Non-linear stress-softening of the bacterial cell wall confers cell shape homeostasis

Abstract

The bacillus - or rod - is a pervasive cellular morphology among bacteria. Rod-shaped cells elongate without widening by reinforcing their cell wall anisotropically to prevent turgor pressure from inflating cell width. Here, we demonstrate that a constrictive force is also essential for avoiding pressure-driven widening in Gram-positive bacteria. Specifically, super-resolution measurements of the nonlinear mechanical properties of the cell wall revealed that across a range of turgor pressure cell elongation directly causes width constriction, similar to a “finger trap” toy. As predicted by theory, this property depends on cell-wall anisotropy and is precisely correlated with the cell’s ability to maintain a rod shape. Furthermore, the acute non-linearities in the dependence between cell length and width deformation result in a negative-feedback mechanism that confers cell-width homeostasis. That is, the Gram-positive cell wall is a “smart material” whose exotic mechanical properties are exquisitely adapted to execute cellular morphogenesis.

Introduction

The peptidoglycan cell wall is a covalently cross-linked polymer network that defines the size and shape of bacterial cells (Fig. 1A). Three key processes mediate expansion of the wall during cell growth: peptidoglycan synthesis¹, enzymatic hydrolysis of the peptide moieties², and mechanical deformation of the wall by the large intracellular turgor pressure³ (≈ 1–30 atm, depending on species^{4, 5}). The primary protein machinery that executes peptidoglycan synthesis during the growth of rod-shaped bacteria is the Rod complex, a heterocomplex of 5 proteins that is scaffolded by oligomers of bacterial actin-homologues^6–8. These transmembrane complexes synthesize peptidoglycan processively, resulting in anisotropic cell wall microstructure in which the glycan moieties are oriented approximately circumferentially⁹ ($\theta$, Fig. 1A) and are connected to one another via the peptide moieties.

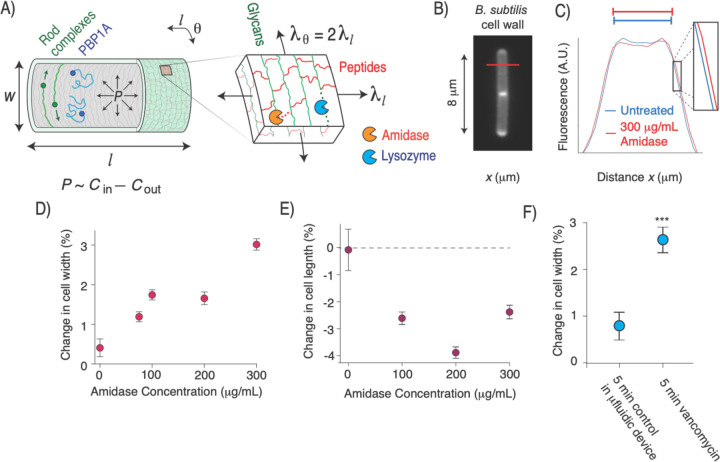
Figure 1. Exogenous peptide digestion causes cell widening.

A) Diagram of the Gram-positive cell wall including its modes of synthesis and cell surface co-ordinate system $\left(l,\theta \right)$. P: turgor pressure. B) B. subtilis cell wall labeled with the fluorescent D-amino acid HADA. C) Mean fluorescent profile across the width of the labeled cell wall (red line in B) before and after 30 s amidase treatment. D) Mean change in cell width upon amidase treatment. Error bars indicate +/− 1 s.e.m. n=15–50 cells across two technical replicates per data point. E) Mean change in cell length upon amidase treatment, controlling for cell growth. Error bars indicate +/− 1 s.e.m. n=20–50 cells across two technical replicates per data point. F) Change in cell width during minutes growth in the microfluidic chip (control) and during 5 minutes of treatment with 10 mg/mL vancomycin. *: p=10⁻²,**: 10⁻³,***: p<10⁻⁴, compared to untreated control.

It is widely believed that the oriented glycans polymers promote rod-shaped growth by mechanically reinforcing the cell wall in the circumferential direction, effectively “girdling” the cell to prevent turgor pressure from driving cell widening¹⁰. Additionally, it is commonly assumed that peptides are oriented longitudinally¹¹ ($l$, Fig. 1A). If so, hydrolysis of load-bearing peptides would tend to cause cellular elongation rather than widening.

This model, however, is not sufficient to prescribe rod-shaped morphogenesis. Glycans are not oriented strictly circumferentially⁹ nor are they infinitely stiff⁴. Similarly, peptides are not oriented strictly longitudinally, and in Gram-positive bacteria the requirement for peptides to connect glycans across the thickness of the cell wall make this impossible. Finally, inflation of the cell by turgor pressure causes anisotropic surface tension in the cell wall whereby the circumferential tension is twice the longitudinal tension¹² (${\lambda }_{\theta }=2{\lambda }_l$; Fig. 1A). Therefore, based on first principles, hydrolysis of peptide moieties during cell growth is expected to lead to both elongation and widening.

Peptide hydrolysis causes cell widening

To explicitly demonstrate this principle, we measured the change in cell width in response to exogenous digestion of cell-wall peptides in the Gram-positive bacterium Bacillus subtilis. To do so, we used microfluidics to acutely perfuse single bacterial cells with a purified recombinant amidase (Fig. 1A) derived from the lytic bacteriophage SPP1¹³. We labeled the cell wall with a fluorescent D-amino acid¹⁴ and developed a super-resolution method to quantify small changes (<1%) in cell width (Fig. 1B,C). As hypothesized, amidase perfusion led to a dose-dependent increase in width (Fig. 1D). Surprisingly, when controlling for cell growth, amidase also caused a decrease in cell length (Fig. 1E, Methods). Perfusion of lysozyme, which digests the glycan moieties led to the same qualitative effects (Fig. S1A,B).

As an alternative method to measure the effect of hydrolysis on cell width, we perfused cells with an inhibitory concentration of vancomycin, which prevents cell wall synthesis without completely inhibiting hydrolysis¹⁵, leading eventually to lysis (Fig. S1C). This treatment also caused cell widening even before it had an effect on elongation rate (Fig. 1F,S1C). Together, these data indicate that peptidoglycan hydrolysis, when unbalanced by synthesis, leads to cell widening.

In light of these data, we hypothesized that to avoid slow increases in cell width during the peptidoglycan hydrolysis required for cell growth, cells exert a radially constrictive force on the cell wall to counteract turgor pressure. It was previously shown computationally that applying pre-tension to nascent glycan polymers could prevent pressure-driven widening¹⁶, but this mechanism was not tested, nor is there an obvious molecular motor within the Rod complex that could exert tension on the cell wall.

Bacteria exhibit finger-trap mechanics

To probe the magnitude of the constrictive force that would be required to counterbalance inflation, we first measured the mechanical properties of the cell wall. Atomic force microscopy is commonly used to measure the deformation of the cell wall in response to indentation forces⁴, but its deformation with respect to changes in surface tension is more relevant to cellular morphogenesis. We therefore subjected B. subtilis cells to a microfluidics-based “osmotic force-extension” assay that we previously developed for Gram-negative bacteria¹⁷ In this assay, single cells are subjected to a series of osmotic shocks (Fig. 2A), which cause acute changes in pressure. These pressure variations deform the cell wall (Fig. 2B), and the dependence of this deformation (the longitudinal and circumferential strains, ${\epsilon }_l$ and ${\epsilon }_{\theta }$) on shock magnitude yields an empirical measurement of the anisotropic mechanical properties of the cell wall (Fig. 2C,D).

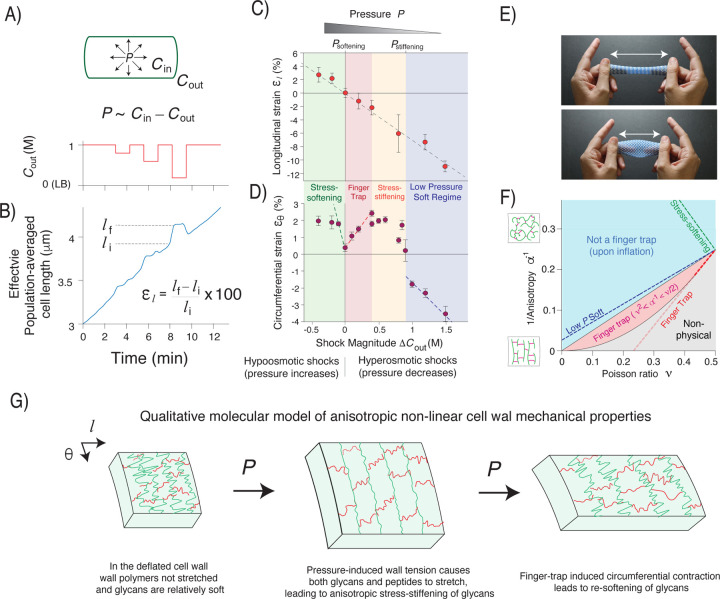
Figure 2. The cell wall exhibits anisotropic stress-stiffening and stress-softening.

A) (top) Diagram of inflated cell wall. P: turgor pressure, C_in: cytosolic osmolarity, C_out: extracellular osmolarity. (bottom) Extracellular osmolarity versus time during an osmotic force extension experiment. B) Effective population-averaged cell length versus time during the osmotic force extension experiment. C) Longitudinal strain versus shock magnitude across several osmotic force extension experiments. n=20–60 cells across 1–3 replicate experiments per shock magnitude. Error bars: +/− 1 s.e.m. The dotted line is a linear regression. D) Circumferential strain versus shock magnitude across several osmotic force extension experiments. n=74–174 1–2 replicate experiments per shock magnitude. Error bars: +/− 1 s.e.m. The dotted lines are linear regressions to linear regimes from three regions of parameter space. E) A macroscopic finger trap. F) The mechanical behavior of an inflated linear elastic cylindrical cell, versus anisotropy and Poisson ratio. The dotted lines are the behavior constrained by slopes of the regressions in C) and D). G) Qualitative molecular model of the anisotropic non-linear cell wall mechanical properties, based on experimental results.

As expected, hyperosmotic shocks, which decrease pressure, caused longitudinal contraction of the cell wall (negative longitudinal strain, ${\epsilon }_l<0$), whereas hypoosmotic shocks caused longitudinal stretching (${\epsilon }_l>0$). Moreover, longitudinal strain was inversely proportional to shock magnitude and reversible (Fig. 2B,C), demonstrating that the cell wall is linearly elastic in this dimension.

As expected, small hypoosmotic shocks, which increase turgor pressure, caused circumferential stretching of the cell wall (Fig. 2C). Counterintuitively, small hyperosmotic shocks also caused circumferential stretching. As a result, in this regime variation in pressure had the opposite effect on cell length and width, similar to the opposite effect that peptidoglycan hydrolysis had (Fig. 1D,E,S1A,B). This behavior is reminiscent of a finger-trap toy in which longitudinal tension causes circumferential constriction due to mechanical coupling between the two directions (Fig. 2D). Finger-trap mechanics are more surprising in the case of a pressurized cell where the circumferential surface tension is twice that of the longitudinal tension (Fig. 1A).

Bacterial cells exhibited approximately linear finger-trap behavior for hyperosmotic shocks up to 400 mM (Fig 2C), however, we observed dramatic non-linear behavior outside this range. First, for hyperosmotic shocks between 400 – 800 mM, the circumferential strain plateaued. At ≈800 mM, we observed a sharp decrease in strain, whereas for larger shocks circumferential strain decreased linearly. Second, since small hypoosmotic shocks caused swelling of cell width, steady-state growth occurs at a sharp non-linear transition.

The cell wall exhibits anisotropic strain-stiffening and -softening

Because the dependence of mechanical strains were approximately linear within low-pressure and finger-trap mechanical regimes, it was instructive to use linear elasticity theory to interpret these data. For an anisotropic two-dimensional material, linear elasticity is given by:

$$\left(\begin{array}{c}{\epsilon }_l\\ {\epsilon }_{\theta }\end{array}\right)=\frac{1}{E_l}\frac{1}{\alpha \left({\alpha }^{-1}-v^2\right)}\left(\begin{array}{cc}1& -v\\ -v& {\alpha }^{-1}\end{array}\right)\left(\begin{array}{c}{\lambda }_l\\ {\lambda }_{\theta }\end{array}\right)$$

where $E_l$ is the longitudinal elastic modulus (in 2D), $\alpha =E_{\theta }/E_l$ is the mechanical anisotropy (ratio of the principal elastic moduli), and $v$ is a Poisson ratio (Methods). The surface tensions, ${\lambda }_l=PR/2$ and ${\lambda }_{\theta }=PR$, balance pressure¹². Imposing the condition that ${\epsilon }_l$ and ${\epsilon }_{\theta }$ have opposite signs when pressure is altered reveals that the cell behaves as a finger trap if ${\alpha }^{-1}<v/2$, that is, if the cell wall is sufficiently anisotropic (Fig. 2F).

Although the empirical dependence of the strains on osmotic shock magnitude (Fig. 2C,D) does not uniquely define $\alpha$ and $v$, it constrains them to a slice of parameter space (Fig. 2F). In the finger-trap regime, this simple analysis demonstrates that the effective Poisson ratio is between $0.45<v<0.5$ and $\alpha$ is as high as is physically possible within that range, assuming there is no other source of tension other than pressure.

A similar analysis for the mechanical behavior in the low-pressure regime demonstrates that the cell wall has a lower value of anisotropy than in the finger trap regime (Fig. 2F). Since the linear dependence of the longitudinal strain is independent of pressure (Fig. 2C), this means that the transition from the low-pressure regime to the finger-trap regime reflects anisotropic stress-stiffening⁴ exclusively in the circumferential direction. Additionally, we noted that the sharp change in circumferential strain at the transition between the low-pressure regime and the stress-stiffening regime is qualitatively equivalent to “slack” in the circumferential direction (i.e. a large increase in deformation across a small increase in pressure).

The observation that cells do not behave as a finger trap for hypoosmotic shocks indicate that the wall is softening circumferentially in response to increases in pressure beyond the steady-state value. Although the deformation is not linear in this regime, we estimated the degree of softening for very small increases in pressure, which indeed revealed that in this regime the cell wall is quantitatively much softer than it is in the finger trap regime, as well as in the low pressure regime (Fig. 2F).

Together, our data suggest a qualitative model of B. subtilis cell wall mechanics (Fig. 2G). First, at low pressures the cell wall is relatively soft in the circumferential direction because the glycan moieties are not fully extended (circumferential strain is low). For example, the glycans may be in shorter folded conformations. In this soft state, the glycans can be thought of as circumferential slack. Therefore, increasing pressure causes the cell wall to stretch circumferentially, and causes the cell to widen. However, eventually the glycans become taut, causing the wall to stiffen in the circumferential direction, eventually leading to finger-trap mechanics. In this state, as pressure increases the cell wall contracts circumferentially, decreasing cell width. Finally, this contraction eventually causes glycans to exit their taut state, leading to softening of the cell wall in the circumferential direction and loss of finger trap mechanics. Further increases in pressure therefore cause cell widening. Interestingly, not only does finger-trap behavior inherently depend on mechanical coupling between the longitudinal and circumferential coupling, but the circumferential stiffening and softening must also depend on longitudinal strain since otherwise as soon as the finger trap was engaged it would contract the wall out of the finger-trap regime.

Finger-trap mechanics are correlated with cell-width control

Because finger-trap mechanics correspond to constriction of cell width upon elongation, our results raised the possibility that this behavior was required to avoid runaway widening during cell growth. To explore this hypothesis theoretically, we first constructed a simple physical model for the irreversible mechanical expansion of a linear elastic layered cell wall that accounts for variation of cell length and width (Fig. 3A). The specific spatial relationship of peptidoglycan synthesis and hydrolysis during cell growth is unknown, but since rod complexes are membrane-bound it is believed that synthesis of non-load-bearing peptidoglycan occurs proximal to the membrane whereas the hydrolysis of load-bearing peptidoglycan required for cell growth occurs distally¹⁸. We therefore considered a model in which anisotropic peptidoglycan is added to the inner face of the cell wall at a constant rate and removed at the same rate from the outer face via hydrolysis (Methods). Since the cell wall is under tension, removal of load-bearing peptidoglycan dissipates energy and causes irreversible deformation, or growth.

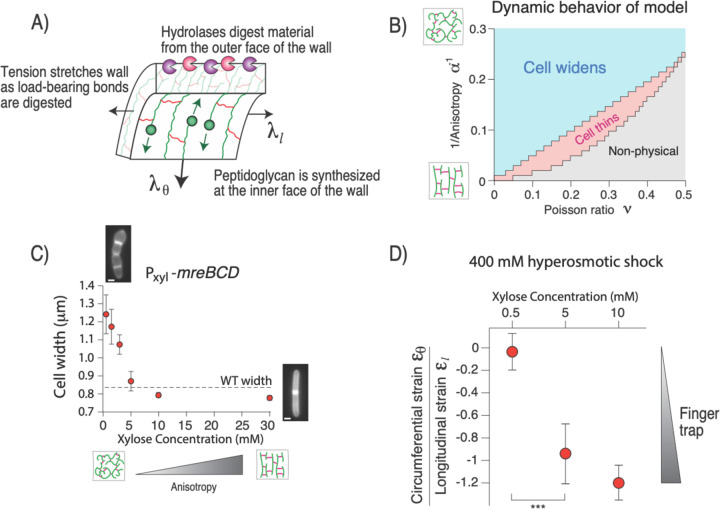
Figure 3. Finger trap mechanics are correlated with cell-width control.

A) Diagram of the components of the theoretical linear elastic model for cell growth. B) Dynamic behavior of the model versus the anisotropy and Poisson ratio of the cell wall. C) Cell width versus induction of mreBCD. n=22–57 cells across 1 replicate per induction level. Error bars: +/− 1 s.d. D) Ratio of circumferential strain and longitudinal strain upon 400 mM hyperosmotic shock for three induction levels of mreBCD. The more negative the ratio is, the more of a finger trap the cell wall is. Values were calculated from n=26–90 cells across 1–3 experiments (circumferential strain) and n=60–78 cells across 1 experiment (longitudinal strain) per induction level. Error was propagated from the s.e.m. for each respective measurement. ***: p<10⁻⁴.

When we solved this model computationally across $\alpha$ and $v$, we found that the region of parameter space in which cell width decreases dynamically was identical to the region where the cell wall behaves as a finger trap mechanically (Fig. 3B). Conversely, in the region of parameter space where cell width increases upon inflation, the cell widens during simulations of cell growth. The reason for the correspondence between the elastic behavior and growth-dynamics is simple: when load-bearing peptidoglycan is removed from the cell wall, the wall must deform in order to balance pressure, and since we analyzed a linear model, the cell wall deforms as a finger trap regardless of the strain distribution along the proximo-distal axis (Fig. 3A).

Therefore, our model made the strong prediction that the cell wall must behave as a finger trap, mechanically, in order to maintain rod shape during growth. We tested this explicitly by genetically manipulating cell-wall mechanical properties and measuring the effect on cell width. While it is not possible to specifically tune the Poisson ratio of the cell wall independently, anisotropy can be systematically altered by titrating components of Rod complex (specifically the mreBCD operon) via inducible expression¹⁹. When biosynthetic flux through the Rod complex is reduced, the balance is accommodated by PBP1A, a non-essential enzyme that synthesizes peptidoglycan isotropically (Fig. 1A). Therefore, when the relative expression of the Rod complex is reduced beyond wild-type levels, cell width acutely increases and cells partially lose rod shape (Fig. 3C).

As our model predicted, for Rod-complex expression high enough to generate well-shaped rods, modest hyperosmotic shock led to circumferential stretching (finger trap mechanics; Fig. 3D). Conversely, when Rod complex expression was reduced below this threshold cells began to lose rod shape and no longer stretched circumferentially upon hyperosmotic shock. That is, there was a precise correlation between whether the cell maintained a rod shape and whether the cell exhibited finger-trap mechanics. Importantly, for an induction level of 0.5 mM, well below that required for rod-shaped growth, linear elasticity analysis reveals that the cell wall is still highly anisotropic ($\alpha \text{>}4$), demonstrating that finger-trap mechanics, rather than anisotropy alone, is the critical factor underlying the mechanics of rod-shaped morphogenesis.

Pressure-induced wall softening confers width homeostasis

Our analysis explained how cells avoid inflationary widening during cell growth. However, the dynamics of this model are inherently unstable: if the cell wall is not a finger trap then the cell widens ad infinitum during growth, while if the wall is a finger trap then cell width asymptotically approaches zero during growth (Fig. 3B).

However, the linear model ignored the non-linear stress-softening transition (Fig. 2D). Conspicuously, during steady-state growth the cell wall is inflated precisely to this transition. Given this observation, and because circumferential softening leads to widening (Fig. 3B), we posited that this transition could confer an intrinsic mechanism for homeostatic control of cell width if turgor pressure is inversely dependent on cell width (Fig. 4A). In this picture, if a cell is wider than its steady-state width, then turgor pressure would be correspondingly lower than its steady-state value and the cell would be a finger-trap, leading to thinning. However, as the cell thins, turgor pressure increases until the cell wall reaches the stress-softening transition. At this point, further increase in pressure causes widening, which decreases pressure, thereby keeping the cell wall at the transition and maintaining cell width. To sum, the non-linear stress-softening transition itself would impose width homeostasis if pressure increased with decreasing width.

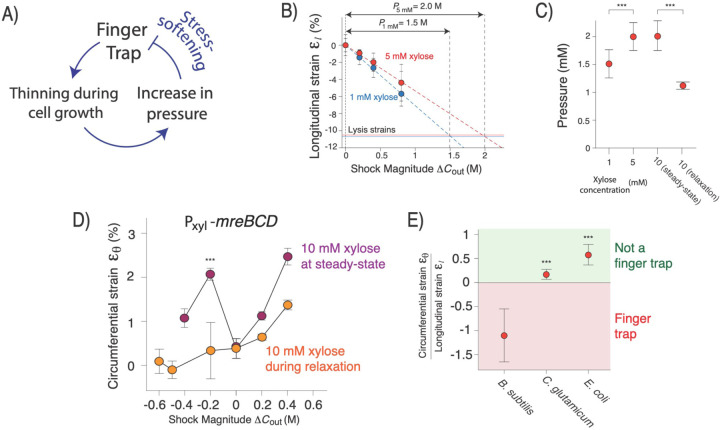
Figure 4. Strain-softening confers cell width homeostasis.

A) Model for negative feedback regulation of cell width mediated by finger-trap mechanics and strain-softening. B) Method for measuring turgor pressure. Cells were lysed with detergent to determine the degree to which the cell wall was stretched longitudinally and then an osmotic force extension assay was performed to determine the hyperosmotic shock magnitude that contracted the cell wall to the rest length. C) Pressure versus induction of mreBCD. n=20–72 cells across 1–2 replicate experiments for measurement of lysis strains. n=83–168 cells across 1–2 replicate experiments for osmotic force extension measurements. Error was propagated from the s.d. of the lysis strain and the standard error of the regression of the osmotic force extension experiments. D) Circumferential strain versus shock magnitude across several osmotic force extension experiments for 10 mM induction of mreBCD. In one set of experiments the cells were growing at steady-state width, in the other they were dynamically relaxing to steady-state from a larger width. n=20–62 cells across 1–2 experimental replicates per shock magnitude. ***: p<10⁻⁴, comparing two conditions at −0.2 M shock magnitude. E) Ratio of circumferential strain and longitudinal strain upon 400 mM hyperosmotic shock for wild-type B. subtilis, C. glutamicum, and E. coli. B. subtilis statistics are the same as in Fig. 2C,D. For C.g., n=20–30 cells across 1 experiment for circumferential strain and n= 306 across 1 experimental for longitudinal strain. For E.c. circumferential strain n=22–37 cells across two experimental replicates and for longitudinal strain n=238 cell across 3 experimental replicates. Error was propagated from the s.e.m. for each respective measurement. ***: p<10⁻⁴, compared to B. subtilis.

An inverse dependence of pressure on cell width, $P\propto R^{-1}$, is predicted by empirical bacterial growth laws²⁰ if pressure is proportional to the mass density of the cytoplasm. We explicitly tested for an inverse correlation between turgor pressure and width in two ways. First, we measured steady-state pressure at several levels of Rod complex expression that yield a range of widths. To measure pressure, for each expression level we performed our longitudinal osmotic-force-extension assay in one experiment, and in a second experiment we lysed cells and measured length contraction upon loss of turgor pressure. We extrapolated the osmotic-force-extension curve to quantify the magnitude of hyperosmotic shock that caused contraction of cell length to the same degree as cell lysis, which gives an empirical measurement of turgor pressure in units of osmolarity (Fig. 4B). We found that pressure was markedly decreased in expression levels that resulted in wide, semi-amorphous cells (Fig. 4C).

Second, our model predicts that if cells are transiently forced to be wider than their steady-state width for a given Rod complex expression level, then pressure will be lower. To test this, we cultured cells at a low expression level of Rod complex that yields wide cells (1 mM xylose), acutely induced higher expression that yields thinner cells (10 mM xylose), and measured pressure during dynamic relaxation to steady-state (Fig. S2). As hypothesized, for the same induction level cells had a lower pressure during relaxation than after reaching steady-state width (Fig. 4C).

Finally, a central prediction of our model is that for cells that are wider than their steady-steady width but are dynamically relaxing to it (Fig. S2), that the cell wall will not be inflated to the stress-softening transition. To test this, as before we cultured cells to steady-state growth at low Rod-complex expression, acutely induced high Rod-complex expression, and then performed circumferential osmotic-force-extension experiments during and after relaxation to steady-state. As for wild-type bacteria, both hypo- and hyperosmotic shocks caused swelling of width for cells grown to steady-state at high expression (Fig. 4D). Conversely, for cells that were dynamically relaxing to steady-state hypoosmotic shocks up to 600 mM caused constriction of cell with. In other words, during relaxation, the cells were squarely in the finger trap regime. The validation of this non-intuitive prediction strongly supports our model.

Finger-trap mechanics are unique to Gram-positive rod-shaped bacteria

Finally, we tested the generality of the finger-trap mechanism of cell width control across other bacteria. Interestingly, Corynebacterium glutamicum, another rod-shaped Gram-positive bacterium does not exhibit finger trap mechanics for hyperosmotic shocks. This makes sense, however, in light of the fact that C. glutamicum elongates via polar growth rather than the “diffuse” growth used by B. subtilis. For polar growth, cell width must be maintained through control of the size of the polar growth zone. Previous measurements of E. coli cell geometry in response to osmotic shocks did not indicate finger-trap mechanics²¹, a result we confirmed (Fig. 4D). This suggests that Gram-negative bacteria must also use another mechanism to control width in spite of turgor pressure, which is however much lower than in Gram-positive bacteria⁴; this will be an interesting subject for further study.

Discussion

Transduction of forces within eukaryotic cells is mediated by a variety of molecular mechanosensors²² that elicit biochemical and genetic responses that can, in turn, manipulate forces within the cell. For example, when force is applied to branched actin networks, the network rapidly increases the amount of force it can sustain through structural alterations to the network, a process that is encoded in the biochemistry of actin-binding proteins²³. We found that like actin, the Gram-positive bacterial cell wall is a “smart material” that internally senses and responds to forces. However, the cell wall employs a quintessentially prokaryotic paradigm whereby negative-feedback regulation of cell width is intrinsic to the acute non-linear properties of the wall, when coupled to simple dependence of turgor pressure on cell size. By analyzing this mechanical feedback system in tandem with genetic and biochemical circuits involved in cell-width maintenance we expect to be able to understand quantitatively and precisely how bacterial cell shape is robustly controlled across dynamic environments. Finally, the anisotropic strain-stiffening and strain-softening of the cell wall is exotic from a mechanical perspective and deserves to investigated from a materials science perspective.

Materials and Methods

Bacterial strains and growth condition.

The strains used in this study are listed in Table S1. Cells were grown in Luria-Bertani (LB) medium at 37°C with continuous shaking. For promoter induction of the strain Pxyl-mreBCD, cells cultured overnight in LB supplemented with 3mM xylose, were diluted in fresh media with the indicated amount of xylose until exponential phase was reached. Hypoosmotic shocks were done by using media supplemented with the indicated amount of sorbitol; for hypoosmotic shocks, cells from overnight culture were diluted in LB medium supplemented with 1M sorbitol; lower concentration of sorbitol were used to shock the cells. Corynaebacterium glutamicum cells were grown at 30°C in Brain Heart Infusion medium (BHI); to perform osmotic shocks BHI media was supplemented with the indicated amount of sorbitol.

Microscopy in microfluidic devices.

Time-lapse movies were taken using the Nikon Eclipse Ti2 inverted fluorescence microscope integrated with a BSI sCMOS camera and controlled by Nikon Elements software. An oil-immersion 100X object (NA 1.40) was used for imaging. Cells were maintained during imaging at a constant temperature using a microscope live-cell imaging chamber (Haison). Phase-contrast images were acquired at a frame rate of 10 seconds to measure cell length. Cell tracking was performed using custom MATLAB (Mathworks, Natick, MA, USA) software.

Osmotic force extension assays.

To perform the osmotic-force-extension assay consecutive osmotic shocks were performed using commercial microfluidic plates (BA04, CellASIC, Millipore-Sigma) controlled by the ONIX microfluidic platform. Overnight cells were diluted in fresh media and grown until early exponential phase. Cells were then harvested in the microfluidic chamber at 37°C for 30 min with no shaking to achieve steady-state growth. Prior to the experiments the channels were primed with the desired media for 30 minutes at a pressure of 4psi. The cells were then loaded into the perfusion chamber and osmotic shocks were performed by perfusing media supplemented with the desired sorbitol concentration at a constant pressure of 8 psi. Typically, osmotic shocks were performed every 5 min for a duration of 3 min each. Alexa Fluor 647 dye was added to the media used between the shocks to track media switching. To calculate the change in length resulting from osmotic shock, we determined the intervals of the shocks when the medium was exchanged. Then, for every cell, we calculated the longitudinal strain during each osmotic shock using the formula ${\epsilon }_l=\left(l_f-l_i\right)/l_i$, where $l_i$ is the length of the cell at the beginning of the interval and $l_f$ is the maximum length of the cell during the interval.

Super-resolution measurement of single-cell width deformation.

To perform single-cell measurements of width deformation upon osmotic shocks (or enzyme treatment), the cell wall of B. subtilis was labelled with fluorescent D-aminoacids (FDDAs, Biotorchis). Before the experiments, cells cultured overnight were diluted in fresh media and cultured until early exponential phase was reached (0.3–0.4 OD). 10mM of RADA was added to the culture 1 hour before the microfluidic experiment. The same concentration of fluorescent D-amino acids was added to the cell loading well. Cultures were back-diluted X100 into the loading well. One image was taken 30 s before the osmotic shock and one image was taken 30 s after the osmotic shock. To track the switching of the media, 0.5mM Alexa Fluor 647 was added to the media used between the shocks.

To quantify changes in width with extreme sub-pixel precision, we developed a fit-free method. Images of labeled single cells pre- and post-shock were computationally aligned by rotating them along a vertical axis. In each image, the portions of the cell containing the septa was cropped, leaving only the cylindrical portion of the cell. Each image was then averaged along the vertical axis to obtain a single-cell average of the fluorescence profile across the width of the cell (Fig. 1C). To calculate circumferential strain without fitting profiles, we normalized the pre- and post- profiles and then scaled one of them along the horizontal (width) axis at sub-pixel intervals, and performed cross-correlation with the other profile.

To measure the circumferential strain versus shock magnitude during dynamic relaxation of cell width (Fig. 4D), we first took a standard curve of width versus time of strain ER476 upon increased induction from 1 mM xylose to 10 mM xylose. We back-diluted an overnight culture induced with 3 mM xylose X100 into LB+1mM xylose. We grew this culture to exponential phase before back-diluting it X100 into LB+10 mM xylose. We then measured cell width on LB agarose pads supplemented with 10 mM xylose every 20 minutes. This confirmed that width began decreasing within 15 minutes after the increase in induction (Fig. S2). Therefore, to measure circumferential strain upon osmotic shock during relaxation, we prepared circumferential osmotic force extension assays at 1 mM xylose induction, as described above, but once we loaded cells into the imaging chamber we perfused them with 10 mM xylose for 15 minutes prior to performing the osmotic shocks. We performed a similar protocol to measure lysis strain during relaxation (see below).

To measure changes in cell width in C. glutamicum 0.5mM of RADA was used to label the cells 1 hour before the experiments. For E. coli MG1655, the cell wall was labelled with HADA for 1 hour.

Spp1 endolysin purification.

The bacteriophage endopeptidase, Spp1Lys, was purified by using a previously established protocol¹³, from E. coli strain CG/pIV::25His. Cells were grown at constant shaking at 28°C until an OD of 0.6–0.8, after that cells were transferred at 42°C for 30 min and at 16°C for 14 hours to induce protein expression. Cells were collected by centrifugation (4000rpm for 30minutes at 4°C) and resuspended in lysis buffer (20mM Hepes, 500mM NaCl, 20mM imidazole, 1% glycerol and 1mM DTT [pH 6.5]). Resuspended cells were lysed by sonication. The supernatant was collected after centrifugation (10000 rpm for 30 min at 4°C) and the enzyme was purified using a column packed with Ni Sepharose High Performance histidine-tagged protein purification resin (Cytiva). The elution buffer was the same as the lysis buffer except that the concentration of imidazole was 500mM. The eluted fraction containing the purified protein was concentrated and the buffer was exchanged to a phosphate-based buffer (50mM phosphate-Na, 500mM NaCl, 25% glycerol, and 1mM DTT [pH6.5]) using a HisTrap Desalting column (Cytiva, 5mL). Whole extract, lysate, and eluted fractions were analyzed by SDS-PAGE and western blot. For western blot, proteins were transferred to a polyvinylidene difluoride membrane using Trans-Blot Turbo system (Biorad). For the detection of SPP1Lys an antibody against the His-tag was used and visualized with a ChemiDoc imaging System. Protein concentrations were determined using a nanodrop ($\text{ε}=32.89$, M.W.=30.705). The purified enzymes were divided into small aliquots and kept at −80°C in the eluted buffer.

Hydrolysis assay.

Hydrolysis experiments were performed in microfluidic devices at 37C. Lyophilized powder of lysozyme (Sigma Aldrich) was dissolved in the desired media before the experiments. Purified Spp1 was added directly to the media in the designated chamber at the indicated concentration. Cells were grown in rich media in the growing chamber for 5 minutes prior to the perfusion of the hydrolases. To control for cell lysis, 0.1μM of propidium iodide (Sigma Aldrich) was added to the media with the enzymes. To measure changes in width and length, images were taken 1 minute before and after adding the enzymes, ensuring that cells were not lysed. The measurements were done using custom MATLAB scripts.

Theoretical phase space.

The theoretical phase space associated with linear elasticity was calculated from Eq. 1. Note that in Eq. 1 the Poisson ratio, $v$, cannot be defined in the traditional manner since the cell wall is anisotropic. The boundary between the finger trap regime and the no-finger trap regime comes from solving Eq. 1 for the condition ${\epsilon }_{\theta }=0$. The condition that ${\alpha }^{-1}>v^2$ results from substituting the thin shell approximation for the principal surface tensions, ${\lambda }_l=PR/2$ and ${\lambda }_{\theta }=PR$, into Eq. 1 and imposing the physicality condition that the moduli $E_l$, $E_{\theta }$, and $E_{l\theta }$ must be greater than zero. Note that this constraint only strictly applies in the limit of the thin shell approximation, which is likely to be approximately true for B. subtilis since the thickness of the cell wall is ≈ 40 nm and the radius of the cell is ≈ 400 nm. However, contributions of normal stress to the balance of turgor pressure would shift this boundary.

The slices through parameter space that constrain the mechanical properties of the low pressure, finger trap, and stress-softened regimes were found by first finding the slopes of the regression to the circumferential strain versus shock magnitude in the three regimes (slopes $m_{\text{θ}}$’s of dotted lines in Fig. 2D), and then substituting these as well as the slope of the regression to longitudinal strain versus shock magnitude, $m_l$ into Eq. 1 as ${\epsilon }_{l,\theta }=m_{l,\theta }\Delta {\text{C}}_{out}$. This assumes that in each of these three regimes the cell wall is a linear material near an appropriate reference state. Rather than assuming that the material is linear globally (it obviously is not) this analysis is simply a way to estimate the relative local mechanical properties in the three regimes. Furthermore, all materials are linear for small deformations and non-linear for large deformations, and whether the reference state is the rest state need not affect whether the material behaves locally like a linear elastic material with given parameters $\alpha$ and $v$.

Cell lysis assay.

To measure changes in dimensions in response to lysis, we lysed cells with 5% N-lauroylsarcosine sodium salt. The detergent dissolves the plasma membrane causing the release of the cytoplasmic contents. The cell depleted of the turgor pressure shrinks to its rest length. To measure the change in length in response to lysis, images were taken 1 min before the addition of the detergent and after the detergent was washed away using LB. To calculate changes in dimensions for different levels of Rod complex induction, cells grown overnight in LB with 5mM xylose were back diluted in LB supplemented with the amount of xylose needed to generate cells with the desired diameter (0.5mM, 5mM, and 30mM). The same xylose concentrations were added to the media with detergent and the washing media. The measurements and the calculation of the percentages of change in width and length were done using costume made scripts as described before.

Pressure measurements.

To measure pressure osmotic force extension experiments were combined with measurements of lysis strains. Pressure was calculated from the regression of the osmotic force extension curves, as the hyperosmotic shock magnitude that caused contraction of the cell wall to the rest length observed upon lysis.

Mathematical model of cell morphogenesis.

To model morphogenesis of a rod-shaped cell where width could change dynamically, we considered a cylindrical cell wall with a constant thickness of 40 nm and pressure of 10 atm. To balance pressure, making the thin-shell approximation, the total longitudinal tension borne by the cell wall is ${\lambda }_l=\frac{PR}{2}$ and the circumferential tension is ${\lambda }_{\theta }=PR$. We discretized the cell wall into 100 layers and allowed the stress and strain to vary across the thickness of the cell wall given these global force-balance constraints. To model dynamic growth and morphogenesis of the cell, we defined an arbitrarily small time step. During each time step we removed one layer (1/100^th of wall thickness) from the outer surface of the cell wall and added a unstretched layer to the inner surface of the wall, and then allowed the cell wall to deform to satisfy the global force balance constraints using a standard energy minimization routine.