Highly prevalent putative quadruplex sequence motifs in human DNA

Abstract

We report here the results of a systematic search for the existence and prevalence of potential intramolecular G-quadruplex forming sequences in the human genome. We have also examined the tendency for particular sequences of ‘loop’ regions to occur in particular positions with respect to the G-tracts in a quadruplex. Using arithmetic ratio and probability techniques we have discovered frequent and systematic occurrence of certain sequence types, the most prominent being a potential quadruplex containing CCTGT in the first ‘loop’ position. Being able to highlight types of potential quadruplex sequences in G-rich regions is an important step in searching for biologically relevant sequences and finding their function.

INTRODUCTION

Four-stranded G-quadruplex structures are the resultant of the folding of guanine-rich nucleic acid sequences (1–3) into higher-order structures. They can form most readily from a single strand of nucleic acid, as at the 3′ end of telomeric DNA (4–9). They can also be extruded from double stranded DNA (10), especially under the influence of a small-molecule ligand such as the porphyrin molecule TMPyP, which binds preferably to some quadruplexes rather than duplex DNA, pushing the equilibrium to the former structure (11–13). Some of these quadruplex sequences have been considered as potential therapeutic targets for small molecules since they have been reported to occur within the regulatory regions of several oncogenes (1). A well-studied example is the G-rich promoter element of the c-myc oncogene, for which G-quadruplex formation has been suggested as a molecular switch for gene expression (11–16). This quadruplex is exceptionally stable, and is readily formed in preference to remaining in a duplex structure, at least within short DNA sequences.

In this paper, we have started to address the use of bioinformatics tools, and in the accompanying one from our collaborators (17), the more general question of the number and nature of putative quadruplex sequences within the human (and other) genome(s). Such sequences, and the individual quadruplex structures, may be novel targets for therapeutic intervention, analogous to the selective interference with telomere maintenance by molecules that bind to and stabilize telomeric DNA quadruplexes (18–22). Structural data on quadruplexes is as yet relatively sparse; however, those structures that are known, from X-ray crystallography and NMR studies, show a wide diversity of features (7,9,16,23–26).

We have carried out a survey of all possible short quadruplex sequences in the human genome and have attempted to identify some of the most commonly occurring sequences. Our analysis of these sequences has highlighted some motifs, which stand out as being in a separate class from the rest of the potential quadruplexes, and therefore may have an important function. Categorization of short sequences like quadruplexes within the human genome is not straightforward. Unlike conventional gene sequences, the differences between the sequences is not large but is rather a continuum where, for example, trying to isolate a sequence or family of sequences on the grounds of uniqueness is difficult since there are always many very similar sequences that occur with similar frequencies. The number of combinations of bases that are possible for loop sequences of the size that we are considering is similar to the number of distinct loop sequences that exist (Table 1). Because there are no islands of unique sequence as such, finding correlations between possible quadruplex and function is made more difficult.

Table 1.

Number of quadruplex sequences occurring in human genomic DNA

	Number of quadruplexes	Number of unique quadruplexes	Number of unique loop sequences (number observed/number possible)
Un-restricted dataset	5 713 900	3 166 800	20 492/21 844
Arbitrary dataset	375 157	226 157	10 551/12 289

It has been demonstrated that the stability and the folding topology of a quadruplex is dependent on the sequence of the loop regions (27–29). Therefore, we would expect trends in the sequence of the loops derived from a genome-wide survey of potential quadruplex sequences to reflect the relative stability and possibly the functionality of a particular sequence. Trends in loop sequence were discovered here through inequalities in the distribution of sequences across each of the three loop regions within a quadruplex sequence, i.e. examining whether a particular sequence occurs more in the first, second or third loops. It is important to emphasize that in the absence of appropriate biophysical, biochemical and structural data, we can only assign sequences as being putative quadruplex-forming. Indeed the available evidence (28) strongly suggests that many such sequences do not actually form stable quadruplexes.

METHODS

We define a potential quadruplex sequence as a sequence with four runs of guanine between three and five bases long, separated by regions of DNA, which we will call here loop regions L1, L2 and L3, containing between one and seven bases that may or may not themselves contain guanines. The lengths of each of these were restrained for practical reasons (an arbitrary cut-off of a maximum loop-length of 7 nt had to be applied because a loop unrestrained in length would make searching for sequences difficult) and also because of the evidence to date (29) that quadruplexes exist as short nucleic acid sequences.

We thus define a general quadruplex sequence as

$${\text{G}}_{3-5}{\text{N}}_{\text{L}1}{\text{G}}_{3-5}{\text{N}}_{\text{L}2}{\text{G}}_{3-5}{\text{N}}_{\text{L}3}{\text{G}}_{3-5},$$

where N_L1–3 are loops of unknown length, although within the limits 1 < N_L1–3 < 7 nt.

The examination of the distribution of loop sequence was carried out in several different ways:

1. The total number of times that a particular loop sequence appears.

2. The distribution of loop sequences with respect to loop position, by taking a particular loop sequence and examining the number of times that it occurred in each loop position, N_L1, N_L2 or N_L3. We then looked at the ratio between the highest and lowest values for these populations.

3. The probability of a given distribution in each of the three loops occurring, given an equal likelihood of each sequence occurring in each loop region L1, L2 or L3.

It is possible for a single sequence to have a number of different quadruplex topologies (Figure 1) and several different isomers of a sequence fold may lend stability to the system. Not only are there a number of distinct quadruplex fold motifs that have been identified by X-ray crystallography and NMR, but there can be a number of choices about which nucleotides in a quadruplex sequence are members of the G-quartet and which are within loop regions. This complicates the analysis of the loop distribution since not only is it impossible to determine the ‘correct’ choice of bases for each loop region from just sequence data but the same sequence could at least in principle be involved in different alternative and dynamic structures. To overcome some of these difficulties we have used two distinct sets of data. In the first instance, we include all the sequences that could be considered as belonging to loop regions. In some cases this can include many overlapping sequences. However this data will contain some loop sequences, which may otherwise be missed out of the second dataset. In the second case, we have included only sequences that do not overlap with one another. In order to overcome some of the ambiguity illustrated in Figure 1a, we have removed leading and trailing guanines, and loops that consisted of guanines only were reduced to a single G.

Figure 1.

Ways in which quadruplex-fold ambiguity can occur. (a) Shaded regions represent the guanines contributing to the G-quartets and the unshaded regions the loops. Regions of high guanine density tend to have more quadruplex hits which in some cases lead to many hits for a single region of DNA. (b) Overlapping quadruplexes. In the first (un-restricted) dataset, the above sequence would produce five possible quadruplex folds, and in the second (arbitrary) dataset, this sequence would only have been counted as two distinct quadruplexes.

Obtaining and preparing the data

Version 20.34c of the Ensembl human genome database (30) was downloaded from the Ensembl website in the form of SQL dumps of the Ensembl MySQL database, as were the software tools to access the database using the Perl scripting language (Perl API). The Ensembl tables were then compiled into the relational database program MySQL.

The database was searched for quadruplex sequences in two steps. First, Ensembl Perl API was used to extract assembled lengths of 2 000 000 bases, which were then searched for potential quadruplex sequences using a C++ program developed by A. K. Todd. A list of all combinations of loop length (1–7 nt) and guanine run length (3–5 nt) was generated and each was compared against the total genomic sequence. The results were broken down into the following fields: (i) individual chromosome, (ii) position in the chromosome, (iii) function (intron, exon or other), (iv) sequence of the extracted loop regions and (v) strand on which the hit occurred. The results were then compiled into mySQL tables and added to our local implementation of the Ensembl database. This set of tables included all potential quadruplex sequences including those where a region of DNA could contain more than one potential quadruplex sequence. This raw data is available on request from alan.todd@ulsop.ac.uk

As demonstrated in Figure 1, a single sequence may have more than one possible quadruplex folding topology. Also more than one loop sequence for a particular loop position L1, L2 or L3 may be possible. We will refer to these problems as quadruplex fold ambiguity. An arbitrary choice of a quadruplex sequence will bias the results of many types of analyses of quadruplex. However, it may also be necessary for finding the number of times a particular motif occurs. Therefore, we have examined our data in two ways. First, a list of loop sequences was compiled, which included overlapping sequences and all possible choices of loop region. We will refer to this as the un-restricted dataset. A second list was also generated in which the quadruplex motif was found but this time, if overlapping sequences occurred, only the first one encountered would be considered. This list was further modified by removing any leading or trailing guanines from the loop sequence, as these would otherwise lead to ambiguity in the loop sequence. This also prevented the inclusion of a particular loop region more than once in the list. Where loop regions were made up entirely of guanines, these were reduced to a single guanine base. This will be referred to as the arbitrary dataset.

Data analysis

The contents of datasets were ranked in the following way:

1. By overall loop composition for each hit.

2. By the number of times each loop sequence occurs.

3. By population of loop position:

   1. By looking at the number of times each particular loop sequence occurs in each loop position and finding the ratio between the maximum and minimum of these populations. Where there was a population of 0 this was counted as 1.
   2. By probability of loop distribution, given an equal likelihood that a quadruplex sequence can occur in each of the loops.

Calculating probability scores

Given an equal likelihood that a particular loop sequence can be found in any of the three loop positions, the probability that a loop distribution [a, b or c] occurs is given by the equation

$$P=\frac{(a+b+c)!}{a!b!c!3^{a+b+c}},$$ 1

where a,b and c represent the observed populations of a particular sequence in loop positions L1, L2 and L3, respectively. Because of the impracticality of working with the very large numbers that are generated when using factorials we need to work in log space, so for our probability score the negative log of the probability was calculated as in Equation 2:

$$\begin{array}{c}-logP=(a+b+c)log3+{\displaystyle \sum _{n=1}^a}logn+{\displaystyle \sum _{n=1}^b}logn\\ +{\displaystyle \sum _{n=1}^c}logn-{\displaystyle \sum _{n=1}^{a+b+c}}logn.\end{array}$$ 2

Therefore the higher the score, the less probable the distribution. Derivations of Equations 1 and 2 are based on an exercise in reference (31), and are given in the Supplementary Material.

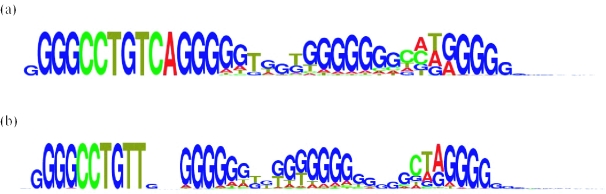
Two types of quadruplex sequences which stood out, those which contained CCTGTT and CCTGTCA in the first loop, were selected from the database and multiple sequence alignment of these two quadruplex sequence types were carried out using CLUSTAL W version 1.85 (32). Figure 2, which shows the consensus sequences containing them, was generated with the program MakeLogo (33). The data used in constructing Figure 2 is available in the Supplementary Material.

Figure 2.

Consensus sequences for (a) CCTGTCA and (b) CCTGTT sequence types. Diagrams were generated with the program MakeLogo (33). A total of 1956 sequences were used to find the consensus sequence for CCTGTCA and 2361 sequences for the CCTGTT type. The height of each letter is proportional to the number of times each base appeared in that position.

RESULTS AND DISCUSSION

Table 1 gives a summary of the number of quadruplexes in both datasets. A large number of potential quadruplex sequences were found on the initial search, which was reduced by ∼15-fold when the overlapping sequences were rejected (5713900 → 375157). The number of distinct (i.e. unique) quadruplexes is similarly reduced, from 3166800 to 226157; each quadruplex sequence occurs only once in this category. Table 1 also shows that some loop sequence combinations were not detected since the number of unique sequences that were observed is less than the total number possible. Overall, 375157 putative quadruplex sequences have been located in the genome. This agrees remarkably well with the estimate of 376 000 by a distinct approach (17). Tables 2 and 3 represent two ways in which the arbitrary dataset has been examined to search for inequalities in the distribution of sequences by loop position, ranked by ratio and probability respectively, and show the top 40 occurrences in each set. Tables 4 and 5 are the corresponding tables for the un-restricted dataset.

Table 2.

Top 20 loop sequence by maximum ratio of population in loop position, for the arbitrary dataset

	Sequence	Ratio of max and min populations	Population in loop a	Population in loop b	Population in loop c
1	CCTGTCA	309	1239	5	4
2	CCTGTT	140	1266	18	9
3	CCTGTC	139	836	8	6
4	CCTGTTA	90	90	1	0
5	ATCTCCA	74	1	5	74
6	TGGTCTT	58	3	1	58
7	CCTATCA	53	53	1	0
8	TCTGTCA	51	51	3	0
9	TAGCACA	42	0	5	42
10	CCTATC	38	38	1	1
11	CCTATT	37	75	4	2
12	CCTTTCA	37	37	1	0
13	CTTGGC	36	13	16	471
14	TAGCATT	34	1	0	34
15	CCTGTCC	30	30	0	3
16	CCTGTTT	29	58	4	2
17	CTTGTCA	29	58	4	2
18	CCTGTGA	28	28	8	1
19	CCAGTC	28	28	1	3
20	ACCTGTC	27	27	1	2

Table 3.

Top 20 loop sequence by probability for the arbitrary dataset. Sequences 5,6,7 and 10 also feature in Table 2

	Sequence	−Log probability	Population in loop a	Population in loop b	Population in loop c
1	T	3277	53 234	37 657	30 515
2	A	2873	51 361	63 872	78 523
3	AGGT	2413	1516	6448	1470
4	G	1319	7183	8375	14 065
5	CCTGTCA	1313	1239	5	4
6	CCTGTT	1275	1266	18	9
7	CCTGTC	855	836	8	6
8	TT	494	7437	5530	4122
9	TC	458	3181	1774	1283
10	CTTGGC	421	13	16	471
11	TCTGA	412	737	115	85
12	AGGA	405	1932	3559	3972
13	CTA	316	769	2068	1481
14	AGT	295	2767	4447	2682
15	TGGA	287	2573	1379	1282
16	CAA	175	1035	1928	1876
17	ACTCA	175	428	79	108
18	AGC	173	973	1826	1042
19	ACTT	173	674	225	223
20	AAAT	152	324	299	781

Table 4.

Top 20 loop sequence by maximum ratio of population in loop position for un-restricted dataset

	Sequence	Ratio of max and min populations	Population in loop a	Population in loop b	Population in loop c
1	TAGCATT	1058	1	0	1058
2	CCTGTTG	990	10 897	79	11
3	CCTGTCG	949	7592	40	8
4	CCTGTCA	714	12 138	39	17
5	CCTATCA	467	467	2	0
6	CCTATCG	352	352	2	0
7	GCCTATT	336	336	1	3
8	CCTGTT	332	12 308	113	37
9	CCTTTCA	310	310	4	1
10	GCCTGTT	303	6373	61	21
11	TCTGTCG	287	287	0	3
12	CCTATTG	268	537	10	2
13	CCTGTC	267	8553	104	32
14	CCTGTTA	221	885	4	5
15	CCTATC	203	407	3	2
16	GCCTATC	203	203	2	1
17	GACTCAA	190	190	7	1
18	GCCTGTC	179	4679	89	26
19	ACTGTCA	173	173	0	10
20	CCAGTTG	165	165	0	2

Table 5.

Top 20 loop sequence by probability, for the unrestricted dataset. Sequences 11, 12, 14 and 19 also feature in Table 4

	Sequence	−Log probability	Population in loop a	Population in loop b	Population in loop c
1	GA	63 611	117 903	163 870	340 624
2	GGA	51 459	34 048	67 293	165 738
3	GGGA	48 837	9892	31 567	102 345
4	A	38 358	273 627	300 495	492 842
5	GTGGG	25 655	55 719	11 578	8617
6	TGGG	24 126	62 418	15 377	12 614
7	TGG	22 161	101 363	41 802	32 928
8	GTGG	22 104	82 252	30 832	22 040
9	TG	17 189	153 386	86 943	72 114
10	GTG	16 479	114 504	61 257	46 660
11	CCTGTCA	13 009	12 138	39	17
12	CCTGTT	12 795	12 308	113	37
13	GT	12 062	143 082	88 734	75 429
14	CCTGTTG	11 518	10 897	79	11
15	T	10 975	220 140	154 559	136 752
16	GGAGGG	10 793	4373	25 445	5925
17	GGGAGGG	9174	2588	19 101	4022
18	GGGAGG	8778	4447	22 995	6125
19	CCTGTC	8775	8553	104	32
20	GAGGG	8557	8102	29 589	9460

Distribution of loop sequence by position

Unusual distributions are easier to spot for longer loop sequences. This is because there is a much lower probability that these longer sequences would occur by chance than a short one or two base sequences. Since low populations have a major effect on the ratio, simply looking at the ratio between the populations in each loop position highlights sequences that have a low population in one of the positions (Table 2).

The differences between Tables 2 and 4 show the merits of using both data sets. e.g. the highest ratio in Table 4 (TAGCATT) occurs in 14th place in Table 2. This difference is because the sequences in which TAGCATT occur are very G-rich and have many possible choices of loop sequence so although the un-restricted dataset is an unbiased choice of loop sequence Table 4 artificially raises the population of some sequences. In both tables the most commonly occurring motifs contain CCTGT or CCTAT in the first loop position with CCTGTCA the most frequent and CCTGTT the next most frequent.

The number of possible sequences for a stretch of DNA is equal to 4^N where N is the number of bases. This means that there are fewer sequences for a population to be distributed across for shorter loops. The shorter the sequence, the fewer the number of changes required to distribute the population across the spectrum of possible sequences. As a result the only sequences that occur infrequently in any given loop position are the longer sequences. We find therefore that using a ratio of populations does not highlight short sequences. The probability technique that we used, greatly reduces this bias towards long sequences, with Tables 3 and 5 showing that guanine-rich sequences with single A and T bases have the least probable distribution.

Several sequences occur in both the ratio tables (Tables 2 and 4) and the probability tables (Tables 3 and 5); ATCTCCA and CCTTGGC tend to occur in the third loop position and many of the CCTGT which tend to occur on the first loop position.

The most frequently occurring loops are those containing single A and single T bases, as seen in Table 6, which one derived from the arbitrary dataset. Study of these quadruplex sequences and surrounding DNA reveals that there are large G-rich regions interspersed with single A or T bases. The c-myc sequence (11,13) is a member of this type.

Table 6.

Most popular loop sequences for the arbitrary dataset

	Sequence	Population	Population in loop a	Population in loop b	Population in loop c
1	A	193 756	51 361	63 872	78 523
2	T	121 406	53 234	37 657	30 515
3	C	44 020	14 983	14 907	14 130
4	AA	40 026	12 778	13 717	13 531
5	CT	32 472	11 637	10 554	10 281
6	CA	32 070	10 781	10 846	10 443
7	G	29 623	7183	8375	14 065
8	AT	19 957	6789	7242	5926
9	AGA	19 144	5377	6919	6848
10	TT	17 089	7437	5530	4122
11	TA	12 641	4744	4329	3568
12	CC	10 955	3646	3726	3583
13	AGT	9896	2767	4447	2682
14	AGGA	9463	1932	3559	3972
15	AGGT	9434	1516	6448	1470
16	TGA	9237	3006	2849	3382
17	AAA	7839	2393	2970	2476
18	CCT	7151	2540	2298	2313
19	TGT	6619	2530	2307	1782
20	CCA	6269	2105	2048	2116

CCTGT sequences

The CCTGT sequences were examined in more detail because they were the logical choice to illustrate certain aspects of the sequences that come to light when looking at quadruplexes in such a way. Although, it may not necessarily be representative of the sequences that our methods have flagged, it is useful in an illustrative capacity. Although some sequences may be rigidly conserved throughout, the CCTGT type, shows a degree of variability. In order to determine whether the rest of the sequences that had the CCTGT motif in the first loop were consistent in the rest of the quadruplex we extracted all of the CCTGT sequences from the arbitrary dataset and ranked them by population. Table 7 shows the top 40 sequences. There were 3524 sequences that contained CCTGT in one of the loop regions. The most common loop sequences were T for the second loop and CTA for the third loop, both of which occur in Table 5. Looking at the whole table we see a large variability in quadruplex sequences that contain CCTGT. Only the top 526 sequences occur more than once, which leaves 2998 unique sequences. This variability makes it difficult to find a consensus sequence that contains non-guanines in the second loop. However, the most commonly occurring sequences are very similar.

Table 7.

Quadruplex sequences containing CCTGT in the first loop

	Loop a	Loop b	Loop c	Length of G-run	Population
1	CCTGTCA	T	CTA	3	39
2	CCTGTT	T	CTA	3	38
3	CCTGTCA	T	CTA	4	37
4	CCTGTC	T	CTA	3	35
5	CCTGTCA	T	CT	3	23
6	CCTGTCA	T	CT	4	22
7	CCTGTCA	T	CAA	3	21
8	CCTGTC	T	CTA	4	21
9	CCTGTT	T	CAA	3	20
10	CCTGTT	T	CTA	4	18
11	CCTGTT	T	A	3	18
12	CCTGTC	T	CT	3	18
13	CCTGTCA	T	CAA	4	16
14	CCTGTC	T	CAA	3	16
15	CCTGTT	T	CT	4	15
16	CCTGTT	TT	CTA	3	15
17	CCTGTCA	TT	CTA	3	13
18	CCTGTC	TT	CAA	3	12
19	CCTGTT	A	T	3	12
20	CCTGTT	T	CT	3	12
21	CCTGTT	AT	CAA	3	11
22	CCTGTC	T	CT	4	11
23	CCTGTCA	TT	CTA	4	11
24	CCTGTCA	AT	CTA	3	10
25	CCTGTT	TT	CT	3	10
26	CCTGT	T	T	3	10
27	CCTGTCA	TGA	CTA	4	10
28	CCTGTT	T	T	3	10
29	CCTGTC	T	CAA	4	10
30	CCTGTCA	T	AGGCAA	3	9
31	CCTGTT	AT	CTA	3	9
32	CCTGTT	T	TGA	3	9
33	CCTGTCA	TGGA	CTA	3	9
34	CCTGTCA	TT	CAA	3	9
35	CCTGTT	G	T	3	9
36	CCTGTCA	T	ACTA	4	9
37	CCTGTT	T	CAA	4	9
38	CCTGTT	AGT	CTA	3	8
39	CCTGTC	AT	CAA	3	8
40	CCTGTCA	T	ACTA	3	8

Consensus sequences were generated from the multiple sequence alignments of the quadruplex sequences that contained CCTGTT and CCTGTCA in the first loop (Figures 2a and b, respectively). The variability of the second loop and the length of the G-runs surrounding it result in a somewhat incoherent result for the consensus sequence. The consensus sequences for both of these types have only two regions that do not contain guanines. For the CCTGTT type sequences the third loop has the sequence CTA, which is consistent with the most commonly occurring CCTGT type sequence shown in Figure 2a. For the CCTGTCA type sequence the third loop has a similar sequence, CT, which also features highly in the most frequently occurring overall sequences.

We have also examined where the CCTGTT and CCTGTCA sequences occurred with respect to DNA function (Table 8). The relative distributions of CCTGTT and CCTGTCA appear to be similar, whereas the distribution of these two subsets is different from the distribution when all quadruplex sequences are considered. Not only is the proportion of CCTGTT and CCTGTCA quadruplex sequences within genes markedly lower than for the overall quadruplex population but also there seems to be a larger number on the minus strand, suggestive that these sequences could form RNA secondary structures (34) which would, in some cases be undesirable.

Table 8.

Sequence distribution by DNA function for the arbitrary dataset

	All quadruplexes	CCTGTT quadruplexes	CCTGTCA quadruplexes
Intergenic regions	223 321 (60%)	1193 (76%)	1490 (77%)
Within genes (plus strand)	75 189 (20%)	170 (11%)	162 (8%)
Within genes (minus strand)	76 647 (20%)	212 (13%)	290 (15%)
Of which within exons	14 009	1	2

The numbers represent the number of quadruplex sequences occuring within the given type of DNA. Number totally within exons 12 393.

Despite variability in the loop sequences that the CCTGT-type potential quadruplex structures show, they frequently occur in the context of quadruplex sequence and this may be evidence of quadruplex structure. Our analysis shows that there are a large number of sequences in the human genome, many of which occur systematically, which could potentially form G-quadruplexes. We have demonstrated that it is possible to use sequence data alone to isolate unique sequence types within these. Further sequence analyses are possible and with the knowledge we can begin to interpret experimental evidence, e.g. correlate location of quadruplex sequences with RNA expression levels. We may also be able to correlate the occurrence of particular quadruplex sequence types by proximity to particular families of proteins.