Prevalence of quadruplexes in the human genome

Abstract

Guanine-rich DNA sequences of a particular form have the ability to fold into four-stranded structures called G-quadruplexes. In this paper, we present a working rule to predict which primary sequences can form this structure, and describe a search algorithm to identify such sequences in genomic DNA. We count the number of quadruplexes found in the human genome and compare that with the figure predicted by modelling DNA as a Bernoulli stream or as a Markov chain, using windows of various sizes. We demonstrate that the distribution of loop lengths is significantly different from what would be expected in a random case, providing an indication of the number of potentially relevant quadruplex-forming sequences. In particular, we show that there is a significant repression of quadruplexes in the coding strand of exonic regions, which suggests that quadruplex-forming patterns are disfavoured in sequences that will form RNA.

INTRODUCTION

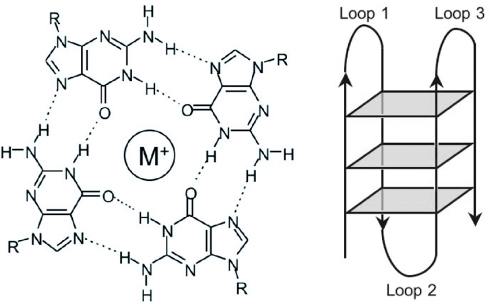
Nucleic acid sequences rich in guanine are capable of forming four-stranded structures called G-quadruplexes, stabilized by Hoogsteen hydrogen bonding between a tetrad of guanine bases (see Figure 1) (1,2). Telomeric repeats in a variety of organisms (3,4) have been shown to form these structures in vitro and high-resolution structures of the human telomeric sequence d(T₂AG₃)_n have been solved by NMR spectroscopy (5) and X-ray crystallography (6). Quadruplexes have also been shown to exist in vivo in Stylonychia lemnae macronuclei (7). The formation of these telomeric quadruplexes has been shown to decrease the activity of the enzyme telomerase (8), which is responsible for elongating telomeres. Since elevated telomerase activity has been implicated in ∼85% of cancers (9), this has become a significant strategy for drug development (10) and molecules that bind to and stabilize G-quadruplexes have been identified (9). A number of proteins that interact specifically with G-quadruplexes have also been reported, including the helicases implicated in Bloom's (11) and Werner's (12) syndromes the Saccharomyces cerevisiae protein RAP1 (13,14) and the artificially selected zinc finger protein Gq1 (15).

Figure 1.

Left: hydrogen bond pattern in a G-tetrad. A monvalent cation occupies the central position. Right: Schematic diagram of a unimolecular G-quadruplex structure.

Recently, there has been growing interest in quadruplex-forming sequences elsewhere in the genome. There has been particular focus on the quadruplex formed by the nuclease-hypersensitive element of the c-myc promoter (16–19) and structural studies have been performed on this sequence (20,21). Other potential quadruplex-forming sequences include the fragile X syndrome repeat d(CGG)_n (12,22,23), and the Cystatin B promoter (24), which has a region with sequence (CGCG₄CG₄)₄ and is involved in epilepsy. G-rich strands of the human insulin gene can form quadruplexes (25), as can the mouse Ms6-hm hypervariable satellite repeat (26), with sequence (CAGGG)_n. It has recently been proposed that the promoter regions of the RET protooncogene (27) and Ki-ras (28) can each form a quadruplex. G-rich RNA can also fold into quadruplex structures, e.g. the insulin-like growth factor II mRNA (29).

To date, however, there has not been significant attention focused on the more general question of identifying candidate sequences throughout the genome. There has also been no study of the general prevalence of putative quadruplex sequences (PQS) throughout the genome and how it compares with the chance frequency. In this paper, we outline a new rule for the prediction of PQS based on the primary DNA sequence and describe a program that can search DNA for these sequences. We then investigate the frequency of these sequences and the distribution of lengths of the loops joining the tetrad stacks within those sequences. A paper by Todd et al. (30) addresses the question of the loop sequences in detail.

MATERIALS AND METHODS

The quadruplex folding rule and the quadparser algorithm

In order to identify and investigate novel quadruplex-forming sequences, it is helpful to to identify PQS rapidly and simply, based purely on their sequence. Biophysical techniques, such as circular dichroism (14,31), NMR spectroscopy (5) and ultraviolet melting (32), can then be used for the confirmation of the structure for such candidates. No rule will be absolutely accurate, but from our previous work and examining the literature (vide infra), we have developed a simple ‘Folding Rule’ describing sequences that may form quadruplexes. Four aspects were considered in developing this rule: strand stoichiometry; the number of stacked tetrads in the quadruplex core; the presence of mutations or deletions; and the length and composition of loops. This rule predicts sequences that could form a quadruplex, but does not preclude the possibility of some or all of the motifs forming an alternative structure.

Strand stoichiometry

Quadruplexes can be uni-, bi- or tetramolecular. Since under physiological conditions the strand concentration of DNA is relatively low (in the order of nM), except in rare exceptions such as S.lemnae macronuclei (7), interstrand quadruplexes will be strongly disfavoured, and we have limited our analysis to sequences that may form from intramolecular structures.

Number of tetrads

G-quadruplex structures can, in principle, form from any number of G-tetrad stacks. In general, the stability increases with increasing numbers of stacks. Single G-tetrads have only been reported in highly concentrated guanine solutions at mM concentrations (1), and are unlikely to be physiologically relevant. There are a few examples of double-stack quadruplexes, such as the thrombin-binding aptamer (33,34) and the sequences identified as responsible for the fragile X syndrome (22). However, because these are in general less stable with regard either to single-stranded forms or duplex formation (35), we have only considered sequences capable of forming three or more G-tetrad stacks.

Discontinuities in G-tracts

Does a quadruplex have to be made up of perfect guanine tetrads, or can it tolerate discontinuities in the guanine bases? A few studies have recently been published identifying tetrads not purely comprising guanine (36–40), but most of these are artificially designed sequences, where a mixed tetrad is stabilized by flanking G-tetrads. In addition, recently there have been structures identified as having ‘slipped’ structures (41), where two quadruplexes slide against each other, or intrastrand leaps (42), in which a particular stack of guanines comes from more than one consecutive series of bases, but these are also artificial structures. We have performed a study (data not shown) to explore the effects of guanine replacements and deletions on a variant of the human telomeric sequence d(GGTTAG)_n. The variations result in sequences with significantly lower stability and for that reason we have restricted our analysis to include only sequences with no discontinuities in the G-tracts.

Loop length and composition

An intramolecular quadruplex must have three loops to link the tetrads together, and they play a large role in determining both the stability and folding pattern of the quadruplex. We have investigated this effect using biophysical techniques and molecular modelling, and this is described in detail elsewhere (43). In summary, loops with lengths from 1 to 7 bases were found to form quadruplexes, with stability decreasing as length increased. In principle, there is no reason to believe that structures cannot form with loops of 8 or more bases, but due to the predicted decrease in stability, we have limited the length to 7 bases.

Folding Rule

The above considerations led us to propose the following Folding Rule:

‘A sequence of the form d(G₃₊N_1–7G₃₊N_1–7G₃₊N_1–7G₃₊) will fold into a quadruplex under near-physiological conditions.’

In this rule, N refers to any base, including guanine, and the near-physiological conditions are 100 mM KCl and 10 mM Tris–HCl (pH 7.4).

Quadparser algorithm

We have developed a computer algorithm to identify PQS from genomic data in the FASTA format, which we have termed quadparser. It can rapidly analyse large amounts of genomic data and report on the number, position and other parameters for identified quadruplexes. It can process the entire human genome sequence in ∼20 min on a 1.25 MHz G4 processor. It is written in C and is available as Supplementary Material. The output formats and patterns it searches can be customized. Throughout this work, we have used the NCBI build 34 version of the human genome sequence.

Explicit solution to Bernoulli model

An explicit solution for the frequency of quadruplexes in DNA was calculated for the case in which each DNA base is independent. By considering the chance of obtaining four runs of at least three guanines and the chance of obtaining each of the possible loops, a polynomial expression in terms of the probability p of any base being guanine may be derived. The full solution is shown in the Supplementary Material, and yields the density of PQS sequences as:

$$\begin{array}{c}\rho \left(\text{PQS}\right)=343p^{12}-882p^{13}+756p^{14}-1098p^{15}\\ +2835p^{16}-3357p^{17}+2484p^{18}\dots \end{array}$$

Markov windowed model

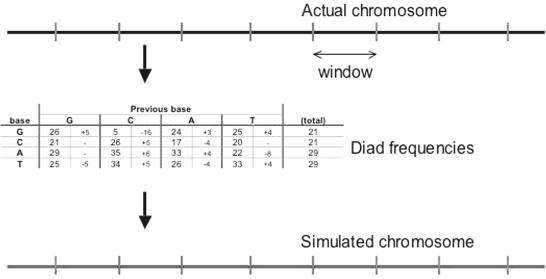
A more complex model of DNA may be obtained by using a Markov model, and basing the model on a series of individual windows to account for the heterogeneity of DNA regions. The DNA was separated in windows of defined size ranging from 50 to 4000 bp, beginning at the 5′ end of the sequence, as described in NCBI build 34. DNA diad frequencies were then obtained for each window by considering the first base and the next base, and incrementing the number of observations of that combination by one, before proceeding to the next base until the end of the window. In this manner, a 4 × 4 matrix was created, referring to all combinations of bases, and was converted from number in probabilities. A simulate was then generated, by generating the first base randomly according to the base frequencies, and then the second and subsequent bases based on the 4 × 4 matrix of probabilities, in each case using the probability matrix. After this simulation was complete, the next window was studied and the process repeated (Figure 2).

Figure 2.

Process for generating Markov windowed simulates. A real chromosome (top) is separated into discrete windows. For each of these, a table of base and diad frequencies is generated (middle), which is then used to generate a simulated window (bottom), which are then joined to produce the replicate chromosome.

PQS density in exons

Sequences of exons identified in ENSEMBL were downloaded using the EnsMart feature. The focus was set to ‘Ensembl genes’ and the species to ‘Homo Sapiens’. The filter was restricted to ‘known genes’ and the output was set to give ‘exon sequences only’ with one output per gene. The output format was FASTA, and the sequences were analysed using quadparser.

Loop counts

Quadparser may be instructed to count the loop lengths of each PQS it identifies, rather than outputting the full sequence. Loops were defined as commencing from the end of a run of three or more G's and finishing before the next run of three or more G's. Runs of seven or more G's were treated as having as many runs of GGG as could be managed with loops of at least 1 base, and were assumed to have equally distributed loops. All possible quadruplexes were counted, including overlapping sequences. For statistical analysis, the results were output as a 7 × 7 × 7 array, corresponding to frequencies for each possible combination of loop lengths.

RESULTS AND DISCUSSION

Prevalence of quadruplexes in the human genome

To date, there have been no reports of the total number of potential quadruplexes present in the human genome; rather, individual sequences have been examined in detail. Understanding the prevalence is important, because it leads to the identification of more sequences of potential biological interest, and also because in order for quadruplexes to be useful as therapeutic targets, a quadruplex ligand must ideally be specific for only one quadruplex in the genome. Furthermore, a genome-wide analysis of quadruplex-like elements prevalence may reveal indications of whether evolution has influenced the occurrence of such motifs.

The quadparser algorithm, using the folding rule described above, can identify and count all the PQS in the genome. Where there is more than one possible quadruplex from a given sequences of four runs of Gs, it counts only one, by assuming that all the Gs in a run do not belong to loops. This is done to avoid multiple-counting, and because it is hard to unambiguously assign which G's are in a tetrad. Indeed, it has been shown in the literature (17,20) that in the case of the PQS in the promoter of c-myc, d(AGGGTGGGGAGGGTGGGG), an ensemble of four structures is formed, each utilizing in the tetrads either the first or fourth G of the underlined runs. When there are more than four runs of d(GGG), it counts the maximum number of quadruplexes that could be formed at any given time using consecutive guanine runs. [i.e. a sequence d(GGGTTA)₈ would yield a count of 2]. Other approaches to counting have also been employed, such as counting the maximum number of potential quadruplexes [5 for the example of d(GGGTTA)₈]. These give results similar to those described here (data not shown). Because genomic data are normally supplied as a single strand, quadparser has been used to count both G-rich patterns (‘G-patterns’) and ‘C-patterns’, C-rich sequences of the same form as the G-patterns. These have no direct meaning, but do mean that a G-quadruplex could be formed in the strand complementary to that for which the sequence was obtained. ‘A-patterns’ and ‘T-patterns’ refer to A- and T-rich sequences of the same form and have no known physical meaning, but are used as statistical controls. ‘GC-patterns’ refer to both G-patterns and C-patterns and likewise for AT-patterns.

The results from counting the number of PQS in the human genome are shown in Table 1. This shows a total of 376 000 GC-patterns and 3 260 000 AT-patterns. The excess of AT-patterns is caused by the excess of A and T over G and C in the human genome (29% versus 21%). Some of the GC-patterns are located in regions with simple repeats, such as the telomeres. However, by counting the total number of sequences found, counting concatenated sequences as one, it can be shown that that such repeats account for ∼20 000 of those found, still leaving a very considerable number elsewhere. The number of GC-patterns identified accords well with the results of an independent study by our collaborators using a different approach (30), which found 375 000 GC-patterns.

Table 1.

Number of X-patterns of the form d(X₃₊N_1–7X₃₊N_1–7X₃₊N_1–7X₃₊) where X refers to the base being examined, for the whole human genome (NCBI build 34, accessed via ENSEMBL)

G-patterns	188 836	A-patterns	1 624 670
C-patterns	187 610	T-patterns	1 638 487
Total GC-patterns	376 446	Total AT-patterns	3 263 157

G-patterns have a physical reality, and C-patterns identify G-patterns in the complementary strand. A- and T-patterns have no known physical meaning.

In the remaining sections of this paper, we describe the outcome of studies aimed at investigating the frequency, distribution and sequence pattern of PQS.

Comparison of native PQS frequency with that of shuffled DNA

Evidence of evolutionary selective pressures acting on these sequences would provide support for the functional relevance of these sequences. This may be examined by comparing the number of putative GC-quadruplexes actually found to the number predicted for randomized DNA sequences. If PQS have a physiological consequence, then they may occur more or less frequently than expected owing to evolutionary pressures. To investigate the expected frequency of PQS in DNA, we needed to develop a model for randomized DNA. The simplest such model is to treat DNA as a sequence of independent bases (a Bernoulli stream), each occurring with a probability equivalent to their frequency in the human genome. There are approximate methods (44,45) for calculating the expected number of PQS given a certain base frequency, and we have solved this problem explicitly as well. This gives the expected density of PQS, ρ(PQS), as a function of p, the probability of any individual base being guanine:

$$\begin{array}{c}\rho \left(\text{PQS}\right)=343p^{12}-882p^{13}+756p^{14}-1098p^{15}\\ +2835p^{16}-3357p^{17}+2484p^{18}\dots \end{array}$$

However, applying this solution to the entire human genome gives predicted frequencies for GC-patterns of 8300 and for AT-patterns of 304 000. These results are clearly significantly lower than those actually found, by more than an order of magnitude. Since the discrepancy between real genomic data and prediction arises for both ‘real’ GC-patterns and ‘control’ AT-patterns, this is suggestive of shortcomings in the model used for DNA.

There are two reasons why this simple Bernoulli model may be oversimplistic. First, DNA exhibits considerable structure on the diad base level, shown in Table 2, and as described previously by others (46,47). This means that some bases are more likely to occur after others. As an example, there is only a 5% chance of finding a G after a C, although there is a 21% chance in general of finding a G in any particular position. In particular, homodiads are relatively frequent, which means that quadruplex-forming sequences will be considerably more frequent. Second, DNA is not homogenous with respect to base composition, and has regions that are relatively rich in each base. Since the number of quadruplexes found is a very strong function of base density, this factor will have a large impact.

Table 2.

Diad analysis of every human chromosome

Base	Previous base								Total
	G		C		A		T
G	0.26	+0.05	0.05	−0.16	0.24	+0.03	0.25	+0.04	0.21
C	0.21	—	0.26	+0.05	0.17	−0.04	0.20	—	0.21
A	0.29	—	0.35	+0.06	0.33	+0.04	0.22	−0.08	0.29
T	0.25	−0.05	0.34	+0.05	0.26	−0.04	0.33	+0.04	0.29

Vertical lines show the percentage probabilities of each base following a given base, and then the deviation from the percentage probabilities expected if each base was independent. For clarity, data resulting from the borders of unsequenced regions of DNA have been suppressed.

In order to develop a better model of DNA, we have produced simulated chromosomes based on real chromosomes using a windowing procedure and generating simulated DNA while preserving the native diad frequency using a Markov model. In summary, we take the first n bases of the chromosome being studied, where n is the window size, and count the diad frequencies. These are then used to generate n bases, which are used as the beginning of the simulated chromosome. The next n real bases are then taken, a shuffled version generated and added to the simulated chromosome. This is continued until the end of the real chromosome.

Replicates of the entire human genome were generated using this method, and the number of GC- and AT-patterns found was calculated using quadparser. These numbers vary considerably with the window size, and the results are shown in Table 3 for window sizes from 50 to 4000 bases. Five repeats of each simulation were performed, and the SD was <1% in all cases. Large window sizes tend to produce fewer PQS, because they average out smaller base-rich islands. Smaller window sizes give results with more repeated units, resulting in more PQS being identified. For extremely small window sizes, i.e. a few bases, the Markov approach is not satisfactory (data not shown), and for a window size of one base, an exact replica of the initial chromosome is generated. Comparing the results found using this Markov windowed method with those found in the real human genome, it is seen that for window sizes ≥150, there are fewer predicted sequences than actually found for both GC- and AT-patterns. For window sizes between 75 and 150, there are more GC-patterns than actually found, but fewer AT-patterns. It is interesting to note that at a window size of 75, the algorithm correctly predicts the number of AT-patterns, i.e. 3 260 000, but predicts 37% more GC-patterns than actually found. For smaller windows, more of both types of patterns are predicted than found.

Table 3.

Total number of GC- and AT-patterns found in the real human genome and simulates using various methods

Method	GC-patterns	AT-patterns
Markov, size 50	687 k	4.01 M
Markov, size 75	514 k	3.26 M
Markov, size 100	420 k	2.81 M
Markov, size 150	320 k	2.29 M
Markov, size 200	269 k	2.02 M
Markov, size 400	185 k	1.56 M
Markov, size 1000	123 k	1.20 M
Markov, size 2000	93 k	1.02 M
Markov, size 4000	75 k	0.89 M
Bernoulli	8 k	0.30 M
Real human genome	376 k	3.26 M

In the window methods, simulates were generated conserving diad base frequencies in windows of the size shown. Five independent analyses were performed, and the SD was in all cases <1%. The ‘Bernoulli’ method treats DNA as a stream of independent bases, with base frequencies homogenous across each chromosome. The Markov model that correctly predicted the number of AT-patterns (window size 75 bp) is shown in boldface.

The ratios of patterns for each base under different simulation conditions are shown in Table 4 for each case, normalized to the predicted number of T-patterns = 1. This shows that in all cases, a ‘pseudo-Chargaff’ rule applies, with roughly as many G-patterns as C-patterns, and similarly with A and T.

Table 4.

Frequencies of X-patterns of the form d(X₃₊N_1–7X₃₊N_1–7X₃₊N_1–7X₃₊) for x = G, C, A, T under various conditions, normalized such that the frequency of T-patterns in each column is 1

X	Relative frequencies, normalized to T = 1
	Actually observed	Bernoulli	Markov 50 bp	Markov 75 bp	Markov 100 bp	Markov 150 bp	Markov 200 bp	Markov 400 bp	Markov 1000 bp	Markov 2000 bp	Markov 4000 bp
G	0.12	0.03	0.17	0.16	0.15	0.14	0.13	0.12	0.10	0.09	0.08
C	0.12	0.03	0.17	0.16	0.15	0.14	0.13	0.12	0.10	0.09	0.08
A	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.99
T	1	1	1	1	1	1	1	1	1	1	1

The actually observed data are taken from the NCBI build 34 of the human genome. The Bernoulli model and Markov models are described elsewhere in the text, and the number below the word ‘Markov’ refers to the window size used. It can be clearly seen throughout these data that the pseudo-Chargaff rule G = C and A = T holds, to be within 1%. This also shows that the relative depletion of GC-patterns increases with increasing window size.

Location of putative quadruplexes

Using the ENSEMBL database, it is possible to classify regions of the genome as related to genes. This information was used to investigate the number of putative quadruplexes in genes, and specifically within the exonic regions. These results show marked differences in terms of base composition and frequency of quadruplex-forming patterns. The exonic regions have been determined using the annotations within ENSEMBL. They have a base ratio that closely approximates equality (G:C:A:T 1.05:1.04:1.07:1), and diad repeat ratios that deviate less far from a Bernoulli model than the rest of the genome (GG:CC:AA:TT 0.98:1.07:1.05:1 for exons, against 0.78:0.79:1.00:1 for the whole genome) (see Table 5). There are still some differences in these parameters between the four bases, and as a result they give rise to different predicted X-pattern frequencies, based on a windowed Markov model of the exons, as described previously. These ratios are G:C:A:T 0.91:1.10:1.21:1. Examination of the actual exonic regions reveals a very different ratio, with the observed frequencies of X-patterns being in the ratio 0.48:0.83:0.93:1.

Table 5.

Frequencies of bases, diads and patterns for each base the exonic regions

Base	Frequency	Diad repeat frequency	Observed pattern frequency	Markov predicted pattern frequency	Observed/Markov predicted frequency ratio
G	0.25	0.27	0.48	0.91	0.53
C	0.25	0.29	0.83	1.10	0.75
A	0.26	0.29	0.93	1.21	0.77
T	0.24	0.27	1	1	1

Frequency lists the frequency of each bases in the relevant region. Diad repeat frequency refers to the chance that after a given base, the same base will be repeated. The observed and predicted pattern frequencies refer to the relative frequencies of patterns of the form d(X₃₊N_1–7X₃₊N_1–7X₃₊N_1–7X₃₊) for X=G, C, A, T, normalized to 1 for the frequency of T-patterns, either in the actual human genome or in a simulate using a Markov model with a window size of 75 bp. The data show that the G-patterns are dramatically underrepresented, and there is a weaker effect on C-patterns, and another on A-patterns.

One feature throughout these results is that the ‘pseudo-Chargaff’ rule that applies for the whole genome need not and does not apply to the case of exons, since the two DNA strands are distinct in exonic regions, with only one of them being transcribed to form RNA. However, does this show a bias with respect to quadruplex location as well? To investigate this, we considered the differences between the predicted ratio of X-patterns, compared with the observed ratio. This is given in Table 5, and gives a ratio of observed/predicted of {0.53, 0.76, 0.76, 1} for {G, C, A, T}.

The most marked effect observable from these results is the considerable suppression of the G-patterns compared with that predicted. This effect is greater than that observed for C-patterns, which have a suppression of an order similar to the effects on A-patterns. Why is this difference observed? One discriminating factor is the fact the G-rich codons do not code for the same amino acids as C-rich codons, but the discrimination is not sufficient to account for our observations, although it may form part of the explanation. An alternative explanation is based on the observation that the G-patterns would lead to potential quadruplexes in the mRNA strand in addition to the DNA duplex, whereas C-patterns could only lead to quadruplexes in the DNA. This evidence is consistent with an evolutionary pressure reducing the number of quadruplexes allowed to form in mRNA. To date, there has been relatively little work focused on RNA quadruplexes, although it has evoked some interest (29,48,49). These results suggest that RNA quadruplexes could play a significant role and should be investigated further.

Distribution of loop lengths

It has been previously shown that the length of the loops linking the runs of oligo(G) sequences plays a significant role in determining the stability of the resultant quadruplexes (43,50). We, therefore, hypothesized that if there were selective pressures acting on sequences with the potential to form quadruplexes, this would be evident in the distribution of loop lengths as well as the overall number. Any indication of deviation from randomness would indicate some kind of selective pressure, and by examining the direction of the deviation, it might be possible to rationalize the pressures observed.

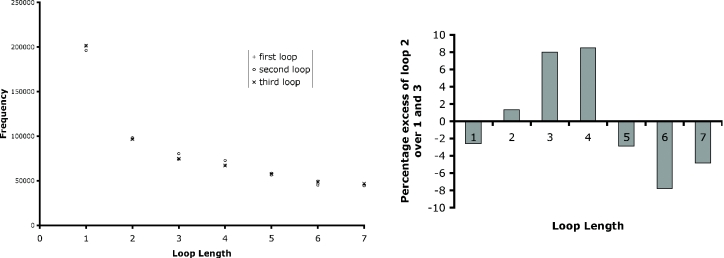
The simplest approach to this question is to consider the distribution of loop lengths for each loop (first, second or third). This study has been performed, and the frequency results are shown in Figure 3. All possible quadruplexes were considered. These results show that loops 1 and 3 display the same properties as each other, but that loop 2 behaves significantly differently. This is emphasized in the right-hand side of Figure 3, where the excess/decrease of loop 2 frequencies over the frequencies for loops 1 and 3 is shown for each possible length for the real human genome. The same study was performed on GC-patterns in simulated DNA (using the Markov windowed model) and on AT-patterns, both simulated and real. None of these showed any significant deviations, in the manner observed for real GC-patterns.

Figure 3.

Left: frequency distributions of loops of lengths 1–7 bases for the entire human genome. Right: percentage excesses of loop 2 counts over the averages of loops 1 and 3 for the entire human genome.

This result demonstrates that there is a non-random behaviour demonstrated by sequences capable of forming quadruplexes. However, a more detailed analysis is required in order to be able to make comments about the nature and significance of the non-randomness observed. In order to do this, the number of sequences in the genome with loop lengths {i, j, k} was counted. The results are represented as a mosaic plot in Figure 4. The most common set of loop lengths was {1, 1, 1}, which accounted for 8% of all PQS. Table 6 lists the 20 most common loop length combinations, which account for 32% of all PQS. Many of these have single-base loops, a trend also observed in an independent study by our collaborators (30). Table 6 also lists the 20 least common loop length combinations, which generally include longer loops. It is also noteworthy than in none of the least common loop length combinations is the length of loops 1 and 3 the same. Thus, such sequences are over-represented in the cases of the most common loop length combinations. The full dataset of loop length combinations is given in Supplementary Material.

Figure 4.

Mosaic plot representing the loop lengths of all putative quadruplexes found in the human genome. The seven principle columns represent the lengths of the first loop, the seven rows the lengths of the second loop, and the seven segments in each box the lengths of the third loop. The area of each box is proportional to the number of sequences found with that combination of loop lengths. The plot was produced using the program R, (http://www.r-project.org) using the command mosaicplot.

Table 6.

The 20 most common and 20 least common sets of observed PQS loop lengths

Most common loop lengths				Least common loop lengths
Loop 1	Loop 2	Loop 3	Number	Loop 1	Loop 2	Loop 3	Number
1	1	1	47 475	6	5	7	441
1	4	1	11 328	7	6	5	441
1	2	1	10 656	7	6	3	447
1	1	2	10 415	5	6	7	447
2	1	1	10 040	6	6	7	449
2	2	2	9411	6	7	7	450
1	3	1	9127	7	5	6	452
1	5	1	7799	5	7	6	484
5	1	1	7379	5	5	7	501
1	1	5	7337	5	6	3	505
3	3	3	6827	7	7	6	505
3	1	1	6458	6	6	5	506
1	1	3	6403	5	6	6	511
1	1	4	6196	3	6	7	521
4	1	1	6189	7	6	6	523
2	2	1	5123	6	7	3	525
1	2	2	5046	7	7	4	528
2	1	2	4780	3	7	6	533
1	6	1	4556	5	7	7	536
6	1	1	4462	6	7	5	538

Loops are numbered from 5′ to 3′ of the G-rich strand.

We initially attempted to represent these data as three independent distributions. However, it was immediately obvious that there are patterns within these data that deviate from randomness. In particular, it is clear that there is a peak in frequency for values where the length of the first loop is equal to that of the third loop (i = k). As a result, attempts to fit the data to a model involving three independent distributions (one for each loop) left as a residue a ‘spine’ of excess sequences occurring along this diagonal. This implies that there are more sequences than expected with two of the loops being of equal length. In order to fit this excess into the model, an extra term in the frequency expression is required, giving the relationships shown below, where N_{ik} is the predicted count with first loop length i and third loop length k, β_i and β_k are the two independent distributions, a is a constant describing the population of the ‘spine’ and α_i describes the distribution of sequences along the spine:

$$\begin{array}{c}{N}_{\left\{ik\right\}}=a•{\alpha }_i+(1-a){\beta }_i{\beta }_k\text{for}i=k,\\ N_{\left\{ik\right\}}=(1-a){\beta }_i{\beta }_k\text{for}i\ne k.\end{array}$$

This is called diagonal quasi-independence (51), and corresponds to a probability mixture model, in which with probability a, the loop lengths are constrained to be the same, and with probability (1 − a), they are independent. Fitting the observed data to the model allows the calculation of a value for a of 0.09, implying that ∼10% of the potential quadruplex patterns show a high correlation between the lengths of loops 1 and 3.

A correlation between loops in these GC-patterns is very hard to explain while only considering duplex DNA. However, it is perhaps more reasonable to expect that loop length correlations could affect the properties (e.g. stability) of DNA in the quadruplex form. This observation of strong patterns in at least 10% of the GC-patterns is suggestive that at least this fraction of quadruplexes may have distinct physical and/or functional properties in vivo. Despite a few studies (43,50) on the effect of loop length on quadruplex stability, it is not yet clear exactly how the loops control the stability. It is likely that the sequence of the loops must play a role, but this is not yet understood in any detail. These statistical correlations suggest further biophysical studies on quadruplex loop lengths and loop sequences would be worthwhile in the future. Given the frequency results shown in Table 6, a focus on sequences with relatively short loops would be a promising approach.

CONCLUSIONS

The human genome contains a large number of sequences that have the potential to form quadruplexes. In principle, as many as 376 000 quadruplexes could exist simultaneously. It is unlikely that anything like this number would exist at the same time, as there is likely to be a dynamic equilibrium between quadruplex and other structural forms of DNA (e.g. duplex), and furthermore the DNA structure will be subject to influence of chromatin structure, many classes of DNA-binding proteins, and also the cell-type and its state. That the number of putative genomic quadruplexes is so high does raise an important selectivity challenge for quadruplex recognition either by natural or unnatural molecules.

Simple modelling of DNA as a series of independent bases is unsatisfactory for predicting the number of PQS, owing to chromosome heterogeneity and details of the diad composition of genomic DNA. A Markov chain approach was used to generate DNA simulates in windows. We have demonstrated how the predictions of PQS and AT-patterns vary as a function of the window size. In all cases studied (window sizes from 50 to 4000 bases), the predictions of the Markov model were closer to the actual frequencies in the human genome than those of the Bernoulli approach.

The differentiation between G- and C-patterns in exonic regions suggests that there is another level of selection occurring, with suppression of potential quadruplexes in mRNA sequences. Similarly, where there are potential quadruplexes in the genome, there are strong correlations in the lengths of the loops. This could potentially be another mechanism for reducing their formation.

Further evidence for the in vivo significance of these quadruplex-forming sequences comes from the observation, both in this paper and the accompanying one (30), that the putative loops exhibit significant non-random structure. We show here that there are correlations between the lengths of the loops, in a way that would be very hard to rationalize if the sequences exist solely as duplex DNA.

Suppression of genomic G-quadruplexes could indicate that they have been selected against in evolution. They may broadly interfere with normal cellular activities, such as replication and transcription, by blocking access to DNA. The existence of helicases (11,12) that are required to specifically unwind G-quadruplex structures during transcription supports this argument. The sequences that remain may have a role in gene regulation or many other activities, and further detailed studies will be required to confirm that they do indeed form quadruplexes, and what roles they have.

Having located all of these PQS identified by the quadparser algorithm, they may be used for a variety of purposes to examine particular genes or other regions of interest, and we are actively investigating such interesting potential quadruplexes. A full dataset of genomic coordinates for all potential quadruplexes are available from the authors in DAS format, which may be uploaded to the ENSEMBL website for visualization. We are currently investigating the biophysical properties and physiological function of a number of these sequences, and performing further bioinformatic studies across the whole genome to investigate their correlations with other genomic features, such as single nucleotide polymorphisms, nuclease hypersensitive regions, promoter regions and regions of high cross-genome conservation.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.