Abstract
The identification of potential interactions and relationships between diseases and drugs is significant in public health care and drug discovery. As we all know, experimenting to determine the drug-disease interactions is very expensive in both time and money. However, there are still many drug-disease associations that are still undiscovered and potential. Therefore, the development of computational methods to explore the relationship between drugs and diseases is very important and essential. Many computational methods for predicting drug-disease associations have been developed based on known interactions to learn potential interactions of unknown drug-disease pairs. In this paper, we propose 3 new main groups of meta-paths based on the heterogeneous biological network of drug-protein-disease objects. For each meta-path, we design a machine learning model, then an integrated learning method is formed by these models. We evaluated our approach on 3 standard datasets which are DrugBank, OMIM, and Gottlieb’s dataset. Experimental results demonstrate that the proposed method is better than some recent methods such as EMP-SVD, LRSSL, MBiRW, MPG-DDA, SCMFDD,. . . in some measures such as AUC, AUPR, and F1-score.
Keywords: Drug-disease associations, knowledge graph embeddings, structural representation, drug repositioning, drug development
Introduction
As traditional drug development faces sufficiently long procedures including target discovery, discovery screening, lead optimization, ADMET (Absorption, Distribution, Metabolism, Excretion and Toxicity) testing, development and registration, the process is usually complicated and costly and it carries a high risk of failure. The pharmaceutical product development is still in need of at least 10 to 15 years and this can cost between $500 million and $2 billion, 1 with substantial investments directed toward basic science, technology development, and the exploration of new organizational and management models.
In particular, newly discovered usages of existing drugs seems to bring the development cost down much compared with “de novo” drug discovery and development. 2 Much recent publications3 -14 have considered closely on drugs repurposing where additional indications were discovered unexpectedly. While Chlorpromazine (dopamine receptor blockade) was initially developed to treat Antiemetic/antihistamine, a tranquilizing effect of the drug was discovered by Heri Laborit and it became a staple of psychiatric treatment. Very recently, Galantamine (acetylcholinesterase inhibition) 15 which was considered as a drug for treating polio, paralysis and anesthesia had its new usage approved in many countries for Alzheimer’s disease. Importantly, as repositioning drug candidates have frequently been tested in development for their initial indication, a variety of phases common to de novo drug discovery and development can be avoided. So, the drug repositioning provides a chance of reducing time and risk of development. It is with the drug repositioning concept that many researchers choose to explore drug-disease association for predicting new usage for existing drugs. This may be due to the assumption that similar drugs tended to treat similar diseases. 16
We can note a recent sharp growth of biological data for genome sequences, gene expression status, protein interactions and patients. In addition, most databases are dedicated to a specific type of information, and the relationship between different datasets, for example between gene production and epigenetic status, is still deficiently understood. With this complex data landscape, combining different datasets gives an integrated heterogeneous dataset that is almost always as good as, and in several cases significantly better than, a dataset alone. Also note that, heterogeneous transfer learning methods, where heterogeneous networks take place throughout biological data, have been implemented with promising results. 17 The approach is adapted in our article to set up a heterogeneous network allowing drug repositioning with appropriate proteins’ information. There is evidence that if information of associations between drugs, protein and diseases is available then a heterogeneous network with Singular Value Decomposition (SVD) can learn relying on some meta-paths. 18
Concerning the meta-paths, it is important for drug repositioning, and all other transfer learning methods, that a clear logical structure of meta-paths is needed to be defined. In this work, we present a new method for detection of new drug-disease association based on meta-paths. The first major contribution has come in the way of finding out drug-drug associations, protein-protein associations, disease-disease associations and heterogeneous network construction from the associations. The second, we propose to analyze the drug-disease associations by presenting drug-disease associations through 3 creative meta-paths. As far as the drug-disease associations are combined from these meta-paths, latent features are extracted with data dimension reduction. Finally, we apply an appropriate classification model for the heterogeneous network. The proposed approach is designed for drug repositioning in a biological heterogeneous network and can be an effective model for label transferring as well as on other heterogeneous data.
Related Work
It is significant to understand what the expert currently studies when checking drug-disease association in drug repurposing. A large number of computational works have attempted to define a method of presenting drug-disease association or design drug re-purpose learning model. A detailed review of works related to our approach is shown now in 2 subsections.
Drug-disease association presentation
Differences in feature extraction, similarity estimation, and matrix factorization are just some approaches that play a role for presenting drug-disease association. In particular, the association of drug-protein, drug-disease and protein-disease are encoded in binary labels indicating the presence or absence of an interaction. Feature vectors with certain length, often accompanied with the binary labels are used for presenting the features of drug-disease association. 19 To improve performance as well as the efficiency, some works implemented dimension reduction techniques to transform feature arrays from a high-dimensional space into a low-dimensional space, retaining meaningful properties of the drug-disease association. In order to forecast drug-disease interaction, different techniques can be implemented, some of them are: Support Vector Machines (SVM), 17 and Random Forest. 3 However, SVM performs poorly on highly imbalanced data, especially in complex tasks. In this study, only the weighted SVM model was considered without any data sampling or filtering, which may not be sufficient to address the issue of data imbalance. Meanwhile, the limitations of Random Forests, such as high computational complexity and difficulty in explaining the model, could also apply in this case, based on the general nature of these limitations for this method in other studies.
The similarity measure that associations are labeled based on their features’ similarity has been addressed in this domain. Because the drug-drug and disease-disease similarity measures can be performed through similarity or distance functions, prediction of interaction can be estimated: Using the matrix consisting of known drug and disease interaction, similarity measures can produce estimation for unknown drug and disease pairs. A number of similarity based methods, including Zhang et al, 4 Shi et al 5 has been proposed addressing the similarity scores of either drug-drug, disease-disease or drug-disease associations. Furthermore, Euclidean distance was used in a nearest neighbor algorithm applied to the interaction. 6 The genomic similarity of protein sequences, and pharmacological similarity of drugs, in cooperation with topological properties of drugs-protein-disease network were also suggested for drug-disease interaction prediction. 7 Actually, proportion of known drug-disease interactions and total number of interactions is very low and this is the main disadvantage of the similarity-based methods.
We are also examining whether study works that are related to factors of the features of drug-disease interactions. More interesting might be the matrix factorization that can represent drug-disease interactions by factors. This is surely possible when there are consistent associations between the characteristics of drugs and the characteristics of the diseases. Unlike the similarity approach based on characteristics of drugs and the characteristics of the diseases, the matrix factorization is based on measurement of the strength of the drug-disease interactions, when drugs and diseases are located within the same spatial region. 8 Mentioned above works outlined different ways to present features for drug-disease association. The proposed method in this paper uses binary class for presenting drug disease association and the matrix factorization approach for getting major factors of feature matrices. However, we propose to implement novel 3 meta-paths instead of using similarity measurement.
Drug re-purpose learning model design
Research in recent years shows that few experts described specific concepts like network, deep learning and hybrid methods for the designing of drug re-purpose learning models. Consider network-based methods where data structure is a set of objects represented by nodes and their relationships shown by edges. The attention of the methods is gained for machine learning research by the high network power. Alternative semi-supervised heterogeneous network embedding was noted by Song et al. 9 Specifically, the network is set up by similarity of drugs, drug-disease, and protein-protein interaction. On other hand, a multi-graph based method was proposed by Zhao et al 10 where graph convolution network was implemented with graph embedding approach for representing features of drug-disease associations. Good works adapting networks for drug-disease heterogeneous data can be seen in convolutional neural networks by Öztürk et al, 11 and in multiple layer perceptions by You et al. 12
In the deep learning direction, Zhao et al 13 recommended a geometric deep learning method for solving the drug-disease associations problem with heterogeneous information. The projection of geometric prior knowledge of network structure to a latent feature space was addressed for feature representation.
Most of the methods introduced above are really good at completing 1 task or working with 1 dataset. There are methods that are combinations of existing methods which were applied in the field or were transferred from other fields. We see that combinations can be performed from feature-based methods, matrix factorization, networks and deep learning. Thus, the feature-based and similarity-based machine learning approaches were essentially integrated by Agarwal et al. 14 Such hybrid methods are generally constructive and productive by optimizing the feature extraction for extracting the complex hidden features of drugs and diseases. Joining 2 machine learning methods in Drug-Disease Interaction prediction often yields favorable results as they can fully exploit the potential of partial methods simultaneously. However, one should be able to handle the high complexity, either computational or operational caused by integration. In drug repurpose learning model design, we selected the hybrid approach to attract advantages of partial methods including feature extraction, SVD and new 3 meta-paths that were designed specifically to deal with the heterogeneous drug and disease data.
The Method
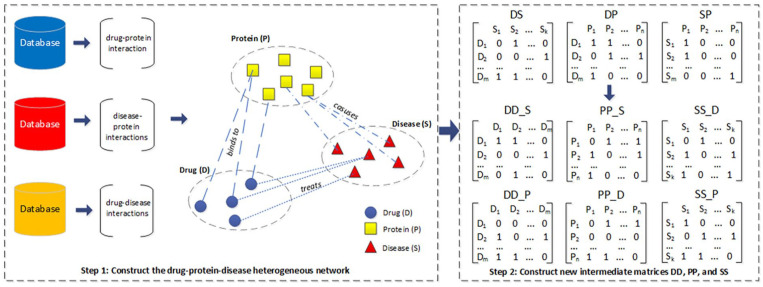
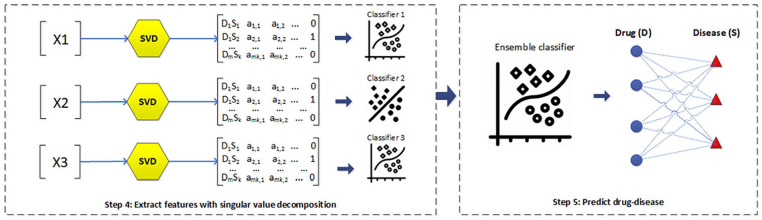
In this section, the essential tasks of our method are outlined for predicting drug-disease associations. As part of the story, we describe a heterogeneous network that takes place throughout biological databases related to drug, protein and disease, see step 1 in Figure 1. Then, the network can be extended by adding the relationships of drug-drug, protein-protein, and disease-disease. We will build 6 new matrices, which describe the connections, see step 2 in Figure 1. To ease drug-disease associations prediction, our suggestion is to bring the new constructed matrices into learning—to have three paths which actually reflect the drug-disease associations, see step 3 in Figure 1. We shall see that features can be extracted from the drug-disease associations and used for learning in the final task, see steps 4 and 5 in Figure 1.
Figure 1.
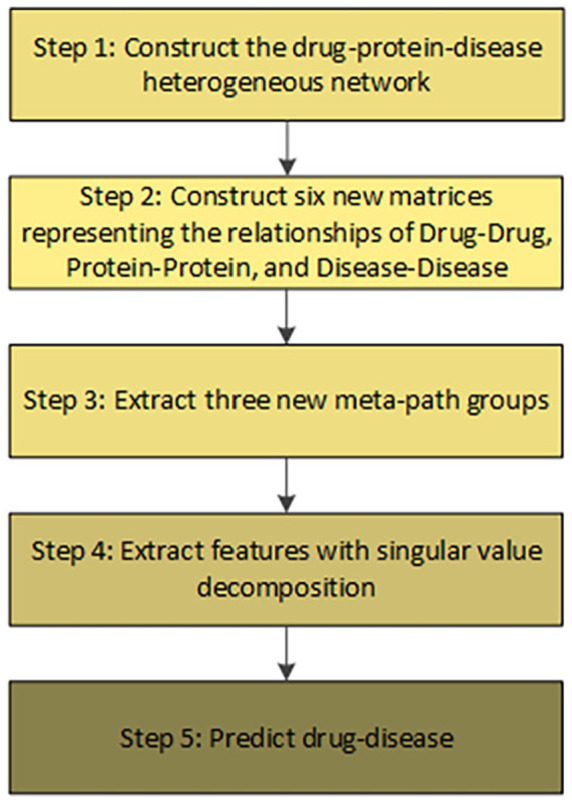
General workflow containing 5 main steps.
Heterogeneous network construction
To avoid being distracted by the details, we use for drug, for protein and for disease. Also, means a set of drugs once the drug data are available for study. Similarly, is a set of proteins and is a set of diseases. Certainly, we need biological data that cover the “binds to” link between drugs and proteins, “causes/caused by” link between proteins and diseases, “treated/treated by” link between drugs and diseases. There are 3 possible types of associations. Here, we have used a binary matrix that presents the drug-protein associations. If drug is associated with protein , then the element is set to 1, otherwise set to 0. Indeed, the disease-protein associations can be coded in a binary matrix , and the drug-disease association is expressed by a binary matrix .
Heterogeneous network
Let be a network, where denotes the set of nodes , and represents links set . Its network schema, is a meta-template of , where and represent node type sets and edge type sets, respectively.
The elements of the heterogeneous network in Table 1 demonstrates that the network contains interconnected nodes and links of different types. A heterogeneous network can represent interconnected nodes of various types, including drugs, diseases, and proteins. So, step 1 in Figure 2 shows the nodes in 3 colors according to the types. The edges of the networks are displayed in 3 types of lines for indicating divergent types of edges.
Table 1.
Elements of the heterogeneous network of drug-protein-disease.
| Type | Property |
|---|---|
| Nodes (N) | Drug (D) |
| Protein (P) | |
| Disease (S) | |
| Relations (R) | Drug-Protein (DP) |
| Disease-Protein (SP) | |
| Drug-Disease (DS) |
Figure 2.
Construct the drug-protein-disease heterogeneous network and 6 new matrices representing the relationships of drug-drug, protein-protein, and disease-disease.
Network expansion by adding associations
In designing a heterogeneous network, there are choices about the types of edges. The constructed network has edges for drug-protein, disease-protein and drug-disease associations. We propose to append 3 new types of edges which are drug-drug, disease-disease, and protein-protein.
The drug-drug association
Specifying drug-drug association is very noteworthy and it can be actually carried out by studying the drug-disease or drug-protein association. Of course, association between two drugs can be established if there exists a disease that both drugs are associated with. The drug-drug association created by disease as intermediary is represented by a matrix . Similarly, drug-drug association can be observed by checking drug-protein association. It has to mark an association for two drugs whenever there exists a protein that is associated with both drugs. The drug-drug association created by protein as an intermediary is represented by matrix .
The protein-protein association
We have looked at techniques for defining this association. One way of detecting protein-protein association is to search a drug as an intermediary for protein-drug-protein association to calculate the association matrix . With availability of protein-disease association, we can of course instantly evaluate protein-disease-protein relation to get protein-protein association. This resulted a matrix .
The disease-disease association
You can see that this kind of association matches one disease to another. What we have done is to extract disease-drug-disease relation by checking drug-disease association. Once 2 diseases are associated with the same drug, they are marked as associated in the matrix . Next each of disease-protein disease link in described disease-protein association is the base for clarifying the disease-disease association in its appropriate matrix . This aforementioned act of associating operations with intermediaries allowed us to yield 6 association matrices, as indicated in Step 2 of Figure 2.
New three meta-paths
Meta-path
In a heterogeneous network, a meta-path X is defined as a path on a schema representing a sequence of node types connected by specific edge types:
where and
A common point of view is that a meta-path for drug disease association will start by a drug and end by a disease ( = Drug and = Disease). In the previous study, Wu et al 18 showed 5 meta-paths effective for estimating drug-disease associations. In this study, we propose new 3 meta-paths to predict potential drugs for diseases. The meta-path design can reasonably maintain the most logical solution designed currently practical. It contains some definite estimations, each of which out-turns association. The first design that a meta-path should cover DD, DS, and SS by DD ∙ DS ∙ SS. This path takes 2 options of drug-drug association DD which are DD_S, DD_P, and 2 options of disease-disease association SS that are SS_D, SS_P. By having combinations of the 2 options the first meta-path contains 4 sub-meta-paths:
| (1) |
| (2) |
| (3) |
| (4) |
When studying associations of and we can look at a meta-path that covers the associations by having particular drug-drug association and protein-protein association The and associations have alternative options including and Then, the whole 4 sub-paths for this meta-paths can be described as follows:
| (5) |
| (6) |
| (7) |
| (8) |
If we look at 3 associations of drug-drug protein-protein and disease-disease , the associations of drug-protein and protein-disease insists on preserving completely different paths for drug-disease association. For all possible combinations of options of and the meta-path of has 8 sub-paths:
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
So, in general, for producing drug-disease association each new meta-path has its sub-paths.
Feature extraction
As defined by Wu et al, 18 the element of the transition matrix represents the number of paths from the drug to the disease according to the corresponding meta-path. It seems like an act of getting row in the transition matrix to build features for drug . Similarly, column can be used to build features for disease . In this form of programing, the mentioned above features of drug-disease association are grouped together to represent features of the association. Here, the number of drugs is and the number of diseases is , then the number of features representing the drug-disease interaction will be . In Figure 3, we mark for the feature matrices provided by each combination of sub-paths of 3 meta paths.
Figure 3.
Extract features with singular value decomposition, then predict drug-disease.
However, as we know, the number of known drug disease pairs is extremely small, compared with the total number of drug-disease pairs. Therefore, this considerably affects the construction of an effective machine learning model. It is, of course, possible to apply the singular value decomposition (SVD) to extract some small features in our work. Some studies have also expressed that in the task of dimensionality downgrading using SVD in the prediction problem on a heterogeneous biological network, useful data will not be altered, but redundant information will be taken out. 20 Note, as an interesting contribution, that the proposed 3 meta-paths with their 128 subpaths reflect many aspects integrated in the heterogeneous network, thereby revealing many relationships between drug disease treatment. Then, the base classifiers of each metapath were constructed to predict the relationship between drug-disease treatment. Finally, we integrated these base classifiers together to create an ensemble classifier as shown in Figure 3. The classifier used in our method is the ensemble classifier with a voting strategy for selecting the best one.
Prediction of drug-disease associations
It would be necessary to apply an ensemble classifier for improving performance. Suppose is a feature vector of a drug-disease pair with an unknown label, and is the prediction probability of each base classifier. Then, the final prediction result of the ensemble model is the average value of .
| (17) |
In summary, as data were collected from different biological databases, we integrate them to form a mixed drug protein-disease bio-network. We explained how 128 subpaths of three new meta-paths enriched associations for the heterogeneous network. This noticeably aids the process of constructing feature vector data that represent the relationship between drug and disease in the network.
Experiments
The study for evaluating the prediction of new drug disease interactions by considering available interaction between drugs, proteins and diseases. The description of data and parameters used in our experiments will be outlined and discussion of learning results will be followed in this section.
Data
Our study on searching drugs for diseases requires reliable and accurate data of drug-disease, drug-protein and disease-protein. The resources of the data are available from OMIM, 21 Gottlieb’s data set, 22 DrugBank. 23 and selected by Wu et al 18 as shown in Table 2. Actually, the data was provided by the sources with a big variation of formats and data types due to different data sources. In the OMIM, 21 by checking 449 diseases and 1147 proteins, 1365 disease-protein interactions were reported. At the same time, Gottlieb’s data set provided 1827 drug disease interactions addressing 302 diseases and 551 drugs. By the DrugBank, 23 4642 drug-protein interactions were gathered from 1186 drugs and 1147 proteins. The first significant notice is the heterogeneity of the dataset, collected from different sources. Second, for studying the relation between a drug and a disease, it is to check whether the route lies within the network of the diseases, proteins and drugs that connect a particular drug and a specific disease. Since the network consists of edges that were constructed from mentioned above different sources, the network is surely heterogeneous.
Table 2.
Data in experiments. 18
| Object | Number | Interaction | Number | Ratio |
|---|---|---|---|---|
| Drug | 1186 | Drug-protein | 4642 | 1:293 |
| Protein | 1467 | Protein-disease | 1365 | 1:377 |
| Disease | 449 | Disease-protein | 1827 | 1:291 |
Parameters
In the algorithm 1 for meta-path 1, the drug parameter has 2 parameters for calculating drug-drug association , we marked m1d0 and for the case of running sub-paths of the meta-path with , and accordingly. Considering the disease parameter , the notes of and serves the sub-paths of the first meta-path with , and appropriately. By the same way, the second meta-path and the third path contains parameters. There are options, which are combinations of input parameters for metapath 1, options for in meta-path 2 and options for in meta-path 3 according to the described method in Section 3. Thus, there are learning options in total. In training for each learning option, the 3 meta paths have been performed and then an ensemble method was conducted from the paths to get ensemble learning.
To enable cross validation, the data of drug-disease interaction in each learning option were split randomly 5 times, providing a training set and a test set each time. Several metrics that include ACC, PRE, REC, MCC, F1 (A1-A5) were implemented in the cross validation to evaluate performance of learning. The Area Under Precision-Recall Curve (AUPR) and Area Under Receiver Operating Characteristic Curve (AUC) were used in our tests.
Discussion
We may illustrate the selected parameters corresponding to the possible value of accuracy. The map in Figure 4 explores the correspondence by using vertical axis for parameters of path 1 and path 2, while horizontal axis is covered by parameters of path 3. In particular, the accuracy which is higher than 0.9 has been seen in several places of the map. To report the best results of implementing 3 paths by 28 options, Table 3 uses a particular note for an option consisting of parameters. At the path 1, the note of m1(ds) is to show parameter of drug (d) for accuracy varying from 0.906 to 0.908. Actually, there is only 1 note of for path 1 that requires updating the prior of drug by drug-protein interactions and the prior of disease by disease-protein interactions. However, the third path needs the prior of disease update by disease-drug interactions as the number of 0 can be seen at the end of all notes in the third column and disease and where can be 0 or 1. So that, the note of in the case means . Table 3 shows 7 the best options for accuracy varying from 0.906 to 0.908. Actually, there is only 1 note of for path 1 that requires updating the prior of drug by drug-protein interactions and the prior of disease by disease-protein interactions. However, the third path needs the prior of disease update by disease-drug interactions as the number of 0 can be seen at the end of all notes in the third column.
Figure 4.
Accuracy by ensemble path given parameters of each meta-path.
Table 3.
The best results of ensemble path by parameters of 3 meta-path.
| m1(ds) | m2(ds) | m3(ds) | AUPR | AUC | PRE | REC | ACC | MCC | F1 |
|---|---|---|---|---|---|---|---|---|---|
| 1-1 | 1-1-0 | 0-0-0 | 0.968 | 0.963 | 0.895 | 0.922 | 0.908 | 0.816 | 0.908 |
| 1-1 | 1-1-1 | 0-0-0 | 0.968 | 0.963 | 0.895 | 0.922 | 0.908 | 0.816 | 0.908 |
| 1-1 | 1-0-0 | 0-1-0 | 0.968 | 0.963 | 0.903 | 0.914 | 0.907 | 0.815 | 0.909 |
| 1-1 | 1-0-1 | 0-1-0 | 0.968 | 0.963 | 0.903 | 0.914 | 0.907 | 0.815 | 0.909 |
| 1-1 | 0-1-0 | 1-0-0 | 0.966 | 0.960 | 0.906 | 0.910 | 0.906 | 0.813 | 0.908 |
| 1-1 | 0-1-1 | 1-0-0 | 0.966 | 0.960 | 0.906 | 0.910 | 0.906 | 0.813 | 0.908 |
| 1-1 | 1-1-0 | 0-1-0 | 0.967 | 0.963 | 0.897 | 0.915 | 0.906 | 0.811 | 0.906 |
| 1-1 | 1-1-1 | 0-1-0 | 0.967 | 0.963 | 0.897 | 0.915 | 0.906 | 0.811 | 0.906 |
Furthermore, the available results of related works are summarized in a comparative report. By incorporating drug chemistry information and gene ontology annotation information, Liang et al 24 proposed the Laplacian regularized sparse subspace learning (LRSSL) approach for predicting drug-disease interactions.24 Luo et al 25 used the Bi-Random walk algorithm (MBiRW)25 with analysis of medications and disorders for evaluating new drug-disease interactions. In applying meta-paths with ensemble learning methods, Kawichai et al 26 associated drugs and diseases by Gene ontology terms.
To estimate drug-disease interactions, a linear neighborhood similarity 27 and a network topological similarity 10 were introduced by Zhang et al. It is then possible to implement a similarity constrained matrix factorization method (SCMFDD) analyzing drug features, and disease semantics and information of drug-disease associations. 20 After representing similarities and interactions between diseases, medications, and therapeutic targets, a three-layer heterogeneous network model (TL-HGBI) was proposed by Wang et al 28 like a computational framework. Tho Dang et al 29 implemented the EMP-SVD 18 in other new 5 meta-paths and that improved some performance metrics.
As SVD was proposed to extract some small features, it’s essential to show the effect of the SVD by small experiment where SVD was not used in our method and all features were used for training. The scores of the experiment can be seen in Table 4 with ACC = 0.848, which is lower than the case with SVD. The method has its major three meta paths. For instance, the method with 1 meta path consists of 1 time running EMP-SVD proposed by Wu et al. 18 The method designed with 2 meta paths consists of first run of the EMP-SVD and then run different combination , , , , as presented in Section 3.3. The best score of the experiment of the method with 2 meta paths is also included in Table 4. Actually, the score is not as good as the 1 for 3 meta paths.
Table 4.
Performance of related methods.
| Methods | AUPR | AUC | PRE | REC | ACC | MCC | F1 |
|---|---|---|---|---|---|---|---|
| EMP-SVD 18 | 0.956 | 0.951 | 0.913 | 0.854 | 0.876 | 0.755 | 0.882 |
| LRSSL 24 | 0.881 | 0.861 | 0.864 | 0.732 | 0.770 | 0.553 | 0.790 |
| MBiRW 25 | 0.952 | 0.942 | 0.867 | 0.901 | 0.884 | 0.769 | 0.884 |
| MPG-DDA 26 | 0.944 | 0.930 | 0.886 | 0.842 | 0.867 | NA | 0.863 |
| PREDICT 30 | 0.908 | 0.895 | 0.809 | 0.850 | 0.830 | 0.662 | 0.828 |
| SCMFDD 20 | 0.836 | 0.854 | 0.926 | 0.713 | 0.774 | 0.575 | 0.805 |
| TL-HGBI 28 | 0.852 | 0.846 | 0.829 | 0.750 | 0.774 | 0.552 | 0.787 |
| Five Paths 29 | 0.962 | 0.956 | 0.882 | 0.901 | 0.889 | 0.780 | 0.889 |
| Our method with 3 paths no SVD | 0.923 | 0.920 | 0.867 | 0.838 | 0.848 | 0.696 | 0.852 |
| Our method with 2 paths | 0.845 | 0.833 | 0.822 | 0.731 | 0.756 | 0.518 | 0.773 |
| Our method | 0.968 | 0.963 | 0.895 | 0.922 | 0.908 | 0.816 | 0.908 |
The best scores are printed in bold.
In this study, we proposed to analyze the drug-disease associations by presenting drug-disease associations through three novel meta-paths. Through experiments, it has also been proven that this is a new point and main contribution of the article, demonstrating the role of these three new meta-paths. However, a limitation of the article is that it has not been scientifically explained using biomedical bases to see the practical significance. If it can be done, it will be a groundbreaking contribution. This is really very difficult, and currently research is mainly doing what we do, which is to prove it through experiments and measurements for evaluation.
Case Studies
When transferring drug-disease associations from known associations to new associations, new drug-disease associations can be checked with literature for confirmation or disapproval reports. We used the label transfer method with 3 paths for searching for a new association of drug- disease from the dataset covering drug-disease, disease-protein and drug-protein association. A number of new associations of drug-disease are found while they were both unassociated in the initial dataset and unassociated by the original 5 paths methods.
For each new found drug-disease association we search available publications of the drug and its uses in treatment of the disease. Many drug-disease associations are created by the label transferring method but no report of the association cannot be found. Although it is hard to derive publication for new associations, we can instead obtain confirmation for some drug-disease associations. Thus, by raising association of the drug of fludrocortisone and the disease of hypertension from label transfering, we have found a paper of Veazie et al 31 on this association. The disease of orthostatic hypotension is an overstated drop in blood pressure while standing. This is the effect of a diminish in cardiac output or defective or insufficient vasoconstrictor mechanisms. The drug fludrocortisone is a mineralocorticoid that expands blood volume and blood pressure. Fludrocortisone is regarded as the first- or second-line pharmacological therapy for disease of orthostatic hypotension alongside mechanical and positional methods.
For instance, a new association of the oseltamivir drug and the encephalopathy disease is created by our label transfer method. Encephalopathy is described for any disease of the brain that changes brain structure or function. In the market, oseltamivir is sold under the brand name Tamiflu and it is an antiviral drug. A common way of using oseltamivir is to prevent and to treat influenza A and influenza B, viruses which cause the flu. In what follows, a case of treatment with oseltamivir for encephalopathy was reported in detail by Yen et al. 32 Here, flu-like symptoms and progressive encephalopathy were observed for a 25-year old female patient. With assistance of nasopharyngeal swab Polymerase Chain Reaction Influenza B was detected. The patient was treated with oseltamivir and patient’s mental status retaken within days.
Conclusions
We presented a new method for enhancing performance of drug-disease interaction prediction and applied it to the analysis of biomedical heterogeneous data. The method includes 3 paths designed for training a dataset of interactions between 3 objects: drug, protein and disease. The contribution of this paper is to present only 3 meta-paths with a full 27 options which allows us to update the prior of mentioned above objects by their related interactions with neighbor objects. In experiments, all the learning options were tested with cross validation permitting us to see which options can improve accuracy. As a result the method succeeded in enhancement for most of all performance metrics, including accuracy and F1-measure. The integration of the use of prior update, the use wherever applicable for heterogeneous biomedical heterogeneous data, and the way to make training flexible, yields an computational framework effective for data collected from different sources.
Acknowledgments
We acknowledge support from the Vietnam Ministry of Education and Training, Hanoi National University of Education, Electric Power University, and Academy of Policy and Development.
Appendix
Consider a test that provides , and which are the number of true positive samples, true negative samples, false positive samples and false negative samples, correspondingly.33-36 A number of classification metrics can be been estimated to enable the performance evaluation:
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
Footnotes
Credit Authorship Contribution Statement: Nam Anh Dao: Conceptualization of this study, Software. Manh Hung Le: Data curation, Writing - Related woks. Xuan Tho Dang: Data curation, Methodology. Xuan Tho Dang et al.: Preprint submitted to Evolutionary Bioinformatics.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was funded by the Vietnam Ministry of Education and Training, project B2022-SPH-04.
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
ORCID iDs: Nam Anh Dao  https://orcid.org/0000-0002-0536-8686
https://orcid.org/0000-0002-0536-8686
Xuan Tho Dang  https://orcid.org/0000-0002-7654-5942
https://orcid.org/0000-0002-7654-5942
References
- 1. Adams CP, Brantner VV. Estimating the cost of new drug development: is it really 802 million dollars? Health Aff. 2006;25:420-428. [DOI] [PubMed] [Google Scholar]
- 2. Ashburn TT, Thor KB. Drug repositioning: identifying and developing new uses for existing drugs. Nat Rev Drug Discov. 2004;3:673-683. [DOI] [PubMed] [Google Scholar]
- 3. Olayan RS, Ashoor H, Bajic VB. DDR: efficient computational method to predict drug–target interactions using graph mining and machine learning approaches. Bioinformatics. 2018;34:3779-3779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Zhang X, Li L, Ng MK, Zhang S. Drug-target interaction prediction by integrating multiview network data. Comput Biol Chem. 2017;69:185-193. [DOI] [PubMed] [Google Scholar]
- 5. Shi JY, Yiu SM, Li Y, Leung HC, Chin FY. Predicting drug-target interaction for new drugs using enhanced similarity measures and super-target clustering. Methods. 2015;83:98-104. [DOI] [PubMed] [Google Scholar]
- 6. He Z, Zhang J, Shi XH, et al. Predicting drug-target interaction networks based on functional groups and biological features. PLoS One. 2010;5:1-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Takarabe M, Kotera M, Nishimura Y, Goto S, Yamanishi Y. Drug target prediction using adverse event report systems: a pharmacogenomic approach. Oxford Academic. 2012;28:i611-i618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Zhang R. An ensemble learning approach for improving drug target interactions prediction. Proceedings of the 4th International Conference on Computer Engineering and Networks. 2004:433-442. [Google Scholar]
- 9. Song F, Tan S, Dou Z, Liu X, Ma X. Predicting combinations of drugs by exploiting graph embedding of heterogeneous networks. BMC Bioinformatics. 2022;23:34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Zhao BW, You ZH, Wong L, et al. MGRL: predicting drug-disease associations based on multi-graph representation learning. Front Genet. 2021;12:515:1-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Öztürk H, Özgür A, Ozkirimli E. DeepDTA: deep drug-target binding affinity prediction. Bioinformatics. 2018;34:i821-i829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. You J, McLeod RD, Hu P. Predicting drug-target interaction network using deep learning model. Comput Biol Chem. 2019;80:90-101. [DOI] [PubMed] [Google Scholar]
- 13. Zhao BW, Su XR, Hu PW, et al. A geometric deep learning framework for drug repositioning over heterogeneous information networks. Brief Bioinform. 2022;23:384. [DOI] [PubMed] [Google Scholar]
- 14. Agarwal S, Dugar D, Sengupta S. Ranking chemical structures for drug discovery: a new machine learning approach. J Chem Inf Model. 2010;50:716-731. [DOI] [PubMed] [Google Scholar]
- 15. Geerts H, Guillaumat PO, Grantham C, et al. Brain levels and acetylcholinesterase inhibition with galantamine and donepezil in rats, mice, and rabbits. Brain Res. 2005;1033:186-193. [DOI] [PubMed] [Google Scholar]
- 16. Xuan P, Zhao L, Zhang T, Ye Y, Zhang Y. Inferring drug-related diseases based on convolutional neural network and gated recurrent unit. Molecules. 2019;24:2712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Ding Y, Tang J, Guo F. Identification of drug-target interactions via multiple information integration. Inf Sci. 2017;418-419:546-560. [Google Scholar]
- 18. Wu G, Liu J, Yue X. Prediction of drug-disease associations based on ensemble meta paths and singular value decomposition. BMC Bioinformatics. 2019;20:134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Shi H, Liu S, Chen J, et al. Predicting drug-target interactions using lasso with random forest based on evolutionary information and chemical structure. Genomics. 2019;111:1839-1852. [DOI] [PubMed] [Google Scholar]
- 20. Zhang W, Yue X, Lin W, et al. Predicting drug-disease associations by using similarity constrained matrix factorization. BMC Bioinformatics. 2018;19:233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. O’Boyle NM, Banck M, James CA, et al. Open Babel: an open chemical toolbox. J Cheminform. 2011;3:33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Smith TF, Waterman MS, Burks C. The statistical distribution of nucleic acid similarities. Nucleic Acids Res. 1985;13:645-656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Weininger D. Smiles. A chemical language and information system. 1. Introduction to methodology and encoding rules. J Chem Inf Comput Sci. 1988;28:31-36. [Google Scholar]
- 24. Liang X, Zhang P, Yan L, et al. Lrssl: predict and interpret drug-disease associations based on data integration using sparse subspace learning. Bioinformatics. 2017;33:1187-1196. [DOI] [PubMed] [Google Scholar]
- 25. Luo H, Wang J, Li M, et al. Drug repositioning based on comprehensive similarity measures and bi-random walk algorithm. Bioinformatics. 2016;32:2664-2671. [DOI] [PubMed] [Google Scholar]
- 26. Kawichai T, Suratanee A, Plaimas K. Meta-path based gene ontology profiles for predicting drug-disease associations. IEEE Access. 2021;9:41809-41820. [Google Scholar]
- 27. Zhang W, Yue X, Liu F, et al. A unified frame of predicting side effects of drugs by using linear neighborhood similarity. BMC Syst Biol. 2017;11:101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Wang W, Yang S, Zhang X, Li J. Drug repositioning by integrating target information through a heterogeneous network model. Bioinformatics. 2014;30:2923-2930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Tho Dang X, Hung Le M., Anh Dao N. Drug repositioning for drug disease association in meta-paths. In: Phuong NH, Kreinovich V, eds. Deep Learning and Other Soft Computing Techniques: Biomedical and Related Applications. Springer Nature; 2023:39-51. [Google Scholar]
- 30. Zeng X, Zhu S, Liu X, et al. deepDR: a network-based deep learning approach to in silico drug repositioning. Bioinformatics. 2019;35:5191-5198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Veazie S, Peterson K, Ansari Y, et al. Fludrocortisone for orthostatic hypotension. Cochrane Database Syst Rev. 2021;5:CD012868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Yen J, Al Moamen A, Margolesky J. Influenza B-associated encephalitis with rapid improvement with oseltamivir. Neurol Sci. 2021;42:745-747. [DOI] [PubMed] [Google Scholar]
- 33. Anh DN, Hung BD, Huy PQ, Tho DX. Feature analysis for imbalanced learning. J Adv Comput Intell Intell Inform. 2020;24(5):648-655. [Google Scholar]
- 34. Dang XT, Hirose O, Saethang T, et al. A novel over-sampling method and its application to miRNA prediction. J of Biomed Sci Eng. 2013;6(02):236-248. [Google Scholar]
- 35. Hung BD, Anh DN, Tho DX. Relabeling with mask-S for imbalanced class distribution. In: Frontiers in Intelligent Computing: Theory and Applications: Proceedings of the 7th International Conference on FICTA (2018). Vol. 1. Singapore: Springer, 2020:31-41. [Google Scholar]
- 36. Dang XT, Bui DH, Nguyen TH, Nguyen TQV, Tran DH. Prediction of autism-related genes using a new clustering-based under-sampling method. In 2019 11th International Conference on Knowledge and Systems Engineering (KSE), October 2019, pp. 1-6. IEEE. [Google Scholar]