Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps

Abstract

We provide a framework for structural multiscale geometric organization of graphs and subsets of 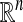. We use diffusion semigroups to generate multiscale geometries in order to organize and represent complex structures. We show that appropriately selected eigenfunctions or scaling functions of Markov matrices, which describe local transitions, lead to macroscopic descriptions at different scales. The process of iterating or diffusing the Markov matrix is seen as a generalization of some aspects of the Newtonian paradigm, in which local infinitesimal transitions of a system lead to global macroscopic descriptions by integration. We provide a unified view of ideas from data analysis, machine learning, and numerical analysis.

The geometric organization of graphs and data sets in 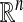is a central problem in statistical data analysis. In the continuous Euclidean setting, tools from harmonic analysis, such as Fourier decompositions, wavelets, and spectral analysis of pseudo-differential operators, have proven highly successful in many areas such as compression, denoising, and density estimation (1, 2). In this paper, we extend multiscale harmonic analysis to discrete graphs and subsets of 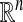. We use diffusion semigroups to define and generate multiscale geometries of complex structures. This framework generalizes some aspects of the Newtonian paradigm, in which local infinitesimal transitions of a system lead to global macroscopic descriptions by integration, the global functions being characterized by differential equations. We show that appropriately selected eigenfunctions of Markov matrices (describing local transitions, or affinities in the system) lead to macroscopic representations at different scales. In particular, the top eigenfunctions permit a low-dimensional geometric embedding of the set into 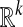, with k << n, so that the ordinary Euclidean distance in the embedding space measures intrinsic diffusion metrics on the data. Many of these ideas appear in a variety of contexts of data analysis, such as spectral graph theory, manifold learning, nonlinear principal components, and kernel methods. We augment these approaches by showing that the diffusion distance is a key intrinsic geometric quantity linking spectral theory of the Markov process, Laplace operators, or kernels, to the corresponding geometry and density of the data. This opens the door to the application of methods from numerical analysis and signal processing to the analysis of functions and transformations of the data.

Diffusion Maps

The problem of finding meaningful structures and geometric descriptions of a data set X is often tied to that of dimensionality reduction. Among the different techniques developed, particular attention has been paid to kernel methods (3). Their nonlinearity as well as their locality-preserving property are generally viewed as a major advantage over classical methods like principal component analysis and classical multidimensional scaling. Several other methods to achieve dimensional reduction have also emerged from the field of manifold learning, e.g., local linear embedding (4), Laplacian eigenmaps (5), Hessian eigenmaps (6), local tangent space alignment (7). All these techniques minimize a quadratic distortion measure of the desired coordinates on the data, naturally leading to the eigenfunctions of Laplace-type operators as minimizers. We extend the scope of application of these ideas to various tasks, such as regression of empirical functions, by adjusting the infinitesimal descriptions, and the description of the long-time asymptotics of stochastic dynamical systems.

The simplest way to introduce our approach is to consider a set X of normalized data points. Define the “quantized” correlation matrix C = {c_ij}, where c_ij = 1 if (x_i·x_j) > 0.95, and c_ij = 0 otherwise. We view this matrix as the adjacency matrix of a graph on which we define an appropriate Markov process to start our analysis. A more continuous kernel version can be defined as c_ij = e^{(1–(x_i·x_j)/ε)} = e^{–(∥x_i–x_j∥2/2ε)}. The remarkable fact is that the eigenvectors of this “corrected correlation” can be much more meaningful in the analysis of data than the usual principal components as they relate to diffusion and inference on the data.

As an illustration of the geometric approach, suppose that the data points are uniformly distributed on a manifold X. Then it is known from spectral graph theory (8) that if W = {w_ij} is any symmetric positive semi-definite matrix, with nonnegative entries, then the minimization of

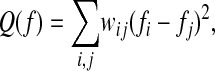where f is a function on the data set X with the additional constraint of unit norm, is equivalent to finding the eigenvectors of D^–1/2WD^1/2, where D = {d_ij} is a diagonal matrix with diagonal entry d_ii equal to the sum of the elements of W along the ith row. Belkin et al. (5) suggest the choice w_ij = e^{–(∥x_i – x_j∥2/ε)}, in which case the distortion Q clearly penalizes pairs of points that are very close, forcing them to be mapped to very close values by f. Likewise, pairs of points that are far away from each other play no role in this minimization. The first few eigenfunctions {φ_k} are then used to map the data in a nonlinear way so that the closeness of points is preserved. We will provide a principled geometric approach for the selection of eigenfunction coordinates.

This general framework based upon diffusion processes leads to efficient multiscale analysis of data sets for which we have a Heisenberg localization principle relating localization in data to localization in spectrum. We also show that spectral properties can be employed to embed the data into a Euclidean space via a diffusion map. In this space, the data points are reorganized in such a way that the Euclidean distance corresponds to a diffusion metric. The case of submanifolds of 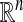is studied in greater detail, and we show how to define different kinds of diffusions to recover the intrinsic geometric structure, separating geometry from statistics. More details on the topics covered in this section can be found in ref. 9. We also propose an additional diffusion map based on a specific anisotropic kernel whose eigenfunctions capture the long-time asymptotics of data sampled from a stochastic dynamical system (10).

Construction of the Diffusion Map. From the above discussion, the data points can be thought of as being the nodes of a graph whose weight function k(x, y) (also referred to as “kernel” or “affinity function”) satisfies the following properties:

• k is symmetric: k(x, y) = k(y, x),

• k is positivity preserving: for all x and y in X, k(x, y) ≥ 0,

• k is positive semi-definite: for all real-valued bounded functions f defined on X,

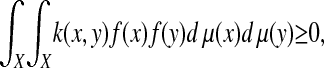where μ is a probability measure on X.

The construction of a diffusion process on the graph is a classical topic in spectral graph theory [weighted graph Laplacian normalization (8)], and the procedure consists in renormalizing the kernel k(x, y) as follows: for all x ε X,

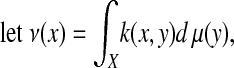and set

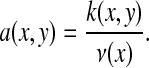Notice that we have the following conservation property:

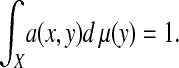[1]

Therefore, the quantity a(x, y) can be viewed as the probability for a random walker on X to make a step from x to y. Now we naturally define the diffusion operator

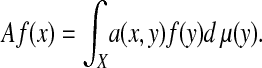As is well known in spectral graph theory (8), there is a spectral theory for this Markov chain, and if à is the integral operator defined on L²(X) with the kernel

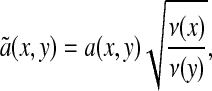[2]

then it can be verified that à is a symmetric operator. Consequently, we have the following spectral decomposition

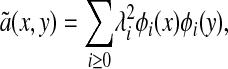[3]

where λ₀ = 1 ≥ λ₁ ≥ λ₂ ≥.... Let ã⁽m)(x, y) be the kernel of Ã^m. Then we have

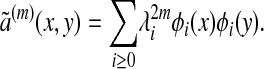[4]

Lastly, we introduce the family of diffusion maps {Φ_m} by

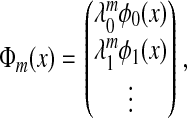and the family of diffusion distances {D_m} defined by

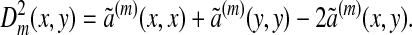The quantity a(x, y), which is related to ã(x, y) according to Eq. 2, can be interpreted as the transition probability of a diffusion process, while a^(m)(x, y) represents the probability of transition from x to y in m steps. To this diffusion process corresponds the distance D_m(x, y), which defines a metric on the data that measures the rate of connectivity of the points x and y by paths of length m in the data, and, in particular, it is small if there are a large number of paths connecting x and y. Note that, unlike the geodesic distance, this metric is robust to perturbations on the data.

The dual point of view is that of the analysis of functions defined on the data. The kernel ã^(m)(x, ·) can be viewed as a bump function centered at x that becomes wider as m increases. The distance D_2m(x, y) is also a distance between the two bumps ã^(m)(x, ·) and ã^(m)(y, ·):

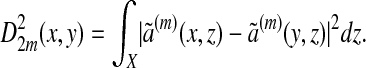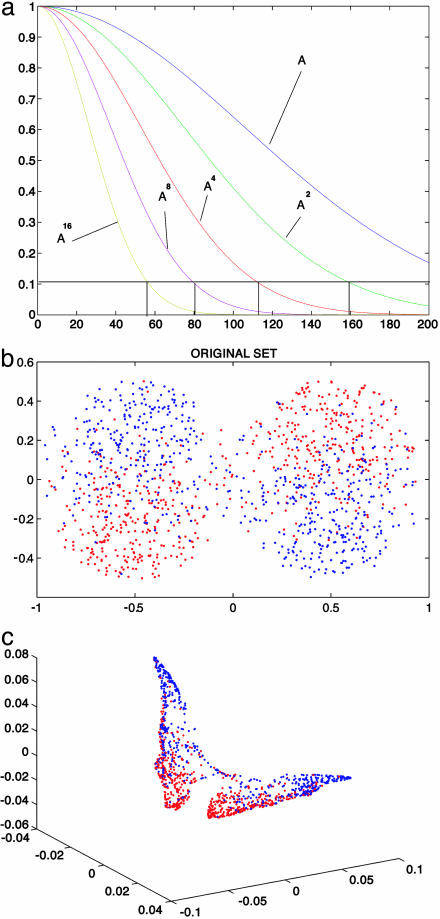
The eigenfunctions have the classical interpretation of an orthonormal basis, and their frequency content can be related to the spectrum of operator A in what constitutes a generalized Heisenberg principle. The key observation is that, for many practical examples, the numerical rank of the operator A^(m) decays rapidly as seen from Eq. 4 or from Fig. 1. More precisely, since 0 ≤ λ_i ≤ λ₀ = 1, the kernel ã^(m)(x, y), and therefore the distance D_m(x, y), can be computed to high accuracy with only a few terms in the sum of 4, that is to say, by only retaining the eigenfunctions φ_i for which 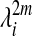exceeds a certain precision threshold. Therefore, the rows (the so-called bumps) of A^m span a space of lower numerical dimension, and the set of columns can be down-sampled. Furthermore, to generate this space, one just needs the top eigenfunctions, as prescribed in Eq. 4. Consequently, by a change of basis, eigenfunctions corresponding to eigenvalues at the beginning of the spectrum have low frequencies, and the number of oscillations increase as one moves further down in the spectrum.

Fig. 1.

The spectra of powers of A (a), and the diffusion embedding of a mixture of two materials with different heat conductivity (b and c). The original geometry (b) is mapped as a “butterfly” set, in which the red (higher conductivity) and blue phases are organized according to the diffusion they generate: the cord length between two points in the diffusion space measures the quantity of heat that can travel between these points.

The link between diffusion maps and distances can be summarized by the spectral identity

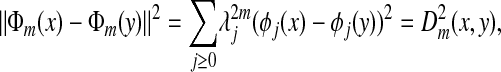which means that the diffusion map Φ_m embeds the data into a Euclidean space in which the Euclidean distance is equal to the diffusion distance D_m. Moreover, the diffusion distance can be accurately approximated by retaining only the terms for which 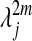remains numerically significant: the embedding

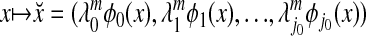satisfies

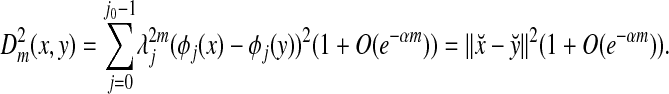Therefore, there exists an m₀ such that for all m ≥ m₀, the diffusion map with the first j₀ eigenfunctions embeds the data into 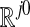in an approximately isometric fashion, with respect to the diffusion distance D_m.

The Heat Diffusion Map on Riemannian Submanifolds. Suppose that the data set X is approximately lying along a submanifold 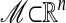, with a density p(x) (not necessarily uniform on ℳ). This kind of situation arises in many applications ranging from hyperspectral imagery to image processing to vision. For instance, in the latter field, a model for edges can be generated by considering pixel neighborhoods whose variability is governed by a few parameters (11, 12).

We consider isotropic kernels, i.e., kernels of the form

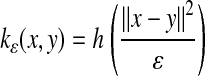In ref. 5, Belkin et al. suggest to take k_ε(x, y) = e^{–(∥x–y∥2/ε)} and to apply the weighted graph Laplacian normalization procedure described in the previous section. They show that if the density of points is uniform, then as ε → 0, one is able to approximate the Laplace–Beltrami operator Δ on ℳ.

However, when the density p is not uniform, as is often the case, the limit operator is conjugate to an elliptic Schrödinger-type operator having the more general form Δ + Q, where Q(x) = Δp(x)/p(x) is a potential term capturing the influence of the nonuniform density. By writing the nonuniform density in a Boltzmann form, p(x) = e^–U(x), the infinitesimal operator can be expressed as

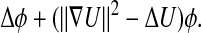[5]

This generator corresponds to the forward diffusion operator and is the adjoint of the infinitesimal generator of the backward operator, given by

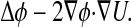[6]

As is well known from quantum physics, for a double well potential U, corresponding to two separated clusters, the first nontrivial eigenfunction of this operator discriminates between the two wells. This result reinforces the use of the standard graph Laplacian for computing an approximation to the normalized cut problem, as described in ref. 13 and more generally for the use of the first few eigenvectors for spectral clustering, as suggested by Weiss (14).

To capture the geometry of a given manifold, regardless of the density, we propose a different normalization that asymptotically recovers the eigenfunctions of the Laplace–Beltrami (heat) operator on the manifold. For any rotation-invariant kernel k_ε(x, y) = h(∥x – y∥²/ε), we consider the normalization described in the box below. The operator A_ε can be used to define a discrete approximate Laplace operator as

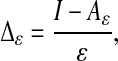and it can be verified that Δ_ε = Δ₀ + ε^1/2R_ε, where Δ₀ is a multiple of the Laplace–Beltrami operator Δ on ℳ, and R_ε is bounded on a fixed space of bandlimited functions. From this, we can deduce the following result.

Theorem 2.1. Let t > 0 be a fixed number, then as ε → 0, 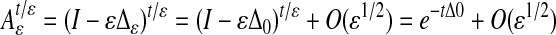and the kernel of 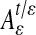is given as

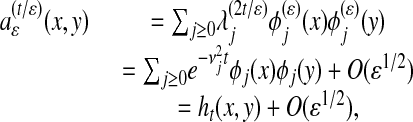where 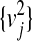and {φ_j} are the eigenvalues and eigenfunctions of the limiting Laplace operator, h_t(x, y) is the heat diffusion kernel at time t, and all estimates are relative to any fixed space of bandlimited functions.

Approximation of the Laplace–Beltrami Diffusion Kernel.

1. Let p_ε(x) = ∫_X k_ε(x, y)p(y)dy, and form the new kernel k̂_ε(x̆, y) = k_ε(x, y)/p_ε(x)p_ε(y).

2. Apply the weighted graph Laplacian normalization to this kernel by defining v_ε(x) =∫_Xk̂_ε(x, y)p(y)dy, and by setting a_ε(x, y) = k̂_ε(x, y)/v_ε(x).

Then the operator A_εf(x) = ∫_X a_ε(x, y)f(y)p(y)dy is an approximation of the Laplace–Beltrami diffusion kernel at time ε.

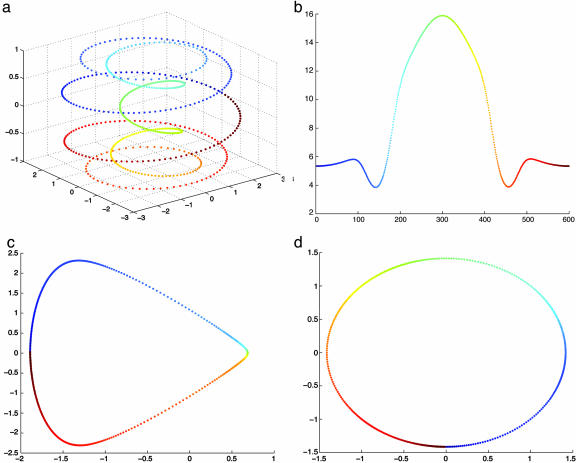
For simplicity, we assume that on the compact manifold ℳ, the data points are relatively densely sampled (each ball of radius 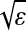contains enough sample points so that integrals can approximated by discrete sums). Moreover, if the data only covers a subdomain of ℳ with nonempty boundary, then Δ₀ needs to be interpreted as acting with Neumann boundary conditions. As in the previous section, one can compute heat diffusion distances and the corresponding embedding. Moreover, any closed rectifiable curve can be embedded as a circle on which the density of points is preserved: We have thus separated the geometry of the set from the distribution of the points (see Fig. 3 for an example).

Fig. 3.

Original spiral curve (a) and the density of points on it (b), embedding obtained from the normalized graph Laplacian (c), and embedding from the Laplace–Beltrami approximation (d).

Anisotropic Diffusion and Stochastic Differential Equations. So far we have considered the analysis of general data sets by diffusion maps, without considering the source of the data. One important case of interest is when the data x is sampled from a stochastic dynamical system. Consider, therefore, data sampled from a system 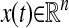whose time evolution is described by the following Langevin equation

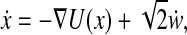[7]

where U is the free energy and w(t) is the standard n-dimensional Brownian motion. Let p(y, t ; x, s) denote the transition probability of finding the system at location y at time t, given an initial location x at time s. Then, in terms of the variables {y, t}, p satisfies the forward Fokker–Planck equation (FPE), for t > s,

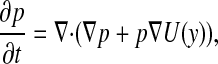[8]

whereas in terms of the variables {x, s}, the transition probability satisfies the backward equation

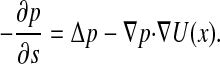[9]

As time t → ∞, the solution of the forward FPE converges to the steady-state Boltzmann density

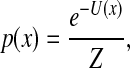[10]

where the partition function Z is the appropriate normalization constant.

The general solution to the FPE can be written in terms of an eigenfunction expansion

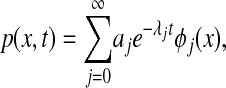[11]

where λ_j are the eigenvalues of the Fokker–Planck operator, with λ₀ = 1 > λ₁ ≥ λ₂ ≥..., and with φ_j(x) the corresponding eigenfunctions. The coefficients a_j depend on the initial conditions. A similar expansion exists for the backward equation, with the eigenfunctions of the backward operator given by ψ_j(x) = e^U(x)φ_j(x).

As can be seen from Eq. 11, the long time asymptotics of the solution is governed only by the first few eigenfunctions of the Fokker–Planck operator. Whereas in low dimensions, e.g., n ≤ 3, approximations to these eigenfunctions can be computed via numerical solutions of the partial differential equation, in general, this is infeasible in high dimensions. On the other hand, simulations of trajectories according to the Langevin Eq. 7 are easily performed. An interesting question, then, is whether it is possible to obtain approximations to these first few eigenfunctions from (large enough) data sampled from these trajectories.

In the previous section we saw that the infinitesimal generator of the normalized graph Laplacian construction corresponds to a Fokker–Planck operator with a potential 2U(x) (see Eq. 6). Therefore, in general, there is no direct connection between the eigenvalues and eigenfunctions of the normalized graph Laplacian and those of the underlying Fokker–Planck operator 8. However, it is possible to construct a different normalization that yields infinitesimal generators corresponding to the potential U(x) without the additional factor of two.

Consider the following anisotropic kernel.

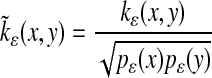[12]

A similar analysis to that of the previous section shows that the normalized graph Laplacian construction that corresponds to this kernel gives in the asymptotic limit the correct Fokker–Planck operator, e.g., with the potential U(x).

Since the Euclidean distance in the diffusion map space corresponds to diffusion distance in the feature space, the first few eigenvectors corresponding to the anisotropic kernel (Eq. 12) capture the long-time asymptotic behavior of the stochastic system (Eq. 7). Therefore, the diffusion map can be seen as an empirical method for homogenization (see ref. 10 for more details). These variables are the right observables with which to implement the equation-free complex/multiscale computations of Kevrekidis et al. (see refs. 15 and 16).

One-Parameter Family of Diffusion Maps. In the previous sections, we showed three different constructions of Markov chains on a discrete data set that asymptotically recover either the Laplace–Beltrami operator on the manifold, the backward Fokker–Planck operator with potential 2U(x) for the normalized graph Laplacian, or U(x)for the anisotropic diffusion kernel.

In fact, these three normalizations can be seen as specific cases of a one-parameter family of different diffusion maps, based on the kernel

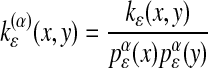[13]

for some α > 0.

It can be shown (9) that the forward infinitesimal operator generated by this diffusion is

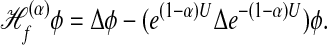[14]

One can easily see that the interesting cases are (i) α = 0, corresponding to the classical normalized graph Laplacian; (ii) α = 1, yielding the Laplace–Beltrami operator; and (iii) α = 1/2 yielding the backward Fokker–Planck operator.

Therefore, while the graph Laplacian based on a kernel with α = 1 captures the geometry of the data, with the density e^–U playing absolutely no role, the other normalizations take into account also the density of the points on the manifold.

Directed Diffusion and Learning by Diffusion

It follows from the previous section that the embedding that one obtains depends heavily on the choice of a diffusion kernel. In some cases, one is interested in constructing diffusion kernels that are data- or task-driven. As an example, consider an empirical function F(x) on the data. We would like to find a coordinate system in which the first coordinate has the same level lines as the empirical function F. For that purpose, we replace the Euclidean distance in the Gaussian kernel by the anisotropic distance.

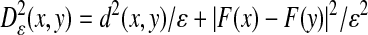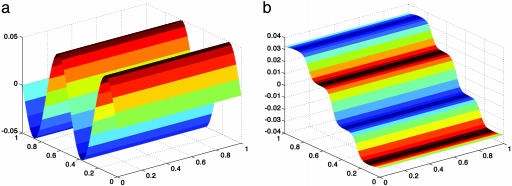
The corresponding limit of 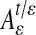is a diffusion along the level surfaces of F from which it follows that the first nonconstant eigenfunction of A_ε has to be constant on level surfaces. This is illustrated in Fig. 4, where the graph represents the function F and the colors correspond to the values of the first nontrivial eigenfunction. In particular, observe that the level lines of this eigenfunction are the integral curves of the field orthogonal to the gradient of F. This is clear since we forced the diffusion to follow this field at a much faster rate, in effect integrating that field. It also follows that any differential equation can be integrated numerically by a nonisotropic diffusion in which the direction of propagation is faster along the field specified by the equation.

Fig. 4.

The original function f on the unit square (a), and the first nontrivial eigenfunction (b). On this plot, the colors corresponds to the values of f.

We now apply this approach to the construction of empirical models for statistical learning. Assume that a data set has been generated by a process whose local statistical properties vary from location to location. Around each point x, we view all neighboring data points as having been generated by a local diffusion whose probability density is estimated by p_x(y) = c_xexp(–q_x(x – y)), where q_x is a quadratic form obtained empirically by PCA from the data in a small neighborhood of x. We then use the kernel a(x, z) = ∫ p_x(y)p_z(y)dy to model the diffusion. Note that the distance defined by this kernel is (∫;p_x(y) – p_z(y);²dy)^1/2, which can be viewed as the natural distance on the “statistical tangent space” at every point in the data. If labels are available, the information about the labels can be incorporated by, for example, locally warping the metric so that the diffusion starting in one class stays in the class without leaking to other classes. This could be obtained by using local discriminant analysis (e.g., linear, quadratic, or Fisher discriminant analysis) to build a local metric whose fast directions are parallel to the boundary between classes and whose slow directions are transversal to the classes (see, e.g., ref. 1).

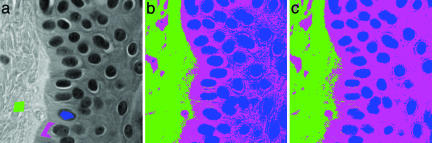
In data classification, geometric diffusion provides a powerful tool to identify arbitrarily shaped clusters with partially labelled data. Suppose, for example, we are given a data set X with N points from C different classes. Assume our task is to learn a function L: X → {1,..., C} for every point in X but we are given the labels of only s << N points in X. If we cannot infer the geometry of the data from the label points only, many parametric methods (e.g., Gaussian classifiers) and nonparametric techniques (e.g., nearest neighbors) lead to poor results. In Fig. 5, we illustrate this with an example. Here, we have a hyperspectral image of pathology tissue. Each pixel (x, y) in the image is associated with a vector {I(x, y)}_λ that reflects the material's spectral characteristics at different wavelengths λ. We are given a partially labelled set for three different tissue classes (marked with blue, green, and pink in Fig. 5a) and are asked to classify all pixels in the image using only spectral, as opposed to spatial, information. Both Gaussian classifiers and nearest-neighbor classifiers (see Fig. 5b) perform poorly in this case as there is a gradual change in both shading and chemical composition in the vertical direction of the tissue sample.

Fig. 5.

Pathology slice with partially labeled data (a), tissue classification from spectra by using 1-nearest neighbors (b), and tissue classification from spectra by using geometric diffusion (c). The three tissue classes are marked with blue, green, and pink.

The diffusion framework, however, provides an alternative classification scheme that links points together by a Markov random walk (see ref. 17 for a discussion): let χ_i be the ℒ¹-normalized characteristic function of the initially labelled set from class i. At a given time t, we can interpret the diffused label functions (A^tχ_i)_i as the posterior probabilities of the points belonging to class i. Choose a time τ when the margin between the classes is maximized, and then define the label of a point x ε X as the maximum a posteriori estimate L(x; τ) = argmax_iA^τχ_i. Fig. 5c shows the classification of the pathology sample using the above scheme. The latter result agrees significantly better with a specialist's view of correct tissue classification.

In many practical situations, the user may want to refine the classification of points that occur near the boundaries between classes in state space. One option is to use an iterative scheme, where the user provides new labelled data where needed and then restarts the diffusion with the new enlarged training set. However, if the total data set X is very large, an alternative, more efficient, scheme is to define a modified kernel that incorporates both previous classification results and new information provided by the user: for example, assign to each point a score s_i(x) ε [0, 1] that reflects the probability that a point x belongs to class i. Then use these scores to warp the diffusion so that we have a set of class-specific diffusion kernels {Ã_i}_i that slow down diffusion between points with different label probabilities. Choose, for example, in each new iteration, weights according to k̃_i(x, y) = k(x, y)s_i(x)s_i(y), where s_i = A^τχ_i are the label posteriors from the previous diffusion, and renormalize the kernel to be a Markov matrix. If the user provides a series of consistent labelled examples, the classification will speed up in each new iteration and the diffusion will eventually occur only within disjoint sets of samples with the same labels.

Summary

In this article, we presented a general framework for structural multiscale geometric organization of graphs and subsets of 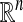. We introduced a family of diffusion maps that allow the exploration of both the geometry, the statistics and functions of the data. Diffusion maps provide a natural low-dimensional embedding of high-dimensional data that is suited for subsequent tasks such as visualization, clustering, and regression. In the companion article (18), we introduce multiscale methods that allow fast computation of functions of diffusion operators on the data and also present a scheme for extending empirical functions.

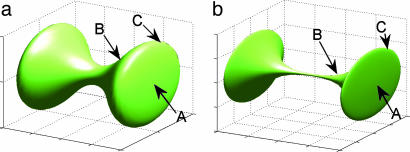
Fig. 2.

A dumbbell (a) is embedded by using the first three eigenfunctions (b). Because of the bottleneck, the two lobes are pushed away from each other. Observe also that in the embedding space, point A is closer to the handle (point B) than any point on the edge (like point C), because there are many more short paths joining A and B than A and C.