Abstract
The acidity constants for (N3)H of the uridine-type ligands (U) 5-fluorouridine, 5-chloro-2′-deoxyuridine, uridine, and thymidine (2′-deoxy-5-methyluridine) and the stability constants of the M(U–H)+ complexes for M2+ = Mg2+, Ca2+, Sr2+, Ba2+, Mn2+, Co2+, Ni2+, Cu2+, Zn2+, Cd2+, and Pb2+ were measured (potentiometric pH titrations; aqueous solution; 25°C; I = 0.1 M, NaNO3). Plots of 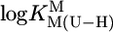 vs.
vs. 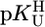 result in straight lines that are compared with previous plots for simple pyridine-type and o-amino(methyl)pyridine-type ligands as well as with the stabilities of the corresponding M(cytidine)2+ complexes. The results indicate monodentate coordination to (N3)– in M(U–H)+ for Co2+ and Ni2+. For the M(U–H)+ species of Cd2+, Zn2+, or Cu2+, increased stabilities imply that semichelates form, i.e., M2+ is (N3)–-bound and coordinated water molecules form hydrogen bonds to (C2)O and (C4)O; these “double” semichelates are in equilibrium with “single” semichelates involving either (C2)O or (C4)O and possibly also with four-membered chelates for which M2+ is innersphere-coordinated to (N3)– and a carbonyl oxygen. For the alkaline earth ions, semichelates dominate with the M2+ outersphere bound to (N3)– and innersphere to one of the carbonyl oxygens. Mn(U–H)+ is with its properties between those of Cd2+ (which probably also hold for Pb2+) and the alkaline earth ions. In nucleic acids, M2+–C(O) interactions are expected, if support is provided by other primary binding sites. (N3)H may possibly be acidified via carbonyl-coordinated M2+ to become a proton donor in the physiological pH range, at which direct (N3)– binding of M2+ also seems possible.
result in straight lines that are compared with previous plots for simple pyridine-type and o-amino(methyl)pyridine-type ligands as well as with the stabilities of the corresponding M(cytidine)2+ complexes. The results indicate monodentate coordination to (N3)– in M(U–H)+ for Co2+ and Ni2+. For the M(U–H)+ species of Cd2+, Zn2+, or Cu2+, increased stabilities imply that semichelates form, i.e., M2+ is (N3)–-bound and coordinated water molecules form hydrogen bonds to (C2)O and (C4)O; these “double” semichelates are in equilibrium with “single” semichelates involving either (C2)O or (C4)O and possibly also with four-membered chelates for which M2+ is innersphere-coordinated to (N3)– and a carbonyl oxygen. For the alkaline earth ions, semichelates dominate with the M2+ outersphere bound to (N3)– and innersphere to one of the carbonyl oxygens. Mn(U–H)+ is with its properties between those of Cd2+ (which probably also hold for Pb2+) and the alkaline earth ions. In nucleic acids, M2+–C(O) interactions are expected, if support is provided by other primary binding sites. (N3)H may possibly be acidified via carbonyl-coordinated M2+ to become a proton donor in the physiological pH range, at which direct (N3)– binding of M2+ also seems possible.
Keywords: chelate formation, equilibrium constants, metal ion complexes, nucleic acids, nucleobase properties
The importance of metal ion–nucleic acid interactions in the metabolic machinery is well recognized and applied, e.g., in medicinal chemistry (1). Crystal-structure analyses of nucleic acids (2), especially RNAs (3), show that metal ions coordinate to the phosphate-diester bridges as well as to nucleobase residues, and they are important for folding and catalysis of ribozymes (3–5).
The N7 sites of purine residues are exposed in the major groove of DNA (2) and accessible for metal ion binding (6). Maybe this is one reason why their metal ion-coordinating properties are relatively well studied (6–11) in contrast to those of pyrimidine-nucleobase residues (8–10). In fact, the stabilities and solution structures of cytidine (Cyd) complexes of biologically relevant metal ions were quantified only recently (12). Knowledge on uridine complexes is scarce: The carbonyl oxygens (C2)O and (C4)O of uracil residues in low (2, 13) and high (2, 3, 14, 15) molecular weight derivatives may interact in the solid state with metal ions, but in aqueous (aq) solution monodentate carbonyl-oxygen ligands bind only if correctly positioned by primary sites (16).
In a recent study (17) with Mg2+, Ca2+, Mn2+, Zn2+, and Cd2+ (M2+), we showed that (N3)-deprotonated uridine, i.e., (Urd–H)–, forms rather stable M(Urd–H)+ complexes. Until then no reliable stability constants were available (8–10), most likely because hydrolysis of M(aq)2+ was not considered properly (17); this criticism agrees with the judgement (8) “not recommended.”
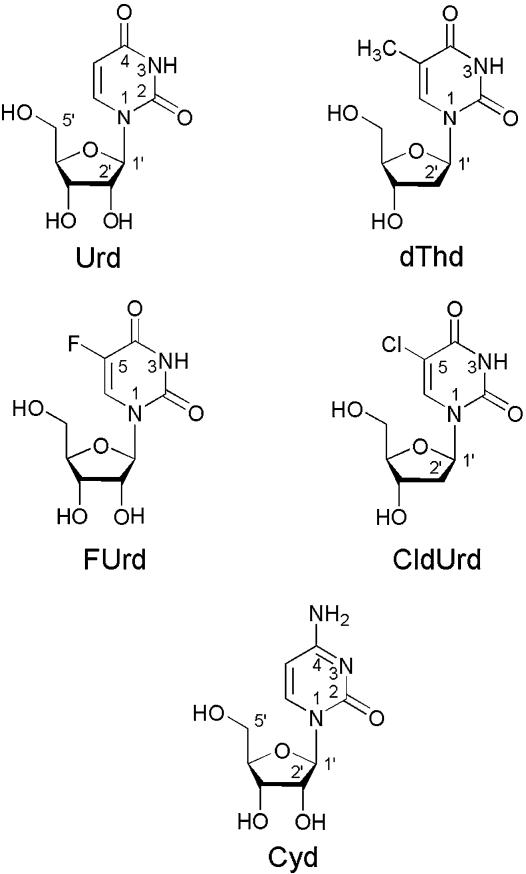
We confirmed our preliminary results (17) and measured the stabilities of M(Urd–H)+ with alkaline earth ions, Mn2+, Co2+, Ni2+, Cu2+, Zn2+, Cd2+, or Pb2+. To interpret the results unequivocally, we extended the study to thymidine (dThd), 5-fluorouridine (FUrd), and 5-chloro-2′-deoxyuridine (CldUrd) (U; Fig. 1) (2, 18). Plots of 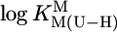 vs.
vs. 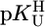 resulted in straight lines and led to the conclusion that in several complexes next to (N3)– also (C2)O/(C4)O participate in M2+ binding.
resulted in straight lines and led to the conclusion that in several complexes next to (N3)– also (C2)O/(C4)O participate in M2+ binding.
Fig. 1.
Chemical structures of Urd, dThd (2′-deoxy-5-methyluridine), FUrd, and CldUrd, as well as of Cyd in their dominating anti conformation (2, 18). For the anti–syn barrier, see ref. 12. The Urds are abbreviated as U and in the (N3)-deprotonated, anionic form as (U–H)– (U minus H); of course, the resulting negative charge at N3 can be delocalized in part to the neighboring carbonyl-oxygens.
Methods
Materials and Potentiometric pH Titrations. FUrd (99%) was from Acros Organics (Geel, Belgium) and Fluka. CldUrd (98%) and dThd (99%) were from Sigma–Aldrich. Urd, the nitrate salts of the metal ions, the buffers, and all other reagents were from previous sources (17).
The pH titrations were made with the equipment and evaluated as described (17). The acidity constants determined at I = 0.1 M (NaNO3) and 25°C are so-called practical, mixed, or Brønsted constants (19), which may be converted into concentration constants by subtracting 0.02 from the measured pKa values (19). The ionic product of water (Kw) does not enter into our calculations, because the difference in NaOH consumption between solutions with and without ligand are evaluated (19). The stability constants are, as usual, concentration constants.
Determination of Equilibrium Constants. The acidity constant 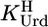 of Urd was determined as described (17). The acidity constants of FUrd and CldUrd (Eq. 2) were measured similarly by titrating 50 ml of aqueous 0.1 mM HNO3 under N2 with 0.8 ml of 0.06 M NaOH with and without 0.6 mM ligand. For FUrd additionally 30 ml of 0.04 mM HNO3 were titrated with 0.7 ml of 0.02 M NaOH with and without 0.3 mM FUrd. The individual results for
of Urd was determined as described (17). The acidity constants of FUrd and CldUrd (Eq. 2) were measured similarly by titrating 50 ml of aqueous 0.1 mM HNO3 under N2 with 0.8 ml of 0.06 M NaOH with and without 0.6 mM ligand. For FUrd additionally 30 ml of 0.04 mM HNO3 were titrated with 0.7 ml of 0.02 M NaOH with and without 0.3 mM FUrd. The individual results for 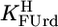 showed no difference between the various conditions and two samples. For the determination of
showed no difference between the various conditions and two samples. For the determination of 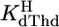 (20), 50 ml of aqueous 0.1 mM HNO3 were titrated under N2 with up to 3 ml of 0.1 M NaOH with and without 0.9 mM dThd. From the difference in NaOH consumption (17, 21) between such a pair of titrations,
(20), 50 ml of aqueous 0.1 mM HNO3 were titrated under N2 with up to 3 ml of 0.1 M NaOH with and without 0.9 mM dThd. From the difference in NaOH consumption (17, 21) between such a pair of titrations, 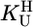 was calculated (
was calculated ( ) by a curve-fitting procedure using a Newton–Gauss nonlinear least-squares program; the final results are the averages of 18–36 independent pairs of titrations (25°C; I = 0.1 M, NaNO3).
) by a curve-fitting procedure using a Newton–Gauss nonlinear least-squares program; the final results are the averages of 18–36 independent pairs of titrations (25°C; I = 0.1 M, NaNO3).
The stability constants 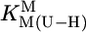 (Eq. 4) were determined under the conditions used for the acidity constants, but NaNO3 was partly or fully replaced by M(NO3)2 (see refs. 17 and 21). The latter was true for Mg2+, Ca2+, Sr2+, and Ba2+ because of the low stability of their complexes; thus, the M2+/ligand ratios were close to 37:1 for the M(dThd–H)+ and close to 56:1 for the other M(U–H)+ systems. For the other M2+, at least two different ratios were used. The stability constants, calculated as described (17, 21) [pH range: lower limit,
(Eq. 4) were determined under the conditions used for the acidity constants, but NaNO3 was partly or fully replaced by M(NO3)2 (see refs. 17 and 21). The latter was true for Mg2+, Ca2+, Sr2+, and Ba2+ because of the low stability of their complexes; thus, the M2+/ligand ratios were close to 37:1 for the M(dThd–H)+ and close to 56:1 for the other M(U–H)+ systems. For the other M2+, at least two different ratios were used. The stability constants, calculated as described (17, 21) [pH range: lower limit,  ; upper limit, neutralization degree of ≈85% or M(aq)2+ hydrolysis], showed no dependence on the excess of M2+ [i.e., no M2(U–H)3+ species, etc. form]; the final results are the average of at least four (typically six) independent pairs of titrations (25°C; I = 0.1 M, NaNO3).
; upper limit, neutralization degree of ≈85% or M(aq)2+ hydrolysis], showed no dependence on the excess of M2+ [i.e., no M2(U–H)3+ species, etc. form]; the final results are the average of at least four (typically six) independent pairs of titrations (25°C; I = 0.1 M, NaNO3).
Results and Discussion
Definition of the Considered Equilibria and Results. The self-association tendency of pyrimidine nucleosides is very small (22) and not of relevance. Similarly, because the ribose moiety of a nucleoside is deprotonated at one of its hydroxy groups only with pKa > 12.0 (23), for the deprotonation of Urd and its derivatives (U), which occurs at (N3)H, only the following equilibrium is relevant in the “neutral” pH range of 3–11:
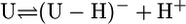 |
[1] |
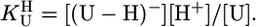 |
[2] |
Indeed, the potentiometric pH data could be fitted perfectly with Eq. 2. The result 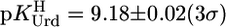 excellently agrees with previous data (see ref. 17). This is true also for dThd (20), which is more basic (
excellently agrees with previous data (see ref. 17). This is true also for dThd (20), which is more basic (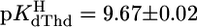 ) because of the methyl substituent and the deletion of the 2′-OH group (Fig. 1). Because, in general, 2′-deoxyribonucleosides are somewhat more basic than their ribonucleoside counterparts (11, 24), ΔpKa = 0.5 fits in the picture. The results
) because of the methyl substituent and the deletion of the 2′-OH group (Fig. 1). Because, in general, 2′-deoxyribonucleosides are somewhat more basic than their ribonucleoside counterparts (11, 24), ΔpKa = 0.5 fits in the picture. The results 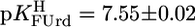 and
and 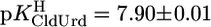 confirm the expectation that a strongly electronegative substituent at position 5 acidifies (N3)H.
confirm the expectation that a strongly electronegative substituent at position 5 acidifies (N3)H.
Under our conditions, the experimental data of the potentiometric pH titrations can be explained fully by considering equilibria 1 and 3, the latter defining complex formation,
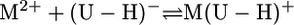 |
[3] |
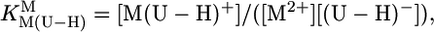 |
[4] |
if the evaluation is not carried into the pH range in which hydrolysis of M(aq)2+ begins. The results according to Eq. 4 for the four uridinate-type ligands in Fig. 1 are listed in Table 1. The stability constants of Cu(Urd–H)+, Cu(dThd–H)+, Zn(dThd–H)+, Pb(Urd–H)+, and Pb(dThd–H)+ could not be determined because of hydrolysis. The reliability of previous data (10) has already been questioned in the Introduction (and ref. 17). However, the present stability constants for M(Urd–H)+ with Mg2+, Ca2+, Mn2+, Zn2+, or Cd2+ excellently agree with our previous values (17).
Table 1.
Logarithms of the stability constants for the 1:1 complexes (Eqs. 3 and 4) formed between several divalent metal ions (M2+) and the uridinate-type (U–H)– ligands shown in their (N3)H protonated form in the upper part of Fig. 1 (potentiometric pH titrations; aq solution; 25°C; I = 0.1 M, NaNO3)
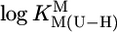 for U = for U =
|
||||
|---|---|---|---|---|
| M2+ | Urd | FUrd | CldUrd | dThd |
| Mg2+ | 0.70 ± 0.06 | 0.54 ± 0.16 | 0.60 ± 0.09 | 0.83 ± 0.10 |
| Ca2+ | 0.82 ± 0.11 | 0.59 ± 0.19 | 0.70 ± 0.07 | 0.88 ± 0.08 |
| Sr2+ | 0.65 ± 0.07 | 0.63 ± 0.14 | 0.53 ± 0.09 | 0.77 ± 0.06 |
| Ba2+ | 0.68 ± 0.15 | 0.65 ± 0.10 | 0.59 ± 0.06 | 0.77 ± 0.06 |
| Mn2+ | 1.36 ± 0.05 | 1.04 ± 0.13 | 1.07 ± 0.08 | 1.38 ± 0.06 |
| Co2+ | 1.60 ± 0.10 | 1.04 ± 0.13 | 1.10 ± 0.17 | 1.71 ± 0.15 |
| Ni2+ | 1.76 ± 0.06 | 1.20 ± 0.15 | 1.27 ± 0.14 | 1.80 ± 0.20 |
| Cu2+ | —* | 3.39 ± 0.04 | 3.55 ± 0.03 | —* |
| Zn2+ | 2.41 ± 0.14 | 1.74 ± 0.04 | 1.81 ± 0.07 | —* |
| Cd2+ | 3.16 ± 0.04 | 2.59 ± 0.05 | 2.70 ± 0.03 | 3.43 ± 0.05 |
| Pb2+ | —* | 2.51 ± 0.08 | 2.69 ± 0.06 | —* |
The acidity constants for U (Eq. 2) are 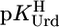 = 9.18 ± 0.02,
= 9.18 ± 0.02, 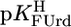 = 7.55 ± 0.02,
= 7.55 ± 0.02, 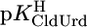 = 7.90 ± 0.01, and
= 7.90 ± 0.01, and 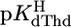 = 9.67 ± 0.02; so-called practical (or mixed) constants are given (see Methods). The errors given are three times the SEM value or the sum of the probable systematic errors, whichever is larger.
= 9.67 ± 0.02; so-called practical (or mixed) constants are given (see Methods). The errors given are three times the SEM value or the sum of the probable systematic errors, whichever is larger.
No stability constant for the M(U—H)+ complex could be determined because of hydrolysis of M(aq)2+.
Preliminary Considerations on the Stability of the M(Urd–H)+ Complexes. The stabilities of M(Urd–H)+ (Table 1, column 2) of the alkaline earth ions appear at first sight relatively high, whereas those for Mn2+, Co2+, Ni2+, and Zn2+ seem to follow the Irving–Williams sequence, although it is somewhat disturbing that Zn(Urd–H)+ is by ≈0.8 log unit more stable than Co(Urd–H)+; usually the stabilities of Co2+ and Zn2+ complexes are similar (25, 26). Therefore, we compared the results with previous ones for simple pyridine-type ligands (PyN) (27). For families of structurally related ligands (L), plots of 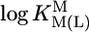 vs.
vs. 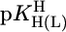 result in straight lines (28) defined by Eq. 5,
result in straight lines (28) defined by Eq. 5,
 |
[5] |
where m represents the slope and b the intercept with the y axis. The parameters for the 3d-transition ions including Zn2+ and Cd2+, determined from equilibrium data within the 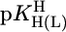 range of 3–6.5, are listed in table 3 of ref. 27. By using
range of 3–6.5, are listed in table 3 of ref. 27. By using 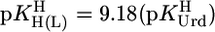 , we extrapolated these data with Eq. 5 to the expected affinity of a neutral PyN, with a basicity that corresponds to the one of (N3)– of uridinate, toward the mentioned M2+ ions. The results for these hypothetical M(PyN)2+ species are listed in Table 2 (column 3).
, we extrapolated these data with Eq. 5 to the expected affinity of a neutral PyN, with a basicity that corresponds to the one of (N3)– of uridinate, toward the mentioned M2+ ions. The results for these hypothetical M(PyN)2+ species are listed in Table 2 (column 3).
Table 2.
Stability constant comparisons for the M(Urd–H)+ complexes between the measured stability constants (Table 1, column 2) and calculated stability constants (Eq. 5) based on 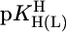 = 9.18 (=
= 9.18 (= 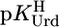 ) for a hypothetical PyN, i.e., for M(PyN)2+ complexes, together with the stability difference logΔ as defined by Eq. 6
) for a hypothetical PyN, i.e., for M(PyN)2+ complexes, together with the stability difference logΔ as defined by Eq. 6
| M2+ | 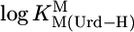 |
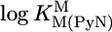 * *
|
logΔ |
|---|---|---|---|
| Mg2+ | 0.70 ± 0.06 | 0.04 ± 0.04 | 0.66 ± 0.07 |
| Ca2+ | 0.82 ± 0.11 | -0.08 ± 0.07 | 0.90 ± 0.13 |
| Sr2+ | 0.65 ± 0.07 | -0.12 ± 0.08 | 0.77 ± 0.11 |
| Ba2+ | 0.68 ± 0.15 | -0.15 ± 0.10 | 0.83 ± 0.18 |
| Mn2+ | 1.36 ± 0.05 | 0.82 ± 0.04 | 0.54 ± 0.06 |
| Co2+ | 1.60 ± 0.10 | 2.14 ± 0.09 | -0.54 ± 0.13 |
| Ni2+ | 1.76 ± 0.06 | 2.83 ± 0.09 | -1.07 ± 0.11 |
| Cu2+ | — | 4.21 ± 0.09 | — |
| Zn2+ | 2.41 ± 0.14 | 2.09 ± 0.05 | 0.32 ± 0.15 |
| Cd2+ | 3.16 ± 0.04 | 2.44 ± 0.05 | 0.72 ± 0.06 |
For the error limits, see the Table 1 legend. The error limits of the derived data, in the above case of logΔ, were calculated according to the error propagation after Gauss.
The first four entries in this column are taken from Equations 6-9 in ref. 27. The other values were calculated according to Eq. 5 with 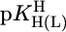 = 9.18 and the straight-line parameters listed in table 3 of ref. 27; the corresponding error limits are the sum of the errors in b (ref. 27, Table 3) and 3 SD values given in table 4 of ref. 27. All values listed in this column refer to I = 0.5 M (NaNO3; 25°C); however, because these PyN are neutral, a change in I from 0.5 to 0.1 M hardly affects (27) the listed values.
= 9.18 and the straight-line parameters listed in table 3 of ref. 27; the corresponding error limits are the sum of the errors in b (ref. 27, Table 3) and 3 SD values given in table 4 of ref. 27. All values listed in this column refer to I = 0.5 M (NaNO3; 25°C); however, because these PyN are neutral, a change in I from 0.5 to 0.1 M hardly affects (27) the listed values.
The affinity of PyN ligands toward Ba2+, Sr2+, Ca2+, and Mg2+ is independent of their basicity in the mentioned 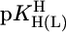 range (27); therefore, the actual M(PyN)2+ stabilities (see equations 6–9 in ref. 27) are listed in Table 2 (column 3). This independence of complex stability on basicity has led to the conclusion (27) that these M2+ form outersphere complexes with PyN.
range (27); therefore, the actual M(PyN)2+ stabilities (see equations 6–9 in ref. 27) are listed in Table 2 (column 3). This independence of complex stability on basicity has led to the conclusion (27) that these M2+ form outersphere complexes with PyN.
Comparisons of the stability constants for the M(Urd–H)+ complexes with those of the corresponding hypothetical M(PyN)2+ species according to Eq. 6,
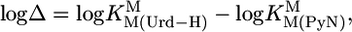 |
[6] |
are listed in Table 2 (column 4). A higher stability for M(Urd–H)+ species is intuitively expected because of the negative charge of uridinate. Yet, there are several caveats: (i) It is strange that the stabilities of Co(Urd–H)+ and Ni(Urd–H)+ are lower than those of their M(PyN)2+ counterparts. Does this indicate a steric inhibition of the (C2)O/(C4)O groups? (ii) The average stability increase of ≈0.5 log unit observed for Mn(Urd–H)+, Zn(Urd–H)+, and Cd(Urd–H)+ might be as expected; however, if so, (iii) then the average stability increase of ≈0.8 log unit for the M(Urd–H)+ complexes of the alkaline earth ions is clearly unexpected. Does this mean that (C2)O/(C4)O participate in M2+ binding?
To answer the indicated questions, we extended the studies to related ligands (Fig. 1) and measured the stabilities of M(FUrd–H)+, M(CldUrd–H)+, and M(dThd–H)+ complexes (Table 1, columns 3–5), for which no stability data existed (8–10) except for a few M(dThd–H)+ values (10), most of which agree poorly with our results, probably because of ignoring previously the hydrolysis of M(aq)2+ (see also Introduction).
Straight-Line Correlations for M(U–H)+ Complexes. For most M2+ systems, four data pairs are available (Table 1) that could be fitted (least squares) to straight lines; their parameters are given in Table 3. It is interesting to determine the deviation from the least-squares line for the stability constant of each individual complex by comparing an expected value calculated with 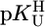 and Eq. 5 with the measured one and to obtain information in this way about the quality of the data. It is satisfying that all deviations are within ±0.07 log unit or less (Table 4, which is published as supporting information on the PNAS web site).
and Eq. 5 with the measured one and to obtain information in this way about the quality of the data. It is satisfying that all deviations are within ±0.07 log unit or less (Table 4, which is published as supporting information on the PNAS web site).
Table 3. Straight-line parameters for M2+ 1:1 complexes formed with uridinate-type ligands, valid for aq solutions at 25°C and I = 0.1 M (NaNO3).
| No. | M2+ | m | b | R* | SD† |
|---|---|---|---|---|---|
| 1 | Mg2+ | 0.122 ± 0.021 | -0.376 ± 0.183 | 0.971 | 0.015 |
| 2 | Ca2+ | 0.125 ± 0.019 | -0.320 ± 0.165 | 0.977 | 0.013 |
| 3 | Sr2+ | 0.076 ± 0.043 | -0.005 ± 0.372 | 0.779 | 0.031 |
| 4 | Ba2+ | 0.062 ± 0.029 | 0.142 ± 0.249 | 0.835 | 0.020 |
| 5 | Mn2+ | 0.178 ± 0.022 | -0.311 ± 0.188 | 0.985 | 0.017 |
| 6 | Co2+ | 0.336 ± 0.023 | -1.519 ± 0.201 | 0.995 | 0.017 |
| 7 | Ni2+ | 0.309 ± 0.035 | -1.141 ± 0.298 | 0.988 | 0.024 |
| 8 | Cu2+ | 0.457 | -0.061 | — | 0.07 |
| 9 | Zn2+ | 0.427 ± 0.047 | -1.516 ± 0.389 | 0.994 | 0.024 |
| 10 | Cd2+ | 0.388 ± 0.024 | -0.354 ± 0.209 | 0.996 | 0.017 |
| 11 | Pb2+ | 0.514 | -1.373 | — | 0.07 |
The slopes (m) and intercepts (b) for the straight reference lines from plots of  were calculated by the least-squares procedure from the measured equilibrium constants listed in Table 1. Straight-line equation (see also Eq. 5): y = m·x + b, where x represents the
were calculated by the least-squares procedure from the measured equilibrium constants listed in Table 1. Straight-line equation (see also Eq. 5): y = m·x + b, where x represents the 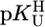 value for the deprotonation of any (N3)H site of a uridine-type ligand and y the calculated stability constant
value for the deprotonation of any (N3)H site of a uridine-type ligand and y the calculated stability constant 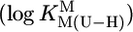 for the corresponding M(U—H)+ complex; the errors given with m and b correspond to one SD (1σ).
for the corresponding M(U—H)+ complex; the errors given with m and b correspond to one SD (1σ).
Correlation coefficient: In the case of small values for the slope (m), the values for R are also expected to be relatively small (see, e.g., entries 3 and 4).
This column lists the SD resulting from the logarithmic differences between the experimentally determined (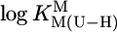 of Table 1) and calculated (Eq. 5) stability constants for a given M(U—H)+ series (Table 4).
of Table 1) and calculated (Eq. 5) stability constants for a given M(U—H)+ series (Table 4).
To provide a reliable error limit for any stability constant calculated with the straight-line parameters of Table 3 and a given 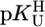 value, the standard deviation (SD) of the (usually) four data points from the relevant least-squares line was calculated (Table 3, column 6, and Table 4). Users of our results are recommended to apply the equations of Table 3 in the
value, the standard deviation (SD) of the (usually) four data points from the relevant least-squares line was calculated (Table 3, column 6, and Table 4). Users of our results are recommended to apply the equations of Table 3 in the 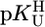 range of 7.5–9.7 with error limits for the calculated
range of 7.5–9.7 with error limits for the calculated 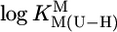 values (Eq. 5) of three times the SD values. For calculated stability constants in the
values (Eq. 5) of three times the SD values. For calculated stability constants in the 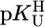 range of <7.5 or >9.7, the error limits given for b should also be considered.
range of <7.5 or >9.7, the error limits given for b should also be considered.
No stability constants were determined for Fe(U–H)+, because traces of Fe3+ present or formed during the experiment make such measurements error-prone. Indeed, only a few constants for Fe2+ complexes exist (8–10). If values are needed, we recommend obtaining an estimate by averaging the corresponding Mn2+ and Co2+ data (25).
Because we worked with an excess of M2+ compared to [U] (see Methods), we could not measure stabilities of Cu(Urd–H)+ and Pb(Urd–H)+ because hydrolysis of the corresponding M(aq)2+ occurred before the onset of complex formation. Yet, for both complexes, stability constants were determined with a M2+/L ratio of 1:1 (29) or an excess of Urd (30, 31). However, based on our results (Table 3), constants for these complexes can be calculated, and for Cu(Urd–H)+ one obtains with 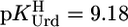 an expected value of
an expected value of 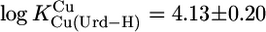 (25°C; I = 0.1 M, NaNO3), which agrees reasonably with the published values of 4.2 ± 0.2 (25°C; I = 1 M, NaNO3) (29) and 4.32 ± 0.06 (20°C; I = 0.1 M, KNO3) (31), especially if one considers the different experimental conditions. We also calculated with the parameters of Table 3 and
(25°C; I = 0.1 M, NaNO3), which agrees reasonably with the published values of 4.2 ± 0.2 (25°C; I = 1 M, NaNO3) (29) and 4.32 ± 0.06 (20°C; I = 0.1 M, KNO3) (31), especially if one considers the different experimental conditions. We also calculated with the parameters of Table 3 and 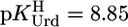 from an earlier study (30) with even more different conditions (37°C; I = 0.15 M, NaNO3)
from an earlier study (30) with even more different conditions (37°C; I = 0.15 M, NaNO3) 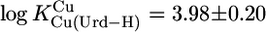 ; this value is nearly 0.6 log units lower than the one (4.57) in ref. 30, which is probably blurred by Cu(aq)2+ hydrolysis.
; this value is nearly 0.6 log units lower than the one (4.57) in ref. 30, which is probably blurred by Cu(aq)2+ hydrolysis.
For Pb(Urd–H)+, one calculates with 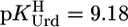 and the parameters of Table 3
and the parameters of Table 3 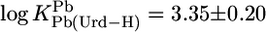 (25°C; I = 0.1 M, NaNO3), which agrees excellently (this view is revised from ref. 17) with the measured (29) value of 3.4 ± 0.25 (20°C; I = 1 M, NaNO3).
(25°C; I = 0.1 M, NaNO3), which agrees excellently (this view is revised from ref. 17) with the measured (29) value of 3.4 ± 0.25 (20°C; I = 1 M, NaNO3).
For M(dThd–H)+, we calculated 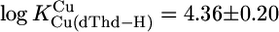 and
and 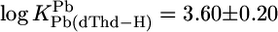 with
with 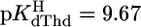 (25°C; I = 0.1 M, NaNO3). The Pb2+ value of 3.7 ± 0.4 of ref. 29 (25°C; I = 1 M, NaNO3) agrees with our result, but the log constant 4.7 ± 0.15 (29) for Cu(dThd–H)+ is somewhat too large, probably because of Cu(aq)2+ hydrolysis. However, four of the six literature values for the Cu2+ and Pb2+ systems are in accord with our calculations, indicating that the straight-line parameters of Table 3 for the two M2+ are reasonably reliable even though they are based only on two data pairs each.
(25°C; I = 0.1 M, NaNO3). The Pb2+ value of 3.7 ± 0.4 of ref. 29 (25°C; I = 1 M, NaNO3) agrees with our result, but the log constant 4.7 ± 0.15 (29) for Cu(dThd–H)+ is somewhat too large, probably because of Cu(aq)2+ hydrolysis. However, four of the six literature values for the Cu2+ and Pb2+ systems are in accord with our calculations, indicating that the straight-line parameters of Table 3 for the two M2+ are reasonably reliable even though they are based only on two data pairs each.
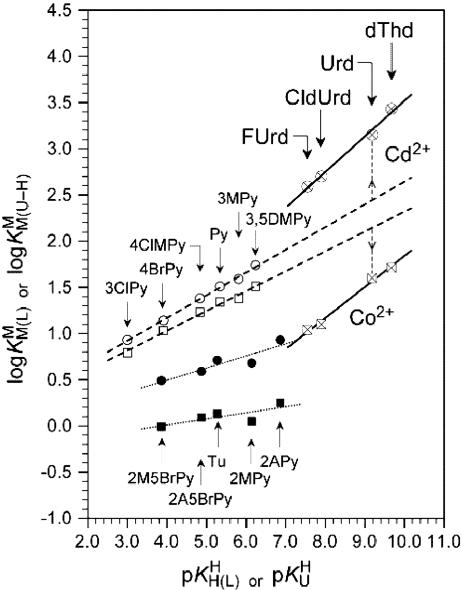
Comparison of the Stabilities of M(U–H)+ Complexes with Those Formed by PyN. It is evident from Fig. 2 that extrapolation of the pyridine-type straight lines (○, □) to 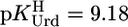 indicates that Cd(Urd–H)+ is more stable than Cd(PyN)2+, whereas Co(Urd–H)+ is less stable than its Co(PyN)2+ counterpart. Furthermore, the Co(U–H)+ straight line is placed (although with a somewhat steeper slope) between the lines of the Co2+ complexes of PyN- and oPyN-type ligands (⊠, ▪, □). This indicates that Co2+ suffers in its coordination to (N3)– of (U–H)– a steric hindrance by the neighboring (C2)O/(C4)O groups that is less pronounced than by an o-amino or o-methyl group. In contrast, in Cd(U–H)+, (C2)O/(C4)O facilitate Cd2+ binding, leading to an increased stability (⊗, •, ○). These observations conform to the data shown in Table 2.
indicates that Cd(Urd–H)+ is more stable than Cd(PyN)2+, whereas Co(Urd–H)+ is less stable than its Co(PyN)2+ counterpart. Furthermore, the Co(U–H)+ straight line is placed (although with a somewhat steeper slope) between the lines of the Co2+ complexes of PyN- and oPyN-type ligands (⊠, ▪, □). This indicates that Co2+ suffers in its coordination to (N3)– of (U–H)– a steric hindrance by the neighboring (C2)O/(C4)O groups that is less pronounced than by an o-amino or o-methyl group. In contrast, in Cd(U–H)+, (C2)O/(C4)O facilitate Cd2+ binding, leading to an increased stability (⊗, •, ○). These observations conform to the data shown in Table 2.
Fig. 2.
Comparison of the 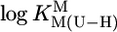 vs.
vs. 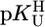 relationship (⊗, ⊠) for the uridinate-type (U–H)– ligands shown in Fig. 1 for their Co2+ (⊠, □, ▪) and Cd2+ (⊗, ○, •) complexes with the corresponding
relationship (⊗, ⊠) for the uridinate-type (U–H)– ligands shown in Fig. 1 for their Co2+ (⊠, □, ▪) and Cd2+ (⊗, ○, •) complexes with the corresponding 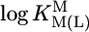 vs.
vs. 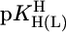 relationships for PyN [L = PyN = 3-chloropyridine (3ClPy), 4-bromopyridine (4BrPy), 4-(chloromethyl)pyridine (4ClMPy), pyridine (Py), 3-methylpyridine (3MPy), and 3,5-dimethylpyridine (3,5DMPy) (from left to right)] (○, □) and for o-substituted PyN [L = oPyN = 2-methyl-5-bromopyridine (2M5BrPy), 2-amino-5-bromopyridine (2A5BrPy), tubercidin (7-deazaadenosine, Tu), 2-methylpyridine (2MPy) and 2-aminopyridine (2APy)] (•, ▪). The reduced stability of the M(oPyN)2+ complexes reflects the steric inhibition of an o-amino or o-methyl group. The data pairs for the M(U–H)+ complexes are from Table 1, and those for the M(PyN)2+ and M(oPyN)2+ species are from table 3 in ref. 27. The least-squares straight reference lines are drawn according to Eq. 5 (see Table 3 and ref. 27). The plotted equilibrium constants (aq solution; 25°C) for the M2+/(U–H)– systems (Table 1) refer to I = 0.1 M (NaNO3), and those for the M2+/PyN or oPyN systems refer to I = 0.5 M (NaNO3); this change in I from 0.1 to 0.5 M is of no significance, because the latter ligands do not carry a charge, and the shifts in
relationships for PyN [L = PyN = 3-chloropyridine (3ClPy), 4-bromopyridine (4BrPy), 4-(chloromethyl)pyridine (4ClMPy), pyridine (Py), 3-methylpyridine (3MPy), and 3,5-dimethylpyridine (3,5DMPy) (from left to right)] (○, □) and for o-substituted PyN [L = oPyN = 2-methyl-5-bromopyridine (2M5BrPy), 2-amino-5-bromopyridine (2A5BrPy), tubercidin (7-deazaadenosine, Tu), 2-methylpyridine (2MPy) and 2-aminopyridine (2APy)] (•, ▪). The reduced stability of the M(oPyN)2+ complexes reflects the steric inhibition of an o-amino or o-methyl group. The data pairs for the M(U–H)+ complexes are from Table 1, and those for the M(PyN)2+ and M(oPyN)2+ species are from table 3 in ref. 27. The least-squares straight reference lines are drawn according to Eq. 5 (see Table 3 and ref. 27). The plotted equilibrium constants (aq solution; 25°C) for the M2+/(U–H)– systems (Table 1) refer to I = 0.1 M (NaNO3), and those for the M2+/PyN or oPyN systems refer to I = 0.5 M (NaNO3); this change in I from 0.1 to 0.5 M is of no significance, because the latter ligands do not carry a charge, and the shifts in 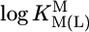 and
and 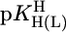 go “parallel” to each other (27).
go “parallel” to each other (27).
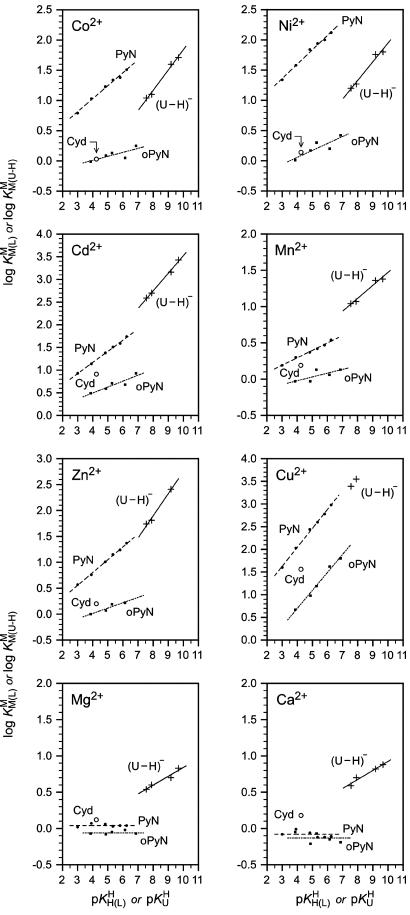
Fig. 3 allows a direct comparison between the properties of different M2+ and their coordination tendency toward (U–H)–-type and PyN or o-amino(methyl)pyridine-type ligands (27). The straight lines are defined by the same ligands as those shown in Fig. 2 (compare from left to right). The given data points for the M(Cyd)2+ complexes facilitate additional structural interpretations. Note that Cyd (Fig. 1) offers the pyridine-type N3, but an o-NH2 group next to it may inhibit M2+ coordination, whereas an o-(C)O group may facilitate it (12). No stability data for Sr(U–H)+ and Ba(U–H)+ are plotted, because they correspond to those of Mg(U–H)+ and especially Ca(U–H)+. Pb(U–H)+ complexes (Table 1) do not appear, because no reference lines for PyN and oPyN ligands are available.
Fig. 3.
Comparison of the 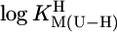 vs.
vs. 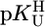 relationships (+) for eight different metal ions with the corresponding
relationships (+) for eight different metal ions with the corresponding 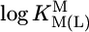 vs.
vs. 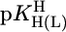 relationships (27) for simple PyN (•), sterically inhibited o-amino(methyl)pyridine-type ligands (oPyN) (▪), and M2+/Cyd (12) systems (○). For the definition and source of the data points, see the Fig. 2 legend (compare from left to right). The straight reference line for the Zn2+/oPyN system (see table 3 of ref. 27) is based only on the first four data points; Zn2+/2APy is neglected in the calculations because the stability constant carries a large error caused by the very low formation degree of Zn(2APy)2+ (27).
relationships (27) for simple PyN (•), sterically inhibited o-amino(methyl)pyridine-type ligands (oPyN) (▪), and M2+/Cyd (12) systems (○). For the definition and source of the data points, see the Fig. 2 legend (compare from left to right). The straight reference line for the Zn2+/oPyN system (see table 3 of ref. 27) is based only on the first four data points; Zn2+/2APy is neglected in the calculations because the stability constant carries a large error caused by the very low formation degree of Zn(2APy)2+ (27).
Structural Considerations on the M(U–H)+ Complexes. The upper part of Fig. 3 reveals that the data points for Co(Cyd)2+ and Ni(Cyd)2+ fit on their reference lines defined by the oPyN ligands, whereas those for Cd(Cyd)2+ and Mn(Cyd)2+ are above the reference lines. This means that the steric inhibition exercised by the o-amino group at C4 of Cyd (Fig. 1) is offset partly by an interaction of the (N3)-coordinated Cd2+ and Mn2+ ions with (C2)O, giving rise to chelates (12). The same may be surmised for Cd(U–H)+ and Mn(U–H)+, which show an enhanced stability compared with that of the corresponding M(PyN)2+ complexes. In contrast, no M(Cyd)2+ chelates form with Co2+ and Ni2+. They simply coordinate in a monodentate fashion to N3 of Cyd, and the position of the (U–H)– reference lines implies the same for the Co(U–H)+ and Ni(U–H)+ species.
Comparison of the relative positions of the data for Zn(U–H)+ and Cu(U–H)+ in Fig. 3 with those for Cd(U–H)+ and Mn(U–H)+ indicates that chelate formation involving (C2)O/(C4)O is also important in these species, although possibly a bit less.
The stability of the complexes of Mg2+ and Ca2+ does not depend on the basicity of the pyridine nitrogen (Fig. 3, Bottom), indicating that outersphere complexes are formed (27). If a water molecule is between the liganding N site and M2+, then a change in the basicity of the ligand is reflected only little or not at all in complex stability. Of course, such outersphere species are not very stable, and the steric inhibition of the ortho substituent is small (≈0.05–0.10 log unit).
Of additional relevance is that the data points for Mg(Cyd)2+ and Ca(Cyd)2+ are above both pyridine-type reference lines, indicating a strong participation of (C2)O in M2+ binding. Indeed, in accord with a crystal structure analysis of a Ba2+ complex (2), it has been proposed (12) that (C2)O is innersphere-coordinated and a semichelate forms, involving an outersphere coordination of an M2+-bound water molecule to N3. A (C2)O-Ba2+ binding is also known from an x-ray crystal structure of a Ba2+-Urd 5′-monophosphate complex (2). Because in uridinate-type ligands the negative charge is not solely located at (N3)– but partly also at (C2)O and (C4)O, this type of semichelate also quite likely occurs in M(U–H)+ species of Mg2+, Ca2+, Sr2+, and Ba2+; in accord herewith, complex stability depends somewhat on ligand basicity, i.e., the slopes m of the straight lines vary between 0.062 (Ba2+) and 0.122 (Mg2+) (Table 3). This is expected for M2+ binding to oxygen donors with a (partial) negative charge; e.g., for 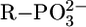 ligands, m varies between 0.087 (Ba2+) and 0.208 (Mg2+) (16, 26). These slopes are more pronounced because the amount of negative charge at the ligating site in
ligands, m varies between 0.087 (Ba2+) and 0.208 (Mg2+) (16, 26). These slopes are more pronounced because the amount of negative charge at the ligating site in 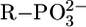 is higher.
is higher.
It is unfortunate that an exact quantitative evaluation of the extent of chelate formation is not possible for the M(U–H)+ complexes because no (N3)– reference lines are available that would need to be defined by simple negatively charged (N3)– ligands having no carbonyl groups in their ortho positions, a goal hard to achieve. However, based on the results for the M(Cyd)2+ complexes (12), lower limits for the chelate-formation degrees of the M(U–H)+ species can be assessed; “lower limits” because in (U–H)– there is no steric hindrance by an o-NH2 group, and two (C)O groups (not only one; see Fig. 1) may participate in complex formation. For Mg(U–H)+ as well as for the Mn2+ and Zn2+ complexes this lower limit is 30% and for Ca2+, Sr2+, and Ba2+ is >50%. No chelate formation is anticipated for Co(U–H)+ and Ni(U–H)+ but more than 60% and 80% for Cd(U–H)+ and Cu(U–H)+, respectively. Clearly, chelate formation is substantial for some M(U–H)+ species.
Conclusions
Above it was concluded that M2+ in Co(U–H)+ and Ni(U–H)+ is bound in a monodentate fashion to (N3)– of the uridinates, as observed previously for Co2+ in the solid state coordinating to N3 of a Cyd residue (2). For all other M2+ chelates, formation must be surmised, but the available data only allow an estimation of the lower limit of their formation degrees.
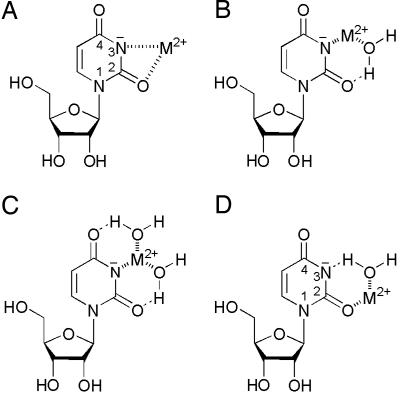
Solid-state studies (2) of complexes containing a Cyd residue and Cd2+, Zn2+, or Cu2+ show that distorted four-membered chelates form (see ref 12 and references therein); corresponding structures are expected for the uridinates (Fig. 4A). It is interesting that 2-thiouridine is also an effective ligand in its (N3)–-deprotonated form, and there is spectroscopic evidence, mainly from NMR and for Cd2+ (32), that in aqueous solution four-membered chelates involving (N3)– and the (C2)S site form (32, 33). The larger size of S, compared to O, favors chelate formation of small and distorted rings, as is known from purine derivatives in which five-membered chelates involving N7 and (C6)S occur (34). However, in aqueous solution, it is highly likely that uridinates form in addition to four-membered rings, so-called semichelates, in which M2+ is innersphere-bound to (N3)– and an M2+-coordinated water interacts outersphere with (C2)O (Fig. 4B). Of course, a structure with two semichelates (Fig. 4C) is possible also, and this could well give rise to large, relative stability enhancements as observed (e.g., with Cd2+).
Fig. 4.
Possible metal ion-binding modes in the chelates formed in equilibrium by the M(U–H)+ complexes in aqueous solution (see Conclusions). The negative charge in the uridinate structures is shown on N3, but it can be delocalized in part to the neighboring C(O) groups.
Based on the results of Fig. 3 one may propose for Mn(U–H)+ the same structures as discussed for the Cd2+, Zn2+, or Cu2+ complexes. However, there is also a crystal structure in which Mn2+ coordinates to (C2)O of a Cyd residue with a rather short bond (2.08 Å) (2, 35). Considering the partial delocalization of the negative charge from (N3)– to (C2)O and (C4)O, a semichelate as shown in Fig. 4D or the analogous one involving (C4)O may well exist in aqueous solution in equilibrium.
The same two semichelates (Fig. 4D) are expected to occur with Mg2+, Ca2+, Sr2+, and Ba2+, and in solution this is ascertained from the stability enhancements, Ca2+ being especially favored; maybe its size allows a perfect fit to the ligating sites in (U–H)–. In any case, Ca2+ coordinates innersphere to (C4)O of Urd in an RNA tetraplex (36); this is also true for small RNAs and Ba2+ (37), as well as (C2)O and Sr2+ (3).
The lack of reference lines for Pb(PyN)2+ and Pb(oPyN)2+ prevents comparisons with the stability data of Pb(U–H)+. However, based on the so-called stability ruler (38), similar properties and chelate structures are expected, as for Cd(U–H)+, and the stability constants shown in Table 1 confirm this. Furthermore, C(O) interactions are likely of relevance in Pb2+ complexes of RNA (3, 14, 15). For example, in the leadzyme Pb2+ is suggested to bind, next to other sites, to the (C2)O group of a uracil residue (3). Similarly, with yeast phenylalanine tRNA, a strikingly short bond of 2.2 Å exists between (C4)O and Pb2+ (15), which confirms the affinity of Pb2+ toward carbonyl groups.
With regard to biological systems one also may ask: Is deprotonation of the (N3)H site of a Urd residue expected to occur under physiological conditions? At pH 7.6, a small fraction of ≈2.6% of (Urd–H)– exists. With dThd, because of its higher pKa value, the amount is even smaller, whereas for the artificial analogues it increases; e.g., ≈50% of FUrd is deprotonated at N3 under these conditions. Complex formation at pH 7.6, e.g., between Urd and Zn2+ in 10–3 M solutions, is also small; only ≈0.7% exist as Zn(Urd–H)+. Of course, increase of the concentration of one component will increase the formation degree significantly; this is also true if Zn2+ is pushed into a favorable steric orientation by other primary binding sites. Remarkably, in a recent study (39) on a novel Zn2+-catalyzed cleavage site between C3 and U4 in the catalytic core of the hammerhead ribozyme it was discovered that cleavage at U4 occurs only after the one at A9; i.e., there is a sequential cleavage mechanism. This U4 cleavage is connected with a pH-dependent conformational change and occurs only at pH > 7.9, reaching a maximum at pH ≈ 8.5. Indeed, such a conformational change evidently occurs with an apparent pKa of ≈8.5 (40). Considering our results, this observation may well be connected with a deprotonation at (N3)H of U4. Of interest is also the recent proposal (41) that an (N1)-deprotonated site of a guanosine residue participates in the catalysis of the hairpin ribozyme; it is also interesting that the pKa values for the deprotonation of (N1)H of guanosine (9.22) (11) and of (N3)H of Urd (9.18) are very similar. Furthermore, metal ion coordination at a nucleobase residue may heavily perturb its acid–base properties (7, 42).
Finally, it seems quite feasible under biological conditions that two ions like Mg2+, Mn2+ or Zn2+, coordinate with the help of primary binding sites to both (C2)O and (C4)O groups, acidifying (N3)H such that it becomes a proton donor, e.g., in a ribozyme reaction. That two metal ions may be in close neighborhood and coordinate simultaneously to the same nucleobase residue has been shown recently (43) for purine residues in aqueous solution.
Supplementary Material
Acknowledgments
This work is dedicated to Professor Dr. Hans H. Brintzinger on the occasion of his 70th birthday with all best wishes for his future endeavors. The competent technical assistance of Mrs. Astrid Sigel and stimulating discussions with members of the COST D20 Programme are gratefully acknowledged, as is support by the Swiss National Science Foundation, the State Secretariat for Education and Research (COST D20) (to H.S.), and the Austrian Science Foundation (COST D13) (to W.L.).
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: Urd, uridine; Cyd, cytidine; aq, aqueous; dThd, thymidine; FUrd, 5-fluorouridine; CldUrd, 5-chloro-2′-deoxyuridine; PyN, pyridine-type ligands.
References
- 1.Sigel, A. & Sigel, H., eds. (2004) Metal Complexes in Tumor Diagnosis and as Anticancer Agents (Metal Ions in Biological Systems) (Dekker, New York), Vol. 42, pp. 1–534. [Google Scholar]
- 2.Aoki, K. (1996) Met. Ions Biol. Syst. 32, 91–134. [Google Scholar]
- 3.Wedekind, J. E. & McKay, D. B. (2003) Biochemistry 42, 9554–9563. [DOI] [PubMed] [Google Scholar]
- 4.Sigel, R. K. O., Vaidya, A. & Pyle, A. M. (2000) Nat. Struct. Biol. 7, 1111–1116. [DOI] [PubMed] [Google Scholar]
- 5.Sigel, R. K. O. & Pyle, A. M. (2003) Met. Ions Biol. Syst. 40, 477–512. [PubMed] [Google Scholar]
- 6.Sletten, E. & Frøystein, N. Å. (1996) Met. Ions Biol. Syst. 32, 397–418. [PubMed] [Google Scholar]
- 7.Sigel, H. (2004) Pure Appl. Chem. 76, 1869–1886. [Google Scholar]
- 8.Smith, R. M. & Martell, A. E. (2001) NIST Critically Selected Stability Constants of Metal Complexes (U.S. Dept. of Commerce, Natl. Inst. of Standards and Technology, Gaitherburg, MD), Reference Database 46, Version 6.4.
- 9.Murray, F. & May, P. M. (2001) Joint Expert Speciations System (JESS) (Div. of Water Technology, CSIR, Pretoria, South Africa; and School of Math. and Phys. Sci., Murdoch University, Murdoch, Western Australia), Version 6.0.
- 10.Pettit, L. D. & Powell, H. K. J. (2001) IUPAC Stability Constants Database (Academic Software, Timble, Otley, West Yorkshire, U.K.), Release 5, Version 5.16.
- 11.Da Costa, C. P. & Sigel, H. (2003) Inorg. Chem. 42, 3475–3482. [DOI] [PubMed] [Google Scholar]
- 12.Knobloch, B. & Sigel, H. (2004) J. Biol. Inorg. Chem. 9, 365–373. [DOI] [PubMed] [Google Scholar]
- 13.Fischer, B., Preut, H., Lippert, B., Schöllhorn, H. & Thewalt, U. (1990) Polyhedron 9, 2199–2204. [Google Scholar]
- 14.Sundaralingam, M., Rubin, J. R. & Cannon, J. F. (1984) Int. J. Quantum Chem. Quantum Biol. Symp. 11, 355–366. [Google Scholar]
- 15.Brown, R. S., Dewan, J. C. & Klug, A. (1985) Biochemistry 24, 4785–4801. [DOI] [PubMed] [Google Scholar]
- 16.Sigel, H. & Kapinos, L. E. (2000) Coord. Chem. Rev. 200–202, 563–594. [Google Scholar]
- 17.Knobloch, B., Da Costa, C. P., Linert, W. & Sigel, H. (2003) Inorg. Chem. Commun. 6, 90–93. [Google Scholar]
- 18.Davies, D. B., Rajani, P. & Sadikot, H. (1985) J. Chem. Soc. Perkin Trans. 2, 279–285. [Google Scholar]
- 19.Sigel, H., Zuberbühler, A. D. & Yamauchi, O. (1991) Anal. Chim. Acta 255, 63–72. [Google Scholar]
- 20.Moreno-Luque, C. F., Freisinger, E., Costisella, B., Griesser, R., Ochocki, J., Lippert B. & Sigel, H. (2001) J. Chem. Soc. Perkin Trans. 2, 2005–2011. [Google Scholar]
- 21.Sigel, R. K. O., Song, B. & Sigel, H. (1997) J. Am. Chem. Soc. 119, 744–755. [Google Scholar]
- 22.Yamauchi, O., Odani, A., Masuda, H. & Sigel, H. (1996) Met. Ions Biol. Syst. 32, 207–270. [Google Scholar]
- 23.Sigel, H., Massoud, S. S. & Corfù, N. A. (1994) J. Am. Chem. Soc. 116, 2958–2971. [Google Scholar]
- 24.Acharya, P., Cheruku, P., Chatterjee, S., Acharya, S. & Chattopadhyaya, J. (2004) J. Am. Chem. Soc. 126, 2862–2869. [DOI] [PubMed] [Google Scholar]
- 25.Kapinos, L. E., Song, B. & Sigel, H. (1999) Chem. Eur. J. 5, 1794–1802. [Google Scholar]
- 26.Sigel, H. & Song, B. (1996) Met. Ions Biol. Syst. 32, 135–205. [Google Scholar]
- 27.Kapinos, L. E. & Sigel, H. (2002) Inorg. Chim. Acta 337, 131–142. [Google Scholar]
- 28.Martin, R. B. & Sigel, H. (1988) Comments Inorg. Chem. 6, 285–314. [Google Scholar]
- 29.Fiskin, A. M. & Beer, M. (1965) Biochemistry 4, 1289–1294. [DOI] [PubMed] [Google Scholar]
- 30.Casassas, E., Izquierdo-Ridorsa, A. & Tauler, R. (1990) J. Inorg. Biochem. 39, 327–336. [DOI] [PubMed] [Google Scholar]
- 31.Lomozik, L., Jastrzab, R. & Gasowska, A. (2000) Polyhedron 19, 1145–1154. [Google Scholar]
- 32.Kowalik-Jankowska, T., Varnagy, K., Swiatek-Kozlowska, J., Jon, A., Sovago, I., Sochacka, E., Malkiewicz, A., Spychala, J. & Kozlowski, H. (1997) J. Inorg. Biochem. 65, 257–262. [Google Scholar]
- 33.Swiatek-Kozlowska, J., Brasun, J., Dobocz, A., Sochacka, E. & Glowacka, A. (2003) J. Inorg. Biochem. 93, 119–124. [DOI] [PubMed] [Google Scholar]
- 34.Dubler, E. (1996) Met. Ions Biol. Syst. 32, 301–338. [Google Scholar]
- 35.Aoki, K. (1976) J. Chem. Soc. Chem. Commun. 748–749.
- 36.Deng, J., Xiong, Y. & Sundaralingam, M. (2001) Proc. Natl. Acad. Sci. USA 98, 13665–13670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kacer, V., Scaringe, S. A., Scarsdale, J. N. & Rife, J. P. (2003) Acta Crystallogr. D 59, 423–432. [DOI] [PubMed] [Google Scholar]
- 38.Martin, R. B. (1996) in Encyclopedia of Molecular Biology and Molecular Medicine, ed. Meyers, R. A. (VCH, Weinheim, Germany), Vol. 1, pp. 125–134. [Google Scholar]
- 39.Borda, E. J., Markley, J. C. & Sigurdsson, S. T. (2003) Nucleic Acids Res. 31, 2595–2600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Murray, J. B., Dunham, C. M. & Scott, W. G. (2002) J. Mol. Biol. 315, 121–130. [DOI] [PubMed] [Google Scholar]
- 41.Bevilacqua, P. C. (2003) Biochemistry 42, 2259–2265. [DOI] [PubMed] [Google Scholar]
- 42.Garijo-Añorbe, M., Lüth, M. S., Roitzsch, M., Morell-Cerdà, M., Lax, P., Kampf, G., Sigel, H. & Lippert, B. (2004) Chem. Eur. J. 10, 1046–1057. [DOI] [PubMed] [Google Scholar]
- 43.Knobloch, B., Sigel, R. K. O., Lippert, B. & Sigel, H. (2004) Angew. Chem. Int. Ed. 43, 3793–3795. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.