Prion and water: Tight and dynamical hydration sites have a key role in structural stability

Abstract

The propensity to form fibril in disease-related proteins is a widely studied phenomenon, but its correlation, if any, with structural characteristics of the associated proteins is not clearly understood. However, the observation has been made that some proteins that readily form amyloid have a significant number of backbone H bonds that are exposed to solvent molecules, suggesting that these regions have a propensity toward protein interaction and aggregation [Fernandez, A. & Scheraga, H. A. (2003) Proc. Natl. Acad. Sci. USA 100, 113–118]. High-resolution x-ray structures of the sheep and human C-terminal prion protein have provided a useful description of surface and partially buried waters. By molecular dynamics simulations, we investigated the structural role of these water molecules. The solvent dynamical behavior on the protein surface reveals significant features about the stability and the potential interactions of the prion protein. The protein presents regions of tightly bound conserved waters that are necessary to hold in place local elements of the fold, as well as regions where the local water is in fast exchange with bulk water. These results are evidenced by a map of the spatial distribution entropy of the solvent around the protein. The particular behavior of the solvent around these regions may be crucial in the folding stability and in terms of aggregation loci.

Globular proteins or the soluble domains of membrane proteins have evolved in an aqueous environment, and therefore, protein–water interactions have an essential role in defining their folding and their general properties. However, there are proteins that can aggregate readily to form structurally well defined insoluble fibrillar polymers, named amyloids; such proteins appear to possess significant populations of nonnative folding states through which the fibers initiate. These amyloid-forming proteins are associated with several neurodegenerative diseases, such as Alzheimer's disease, Parkinson's disease, and Huntington's disease; chronic wasting disease; transmissible spongiform encephalopathy; and bovine spongiform encephalopathy (1–3).

In particular, it has been suggested that prion diseases are caused by a conformational change of the soluble cellular prion protein (PrP^C), which is rich in α-helix, to its β-sheet-rich insoluble isoform scrapie PrP (PrP^Sc) (3–5).

Because solubilization and aggregation are equilibrium processes, water interactions have a key role in the factors that define which state the protein will adopt. This task is apparent from the effect of system properties (pH, temperature, pressure, and concentration) on the formation of aggregates.

It has been observed by Fernandez et al. (6–8) that disease-related amyloidogenic proteins and, especially, PrP^Cs have a large number of under-dehydrated H bonds (UDHBs). These are backbone H bonds that are not protected against water interaction by flanking hydrophobic residue. As a result, the packing of H bonds is less stable, and the regions with a high concentration of UDHBs are structurally more labile. The loci of these “defects” on the protein surface are correlated with local destabilization and the favoring of partially unfolded structures with a consequent potential for aggregation (6, 9). This observation links amyloidogenic propensity and structural instability. At the same time, data from NMR measurements of the amide proton exchange protection factors reveal that the pattern of protection is very well correlated with the core structure of the native PrP^C (10–12). Further aspects of the PrP–water interaction have been provided by high-pressure spectroscopy and pressure-perturbation calorimetry (13). The study pointed out a different nature of hydration for the amyloidogenic form.

The full-length mature prion is a glycoprotein consisting of ≈210 aa, and its 3D structure is divided in two domains: an N-terminal domain that is flexible and disordered and a C-terminal globular domain that is structured. The C-terminal region of the PrP^C presents a mainly α-fold composed of three helixes: helix (H)1, H2, and H3, as well as one short segment of double-stranded antiparallel β-sheet (strand 1, β1; strand 2 β2). Also, there are ≈15 structurally conserved waters in the available x-ray structures of the human PrP (huPrP) and of sheep PrP (shPrP) variants (14–16), indicating that the folding process led to specific water internalization.

These data raise the following questions. What is the role of the highly conserved waters; and how does the surrounding solvent influence the PrP^C stability especially in the poorly protected regions? An answer to these questions will represent a step toward understanding the relation between solvation behavior of the PrP and its aggregation.

Experimental evidence for the dynamics of solvent at a protein surface is very hard to obtain. Much of the experimental information about protein hydration dynamics has come from magnetic relaxation techniques (17). Techniques that use super-cooled protein solutions would allow more characterization of surface dynamics (18).

However, a powerful method to study the distribution and the mobility of water around proteins is provided by molecular dynamics (MD) simulations. MD calculations have also been used to estimate the effects of water binding on protein flexibility (19). Although a number of MD studies have been carried out on the PrP, most of them have concentrated on modeling the structural processes leading to the scrapie PrP (PrP^Sc) form, for which limited structural data are available (6, 20–22).

In this study, we provide an extensive analysis of the PrP hydration supported by MD simulations. We identify tightly bound water sites that correlate with the structurally conserved waters identified by x-ray analysis. Also, the dynamical behavior of water on the protein surface derived from the simulations revealed features about the stability and the potential interactions of the PrP. Therefore, we calculate a map of the spatial distribution entropy of the solvent around the protein to clarify the nature of high and low solvent-density spots.

We focused on specific conserved water molecules and found that their structural role could be explained at an atomic level. We also studied the structural and solvation consequences of a pathogenic point mutation associated with Gerstmann–Straussler–Scheinker disease (Q217R) because our data suggest that it is linked to one of the structurally conserved waters.

Materials and Methods

MD Set Up. Several 10-ns-long MD simulations have been performed, starting on the following five prion C terminus structures: x-ray shPrP (PDB ID code 1UW3) (14); x-ray shPrP variants ARR, ARQ, and VRQ bound to antibody (PDB ID codes 1TQC, 1TPX, and 1TQB, respectively) (15); and NMR huPrP structures at pH 7 (PDB ID code 1HJN; model 1) (12). The x-ray huPrP (PDB ID code 1I4M) (16) has not been used for MD calculations but only for structural comparisons because the structure is a swapped dimer. All of the computations have been performed with the gromacs simulations package (23) with the gromos96 force field (24). The simulations were carried out in the npt ensemble with periodic boundary conditions at a constant temperature of 300 K. The Berendsen algorithm (25) has been applied for the temperature and pressure coupling. The particle-mesh Ewald method (PME) (26) was used to calculate the electrostatic contribution. The x-ray waters, when present, were not included in the starting structures, to avoid any bias. Because pH value of the simulation was 7, the protonation states of pH-sensitive residues were as follows: Arg and Lys were positively charged, Asp and Glu were negatively charged, and His was neutral. The net charge of the protein was neutralized by the addition of Cl^– and Na⁺ ions. In each simulation, the initial shortest distance between the protein and the box boundaries was 1.5 nm. The remaining box volume was filled with the extended simple point charge (SPCE) water model (27), and periodic boundary conditions were applied.

Water Density Function. The MD solvent density distribution was evaluated from the water oxygen atom positions as described by Lounnas and Pettitt (28, 29). For each frame, the atom coordinates were transformed by superimposing the current model onto a reference model. For the water positions, the boundary conditions are applied. The density function is then calculated for a discrete 0.05-nm step 3D grid. The space surrounding the protein is divided in two shells. The first region describes the water around the protein and comprises the region from the protein center of mass to a maximum distance of 0.6 nm from the protein surface. The second region goes from 0.6–0.8 nm from the protein surface and represents the bulk solvent shell. The MD hydration sites (MDHS) are assigned as the local maxima of the function, following the restrictions to be the highest value in a radius of 0.14 nm with a minimum density of 1.7 times the value of bulk water. To exclude any bias due to the superimposition of structures in the map building, we repeated the calculation several times for each map by using different regions of the protein as reference set.

Time-Autocorrelation Function and Residence Time. The time autocorrelation function P(τ), as described in previous MD studies (28), provides an estimation of the water exchange rate (residence time) in the hydration site.

The adopted formula is as follows:

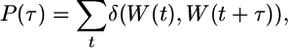[1]

where the delta function δ(W(t), W(t + τ)) assigns 0 or 1, respectively, whether or not the indexes of the waters residing in the hydration site at times t and t + τ differ. The resulting time-autocorrelation function is fitted by an exponential model.

Calculation of the Free Energy of the Water Binding. One of the advantages of MD simulations is in the possibility of calculating the free-energy difference between two states a and b of the studied system. In this work, following the double-decoupling method (30), the free energy of binding of a water molecule to the protein was calculated by dividing the process in two steps; the water was transferred first from the bulk to the gas phase and, second, to the binding site. Both the contributions were calculated with the slow-growth method. The free-energy difference is computed with the following integral:

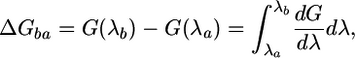[2]

where λ is the reaction coordinate, which is 0 in state a and 1 in state b. The derivate of the free energy with respect to λ can be written as follows:

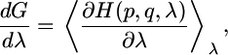[3]

where H(p, q, λ) is the classical Hamiltonian that is a function of Cartesian coordinates, conjugate momenta, and λ, respectively.

Solvent Entropy. The spatial distribution of the solvent around the protein was used to map the solvent entropy. The solvent entropy map was computed in a 0.1-nm-spaced grid, each node of which was connected to a narrower grid of 0.02-nm mesh size, which takes into count of the water distribution around the node. The solvent entropy for a generic node of the map is calculated according to the following equation:

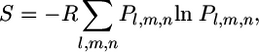[4]

where P_l,m,n is the probability of finding a water in the subvolume l, m, n of the space surrounding the node, and R is the gas constant.

Results and Discussion

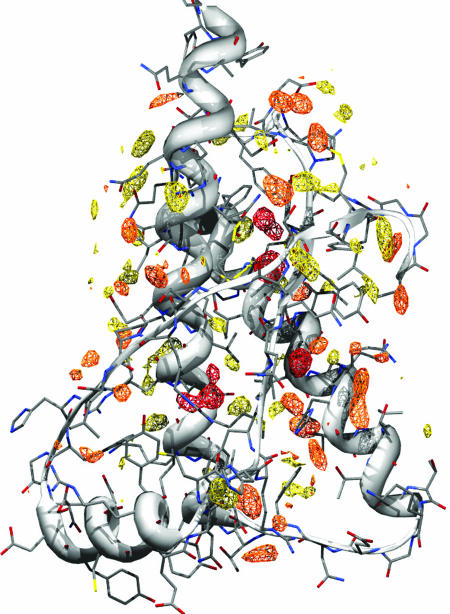
Hydration Sites Map and Comparison with X-Ray Waters. The study of the prion solvation features was made by the analysis of MD simulations. We focused on how the water surrounds the PrP by mapping the solvent density around the protein. Time-averaged water density maps have been calculated for all of the MD simulations (see Materials and Methods). The MDHS are identified as local maxima in the density function. We observed a good consistency among the MDHS in the five different simulations of the various prion structures. In Fig. 1, the shPrP structure (PDB ID code 1UW3) (14) is shown, with high MD water-density sites shown as contours.

Fig. 1.

Prion solvation map. MD water high-density sites contoured at 2.5 times the bulk solvent density. The reference structure is the shPrP (PDB ID code 1UW3). Yellow, orange, and red indicate low (τ < 70 ps), medium (70 < τ < 500 ps), and long (τ > 500 ps) residence time, respectively. A stereoview is shown in Fig. 6, which is published as supporting information on the PNAS web site.

Comparison of MD water positions and those that appear in x-ray analysis is difficult because the vitrified solvent is trapped at 100 K. Nevertheless, the long residence time MDHS show a very good correlation with x-ray defined waters, especially when compared with equivalent waters among the various crystal structures; therefore, these are the structurally conserved waters. For waters with shorter residence times the correlation with the x-ray defined waters is poorer. However, a similar lack of correlation is apparent among the surface crystallographic waters in the different crystal structures. This finding is most probably a consequence of their different solution compositions and lattice contacts, and it illustrates how delicate the balance is of factors that position solvent and surface side-chains.

Recent NMR studies on the structural mobility of the huPrP have identified regions in which the amide protons are protected (10–12). Interestingly, the unprotected regions match those suggested by Fernandez et al., and they are, according to his definition, “underwrapped” (6, 9). The observation that the two C-terminal turns from H2 and H3 show an equilibrium with an unfolded form (11), as well as the fact that these segments are also found to be unprotected from water, suggest that there are structural defects in these regions that may promote unfolding. On the basis of these observations, we decided to analyze the behavior of the different structural elements with respect to water.

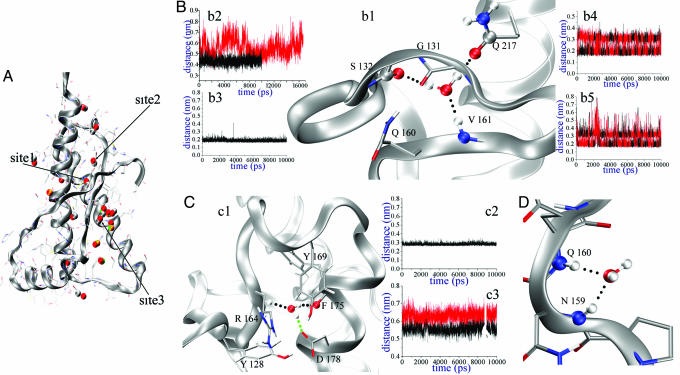
As described above, we identified localized waters (referred as to “sharp spots”) and surfaces of the protein in which the water is highly mobile as in the bulk phase. We refer to these as “smooth spots.” The distribution of the MDHS residence times (see Fig. 7, which is published as supporting information on the PNAS web site) shows three tightly bound waters with a residence time of >1.5 ns; we call these Sites1–3, respectively (Fig. 2A).

Fig. 2.

Structural details on Sites1–3. (A) General map of conserved x-ray waters. The reference structure is the shPrP (PDB ID code 1UW3). The color-coding of the water is as follows: red, PDB ID code 1I4M (huPrP); gray, PDB ID code 1UW3 (shPrP); green, PDB ID code 1TPX (shPrP); and gold, PDB ID code 1TQB (shPrP). A close-up view of Site1–3 is provided in Fig. 8, which is published as supporting information on the PNAS web site. (B) Site1 MD structural arrangements. (b1) MD interactions. (b2) S132 carbonyl O–V161 amide N distances with (black) and without (red) the water. (b3) Water O–V161 amide H distance in the MD. (b4) Water H–S132 carbonyl O distances. (b5) Water H–Q217 sidechain O distances. (C) Site2 MD structural arrangements. (c1) Structural overview. (c2) Water O–R164 amide N distance in the MD. (c3) Y169 amide N–F175 carbonyl O distances with (black) and without (red) the water. (D) MD water–backbone–amides interactions in Site3.

Sharp Spots and Structurally Conserved Waters. Table 1 lists the MD residence times calculated for the position of the waters that are determined in all of the available x-ray structures. For the sheep variant ARR (PDB ID code 1TQC) (15), only a few waters on the antibody have been localized; therefore, it has not been considered in our analysis. These residence times differ from the ones calculated on the maxima of the MD water density. In this case, to estimate the residence time for the x-ray waters, the central position for the autocorrelation function calculation coincides with the x-ray coordinates. The sites were sorted on the basis of their residence times. As shown, there is a remarkable difference in the residence time of the first sites (especially for Sites 1–3) and the remaining set. These sites are partially buried and correspond to some of the structurally conserved x-ray waters; their structural features are described in detail below.

Table 1. Highest residence time calculated for the x-ray conserved waters.

Site	1l4M	1UW3	1TOB	1TPX	τ, ps
Site1	62	1	4	8	>1,000
Site2	53	29	—	—	>1,000
Site3	60	22	—	—	>1,000
Site4	44	—	34	43	342.904
Site5	22	—	31	22	234.506
Site6	75	—	—	—	187.937
Site7	13	—	6	4	182.741
Site8	72	23	—	70	77.448

The four center columns are labeled with PDB ID codes, which refer to the water numbering in the respective PDB files.

The first analyzed site (Site1; Fig. 2Bb1) represents an example of synergistic protein–water interactions. The water connects three protein regions that are separate in sequence and belong to different secondary structural elements (β1, β2, and H3). This water bridges the amide of V161 (Fig. 2Bb3), the carbonyl of S132, and the Q217 side-chain oxygen (Figs. 2B b4 and b5). The water molecule is locked in the site in all of the simulations that we performed on the shPrP. In the huPrP, sporadic water exchanges are caused by a slight displacement of the Q217 residue in this site, which somewhat impedes the restructuring of the water. The site is located at the end of the β-sheet whose natural prolongation should involve an additional H bond between the amide of V161 and the carbonyl of G131. However, this bond is prevented by the interaction of the side chain of Q160 with the carbonyl of G131. Given this structural arrangement, Site1 water is essential in stabilizing the fold by connecting the amide of V161 and the carbonyl of S132 and, thus, tightening the structural elements to the general framework of the structure. Removal of this water during the simulation destabilizes the site (Fig. 2Bb2), producing fluctuations in the S132 position as large as 4 Å. This site is of special interest because the involved water is present in all of the x-ray prion structures (Table 1). The calculated free energy of binding for this water molecule (see Materials and Methods) is –25.82 kJ·mol^–1. This result is in the range of values calculated with different techniques for the water binding free energy in deep pockets of proteins (30), and it provides an estimation of the local stabilization due to the protein–water interactions.

Site2 has a long residence time and has been located in huPrP and shPrP (PDB ID codes 1UW3 and 1I4M) (Fig. 2Cc1). The site is in a cavity positioned between the end of β2 and the H2 segments and enclosed by residues Y128, R164, Y169, F175, and D178. Some of these residues (Y128, R164, and D178) have a key role for the β-sheet stability and the cohesion of secondary-structure elements β1, β2, and H2 (31, 32). During the simulations, the burial of the site prevents solvent exchange with the bulk solution (Fig. 2Cc2). The water is sited next to the loop region indicated as the putative epitope for the protein–X binding (12). This loop has been found to be either flexible or rigid in different structures. Indeed, it is poorly defined in all available mammalian PrP structures derived by NMR, apart from the elk PrP structure (33). The calculations reveal a water-mediated interaction between the backbone oxygen of F175 and the amide of R164 that bridges the end points (164–175) of the loop. Also, the water interacts with the side chains of D178 or F175. As a result, the loop flexibility (which may be relevant for the protein–X binding) may be affected by the strength of the water-mediated H bond. In fact, the artificial removal of the water during the simulations causes the pocket to swell, as confirmed by an increase of almost 2 Å in the distance between the backbones of F175 and R164 (Fig. 2Cc3). The calculated water-binding free energy is –21.11 kJ·mol^–1. The two estimated binding free energies for Site1 and Site2 are very similar, with a tighter bound water for Site1.

Site3 water interacts with the backbone amides of two vicinal residues (N1591-Q160), which are part of a bend (Fig. 2D) where the orientation of the amides enhances a dipolar coupling with the water. This hydration site is conserved in the shPrP (PDB ID code 1UW3) and displaced in the huPrP (PDB ID code 1I4M), where it interacts only with N159 amide (Table 2). This MDHS is largely occupied during the simulation by the same water molecule, with a few occasions of exchange with other water molecules. The bend, which precedes the β2 strand, remains stable and hydrated during the simulation.

Table 2. H-bond distances (Å) between water oxygen and protein atoms.

		MD simulations					X-ray structures
Site	Protein atom	shPrP	shPrP ARO	shPrP VRO	shPrP ARR	huPrP	shPrP 1UW3	shPrP 1TPX	shPrP 1TQB	huPrP 1l4M
Site1	S132—O	2.83	2.53	2.86	2.88	3.01	2.46	2.76	2.64	2.96
Site1	V161—N	2.87	3.49	2.92	2.89	3.39	2.97	2.81	2.87	3.04
Site1	Q217—OE1	2.83	2.91	3.42	3.10	4.07	3.93	2.88	2.92	2.78
Site2	R164—N	3.01	2.91	2.87	2.85	2.84	3.37	—	—	2.98
Site2	F175—O	2.83	3.01	3.11	3.09	3.07	3.05	—	—	3.01
Site3	N159—N	2.89	3.11	2.88	2.88	2.88	2.42	—	—	3.41
Site3	Q160—N	3.02	3.18	2.99	3.02	3.03	3.27	—	—	4.13

The water–protein interactions for Sites1–3 are given in summary in Table 2 for all of the x-ray structures and the MD simulations. Overall, there are slight differences among the various x-ray structures and MDHS. The main origin of these differences can be ascribed to variations in protein environment. In the MD simulation, there are no constraints to the protein motions, whereas lattice contacts influence, to a degree, the structures and molecule motions. Nevertheless, the differences in H-bond distances among MD simulations and the various x-ray structures are encouraging, apart from a few cases (Site3–Q160 in PDB ID code 1I4M, and Site1–Q217 in PDB ID code 1UW3).

Effects of the Q217R Mutation on Site1. Substituting the Q217 with R (a mutation linked with Gerstmann–Straussler–Scheinker disease) (34, 35) in the simulations has the immediate effect of expelling the water from Site1, because the original pocket is now filled by the larger R217 side chain.

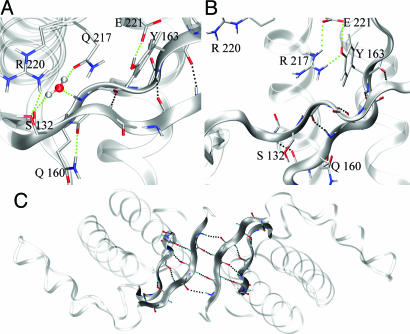
Moreover, the presence of R217 causes another major rearrangement involving the adjacent R220. The two positive charges repel each other, pushing the R220 side chain away. As observed in all of the crystal structures (except the shPrP PDB ID code 1UW3), R220 interacts with S132, causing the last segment of β1 to bulge and unzip from the facing strand β2 (Fig. 3A). When R220 displaced, this segment can relax, and the H bond between the G131 carbonyl and the V161 amide H can be formed. The H bond has the effect of elongating and stabilizing the β-sheet, which is then further stabilized by a fifth H bond that links the amide of A133 to the carbonyl of N159 (Fig. 3B). Perhaps, the whole mechanism could be taken as an example of structural optimization in the proximity of an unprotected H bond. In the wild type, the carbonyl of G131 and the amide H of V161 are prevented from H bonding by their surrounding side chains. Instead, they establish alternative interactions. Because in the crystal this particular β-sheet brings the native shPrP monomers together to form a dimer stabilized by a four-stranded antiparallel sheet (14), we propose that this dimerization is a model for the initial step in eventual polymerization (Fig. 3C). This model agrees well with recent findings that confirm the model of intermolecular β-sheet formation as a widespread mechanism of protein aggregation (36).

Fig. 3.

Q217R mutation. (A) MD wild-type main interaction in the Site1 region. (B) Effect of Q217R mutation on the local MD simulated structure, with relative structural rearrangements in the pocket. (C) Dimerization model based on the MD mutation and x-ray symmetry contact (PDB ID code 1UW3; crystal packing).

Smooth Spots and Surfaces with Under-Protected H Bonds. The original intention in calculating the water density map was to investigate the solvent behavior in the neighborhood of the under-protected regions (H1, C-terminal H2, loop H2–H3, and C-terminal H3) of the PrP for which the backbone H bonds are exposed to surrounding water. In these regions, we expected to find well defined and relatively stable waters interacting with the polar atoms of the protein and, thus, compensating for the under-protection of the main-chain H bonds. Unexpectedly, however, we did not find any particularly localized hydration site in these regions.

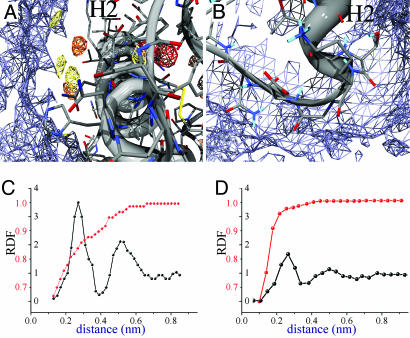
The water entropy-distribution map (see Materials and Methods) reveals the structural and dynamical properties of water around the protein molecule. The higher values in the entropy distribution shown in Fig. 4 by blue contours, resemble those of bulk solvent. By focusing on the middle region of H2 (Fig. 4A), we observe two different organizations of the water. The highdensity regions show a progressive attenuation of the entropy approaching the protein surface, because of the three-dimensional organization of the waters at this surface. The bulk solvent is not directly in contact with the protein, which is largely enveloped by structured waters (protected regions in the NMR experiments) (10–12). A different picture emerges in the proximity of the unprotected regions (Fig. 4B); the entropy map, even close to the protein surface, resembles that of the bulk solvent.

Fig. 4.

Water entropy-distribution maps around H2. The high-entropy contours are shown in blue. (A) Close-up view of the middle regions of H2. The water-density contours as in Fig. 1. (B) H2 C-terminal with H2–H3 loop. (C) Radial distribution function vs. distance from the protein surface on the sharp spots. Water density is shown in black, and entropy is shown in red. Both the density and the entropy have been normalized with respect to the value assumed in the bulk solvent. (D) Radial distribution function on the smooth spots. Colors and lines are as described for C.

Entropy and density radial-distribution functions are different in the sharp and smooth solvent regions, as shown in Fig. 4 C and D, respectively. Sharp spot regions present well defined first- and second-solvation shells and a gradual increase in entropy, contrary to the smooth spots regions that present an abrupt increase in entropy.

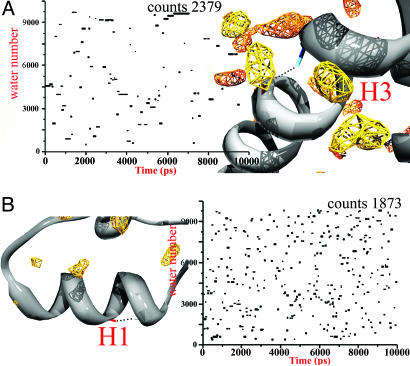
Solvent–backbone H-bond exchanges were followed by analyzing the evolution of the interacting water with time; waters are followed by means of identification numbers (Fig. 5). A R208–E212 H bond occurs in H3 (Fig. 5A) and is surrounded by MDHS with fast and medium residence times. Only a limited number of waters are found to be in direct contact with the H-bond. The interactions in the protected surfaces last, on average, for a relatively long time compared with the times observed in the unprotected regions (Fig. 5B). The scattered plot resulting in the latter regions indicates a very fast water exchange, which is similar to the behavior in the bulk solvent.

Fig. 5.

Time evolution of solvent-backbone H-bond exchange. Index numbers of interacting waters with a specific H bond during the simulation are given. The H-bonds R208–E212 (A) and V189–T193 (B) are shown. The counts are the total number of “visits” of the waters around the analyzed regions. The water-density contours are as shown in Fig. 1.

The backbone time-averaged RMS fluctuation (data not shown) reveals a close correspondence between flexible and bulk solvated regions, raising the following questions: Can the bulk water at the unprotected surfaces result from protein vibrations, or is the intrinsic flexibility at the unprotected surface enhanced by the lack of structured waters around it? To answer these questions, we repeated the MD simulations, keeping the protein rigid by restraining the main-chain atom positions and, hence, preventing the effect of the backbone flexibility. The resulting density map (data not shown) is essentially the same as that obtained with the previous calculations, suggesting that the specific hydration profiles obtained in the calculations are a property of the protein local sequence and conformation.

Conclusion

In this study, we studied the PrP hydration patterns with MD simulations, which provided enough data to address the starting questions on the role of the structurally conserved waters and the organization of the water at “unprotected” H-bond sites.

By selectively removing the waters with longer residence times, we observed destabilization of structural elements in crucial regions of the fold; therefore, we explained at an atomic level the water structural role and calculated their free energy of binding to the protein.

Also, we found that one of the structurally conserved waters appears to have a key role in holding in place a residue involved in a pathogenic mutation associated with Gerstmann–Straussler–Scheinker disease (34, 35). In the calculations, there are conformational rearrangements arising from the mutation Q217R that lead to an elongation of the β-strand. Note that in the shPrP crystal the monomers form a weak dimer through the β-sheet interactions between 129 and 132. We propose that the elongation of the β-sheet at 133 and 159, shown in the simulated mutated conformer, is a step in a more stable dimerization process, which leads to fiber formation.

The water-density analysis exhibits a pattern of dual behavior of water with respect to the protein surface that can be explained by analysis of the local configurational solvent entropy. With our simulations, we describe at an atomic-level regions where localized water molecules possess a low solvent entropy and constitute a separate layer between protein surface and bulk solvent. Also, we observed protein surface patches that are in contact with highly mobile waters having high entropy, reminiscent of the bulk solvent. This high solvent entropy could compensate for the loss in energy of exposing main-chain H bond during the folding. Also, our data suggest that these regions could be more likely to have their H-bond atoms interacting with the adjacent water, lowering the activation required to unfold. These surfaces, which are more prone to interact under particular conditions, may lead to polymerize into fibers.