On the orientation of the backbone dipoles in native folds

Abstract

The role of electrostatic interactions in determining the native fold of proteins has been investigated by analyzing the alignment of peptide bond dipole moments with the local electrostatic field generated by the rest of the molecule with and without solvent effects. This alignment was calculated for a set of 112 native proteins by using charges from a gas phase potential. Most of the peptide dipoles in this set of proteins are on average aligned with the electrostatic field. The dipole moments associated with α-helical conformations show the best alignment with the electrostatic field, followed by residues in β-strand conformations. The dipole moments associated with other secondary structure elements are on average better aligned than in randomly generated conformations. The alignment of a dipole with the local electrostatic field depends on both the topology of the native fold and the charge distribution assumed for all of the residues. The influences of (i) solvent effects, (ii) different sets of charges, and (iii) the charge distribution assumed for the whole molecule were examined with a subset of 22 proteins each of which contains <30 ionizable groups. The results show that alternative charge distribution models lead to significant differences among the associated electrostatic fields, whereas the electrostatic field is less sensitive to the particular set of the adopted charges themselves (empirical conformational energy program for peptides or parameters for solvation energy).

Charge–charge and ionizable group–peptide dipole interactions have been proposed to play a relevant role in the stabilization of proteins (1) and in determining the native fold (2). Although a quantitative analysis of the relative stability of the native fold requires consideration of a delicate balance among all physical forces, we concentrate here on how electrostatic interactions can be identified as an important determination of the backbone conformation of the native structure.

It is well known that the CO and NH dipoles in an α-helix are electrostatically aligned nearly parallel to the axis of the helix (3), and that the alignment of peptide dipoles in various types of secondary structure elements is significant in determining the 3D structure (4) and stability of globular proteins (5, 6). The concept of the preferential alignment of the backbone dipole moments (μ) with the local electrostatic field (E) (see Fig. 1) was used by Piela and Scheraga (7) and by Ripoll and Scheraga (8) to develop procedures to surmount the multiple-minima problem in the conformational analysis of peptides and proteins. The charges used in these procedures to define μ, shown in Fig. 1, are ECEPP/3 (empirical conformational energy program for peptides) charges (9) that differ from other charges, e.g., PARSE (parameters for solvation energy) charges (10).

Fig. 1.

Ball and stick representation of a peptide unit showing the atoms and bonds that lie in the peptide plane. The ECEPP/3 charges (in electronic charge units) of those atoms associated with μ are indicated. The expressions given by Eqs. 2 and 3, respectively, are used to compute μ_i and the position, r_i, where μ is located. The value of E(r_i), the local electrostatic field, is computed either by solving the Poisson equation numerically when solvent is present, or by using Eq. 4 in the absence of solvent.

Approximately 50% of the residues in proteins fit in the most common secondary structure classes (11), such as α-helix or β-sheet, and the rest are associated with statistical coil fragments or loop regions. The question then arises as to how the μ's in proteins behave.

We view the native fold as the net effect of different interactions such as van der Waals, electrostatic, and solvent polarization, among others. If the electrostatic interactions were dominant, then it would be expected that all of the dipoles would be well aligned with the local electrostatic field. On the other hand, if the role of electrostatics is irrelevant, then the dipoles should not have a preferential orientation with respect to the local electrostatic field. The purpose of this work is to explore the extent of the alignment of the peptide units in the local electrostatic field and the dependence of this extent on the adopted representation of the electrostatic charge distribution. In an attempt to clarify the role of electrostatic interactions in determining the native conformation, we have analyzed a relatively large set of experimentally solved protein structures. Particular emphasis has been placed on comparing different representations of the electrostatic field.

Proteins contain ionizable groups whose ionization states depend on a number of variables, among them the pK_a, the pH of the solution, and the interaction with neighboring groups. As a consequence, the charge distribution and the conformation of a protein are coupled (12). A computational treatment of this effect is quite difficult, and simplifications of this problem are adopted in most theoretical studies carried out at present. Typically, charge assignment in molecular mechanics and molecular dynamics calculations on proteins with explicit solvent are carried out by using the Null/Zero model (13). In this model, any ionizable residue is assigned a zero or ±1e charge (adding or subtracting a H⁺ atom) without consideration of nearby interacting groups. On the other hand, it is common in molecular mechanics calculations with implicit solvent to assume that all residues are neutral to avoid overestimating the electrostatic contributions.

Consequently, calculations of E in this work range from simple representations, in which the molecule is considered in isolation with all residues in a neutral state, to more sophisticated ones in which the problem of ionization equilibria, as well as the electrostatic effects of solvation, are considered (14).

The present study has also enabled us (i) to assess the accuracy of using a fixed (neutral or charged) distribution in molecular modeling and simulations, instead of the appropriate but more complex and time-consuming representation that considers variable ionization states of the ionizable residues; and (ii) to test the validity of the assumption that μ's are locally optimally oriented with E. The latter assumption is used in protein structure prediction approaches such as the self-consistent electric field (SCEF) (7) and the electrostatically driven Monte Carlo (EDMC) (8) methods.

Materials and Methods

Conversion of the Native Structures from Flexible to Rigid ECEPP/3 Geometry. To carry out the present study, the experimentally determined conformations (i) were regularized, i.e., all residues were replaced by the standard ECEPP/3 residues in which bond lengths and bond angles are fixed (rigid geometry approximation), and (ii) hydrogen atoms were added.

The conversion process was carried out by generating the new rigid-geometry conformation from the N terminus by adding one residue at a time and minimizing the rms deviation (rmsd) between all heavy atoms in the generated fragment and the corresponding fragment in the experimental structure. The procedure was iterated until the C-terminal group was added to the chain. The final conformations resulting from this regularization procedure are quite close to the experimental ones in practically all of the cases, with rmsd values for all of the heavy atoms ranging from 0.1 to 0.8 Å.

The experimental set of structures contains 112 proteins and was obtained from the Protein Data Bank (PDB) (15). These proteins are identified by a four-letter PDB code followed in some cases by an extra single number or letter to indicate the particular monomer used in the calculations. The list is the following: 1ACX, 1AZU, 1BBP_A, 1BDD, 1BDS, 1BMV_A, 1BMV_B, 1CBH, 1CC5, 1CDT_A, 1CRN, 1E0L, 1ECA, 1FC2_C, 1FKF, 1FND, 1FSL, 1FXI, 1GAB, 1GDL, 1GPL, 1HIP, 1IL8_A, 1L58, 1LMB, 1MCP, 1MRT, 1OVO_A, 1PAZ, 1PPT, 1PRC_C, 1PRC_H, 1PRC_L, 1PRC_M, 1PYP, 1R09, 1RBP, 1RHD, 1S01, 1SH1, 1TGS_I, 1TNF_A, 1UBQ, 1VII, 256B_A, 2AAT, 2AK3_A, 2ALP, 2CAB, 2CCY_A, 2CYP, 2FOX, 2GBP, 2GLS, 2GMZ, 2GN5, 2I1B, 2LTN_B, 2MEV_4, 2MHU, 2OR1_L, 2PAB_A, 2PCY, 2PHH, 2SNS, 2SOD_B, 2STV, 2TGP_I, 2TMV_P, 2TSC_A, 2UTG_A, 2WRP_R, 3AIT, 3BLM, 3CD4, 3CLA, 3CLN, 3EBX, 3HMG_A, 3HMG_B, 3ICB, 3PGM, 3RNT, 3SDH, 3TIM, 4BP2, 4CMS, 4CPA_I, 4CPV, 4GR1, 4PFK, 4RHV_4, 4RXN, 4TS1, 4XIA_A, 5CYT, 5ER2_E, 5HVP_A, 5LYZ, 6CPA, 6CPP, 6CTS, 6DFR, 6HIR, 6TMN_E, 7CAT_A, 7RSA, 8ABP, 8ADH, 9API_B, 9PAP, and 9WGA.

Secondary Structure Assignment. The Dictionary of Secondary Structure of Proteins (16) was used to classify the residues of the set of 112 native proteins. Subsequently, the residues were grouped in three different classes, alpha (α), beta (β), and loop (Λ), following the scheme of Rost and Sander (11). A dipole moment was associated with the α or β class if the corresponding peptide unit is located between two residues in α-helical or β-strand conformations, respectively. Otherwise, the dipole moment was assigned to the Λ class.

Stiffness of the Polypeptide Chain. As for polymers in general (17), bond-angle restrictions in real polypeptide chains determine that the direction assumed by a given main chain bond is strongly influenced by the direction of a few preceding bonds in the chain. These restrictions give rise to a local stiffness of the protein backbone. To investigate the effect of this local stiffness of the polypeptide chain on the alignment between μ and E, we selected seven proteins (PDB ID codes 1BDD, 1E0L, 1FSD, 3ICB, 4RXN, 1RBP, and 2GBP) and generated 1,000 random conformations for each.

All backbone and side-chain dihedral angles of these random conformations were chosen randomly between 180.0° and –180.0°, with the exception of the dihedral angles ω of the peptide group that were always chosen in the trans (180.0°) conformation. Local energy minimization was carried out for each conformation by using a simplified force field based on a soft-sphere model (18) to remove atomic overlaps. No electrostatic term was included in these energy minimizations to avoid bias in the alignment of μ and E.

Computation of the Alignment Between μ and E. The current study was carried out by analyzing the alignment of the μ's with E's in native proteins generated by (i) the protein molecule itself, and (ii) the protein molecule plus its aqueous solvent.

To assess the robustness of the computed results, we considered two different sets of partial atomic charges as given by ECEPP/3 (9, 19–21) and PARSE (10), respectively. In addition, we investigated the effects of the following alternative assignments of the charge distribution in the protein. (i) The ionizable residues were assigned charges obtained by solving the multiple titration binding problem, computed at the experimental pH. Computations of the average degree of ionization of ionizable residues in a subset of 22 proteins was carried out by using the multiboundary element method of Vorobjev and Scheraga (22). (ii) The ionizable residues were assigned charges dictated by the Null or Zero model (13), by adding or subtracting a proton (H⁺), depending on the group's intrinsic pK_a and the pH of the solution, and by neglecting the effects of nearby interacting groups. (iii) All residues were assigned neutral charges.

The angle θ_i between the local electrostatic field, E_i(r_i), and the ith dipole moment, μ_i(r_i) (see Fig. 1), is used as a measure of the alignment between the two vectors, and is computed as

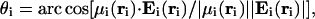[1]

where

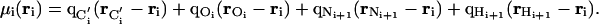[2]

The quantities E_i(r_i) and μ_i(r_i) are evaluated at position r_i (with respect to an arbitrary origin). The vector r_i is chosen, by convention, as a charge-weighted average of the positions of the C′, O, N, and H atoms forming the ith peptide plane, i.e.,

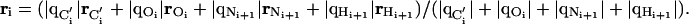[3]

The computation of the local electrostatic field due to the protein molecule itself is carried out by using Coulombs law:

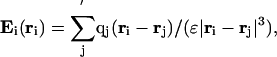[4]

where the sum runs over all of the atoms of the molecule except (as indicated by the prime in the summation symbol) for (i) those forming the peptide unit i and (ii) a predetermined set associated with the local stiffness of the chain, q_j is the charge of atom j located at position r_j, and ε is the dielectric constant in which the charges are embedded (the protein environment), assumed to be 4.

Calculations of E were carried out by considering two alternative groups of excluded atoms: (i) the short window (SW) containing atoms forming the peptide unit i, as well as the preceding and following C^α atoms (Fig. 1); and (ii) the long window (LW) containing atoms in the SW plus the atoms of the preceding and following peptide units. Our LW definition resembles the one used by Avbelj and Moult (23) to analyze the role of electrostatics of the main chain atoms on the conformational preference of amino acid residues in proteins.

Computation of the local electrostatic field due to both the protein molecule and its aqueous environment was carried out by solving the Poisson equation numerically with the program delphi (24). In these calculations, the molecule was considered as a low-dielectric cavity (ε_prot = 4) immersed in a cubic grid (65 × 65 × 65 grid points) assumed to be filled with water (ε_H2O = 78.3). Partial charges were assigned to each of the atoms of the protein. The focusing feature from the program delphi with Coulombic boundary conditions was used to obtain precise values of the electrostatic field. The value of E at a given position (e.g., the position at which a particular μ is computed) was obtained by interpolation between the grid values from the final delphi run.

Because the calculation of the local electrostatic field, E, requires the exclusion of the charges associated with the ith dipole moment and the neighboring atoms (i.e., SW or LW; see the prime on Σ of Eq. 4), N – 1 runs with the program delphi were needed to compute E at the position of each dipole in a protein that contains N residues.

In treating the ionizable residues, the charges were assigned by the following procedure. An atom i, belonging to an ionizable residue j, was assigned a charge, q_i, that resulted from a linear interpolation between the uncharged and fully charged states, i.e.,

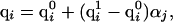[5]

where 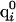is the partial charge of the ith atom in the uncharged state of the jth ionizable residue, 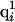is the partial charge of the ith atom in the charged state of the jth ionizable residue, and α_j is the degree of ionization of the jth ionizable residue computed by the procedure adopted to obtain the charge distribution. A special treatment was needed for ionizable residues in the first and last positions in the sequence when the end-groups of the polypeptide chain were also ionizable. In those cases, a double interpolation scheme was derived to assign the charges described by

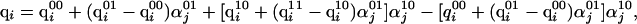[6]

where 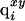is the partial charge of the ith atom that depends on the state of ionization of the end group and the neighboring residue (if it is ionizable); the first superscript, x, indicates the ionization state of the end group (x = 0 indicates that it is in the uncharged state, and x = 1 indicates that the end group is fully charged). Similarly, the second superscript, y, indicates the ionization state of the neighboring ionizable residue (y = 0 indicates that it is in the uncharged state, and y = 1 indicates that the residue is fully ionized). Finally, and represent the degree of ionization of the end group and neighboring ionizable residue, respectively.

Results

Analysis of the Dipole-Field Alignment in the Gas Phase. Randomly generated conformations. The average angle between the μ's and E's computed with the SW for the set of 112 proteins in the gas phase is ≈46°. This result indicates that the local E, on average, has a component parallel to μ and pointing in the same direction. However, the bond-angle restrictions in the polypeptide chain can be largely responsible for the observed alignment between the μ's and E's. To investigate further the effect of the local environment on the direction of the electrostatic field, a set of randomly generated conformations was studied. The influence of the local stiffness on the direction of the electrostatic field in 1,000 randomly generated conformations is illustrated by an analysis of the alignment between the μ's and E's for seven proteins (Fig. 2).

Fig. 2.

Plot of the average angle θ_i between μ_i and E_i, computed from sets of 1,000 randomly generated conformations for each of the seven specified proteins. To analyze the effect of the stiffness of the polypeptide chain, the electrostatic field was computed by using Eq. 4, by excluding atoms defined by (i) the SW (circles) and (ii) the LW (squares)_. Each conformation was energy-minimized by using a soft-sphere potential (16) to relieve atomic overlaps.

Comparison of the average alignment, θ, using the SW (≈60°) and LW (≈84°), indicates that the local electrostatic field is strongly influenced by the local structure around the peptide unit. Because our aim is to investigate the effect of the long-range electrostatic interactions on the organization of the polypeptide chain in native folds, from here on, the analysis will be focused on the electrostatic field computed by using the LW in Eq. 4.

Native proteins. Analysis of the alignment of μ and E was carried out for different secondary structure elements in the set of 112 protein structures. The electrostatic field was computed by using Eq. 4 with the LW set of excluded atoms. The α structural class encompasses 30.7% of the total number of μ's in the set, while the β and Λ classes contain 16.1% and 53.2% of the μ's, respectively. The μ's in the α class show the best alignment with the electrostatic field with an average value of 31.1°± 16.4°. Even though μ's associated with the β and Λ classes show average values (50.5°± 31.1° and 61.5°± 35.4°, respectively) lower than randomly generated conformations (84°± 34.7°; see Fig. 2), their standard deviations are significantly larger than those of the α class.

Analysis of the Dipole-Field Alignment in Aqueous Solvent. Alignment of μ and E in native proteins. As already mentioned, the native structure should be the result of a balance of different interactions. In particular, the electrostatic effects include contributions from the solvent. To account for these contributions, the Poisson equation was solved numerically by using the program delphi, and the local electrostatic field at each dipole position was computed for a reduced set of proteins.

To assess the robustness of the computed results, the average value of the angle between μ and E was computed with two different sets of charges: the ECEPP/3 and PARSE charges, respectively. In addition, to estimate the differences between different charge-parameter sets and different representations of the charge distributions (i.e., alternative ionization states of the molecule), the angle between their respective electrostatic fields was computed. A distribution based on the solution of the Poisson equation that considers 2^ζ ionization states of a given protein, with ζ being the number of ionizable residues, is taken as the most accurate representation of electrostatic effects. Consequently, the values of E obtained in delphi calculations with the boundary element method (BEM) states of ionization (22) were used as a reference with which to measure the quality of the other two simplified representations of the charge distribution.

These particular calculations were carried out on a set of 22 native proteins. Average values of θ over 22 proteins, for μ's associated with the α, β and Λ classes, were obtained by using charge distributions given by (i) a solution of the problem of multiple titration as given by the BEM, (ii) the Null/Zero approximation, and (iii) assuming neutral charges for all residues, respectively. Averages computed by using ECEPP/3 (see Fig. 3) and PARSE charges (data not shown) led to very similar values. Both sets of charges show that dipole moments are preferentially oriented with respect to the local electrostatic field, with θ (α) < θ (β) < θ (Λ), i.e., with a similar tendency as observed for gas phase calculations on the larger set of 112 proteins. Analysis of the angle between μ and E (see Fig. 3) indicates also that the average values are affected only slightly by the assumed charge distribution.

Fig. 3.

Bar diagram indicating the average value of the angle θ_i between μ_i and E_i, computed for sets of dipole moments associated with the α, β, and Λ classes (see text). The analysis was carried out on a subset of 22 experimental structures by assuming that the molecules were embedded in aqueous solution (ε = 78.3) and considering three alternative charge distributions: (i) all residues in a neutral state (gray bars), (ii) residues charged according to the Null/Zero model (white bars), and (iii) charges of ionizable residues determined by BEM (black bars). The results were obtained by using ECEPP/3 charges.

Difference between alternative electrostatic field representations in native proteins. The previous analysis might, at first sight, lead to the conclusion that the optimal orientation of μ and E does not depend on either the charge set or the adopted charge distribution or even on the solvent. However, this analysis, although important, should be complemented with the results of the relative orientations of the E's because of the different sets of charges, their corresponding distribution, and by analysis of the solvent effect. The angles (Ω) between representations of the electrostatic fields vary from protein to protein and are presented in Table 1. As expected, for most of the proteins, the Null/Zero distribution leads to E's that are more similar to those obtained from the BEM distribution (Ω values listed in the third and fourth columns of Table 1) than the E's generated by the neutral distribution (Ω values listed in the fifth and sixth of Table 1). Among all 22 proteins, the best agreements between the associated E's and the reference from the BEM distribution were found for protein 9API_B with Ω = 1.9°, using ECEPP/3 charges, and for protein 2OR1_L with Ω = 1.5°, using PARSE charges.

Table 1. Average Ω angle between alternative representations of the electrostatic field considering solvent.

		Average angle Ω between electrostatic field vectors,‡ degrees
		Null/Zero model and BEM method§		Neutral and BEM method¶
Protein name,* PDB code	Disagreement in the assignment of charge† (%)	ECEPP/3	PARSE	ECEPP/3	PARSE
1BDD	65 (50)	21.8	12.4	19.4	10.3
1BDS	20 (20)	18.7	17.6	20.2	18.0
1CDT_A	41 (35)	28.5	29.2	31.8	22.0
1CRN	17 (0)	7.6	5.0	17.9	11.6
1E0L	23 (18)	17.1	11.6	40.5	18.5
1FC2_C	27 (27)	7.7	4.4	25.6	15.0
1GAB	15 (15)	18.1	11.6	19.6	11.2
1MRT	0 (0)	2.7	2.1	29.8	20.2
1OVO_A	0 (0)	11.3	6.4	33.8	25.2
1PPT	8 (8)	8.7	4.7	24.0	15.1
1SH1	50 (20)	34.0	24.8	26.6	22.3
1TGS_1	15 (15)	18.0	9.1	33.7	22.0
1VII	25 (25)	4.6	2.6	16.2	11.0
2LTN_B	0 (0)	15.1	27.0	33.3	33.2
2MHU	0 (0)	11.4	8.6	27.4	20.8
2OR1_L	7 (0)	2.2	1.5	21.6	13.0
2TGP_I	0 (0)	32.3	21.9	32.9	17.0
3ICB	21 (11)	16.4	13.7	25.5	14.6
4CPA_I	22 (0)	11.9	12.4	55.3	43.5
4RXN	30 (22)	27.5	18.8	44.9	27.7
6HIR	10 (10)	14.8	8.7	38.9	20.6
9API_B	0 (0)	1.9	2.6	37.2	26.8

The value of E is computed with solvent polarization included, as a solution of the Poisson equation with delphi, as explained in Materials and Methods.

^*Four-letter code used to designate the protein in the PDB. An extra single letter that follows the PDB code indicates the particular monomer used in the calculation.

^†To decide whether the average degree of charge computed by the BEM is different from the assignment of the Null/Zero model (1/0), the following criterion was adopted. If the average degree of charge computed at a fixed pH for a given ionizable residue differs by more than a predefined percentage from the integer values 1 or 0, the charge assignment is considered different. Predefined difference values of 10% or 30% between both assignments were used here. The values listed correspond to the percentage of all ionizable groups for which the BEM and Null/Zero model disagree in the charge assignment by > 10% or, within parentheses, by > 30%.

^‡Angles between representations of electrostatic fields as explained in Difference between alternative electrostatic field representations in native proteins. For each protein, two values are listed; the first corresponds to calculations with the ECEPP/3 charge set, and the second one corresponds to calculations with the PARSE charge set.

^§Values obtained with electrostatic fields computed by using the distributions of charges as given by the Null/Zero model or the BEM model.

^¶Values obtained with electrostatic fields computed by using the distributions of charges as given by neutral approximation or the BEM model.

Fig. 4 shows the values of the angle, Ω_i, between E_i vectors computed at position r_i (where μ_i is located), by using the Null/Zero and the BEM distributions (black bars) and the Neutral and BEM distributions (gray bars), using PARSE charges in both cases, for the protein 1OVO_A. For this protein, using the Null/Zero charge distribution as an approximation of the more reliable BEM distribution leads to a more accurate representation of the electrostatic field than the use of the neutral charge distribution.

Fig. 4.

Black bars indicate differences in the values of the angle Ω_i between electrostatic field computed at r_i (see Eq. 3) by using the Null/Zero and the BEM distributions for the protein 1OVO_A. The gray bars correspond to the differences in the values of the angle Ω_i computed by using the Neutral and the BEM distributions. Each letter on the abscissa indicates the secondary structure class of each particular dipole moment from the N to C terminus in the structure of 1OVO_A.

However, straightforward use of the Null/Zero charge distribution does not always guarantee an accurate representation of E. Fig. 5 shows a similar diagram of the Ω_i between E_i vectors computed by using the Null/Zero and the BEM distributions and ECEPP/3 charges for the protein 1SH1. The structure of this protein was obtained by NMR methods at pH 5. Computation of the average degree of charge of the ionizable groups shows that 6 of 18, namely the N-terminal group, Asp-7, Glu-8, Lys-32, Asp-42, and Arg-45, differ by at least 30% from the estimation provided by the Null/Zero model. For this protein, the agreement in the relative orientations of E between the Null/Zero and BEM distributions shown in Fig. 5 is quite poor.

Fig. 5.

Bar diagram showing the differences in the values of the angle Ω_i between the electrostatic field computed at r_i (see Eq. 3) by using the Null/Zero and the BEM distributions for the protein 1SH1. Hatched bars indicate those ionizable residues for which the charge assignments given by the Null/Zero model and the BEM differ by >30%. Each letter on the abscissa indicates the secondary structure class of each particular dipole moment from the N to C terminus in the structure of 1SH1.

These two examples illustrate the difficulties in replacing the actual charge distribution (i.e., the distribution derived from the BEM method) by an alternative one such as that based on neutral charges or the one derived from the Null/Zero model. Therefore, effort should be directed to include the most accurate charge distribution, such as that obtained with the BEM, for molecular simulations.

Energetic analysis of the orientation of the backbone dipoles with the electrostatic field in native proteins. The average dipole energy, 〈–(μ·E)〉, and the average magnitude of E, 〈|E|〉, for each structural class was computed for the proteins listed in Table 1. Results from this analysis are presented in Table 2, which shows that the average alignment energies are significantly more negative for dipoles of the α class than for those in β or Λ class, independent of the set of charges or the charge distribution method used in the computations. However, for the β and Λ classes, the relative alignment energies depend on the set of charges. An interesting observation from Table 2 is that the average magnitudes of E computed for the α and Λ class are comparable but two to four times larger than those computed for the β class.

Table 2. Energetics of the alignment between μ and E in solution.

Structural class	Average dipole energy* 〈-(μ·E)〉, kcal·mol-1		Average field† 〈|E|〉, kcal·mol-1·e-1·Å-1
	Neutral‡	BEM§	Neutral‡	BEM§
α	-1.11 (-4.72)	-1.28 (-4.97)	2.52 (5.28)	2.89 (5.52)
β	-0.42 (-1.47)	-0.45 (-1.53)	1.12 (1.96)	1.24 (2.00)
Λ	-0.19 (-1.98)	-0.29 (-2.18)	3.45 (4.84)	3.79 (5.05)

The set of 22 proteins listed in Table 1 was used for these computations.

^*Values were computed as (1/N) Σ_i^N (-|μ_i(r_i)||E_i(r_i)| cos θ_i), with N being the number of μs contained in the particular structural class (values of N for the α, β, and Λ classes are 266, 119, and 636, respectively). In each column, two values are listed for each structural class; the first one corresponds to calculations with the ECEPP/3 charge set, the second one, in parentheses, corresponds to calculations with the PARSE charge set. The average values of μ are 0.54 eÅ and 1.07 eÅ, (1eÅ = 4.8 Debye) for the ECEPP and PARSE sets, respectively.

^†Values were computed as (1/N) Σ_i^N|E_i(r_i)|. See item * for additional explanation.

^‡Values were computed assuming a neutral charge distribution.

^§Values were computed assuming the BEM charge distribution.

Although the energies presented in Table 2 are quite dependent on the set of charges adopted, these numbers argue in favor of an important role of the alignment of μ's with E's in the stabilization of the whole backbone conformation.

Discussion and Conclusions

The results from this work (see Analysis of the Dipole-Field Alignment in the Gas Phase in Results) show that the actual electrostatic field acting on a given μ has a significant component due to the local environment that dominates the alignment, regardless of the secondary structure class, leading to average angles between the μ's and E's of ≈60° in randomly generated conformations (Fig. 2, E's computed with the SW) and ≈46° for our set of 112 proteins in the gas phase. When the local contribution due to the backbone atoms of neighboring residues is excluded (i.e., for E's computed with the LW), the dipole moments of the main chain, in particular those μ's associated with α-helical and β-strand conformations, remain on average well aligned. A significant finding from this work is that this alignment is not restricted only to those μ's from peptide units associated with secondary structure motifs such as α-helices and β-strand but extends also to μ's associated with loop and statistical coil regions.

When an implicit solvent model (delphi) was used to compute solvent polarization, a significant dependence of the average orientation of E as function of different distribution of charges was found for some proteins (see Figs. 4 and 5), suggesting that protein conformation is sensitive to the charge distribution. Because the observed pKs of the ionizable groups depend on the conformation of the molecule and on the environment of these groups in the macromolecule (25), an erroneous selection of a model for the charge distribution could have important consequences on folding simulations.

The results of this work (i) are consistent with previous studies (1–5) that postulate a relevant role for electrostatic interactions in stabilizing the native fold; (ii) argue strongly for a relevant role for electrostatic forces in determining the direction of the main chain in the native conformation; (iii) go beyond current knowledge by showing that the backbone dipole orientation with respect to the electrostatic field is not restricted to α-helices and β-strands; and (iv) show the importance of an adequate choice of the charge distribution to represent the electrostatics.

In the same way that burial of nonpolar amino acids is an indication of the importance of hydrophobic effects in proteins, we consider that the alignment of the backbone dipole moments with the electrostatic field generated by the whole molecule and the surrounding solvent (but excluding the local environment of the dipole), described in this work, is a footprint that highlights the relevance of the electrostatic forces in determining the native fold.

Finally, although the multiple-minima problem remains as one of the most formidable unsolved challenges in the conformational analysis of proteins, the results of the present study validate the assumption of optimal alignment of μ and E on which the SCEF and EDMC global optimization methods are based.