Electrostatic mechanism of nucleosomal array folding revealed by computer simulation

Abstract

Although numerous experiments indicate that the chromatin fiber displays salt-dependent conformations, the associated molecular mechanism remains unclear. Here, we apply an irregular Discrete Surface Charge Optimization (DiSCO) model of the nucleosome with all histone tails incorporated to describe by Monte Carlo simulations salt-dependent rearrangements of a nucleosomal array with 12 nucleosomes. The ensemble of nucleosomal array conformations display salt-dependent condensation in good agreement with hydrodynamic measurements and suggest that the array adopts highly irregular 3D zig-zag conformations at high (physiological) salt concentrations and transitions into the extended “beads-on-a-string” conformation at low salt. Energy analyses indicate that the repulsion among linker DNA leads to this extended form, whereas internucleosome attraction drives the folding at high salt. The balance between these two contributions determines the salt-dependent condensation. Importantly, the internucleosome and linker DNA–nucleosome attractions require histone tails; we find that the H3 tails, in particular, are crucial for stabilizing the moderately folded fiber at physiological monovalent salt.

Chromatin folding and the dynamic interplay between chromatin structures and various cellular factors directly regulate fundamental gene expression and silencing processes (1–4). Extensive studies have probed the structural and dynamic properties of chromatin and the molecular mechanisms that determine these properties (5–8). Nonetheless, questions remain concerning how a chain of nucleosomes connected by linker DNA folds into a condensed 30-nm chromatin fiber under physiological conditions (9) and what the exact arrangements of nucleosomes in the 30-nm fiber are (6). Two principal architectures of fiber arrangement proposed are the solenoid and zig-zag models. They differ significantly in how the linker DNA is arranged within the condensed chromatin fiber. In the solenoid model, the linker DNA is bent such that the consecutive nucleosomes interact with each other and form a helix (10–14); in the zig-zag model, the linker DNA remains straight and crosses the fiber axis so that the consecutive nucleosomes appear at the opposite side of the fiber axis (5, 15–18).

The structure of chromatin strongly depends on the salt environment, both in terms of the valence of the ions and their concentration in solution (1). At low salt concentrations, chromatin adopts the extended “beads-on-a-string” conformation, whereas at high salt concentrations it folds into compact forms. In the presence of linker histones (H1 or H5) under physiological salt conditions, chromatin forms the folded 30-nm fiber. The histone tails are known to be crucial for the folding of chromatin fibers (19–21; reviewed in ref. 22). The tail domains, accounting for ≈50% of the positive charges of the histone octamer, are located at the N-terminal portions of H2A, H2B, H3, and H4, and the C terminus of H2A. They are also targets for posttranslational modifications by many enzymes (reviewed in refs. 23 and 24) and are essential for the formation of highly ordered structures (25).

It has been established that the folding of chromatin is mostly attributed to the electrostatic free energy among linker DNA segments (26). However, the internal forces that govern the structure and dynamics of chromatin are not well understood. Only recently, with the advent of single molecule techniques, have these basic physical properties been measured (reviewed in ref. 27). Cui and Bustamante (28) estimated a 3.4 k_BT attractive energy per nucleosome at physiological ionic strength. Simulations showed that the nucleosome–nucleosome interaction played a major role in determining the mechanical properties of chromatin (29). A similar conclusion regarding the internucleosome attraction also was obtained in a theoretical analysis (30) of a two-angle model of chromatin (17).

Because of the size and complexity of chromatin, computational studies have been based on coarse-grained models (29, 31–34). For example, a dinucleosome was simulated on nucleosome-constrained circular DNA (31); strings of 4–24 nucleosomes were modeled by virtual bonds, and their structures were determined by geometric parameters (32); the nucleosome was represented by a spherical bead and the interaction between nucleosomes was modeled by a simple spherical isotropic step-like potential (29). A more realistic model considered nucleosomes as oblate ellipsoids, with internucleosome interactions described by the anisotropic Gay–Berne potential (34). Another approach (33) uses the Discrete Surface Charge Optimization (DiSCO) representation of the nucleosome (35). Based on the pioneering nucleosome crystal structure (36), the nucleosome is represented by a few hundred effective charges located on a regular disk and a cylinder, thereby capturing essential electrostatic and structural features of the nucleoprotein complex. Recently, the DiSCO model was further improved by an irregular-surface representation to include the fine surface details and reproduce the electrostatics interactions better (37) (see Fig. 1a).

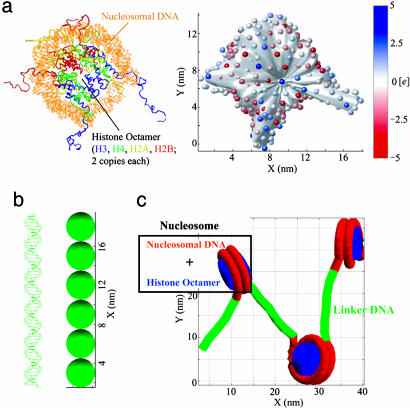
Fig. 1.

Models of nucleosome and linker DNA. (a Left) Crystal structure of nucleosome with complete modeled histone tails (PDB ID code 1KX5). (a Right) DiSCO model of the nucleosome with 300 effective charges located on an irregular surface. The surface was reduced by5Åto show the positions of the charges. The color scale indicates the value of each charge in the unit of e. (b Left) Linker DNA that connects two nucleosomes. (b Right) DNA bead model with six beads of 3-nm diameter. (c) Simplified representation of a short nucleosomal array showing how linker DNA connects nucleosomes.

To investigate the mechanism of the salt-dependent folding of the nucleosomal array in the absence of linker histones and dissect structural features of the array at different salt concentrations, we apply here the new irregular DiSCO model (37) to an array system in which all histone tails are incorporated as the model described in the recent crystal structure [Protein Data Bank (PDB) ID code 1KX5; Fig. 1a] by Davey et al. (38). Because salt effects are incorporated by means of a physical model, the nonlinear Poisson–Boltzmann equation solved at different salt concentrations to determine a set of nucleosome charges (35, 37), these analyses become possible. The effect of each histone tail on the stability, as well as salt-dependent folding and unfolding processes based on initial models (two solenoids and two zig-zags with different nucleosome orientations), are explored.

Our simulations reproduce the observed salt-dependent condensation and suggest that nucleosomal arrays adopt irregular 3D zig-zag conformations at high monovalent salt concentrations. The salt-dependent condensation is governed by electrostatic interactions, including the linker DNA–nucleosome and internucleosome attractions in addition to the repulsion between linker DNA units. Under physiological conditions, the major contribution to the folding and stability of the nucleosomal array arises from the internucleosome interactions. We also find that the histone tails, especially the H3 tails, are responsible for the internucleosome attraction and most of the linker DNA–nucleosome interactions.

Computational Methods

DiSCO Model. The details of constructing the DiSCO model with irregular surface are described in ref. 37. Briefly, 300 discrete charges were uniformly distributed on an irregular surface (Fig. 1a), which was built to represent the smoothed molecular surface of the nucleosome (PDB ID code 1KX5; with model of complete histone tails; Fig. 1a). The electrostatic potential of the nucleosome was obtained by solving the nonlinear Poisson–Boltzmann equation with the program qnifft 1.2 (39–41). The atomic charges and radii were set by the CHARMM27 force field (42). The discrete charges were optimized with the truncated Newton program tnpack (43–45), integrated in the disco software package to reproduce with Debye–Hückel approximation the electric field in the region 0.5 nm away from the model surface (37).

These nucleosomes were linked together with six DNA beads of 3-nm diameter represented by the elastic DNA approach (46–48) (see Fig. 1b). The linker DNAs connected to nucleosomes at the entry and exit points of nucleosome DNA that wrap 1.75 turns on the core (33). The default local geometry of linker DNA at the entry–exit point was such that these linker DNAs had the same orientation and phase as the nucleosomal DNA. The electrostatic and elastic properties of the DNA segments were as described in ref. 33. With this approach, the electrostatic interactions for both the internucleosome and the linker DNA–nucleosome were incorporated explicitly into the simulation of a 48-unit chromatin fiber (33), unlike other approaches.

The DiSCO model has been applied to Brownian dynamics simulations of dinucleosome, trinucleosome, and 48-mer chromatin fiber (33), as well as supercoiled DNA bound to Hin and Fis proteins (49, 50). In these applications, good agreement with experiments has been demonstrated.

Energy Terms. The total energy of the system includes stretching, twisting, bending energy, electrostatic interaction, and excluded volume effect (see Supporting Appendix, which is published as supporting information on the PNAS web site, and ref. 33 for details). All energy parameters are listed in Table 3, which is published as supporting information on the PNAS web site. Except for the excluded volume parameters (σ₁ and σ₂), which are reduced by 0.5 nm to accommodate the inclusion of the histone tails, all parameters were the same as in ref. 33.

Monte Carlo (MC) Simulation. We used the standard Metropolis method (51) in our MC sampling to generate the ensemble of nucleosomal array conformations in equilibrium at given salt concentrations. As in previous DNA simulations (46), two types of moves were used. For the local move, one bead (either a DNA bead or nucleosome core particle) was randomly selected and perturbed; the movement orientation was uniformly distributed in the space, and the amplitude was within [0, 0.05 nm]. For the global move, after a bead was randomly selected, the shorter part of the array was rotated along a random axis that passed through the selected bead; the orientation of the axis was uniformly distributed in space, and the rotation angle was uniformly distributed within [0, 5°] (or [0, 10°] at 10 and 30 mM). The acceptance ratio was ≈0.5 (0.6–0.7 for 10 and 30 mM). Each MC simulation involved at least 2 million steps with the last 1.5 million steps used to calculate system properties. The run test method was used to determine MC sample sizes and ensure uncorrelated samples, as applied in ref. 52 and implemented in program mmc (http://inka.mssm.edu/~mezei/mmc). We found that after 4,098 steps for the energy and 8,196 steps for the sedimentation coefficient, the data became independent; therefore we sampled every 5000th for energy and 10000th for sedimentation coefficient for analysis.

Sedimentation Coefficient Calculation. We calculated the sedimentation coefficient for a given conformation of the nucleosomal array with the method developed by Bloomfield et al. (53) following the Kirkwood approach (54), as applied to nucleosomal arrays in refs. 19 and 55. By neglecting the contribution of linker DNA, sedimentation coefficient s_20,w can be approximated as

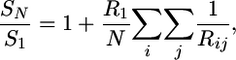[1]

where S_N represents s_20,w for a rigid structure consisting of N nucleosomes of radius R₁, R_ij is the distance between two nucleosomes, and S₁ is s_20,w of a mononucleosome. This approach assumes spherical nucleosomes, a reasonable approximation. We use R₁ = 5.5 nm and S₁ = 11.1 Svedberg (S; 1 S = 10^-13 sec) as in previous applications (19). We also used the program hydro (56) for the calculation with radius of nucleosome core particle and DNA bead as 5.0 and 1.5 nm (33). These two methods gave similar results (<0.6S differences).

All computations were performed on an Origin 2000 processor at New York University. One million MC steps took ≈4–5 days of central processing unit time.

Results

Pathway of Linker DNA Within Moderately Folded Nucleosomal Array. Hydrodynamic analyses of the reconstituted homogeneous 208–12 nucleosomal array (12 core histone octamers and 12 tandem repeats of 208-bp DNA) revealed that the array forms a moderately folded structure, not the maximally condensed 30-nm fiber, at monovalent salt concentrations up to 200 mM (19, 55). Nonetheless, these experiments do not provide structural information regarding the pathway of linker DNA in the array. To determine whether the solenoid or the zig-zag model is favorable under these conditions, we constructed four initial configurations by using our basic chromatin model in which nucleosomes represented as effective charges are linked to one another by DNA represented by elastic beads (Fig. 1).

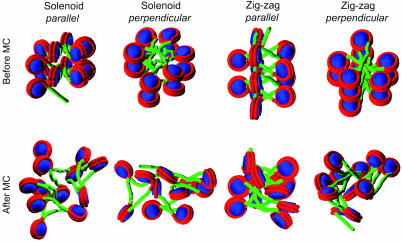
The solenoid model in refs. 10 and 13 has six nucleosomes per helix turn and an 11-nm helix pitch. For a less condensed form (without linker histones), we set six nucleosomes per helix turn but a 14-nm helix pitch. The distance from the center of a nucleosome to the helix axis was set to 13 nm, and the linker DNA connecting two consecutive nucleosomes was bent. This solenoid 12-nucleosomal array thus formed two turns of the helix, as shown in Fig. 2. Although it has been shown that the disk planes of nucleosomes in the condensed 30-nm fiber are roughly parallel to the fiber helix axis (11), we considered both parallel and perpendicular orientations (Fig. 2). The zig-zag model in ref. 5 has 5.9 nucleosomes per 11 nm at 80 mM monovalent salt concentration. For a less condensed form, we set five nucleosomes per helix turn and a 14-nm helix pitch. The distance from the center of a nucleosome to the helix axis was set to 13 nm, but the linker DNA was straight and connected two consecutive nucleosomes on the opposite sides of the array helix axis. In addition, both parallel and perpendicular orientations of nucleosomes were considered (Fig. 2).

Fig. 2.

Structures of nucleosomal arrays before and after MC simulations from different initial models. The initial models are constructed with nucleosome disk planes either parallel or perpendicular to the array helix axis before 2 million steps (6 million steps for the solenoid model with parallel nucleosomes) of MC simulations.

From these four initial models, we performed MC simulations for 2 million steps to sample the favorable conformations at the 200 mM monovalent salt concentration. Their final conformations are shown in Fig. 2.

The linker DNA in the two zig-zag models remains straight (Fig. 2), and the bent linker DNA in the solenoid model with perpendicular nucleosomes becomes straight (Fig. 2). Thus, this solenoid structure converges to the zig-zag model. The solenoid model with parallel nucleosomes retains bent linker DNA (within 2 million MC steps) but has not converged after 2 million steps of simulation (Fig. 3); only longer simulations (≈5 million steps) are required for its linker DNA to become straight (see Fig. 7, which is published as supporting information on the PNAS web site). These results suggest that at high monovalent salt concentrations, in the absence of linker histones, the linker DNA in the nucleosomal array would not adopt bent forms due to unfavorable bending energy; instead, the array forms irregular zig-zag conformations with the linker DNA mainly extended.

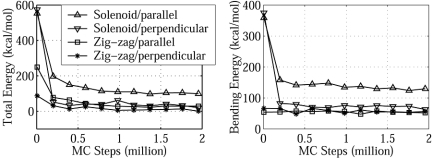
Fig. 3.

Total and bending energies as a function of MC steps for different initial models at 200 mM. Four different initial structures, representing the solenoid and zig-zag models with both parallel and perpendicular nucleosome orientations, are shown in Fig. 2. Data points are collected every 5,000 MC steps but are plotted every 200,000 steps.

The two zig-zag models both converge to irregular structures with largely extended linker DNA and highly irregular nucleosome orientations (Fig. 2), regardless of the initial orientations. We chose the zig-zag model with perpendicular nucleosomes rather than parallel nucleosomes as the initial conformation for the remaining studies, because the former has a lower total energy (16 vs. 30 kcal/mol; Fig. 3) and reproduces experimental sedimentation coefficients better (e.g., 40 vs. 43 S at 200 mM; the former is closer to the experimental value in Fig. 4).

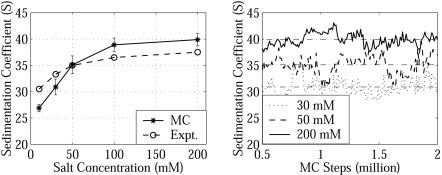
Fig. 4.

Sedimentation coefficients s_20,w as a function of salt concentration and MC steps. The experimental values (Expt.) are from ref. 55. Calculation of s_20,w uses Eq. 1; every 10000th sample is used for the mean and standard deviation calculation.

Salt-Dependent Condensation of the Nucleosomal Array. We simulated the array's salt-dependent condensation by computing s_20,w from MC trajectories at a series of salt concentrations of 10, 30, 50, 100, and 200 mM. Results, shown in Fig. 4 together with data from hydrodynamic measurements (55), reveal conformational changes from extended (27 S at 10 mM) to compact (40 S at 200 mM) forms with close reproduction of the experimental results. Discrepancies at high and low salt may arise from dissociation and ion heterogeneity factors, respectively. At high salt, some histone octamers may dissociate from the nucleosomal DNA (55, 57–59; reviewed in ref. 60), affecting the measurements (55). At low salt, experimentally measured values reflect a buffer with given NaCl concentrations but also other ions, whereas our calculations account only for monovalent salt; there are also charge effects on the measured values well known for polyelectrolytes at low salt.

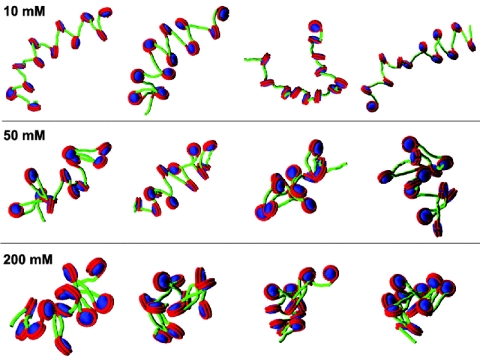
We also note a wide distribution of s_20,w in our simulations (Fig. 4), pointing to a heterogeneous conformational ensemble at a given salt concentration, in equilibrium between extended and compact forms. An increase of the salt concentration shifts the equilibrium to more compact forms, as shown in both Fig. 4 (s_{20, w}) and Fig. 5 (MC snapshots), but the ensembles are still heterogeneous because of entropic effects.

Fig. 5.

Snapshots of the nucleosomal array at different salt concentrations. From left to right, the snapshots are taken after 0.5 million, 1 million, 1.5 million, and 2 million steps of the MC simulations.

Structural Features of the Salt-Dependent Condensation. Detailed structural features of the salt-dependent condensation can be gleaned from averages and standard deviations of the radius of gyration (R_g), the angle (θ) formed by lines connecting three consecutive nucleosomes, and the dihedral angle (ϕ) formed by four consecutive nucleosomes (see Table 4, which is published as supporting information on the PNAS web site). An increase of the salt concentration from 10 to 200 mM decreases R_g from 41 to 19 nm, decreases θ from 64° to 41°, and decreases ϕ from 147° to 58° corresponding to the condensation of an extended beads-on-a-string conformation. These variables' distributions also change dramatically (see Fig. 8, which is published as supporting information on the PNAS web site). Both θ and ϕ are widely distributed at all salt concentrations; at high salt, this behavior indicates irregular zig-zag conformations with some structural heterogeneity.

Energetic Features of the Salt-Dependent Condensation. To interpret the driving force behind the salt-dependent condensation, we compared the energy components at different salt concentrations (see Table 5, which is published as supporting information on the PNAS web site). The total energy drops from 145 kcal/mol at 10 mM to 16 kcal/mol at 200 mM. The electrostatic energy change from 3 kcal/mol (10 mM) to -117 kcal/mol (200 mM) accounts for>90% of the total energy change.

We dissect the electrostatic energy into linker–linker, linker DNA–nucleosome, and internucleosome components in Table 1. The repulsion between linker DNA is 46 kcal/mol at low salt vs. 9 kcal/mol at high salt due to the stronger screening effect at high salt concentrations, even though the linker DNAs are closer to each other in more compact forms. Both the linker DNA–nucleosome and internucleosome attractions become much stronger at high salt (Table 1). Significantly, 80% of the internucleosome attraction increase stems from neighboring nucleosome interactions (nucleosomes i with i - 2 and i + 2 in the zig-zag model because nucleosomes i - 1 and i + 1 are both on the opposite side of the array helix axis). This attraction directly leads to the collapse of the angle θ and significantly contributes to the condensation of the array.

Table 1. Energy components of electrostatic interactions.

Salt, mM	Linker–linker, kcal/mol	Linker–nucleosome, kcal/mol	Internucleosome, kcal/mol	Total, kcal/mol
10	46 ± 2	-44 ± 5	1 ± 0	3 ± 5
30	25 ± 3	-60 ± 6	-12 ± 6	-48 ± 8
50	19 ± 3	-62 ± 5	-43 ± 8	-86 ± 8
100	14 ± 3	-67 ± 6	-54 ± 8	-108 ± 10
200	9 ± 2	-71 ± 6	-55 ± 6	-117 ± 8

Values are ±SD.

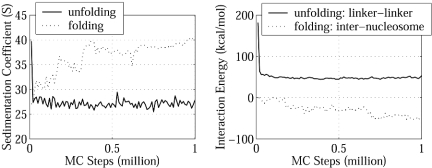
Folding/Unfolding of the Nucleosomal Array. To better understand the driving force for chromatin folding and unfolding, we analyzed two MC simulations (1 million steps each) that simulate unfolding at 10 mM starting from a compact structure obtained at 200 mM and folding at 200 mM starting from an extended form obtained at 10 mM.

During unfolding, the strong repulsion among the linker DNA in the compact form at low salt concentration drives the array into an extended form to relieve this unfavorable linker-linker interaction. After 10⁵ MC steps, the repulsion drops from the initial 182 kcal/mol value to 46 kcal/mol, and the array reaches equilibrium around the extended 27S form (Fig. 6). In equilibrium, the repulsion is mostly compensated by the favorable linker DNA–nucleosome interaction, whereas the internucleosome interaction makes a negligible contribution (1 kcal/mol; Table 1).

Fig. 6.

Unfolding and folding simulations of nucleosomal array. (Left) s_20,w during the unfolding simulation at 10 mM and the folding simulation at 200 mM. (Right) Linker–linker interaction energy during the unfolding simulation at 10 mM and internucleosome interaction energy during the folding simulation at 200 mM.

During folding, the repulsion among linker DNA is only a few kilocalories per mole and thus does not determine the folding process. Instead, the internucleosome attraction dominates this process: the associated energy drops from 0 to -55 kcal/mol as s_20,w increases from 27 to 40 S (Fig. 6). In this process, the linker DNA–nucleosome interaction is always favorable, as in the unfolding process, but here it changes little and exhibits no correlation to the array folding.

These results suggest that folding and unfolding have different driving forces. At low salt concentrations, it is the repulsion among linker DNA that drives the nucleosomal array to adopt an extended form; at high salt concentrations, the attraction between nucleosomes drives and stabilizes the folding of the array.

Role of Histone Tails in Stabilizing the Moderately Folded Array. How can the nucleosomes with a net charge each of approximately -144 e induce strong attractive forces? The positive potential regions of the nucleosome are mainly located in the histone tail domains that protrude from the nucleosome core. Because most of the nucleosomes as well as the linker DNAs are negatively charged, these tails may drive the favorable linker DNA–nucleosome and internucleosome interactions. To estimate the contribution of histone tails to these interactions, we have constructed different DiSCO models in which we set the charges in some of the histone tails to neutral and recalculated the electrostatic interactions in the moderately folded array at 200 mM obtained above.

When all histone tails are set to neutral, the linker DNA–nucleosome interaction changes from -71 kcal/mol (Table 1) to -9 kcal/mol (Table 2), the internucleosome interaction changes from favorable -55 kcal/mol (Table 1) to unfavorable 7 kcal/mol (Table 2), and the total electrostatic energy changes from -117 kcal/mol (Table 1) to 7 kcal/mol (Table 2). Therefore, the histone tails dominate the favorable electrostatic interactions responsible for the stability of the folded forms of the array at high salt concentrations, modulating the linker DNA–nucleosome and internucleosome interactions.

Table 2. Contribution of histone tail domains to the electrostatic interactions at 200 mM salt concentration.

Tails neutralized	Linker–nucleosome, kcal/mol	Internucleosome, kcal/mol	Total electrostatics, kcal/mol
All	-9 ± 4	7 ± 4	7 ± 6
H2A	-36 ± 5	-14 ± 4	-41 ± 6
H2B	-38 ± 5	-13 ± 4	-43 ± 6
H3	-10 ± 4	1 ± 3	-1 ± 6
H4	-37 ± 5	-7 ± 5	-36 ± 6

The linker–linker interaction is 9 kcal/mol, unchanged from Table 1. Values are ±SD.

To further dissect the contribution of different tails, we set the tails of each type of histone to neutral while keeping the rest of the tails intact. With H3 tails neutral, the linker DNA–nucleosome interaction is reduced to -10 kcal/mol (close to -9 kcal/mol when all tails are neutralized), the internucleosome interaction becomes unfavorably 1 kcal/mol, and the total electrostatic energy is -1 kcal/mol only (Table 2). Although neutralization of each of the H4, H2A, and H2B tails also reduces the favorable interactions, these interactions remain attractive, and the total electrostatic interactions remain favorable (Table 2). These calculations suggest that the most important contribution to the favorable electrostatic interactions of compact forms at high salt comes from the H3 tail domains, which determine the overall favorable linker DNA–nucleosome and internucleosome interactions.

The above results consider neutralized histone tails without resimulating the array at 200 mM. To examine the effect of histone tails on stability, we simulated trypsinized nucleosomal arrays in which given histone tails were excised. As expected, the array with tailless histones unfolds at 200 mM, and its average s_20,w is 31 S. Importantly, we find that the array missing only H3 tails cannot achieve the compact form 40 S either at 200 mM; instead, it adopts extended forms with an average s_20,w of 32 S. However, removal of any other histone tail has no effect on the stability of the array at 200 mM, and all of the arrays remain in the compact 40S form during the simulations. The unique features of the H3 tail domains in our DiSCO model (longest extensions from the core and proximity to both the entry and the exit of linker DNA) may explain why H3 tails are so important for the folding and stability of chromatin.

Therefore, the internucleosome attraction comes from the interactions of one nucleosome's positively charged histone tails with another's negatively charged nucleosome cores (particularly the nucleosomal DNA). The attraction increases at high salt because the repulsion between linker DNA is screened, allowing closer approach between the positive tails and negative DNA.

Discussion

The strong salt dependence of chromatin structures indicates that electrostatic interactions play a major role in chromatin folding. Our computational study of the 12-unit nucleosomal array has quantitatively analyzed this behavior and compared it with available experimental data to provide further insights into its structural and energetic features. The change of s_20,w with the salt from our simulations is in good agreement with the hydrodynamic measurements (55).

Our results also suggest that a highly irregular 3D zig-zag conformation with linker DNA mainly extended is preferred by the nucleosomal array at high monovalent salt concentrations. At low salt, the array becomes extended. The structural changes during the reversible folding process are mirrored by reduction of both the angle θ and the dihedral angle ϕ. We propose that, in addition to the collapse of θ (5, 7, 9), the substantial decrease of ϕ also contributes significantly to the condensation of the array. Of course, all simulations are subject to the well known sampling limitations, although MC trajectories sample a wide range. Because all our simulations lead to irregular zig-zag conformations at high salt, they are likely representative.

Through disulfide cross-links between nucleosome particles, Dorigo et al. (61) demonstrated the compact arrays formed in the presence of divalent ions adopted a two-start helix with straight linker DNA, not the solenoid model. Our predicted zig-zag model is consistent with their topologies in the zig-zag class and represents an intermediate folded state formed with monovalent ions on the pathway from an extended form to the final most condensed 30-nm form.

In a theoretical analysis of the electrostatic mechanism of chromatin folding, Clark and Kimura (26) concluded that the mechanism of chromatin folding was essentially electrostatic in nature and proposed the major role of repulsion between linker DNA in determining the stability of chromatin fiber. Our results suggest that the repulsion among linker DNA dominates at low salt, but favorable internucleosome interactions dominate at high salt. Thus, the present studies demonstrate the importance of the internucleosome interaction for the folding and stability of chromatin fiber at physiological salt concentrations, as suggested by van Holde, Zlatanova, and coworkers (7, 9) and indicated by the single molecular experiments on the chromatin fiber (28).

We also traced the origin of the favorable internucleosome interaction to the histone tail domains, especially of H3 (Table 2). At high salt, the repulsion between linker DNA is screened, allowing stronger attraction between one nucleosome's positively charged histone tails and another's negatively charged nucleosome cores. In an experimental study of a nucleosome solution without linker DNA (62), it was found that at low salt concentrations (<50 mM) the histone tails collapsed to interact with its own nucleosomal DNA and the internucleosome interactions were unfavorable, whereas at high salt concentrations (>50 mM) the histone tails extended from the nucleosome to form favorable internucleosome interactions. The origin of the observed internucleosome attraction was further attributed to the histone tail domains by comparing the intact nucleosome solution and the tailless nucleosome solution (63).

The present approach, which includes all histone tails modeled, allowed us to investigate these forces because the effective charges in the DiSCO model are derived directly from the nucleosome's electrostatic potential, and thus salt effects are naturally incorporated (35, 37). Prior simulations used simpler approximations. For example, in the simulations of pulling chromatin fibers, the interactions involving nucleosomes included nucleosome–DNA excluded volume effects and short-range internucleosome attraction (29); this short-range attraction was modeled by an isotropic hard-core potential in which the depth of the attractive well was adjusted to increase with salt concentration. Thus, in the absence of imposed stretching forces, the fiber condensation at high salt concentration was induced by adjustment of a parameter, the decrease of the effective nucleosome diameter. In the study of chromatin folding by Langowski's group, the internucleosome interaction was described by a Gay–Berne potential, a generalization of Lennard–Jones potential for objects with ellipsoidal symmetry (34). However, their focus was on modeling chromatin at near-physiological ionic conditions; thus the effects of the ionic strength on the nucleosomal interactions and on the geometrical parameters were not modeled; it was suggested that reparameterizing the Gay–Berne potential according to the experimental salt-dependence of the linear mass density of the chromatin fiber is required to explore salt-dependent behavior.

Our present chromatin model treats nucleosomes, including the histone tails, as rigid bodies; these bodies can translate/rotate as a whole; only the linker DNA is fully flexible, within our resolution (Fig. 1). Clearly, the histone tails are flexible and rearrange to different locations depending on the context in which they are isolated or assembled (64, 65; reviewed in refs. 22 and 60). Still, we expect that the flexible histone tails would adjust their conformations in chromatin to form favorable linker DNA–nucleosome interactions as well as internucleosome and intranucleosome interactions. In fact, we have tested different orientations of histone tails in our DiSCO model and found that the exact positions of the tails do not matter. The array stays in moderate folded forms at high salt as long as the tails protrude from nucleosome cores; the tails prefer protrusion at high salt as observed in experiments (62). Another approximation in the present model is our use of Debye–Hückel approximation, which accounts for neither the nonlinear effect from the polyelectrolyte feature of both the linker DNA and the nucleosomal DNA nor the contribution of desolvation terms. Although this macroscopic model of the nucleosome is reasonable, as demonstrated by a good agreement with experiments, and allows systematic exploration of general features, more realistic and refined models of the nucleosome are required to address questions such as the effects of posttranslational modifications (most on the histone tails) and histone variants on the nucleosomal array and chromatin fiber.