Abstract
General anesthesia can be caused by various, chemically very different molecules, while several other molecules, many of which are structurally rather similar to them, do not exhibit anesthetic effects at all. To understand the origin of this difference and shed some light on the molecular mechanism of general anesthesia, we report here molecular dynamics simulations of the neat dipalmitoylphosphatidylcholine (DPPC) membrane as well as DPPC membranes containing the anesthetics diethyl ether and chloroform and the structurally similar non-anesthetics n-pentane and carbon tetrachloride, respectively. To also account for the pressure reversal of anesthesia, these simulations are performed both at 1 bar and at 600 bar. Our results indicate that all solutes considered prefer to stay both in the middle of the membrane and close to the boundary of the hydrocarbon domain, at the vicinity of the crowded region of the polar headgroups. However, this latter preference is considerably stronger for the (weakly polar) anesthetics than for the (apolar) non-anesthetics. Anesthetics staying in this outer preferred position increase the lateral separation between the lipid molecules, giving rise to a decrease of the lateral density. The lower lateral density leads to an increased mobility of the DPPC molecules, a decreased order of their tails, an increase of the free volume around this outer preferred position, and a decrease of the lateral pressure at the hydrocarbon side of the apolar/polar interface, a change that might well be in a causal relation with the occurrence of the anesthetic effect. All these changes are clearly reverted by the increase of pressure. Furthermore, non-anesthetics occur in this outer preferred position in a considerably smaller concentration and hence either induce such changes in a much weaker form or do not induce them at all.
1. Introduction
General anesthesia has been used in surgical practice for more than 150 years. However, the molecular mechanism behind the phenomenon of general anesthesia is still largely unknown. Meyer1 and Overton2 realized, independently from each other, at the dawn of the 20th century that the efficiency of general anesthetics is proportional to their olive oil/water partition coefficient, and they concluded that the site of action of general anesthesia must be the plasma membrane of the cells. It was widely assumed that general anesthetics act indirectly by altering some properties of the cell membrane, which modify the function of certain membrane-bound proteins. However, no membrane property was found for a long time that might possibly underlie the anesthetic effect. The lack of success of these so-called lipid theories gave rise to the idea in the 1970s that general anesthetics might directly bind to certain membrane proteins and modify their function via specific protein–substrate interactions.3−6 However, these protein theories also failed so far to identify the proteins involved in this process and characterize their specific interaction with general anesthetics.
The difficulty stems from the vast chemical variety of general anesthetics: alcohols (e.g., ethanol), ethers (e.g., diethyl ether), halogenated hydrocarbons [e.g., chloroform (CF), halothane], cyclic hydrocarbons (e.g., cyclopropane), and even certain inorganic molecules (e.g., NO2) and noble gases (e.g., Xe) can act as general anesthetics. The problem is further complicated by the fact that several molecules with no anesthetic potency are structurally rather similar to some general anesthetics. Thus, for instance, while xenon, decanol, and CF are all rather effective general anesthetics, argon, hexadecanol, and carbon tetrachloride (CT) do not show any anesthetic effect. In certain cases, i.e., when the two molecules differ only in the chain length, this difference in their behavior is well explained,7−9 while in other cases, the origin of their different behavior is far from being fully understood.
The aforementioned large chemical variety of general anesthetics practically excludes any general protein–substrate mechanism, valid for all anesthetics. Further, it is very difficult to imagine any evolutionary mechanism that would lead to the development of any specific interaction of proteins with a chemically totally inactive species, such as xenon, which is not even present in a considerable concentration on Earth. It is also to be noted that anesthetics exert action not only on human patients but on species spanning the evolutionary tree of life.10 The explanation of the molecular mechanism of general anesthesia is further exacerbated by the long known experimental fact that the anesthetic effect is reverted at elevated pressures.11−15 Therefore, any explanation of this mechanism has to account not only for the chemical variety of general anesthetics and the markedly different behavior of chemically and structurally rather similar molecules but also for the pressure reversal of anesthesia.
The first membrane property that was found to be correlated with the presence of anesthetics was the molar volume of the membrane. Thus, more than half a century ago, Mullins realized that the molar volume of the membranes is increased by anesthetics but it decreases at high pressures and hypothesized that anesthesia occurs if the molar volume of the membrane exceeds a critical threshold value.16 This critical volume hypothesis was later rationalized by assuming that anesthetics increase the thickness of the membrane by pushing the two membrane leaflets farther away from each other17,18 and/or by ordering the lipid tails, thus making the lipid molecules more elongated.19 However, both experimental20,21 and computer simulation results22−34 turned out to be rather controversial in this respect, showing that the membrane thickness can decrease in the presence of anesthetics20,24−28 or simply be insensitive to it.21,29−32 Existing results suggest that the change of this property depends on the anesthetic molecule used.34 Interestingly, the possibility that the change of the molar volume might also be governed by changes in the molar surface area (or surface density) of the membrane was not considered until the millennium. In their pioneering studies, Ly et al. finally got rid of the assumption that the lateral membrane density is not affected by the presence of anesthetics and demonstrated experimentally that anesthetics, in fact, induce a lateral swelling of the membrane,35,36 an effect that is clearly reverted by increasing pressure. This finding was later supported by numerous computer simulation studies.17,18,24−34,37−43 Anesthetic-induced increase (and pressure-induced decrease) of the membrane fluidity was also often thought to be an effect that is behind the molecular mechanism of anesthesia.9,44−49 In accordance with this idea, the lateral mobility of the lipid molecules was also found to increase in the presence of various general anesthetics.25,33,39−41,50−53 This increased lateral mobility of the lipid molecules can be, however, also well explained by the above changes of the lateral density.33,34
In 1997, Cantor presented thermodynamic arguments demonstrating that if anesthesia is caused by the switch between two conformations of a membrane-bound (e.g., channel-forming) protein and anesthetics alter the lateral pressure profile across the membrane in such a way that it alters the cross-sectional area profile of both conformers of this protein non-uniformly, the ratio of the active and passive conformers depends exponentially on the anesthetic concentration.54,55 Testing the validity of this lateral pressure hypothesis experimentally is, however, severely hindered by the fact that it is practically impossible to measure the variation of the lateral component of the pressure along the membrane normal with sub-nanometer resolution. Further, the calculation of the lateral pressure profile in computer simulations is also impeded by several technical and conceptual difficulties, originating from the fact that pressure is an inherently non-local quantity, and hence localization of its components, needed to calculate their profiles, cannot be done unambiguously.56,57 Having a reasonably accurate and computationally efficient method in hand,58 we have previously demonstrated that relevant changes of the lateral pressure profile in this respect can be expected near the boundary between the polar and apolar membrane domains, close to the region of the ester groups of phospholipid bilayers.33,59
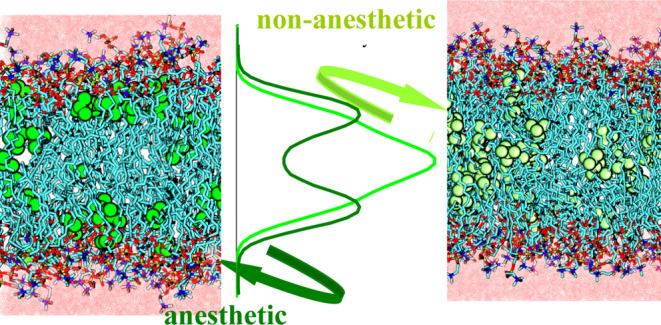
In a set of earlier studies, we were searching for membrane properties the change of which might possibly be related to the molecular mechanism of general anesthesia.31−33,59 In these studies, we followed the approach that such properties have to change in the same way upon adding any general anesthetic and in the opposite way upon increasing the pressure. Further, this pattern of changes has to be present in membranes of various compositions33 and under different thermodynamic conditions.31 In accordance with the general picture emerging from recent experimental60 as well as computer simulation investigations,34 we found that anesthetics have, in general, two preferred positions along the membrane normal, namely, at the apolar side of the polar/apolar interface and in the middle of the membrane. The relative strengths of these two positional preferences may vary from anesthetic to anesthetic,31−33 and the latter preference might even vanish in certain cases (e.g., for ethanol25,27,38,39,45,52 or ketamine30). However, a large fraction of the general anesthetics is always located in the former of the two preferred positions, leading to a decrease of the lateral density of the membrane. This lateral swelling, which clearly satisfies all of our above criteria,31−33 gives rise to the increase of the lateral mobility of the lipid molecules, an effect that, although correlated, seems not to be in a causal relation with anesthesia,33 as well as to the increase of the free volume around the outer preferred position of the anesthetics,33,59 and, as a consequence, to the decrease of the lateral pressure at the polar/apolar interface.33,59 Provided that the other hypotheses of Cantor54,55 are also valid, these changes can provide a possible causal explanation of the phenomenon of general anesthesia.
However, if the above chain of changes of the various membrane properties is indeed related to the anesthetic effect, it also has to explain why certain molecules that are chemically similar to some general anesthetics do not exhibit anesthetic effects. In other words, the above pattern of changes cannot be valid for non-anesthetics: relevant membrane properties cannot be changed in the same way or, at least, to the same extent by anesthetics and non-anesthetics. In this paper, we present a detailed comparative computer simulation investigation of the effect of general anesthetics and structurally similar non-anesthetics on the properties of the dipalmitoylphosphatidylcholine (DPPC) lipid membrane. DPPC, being one of the major constituents of the plasma membranes of living cells, is widely used in modeling lipid membranes and has also been considered in our previous studies.31−33,59 In the current analyses, we consider only those membrane properties that might be related to the effect of anesthesia in light of our previous studies. Thus, here, we analyze the distribution of the anesthetic and non-anesthetic solutes along the bilayer normal, the area and volume per lipid, the thickness of the membrane, the lateral diffusion of the lipid molecules, as well as the profiles of the free volume and lateral pressure along the membrane normal. In addition, we also analyze the effect of the solutes on the local order of the lipid tails, a property the change of which turned out so far to be model-dependent; nevertheless, its possible relation with the anesthetic effect could not have been fully excluded yet.31−33 For this purpose, we have chosen two general anesthetics of markedly different structures, namely, diethyl ether (DE) and CF, whereas as non-anesthetics, we use n-pentane (PE, differing from DE only by substituting its O atom by an isoelectronic CH2 group) and CT (differing from CF by substituting its H by another Cl atom). The schematic chemical structure of these molecules as well as of DPPC is shown in Figure 1. It should be noted that although PE is sometimes also regarded as a weak general anesthetic, its anesthetic efficiency is an order of magnitude smaller than that of DE,61,62 and hence, we simply consider it here as a non-anesthetic.
Figure 1.
Schematic structure of the anesthetic and non-anesthetic molecules considered in this study and of DPPC. The numbering of the tail C atoms used in the paper is also indicated.
The remainder of the paper is organized as follows. In Section 2, details of the performed computer simulations are given. The obtained results are presented and detailed in Section 3. Finally, in Section 4, the obtained results are discussed in terms of explaining the molecular mechanism of general anesthesia, and the conclusions of this study are drawn.
2. Methods
2.1. Molecular Dynamics Simulations
Molecular dynamics simulations of the fully hydrated neat DPPC membrane as well as DPPC membranes containing DE, PE, CF, and CT molecules have been performed on the isothermal-isobaric (N,p,T) ensemble at 330 K. Simulation of the neat DPPC bilayer has only been performed at 1 bar, while the membranes with dissolved anesthetic or non-anesthetic molecules have been simulated both at 1 and 600 bar. The two membrane layers consisted of 128 DPPC molecules each, being hydrated by 7680 water molecules. The ratio of the water and DPPC molecules of 30 has thus exceeded the threshold value of 29.1, required for full hydration.63 In addition, the respective systems have also included 192 DE or PE and 112 CF or CT molecules, corresponding roughly to a 1 M concentration of DE and PE and a 0.6 M concentration of CF and CT in the hydrocarbon phase of the membrane. It should be noted that these concentrations of the anesthetic molecules well exceed what is needed for anesthesia. Similarly, the pressure of 600 bar, considered in the high-pressure simulations, is also much higher than what is needed for pressure reversal. We have used these exaggerated concentration and pressure values, following the idea of Oh and Klein,29 to amplify their effect on the membrane properties, thus making the real changes of these properties safely larger than their statistical noise.
The DPPC, DE, and PE molecules have been described by the all-atom CHARMM36 force field,64 while the parameters of the CF and CT molecules have been obtained using the SwissParam server,65,66 which provides CHARMM-compatible parameters for small organic molecules. Finally, water molecules have been described by the rigid, three-site, CHARMM-compatible modified TIP3P (mTIP3P) potential.67 Thus, the intramolecular part of the total potential energy of the system has consisted of terms corresponding to bond stretching, bond angle bending, and torsional rotation. The geometry of the water molecules has been kept fixed by means of the SETTLE algorithm,68 while all other chemical bonds involving an H atom have been constrained using the LINCS algorithm.69 The intermolecular term of the total potential energy has been calculated as the sum of the Lennard-Jones and charge–charge Coulomb contributions of all atom pairs. All interactions have been truncated to zero beyond the group-based cut-off distance of 12 Å. The long-range part of the electrostatic interaction has been accounted for by means of the Particle Mesh Ewald method in its smooth implementation70 using the mesh spacing of 1.2 Å.
The simulations have been performed by the GROMACS 5.1 program package,71 while for the calculation of the lateral pressure profile, an in-house modified version72 of this program has been used, which also determines the contribution of each particle to the lateral pressure. Equations of motion have been integrated in time steps of 2 fs using the Verlet algorithm.73 The temperature of the system has been kept constant by means of the Nosé–Hoover thermostat74,75 using a time constant of 1 ps. The pressure has been controlled by the Parrinello–Rahman barostat76 using semi-isotropic coupling and the coupling time of 5 ps. Initial configurations have been created using equilibrium configurations of our previous simulations of a neat and a DE-containing DPPC membrane.33 After a short energy minimization, the systems have been equilibrated for 20 ns. Then, in the production phase of the simulations, a 100 ns long trajectory of each system has been generated for the detailed analyses. Equilibrium snapshots of the systems containing dissolved anesthetics or non-anesthetics at 1 bar are shown in Figure 2.
Figure 2.

Equilibrium snapshots of the DPPC membranes containing dissolved DE (top left), PE (bottom left), CF (top right), and CT (bottom right) molecules, as obtained from the 1 bar simulations.
2.2. Calculation of the Lateral Pressure Profile
To calculate the profile of the lateral pressure, pL, along the membrane normal axis, the lateral components of the pressure tensor have to be decomposed to contributions that can be assigned to well-defined spatial positions. However, while the kinetic part of the pressure tensor elements (i.e., V–1∑imivaivbi, where mi and vi are the mass and velocity of the ith atom, a and b denote the corresponding spatial directions, and V is the volume of the system) consists of contributions located at the positions of the individual atoms, and for which such a decomposition can be trivially done, the interaction (or virial) term of the pressure tensor elements can be written as
| 1 |
where fij is the force acting between atoms i and j and the brackets ⟨...⟩ denote ensemble averaging. This equation contains an integral over an open path, Cij, connecting atoms i and j, parameterized by the vector s, and hence the result is inevitably path-dependent. Among the possible reasonable integration contours that provide compatible results with each other,57 the use of the Harasima path77 has several advantages. Thus, it can be used even in cases when the potential energy of the system is not fully pairwise additive,57 such as the reciprocal space part of the long range correction calculated by Ewald summation73,78,79 or by any of its particle mesh variants.70,80 This way, changing the potential function in an a posteriori evaluation of the lateral pressure profile (i.e., using a large cut-off instead of the Ewald-based long range correction) can simply be avoided.58 Further, this way, the lateral pressure contributions are distributed between the individual atoms,81 and hence lateral pressure contributions can be treated as if they were additive properties of the individual atoms,58,81 which enables a computationally very efficient, on-the-fly calculation of the lateral pressure profile. It should finally be noted that the interfacial tension can be calculated as the integral of the difference between the normal and lateral pressure components along the interface normal. Since the former component is constant across the entire system due to the requirement of mechanical stability, the lateral pressure profile is practically identical, apart from a minus sign, to that of the interfacial tension at atmospheric pressure.
3. Results
3.1. Density Profiles
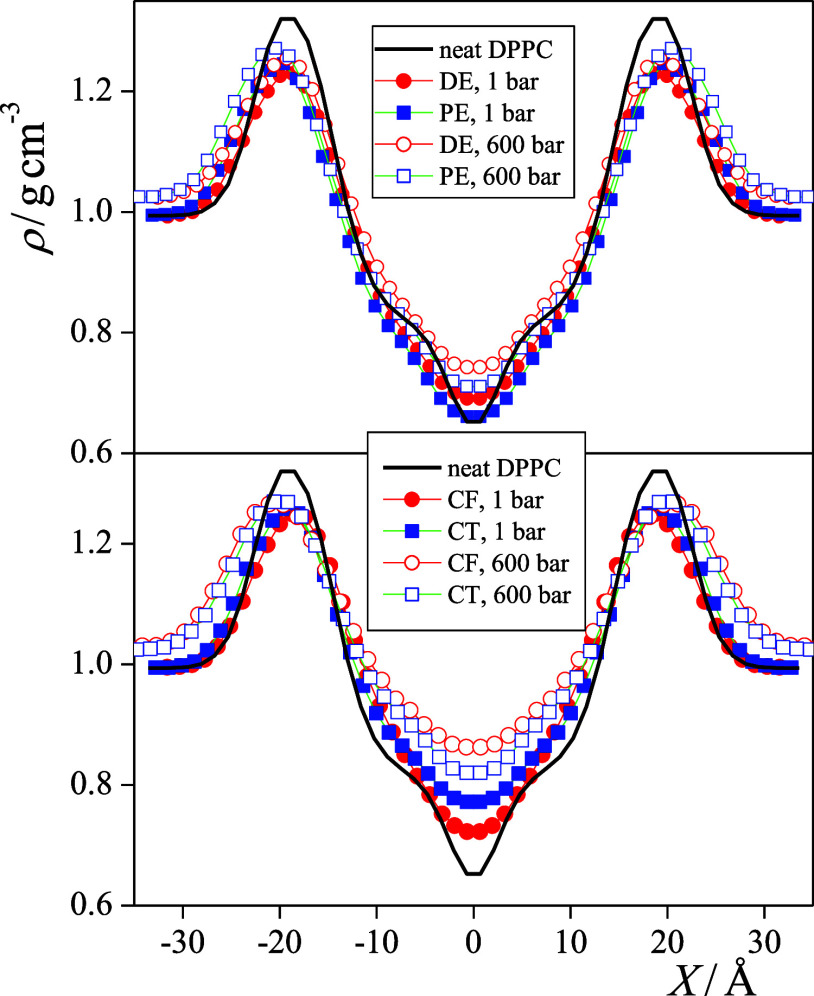
The mass density profiles of the nine systems along the membrane normal axis, X, are shown in Figure 3. All the density profiles shown are averaged over the two leaflets of the membrane. The profiles are characterized by a high-density region around |X| = 20 Å, corresponding to the crowded domain around the lipid headgroups and a low-density region in the middle of the membrane, around X = 0 Å. In the case of the neat DPPC membrane, the density exhibits a sudden drop close to the middle of the bilayer, indicating that not all the hydrocarbon chains reach this region. The presence of all solutes considered increases the density here, reflecting the simple fact that additional molecules prefer to stay in the region where there is the largest available free volume. The solute molecules located in the middle of the membrane are, however, not expected to be related to the anesthetic effect as the density increases further rather than being reverted by the increase of pressure. Consistently, there is no systematic difference between the behavior of the anesthetics and that of the non-anesthetics in this respect. This claim is also consistent with the earlier finding that some of the general anesthetics, such as ethanol25,27,38,39,45,52 and ketamine,30 do not accumulate in the middle of the membrane at all.
Figure 3.
Mass density profiles of the membranes simulated along their normal axis, X. Black solid line: neat DPPC membrane without any dissolved molecule (simulated at 1 bar), red circles: membranes with anesthetics, and blue squares: membranes with non-anesthetics. Filled and open symbols correspond to the systems at 1 and 600 bar, respectively. Top panel: membranes containing the DE/PE anesthetic/non-anesthetic pair; bottom panel: membranes containing the CF/CT anesthetic/non-anesthetic pair. The profiles shown are averaged over the two leaflets of the membrane.
The presence of any kind of dissolved molecules leads to a decrease of the density in the crowded region of the headgroups. However, no clear tendency is apparent concerning the position and height of this density peak apart from the fact that the increase of the pressure leads to the increase of the density both in the headgroup region and in the aqueous phase.
The contribution of the different molecules and groups of the DPPC molecule to the overall density profiles is shown in Figure 4 for all the solute-containing membranes considered. As seen, the high-density region around X = ±20 Å indeed covers the region of the negatively charged PO4 groups, encloses the vast majority of the esteric C=O groups, and contains a considerable amount of water. The density of water drops rapidly toward the middle of the membrane and vanishes beyond the region of the esteric C=O groups of DPPC. Thus, the roughly 20 Å wide hydrocarbon core in the middle of the membrane is practically free from water and the polar groups of DPPC. The solute molecules are almost exclusively distributed within this apolar region of the hydrocarbon chains.
Figure 4.
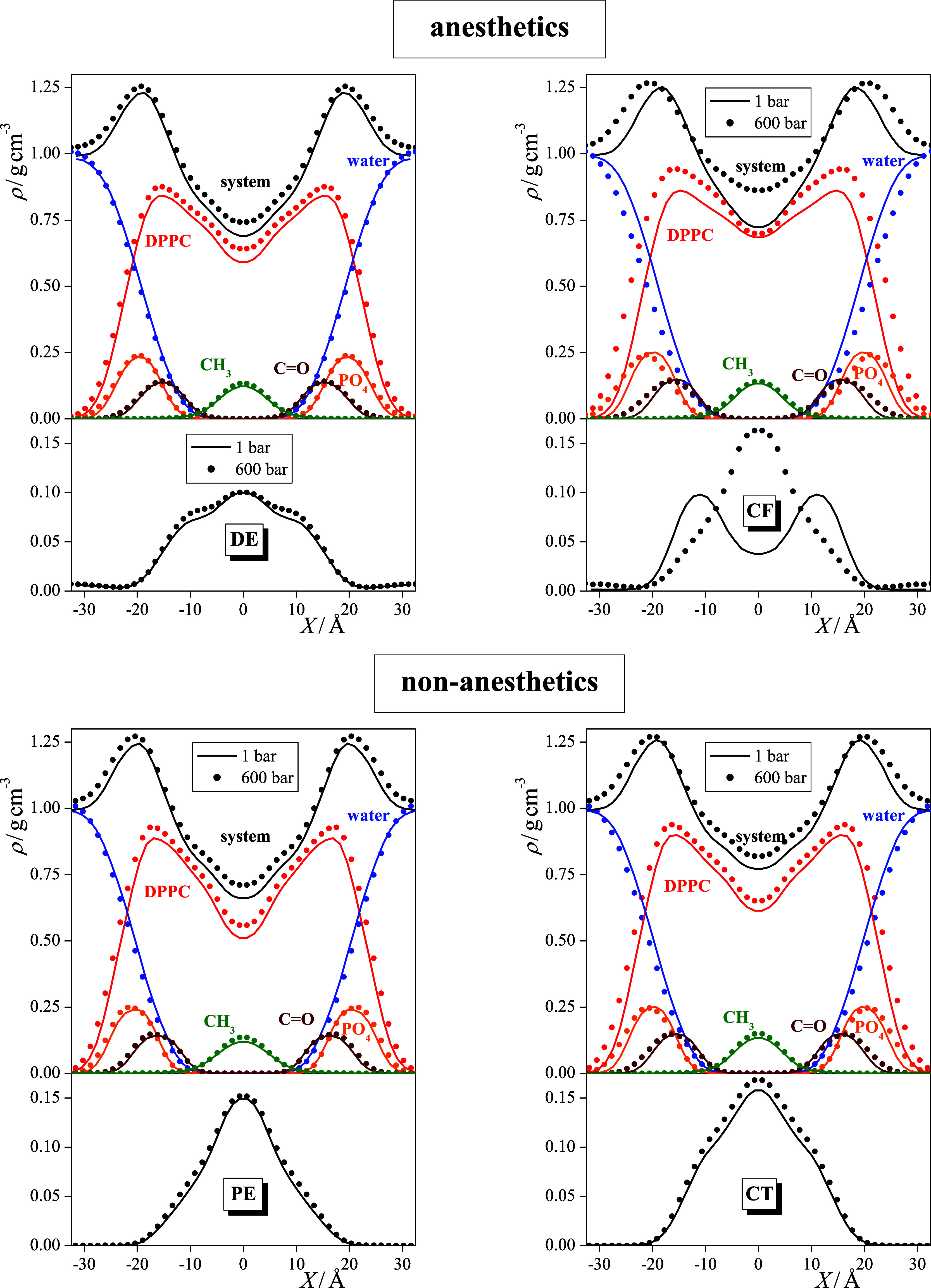
Mass density profiles of the membranes, containing dissolved DE (top left), PE (bottom left), CF (top right), and CT (bottom right) molecules, along the membrane normal axis, X, and contributions of various molecules and groups to these profiles. Top panels: black: entire system, blue: water molecules, red: DPPC molecules, orange: PO4 groups, brown: esteric C=O groups, and green: chain terminal CH3 groups. Bottom panel: profile of the dissolved anesthetic or non-anesthetic molecules. Solid lines and symbols correspond to systems at 1 bar and 600 bar, respectively. The profiles shown are averaged over the two leaflets of the membrane.
Not surprisingly, the increase of pressure leads not only to the increase of the overall density but also to that of most of the different molecules and groups. A clear exception in this respect is water, the density of which is decreased by increasing pressure within the membrane (while it is evidently increased in the aqueous phase, see Figure 3). In other words, pressure “squeezes out” water from the membrane. It is also interesting to see that the position of the high-density peak of the entire membrane as well as the density peaks corresponding to the PO4 and esteric C=O groups are shifted farther from the middle of the bilayer with increasing pressure. This finding is somewhat counterintuitive as it indicates that at high pressure, the membrane is thicker than at 1 bar. This behavior is probably caused by the ordering effect of the pressure on the lipid tails, namely, that at high pressure, the conformation of the lipid tails is straighter than at ambient pressure, which moves the lipid heads farther away from each other. This point will be addressed in detail in a subsequent subsection. It is, however, to be noted that there is no clear difference in the arrangement of the different groups of DPPC along the membrane normal in the systems containing anesthetic and non-anesthetic solutes.
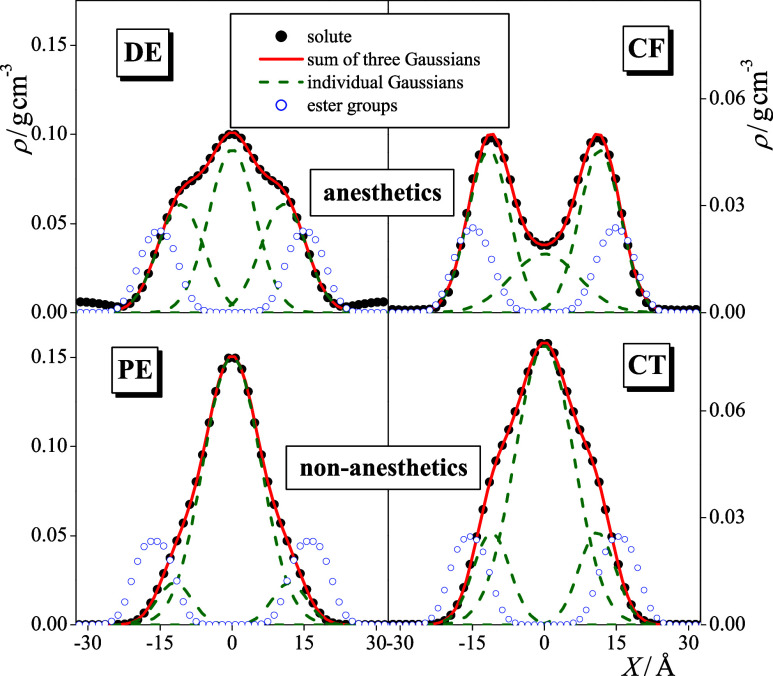
As it has already been stated, the solute molecules considered infiltrate the entire hydrocarbon interior of the DPPC bilayer in every case. Although the distributions of these molecules are markedly different from each other, it is seen that, besides accumulating in the middle of the membrane, they always prefer to stay close to the boundary of this hydrocarbon phase. This preference is reflected in the occurrence of either a distinct peak or, at least, a shoulder of the density profiles around X = ±10 Å (see the lower panels of Figure 4). In fact, the density profile of the solute molecules can be very well fitted by the sum of three Gaussian functions, one of which is centered in the middle of the membrane, i.e., at X = 0 Å, while the other two are mirror images of each other. This is illustrated in Figure 5, showing this three-Gaussian fit of the density profiles of all the four solutes considered at 1 bar. Further, the position of the outer Gaussian, |X2|, as well as the relative weights of the inner and outer Gaussians, w1 and w2, respectively, are collected and presented in Table 1 (w2 being the weight of the two outer Gaussians together). Figure 5 also shows the density profiles of the esteric C=O groups, demonstrating that it is very close to the position of the outer of the fitted Gaussian functions, being only about 3–4 Å farther from the middle of the membrane.
Figure 5.
Mass density profiles of the dissolved DE (top left), PE (bottom left), CF (top right), and CT (bottom right) molecules along the membrane normal axis, X, as obtained at 1 bar (black filled circles), together with their fits with the sum of 3 Gaussian functions (red solid lines) and the individual Gaussians (green dashed lines). The density profile of the esteric C=O groups are also shown for reference (blue open circles). Scales at the left and right sides correspond to the densities of the dissolved molecules and fitted Gaussians and to that of the esteric C=O groups, respectively. The profiles shown are averaged over the two leaflets of the membrane.
Table 1. Peak Position of the Outer Gaussian and Relative Weights of the Inner and Outer Gaussian Functions Used to Fit the Density Profiles of the Anesthetic and Non-Anesthetic Molecules in the DPPC Membrane and Solvation Free Energy Difference between the Two Preferred Positionsa.
| system | |X2|/Å | w1 (%) | w2 (%) | ΔG/kJ mol–1 |
|---|---|---|---|---|
| DPPC + DE | 10.7 | 43.4 | 56.6 | –0.7 |
| DPPC + PE | 12.0 | 84.1 | 15.9 | 4.6 |
| DPPC + CF | 11.6 | 22.9 | 77.1 | –3.3 |
| DPPC + CT | 11.0 | 70.8 | 29.2 | 2.4 |
The position of the inner Gaussian is always X1 = 0 Å.
Here, a clear and marked difference is seen between the behaviors of the anesthetic and non-anesthetic solutes based on the relative weights of these Gaussians (see Table 1). Thus, for both pairs, about three times more anesthetic than non-anesthetic molecules are accumulated in this outer preferred position, close to the boundary of the hydrocarbon phase than non-anesthetic solutes. Further, for anesthetics, always more than half of the molecules are located in this outer preferred position, while at least 70% of the non-anesthetic solutes are accumulated in the middle of the membrane. Considering that the solvation free energy profile, G(X), is related to the number density profile, ρ(X), simply as G(X) = −RT ln ρ(X) + C, where R is the gas constant and C is an additive constant, the solvation free energy difference between the outer and inner preferred positions can be estimated using a two-state model, as
| 2 |
where ρ1(X) and ρ2(X) are the density profiles corresponding to the inner and two outer Gaussians, respectively. The ΔG values obtained this way are also included in Table 1. As seen, the difference between the ΔG values obtained for anesthetics and the corresponding non-anesthetics is about 5.5 kJ/mol, i.e., 2 RT at the simulation temperature in both cases.
The observed difference in the affinities of the anesthetic and non-anesthetic solutes to the two preferred positions is likely related to the fact that while the investigated non-anesthetics are fully apolar, their anesthetic counterparts are weakly polar. As a consequence, the interaction of the small dipole moment of the anesthetic molecules with the polar region of the headgroups and, in particular, with the dipole moments of the ester groups, is a driving force of the strong enrichment of the anesthetics close to the outer boundary of the hydrocarbon phase (although this driving force is certainly not strong enough to bring them even out from the apolar region). On the other hand, the driving force of the preference of apolar non-anesthetics for staying at the boundary of the apolar phase is the enhancement of their Lennard-Jones interaction upon approaching the high-density region of the headgroups. More specifically, as we have shown recently, the preference for the outer position of apolar solutes is resulted from the interplay of their increasing attraction and the decreasing free volume available for them upon going farther away from the middle of the bilayer.82 However, in view of the lack of an additional dipolar interaction, as in the case of the non-anesthetic molecules, this driving force is certainly weaker than that caused by the larger availability of empty space in the middle of the bilayer. As a consequence, the preference of the apolar non-anesthetics for the outer position is considerably weaker than for the middle of the membrane. This finding is consistent with our earlier claim33,59 that the anesthetic effect is caused by the molecules that are accumulated at the boundary of the hydrocarbon region of the membrane. These results clearly demonstrate that there is a marked difference between the behaviors of general anesthetics and structurally similar non-anesthetics in this respect.
3.2. Membrane Dimensions
The average area per lipid, Al, thickness, l, and volume per lipid, Vl, of the nine membranes simulated are collected and presented in Table 2. The thickness of the membrane is estimated by the distance of the peak positions of the PO4 density profile at the two sides of the membrane, while the average area and volume per lipid is calculated as
| 3 |
and
| 4 |
respectively, where LY and LZ are the edge lengths of the basic box within the plane of the bilayer and NDPPC is the number of DPPC molecules in the basic box. The Al and Vl values obtained for the neat DPPC membrane agree very well with existing experimental data of 62 ± 2 and 62.9 ± 0.9 Å2 (area per lipid)63,83 and 1232 Å3 (volume per lipid).84
Table 2. Average Thickness, Molecular Surface Area, and Volume of the Membranes Simulateda.
| system | area
per lipid (Å2) |
membrane
thickness (Å) |
volume
per lipid (Å3) |
|||
|---|---|---|---|---|---|---|
| 1 bar | 600 bar | 1 bar | 600 bar | 1 bar | 600 bar | |
| DPPC | 61.9 | 39.7 | 1228 | |||
| DPPC + DE | 70.0 | 65.4 | 38.6 | 40.5 | 1351 | 1325 |
| DPPC + PE | 67.0 | 62.0 | 40.6 | 42.2 | 1359 | 1309 |
| DPPC + CF | 67.7 | 63.9 | 38.7 | 42.1 | 1309 | 1341 |
| DPPC + CT | 65.6 | 59.7 | 40.2 | 41.1 | 1318 | 1227 |
Error bars are below 0.3 Å2, 0.1 Å, and 10 Å3, respectively.
As seen from Table 2, the presence of all solutes induces a clear increase of the area per headgroup, but this change is considerably, i.e., more than 50%, larger for the anesthetic solutes than for the corresponding non-anesthetics. This is in a clear accordance both with the experimental results of Ly et al.35,36 and with our earlier finding that anesthetics are accumulated in a considerably higher concentration at the outer boundary of the hydrocarbon phase than non-anesthetics. It also indicates that the observed increase of the area per lipid (or decrease of the lateral density) of the membrane is caused by the solute molecules located in their outer preferred position. Considering also that this solute-induced decrease of the lateral density is clearly reverted by the increase of the pressure, this effect is likely related to the molecular mechanism of anesthesia.
Considering the thickness of the membrane, it is seen that while the presence of anesthetics, in accordance with the results of some of the early experiments,20 leads to its decrease, that of the non-anesthetics result in its increase. This difference can again be explained by the different distributions of these molecules along the membrane normal axis. Thus, non-anesthetics are largely accumulated in the middle of the membrane, and hence they push the two leaflets farther away from each other. On the other hand, anesthetics prefer positions among the lipid molecules close to the boundary of the hydrocarbon phase, thus pushing the DPPC molecules laterally farther away from each other. This increase of the empty space between the neighboring lipid molecules allows them larger conformational flexibility, which eventually leads to their smaller head-to-tail distance and hence to a decrease of the membrane thickness. Interestingly, the increase of the pressure results in larger membrane thickness values, presumably because of the straightening of the lipid tails, as it has been discussed in the previous subsection.
The change of the volume per lipid due to the presence of solutes of different natures and to the pressure does not show such a clear picture as it reflects the combined changes of both the area per lipid and the membrane thickness. Thus, the addition of solute molecules induces an increase of Vl even if it corresponds to a decrease of the membrane thickness. This change is understandable, considering that any solute simply increases the number of atoms inside the membrane, and hence a larger volume is needed to accommodate them. On the other hand, the increase of the pressure results in a decrease of the volume per lipid in most of the cases, in accordance with what is expected from elemental physical chemistry. However, there is also an exception in this respect, namely, the case of CF, where the volume per lipid is found to increase slightly with increasing pressure. To understand this result and resolve the seeming contradiction, it has to be emphasized that the volume per lipid calculated according to eq 3 does not account for the aqueous phase of the system (i.e., what is beyond the density peak of the PO4 groups). Thus, while the density between the regions of the PO4 groups in the two leaflets decreases slightly due to the aforementioned straightening of the lipid tails and to the fact that high pressure pushes the CF molecules into the middle of the bilayer (see the top right panel of Figure 4), the density of the entire system, including also the aqueous phase, still increases. Furthermore, the volume per lipid does not take into account the dissolved molecules, and hence it does not even correspond to the real (mass) density of the membrane interior (its reciprocal is the number density of the lipid molecules irrespective of whether there are any other molecules between them or not). Thus, as clearly seen from the top right panel of Figure 4, even if the volume per lipid of the CF containing membrane is larger, the mass density of even the membrane interior is higher at higher pressure, as expected.
Nevertheless, among the three membrane dimensions considered, it is the area per lipid that not only shows a clear trend with both the nature (i.e., anesthetics vs. non-anesthetics) of the solute and the pressure and hence changes consistently with both the anesthetic effect and its pressure reversal, but it is also in a clear causal relation both with the distribution of the solute molecules along the membrane normal and with the further changes discussed in the following subsections, which eventually trigger the anesthetic effect.
3.3. Order Parameters of the Hydrocarbon Tails
The local orientational order of the DPPC molecules around their individual C atoms can be conveniently characterized by the deuterium order parameter, SCD, which can be calculated as85,86
| 5 |
In this equation, γ denotes the angle formed by a C–H bond involving the C atom of interest and the membrane normal, and the brackets ⟨...⟩ denote ensemble averaging. The value of SCD calculated for all C atoms along the hydrocarbon tail characterizes the orientational order along the entire tail. The main advantage of using SCD instead of other local order parameters is that it is also accessible experimentally, performing nuclear magnetic resonance (NMR) measurements of selectively deuterated samples.
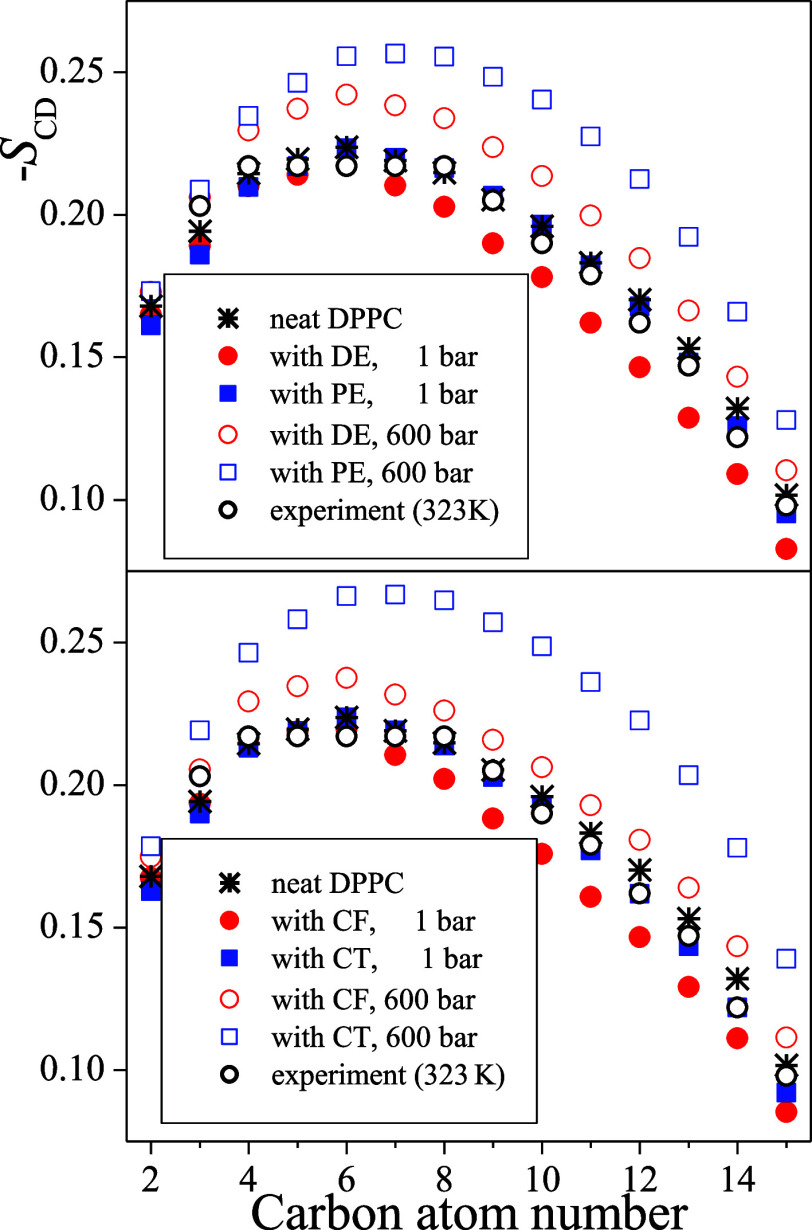
The SCD profiles along the lipid tails are shown in Figure 6 as obtained in the nine systems simulated. The numbering of the C atoms starts from that bound to the ester group and goes toward the chain terminal CH3 group, as shown in Figure 1. It should be noted that the SCD values shown are averaged over the two lipid tails; however, apart from those corresponding to the first C atom, the values obtained along the two chains are always rather close to each other. The profile obtained in the neat DPPC membrane is also compared with experimental data, obtained by Douliez et al. at 323 K.87 The simulation results agree rather well with the experimental data apart from the small (i.e., about 7 K) temperature shift.
Figure 6.
Profile of the deuterium order parameter along the hydrocarbon tails of the DPPC molecules. The numbering of the C atoms is shown in Figure 1. Black asterisks: simulation results in the neat DPPC membrane; black open circles: experimental data of Douliez et al., obtained in the neat DPPC membrane at 323 K (ref (87)); red circles: membranes with anesthetics; and blue squares: membranes with non-anesthetics. Filled and open symbols correspond to the systems at 1 and 600 bar, respectively. Top panel: membranes containing the DE/PE anesthetic/non-anesthetic pair; bottom panel: membranes containing the CF/CT anesthetic/non-anesthetic pair. The estimated uncertainty of the data points is always below 0.005, being smaller than the symbols.
The obtained results show that in the presence of anesthetics, which are located preferentially close to the ester groups (i.e., among the first few C atoms along the hydrocarbon chains), the orientational order is consistently lower at the end of the tail, around the last 6–9 C atoms, than in the neat membrane. This result is in a clear accordance with our above finding that the anesthetic molecules located close to the boundary of the apolar region push the DPPC tails farther away from each other in lateral directions. This increased surface area occupied by the individual DPPC molecules give larger conformational flexibility to their tails, resulting in the observed decrease of the orientational order parameter. On the other hand, no such change is seen in the presence of non-anesthetics, which are preferentially located in the middle of the membrane, between the two leaflets of DPPC. Further, the increase of the pressure results in a marked increase of the orientational order along the entire chain in all cases, confirming our explanation of the pressure-induced thickening of the membrane (see Section 3.2). These results indicate that the order parameter profile of the lipid tails is correlated with the occurrence of the anesthetic effect although it is most likely not in a causal relation with it.
3.4. Lateral Mobility of the Lipid Molecules
The lateral mobility of the DPPC molecules is characterized here by their diffusion coefficient within the plane of the bilayer, D||, calculated through the Einstein relation73 as
| 6 |
In this equation, 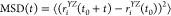 is the mean squared displacement of the
lipid molecules within the plane of the membrane, YZ, t stands for the time, rYZi(t0) and rYZi(t0 + t) are the positions
of the ith DPPC molecule (represented by that of
its P atom) in the YZ plane at times t0 and t0 + t, respectively, and the brackets ⟨...⟩ denote ensemble
averaging. The value of D|| has been obtained
from the slope of the linear fit to the MSD vs t data.
To ensure that the DPPC molecules left the ballistic regime and performed
diffusive motion, the first 2 ns of the data have been omitted from
the fitting. No finite size correction88 has been applied as we focus here on the change of D|| rather than on its accurate value.
is the mean squared displacement of the
lipid molecules within the plane of the membrane, YZ, t stands for the time, rYZi(t0) and rYZi(t0 + t) are the positions
of the ith DPPC molecule (represented by that of
its P atom) in the YZ plane at times t0 and t0 + t, respectively, and the brackets ⟨...⟩ denote ensemble
averaging. The value of D|| has been obtained
from the slope of the linear fit to the MSD vs t data.
To ensure that the DPPC molecules left the ballistic regime and performed
diffusive motion, the first 2 ns of the data have been omitted from
the fitting. No finite size correction88 has been applied as we focus here on the change of D|| rather than on its accurate value.
The D|| values obtained in the different membranes are collected and presented in Table 3. The (uncorrected) value of 17.4 μm2/s, obtained in the neat DPPC bilayer, agrees very well with the experimental data of 17.8 μm2/s.89 As seen, all the four solutes considered increase the lateral mobility of the DPPC molecules; however, this increase is considerably larger for anesthetics than for the corresponding non-anesthetics. Further, the increase of the pressure to 600 bar leads to a substantial decrease of the lateral mobility of DPPC.
Table 3. Lateral Diffusion Coefficient of the DPPC Molecules (in μm2/s Units) in the Different Membranes Simulated.
| system | 1 bar | 600 bar |
|---|---|---|
| DPPC | 17.4 (17.8)a | |
| DPPC + DE | 35.6 | 17.3 |
| DPPC + PE | 31.4 | 17.4 |
| DPPC + CF | 33.9 | 11.4 |
| DPPC + CT | 24.8 | 12.5 |
Value in parenthesis is experimental data from ref (89).
The behavior of the lateral diffusion coefficient of DPPC exhibits a clear correlation with the area per lipid as the higher area per lipid corresponds, in general, to larger lateral diffusion coefficient values. This is not surprising, considering that the higher area per lipid (i.e., lower lateral density of the membrane) provides more space for the DPPC molecules to move. This additional space is created by all solute molecules considered, but to a considerably larger extent by the anesthetics than the corresponding non-anesthetics, while it is removed by the increase of pressure.
3.5. Free Volume Profile
To investigate the distribution of the additional empty space created by the solute molecules along the membrane normal axis, X, we have calculated the fraction of the empty volume, ϕ, along this axis in the different systems. For this reason, a set of 5 × 105 test points per sample configuration has been considered, and it has been checked for each test point whether it is covered by any of the atoms in the system. The diameter of each atom has been estimated by its Lennard-Jones distance parameter, σ. The fraction of the empty volume has then simply been calculated as the ratio of the number of test points not covered by any atom and that of all the test points considered.
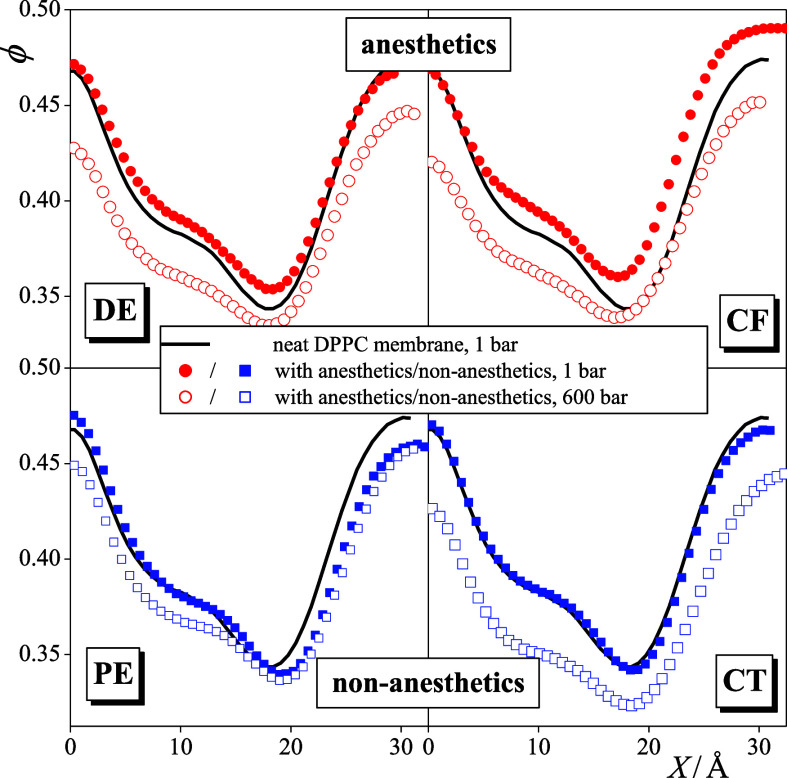
The profile of the empty volume fraction along the membrane normal, ϕ(X), is shown in Figure 7 as obtained in the different systems simulated. To magnify the effect of the solute molecules, these profiles (being symmetrized over the two membrane leaflets) are only shown in one side of the bilayer. The obtained ϕ(X) profiles exhibit a maximum at X = 0 Å, i.e., in the middle of the bilayer, a minimum around |X| = 20 Å in the crowded region of the headgroups, and a shoulder around |X| = 10 Å at the outer boundary of the hydrocarbon region. These features are in clear accordance with the obtained density profiles (see Figures 3 and 4). More importantly, the obtained results clearly show that the addition of anesthetics increases the fraction of the free volume at the outer boundary of the hydrocarbon phase as well as in the headgroup region, while no such effect is caused by the corresponding non-anesthetics. This result is understandable, considering that anesthetics occur in considerably higher concentrations at the outer boundary of the hydrocarbon region, hence causing a noticeably larger lateral swelling of the membrane than the corresponding non-anesthetics. This finding is consistent with the claim that the lateral swelling of the membrane is caused by the anesthetic molecules that stay in their outer preferred position, pushing the DPPC molecules laterally farther away from each other and thus creating some additional empty space, and not by those staying in the middle of the membrane, where no such increase of the empty space is observed. Finally, as it is clearly seen from Figure 7, the increase of the pressure decreases the fraction of the free volume all along the membrane normal axis, in particular, at the relatively loosely packed hydrocarbon interior of the bilayer, thus reverting the increase caused by the presence of the anesthetic molecules.
Figure 7.
Profile of the fraction of free volume along the membrane normal axis, X, as obtained in the neat DPPC membrane as well as in membranes containing DE (top left), PE (bottom left), CF (top right), and CT (bottom right). Black solid lines: neat DPPC membrane; red circles: membranes with anesthetics; and blue squares: membranes with non-anesthetics. Filled and open symbols correspond to the systems at 1 and 600 bar, respectively. To magnify the effect of the solute molecules, the profiles (being already symmetrized over the two leaflets) are only shown in one side of the membrane.
3.6. Profile of Lateral Pressure
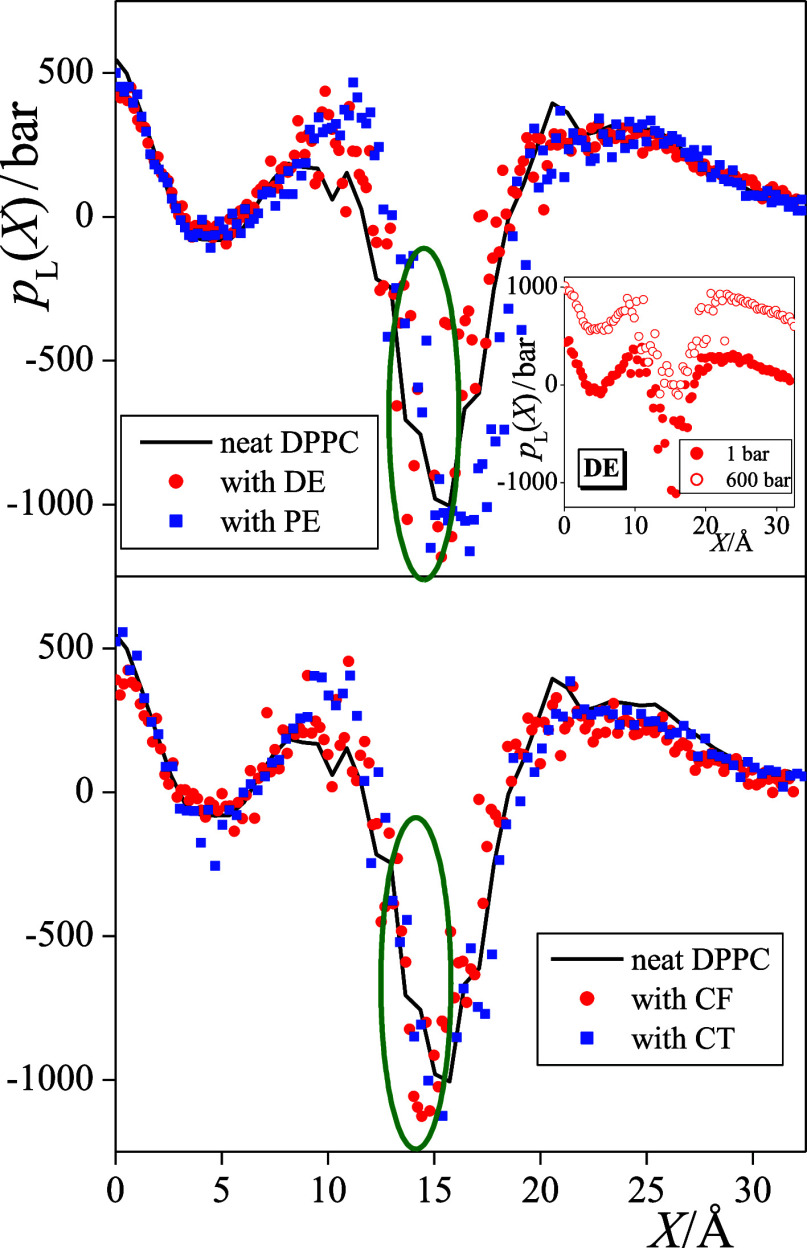
The lateral pressure profiles along the membrane normal axis, pL(X), are shown in Figure 8 as obtained from the simulations at 1 bar. Since these calculations are still rather demanding and the increase of the overall pressure strongly shifts the entire profile to higher lateral pressure values while the effect of the anesthetics on this profile is rather subtle, we have not calculated the pL(X) profiles in the 600 bar systems. The strong upward shift of the pL(X) profile due to the increase of the overall pressure is illustrated in the inset of Figure 8 using the pL(X) data of the DE-containing membrane from our previous publication.33 To magnify the aforementioned subtle effect of the anesthetics, the (symmetrized) pL(X) profiles are also shown in one side of the bilayer only.
Figure 8.
Profile of the lateral pressure along the membrane normal axis, X, as obtained from the simulations performed at 1 bar. Black solid lines: neat DPPC membrane; red circles: membranes with anesthetics; and blue squares: membranes with non-anesthetics. Top panel: membranes containing the DE/PE anesthetic/non-anesthetic pair and bottom panel: membranes containing the CF/CT anesthetic/non-anesthetic pair. Encircled is the membrane domain in which the lateral pressure is decreased by the anesthetics. To magnify the effect of the solute molecules, the profiles (being already symmetrized over the two leaflets) are only shown in one side of the membrane. The inset shows the lateral pressure profiles obtained in the DE-containing membrane at 1 bar (filled circles) and 600 bar (open circles) from a previous publication (ref (33)).
The obtained pL(X) profiles exhibit a peak in the middle of the membrane, and one in the region of the headgroups, while a clear and deep minimum is seen at the boundary of the hydrocarbon and aqueous domains, around |X| = 15 Å. Further, while the lateral pressure is positive in most parts of the membrane, it deeply extends to negative values in this minimum, i.e., at the boundary of the apolar and polar domains. This finding is understandable, considering that negative values of lateral pressure indicate a positive contribution to the interfacial tension and vice versa.90
Considering the effect of the anesthetic and non-anesthetic solutes on the lateral pressure profile, it is seen that the presence of the anesthetics results in a decrease of pL(X) in a narrow region, between the |X| values of about 13 and 16 Å, i.e., at the hydrocarbon side of the apolar/polar interface. This domain is located slightly, i.e., by about 2–3 Å farther from the middle of the bilayer than the outer preferred position of the anesthetic molecules (see Figure 5). This apparent decrease of the lateral pressure evidences the weakening of the interaction between the lipid molecules that are pushed laterally farther away from each other by the nearby anesthetics. Since non-anesthetics occur in this outer preferred position in a considerably smaller concentration than the corresponding anesthetics, they do not induce such a decrease of the lateral pressure in this narrow region. It should finally be emphasized that the increase of the overall pressure clearly reverts this anesthetic-induced decrease of lateral pressure.
At this point, we should recall the hypothesis of Cantor, namely, that anesthesia is caused by anesthetic-induced non-uniform changes in the lateral pressure profile,54,55 which has to be reverted by the increase of pressure. Thus, we can conclude that the above-discussed decrease of lateral pressure at the inner side of the hydrocarbon/aqueous interface, caused by the nearby anesthetic molecules staying in their outer preferred position, is in a causal relation with the occurrence of the anesthetic effect. This view is also supported by the finding that structurally similar but completely apolar non-anesthetics are accumulated in a considerably smaller concentration in this outer preferred position than the corresponding anesthetics, and hence they do not induce such a decrease of lateral pressure at the hydrocarbon/aqueous interface. Finally, it should be noted that here we found such changes of the lateral pressure profile at the hydrocarbon side of the apolar/polar interface in the presence of anesthetics that are also compatible with the phenomenon of pressure reversal. Therefore, our results suggest that the relevant conformational changes of the transmembrane proteins, such as the TREK-1 potassium channel,91 that can be related to the anesthetic effect are also expected here. Further investigation of the problem would therefore involve membrane simulations in the presence of both general anesthetics and such proteins.
4. Discussion and Conclusions
In a set of our previous publications,31−33,59 we were looking for various membrane properties that change in accordance with what we know about general anesthesia, i.e., they change in a certain way upon adding any kind of general anesthetic and in the opposite way upon applying pressure. We found, in accordance with numerous similar computer simulation studies performed in the past two decades,34 that the average area per lipid is such a property, and its systematic change induces similar changes, being still compatible with the phenomenon of general anesthesia, in a number of other membrane properties (e.g., lateral mobility, tail order, profiles of the free volume, and lateral pressure). These changes turned out to be independent from the anesthetic molecule considered32 as well as from the composition33 and phase31,33 of the membrane. However, one piece of information was still missing: such changes should not occur at all or, at least, not at the same extent in the presence of dissolved molecules having no anesthetic effect. The present study is intended to fill this gap, demonstrating that non-anesthetics, even if they are chemically or at least structurally rather similar to certain anesthetics, do not induce such changes of the membrane properties or induce them to a much smaller extent.
Having these results, now we are in the position of proposing a molecular mechanism of general anesthesia, which is also compatible with its well-known pressure reversal. The key point in this respect is the distribution of the anesthetic molecules along the membrane normal, namely, their strong preference for staying close to the boundary of the hydrocarbon phase. The majority of the general anesthetics are weakly polar, and hence, while they are still dissolved in the hydrocarbon phase, the favorable interaction of their small dipole moment with the region of the polar headgroups represents a stronger driving force than the larger space available in the middle of the membrane. On the other hand, non-anesthetics that are dissolved in the hydrocarbon phase are generally apolar; hence, their distribution along the membrane normal is driven primarily by steric effects, and thus their main preference is to stay in the middle of the membrane.
The anesthetic molecules, staying thus between the lipid tails, push the lipid molecules farther away from each other, giving rise to a decrease of the lateral density (i.e., increase of the area per lipid) of the membrane, an effect that is clearly reverted at high pressure. This behavior is in a clear accordance with the half-a-century-old critical volume hypothesis, suggesting that general anesthesia occurs if the volume per lipid goes above a certain threshold value.16 However, this hypothesis can also be refined in light of the recent findings, namely, that instead of the volume, the surface area per lipid has to exceed a certain value. This refinement is particularly important in light of the fact that a number of anesthetics induce a thinning, while pressure induces a thickening of the membrane, an effect that, at least partly, compensates for the surface area-induced changes of the membrane volume.
The decreased lateral density triggers a number of other changes in the membrane properties, such as the increase of the free volume, decrease of the order of the lipid tails close to the region where anesthetics are preferentially staying, or the increase of the lateral mobility of the lipid molecules. However, although these changes are certainly correlated with the occurrence of the phenomenon of general anesthesia, they are not necessarily in a causal relation with it.
To understand the direct cause of the anesthetic effect, the pioneering work of Cantor54,55 has to be considered. Thus, based on thermodynamic arguments, Cantor demonstrated that conformational changes of certain membrane-bound proteins, which turn on the anesthetic effect, could be triggered by non-uniform changes in the profile of lateral pressure. Considering also the phenomenon of pressure reversal, these changes should be such that the lateral pressure is decreased by the anesthetics in certain membrane regions. Clearly, the decreased lateral density, caused by the anesthetic molecules staying between the lipid tails, can induce such a systematic decrease of lateral pressure at the vicinity of the preferred position of the anesthetics along the membrane normal, i.e., at the hydrocarbon side of the apolar/polar interface. On the other hand, non-anesthetics, mostly accumulated in the middle of the bilayer, and thus staying in a much smaller concentration between the lipid tails than anesthetics, cannot induce a noticeable decrease of the lateral pressure in this region. Thus, unlike the anesthetic-induced changes in the lateral mobility or ordering of the lipid tails, those of the lateral pressure profile might indeed well be in a causal relation with the phenomenon of anesthesia.
After the seminal finding of Cantor,54,55 the task of explaining the molecular mechanism of general anesthesia was simplified to the task of explaining how and where the general anesthetics can alter the lateral pressure profile in such a way that is consistent (i) with the occurrence of the anesthetic effect in the presence of any kind of general anesthetics, (ii) with the lack of such an effect in the presence of non-anesthetics, and (iii) also with the pressure reversal of anesthesia. The present work, together with the picture that emerged from a number of similar studies in the past two decades,34 can now fill this gap.
Acknowledgments
This work has been supported by the Hungarian NKFIH Foundation under Project nos. 134596 and TKP2021-NVA-14.
Author Present Address
⊥ Department of Theoretical Biophysics, Max Planck Institute of Biophysics, Max von Laue Street 3, D-60438 Frankfurt am Main, Germany
The authors declare no competing financial interest.
References
- Meyer H. Zur Theorie der Alkoholnarkose. N. Schmied. Arch. Pharmacol. 1899, 42, 109–118. 10.1007/bf01834479. [DOI] [Google Scholar]
- Overton E.Studien über die Narkose zugleich ein Beitrag zur allgemeinen Pharmakologei; Gustav Fischer Verlag: Jena, 1901. [Google Scholar]
- Franks N. P.; Lieb W. R. Where Do General Anesthetics Act?. Nature 1978, 274, 339–342. 10.1038/274339a0. [DOI] [PubMed] [Google Scholar]
- Franks N. P.; Lieb W. R. Molecular and cellular mechanisms of general anaesthesia. Nature 1994, 367, 607–614. 10.1038/367607a0. [DOI] [PubMed] [Google Scholar]
- Mitchell D. C.; Lawrence J. T. R.; Litman B. J. Primary Alcohols Modulate the Activation of the G Protein-Coupled Receptor Rhodopsin by a Lipid-Mediated Mechanism. J. Biol. Chem. 1996, 271, 19033–19036. 10.1074/jbc.271.32.19033. [DOI] [PubMed] [Google Scholar]
- Mihic S. J.; Ye Q.; Wick M. J.; Koltchine V. V.; Krasowski M. D.; Finn S. E.; Mascia M. P.; Valenzuela C. F.; Hanson K. K.; Greenblatt E. P.; et al. Sites of Alcohol and Volatile Anesthetic Action on GABAA and Glycine Receptors. Nature 1997, 389, 385–389. 10.1038/38738. [DOI] [PubMed] [Google Scholar]
- Mohr J. T.; Gribble G. W.; Lin S. S.; Eckenhoff R. G.; Cantor R. S. Anesthetic Potency of Two Novel Synthetic Polyhydric Alkanols Longer than the n-Alkanol Cutoff: Evidence for a Bilayer-Mediated Mechanism of Anesthesia?. J. Med. Chem. 2005, 48, 4172–4176. 10.1021/jm049459k. [DOI] [PubMed] [Google Scholar]
- Cantor R. S. Breaking the Meyer-Overton Rule: Predicted Effects of Varying Stiffness and Interfacial Activity on the Intrinsic Potency of Anesthetics. Biophys. J. 2001, 80, 2284–2297. 10.1016/s0006-3495(01)76200-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Græsbøll K.; Sasse-Middelhoff H.; Heimburg T. The Thermodynamics of General and Local Anesthesia. Biophys. J. 2014, 106, 2143–2156. 10.1016/j.bpj.2014.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelz M. B.; Mashour G. A. The Biology of General Anesthesia from Paramecium to Primate. Curr. Biol. 2019, 29, R1199–R1210. 10.1016/j.cub.2019.09.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson F. H.; Flagler E. A. Hydrostatic Pressure Reversal of Narcosis in Tadpoles. Science 1950, 112, 91–92. 10.1126/science.112.2899.91-a. [DOI] [PubMed] [Google Scholar]
- Johnson S. M.; Miller K. W. Antagonism of Pressure and Anaesthesia. Nature 1970, 228, 75–76. 10.1038/228075b0. [DOI] [PubMed] [Google Scholar]
- Lever M. J.; Miller K. W.; Paton W. D. M.; Smith E. B. Pressure Reversal of Anaesthesia. Nature 1971, 231, 368–371. 10.1038/231368a0. [DOI] [PubMed] [Google Scholar]
- Halsey M. J.; Wardley-Smith B. Pressure Reversal of Narcosis Produced by Anesthetics, Narcotics and Tranquillisers. Nature 1975, 257, 811–813. [DOI] [PubMed] [Google Scholar]
- Trudell J. R.; Payan D. G.; Chin J. H.; Cohen E. N. The Antagonistic Effect of an Inhalation Anesthetic and High Pressure on the Phase Diagram of Mixed Dipalmitoyl-Dimyristoylphosphatidylcholine Bilayers. Proc. Natl. Acad. Sci. U.S.A. 1975, 72, 210–213. 10.1073/pnas.72.1.210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mullins L. J. Some Physical Mechanisms in Narcosis. Chem. Rev. 1954, 54, 289–323. 10.1021/cr60168a003. [DOI] [Google Scholar]
- Booker R. D.; Sum A. K. Biophysical Changes Induced by Xenon on Phospholipid Bilayers. Biochim. Biophys. Acta 2013, 1828, 1347–1356. 10.1016/j.bbamem.2013.01.016. [DOI] [PubMed] [Google Scholar]
- Moskovitz Y.; Yang H. Modelling of noble anaesthetic gases and high hydrostatic pressure effects in lipid bilayers. Soft Matter 2015, 11, 2125–2138. 10.1039/c4sm02667e. [DOI] [PubMed] [Google Scholar]
- Haydon D. A.; Hendry B. M.; Levinson S. R.; Requena J. The molecular mechanisms of anaesthesia. Nature 1977, 268, 356–358. 10.1038/268356a0. [DOI] [PubMed] [Google Scholar]
- Trudell J. R.; Hubbell W. L.; Cohen E. N. The effect of two inhalation anesthetics of the order of spin-labeled phospholipid vesicles. Biochim. Biophys. Acta 1973, 291, 321–327. 10.1016/0005-2736(73)90485-9. [DOI] [PubMed] [Google Scholar]
- Franks N. P.; Lieb W. R. The structure of lipid bilayers and the effects of general anaesthetics. J. Mol. Biol. 1979, 133, 469–500. 10.1016/0022-2836(79)90403-0. [DOI] [PubMed] [Google Scholar]
- Tu K.; Tarek M.; Klein M. L.; Scharf D. Effects of Anesthetics on the Structure of a Phospholipid Bilayer: Molecular Dynamics Investigation of Halothane in the Hydrated Liquid Crystal Phase of Dipalmitoylphosphatidylcholine. Biophys. J. 1998, 75, 2123–2134. 10.1016/s0006-3495(98)77655-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koubi L.; Tarek M.; Klein M. L.; Scharf D. Distribution of Halothane in a Dipalmitoylphosphatidylcholine Bilayer from Molecular Dynamics Calculations. Biophys. J. 2000, 78, 800–811. 10.1016/s0006-3495(00)76637-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee B. W.; Faller R.; Sum A. K.; Vattulainen I.; Patra M.; Karttunen M. Structural effects of small molecules on phospholipid bilayers investigated by molecular simulations. Fluid Phase Equilib. 2005, 228–229, 135–140. 10.1016/j.fluid.2005.03.002. [DOI] [Google Scholar]
- Patra M.; Salonen E.; Terama E.; Vattulainen I.; Faller R.; Lee B. W.; Holopainen J.; Karttunen M. Under the Influence of Alcohol: The Effect of Ethanol and Methanol on Lipid Bilayers. Biophys. J. 2006, 90, 1121–1135. 10.1529/biophysj.105.062364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frischknecht A. L.; Frink L. J. D. Alcohols Reduce Lateral Membrane Pressures: Predictions from Molecular Theory. Biophys. J. 2006, 91, 4081–4090. 10.1529/biophysj.106.091918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griepernau B.; Böckmann R. A. The Influence of 1-Alkanols and External Pressure on the Lateral Pressure Profiles of Lipid Bilayers. Biophys. J. 2008, 95, 5766–5778. 10.1529/biophysj.108.142125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurtovenko A. A.; Anwar J. Interaction of Ethanol with Biological Membranes: The Formation of Non-bilayer Structures within the Membrane Interior and their Significance. J. Phys. Chem. B 2009, 113, 1983–1992. 10.1021/jp808041z. [DOI] [PubMed] [Google Scholar]
- Oh K.-J.; Klein M. L. Effects of Halothane on Dimyristoylphosphatidylcholine Lipid Bilayer Structure: A Molecular Dynamics Simulation Study. Bull. Korean Chem. Soc. 2009, 30, 2087–2092. 10.5012/bkcs.2009.30.9.2087. [DOI] [Google Scholar]
- Jerabek H.; Pabst G.; Rappolt M.; Stockner T. Membrane-Mediated Effect on Ion Channels Induced by the Anesthetic Drug Ketmine. J. Am. Chem. Soc. 2010, 132, 7990–7997. 10.1021/ja910843d. [DOI] [PubMed] [Google Scholar]
- Darvas M.; Hoang P. N. M.; Picaud S.; Sega M.; Jedlovszky P. Anesthetic Molecules Embedded in a Lipid Membrane: A Computer Simulation Study. Phys. Chem. Chem. Phys. 2012, 14, 12956–12969. 10.1039/c2cp41581j. [DOI] [PubMed] [Google Scholar]
- Fábián B.; Darvas M.; Picaud S.; Sega M.; Jedlovszky P. The effect of anaesthetics on the properties of a lipid membrane in the biologically relevant phase: a computer simulation study. Phys. Chem. Chem. Phys. 2015, 17, 14750–14760. 10.1039/c5cp00851d. [DOI] [PubMed] [Google Scholar]
- Hantal G.; Fábián B.; Sega M.; Jójárt B.; Jedlovszky P. Effect of General Anesthetics on the Properties of Lipid Membranes of Various Compositions. Biochim. Biophys. Acta Biomembr. 2019, 1861, 594–609. 10.1016/j.bbamem.2018.12.008. [DOI] [PubMed] [Google Scholar]
- Jedlovszky P.Simulation of Membranes Containing General Anesthetics. In Biomembrane Simulations. Computational Studies of Biological Membranes; Berkowitz M. L., Ed.; Taylor and Francis: New York, 2019; pp 177–198. and references therein. [Google Scholar]
- Ly H. V.; Block D. E.; Longo M. L. Interfacial Tension Effect of Ethanol on Lipid Bilayer Rigidity, Stability, and Area/Molecule: A Micropipet Aspiration Approach. Langmuir 2002, 18, 8988–8995. 10.1021/la026010q. [DOI] [Google Scholar]
- Ly H. V.; Longo M. L. The Influence of Short-Chain Alcohols on Interfacial Tension, Mechanical Properties, Area/Molecule, and Permeability of Fluid Lipid Bilayers. Biophys. J. 2004, 87, 1013–1033. 10.1529/biophysj.103.034280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stimson L. M.; Vattulainen I.; Róg T.; Karttunen M. Exploring the Effect of Xenon on Biomembranes. Cell. Mol. Biol. Lett. 2005, 10, 563–569. [PubMed] [Google Scholar]
- Griepernau B.; Leis S.; Schneider M. F.; Sikor M.; Steppich D.; Böckmann R. A. 1-Alkanols and Membranes: A Story of Attraction. Biochim. Biophys. Acta 2007, 1768, 2899–2913. 10.1016/j.bbamem.2007.08.002. [DOI] [PubMed] [Google Scholar]
- Dickey A. N.; Faller R. How Alcohol Chain-Length and Concentration Modulate Hydrogen Bond Formation in a Lipid Bilayer. Biophys. J. 2007, 92, 2366–2376. 10.1529/biophysj.106.097022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reigada R. Influence of Chloroform in Liquid-Ordered and Liquid-Disordered Phases in Lipid Membranes. J. Phys. Chem. B 2011, 115, 2527–2535. 10.1021/jp110699h. [DOI] [PubMed] [Google Scholar]
- Yamamoto E.; Akimoto T.; Shimizu H.; Hirano Y.; Yasui M.; Yasuoka K. Diffusive Nature of Xenon Anesthetic Changes Properties of a Lipid Bilayer: Molecular Dynamics Simulations. J. Phys. Chem. B 2012, 116, 8989–8995. 10.1021/jp303330c. [DOI] [PubMed] [Google Scholar]
- Reigada R. Atomistic Study of Lipid Membranes Containing Chloroform: Looking for a Lipid-Mediated Mechanism of Anesthesia. PLoS One 2013, 8, e52631 10.1371/journal.pone.0052631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J.; Chen L.; Wang Y.; Wang X.; Zeng S. Exploring the Effects on Lipid Bilayer Induced by Noble Gases via Molecular Dynamics Simulations. Sci. Rep. 2015, 5, 17235. 10.1038/srep17235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janoff A. S.; Miller K. W.. Biological Membranes; Chapman D., Ed.; Academic Press: London, 1982; pp 417–476. [Google Scholar]
- Forrest B. J.; Rodham D. K. An anaesthetic-induced phosphatidylcholine hexagonal phase. Biochim. Biophys. Acta 1985, 814, 281–288. 10.1016/0005-2736(85)90446-8. [DOI] [Google Scholar]
- Kaminoh Y.; Tashiro C.; Kamaya H.; Ueda I. Depression of Phase-Transition Temperature by Anesthetics: Nonzero Solid Membrane Binding. Biochim. Biophys. Acta 1988, 946, 215–220. 10.1016/0005-2736(88)90395-1. [DOI] [PubMed] [Google Scholar]
- Kaminoh Y.; Nishimura S.; Kamaya H.; Ueda I. Alcohol Interaction with High Entropy States of Macromolecules: Critical Temperature Hypothesisfor Anesthesia Cutoff. Biochim. Biophys. Acta 1992, 1106, 335–343. 10.1016/0005-2736(92)90014-d. [DOI] [PubMed] [Google Scholar]
- Heimburg T.; Jackson A. D. The Thermodynamics of General Anesthesia. Biophys. J. 2007, 92, 3159–3165. 10.1529/biophysj.106.099754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sierra-Valdez F. J.; Ruiz-Suárez J. C. Noble Gases in Pure Lipid Membranes. J. Phys. Chem. B 2013, 117, 3167–3172. 10.1021/jp400367t. [DOI] [PubMed] [Google Scholar]
- Chanda J.; Bandyopadhyay S. Distribution of Ethanol in a Model Membrane: A Computer Simulation Study. Chem. Phys. Lett. 2004, 392, 249–254. 10.1016/j.cplett.2004.05.072. [DOI] [Google Scholar]
- Pickholz M.; Saiz L.; Klein M. L. Concentration Effects of Volatile Anesthetics on the Properties of Model Membranes: A Coarse-Grain Approach. Biophys. J. 2005, 88, 1524–1534. 10.1529/biophysj.104.044354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chanda J.; Bandyopadhyay S. Perturbation of Phospholipid Bilayer Properties by Ethanol at a High Concentration. Langmuir 2006, 22, 3775–3781. 10.1021/la053398r. [DOI] [PubMed] [Google Scholar]
- Terama E.; Ollila O. H. S.; Salonen E.; Rowat A. C.; Trandum C.; Westh P.; Patra M.; Karttunen M.; Vattulainen I. Influence of Ethanol on Lipid Membranes: From Lateral Pressure Profiles to Dynamics and Partitioning. J. Phys. Chem. B 2008, 112, 4131–4139. 10.1021/jp0750811. [DOI] [PubMed] [Google Scholar]
- Cantor R. S. Lateral Pressures in Cell Membranes: A Mechanism for Modulation of Protein Function. J. Phys. Chem. B 1997, 101, 1723–1725. 10.1021/jp963911x. [DOI] [Google Scholar]
- Cantor R. S. The Lateral Pressure Profile in Membranes: A Physical Mechanism of General Anesthesia. Biochemistry 1997, 36, 2339–2344. 10.1021/bi9627323. [DOI] [PubMed] [Google Scholar]
- Schofield P.; Henderson J. R. Statistical Mechanics of Inhomogeneous Fluids. Proc. R. Soc. London, Ser. A 1982, 379, 231–246. 10.1098/rspa.1982.0015. [DOI] [Google Scholar]
- Sonne J.; Hansen F. Y.; Peters G. H. Methodological Problems in Pressure Profile Calculations for Lipid Bilayers. J. Chem. Phys. 2005, 122, 124903. 10.1063/1.1862624. [DOI] [PubMed] [Google Scholar]
- Sega M.; Fábián B.; Jedlovszky P. Pressure Profile Calculation with Mesh Ewald Methods. J. Chem. Theory Comput. 2016, 12, 4509–4515. 10.1021/acs.jctc.6b00576. [DOI] [PubMed] [Google Scholar]
- Fábián B.; Sega M.; Voloshin V. P.; Medvedev N. N.; Jedlovszky P. Lateral Pressure Profile and Free Volume Properties in Phospholipid Membranes Containing Anesthetics. J. Phys. Chem. B 2017, 121, 2814–2824. 10.1021/acs.jpcb.7b00990. [DOI] [PubMed] [Google Scholar]
- Hauet N. F.; Artzner F.; Boucher F.; Grabielle-Madelmont C.; Cloutier I.; Keller G.; Lesieur P.; Durand D.; Paternostre M. Interaction between Artificial Membranes and Enflurane, a General Volatile Anesthetic: DPPC-Enflurane Interaction. Biophys. J. 2003, 84, 3123–3137. 10.1016/s0006-3495(03)70037-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin L.; Laster M. J.; Taheri S.; Eger E. I. II; Koblin D. D.; Halsey M. J. Is There a Cutoff in Anesthetic Potency for the Normal Alkanes?. Anesth. Analg. 1993, 77, 12–18. 10.1213/00000539-199307000-00004. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Eger E. I. II; Dutton R. C.; Sonner J. M. Inhaled Anesthetics Have Hyperalgesic Effects at 0.1 Minimum Alveloar Anesthetic Concentration. Anesth. Analg. 2000, 91, 462–466. 10.1097/00000539-200008000-00044. [DOI] [PubMed] [Google Scholar]
- Nagle J. F.; Zhang R.; Tristram-Nagle S.; Sun W.; Petrache H. I.; Suter R. M. X-Ray Structure Determination of Fully Hydrated Lα Phase Dipalmitoylphosphatidylcholine Bilayers. Biophys. J. 1996, 70, 1419–1431. 10.1016/s0006-3495(96)79701-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klauda J. B.; Venable R. M.; Freites J. A.; O’Connor J. W.; Tobias D. J.; Mondragon-Ramirez C.; Vorobyov I.; MacKerell A. D.; Pastor R. W. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zoete V.; Cuendet M. A.; Grosdidier A.; Michielin O. SwissParam, a Fast Force Field Generation Tool For Small Organic Molecules. J. Comput. Chem. 2011, 32, 2359–2368. 10.1002/jcc.21816. [DOI] [PubMed] [Google Scholar]
- SIB . SwissParam. https://www.swissparam.ch (accessed Feb 23, 2023).
- Neria E.; Fischer S.; Karplus M. Simulation of Activation Free Energies in Molecular Systems. J. Chem. Phys. 1996, 105, 1902–1921. 10.1063/1.472061. [DOI] [Google Scholar]
- Miyamoto S.; Kollman P. A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
- Hess B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 116–122. 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Pronk S.; Páll S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; van der Spoel D.; et al. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- GitHub . Marcello-Sega/gromacs. The code is freely available at https://github.com/Marcello-Sega/gromacs/tree/virial/ (accessed Jan 27, 2023).
- Allen M. P.; Tildesley D. J.. Computer Simulation of Liquids; Clarendon Press: Oxford, 1987. [Google Scholar]
- Nosé S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 1984, 52, 255–268. 10.1080/00268978400101201. [DOI] [Google Scholar]
- Hoover W. G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 1985, 31, 1695–1697. 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Harasima A.Molecular Theory of Surface Tension. Advances in Chemical Physics; Wiley, 1958; Vol. 1, pp 203–237. [Google Scholar]
- Ewald P. Die Berechnung Optischer und Elektrostatischer Gitterpotentiale. Ann. Phys. 1921, 369, 253–287. 10.1002/andp.19213690304. [DOI] [Google Scholar]
- de Leeuw S. W.; Perram J. W.; Smith E. R. Simulation of Electrostatic Systems in Periodic Boundary Conditions. I. Lattice Sums and Dielectric Constants. Proc. R. Soc. London, Ser. A 1980, 373, 27–56. 10.1098/rspa.1980.0135. [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Sega M.; Fábián B.; Jedlovszky P. Layer-by-Layer and Intrinsic Analysis of Molecular and Thermodynamic Properties Across Soft Interfaces. J. Chem. Phys. 2015, 143, 114709. 10.1063/1.4931180. [DOI] [PubMed] [Google Scholar]
- Rózsa Z. B.; Fábián B.; Hantal G.; Szőri M.; Jedlovszky P. Effect of Xenon, an Apolar General Anaesthetic on the Properties of the DPPC Bilayer. J. Mol. Liq. 2023, 122405 10.1016/j.molliq.2023.122405. [DOI] [Google Scholar]
- Nagle J. F. Area/Lipid of Bilayers from NMR. Biophys. J. 1993, 64, 1476–1481. 10.1016/s0006-3495(93)81514-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiener M. C.; Tristram-Nagle S.; Wilkinson D. A.; Campbell L. E.; Nagle J. F. Specific Volumes of Lipids in Fully Hydrated Bilayer Dispersions. Biochim. Biophys. Acta Biomembr. 1988, 938, 135–142. 10.1016/0005-2736(88)90153-8. [DOI] [PubMed] [Google Scholar]
- López-Cascales J. J.; García de la Torre J.; Marrink S. J.; Berendsen H. J. C. Molecular dynamics simulation of a charged biological membrane. J. Chem. Phys. 1996, 104, 2713–2720. 10.1063/1.470992. [DOI] [Google Scholar]
- Mezei M.; Jedlovszky P.. Statistical Thermodynamics via Computer Simulation to Characterize Phospholipid Interactions in Membranes. In Methods in Molecular Biology; Dopico A. M., Ed.; Methods in Membrane Lipid; Humana Press: Totowa, NJ, 2007; Vol. 400, pp 127–144. [DOI] [PubMed] [Google Scholar]
- Douliez J. P.; Léonard A.; Dufourc E. J. Restatement of Order Parameters in Biomembranes: Calculation of C-C Bond Order Parameters from C-D Quadrupolar Splittings. Biophys. J. 1995, 68, 1727–1739. 10.1016/s0006-3495(95)80350-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vögele M.; Hummer G. Divergent Diffusion Coefficients in Simulations of Fluids and Lipid Membranes. J. Phys. Chem. B 2016, 120, 8722–8732. 10.1021/acs.jpcb.6b05102. [DOI] [PubMed] [Google Scholar]
- Orädd G.; Westerman P. W.; Lindblom G. Lateral Diffusion Coefficients of Separate Lipid Species in a Ternary Raft-Forming Bilayer: A Pfg-NMR Multinuclear Study. Biophys. J. 2005, 89, 315–320. 10.1529/biophysj.105.061762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sega M.; Fábián B.; Horvai G.; Jedlovszky P. How Is the Surface Tension of Various Liquids Distributed along the Interface Normal?. J. Phys. Chem. C 2016, 120, 27468–27477. 10.1021/acs.jpcc.6b09880. [DOI] [Google Scholar]
- Pavel M. A.; Petersen E. N.; Wang H.; Lerner R. A.; Hansen S. B. Studies on the Mechanism of General Anesthesia. Proc. Natl. Acad. Sci. U.S.A. 2020, 117, 13757–13766. 10.1073/pnas.2004259117. [DOI] [PMC free article] [PubMed] [Google Scholar]