Abstract
Mechanical force has repeatedly been highlighted to be involved in T cell activation. However, the biological significance of mechanical force for T cell receptor signaling remains under active consideration. Here, guided by theoretical analysis, we provide a perspective on how mechanical forces between a T cell and an antigen-presenting cell can influence the bond of a single T cell receptor major histocompatibility complex during early T cell activation. We point out that the lifetime of T cell receptor bonds and thus the degree of their phosphorylation which is essential for T cell activation depends considerably on the T cell receptor rigidity and the average magnitude and frequency of an applied oscillatory force. Such forces could be, for example, produced by protrusions like microvilli during early T cell activation or invadosomes during full T cell activation. These features are suggestive of mechanical force being exploited by T cells to advance self–nonself discrimination in early T cell activation.
Keywords: TCR, mechanical force, T cell activation, catch bond, self–nonself discrimination
Over the last couple of years mechanical force has become known to be involved in all stages of T cell activation (1–3). Already at first contact between a T cell and an antigen-presenting cell (APC), when T cell protrusions like ruffles and microvilli initiate T cell receptor (TCR) binding to peptide major histocompatibility complexes (pMHCs) on the APC, mechanical forces affect their interaction (4, 5). Strikingly, these interactions are dynamic and physical in nature with T cell protrusions constantly touching the APC surface, pushing through its glycocalyx, and pulling back (6, 7). Thereby they aim to bring TCRs into close proximity of and to engage with the pMHCs on the APC.
Upon engagement of a single TCR–pMHC bond (8–10), TCR phosphorylation occurs through recruitment of kinases within a few seconds (8, 10). By increasing the lifetime of the TCR–pMHC bond, the number of total TCR phosphorylation events is enhanced (11). The number of total TCR phosphorylation events and thus the duration of the bond lifetime is thought to determine whether to activate a T cell or not (11, 12), both, in vitro (13, 14) and in vivo (9).
Initial T cell activation then leads to the formation of TCR microcluster, of the central supramolecular activation complex, and ultimately of the immunological synapse (IS) within minutes, which marks full T cell activation (15). If the recognized peptide antigen was nonself, then naive T cells differentiate into T cell effectors over hours and days (15, 16).
The process of TCR–pMHC recognition must be highly specific (17, 18), since T cells are capable of identifying few nonself pMHCs among a vast excess of self pMHCs (19–21). The ability to discriminate between self and nonself is commonly accepted to be largely amplified by kinetic proofreading (22, 23). Kinetic proofreading is at play at the single TCR–pMHC bond during early T cell activation and at the IS during full T cell activation (12).
Whereas biochemical events involved in TCR signaling are increasingly well understood, the importance of mechanical force for TCR–pMHC binding remains under discussion. Al-Aghbar et al. recently concluded that mechanical force may be involved in all stages, from early T cell activation to T cell effector differentiation (24). Mechanical force can contribute to the organization of the T cell membrane topography (25) and T cell cytoskeletal nanostructure (26, 27), which together with the mechanical properties of the T cell govern antigen extraction from the APC (28).
The uncertainty about the importance of mechanical force for antigen recognition might in part be due to the fact that the mechanical forces acting on TCR–pMHC bonds are diverse. For example, T cell microvilli during early T cell activation and invadosomes during full T cell activation generate a combination of constant and fluctuating mechanical forces in the pico-newton (pN) range. Furthermore, mechanical forces can have different effects on bond lifetime: Slip bonds break faster upon application of a mechanical force. In contrast, catch bonds are stabilized by an applied moderate mechanical force. For TCR–pMHC bonds, depending on the TCR involved, both, slip and catch bond behaviors have been reported (29).
Mechanical forces with constant amplitude over time have been experimentally shown to affect the lifetime of TCR–pMHC bonds (29). Consistently, the self–nonself discrimination by the TCR has been found to be impaired in the absence of mechanical force (30), highlighting their importance in differentiating between self and nonself pMHCs with consequences for autoimmune diseases and antitumor responses (31).
In an elegant study, Feng et al. uncovered recently that mechanics drives self–nonself discrimination of the αβTCR (32) but not of the γδTCR (33). TCR allostery, that is, the transmission of signals to distal TCR sites via changes in protein structure, could provide a molecular explanation for the TCR–pMHC response to mechanical force (34–37). TCR allostery warrants further investigation, though (38, 39), as allosteric rearrangements are thought to act on the microsecond time scale, where thermodynamic fluctuations dominate (34), or might even dominate the catch-bond curve (40).
However, although there are ample indications that T cell APC biomechanics may be of importance for TCR signaling, a direct influence of mechanical force on TCR–pMHC binding remains to be shown (3, 41, 42). Recent efforts to quantify small mechanical forces imposed on TCR via quantitative Foerster fluorescence resonance energy transfer (FRET) did not detect force (43). Possibly, in addition to technical limitations of the applied methodology, this could be because fluctuating and constant mechanical forces have not been considered separately in the contexts of early and full T cell activation. Furthermore, subsets of T cells have distinct mechanical properties and are known to produce various cell protrusions like dynamic microvilli and more static invadosomes at different stages of T cell activation (5).
In the following, to address some of these open questions, we discuss a simple effective theoretical description of TCR phosphorylation to provide a perspective on how mechanical forces between a T cell and an APC influence the lifetime of a single TCR–pMHC during early T cell activation. We show that the number of TCR phosphorylation events for catch and slip bonds can depend dramatically on the average magnitude and the frequency of an applied mechanical force. We also discuss how the TCR rebinding to APC as well as TCR rigidity influence this number.
Theory Indicates That Mechanical Force Matters in Early T Cell Activation
To discuss the role of mechanical force in early T cell activation, we consider an effective theoretical description of a single TCR–pMHC bond during the initial interaction between a T cell and an APC (Fig. 1A). We first explore the dependence on an applied constant mechanical force of TCR phosphorylation for a TCR–pMHC bond with catch bond property. We then expand the discussion to fluctuating mechanical forces and present the dependence on mechanical force frequency. We consider the possibility of TCR to pMHC-complex rebinding and its effects on TCR phosphorylation in presence of both constant and oscillatory mechanical forces with catch and slip bond features. We ask then how TCR rigidity influences the activation of T cells. Finally, we consider the time course of the degree of TCR phosphorylation in presence of dephosphorylation and a finite number of phosphorylation sites. Note, we refer to mechanical force simply as force in the following sections.
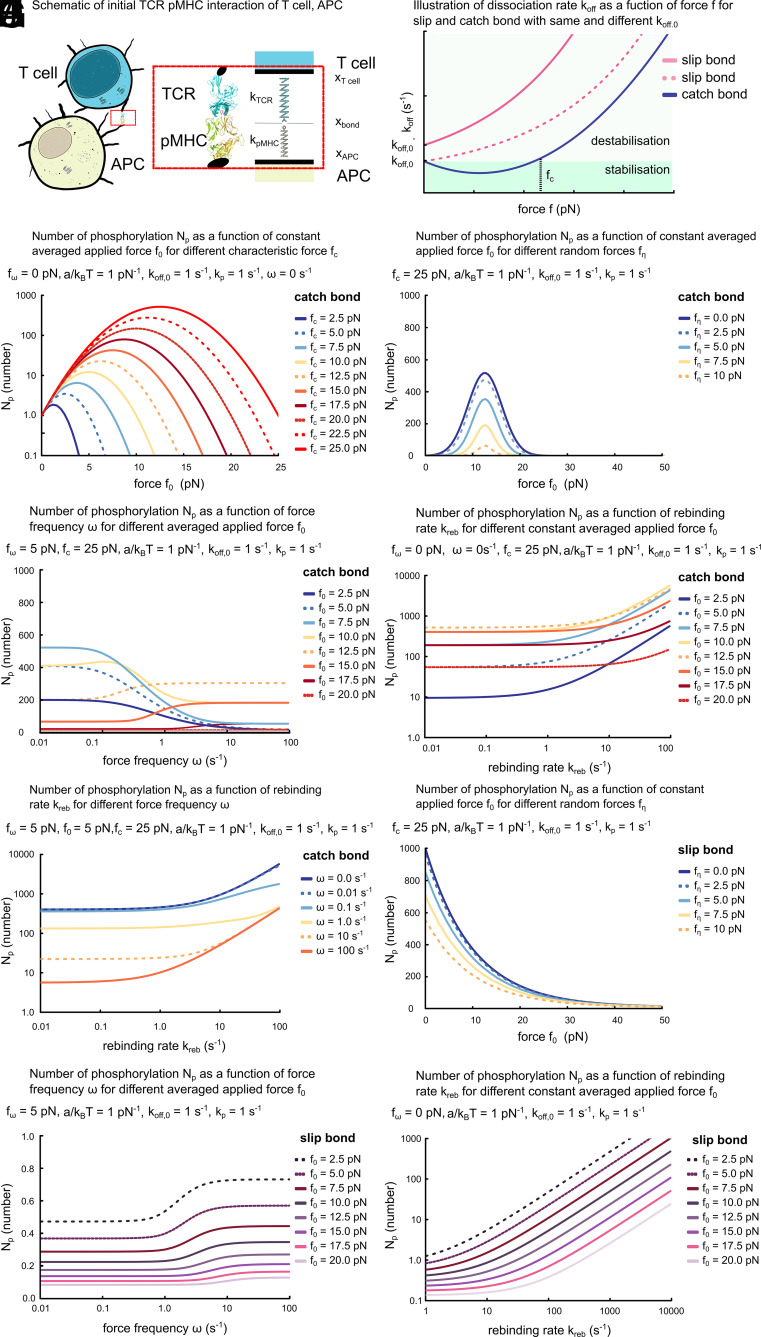
Fig. 1.
Effects of mechanical force on early stages of T cell activation. (A) Schematic of initial TCR–pMHC interaction between T cell and APC. (B) Illustration of the force dependence of for a slip and a catch bond. (C–J) Number of total TCR phosphorylation as a function of external average force in absence (C) and in presence of force fluctuations (D and H), force frequency (E and I), and rebinding rate (F, G, and J). Parameter values (if not varied): pN, pN, s−1, pN−1, and .
Many molecular aspects of how TCR phosphorylation leads to early T cell activation are actively investigated and require further research. Yet, the decision-making of a T cell to either activate or not is known to depend on the overall total phosphorylation of a single TCR integrated over time rather than TCR phosphorylation at a given point in time (44). For this reason, we opt first for studying the cumulative number of TCR phosphorylation events as a proxy. In this context, we neglect TCR dephosphorylation and consider the number of phosphorylation sites to be not limiting phosphorylation. Furthermore, we only consider the dynamics of the TCR–pMHC binding at the time after the bond is first formed and do not account for the process of bond formation. The latter would explicitly require to account for cell-shape changes like microvilli formation that bring the TCR in the vicinity of a pMHC. Later, we extend our description as indicated above.
The quality of the TCR–pMHC bond typically depends on the TCR affinity to the pMHC, the value of which is given by its bond lifetime . In the simplest case, the bond lifetime is then given by the bare off rate of the TCR from the pMHC through . As a consequence, , where is the phosphorylation rate while the TCR–pMHC bond is intact. This relation typically does not hold upon application of a force , for example, by the T cell as discussed above. We now compute as a function of an applied force , where we assume for simplicity that this force is always directed along the direction of the bond.
Number of Total TCR Phosphorylation Depends on Constant Force.
According to their definition, slip bonds are weakened by an applied force, whereas catch bonds can be strengthened (Fig. 1B). The figure illustrates that, for a catch bond, the dissociation rate in absence of a force is typically lower than the corresponding rate of a slip bond, . On this basis, self-peptide antigens have been suggested to form slip bonds, and nonself-peptide antigens to form catch bonds (45). Thereby, application of a force by the T cell on the TCR–pMHC bond could enhance self–nonself discrimination.
We follow the common Bell and Evans approach to characterize the force dependence of slip and catch bonds (Fig. 1B) (46, 47), with for a slip bond, and for a catch bond. In these expressions, is a characteristic force, a molecular length scale, and thermal energy. Being molecular quantities, should be on the order of a few pN and a few nanometers (nm). The thermal energy pNnm with Boltzmann constant is considered at room temperature.
We can then compute for an external force with constant phosphorylation rate . Let be the probability of the bond to be intact at time . The number of phosphorylated TCR residues at time evolves according to
| [1] |
where . The number is then given by as . The time evolution of the probability follows
| [2] |
with , reflecting our choice to consider only the period after bond formation, and dissociation rate . Using Eqs. 1 and 2, we obtain . For a slip bond and in presence of a constant force , we have . An applied constant force thus always leads to a decrease in .
In contrast, for a constant force acting on a catch bond, we obtain . Depending on the values of and , an applied constant force can thus increase or decrease . The increase of the number of total TCR phosphorylation can be several orders of magnitude for an applied external force in the range of a few pN and depending on the value of (Fig. 1C). To this end, we used pN−1 (13, 35), s−1 (30, 48), s−1 (30, 48). Note, for reasons of simplicity the case for a slip bond in the presence of constant force is not shown. Together, a constant force acting on a single TCR–pMHC bond can enhance TCR phosphorylation during early T cell activation.
One might wonder about the dependence of the results presented in Fig. 1C on parameter values. Note that forces enter Eqs. 1 and 2 only through the rate . As a consequence, remains unchanged when changing the forces , by a common factor . This scaling can be used to infer the value of for other parameter values. Furthermore, is proportional to and inversely proportional to .
Force Fluctuations Increase Differences between Number of Total TCR Phosphorylations for Catch Bonds.
We now expand the discussion to fluctuating, that is, time-dependent forces. Explicitly, we consider a constant force of value . The amplitude of the variation is , such that , where is a random variable that is uniformly distributed in and for . The number of total TCR phosphorylation peaks at 10 to 15 pN and the increases of persists in the presence of force fluctuations (Fig. 1D).
In addition, cells might themselves exert an oscillating force. We thus consider now . Forces applied to a TCR–pMHC bond formed at the encounter of a T cell and an APC may be more complicated and contain various different frequencies. We chose the given form, because, a general time dependence can always be decomposed in terms of cosines and sines, and the dependence of on is instructive. We will exemplify the case for the cosine such that the force is maximal at time .
For a quantitative assessment of the number of total TCR phosphorylation in the presence of an oscillating force, we numerically solved Eqs. 1 and 2 with parameters pN and pN (13, 35), as well as pN−1 and s−1 as above. The values of approach those for a constant force for small force frequencies (Fig. 1E). Explicitly, we consider a spectrum of force frequencies as T cells would likely experience them in a realistic biological scenario, as well as individual force frequencies because a spectrum of force frequencies can mathematically be divided into a linear combination of the individual frequencies, which ultimately determine their effects on the single TCR–pMHC bond. Importantly, for higher force frequencies, can increase several fold, if pN (Fig. 1E). Note, that a scaling relation similar to the static case holds: Multiplication of , , , and by leaves invariant.
From the graphs, we also deduce that force fluctuations can compensate at least partially the reduction in for a nonoptimal average applied force. In this context, optimal means that it leads to the maximal extension of the catch bond’s lifetime and thus largest value of . This reduction is a consequence of the nonlinear dependence of on the force . It is weaker close to the optimal force that minimizes for a catch bond. Thus, the fluctuations will drive the force closer to the optimal value for longer times than away from it. This effect vanishes, if is such that fluctuations drive the force mostly away from its optimal value. In this case, for pN, decreases with increasing force frequency (Fig. 1E).
For intermediate values of the average force , exhibits a maximum at finite force frequency (Fig. 1E). This nonmonotonic dependence of on the applied average force results from a competition between the two effects discussed in the previous paragraph. Note, that the force is at its maximal value for . In case the applied force starts at its minimal value, , only small increases in are observed.
Let us highlight that fluctuations of forces acting on single TCR–pMHCs are inevitable, as they are subject to molecular noise. Together the analysis suggests that high force frequency fluctuations compensate partially for applying a nonoptimal force and the strongest effect is observed for intermediate values of the average force.
Rebinding of TCR to pMHC Strongly Affects Number of Total TCR Phosphorylations for Catch Bonds.
Having highlighted the role of constant and fluctuating force on the number of total TCR phosphorylations, in this section, we examine effects of rebinding of TCR to pMHC in the biological scenario when the T cell and APC remain juxtaposed after the unique TCR–pMHC bond is broken. From the physics perspective, this could occur if receptor ligand diffusion is slow compared reaction kinetics or if integrins such as CD2 or ICAM-I on the two cells engage in addition to the initial TCR–pMHC bond.
In light of this, we now consider a state from which the TCR–pMHC bond can reform in addition to the bound and unbound states. In this new state, no phosphorylation occurs. If denotes again the probability that the TCR–pMHC bond is formed at time , and the probability that the system is in the state from which the bond can reform, then the dynamic equations are
| [3] |
| [4] |
| [5] |
with is the rate of reforming the bond and the rate of complete unbinding. Initially, we have , , and . Also, is considered to be independent of the applied force. In contrast, , that is, we assume the juxtaposition of T cell and APC surface to behave like a slip bond. In case is independent of the applied force or even behaved as a catch bond, the results below underestimate the number of total TCR phosphorylation .
We again consider first the case of a constant applied force (Fig. 1F). can then be obtained analytically. For all constant forces, its value strongly increases monotonically with the rebinding rate . The value of is larger than the corresponding value in absence of rebinding as rebinding can ’rescue’ an initial unbinding event. Note that the dependence of on is nonmonotonic for a fixed value of .
Similarly, in the case of an oscillating force with , is monotonically increasing with the rebinding rate for a range of force frequencies (Fig. 1G). Consistent with the constant force, decreases monotonically with for a given value . Together, this highlights that rebinding of TCR to pMHC can strongly affect number of total TCR phosphorylations for catch bonds during early T cell activation.
Effects of Force on Slip Bonds.
For a slip bond, the number of total TCR phosphorylations decreases compared to the force-free situation in the presence of a constant force as discussed above. This is also the case when applying a stochastic force with as above (Fig. 1H) or an oscillating force (Fig. 1I). increases with a sigmoidal dependence as a function of force frequency . For low frequencies, tends toward the value for a constant force . For , in contrast, tends toward the value of a constant force .
Interestingly, still decreases with in the case of a constant external force for a given rebinding rate (Fig. 1J). But strongly increases monotonically without an upper bound as a function of , suggesting that the increasingly rapid rebinding ’protects’ the bond from breaking and thus stabilizes it for increasingly longer periods as the value of is increased. Together, this analysis highlights that rebinding of TCR to pMHC can strongly affect the number of total TCR phosphorylations for slip bonds during early T cell activation.
Effects of TCR Rigidity on Total Number of TCR Phosphorylations.
Above, we considered forces directly acting on the TCR–pMHC bond. From the molecular mechanics perspective, the force exerted by the T cell is transmitted to the bond through the TCR, and the mechanical properties of the TCR, i.e. its rigidity, affect this transmission.
To account for TCR rigidity in the analysis based on Eqs. 1 and 2, we capture TCR deformation in terms of an extension of the molecule along the direction determined by the applied force. Let denote the position of the point at which the TCR is anchored to the T cell surface and the position of the bond along this direction. We assume that, in the situations of interest, the mechanical properties of both, the TCR and the pMHC, can be captured by linear springs. The corresponding spring constants are and . The positions and are measured relative to their positions at which the two springs are stress-free. Finally, the rest length of the TCR is given by and dissipation during length changes of the respective molecules is captured by the constants and , which have units of a friction coefficient (pN/(nm/s)).
Due to the negligible mass of the TCR and the pMHC, the dynamics of the bond is overdamped and the dynamic equations read
| [6] |
| [7] |
The lifetime of the bond is affected by the mechanical stress it is exposed to. This stress, which has the units of a force and is denoted by , is given by . The dependence on of the unbinding rate is as above. The dynamics remains unchanged if all forces, the friction coefficients and , and the spring constants and are multiplied by the same factor.
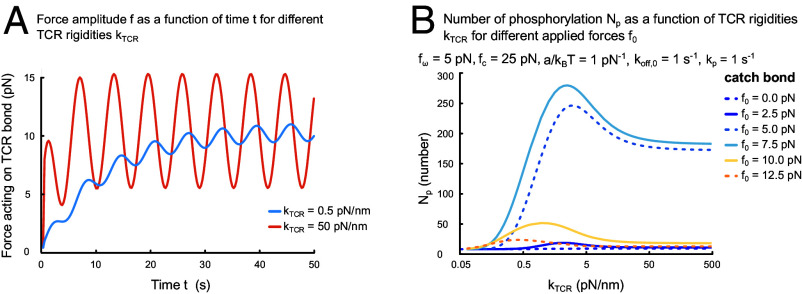
Solving the dynamic equations numerically, we find that the force amplitude depends on TCR rigidity (Fig. 2A). For these computations, we assume that the TCR–pMHC bond is stress-free at the time of formation, , and used spring constants of pN/nm and 50 pN/nm. Although, as expected, in both cases the same average stress is eventually reached, for the softer spring, the duration of the transient regime is about 5 times longer and the oscillation amplitude about 5 times smaller than for the stiffer spring. This result shows that a soft TCR can “buffer” part of the force applied by the T cell for several seconds.
Fig. 2.
Effects of TCR rigidity on early T cell activation. (A) Force amplitude as a function of time for pN/nm (blue) and pN/nm (red) and pN/nm, nm, pN/(nm/s), pN, pN, and s−1. (B) Number of total phosphorylation events as a function of TCR rigidity for different applied forces . Parameter values (if not varied) as in (A) and pN, pN−1, and .
The number of total TCR phosphorylations also depends on the TCR rigidity for different values of the constant force (Fig. 2B). For pN, the effect of varying the spring constant can be dramatic, leading to an increase of by two orders of magnitude. The size of the effect depends sensitively on the value of . Together, these results suggest that TCR rigidity is an important determinant of how the TCR–pMHC bond responds to force.
Time Course of Phosphorylated TCRs.
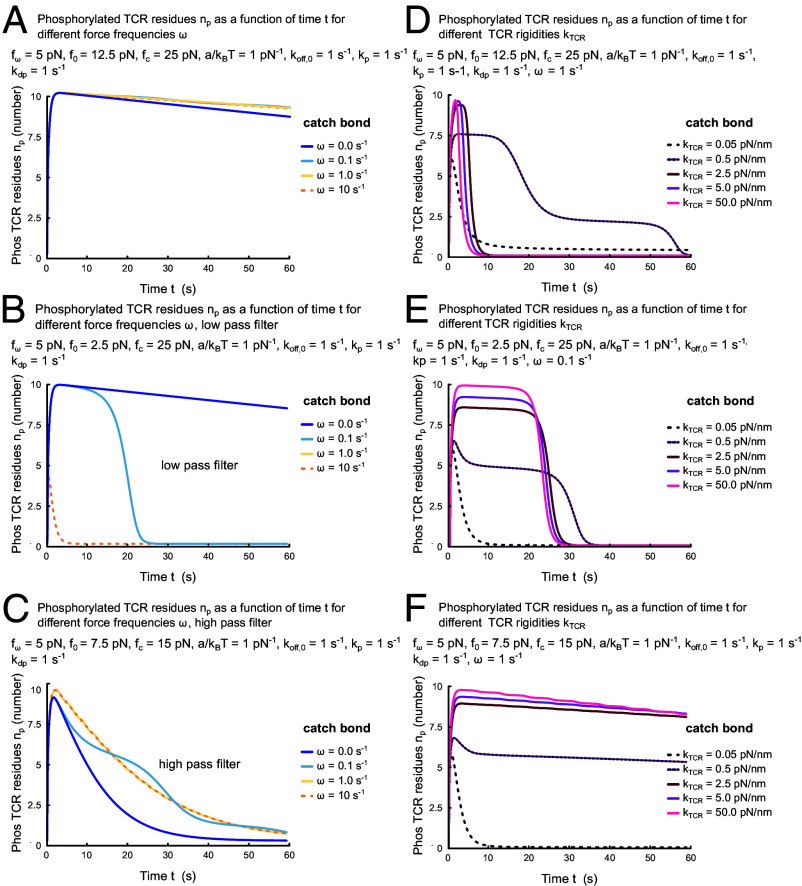
Having considered the cumulative number of TCR phosphorylation events as a proxy for T cell decision-making, we now study the underlying time course of the number of phosphorylated TCR residues in the presence of force. The time course consideration provides a quantitative understanding of how force influences the T cell’s decision-making over a period within its activation time scale of 60 s. This is the window in which the earliest activation marker calcium is released into the T cell’s cytosol (49). For this part, we also consider TCR dephosphorylation at rate and a finite number of TCR phosphorylation residues . We include these effects by modifying Eq. 1 to read
| [8] |
For a quantitative assessment of in the presence of oscillating force, we solved (Eq. 8) with parameters /s (50) and (50). We find that for an average force pN, pN and independently of the force frequency , the number of phosphorylated sites is close to its steady state value for , , during more than 60 s (Fig. 3A). This is different for pN, for which the time with increases with decreasing force frequency (Fig. 3B). For these parameters, the TCR–pMHC bond acts as a low-pass filter for oscillating forces. In contrast, for pN there is no plateau and decreases with decreasing force frequency, making the TCR–pMHC bond act as a high pass filter (Fig. 3C).
Fig. 3.
Time dependence of the number of phosphorylated TCR residues when forces act directly on the TCR–pMHC bond (A–C) and for finite TCR rigidities. Parameter values are pN, pN−1, s−1, and as well as pN and pN (A and D), pN and pN (B and E), and pN and pN (C and F). In (D–F), additionally, pN/nm, nm, pN/(nm/s).
Similarly, the time course can depend dramatically on TCR rigidity (Fig. 3D–F). The duration of the plateau phases can be reduced by an order of magnitude (Fig. 3D) or an extended plateau phase can be generated (Fig. 3F). Alternatively, the height of the plateau phase can be affected (Fig. 3E). The results show that, in general, the dependence of early T cell activation on force is complicated. Together, they further support that TCR rigidity is an important determinant of how the TCR–pMHC bond responds to force.
Implications of Mechanical Force for T Cell Activation
Most efforts to explain self–nonself discrimination in T cell activation have focused on biological signaling mechanisms. Undoubtedly, however, TCR–pMHC bonds are exposed to fluctuating force. Our theoretical analysis suggests that the number of total TCR phosphorylation and thus early T cell activation critically depends on the force applied to a TCR–pMHC. According to our analysis, a minimal force amplitude of 7.5 pN and a spectrum of force frequencies from 0.1 to 10 Hz would be ideal to exploit these mechanical properties of TCR–pMHC bonds by a T cell (Fig. 1C–F) and (Fig. 3A–C). Consistent with our findings in the presence of fluctuating forces, molecular dynamics simulations (51) and biomembrane force probes (52) suggest that the force leading to the maximal lifetime of a TCR–pMHC bond is around 10 to 15 pN. In our computations, this value depends on parameter values, notably, the molecular length scale , which defines an interaction volume between the TCR and pMHC. Although remains unchanged when changing the forces , by a factor , decreasing the interaction volume by results in proportional changes in the respective forces. As a consequence, this could mean that the TCR–pMHC bears larger characteristic forces for smaller volumes and smaller forces for larger volumes.
Forces with these characteristics could be produced by microvilli (5). Microvilli are dynamic with characteristic time scales on the right order of magnitude. For this reason, we encourage experimental investigation of the role of microvilli in self–nonself discrimination in T cell activation.
To date, as detailed above, experiments disagree on whether force is relevant in T cell activation (2, 3, 29, 31, 32, 43, 53). We discuss in the following how our findings could provide a consistent frame for interpreting the multitude of experimental results. We then indicate which experiments would be particularly helpful to elucidate the role of force in early T cell activation and, finally, speculate about the role played by force in self–nonself discrimination. Before delving on these points, let us discuss potential limitations of our analysis.
Potential Limitations of the Theoretical Analysis.
In the simple theoretical analysis, we opted for neglecting molecular details and instead employed an effective description. This aids to focus on generic properties of the TCR–pMHC bond that are independent of structural and signaling pathway complexities. Hence, direct comparison of our results to specific experimental data should be made with caution. Eventually, one would like to relate structural properties of the TCR and TCR–pMHC bonds quantitatively to the effects of force on bond lifetime. This requires a more detailed approach as can be provided by molecular dynamics simulations. Nevertheless, our effective description should yield correct orders of magnitude for bond lifetimes and can serve as a conceptual guide for more detailed computations and future experiments.
We initially investigated the cumulative number of TCR phosphorylation events as a quantitative readout of bond lifetime. Assuming that the number of TCR phosphorylation sites is not limiting, we did not need to account for dephosphorylation events. Later on, to understand the effects of force on the time scale of early T cell activation, we considered a finite number phosphorylated TCR residues and their dephosphorylation. Although many molecular details remain to be understood, the relationship between bond lifetime and early T cell activation is almost certainly more complicated. Yet, in addition to allowing for a transparent discussion of the effects of force on TCR–pMHC bonds, we expect our description to capture qualitatively the effect of force on early T cell activation.
Also, we did not account for the dynamics and mechanics of the T cell and APC environments on bond lifetime, for example, the dynamics of the T cell plasma membrane and cytoskeleton that directly couple to the TCR and the pMHCs on the APC. First studies suggest that they do play a role (26), but additional investigations are needed in this context. Further, we did not consider the role of coreceptors. For example, TCR–pMHC–CD4 bond lifetimes have been shown to be prolonged by force (27). Such studies might indicate experiments that would allow to further probe the role of force in early T cell activation.
As a final point, let us stress that spatial aspects of the dynamics leading to early T cell activation merit a detailed investigation. Even though, we do not expect a full spatiotemporal analysis to qualitatively affect our conclusions, for example, important quantitative differences likely exist between passive transport by diffusion and active transport driven by molecular motors of kinases to the TCR. Also, it might be interesting to investigate the dependence of IS position in later stages of T cell activation on kinase transport (54) for a theoretical study of localization in Ca2+-signaling.
A Common Theoretical and Experimental Framework for Early T Cell Activation.
To a large extent, experiments on the role of force in TCR–pMHC binding are so far not quantitatively comparable among each other, chiefly owing to differences in measurement techniques and their sensitivity. For instance, the single TCR–pMHC binding quantifications stem mostly from optical tweezers in the context of early T cell activation (2, 32), whereas for TCR–pMHC binding at the IS, FRET force sensors were employed in presence of fluid supported lipid bilayers (43). For these reasons, differences in the outcomes of the experiments must be interpreted with care. They might be resolved with improved experimental techniques. Yet, such differences might also turn out to be real. Our analysis suggests a number of possible reasons.
First, the applied force amplitude matters. Depending on its value, total TCR phosphorylation might be enhanced or reduced for catch bonds. Our computations suggest that differences of even a few pN in the applied force amplitude could make a large difference (Fig. 1C). An increase by 1 pN could augment or decrease TCR phosphorylation by an order of magnitude.
Second, the force frequency of a fluctuating applied force also affects TCR phosphorylation, albeit less dramatically. Maximal changes are about a factor of 5 and can either increase or decrease TCR phosphorylation, depending on the average applied force (Fig. 1D). Compared to its dependence on the force amplitude, TCR phosphorylation’s dependence on the force frequency is thus much less sensitive. Furthermore, force frequencies exist above and below at which TCR phosphorylation is essentially independent of the force frequency (Fig. 1D). This behavior holds true for slip bonds (Fig. 1H).
Third, when analyzing T cell activation in the presence of force, it is also essential to consider the TCR subtype. Indeed, αβTCR exhibit catch bond behavior (32), whereas γδTCR have been found to behave like slip bonds (33). At the outset, 90 percent of all T cells are known to be αβTCR (55). The molecular structural and signaling pathway differences through which αβTCR and γδTCR signal remain under active investigation. The presented analysis above suggests that a constant force acting on a catch bond could enhance TCR phosphorylation multiple orders of magnitude. Similarly, dynamic forces acting on single catch bonds could enhance TCR phosphorylation up to five-fold. This is consistent with single molecule TCR–pMHC experiments on αβTCR (29).
Finally, the rigidity of the TCR has also a strong effect on the lifetime of the TCR–pMHC bond and thus on TCR phosphorylation (Figs. 2B and 3 D and E) (56). Experimental evidence for these findings will rely on direct measurements of TCR rigidity which is technically challenging but single-molecule experiments (40, 57) and molecular simulations indicate that it seemingly depends on the effective length extension of the TCR complex and its conformational changes (58, 59). Consistent with the time scale of calcium release in activating T cells (49), the phosphorylated TCR residues act as low pass or high pass filter for the influencing force frequencies (Fig. 3A–C).
In summary, the presented effective theoretical analysis suggests that self–nonself discrimination in early T cell activation depends sensitively on a number of mechanical parameters. The findings are consistent with measurements in which force on the TCR induces signaling events depending on its magnitude, duration, frequency, and timing, such that agonists form catch bonds that trigger the T cells, whereas antagonists form slip bonds that fail to activate (52). Comparison between outcomes of different experiments can only be meaningful if these parameters are accounted for.
Future Experiments of Early T Cell Activation.
A remedy for improving measurements and quantitative comparison of force in TCR–pMHC binding across both early and full T cell activation could be offered by combining molecular FRET-based sensors (43) and superresolution traction force microscopy (TFM) (60, 61). Astigmatic TFM provides the biologically demanded spatiotemporal sensitivity adequate for TCR–pMHC binding including acquisition speed and spatiotemporal mapping of the direction and magnitude of the generated force vector with pN-sensitivity. Complementary, the FRET sensors can probe force magnitudes of the TCR–pMHC molecules. This combined usage of TFM and FRET sensors would provide two independent measurements of the forces in a single experiment acting on single TCR–pMHCs, for example, through T cells presenting ruffles and microvilli during early T cell activation (5) or invadosomes across the whole contact interface of the IS during full T cell activation (62–64). The experiments could be further expanded to include measurements of the T cell and APC membrane mechanics, e.g., with tension probes (65).
Let us note that engineered changes of TCR rigidity can yield valuable insights into the role of mechanics for early T cell activation. Such efforts to engineer the TCR may consider that both stiffer TCR bulk domains and softer flexible domains contribute to TCR rigidity. To this end, the αβTCR and γδTCR rigidities would be expected to differ because their number of softer flexible do mains is different. As highlighted above, although single-molecule assays (40, 57) and molecular simulations suggest that TCR rigidity depends on TCR length extension and conformational changes upon binding (58, 59), electron microscopy structures suggest a lack of conformational changes in the extracellular regions of some αβTCRs upon pMHC-II binding (38, 39). Conformational changes involved in TCR–pMHC binding could be captured in our approach by considering that TCR rigidity dynamically evolves under an applied force. In this way, TCR rigidity changes contribute to the force balance of the TCR–pMHC binding interaction, which in turn rescales the characteristic force amplitude typically at 10 pN with changing smaller or larger interaction volumes as discussed above. Consequently, a very soft TCR could effectively mechanically isolate the TCR–pMHC form the T cell and thus provide a qualitative insight into how T cell activation depends on mechanics.
Importance of TCR Force Sensitivity in Early T Cell Activation.
The high sensitivity of TCR phosphorylation on the applied force might appear as a flaw in the evolutionary design of TCR–pMHC bonds. Nevertheless, in the context of self–nonself discrimination, this “bug” might really be an advantageous feature. The mechanical parameters characterizing a TCR–pMHC bond depend on the TCR-peptide antigen pair. As the theoretical analysis suggests, slight differences in these parameters, notably the value of characteristic force , can have a strong effect on TCR phosphorylation. Whether mechanical properties of TCR–pMHC bonds indeed play a role in the discrimination between self and nonself requires experimental investigations. We now discuss this possible role from a theoretical point of view.
Self–Nonself Discrimination in Early T Cell Activation.
Adopting the currently accepted view that phosphorylation of the TCR is directly linked to early T cell activation, force has multiple effects on this process. In the theoretical analysis, the parameters characterizing the TCR–pMHC and depending on the peptide antigen are and . In the context of self–nonself discrimination and for a catch bond like αβTCR–pMHC, the putative dependence of on the peptide seems particularly relevant. Indeed, for a fixed applied constant force, the value of decides about whether TCR phosphorylation will increase or decrease compared to the force-free case. Assuming that a self-peptide leads to a value of that is 2.5 pN larger than for a nonself-peptide, TCR phosphorylation can differ by an order of magnitude between the two peptides. In this way, an applied force can significantly contribute to self–nonself discrimination. Let us speculate on features of TCR base level phosphorylation. An intriguing consequence arises from the effective description suggesting that if a large number of TCRs were simultaneously bound to self, a single TCR bond to non-self might not be detectable. Consequently, TCR self-nonself discrimination would potentially transiently break down.
The presented analysis revealed that mechanical improvement of self–nonself discrimination is very sensitive to actual values (Fig. 1C), because small differences in , but also in strongly affect the absolute values of TCR phosphorylation. While this might be perceived as a problem for using force to enhance self–nonself discrimination, we would argue that evolution could optimize the force exerted by T cells on APCs such that self-peptides do not lead to T cell activation. It will be interesting to investigate whether a combination of kinetic proofreading and force can robustly sharpen the discrimination between self and nonself.
Self–Nonself Discrimination at the IS.
In contrast to αβTCR, for γδTCR, which exhibit slip bond behavior, the magnitude of the average applied force does not aid the discrimination between self and nonself antigens. Nevertheless, oscillatory force can minimally enhance the number of total TCR phosphorylation in the absence of rebinding and vastly in the presence of rebinding. This might be irrelevant during early T cell activation, but makes a significant contribution at the IS.
Let us highlight in this context again that a single TCR–pMHC bond has experimentally indeed been demonstrated to be detected by CD8+ and CD4+ T cells (19, 20). But at least 10 pMHCs have been shown to be required to induce IS formation in T cells (20, 66). Importantly, it is therefore still not fully established whether a single TCR–pMHC bond activates T cells as the self-peptide also directly interacts with the TCR for positive selection (67).
Indeed, self–nonself discrimination at the IS differs from early T cell activation (67, 68), because at the IS, the T cell interprets multiple TCRs organized in clusters and interacting with pMHCs instead of individual TCR–pMHCs. The role of TCR avidity, the effective , for TCRs within TCR clusters must therefore be carefully considered for the different force parameters in theoretical descriptions in future discussions. After all, TCR rebinding led to improvements in TCR phosphorylation only at large during early T cell activation (Fig. 1H). Experimentally, TCR avidity is known to be important at the IS (55, 69).
Biochemistry, Biomechanics, and Mechanobiology.
Although the majority of efforts to adequately explain T cell activation have previously prioritized biochemistry, many of its processes profoundly depend on mechanics. Force acts across a variety of length scales, from the human organism down to tissues, single cells, and molecules such as the TCR. This theoretical discussion highlights the force’s influence on a single TCR–pMHC during early T cell activation. Emerging evidence indicates indeed that the mechanics of the TCR, the pMHC, the T cell surface, and APC surface all together dynamically contribute to TCR mechanics. Now, this discussion may be suggestive that the question may no longer be whether TCRs depend on force. Rather, we can proceed to investigate T cell mechanobiology (70), that is, to determine how mechanical force affects TCR function and behavior, and decision-making of T cells.
Acknowledgments
M.F. acknowledges generous funding from the Rosalind Franklin Institute (EP/T033452/1) and the Kennedy Trust for Rheumatology Research, and the Engineering and Physical Sciences Research Council (EP/X033015/1). K.K. gratefully acknowledges financial support by Swiss NSF through Sinergia grant CRSII5_183550.
Author contributions
M.F. and K.K. designed research; performed research; analyzed data; and wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Contributor Information
Marco Fritzsche, Email: marco.fritzsche@kennedy.ox.ac.uk.
Karsten Kruse, Email: karsten.kruse@unige.ch.
Data, Materials, and Software Availability
There are no data underlying this work.
References
- 1.Basu R., et al. , Cytotoxic T cells use mechanical force to potentiate target cell killing. Cell 165, 100–110 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Huang J., et al. , The kinetics of two-dimensional TCR and pMHC interactions determine T-cell responsiveness. Nature 464, 932–936 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Harrison D. L., Fang Y., Huang J., T-cell mechanobiology: Force sensation, potentiation, and translation. Front. Phys. 7, 2019 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fritzsche M., et al. , Cytoskeletal actin dynamics shape a ramifying actin network underpinning immunological synapse formation. Sci. Adv. 3, e1603032 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cai E., et al. , Visualizing dynamic microvillar search and stabilization during ligand detection by T cells. Science 356, eaal3118 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Moeckl L., The emerging role of the mammalian glycocalyx in functional membrane organization and immune system regulation. Front. Cell Dev. Biol. 8, 253 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Razvag Y., et al. , T cell activation through isolated tight contacts. Cell Rep. 29, 3506–3521.e6 (2019). [DOI] [PubMed] [Google Scholar]
- 8.Sykulev Y., Joo M., Vturina I., Tsomides T. J., Eisen H. N., Evidence that a single peptide-MHC complex on a target cell can elicit a cytolytic T cell response. Immunity 4, 565–571 (1996). [DOI] [PubMed] [Google Scholar]
- 9.Huang J., et al. , A single peptide-major histocompatibility complex ligand triggers digital cytokine secretion in CD4+ T cells. Immunity 39, 846–857 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shah K., Al-Haidari A., Sun J., Kazi J., T cell receptor (TCR) signaling in health and disease. Signal Transduct. Target Ther. 6, 412 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu B., Chen W., Evavold B. D., Zhu C., Antigen-specific TCR-pMHC catch bonds trigger signaling by fast accumulation of force-prolonged bond lifetimes. Cell 157, 357–368 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Courtney A. H., Lo W. L., Weiss A., TCR signaling: Mechanisms of initiation and propagation. Trend. Biochem. Sci. 43, 108–123 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sasmal D. K., et al. , TCR-pMHC bond conformation controls TCR ligand discrimination. Cell. Mol. Immunol. 17, 203–217 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Huppa J. B., et al. , TCR-peptide-MHC interactions in situ show accelerated kinetics and increased affinity. Nature 463, 963–967 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Varma R., Campi G., Yokosuka T., Saito T., Dustin M. L., T cell receptor-proximal signals are sustained in peripheral microclusters and terminated in the central supramolecular activation cluster. Immunity 25, 117–127 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Huppa J. B., Gleimer M., Sumen C., Davis M. M., Continuous T cell receptor signaling required for synapse maintenance and full effector potential. Nat. Immunol. 4, 749–755 (2003). [DOI] [PubMed] [Google Scholar]
- 17.Lanzavecchia A., Lezzi G., Viola A., From TCR engagement to T cell activation a kinetic view of T cell behavior. Cell 96, 1–4 (1999). [DOI] [PubMed] [Google Scholar]
- 18.Henry N., Hivroz C., Early T-cell activation biophysics. HFSP J. 3, 401–411 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Irvine D. J., Purbhoo M. A., Krogsgaard M., David M. M., Direct observation of ligand recognition by T cells. Nature 419, 845–849 (2002). [DOI] [PubMed] [Google Scholar]
- 20.Purbhoo M. A., Irvine D. J., Huppa J. B., David M. M., T cell killing does not require the formation of a stable mature immunological synapse. Nat. Immunol. 5, 524–530 (2004). [DOI] [PubMed] [Google Scholar]
- 21.Manz B. N., Jackson B. L., Petit R. S., Dustin M. L., Grove J., T-cell triggering thresholds are modulated by the number of antigen within individual T-cell receptor clusters. Proc. Natl. Acad. Sci. U.S.A. 108, 9089–9094 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.McKeithan T. W., Kinetic proofreading in T-cell receptor signal transduction. Proc. Natl. Acad. Sci. U.S.A. 92, 5042–5046 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Britain D. M., Town J. P., Weiner O. D., Progressive enhancement of kinetic proofreading in T cell antigen discrimination from receptor activation to DAG generation. eLife 11, e75263 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Al-Aghbar M. A., Jainarayanan A. K., Dustin M. L., Roffler S. R., The interplay between membrane topology and mechanical forces in regulating T cell receptor activity. Commun. Biol. 5, 40 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Klotzsch E., Stiegler J., Ben-Ishay E., Gaus K., Do mechanical forces contribute to nanoscale membrane organisation in T cells? Biochim. Biophys. Acta Mol. Cell Res. 1853, 822–829 (2015). [DOI] [PubMed] [Google Scholar]
- 26.Colin-York H., et al. , Cytoskeletal control of antigen-dependent T cell activation. Cell Rep. 26, 3369–3379.e5 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rushdi M. N., et al. , Cooperative binding of T cell receptor and CD4 to peptide-MHC enhances antigen sensitivity. Nat. Commun. 13, 7055 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Spillane K. M., Tolar P., B cell antigen extraction is regulated by physical properties of antigen-presenting cells. J. Cell Biol. 216, 217–230 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Choi H. K., et al. , Catch bond models explain how force amplifies TCR signaling and antigen discrimination. Nat. Commun. 14, 2616 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pettmann J., et al. , The discriminatory power of the T cell receptor. eLife 10, e67092 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pettmann J., et al. , Mechanical forces impair antigen discrimination by reducing differences in T-cell receptor/peptide-MHC off-rates. EMBO J. 42, e111841 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Feng Y., et al. , Mechanosensing drives acuity of T-cell recognition. Proc. Natl. Acad. Sci. U.S.A. 114, E8204–E8213 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mallis R. J., Duke-Cohan J. S., Das D. K., Reinherz E. L., Molecular design of the T cell receptor ectodomain encodes biologically fit ligand recognition in the absence of mechanosensing. Proc. Natl. Acad. Sci. U.S.A. 118, e2023050118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lanz A. L., et al. , Allosteric activation of T cell antigen receptor signaling by quaternary structure relaxation. Cell Rep. 36, 109375 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wu P., et al. , Mechano-regulation of peptide-MHC class I conformations determines TCR antigen recognition. Mol. Cell 73, 1015–1027.e7 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Natarajan K., et al. , An allosteric site in the T-cell receptor C domain plays a critical signalling role. Nat. Commun. 8, 15260 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rangarajan S., et al. , Peptide-MHC (pMHC) binding to a human antiviral T cell receptor induces long-range allosteric communication between pMHC- and CD3-binding sites. J. Biol. Chem. 293, 15991–16005 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Susac L., et al. , Structure of a fully assembled tumor-specific T cell receptor ligated by pMHC. Cell 185, 3201–3213.e19 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Saotome K., et al. , Structural analysis of cancer-relevant TCR-CD3 and peptide-MHC complexes by cryoEM. Nat. Commun. 14, 2401 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Das D. K., et al. , Pre-T cell receptors (Pre-TCRs) leverage V complementarity determining regions (CDRs) and hydrophobic patch in mechanosensing thymic self-ligands. J. Biol. Chem. 291, 25292–25305 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Pageon S. V., Govendir M. A., Kempe D., Biro M., Mechanoimmunology: Molecular-scale forces govern immune cell functions. Mol. Biol. Cell 29, 1919–1926 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Liu B., Kolawole E. M., Evavold B. D., Mechanobiology of T cell activation: To catch a bond. Annu. Rev. 37, 65–87 (2022). [DOI] [PubMed] [Google Scholar]
- 43.Goehring J., et al. , Temporal analysis of T-cell receptor-imposed forces via quantitative single molecule FRET measurements. Nat. Commun. 12, 2502 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Malissen B., Bongrand P., Early T cell activation: Integrating biochemical, structural, and biophysical cues. Annu. Rev. Immunol. 33, 539–561 (2015). [DOI] [PubMed] [Google Scholar]
- 45.Liu B., Kolawole E. M., Evavold B. D., Mechanobiology of T cell activation: To catch a bond. Annu. Rev. Cell Dev. Biol. 37, 65–87 (2021). [DOI] [PubMed] [Google Scholar]
- 46.Bell G. I., Models for the specific adhesion of cells to cells. Science 200, 618–627 (1978). [DOI] [PubMed] [Google Scholar]
- 47.Evans E. A., Calderwood D. A., Forces and bond dynamics in cell adhesion. Science 316, 1148–1153 (2007). [DOI] [PubMed] [Google Scholar]
- 48.Xiong Y., Kern P., Chang H. C., Reinherz E. L., Lang M. J., T Cell Receptor Binding to a pMHCII Ligand Is Kinetically Distinct from and Independent of CD4. J. Biol. Chem. 276, 5659–5667 (2021). [DOI] [PubMed] [Google Scholar]
- 49.Lee A. M., Colin-York H., Fritzsche M., CalQuo 2: Automated Fourier-space, population-level quantification of global intracellular calcium responses. Sci. Rep. 7, 5416 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Goyette J., et al. , Dephosphorylation accelerates the dissociation of ZAP70 from the T cell receptor. Proc. Natl. Acad. Sci. U.S.A. 119, e2116815119 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hwang W., Mallis R. J., Lang M. J., Reinherz E. L., The TCR mechanosensor exploits dynamic ectodomain allostery to optimize its ligand recognition site. Proc. Natl. Acad. Sci. U.S.A. 117, 21336–21345 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Liu B., Chen W., Evavold B. D., Zhu C., Accumulation of dynamic catch bonds between TCR and agonist peptide-MHC triggers T cell signaling. Cell 157, 357–368 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Klotzsch E., Schuetz G. J., Improved ligand discrimination by force-induced unbinding of the T cell receptor from peptide-MHC. Biophys. J. 104, 1670–1675 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Wasnik V. H., Lipp P., Kruse K., Positional information readout in Ca2+ signaling Phys. Rev. Lett. 123, 058102 (2019). [DOI] [PubMed] [Google Scholar]
- 55.Purcarea A., et al. , Signatures of recent activation identify a circulating T cell compartment containing tumor-specific antigen receptors with high avidity. Sci. Immunol. 7, eabm2077 (2022). [DOI] [PubMed] [Google Scholar]
- 56.O. Staufer et al., Solution structure and synaptic analyses reveal molecular mechanisms of bispecific T cell engagers. bioRxiv [Preprint] (2023). 10.1101/2022.06.15.496334 (Accessed 1 December 2023). [DOI]
- 57.Das D. K., et al. , Force-dependent transition in the T-cell receptor -subunit allosterically regulates peptide discrimination and pMHC bond lifetime. Proc. Natl. Acad. Sci. U.S.A. 112, 1517–1522 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Prakaash D., Cook G. P., Acuto O., Kalli A. C., Multi-scale simulations of the T cell receptor reveal its lipid interactions, dynamics and the arrangement of its cytoplasmic region. PLoS Comput. Biol. 17, e1009232 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Eerden F. J., et al. , TCR-pMHC complex formation triggers CD3 dynamics. eLife 12, RP88065 (2023). [Google Scholar]
- 60.Barbieri L., et al. , Two-dimensional TIRF-SIM-traction force microscopy (2D TIRF-SIM-TFM). Nat. Commun. 12, 2169 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Li D., et al. , Astigmatic traction force microscopy (aTFM). Nat. Commun. 12, 2168 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Stinchcombe J. C., et al. , Ectocytosis renders T cell receptor signaling self-limiting at the immune synapse. Science 380, 818–823 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sage P. T., et al. , Antigen recognition is facilitated by invadosome-like protrusions formed by memory/effector T cells. J. Immunol. 188, 3686–3699 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Kumari S., et al. , Actin foci facilitate activation of the phospholipase C- in primary T lymphocytes via the WASP pathway. eLife 4, e04953 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Colom A., et al. , A fluorescent membrane tension probe. Nat. Chem. 10, 1118–1125 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Krogsgaard M., Li Q. J., Huppa J. B., Huse M., Davis M. M., Agonist/endogenous peptide-MHC heterodimers drive T cell activation and sensitivity. Nature 434, 238–243 (2005). [DOI] [PubMed] [Google Scholar]
- 67.Juang J., et al. , Peptide-MHC heterodimers show that thymic positive selection requires a more restricted set of self-peptides than negative selection. J. Exp. Med. 207, 1223–1234 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Dustin M. L., What counts in the immunological synapse? Mol. Cell 54, 255–262 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Fahmy T. M., Bieler J. G., Edidin M., Schneck J. P., Increased TCR avidity after T cell activation: A mechanism for sensing low-density antigen. Immunity 14, 135–143 (2001). [PubMed] [Google Scholar]
- 70.Gunasinghe S. D., Peres N. G., Goyette J., Gaus K., Biomechanics of T cell dysfunctions in chronic diseases. Front Immunol. 12, 600829 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
There are no data underlying this work.