Abstract
In 2018, the ATHLETIC campaign was conducted at the University of Colorado Dal Ward Athletic Center and characterized dynamic indoor air composition in a gym environment. Among other parameters, inorganic particle and gas-phase species were alternatingly measured in the gym’s supply duct and weight room. The Indoor Model of Aerosols, Gases, Emissions, and Surfaces (IMAGES) uses the inorganic aerosol thermodynamic equilibrium model, ISORROPIA, to estimate the partitioning of inorganic aerosols and corresponding gases. In this study herein, measurements from the ATHLETIC campaign were used to evaluate IMAGES’ performance. Ammonia emission rates, nitric acid deposition, and particle deposition velocities were related to observed occupancy, which informed these rates in IMAGES runs. Initially, modeled indoor inorganic aerosol concentrations were not in good agreement with measurements. A parametric investigation revealed that lowering the temperature or raising the relative humidity used in the ISORROPIA model drove the semivolatile species more toward the particle phase, substantially improving modeled-measured agreement. One speculated reason for these solutions is that aerosol water was enhanced by increasing the RH or decreasing the temperature. Another is that thermodynamic equilibrium was not established in this indoor setting or that the thermodynamic parametrizations in ISORROPIA are less accurate for typical indoor settings. This result suggests that applying ISORROPIA indoors requires further careful experimental validation.
Keywords: Inorganic aerosols, Indoor modeling, ATHLETIC, IMAGES, ISORROPIA
Short abstract
This work applies an indoor aerosol model, IMAGES, that estimates the partitioning of inorganic aerosol components and their corresponding gas-phase species with ISORROPIA by leveraging measurements from a university athletic center and derived relationships between occupancy and nitric acid deposition, particle deposition, and ammonia emissions. This study highlights that applying ISORROPIA indoors can sometimes result in inaccurate gas-particle partitioning. However, forcing the model to predict increased particle water by either adjusting relative humidity up or temperature down will result in accurate gas-particle partitioning.
1. Introduction
Residents of industrialized
countries spend most of their time
indoors where they are exposed to air pollution from indoor sources
or of outdoor origin.1 One major class
of these pollutants includes particulate matter (PM), which is causally
associated with morbidity and mortality2−5 and is composed of organic aerosols (OA)
and inorganic aerosols (IA).6−8 Major components of IA are sulfate
( ), ammonium (
), ammonium ( ), and nitrate (
), and nitrate ( ), which interact with inorganic gases such
as ammonia (NH3) and nitric acid (HNO3). Due
to differences in source and loss processes between indoor and outdoor
environments, some pollutants may exist at much higher or lower concentrations
indoors than in the ambient air.2
), which interact with inorganic gases such
as ammonia (NH3) and nitric acid (HNO3). Due
to differences in source and loss processes between indoor and outdoor
environments, some pollutants may exist at much higher or lower concentrations
indoors than in the ambient air.2
NH3 is one example of a pollutant that often exists at higher concentrations indoors than outdoors due to substantial indoor sources.9−12 Indoor NH3 is often sourced from certain cooking and cleaning activities, emissions from building materials, and emissions from occupants.9,13−18 Indoor NH3 emissions are essential to understand since NH3 contributes to the formation of IA and because NH3 influences gas-to-particle partitioning by neutralizing acidic species.19−21 Recent decreases in the use of NH3-based cleaning products and increased use of low-emitting building materials may cause building occupants to be the dominant source of indoor NH3.19 Thus, the effects of human-emitted NH3 on indoor air quality have become a topic of interest.22
Beko et al.23 outlined the Indoor Chemical Human Emissions and Reactivity (ICHEAR) project, which examined the role of human emissions on indoor chemistry. As part of this project, Li et al.19 characterized how human NH3 emission rates varied in a test chamber as a function of temperature (T), relative humidity (RH), human subject age and clothing characteristics, and ozone (O3) concentration. They found that NH3 emissions were affected mainly by T, age of the human subject, and clothing, but these emissions rates were negligibly influenced by RH and O3. As part of the ATHLETic center study of Indoor Chemistry (ATHLETIC) field campaign, Finewax et al.24 investigated the impacts of human exercise on NH3 emissions as well as other activities on different species. They concluded that an occupant’s NH3 emissions increased with their metabolic rate.
Previously, Berman et al.25 incorporated the IA thermodynamic equilibrium model, ISORROPIA,26,27 into the existing Indoor Model of Aerosols, Gases, Emissions, and Surfaces (IMAGES)28,29 framework to better consider indoor IA partitioning and concentrations. ISORROPIA simulates the gas-particle partitioning of inorganic species with known values of temperature, RH, and total concentrations (gas + particle) of inorganic species and is described in Section 2.2. IMAGES is a platform that initially only simulated organic aerosol (OA) concentration, composition, partitioning behavior, and secondary formation using the 2D-volatility basis set framework, which replicates thermodynamic principles provided by OA absorptive partitioning theory.30−32 Berman et al.25 extended IMAGES to incorporate the inorganic aerosol thermodynamic equilibrium model, ISORROPIA. Berman et al.25 tested the model against measured data in a classroom33 and used T and the difference between indoor and outdoor CO2 (ΔCO2, ppm to estimate NH3 concentrations from occupants. However, rigorous evaluation of the approach was difficult since the validation measurements did not include concentrations of NH3 or HNO3, which also precluded evaluating whether ISORROPIA predicted the IA partitioning well.33
The work herein builds upon Berman et al.25 by first evaluating ISORROPIA partitioning with measured indoor concentrations. Results will show that ISORROPIA required either a decrease in the input T or an increase in the input RH for simulated partitioning to agree with measurements, since either change pushed aerosol species concentrations toward the particle phase. Next, particle, gas, and occupancy data from the ATHLETIC campaign were used to derive relationships of net NH3 emissions, the deposition velocity of particles, and the deposition velocity of HNO3 to observed dynamic occupancy. Using these relationships and the ATHLETIC campaign’s robust measurements of inorganic species, occupancy, and environmental conditions, the application of IMAGES with the adjusted thermodynamic inputs was evaluated.
2. Methods
2.1. ATHLETIC Campaign Measurements
Measurements
from the ATHLETIC campaign defined the scope of this work. Using various
instruments described by Claflin et al.34 and in Table 1 of Finewax et al.,24 time-resolved
measurements of T, RH,  ,
,  ,
, 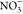 , NH3, HNO3, and CO2 were taken in the Dal Ward Athletic Center’s weight
room and supply duct University of Colorado, Boulder. Specifically,
an Aerodyne HR-TOF-AMS measured nonrefractory particle composition
(i.e.,
, NH3, HNO3, and CO2 were taken in the Dal Ward Athletic Center’s weight
room and supply duct University of Colorado, Boulder. Specifically,
an Aerodyne HR-TOF-AMS measured nonrefractory particle composition
(i.e., 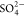 ,
,  ,
, 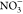 less than 1 μm in aerodynamic diameter),35 an Aerodyne/TOFWERK I-CIMS measured HNO3, a Picarro SI2108 measured NH3, and a Picarro
G2401 measured CO2, supply temperature and RH.24,34,36−39 These instruments were placed
on the balcony and a nearby supply air register and alternated between
the two sampling locations every 5–10 min. Detailed information
about the measurement campaign and the instrumentation used are described
in detail in Finewax et al.24 and Claflin
et al.34 However, the limits of detection
can be found in Table S1. The aerosol richinorganic
species might contain some organic contribution,40,41 although that effect is likely small for this data set based on
the analysis in this work (Section 3.3).42 The University of Colorado
(CU) Facilities management provided room temperature, and room RH
was derived by Claflin et al.34 by using
building temperature, local pressure, and H2O mixing ratio
measured by the Picarro instruments. The weight room’s temperature
was controlled at ∼293 K; this value was assumed when any weight
room temperature data was missing.
less than 1 μm in aerodynamic diameter),35 an Aerodyne/TOFWERK I-CIMS measured HNO3, a Picarro SI2108 measured NH3, and a Picarro
G2401 measured CO2, supply temperature and RH.24,34,36−39 These instruments were placed
on the balcony and a nearby supply air register and alternated between
the two sampling locations every 5–10 min. Detailed information
about the measurement campaign and the instrumentation used are described
in detail in Finewax et al.24 and Claflin
et al.34 However, the limits of detection
can be found in Table S1. The aerosol richinorganic
species might contain some organic contribution,40,41 although that effect is likely small for this data set based on
the analysis in this work (Section 3.3).42 The University of Colorado
(CU) Facilities management provided room temperature, and room RH
was derived by Claflin et al.34 by using
building temperature, local pressure, and H2O mixing ratio
measured by the Picarro instruments. The weight room’s temperature
was controlled at ∼293 K; this value was assumed when any weight
room temperature data was missing.
The weight room’s
volume was estimated to be 1700 m3 with a constant supply
airflow of 200 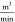 delivered by the building’s heating,
ventilation, and air conditioning (HVAC) system, resulting in a room
air exchange rate of ∼7 h –1. Occupants throughout
time were counted from video recordings of the gym’s main room
and balcony.24 This modeling study considered
the portion of the campaign from November 7–19, 2018, corresponding
to the timesteps where complete concentration data in the supply duct
and weight room (i.e., concentration measurements of
delivered by the building’s heating,
ventilation, and air conditioning (HVAC) system, resulting in a room
air exchange rate of ∼7 h –1. Occupants throughout
time were counted from video recordings of the gym’s main room
and balcony.24 This modeling study considered
the portion of the campaign from November 7–19, 2018, corresponding
to the timesteps where complete concentration data in the supply duct
and weight room (i.e., concentration measurements of 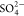 ,
,  ,
, 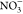 , NH3, and HNO3 in
the supply duct and weight room), and humidity data in the weight
room were all available. However, HNO3 measurements were
missing in the supply duct for 12 h on November 10, and supply duct
NH3 concentrations were missing between November 12 and
November 15. Since these values are needed for the IMAGES modeling,
the portion of the data set where these significant data gaps existed
were not included in the IMAGES simulations. The preprocessing necessary
to provide a uniform time step for use in IMAGES as well as the time
periods of the ATHLETIC campaign modeled with IMAGES are provided
in Section S1 of Supporting Information (SI). Additionally, how often inorganic concentration measurements go
below the limits of detection are provided in Table S2.
, NH3, and HNO3 in
the supply duct and weight room), and humidity data in the weight
room were all available. However, HNO3 measurements were
missing in the supply duct for 12 h on November 10, and supply duct
NH3 concentrations were missing between November 12 and
November 15. Since these values are needed for the IMAGES modeling,
the portion of the data set where these significant data gaps existed
were not included in the IMAGES simulations. The preprocessing necessary
to provide a uniform time step for use in IMAGES as well as the time
periods of the ATHLETIC campaign modeled with IMAGES are provided
in Section S1 of Supporting Information (SI). Additionally, how often inorganic concentration measurements go
below the limits of detection are provided in Table S2.
ATHLETIC campaign measurements were used to evaluate ISORROPIA’s performance in indoor environments (Section 2.2), explore drivers of modeled-measured agreement for ISORROPIA in our data set (Section 2.3), and selectively constrain IMAGES (Section 2.4), which also necessitated deriving deposition and emission rates as a function of occupancy (Section 2.5). Given the species measured, particulate matter is assumed to be entirely composed of ammonium-sulfate, ammonium-nitrate, and water.
2.2. ISORROPIA Evaluation Using Weight Room Measurements
ISORROPIA is an inorganic aerosol thermodynamic equilibrium model
that estimates the gas-to-particle partitioning of IA species when
given T, RH, and total (gas + particle) concentrations
and is described in detail elsewhere.26,27 However, to
briefly summarize, ISORROPIA formulates the aerosol-gas partitioning
problem formulated as either forward or reverse. In forward problems,
known values of temperature, RH, and total (gas + aerosol) concentrations
of sodium, sulfate, ammonium, nitrate, chloride, magnesium, potassium,
and calcium are used to calculate the gas phase concentrations of
ammonia (NH3), hydrochloric acid (HCl), and nitric acid
(HNO3), as well as the aerosol concentrations of hydrogen
(H+), sodium (Na+), 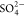 , bisulfate (
, bisulfate (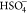 ),
),  ,
, 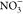 , CL–, calcium (Ca2+), potassium (K+), magnesium (Mg2+),
and water (H2O).26 When solving
the reverse problem, ISORROPIA uses the aerosol phase concentrations
of the inputs to calculate the corresponding gas phase concentrations
of species in equilibrium.26,27 This work uses the
forward mode since measurements of
, CL–, calcium (Ca2+), potassium (K+), magnesium (Mg2+),
and water (H2O).26 When solving
the reverse problem, ISORROPIA uses the aerosol phase concentrations
of the inputs to calculate the corresponding gas phase concentrations
of species in equilibrium.26,27 This work uses the
forward mode since measurements of 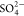 ,
,  ,
, 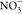 , NH3, and HNO3 are
given (Section 2.1), thus fully constraining the sulfate-nitrate-ammonium system. Additionally,
the aerosol can be in a thermodynamically metastable or stable state.
In the metastable case, salts do not precipitate under supersaturated
conditions. Therefore, aerosols will always be aqueous.26,27 In the latter, salts precipitate if saturation is exceeded; thus,
aerosols can exist as solid or aqueous species.26,27
, NH3, and HNO3 are
given (Section 2.1), thus fully constraining the sulfate-nitrate-ammonium system. Additionally,
the aerosol can be in a thermodynamically metastable or stable state.
In the metastable case, salts do not precipitate under supersaturated
conditions. Therefore, aerosols will always be aqueous.26,27 In the latter, salts precipitate if saturation is exceeded; thus,
aerosols can exist as solid or aqueous species.26,27
Since ISORROPIA is used in atmospheric models such as GEOS-Chem and the Community Multiscale Air Quality model (CMAQ), it has been evaluated extensively with outdoor measurements.26,27,43−49 However, Berman et al.25 represents the only known indoor application of ISORROPIA to explicitly simulate indoor thermodynamics; yet, that work excluded a comprehensive evaluation of the applicability of ISORROPIA indoors because NH3 and HNO3 measurements were not available for that study. Since these gases were measured by the ATHLETIC campaign, the applicability of ISORROPIA to this indoor environment was comprehensively evaluated here.
To do so, ISORROPIA was used to partition the total (i.e., gas + particle concentrations, where gas and particle concentrations were measured separately) concentration of each inorganic species in the room air between the aerosol and gas phase whenever complete data was available (∼96% of the time during November 7–19, 2018). The resulting modeled aerosol and gas phase concentrations were then compared to room air measurements. ISORROPIA’s metastable mode, which prevents saltation (solid formation) in the aerosol phase, was used during this evaluation. Since saltation is kinetically limited, using ISORROPIA’s metastable mode is a reasonable assumption for this fast-changing environment. Still, an evaluation using ISORROPIA’s stable mode, which allows particles to be aqueous or solids and did not produce markedly better agreement, is shown in Section S2 of the SI.
2.3. Optimizing Indoor Environmental Conditions To Be Used in IMAGES
Because we observed during this phase
that the ISORROPIA-partitioned  and
and 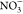 concentrations were often underpredicted
using the provided room T and RH (RHroom,meas) directly (Section 3.1), a parametric study of the influences of T and RH on chemical partitioning was done with ISORROPIA. Both lower T and higher RH increase the tendency for species to condense.
Thus, modifying T or RH will shift the partitioning
in ISORROPIA. ISORROPIA was executed with each unique combination
of T and RH over the entire timeseries of measured
room concentrations. Results from this parametric test are discussed
in Section S2 and were used to inform the
environmental conditions necessary to produce satisfactory agreement
between the model and measurements.
concentrations were often underpredicted
using the provided room T and RH (RHroom,meas) directly (Section 3.1), a parametric study of the influences of T and RH on chemical partitioning was done with ISORROPIA. Both lower T and higher RH increase the tendency for species to condense.
Thus, modifying T or RH will shift the partitioning
in ISORROPIA. ISORROPIA was executed with each unique combination
of T and RH over the entire timeseries of measured
room concentrations. Results from this parametric test are discussed
in Section S2 and were used to inform the
environmental conditions necessary to produce satisfactory agreement
between the model and measurements.
ISORROPIA compared better with the measured indoor concentrations at specific T and RH combinations within the parametric test described in the previous paragraph. Since ISORROPIA simulates the IA partitioning in IMAGES, the T and RH values fed to ISORROPIA were chosen to minimize the partitioning error as defined by the difference of the modeled partitioning fractions from the measured (though the reasons for this error were indiscoverable in this study design) rather than reflecting actual conditions. The indoor T was reasonably constant (∼293 K) during the ATHLETIC campaign (Section 2.1), so the indoor RH was optimized for a constant T of 293 K to best match the chemical partitioning.
The RH value that resulted
in the best partitioning agreement between
the volatile species (RHroom,opt) was determined
by first calculating the weighted averages (εroom) of measured and ISORROPIA-modeled indoor
particle fraction of 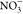 (
(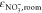 ) and
) and  (
(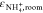 ) (i.e,
) (i.e, 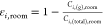 ). The εroom was calculated to combine all the partitioning information
in a single metric for each measurement time:
). The εroom was calculated to combine all the partitioning information
in a single metric for each measurement time:
| 1 |
where 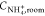 and
and 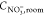 (
(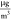 ) are the concentrations of
) are the concentrations of  and
and 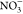 in the weight room. Next, using an orthogonal
regression, statistics for the line of best fit (i.e., the correlation
coefficient, R2, the slope, m, and the y-intercept, b) between
measured and ISORROPIA-modeled εroom were calculated and used to compute
the distance (d) between a perfect one-to-one correlation
(where R2 = 1, m = 1,
and b = 0), and the actual correlation:
in the weight room. Next, using an orthogonal
regression, statistics for the line of best fit (i.e., the correlation
coefficient, R2, the slope, m, and the y-intercept, b) between
measured and ISORROPIA-modeled εroom were calculated and used to compute
the distance (d) between a perfect one-to-one correlation
(where R2 = 1, m = 1,
and b = 0), and the actual correlation:
| 2 |
Finally, the case where d was at a minimum was chosen as the optimal condition, which at 293 K was an RH of 98%. Although an RH of 98% is not a realistic indoor value, this value was determined algorithmically to provide the best partitioning agreement. Therefore, setting the RH to 98% in this work makes up for a missing kinetic term, whose source is unclear. Therefore, results using this value are shown in Section 3.1. More details concerning the results of this optimization technique can be found in Section S3.
2.4. IMAGES Model Overview
The comprehensive
indoor thermodynamic particle model, IMAGES, was employed to simulate
IA concentrations in the weight room. Specifically, IMAGES uses a
well-mixed box model to inform a mass balance that describes total
(including gas and particle phases) indoor concentrations of any contaminant
species i (Ci,room,  ) when given its source rate (Si,
) when given its source rate (Si, 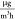 ) and first-order loss rate coefficient
(li, h–1):
) and first-order loss rate coefficient
(li, h–1):
| 3 |
IMAGES uses ISORROPIA to estimate gas- and
particle-phase fractions for each IA species.25 Specifically, the concentrations of 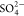 ,
,  ,
, 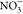 , NH3, and HNO3 were
modeled to simulate the measurements from the ATHLETIC campaign. A
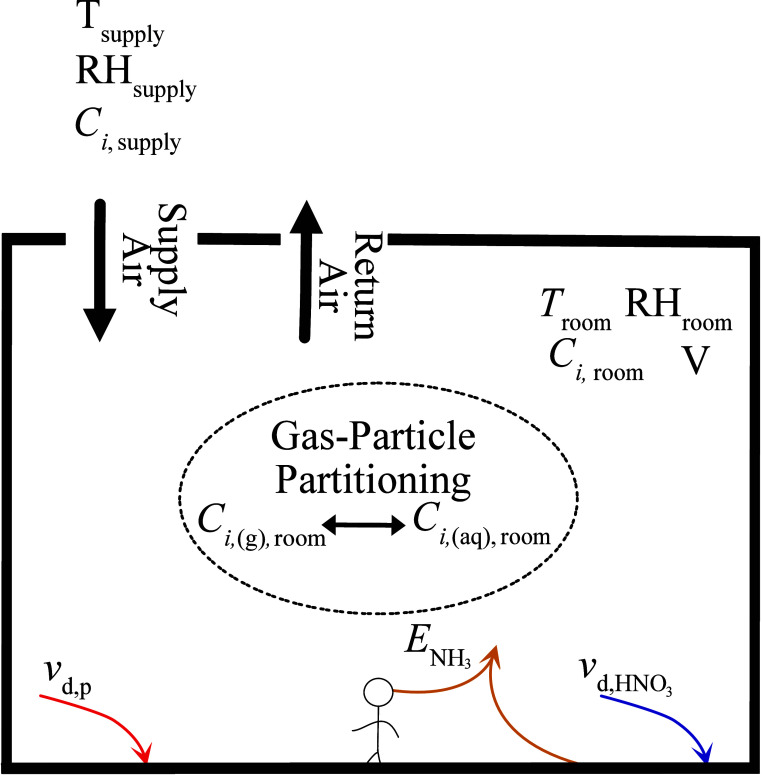
schematic that illustrates how IMAGES and ISORROPIA interact is displayed
in Figure 1.
, NH3, and HNO3 were
modeled to simulate the measurements from the ATHLETIC campaign. A
schematic that illustrates how IMAGES and ISORROPIA interact is displayed
in Figure 1.
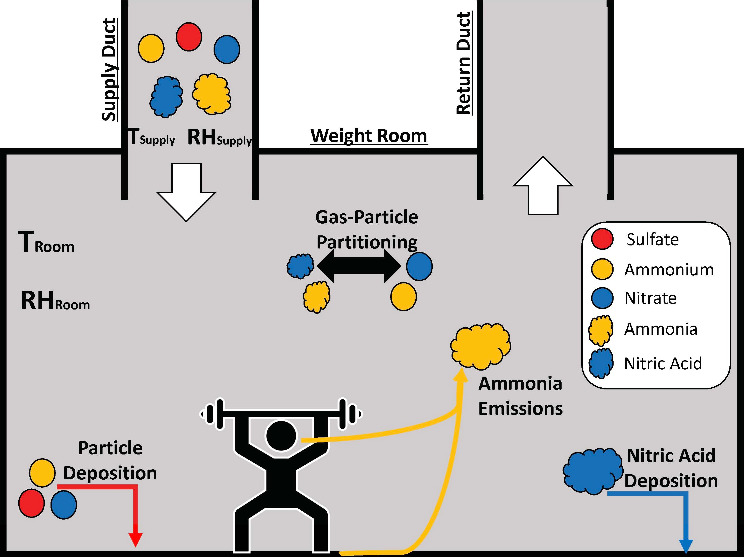
Figure 1.
Schematic of IMAGES as applied to modeling the ATHLETIC Campaign. Temperature, RH, and inorganic particle and gas concentrations were measured in the supply duct and room. Modeled processes in the space include particle deposition, HNO3 deposition, and NH3 emissions. ISORROPIA determined gas-particle partitioning.
Measurements were taken in the supply duct and
weight room of a
gym (Section 2.1),
and so the modeled source and loss rates reflect those observations.
The weight room was designed to have a constant volume flow delivered
by the building’s HVAC system. When air is supplied to a room,
gases and particles from the supply duct are introduced as a source.
Additional indoor sources of NH3 exist, including emissions
from building materials or occupants (which are elevated during exercise).24,34 Therefore, the source rate, Si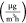 , for each total quantity (gas + particle)
of species, i, is
, for each total quantity (gas + particle)
of species, i, is
| 4 |
where 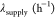 is the supply air exchange rate;
is the supply air exchange rate; 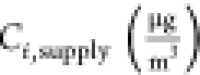 is the supply duct concentration; V (m3) is the room volume; and
is the supply duct concentration; V (m3) is the room volume; and 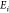 (
(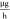 is the net indoor emission rate.
is the net indoor emission rate.
Air is assumed to leave the weight room through an HVAC return at the same rate as it is supplied. Particles and gases either are removed with the return air or deposit onto surfaces.50−53
Therefore, the loss rate, li (h–1) of each total quantity (gas + particle) of species, i, is defined as
| 5 |
where lg,i represents gas-phase losses; lp,i represents particle-phase losses; βp (h–1) and βg,i (h–1) are the net particle and gas deposition rates; and εi,room is the particle fraction of species i in the weight room, as determined by ISORROPIA.54,55
2.5. Relating Emissions and Deposition Rates to Occupancy
Emission and deposition parameters directly impact
indoor gas and particle concentrations and may vary with occupancy.
Thus, estimates of ENH3, the net deposition
velocity of particles (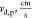 ), and the net deposition velocity of HNO3 (
), and the net deposition velocity of HNO3 (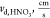 ) were derived as functions of the number
of occupants or the change in indoor CO2 concentrations
from estimated outdoor concentrations, ΔCO2 (Section S3). Specifically, the emission and deposition
rates were computed at every time step by constraining eqs 3–5 with measured values of the supply duct and room concentrations.
A surface-area-to-volume ratio
) were derived as functions of the number
of occupants or the change in indoor CO2 concentrations
from estimated outdoor concentrations, ΔCO2 (Section S3). Specifically, the emission and deposition
rates were computed at every time step by constraining eqs 3–5 with measured values of the supply duct and room concentrations.
A surface-area-to-volume ratio 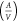 of 2.5 m–1 was assumed
to obtain
of 2.5 m–1 was assumed
to obtain 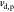 and
and 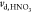 (
(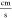 from βp and βHNO3 (h–1), respectively, which was informed
by Manuja et al.24 In this procedure, βp was computed first by considering only measured
from βp and βHNO3 (h–1), respectively, which was informed
by Manuja et al.24 In this procedure, βp was computed first by considering only measured 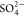 because it is nonvolatile and, thus, has
no gas-phase sources or losses,2,33 leaving βp as the only unknown variable in the mass balance. Assuming
internally mixed particles (i.e., βp applies uniformly
to all species),56 this time-resolved βp could then be used as input to determine
because it is nonvolatile and, thus, has
no gas-phase sources or losses,2,33 leaving βp as the only unknown variable in the mass balance. Assuming
internally mixed particles (i.e., βp applies uniformly
to all species),56 this time-resolved βp could then be used as input to determine  at each measurement time since
at each measurement time since  is the only unknown variable in the mass
balance on
is the only unknown variable in the mass
balance on 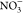 and HNO3. Similarly, using the
mass balance on
and HNO3. Similarly, using the
mass balance on  and NH3, the net emission rate,
and NH3, the net emission rate, 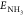 , can be determined.
, can be determined.
It was hypothesized
that the inferred 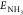 ,
, 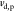 , and
, and 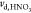 would increase as a function of occupancy.9,54 Linear regressions were used to develop functional forms of each
parameter based on occupancy values. Only data points where all concentrations
fell above the detection limit were considered when creating these
relationships. If a concentration value fell below the detection limit,
that data points and the one at the previous time step, which informs
the deposition and emission values (Section S4), were removed from the linear regression. As such, 2.2% of the
data was removed from the linear regressions with this method. The
limit of detection values for each species can be found in Table S1 of the SI. Relationships for when no values were removed from the linear regression
are also included in Section S4. These
linear relationships were used to provide
would increase as a function of occupancy.9,54 Linear regressions were used to develop functional forms of each
parameter based on occupancy values. Only data points where all concentrations
fell above the detection limit were considered when creating these
relationships. If a concentration value fell below the detection limit,
that data points and the one at the previous time step, which informs
the deposition and emission values (Section S4), were removed from the linear regression. As such, 2.2% of the
data was removed from the linear regressions with this method. The
limit of detection values for each species can be found in Table S1 of the SI. Relationships for when no values were removed from the linear regression
are also included in Section S4. These
linear relationships were used to provide 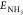 and
and 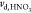 as a function of occupancy or ΔCO2 when running IMAGES. However, since the correlation between vd,p and both occupancy and ΔCO2 was so low, a constant value taken from the average vd,p (0.0054
as a function of occupancy or ΔCO2 when running IMAGES. However, since the correlation between vd,p and both occupancy and ΔCO2 was so low, a constant value taken from the average vd,p (0.0054 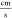 ) was used instead.
) was used instead.
3. Results and Discussion
3.1. Indoor ISORROPIA Evaluation
ISORROPIA was first run in a standalone evaluation using the measured inorganic species and environmental conditions to directly evaluate ISORROPIA’s ability to recreate the observed indoor IA partitioning. Since measured room concentrations were used directly, neither IMAGES nor its mass balance parameters were utilized for this evaluation.
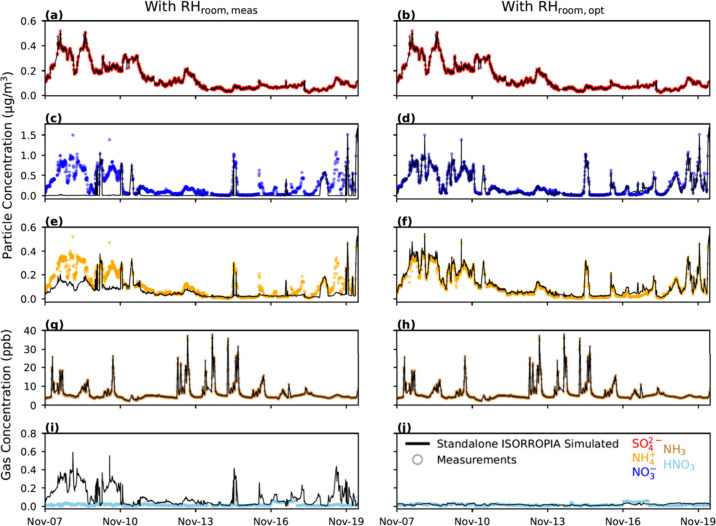
Figures 2 and 3 include the evaluation of ISORROPIA against measured concentrations
with either measured or optimized T and RH values.
For these runs, the 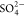 consistently agreed strongly between measured
and ISORROPIA-partitioned fractions (Figures 2a and 3a) since
consistently agreed strongly between measured
and ISORROPIA-partitioned fractions (Figures 2a and 3a) since 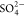 is nonvolatile and, thus, always in the
particle phase.2 However, ISORROPIA did
not estimate
is nonvolatile and, thus, always in the
particle phase.2 However, ISORROPIA did
not estimate 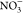 , HNO3, and
, HNO3, and  concentrations in good accordance with
observations when the real-time RHroom,meas was used as
input. When RHroom,meas was used as input to ISORROPIA,
it frequently predicted that nitrate would be gaseous when particle-bound
nitrate was observed in reality (Figure S3). For instance, Figure 2c,I shows that the ISORROPIA-partitioned HNO3 values
closely align with the measured
concentrations in good accordance with
observations when the real-time RHroom,meas was used as
input. When RHroom,meas was used as input to ISORROPIA,
it frequently predicted that nitrate would be gaseous when particle-bound
nitrate was observed in reality (Figure S3). For instance, Figure 2c,I shows that the ISORROPIA-partitioned HNO3 values
closely align with the measured 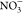 at various times between Nov 7 and Nov
10. This inaccurate partitioning leads to a considerable overprediction
of HNO3 and underprediction of
at various times between Nov 7 and Nov
10. This inaccurate partitioning leads to a considerable overprediction
of HNO3 and underprediction of 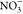 (Figure 3c,e). Still, HNO3 may not be a meaningful
metric to compare given its low concentration magnitude.
(Figure 3c,e). Still, HNO3 may not be a meaningful
metric to compare given its low concentration magnitude.
Figure 2.
Time series of standalone ISORROPIA simulated (black line) particle and gas concentrations using RHroom,meas (left column) and RHroom,opt (right column). Measured concentrations (circle markers) are shown for comparison.
Figure 3.
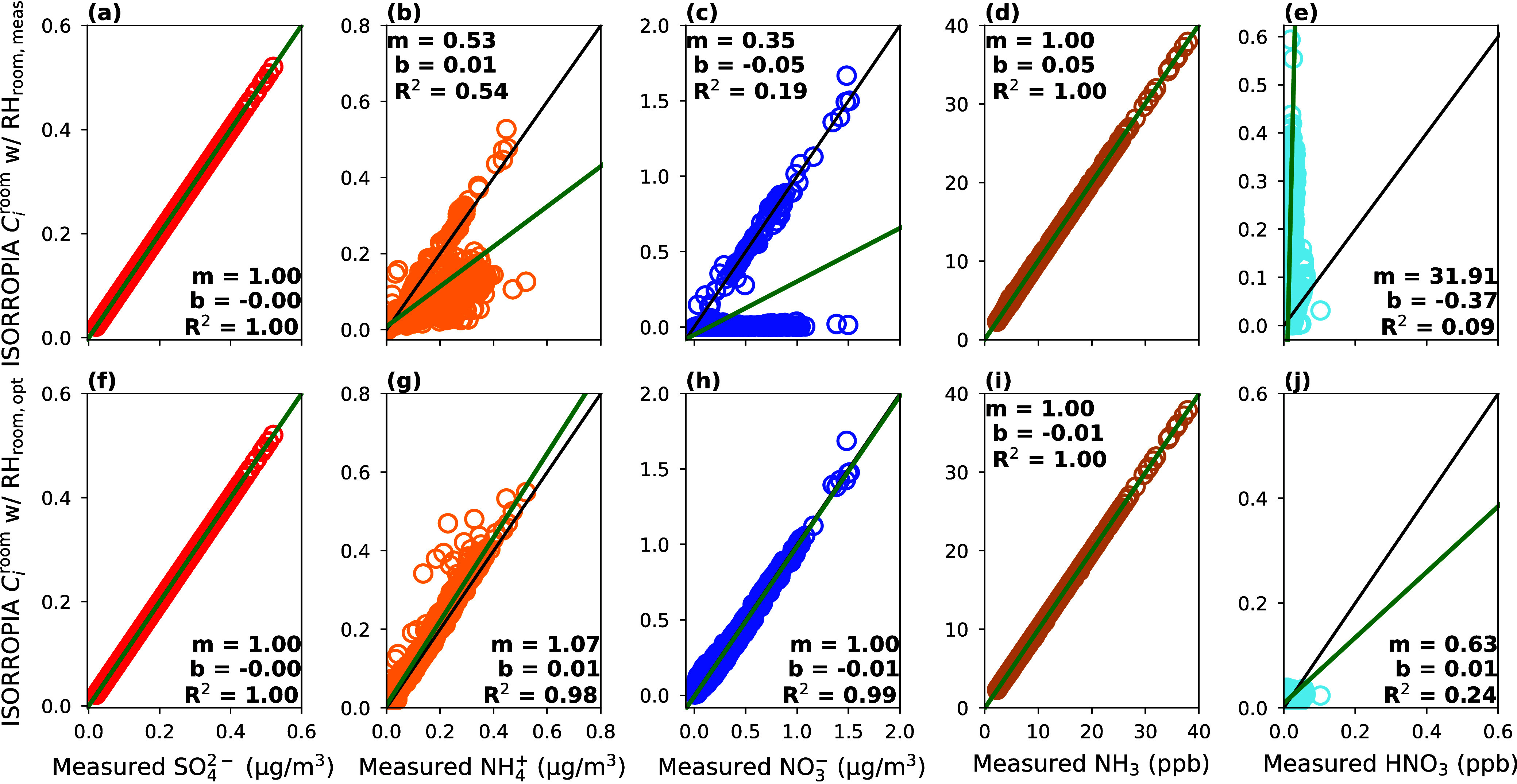
Comparison of standalone ISORROPIA simulated concentrations against measured concentrations using RHroom,meas (a–e) and RHroom,opt (f–j) as inputs to ISORROPIA. The green line represents the line of best fit calculated with an orthogonal regression, while the black line is the 1:1 line. The correlation coefficient, R2; slope, m; and y-intercept, b, are displayed for each regression.
Similarly, when RHroom,meas was used
as input to ISORROPIA,  was underpredicted often (Figure 2e). Specifically,
was underpredicted often (Figure 2e). Specifically,  was always underpredicted when
was always underpredicted when  was simulated to be completely evaporated.
Since
was simulated to be completely evaporated.
Since  was measured at low concentrations, an
underprediction of it by ISORROPIA resulted in a large relative error
(Figures 2e and 3b). Nevertheless, measured and ISORROPIA-partitioned
NH3 were in good agreement (Figure 3d), which is possible given the excess NH3 attributable to indoor sources.
was measured at low concentrations, an
underprediction of it by ISORROPIA resulted in a large relative error
(Figures 2e and 3b). Nevertheless, measured and ISORROPIA-partitioned
NH3 were in good agreement (Figure 3d), which is possible given the excess NH3 attributable to indoor sources.
The ISORROPIA evaluation
improves significantly when using RHroom,opt of 98% (Figures 2 (right column)
and 3f–j).
According to the best-fit statistics, HNO3 is somewhat
under-predicted by ISORROPIA, which is likely driven by the majority
of  being in the particle phase and may be
complicated by the difficulty of measuring HNO3 (Figure 3j). Still, m, b, and R2 are close to 1.0, 0.0, and 1.0 for the remaining species (Figure 3f–i). Setting
the indoor RH to 98% (RHroom,opt) in the ISORROPIA model
drives semivolatile species to the particle phase, improving modeled-measured
agreement. Similar behavior could occur at other RH input values when
combined with lower temperature inputs, as shown in the optimized
environmental condition results (Section S2). This outcome may suggest that the assumption of thermodynamic
equilibrium, made by ISORROPIA, may not apply to this indoor setting.
For instance, the high air exchange rate may have reduced the residence
time of aerosols in the weight room, preventing them from ever reaching
thermodynamic equilibrium. Furthermore, ISORROPIA is run under rather
exotic conditions in this modeling scenario, where typical uses of
ISORROPIA apply it to outdoor conditions. Alternatively, this outcome
may indicate that there is a condensation driver that is not included
in our model but has not been uncovered in this work.
being in the particle phase and may be
complicated by the difficulty of measuring HNO3 (Figure 3j). Still, m, b, and R2 are close to 1.0, 0.0, and 1.0 for the remaining species (Figure 3f–i). Setting
the indoor RH to 98% (RHroom,opt) in the ISORROPIA model
drives semivolatile species to the particle phase, improving modeled-measured
agreement. Similar behavior could occur at other RH input values when
combined with lower temperature inputs, as shown in the optimized
environmental condition results (Section S2). This outcome may suggest that the assumption of thermodynamic
equilibrium, made by ISORROPIA, may not apply to this indoor setting.
For instance, the high air exchange rate may have reduced the residence
time of aerosols in the weight room, preventing them from ever reaching
thermodynamic equilibrium. Furthermore, ISORROPIA is run under rather
exotic conditions in this modeling scenario, where typical uses of
ISORROPIA apply it to outdoor conditions. Alternatively, this outcome
may indicate that there is a condensation driver that is not included
in our model but has not been uncovered in this work.
Among many more potential explanations, some hypotheses are initially proposed for this observed need for a larger aerosol liquid water content for better modeled-measured agreement. These hypotheses include hysteresis, HVAC impacts, or a combination of the two; both pathways are difficult to test from the data and experimental design of the ATHLETIC campaign. For instance, setting the RH to a high value may reflect the possible history of the particles that deliquesced outdoors or in the HVAC system before coming into the weight room. Despite no active cooling (Figure S3) and the outdoor RH (RHout) not consistently being high (Figure S2), other T and RH extremes were thought to exist in parts of the HVAC zone that were not explicitly measured but could be significant. However, according to CU’s building management, only minimal heating occurred in the facility during the ATHLETIC campaign. Therefore, this hypothesis was deemed unlikely.
Furthermore, complexities in measurements were also considered as contributing to inaccuracies in standalone ISORROPIA simulated concentrations. Specifically, gases prone to partitioning to surfaces, like HNO3, may be reduced during the sampling process, so the measured HNO3 may under-represent what exists in the room air. However, increasing the HNO3 concentration to account for inlet losses of HNO3 led to a rejection of this possibility since the agreement of ISORROPIA-partitioned concentrations with measurements did not improve (Figures S6 and S7). Therefore, measurement uncertainties are not obviously causing inaccuracies in standalone ISORROPIA simulated concentrations.
Additionally, organic aerosol (OA) has relatively no impact on the total ALW needed to explain these observations, as shown in Figure S8 of the SI. To summarize, the OA ALW was found for the ATHLETIC observations using κOA parametrization from Rickards et al.,57 where κ is a single hygroscopicity parameter that describes the degree of hygroscopic growth for an aerosol component. Figure S8 shows that OA ALW is negligible compared to IA ALW. Therefore, omitting OA ALW is not to be blamed for the partitioning discrepancies. Thus, why ISORROPIA requires more water to be driven to the particle to perform well in the setting of the ATHLETIC campaign remains an open question.
Poor agreement at RHroom,meas is consistent with previous outdoor modeling campaigns when modeling species at RH values below 20%. For instance, Guo et al.46 had discarded data where the RH was below 20% since ISORROPIA is problematic in this RH range. For instance, at these low RH ranges, the activity coefficients associated with these highly concentrated solutions are uncertain, resulting in uncertainties in ISORROPIA’s pH predictions.46 Colorado occupies an “arid” climate zone,58 where indoor RH tends be especially low in colder months.28 Accordingly, the measured room RH is often below 20% (Figure S2). Thus, this poor agreement could result from ISORROPIA’s low trustworthiness in this RH domain. Although some data points fall on the one-to-one line in Figure 3b,c, ISORROPIA predicts an unrealistically high pH for these values (Figures S9 and S10). Using RHroom,opt instead puts the pH in a more realistic indoor range of ∼3 (Figures S11 and S12).22
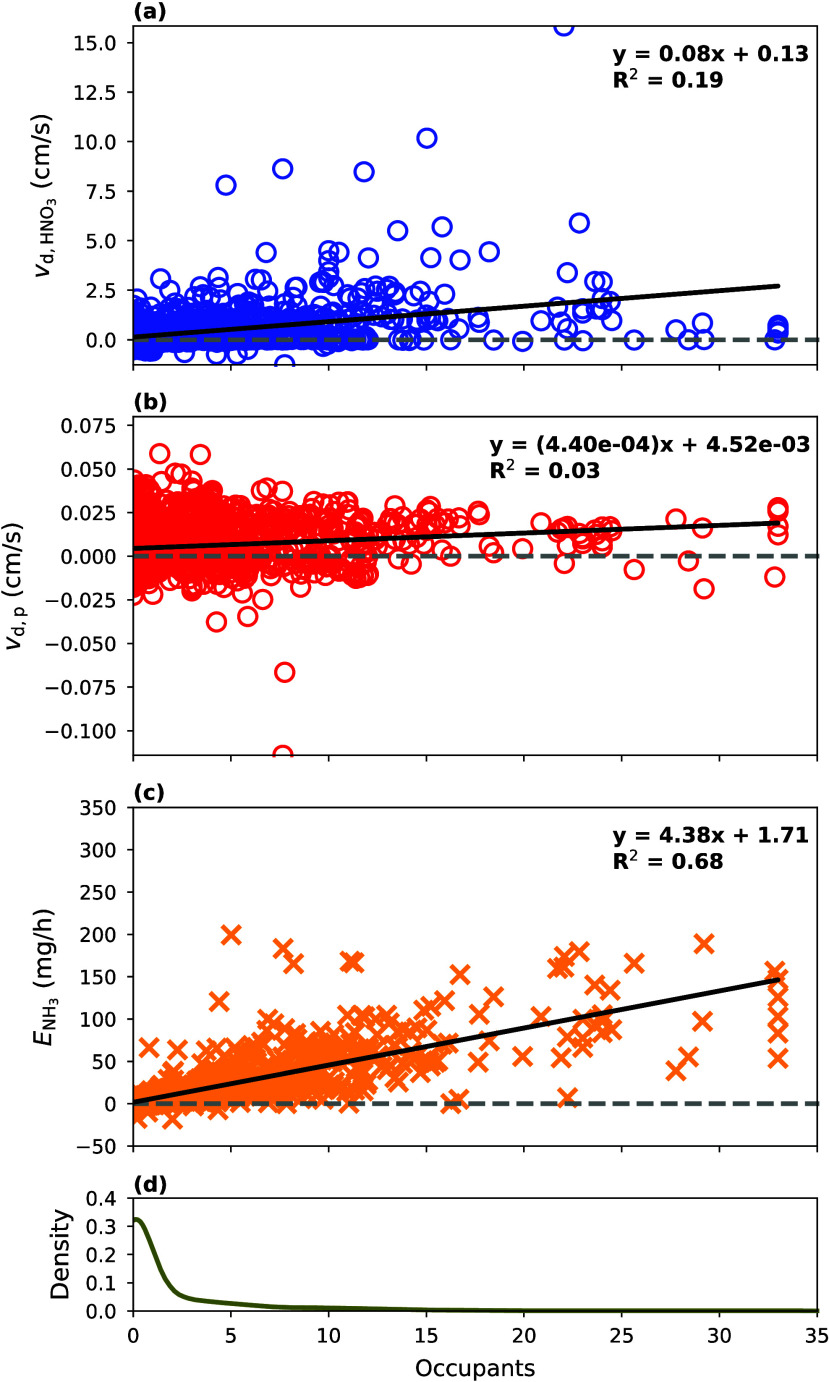
3.2. Emissions and Deposition Relationship with Occupancy
Linear relationships of  ,
, 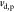 , and
, and  to occupancy (Figure 4) and ΔCO2 (Figure S15) were derived to constrain those inputs
for forward run IMAGES simulations. Occupancy was weakly correlated
with
to occupancy (Figure 4) and ΔCO2 (Figure S15) were derived to constrain those inputs
for forward run IMAGES simulations. Occupancy was weakly correlated
with 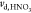 (R2 = 0.19)
and
(R2 = 0.19)
and 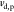 (R2 = 0.03).
The
(R2 = 0.03).
The 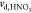 had a stronger correlation with occupancy
than
had a stronger correlation with occupancy
than 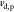 did possibly because of the affinity of
HNO3 for the water in human sweat. For instance, HNO3 may be more likely to deposit onto people with sweat on them
than without. Still, occupancy does not seem to appreciably influence
these deposition velocities given the small slope of their fits (m = 0.08 for
did possibly because of the affinity of
HNO3 for the water in human sweat. For instance, HNO3 may be more likely to deposit onto people with sweat on them
than without. Still, occupancy does not seem to appreciably influence
these deposition velocities given the small slope of their fits (m = 0.08 for 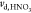 with respect to occupancy and m = 4.4 × 10–4 for
with respect to occupancy and m = 4.4 × 10–4 for 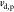 with respect to occupancy). The y-intercept depicted in Figure 4a,b is the deposition velocity of HNO3 and particles onto surfaces in the weight room without occupants
present. The standard error for these slopes are shown in Table S3.
with respect to occupancy). The y-intercept depicted in Figure 4a,b is the deposition velocity of HNO3 and particles onto surfaces in the weight room without occupants
present. The standard error for these slopes are shown in Table S3.
Figure 4.
Linear relationships relating the number
of occupants to 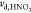 (a),
(a), 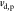 (b), and
(b), and 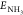 (c), and a probability density function
(d) shows the distribution of occupancy. The best fit line (black
line), best-fit equation, and R2 value
are displayed in each plot (a–c).
(c), and a probability density function
(d) shows the distribution of occupancy. The best fit line (black
line), best-fit equation, and R2 value
are displayed in each plot (a–c).
These deposition values might be weakly correlated
to occupancy
because the generally small number of people in the gym may not increase
the total surface area by a large extent relative to the area without
occupants. Manuja et al.54 suggest that
only the first few largest items in the room contribute significantly
to the total surface area. For instance, using the formula described
in Dubois and Dubois59 to estimate body
surface area (BSA) given body weight and height, the average adult
American male (∼175 cm, ∼91 kg according to the Centers
for Disease Control and Prevention) has a BSA of ∼2.07 m2. Assuming all occupants have about the same BSA, the 35 occupants
would contribute to less than 2% of the total surface area (using V = 1700 m3 and  = 2.5 m–1) in the gym.
Further, the order of magnitude of the near-constant
= 2.5 m–1) in the gym.
Further, the order of magnitude of the near-constant 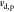 here aligns with previous indoor measurement
campaigns such as Xu et al.60 and Offerman
et al.61 Similarly, the range of
here aligns with previous indoor measurement
campaigns such as Xu et al.60 and Offerman
et al.61 Similarly, the range of 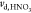 here (0.13–2.93
here (0.13–2.93 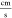 ) agrees with indoor measurements from Salmon
et al.62 (0.24–1.34
) agrees with indoor measurements from Salmon
et al.62 (0.24–1.34 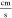 ) and estimates from Lunden et al.63 (0.56
) and estimates from Lunden et al.63 (0.56 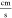 ).
).
Results demonstrate that occupancy
is relatively well correlated
with the net 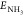 (R2 = 0.68; Figure 4c).
(R2 = 0.68; Figure 4c). 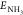 being correlated with occupancy agrees
with the findings of previous indoor field campaigns.14,64 For instance, the per person
being correlated with occupancy agrees
with the findings of previous indoor field campaigns.14,64 For instance, the per person 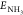 computed here as the slope of the linear
fit (∼4.38
computed here as the slope of the linear
fit (∼4.38 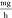 ) is on par with
) is on par with 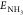 estimated from past studies (Furukawa et
al.:64 ∼5.9
estimated from past studies (Furukawa et
al.:64 ∼5.9 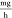 and Li et al.:19 0.4–5.2
and Li et al.:19 0.4–5.2 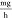 ). When no occupants are present, NH3 emissions still occur from building materials, and the y-intercept displayed in Figure 4c could represent the net NH3 emission
rate attributed to the building source.13 However, this value is hard to compare to
). When no occupants are present, NH3 emissions still occur from building materials, and the y-intercept displayed in Figure 4c could represent the net NH3 emission
rate attributed to the building source.13 However, this value is hard to compare to 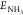 from previous studies since it depends
on multiple building parameters such as T, RH, and
the air exchange rate.13 In the next set
of IMAGES runs, the observed number of occupants in a room were used
in the best-fit equations, displayed in Figure 4 (and Figure S15 when given ΔCO2), to estimate
from previous studies since it depends
on multiple building parameters such as T, RH, and
the air exchange rate.13 In the next set
of IMAGES runs, the observed number of occupants in a room were used
in the best-fit equations, displayed in Figure 4 (and Figure S15 when given ΔCO2), to estimate 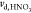 and
and 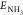 at each time step within IMAGES. However,
since the
at each time step within IMAGES. However,
since the 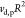 value was near 0, a constant value of 0.0054
value was near 0, a constant value of 0.0054 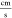 , taken from the average computed
, taken from the average computed 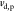 , was used instead.
, was used instead.
3.3. IMAGES Evaluation
Room concentrations
of inorganic particle and gas species were simulated using IMAGES
for the ATHLETIC campaign based on measured supply airstream concentrations
and room conditions, and the computed room concentration results were
evaluated against room measurements. The degree to which RHroom,opt influenced IMAGES results was again assessed by running IMAGES with
RHroom,meas and RHroom,opt. The results presented
here use the occupancy-based relationships of 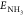 and
and 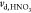 , and a constant
, and a constant 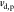 to determine deposition and emission parameters
as described in Section 2.5. Results using the ΔCO2-based relationships
instead are shown in Section S4.
to determine deposition and emission parameters
as described in Section 2.5. Results using the ΔCO2-based relationships
instead are shown in Section S4.
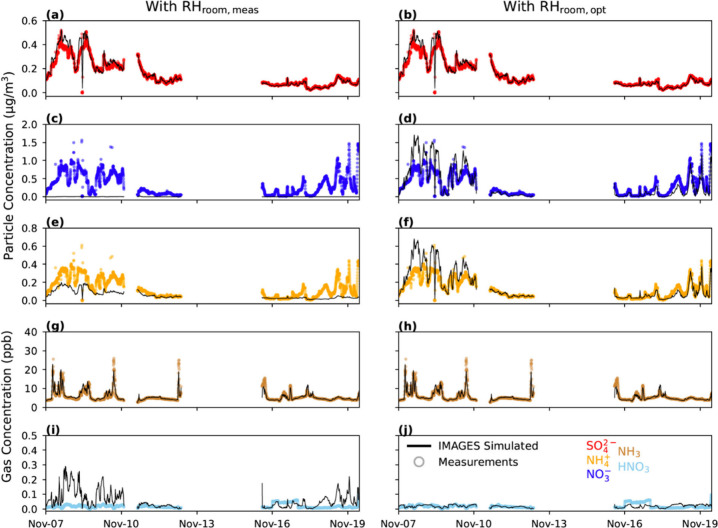
The agreement of IMAGES results with measured room concentrations
was strongly driven by the indoor RH used in the simulations and whether
ISORROPIA well-predicted IA partitioning. For instance, when running
IMAGES at measured T and RH conditions, IMAGES underestimates  and always allocates nitrate to the gas
phase, but simulates
and always allocates nitrate to the gas
phase, but simulates 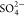 and NH3 well (Figure 5 left column and Figure 6a–e). Conversely, running
IMAGES with RHroom,opt improves the agreement of modeled
and measured concentrations of
and NH3 well (Figure 5 left column and Figure 6a–e). Conversely, running
IMAGES with RHroom,opt improves the agreement of modeled
and measured concentrations of 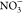 , HNO3, and
, HNO3, and  . For instance, the IMAGES timeseries of
HNO3 more closely follows HNO3 measurements
when using RHroom,opt (Figure 5, right column) rather than measured
. For instance, the IMAGES timeseries of
HNO3 more closely follows HNO3 measurements
when using RHroom,opt (Figure 5, right column) rather than measured  , which it follows when using RHroom,meas (Figure 5 left column).
This outcome was expected since similar results were presented in Section 3.1, in which the
applicability of ISORROPIA in the weight room was evaluated independently.
, which it follows when using RHroom,meas (Figure 5 left column).
This outcome was expected since similar results were presented in Section 3.1, in which the
applicability of ISORROPIA in the weight room was evaluated independently.
Figure 5.
Time series of IMAGES simulated (solid lines) particle and gas concentrations using RHroom,meas (left column) and RHroom,opt (right column). Measured concentrations (circle markers) are shown for comparison.
Figure 6.
Comparison of IMAGES simulated and measured concentrations using RHroom,meas (a–e) and RHroom,opt (f–j) as model inputs. The green line represents the line of best fit calculated with an orthogonal regression, while the black line is the 1:1 line. The correlation coefficient, R2; slope, m; and y-intercept, b, are displayed for each regression.
After running IMAGES with the optimized RHroom,opt of
98% to correct the observed partitioning error associated with using
ISORROPIA in this indoor setting,  and
and  are slightly overpredicted (m = 1.62 and 1.54, respectively), and NH3 and HNO3 are a bit underpredicted (m = 0.85 and 0.23, respectively).
The poor HNO3 agreement may be driven by its almost negligible
concentration. The fact that
are slightly overpredicted (m = 1.62 and 1.54, respectively), and NH3 and HNO3 are a bit underpredicted (m = 0.85 and 0.23, respectively).
The poor HNO3 agreement may be driven by its almost negligible
concentration. The fact that 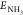 ,
, 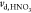 and
and 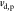 occupancy-based estimations were used at
each time step may explain these discrepancies between measurements
and simulations, since the amount of mass in each phase may deviate
from the measurements if the deposition and emission rates were inconsistent
with those in reality. Although the actual emission and deposition
rates at every step could have been used to produce more accurate
results, estimating
occupancy-based estimations were used at
each time step may explain these discrepancies between measurements
and simulations, since the amount of mass in each phase may deviate
from the measurements if the deposition and emission rates were inconsistent
with those in reality. Although the actual emission and deposition
rates at every step could have been used to produce more accurate
results, estimating 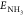 ,
, 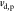 , and
, and 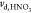 with occupancy (or ΔCO2) data is more valuable since they can be applied to future modeling
domains. Still, IMAGES simulations predict IA concentrations well
when using the occupant-based relationships with RHroom,opt, but poorly estimates them when using RHroom,meas. Similar
results for the ΔCO2-based relationships are shown
in Section S4. This result suggests that
the deviation from the predicted equilibrium is the primary factor
affecting the IMAGES performance when the RH is not optimized rather
than the occupancy-based emission and deposition trends.
with occupancy (or ΔCO2) data is more valuable since they can be applied to future modeling
domains. Still, IMAGES simulations predict IA concentrations well
when using the occupant-based relationships with RHroom,opt, but poorly estimates them when using RHroom,meas. Similar
results for the ΔCO2-based relationships are shown
in Section S4. This result suggests that
the deviation from the predicted equilibrium is the primary factor
affecting the IMAGES performance when the RH is not optimized rather
than the occupancy-based emission and deposition trends.
Still,
a sensitivity analysis where 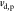 and
and  were varied was performed. For this sensitivity
test,
were varied was performed. For this sensitivity
test,  was set to either 0
was set to either 0 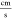 , 0.0058
, 0.0058 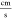 (the average of the trend line in Figure 4b), or 0.03
(the average of the trend line in Figure 4b), or 0.03 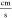 (the 95th percentile of the trend line
in Figure 4b). Additionally,
(the 95th percentile of the trend line
in Figure 4b). Additionally, 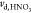 was set to either 0
was set to either 0 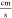 , 0.28
, 0.28 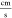 (the average of the trend line in Figure 4a), or 1.22
(the average of the trend line in Figure 4a), or 1.22 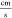 (the 95th percentile of the trend line
in Figure 4a). Results
from this sensitivity analysis are shown in Figures S20 and S21 of the SI. To summarize,
the model was not sensitive to changes in particle deposition. However,
omitting
(the 95th percentile of the trend line
in Figure 4a). Results
from this sensitivity analysis are shown in Figures S20 and S21 of the SI. To summarize,
the model was not sensitive to changes in particle deposition. However,
omitting 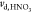 returned a portion of data points where
the modeled semivolatile particle species concentrations agreed with
measurements, which corresponded to the cases when ISORROPIA estimated
unrealistically high pH values. Increasing
returned a portion of data points where
the modeled semivolatile particle species concentrations agreed with
measurements, which corresponded to the cases when ISORROPIA estimated
unrealistically high pH values. Increasing 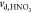 eliminated any
eliminated any 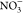 . Additionally, a sensitivity analysis was
conducted where A/V was set to 0.5
m–1, 2.5 m–1, or 10 m–1. These results show that the modeled-measured agreement did not
improve by increasing A/V. However,
lowering A/V returned some data
points where the modeled semivolatile particle species matched measured
concentrations. However, the cases where good agreement occurred were
due to ISORROPIA estimating unrealistically high pH values (as discussed
in Section 3.1).
Results from this sensitivity test can be found in Figure S22 of the SI.
. Additionally, a sensitivity analysis was
conducted where A/V was set to 0.5
m–1, 2.5 m–1, or 10 m–1. These results show that the modeled-measured agreement did not
improve by increasing A/V. However,
lowering A/V returned some data
points where the modeled semivolatile particle species matched measured
concentrations. However, the cases where good agreement occurred were
due to ISORROPIA estimating unrealistically high pH values (as discussed
in Section 3.1).
Results from this sensitivity test can be found in Figure S22 of the SI.
4. Conclusions
The thermodynamic inorganic
aerosol model ISORROPIA that was recently
integrated into our comprehensive indoor aerosol model, IMAGES, was
applied here to simulate the partitioning of inorganic particle- and
gas-phase species in a weight room with occupants during the ATHLETIC
indoor measurement campaign. The measurements in this campaign provided
the first opportunity to evaluate the performance of ISORROPIA indoors.
Linear relationships, which related 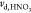 ,
, 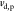 , and
, and 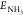 to occupancy, were derived from measurements
since these parameters were unknown but were required for indoor modeling
with IMAGES.
to occupancy, were derived from measurements
since these parameters were unknown but were required for indoor modeling
with IMAGES. 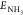 correlated strongly with occupancy, but
correlated strongly with occupancy, but  and
and 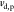 did not since the occupants contributed
little to the total surface area in the gym. Still, the range of estimated
did not since the occupants contributed
little to the total surface area in the gym. Still, the range of estimated 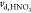 ,
, 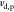 , and
, and 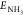 agreed well with values from previous studies.
agreed well with values from previous studies. 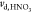 and
and 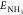 correlations and a constant
correlations and a constant 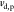 were used during the indoor modeling to
parametrize deposition and emission rates using the observed occupancy
at the model time steps.
were used during the indoor modeling to
parametrize deposition and emission rates using the observed occupancy
at the model time steps.
IMAGES only performed well when the aerosol liquid water content in ISORROPIA was made greater than measured indoor environmental conditions of air temperature and RH would suggest. The necessary increase of the indoor RH to a higher RHroom,opt was determined in an independent parametric analysis since T was relatively constant throughout the campaign. ISORROPIA not accounting for hysteresis effects was hypothesized to play a role in why ISORROPIA-partitioned concentrations agreed with measurements when the measured RH was used. However, this hypothesis, as well as inlet losses of HNO3 contributing to the poor agreement were deemed unlikely. Other possible explanations could be evaluated in the future, such as the building walls being more complex than this model assumes, as they may act as a source or sink of inorganic species depending on conditions. Estimating deposition and emission rates also contributes to the slight overpredictions of particles and underpredictions of gases. Ultimately, IMAGES simulations predicted indoor IA concentrations in a gym with people with good agreement with measurements when RH was optimized with observations.
Therefore, with IMAGES, detailed modeling can be performed to understand better how aerosols’ physical state and composition changes, such as when transported from the supply duct to the room. Knowing the physical state and composition of contaminants is crucial. For example, aerosol composition influences their physicochemical properties, such as volatility, hygroscopicity, and density, which affect aerosol behavior. However, an increased RH (or decreased T) was required to obtain accurate inorganic partitioning for this modeling scenerio, Depending on why changes in RH or T were needed here, this fix may or may not work in future modeling scenerios. Therefore, future work will build upon this study by looking into ISORROPIA’s indoor partitioning error. Additionally, an air handling unit (AHU) module will be developed, enabling researchers to simulate how aerosols’ physical state and composition alter during outdoor-to-indoor transport.
Acknowledgments
The Alfred P. Sloan Foundation provided funding for this work (Grant No. 2019-12301). The Alfred P. Sloan Foundation also funded the ATHLETIC Campaign and provided the input data for this work (Grant Nos. G-2016-7173 and G-2019-12444). In addition to the Sloan Foundation support, H.G., P.C.J., J.L.J., D.P., D.A.D., A.V.H., and B.A.N. also acknowledge support from NASA Earth Sciences Division (Grant Nos. 80NSSC21K1451 and 80NSSC23K0828) and the Balvi Filantropic Fund (A27). The authors thank Jason DePaepe, Shawn Herrera, MT Eisner, Jennifer Green, and Jeremy Johnson at the University of Colorado Athletics and Facilities for hosting the sampling site and supporting this study.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsestair.4c00060.
The SI starts with a note on how the ATHLETIC Campaign data was preprocessed for use with IMAGES. Then, the SI gives more information about how ISORROPIA performed indoors by (1) describing in detail the parametric test that was initially discussed in Section 2.2, (2) analyzing the various hypotheses made for why ISORROPIA needs a high RH or low temperature to produce accurate gas-particle partitioning, and (3) showing how ISORROPIA performed indoors when it is run using the stable mode. Next, the SI describes how we determined that running ISORROPIA with an RH of 98% would produce the most accurate gas-particle partitioning results. Then, emission and deposition rate trends as they relate to ΔCO2 are shown. Additionally, how outliers were found from these emission and deposition trends is described. Finally, IMAGES is run and evaluated using the ΔCO2-based deposition and emission trends (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Klepeis N. E.; Nelson W. C.; Ott W. R.; et al. The National Human Activity Pattern Survey (NHAPS): a resource for assessing exposure to environmental pollutants. Journal of Exposure Analysis and Environmental Epidemiology. 2001, 11 (3), 231–252. 10.1038/sj.jea.7500165. [DOI] [PubMed] [Google Scholar]
- Johnson A. M.; Waring M. S.; DeCarlo P. F. Real-time transformation of outdoor aerosol components upon transport indoors measured with aerosol mass spectrometry. Indoor Air. 2017, 27 (1), 230–240. 10.1111/ina.12299. [DOI] [PubMed] [Google Scholar]
- Pope C. A.; Coleman N.; Pond Z. A.; Burnett R. T. Fine particulate air pollution and human mortality: 25+ years of cohort studies. Environmental Research 2020, 183, 108924. 10.1016/j.envres.2019.108924. [DOI] [PubMed] [Google Scholar]
- Wang G. H.; Zhang R. Y.; Gomez M. E.; et al. Persistent sulfate formation from London Fog to Chinese haze. Proceedings of the National Academy of Sciences of the United States of America. 2016, 113 (48), 13630–13635. 10.1073/pnas.1616540113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie Y. Y.; Zhao B. Chemical composition of outdoor and indoor PM2.5 collected during haze events: Transformations and modified source contributions resulting from outdoor-to-indoor transport. Indoor Air. 2018, 28 (6), 828–839. 10.1111/ina.12503. [DOI] [PubMed] [Google Scholar]
- Logue J. M.; McKone T. E.; Sherman M. H.; Singer B. C. Hazard assessment of chemical air contaminants measured in residences. Indoor Air. 2011, 21 (2), 92–109. 10.1111/j.1600-0668.2010.00683.x. [DOI] [PubMed] [Google Scholar]
- Weschler C. J. Ozone’s impact on public health: Contributions from indoor exposures to ozone and products of ozone-initiated chemistry. Environmental Health Perspectives. 2006, 114 (10), 1489–1496. 10.1289/ehp.9256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weschler C. J.; Nazaroff W. W. Semivolatile organic compounds in indoor environments. Atmos. Environ. 2008, 42 (40), 9018–9040. 10.1016/j.atmosenv.2008.09.052. [DOI] [Google Scholar]
- Ampollini L.; Katz E.; Bourne S.; et al. Observations and Contributions of Real-time Indoor Ammonia Concentrations During HOMEChem. Environ. Sci. Technol. 2019, 53 (15), 8591–8598. 10.1021/acs.est.9b02157. [DOI] [PubMed] [Google Scholar]
- Li Y. Q.; Harrison R. M. Comparison of Indoor and Outdoor Concentrations of Acid Gases, Ammonia and Their Associated Salts. Environmental Technology. 1990, 11 (4), 315–326. 10.1080/09593339009384868. [DOI] [Google Scholar]
- Liang C. S. K.; Waldman J. M. Indoor Exposures To Acidic Aerosols At Child And Elderly Care Facilities. Indoor Air. 1992, 2 (4), 196–207. 10.1111/j.1600-0668.1992.00002.x. [DOI] [Google Scholar]
- Nazaroff W. W.; Weschler C. J. Indoor acids and bases. Indoor Air. 2020, 30 (4), 559–644. 10.1111/ina.12670. [DOI] [PubMed] [Google Scholar]
- Bai Z.; Dong Y.; Wang Z.; Zhu T. Emission of ammonia from indoor concrete wall and assessment of human exposure. Environment International. 2006, 32 (3), 303–311. 10.1016/j.envint.2005.06.002. [DOI] [PubMed] [Google Scholar]
- Li M. Z.; Weschler C. J.; Beko G.; Wargocki P.; Lucic G.; Williams J. Human Ammonia Emission Rates under Various Indoor Environmental Conditions. Environ. Sci. Technol. 2020, 54 (9), 5419–5428. 10.1021/acs.est.0c00094. [DOI] [PubMed] [Google Scholar]
- Nose K.; Mizuno T.; Yamane N.; et al. Identification of ammonia in gas emanated from human skin and its correlation with that in blood. Anal. Sci. 2005, 21 (12), 1471–1474. 10.2116/analsci.21.1471. [DOI] [PubMed] [Google Scholar]
- Schmidt F M; Vaittinen O; Metsala M; Lehto M; Forsblom C; Groop P-H; Halonen L; et al. Ammonia in breath and emitted from skin. Journal of Breath Research 2013, 7 (1), 017109. 10.1088/1752-7155/7/1/017109. [DOI] [PubMed] [Google Scholar]
- Španel P.; Dryahina K.; Smith D. The concentration distributions of some metabolites in the exhaled breath of young adults. Journal of Breath Research 2007, 1 (2), 026001. 10.1088/1752-7155/1/2/026001. [DOI] [PubMed] [Google Scholar]
- Turner C.; Spanel P.; Smith D. A longitudinal study of ammonia, acetone and propanol in the exhaled breath of 30 subjects using selected ion flow tube mass spectrometry, SIFT-MS. Physiological Measurement. 2006, 27 (4), 321–337. 10.1088/0967-3334/27/4/001. [DOI] [PubMed] [Google Scholar]
- Li M.; Weschler C.; Bekö G.; Wargocki P.; Lucic G.; Williams J. Human Ammonia Emission Rates under Various Indoor Environmental Conditions. Environ. Sci. Technol. 2020, 54, 5419–5428. 10.1021/acs.est.0c00094. [DOI] [PubMed] [Google Scholar]
- Zhang L.; Chen Y. F.; Zhao Y. H.; et al. Agricultural ammonia emissions in China: reconciling bottom-up and top-down estimates. Atmospheric Chemistry and Physics. 2018, 18 (1), 339–355. 10.5194/acp-18-339-2018. [DOI] [Google Scholar]
- Zhu L.; Henze D. K.; Cady-Pereira K. E.; et al. Constraining U.S. ammonia emissions using TES remote sensing observations and the GEOS-Chem adjoint model. Journal of Geophysical Research: Atmospheres 2013, 118, 3355–3368. 10.1002/jgrd.50166. [DOI] [Google Scholar]
- Liu C.; Wang H.; Guo H. Redistribution of PM2.5 associated nitrate and ammonium during outdoor to indoor transport. Indoor Air. 2019, 29 (3), 460–468. 10.1111/ina.12549. [DOI] [PubMed] [Google Scholar]
- Beko G.; Wargocki P.; Wang N. J.; et al. The Indoor Chemical Human Emissions and Reactivity (ICHEAR) project: Overview of experimental methodology and preliminary results. Indoor Air. 2020, 30 (6), 1213–1228. 10.1111/ina.12687. [DOI] [PubMed] [Google Scholar]
- Finewax Z.; Pagonis D.; Claflin M. S.; et al. Quantification and source characterization of volatile organic compounds from exercising and application of chlorine-based cleaning products in a university athletic center. Indoor Air. 2021, 31 (5), 1323–1339. 10.1111/ina.12781. [DOI] [PubMed] [Google Scholar]
- Berman B. C.; Cummings B. E.; Avery A. M.; DeCarlo P. F.; Capps S. L.; Waring M. S. Simulating indoor inorganic aerosols of outdoor origin with the inorganic aerosol thermodynamic equilibrium model ISORROPIA. Indoor Air. 2022, 32 (7), e13075. 10.1111/ina.13075. [DOI] [PubMed] [Google Scholar]
- Fountoukis C.; Nenes A. ISORROPIA II: a computationally efficient thermodynamic equilibrium model for K+-Ca2+-Mg2+-Nh(4)(+)-Na+-SO42-NO3-Cl-H2O aerosols. Atmospheric Chemistry and Physics. 2007, 7 (17), 4639–4659. 10.5194/acp-7-4639-2007. [DOI] [Google Scholar]
- Nenes A.; Pandis S. N.; Pilinis C. ISORROPIA: A New Thermodynamic Equilibrium Model for Multiphase Multicomponent Inorganic Aerosols. Aquatic Geochemistry. 1998, 4, 123–152. 10.1023/A:1009604003981. [DOI] [Google Scholar]
- Cummings B. E.; Li Y.; DeCarlo P. F.; Shiraiwa M.; Waring M. S. Indoor aerosol water content and phase state in U.S. residences: impacts of relative humidity, aerosol mass and composition, and mechanical system operation. Environmental science-processes & impacts. 2020, 22 (10), 2031–2057. 10.1039/D0EM00122H. [DOI] [PubMed] [Google Scholar]
- Shiraiwa M.; Carslaw N.; Tobias D. J.; et al. Modelling consortium for chemistry of indoor environments (MOCCIE): integrating chemical processes from molecular to room scales. Environ. Sci-Process Impacts. 2019, 21 (8), 1240–1254. 10.1039/C9EM00123A. [DOI] [PubMed] [Google Scholar]
- Donahue N. M.; Kroll J. H.; Pandis S. N.; Robinson A. L. A two-dimensional volatility basis set - Part 2: Diagnostics of organic-aerosol evolution. Atmos Chem. Phys. 2012, 12 (2), 615–634. 10.5194/acp-12-615-2012. [DOI] [Google Scholar]
- Jimenez J. L.; Canagaratna M. R.; Donahue N. M.; et al. Evolution of Organic Aerosols in the Atmosphere. Science. 2009, 326 (5959), 1525–1529. 10.1126/science.1180353. [DOI] [PubMed] [Google Scholar]
- Pankow J. F. An Absorption-Model of Gas-Particle Partitioning of Organic-Compounds in the Atmosphere. Atmos. Environ. 1994, 28 (2), 185–188. 10.1016/1352-2310(94)90093-0. [DOI] [Google Scholar]
- Avery A. M.; Waring M. S.; DeCarlo P. F. Seasonal variation in aerosol composition and concentration upon transport from the outdoor to indoor environment. Environ. Sci-Process Impacts. 2019, 21 (3), 528–547. 10.1039/C8EM00471D. [DOI] [PubMed] [Google Scholar]
- Claflin M. S.; Pagonis D.; Finewax Z.; et al. An in situ gas chromatograph with automatic detector switching between PTR- and EI-TOF-MS: isomer-resolved measurements of indoor air. Atmospheric Measurement Techniques. 2021, 14 (1), 133–152. 10.5194/amt-14-133-2021. [DOI] [Google Scholar]
- Guo H.; Campuzano-Jost P.; Nault B. A.; et al. The importance of size ranges in aerosol instrument intercomparisons: a case study for the Atmospheric Tomography Mission. Atmos Meas Technol. 2021, 14 (5), 3631–3655. 10.5194/amt-14-3631-2021. [DOI] [Google Scholar]
- Canagaratna M. R.; Jayne J. T.; Jimenez J. L.; et al. Chemical and microphysical characterization of ambient aerosols with the aerodyne aerosol mass spectrometer. Mass Spectrometry Reviews. 2007, 26 (2), 185–222. 10.1002/mas.20115. [DOI] [PubMed] [Google Scholar]
- DeCarlo P. F.; Kimmel J. R.; Trimborn A.; et al. Field-deployable, high-resolution, time-of-flight aerosol mass spectrometer. Anal. Chem. 2006, 78 (24), 8281–8289. 10.1021/ac061249n. [DOI] [PubMed] [Google Scholar]
- Guo H. Y.; Campuzano-Jost P.; Nault B. A.; et al. The importance of size ranges in aerosol instrument intercomparisons: a case study for the Atmospheric Tomography Mission. Atmospheric Measurement Techniques. 2021, 14 (5), 3631–3655. 10.5194/amt-14-3631-2021. [DOI] [Google Scholar]
- Moravek A.; VandenBoer T. C.; Finewax Z.; et al. Reactive Chlorine Emissions from Cleaning and Reactive Nitrogen Chemistry in an Indoor Athletic Facility. Environ. Sci. Technol. 2022, 56 (22), 15408–15416. 10.1021/acs.est.2c04622. [DOI] [PubMed] [Google Scholar]
- Day D. A.; Campuzano-Jost P.; Nault B. A.; et al. A systematic re-evaluation of methods for quantification of bulk particle-phase organic nitrates using real-time aerosol mass spectrometry. Atmos Meas Technol. 2022, 15 (2), 459–483. 10.5194/amt-15-459-2022. [DOI] [Google Scholar]
- Schueneman M. K.; Nault B. A.; Campuzano-Jost P.; et al. Aerosol pH indicator and organosulfate detectability from aerosol mass spectrometry measurements. Atmos Meas Technol. 2021, 14 (3), 2237–2260. 10.5194/amt-14-2237-2021. [DOI] [Google Scholar]
- Farmer D. K.; Matsunaga A.; Docherty K. S.; et al. Response of an aerosol mass spectrometer to organonitrates and organosulfates and implications for atmospheric chemistry. Proceedings of the National Academy of Sciences of the United States of America. 2010, 107 (15), 6670–6675. 10.1073/pnas.0912340107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bey I.; Jacob D. J.; Yantosca R. M.; et al. Global modeling of tropospheric chemistry with assimilated meteorology: Model description and evaluation. J. Geophys Res-Atmos. 2001, 106 (D19), 23073–23095. 10.1029/2001JD000807. [DOI] [Google Scholar]
- Byun D.; Schere K. L. Review of the Governing Equations, Computational Algorithms, and Other Components of the Models-3 Community Multiscale Air Quality (CMAQ) Modeling System. Applied Mechanics Reviews. 2006, 59 (2), 51. 10.1115/1.2128636. [DOI] [Google Scholar]
- Capps S. L.; Henze D. K.; Hakami A.; Russell A. G.; Nenes A. ANISORROPIA: the adjoint of the aerosol thermodynamic model ISORROPIA. Atmospheric Chemistry and Physics. 2012, 12, 527–543. 10.5194/acp-12-527-2012. [DOI] [Google Scholar]
- Guo H.; Sullivan A. P.; Campuzano-Jost P.; Schroder J. C.; Lopez-Hilfiker F. D.; Dibb J. E.; Jimenez J. L.; Thornton J. A.; Brown S. S.; Nenes A.; Weber R. J. Fine particle pH and the partitioning of nitric acid during winter in the northeastern United States. J. Geophys Res-Atmos. 2016, 121 (17), 10355–10376. 10.1002/2016JD025311. [DOI] [Google Scholar]
- Hennigan C. J.; Izumi J.; Sullivan A. P.; Weber R. J.; Nenes A. A critical evaluation of proxy methods used to estimate the acidity of atmospheric particles. Atmos Chem. Phys. 2015, 15 (5), 2775–2790. 10.5194/acp-15-2775-2015. [DOI] [Google Scholar]
- Pye H. O. T.; Nenes A.; Alexander B.; et al. The acidity of atmospheric particles and clouds. Atmos Chem. Phys. 2020, 20 (8), 4809–4888. 10.5194/acp-20-4809-2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S. J.; Gao M.; Xu W. Q.; et al. Fine-particle pH for Beijing winter haze as inferred from different thermodynamic equilibrium models. Atmospheric Chemistry and Physics. 2018, 18 (10), 7423–7438. 10.5194/acp-18-7423-2018. [DOI] [Google Scholar]
- Chen C.; Ji W.; Zhao B. Size-dependent efficiencies of ultrafine particle removal of various filter media. Build Environ. 2019, 160, 106171. 10.1016/j.buildenv.2019.106171. [DOI] [Google Scholar]
- El Orch Z.; Stephens B.; Waring M. S. Predictions and determinants of size-resolved particle infiltration factors in single-family homes in the U.S. Build Environ. 2014, 74, 106–118. 10.1016/j.buildenv.2014.01.006. [DOI] [Google Scholar]
- Lai A. C. K.; Thatcher T. L.; Nazaroff W. W. Inhalation Transfer Factors for Air Pollution Health Risk Assessment. Journal of the Air & Waste Management Association (1995). 2000, 50 (9), 1688–1699. 10.1080/10473289.2000.10464196. [DOI] [PubMed] [Google Scholar]
- Riley W. J.; McKone T. E.; Lai A. C. K.; Nazaroff W. W. Indoor particulate matter of outdoor origin: Importance of size-dependent removal mechanisms. Environ. Sci. Technol. 2002, 36 (2), 200–207. 10.1021/es010723y. [DOI] [PubMed] [Google Scholar]
- Manuja A.; Ritchie J.; Buch K.; et al. Total surface area in indoor environments. Environ. Sci-Process Impacts. 2019, 21 (8), 1384–1392. 10.1039/C9EM00157C. [DOI] [PubMed] [Google Scholar]
- Thatcher T. L.; Lai A. C. K.; Moreno-Jackson R.; Sextro R. G.; Nazaroff W. W. Effects of room furnishings and air speed on particle deposition rates indoors. Atmos. Environ. 2002, 36 (11), 1811–1819. 10.1016/S1352-2310(02)00157-7. [DOI] [Google Scholar]
- Katz E. F.; Guo H. Y.; Campuzano-Jost P.; et al. Quantification of cooking organic aerosol in the indoor environment using aerodyne aerosol mass spectrometers. Aerosol Sci. Technol. 2021, 55 (10), 1099–1114. 10.1080/02786826.2021.1931013. [DOI] [Google Scholar]
- Rickards A. M. J.; Miles R. E. H.; Davies J. F.; Marshall F. H.; Reid J. P. Measurements of the Sensitivity of Aerosol Hygroscopicity and the κ Parameter to the O/C Ratio. J. Phys. Chem. A 2013, 117 (51), 14120–14131. 10.1021/jp407991n. [DOI] [PubMed] [Google Scholar]
- Briggs R. S.; Lucas R. G.; Taylor Z. T. Climate Classification for Building Energy Codes and Standards: Part 1 - Development Process. ASHRAE Transactions. 2003, 109, 109–121. [Google Scholar]
- Dubois D.; Dubois E. F. Nutrition Metabolism Classic - a Formula to Estimate the Approximate Surface-Area if Height and Weight Be Known (Reprinted from Archives Internal Medicine, Vol 17, p 863, 1916). Nutrition 1989, 5 (5), 303–311. [PubMed] [Google Scholar]
- Xu M. D.; Nematollahi M.; Sextro R. G.; Gadgil A. J.; Nazaroff W. W. Deposition of Tobacco-Smoke Particles in a Low Ventilation Room. Aerosol Sci. Technol. 1994, 20 (2), 194–206. 10.1080/02786829408959676. [DOI] [Google Scholar]
- Offermann F. J.; Sextro R. G.; Fisk W. J.; et al. Control of Respirable Particles in Indoor Air with Portable Air Cleaners. Atmos. Environ. 1985, 19 (11), 1761–1771. 10.1016/0004-6981(85)90003-4. [DOI] [Google Scholar]
- Salmon L. G.; Nazaroff W. W.; Ligocki M. P.; Jones M. C.; Cass G. R. Nitric-Acid Concentrations in Southern California Museums. Environ. Sci. Technol. 1990, 24 (7), 1004–1013. 10.1021/es00077a009. [DOI] [Google Scholar]
- Lunden M. M.; Revzan K. L.; Fischer M. L.; et al. The transformation of outdoor ammonium nitrate aerosols in the indoor environment. Atmos. Environ. 2003, 37 (39–40), 5633–5644. 10.1016/j.atmosenv.2003.09.035. [DOI] [Google Scholar]
- Furukawa S.; Sekine Y.; Kimura K.; Umezawa K.; Asai S.; Miyachi H. Simultaneous and multi-point measurement of ammonia emanating from human skin surface for the estimation of whole body dermal emission rate. Journal of Chromatography B-Analytical Technologies in the Biomedical and Life Sciences. 2017, 1053, 60–64. 10.1016/j.jchromb.2017.03.034. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.