A two-dimensional vertex model for curvy cell–cell interfaces at the subcellular scale

Abstract

Cross-sections of cell shapes in a tissue monolayer typically resemble a tiling of convex polygons. Yet, examples exist where the polygons are not convex with curved cell–cell interfaces, as seen in the adaxial epidermis. To date, two-dimensional vertex models predicting the structure and mechanics of cell monolayers have been mostly limited to convex polygons. To overcome this limitation, we introduce a framework to study curvy cell–cell interfaces at the subcellular scale within vertex models by using a parametrized curve between vertices that is expanded in a Fourier series and whose coefficients represent additional degrees of freedom. This extension to non-convex polygons allows for cells with the same shape index, or dimensionless perimeter, to be, for example, either elongated or globular with lobes. In the presence of applied, anisotropic stresses, we find that local, subcellular curvature or buckling can be energetically more favourable than larger scale deformations involving groups of cells. Inspired by recent experiments, we also find that local, subcellular curvature at cell–cell interfaces emerges in a group of cells in response to the swelling of additional cells surrounding the group. Our framework, therefore, can account for a wider array of multicellular responses to constraints in the tissue environment.

1. Introduction

Isolated cells take on a multitude of convex and non-convex shapes as determined by their underlying cytoskeletal morphology and their environment. Cells packed together to form a tissue can take on different shapes (from isolated cells), given the additional interactions between them. Interestingly, cells in a number of tissues take on convex polyhedral shapes, such as truncated octahedrons [1–3]. The observation of these convex polyhedra in cultured lung epithelial tissue and other tissues motivated a comparison with soap bubble arrangements, which then led to the birth of vertex models [4,5]. In vertex models, tissue cells are treated as deformable polyhedrons forming a space-filling packing with some energetic cost to the cellular deformation [6,7]. Indeed, vertex modelling has provided key insights into understanding how cells interact with each other in tissues [8–22]. For instance, a predicted rigidity transition in disordered tissues [12] was discovered during a period of fast tail growth in zebrafish embryos [23,24]. Cells in the mesodermal progenitor zone (MPZ) act as a liquid with cells exchanging neighbours. However, when cells become part of the presomitic mesoderm (PSM), they act more as solids, with a decrease in cell-to-cell contact variations. In vitro tissues have also been shown to exhibit glassy behaviour and superelasticity, with these properties also emerging in vertex models [25–27].

To date, vertex modelling of tissues has focused on polygons or polyhedrons with straight edges (SEs). And yet, there are numerous examples of both plant and animal tissues containing cells with curved edges (CEs) [28–30] (see figure 1). CEs are possible presumably owing to the underlying reorganization of the actomyosin cortex. Moreover, they allow cells to readily increase their surface area/perimeter while maintaining their volume/area. For instance, a study focusing on the rigidity transition in a monolayer of MCF10A cells found that in the control case, the cell–cell interfaces were curved at the subcellular scale [28]. However, when they elevated a regulator of endocytosis, RAB5A, the cell–cell interface became less curved and the cells could more easily pass each other to form a fluid. Intriguingly, RAB5A not only regulates endocytosis by mediating the fusion rate of endosomes with endocytic vesicles, it also triggers lamellipodia formation in fibroblasts and so is involved with actin cytoskeletal reorganization [32]. As lamellipodia are typically broad protrusions involving a branched dendritic network [33,34], the curved interfaces straighten out.

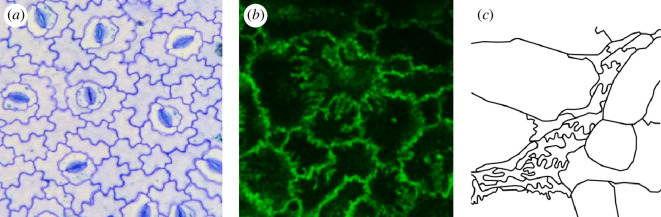
Figure 1.

Curvy cell–cell interfaces in plant and animal cells. (a) Cross-section of a monolayer of plant cells. This is a cropped image originally taken by Karl Az and is licensed under CC BY 4.0 [31]. (b) Cross-section of a monolayer of MCF10A cells with cell–cell interfaces fluorescently labelled in green. (Unpublished image with permission from G. Scita.) (c) Drawing of a cross section of a monolayer of cells in the larval Drosophila dermis during development based on images from [30].

More recently, experiments by Rigato et al. [30] discovered curved cell–cell interfaces in a cell monolayer of the larval Drosophila epidermis. This epidermis is made up of larval epithelial cells and histoblasts. The histoblasts typically cluster in groups of 5–17 cells. These groups are surrounded by larval epithelial cells. The histoblasts begin as SE polyhedrons; however, over time their apical surface actively shrinks, causing their adherens junctions to fold and form a characteristic wavy pattern on the apical surface. As larval epithelial cells expand, histoblasts are forced to adjust their shape to accommodate their own growth within the shrinking space available, inducing a type of folding of the actomyosin cortex with each cell. This dynamic change in histoblast morphology underscores the importance of cell confinement in the larval epidermis, which is presumably at the heart of this remarkable cell shape transformation.

Based on the prevalence of cells in essentially close-packed tissues with curved cell–cell interfaces and the recent study demonstrating a transition from SEs to CEs, we modify the classic version of the two-dimensional vertex model [35–37] to create a version suitable for tissues with curved cell–cell interfaces at the subcellular scale. We do so by replacing a straight line between two vertices with a parametrized curve described by several Fourier coefficients. This approach will allow us to go beyond simple arcs between vertices [38] and does not involve increasing the number of vertices with SEs (shared or not shared between cells) to allow for cell shapes that change convexity [39–41]. We will explore under what conditions straight cell–cell interfaces are energetically favourable and under what conditions curved cell–cell interfaces are energetically favourable. Our exploration will focus on a simple ordered tiling as well as the experimental situation described in the work of Rigato et al. It will yield novel mechanical insights into the multitude of ways cells regulate their shape at the subcellular (or intra-cellular scale) leading to new emergent phenomena at the tissue scale.

2. Model and methodology

While the mechanics of solid-like cellular tissue can be represented by continuous elastic fields at large enough wavelengths [42], here, we consider a cellular-based approach to study the structure of cells as their cell–cell interfaces deviate from straight geometries to curved geometries in the presence of applied stresses. Let us begin with the mechanical energy $E_{\alpha }$ for the $\alpha$ th cell within a cellular packing [8,9,12] with cross-sectional area $A_{\alpha }$ and cross-sectional perimeter $P_{\alpha }$ :

$$E_{\alpha }=K_A{(A_{\alpha }-A_0)}^2+K_P{P}_{\alpha }^2+\gamma P_{\alpha }.$$ (2.1)

The first term captures the cell’s bulk elasticity [43,44] with $K_A$ denoting area stiffness and $A_0$ the target area. The second term in the cell mechanical energy is quadratic in the cell cross-sectional perimeter $P_{\alpha }$ and models the active contractility of the intracellular actomyosin cortex with elastic constant $K_P$ [8]. Finally, the last term represents an interfacial tension $\gamma$ set by a competition between the cortical tension and the energy of cell–cell adhesion [45,46] between two cells in contact. Note that for a single cell, $\gamma$ denotes the surface tension of a cell. For simplicity, we assume that all four parameters— $K_A$ , $A_0$ , $K_P$ and $\gamma$ —are the same for each cell.

The addition of a constant to the mechanical energy, which does not affect the forces, allows one to complete the square to obtain

$$E_{\alpha }=K_A{(A_{\alpha }-A_0)}^2+K_P{(P_{\alpha }-P_0)}^2,$$ (2.2)

with $P_0=-\gamma /(2K_P)$ as the effective target perimeter. This energy can be non-dimensionalized such that

$${\displaystyle ϵ=\frac{1}{K_A{A}_0^2}{E}_{\alpha }={\left(a_{\alpha }-1\right)}^2+\frac{K_P}{\left(K_A{A}_0\right)}{\left(p_{\alpha }-p_0\right)}^2,}$$ (2.3)

where $a_{\alpha }=A_{\alpha }/A_0$ and $p_{\alpha }=P_{\alpha }/\sqrt{A_0}$ are the rescaled shape functions for area and perimeter. Moreover, $p_0=P_0/\sqrt{A_0}$ is the target shape index, a quantity that plays a crucial role in determining the mechanics of tissues in two dimensions. To be specific, a regular hexagon corresponds to $p_0^{hex}=2\sqrt{2}\sqrt[4]{3}\approx 3.72$ and a regular pentagon to $p_0^{pent}=2\sqrt{5}{(5-2\sqrt{5})}^{1/4}\approx 3.81$ . Wavy cell shapes are also expected to have target shape indices larger than the circle as they also deviate from the circle in a manner different from a convex polygon.

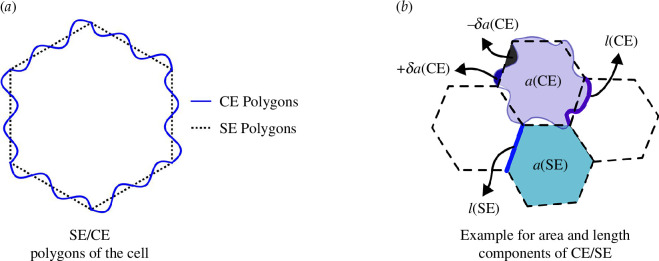
A deformable cell is now described as a combination of a SE polygon and a CE polygon, as shown in figure 2. As the CEs extend the cellular geometry by incorporating a continuous field, which introduces, in principle, infinite degrees of freedom at each edge, in practice, the additional degrees of freedom to capture curvature between two vertices will be constrained in several ways. First, we chose the mathematical expression $c^{(1)}\sin \theta +c^{(2)}\sin 2\theta +c^{(3)}\sin 3\theta +c^{(4)}\sin 4\theta$ to parametrize each CE. In addition to constraining the endpoints to match those of the SE solutions in certain cases, the sinusoidal function more readily ensures that ${\displaystyle \delta a^{\left(\mathrm{C}\mathrm{E}\right)}}$ in figure 2b is zero even if the edge length changes. While this choice is not necessary, it makes it easier to calculate the $c^{(r)}$ ’s. We will address additional constraints below. Also, we exclude overhangs in our formulation for now.

Figure 2.

Representation of SE/CE polygons. (a) A polygon can be constructed with CEs and with SEs. (b) Area and length components can be obtained separately for the CEs and SEs. Note that ${\displaystyle \pm \delta a^{\left(\mathrm{C}\mathrm{E}\right)}}$ represents relative area differences as compared with SE polygons. Signs indicate whether the area was subtracted from, or added to, the area of the SE polygon.

For the CE model, we connect vertex pairs using a parametrized curve within the range $t\in [0,1]$ . The number of polygon vertices is equal to the number of edges for the single cell, so we define coefficients $c_{\alpha ,i}^{(j)}$ to describe the $j$ th coefficient of the cell edge $i$ between vertices $i$ and $i+1$ and for cell $\alpha$ (equivalently, the $k$ th edge of the entire cell array). We now use an index $k$ to represent edges explicitly. The polygon’s area (and perimeter) depends on indices $\alpha$ and $k$ . Given our parametrization, the coordinate for a vertex $i$ associated with a CE $v_k(t)$ and its associated curve $c_k(t)$ in terms of the Cartesian coordinate vector components $(x,y)$ :

$${\displaystyle \begin{array}{rl}{c}_k\left(t\right)=& c_{\alpha ,i}\left(t\right)\\ =& c_{\alpha ,i}^{\left(1\right)}\sin \left(\pi t\right)+c_{\alpha ,i}^{\left(2\right)}\sin \left(2\pi t\right)+c_{\alpha ,i}^{\left(3\right)}\sin \left(3\pi t\right)+c_{\alpha ,i}^{\left(4\right)}\sin \left(4\pi t\right),\end{array}}$$ (2.4)

$$v_k(t)=v_{\alpha ,i}(t)=(f_{\alpha ,i}(t),g_{\alpha ,i}(t)),$$ (2.5)

$${\displaystyle \begin{array}{c}{f}_{\alpha ,i}\left(t\right)=\left(1-t\right)x_{\alpha ,i}+t{x}_{\alpha ,i+1}+\frac{c_{\alpha ,i}\left(t\right)\left(x_{\alpha ,i}+x_{\alpha ,i+1}\right)}{\sqrt{{\left(x_{\alpha ,i}+x_{\alpha ,i+1}\right)}^2+{\left(y_{\alpha ,i}+y_{\alpha ,i+1}\right)}^2}},\end{array}}$$ (2.6)

$${\displaystyle \begin{array}{c}{g}_{\alpha ,i}\left(t\right)=\left(1-t\right)y_{\alpha ,i}+t{y}_{\alpha ,i+1}+\frac{c_{\alpha ,i}\left(t\right)\left(y_{\alpha ,i}+y_{\alpha ,i+1}\right)}{\sqrt{{\left(x_{\alpha ,i}+x_{\alpha ,i+1}\right)}^2+{\left(y_{\alpha ,i}+y_{\alpha ,i+1}\right)}^2}},\end{array}}$$ (2.7)

where the bold type indicates a vector quantity. This parametrization has certain singularities for several specifically angled edges, such as a horizontal line, in which case a different parametrization can be used (see appendix A for a few more details). The SE equivalent for ${\displaystyle {\mathbf{v}}_k^{\left(\mathrm{S}\mathrm{E}\right)}}$ is

$${\displaystyle {\mathbf{v}}_k^{\left(\mathrm{S}\mathrm{E}\right)}\left(t\right)={\mathbf{v}}_{\alpha ,i}^{\left(\mathrm{S}\mathrm{E}\right)}\left(t\right)=\left(f_{\alpha ,i}^{\left(\mathrm{S}\mathrm{E}\right)}\left(t\right),g_{\alpha ,i}^{\left(\mathrm{S}\mathrm{E}\right)}\left(t\right)\right),}$$ (2.8)

$${\displaystyle f_{\alpha ,i}^{\left(\mathrm{S}\mathrm{E}\right)}\left(t\right)=\left(1-t\right)x_{\alpha ,i}+t{x}_{\alpha ,i+1},}$$ (2.9)

$${\displaystyle g_{\alpha ,i}^{\left(\mathrm{S}\mathrm{E}\right)}\left(t\right)=\left(1-t\right)y_{\alpha ,i}+t{y}_{\alpha ,i+1}.}$$ (2.10)

With this information, in addition to computing their perimeter, we can also trivially compute their area by determining the polygon centre, given by the average of the vertex coordinates, and then dividing up the polygon into triangles each with areas ${\displaystyle A_{\alpha ,i}^{\left(\mathrm{S}\mathrm{E}\right)}}$ and whose endpoints consist of the polygon centre and the two vertices $i$ and $i+1$ , or

$${\displaystyle A_{\alpha ,i}^{\left(\mathrm{S}\mathrm{E}\right)}=\frac{1}{2!}\left|\begin{array}{ccc}{x}_{\alpha ,i}& y_{\alpha ,i}& 1\\ x_{\alpha ,i+1}& y_{\alpha ,i+1}& 1\\ x_{\alpha ,c}& y_{\alpha ,c}& 1\end{array}\right|,}$$ (2.11)

where vertical lines indicate the determinant. The total polygon area is the sum of such triangular areas.

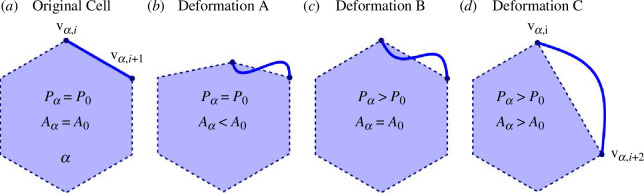
A similar approach to compute the cell area for the CE model can be performed using the parametrization for each CE in a polygon. However, there are several possibilities now that the Euclidean distance between vertices and the edge length, or contour length, between vertices can be different. In figure 3, deformation type A denotes cell side contraction where initial side lengths are maintained but the Euclidean distance of pairs $(i,i+1)$ is reduced. In other words, the area of the cell decreases while its perimeter remains the same. Deformation type B refers to the elongation of cell edges while maintaining the same Euclidean distance between pairs $(i,i+1)$ , or the cell area remaining fixed while its perimeter increases. Deformation type C results in the cell perimeter increasing while the area decreases, as shown in figure 3, as the junction angle at a vertex flattens. For the time being, we will not explore in detail the subcellular mechanisms driving these shape changes other than to state that deformation type B change, for example, could be induced by radially oriented microtubules or localized branched actin structures [34,47]. Moreover, the retraction of microtubules lead to an increase in acto-myosin cortex contraction, observed in individual migrating cells, which may lead to deformation type A [48]. In any event, subcellular curvature may arise from different biophysical mechanisms that involve both internal and external forces.

Figure 3.

Potential types of deformations in the CE model. (a) Original cell shape. (b) Deformation type A (perimeter preserved): initial side lengths are conserved while the Euclidean distance of pairs $(i,i+1)$ decreases. (c) Deformation type B (area conserved): side lengths are increased while the Euclidean distance of pairs $(i,i+1)$ is conserved. (d) One of the possible cases in deformation type C (vertex removed: the junction angle between a line $(v_i,v_{i+1})$ and $(v_{i+1},v_{i+2})$ becomes zero while the sum of initial side length of pairs $(i,i+1)$ and $(i+1,i+2)$ is conserved (a point $v_{i+1}$ is hidden inside of the straight line)).

To compute the area under each parameterized curve to find the total area of the cell, we find the areas deviating from the SE model, keeping track of signs and add them to the SE polygon area. The sign of area segments is positive when a curve segment is located outside the SE polygon version and negative when the curve segment is located inside (see figure 2b ). Specifically, the deviation in area $\delta a_{\alpha }$ for polygon $\alpha$ , for a Euclidean distance between two vertices denoted by $d$ and index $j$ denoting breaking up each CE into subsections, is given by

$${\displaystyle {\displaystyle \delta a_{\alpha }^{\left(\mathrm{C}\mathrm{E}\right)}=\sum _{j}dt\cdot \{\begin{array}{l}\begin{array}{cc}d\left({\mathbf{v}}_{\alpha ,i}\left(j\cdot dt\right),{\mathbf{v}}_{\alpha ,i}^{\left(\mathrm{S}\mathrm{E}\right)}\left(j\cdot dt\right)\right)& \text{(outside)}\\ -d\left({\mathbf{v}}_{\alpha ,i}\left(j\cdot dt\right),{\mathbf{v}}_{\alpha ,i}^{\left(\mathrm{S}\mathrm{E}\right)}\left(j\cdot dt\right)\right)& \text{(inside)}\text{.}\end{array}\end{array}}}$$ (2.12)

For lengths of shared edges between cells $\alpha$ and $\beta$ and corresponding $(i,i+1)$ and $(i^{\prime },i^{\prime }+1)$ vertex pairs,

$${\displaystyle {\displaystyle l_k^{(\mathrm{C}\mathrm{E})}=\begin{array}{l}\{\begin{array}{ll}\sum _{j}d({\mathbf{v}}_{\alpha ,i}(j\cdot dt),{\mathbf{v}}_{\alpha ,i}(j+1\cdot dt))& \text{(for cell }\alpha )\\ \sum _{j}d({\mathbf{v}}_{\beta ,i^{\mathrm{\prime }}}(j\cdot dt),{\mathbf{v}}_{\beta ,i^{\mathrm{\prime }}}(j+1\cdot dt))& \text{(for cell }\beta ).\end{array}\end{array}}}$$ (2.13)

The result for $v_{\alpha ,i}=v_{\beta ,i^{\prime }},v_{\alpha ,i+1}=v_{\beta ,i^{\prime }+1}$ is identical for either choice. Thus, we will simply note above as

$${\displaystyle {\displaystyle l_k^{\left(\mathrm{C}\mathrm{E}\right)}=\sum _{j}d\left({\mathbf{v}}_k\left(j\cdot dt\right),{\mathbf{v}}_k\left(j+1\cdot dt\right)\right).}}$$ (2.14)

To numerically determine $dt$ we set substantive deviations of $c^{(1)}=c^{(2)}=c^{(3)}=c^{(4)}=0.05$ and adopted $dt=\frac{1}{40}$ to balance computational speed with precision up to two decimal places to compute cell areas and perimeters. Smaller $dt$ s will yield higher precision results.

We also impose additional soft constraints on both the SE and CE models with the additional resistance contributions to the energy of each cell. For instance, we impose a vertex resistance energy function in which vertex positions are quadratically penalized to deviate from some target position as controlled by coefficient ${\displaystyle K_R}$ and summed over vertices $i$ . Such energy contributions model the friction of the epithelium on a substrate, which can be either organic or inorganic, and represents the third dimension of space discarded in our two-dimensional approach. In in vitro experiments, the substrate can be rigid or soft, while in in vivo experiments, the substrate is the extracellular matrix attached to the cell monolayer [30,49]. The quadratic choice is inspired by the Winkler model [50], which is very popular in solid mechanics because of its simplicity (the links are represented by a collection of springs), although more sophisticated extensions have been proposed. Therefore, the SE energy function takes the form: ${\displaystyle E^{\left(\mathrm{S}\mathrm{E}\right)}={\mathcal{A}}^{\left(\mathrm{S}\mathrm{E}\right)}+{\mathcal{P}}^{\left(\mathrm{S}\mathrm{E}\right)}+{\mathcal{R}}^{\left(\mathrm{S}\mathrm{E}\right)}}$ .

For models with continuously CEs, and as mentioned previously, there is a vertex resistance energy function enforcing fixed positions for two endpoints of a CE by quadratically penalizing deviations from target positions and controlled by coefficient $K_{R1}$ . An edge curvature resistance function ( ${\displaystyle {\mathcal{R}}_2}$ ) exists as well by quadratically penalizing too large deviations from target coefficients in the sinusoidal harmonics defining the curves, and summed over edges $k$ and harmonics $j$ to assist with the minimization process. Note that ${\mathcal{R}}_2$ can be considered as a measure of the wall stiffness since large values limit their distortion. Formally, the CE model energy function takes the form: ${\displaystyle E^{\left(\mathrm{C}\mathrm{E}\right)}={\mathcal{A}}^{\left(\mathrm{C}\mathrm{E}\right)}+{\mathcal{P}}^{\left(\mathrm{C}\mathrm{E}\right)}+{\mathcal{R}}^{\left(\mathrm{C}\mathrm{E}\right)}\text{with}{\mathcal{R}}^{\left(\mathrm{C}\mathrm{E}\right)}={\mathcal{R}}_1^{\left(\mathrm{C}\mathrm{E}\right)}+{\mathcal{R}}_2^{\left(\mathrm{C}\mathrm{E}\right)}}$ .

While both models share similar energy components, the resistance term ( ${\displaystyle \mathcal{R}}$ ) in the SE model addresses two potential scenarios. The first is vertex displacement resistance, which penalizes quadratic deviations of vertex positions owing to friction of the substrate. For the CE model, we represent the CEs using sinusoidal harmonics with four coefficients ( $c^{(j)}$ ). In our analysis, we set small initial values for these coefficients (e.g. $c^{(j)}=0.01$ ) using the ${\displaystyle {\mathcal{R}}_2^{\left(CE\right)}}$ function with small $K_{R2}$ . The target Fourier coefficients are empirically chosen to constrain the amount of curvature along the cell–cell interface to more readily find local minima. Indeed, there are physical constraints on the curvature owing to the structure of the cytoskeleton and its ability to form filopodia and lamellipodia. Since our model does not contain detailed information about cytoskeleton organization in terms of lamelipodia and filopodia, we make empirical choices for the target values of the Fourier coefficients and study the sensitivity of the results of such choices.

With fixed positions for SE cells, the CE model involves four more unknowns (harmonic coefficients) per CE or more degrees of freedom. To ensure solution convergence with these additional degrees of freedom, we use the ${\displaystyle \mathcal{R}}$ function as an additional constraint. We have also studied how strongly the energy minimized solutions depend on these additional energy contributions (see appendix A for more discussion on the relationship between degrees of freedom and constraints). If we assume that we have $2V$ number of unknowns for position vectors and $4E$ unknowns for curvy edge functions for $V$ number of vertices and $E$ number of edges, by adding the resistance function ${\displaystyle {\mathcal{R}}_1=\frac{1}{2}{K}_{R1}\cdot \sum _i\left({\left(x_i-x_i\left(0\right)\right)}^2+{\left(y_i-y_i\left(0\right)\right)}^2\right)}$ and ${\displaystyle {\mathcal{R}}_2=K_{R2}\cdot \sum _i{\left(c_i-c_t\right)}^2}$ , we introduce an equal number of constraints to the system, which stabilizes the simulation.

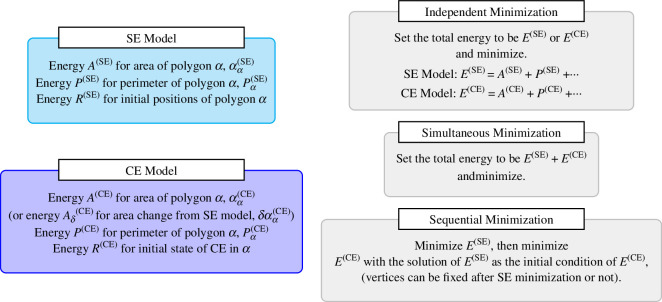
Finally, in terms of the energy minimization procedure, as elaborated on in figure 4, we illustrate our scheme for evaluating the energy using polygons with SEs and polygons with CEs. We may first minimize the SE model and then the CE model. Alternatively, we can also minimize the two models simultaneously.

Figure 4.

Computational methods for evaluating cell shapes from given energies. Either SE model, CE model, or SE + CE model can be taken for analysis and, based on the problem at hand, optimization can be performed once or separately.

3. Properties of the curved edge model

One measure characterizing cell shape is the cell shape index $p$ , or its dimensionless perimeter. We now compare minimal energy solutions for both SE solutions and CE solutions for single cells and for ordered multi-cellular tilings, focusing on regular, hexagonal cells for simplicity.

3.1. Transition from convex to non-convex for a single cell

As the target shape index is typically a parameter of interest, we begin with a regular hexagon and then increase the target shape index and look for minimal-energy states. For a regular hexagon, the cell shape index $p_{\alpha }$ (with $a_{\alpha }=1$ ) is as follows:

$${\displaystyle p_{\alpha }=\frac{6l^{\left(\mathrm{C}\mathrm{E}\right)}}{\sqrt{6a^{\left(\mathrm{C}\mathrm{E}\right)}}}=\frac{\sqrt{6}{l}^{\left(\mathrm{C}\mathrm{E}\right)}}{\sqrt{a^{\left(\mathrm{C}\mathrm{E}\right)}}}=\sqrt{6}{p}^{\left(\mathrm{C}\mathrm{E}\right)},}$$ (3.1)

where ${\displaystyle l^{\left(\mathrm{C}\mathrm{E}\right)}}$ and ${\displaystyle a^{\left(\mathrm{C}\mathrm{E}\right)}}$ represent the side length and area of one of the six wedges in the CE model. We also consider the energy function from equation (2.3) with $a_{\alpha }=1$ (equivalently, the area term is negligible). Thus, the energy takes the form:

$${\displaystyle \begin{array}{c}E\left(p\right)=K_{SI}{\left(\sqrt{6}{p}^{\left(\mathrm{C}\mathrm{E}\right)}-p_0\right)}^2\\ =K_{SI}{\left(\frac{\sqrt{6}\cdot l^{\left(\mathrm{C}\mathrm{E}\right)}}{\sqrt{\frac{\sqrt{3}}{4}+\delta a^{\left(\mathrm{C}\mathrm{E}\right)}}}-p_0\right)}^2,\end{array}}$$ (3.2)

where $K_{SI}=\frac{K_P}{(K_A{A}_0)}$ , ${\displaystyle l^{\left(\mathrm{C}\mathrm{E}\right)}}$ is the arc length of a wedge, ${\displaystyle \delta a^{\left(\mathrm{C}\mathrm{E}\right)}}$ is the area between the CE and the SE (as shown in figure 2b ), and $p_0$ represents the target shape index.

In figure 5, we show the results of minimizing ${\displaystyle min\left(E\left(p\right)+{\mathcal{R}}_2^{\left(\mathrm{C}\mathrm{E}\right)}\right)}$ with $K_{SI}=10$ , $K_{R2}=0.001$ and each target Fourier coefficient $c_t$ for $K_{R2}\cdot {\displaystyle {\sum }_i{(c_i-c_t)}^2}$ is given by $c_t=0.01$ in ${\displaystyle {\mathcal{R}}_2^{\left(\mathrm{C}\mathrm{E}\right)}}$ . Note that we also fix the vertices in the CE minimization to preserve the six-fold symmetry. To test the robustness of our results, we vary $K_{R2}$ from $0.001$ to $0.1$ , as well as vary $c_t$ , to show that there are predominantly changes in the third decimal place for the cell shape index as indicated in table 1. As we increase the target cell shape index, the cells transition from convex to non-convex shapes. Such a transition does not occur in the SE model for a hexagon. Note that the convex–non-convex transition occurs slightly below the shape index of a regular hexagon (with unit area). As $K_{R2}\to 0$ , this transition takes place at the regular hexagon. However, again, for some range of $K_{R2}$ , the solutions are robust. Moreover, for convex, regular polygons, as the shape index increases, the number of edges decreases with the triangle being the minimal number of edges (see table 2). With a CE model, to increase their shape index, regular shapes can either decrease the number of edges or transition to non-convex shapes to increase their shape index. Of course, cells can also become irregular to increase their shape index as will be discussed in the next subsection.

Figure 5.

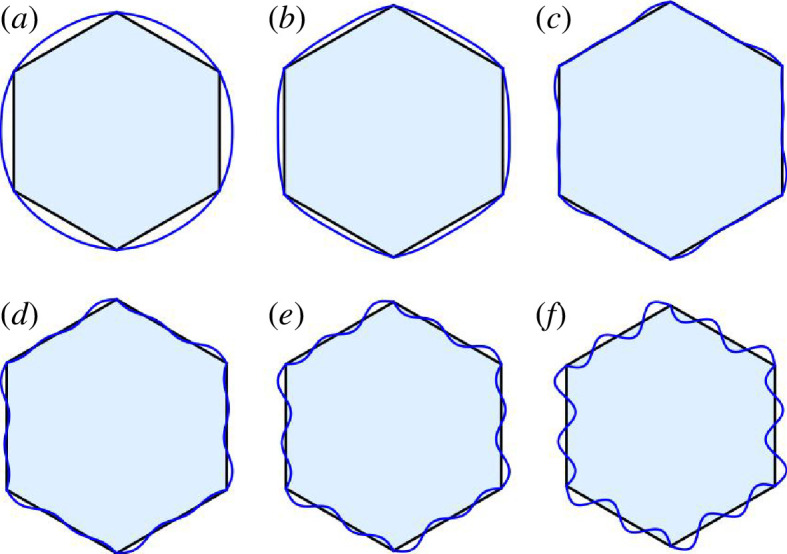
Different shape indices of CE cells were simulated and compared with a regular hexagon. The target shape index of each shape is (a) 3.55, (b) 3.6, (c) $\frac{2\sqrt{6}}{3^{1/4}}\simeq 3.72$ , (d) 3.8, (e) 4 and (f) 4.5.

Table 1.

Measured shape index $p_{\alpha }$ with different coefficients (equation (3.2) with ${\displaystyle p_{\alpha }=\sqrt{6}{p}^{\left(\mathrm{C}\mathrm{E}\right)},p_0=3.55}$ ).

( $K_{SI}=10$ )	$c_t=0.01$	$c_t=0.02$	$c_t=0.03$	$c_t=0.04$	$c_t=0.05$
$K_{R2}=0.001$	3.54995	3.55003	3.55002	3.55002	3.55002
$K_{R2}=0.01$	3.55027	3.55024	3.55022	3.55020	3.55019
$K_{R2}=0.1$	3.55216	3.55199	3.55183	3.55170	3.55158

Table 2.

Shape index.

	circle	decagon	octagon	hexagon	square	triangle
number of edges	–	12	8	6	4	3
shape index	3.54491	3.58630	3.64072	3.72242	4	4.55901

3.2. Expansion of the zero-energy solution space

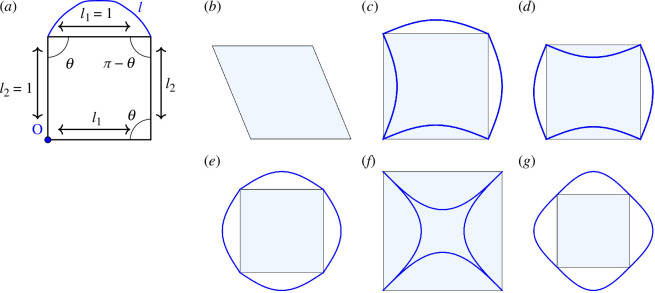
Using the energy functional in equation (2.3) for a single cell, it has been shown that there exists a compatibility–incompatibility transition as the target shape index increases where the shapes eventually become zero-energy solutions, i.e. their shapes are compatible with the energy [22]. For instance, for six-sided polygons, the location of the transition occurs at the target shape index of the regular hexagon. This analysis has been recently extended to three dimensions to also demonstrate such a transition [51]. For the CE model, its additional degrees of freedom thus allow for greater compatibility and, therefore, an expansion of the zero-energy solution space. To more concretely illustrate this point, we will focus on a simplified model using a single sine curve, i.e. $c_2=c_3=c_4=0$ . This example, depicted in figure 6, captures the essence of CE behaviour while remaining tractable for calculations. For the SE model, the compatibility–incompatibility transition occurs at $p_0=4$ .

Figure 6.

A simple rectangular cell model. Different representations of cells with the same shape index $p_{\alpha }\simeq 4.17$ (a–d) as well as limits on the shape index (e–g) for the regular case. (a) The model can be described with two different edge lengths $l_1,l_2$ and an angle $\theta$ . (b–d) Different representations of cells with the same shape index $p_{\alpha }\simeq 4.17$ : (b) $\theta =\frac{1.5\pi }{4}$ , (c,d) $\theta =\frac{\pi }{2},c_1=0.132$ for two edges ( $c_1=-0.132$ for the other two edges). (e,f) Limits on the shape index for the regular model. (e) The minimum shape index with $c_1=0.213$ , (f) the maximum perimeter based on the square with $c_1=-0.32$ , and (g) the convex counterpart of (f).

Using a single sinusoid parametrized by the coefficient $c_1$ , we can describe points along a CE:

$$(x,y)=(f(t),g(t))\text{for }t\in [0,1],$$ (3.3)

$$f(t)=t,$$ (3.4)

$$g(t)=c_1\sin \pi t.$$ (3.5)

We can also compute the edge length of CE component by $l$ :

$${\displaystyle \begin{array}{c}l=\int \sqrt{f^{\mathrm{\prime }}{\left(t\right)}^2+g^{\mathrm{\prime }}{\left(t\right)}^2}dt={\int }_0^1\sqrt{1+c_1^2{\pi }^2\cos \pi t^2}dt\\ =\sqrt{1+c_1^2{\pi }^2}{\int }_0^1\sqrt{1-\frac{c_1^2{\pi }^2}{1+c_1^2{\pi }^2}\sin \pi t^2}dt=2\frac{\sqrt{1+c_1^2{\pi }^2}}{\pi }E\left(\frac{c_1^2{\pi }^2}{1+c_1^2{\pi }^2}\right).\end{array}}$$ (3.6)

This allows us to compute the side length of the curved segment using an integral expression equation (3.6), which involves the complete elliptic integral of the second kind. Assuming equal side lengths for the edges and focusing solely on angle changes, the perimeter is directly proportional to the side length. Interestingly, if we fix the area to $1$ , both the perimeter and the shape index increase as we adjust the amplitude of the sine function (represented by $c_1$ ).

If we consider the area of the SE polygon as ${\displaystyle a^{\left(\mathrm{S}\mathrm{E}\right)}}$ , then we obtain

$${\displaystyle a^{\left(\mathrm{S}\mathrm{E}\right)}=l_1{l}_2\sin \theta .}$$ (3.7)

The fixed perimeter of $2l_1+2l_2=4$ allows for calculation of the desired angle using the shape index. For the SE polygon case, there are two solutions when $\theta \ne \frac{\pi }{2}$ , and a single solution when $\theta =\frac{\pi }{2}$ . Varying the values of $l_1$ and $l_2$ can yield additional solutions, but a single representation (up to global rotations) for $\theta =\frac{\pi }{2}$ remains when $l_1$ and $l_2$ are known. The CE approach offers a larger range of shapes when changing the shape index of a square ( $\theta =\frac{\pi }{2}$ ) as compared with the SE case, where the shape index and angle are determined by a fixed perimeter. Figure 6b–d showcases this range, demonstrating different CE representations for squares with the same shape index $p_{\alpha }\simeq 4.17$ . Thus, the zero-energy solution space is now higher dimensional as it now depends on $c_1$ as well.

With the CEs, the compatible–incompatible transition for a single cell now occurs near the shape index of the circle (relaxing the tiling condition, though one can consider cells of different concavities in a tiling), which is $c_1=0.213$ with $p_{\alpha }=3.55562$ , as shown in figure 6e . We can also consider the limit of the CE model from regular SE-based vertex coordinates for this four-sided polygon when $\theta =\frac{\pi }{4}$ , that is, when the edges potentially overlap with minimum area. If we use a single sine function, we have $c_1=0.32$ with shape index $11.32360$ as the limit, which can be seen in figure 6f . From its convex counterpart in figure 6g , i.e. rearranging curves to be outside the polygon, we can easily see that the extremum occurs closest to the shape of the extended square. Thus, the compatibility–incompatibility transition point no longer occurs at $p_0=4$ but at a shape index much closer to the circle.

3.3. A tiling of hexagonal shapes

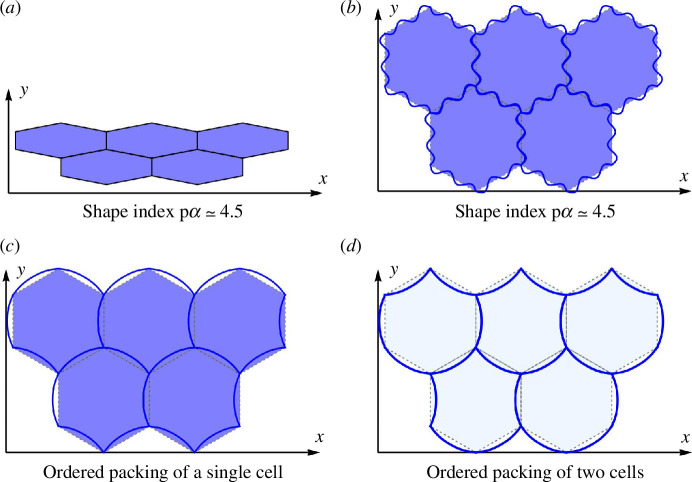
Consider a tiling of ordered polygons as shown in figure 7a . Here, we have focused on a specific change for a given deformation, which is one of many possible shape changes, at least in the compatible regime. The polygons indeed remain hexagonal, though their shape index has increased as the polygons have become irregular with the distances between some vertices decreasing and between other vertices increasing (and the area remaining fixed). However, suppose there is a change in shape index resulting from the stretching of the edges while maintaining the total area without an overall anisotropy developing, as shown in figure 7b . To do so in the SE model becomes complicated, requiring additional vertices on the edges to capture the CEs, but not with the CE model.

Figure 7.

Tiling of SE and CE shapes for the same shape index and example of circular tiling. (a) Hexagonal cell array with shape index $p_{\alpha }\simeq 4.5$ . (b) CE model with six-fold symmetry with $p_{\alpha }\simeq 4.5$ . (c) Three edges are concave and others are convex in orientation relative to the hexagon. The shape index of this cell is $p_{\alpha }=3.89811$ . (d) Two different cells so that, on average, three edges are concave and others are convex with $p_{\alpha }=3.83190$ and $3.9679$ .

We can also create an ordered array of cells with two different shape indices from a single-ordered SE cell array. Motivated by circular cross-sectional cell shapes in the mouse ear epidermis [38], consider the case of a circular-edged tile emerging from a regular hexagonal array, as shown in figure 7c,d . As the area of individual cells decreases owing to the CEs, their opposite edges morph into concave shapes. Interestingly, despite these variations, the average cell area for this circular arrangement approaches that of the original hexagon. From equation (3.2), we have

$${\displaystyle p_{\alpha }=\sqrt{6}{p}^{\left(\mathrm{C}\mathrm{E}\right)}=\frac{6\cdot l^{\left(\mathrm{C}\mathrm{E}\right)}}{\sqrt{6\cdot a^{\left(\mathrm{C}\mathrm{E}\right)}}}=\frac{\sqrt{6}\cdot l^{\left(\mathrm{C}\mathrm{E}\right)}}{\sqrt{\frac{\sqrt{3}}{4}+\delta a^{\left(\mathrm{C}\mathrm{E}\right)}}}.}$$ (3.8)

While each cell retains the identical perimeter of $2\pi$ (based on the initial hexagonal array with radius $r=1$ ), their areas differ slightly owing to the CEs. We quantify this difference with ${\displaystyle \pm 6\delta a^{\left(\mathrm{C}\mathrm{E}\right)}}$ , where ${\displaystyle \delta a^{\left(\mathrm{C}\mathrm{E}\right)}}$ represents the area beneath a single-curved segment. For a circle with a target shape index of $p_{\alpha }=3.54491$ as in figure 5a , applying the shape index equations with ${\displaystyle l^{\left(\mathrm{C}\mathrm{E}\right)}=\frac{2\pi }{6}}$ ( $\frac{1}{6}$ times perimeter of the unit circle) yields a required ${\displaystyle \delta a^{\left(\mathrm{C}\mathrm{E}\right)}}$ of approximately $0.09059$ .

While neighbouring cells in this circular pattern can adopt different shape indices based on their CE orientations, as illustrated by comparing figure 5a,b , this freedom ultimately results in a slightly higher average shape index for the entire circular array compared with the hexagonal tiling. This occurs even though the area remains the same, because the increased perimeter of the circular array outweighs the unchanged area in terms of affecting the shape index calculation. However, while the SE solution has the lower energy in this case, it may not be compatible with the symmetry and/or boundary conditions of the system at hand. More generally, energetically preferred shapes depend on the relative weight of the area and perimeter terms in the energy equation (2.3). To be concrete, consider a unit circle and a regular hexagon of unit edge length with the desired shape of a circle:

$${\displaystyle e_{\alpha }={\left(a_{\alpha }-1\right)}^2+K_{SI}{\left(p_{\alpha }-\frac{2\pi }{\sqrt{\pi }}\right)}^2.}$$ (3.9)

For the regular hexagon, this becomes

$${\displaystyle e_{\text{hex}}={\left(\frac{3\sqrt{3}}{2\pi }-1\right)}^2+K_{SI}{\left(\frac{6}{\sqrt{\pi }}-\frac{2\pi }{\sqrt{\pi }}\right)}^2.}$$ (3.10)

Figure 7c has the same area term as the hexagon, but a different perimeter term:

$${\displaystyle e_{\text{8(c)}}={\left(\frac{3\sqrt{3}}{2\pi }-1\right)}^2+K_{SI}{\left(\frac{2\pi }{\sqrt{\pi }}-\frac{2\pi }{\sqrt{\pi }}\right)}^2.}$$ (3.11)

Figure 7d has a slightly modified area term depending on the cell type (represented by $\pm$ ):

$${\displaystyle e_{\text{8(d)}}={\left(\frac{\frac{3\sqrt{3}}{2}\pm 0.09059}{\pi }-1\right)}^2+K_{SI}{\left(\frac{2\pi }{\sqrt{\pi }}-\frac{2\pi }{\sqrt{\pi }}\right)}^2.}$$ (3.12)

While the dimensionless energy $e_{\alpha }$ ultimately depends on the specific values of $K_{SI}$ for the hexagonal case, the dimensionless perimeter term from ${(P_{\alpha }-2\pi )}^2\frac{1}{\pi }={(p_{\alpha }-\frac{2\pi }{\sqrt{\pi }})}^2$ vanishes for figure 7c,d , which can make the shapes shown in figure 7c the energetically favourable choice.

4. Multicellular response to applied stresses

For the first case, we will consider a line of cells in the presence of applied, anisotropic stress. In the second case, inspired by recent experiments [30], we will explore how a group of cells can be compressed by surrounding cells. We study this latter phenomenon in both ‘ordered’ and ‘disordered’ scenarios.

4.1. Curved edges induced by anisotropic stress

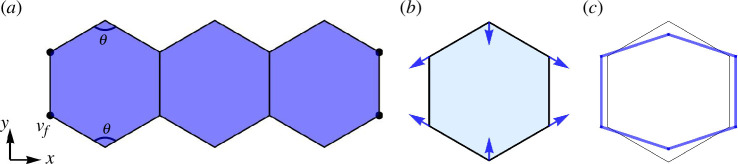
Imagine a line of cells under ‘anisotropic’ stress, meaning that each cell experiences pressure from different directions with different intensities. This non-uniform force field may cause ‘stress-induced subcellular buckling’, depending on the boundary conditions. As depicted in figure 8b,c , each cell in the line experiences a unique stress pattern that mimics local anisotropic forces but does not perfectly mimic stretching [53]. As shown in figure 8, we have developed a simple energy function that adjusts the top and bottom angles of a hexagon to induce the transformation from a hexagon into a rectangle and vice versa. This transformation includes a change in the length of corresponding edges (see figure 8c ):

Figure 8.

A basic model for evaluating local deformations under anisotropic stress. Let $v_f$ denote the fixed vertices at the end of the hexagonal cell array, marked by black-coloured points. The angle $\theta$ indicates the top/bottom angles that can convert hexagonal cells into rectangular shapes. The hexagon is changing its angle owing to a uniform anisotropic stress [52]. Blue arrows in (b) represent the forces applied at each vertex. The blue hexagon in (c) illustrates the change in shape in response to the applied stress.

$${\displaystyle {\displaystyle {\epsilon }_{\theta }=\frac{K_T}{2}\sum _{\alpha }{\left({\theta }_{\alpha }-{\theta }_t\right)}^2,}}$$ (4.1)

with $\theta$ as denoted in figure 8a . To drive the cell shape change from hexagon to rectangle, we minimized the top and bottom angles of each hexagon, as opposed to all angles, as our chosen target angle ( ${\theta }_t=\pi$ ) induces changes in all angles of the polygons given the other energetic contributions. To study the stress-induced deformations, we implemented independent optimizations for the SE and CE models.

The energy function for both models is given by ${\displaystyle E={\epsilon }_{\theta }+\mathcal{A}+\mathcal{P}+\mathcal{R}}$ , parametrized by ${\theta }_t$ , $A_0$ , $P_0$ , $x_t$ and $y_t$ , directed both SE and CE simulations. While $A_0$ , $x_t$ and $y_t$ correspond to those of a regular hexagon, $P_0$ took non-uniform values between $6$ and $6.24$ (see table 3) with shape index to be $3.79549$ in figure 9a and $3.75973$ in figure 9b on average, except for two half-hexagonal boundary cells in figure 9b . This range of $P_0$ is used to help induce global buckling. Also note that we have fixed boundary vertices and boundary cell walls. Control parameters are identical for both models: $K_T=2$ , $K_A=1$ , $K_P=3$ (or $K_A^{\prime }=1$ , $K_P^{\prime }=3$ ) and $K_{R1}=1$ . The resistance vertex function is implemented to prevent vertex flipping. In the CE model, we used additional parameters, $K_{R2}=0.01$ and $c_t=0.05$ .

Table 3.

Average shape index of individual cells (from the equation $p_{\alpha }=\frac{P_{\alpha }}{\sqrt{A_{\alpha }}}$ ).

	$p_0$	$p_{\alpha }$ of SE models	$p_{\alpha }$ of CE models
single row cell array (figure 9c )	3.79549	4.35291	3.81628
double row cell array (figure 9d )	3.75973	4.11177	3.92456

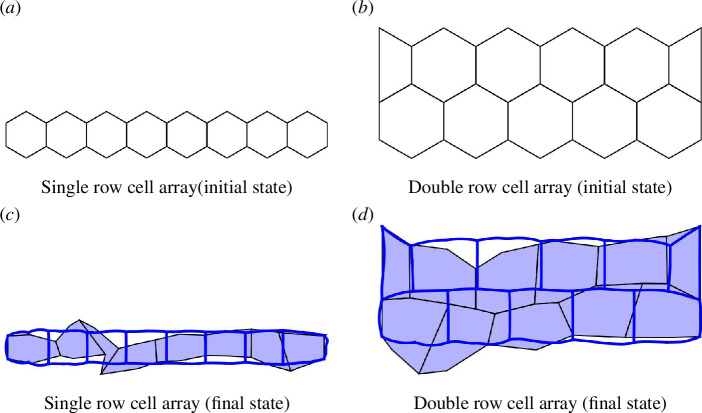
Figure 9.

Subcellular buckling simulation of single and double array cells for a fixed boundary. (a,b) Initial cell shape, (c,d) blue lines represent cells with CEs and light blue shaded cells represent cells with SEs.

Examining figure 9c,d , we observe a notable difference in chain shape. The curved model shows a less deformed chain shape to reach the target angle of ${\theta }_t=\pi$ globally as compared with the SE model. This configuration is owing to the increased degrees of freedom provided by the CEs. These added degrees of freedom allow the cells to energetically conform to the desired ${\theta }_t=\pi$ with smaller deformations at larger length scales over multiple cells such that subcellular buckling emerges as opposed to multicellular buckling.

Beyond the impact of CEs, confinement plays a crucial role in shaping cell morphology. The availability of space at the top and bottom can introduce distinct constraints, even within the same model. For example, comparing figure 9c,d , we see that the restructuring of the cells occurs in double arrays to satisfy ${\theta }_t=\pi$ , going beyond top/bottom flattening. This suggests that cells in confined spaces adapt their arrangements to meet target conditions, highlighting the interplay between shape flexibility and confinement. Furthermore, the CE model is expected to have lower energy costs associated with shape changes owing to its proximity to the target shape index of $3.79549$ (figure 9a ) and $3.75973$ (figure 9b ). We note that owing to the two boundary tetragonal cells in figure 9b , there is a slight increase in the shape index compared with the hexagonal one for figure 9d . Without these two cells, we obtain $p_{\alpha }=4.04877$ and $3.81244$ for the SE and CE models in figure 9d .

4.2. Compression-induced curved edges

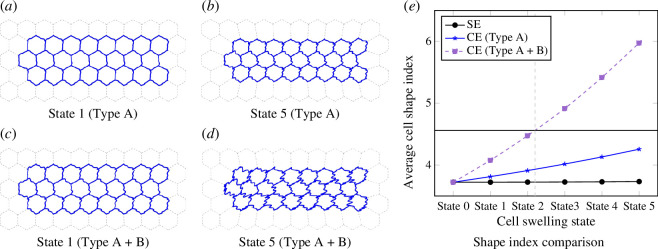
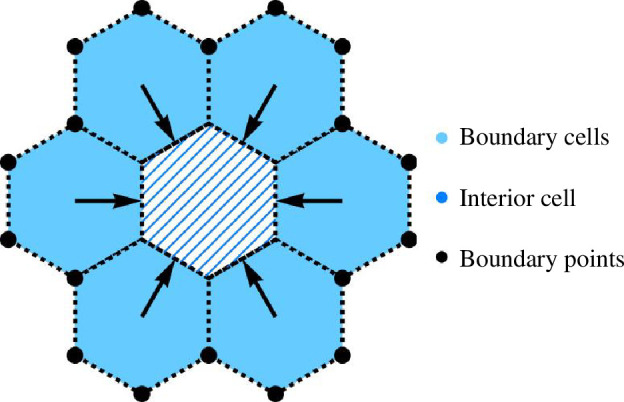
We now focus on the compression of a group of cells in both disordered and ordered scenarios surrounded by boundary cells. For the ordered case, we modified the target parameters in a way that mimics the swelling of boundary cells [54]. This mechanism uses vertex position data from the previous minimized state to evaluate and determine the next minimized state. Figure 10 shows the cell array used in the simulations. Details are provided in appendix A. For both the ordered and disordered cases, we use a simultaneous optimization approach. We define constraints governing the relative increase or decrease in area and perimeter compared with the initial state (figure 1c ; refer also to figure 11). Simulations were conducted using Mathematica software [55], specifically employing the NMinimize function for optimization.

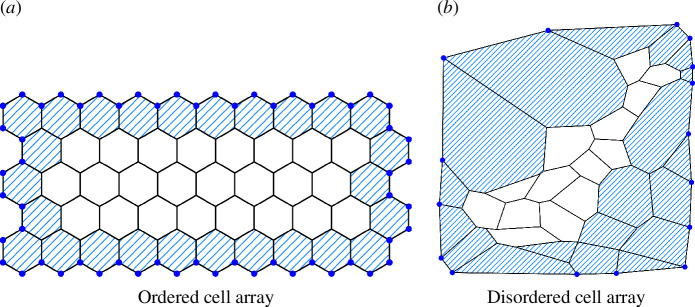
Figure 10.

Ordered/disordered cell array used in the simulations. Interior cells are painted white, while boundary cells are represented by blue diagonal stripes. For the ordered (a) scenario, we conduct simulations on 24 interior cell arrays to investigate subcellular buckling caused by compression by the boundary cells. In the case of disordered cell array in (b), we used a graph inspired by experiments reported in [30] (see figure 11).

Figure 11.

(a–c) Extracted from the experimental data of Rigato et al. (d–f) Disordered cell simulation results. (a) SE cell vertex model for (b). (b,c) Drawings from fig. 1a in [30]. (d) Cell ID of each polygon. (e,f) Simulation results of state 0,3 using the parameters listed in table 4.

4.2.1. Ordered case

To study the ordered system under compression by a group of surrounding cells that are swelling, we

1. increase the target boundary cell area by 5%

2. decrease the target boundary cell perimeter by 5%.

These percentage changes are similar to the disordered case, which is directly relevant to experiments [30]. States 1–5 refer to this increase in area/decrease in perimeter for each consecutive step. The ordered simulation evaluates two different subcellular buckling mechanisms in terms of deformation types A and B. In deformation type A, again, we imagine a cell contracting while maintaining its edge length, resulting in the curved edge length remaining the same as the initial edge length, but the straight edge length becoming smaller. On the other hand, deformation type B involves stretching the side length while maintaining the distance from vertex to vertex, so the straight edge length remains the same while the curved edge length increases.

1. Deformation type A (figure 3b )

   • —Cells maintain their initial edge length while contracting their area.
   • —Shape index remains relatively stable, indicating that the SE behaviour is energetically favourable.

2. Deformation type A + B (figure 3b,c )

   • —Side length increases to approximately 1.4 during cell contraction, mirroring the disordered case.
   • —Significant rise in shape index, suggesting a transition towards CE behaviour.

Note the combination of deformation type A + B is not equivalent to deformation type C, the latter of which does not conserve the number of vertices.

Our simulations show that both area contraction and perimeter expansion are necessary for curved edge morphologies. The transition from SE to CE behaviour, as observed in deformation type A + B, begins at state 2 when the SE shape index limit ( $p_{\alpha }~4.56$ for regular triangles) is used as the transition point, which is represented in figure 11e . See appendix A for more simulation details.

Figure 12.

Simulation results and shape index comparison for an ordered collection of cells. In (a–c) the cell edges show wavy shapes and the cell shape indices are less than $p_{\alpha }~4.56$ , still not significant compared with (d) where the cell shape index is greater than $p_{\alpha }~4.56$ . (e) The black horizontal line represents shape index of the regular triangle. A transition point $p_{\alpha }~4.56$ is represented by the dashed grey vertical line.

4.2.2. Disordered cell simulation

As mentioned previously, in development, larval epithelial cells and histoblasts compete for limited space on the growing larval body surface (even in the absence of cell division) [30]. Histoblasts undergo a remarkable morphological transformation from convex polygons into cells with CEs, as shown in figure 12a–c , as surrounding larval epithelial cells swell to compress the histoblasts. Our simulation focuses on the two-dimensional aspects of this process, where readily available information on cell area and perimeter allows one to analyse the shape changes observed in the experiments. Given the lack of specific data for individual boundary and histoblasts, we selected parameters by comparing figures from [30] and opted for a smaller value for the scaling factor ( $s$ ) than the reported average given sample-to-sample fluctuations. table 4 details the chosen conditions and parameter values for this disordered case.

Table 4.

Disordered cell constraints.

	state 0	state 1	state 2	state 3
Bd. SE area	$s_a^{(SE)}=1$	$1.01$	$1.02$	$1.05$
Bd. SE peri.	$s_p^{(SE)}=1$	$\sqrt{1.01}$	$\sqrt{1.02}$	$\sqrt{1.05}$
Int. SE area	$s_a^{(SE)}=1$	$0.9$	$0.85$	$0.75$
Int. SE peri.	$s_p^{(SE)}=1$	$\sqrt{0.9}$	$\sqrt{0.85}$	$\sqrt{0.75}$
Int. CE area	$s_a^{(CE)}=1$	$1$	$1$	$1$
Int. CE peri.	$s_p^{(CE)}=1$	$1$	$1.1$	$1.4$
images from Rigato et al.	fig. 1a	fig. 1b	fig. 1c	fig. 1d

Bd., boundary (border) cells; Int., interior (inner) cells; peri., perimeter of the cell.

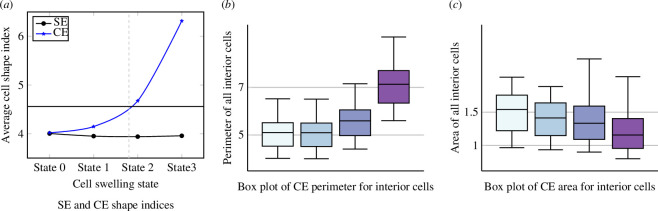
Figure 12 depicts our findings. Figure 12a shows the SE cell vertex model, which serves as the starting point for our analysis. Figure 12a,c features drawings adapted from fig. 1a/d in [30] showcasing the configuration of cells. Figure 12d displays the assigned cell IDs for each polygon. Finally, figure 12e,f presents the simulation results for states 0 and 3, respectively, achieved using the conditions specified in table 5. Each state denotes a further increment in time as the boundary cells swell. With our parametrization choice given in equations (2.6) and (2.7), we observe anisotropic CEs in figure 12f , which are similar to those depicted in figure 12c . Figure 13a shows the average cell shape indices for the disordered system for each boundary cell swelling state. We exclude cell IDs as 1 and 9 owing to their significantly higher shape index (>5) as compared with other cells (approximately 4). To compare our results with those of the experiments, we collect data for both area and perimeter of CE cells. Figure 13 aligns well with the general trends observed in fig. 1f,g of the experimental average values reported in [30].

Table 5.

Ordered cell constraints (SE).

	state 0	state 1	state 2	state 3	state 4	state 5
Bd. SE area	$s_a^{(SE)}=1$	${1.05}^1$	${1.05}^2$	${1.05}^3$	${1.05}^3$	${1.05}^5$
Bd. SE peri.	$s_p^{(SE)}=1$	$\sqrt{{1.05}^1}$	$\sqrt{{1.05}^2}$	$\sqrt{{1.05}^3}$	$\sqrt{{1.05}^4}$	$\sqrt{{1.05}^5}$
Int. SE area	$s_a^{(SE)}=1$	${0.95}^1$	${0.95}^2$	${0.95}^3$	${0.95}^4$	${0.95}^5$

Bd., boundary (border) cells; Int., interior (inner) cells; peri., perimeter of the cell.

Figure 13.

Perimeter and area of all interior CE cells and comparison of SE and CE shape indices for disordered cells (*excluding cell IDs 1 and 9). The solid black horizontal line represents a shape index of $4.56$ , which is the shape index of a regular triangle. A dashed grey vertical line represents the transition point from SE- to CE-dominated cells.

Our analysis also sheds light on the transition point from SE to CE behaviour. For regular polygons, the triangle shape index is the highest. As the shape index increases, the number of edges decreases while the number of edges per vertex increases, aligning with the findings of Lin et al. [56]. We can expect a transition to a CE-dominated regime when the shape index exceeds a critical value, approximately $p_{\alpha }~4.56$ for a SE cell limit. At this point, cell edge buckling, similar to those observed in state 2 of figure 11e , becomes likely. Alternative criteria can be used for conditions where the initial average cell shape index for SE cells exceeds 4.56. For example, the region dominated by wavy cell edges can be identified by calculating the difference in the average shape index. These conditions apply to both area decreasing and perimeter increasing.

To facilitate further comparison with the results of the experiments, we converted the dimensionless shape index $p_{\alpha }$ to circularity $C$ using the following equation:

$${\displaystyle C=\frac{4\pi a}{p^2}=\frac{4\pi }{p_{\alpha }^2}.}$$

For state 0, the circularity is $C=0.77472$ , and for state 3, it becomes $C=0.31290$ (again, excluding cell IDs 1 and 9). While similar trends to the experiment are observed, we do not yet have a quantitative agreement with experiments. As we do not yet have information distinguishing changes between the boundary cells and the histoblasts, as evidenced by the differences between figure 12c,f , it is clear that the boundary cells are not identical (especially top/bottom and bottom left). We will incorporate such details in future work to ultimately yield a quantitative comparison with experiments.

5. Discussion

We have introduced a CE vertex model for curved cell–cell interfaces in tissues at the subcellular scale using a parametric function to quantify the edge between two vertices. We can now explore non-convex cell shapes in a tiling without adding more vertices explicitly. From a cell shape index perspective, there are now two ways to increase the cell shape index, either by remaining convex and becoming more elongated or by remaining globular and becoming more non-convex. Which shape change pathway a cell takes depends on a multitude of factors, including the morphology of the underlying cytoskeleton. For instance, in cell monolayer experiments discovering that the upregulation of RAB5A induced an unjamming transition, the cells morphed from non-convex to convex shapes [28]. As the cells become convex, they can then perhaps undergo T1 transitions at very little energetic cost and so the system fluidizes, provided the cell shape index is high enough [12]. In other words, perhaps cell non-convexity helps put a brake on cell fluidization. Therefore, in addition to the target cell shape index parameter, topology of the tiling [57] and applied shear [58] as drivers of a rigidity transition, we perhaps should add yet another axis of the fraction of convex cells to the rigidity transition phase diagram. Interestingly, recent work has demonstrated that when a polygon, consisting of two-body springs and an area spring constraint, is subjected to expansive strain, the convexity of the polygon is a necessary condition to generate a state of self-stress, or rigidity, while a cyclic configuration of the polygon is a sufficient condition for the self-stress [59].

While cellular non-convexity may place a brake on cell fluidization, how then can cells adjust in the presence of applied compression? Our results indicate that as cells become increasingly non-convex, they can respond to applied compression without giving up their area by becoming more like jigsaw puzzle pieces. This phenomenon is presumably widely observed in plant cells because plant cells, which contain cell walls, are not motile. As depicted in figure 1a , Bidhendi et al. [60] established that the cell wall shaping process relies on spatially confined, feedback-augmented stiffening of the cell wall in the periclinal walls. Moreover, Belteton et al. [29] demonstrated that tensile forces and the microtubule–cellulose synthase systems dictate the patterns of interdigitated growth. Finally, experiments in Drosophila [30] demonstrate similar behaviour in which a group of cells eventually develops significant non-convexity to accommodate the compression by surrounding swelling cells. It would be interesting to search for other examples of this convex to non-convex transition in other instances in animal tissues.

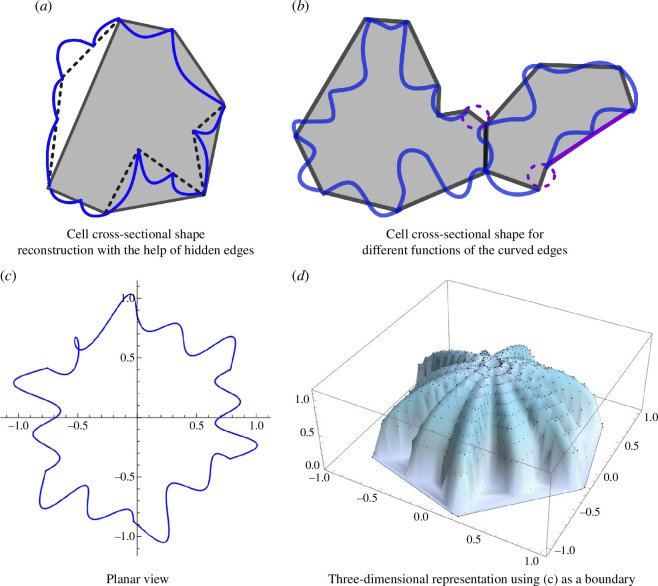
We envision future extensions to the model we have introduced here that remain distinct from other approaches to capture edge cell curvature [40,41]. For example, if concave polygons are to be avoided for technical purposes, the CE model can be extended by adding more vertex points and different curve functions can be selected for the CE model to improve the representation of cellular shape profiles. Simply, invisible vertex points can be added on each edge. Figure 14a has hidden edges (for invisible vertex points) to simulate cells with lobes. Representing lobes in the simulations may involve folding certain edges. By implementing invisible vertex points, cell profiles can be accurately represented and convex polygons can be maintained for the SE model (grey-shaded polygon in figure 14a ). The possibility of setting angles between hidden edges to zero enables the representation of a wider range of shapes. Figure 14a shows an example with hidden edges inspired by fig. 2a in [28]; figure 14b is the demonstration of the complicated cell structure inspired by figure 1a and fig. 1 in [62].

Figure 14.

Possible extensions of the CE model. (a) Cell reconstruction with the help of hidden edges. Black solid lines filled with grey shade represent SE components and dashed lines depict hidden edges. (b) Cell reconstruction for different functions of the CEs. Two dashed purple circles represent edges with zero curvature, and two purple lines show two SEs forming a line similar to deformation type C in figure 3. (c) A single-cell example with a singular point. (d) The three-dimensional representation using the bounded spherical balloon equation in [61]. The singular boundary point is ignored in the calculation.

Because we are using parametrized curves at two fixed ends that correspond to the edges of the straight polygon, we may get unintended results during the optimization. For example, when implementing sinusoids as the parametric function, there can be overlaps resulting from adjacent edges, as shown in figure 14c . These points of overlap can be a source of error in the evaluation of the correct perimeter and area. In addition, if we look in three dimensions, these points will generate several boundary points; therefore, some of them will have to be recalculated or omitted, as shown in the figure 14d . To achieve more accurate cell profiles, one may consider using different coefficients for sinusoidal harmonics, such as ${(c_i)}^2$ instead of $c_i$ , or limiting $c_i$ to be positive or small enough, will presumably avoid such singular points. Another approach to avoid singular points is by imposing constraints on the slope of the two endpoints. Moreover, instead of sine functions, other trigonometric functions, such as elliptic functions, hypergeometric functions or Bézier type functions [63] can be chosen to generate different edge profiles.

Finally, our analysis has so far been restricted to two dimensions. However, we can model the three-dimensional shape of a non-convex cell using two-dimensional representations of the cell’s boundary. Re-optimization with constraints can then be performed in two- or three-dimensional computations, as shown in figure 14d serving as initial parameters. By conceptualizing the shape of a cell as two-dimensional surface sheets, we can perform minimum energy calculations [64,65] to ultimately study the three-dimensional aspects of cellular non-convexity at the subcellular scale.

Appendix A

A.1. More on the methodology

This section addresses more of the technical details for our CE model. Let us first address the issue of how many Fourier coefficients to include in the computation from a constraint counting perspective. For the cellular packings we considered, there are approximately two-thirds of the number of vertices where the number of edges is equal to the number of vertices. Suppose we have a total of $N$ number of packed cell arrays with boundaries. In general, the relation between the number of cells $N$ , the number of edges $E$ and the number of vertices $V$ is as follows:

$$V=\alpha E,$$ (A 1)

$$N=E-V+1\text{(for open boundary)},$$ (A 2)

$$\text{ or }N=E-V\text{(for periodic boundary)},$$ (A 3)

$$N=(1-\alpha )E+1(\text{or }N=(1-\alpha )E),$$ (A 4)

where $\alpha$ is the ratio of the total number of vertices to the number of edges. For example, $\alpha =\frac{2}{3}$ for a cell packing with periodic boundary conditions. From the energy functional (without the resistance contributions), there are $2N$ constraints. Using equation (A 4), we obtain the number of constraints by comparing the number of degrees of freedom in terms of $E$ , and we can deduce whether the system is marginal, under-constrained or over-constrained. For our case, if we ignore boundary edges for the open boundary case, we have about $E^{\prime }=\frac{2}{3}E$ number of shared edges. This number can be adjusted by the ratio of boundary edges to interior edges. Similarly, we have $V^{\prime }=\frac{2}{3}{E}^{\prime }$ number of shared vertices between cells. So the number of degrees of freedom is $(\frac{4}{9}\cdot 2+\frac{2}{3}\cdot 4)E=\frac{32}{9}E$ , with the second term accounting for the four Fourier coefficients. By inserting $\alpha =\frac{2}{3}$ into equation (A 4), $N~\frac{1}{3}E$ such that $2N=\frac{2}{3}E<\frac{32}{9}E$ and so the system is under-constrained. Including the resistance function as constraints may result in a slightly over-constrained system. Still, there are fewer unknowns for the CE model as compared with adding more SE vertices $V^{*}$ because the number of unknowns is increased to $2(V^{*}+V)$ even though the number of constraints remains the same.

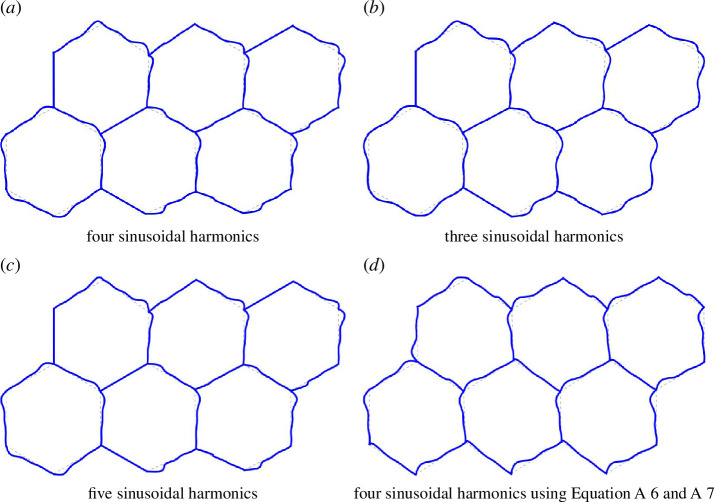
Next, we check how the number of Fourier coefficients affect our results, at least for one cell packing. Figure 15a,c illustrates the minimal energy configurations for three, four and five Fourier coefficients. It is evident that smaller numbers may result in rounded profiles. However, the results of the four and five frequency simulations showed minimal differences. The measured ${\displaystyle P_{\alpha }^{\left(\mathrm{C}\mathrm{E}\right)}}$ were $6.20037$ (three harmonics)/ $6.20103$ (four harmonics)/ $6.20144$ (five harmonics), i.e. a change in the third decimal place.

Figure 15.

Exploring different numbers of Fourier coefficients as well as the curve parametrization in the CE model.

Figure 16.

A model for swelling of the boundary cells. Fixed boundary points are symbolized as black points. Boundary cells are marked with blue shading, and interior cells are represented by blue diagonal stripes, surrounded by boundary cells. Black arrows indicate the direction of swelling.

The parametrization implemented equations (2.6) and (2.7) have several singularities. Here, we introduce another parametrization that may be useful for other cell packing geometries. The parametrization is

$$v_k(t)=v_{\alpha ,i}(t)=(f_{\alpha ,i}(t),g_{\alpha ,i}(t)),$$ (A 5)

$${\displaystyle \begin{array}{c}{f}_{\alpha ,i}\left(t\right)=\left(1-t\right)x_{\alpha ,i}+t{x}_{\alpha ,i+1}-\frac{c_{\alpha ,i}\left(t\right)\left(x_{\alpha ,i}-x_{\alpha ,i+1}\right)}{\sqrt{{\left(x_{\alpha ,i}-x_{\alpha ,i+1}\right)}^2+{\left(y_{\alpha ,i}-y_{\alpha ,i+1}\right)}^2}},\end{array}}$$ (A 6)

$${\displaystyle \begin{array}{c}{g}_{\alpha ,i}\left(t\right)=\left(1-t\right)y_{\alpha ,i}+t{y}_{\alpha ,i+1}+\frac{c_{\alpha ,i}\left(t\right)\left(y_{\alpha ,i}-y_{\alpha ,i+1}\right)}{\sqrt{{\left(x_{\alpha ,i}-x_{\alpha ,i+1}\right)}^2+{\left(y_{\alpha ,i}-y_{\alpha ,i+1}\right)}^2}}.\end{array}}$$ (A 7)

Using this alternative parametrization does not significantly affect the minimized cell structures (see figure 15a,d ). It is worth noting that figure 15d does not have perfectly flat edges at certain angles.

A.2 Simulation conditions for compression-induced curved edges

To study the deformation of the interior cells as a result of swelling boundary cells, we establish a scaling factor $s$ for the $m$ th state of cell $\alpha$ as stated below:

$${\displaystyle A_0^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)=s_a^{\left(\mathrm{S}\mathrm{E}\right)}\cdot A_0,}$$ (A 8)

$${\displaystyle P_0^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)=s_p^{\left(\mathrm{S}\mathrm{E}\right)}\cdot P_0,}$$ (A 9)

$${\displaystyle A_0^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)=s_a^{\left(\mathrm{C}\mathrm{E}\right)}\cdot A_0,}$$ (A 10)

$${\displaystyle P_0^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)=s_p^{\left(\mathrm{C}\mathrm{E}\right)}\cdot P_0,}$$ (A 11)

where $A_0$ and $P_0$ are the area and perimeter of the unit-length regular hexagon. Both SE cell characteristics and CE cell characteristics are determined by the area, perimeter and the cell index $\alpha$ . If ${\displaystyle s_p^{\left(\mathrm{S}\mathrm{E}\right)}=\sqrt{s_a^{\left(\mathrm{S}\mathrm{E}\right)}}}$ , then the target shape index for the $m$ th state ${\displaystyle p_0^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)}$ will be

$${\displaystyle p_0^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)=\frac{P_0^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)}{A_0^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)}=\frac{s_p^{\left(\mathrm{S}\mathrm{E}\right)}\cdot P_0}{\sqrt{s_a^{\left(\mathrm{S}\mathrm{E}\right)}\cdot A_0}}=\frac{s_p^{\left(\mathrm{S}\mathrm{E}\right)}\cdot P_0}{\sqrt{s_a^{\left(\mathrm{S}\mathrm{E}\right)}}\cdot \sqrt{A_0}}=\frac{P_0}{\sqrt{A_0}}.}$$ (A 12)

Thus, the shape index of SE remains unchanged. Then we can define the following energy functions in the form of ${\displaystyle {\mathcal{W}}^{(\ast )}\left(m\right)=\frac{K_W}{2}\sum _{\alpha }{\left(W_{\alpha }^{(\ast )}\left(m\right)-W_0^{(\ast )}\left(m\right)\right)}^2}$

$${\displaystyle {\displaystyle {\mathcal{A}}^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)=\frac{K_A}{2}\sum _{\alpha }{\left(A_{\alpha }^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)-s_a^{\left(\mathrm{S}\mathrm{E}\right)}{A}_{\alpha ,0}\right)}^2,}}$$ (A 13)

$${\displaystyle {\displaystyle {\mathcal{P}}^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)=\frac{K_P}{2}\sum _{\alpha }{\left(P_{\alpha }^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)-s_p^{\left(\mathrm{S}\mathrm{E}\right)}{P}_{\alpha ,0}\right)}^2,}}$$ (A 14)

$${\displaystyle {\displaystyle {\mathcal{A}}^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)=\frac{K_A^{\mathrm{\prime }}}{2}\sum _{\alpha }{\left(\delta a_{\alpha }^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)\right)}^2\to 0\text{(conserved),}}}$$ (A 15)

$${\displaystyle {\displaystyle {\mathcal{P}}^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)=\frac{K_P^{\mathrm{\prime }}}{2}\sum _{\alpha }{\left(P_{\alpha }^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)-s_p^{\left(\mathrm{C}\mathrm{E}\right)}{P}_{\alpha ,0}\right)}^2,}}$$ (A 16)

where ${\displaystyle \delta a_{\alpha }^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)}$ denotes an area under the curve such that ${\displaystyle \delta a_{\alpha }^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)+s_a^{\left(\mathrm{C}\mathrm{E}\right)}\cdot A_{\alpha ,0}=A_{\alpha }^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)}$ (because the area is conserved when simulating curved edges for ${\displaystyle s_a^{\left(\mathrm{C}\mathrm{E}\right)}=1}$ , we get ${\displaystyle A_{\alpha }^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)=A_{\alpha ,0}}$ ). We set $K_A=1,K_P=1,K_A^{\prime }=2,$ and $K_P^{\prime }=2$ . Figure 16 illustrates the swelling of the boundary cells with immovable boundaries (represented by black points), accompanied by the compression of interior cells. In the ordered scenario, we use an 8 × 3 array of inner cells and impose three rows of cells with central cells undergoing vertical compression from top and bottom. For the disordered case, we convert a hand-drawn vector image into a Mathematica graph object [55]. Figure 10 illustrates the use of both disordered and ordered cell arrays in the simulation.

As obtaining precise initial configurations from the experimental images is challenging owing to the curved edges, we use the same initial parameters for the different states via the resistance function. However, in the ordered case, to mimic the continuous area expansion of the boundary cells, we implement a feed-forward loop that uses the vertex position data of the previous state to evaluate the next state. Therefore, resistance functions for a state $m$ can be evaluated by

$${\displaystyle {\displaystyle \begin{array}{c}{\mathcal{R}}^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)=\frac{K_R}{2}\sum _i\left({\left(x_i\left(m\right)-x_i\left(0\right)\right)}^2+{\left(y_i\left(m\right)-y_i\left(0\right)\right)}^2\right)\text{(disordered)},\end{array}}}$$ (A 17)

$${\displaystyle {\displaystyle \begin{array}{c}{\mathcal{R}}^{\left(\mathrm{S}\mathrm{E}\right)}\left(m\right)=\frac{K_R}{2}\sum _i\left({\left(x_i\left(m\right)-x_i\left(m-1\right)\right)}^2+{\left(y_i\left(m\right)-y_i\left(m-1\right)\right)}^2\right)\text{(ordered),}\end{array}}}$$ (A 18)

$${\displaystyle {\displaystyle {\mathcal{R}}_2^{\left(\mathrm{C}\mathrm{E}\right)}\left(m\right)=\frac{K_{R2}}{2}\sum _k\sum _{j=1}^4{\left(c_k^{\left(j\right)}\left(m\right)-0.05\right)}^2.}}$$ (A 19)

We run simulations for $K_R=0.1,K_{R1}=0,$ and $K_{R2}=0.2$ . Moreover, $(x_i(0),y_i(0))$ denotes the initial position for the $i$ th vertex and $(x_i(m),y_i(m))$ denotes the position at the $i$ th vertex in the mth state. In order to reduce computation time, we separate the SE and CE contributions for the ordered cases, as depicted in table 6. We start with SE conditions in table 5, using its data as input for both the type A and type A + B simulations indicated in tables 7 and 8. Thus, a comparison between CE types A and A + B can be made without factoring in the SE cell shape index. The constraints are chosen to correspond the disordered scenario. For example ${(1.07)}^2\simeq 1.145$ , which matches state 2 in the disordered scenario (Tables 5, 7 and 8), and ${(1.07)}^5\simeq 1.403$ , which matches state 5.

Table 6.

Optimization methods.

	optimization methods
disordered	simultaneous (SE and CE)
ordered (type A)	sequential (SE first)
ordered (type A + B)	sequential (SE first)

Table 7.

Ordered cell (CE, type A + B)

	state 0	state 1	state 2	state 3	state 4	state 5
Int. CE area	${\displaystyle s_a^{\left(CE\right)}=1}$	1	1	1	1	1
Int. CE peri.	${\displaystyle s_p^{\left(CE\right)}=1}$	1	1	1	1	1

Table 8.

Ordered cell (CE, type A + B).

	state 0	state 1	state 2	state 3	state 4	state 5
Int. CE area	${\displaystyle s_a^{\left(CE\right)}=1}$	$1$	$1$	$1$	$1$	$1$
Int. CE peri.	$s_p^{(CE)}=1$	${1.07}^1$	${1.07}^2$	${1.07}^3$	${1.07}^4$	${1.07}^5$

Int., interior (inner) cells; peri., perimeter of the cell.

Ethics

This work did not require ethical approval from a human subject or animal welfare committee.

Data accessibility

This article has no additional data.

Declaration of AI use

We have not used AI-assisted technologies in creating this article.

Authors’ contributions

K.K.: conceptualization, methodology, software, validation, writing—original draft; J.M.S.: conceptualization, formal analysis, funding acquisition, methodology, project administration, supervision, writing—original draft; M.B.A.: conceptualization, formal analysis, methodology, validation, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

J.M.S. acknowledges financial support from NSF-PHY-PoLS-2014192. M.B.A. acknowledges the financial support from ITMO Cancer of Aviesan within the framework of the 2021–2030 Cancer Control Strategy, on funds administrated by Inserm (PCSI 2021, MCMP 2022).