Recent advances toward intraoctahedral phase change in metal halide perovskite nanomaterials

Summary

Metal halide perovskite nanomaterials (PeNMs) are among the next generation of optoelectronic materials due to their unique crystal structure and diverse phase change behaviors, which have the potential to dynamically tune the device performances. In this review, the research progress on the phase change of PeNMs is comprehensively reviewed and summarized. First, the basic structure and composition, as well as the phase change mechanism are introduced. Then, the influence of the phase change on the optoelectronic properties of PeNMs is discussed in detail, including the regulation of the energy band structure, carrier transport properties, lattice strain and distortion, and the evolution of the photoexcited state. Finally, current challenges and future development trends are projected. This review promotes the understanding of the phase change of PeNMs, which will be useful for the innovative design and application of related optoelectronic devices.

Graphical abstract

Applied sciences; Materials science; Nanomaterials

Introduction

Metal halide perovskite nanomaterials (PeNMs) have attracted immense interest in recent years due to their facile synthesis and exceptional optoelectronic properties. They exhibit remarkable properties such as high photoluminescence quantum yields (PLQYs),¹ tunable photoluminescence (PL) emission,² and long carrier diffusion lengths,³ which make them promising candidates for various applications, including photovoltaics,⁴ light-emitting diodes (LEDs),⁵ lasers,⁶ and photodetectors.⁷

One intriguing aspect of PeNMs is their ability to undergo phase changes, which can significantly affect their structural, optical, and electronic properties. Phase changes in these materials can occur due to various stimuli, such as temperature,⁸ pressure,⁹ or external fields.¹⁰ Tracing back to its origin, this behavior is mainly governed by the interplay between the organic and inorganic frameworks, as well as the halide composition.¹¹ For example, the organic cation plays a crucial role in stabilizing the perovskite structure and influencing the phase change temperatures.¹² Meanwhile, the choice of halide anions (e.g., Cl, Br, I) can significantly affect the structural, optical, and thermal properties of PeNMs, thereby modulating their phase change properties.¹³

Although PeNMs possess promising attributes, there are still limitations in regulating the phase change properties of the materials. One major challenge is the complex interplay between various factors influencing phase changes, making it difficult to predict and precisely control these changes. Additionally, the stability of different phases under various environmental conditions remains a significant concern, potentially limiting the practical applications of PeNMs various optoelectronic devices. Furthermore, the reversibility and cyclability of phase changes in PeNMs are critical aspects that require further investigation, as they directly impact the long-term performance and reliability of devices utilizing these materials. Another pressing limitation is the current gap between laboratory-scale demonstrations and large-scale, commercially viable production of phase-change PeNMs. Scaling up synthesis processes while maintaining precise control over composition and phase behavior presents a significant hurdle for industrial adoption.

In order to overcome the previous challenges, the understanding and controlling these phase changes is crucial to tailoring the properties of PeNMs, and realizing their full potential in various applications. In recent years, remarkable progress has been made in understanding and manipulating phase changes in PeNMs, including compositional engineering,^14,15 and phase changes induced by external stimulus.^16,17 These advances have not only shed light on the fundamental mechanisms governing phase changes, but have also paved the way for the development of optoelectronic functional materials with tunable properties.

Unfortunately, a comprehensive overview is still lacking to facilitate a deeper understanding of the fundamental mechanisms, as well as to better exploit phase changes for tailoring the properties of PeNMs for optoelectronic applications. Therefore, this manuscript aims to provide a comprehensive review of the recent advances in the field of phase change in PeNMs. A systematic literature review (SLR) of journal articles published between 2013 and 2023 on the topic of the phase change in PeNMs, and an overview of the study method was presented in Figure 1. There are 73 journal articles were analysed by categorizing them into category 1 (35 articles) and category 2 (38 articles). This manuscript will cover the fundamental principles underlying phase changes, the different types of phase changes observed in these materials, and the strategies used to induce and control these changes. In addition, the review will highlight the potential applications of phase change PeNMs in optoelectronics, energy conversion, and other emerging fields. By synthesizing the latest research findings, this review will stimulate further exploration and exploitation of phase changes in PeNMs, ultimately driving the development of innovative technologies and materials.

Figure 1.

SLR methodology adopted in this study

Fundamentals of phase change

Crystal structure and composition

The general chemical formula of standard PeNMs is ABX₃, where A, B, and X are monovalent cations, divalent metal cations, and monovalent halogen anions, respectively. The A-site cation plays a crucial role in determining the structural and thermal stability of the perovskite phase, while the B-site cation and the X-site halide ions influence the electronic and optical properties. The crystal structure of PeNMs consists of a pseudo-cubic array of corner-sharing [BX₆]^4- octahedra with the A-site cation located in the cubic octahedron cavity, and the coordination number is 12.¹⁸ The geometric stability of the structure can be evaluated by the Goldschmidt tolerance factor (t):¹⁹

$$t=\frac{R_A+R_B}{\sqrt{2}\left(R_B+R_X\right)}$$ (Equation 1)

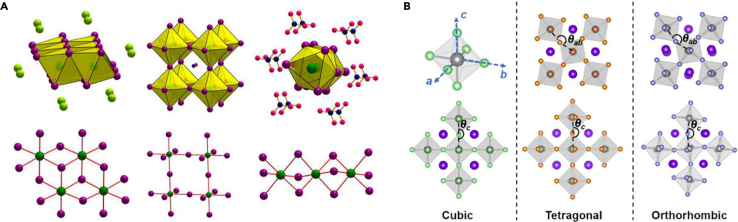
where R_A, R_B, and R_X are the ionic radii of A, B, and X, respectively. Ideally, when the tolerance factor t reaches 1, the crystal possesses a strictly cubic structure. Any deviation from t = 1 indicates that the unit cell structure is deformed, resulting in the low symmetry. Generally, when 0.76 < t < 1.13, a stable perovskite structure can exist.²⁰ If t < 0.76, the A-site cation is too small to fully occupy the cavity of the cubic octahedral [BX₆]^4-, resulting in serious distortion occurs in the perovskite framework. And the preferred structure is A₄BX₃-type, which can be described as a double chain of [BX₅]^3- (Figure 2A).²¹ On the other hand, if the A-site cation is too large (t > 1.13), the angle sharing octahedral network is excluded. The preferred structure consists of single chains of face-sharing octahedra. Simultaneously, densely packed cations can induce the change of perovskite structure toward a lower dimensionality (for example, Aurivillius,²² Ruddlesden-Popper,²³ and Dion-Jacobson phases.²⁴ Obviously, for the previous cases, the crystal structure is no longer the typical perovskite type.

Figure 2.

The crystal structure of PeNMs changes when the phase change occurs

(A) Established structural motifs for the ABX₃ perovskite as a function of the ionic radii of A⁺, B²⁺, and X^– ions expressed with a tentative tolerance factor value. Adapted from the study by Stoumpos et al.²¹

(B) Schematic diagram of the three phase change structures of PeNMs. Adapted from the study by Chen et al.²⁵

Therefore, only the phase changes behavior in the case of 0.76 < t < 1.13, that is, intraoctahedral phase change, will be discussed in this review. In this range, the tilting of the octahedra does not change the overall three-dimensional architecture, but can significantly change the X-Pb-X angle from an ideal 180° to as low as 150°, where the structure type changes or becomes amorphous. The crystal phases can be classified as orthorhombic (γ), tetragonal (β), and cubic (α), as shown in Figure 2B. Theoretical calculations have predicted that the origin of the phase change is related to the [PbX₆]^4- octahedral tilting coupled with the rotation of A-site cation from in-plane [010] direction toward out-of-plane c-direction.²⁶ The space group of the α-phase of PeNMs is Pm3m, which belongs to the equiaxed crystal system. In this phase, the lattice unfolds seamlessly, the cation is located at the corner of the cube, the anion is located in the center of the surface, and the B-site cation occupies the cavity. From the dense stacking point of view, due to the similar ionic radii of A and X, the structure can be regarded as the formation of A and X atomic layers by the hexagonal packing along the [111] direction, and B filling in the octahedral voids. Therefore, this structure is prone to the disorder orientation or fluidity of organic cations under the external stimulation or the arrangement of atoms space, which is difficult to be bound in octahedral lattice, leading to the phase change. With the decrease of symmetry, PeNMs undergo a transition to the β-phase (P4mm), which is characterized by elongation along one axis. Further reduction in symmetry leads to the appearance of the γ-phase (Pnma), where the crystal distortion is exacerbated, resulting in unequal lattice parameters along the three orthogonal axes. The change between these phases has a profound effect on the optical, electronic, and structural properties of PeNMs. Changes in the cross-phase bandgap modulate the light absorption and emission characteristics, while changes in charge transport affect the performance and stability of the device. Therefore, understanding the complex relationship between phase change and material properties is essential to tailor PeNMs for specific applications.

Factors, mechanism, and manipulation of phase change

Temperature

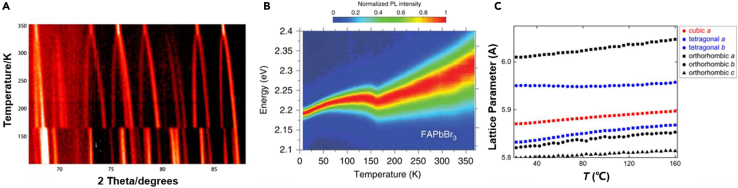
Temperature is the primary driving force of phase change in PeNMs. In 2015, Hansen’s group used high-resolution powder neutron diffraction to observe the temperature-dependent phase change behavior in MAPbI₃ for the first time.²⁷ As shown in Figure 3A, the crystal structure change from the γ-to the β-phase, and from the β-to the α-phase occurred at 165 and 327 K, respectively. Although the MA⁺ cation is oriented toward an open face of the distorted cube formed by the linked [PbI₆]^4- octahedra at all temperatures, its position changes during the two-phase change processes. At low temperature, the orientation of MA⁺ cation is fixed as a result of the hydrogen bonding between the NH₃ groups and the framework iodide atoms. With the increase of temperature, the thermal motion of the cation increases and the NH-I interactions become weaker. At the change to the β-phase at 165 K, MA⁺ cation becomes rotational disordered in the ab plane, and disordered over four similar orientations as found for the γ-phase, which direct toward the distorted cube faces, <100>, <010>, <−100>, and <0–10>. At this point, the MA⁺ cation deviates slightly from the center of the unit cell. Upon further heating toward room temperature, the free motion of the MA⁺ cation increases and slowly migrates toward the central of the perovskite A-site cavity before 327 K. In the α-phase, the MA⁺ cation appears to remain oriented toward the cube faces orientationally disordered over six positions, although there is a high degree of positional and thermal disorder exists in this phase.

Figure 3.

Effect of temperature on phase change of PeNMs

(A) Stacked plot, viewed vertically, of part of the neutron powder diffraction data (67–88°) collected from MAPbI₃ over the temperature range 100–352 K. Adapted from the study by Weller et al.²⁷

(B) Color plots of normalized steady-state PL spectra of FAPbBr₃ at temperatures between 10 and 370 K. Adapted from the study by Wright et al.²⁸

(C) Evolution of the lattice parameters of the α-, β-, and γ-phase fits as a function of temperature. Adapted from the study by Cottingham et al.²⁹

The phase change mechanism in another common organic-inorganic hybrid perovskite FAPbX₃ is also similar to the aforementioned. Masada et al. performed the temperature dependent PL measurement of FAPbBr₃.³⁰ As shown in Figure 3B, the large photon energy redshift that occurs near 90 K can be ascribed to the structural phase change, because the β-phase has a narrower bandgap than the γ-phase. Compared with MAPbBr₃, FAPbBr₃ exhibited a lower phase change temperature, which is generally associated with larger energy shifts because it marks a strong reduction in the degree of rotational freedom of the organic cation.²⁸

The phase change behavior in all-inorganic CsPbX₃ is similar to that in organic-inorganic PeNMs. The temperature dependent PL spectrum showed that they have two phase changes during the temperature range of 80–370 K.³¹ Withe the increase of temperature, their photon energies firstly blue-shifted and then red-shifted. Besides the change in photon energy, the PL intensity against temperature is another parameter to determine the phase change. Lohar et al. reported a sudden jump in PL intensity during the temperature change of CsPbCl₃, which corresponds to the phase change of the structure.³² However, it is worth to mention that the phase change mechanism of the all-inorganic CsPbX₃ is not the movement of A-site cation, but through an order-disorder process, such as the formation of twin boundaries. Cottingham and Brutchey determined the temperature ranges of CsPbBr₃ for the γ- to β- and β- to α-phase changes to be 323 to 332 K, and from 381 to 390 K, respectively, based on the temperature dependent synchrotron X-ray diffraction (XRD) measurement.²⁹ The influence of temperature on the magnitude of the distortion was also evaluated through the evolution of the lattice parameters. It was found that the magnitude of the local distortion is weakly dependent on temperature below 433 K, which is consistent with the phase changes in CsPbBr₃. In addition, the evolution of the lattice parameter R_w and atomic positions of Br in Figure 3C were all smooth in the vicinity of the phase changes, suggesting that the reorientation of tilting patterns to form twinned domains may occur in a gradual, rather than stepwise manner.

Pressure

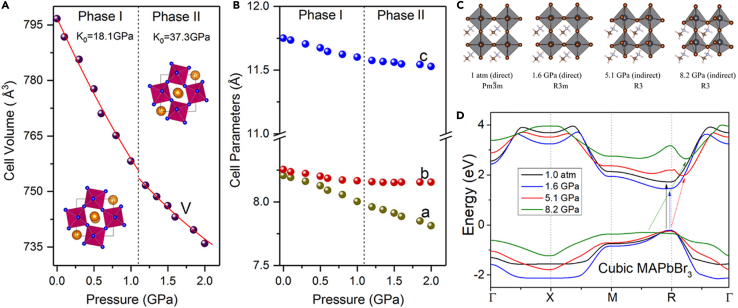
Due to the inherent properties of ionic crystals, PeNMs are extremely sensitive to pressure, which can be used to study their structural and electronic behaviors. Figure 4A shows the XRD pattern of MAPbBr₃ collected under different pressures during compression up to 34.0 GPa and decompression.³³ A subtle structure change occurs at very low pressure (0.4 GPa) with the appearance of several small peaks at 6.3° and 7.4°. Another phase change occurs from 1.8 GPa as evidenced by the apparent splitting of the peak located around 8°. Along with the increase of applied pressure (above 2.0 GPa), broad bands induced by amorphization dominate the XRD data. After decompression, the amorphous phase returns to the original MAPbBr₃ form, and its XRD pattern can be indexed again by using the Pm3m unit cell with almost the same parameters. The tilting distortion of [PbBr₆]^4- octahedral dominates the phase changes (a⁺a⁺a⁺ for Pm3m, a⁺b^–b^– for Pnma) during the pressurization, and the order of the long-range orientation of the MA⁺ cation does not change, only contributing to the broad diffraction background. Only in the process of change to amorphous, the long-range order of MA is destroyed. The two discontinuous phase changes during compression are characterized by the considerable changes in both cell parameters (a, b, c) and cell volumes. Meanwhile, the bandgap evolution in Figure 4B was evaluated by in situ PL measurement as a function of pressure up to 20.7 GPa. An anomalous peak shift was observed upon compression: first a gradual redshift in the 0–1 GPa region, and followed by a blueshift above 1 GPa. The abnormal PL/bandgap evolutions were attributed to the competition between the compression effect and the destruction of the long-range ordering of MA molecules. The optical properties of the sample can be restored when the pressure is released, in accordance with the tendency of XRD. Due to the pressure-induced amorphization, MAPbBr₃ showed a rapid increase of the resistance, for the applied pressure increases above 2.0 GPa. Similarly, FAPbI₃ underwent a phase change from a cubic Pm3m to a cubic supercell Pm3m in the pressure range of 0–3 GPa, followed by an amorphization process.⁹ The evolutions of the absorption and PL spectra of FAPbI₃ as a function of pressure in Figure 4C show a strong correlation with the crystal structure changes, which is consistent with the band structure calculation based on density functional theory (DFT).

Figure 4.

Effect of pressure on phase change of PeNMs

(A) Integrated 1D XRD profiles of MAPbBr₃.

(B) The calculated partial DOS from each element. Adapted from the study by Wang et al.³³

(C) Absorption and PL evolutions during the pressure cycle. Adapted from the study by Zhu et al.⁹

Xiao et al. carried out an in situ high-pressure PL measurement to investigate the optical properties of CsPbBr₃.³⁴ The PL peak displayed a redshift in wavelength and gradually became broad with an increase in pressure. Additionally, the PL intensity decreased sharply upon compression to 1.21 GPa, after which the fluorescence was abrupt quenched and was governed by the structure-related change. The optical photographs clearly revealed the darkening trend of the PL brightness in CsPbBr₃, accompanied by the color changes from bright green to dark green. Furthermore, they revealed the pressure-induced phase change mechanism in CsPbBr₃ based on the first-principles calculation. It is known that the valence band maximum (VBM) of CsPbBr₃ was identified as the antibonding hybridization between the Pb 6s and Br 4p orbitals, whereas the conduction band minimum (CBM) state was governed by the orbital interactions between Pb 6p and Br 4s orbitals in the [PbBr₆]^4- octahedral network. When pressure was applied, CBM was mostly a nonbonding localized state of Pb 6p orbitals, which is less sensitive to external pressure stimulus. Therefore, the bandgap evolution of CsPbBr₃ was initially determined by the change of VBM. With the increase of pressure, the enhanced orbital coupling between the Pb 6s and Br 4p states pushed up the VBM due to its antibonding character, which explains the redshift of the bandgap with pressure. As CsPbBr₃ was subjected to pressure beyond 2.0 GPa, the CBM happened to be dominated by the strong coupling of the Pb 6p and Br 4p orbitals. Accordingly, the blue jump can be interpreted from the significant shift to higher energy level of the CBM by the exertion of pressure, thereby leading to the wider bandgap. Obviously, whether it is organic-inorganic or all-organic PeNMs, the phase change caused by pressure is only related to the degree of distortion of the octahedron, while the influence of the A-site cation is almost negligible.

External field

Light is the most commonly applied external field for PeNMs. The photoinduced phase change in PeNMs is non-equilibrium, resulting from the rapid deposition of pulse-induced energy into the lattice. In the case of CsPbBr₃, the photo-induced reversible phase change was observed by time-resolved XRD measurements (Figure 5A).¹⁰ It is needed to mention that CsPbI₃ underwent an γ- to α-phase change directly without the β-phase. Under an excitation fluence of 4.8 mJ/cm², the high symmetry cubic diffraction peaks shift to lower Q values due to the thermal lattice expansion. During the first 80 ps, a decrease in diffraction intensity without peak shifts is observed as shown in Figure 5B, suggesting the change from γ- to α-phase. Interestingly, the structural change is reversible. From 80 to 320 ps (Figure 5C), the cubic diffraction peaks spontaneously return to their original position and γ-peaks recover. However, the reversible phase change is strongly related to the photoexcitation fluence. The high fluences induce an irreversible change to amorphous structure (melting) due to the photoinduced structural degradation. The prolonged illumination may cause unavoidable heating, which might be another factor that can induce structural variation of PeNMs. Recently, Lu et al. investigated the internal mechanism of the light-induced phase change of CsPbBr₃ PeNMs via DFT simulations.³⁵ They found that although CsPbBr₃ tends to appear in the γ-structure, it can be changed easily by external stimulus, and the transition of photogenerated carrier plays the decisive role in this process. When the photogenerated carrier transits from VBM to CBM in the reciprocal space, they actually transit from Br⁻ ions to Pb²⁺ ions in the real space, which are taken away by the Br atoms with higher electronegativity from Pb atoms during the initial formation of the lattice. This charge transition releases the distortion of the Pb-Br octahedral framework and expands the CsPbBr₃ lattice, providing possibilities to the phase change from the γ- to β-structure. This phase change is a self-accelerating positive feedback process, increasing the light absorption efficiency of the CsPbBr₃ PeNMs, which is of great significance for the widespread promotion and application of the photostriction effect.

Figure 5.

Effect of external field on phase change of PeNMs

(A) Time-resolved XRD pattern of CsPbBr₃ at various times following excitation at 4.8 mJ cm⁻² along with the static XRD pattern for reference on peak positions.

(B) Zoomed in time-resolved XRD for 80 ps in the Q range of 1.6–2.1 Å⁻¹.

(C) Time-resolved XRD pattern for the [200] peak normalized such that the maximum ΔS = 1. The arrow denotes how the pattern evolves in time. Adapted from the study by Kirschner et al.¹⁰

(D) PL intensity temperature dependence associated with the phonon-assisted PL quenching and the phonon-assisted structural phase change.

(E) The multiple Mott equation fit of the temperature dependences of the PL integrated intensities.

(F) The range of the γ- to β-phase change in MAPbBr₃/ZnO (30 nm). Adapted from the study by Xiao et al.³⁴

The electric field can also affect the phase change in PeNMs. In Figure 5, we reported the expansion of the phase temperature in MAPbBr₃ by the interfacial electric field.³⁶ The temperature dependent PL experiments revealed that the PL quenching in the γ-phase involves twist mode (TO)-phonons. Thus, the γ- to β-phase change occurs due to the activation of MA torsional (MAT) phonons. In contrast, the β- to α-phase change involves MA internal (MAI)-phonons. We also note that the γ- to β-structural phase change is spread out over the range of 70–140 K, which is believed to be due to the configurational entropy loss and the corresponding structural phase instability when free rotations of MA⁺ cation are no longer restricted strongly by a long-range polar order. The resulted local field fluctuations in MAPbX₃ and the liquid-like motion of MA⁺ cations weaken and smooth distortions of [PbX₆]^4- octahedra that are responsible for band edge carrier recombination, thus eliminating the step-like shift of the corresponding absorption and PL bands. Therefore, it can be concluded that the interfacial electric field caused by dynamic charge separation can enhance the configurational entropy loss and the liquid-like motion of MA⁺ cation, extend the range of the γ- to β-structural phase instability from 70 to 230 K, and significantly shift the β- to α-phase change to the temperatures beyond room temperature. More importantly, the effect is dependent on the applied layer thickness (the strain and electric field induced effects) and the photoexcited carrier density, thus allowing one to control the structural phase instability range in MAPbBr₃.

Zeng et al. explained the mechanism of the influence of electric field on the phase change in more depth.³⁷ They reported for the first time the triggering phase change from γ- to β-phase in CsPbBr₃ using above-bandgap illumination with a low energy threshold (1.6 mW cm⁻²). This photon-induced structure reorganization was reversible and presented a fast and controllable response (<0.5 s) to light on/off. Raman spectroscopy and DFT calculations revealed that such a dynamic structure reorganization is caused by the transition of torsion direction in Pb-Br octahedral, while the diffusion potential difference induced local Coulombic field was proved to drive this process. Under the electric field, a shear force occurs in the lattice leading to the change of structure, further leading to the changes of other physical properties. Therefore, the electric field from photogenerated charged carriers has a noticeable effect on the accelerated phase transformation. In general, it is reasonable to believe that the local electric field is formed in CsPbBr₃ due to separation of isopotential surface in photogenerated hole and electron. For instance, terahertz spectroscopy has confirmed a negligible influence of surface defects in trapping carriers and a remarkably electron mobility (≈1000 cm² V⁻¹ s⁻¹),³⁸ whereas the hole possesses quite low mobility (≈52 cm² V⁻¹ s⁻¹).³⁹ Concerning unbalance in charge carrier mobility, the diffusion potential difference is proposed to represent a predominant role in phase change.

Size

The influence of size on the phase change behavior is reflected more in the manipulation of the phase change temperature. Sychugov’s group reported the strong size-dependent effect on temperature-induced phase changes in individual MAPbBr₃.⁴⁰ As shown in Figures 6A and 6B, the large PeNMs with the size about 4 nm revealed a clear α- to β-phase change at 150 K, as derived from the PL spectra and lifetimes data. In contrast, the phase change was absent in smaller PeNMs with the size around 2 nm. Moreover, the influence of size on the paraelectric-ferroelectric phase change temperature was investigated based on the Ginzburg-Landau-Devonshire theory (Figure 6C). The calculated α- to β-phase change temperature was predicted to be 120 K for the PeNMs with size of 4 nm, which is in good agreement with the experimental value. When the size is decreased to 2 nm, the phase change temperature becomes close to 0 K, implying that the material maintains the α-phase. One possible reason for this phenomenon is the size-dependent free energy, which makes the phase change less favorable in smaller PeNMs. Another explanation is the lack of the “anti-Varshni” trend, that is, the narrower bandgap at lower temperature. The PeNMs with small size showed the same PL behavior between 80 and 295 K, which may reflect a subtle interplay between the opposite effects of a standard bandgap narrowing (blueshift, Varshni trend) and perovskite-specific band edge rearrangement (redshift, anti-Varshni trend). Moreover, the winder PL linewidth of PeNMs with smaller size may be due to a higher sensitivity of the exciton to surrounding charges, the so-called quantum Stark effect. The research also showed that the phase change temperature of FAPbBr₃ PeNMs is size dependent.⁴¹ With the decrease of size, the phase change temperature is lower.

Figure 6.

Effect of size on phase change of PeNMs

(A and B) Distribution of PL peak positions and statistical distribution of FWHM as a function of temperature, respectively. The blue and green bars represent the single smaller and larger sized MAPbBr₃, respectively.

(C) Dependence of the Curie temperature and Gibbs free energy on the diameter of PeNMs. The inset is the schematic diagram of the size-dependent phase change. Adapted from the study by Cao et al.³⁵

(D) Change pressure at which the PL turns from a red-shift to a blue-shift as a function of size. The dotted line and dash-dotted line are the change pressure in bulk and PeNMs. Adapted from the study by Xue et al.³⁷

Similarly, the size of PeNMs also affects the pressure critical point of the phase change. Theoretically, the surface-to-volume ratio of NCs increases with decreasing size, which leads to the change of surface energy. In other words, a higher pressure is usually required to convert smaller NCs to another phase. However, the phase change of PeNMs only causes changes of the tilting angle and the [PbX₆]^4- octahedra distortion, which means that the situation may be different. For instance, it has been observed in Figure 6D that the phase change pressure decreases with the size decrease of PeNMs. The isostructural phase change pressures and PL pressure coefficients of CsPbBr₃ PeNMs have been investigated to explain this phenomenon.⁴² For the smaller size, the fluctuation length scale that can cause an isostructural phase change involving a different octahedral tilt is shorter. Low energy Raman spectroscopy results on CsPbBr₃ have shown that local polar fluctuations at room temperature cause the Cs⁺ ion to be displaced off the center, which induces the tilting in the octahedra. With a higher surface-to-volume ratio, surface fluctuations may be more likely to induce a coherent phase change than that in larger PeNMs, resulting in a lower change pressure.

Composition

The phase change is ultimately a change of the crystal structure. Therefore, the components, especially the A-site cation restricted by the octahedron possesses an impact on the phase change behavior. Due to the lack of relevant comparisons of PeNMs, the trend in single crystals can be inferred. Mannino et al. studied the phase change process in CsPbBr₃, MAPbBr₃, and FAPbBr₃ single crystals based on DFT calculation.⁴³ In the case of materials with similar sizes, the phase change temperatures are very different. In the temperature range of 183–363 K, they claimed that all the samples undergo lattice changes at least from β- to α-phase. The change temperatures were 235, 265, and 361 K for MAPbBr₃, FAPbBr₃, and CsPbBr₃, respectively. More importantly, the β- to α-phase change is optically continuous, indicating a structural relationship between the two phases. In contrast, the discontinuity for the γ- to β-phase change could be attributed to a sharp structural change related to the difference of the A-cation, which influences the vibrational properties of the system. The change of anion also has an impact on the phase change. Yi and co-workers investigated the phase change of CsPbX₃ (X = Cl, Br, I).⁴⁴ They found that only the phase change behavior in CsPbCl₃ occurs at around 193 K, i.e., the PL peak blueshifted to the phase change temperature, followed by a redshift until room temperature. Meanwhile, the PL lifetimes of CsPbBr₃ and CsPbI₃ increased continuously with the temperature, while the PL lifetime of CsPbCl₃ decrease with the increase of temperature and then increased above the phase change temperature.

Compared to other strategies, controlling the phase change behavior in PeNMs by doping is perhaps the simplest approach. Li et al. change the phase of CsPbBr₃ from α- to γ-phase via anion exchange reactions. The results from the transmission electron microscopy (TEM) images and XRD patterns indicate that the addition of Cl⁻ anions does not affect the crystallinity, monodispersity, and morphology of CsPbBr₃, while the addition of I⁻ anions changes the PeNMs from α- to γ-phase (Figure 7A).⁴⁵ In addition to the substitution between halogen anions, other ions also play an important role in regulating the phase change behavior of PeNMs. We investigated the phase stability of MA_xFA_1-xPbI₃ with respect to temperature.⁴⁶ With the increase of x, the sample showed a gradually decrease in size due to the smaller size of MA ions, which results in the larger Pb-I-Pb bond angle in the crystal. We studied the x-dependent phase change temperature as shown in Figures 7B and 7C, which show an initial increase and then a decrease with x due to the uniform strain distribution. When the proportions of MA and FA are comparable, the strains induced by MAPbI₃ and FAPbI₃ will compensate with each other due to the different phase behaviors caused by cation rotation. Since the strains are uniformly distributed while the cations are randomly distributed, the structure is stable within the whole temperature range. Similarly, Vigil et al. reported the tunable phase change in FA_xCs_1-xPbI₃.⁴⁷ The structure decreases in symmetry from the α- to β- to γ-phases with the decrease of x. And the corresponding α- to β- and β- to γ-phase changes occur between x = 0.75–0.5 and x = 0.25–0.1, respectively. Moreover, the doping-induced structural phase changes occurring in Ni²⁺-doped CsPbCl₃ has been revealed.⁴⁸ They performed the Carr-Parrinello molecular dynamics calculations on the 3 × 3 × 3 CsPbCl₃ supercells without and with Ni²⁺ ion replacement (Figure 7D). Starting from the cubic phase of the crystal structure, the pristine CsPbCl₃ becomes the γ-phase after undergoing a strong thermal fluctuation at room and cryogenic temperatures. In the Ni²⁺-doped sample, at room temperature, the Pb-Cl-Pb bonds away from Ni²⁺ dopant center undergoes strong fluctuation with the average tilting angle between 148° and 169° (Figure 7E), while the Ni-Cl-Pb bonds surrounding the Ni dopant can recover to 175° after 3 ps, because the dopants with a smaller ionic radius can release the lattice strain. When the temperature decreases from 300 to 100 K, the Ni-Cl-Pb tilting around the Ni²⁺ dopant of CsPbCl₃ supercell shows an average tilting angle between 165° and 175° (see Figures 7E–7G), corresponding to a small temperature induced change. It can be concluded that Ni²⁺ doping leads to the coexistence of dual subdomains of α- and γ-phases, and retards the phase change from α- to γ-phase in the CsPbCl₃. The variation of phase changes can be attributed to the release of lattice strain due to the size mismatch between Ni²⁺ and Pb²⁺ ions, and the temperature insensitive local structural change in the doped region.

Figure 7.

Effect of composition on phase change of PeNMs

(A) XRD patterns of mixed halide CsPbX₃. Adapted from the study by Liu et al.⁴⁰

(B and C) Temperature range and PL peak energy range for the phase change from γ to β of MA_xFA_1-xPbI₃ (x = 0.8, 0.6, 0.4 and 0.2), respectively. Adapted from the study by Cho et al.⁴¹

(D) Illustrations of the four Pb-Cl-Pb band angles taken from 3 × 3 × 3 CsPbCl₃ supercells with and without Ni²⁺ ion replacement.

(E–G) The Pb-Cl-Pb bond angle evolution starting from initial cubic-phase CsPbCl₃ without and with Ni²⁺ ion replacement at 300, 200, and 100 K. Adapted from the study by Mannino et al.⁴³

Defect

Although PeNMs possess a high defect tolerance, the influence of defect on the phase change behavior should be taken into consideration. The process of the solid-solid phase change depends on the local properties of the material and in particular the presence of structural and chemical defects. Theoretically, the random local field defects are particularly important for first-order phase change between phases with different symmetries, since the difference in the local concentration of such defects can induce phase change at different temperatures and spatial locations. Based on this phenomenon, Dobrovolsky studied the phase change process in methylammonium lead triiodide by micro-PL spectroscopy and super-resolution imaging (Figure 8A).⁴⁹ They found that upon cooling from 160 to 140 K, the crystal with higher defect density readily transforms to the high bandgap γ-phase at higher temperatures, while the crystal with fewer defects retains the β-phase as shown in Figure 8B. Upon irradiation with ultraviolet light, both phases are excited, and most of the moving charge migrates to the low bandgap square domain due to the funnel effect. At the same time, these domains have a lower defect concentration, which together leads to an increase in the PL intensity. Meanwhile, the decrease in domain size is the reason for the blueshift of the β-phase PL spectrum when cooling over the phase change region. In their proposed model, the closer the temperature to 140 K, the smaller the sizes of the β-inclusions (Figure 8C). Smaller domain sizes imply larger stress from the bulk γ-phase surrounding the β-nanoinclusions, which results in a blueshift of the emission. The nature of the defect is also important. It is generally accepted that a wide variety of intrinsic defects (vacancies, substitutions, and interstitials) are possible in MAPbI₃.⁵⁰ In principle, defects which influent the phase change can be of various types and physical locations. The phase change can even be induced or prevented by a grain boundary in a polycrystal. However, for the phase change of samples with PL enhancement, the defect must be the main channel of nonradiative recombination, that is, the defect should have a relatively deep level in the bandgap, such as I_MA, I_Pb, and Pb_I substitutions, and Pb_i interstitials.

Figure 8.

Effect of defect on phase change of PeNMs

(A) 2D map of PL spectrum vs. temperature.

(B) Variation of the normalized spectrally integrated PL intensity.

(C) The proposed model of the phase change in a perovskite crystal with defects. Adapted from the study by Yi et al.⁴⁴

(D–F) The Pb-Cl-Pb bond angle evolution starting from initial cubic-phase CsPbCl₃ with and without Cl vacancy at 290, 200, and 100 K, respectively. And the corresponding snapshots obtained from the Car-Parrinello molecular dynamics calculations. Adapted from the study by Pang et al.⁴⁶

The reversible phase change behavior of CsPbCl₃ is also closely related to structural defects (Cl vacancy).⁵¹ Highly defective CsPbCl₃ are quasi-α-phase at room temperature, in which the α-subdomains gradually convert to the γ-phase upon cooling. In contrast, high-quality PeNMs show a strongly retarded phase change from mixed α- and γ-subdomains at room temperature. Car-Parrinello molecular dynamics simulations as shown in Figures 8D–8F revealed the mechanisms: (i) the Cl vacancy induces a strong local lattice deformation, and more easily leads to a large Pb-Cl-Pb tilting at low temperatures, resulting in lattice contraction; (ii) for the PeNMs with high quality, the smaller Pb-Cl-Pb tilting releases lattice strain, which can suppress the change from quasi-α- to γ-phase. Importantly, the reversible defect-triggered phase change was also found in other CsPbX₃.

Influence of phase change

Phase changes in PeNMs have profound effects on their structural, electronic, and optical properties due to the intrinsic relationship between the crystal structure and the functionalities of materials. In this section, we will explore various aspects of how phase changes modulate the behavior of PeNMs, shedding light on the underlying mechanisms and their implications for optoelectronic applications.

Lattice strain

The phase change in PeNMs can inevitably induce significant lattice strains and structural distortions within the crystal lattice, leading to the change of bond lengths, bond angles, and coordination environments of the constituent ions. For example, the β- to α-phase change in MAPbI₃ involves a contraction of c-axis and an expansion of a-axis, which results in a distortion of the [PbBr₆]^4- octahedral framework.⁵² The time-resolved XRD showed the β- to α-phase change, as evidenced by the decrease of intensity from the distinct β (211) peak, which completely disappears by 373 K. The phase change was further verified by the appearance of cubic features. For the same temperature range, the β (004) and (220) peaks shifted toward each other, corresponding to contraction along the (001) planes (shortening of the c lattice parameter) and expansion along the (110) planes (lengthening of a lattice parameter) as the [PbI₆]^4– octahedra rotate, and finally merged into the cubic (200) peak. The three closely spaced β (114), (222), and (310) peaks were also observed the change to the single cubic (210) peak. Upon further heating above 373 K, the cubic (200) and (210) peaks shifted to a lower Q, indicating expansion of the cubic crystal lattice.

The high pressure XRD experiments as shown in Figure 9A provide more detail evidences of the α- to β-phase change process in CsPbBr₃, which is accompanied by two processes.⁵³ First, the volume compression is mainly due to the contraction of Pb-Br bond, and the octahedral distortion mainly leads to volume compression, and then the volume compression is mainly due to the tilting and rotation of the octahedron. The a-axis shows the greatest compressibility compared to b- and c-axis throughout the entire compression process (Figure 9B). At ambient conditions, parameters a and b are similar, but due to the difference in the compression ratio, the disparity between a and b gradually increases with the increase of pressure. In particular, a and c maintain a continuous contraction, while parameter b abruptly maintains zero compression due to the structural phase change. This particular phenomenon is due to the fact that the Pb-Br bonding network constitutes a structure similar to the “wine rack” at the ab plane. Pb²⁺ acts as a hinge fulcrum, and the Pb-Br bonds act as arms. The Pb-Pb-Pb angle in the a-axis direction is an obtuse angle under ambient conditions. The degree of obtuse angle gradually increases, and Pb-Br bonds gradually stiffen with pressure. When the obtuse angle increases to the critical value and the Pb-Br bonds are sufficiently stiffened, the tension and the external pressure in the b axis direction cancel each other, which results in zero compression.

Figure 9.

Influence of phase change on lattice strain and band structure of PeNMs

(A and B) Unit cell volume and cell parameter evolutions of CsPbBr₃ under pressure and fit parameters. Adapted from the study by Ma et al.⁴⁸

(C) Evolution of MAPbBr₃ structures under four critical pressure values.

(D) Band structures close to the Fermi level under four critical pressure values. Adapted from the study by Yin et al.⁵⁰

Band structure

As aforementioned, the VBM is determined by the antibonding hybridization between the np-orbitals of X and 6s-orbitals of Pb, while the CBM is mostly a nonbonding localized state of Pb 6p orbital, and is thus not sensitive to the change of crystal structure.² Thus, the phase change stemming from the octahedral distortion is bound which lead to changes of the energy band structure, especially VBM. Ideally, it is expected that all bandgap changes of ABX₃-type PeNMs to be very similar. However, this is not the case. A-site cation has a strong influence on the bandgaps, although it is indirect and lies in its structure directing role. It can deform the perovskite lattice in a cation-specific way through steric and Coulombic interactions. The octahedral tilting is then responsible for the changes in the electronic structure near the band edges, leading to the change of bandgap. Many studies have shown that as the perovskites change from the α- to the β- and the γ-phases, the bandwidth narrows in favor of the increased density of states (DOS) on VBM, and the bandgap increases. This can be understood intuitively by visualizing the overlap between the orbitals of Pb and X. In the ideal undistorted perovskite crystal structure, the axial orbital overlap between the X p-orbitals and the Pb s- and p-orbital is optimal, and this overlap leads to a significant broadening of the s-type valence band, thereby significantly increasing the bandwidth and narrowing the bandgap. With the tilting of the octahedra, the axial orbital mixing will become weaker, which results in a narrow bandwidth. Therefore, optimal electronic properties were expected to be found in the higher symmetry perovskites with a linear Pb-X-Pb angle.

For example, the bandgaps of FAPbBr₃ for the γ-, β-, and α-phase were calculated to be about 2.15, 1.96, and 1.85 eV, respectively,⁵⁴ due to the improvement of the crystal symmetry and the associated spin-orbit coupling effects. In more detail, Huang et al. studied the band structure evolution of PeNMs based on the DFT calculation in as shown in Figures 9C and 9D.⁵⁵ When the environment changes (such as increase pressure), the bandgap of PeNMs narrows first and then widens. This can be explained in terms of electronic landscape as follows. First, the shortening of Pb-X bond length facilitates the coupling effect, pushing up the VBM and narrowing the bandgap. With the further increase of pressure, the electron cloud distance between Pb 6s and Br 4p orbitals finally reaches a minimum, and is ready to increase due to the octahedral rotation evaluated by the aforementioned Pb-Br-Pb angle, so the coupling effect become weaker, which leads to the decrease of VBM and widening of bandgap. When the pressure becomes large enough, pressure induced metallization occurs, and the bandgap begins to narrow down all the way to zero when band crossing occurs, which can be ascribed to the strong coupling effect between Pb 6s and Br 4p orbitals in the small pressed crystal cells. Another research for MAPbI₃ has proposed a deeper understanding for this phenomenon. The phase change under low pressure is only due to the intraoctahedral tilt, while the metallization under high pressure is the intra- and interoctahedral distortions.⁵⁶ For VBM, previously nonbonding I 5p orbitals begin to interact with each other to form antibonding I 5p-I 5p∗ orbitals under sufficient pressure, adding to the existing antibonding character of the Pb 6s-I 5p∗ interactions above this pressure. In the case of the CBM, the strong octahedral distortion induces Pb 6p-Pb 6p bonding interactions. The presence of both antibonding Pb 6p-I 5p∗ and bonding Pb 6p-Pb 6p interactions in the CBM lead to a different energetic trend with pressure from that in the VBM state: the Pb 6p-Pb 6p bonding interaction stabilizes the CBM state. Conversely, the VBM state shows a strong destabilization trend, as it is mainly composed of antibonding interactions. The different trends in VBM and CBM energies, associated with different degrees of destabilization with pressure, reduce the bandgap with compression, until the gap finally closes at a predicted 100 GPa for the high-pressure phase. Thus, the additional orbital interactions (I 5p-I 5p∗ antibonding and Pb 6p-Pb 6p bonding interactions) introduced by the significant octahedral distortion are responsible for the eventual metallization of MAPbI₃.

In addition, the presence of lattice strains and structural distortions can further modulate the energy band structure through the deformation potential effect, which arises from the changes in the interatomic distances and bond angles, altering the overlap between the atomic orbitals and the associated energy levels.⁴⁶

Electronic characteristics

The changes in the crystal structure and electronic band structure during phase changes can influence the carrier generation and recombination processes. For example, the formation of structural defects or distortions can create trapping sites or scattering centers, affecting the carrier mobility and recombination dynamics. Trimpl and co-workers revealed a change in trap density at the phase change.⁵⁷ The trends in PL dynamics showed a slight decrease of recombination rates toward higher temperatures above 250 K, which may be related to a possible phase change. They proposed a trap-mediated recombination model to determine the Auger recombination rate constant R_Auger, which is around 2.1 × 10⁻²⁷ cm⁶ s⁻¹ above the phase change, and increases up to 5.8 × 10⁻²⁷ cm⁶ s⁻¹ with the decrease of temperature under the phase change. The trap density extracted for the high temperature phase is estimated to b 2.5 × 10¹⁵, and 1.5 × 10¹⁶ cm⁻³ for the low temperature phase. The defect density appears to be lower for the high temperature phase, which is positive for photovoltaic applications.

Another explanation for the life extension at high temperatures is related to the disordered nature of organic cations. Shi et al. demonstrate that structural disorder arising from the phase changes is as important as the disorder due to heating in the same phase.⁵⁸ Figure 10A shows the MAPbI₃ simulation cells of the γ-phase heated to 162 K (denoted as Ortho-162 K), the β-phase heated to 162 K (Tetra-162 K), the β-phase heated to 315 K (Tetra-315 K), and the α-phase heated to 315 K (Cubic-315 K). In Figure 10B, the carrier lifetimes increase with the increase of temperature both in the same phase and upon change to the higher temperature phases, because the structural disorder induces partial charge localization, which reduces non-adiabatic coupling and shortening the quantum coherence. They systematically investigated the temperature dependent nonradiative electron-hole recombination process in different phases of MAPbX₃ by performing nanoscale molecular dynamics simulations combined with real-time time dependent density functional theory (TDDFT). The calculations showed that the interaction between the inorganic and organic components depends strongly on the phase. The perovskite geometric structure is relatively ordered up to 162 K in the low temperature γ-phase, where the charge carriers are delocalized, overlap well, interact strongly, and recombine efficiently. The change in the structural symmetry to the β-phase causes slight distortions, and allows stronger atomic fluctuations, which induce partial charge localization. As a result, the electrons and holes overlap less and live longer. When the temperature reaches 315 K, the thermal fluctuations increase significantly, the inorganic lattice becomes more distorted, and the organic cations rotate almost freely. Such a strong structural disorder facilitates charge localization and exciton dissociation. Therefore, the charge carrier lifetime in the higher temperature α-phase is longer than that in the lower temperature β-phase. On the other hand, enhanced thermal atomic fluctuations increase the anharmonicity and activate more phonon modes, favoring faster elastic scattering, and coherence loss. The reduced coupling and shortened coherence time favor longer charge carrier lifetimes at higher temperatures.

Figure 10.

Influence of phase change on electronic and optical properties of PeNMs

(A) Representative geometries of MAPbI₃ for the γ-162 K, β-162 K, β-315 K, and α-315 K phases.

(B) Pure-dephasing functions for the CBM-VBM change in the γ-162 K, β-162 K, β-315 K, and α-315 K MAPbI₃ systems. The inset shows the unnormalized autocorrelation functions of the CBM-VBM bandgaps. Adapted from the study by Zhang et al.⁵³

(C) Temperature-dependent carrier mobility and diffusion length of CsPbBr₃.

(D) The value of exponent changes with Br content in CsPbI_3-xBr_x. Adapted from the study by Trimpl et al.⁵⁷

(E) Pressure dependence of optical absorption of MAPbBr₃. Adapted from the study by Shi et al.⁵⁸

It is known that the maximum achievable carrier mobility in PeNMs is set by the Fröhlich electron-phonon coupling associated with the stretching motion of the Pb-X bonds.⁵⁹ The length and angle of the Pb-X bonds change with the phase change, which naturally affects the carrier mobility. For example, the phase-change dependent charge transport in MAPbI₃ was studied by applying the temperature dependent time-of-flight measurement.⁶⁰ The phase change of MAPbI₃ can easily switch from β- to α-phase at around 310–330 K. For hole measurements, the transient time first increases slightly when the temperature increases from 295 to 310 K, and then decreases rapidly when the temperature further increases to 330 K. As a result, the highest hole mobility reaches 1.95 × 10⁻⁴ cm² V⁻¹ s⁻¹ at 310 K, while the lowest is 5.92 × 10⁻⁵ cm² V⁻¹ s⁻¹ at 325 K. In comparison, the temperature dependence of the electron mobility is slightly different from that of hole mobility. For electron measurements, the transient time increases when the temperature increases from 270 to 330 K, followed by a rapid decrease with the further increase from 330 to 360 K. The highest electron mobility of 1.52 × 10⁻⁴ cm² V⁻¹ s⁻¹ is obtained at 330 K. And at 320 K, both hole (1.32 × 10⁻⁴ cm² V⁻¹ s⁻¹) and electron (9.46 × 10⁻⁵ cm² V⁻¹ s⁻¹) mobilities become most balanced. Meanwhile, when the temperature is increased from 303 to 323 K (phase change), and from 343 to 363 K (pure α-phase), the conductivity of the pure MAPbI₃ film gradually increase. However, the conductivity maintains identical when the temperature changes from 323 to 343 K, which is exactly located within the temperature range of the phase change. The observation indicates that electrical conductivity tends to keep unchanged during the phase change regardless of temperature change.

The structural phase change could induce changes in dielectric and effective mass, both of which are closely related to mobility and carrier diffusion length.⁶¹ Yuan et al. elucidated the mechanism of how the phase change influents the carrier mobility.⁶² There is an abrupt decrease in mobility when the phase of CsPbBr₃ transits from the γ-/β- to α-phase (Figure 10C). When the structure symmetry is improved (γ/β → α), the lattice fluctuation will be changed. This leads to weaker active vibration modes, which results in a decrease of the charge transfers complexity. In addition, the repaid decrease in mobility could be attributed to the decrease in exciton fraction across the γ-/β- to α-phase change, which results from the phase-dependent exciton binding energy. On the other hand, the exponent in Figure 10D shows the lowest value in the case of CsPbI_1.5Br_1.5, indicating acoustic-phonon dominated carrier scattering, which is instigated by the serious imbalance of charge distribution, which results in weak Coulomb binding energy between [PbX₆]⁴⁻ octahedra and the decrease of carrier mobility.

It has been reported that the ionic component of the halide perovskites can be enhanced by the sequential phase changes,¹⁴ which can initiate the displacement of certain atoms from their designated positions in the lattice, and create local charged defects. The charged defects can induce electrostatic potentials, which will locally affect the carrier density but without changing the stoichiometry of the material. This is also one of the reasons for the change of mobility.

Optical properties

The optical properties of PeNMs are strongly dependent on their characteristic structural phases, which produce different band structures. The phase change phenomena in halide PNCs can affect the PL, which is typically accompanied by spectral shape variations.

As discussed earlier, phase changes can lead to shifts in the energy band structure, resulting in changes in the absorption and PL emission spectra of PeNMs, and examples have already been given in the chapters previously, including temperature, pressure, light, and so on. In our previous report, the emission peak of FAPbBr₃ remains almost constant below 100 K. Then, a redshift is observed from 100 to 140 K, which can be attributed to the phase change. With the further increase of temperature, it shows a blueshift, which can be attributed to the stability of the out-of-phase band edge state with the lattice expansion.¹⁷ The high pressure experiments were performed to investigate the optical absorption of MAPbBr₃.⁶³ The absorption edge first shows a redshift with pressure up to around 0.7 GPa, then the absorption edge shows a blueshift under compression up to 3.8 GPa (Figure 10E). These general tunable spectral shifts enable tunable optical properties for specific applications, such as LEDs or photodetectors operated at different wavelengths.

In addition, it has been reported that MAPbI₃ exhibits abnormal luminescence properties during the β- to γ-phase change from 150 to 120 K. Two luminescence features upon the β- to γ-phase change are observed in steady-state PL measurements. β-inclusions in the γ-phase of MAPbI₃ can potentially trap photo-excited excitons due to the narrower bandgap of β-phase. Thus, a large density of free excitons could agglomerate and eventually recombine within these inclusions. Particularly, the excitons with a large binding energy trapped in β-MAPbI₃ during the phase change provides a potential candidate for optoelectronic device applications, especially for lasers since the exciton confinement will decrease the gain threshold.

Several theoretical investigations based on DFT calculations have been conducted to predict and validate the influence of the phase change on the optical properties of PeNMs. Jang et al. predicted the phase dependent structures of MAPbX₃, and then calculated their structural properties with corresponding bandgaps.⁶⁴ All the properties were eventually related to the direct or indirect change in the PL properties. In particular, it was found that the β-phase is marginally (<0.01 eV atom⁻¹) more stable than the α-phase, however, indicating that both structures can exist at room temperature. With respect to the structural composition dependent PL decay lifetime of MAPbX₃, they proposed that the PeNMs with β-phase exhibit more efficient charge separation and slower recombination rate. A similar DFT study elucidated that the bandgap of MAPbI₃ was affected by the change between γ- (1.90 eV) and β-phases (1.82 eV), and this variation also occurred due to the MA⁺ distribution.⁶⁵ The experimental results clearly indicate that the interaction between the MA⁺ and the inorganic framework can affect the crystal structure, which adjusts the electronic structure and the bandgap accordingly. Although the calculated absorption spectrum appeared to be similar in shape to the experimental one, the excitonic peaks showed a redshift with the phase change from γ- to β-structures.

Applications of phase change

Solar cells and emitters

In theory, the phase change modifies the electronic band structure and thereby affects the optoelectronic properties of the perovskite photoactive layer. However, recent studies have shown that in applications that do not involve ferroelectric effect, such as solar cells and LEDs, the performance of the devices is hardly limited by the phase change. For example, Jacobsson et al. demonstrated that MAPbI₃ exhibited only slight change in optical properties over the temperature range from 83 K to 353 K.⁶⁶ They carried out the optical absorption experiment and found that the shift of the absorption onset was rather small with temperature (Figure 11A). Specifically, while the temperature was changed from 353 K down to 83 K, the bandgap shifted from 1.61 to 1.58 eV. And no discontinuities or changes in the slope of the bandgap versus temperature were observed around the phase change temperatures (327 K for the β- to α-phase change, and 160 K for the γ- to β-phase change). From a practical point of view, a bandgap change of 0.03 eV is very small, especially considering a temperature change of nearly 300 K. It can therefore be concluded that the optical properties of PeNMs are almost constant. Therefore, as shown in Figures 11B and 11C, most of the solar cells showed large, but reversible performance changes in this range, which could be attributed to the photogenerated charge carrier separation and transport in the electrical effect, but not the optical effect. Similarly, Quarti et al. have reported that the bandgap of MAPbI₃ does not change sharply across the phase change between β- and α-phase.⁶⁷ They measured the in situ absorption of the materials in the temperature range of 270–420 K. The absorption spectrum shows a monotonous blueshift with the increase of temperature without abrupt change across the phase change temperature. According to the molecular dynamic simulation and XRD measurements, the phase at higher temperature is expected to be cubic on a timescale of 10 ps. On a sub-picosecond timescale, the higher temperature phase is more distorted than that for the cubic symmetry, which is related to the activated motion of organic cations as well as fluctuations in the inorganic framework.

Figure 11.

Effects of phase change on solar cells and emitters based on PeNMs

(A) Absorption at different temperatures.

(B and C) Device performance as a function of temperature from room temperature up to 80°C, and from room temperature down to −190°C, deduced from a scan with a rate of −0.1 V s⁻¹. Adapted from the study by Chin et al.⁶¹

(D) PL emission spectra of PeNMs at the temperature of 120 K with the pumping powers ranging from 0.01 mW to 1 mW. The inset denotes the maximum photon emission energy at each PL measurement.

(E) Lasing threshold in a temperature range from 77 to 240 K.

(F) The wavelength difference (detuning) between the lasing and the spontaneous emission peaks at different temperatures. Adapted from the study by Liang et al.⁶³

The effect of phase change on emitters is basically the same as that in solar cells. However, it is worth mentioning that Kao et al. reported the lasing behavior related to the phase change.⁶⁸ They investigated the coherent light emission properties with different phases of the PeNMs based on the temperature dependent PL measurements. In Figure 11D, a spectral change from spontaneous emission to lasing was observed with the increase of excitation power at a temperature of 120 K. The β-phase can coexist with the γ-phases at different temperatures with different ratios of composition. In the coexisting phases, the β-inclusions can trap more photo-excited carriers than the γ-phase, due to the lower CBM in the β-phases. Upon stronger excitation, the carrier density in β-phase may saturate, and a significant number of carriers may recombine within the γ-phase, hence causing substantial emission at the correspondingly higher energy and thus slight spectral blueshifts before the amplified spontaneous emission (ASE) starts. The presumption of the coexisting states may also indicate that the carrier density and the number of the β-phase are at an equilibrium state at 120 K, giving the lowest power threshold for lasing as indicated in Figure 11E. With the further decrease of temperature, more γ-phases were generated in perovskite thin films, which results in a higher power threshold. Furthermore, under weak excitation, the low number of initially free carriers may just partially fill the sub-gap distribution of states in the β-phase, giving a broadened and downshifted emission observed from the PL spectra. As the temperature exceeded 120 K, the threshold continues to increase because of the thermal broadening of gain spectrum, which is similar to the conventional lasing behavior. Figure 11F represents the peak position difference (detuning) between the lasing mode and the spontaneous emission of PeNMs at different temperatures. The detuning originates from the balance between absorption and light amplification spectra formed by the random cavities. It is shown that the spectral peak positions of the spontaneous emission are quite close to the lasing peaks when the temperature is lower than the characteristic temperature T_c. With the increase of temperature, the lasing wavelength slightly shifted 10 nm within a wide temperature range, while the spontaneous emission showed a dramatic change from 787 to 753 nm, corresponding to an energy difference of about 70 meV. The increase of detuning value could be the results of broadening absorption edge with higher temperature, which pushes the lasing peak away from the spontaneous emission peak.

Sensors

Sensors are needed in various fields such as environmental detection, biomedical detection, and microprocessor monitoring. The reversible phase changes by external stimuli can be reflected in the emission from PeNMs, which makes them suitable for fluorescent sensors. Saraf et al. fabricated a light-harvesting, self-powered tactile sensor capable of operating for at least 72 h after poling under visible light illumination.⁶⁹ The sensor takes advantage of the change from β- (which is ferroelectric) to α-phase (which is not ferroelectric) in MAPbI₃. The proposed ferroelectric properties of the MAPbI₃ films and their effect on generating V_oc and J_sc were investigated by poling under 1.0 sun illumination and ambient conditions. These conditions reflect that light-stimulated ordering of MA⁺ ions enhance the ferroelectric behavior of MAPbI₃, while the presence of O₂ will subdue the proposed p-n junction behavior. The V_oc and J_sc due to ferroelectric polarization were shown in Figures 12A and 12B. When the phase change from β- to α-structure occurs at 330 K, both V_oc and J_sc effects disappear (Figures 12C and 12D), which further confirms the proposed ferroelectric characteristic. The effects are restored on cooling the film back to room temperatures. The sensor decoupled the energy harvesting and pressure sensing, exhibiting a linear response up to 76 kPa with a sensitivity of 0.57 kPa⁻¹. This device could be interesting for remote wearable sensing or continuous monitoring applications.

Figure 12.

Effects of phase change on sensors based on PeNMs

(A and B) V_oc and J_sc cycles after 0.5, 1, 1.5, and 2.5 V μm⁻¹ poling for 5 min.

(C and D) V_oc and J_sc of the MAPbI₃ device before poling at room temperature and after 1 V μm⁻¹ poling for 5 min at room temperature, 330 K, and after cooling to room temperature. OFF refers to V_oc and J_sc measured under dark, and ON refers to V_oc and J_sc measured under 1.0 sun illumination. Adapted from the study by Jang et al.⁶⁴

(E) PL quenching with addition of 0.01 mM nitrophenols in CsPbBr₂I.

(F) Percentage of quenching with the addition of different concentrations of TNP in CsPbBr₂I.

(G) Linear fits of the Stern-Volmer plot for TNP. Adapted from the study by Geng et al.⁶⁵

Aamir et al. demonstrated the potential applications of PeNMs for nitrophenol explosive sensors.⁷⁰ They confirmed that the phase purity of CsPbBr₂I determines the PL intensity, and verified the ability of PeNMs to detect nitrophenols. In Figure 12E, with the successive addition of 2,4,6-trinitrophenol (TNP) into CsPbBr₂I, the PL from the samples quenches monotonically. The addition of 1.6 × 10⁻⁶ mol L⁻¹ of TNP leads to 54% PL quenching with the Stern-Volmer quenching constant (K_sv) of 6.9 × 10⁴ mol L⁻¹. However, after the gradual addition 1 × 10⁻⁵ mol L⁻¹ of TNP, quenching of the PL takes place up to 85% (K_sv = 3.7 × 10⁵ mol L⁻¹) (Figure 12F). In addition, the hydroxyl group can form hydrogen bonding with the PeNMs surface, which can promote efficient electron transfer between the PeNMs and TNP, also leading to the PL quenching. A linear behavior was observed between the TNP concentration and I₀/I as shown in Figure 12G. These results suggest that the as-prepared CsPbBr₂I inorganic PeNMs have comparable PL quenching percentage in relation to CH₃NH₃PbBr₃ hybrid PeNMs. The mechanism of PL quenching can be attributed to either π-π stacking (benzene ring) and/or hydrogen bonding arising from hydroxyl group of TNP with the perovskite structure. It has been reported elsewhere that there is very fast and effective charge separation along with exciton diffusion in perovskite,⁷¹ which could be driving force for the electron transfer from the electron donor perovskite to the electron deficient TNP.

Memory

The hysteresis in the current-voltage responses makes PeNMs a candidate for resistive switching memory devices. At present, most PeNMs-based memories take advantage of the change from the perovskite to the non-perovskite phase, but there is very little research on the change from the γ- to α-phase. Hwang et al. evaluated the MAPbI_3-xBr_x (x = 0, 1, 2, 3) as a component in nonvolatile memory devices.⁷² They quantified the effect of Br incorporation on the electrical properties of the PeNMs with different compositions. With the increase of Br content, the color of the sample changed from semi-transparent dark brown to light brown, then to yellow. XRD patterns indicated that the β-phase of MAPbI_3-xBr_x remained until x = 1 and then changed to α-phase around x = 2. As the β-phase transited to α-phase, the [PbX₆]^4- octahedron rotated along the <001> axis, while the connection to the corner-shared octahedron remains, and this leads to pseudo α-lattice. The resistive switching random access memory (ReRAM) based on PeNMs showed that the reduction in the “set” electric field when Br replaces I (Figure 13A), reduces the power consumption of the device. Figures 13B and 13C evaluated the data retention property of the memory device with a reading voltage of 0.2 V at room temperature. The best device shows the lowest operating electric field of around 3.44 × 10⁴ V cm⁻¹, with long data retention over 10⁴ s and good endurance property. In addition, MAPbI₃ may be a low-cost candidate for ultrahigh capacitance devices.

Figure 13.

Effects of phase change on memory based on PeNMs

(A) Statistical distribution of set electric fields of the hybrid perovskite resistive switching memory.

(B) Data retention characteristics of LRS and HRS states at room temperature.

(C) Switching endurance of perovskite memory device. Adapted from the study by Quarti et al.⁶⁷

(D) Galvanostatic charge-discharge curves of the CH₃NH₃PbI₃ perovskite device at six different temperatures while holding a constant current density of 5 mA cm⁻².

(E) Measured and modeled device discharge curves with current densities of 2, 5, and 10 mA cm⁻² and constant temperature of 300 K.

(F) Cyclic voltammograms of the device at six temperatures and constant scan rate of 5 mV s⁻¹.

(G) Device cyclic voltammograms at scan rates of 2, 5, and 10 mV s⁻¹ and constant temperature of 300 K. Adapted from the study by Kao et al.⁶⁸

Slonopas et al. pressed and sintered the pseudo-β-phase MAPbI₃ that are sandwiched between two gold contacts for supercapacitors.⁷³ In Figure 13D, it can be observed that there is a strong temperature dependence in the charge-discharge curves when a constant current density of 5 mA cm⁻² is maintained. The resulting halide perovskite supercapacitor achieves an energy density of 34.2 Wh kg⁻¹ at 100 Hz at room temperature and a mean areal capacitance of 432 mF/cm². More importantly, the performance of supercapacitor is temperature dependent. A nonlinear jump in the charge time was observed between 150 and 200 K, and was identified again between 300 and 350 K. These discontinuities in temperature dependent charge time are attributed to the perovskite phase change from γ to β, and from β to α at 165 and 330 K, respectively, which leads to the time extension of charge and discharge. The discharge curves are highly linear with temperatures, indicating good electrical double layer performance across a broad range of temperatures. Furthermore, the linearity is observed across the entire discharge regions. This result signifies that the redox process operates at a constant rate in both the inner and outer Helmholtz Plane. These results are indicative of the possibility of utilizing PeNMs for supercapacitor applications. Figure 13E displayed the measured and modeled discharge times of three current densities, and indicated that there is a proportionally large discharge relative to the current density. A good correlation between the measured and modeled data are observed signifying that the capacitor is self-discharging. Discharge in CH₃NH₃PbI₃ is temperature dependent, and can be compensated by implementing heating and cooling elements in conjunction with a feedback controller. Figures 13F and 13G showed the high degree of symmetry in the cyclic voltammetry hysteresis curves at various temperatures and scan rates, respectively. The curves retained their highly rectangular shapes through repeated cycling (5 measurements/device at 3 cycles/measurement). These results indicate high electrochemical stability and capacitance across all perovskite phases.

Conclusions, challenges, and perspectives

The phase change behavior in PeNMs has emerged as an exciting frontier in materials science and nanotechnology. The ability to induce and control reversible phase changes between different structural phases (α, β, γ) offers unique opportunities to tailor the functionalities of these materials. Significant progress has been made in understanding the underlying mechanisms of phase changes, such as temperature, pressure, and light induced changes. Advanced characterization techniques and theoretical modeling have provided valuable insights into the structural dynamics, atomic rearrangements, and associated electronic structure changes during these phase changes.

Although the fields of photovoltaics and optoelectronics are among their most promising applications, the impact of intraoctahedral phase change on both is almost negligible. However, it is worth noting that the phase change behavior has opened up opportunities in other areas beyond optoelectronics, including ferroelectrics, piezoelectrics, and energy storage. The ability to induce ferroelectric and piezoelectric properties through phase changes could lead to the development of new types of sensors, actuators, and energy harvesting devices.

However, before the full potential of phase deformation can be realized, the following challenges needed to be addressed.

• (1)One critical issue is the long-term stability and durability of these materials under various operating conditions. Environmental factors, such as moisture, oxygen, and thermal stress, can significantly affect the phase stability and device performance.
• (2)Another challenge lies in the precise control and tunability of phase changes. While external stimuli such as temperature, pressure, and light can induce phase changes, achieving precise and localized control of these changes remains a formidable task. The development of new strategies for spatial and temporal control of phase changes is crucial for the realization of advanced functionalities and device architectures.
• (3)Lead-free halide PeNMs are another hot topic in research at the moment, due to their environmental benefits. Although the optoelectronic and photovoltaic properties are not yet comparable to those of lead-based halide PeNMs, this kind of PeNMs has a softer lattice, which makes it more susceptible to crystal distortion. This gives lead-free halide PeNMs better ferroelectric, dielectric, piezoelectric, ferromagnetic, and multiferroic properties, making them very suitable for a range of optical, electrical, and magnetic applications. However, the fundamental understanding of the microscopic mechanisms and kinetics of phase change is still lacking for many lead-free systems. Applying advanced computational approaches like first-principles calculations, machine learning etc. in synergy with experiments can unravel change pathways behavior.
• (4)In addition, the integration of PeNMs into existing device platforms and manufacturing processes presents additional challenges, such as thermal/electrical degradation, fatigue, and defect interactions. Research on interface/surface engineering, protective coatings, and composites could mitigate these challenges. In addition, the compatibility with different substrates, scalability, and cost-effective fabrication methods are essential for practical applications.
• (5)
  Although the following applications have not yet been realized, the intraoctahedral phase change in PeNMs may be more widely used in future scenarios:

  • i)
    Neuromorphic computing and artificial intelligence: the ability to dynamically tune the electrical and optical properties of PeNMs through phase changes could enable the development of computational architectures and neuromorphic devices that mimic the behavior of biological neural networks.
  • ii)
    Adaptive optics and tunable optical devices: the modulation of optical properties, such as refractive index and absorption, through phase changes could lead to the development of tunable lenses, filters, and other optical components with applications in imaging, sensing, and communication technologies.
  • iii)
    Responsive and adaptive coatings: phase change PeNMs could be incorporated into smart coatings and surfaces that can dynamically adapt their properties (e.g., wettability, reflectivity, or color) in response to external stimuli, enabling applications in self-cleaning surfaces, energy-efficient windows, and camouflage technologies.

Despite these challenges, the field of phase change metal halide PeNMs holds great promise. Continued research efforts in materials synthesis, characterization, and device development are expected to unlock the full potential of these versatile materials. Interdisciplinary collaborations among chemists, physicists, materials scientists, and engineers will be critical to driving the development of innovative applications and technologies based on phase change perovskites.

Limitations of study

Due to space limit, some important works may not be fully discussed and acknowledged.

Acknowledgments

The authors acknowledge the assistance of SUSTech Core Research Facilities. This work is supported by the National Natural Science Foundation of China (11574130, 62104052), Science, Technology and Innovation Commission of Shenzhen Municipality (JCYJ20220530113015035, JCYJ20210324120204011), and Natural Science Foundation of Guangxi Province (2021GXNSFBA196088).

Author contributions

Conceptualization: X.Z. and R.C.; visualization: X.Z. and S.Z.; writing—original draft: X.Z. and R.Z.; writing—review and editing: X.Z. and S.W.; copyright: X.Z., L.H., P.W., and Z.H.; funding acquisition: R.L. and R.C.; supervision: X.Z. and R.C.

Declaration of interests

The authors declare no competing interest.