Analysis of Ca_1-xSr_xCO₃ phases generated by competitive Sr²⁺ replacement in pre-formed aragonite

Abstract

The ratio of Sr/Ca ions in marine biogenic minerals is considered advantageous for tracking geochemical and biomineralization processes that occur in the oceans. It is debatable, though, whether the ratio in biominerals such as coral skeleton is simply related to values in the seawater environment or controlled by the organism. Recent data show that coral larvae produce partially disordered immature aragonite in Mg-containing Sr-poor calcifying fluids, which transforms into well-ordered aragonite in Mg-depleted Sr-enriched environments, upon animal metamorphosis into the sessile polyp state.

Inspired by the process in young coral, we explored in vitro substitution of Ca by Sr in aragonite by exposing aragonite crystals precipitated a priori to Sr solutions with variable concentrations. The resulting biphasic material, comprised of Sr-doped aragonite and Ca-doped strontianite, was carefully analyzed for foreign cation substitution in each polymorph. This allowed to establish a linear correlation between Sr levels in mineralizing solutions and Sr in aragonite as well as Ca in strontianite. It indicated that ca. 5-fold higher Sr solution concentration is needed for substitution in the crystal to reach the level found in corals. It also provided with Sr levels required for a putative strontianite phase to form.

Graphical abstract

Highlights

• •Young coral skeleton matures via Sr²⁺ upregulation near nascent aragonite crystals.
• •We mimic biomineralization by varying Sr²⁺ levels in 2nd-step mineralizing fluid.
• •Sr/Ca in disordered phases were found to be lower than in crystalline phases.
• •Seven-fold higher [Sr²⁺] in fluid needed to achieve [Sr²⁺] in coral skeleton.

1. Introduction

Aragonite is harnessed by corals, mollusks, and other marine life forms as the material-of-choice for construction of functional hard tissue. Biogenic aragonite is found to be doped by strontium ions in low amounts. The Sr/Ca ratio in coral aragonite skeleton is considered a good proxy for sea surface temperature, relying on the temperature dependence of the ratio in seawater and the premise of direct proportionality of Sr/Ca values in the scleractinia exoskeleton and in surrounding waters [1,2]. Yet, the factors that dictate Sr vs. Ca partitioning between seawater, intracellular compartments and the extracellular fluids that serve as mineralization fronts from which calcium carbonate skeletons grow are far from being understood [[3], [4], [5], [6]]. Studies seeking to trace mechanisms of Sr intake by stony coral [7] pointed to the involvement of ion-selective biological control during calcification, known as a “vital effect” [8]. Yet, Sr transporters, similar to ATPases for calcium, that can actively regulate translocation of Sr ions across the cell membrane, have not been found. Moreover, the poor cationic selectivity of ATPases to Ca ions permits Sr ions to be translocated as well. It also allows the minor ion to bind and inhibit ATPase transport activity either competitively [9] or in mixed-mode [10]. This may explain lower Sr skeletal uptake in seawater with high Ca concentrations and under high calcification rates [6,7].

Corals, at their early larval stage in life, were recently shown to deposit immature aragonite and amorphous calcium carbonate inside Mg-containing compartments in the endoderm [11]. These deposits ripen into larger well-ordered aragonite crystallites with the introduction of Sr ions and decrease of Mg ions upon metamorphosis into polyp [12] suggesting ion modulation as a putative regulatory activity [11]. Sr/Ca ratios in young polyp aragonitic deposits, measured using energy dispersive X-ray data in that work, were higher than in the adult polyp, suggesting ion levels may vary again at later stages of coral life.

Currently, incorporation of the two cations, calcium and strontium, into skeletal material is considered to involve pathways that are kinetically and/or biologically rather than thermodynamically controlled and due to slow diffusion, cation ratios in minerals remain kinetically trapped over time [[13], [14], [15]]. Models of non-isotropic distribution of dopants due to such kinetic effects that partition differently Sr in crystal surface growth zones vs. deep in the core of the crystal [16], help partly explain the variation in coral, including seasonal fluctuations.

In addition to dispersion inside aragonite subunits, Sr was also reported to be present in Scleractinia skeletons as the iso-structural mineral, strontianite (SrCO₃). Using fine structure and near-edge X-ray absorption analysis, as much as 40 % of the cation in coral skeleton was reported to be in a separate strontianite phase [17]. The miscibility gap between the two carbonate phases was first reported to be in the range 0.0058 ≤ x ≤ 0.875 at 25 °C, where x is Sr molar fraction [18]. Thermodynamic stability of the two minerals in a Ca_1-xSr_xCO₃ mixture was maximal when cross doping occurred, i.e., with 0.58 mol% of Sr in aragonite and 12.5 mol% of Ca in strontianite. Later, Ruiz-Hernandez et al. [19] calculated a smaller miscibility gap (0.12 ≤ x ≤ 0.87) which put the lower boundary of the gap outside the typical Sr/Ca ratio in coral skeletal aragonite. These works employed precipitation from a common solution of the two ions. Yet, it would be interesting to elicit Sr/Ca fractionation between mineralizing fluids and solid products in experiments pertaining to the young coral case, whereby the Sr ion is introduced into the fluid phase after the CaCO₃ mineral has already started forming and compare to typical co-precipitation cases [20].

Seeking to further explore coral aragonite mineralization through the transformation from planula to polyp, we designed a two-step in vitro experiment whereby immature aragonite was first precipitated by titrating a Na₂CO₃ solution into a MgCl₂/CaCl₂ solution (Mg:Ca molar ratio, 5:1) and then Sr was incorporated into the pre-formed minerals by titrating a SrCl₂ solution into the reaction mixture. The second step was repeated using a wide range of Sr concentrations. Competitive cation substitution resulted in the formation of Sr-doped aragonite at very low [Sr²⁺] and in the formation of a biphasic mixture of Sr-doped aragonite and Ca-doped strontianite at [Sr²⁺] above a threshold.

Morphological changes in the minerals formed were monitored using electron microscopy. Disordered phases on Sr-aragonite and Ca-strontianite crystal surfaces were characterized using solid-state NMR (ssNMR). Observed lattice unit cell expansions in the two crystal polymorphs were related to Sr concentration in aragonite lattice (and in strontianite lattice) from powder X-ray diffraction (pXRD) analysis. Interestingly, a linear relation was evidenced between dopant concentrations in the crystal and Sr concentration in mineralizing solutions. It was used to correlate unit cell expansion with Sr content in solution and to deduce [Sr²⁺] in solution required to obtain a [Sr²⁺] in aragonite that matches coral skeleton aragonite and values needed to start forming strontianite. Lattice vibrations in Micro-Raman measurements were used to corroborate transitions in the biphasic material. Furthermore, the Sr/Ca ratios inside the two crystalline phases and in precursor solutions were also compared, in select samples, to overall Sr/Ca ratio in the solid precipitate as derived from inductively coupled plasma (ICP) elemental analysis measurements to infer partitioning of the two cations in disordered vs. crystalline phases.

2. Materials and methods

2.1. Materials

Anhydrous sodium carbonate (CAS Number 497-19-8) was purchased from Merck and used as is. Fresh calcium chloride dihydrate (CAS Number 10035-04-8) was purchased from Sigma-Aldrich and magnesium chloride hexahydrate (CAS Number 7791-18-6) was acquired from ACROS; they were used without further processing. Strontium chloride hexahydrate (CAS Number 10025-70-4) was purchased from Merck and used as is. Potassium hydroxide (CAS Number 1310-58-3) was purchased from BIO-LAB and used without processing. Solutions for experiments were prepared using double distilled water (DDW), except for control experiments, in which analytical water was used, Merck (CAS Number 7732-18-5). Details on the control experiments are given in the supporting information.

2.2. Mineral synthesis

A two-step process was devised to emulate the mineralization observed in coral planulae. The precipitation experiments were performed at an ambient temperature (25 ± 3 °C). In the first step, into a 200 ml 50 mM MgCl₂/10 mM CaCl₂ solution stirred at 98 rpm (pre-set to a pH of 9.2 using ∼0.04 ml 0.1M KOH), 100 ml of 20 mM Na₂CO₃ solution was titrated using a peristaltic pump at a rate of 1 ml/min to induce precipitation of calcium carbonate from an alkaline Mg-containing fluid. The solution pH was maintained at 9.2 throughout the titration by adding 50–100 μl aliquots of 0.1M KOH solution as needed, every 5 min. At the end of the titration, the reaction mixture was left unstirred for another 60 min. During this time, the reaction solution pH decreased to 8.4. In the second step, the reaction solution was first corrected to pH 9.2 and stirred at 98 rpm, and then 100 ml 0.09 mM SrCl₂ solution was titrated in, at a rate of 1 ml/min using a peristaltic pump. The pH was controlled and corrected as needed in this step as well, using 50–100 μl aliquots of 0.1M KOH, every 5 min. Dilution effects due to pH corrections (3 ml in the first step and 4 ml in the second step) were negligible. At the end of step 2, the reaction mixture was left for 3 days to allow crystal growth and aging without stirring. At the end of aging, the solid precipitates were filtered and washed with double-distilled water (DDW) and dried in the oven at 37 °C for a week.

Note that the final workup step may have removed minor amounts of leftover amorphous phases at the end of aging and promoted further maturation of crystals and partly disordered phases. The precipitation experiments were repeated using starting SrCl₂ concentrations ranging between 0.09 mM and 90 mM before addition (0.0225 mM and 22.5 mM with dilution accounted for) in step 2. The binary minerals produced, Sr-aragonite and Ca-strontianite, had varying levels of the Sr ions and are denoted as a total mineral Ca_1-xSr_xCO₃ for brevity, where x denotes the molar fraction of Sr in the two crystalline minerals in total.

To explore what mineral phases are formed immediately after the end of the first step, (before SrCl₂ addition), and at the end of the second step, and eliminate any concerns that aging or workup have had major effects on the mineral products, we performed control experiments (I-IV) and measured powder XRD data on the fresh precipitates (Figs. S1–S2). We also performed calculations of mineral and dissolve inorganic carbonate concentrations throughout the titration of Na₂CO₃ in the first step (Fig. S3). For additional details on these control experiments see the supporting information.

2.3. Powder X-ray diffraction

XRD patterns were obtained on a Rigaku SmartLab X-ray diffractometer using Cu Kα radiation (at 40 kV and 30 mA) in Bragg-Brentano geometry. Data were collected over a 2θ range of 15–90° at a step size of 0.0152°. Powder X-ray diffractograms were measured at a scan rate of 1 deg/min (ca. 80 min per sample). For accurate quantitative XRD analysis, such as lattice parameters and reference intensity ratio (RIR) measurements, the samples were mixed with Lab₆ (SRM-NIST 660c) (15 wt%) as an internal standard. Diffractograms were measured at least two times on the samples, with and without Lab₆. Reproducible reflection patterns of the mineral samples were obtained in these measurements. The RIR is defined as the ratio of the intensity of the strongest peak of phase α to the strongest peak of standard s and follows the equation ${RIR}_{\alpha s}=\left(I_{i\alpha }\bullet W_s\right)/\left(I_{js}\bullet W_{\alpha }\right)$, where $W_{\alpha }$ and $W_s$ are the weight fractions of phase α and standard s, respectively.

The patterns were fitted using whole pattern fitting module in the Jade software to refine the lattice parameters. The initial values lattice parameters of aragonite and strontianite were taken from PDF4-ICDD: # 04-008-5421 and # 04-019-1397, respectively, while the internal standard lattice constant was fixed to $a=4.15683\AA$ (# 00-059-0332). A typical fitted pattern is shown in the supporting information (Fig. S4). Assuming the lattice parameters of Sr-aragonite and Ca-strontianite (Ca_1-xSr_xCO₃) solid-mixtures follow Vegard's law, i.e., they are linearly dependent on foreign ion content, x for aragonite (1-x for strontianite), the main cation content (1-x for aragonite and x for strontianite) of each phase in the samples was calculated as well. Additionally, normalized RIR based on Lab₆, $I_{\alpha }/I_{Lab6}$, were determined experimentally from the mixtures of Lab₆ with strontianite SrCO₃ and Lab₆ with aragonite CaCO₃, based on the most intense (111) reflection of Lab₆ and the (111) reflections of strontianite and aragonite. The calculated $\left(I_{SrCO3}/I_{Lab6}\right)/\left(I_{CaCO3}/I_{Lab6}\right)$ ratio was found to be 3.34, very close to the value of $\left(I_{SrCO3}/I_c\right)/\left(I_{CaCO3}/I_c\right)=3.4$ given in the PDF database based on corundum, indicating the absence of preferred orientation of the samples. Finally, the phase weight fractions wt% in the sample were determined using the RIR method, described above in this paragraph. The (111), (021) and (221) reflections of Ca_1-xSr_xCO₃ were chosen since they were free from interference with other diffraction peaks. The RIR value of each Ca_1-xSr_xCO₃ phase was calibrated linearly according to the Ca content, 1-x in Sr-aragonite or x in Ca-strontianite, where the normalized $I_{Ca1-xSrxCO3}/I_{Lab6}$ is equal to 1.00 and 3.34 for $x=1$ and $x=0$, respectively.

2.4. Micro-Raman spectroscopy

Micro-Raman spectroscopy was performed on a Horiba LabRAM HR Evolution (Horiba, France) spectrometer equipped with four laser lines (325, 532, 633, and 785 nm). The system has an 800 mm focal length spectrograph (high resolution, low stray light) with several interchangeable gratings and mounted with an open electrode, front illuminated, cooled CCD detector (Horiba Syncerity). The samples were placed under a modular microscope (Olympus BX-FM) with a suitable objective. For this work, 100x, NA 0.9, (MPlanFL N, Olympus, Japan) objective with spatial resolution better than 1 μm is used. The light from the HeNe laser was dispersed by an 1800 gr/mm grating and the pixel resolution is 0.35 cm⁻¹. Excitation wavelengths of 532, 633 or 785 nm were used to test the sample response and the background signal. Spectra were collected between 100 and 1800 cm⁻¹ with exposure duration of 30–60 s and 2 averages. The acquisition and signal conditioning were done with the Horiba LabSpec 6. The data went through polynomial baseline subtraction and spike removal as is commonly done.

2.5. Solid-state NMR spectroscopy

All solid-state NMR experiments were carried out on an 11.74T Bruker Avance III spectrometer equipped with a 4 mm MAS probe. All measurements were performed at room temperature using a spinning rate of 10 kHz and a SPINAL64 heteronuclear decoupling at a field strength of 85 kHz.

1D ¹³C direct polarization (DP) experiments were recorded using a 3.8 μs ¹³C 30° pulse, 866 repetitions and a recycle delay of 66 s, except for the $X=0.233$ preparation, which employed 744 repetitions and a recycle delay of 360 s. 1D ¹H-¹³C cross polarization (CP) experiments used a 1.67 μs ¹H 65° pulse, a ¹³C lock field of 70 kHz, a ¹H lock field ramped between 60 and 100 kHz, a recycle delay of 1 s, 8k repetitions and a contact time of 3.0 ms. For the preparation with $X=0.233$, a 2.5 μs ¹H 90° pulse, a recycle delay of 4 s, a contact time of 2.0 ms and 15k repetitions were used.

2.6. Scanning electron microscopy (SEM)

SEM was carried out on an FEI environmental scanning electron microscope using a Quanta FEG-250 field-emission gun. All scanning electron micrographs were recorded using an acceleration voltage of 5 kV (except for sample $X=0.5$ which was recorded at 10 kV) and at a beam working distance of 9.3–13.3 mm. Samples were prepared for morphology analysis by suspension in ethanol, sonication for 50 min, and placement on silicon grids until solvent evaporation was complete. The samples were then gold coated prior to measurement.

2.7. Transmission electron microscopy (TEM)

High-resolution TEM (HR-TEM) measurements were carried out on a JEM 2100, JEOL instrument with LaB6 e-beam source at acceleration voltage of 200 kV. Samples were dispersed in ethanol by ultrasonication for 10 min and placed on copper grids prior to measurements.

2.8. Inductively coupled plasma (ICP)

ICP-OES analysis was performed using SPECTRO ARCOS-EOP MultiView FHX2 instrument. Prior to sample analysis, calibration runs using adequate standards for each element were performed as a routine procedure. Quantifications of elemental calcium, strontium and magnesium content in the synthesized minerals were carried out by suspending 20 mg of product powder in 10 ml of 0.1 M HCl and performing two stages of dilution, 10-fold and 100-fold (0.2, 0.02 mg/ml), before injection to the plasma source. Relative errors in Ca and Sr measurements were used to determine errors in Sr/Ca ratios. For the diluted samples, relative errors in these ratios were between 0.65 % and 1.07 %.

3. Results and discussion

3.1. Biphasic crystallization of cross doped aragonite and strontianite

To start we note that the total moles of Sr²⁺ ions added to the solution mixture is represented by its molar fraction $X_{Sr}^{solution}=n_{Sr}^{solution}/\left(n_{Ca}^{solution}+n_{Sr}^{solution}\right)$ or in short as $X$. Since the moles of added Ca²⁺ ions were kept constant in all experiments, the sole effect of Sr²⁺ addition is examined here. The powder X-ray diffractograms of the CaCO₃/SrCO₃ minerals precipitated with increasing X, are shown in Fig. 1. The front diffractogram of pure aragonite ($X=0$) and the back diffractogram of pure strontianite ($X=1$) provide reference fingerprints for the analysis of diffraction patterns for intermediate values of $X$, representing mixtures of the two phases. At low solution [Sr²⁺] $\left(X\le 0.07\right)$, only Sr-doped aragonite is formed with the aragonite reflection peaks shifting to lower angle as more and more Sr is substituted in the crystal. As X is increased ($X>0.07$), a Ca-doped strontianite phase starts forming in growing amounts. The largest reflections (111) and (021) in the patterns of the two phases exhibit broadening for $0.07<X<0.21$ and coalesce at the upper boundary, but from $X>0.23$ and on, they sharpen and become resolvable, indicating growth of larger crystallites from each phase. At $X>0.37$, a complete dissolution of the Sr-aragonite phase and precipitation of only Ca-strontianite takes place, as evident from the diffraction patterns which comprise of the latter mineral reflections exclusively. This dissolution of aragonite phase and reprecipitation of Ca-doped strontianite phase continues also for the highest [Sr²⁺] added ($X=0.818$), as evident from the shifted reflection pattern compared to the pure strontianite phase ($X=1.0$).

Fig. 1.

Propagation of XRD patterns of Ca_1-xSr_xCO₃ minerals with increasing X (side view and top view). At X = 0 and X = 1, pure aragonite and strontianite diffractograms are respectively shown. Reflections from the reference material (LaB₆) are marked by asterisks.

Adsorption onto the faces of the pre-existing aragonite crystallites may be kinetically favorable for the freshly titrated Sr ions, over clustering with dissolved CO₃²⁻ ions to form an initial strontianite nucleate. For higher [Sr²⁺] values ($X>0.07$), the rate of SrCO₃ precipitation becomes comparable to ion substitution in the aragonite crystal and hence, the diffusion layers mixed with the two cation species will lead to doping of the two crystal phases. Strontianite crystal nucleation occurs near the sites of CaCO₃ dissolution and thus partial incorporation of re-dissolved Ca ions into the growing crystal nucleates occurs readily. At the same time, Sr ions in these diffusion layers can readily competitively adsorb onto aragonite crystal growth facets, thus enriching the content of the substituent in the outer crystal layers.

The results from a Rietveld analysis of the diffraction data are summarized in Fig. 2. They depict the $X_{Sr}^{solution}$ dependent changes in the aragonite unit cell parameters (purple circles) as more Sr ions dope the crystal and the strontianite parameters (red circles) as fewer Ca ions substitute the Sr ions in the lattice (Fig. 2C). The results are also shown as a function of Sr/Ca (mol/mol) in Fig. S5 in the SI. A linear change in cell dimensions is observed with the substitution of dopant ions in the two isostructural crystal phases, in accordance with Vegard's law [21] ($a_{mix}={\left(1-x\right)\bullet a}_{Ara}+{x\bullet a}_{Str})$. The unit cells of both doped-aragonite and doped-strontianite expand due to substitution of the larger Sr ions (ionic radius 132 pm), in place of the Ca ions (ionic radius 114 pm) in the lattice. The doping effect on the aragonite cell parameters is significantly smaller since fewer Sr²⁺ ions can replace the much smaller Ca²⁺ ions in the CaCO₃ lattice. For $X>0.37$ , a complete dissolution of the Sr-aragonite phase in favor of Ca-strontianite is observed, manifested by the disappearance of its reflections from the XRD patterns. Note that due to the spacing between experimental points taken and sensitivity limitation of the X-ray diffractometer used, the actual threshold for this discontinuous change (Fig. 2b) can be at any value in the range $0.37<X<0.5$.

Fig. 2.

(A) Dependence of the relative molar fraction of Sr in the crystalline phases, $X_{Sr}^{crystal}$, on the relative molar fraction used in the reaction, $X_{Sr}^{solution}$. (B) Weight fraction of the Ca_1-xSr_xCO₃ phases (Sr-aragonite – purple circles, Ca-strontianite – red circles) as function of solution molar fraction of Sr, $X_{Sr}^{solution}$. (C) The variation of the lattice parameters (a, b, and c) and the volume (V) of Ca_1-xSr_xCO₃ unit cell as a function of solution Sr molar fraction. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

The unit cell dimension and volume changes are shown in Fig. 2C with corresponding linear fitting parameters summarized in Table S1. The relative expansions of the “b” and “c” axes (b/b_o and c/c_o) were two-fold larger than the expansion along the “a” axis (a/a_o), in both strontianite and aragonite as evident from slope values in Fig. S6 (a_o, b_o, c_o denote lattice axes for the pure crystal form). Aragonite unit cell volume expanded by 1.04 % due to Sr doping whereas strontianite unit cell shrunk by as much as ∼10 % by replacing >90 % of Sr ions in the lattice. At $X\le 0.01$, volume and “b”-axis respective expansions of formed Sr-aragonite are 0.015 % and 0.030 %, relative to pure aragonite.

A plot of the Sr ion fractions in the two crystal lattices, $X_{Sr}^{crystal}$ versus the solution molar fraction (Fig. 2A) shows two features of the experimental design: a) incorporation of the larger ion into aragonite crystal is hindered as evidenced by the low Sr/Ca substitution, $X_{Sr}^{crystal}\cong 0.07$, even for $X_{Sr}^{solution}$ values as high as 0.37, beyond which a Sr-aragonite phase is no longer observed. b) Incorporation of Sr over Ca in the strontianite phase is favored for the entire range of $X_{Sr}^{solution}$ as one observes that $X_{Sr}^{crystal}$ >$X_{Sr}^{solution}$ for all values. The relative weight fractions of the two crystal phases in each sample with increasing $X_{Sr}^{solution}$ were also extracted (Fig. 2B). They exhibit, for $0.007<X<0.5$, a linear decrease of aragonite contribution to the total weight of crystalline matter formed, concurrently with a linear increase in strontianite contribution. The apparent discrepancy in the $X$ value at which aragonite phase vanishes here ($X=0.5$), and in the pXRD diffraction data ($X=0.37$) is due to lack of intermediate experimental data points in this range, as noted above. Precipitation throughout step 1 of the reaction was predicted using “Visual Minteq” [22]. It indicated that roughly 9 % of the carbonate added remains as dissolved inorganic carbon (Fig. S3 left) at the end of this step. Therefore, the near absence of strontianite phase for $X<0.07$ is indicative of a preferred competitive binding of the ion on aragonite crystal faces over nucleation of an ab initio SrCO₃ phase, giving rise, through a dissolution-reprecipitation process, to a doped aragonite exclusively. Alternatively, it could be that sensitivity limitations of current experimental techniques preclude detection of the SrCO₃ phase below a certain threshold. This behavior is quite different than the one observed in direct cation co-mixing experiments where the two phases, Ca-strontianite and Sr-aragonite, were observed from start (from very low [Sr²⁺]) [23].

In relation to the biogenic process in corals and other aragonite forming marine organisms, it is evident that bimodal precipitation of Ca-strontianite and Sr-aragonite starting from a pre-formed aragonite phase will be severely limited. Sr molar ratio in mineralizing fluids need to be at least 0.07 for strontianite to start appearing. This leaves a large window of Sr ion concentrations that can serve a functional role such as speeding-up aragonite crystal maturation in coral skeleton while avoiding SrCO₃ phase formation.

3.2. Influence of cation substitution on particle morphology

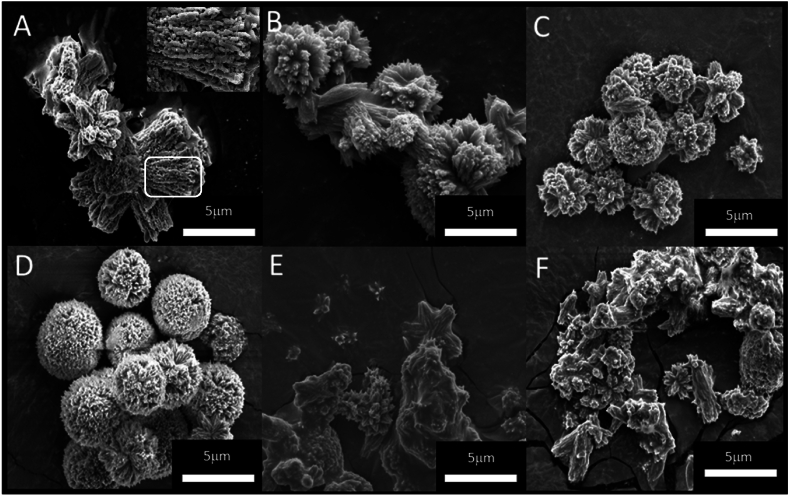
The morphology of mineral particles formed during the two-step reaction, with increasing $X_{Sr}^{solution}$, was explored by scanning electron microscopy (Fig. 3). The particles observed are bundles of Sr-aragonite and Ca-strontianite crystallites at different ratios and doping levels. As aragonite and strontianite crystal lattices are isomorphic, individual crystallites from each of the minerals adopt a similar typical acicular (needle-shaped) morphology. The overall morphology of the assembled particles, however, depends on the relative sizes of grown crystallites, crystal propagation direction and degree of cation replacement by impurities in the crystal. In the various preparations, collections of acicular crystallites are identifiable, collated into radial bundles either in two or three dimensions [24].

Fig. 3.

Scanning electron micrographs showing morphologies of resultant biphasic Ca_1-xSr_xCO₃ minerals formed using various $X_{Sr}^{solution}$ from high to low. (A) $0.818$ (B) $0.5$ (C) $0.13$ (D) $0.1$ (E) $0.047$ (F) $0.0044$. Inset in (A) shows the encircled region in the image, magnified two-fold.

At low $X_{Sr}^{solution}$ , they organize in two dimensions into a shape of star (Fig. 3E and F), reminiscent of the spherulitic growth observed in coral polyps. The crystallites formed in intermediate [Sr²⁺] preparations bundle up into spheroidal morphology (Fig. 3C and D). The crystallites formed with highest Sr concentration (e.g., Fig. 3A) are porous, reflecting a nearly complete Ca ions substitution by Sr ions and an underlying expansion of the aragonite unit cell into the larger unit cell of strontianite. This process takes place through dissolution-reprecipitation which leaves a significant imprint on the integrity of the final crystallites made from the larger basic unit. A SEM image of pure strontianite prepared by direct precipitation is shown for comparison in Fig. S7.

3.3. Dopant contribution to perturbation of molecular and lattice vibrations

Fig. 4 shows the overlaid micro-Raman spectra of biphasic Sr-CaCO₃/Ca-SrCO₃ minerals at increasing $X_{Sr}^{solution}$ values, recorded using a 633 nm excitation laser (full spectra are given in Fig. S8). The same spectra are also shown as a function of Sr/Ca (mol/mol) in Fig. S9. The stretching (Fig. 4A) and bending (Fig. 4C) regions of the carbonate molecular ion vibrations (internal modes) and the lattice vibrations region (Fig. 4E) (external modes) are shown on the left. The internal modes exhibit a shift to lower wavenumber values as more Sr ions substitute Ca ions in the aragonite lattice and as the portion of strontianite in the biphasic product increases. This is owing to the larger ionic mass and the greater distances of Sr ions to CO₃²⁻ ions in the two crystals. The main modes in each region of the Raman spectrum are represented by color coded dots at the bottom of Fig. 4A, C, 4E; they are plotted as a function of $X_{Sr}^{solution}$ in Fig. 4B, D, 4F, respectively.

Fig. 4.

(A, C, E) Active vibrational regions in the Raman spectra on the Ca_1-xSr_xCO₃ precipitates with increasing $X_{Sr}^{solution}$ from $X$ = 0 (bottom) to $X$ = 1 (top), recorded using a 633 nm laser. The peak vibrational modes (three stretching, three bending, and five lattice) are annotated by color coded dots at the bottom of A, C, E. (B, D, F) Peak positions (in cm⁻¹) in the corresponding spectral regions (A, C, E) are plotted as a function of $X_{Sr}^{solution}$, showing changes in vibration frequency with increase in Sr substitution in aragonite and decrease in Ca substitution in strontianite. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Two modes, 1085 cm⁻¹ (A_g) and 205 cm⁻¹ (B_2g), remain unscathed for the entire range of $X_{Sr}^{solution}$ at which they appear ($0\le X\le 0.3$), representing either vibrations less sensitive to the cation identity or crystal regions where Sr ions have not doped (zonal substitution) [20] and that retained pure aragonite modes [25]. For 1083 cm⁻¹ stretching, 190 cm⁻¹ (B_3g) and 180 cm⁻¹ (B_2g) lattice modes, a discontinuity is observed at $X=0.25$ pointing to a change in the character of these modes from doped aragonite to doped strontianite. The modes in the latter polymorph exhibit a much stronger dependence on $X$. Other modes belonging to Ca-strontianite, 1076 and 699 cm⁻¹, are only evident after the discontinuity at $X\ge 0.25$, highlighting the requirement for a high concentration of Sr ions in the two-step synthesis route for dissolution and reprecipitation to be extensive and for the disappearance of the pure aragonitic phase $X\ge 0.3$. This is in contrast to the linear decrease in band wavenumber with increase in $X$, for preparations where the two cations are co-mixed in a single step and resulting in solid-solution formation from start [23]. In preparations with intermediate $X\cong 0.38-0.67$, vibrational peaks are broader and occasionally merge into wide bands indicative of some disorder in the arrangement of cations [23].

In the stretching region (Fig. 4A), the peak observed at low $X_{Sr}^{solution}$ is composed of two modes at 1085 and 1083 cm⁻¹. The low wavenumber peak further splits into two for $X>0.2$ (see Fig. 4), as a doped strontianite mode becomes visible in the spectrum. The highest and lowest peaks agree well with previous reports [23] (1072 cm⁻¹ for strontianite and 1085 cm⁻¹ for aragonite). The anti-symmetric stretching (B_2g) is observed at 1070 cm⁻¹ and 1083 cm⁻¹ for strontianite and aragonite, respectively [25]. The linear decrease of the 1083 cm⁻¹ stretching mode with $X_{Sr}^{solution}$ for values $>0.2$ (fitting parameters: slope 11.1, intercept 1082.5) is similar to the one reported by Alia et al. [23] employing simultaneous co-precipitation of the two cations at 76 °C. This indicates that for high enough $X$, dissolution recrystallization barriers are minimal and Sr ion partitioning between the two phases follows the thermodynamics of a solid solution.

The antisymmetric bending region of the Raman spectra shows two peaks at 701 and 705 cm⁻¹ for aragonite and at 695 and 699 cm⁻¹ for strontianite. These peaks are respectively attributed to B_3g and A_g/B_1g modes in each crystal phase [25], with some controversy reported over this assignment [23]. Interestingly, the higher 705 cm⁻¹ band (orange) exhibits a small decrease with X and vanishes for $X>0.5$. The low wavenumber band 699 cm⁻¹ (green) starts appearing earlier, for $X\ge 0.26$, reaching 695 cm⁻¹ for $X=1$. These bending modes show an overlap of the two minerals for $0.26\le X\le 0.5$. The aragonitic 701 cm⁻¹ band transforms monotonically into the strontianite band at 699 cm⁻¹ over the range of X values.

The low wavenumber modes exhibit some additional interesting effects of the cationic substitution on the lattice. The prominent mode, from concerted libration motion of carbonate ions in the lattice at 152 cm⁻¹ (B_1g) for aragonite (orange) and at 147 cm⁻¹ for strontianite (cyan), exhibits a monotonous shift with $X$ between the two values. The two small aragonite modes at 180 cm⁻¹ (B_2g) (grey) and 190 cm⁻¹ (B_3g) (yellow) show notable and unusual shift with $X$, first to higher and then to lower wavenumbers, settling at 171 cm⁻¹ and 179 cm⁻¹ respectively, for strontianite. Their non-monotonic change may point to a phase transition at $0.3\le X\le 0.5$.

3.4. Crystalline and disordered layers

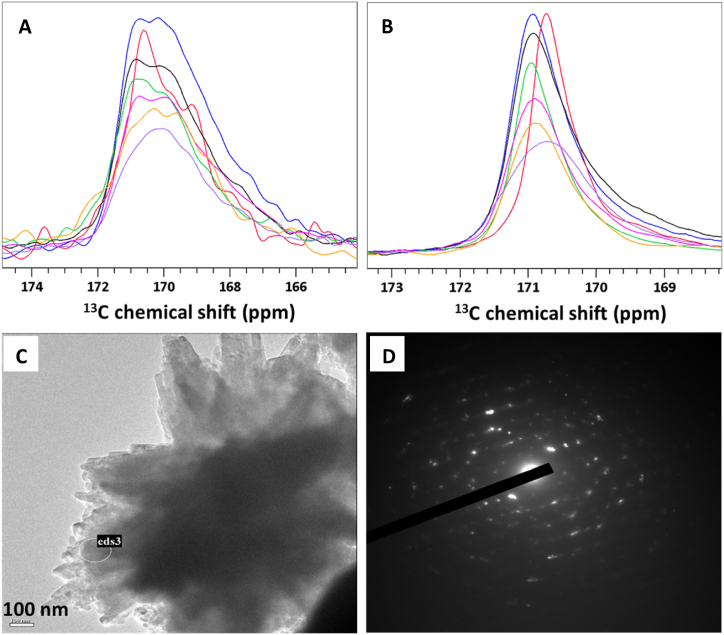
To further characterize bulk crystalline and surface phases, ¹³C direct polarization (DP) and cross polarization (CP) measurements were carried out under MAS on select preparations. ¹³C DP experiments are typically used to identify the carbons in the bulk of carbonate based mineral samples, whereas ¹³C CP experiments are sensitive to the terminal layers on the surfaces of crystallites where water and other ¹H bearing species such as HCO₃⁻ and OH⁻ can be found. CP and DP spectra for preparations with $X=0.0044,0.13,0.23,0.26,0.33$ are shown in Fig. 5A and B, respectively. The DP spectrum of pure strontianite (red) shows a carbonate peak at 170.7 ppm, reported for the first time, and the DP spectrum of pure aragonite (blue) shows typical narrow carbonate peak at 170.9 ppm.

Fig. 5.

(A) 1D ¹³C CP spectrum and (B) 1D ¹³C DP spectrum of ¹³C labeled Ca_1-xSr_xCO₃ prepared using $X_{Sr}^{solution}$ of 0.0044 (black), 0.13 (green), 0.23 (pink), 0.26 (orange), 0.33 (purple). Analogous spectra of pure aragonite (blue) and pure strontianite (red) are also shown. (C) Transmission electron image of mineral prepared using $X=0.33$. (D) Electron diffraction pattern taken at the region encircled in (C) marked as eds3. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

This small chemical shift difference underscores the minute changes in electronic environment around the CO₃²⁻ ion in the two iso-crystals, compared to different polymorphs of CaCO₃, for instance. In the mixed minerals spectra, the single peak observed appears at intermediate chemical shifts between 170.9 and 170.7 and is broader than in the pure crystal phases pointing to lower order in the crystallites formed in the mixtures. Despite the small window of resonance frequencies separating SrCO₃ from CaCO₃, as $X$ is increased and doped versions of the two phases are formed, a shift of the peak maximum from 170.9 ppm upfield is noted. This peak first broadened with increase of $X$ until $X=0.23$ and then narrowed back down for higher $X$, unlike in pXRD and Raman where broadening was observed for $X=0.5$. Deconvolution of the carbonate peak (see Fig. S10, for exemplary deconvolution) indicated it is comprised of two lines with resonance frequencies similar to pure aragonite and strontianite. These analyses were challenging to quantify in terms of doping level or relative proportion of each crystal phase in the sample given the limited resolution (see Table S2).

¹³C CP spectra of the same samples exhibit broader peaks, reflecting a higher disorder in surface phases. In the aragonite CP spectrum (blue), much like in the DP spectrum, the strongest peak appears downfield relative to the same peak in the strontianite spectrum (red). A broader shoulder composed of several weaker lines is also observed upfield of the main peak, associated with disordered phases akin to the crystalline phase they terminate e.g., a proto-aragonitic amorphous calcium carbonate (pa-ACC) phase for the sample of pure aragonite and a proto-strontianite amorphous strontium carbonate (ps-ASC) for the pure strontianite sample. For the mixed minerals CP spectra, various combinations of disordered phases are observed.

Exemplary TEM image and selected area electron diffraction data for the 0.33 sample are also shown in Fig. 5C and D. The crystallites observed have a thickness of 35 nm like the size deduced from XRD reflection width. They show the typical acicular morphology of strontianite/aragonite, like in the analogous SEM images. The selected area electron diffraction patterns (Fig. 5D) exhibited peaks that are attributable to either strontianite or aragonite. A survey of different areas along the samples showed no evidence for a unique pattern of aragonite or strontianite, suggesting the two crystal phases are inter-mixed, at least at the level distinguishable by the e-beam used (spot diameter ∼ 100 nm).

The Sr/Ca ratios from ICP results of selected in vitro preparations are reported in Table 1. These results can be compared to Sr/Ca ratios from pXRD data, accounting for the dopant content in Ca-strontianite and Sr-aragonite (Fig. 2A) and the relative weights of each mineral in the sample (Fig. 2B). For the $0.0044$ preparation, ICP data show a Sr/Ca ratio of 0.0056, whereas diffraction data indicate an intracrystalline Sr/Ca ratio of ratio 0.0060 in Sr-aragonite. For the $X=0.13$ preparation, ICP shows a Sr/Ca of 0.0093, while the total intracrystalline Sr/Ca (from both crystal phases) is 0.031 which is >3-fold larger. For the $0.818$ preparation, the ratio from ICP, 7.25, and from pXRD, 7.62 are similar, like for 0.0044. The discrepancy in the intermediate Sr sample, between ratios inferred from the two techniques is associated with an amorphous Sr-poor calcium carbonate phase that is undetectable by pXRD. In the high Sr preparation, a single strontianite phase is formed with much lower amorphous form and therefore the results from the two techniques converge. It is noted that in coral skeleton samples the discrepancy between the two techniques is much smaller [26].

Table 1.

Sr/Ca ratio in select synthetic minerals from ICP measurements.

Sample ${\mathit{X}}_{\mathit{S}\mathit{r}}^{\mathit{s}\mathit{o}\mathit{l}\mathit{u}\mathit{t}\mathit{i}\mathit{o}\mathit{n}}$	Ca2+ (wt%)	Mg2+ (wt%)	Sr2+ (wt%)	Sr/Ca mol ratio
0.0044	39.620	–	0.490	0.0056
0.133	35.97	0.094	0.730	0.0093
0.818	3.346	–	53.050	7.25

The comparison between ICP and pXRD underscores the need to account for the sensitivity limitations of any technique used to analyze the various environments in the skeleton. The phases that are undetectable by pXRD measurements, i.e., disordered mineral phases in the bioinspired preparations here and chelating biomolecules in the case of biological skeletal tissue extracts, contain viable information about environmental parameters such as the concentration of the two cations in coral mineralizing fluids. A complete account of these contributions may come at a price of complicating the direct correlation between the cationic ratio and the temperature but may provide information about organism adaptation to environmental changes and may help discriminate processes that are species specific.

The ratios of Ca/Sr ions in disordered minerals can be indirectly extracted from measurements of CO₃²⁻ ion content in these disordered phases using techniques like solid-state NMR, provided that they are resolvable. These measurements, like the ones demonstrated here, will permit a more comprehensive view of the various locations that calcium and strontium ions accommodate.

It is possible, based on the benchmark constructed, to estimate the putative Sr concentration in mineralizing fluids in the second stage of mineralization in young corals. For a typical reported Sr/Ca inside coral skeleton aragonite of 0.9–1.0 mol% ($X_{Sr}^{crystal}=0.0089-0.0099$) [26], a ca. 5-fold higher ratio is required in the secondary fluid at mineralization sites, that is a Sr/Ca of 4.5–5.0 mol% ($X_{Sr}^{solution}=0.047-0.052$). Moreover, in cases where Sr plays a role in maturation of aragonite crystals, higher levels of the dopant in calcifying fluids can be expected. The ion could then promote not only higher incorporation into the crystal but also lead to formation of larger more ordered crystallites. This was observed recently in measurements comparing shallow water and mesophotic corals [27]. For Ca-strontianite to start forming, a Sr/Ca of ca. 11.1 mol% ($X_{Sr}^{solution}=0.1)$ in the secondary mineralizing fluid is needed, in a two-step preparation procedure. Under these conditions, partitioning of dissolved Sr upon precipitation takes place, into a Ca-strontianite phase (2 wt %) with a Sr/Ca of ca. 15 mol% in the crystal and a Sr-aragonite phase (98 wt %) with a Sr/Ca ratio of 2 mol% in the crystal. The latter value is higher than the upper threshold reported for Sr in coral skeleton.

4. Conclusions

Competitive replacement of strontium ions in pre-formed aragonite requires concentrations in mineralizing fluids that are at least five-fold higher than in the final doped crystallites for the typical doping found in coral skeleton. Furthermore, a crystalline phase of SrCO₃ only starts precipitating when dissolved Sr²⁺ mol fraction is larger than 0.1 of divalent cations in these fluids. Sr and Ca distributions in disordered layers can be different than in the crystalline phases and this factor needs to be accounted for when deriving Sr/Ca ratios in coral skeletons using techniques that are focused on crystalline phases, especially in the early life of the organism. On the other hand, measurement of the total skeletal Sr/Ca ratio averages the contribution from the two types of mineral phases and may undercut the ability to quantitate intra-crystalline doping level. Solid-state NMR spectroscopy can serve as a useful technique for mitigation of discrepancies between total Sr/Ca ratios inferred from inductively coupled plasma (ICP) elemental analysis and from pXRD analysis. For a more inclusive analysis of cation ratios in coral skeleton, a multi-technique analysis which includes analysis of disordered phases and nanometer size multiphasic mineral analysis is preferred. This will help resolve substitution mechanisms and expose processes that give rise to the biominerals generated during skeletogenesis.

CRediT authorship contribution statement

Saja Nasser: Writing – original draft, Formal analysis, Data curation. Gili Cohen-Taguri: Formal analysis, Data curation. Tali Mass: Writing – original draft, Conceptualization. Iddo Pinkas: Writing – original draft, Data curation. Gil Goobes: Writing – original draft, Supervision, Project administration, Methodology, Investigation, Formal analysis, Data curation, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the supplementary data to this article: