Abstract
The approaches used in biomedicine to analyze epidemics take into account features such as exponential growth in the early stages, slowdown in dynamics upon saturation, time delays in spread, segmented spread, evolutionary adaptations of the pathogen, and preventive measures based on universal communication protocols. All these characteristics are also present in modern cyber epidemics. Therefore, adapting effective biomedical approaches to epidemic analysis for the investigation of the development of cyber epidemics is a promising scientific research task. The article is dedicated to researching the problem of predicting the development of cyber epidemics at early stages. In such conditions, the available data is scarce, incomplete, and distorted. This situation makes it impossible to use artificial intelligence models for prediction. Therefore, the authors propose an entropy-extreme model, defined within the machine learning paradigm, to address this problem. The model is based on estimating the probability distributions of its controllable parameters from input data, taking into account the variability characteristic of the last ones. The entropy-extreme instance, identified from a set of such distributions, indicates the most uncertain (most negative) trajectory of the investigated process. Numerical methods are used to analyze the generated set of investigated process development trajectories based on the assessments of probability distributions of the controllable parameters and the variability characteristic. The result of the analysis includes characteristic predictive trajectories such as the average and median trajectories from the set, as well as the trajectory corresponding to the standard deviation area of the parameters’ values. Experiments with real data on the infection of Windows-operated devices by various categories of malware showed that the proposed model outperforms the classical competitor (least squares method) in predicting the development of cyber epidemics near the extremum of the time series representing the deployment of such a process over time. Moreover, the proposed model can be applied without any prior hypotheses regarding the probabilistic properties of the available data.
Keywords: Cyber epidemics, Malware, Prediction, Small data, Machine learning, Entropy-extreme model, Qualitative metrics
Graphical Abstract
1. Introduction
1.1. Rationale of research
The modern cybersphere is characterized by features such as a well-developed, vertically organized architecture of information-interacting ecosystems, a tendency towards improvement through built-in heuristic and evolutionary processes, adaptability, and self-regulation of ecosystems within established vertical and horizontal connections, and finally, resilience due to built-in cyber-physical protection mechanisms and vulnerability to spontaneous or provoked malicious impacts. Undoubtedly, if we replace the term "cybersphere" with "biosphere" in this sentence, the formulated definition will remain valid. Based on this fact, we can assert that many scientific concepts and directions oriented towards understanding processes in the biosphere can be adapted for studying target processes in the cybersphere. In particular, models and methods of analyzing the course of biological epidemics used in the biomedical field may be relevant when modeling processes related to cyber epidemics. We will substantiate the reliability of this assertion in a first approximation by the fact that biological and cyber epidemics have many common features. These include:
-
-
Both types of epidemics are characterized by an exponential increase in the number of infected subjects at the initial stage due to existing connections and the absence of specialized protective mechanisms;.
-
-
The dynamics of epidemic development slow down as saturation occurs due to a decrease in the number of vulnerable subjects and the introduction of preventive measures;.
-
-
Both types of epidemics are characterized by a multifactorial time delay between the moment a specific subject is infected and the further spread of the infection;.
-
-
The zonal spread of the epidemic due to the segmental organization of relationships between vulnerable ecosystems;.
-
-
The ability of the epidemic agent to modify, evolve, and adapt;.
-
-
The implementation of preventive measures based on universal protocols for organizing communication between potentially vulnerable subjects, activated in case of suspected epidemic emergence.
For an effective response to cyber threats, it is extremely important to establish a clear information security policy for the target object in advance, whether it is a gadget, office, institution, or multinational corporation. This is necessary because, at the time of an incident, under stress and possible lack of resources, it is essential to follow all the necessary response steps as accurately as possible. The rationality of this approach is confirmed, in particular, by the content of the document NIST SP 800–61 Rev. 2 "Computer Security Incident Handling Guide" [1]. This document is considered a classic in the field of cybersecurity, and its principles remain rational over time, as the framework it proposes can be adapted to modern technologies and current cyber threats. This document describes the organizational and technical aspects of responding to cyber incidents.
In NIST SP 800–61, it is noted that ensuring cybersecurity and preventing cyber incidents is important because the constantly increasing flow of incidents will not allow for a prompt response to each one, which can lead to significant damage. The authors of the document emphasize that cyber risk assessment enables the identification and management of information security risks, as well as the identification of information assets whose security status needs to be monitored primarily. In conditions of limited resources, having a predictive model for the development of cyber epidemics in the arsenal of the information security department can be decisive and prevent colossal financial and reputational losses.
It should be noted that relying specifically on scientifically based models and methods can help identify the onset of cyber epidemics at early stages. It is important to understand that incident data at this stage will be limited and noisy. This fact is fundamental when choosing the basis for constructing relevant models and is thoroughly explored in this article. Obtaining more traditional types of forecasts for the development of cyber epidemics to assess their scale in the short and medium term is a separate and relevant task not addressed in this work.
1.2. State-of-the-art
The main approaches to modeling epidemic processes in general, and cyber epidemics in particular, today include approaches based on the application of statistical models [2], [3] that fit the corresponding time series to existing data; dynamic models [3], [4], based on systems of differential equations describing the dynamics of the main indicators of the epidemic; and network models [5], [6], [7], [8], focused on modeling the dynamics of epidemic processes considering the heterogeneous structure of the environment in which the epidemiological process develops (this is reflected in the uneven development of the epidemic in different populations).
Most approaches of the first type are based on ideas that trace back to population models in biological systems, starting with exponential growth models [9], [10]. Exponential growth models demonstrate their effectiveness in the earliest stages of an epidemic when there is a sharp increase in the number of infected individuals. Over time, as natural (e.g., an increase in the proportion of immune members of the population) or artificial constraints (e.g., the introduction of physical barriers to limit contact between population members) appear, the number of infected individuals decreases. This turning point in the development of the epidemic process, as well as its further dynamics, cannot be predicted by simple exponential growth models. For this reason, logistic models [11], [12] are now actively used for these purposes, which are employed to model the total number of infected individuals.
Dynamic models for predicting the development of an epidemic are also actively used today. Without delving into the details of various dynamic models [13], [14], [15], it is important to note a common property among them: the sensitivity of their parameters. This sensitivity consistently leads to the problem of adequately and robustly estimating these parameters, without which the effective functioning of dynamic models is impossible.
Considering that data on the development of epidemics are most often presented as various time series, scientists frequently use autoregressive models [16], [17] and neural networks [18], [19] for their analysis and forecasting. Well-known forecasting methods such as ARIMA [20], linear regression [16], SMOreg [21], and Gaussian models [18] are also widely used by researchers to describe relevant time series.
The authors of the work [22] reviewed forecasting methods used in cybersecurity and concluded that their effectiveness depends on the context in which they are used and the direction of research. In the study [23], [24]; [33], the task of predicting data leaks was addressed by analyzing time series that reflected the time of the incident and its significance, based on the volume of data that became available to attackers as a result of the leak. The researchers used SARIMAX models and recurrent neural networks as tools. Both models showed representative results. In the study [20], the authors implemented long-term runoff forecasting using ARIMA and SARIMA models. It was found that under conditions of non-stationary data, the SARIMA model outperformed its competitor.
In general, current time series forecasting methods have several common shortcomings, including:
-
1.
Many of the methods used in practice assume linear dependencies, which limits their ability to model complex, nonlinear time series.
-
2.
Traditional methods assume stationarity of the time series being studied, meaning that statistical properties remain constant over time. Transforming a non-stationary series into a stationary form needs to be formalized, which is quite challenging.
-
3.
Most time series forecasting methods are sensitive to anomalous values or outliers in the training data, which can distort predictions. The simplest way to address this issue—by excluding anomalous values from the training sample—is unacceptable in cases of small sample sizes and cannot be automated in many applied tasks (e.g., risk modeling, reliability, and aspects of information security).
-
4.
To obtain accurate forecasts, many models require significant amounts of historical data, which can be problematic for rare events or short-term series.
-
5.
Most current time series forecasting methods do not account for the influence of external factors or changes in the environment in which the studied process is developing.
In reviewing works dedicated to the analysis of various data, it is impossible not to mention artificial intelligence methods. Several research teams are developing models for detecting cyberattacks based on convolutional neural networks (CNN). For example, in the study [23], a method based on such an architecture is proposed for detecting cyberattacks in industrial control systems. The study [25] presents a CNN-based method for detecting web attacks in the code of typed HTTP requests. In the work [26], a CNN-LSTM approach is used to detect malware in near real-time with high accuracy. The study [27] proposes a combined model for detecting DDoS attacks based on LSTM and a Bayesian approach, which, according to the authors, showed satisfactory results. The study [28] utilized architectures like CNN and LSTM for intrusion detection based on data from the CIC-IDS2018 dataset. The research [29] presents an effective intrusion detection mechanism based on a deep autoencoder, using the KDD-CUP'99 dataset for training and testing. However, these approaches are not suitable for analyzing cyber epidemics at early stages when there is not enough quality data for training. In this context, the authors of this article focused on a time-tested foundation – the logistic model enhancing it with the concept of small data entropy analysis [30], [31], [32].
1.3. Main attributes of the research
Section summarizes the characteristic information about the article by formulating the object, subject, purpose, tasks, and the main contribution of the research. The object of the research is the initial stage of the cyber epidemic development process. We consider this stage to last until cybersecurity tools developers introduce specialized protocols for identifying and countering specific threats. In fact, during the initial stage of cyber epidemic development, cybersecurity tools only use heuristic analysis technology to identify threats. The subject of the research includes machine learning methods, static modeling, as well as numerical methods. The purpose of the research is to formalize an entropy-extreme model for predicting the development of cyber epidemics, oriented towards application in the vicinity of the extremum of the corresponding time series under conditions where training data are incomplete or distorted. To achieve the stated purpose, the following research tasks were carried out:
-
-
The research object was adequately represented within the formalism of machine learning theory and mathematical statistics (Section 2.1).
-
-
Mathematical models of the investigated process were formalized according to the stated objective, suitable for application under conditions where there are no a priori hypotheses about the probability properties of the available data (Section 2.2).
-
-
Based on the defined characteristics of the research object model, metrics for qualitative indicators were formulated to evaluate the forecasting effectiveness of the cyber epidemic development process (Section 3).
-
-
The adequacy of the presented mathematical framework was empirically demonstrated, and the rationality of the proposed qualitative metric was illustrated through examples (Section 3).
Finally, we will formulate the main contribution of the research. The authors propose an entropy-extreme model, defined within the machine learning paradigm, to address this problem. The model is based on estimating the probability distributions of its controllable parameters from input data, taking into account the variability characteristic of the last ones. The entropy-extreme instance, identified from a set of such distributions, indicates the most uncertain (most negative) trajectory of the investigated process. Numerical methods are used to analyze the generated set of investigated process development trajectories based on the assessments of probability distributions of the controllable parameters and the variability characteristic. The result of the analysis includes characteristic predictive trajectories such as the average and median trajectories from the set, as well as the trajectory corresponding to the standard deviation area of the parameters’ values.
2. Material and methods
2.1. Basic analytical description of the cyber epidemics development process as a research object
In the first approximation, the dynamics of infection spread in nodes in a cyber system can be described based on the classic formula [11], [12], which characterizes the development of an epidemic in a biological system:
| (1) |
where is the rate of increase in the number of infected nodes, is the number of infected nodes, and is the size of the studied system.
The solution to Eq. (1) is the well-known Fermi-Dirac curve [35] of the form:
| (2) |
where is a coefficient determined as , and represents the initial number of infected nodes in the studied population at the initial moment .
The model of (1), (2) belongs to the class of Logistic Growth Models [34] and is quite effective for predicting the total number of infected nodes in a closed system in the early stages of an epidemic.
We transit to the general form of the model (1):
| (3) |
where the logistic curve is a nonlinear function of three controlled parameters , which determines the transformation of the scalar input argument into the output . In the context of the object under research, the argument is represented as a time stamp, and the ordinate is represented as the cumulative number of infected nodes.
Adapting the target model for forecasting involves evaluating its control parameters based on etalon data during training. With determined estimates of these control parameters, one can formalize the procedure for applying the model to obtain forecasts. Statistical methods and machine learning methods in general aim to compute point or interval estimates of these control parameters of the model, upon which the trained model becomes suitable for forecasting. In general, this approach is effective. However, if the target model is nonlinear, establishing properties of the estimates obtained in this manner can be challenging.
Based on the concept of entropy estimation for small stochastic data [35], the authors propose determining not point estimates of the controlled parameters of the model under research, but their probability distributions along with distributions characterizing the inherent variability in measuring these parameters from real data. Importantly, no prior hypotheses are generated regarding the probabilistic properties of these data. In this scenario, the result of the forecasting will not be a single trajectory but a set of them. Statistical analysis of this set will then yield the desired forecast.
Despite the well-known advantages of continuous mathematical modeling of multidimensional objects, this approach is also recognized for its significant computational complexity. To mitigate this limitation, we will transit to a discrete representation of the nonlinear logistic model (3):
| (4) |
where the parameter characterizes the variability of each iteration in measuring the input of the model (3) (hereafter referred to as variability characteristic), and the variable is the output of the model (3), distorted by the imperfection of measurement of .
The controlled parameters and variability characteristics are represented by respective interval discrete stochastic variables with distributions:
| (5) |
| (6) |
where , are the values of stochastic variables, , are their probabilities of realization, , are the interval values of stochastic variables, is the number of data points, and is the dimensionality of the data space (here and further denoted as ).
2.2. An entropy-extreme concept of predicting the development of cyber epidemics at early stages
The concept of entropy estimation for small stochastic data allows determining the optimal distributions of the controlled parameters of the model (3) as a result of training the latter on etalon data. By "etalon data," we mean the content of a collection summarizing measurements of the "input" and "output" entities of the research object with appropriate accuracy and periodicity. Optimality is achieved by identifying the distributions that correspond to the maximum entropy. In the absence of any prior information regarding the actual characteristics of the model parameters, this approach is rational.
So, we need to solve the problem of conditional maximization of the entropy of the distributions of the controlled parameters of the model (4) and the variability characteristic . In doing so, we should consider the normalization conditions of the corresponding distributions and ensure the equilibrium condition of the averaged output of the model with the reference output of the instance of the modeling object.
The objective function of such an optimization problem is formalized by the expression:
| (7) |
where and are the distributions of the controlled parameters (5) and the variability characteristic (6).
At , the normalization and equilibrium conditions are defined as analytical constructs (8) and (9), respectively:
| (8) |
| (9) |
where represents the etalon data (output of the instance of the modeling object), the function is characterized by expression (3), and quantity characterizes the variability of measuring the arguments of the function .
The balance condition (9) can be specified as:
| (10) |
The sum denoted by the symbol in Eq. (10) generalizes terms (summation occurs for all combinations of values of the stochastic variables ).
We formalize the solution to the optimization problem (7) with constraints (8) and (10) based on Lagrange multipliers . As a result, we obtain expressions dependent on the parameters for calculating the extreme probabilities :
| (11) |
| (12) |
The values of the Lagrange multipliers are determined as a result of solving the system of equations obtained after substituting expressions (11) and (12) into the equilibrium condition (9):
| (13) |
As a result of solving the system of Eq. (13), we obtain the desired entropy-extreme distributions of the controlled parameters and the variability characteristic . Naturally, the solution procedure should employ numerical methods [36], such as Adaptive Moment Estimation (Adam), Truncated Newton Conjugate-Gradient (TNCG), or Levenberg-Marquardt (LM). This concludes the description of the training process for model (4).
As emphasized in Section 2.1, applying the trained model for forecasting is a specific process that needs to be specified. The calculated entropy-extreme distributions of the controlled parameters and the variability characteristic , which adapt model (4) to the training data, can be used for forecasting in two ways.
The first approach involves reducing the calculated values of these parameters to point estimates by averaging and subsequently substituting them into expression (4).
The second approach utilizes the full potential laid out in expressions (5) and (6). It entails computing a set of trajectories at the output of the model (4) for each realization of the corresponding stochastic variables. It's important to note that for each realization of the stochastic variables , the values of the variability characteristic are independently generated in the form of a corresponding set of values .
Let there be a sample of controlled parameters from a distribution with volume , defined according to (11). For each instance , , of controlled parameters, instances of variability characteristics are generated from distribution , defined according to (12). Aggregate these stochastic variable values into a block vector form, defining a set of trajectories at the output of the model (4):
where row vectors of matrix define one trajectory instance at the output of model (4) for a set of controlled parameters and generated variability characteristic values. The details of the formation of the matrix are described in the article [30].
Clearly, the number of trajectories in this case equals . Within the set of calculated trajectories, particular instances of interest include the averaged trajectory (avg), the median trajectory (median), and the standard deviation area (sda). In the proposed parameter space, using a nonlinear least squares method, one can compute the averaged trajectory (competitor). This last trajectory can serve as a widely accepted benchmark against the authors’ approach embodied in the (avg, sda, and median) trajectories.
2.3. The initial data space characteristics
One of the most important elements for our research is the etalon data on the development of cyber epidemics. Selecting based on criteria such as relevance, representativeness, completeness, and balanced representation left us with a single option – the "Windows Malware Dataset with PE API Calls" [37]. In subsequent experiments, we focused on malware categories such as:
-
-
Downloader (facilitates the downloading of various types of content from a remote server to a local device, enabling offline access),
-
-
Trojan (deceives users by pretending to be a legitimate program while performing malicious activities without their knowledge),
-
-
Worm (automatically replicates and spreads across networks, infecting multiple computers by exploiting vulnerabilities),
-
-
Virus (infects files or software by inserting its code, capable of replicating itself and spreading to other computers through infected files or networks),
-
-
Backdoor (Provides covert and unauthorized access to a computer system or network, bypassing normal security mechanisms to enable remote control or data attacks).
For each of these malware categories in the selected dataset, there are 1001 samples provided, including the time of device infection. It's worth noting that the infection dynamics of this malware exhibit pronounced peaks followed by declines, which are later followed by a "second wave" with another peak. The mathematical framework presented in Section 2.2 is aimed at forecasting the increase in the number of infections around these peaks. Considering this, data for model training were selected from the 7 days (a week) leading up to the first peak, which was identified based on the maximum of moving average over this period.
To reduce the computational complexity of the training process, the relevant data was scaled to the interval , but when making predictions, the output values of the trained model were returned to the original scale. Overall, the dataset for each malware category was divided into three non-overlapping segments:
-
-
segment , which contained training data;.
-
-
segment , which contained testing data;.
-
-
segment , which contained prediction data.
This segmentation of the dataset is canonical for machine learning and data analysis: the model is trained on the data from the segment , then, to prevent overfitting and to refine the hyperparameters, the model is validated on the data from the segment , and finally, the trained model is verified on the data from the segment .
2.4. Aspects of training and tuning the authors’ model
When training the model for each malware category, data was used starting from the day when cumulative infection of over 100 Windows devices was first recorded, ending on the seventh day preceding the first extremum. Segment included data for a time interval of the next 14 days. Finally, the segment included data for the subsequent 30 days after the interval covered by the segment . As a result, corresponding segments were defined for each category: , , , , . Note that the starting point with index 0 was the day the dataset authors began observing malware manifestations.
As previously mentioned, data from segments were also used for tuning the hyperparameters of the trained model (4). These hyperparameters include the interval values of stochastic variables (5). Regarding the interval values for the stochastic variable (6), we limited their range by , corresponding to a relative measurement error of the model's input (4) within 25 %. The values of hyperparameters and were set to five: . The coefficient of determination was used as a statistical measure of the consistency of the hyperparameters, where is the output of the trained model (4) without considering the variability characteristic ; is the corresponding etalon value, and is the average value for the entire set of etalon data.
Next we specify the procedure for tuning the hyperparameters of the entropy-extreme model (4). First, we form a package of interval configurations by calculating each element of the configuration instance with the corresponding step. Next, we create a set of trained models by sequentially training model (4) based on each configuration instance from the calculated package. We compare the elements of the set of trained models using the metric on the data from segment . The best instance of the trained model will be considered the one with the highest rating for the average trajectory across the set. The initial interval values are set within 20 % of the point estimate, calculated using the least squares method on the data from the segment .
After implementing the hyperparameter tuning procedure, the entropy-extreme model is retrained on the data obtained by combining segments and : , using the previously determined optimal intervals . Specifically, depending on the type of malware for the studied segments , , the following optimal intervals for the controlled variables , , were determined as a result of hyperparameter tuning:
During prediction, the distribution of the variability characteristic value, determined for the last point from the segment , was used. After retraining, the model is fully ready for prediction. As a typical competitor, a curve calculated using the least squares method for the same data from a segment can be used. Note that in addition to the metric , the Mean Squared Error is also informative for our experiment, where the etalon data is contained in segment .
3. Results and discussion
The section summarizes the results of predicting the daily number of infected Windows devices over the time interval represented in the segments from the original dataset for malware categories such as Downloader, Trojan, Worm, Virus, and Backdoor (see Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5, respectively). The graphs visualized in these figures, labeled as "avg", "median", and "sda", show the results demonstrated by the entropy-extreme model: with averaging over the trajectory set, with the median of the trajectory set, and with averaged parameter values from the distribution, respectively. The graphs labeled "etalon" and "competitor" visualize the etalon data from segments and the prediction results obtained using the least squares method, implemented with the scipy.optimize.curve_fit function in the Python programming environment. The graphs marked "per week" are adaptations of the above-described types of graphs, to which a seven-day moving average has been applied.
Fig. 1.
Total and weekly number of devices infected by downloader-type malware.
Fig. 2.
Total and weekly number of devices infected by Trojan-type malware.
Fig. 3.
Total and weekly number of devices infected by worm-type malware.
Fig. 4.
Total and weekly number of devices infected by virus-type malware.
Fig. 5.
Total and weekly number of devices infected by backdoor-type malware.
The y-axes in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 represent the basic metric (see expression (2)). The graphs on the left side figures depict the daily cumulative dynamics of this metric (“per day”), while the graphs on the right side figures depict the daily infection dynamics with a seven-day moving average (”per week”). For all the mentioned figures, the x-axes represent the observation period of the corresponding studied process, graduated in days.
Here we conduct a brief analysis of the results presented in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5. First of all, it should be noted that the cumulative infection dynamics for all types of malware (left side figures) fully correspond to the form of the chosen approximating function (2). This fact supports the notion that the authors’ approach demonstrated greater similarity to the etalon graphs for all studied types of malware compared to the competitor. Nevertheless, it should be acknowledged that the flexibility of the authors’ approach allows for the use of various methods to generalize the set of trajectories obtained as a result of entropy-extreme analysis (avg, median, sda). In this context, the best results were shown by the avg and median variants. In contrast, when describing the daily infection dynamics with a seven-day averaging (right side figures), the median and sda averaging methods proved to be more effective, while the avg variant showed a significantly worse result than the competitor. It should be noted that the benchmark variant of such a dependency is a function with local extrema, which significantly complicates the process of its adequate description.
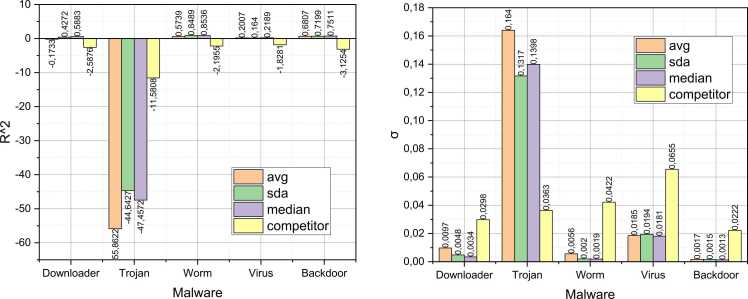
For the completed characterization of the conducted experiments, let's supplement the results presented in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5 with the values of metrics and , demonstrated by the retrained entropy-extreme model on data from segment (Fig. 6) and segment (Fig. 7).
Fig. 6.
The quality of the data from segment . description using the Retrained Model (4).
Fig. 7.
The Quality of the data from segment description using the Retrained Model (4).
Next we analyze the results obtained. We have selected data from the dataset that describe the initial infection scenario of Windows-managed devices by the latest representatives of the respective malware categories. Under these circumstances, conventional cybersecurity measures may not be prepared to counteract such targeted threats effectively – only heuristic detection methods may operate with some probability. Interestingly, the imperfections in the specific threat detection protocols during this period somewhat distort the data presented in the dataset. This circumstance fully justifies the inclusion of the variability characteristic into the model (4). The slowed growth in the number of infected devices after the release of profile updates for cybersecurity tools can be explained by irregularities in updating the databases of the latest threats (this is particularly evident in the case of Virus malware). Additionally, the contradictory picture can also be attributed to overly lenient cybersecurity protocols implemented in institutions and corporations, which afford users excessive degrees of freedom in ambiguous cybersecurity situations.
It is interesting that for the data from the combined training-testing segments (Fig. 6), the typical "competitor" approach based on the least squares method shows higher quality in the metric , compared to the authors’ four-parameter entropy-extreme model, represented by the generalized variants "sda", "median", and "avg". However, the situation changes dramatically in favor of the authors’ approach for the prediction segments .
Аuthor's entropy-extreme approach is characterized by high adaptability due to the selection of the forecasting curve from the trajectory set outputted by the model. Specifically, this selection can favor averaging across the distribution of controlled model parameters ("avg" variant). In such cases, the model becomes equivalent to the typical linear regression approach to forecasting, based on point estimates of controlled parameters. Comparing the "avg" graphs with the etalon graphs in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5, one can observe noticeable inaccuracies in this method of trajectory set generalization by the entropy-extreme model's output (some generated values even fall into the negative domain). This situation can be attributed to the additive noise influencing the output of the model (5), which was set at a high level of 25 % during the experimental setup. The impact of such high variability on the averaged output of the model is particularly pronounced.
Approaches like "sda" and "median" have proven more resilient to the influence of variability characteristics, and incidentally, they demonstrated an advantage over the "competitor" approach. It's also noteworthy that we introduced the variability characteristic into the model (4) to correct for various distortions in the input data. The higher the quality of the investigated data, the lower the value of the indicator can be set, resulting in more accurate forecasts by the authors’ model.
Therefore, the results of the experiments have documented the functionality and effectiveness of the four-parameter entropy-extreme model for predicting the development of cyber epidemics. The model is designed with consideration for application in the vicinity of the extremum of the corresponding time series under conditions where training data are incomplete or distorted. It is noteworthy that the proposed model can be applied without any prior hypotheses regarding the probabilistic properties of the available data.
4. Conclusions
The article explores the challenge of early-stage prediction of cyber epidemics, where data is typically limited, incomplete, and distorted, hindering the use of conventional artificial intelligence models for forecasting. To address this, the authors introduce an entropy-extreme model within the framework of machine learning. This model focuses on estimating probability distributions of controllable parameters from input data, accommodating their inherent variability.
Specifically, the entropy-extreme model identifies the trajectory of the investigated process that exhibits the highest uncertainty (most negative entropy) among a set of distributions derived from input data. Numerical methods are then employed to analyze these trajectories, emphasizing probability distributions of controllable parameters and their variability characteristics.
The analysis yields predictive trajectories such as the average, median, and the ones based on distribution parameters trajectories. In experiments using real data on malware infections in Windows-operated devices, the proposed model demonstrates superior predictive quality compared to the classical least squares method, particularly near critical points in the time series that signify the onset or peak of cyber epidemics.
The results of forecasting the cyber epidemics development on the training-validation (combined) and test segments are demonstrated in the diagrams in Fig. 6, Fig. 7. It should be noted that the authors’ approach shows greater accuracy in describing the combined segment compared to the competitor. This confirms the absence of overfitting. At the same time, the authors’ approach demonstrates better results on the test segment compared to the competitor for all studied classes of malware except Trojan. This fact will be investigated further in the future.
Notably, the entropy-extreme model does not require prior assumptions about the probabilistic properties of the data, making it versatile and robust for forecasting in uncertain and data-scarce environments.
The demonstrated effectiveness of the presented model in forecasting the development of cyber epidemics at early stages enables the formulation of several promising directions for further research based on it. Specifically, there are plans to adapt the entropy-extreme model for classifying cyber threats in conditions of limited incomplete data with high variability. Additionally, it is considered promising to investigate the potential of combining the authors’ approach with dynamic regression models to surpass the current level of forecasting quality in the process of cyber epidemic development.
Funding
The authors would like to extend their gratitude to King Saud University (Riyadh, Saudi Arabia) for funding this research through the Researchers Supporting Project number RSP2024R260.
CRediT authorship contribution statement
Mohammed Al-Maitah: Writing – review & editing, Validation, Resources, Data curation. Krzysztof Grochla: Writing – review & editing, Validation, Resources, Data curation. Wojciech Kempa: Writing – review & editing, Validation, Resources, Data curation. Saad Aldosary: Writing – review & editing, Validation, Resources. Viacheslav Kovtun: Writing – review & editing, Writing – original draft, Visualization, Supervision, Software, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Conceptualization.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors are grateful to all colleagues and institutions that contributed to the research and made it possible to publish its results.
Contributor Information
Viacheslav Kovtun, Email: kovtun_v_v@vntu.edu.ua.
Krzysztof Grochla, Email: kgrochla@iitis.pl.
Mohammed Al-Maitah, Email: malmaitah@ksu.edu.sa.
Saad Aldosary, Email: saldosary@ksu.edu.sa.
Wojciech Kempa, Email: Wojciech.Kempa@polsl.pl.
Data availability
Most data are contained within the article. All the data are available on request.
References
- 1.Cichonski P., Millar T., Grance T., Scarfone K. National Institute of Standards and Technology. 2012. Computer security incident handling guide: Recommendations of the National Institute of Standards and Technology. doi: 10.6028/nist.sp.800-61r2. [Google Scholar]
- 2.S. Yevseiev et al., Models of socio-cyber-physical systems security. Privat Company Technology Center; 2023. Available from: doi: 10.15587/978–617-7319–72-5.
- 3.Temitayo Oluwaseun Abrahams, et al. Vol. 5. Fair East Publishers; 2024. A review of cybersecurity strategies in modern organizations: examining the evolution and effectiveness of cybersecurity measures for data protection; pp. 1–25. (Computer Science & IT Research Journal). [DOI] [Google Scholar]
- 4.Rusnak P., et al. Vol. 243. Elsevier BV; 2024. Importance analysis of a system based on survival signature by structural importance measures. (Reliability Engineering & System Safety). [DOI] [Google Scholar]
- 5.El-Genk M.S., Altamimi R., Schriener T.M. Vol. 154. Elsevier BV; 2021. Pressurizer dynamic model and emulated programmable logic controllers for nuclear power plants cybersecurity investigations. (Annals of Nuclear Energy). [DOI] [Google Scholar]
- 6.Bozorgchenani A., et al. Vol. 237. Elsevier BV; 2023. Novel modeling and optimization for joint Cybersecurity-vs-QoS Intrusion Detection Mechanisms in 5G networks. (Computer Networks). [DOI] [Google Scholar]
- 7.Cheng S., Li J., Luo L., Zhu Y. Vol. 65. Elsevier BV; 2024. Cybersecurity governance and digital finance: evidence from sovereign states. (Finance Research Letters). [DOI] [Google Scholar]
- 8.Chang K., Huang H. Vol. 40. Elsevier BV,; 2023. Exploring the management of multi-sectoral cybersecurity information-sharing networks. (Government Information Quarterly). [DOI] [Google Scholar]
- 9.Wang J., Ang J.B. Vol. 52. Elsevier BV; 2024. Epidemics, disease control, and China’s long-term development; pp. 93–112. (Journal of Comparative Economics). [DOI] [Google Scholar]
- 10.Archibong B., Annan F., Ekhator-Mobayode U. Vol. 211. Elsevier BV,; 2023. The epidemic effect: epidemics, institutions and human capital development; pp. 549–566. (Journal of Economic Behavior & Organization). [DOI] [Google Scholar]
- 11.Liao S., Li X., Niu Y., Xu Z., Cao Y. Vol. 107. Elsevier BV,; 2024. Risk control of epidemic in urban cold-chain transportation. (Sustainable Cities and Society). [DOI] [Google Scholar]
- 12.I. Fedorchenko, et al., Modified genetic algorithm to determine the location of the distribution power supply networks in the city, Zenodo; Dec. 2020. Available from: doi: 10.5281/ZENODO.5163692.
- 13.Alsayaydeh J.A.J., et al. Development of programmable home security using GSM system for early prevention. J Eng Appl Sci. 2021;16(1):88–97. [Google Scholar]
- 14.Zhan J., Wei Y. Vol. 184. Elsevier BV; 2024. Dynamical behavior of a stochastic non-autonomous distributed delay heroin epidemic model with regime-switching. (Chaos, Solitons & Fractals). [DOI] [Google Scholar]
- 15.Tang L., Shen R., Pan X. Vol. 361. Elsevier BV,; 2024. A node-based SIRS epidemic model on two-layer interconnected networks: dynamical analysis of interplay between layers. (Journal of the Franklin Institute). [DOI] [Google Scholar]
- 16.Geng P. Vol. 192. Elsevier BV,; 2022. Estimation of functional-coefficient autoregressive models with measurement error. (Journal of Multivariate Analysis). [DOI] [Google Scholar]
- 17.Berghout T., Benbouzid M., Muyeen S.M. Vol. 38. Elsevier BV; 2022. Machine learning for cybersecurity in smart grids: a comprehensive review-based study on methods, solutions, and prospects. (International Journal of Critical Infrastructure Protection). [DOI] [Google Scholar]
- 18.Oyinloye T.S., Arowolo M.O., Prasad R. Data Science and Management. Elsevier BV,; 2024. Enhancing cyber threat detection with an improved artificial neural network model. [DOI] [Google Scholar]
- 19.Alaoui E.A.A., et al. Vol. 236. Elsevier BV,; 2024. Towards transparent cybersecurity: the role of explainable AI in mitigating spam threats; pp. 394–401. (Procedia Computer Science). [DOI] [Google Scholar]
- 20.Alsayaydeh J.A.J., et al. Development of vehicle ignition using fingerprint. J Eng Appl Sci. 2019;14(23):4045–4053. [Google Scholar]
- 21.Mohammed E.Z., Jameel N.G.M., Shukr A.I., Ghareeb A. Vol. 13. Elsevier BV; 2023. Strategic planning for cancer control: utilizing machine-learning models to predict future incidences. (Results in Control and Optimization). [DOI] [Google Scholar]
- 22.Sarker I.H., Janicke H., Mohsin A., Gill A., Maglaras L. ICT Express. Elsevier BV; 2024. Explainable AI for cybersecurity automation, intelligence and trustworthiness in digital twin: methods, taxonomy, challenges and prospects. [DOI] [Google Scholar]
- 23.Venkatesan V.K., et al. Vol. 11. MDPI AG; 2023. High-performance artificial intelligence recommendation of quality research papers using effective collaborative approach; p. 81. (Systems). [DOI] [Google Scholar]
- 24.Miranda-García A., et al. Vol. 563. Elsevier BV,; 2024. Deep learning applications on cybersecurity: a practical approach. (Neurocomputing). [DOI] [Google Scholar]
- 25.Zaitseva E., Levashenko V., Rabcan J., Kvassay M. Vol. 10. MDPI AG; 2023. A new fuzzy-based classification method for use in smart/precision medicine; p. 838. (Bioengineering). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mochurad L., Hladun Y. Vol. 14. Springer Science and Business Media LLC; 2024. Neural network-based algorithm for door handle recognition using RGBD cameras. (Scientific Reports). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Aydın H., Orman Z., Aydın M.A. Vol. 118. Elsevier BV; 2022. A long short-term memory (LSTM)-based distributed denial of service (DDoS) detection and defense system design in public cloud network environment. (Computers & Security). [DOI] [Google Scholar]
- 28.Kim T.-Y., Cho S.-B. Vol. 456. Elsevier BV; 2021. Optimizing CNN-LSTM neural networks with PSO for anomalous query access control; pp. 666–677. (Neurocomputing). [DOI] [Google Scholar]
- 29.Khaw Y.M., Jahromi A.A., Arani M.F.M., Kundur D. Vol. 17. Elsevier BV,; 2024. Evasive attacks against autoencoder-based cyberattack detection systems in power systems. (Energy and AI). [DOI] [Google Scholar]
- 30.Bisikalo O., et al. Vol. 25. MDPI AG; 2023. Parameterization of the Stochastic model for evaluating variable small data in the Shannon entropy basis; p. 184. (Entropy). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kovtun V., et al. Vol. 13. Springer Science and Business Media LLC; 2023. Stochastic forecasting of variable small data as a basis for analyzing an early stage of a cyber epidemic. (Scientific Reports). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kovtun V., Altameem T., Al-Maitah M., Kempa W. Vol. 10. Elsevier BV; 2024. Entropy-metric estimation of the small data models with stochastic parameters. (Heliyon). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Li X., Zhao Z., Zhao Y., Zhou S., Zhang Y. Vol. 423. Elsevier BV; 2023. Prediction of energy-related carbon emission intensity in China, America, India, Russia, and Japan using a novel self-adaptive grey generalized Verhulst model. (Journal of Cleaner Production). [DOI] [Google Scholar]
- 34.Wang Q., Xiang K., Zhu C., Zou L. Vol. 212. Elsevier BV; 2023. Stochastic SEIR epidemic models with virus mutation and logistic growth of susceptible populations; pp. 289–309. (Mathematics and Computers in Simulation). [DOI] [Google Scholar]
- 35.Kovtun V., et al. Vol. 25. MDPI AG,; 2023. Small stochastic data compactification concept justified in the entropy basis; p. 1567. (Entropy). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Valentine D.T., Hahn B.D. Essential MATLAB for Engineers and Scientists. Elsevier; 2023. Introduction to numerical methods; pp. 293–322. [DOI] [Google Scholar]
- 37.Catak F.O., Ahmed J., Sahinbas K., Khand Z.H. Vol. 7. PeerJ; 2021. Data augmentation based malware detection using convolutional neural networks. (PeerJ Computer Science). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Most data are contained within the article. All the data are available on request.