Improving on polygenic scores across complex traits using select and shrink with summary statistics (S4) and LDpred2

Abstract

Background

As precision medicine advances, polygenic scores (PGS) have become increasingly important for clinical risk assessment. Many methods have been developed to create polygenic models with increased accuracy for risk prediction. Our select and shrink with summary statistics (S4) PGS method has previously been shown to accurately predict the polygenic risk of epithelial ovarian cancer. Here, we applied S4 PGS to 12 phenotypes for UK Biobank participants, and compared it with the LDpred2 and a combined S4 + LDpred2 method.

Results

The S4 + LDpred2 method provided overall improved PGS accuracy across a variety of phenotypes for UK Biobank participants. Additionally, the S4 + LDpred2 method had the best estimated PGS accuracy in Finnish and Japanese populations. We also addressed the challenge of limited genotype level data by developing the PGS models using only GWAS summary statistics.

Conclusions

Taken together, the S4 + LDpred2 method represents an improvement in overall PGS accuracy across multiple phenotypes and populations.

Supplementary Information

The online version contains supplementary material available at 10.1186/s12864-024-10706-3.

Background

Genome-wide association studies (GWAS) have identified associations between common genetic variants and more than 3,300 phenotypes [1], revealing the highly polygenic architecture of many common traits. Polygenic scores (PGS) are a weighted sum of a collection of genome-wide risk alleles for a specific phenotype. Generally, the summary statistics of a genome-wide association study (GWAS) inform the selection and weighting of the common variants in a polygenic model used to calculate a PGS for an individual. Each GWAS variant confers only small risks individually, but their combined effects, when summarized as a PGS, may be substantial. As personalized medicine becomes a larger part of medical care, PGS may be clinically useful to help early detection, individual stratification, and prevention in the general population for a variety of diseases [2–4].

The development of novel methods for PGS estimation allows for different approaches to inform selection of variants and weighting of alleles. In creating a PGS method, it is important that a model is both accurate and computationally feasible. Variants are generally selected by the confidence of association and weighted by their effect on risk as determined from GWAS summary statistics [5, 6]. Additionally, risk variants in high linkage disequilibrium (LD) with each other are often pruned or down-weighted to limit overrepresentation of highly correlated variants from the same association signal [6]. For clinical usage, selection of fewer variants in the model will improve feasibility. For both the GWAS summary statistics and LD reference panel, an ancestry matched cohort is ideal to improve accuracy. Simultaneously, the model’s transferability to other ancestry groups is equally crucial.

Previously, we presented our “select and shrink with summary statistics” (S4) PGS method which accurately and efficiently predicted the polygenic risk of epithelial ovarian cancer [7]. In this paper, we further demonstrated the accuracy of the S4 PGS method in risk predictions of multiple phenotypes, and compared the S4 PGS method to LDpred2 and a combined S4 PGS and LDpred2 model, referred as ‘S4 + LDpred2’ henceforth. LDpred [8, 9] is a commonly utilized Bayesian-based PGS method that uses both a point-normal mixture distribution prior and LD information from a reference panel to estimate posterior mean causal effect sizes to improve accuracy in the PGS [8]. LDpred2 improves the computational efficiency of LDpred, as well as its accuracy when causal variants are in long-range LD regions or are only a small proportion of the total variation [9]. The S4 PGS method uses a continuous shrinkage prior on effect sizes and also allows for improved penalization of rare SNPs by correcting for standard error of the estimate [7]. Recent meta-analyses found no single method consistently outperformed all others, and showed that a combined PGS framework could increase prediction accuracy [10, 11]. In combining S4 PGS with LDpred2, our objective was to investigate whether this combined model enhances prediction accuracy, and more importantly, to improve the model’s generalizability across diverse phenotypes and populations.

Here, we first assessed the feasibility of S4 PGS in diverse phenotypes for which both GWAS summary statistics and genotype level data were available in the UK Biobank [12]. We then combined S4 PGS and LDpred2, and compared it with the standalone methods. Across multiple phenotypes with varying genetic architectures, we found that the combined S4 + LDpred2 method provides overall improved PGS accuracy. We also assessed the performance of PGS models trained in the UK Biobank and validated in Finnish and Japanese populations [13, 14]. Finally, we developed and validated PGS models using only summary statistics, demonstrating the practical viability of S4 + LDpred2. We found that the S4 + LDpred2 method has strong potential for development of accurate PGS across a variety of phenotypes and populations.

Methods

Phenotypes and study populations

We performed PGS modeling and association testing for two quantitative traits: body mass index (BMI), and height; and ten binary diseases: asthma, breast cancer, coronary artery disease, endometrial cancer, inflammatory bowel disease (IBD), major depressive disorder, prostate cancer, schizophrenia, type 1 diabetes, and type 2 diabetes. These phenotypes were chosen to represent a variety of traits, and to include those influenced by epidemiological as well as genetic risk factors.

Published GWAS summary statistics were collected and used as input to form a polygenic model for each trait (Fig. 1, Supplementary Table 1) [15–26]. We collected genotype and phenotype data and GWAS summary statistics of all Europeans from the UK Biobank [12], and only GWAS summary statistics from FinnGen [14] and BioBank Japan [13]. The numbers of case and control samples used in each phenotype are detailed in Supplementary Table 1. European descent was determined in the UK Biobank through the designated Data-Field 22,006, and these individuals were selected for inclusion.

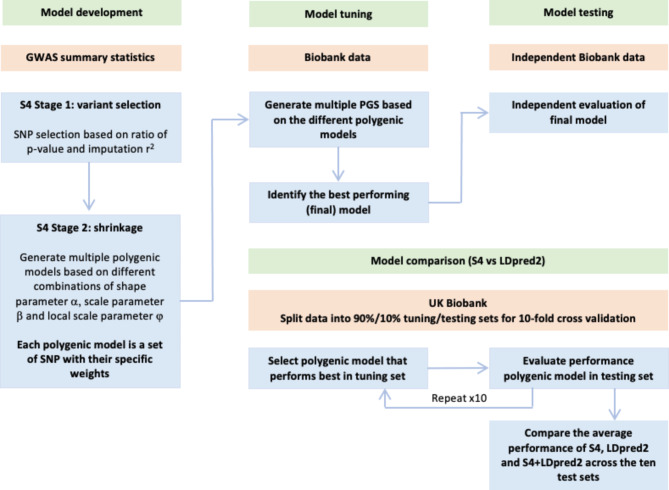
Fig. 1.

S4 PGS model development, tuning, testing, and comparison. We first developed the S4 polygenic models (left), then tuned parameters from Biobank data (middle) and evaluated the best of those models in independent Biobanks data (right). We finally compared S4 PGS with other methods using the average performance across 10-fold cross-validation only by UK Biobank (bottom)

The select and shrink with summary statistics (S4) PGS method

The S4 PGS method had been previously described in Dareng et al. 2022 [7]. We briefly review the main ideas of S4 PGS here. The S4 PGS method is a two-stage approach, where the first stage is variant selection, and the second stage is shrinkage. In the selection stage, the S4 PGS first ranks and selects SNPs from the GWAS summary statistics to include in the model. SNPs pass the defined thresholds, p-value/r², are considered, where the p-value indicates the significance of association in GWAS and r² is the squared correlation between SNPs. Each top GWAS SNP is iteratively added if the correlation with all the other SNPs included is less than 0.85. If the SNP has a correlation below 0.02 with all other SNPs, then a new group is started, helping to reduce computational costs. New SNPs are put into the groups with which they are best correlated. When the p-value divided by the correlation to other SNPs in the model is above a specified threshold (0.02, 0.15, and 0.6 were tested in this analysis) no more SNPs will be chosen. At each threshold, the number of SNPs varies depending on phenotype and density of summary statistics coverage. The threshold of p/r² < 0.6 was not tested on certain phenotypes when computationally infeasible. For BMI, rather than p/r² < 0.6, all SNPs were included as the number of SNPs was still computationally feasible.

In the shrinkage stage, the weight, 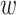, for each of the selected SNPs is calculated using a continuous shrinkage prior on effect sizes. We adapted the PRS-CS algorithm [27] and penalized rarer SNPs by correcting for the standard deviation, which resulted in the selection of fewer SNPs. We considered the global-local scale mixtures of normal:

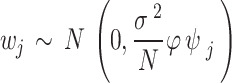, where the variance of 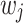scales with the sample size, 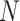, and residual variance, 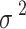. 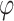is a global scaling parameter shared across all effect sizes, and 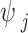is a local SNP-specific scaling parameter. We further assumed an independent gamma-gamma prior on the local scaling parameter, :

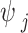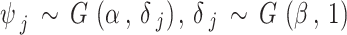, where 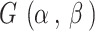denotes the gamma distribution with shape parameter α and scale parameter β. Hence, there are three tuning parameters in the shrinkage stage: 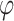is the global shrinkage parameter, α controls the shrinkage of effect estimates around 0, and β controls the shrinkage of larger effect estimates. The performance of the model was minimally impacted by the value of α. Overall, setting α to 0.1 yielded slightly better results when the threshold for selecting variants was at least 0.6, compared to larger values. For smaller threshold values, the differences between α values were negligible, as α mainly influences values near 0. Consequently, α was fixed at 0.1 throughout to simplify the parameter testing process. For the other parameters, 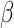was set to a range of values from 0.7 to 100 with increments of 0.1 up to 2.0, increments of 0.2 to 4.0, and eight more increments up to the maximum of 100. The values for 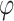were taken as 1, 1.2, 1.5, 2, 2.5, 3, 4, 5, 6, 8 multiplied by factors of 10 from 1e-10 to 1e10. The issue of determining the range of parameter values remains. We selected a metric such that the prior probability of a variant having an absolute effect on the outcome of at least 0.01 was within a specified range. This ensured that the beta values were matched with corresponding 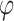values that were reasonable, neither excessively strict nor overly lenient. This process was used to determine the range for the threshold of p/r² = 0.02. Typically, around 700 combinations were tested. For larger thresholds, the values that yielded the best results for the 0.02 threshold, with 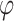set to lower values (since larger thresholds typically require lower 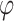values for an equivalent 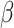), were selected. Approximately 150 parameters were chosen for this latter step. The time required was typically about one hour on a single core for the 0.02 threshold and one day on a single core for the largest threshold.

PGS models development, tuning, testing, and comparison

We compared the PGS prediction performance between S4 PGS, LDpred2, PRS-CS and S4 + LDpred2 [9, 27] (Fig. 1). To maintain a fair comparison, polygenic scores were created as a linear function of 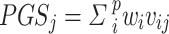, where 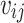represented the dosage of the jth individual for the ith SNP out of p SNPs, and 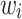represented the weight, i.e. the log of the odds ratio, of the ith SNP. Genotypes were denoted as 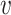, taking on the minor allele dosages of 0, 1 and 2. The S4 PGS method considered SNPs from the entire set of summary statistics, while LDpred2 and PRS-CS focuses only on the Hapmap3 SNPs as recommended by the authors. The three methods used different approaches to select and derive the optimal weights .

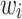We first prepared LD matrices (a set of between SNP pairwise correlations or r²) from the OncoArray genotyping panel for breast, prostate and endometrial cancer and from an Illumina 610 genotyping panel for the other phenotypes [28–30]. The OncoArray panel was chosen as the reference for the cancer phenotypes as the bulk of the samples used in the cancer summary statistics were genotyped on the OncoArray while the Illumina 610 panel was likely to match the non-cancer phenotypes more closely. The phased haplotypes of the 1000 Genomes Project dataset [31] were used in the pseudo-validation process for summary statistics, with FinnGen using the European samples and the Japan Biobank using the Asian samples.

LDpred2 is a popular method for creating a PGS that estimates effect sizes with point-normal prior and a Gibbs sampler. The parameters selected to test the LDpred2 version 1.11.6 model followed the suggestions in the LDpred2 paper [9]. For some of the phenotypes, the best h² coefficient was outside the range suggested within the paper, so extra h² values were generated to select the best fitting model. The aim was to make sure the best fitting model was not an extreme value of h² (either biggest or smallest). LDpred2 assumes that a spike and slab prior fits the data well.

The PRS-CS model is also a Bayesian method that applies a continuous shrinkage prior on effect sizes. This model does not use the same SNP selection method as S4 PGS, which is able to better penalize rarer SNPs. For PRS-CS, the tuning parameter representing global shrinkage, ϕ, was tested at 1e-6, 3e-6, 1e-5, 3e-5 etc. so that the best fitting value lied in the interior of this set of values. This ensured that the best fitting value was close to the global optimum.

We combined the S4 and LDpred2 models by selecting the best models for both S4 and LDpred2 on the tuning set. Then, we fitted a regression model with the outcome as the response and the predictions from the two models as the covariates. We used either the individual weights from the cross-validation or the summary statistics from the FinnGen data (see the subsection below) to estimate the regression coefficients. This gave us a weighted average of the two models that minimized the prediction error on the training set. We applied this combined model on the test set and compared its performance with the other models.

When doing model comparisons, we split UK Biobank data into 90% tuning and 10% testing sets for 10-fold cross-validation [12]. In each cross-validation iteration, we used the 90% tuning data to fine-tune the parameters and select the best performed PGS model. Subsequently, we evaluated this model on the remaining 10% testing data set. Performance was assessed by averaging the area under the receiver operator curve (AUC) values across the ten iterations for categorical variables or averaging correlations for continuous variables. For a comprehensive performance evaluation, besides AUC, we also reported log odds ratio (log OR) normalized by one standard deviation of PGS, which gave a similar measure of effectiveness as the AUC but took into account the covariates. The 95% confidence interval (CI) of log OR per SD was also provided, with a wider confidence interval indicating greater uncertainty in the estimate, while a narrower interval indicates more precise estimation.

PGS performance evaluation in alternative populations

To test applicability to non-European populations, the best PGS models trained in UK Biobank were evaluated in Finnish (FinnGen [14]) and Japanese (BioBank Japan [13]) cohorts (Fig. 1). As no individual level genotypes were available for these cohorts, previous research had developed methods for tuning PGS using summary statistics [32, 33]. Here, we developed a similar evaluation approach, acknowledging that the performance results are inferred and depend on the accuracy of this summary statistic-based approach. We estimated the PGS effects from the summary statistics and variants correlation matrix instead, as follows:

Denote 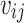to be the value of SNP i for individual j. We can assume that each variant has a mean of 0 without loss of generality. This also means that the constant terms in the regression equation are independent of the other terms (as the dot product between the constant term and any 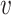is 0). Assume that the polygenic model is 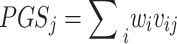. Also, for each variant 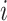, we have the beta coefficient 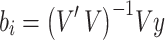, where 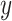is the phenotype outcome and 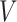is the SNP data matrix, as well as the approximate standard error of beta coefficient 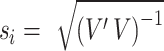. If we set 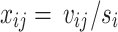, then 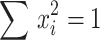and 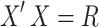, where 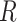is the correlation matrix. We therefore derive,

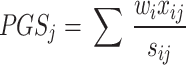We then define the matrix 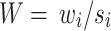, so that 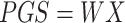. Thus, the estimated beta coefficient of PGS is 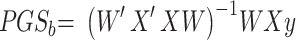and the estimated standard error of PGS is . Since the 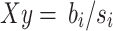for each SNP i is from the summary statistics data, we define 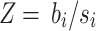. Therefore,

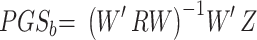For calculating the estimated coefficient per standard deviation, instead of using the coefficient of the unadjusted PGS, we need to estimate the standard deviation of the PGS in the tested dataset. This is done by calculating 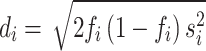for each variant i where 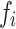is the frequency and 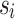is the standard error of the beta estimate. Since the MaCH imputation (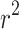) [34] is equal to the variance divided by 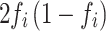, the variance of each variant will generally be less than 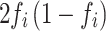. Therefore, the estimate for the population is determined by selecting one of the lower values of d (0.2% percentile). Then:

Estimated standard deviation of PGS in population =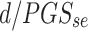

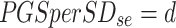This can be extended to regression for several PGSs by defining the matrix 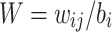where 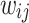is the weight for the ith variant on the jth PGS, and is used when combining the S4 and LDpred2 models.

PGS models tuned by summary statistics

We fitted the polygenic models using the summary statistics from FinnGen as a training set. The summary statistics included the effect size (odds ratio) and the standard error for each genetic variant. We used the odds ratio per standard error as the outcome variable in the parameter estimation step to optimize the different parameters for S4 and LDpred2. We also fitted the S4 + LDPred2 model using the summary statistics and the optimized S4 and LDpred2 models. This was equivalent to maximizing the chi-squared statistic for each variant, which reflected the strength of the association. We applied the PGS model with the best parameters to the different test sets, which consisted of all valid samples for Biobank and the summary statistics for the Biobank Japan.

Results

S4 polygenic predictions of multiple phenotypes in UK Biobank

We applied the S4 PGS method to predict ten complex diseases (asthma, breast cancer, coronary artery disease, endometrial cancer, inflammatory bowel disease, major depressive disorder, prostate cancer, schizophrenia, type 1 diabetes, and type 2 diabetes), and two quantitative traits (body mass index and height) in the UK Biobank [12]. Previously published GWAS summary statistics and individual level genotype data for each disease and trait were used to evaluate the performance of each S4 PGS model. The optimal parameters and performance of best-fitting models for each phenotype are shown in Table 1. Prediction performance metrics included area under the receiver operating characteristic curve (AUC), log odds ratio (log OR) normalized by one standard deviation of PGS, and 95% confidence interval (CI). Among the 12 phenotypes, the AUC values of S4 PGS predictions ranged from 0.56 to 0.79, with better predictions in type 1 diabetes (AUC = 0.79), inflammatory bowel disease (AUC = 0.73), and schizophrenia (AUC = 0.72). PGS associations were accessed by normalized log OR, ranging from 0.22 for major depressive disorder to 1.14 for type 1 diabetes. The number of SNPs selected varied among phenotypes, ranging from 19,584 for type 2 diabetes to 1,239,271 for schizophrenia.

Table 1.

Performance of S4 PGS model on multiple phenotypes in UK Biobank

Phenotype	Number of SNPs	Tuning parameter for best performance			AUC	log OR per SD of PGS		95% CI
		⍺	β	Φ
Quantitative traits
Body mass index	585,796	0.1	4.5	1.20E-04	0.30a	1.468a		1.455–1.482
Height	461,803	0.1	3.8	3.00E-05	0.37a	3.494a		3.478–3.511
Binary diseases
Asthma	425,752	0.1	1.9	2.50E-05	0.60	0.362		0.353–0.372
Breast cancer	357,287	0.1	1.3	4.00E-06	0.66	0.577		0.547–0.607
Coronary artery disease	689,356	0.1	1.3	1.20E-05	0.65	0.585		0.564–0.605
Endometrial cancer	271,090	0.1	4.5	1.50E-04	0.61	0.406		0.345–0.467
Inflammatory bowel disease	358,464	0.1	1.4	2.50E-05	0.73	0.856		0.822–0.890
Major depressive disorder	843,583	0.1	100	3.00E-03	0.56	0.224		0.208–0.240
Prostate cancer	409,227	0.1	1.2	6.00E-06	0.71	0.816		0.786–0.846
Schizophrenia	1,239,271	0.1	100	5.00E-03	0.72	0.858		0.762–0.955
Type 1 diabetes	19,584	0.1	8	1.20E-03	0.79	1.140		1.049–1.231
Type 2 diabetes	874,431	0.1	2.4	5.00E-05	0.66	0.609		0.574–0.645

AUC: area under the receiver operating characteristic (ROC) curve, log OR: log odds ratio, SD: standard deviation, PGS: polygenic score, CI: confidence interval

^a Phenotypes body mass index and height are continuous variables. The prediction accuracy was evaluated by correlation instead of AUC. The association was evaluated by beta coefficient instead of log odds ratio. These applied to all body mass index and height evaluation in this study

S4 PGS performance on various SNP selection thresholds

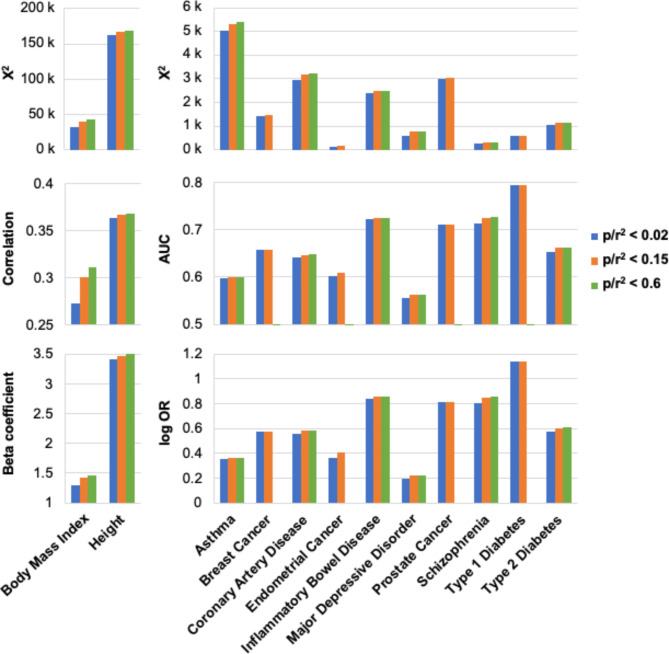
S4 PGS is a parsimonious model which uses the most significant SNPs, resulting in the selection of fewer SNPs. We investigated the influence of SNP selection thresholds on S4 PGS predictions. The threshold was determined by the measure of SNP p-value divided by squared correlation of linkage disequilibrium. We examined thresholds of 0.02, 0.15, and 0.6, which on average used 54,000, 253,000, 731,000 SNPs. For body mass index, rather than the 0.6 threshold, the S4 PGS model was tested with all SNPs, as the number of SNPs was still sufficiently small for the model to run. In general, the inclusion of more SNPs led to better prediction accuracy and association (Fig. 2, Supplementary Table 2). However, this came at the penalty of larger SNP datasets and the need for increasing computational time. For example, the correlations for body mass index were 0.27, 0.3, 0.31 for the three thresholds respectively, and the normalized log ORs were 1.29, 1.42, and 1.47. The only exception was type 1 diabetes, which showed no improvement when increasing the threshold from 0.02 to 0.15. There was little difference in prediction performances when the threshold was increased from 0.15 to 0.6, while the computation time largely increased and models for breast cancer, endometrial cancer, prostate cancer, and type 1 diabetes became computationally infeasible. Even though the various number of SNPs selected also depended on the density of summary statistics coverage and shrinkage parameters of effect estimates, we confirmed through these threshold analyses that the use of threshold 0.15 in this study was ideal in balancing between model performance and computational time.

Fig. 2.

Performance of S4 PGS model across different SNPs selection thresholds. Threshold was determined by p-value divided by r². For each phenotype, chi-square statistics calculated from Likelihood Ratio Test (top), correlations or AUC (middle), and beta coefficient or log Odds Ratio per 1 standard deviation of PGS (bottom) are reported

Combining S4 and LDpred2 improves polygenic score predictions

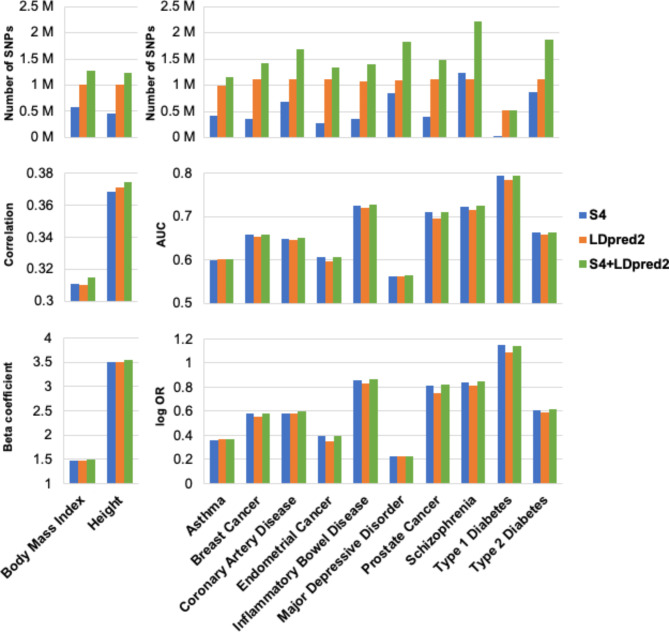
We next sought to compare the S4 PGS method with LDpred2 [9] and the combined S4 + LDpred2 model. LDpred2 was selected due to its reliability in accurately predicting polygenic scores on multiple phenotypes. Overall, the S4 + LDpred2 model performed the best in ten out of 11 phenotypes (Fig. 3, Supplementary Table 3). The S4 + LDpred2 method had better prediction accuracy and association for type 1 diabetes (AUC = 0.793, log OR = 1.14) and Inflammatory bowel disease (AUC = 0.727, log OR = 0.867). S4 PGS and S4 + LDpred2 exhibited noticeable advancement in cancers, including endometrial cancer (AUC = 0.607, log OR = 0.396) and prostate cancer (AUC = 0.711, log OR = 0.822), outperforming LDpred2 (endometrial cancer AUC = 0.597, log OR = 0.351; prostate cancer AUC = 0.695, log OR = 0.755). Consistent with results from previous S4 PGS predictions on epithelial ovarian cancer [7], the S4 PGS methods used noticeably less SNPs than LDpred2 on all phenotypes except schizophrenia. The greatest difference was in type 1 diabetes, where LDpred2 (n = 515,920) had 26-fold increased number of SNPs than S4 PGS (n = 19,584). The comparisons between models were based on the average performance of 10-fold cross-validations for all methods. We note that AUC values from cross-validations were similar to the AUC values derived from full training datasets, indicating overfitting problems were less likely to occur during our model training. We also used bootstrapping to estimate the standard error of the difference between the S4 + LDpred2 models and the LDpred2 models and derived a nominal p-value. The p-values for the difference were significant for all phenotypes (Supplementary Table 4). In brief, our results confirmed that S4 PGS and S4 + LDpred2 methods outperformed LDpred2 in predicting polygenic risk scores on multiple phenotypes.

Fig. 3.

Performance of best-fitting PGS models with 10-fold cross-validation on multiple phenotypes. For each phenotype, number of SNPs used in the respective models (top), correlations or AUC (middle), and beta coefficient or log Odds Ratio per 1 standard deviation of PGS (bottom) are reported

PRS-CS, like S4 PGS, is a widely-used PGS method that employs a shrinkage approach. We conducted the 10-fold cross-validation analysis for PRS-CS using the same set of phenotypes. S4 PGS outperformed PRS-CS in all phenotypes tested (Supplementary Table 5). The S4 PGS method showed the greatest advancement in prediction accuracy and association for prostate cancer (AUC = 0.710, log OR = 0.816) and schizophrenia (AUC = 0.723, log OR = 0.844) compared to PRS-CS (prostate cancer AUC = 0.684, log OR = 0.704; schizophrenia AUC = 0.703, log OR = 0.778). Unlike S4 PGS which used fewer SNPs while varying across phenotypes, PRS-CS models steadily used 1.1 million SNPs per model. When comparing S4, LDpred2, and PRS-CS, PRS-CS exhibited the lowest performance, leading us to exclude it from the combined model.

External validations of PGS models in Finnish and Japanese populations

To assess the applicability of the three PGS methods to other populations we leveraged the existing GWAS summary statistics from FinnGen [14] and BioBank Japan [13]. The best fit model on the whole UK Biobank data for each phenotype and each model was tested on the FinnGen and BioBank Japan populations. Uniformly observed across the three methods: S4 PGS, LDpred2, and S4 + LDpred2, the PGS associations from Finnish and Japanese ancestries were both comparable to the PGS associations obtained from the European cohort in most of the phenotypes (Table 2). Larger log ORs were reported in the FinnGen cohort than UK Biobank for breast cancer, major depressive disorder, and prostate cancer, while inflammatory bowel disease and schizophrenia showed better PGS associations in the UK Biobank. There was no phenotype in which a larger log OR was calculated in BioBank Japan than UK Biobank.

Table 2.

External validation of PGS models in Finnish and Japanese populations. Log OR values with better performance are highlighted in bold

Phenotype	S4			LDpred2			S4 + LDpred2
	χ2	log OR	95% CI	χ2	log OR	95% CI	χ2	log OR	95% CI
FinnGen
Asthma	1603	0.300	0.285–0.315	1640	0.303	0.289-0.318	1687	0.308	0.293–0.322
Breast cancer	3403	0.611	0.590–0.631	3315	0.603	0.582-0.623	3516	0.621	0.600-0.641
Coronary artery disease	4407	0.530	0.514–0.546	4034	0.507	0.491-0.523	4500	0.536	0.520–0.551
Endometrial cancer	123	0.297	0.245–0.350	125	0.3	0.247-0.352	125	0.3	0.248–0.353
Inflammatory bowel disease	1856	0.540	0.515–0.564	1890	0.545	0.520-0.569	1959	0.554	0.530–0.579
Major depressive disorder	1068	0.229	0.215–0.243	1165	0.239	0.226-0.253	1193	0.242	0.228–0.256
Prostate cancer	4761	0.858	0.834–0.882	4005	0.787	0.763-0.811	4865	0.867	0.843–0.892
Schizophrenia	845	0.603	0.563–0.644	856	0.607	0.567-0.648	901	0.623	0.583–0.664
Type 1 diabetes	5755	1.029	1.003–1.056	6159	1.065	1.038-1.091	6133	1.062	1.036–1.089
Type 2 diabetes	5707	0.504	0.491–0.517	5732	0.505	0.492-0.518	6020	0.517	0.504–0.530
BioBank Japan
Quantitative traits
Body mass index	6951	0.186a	0.182–0.191	6829	0.185a	0.180–0.189	7210	0.19 a	0.185–0.194
Height	23,007	0.213a	0.210–0.216	22,562	0.211a	0.208–0.214	23,915	0.217 a	0.215–0.220
Binary diseases
Asthma	599	0.233	0.214–0.251	602	0.233	0.215–0.252	646	0.242	0.223–0.260
Breast cancer	975	0.418	0.392–0.445	953	0.414	0.388–0.440	1028	0.43	0.403–0.456
Endometrial cancer	28	0.154	0.097–0.211	29	0.157	0.100-0.214	29	0.157	0.100-0.214
Major depressive disorder	9	0.105	0.038–0.173	11	0.115	0.048–0.183	11	0.117	0.049–0.184
Prostate cancer	2322	0.701	0.672–0.729	2376	0.709	0.680–0.737	2516	0.729	0.701–0.758
Schizophrenia	14	0.373	0.179–0.568	22	0.468	0.273–0.663	19	0.434	0.239–0.628
Type 1 diabetes	6	0.068	0.011–0.124	2	0.039	-0.017-0.096	5	0.065	0.008–0.121
Type 2 diabetes	4507	0.433	0.421–0.446	4160	0.416	0.404–0.429	4741	0.444	0.432–0.457

^a Phenotypes body mass index and height are continuous variables. The association was evaluated by beta coefficient instead of log odds ratio

When comparing the three methods, S4 + LDpred2 performed better in phenotypes with stronger main effects (such as breast cancer and prostate cancer) and LDpred2 performs better in phenotypes where a very large number of variants contribute (such as major depressive disorder). When accessing the cross-biobank performance, the log ORs of type 1 diabetes in the Japanese population were lower than expected for all three methods (S4 PGS:0.068, LDpred2: 0.039, S4 + LDpred2:0.065). By examining the summary statistics, we discovered that top SNPs for type 1 diabetes in the European population were not significant in the Japanese population (Supplementary Table 6), explaining the discordance. In addition, height and body mass index reported much lower beta coefficients for the Japanese population than the European populations, while the standard errors of the estimates are much less when comparing to the European samples. This observation might be a result of variance in the traits, LD structure, or allele frequency in different populations.

Genotype level data were not available for FinnGen and BioBank Japan, so we evaluated the PGS models predictive performance by estimating PGS effects (joint effects) from GWAS summary statistics (marginal effects) and variants correlation matrix (see Methods). To validate the rationality of this estimation approach, we compared S4 PGS and LDpred2 model results evaluated by directly calculating PGS with results assessed by estimating through summary statistics (Supplementary Table 7). The results from both approaches were similar, except for type 1 diabetes. The chi-squared statistics, log ORs, and confidence intervals show little discrepancy between the two approaches in most of the phenotypes for both S4 PGS and LDpred2, reinforcing the validity of our reported results in cross-biobank analyses. We noted that some variants did not have summary statistics in the GWAS dataset, so the PGS was assessed using only the variants for which summary statistics were available. This may have impacted the performance of type 1 diabetes, where the S4 PGS log OR is 1.14 when directly calculating PGS and 1.27 when estimating from summary statistics. In particular, when S4 PGS overestimated the effect, LDpred2 tended to overestimate the effect and vice-versa. Considering the PGS effect was dominated by the most significant SNPs, this might explain the observed difference.

PGS models optimized and validated by summary statistics

We also aimed to assess the effectiveness of a model developed using summary statistics. To achieve this, we optimized the parameters that yielded the best results based on FinnGen summary statistics rather than the genotyped Biobank samples. We then tested the best fit model for each phenotype on independent test sets, the UK Biobank (Supplementary Table 8) and BioBank Japan populations (Supplementary Table 9). Our findings revealed that in the UK Biobank dataset, S4 + LDpred2 performed the best for all phenotypes except for endometrial cancer (log OR = 0.396) and type 1 diabetes (log OR = 1.084). S4 PGS alone performed better in endometrial cancer (log OR = 0.403) and type 1 diabetes (log OR = 1.109). Additionally, our results for the BioBank Japan aligned with those from the UK Biobank findings, where S4 + LDpred2 combined models performed the best across multiple phenotypes. S4 PGS demonstrated better predictions in type 1 diabetes (log OR = 0.074), while LDpred2 exceled in more accurate predictions of Schizophrenia (log OR = 0.468). These outcomes suggested that a model developed using summary statistics might provide an effective approach for predicting phenotypes across different populations.

Discussion

Genetic risk profiling with PGS can be used to stratify individuals according to their disease risks and could be used to improve screening and prevention strategies and reduce disease mortality [2, 3]. Previously, we had demonstrated the improvement of the S4 PGS method over existing methods in predicting epithelial ovarian cancer risk. Here, we extended the S4 PGS method to 12 phenotypes in UK Biobank, and performed a systematic comparison with LDpred2 and the combined S4 + LDpred2. The S4 + LDpred2 method accurately predicts the PGSs across multiple phenotypes. We assessed the effect of the number of SNPs included in the model on S4 PGS predictive performance by changing the SNP selection threshold. We identified a computationally efficient while accurate threshold, which could be used to guide parameter settings. Furthermore, we explored the applicability of S4 + LDpred2 in modeling joint SNP effects for risk prediction in Finnish and Japanese populations and compared them with common approaches. We also demonstrated the effectiveness of PGS models developed by using only GWAS summary statistics. Our results provided stronger associations with risks of each phenotype.

The UK Biobank and other population-scale biobanks represent a useful resource for testing PGS models. As we have done here, comparing a particular PGS formation method to others across a variety of phenotypes and a variety of ancestries serves as a powerful benchmark of PGS model performance. Recently, a UK Biobank Polygenic Risk Score (PRS) method has been released as a resource of polygenic scores across many diseases and traits, with benchmarking of multiple PGS algorithms or published PGSs [35] against this new method. Notably ovarian cancer was the only phenotype where the UK Biobank generated PRS did not improve on the previously reported PRS, which we previously generated using the S4 PGS method [7]. As population-scale biobanks continue to become available and grow, this benchmarking and comparison of different methods is helpful for developing and improving PGSs.

The S4 PGS model is complementary to LDpred2, contributing to the improved performance observed in the combined S4 + LDpred2 model. The two methods mainly differ in three aspects, which we address in detail below: the type of prior on SNP effect sizes, correlation matrix computation, and SNP selection. The S4 PGS method places a continuous shrinkage prior on SNP effect sizes, and LDpred2 uses the common spike-and-slab prior. The continuous shrinkage prior can model distributions with heavy tails better, whereas it can be more vulnerable if there are inaccuracies in the reference correlation matrix. To reduce the time of computing the variant correlation matrix, S4 PGS partitions SNPs into blocks that are roughly independent of each other, and performs SNP selection for each block. LDpred2 assumes a sparse matrix where for a given SNP, the correlations with other SNPs are set to zero if the genetic distance is greater than 3 centimorgan. The S4 PGS approach reduces computational burden and still maintains accuracy when SNPs are reasonably independent of each other or have only minor effects. Lastly, the S4 PGS method considers all SNPs and selects them based on ranked position by P value, (i.e. the most significant first) that are not excessively correlated with already selected SNPs. This ensures a parsimonious model that requires fewer SNPs. On the other hand, LDpred2 focuses only on the Hapmap3 SNPs, which are better imputed and can be applied in all PGS models.

Further optimization of the S4 PGS models could be achieved by examining the model parameters in greater detail. There are several parameters used to generate the models, as well as the core continuous shrinkage prior parameters. In this study, we primarily assessed the effect of SNPs selection threshold. Parameters such as correlation threshold for adding SNPs into the model, maximum individual correlation, and quality control criteria for summary statistics were set based on our prior experience [7]. A systematic tuning of these thresholds by phenotype may increase the robustness of S4 PGS models.

Conclusions

In conclusion, our results indicated that S4 + LDpred2 provides improvements in risk prediction for multiple phenotypes over more common approaches. Our approach overcomed the computational limitations without loss of accuracy. Besides, S4 + LDpred2 demonstrated applicability to populations from different biobanks. Future works can be focused on the incorporation of epidemiological risk factors or SNPs functional annotations, to further improve the predictive power.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

JPT contributed to data extraction and wrote the codes. JPT and P-CP designed the analytical pipeline. JPT, P-CP, and AAD interpreted the results, drafted the manuscript. SAG, MRJ, and PDP provided feedback on the results. All authors revised the manuscript and approved the final version.

Funding

This work was supported by the National Cancer Institute, grant R00CA256519 (P-CP), Cancer Research UK (PRCPJT\100006) (PDP), Tell Every Amazing Lady About Ovarian Cancer Louisa M. McGregor Ovarian Cancer Foundation (MRJ), and American Cancer Society Research Scholar Grant (RSG-23-1019823-01-CPSH) (MRJ).

Data availability

The S4 PGS program, evaluation codes, and PGS models are freely available at https://github.com/jpt34/S4_programs. Each subfolder includes a README.md file that details the usage. This research has been conducted using the UK Biobank Resource under Application Number 28126.The links to obtain the GWAS summary statistics from UK Biobank are as follows: body mass index (https://portals.broadinstitute.org/collaboration/giant/images/1/15/SNP_gwas_mc_merge_nogc.tbl.uniq.gz), height (https://portals.broadinstitute.org/collaboration/giant/images/0/01/GIANT_HEIGHT_Wood_et_al_2014_publicrelease_HapMapCeuFreq.txt.gz), asthma (https://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST006001-GCST007000/GCST006862/TAGC_meta-analyses_results_for_asthma_risk.zip), breast cancer (https://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST004001-GCST005000/GCST004988/oncoarray_bcac_public_release_oct17%20(1).txt.gz), coronary artery disease (https://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST003001-GCST004000/GCST003116/cad.add.160614.website.txt), endometrial cancer (https://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST006001-GCST007000/GCST006464/GCST006464_GRCh37.tsv.gz), inflammatory bowel disease (https://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST004001-GCST005000/GCST004131/ibd_build37_59957_20161107.txt.gz), major depressive disorder (https://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST005001-GCST006000/GCST005839/MDD2018_ex23andMe.gz), prostate cancer (https://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST006001-GCST007000/GCST006085/meta_v3_onco_euro_overall_ChrAll_1_release.txt), schizophrenia (https://figshare.com/ndownloader/files/34100918), type 1 diabetes (https://datadryad.org/stash/dataset/doi:10.5061/dryad.ns8q3), type 2 diabetes (http://diagram-consortium.org/downloads.html).The FinnGen summary statistics are at https://www.finngen.fi/en/access_results and the form to access the results is available at https://elomake.helsinki.fi/lomakkeet/124935/lomake.html. Release 6 was selected and the phenotype codes are as follows: asthma: J10_ASTHMA, breast cancer: C3_BREAST, coronary artery disease: I9_CORATHER, endometrial cancer: C3_CORPUS_UTERI, inflammatory bowel disease: K11_IBD, major depressive disorder: F5_DEPRESSIO, prostate cancer: C3_PROSTATE, schizophrenia: F5_SCHZPHR, type 1 diabetes: E4_DM1, type 2 diabetes: E4_DM2.For BioBank Japan data, use the format https://pheweb.jp/pheno/ followed by the phenotype. For example, for breast cancer, use https://pheweb.jp/pheno/BrC. The codes are body mass index: BMI, height: Height, asthma: Asthma, breast cancer: BrC, endometrial cancer: EnC, major depressive disorder: Depression, prostate cancer: PrC, schizophrenia: Schizophrenia, type 1 diabetes: T1D, type 2 diabetes: T2D.

Declarations

Ethical approval and consent to participate

An ethical approval is not required for our study. Each biobank has studies approved by the relevant ethics committees and researchers do not require separate ethical approvals. UK Biobank has approval from the North West Multi-centre Research Ethics Committee (MREC) as a Research Tissue Bank (RTB) approval. FinnGen complies with the Biobank Law and the Personal Data Act, approved by the Coordinating Ethics Committee of the Helsinki and Uusimaa Hospital District. Biobank Japan was approved by the research ethics committees at the Institute of Medical Science, the University of Tokyo, the RIKEN Yokohama Institute, and the 12 cooperating hospitals.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.