Abstract
Spectral radiography and fluoroscopy with multi-layer flat-panel detectors (FPD) is being actively investigated in a range of clinical applications. For applications involving contrast administration, maximal contrast resolution is achieved when overlaying background anatomy is completely removed. This calls for three-material decomposition (soft tissue, bone, and contrast) enabled by measurements in three energy channels. We have previously demonstrated the feasibility of such decomposition using a triple-layer detector. While algorithmic solutions can be adopted to mitigate noise in the material basis images, in this work, we seek to fundamentally improve the conditioning of the problem through optimized system design. Design parameters include source voltage, the thickness of the top two CsI scintillators, and the thickness of two copper interstitial filters. The design objective is to minimize noise in the basis image containing contrast, chosen as gadolinium in this work to improve separation from bone. The optimized design was compared with other designs with unoptimized scintillator thickness and/or without interstitial filtration. Results show that CsI thickness optimization and interstitial filtration can significantly reduce noise in the gadolinium image by 35.7% and 42.7% respectively within a lung ROI, which in turn boosts detectability of small vessels. Gadolinium and bone signals are separated in all cases. Visualization of coronary vessels is enabled by the combining optimized system design and regularization. Results from this work demonstrate that three-material decomposition can be significantly improved with system design optimization. Optimized designs obtained from this work can inform imaging techniques selection and triple-layer detector fabrication for spectral radiography.
1. INTRODUCTION
Spectral imaging technology has a long history of investigation in 2D imaging scenarios. Its ability to produce tissue-specific maps can significantly improve contrast resolution of structures of interest by reducing overlaying anatomy. Spectral radiography and fluoroscopy has been explored for both diagnostic (e.g., pulmonary nodule detection,1 coronary diseases evaluation2) and interventional imaging applications (e.g., digital subtraction angiography3, 4).
For applications involving contrast administration, it is often desirable to completely isolate contrast agent from background anatomy in order to maximize the contrast resolution of enhanced structures. Current adoption of 2D spectral imaging has mainly focused on dual-energy acquisition which is typically incapable of separating contrast agent from bone and calcifications. To achieve this purpose, at least three energy channels are required to enable three-material decomposition, for example, into soft tissue, bone, and contrast agent.
In previous work, we have demonstrated the feasibility of three-material decomposition using a triple-layer flat-panel detector (FPD).5 While we have developed algorithmic solutions to achieve good image quality, the decomposition results are inherently limited by low spectral separation among the energy channels which leads to amplified noise in the material basis images. In this work, we seek to improve the decomposition results from a system design perspective. We considered a triple-layer detector design consisting of three CsI scintillator layers and two interstitial filters, each of configurable thickness. Detector design was jointly optimized with x-ray source kV. For initial investigations, we adopted a design objective to minimize variance in the basis image containing contrast. In this work, we focus on gadolinium contrast for improved separability from bone. Results are shown for a thorax phantom for lung and cardiovascular imaging applications.
2. METHODS
2.1. Physics Model of Triple-Layer Flat-Panel Detector
A triple-layer FPD contains three stacked detector layers, each capable of producing a projection measurement. X-ray interactions in each layer harden the beam and change the x-ray spectrum incident on the next layer. Interstitial filtration can additionally be inserted between the detector layers to further enhance spectral separation. The detector is therefore capable of producing three distinct spectral measurements to enable three-material decomposition. The mean detector measurements from the layer () of a triple-layer FPD can be modeled as:
| (1) |
where and represent mass attenuation coefficients and density line integrals of the basis materials, respectively, and denotes the spectrum from the x-ray source after passing through pre-patient filters. The term models filtration as a result of previous detector layer(s) and interstitial filter(s) before the layer as a function of energy, , i.e.,
| (2) |
and models the detection efficiency of the layer scintillator,
| (3) |
In the above equations, and represent linear attenuation coefficients and thicknesses, respectively. Subscripts and denote cesium iodide (CsI) scintillator and interstitial filtration. The term models the quantum gain associated with the conversion from x-ray to optical quanta in CsI and is approximated to be proportional to the x-ray energy. The term captures scalar, non-energy-dependent gain factors including escape fraction, optical coupling, etc. Following the assumptions in Ref.6, is Poisson-distributed while and are deterministic. The measurement covariance is therefore:
| (4) |
2.2. Model-based Projection-Domain Decomposition
Model-based material decomposition can be formulated as the following optimization problem according to a regularized likelihood objective:
| (5) |
where represents the covariance of measurements and is assumed to be a diagonal matrix with its diagonal elements equal to , i.e., . For system optimization, we used the unregularized objective with only the weighted least-squares data fidelity (first term); for material decomposition, we adopted a quadratic penalty (second term) to control image smoothness. A material-basis-dependent regularization strength parameter, where indexes the basis, was empirically set to 10−5,10−4,10−3 for water, calcium, gadolinium, respectively. A Newton’s method, as in previous work,5 was adopted to solve the optimization problem.
2.3. Design Optimization
2.3.1. System Setup
We simulated an imaging system with a triple-layer FPD. The source-to-axis distance is 800mm, source-to-detector distance was 1200mm, and the detector pixel size was 0.42mmx0.42mm. The source spectrum was simulated using Spektr with a fixed pre-patient filter of 10 mm aluminum. A nominal exposure was set to 8 mAs at 100 kV. For other kVs, the mAs was scaled to maintain the overall energy attenuated in the object, i.e., , where was generated at 120 kVp, 8 mAs.
We aim to achieve three-material decomposition into soft tissue, bone, and contrast agent. While iodine is commonly used as the contrast media in x-ray imaging, the attenuation characteristics of iodine is similar to bone and therefore presents a challenging decomposition problem. We therefore investigate another FDA-approved contrast media, gadolinium. For material decomposition, the three basis materials to be esimated, , are water, calcium, and gadolinium.
2.3.2. Optimization Parameters
We optimized a total of five parameters, the source peak voltage (), the thickness of the top two CsI scintillators (, ), and the thickness of two interstitial filters (, ). We fixed the thickness of the bottom scintillator layer to the maximum number considered to maximize x-ray absorption. The parameters and constraints are listed in Table 1. The maximum thickness of the CsI scintillator is 550μm, which is commonly found for single-layer FPDs. We used copper as the interstitial filter material. The maximum thickness was set to 2 mm in consideration of dose efficiency.
Table 1.
Parameters to be optimized
| Parameter | Definition | Constraints |
|---|---|---|
| source peak voltage | 50kV ~ 150 kV | |
| thickness of the first-layer CsI | 0μm ~ 550μm | |
| thickness of the second-layer C-sI | 0μm ~ 550μm | |
| thickness of the third-layer C-sI | 550μm | |
| thickness of the first interstitial filter | 0mm ~ 2mm | |
| thickness of the second interstitial filter | 0mm ~ 2mm |
2.3.3. Optimization Objective and Algorithm
There is a choice of metrics for evaluating spectral system performance. In this work, we are primarily interested optimizing image quality for the visualization of contrast-enhanced structures in the gadolinium basis image. Recognizing that image noise is usually the limiting factor in spectral system performance, we optimized system design to minimize the variance in the gadolinium image.
Using implicit function theorem and Taylor expansion of the objective,7 the basis material covariance can be written as:
| (6a) |
| (6b) |
In the equation above, is the Fisher information matrix and is the Hessian of the penalty function. For simplicity, we ignored for system optimization, assuming that it does not change the rank ordering of system designs. The covariance matrix in this case is equal to and equivalent to the Cramer-Rao lower bound of unbiased estimators. We computed the inverse Fisher information matrix using the ground truth density line integrals and noiseless . Theoretical predictions of the variance of gadolinium was obtained from the corresponding diagonal element of and used in system optimization. The objective function for minimizing variance in the gadolinium image is therefore:
| (7) |
For each combination of material density line integral, , (7) was iteratively solved using the covariance matrix adaptation evolution strategy (CMA-ES).8 The optimization was initialized with the lower bounds of the parameters, and considered converged when the parameter update is smaller than 10−6.
Material decomposition is a nonlinear problem. The optimal system design therefore potentially depends on . We performed system designs for chest imaging, where variations of path lengths of water, calcium, and gadolinium are listed in Table 2. These values were obtained from an XCAT thorax phantom9 and covered the entire thorax region from lung to the heart. Parameter optimization was performed for each combination of material density line integrals.
Table 2.
Basis materials used in optimization
| Basis material | Water | Ca | Gd |
|---|---|---|---|
| Density (mg/ml) | 1000 | 100 | 20 |
| Path length(cm) | 4 | 0 | 0 |
| 8 | 1 | 0.1 | |
| 12 | 2 | 0.2 | |
| 16 | 3 | 0.4 | |
| 20 | 4 | 0.8 | |
| 24 | 5 | 1.6 | |
| 28 | 6 | 3.2 |
3. RESULTS
3.1. Optimized System Design
Results from system optimization are summarized in Fig. 1. We fixed the path lengths of two basis materials, and show how the optimized parameters vary with increasing path length of the third material. The optimal thicknesses of the CsI scintillators and interstitial filters show relatively small changes for different combinations of basis materials. Good performance is achieved in all cases when , , , . The optimized kVs, however, show significant variation for different path lengths. Performance decreases with increasing water and calcium path lengths, but shows a small increase with increasing gadolinium path length. We additionally included comparisons between theoretical prediction of variance in the gadolinium image (Eq.6a) and empirical measurements from 40000 samples. While we obtain good agreement at small water path lengths, significant deviations are observed at water path length greater than 20 cm. We believe this is a regime where the maximum-likelihood estimator is no longer able to yield unbiased estimates. Further investigations to improve theoretical variance prediction are underway.
Figure 1.
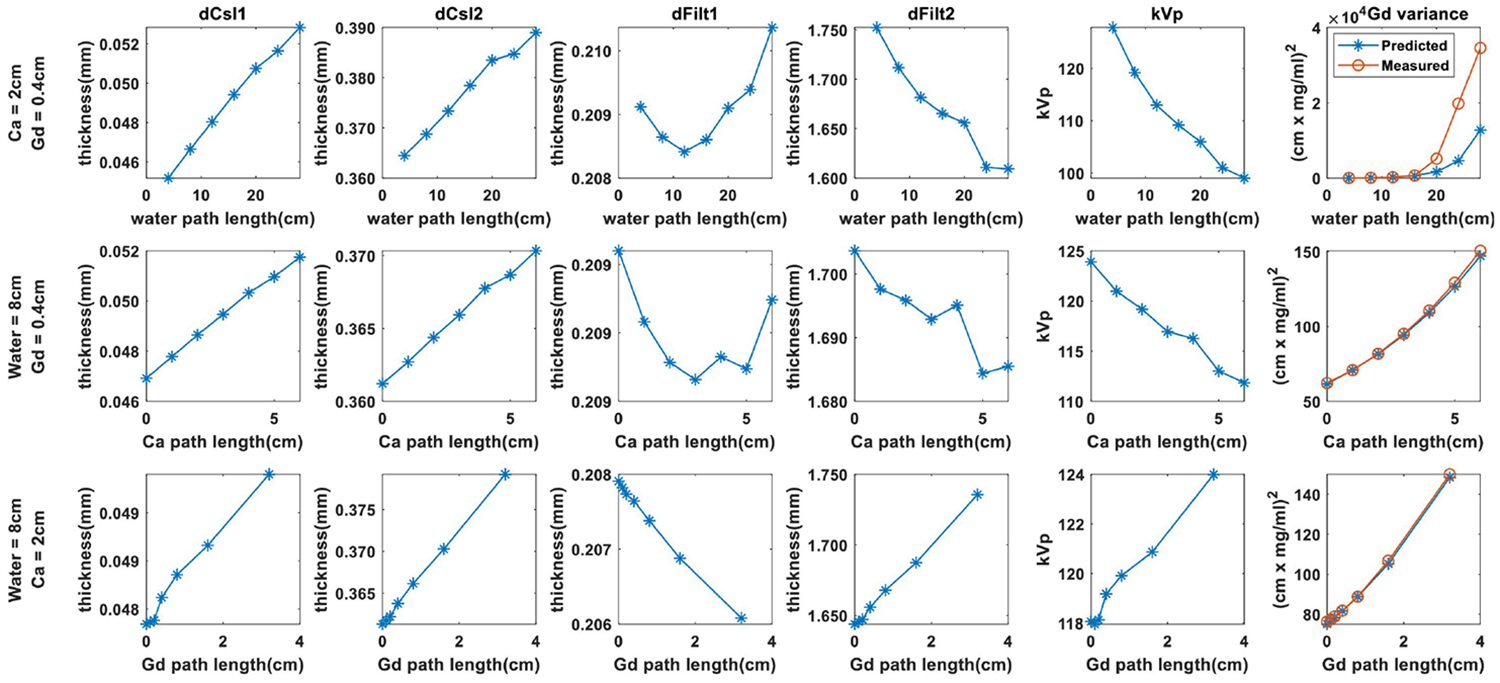
Optimized system parameters for different combinations of material path lengths. The rightmost column shows the predicted vs. measured Gd variance.
The optimal parameters obtained for each point in the thorax phantom are shown in Fig. 2. While such designs are challenging to achieve in reality, these plots nicely illustrates the sensitivity of each parameter to varying combinations of materials. We combined the median value in each parameter map as the optimal system design.
Figure 2.

Optimal system parameters map for a simulated chest phantom.
3.2. Model-based Decomposition of Chest Projections
To compare the imaging performance of different system designs, we simulated chest projections using the XCAT program9 following the physics model of triple-layer FPD (Eq.(1)). All arteries were enhanced by 20 mg/ml of gadolinium. Decomposition results are shown for three different system designs: 1) A detector with equal CsI thickness at 320 μm each and without interstitial filtration; 2) A detector with optimized CsI thicknesses but without interstitial filtration, and 3) A fully optimized design. The kV for all systems are the same at 120 kV. The total CsI thickness is the same for all three designs.
Unregularized model-based decomposition results are summarized in the first three columns in Fig. 3 to ensure fair comparisons. Using the equal-thickness design (first column), both Ca and Gd images exhibit high noise, especially around the spine and heart. Optimizing CsI thickness only without interstitial filtration (second column) is effective in suppressing noise. Inclusion of interstitial filters (third column) further reduces noise and improves the detectability for smaller vessel trees. Results show that CsI thickness optimization and interstitial filtration can reduce the gadolinium noise by 35.7% and 42.7% respectively within the lung ROI. Combining the optimized design and regularized decomposition (fourth column) enables visualization of coronary arteries that overlap with both the heart and spine. Gadolinium contrast and bone are successfully separated.
Figure 3.
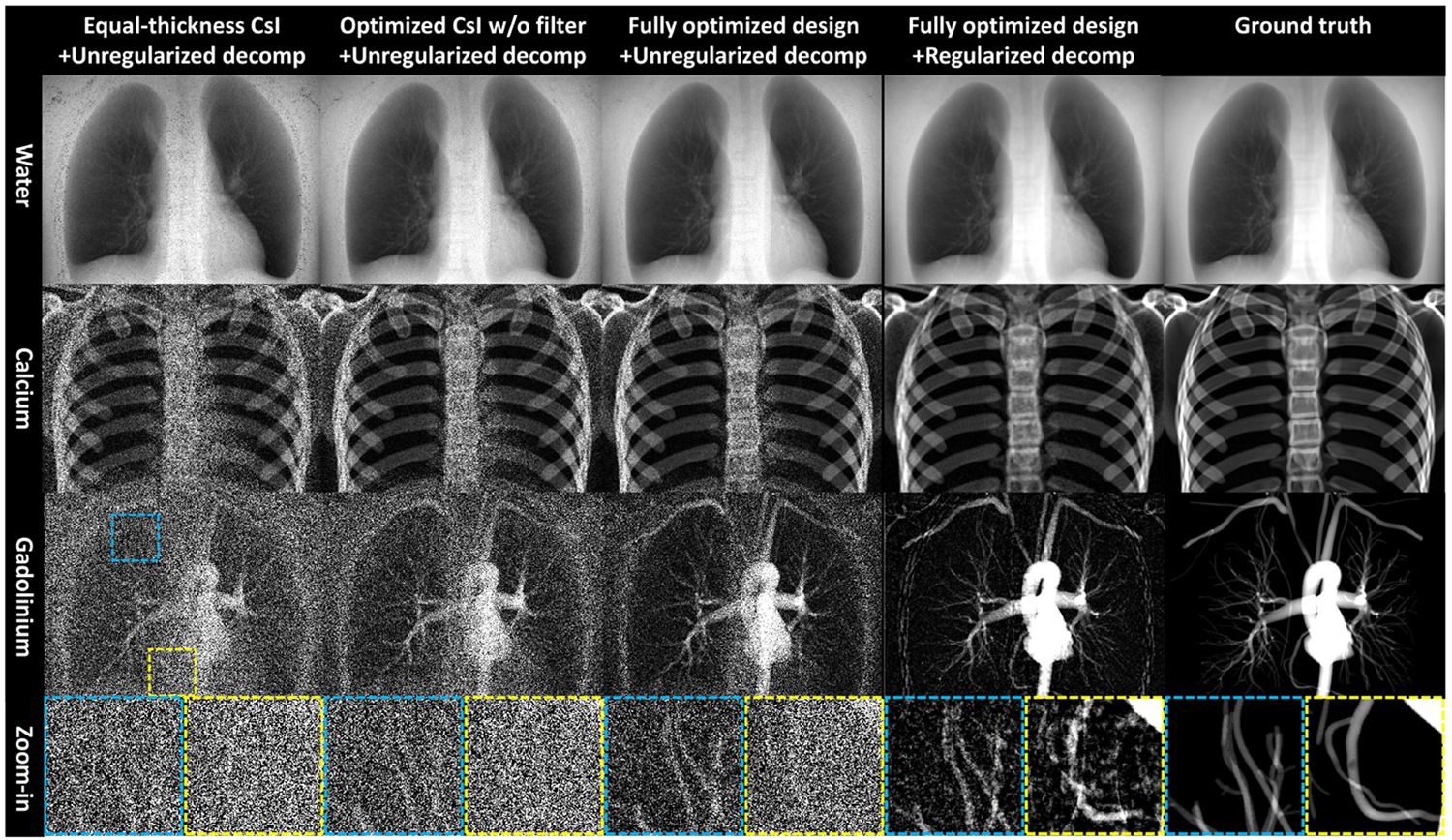
Comparison of three-material material decomposition with different system designs. Display window: water: [6,20]cm×1g/ml, calcium: [0,10]cm×100g/ml, gadolinium: [0,1.6]cm×20mg/ml.
4. CONCLUSION AND DISCUSSION
Three-material decomposition is a highly ill-conditioned problem where high levels of noise often proves detrimental to the detectability of small, low contrast structures. In this work, we performed system optimization of a triple-layer FPD system to improve spectral separability and minimize noise in the resulting material images. We found that optimization of scintillator thickness and inclusion of interstitial filtration are both effective in suppressing noise. Combining optimized design and regularization enables visualization and isolation of contrast-enhanced coronary vessels even in the noisiest region containing the heart and spine. Future work involves improving the accuracy of the theoretical variance predictor by accounting for estimation bias and investigating design objectives beyond variance in the contrast image. Results in this work demonstrate the importance of system design in enhancing spectral imaging performance and provide guidance on technique selection and detector fabrication to enable the clinical translation of three-material decomposition using a triple-layer detector.
ACKNOWLEDGMENTS
This work was supported, in part, by NIH grant R01EB030494.
REFERENCES
- [1].McAdams HP, Samei E, Dobbins III J, Tourassi GD, and Ravin CE, “Recent advances in chest radiography,” Radiology 241(3), 663–683 (2006). [DOI] [PubMed] [Google Scholar]
- [2].Ansari-Gilani K, Tandon YK, Jordan DW, Ciancibello L, Wilson DL, and Gilkeson RC, “Dual-energy subtraction chest radiography: application in cardiovascular imaging,” Journal of Thoracic Imaging 35(3), W75–W81 (2020). [DOI] [PubMed] [Google Scholar]
- [3].Speidel MA, Burton CS, Nikolau EP, Schafer S, and Laeseke PF, “Prototype system for interventional dual-energy subtraction angiography,” in [Medical Imaging 2019: Image-Guided Procedures, Robotic Interventions, and Modeling], 10951, 470–479, SPIE; (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Gang GJ and Stayman JW, “Three-material decomposition using a dual-layer flat panel detector in the presence of soft tissue motion,” in [Medical Imaging 2023: Physics of Medical Imaging], 12463, 188–193, SPIE; (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Jiang X, Stayman JW, and Gang GJ, “Approaches for three material decomposition using a triple-layer flat-panel detector,” in [Medical Imaging 2023: Physics of Medical Imaging], 12463, 182–187, SPIE; (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Tivnan M, Wang W, Gang G, and Stayman JW, “Design optimization of spatial-spectral filters for cone-beam ct material decomposition,” IEEE transactions on medical imaging 41(9), 2399–2413 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Fessler JA, “Mean and variance of implicitly defined biased estimators (such as penalized maximum likelihood): Applications to tomography,” in [5th IEEE EMBS International Summer School on Biomedical Imaging, 2002.], 14–pp, IEEE; (2002). [DOI] [PubMed] [Google Scholar]
- [8].Hansen N, “The cma evolution strategy: A tutorial,” arXiv preprint arXiv:1604.00772 (2016). [Google Scholar]
- [9].Segars WP, Sturgeon G, Mendonca S, Grimes J, and Tsui BM, “4d xcat phantom for multimodality imaging research,” Medical physics 37(9), 4902–4915 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]


