Multiobjective optimal TCSC placement using multiobjective grey wolf optimizer for power losses reduction

Abstract

This study investigates the application of the multiobjective grey wolf optimizer (MOGWO) for optimal placement of thyristor-controlled series compensator (TCSC) to minimize power loss in power systems. Two conflicting objectives are considered: (1) minimizing real and reactive power loss, and (2) minimizing real power loss and TCSC capital cost. The Pareto-optimal method is employed to generate the Pareto front for these objectives. The fuzzy set technique is used to identify the optimal trade-off solution, while the technique for order preference by similarity to the ideal solution suggests multiple optimal solutions catering to diverse utility preferences. Simulations on an IEEE 30 bus test system demonstrate the effectiveness of TCSC placement for power loss minimization using MOGWO. The superiority of MOGWO is confirmed by comparing its results with those obtained from a multiobjective particle swarm optimization algorithm. These findings can assist power system utilities in identifying optimal TCSC locations to maximize their performance.

Introduction

Electrical energy demand across the globe is exponentially rising as a consequence of rapid urbanization and industrialization. On the other hand, deterrents like environmental and economic limitations have contained the installation of new transmission lines and generating plants. Under these circumstances, it has become inevitable for the utilities to operate electric power systems at their full capacities making the system vulnerable to cascaded outages¹. This scenario has led to finding ways to utilize the existing infrastructure more efficiently.

Fortunately, with the emergence of power electronic switching circuits, the concept of the flexible alternating current transmission system (FACTS) introduced by Hingorani and Gyugyi² unfolded as a promising solution for a plethora of electrical engineering issues like power quality, congestion management and power loss reduction^3–7. In⁸, THE AUTHORS PRESENTED A comprehensive review of FACTS devices, their deployment methods and MERITS are presented. To yield the potential benefits of FACTS devices, they should be installed at an optimal location in the power system⁹. TCSC is an exceptional FACTS device that can be introduced into the system at a strategic location to improve the transient stability, augment the power transfer capacity and reduce the loss in power transmission^10–13. ALTHOUGH VARIOUS FACT DEVICES EXIT, TCSC can modify the reactance of the line, thereby augmenting the peak power that can be transferred on that line in addition to diminishing the effective reactive power losses¹⁴. The TCSC can be operated as the capacitive or inductive compensation respectively by directly modifying the reactance of the transmission line. Hence in this study, we explore the BENEFITS of optimal installation of TCSC.

Literature review

In the last decade, umpteen techniques have been proposed for tracing the optimal location of TCSC. A sensitivity index is introduced in¹⁵ for tracing the optimal location of TCSC. To cater TO the optimal location problem of TCSC and other FACTS devices, many researchers suggested the use of intelligent optimization algorithms. In¹⁶, the authors highlighted the application of genetic algorithms (GA) to solve the optimal siting problem of TCSC. A particle swarm optimization (PSO) technique is suggested, considering system loadability and installation cost for optimal TCSC location in¹⁷. The superiority of the bacterial swarming optimization algorithm in solving the optimal location problem over its peers GA and PSO is illustrated in¹⁸. The concept of differential evolution (DE) is used for locating FACTS devices in¹⁹. A strategy taking cues from adaptive particle swarm optimization and DE is suggested in²⁰ to offer an optimal solution for FCATS device installation. A hybrid algorithm combining ant lion optimization, moth flame optimization, and salp swarm optimization is implemented²¹ to locate the optimal position of TCSC.

A whale optimization technique is proposed²² to solve the optimal TCSC installation problem for reactive power planning. The objectives considered are loss minimization and MINIMIZATION OF THE OPERATION COST OF TCSC. SIMILAR WITH THE SAME OBJECTIVES, a study is presented in²³ to solve the optimal TCSC installation problem using some hybrid optimization techniques. Authors in²⁴ explored the BENEFITS of optimal TCSC installation for enhancing the available transfer capability of transmission lines. A technical and economic analysis is presented²⁵, to OPTIMALLY LOCATE TCSC USING THE algorithm. Authors in²⁶ conducted investigations to optimally install multiple FACTS devices INCLUDING TCSC for operational enhancement of the power system. The annual cost of FACTS devices is also considered ONE OF THE OBJECTIVES IN THE multiobjective function formulated. Recently in²⁷, authors solved the optimal positioning problem of the TCSC in the presence of electrical vehicle charging stations using PSO.

Research gap and motivation

The abundant existing literature on power loss minimization and the optimal location of the FACTS device is focused on either solving one objective alone or converting a multiobjective problem into a single objective function by employing weighted sum method. In this method, a weight is given to each objective DEPENDING ON its relative importance. Although this method is simple, it cannot trace the optimal trade-off solution in the non-convex region; consequently, the obtained solution may not be the first-rate optimal solution for the weights chosen²⁸. To avoid such a problem, in this study Pareto optimal method²⁹ is adopted to obtain the Pareto-optimal frontier. Real and reactive power loss, REAL POWER LOSS, AND CAPITAL COST OF TCSC are the two multiobjective functions considered for minimization. We ATTEMPT TO EXPLORE THE CAPABILITIES OF THE multiobjective grey wolf optimizer (MOGWO) presented in³⁰ to solve multiobjective problems under consideration. Further, to underscore the precedence of the MOGWO algorithm, a comparative analysis with MOPSO is also presented.

Contributions of the work

The contributions of this paper are as follows:

1. A Pareto-optimality-BASED multiobjective optimization approach is proposed for optimal installation of TCSC.

2. Two case studies are formulated FOR THE OPTIMAL INSTALLATION of TCSC using the proposed approach. Case study 1, deals with real and reactive power loss as multiple objectives. Whereas, in case 2, the real power loss and capital cost of TCSC are considered in the multiobjective function.

3. A COMPARISON of MOGWO algorithm is performed with MOPSO in solving the multiobjective-BASED OPTIMAL TCSC INSTALLATION PROBLEM.

4. A fuuzy set technique is used to select the optimal trade-off solution from the Pareto-optimal solutions in each case study. However, to provide more diversity in the solutions provided, technique for order preference by similarity to the ideal solution (TOPSIS) methodology is adopted and multiple optimal trade-off solutions are suggested.

Paper orginazation

The remnant of this article is categorized as follows. Section "Thyristor controlled series compensator" is about TCSC and its modelling. In section "Problem formulation", the objective function and the constraints considered are presented. The MOGWO algorithm and the selection of the best optimal solution using the fuzzy and TOPSIS approach ARE DISCUSSED in Section "Optimization methods". In Section "Results and discussion", the results generated are presented and discussed. Finally, the conclusion of the article is presented in Section "Conclusion".

Thyristor controlled series compensator

TCSC is a series compensator that comprises of thyristor thyristor-controlled reactor in parallel with a capacitor, as shown in Fig. 1.

Fig. 1.

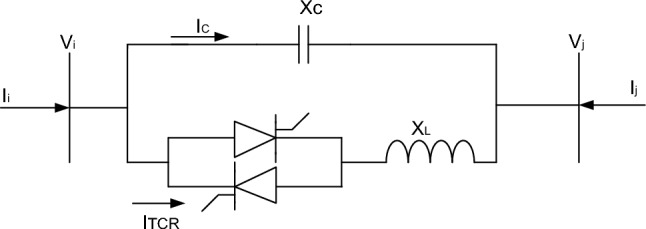
TCSC Model.

In the above model, I_i is the current flow through branch ij, I_j is the current flow through branch ji, V_i is the magnitude of the voltage at bus i and V_j is the magnitude of the voltage at bus j.

In Fig. 1, two thyristors are connected in anti-parallel in series with the inductor. By controlling the firing angle $\prime \alpha \prime$, the TCSC can be operated as either a capacitive compensator or an inductive compensator.

The reactance of the TCSC can be expressed as follows³¹:

$$X_{\mathit{TCSC}}\left(\alpha \right)=\frac{X_C{X}_L(\alpha )}{X_L\left(\alpha \right)-X_C}$$ 1

$$\text{where}{X}_L\left(\alpha \right)=X_L\frac{\pi }{\pi -2\alpha -\text{sin}\alpha }$$ 2

TCSC can be connected to the power transmission line as a series compensator³². In the steady-state analysis, the reactance of TCSC can be adjusted as a static reactance.

The block diagram representation of the transmission line with TCSC is shown in Fig. 2.

$$X_{\mathit{ij}}=X_{\mathit{Line}}+X_{\mathit{TCSC}}$$ 3

$$K_{\mathit{TCSC}}=\frac{X_{\mathit{TCSC}}}{X_{\mathit{Line}}}$$ 4

$$X_{\mathit{TCSC}}=K_{\mathit{TCSC}}{X}_{\mathit{Line}}$$ 5

where $X_{\mathit{ij}}$ is the transmission line reactance with compensation, $X_{\mathit{Line}}$ is the line reactance without compensation,$X_{\mathit{TCSC}}$ is the reactance of TCSC and $K_{\mathit{TCSC}}$ is the degree of compensation. The range of $X_{\mathit{TCSC}}$ to avoid overcompensation is given as⁶:

$$-0.8X_{\mathit{Line}}\le X_{\mathit{TCSC}}\le 0.2X_{\mathit{Line}}$$ 6

Fig. 2.

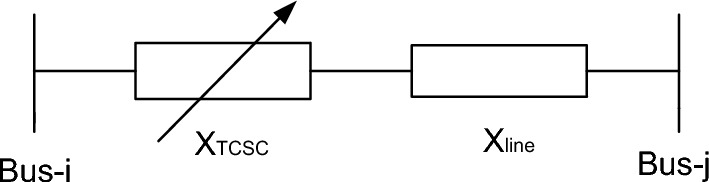
Block diagram of TCSC.

Problem formulation

Objective function

The minimization functions considered are³³:

$${Min(P}_{\mathit{Loss}})=\sum _{m=1}^{\mathit{NL}}{P}_m$$ 7

$$Min(Q_{\mathit{Loss}})=\sum _{m=1}^{\mathit{NL}}{Q}_m$$ 8

where $P_m$ and $Q_m$ are the real and reactive power loss of line m and $\mathit{NL}$ denotes the total number of lines

$$P_m=\left(V_i^2,+,V_j^2,-,2,V_i,V_j,\text{cos},{\delta }_{\mathit{ij}}\right)\left(G_{\mathit{ij}}\right)$$ 9

$$P_m=\left(V_i^2,+,V_j^2,-,2,V_i,V_j,\text{cos},{\delta }_{\mathit{ij}}\right)\left(G_{\mathit{ij}}\right)$$ 10

where V_i and V_j are the ith bus & jth bus voltages, ${\delta }_{\mathit{ij}}$ denotes the phase difference between ith bus & jth bus, G_ij denotes the real part of the admittance between buses i & j and B_ij denotes the imaginary part of line admittance between buses i & j.

The fitness function for reduction of the capital cost of TCSC is framed as per Eq. (11)⁶.

$${\mathit{cost}}_{\mathit{TCSC}}=0.001S^2-0.7130S+153.7$$ 11

where ${\mathit{cost}}_{\mathit{TCSC}}$ is the capital cost of TCSC in US$/KVar, $S$ =$\left|Q_2,-,Q_1\right|$ is the operating range of TCSC in MVar, $Q_1$, and $Q_2$ are reactive power flow through the branch before TCSC installation and after TCSC installation, respectively.

Constraints

The constraints are taken as shown below:

1. Equality Constraints^33,34:

   $$P_{\mathit{gi}}-P_{\mathit{di}}=V_i\sum _{j=1}^{\mathit{Nb}}{V}_j\left(G_{\mathit{ij}},\text{cos},{\delta }_{\mathit{ij}},+,B_{\mathit{ij}},\text{sin},{\delta }_{\mathit{ij}}\right)$$ 12

   $$Q_{\mathit{gi}}-Q_{\mathit{di}}=V_i\sum _{j=1}^{\mathit{Nb}}{V}_j\left(G_{\mathit{ij}},\text{sin},{\delta }_{\mathit{ij}},-,B_{\mathit{ij}},\text{cos},{\delta }_{\mathit{ij}}\right)$$ 13

   where $P_{\mathit{gi}}$ and $P_{\mathit{di}}$ denote the real power generation and demand respectively at bus-$i$, $Q_{\mathit{gi}}$ and $Q_{\mathit{di}}$ denote reactive power generation and demand respectively at bus-$i$, $\mathit{Nb}$ is the total number of buses.

• (b)
  Inequality Constraints³⁴:

  $$V_{\mathit{Li}}^{\mathit{min}}\le V_{\mathit{Li}}\le V_{\mathit{Li}}^{\mathit{max}}$$ 14

  $$V_{\mathit{Gi}}^{\mathit{min}}\le V_{\mathit{Gi}}\le V_{\mathit{Gi}}^{\mathit{max}}$$ 15

  $$Q_{\mathit{Gi}}^{\mathit{min}}\le Q_{\mathit{Gi}}\le Q_{\mathit{Gi}}^{\mathit{max}}$$ 16

  $$Q_c^{\mathit{min}}\le Q_c\le Q_c^{\mathit{max}}$$ 17

  $$T_s^{\mathit{min}}\le T_s\le T_s^{\mathit{max}}$$ 18

  $$X_{\mathit{tcsc}}^{\mathit{min}}\le X_{\mathit{tcsc}}\le X_{\mathit{tcsc}}^{\mathit{max}}$$ 19

  where $V_{\mathit{Li}}$ and $V_{\mathit{Gi}}$ are the values of voltages at $\mathit{thei}\mathit{th}$ load bus and $i\mathit{th}$ generator bus respectively, $Q_{\mathit{Gi}}$ denotes the generated reactive power $ati\mathit{th}$ generator bus, $Q_c$ is reactive power injected by the shunt capacitor at $i\mathit{th}$ bus, $T_s$ is the transformer tap setting of the $X_{\mathit{tcsc}}$ is the reactance of TCSC at line-$m.$

Optimization methods

Multiobjective grey wolf optimizer algorithm

MOGWO algorithm is proposed by Mirjalili et al.³⁰. Like many other infamous metaheuristic optimization algorithms, MOGWO also draws its inspiration from nature. This algorithm simulates the pack hierarchy and the hunting strategy of grey wolves. Grey wolves naturally prefer to forage in packs of 5–12 members. The pack hierarchy of grey wolves consists of four hierarchal levels of wolves, namely alpha (α), beta (β), delta (δ), and omega (ω), with α wolves being the most dominant ones and ω wolves being the least dominant ones. The hunting strategy of grey wolves is yet another intriguing social behavior of grey wolves. Searching, encircling, harassing, and attacking the prey are the main phases of grey wolves hunting strategy. The encircling phase is mathematically modeled as³⁰ :

$$\overrightarrow{D}=\left|\overrightarrow{C}·\overrightarrow{\mathit{Xp}}\left(t\right)-\overrightarrow{X}\left(t\right)\right|$$ 20

$$\overrightarrow{X}\left(t,+,1\right)=\overrightarrow{\mathit{Xp}}\left(t\right)-\overrightarrow{A}·\overrightarrow{D}$$ 21

Here $\overrightarrow{X}\left(t\right)$ and $\overrightarrow{\mathit{Xp}}\left(t\right)$ denote the position vectors of grey wolf and prey respectively for the iteration tth iteration. $\overrightarrow{A}$ and $\overrightarrow{C}$ are the coefficient vectors which are evaluated by equations given below.

$$\overrightarrow{A}=2\overrightarrow{a}·\overrightarrow{r_1}-\overrightarrow{a}$$ 22

$$\overrightarrow{C}=2·\overrightarrow{r_2}$$ 23

The elements of the vector $\overrightarrow{a}$ are decreased linearly from 2 to 0 as the iterations progress and r₁, r₂ represent random vectors in [0, 1]. It is observed that the coefficient vectors $\overrightarrow{A}$ and $\overrightarrow{C}$ have the capacity to control exploration and exploitation. |A|> 1 diverges the grey wolves from the location of the prey, thereby assisting exploration. The coefficient vector $\overrightarrow{C}$ also assists exploration; it takes random values in [0,2]. The random values of $\overrightarrow{C}$ either emphasize (C > 1) or deemphasize (C < 1) the effect of prey in determining the distance. Unlike $\overrightarrow{A},$ the value of $\overrightarrow{C}$ is not decreased linearly; this enables the GWO algorithm to exhibit stochastic behavior through the search process. As a consequence, exploration is favored, and local optima stagnation is avoided. |A|< 1 converges the grey wolves towards the location of prey which assists the exploitation.

The GWO algorithm emulates the pack hierarchy and encircling phase of hunting to determine the best solution for a given problem. During the search process, the α, β, and δ wolves are assumed to possess superior knowledge regarding the location of the prey. The pack hierarchy of grey wolves is mathematically modeled by considering the best solution as α. Consequently, the next best solution as β, and the third best solution as δ. All the other solutions are assumed as ω wolves. The first three best solutions obtained so far are saved, and the other search agents are forced to modify their positions as per the position of α, β, and δ using the following formulas³⁰.

$$\overrightarrow{D_{\alpha }}=\left|\overrightarrow{C_1}\times \overrightarrow{X_{\alpha }}-\overrightarrow{X}\right|$$ 24

$$\overrightarrow{D_{\beta }}=\left|\overrightarrow{C_2}\times \overrightarrow{X_{\beta }}-\overrightarrow{X}\right|$$ 25

$$\overrightarrow{D_{\delta }}=\left|\overrightarrow{C_3}\overrightarrow{·X_{\delta }}-\overrightarrow{X}\right|$$ 26

$$\overrightarrow{X_1}=\overrightarrow{X_{\alpha }}-\overrightarrow{A_1}·(\overrightarrow{D_{\alpha }})$$ 27

$$\overrightarrow{X_2}=\overrightarrow{X_{\beta }}-\overrightarrow{A_2}·(\overrightarrow{D_{\beta }})$$ 28

$$\overrightarrow{X_3}=\overrightarrow{X_{\delta }}-\overrightarrow{A_3}·(\overrightarrow{D_{\delta }})$$ 29

$$\overrightarrow{X}\left(t,+,1\right)=\frac{\overrightarrow{X_1}+\overrightarrow{X_2}+\overrightarrow{X_3}}{3}$$ 30

Two new components are inserted in the GWO algorithm to facilitate multiobjective optimization. The first component is an archive, which is nothing but a memory to store the non-dominated solutions generated so far. The second component is the leader-choosing mechanism that aids in selecting the best solutions from the archive to determine the alpha, beta, and delta wolves.

Multiobjective PSO

Particle swarm optimization algorithm is initially proposed by Dr Kennedy and Dr Eberhart³⁵. This optimization technique mimics the group behavior of bird flocks and fish schools. Shorter running time and the requirement of fewer parameters are some of the noteworthy advantages of PSO. In the PSO algorithm, each particle has a velocity and position. While hovering in the search space, a particle's position is adjusted, balancing the particle's own knowledge and the knowledge of the swarm. The velocity and position equations are as follows³⁴:

$$V_i\left(k,+,1\right)=w\ast V_i\left(k\right)+c1\ast r1\ast \left({\mathit{pbest}}_i,\left(k\right),-,X_i,\left(k\right)\right)+c2\ast r2\ast (gbest\left(k\right)-X_i)$$ 31

$$X_i\left(k,+,1\right)=X_i\left(k\right)+V_i(k+1)$$ 32

where k denotes the present iteration while k + 1 is the next iteration, V_i and X_i represent the velocity and position of the i^th particle, respectively, ${\mathit{pbest}}_i$ is the i^th particle's best value, and $\mathit{gbest}$ denotes the global best value. The flow chart of the algorithms used is presented in Fig. 3.

Fig. 3.

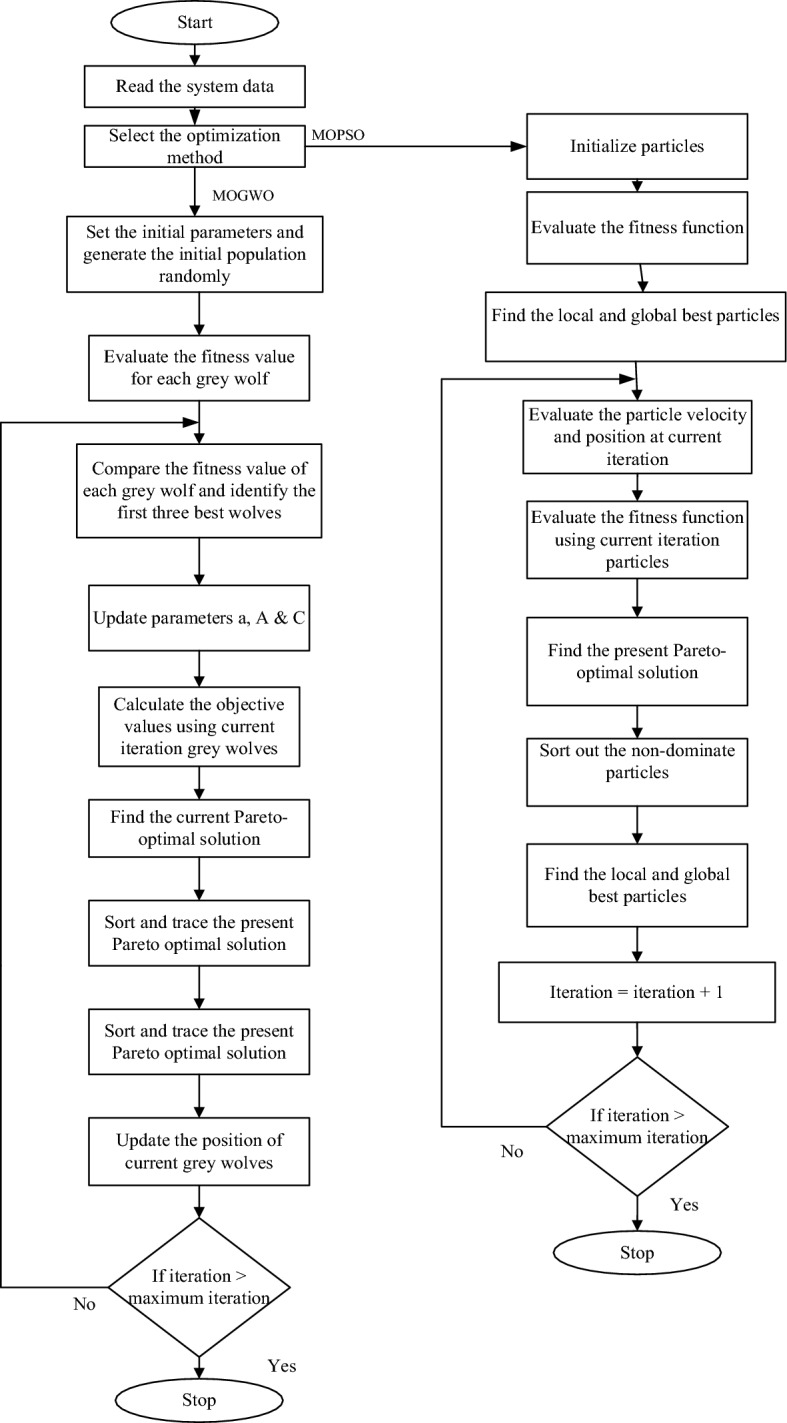
MOPSO and MOGWO flowchart.

Pareto-optimal technique

To provide a solution to conflicting multiple objective functions, the Pareto-optimal technique is explored in this study to generate a Pareto-front. The Pareto-front is a set of compromise solutions denoting the best trade-offs among the conflicting objectives. The idea of dominance is the basic principle of the Pareto-optimal technique. Vector V2 is dominated by vector V1 for the conditions stated below^29,36 .

$$\forall k=\left\{\text{1,2},\cdots \cdots p\},,f_k,(V1),\le ,f_k,(V2)\right)$$ 33

$$\exists l\in \left\{\text{1,2},\cdots .p\},f_l,(V1),<,f_l,\left(V,2\right)\right)$$ 34

where $p$ is the total number of variables.

Selection of optimal trade-off solution

Fuzzy set technique

The optimal trade-off solution from Pareto-front is extracted by the fuzzy set technique³⁷. A fuzzy membership function is developed to this purpose for every objective function, which is given is Eq. (35)³³.

$${\mu }_k\left(x\right)=\left\{\begin{array}{c}\frac{f_k^{\mathit{max}}-f_k\left(x\right)}{f_k^{\mathit{max}}-f_k^{\mathit{min}}},if{f}_k^{\mathit{min}}<f_k<f_k^{\mathit{max}}\\ 1,if{f}_k<f_k^{\mathit{min}}\\ 0,if{f}_k<f_k^{\mathit{max}}\end{array}\right)$$ 35

where $f_k^{\mathit{min}}$ and $f_k^{\mathit{max}}$ for the kth objective function denote the acceptable and unacceptable values, respectively. The membership function³³ is given in Eq. (36).

$${\mu }^r=\frac{{\sum }_{k=1}^{\mathit{NO}}{\mu }_k^r}{{\sum }_{k=1}^{\mathit{ND}}{\sum }_{k=1}^{\mathit{NO}}{\mu }_k^r}$$ 36

where NO and ND respectively denote the number of objective functions and number of solutions in the Pareto-front for the r^th non-dominated solution. The solution corresponding to the maximum membership is the optimal trade-off solution.

Technique for order preference by similarity to an ideal solution

The fuzzy set-based approach presented above identifies a single, optimal trade-off solution from the numerous Pareto-optimal solutions. However, this solution might not be universally preferred by all decision makers (electrical power transmission utilities) due to potential variations in their priorities regarding the study's objectives. To address this limitation, this work employs the TOPSIS method to generate a range of trade-off solutions, catering to a broader spectrum of decision-maker preferences. The following are the steps that makeup TOPSIS³⁸ :

• Step 1: Create a decision matrix with the size $m_1\times m_2$ that contains Pareto optimal solutions, $D=d_{\mathit{ij}}$. In this case, j = 1, 2,…., $m_2$ indicates the objectives or criterion, while i = 1, 2,….,$m_1$ indicates the number of solutions/alternatives.

• Step 2: To create a normalized decision matrix $\left(D_N\right)$., each member of the matrix $D$ is normalized as indicated by the Eq. (37) below³⁸.

  $$d_{n,ij}=\frac{d_{\mathit{ij}}}{\sqrt{\sum _{i=1}^{m_1}{d}_{\mathit{ij}}^2}},\text{i}=1,2,\cdots ,m_1\text{and j}=1,2,{\cdots .,m}_2$$ 37
• Step 3: If necessary, a weighted normalized decision matrix can be created to assign weights to the objectives. If every goal is equally significant, you can skip this stage. The matrix's components are represented as:

  $$w_{\mathit{ij}}=w_j\times d_{n,ij},\text{i}=\text{1,2},\cdots ,m_1\text{and j}=\text{1,2},\cdots ,m_2$$ 38

  where $w_j$ is the decision-makers preference weight assigned to the j^th criterion and ${\sum }_{i=1}^2{w}_j=1$
• Step 4: The weighted normalized choice matrix provides the positive ideal solution (PIS) and the negative ideal solution (NIS)³⁸.

  $$PIS=\left\{\begin{array}{c}{max(w}_{\mathit{ij}})\forall i,ifthetargetrepresentsgain\\ \mathit{min}\left(w_{\mathit{ij}}\right)\forall i,ifthetargetrepresentscost\end{array}\right)$$ 39

  $$NIS=\left\{\begin{array}{c}{max(w}_{\mathit{ij}})\forall i,ifthetargetrepresentscost\\ min(w_{\mathit{ij}})\forall i,ifthetargetrepresentsgain\end{array}\right)$$ 40
• Step 5: As indicated below, calculate the Euclidean distances $d^{+}$ and $d^{-}$ d for every solution derived from PIS and NIS.

  $$d^{+}=\sqrt{\sum _{i=1}^{m_1}{\left(w_{\mathit{ij}},-,P,I,S\right)}^2}$$ 41

  $$d^{-}=\sqrt{\sum _{i=1}^{m_1}{\left(w_{\mathit{ij}},-,N,I,S\right)}^2}$$ 42
• Step 6: The relative closeness index (RCI) is computed for each option using the Euclidean distances determined in the preceding step, as shown below³⁸:

  $$R_i=\frac{d^{+}}{\left(d^{+},+,d^{-}\right)}$$ 43

Among the Pareto optimum solutions, the solution with the highest closeness ratio value will be selected as the BTS.

Results and discussion

To evaluate the effect of TCSC placement on power loss reduction, analysis is performed on an IEEE 30 bus standard system. The structure of the test system is shown in Fig. 4. The parameters considered for the MOGWO and MOPSO are as follows: population size is 50, iterations are 10 and the archive size is 50. To emphasize the merit of TCSC installation, the power loss is computed without TCSC at first and later; the two multiobjective functions are minimized in the presence of TCSC at the optimal site.

Fig. 4.

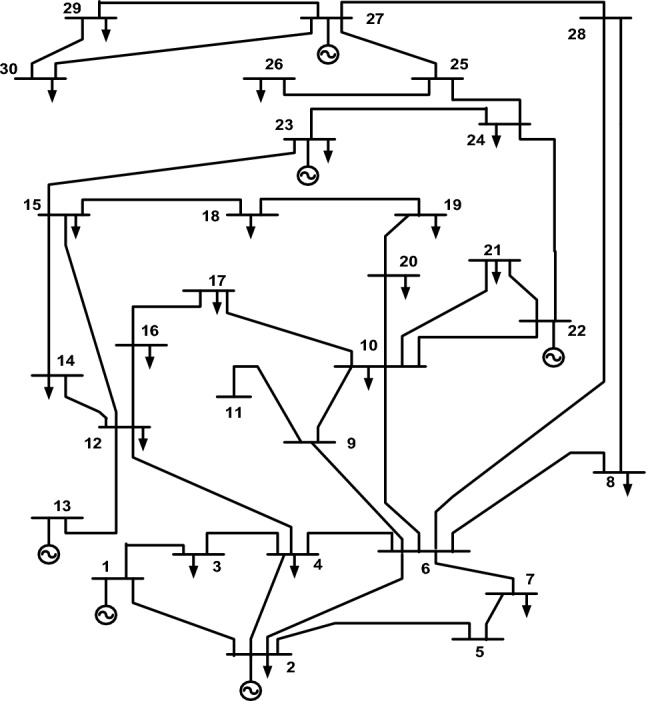
IEEE 30 bus test system.

Power losses reduction without TCSC

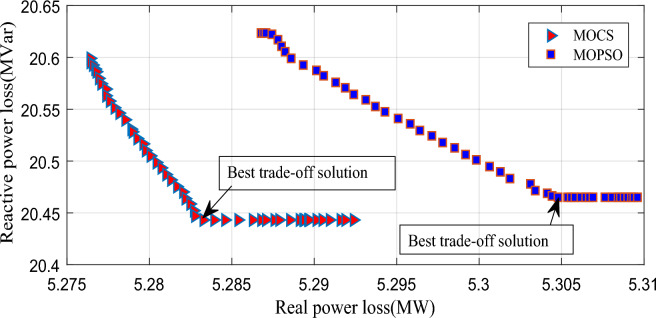
The power loss of the 30 bus system is computed by load flow analysis. The total real power loss and reactive power loss are 5.5933 MW and 21.0658MVar, respectively. These loss values are treated as base case losses for the comparison of results. To the test system, MOGWO and MOPSO algorithms are applied, and the total real and reactive power losses are calculated. The Pareto-optimal solution, thus generated, is presented in Table 1. The optimal trade-off solution is captured from the Pareto-optimal frontier by the fuzzy set technique. The optimal trade-off solution found from the Pareto-optimal frontier of the MOPSO algorithm is 5.3048 MW and 20.4656 MVar. The optimal trade-off solution obtained from the Pareto-optimal frontier of the MOGWO algorithm is 5.2833 MW and 20.4436 MVar. It is visible that the MOGWO algorithm gave relatively better results. The comparative depiction of results from both algorithms is presented in Fig. 5.

Table 1.

MOGWO and MOPSO comparison.

	MOGWO		MOPSO
Solution No	Real power losses (MW)	Reactive power losses (MVar)	Real power losses (MW)	Reactive power losses(MVar)
1	5.2764	20.5992	5.2868	20.6241
2	5.2764	20.5958	5.2868	20.6238
3	5.2766	20.5926	5.2869	20.6236
4	5.2767	20.5893	5.2871	20.6231
5	5.2768	20.5861	5.2874	20.6223
6	5.2769	20.5804	5.2878	20.6165
7	5.2771	20.5747	5.2880	20.6106
8	5.2774	20.5691	5.2882	20.6049
9	5.2774	20.5634	5.2886	20.5991
10	5.2776	20.5574	5.2893	20.5932
11	5.2779	20.5516	5.2901	20.5876
12	5.2782	20.5457	5.2906	20.5819
13	5.2785	20.5396	5.2913	20.5760
14	5.2789	20.5312	5.2919	20.5702
15	5.2790	20.5279	5.2924	20.5645
16	5.2793	20.5221	5.2931	20.5587
17	5.2796	20.5162	5.2937	20.5528
18	5.2798	20.5104	5.2943	20.5471
19	5.2801	20.5046	5.2951	20.5413
20	5.2804	20.4987	5.2958	20.5357
21	5.2807	20.4930	5.2964	20.5299
22	5.2810	20.4872	5.2971	20.5240
23	5.2813	20.4816	5.2978	20.5183
24	5.2817	20.4757	5.2985	20.5124
25	5.2820	20.4698	5.2992	20.5066
26	5.2822	20.4643	5.2998	20.5010
27	5.2825	20.4586	5.3006	20.4952
28	5.2827	20.4526	5.3013	20.4894
29	5.2828	20.4472	5.3019	20.4837
30	5.2833	20.4436	5.3031	20.4780
31	5.2839	20.4433	5.3034	20.4721
32	5.2846	20.4431	5.3041	20.4692
33	5.2854	20.4431	5.3044	20.4659
34	5.2863	20.4431	5.3048	20.4656
35	5.2868	20.4428	5.3054	20.4654
36	5.2871	20.4428	5.3056	20.4652
37	5.2876	20.4428	5.3058	20.4650
38	5.2879	20.4428	5.3062	20.4650
39	5.2885	20.4428	5.3065	20.4649
40	5.2891	20.4428	5.3067	20.4649
41	5.2893	20.4427	5.3069	20.4649
42	5.2894	20.4427	5.3076	20.4649
43	5.2896	20.4427	5.3081	20.4649
44	5.2897	20.4427	5.3084	20.4648
45	5.2901	20.4427	5.3086	20.4648
46	5.2905	20.4427	5.3088	20.4648
47	5.2909	20.4427	5.3090	20.4648
48	5.2916	20.4426	5.3092	20.4648
49	5.2919	20.4426	5.3094	20.4648
50	5.2924	20.4426	5.3096	20.4647

Fig. 5.

Pareto-frontier comparison without TCSC.

Power losses reduction with TCSC

The power loss of the test system considered is computed considering TCSC.Table 2 presents the overall system losses after the installation of TCSC. It can be noted from Table 2 that the total losses of the system are lowest when TCSC is located at line joining buses 27–29. Therefore the optimal site for installing TCSC in the system under consideration is the line joining buses 27 and 29. With TCSC at its optimal site two different cases related to the two multiobjective minimization functions are studied.

Table 2.

System losses considering TCSC.

Line No	From bus-to bus	Power loss		Line No	From bus–to bus	Power loss
		$P_{\mathit{Loss}}$(MW)	$Q_{\mathit{Loss}}$(MVAR)			$P_{\mathit{Loss}}$(MW)	$Q_{\mathit{Loss}}$(MVAR)
1	1–2	6.2189	21.2073	22	15–18	5.6409	21.1456
2	1–3	6.1119	21.5027	23	18–19	5.6466	21.1860
3	2–4	5.7564	21.0080	24	19–20	5.6808	21.2499
4	3–4	5.6268	20.8843	25	10–20	5.6001	21.0748
5	2–5	6.2614	21.0076	26	10–17	5.6043	21.1404
6	2–6	5.9868	21.1433	27	10–21	5.6182	21.1075
7	4–6	5.7239	21.1022	28	10–22	5.6182	21.0967
8	5–7	6.2226	21.7256	29	21–22	5.7648	21.4997
9	6–7	5.6841	20.8136	30	15–23	5.6288	21.1426
10	6–8	5.5868	20.6692	31	22–24	5.6372	21.0740
11	6–9	5.5423	21.3805	32	23–24	5.6218	21.1226
12	6–10	5.5986	21.0992	33	24–25	5.6164	21.1109
13	9–11	5.6094	22.1306	34	25–26	5.6052	21.0455
14	9–10	5.6324	21.2136	35	25–27	5.6268	21.0607
15	4–12	5.8303	23.0641	36	28–27	5.3946	20.4586
16	12–13	5.7334	21.3289	37	27–29	5.3810	20.1497
17	12–14	5.6085	21.0659	38	27–30	5.4056	20.2408
18	12–15	5.6525	21.1366	39	29–30	5.8092	21.8134
19	12–16	5.6232	21.1439	40	8–28	5.6232	21.1439
20	14–15	5.6108	21.1308	41	6–28	5.5696	21.1308
21	16–17	5.6142	21.1446

Case a: real and reactive power losses

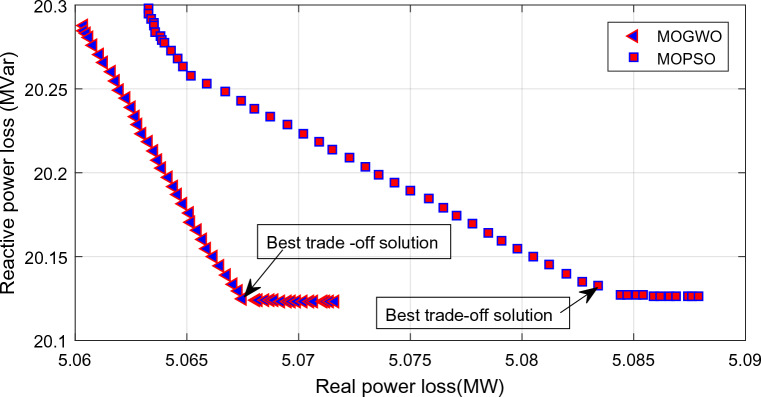
After placing the TCSC at its optimal site, MOGWO and MOPSO algorithms are applied to the test system, and the multiobjective function relating to total real and reactive power losses is solved. The Pareto-optimal solution, thus generated, is presented in Table 3. The optimal trade-off solution is captured from the Pareto-optimal frontier by the fuzzy set technique. The optimal trade-off solution found from the Pareto-optimal frontier of the MOPSO algorithm is 5.0834 MW and 20.1323 MVar. The optimal trade-off solution obtained from the Pareto-optimal frontier of the MOGWO algorithm is 5.0675 MW and 20.1246 MVar. The reduction in real power losses when compared with the base case is 9.11% and 9.4% by MOPSO and MOGWO respectively. In the case of reactive power losses, the reduction is seen as 4.44 and 4.48% by MOPSO and MOGWO respectively. The MOGWO algorithm gave relatively better results. The results attained indicate that the installation of TCSC and the application of MOGWO and MOPSO algorithms minimized the power losses. It is also visible that the MOGWO algorithm gave relatively better results. The comparative depiction of results from both algorithms after locating TCSC at its optimal site is presented in Fig. 6.

Table 3.

MOGWO and MOPSO comparison with TCSC–case a.

	MOGWO		MOPSO
Solution No	Real power losses (MW)	Reactive power losses (MVar)	Real power losses (MW)	Reactive power losses (MVar)
1	5.0604	20.2880	5.0633	20.2980
2	5.0604	20.2850	5.0633	20.2945
3	5.0605	20.2830	5.0634	20.2915
4	5.0606	20.28110	5.0635	20.2890
5	5.0608	20.2759	5.0635	20.2875
6	5.0611	20.2706	5.0636	20.2840
7	5.0613	20.2654	5.0638	20.2815
8	5.0616	20.2601	5.0639	20.2795
9	5.0618	20.2547	5.0640	20.2778
10	5.0620	20.2494	5.0643	20.2729
11	5.0623	20.2442	5.0646	20.2681
12	5.0625	20.2390	5.0648	20.2631
13	5.0627	20.2337	5.0652	20.2582
14	5.0628	20.2285	5.0659	20.2533
15	5.0630	20.2233	5.0667	20.2482
16	5.0633	20.2182	5.0674	20.2432
17	5.0635	20.2130	5.0680	20.2383
18	5.0637	20.2077	5.0687	20.2334
19	5.0639	20.2024	5.0695	20.2284
20	5.0642	20.1972	5.0702	20.2235
21	5.0644	20.1920	5.0709	20.2187
22	5.0646	20.1869	5.0715	20.2138
23	5.0648	20.1815	5.0723	20.2089
24	5.0651	20.1761	5.0730	20.2039
25	5.0652	20.1708	5.0736	20.1990
26	5.0655	20.1654	5.0743	20.1941
27	5.0657	20.1601	5.0750	20.1893
28	5.0659	20.1549	5.0758	20.1843
29	5.0662	20.1497	5.0765	20.1794
30	5.0665	20.1445	5.0771	20.1744
31	5.0668	20.1392	5.0778	20.1695
32	5.0671	20.1338	5.0785	20.1645
33	5.0673	20.1293	5.0791	20.1597
34	5.0675	20.1246	5.0798	20.1547
35	5.0681	20.1241	5.0805	20.1498
36	5.0682	20.1240	5.0812	20.1449
37	5.0685	20.1238	5.0820	20.1399
38	5.0687	20.1238	5.0827	20.1351
39	5.0689	20.1238	5.0834	20.1323
40	5.0692	20.1236	5.0844	20.1275
41	5.0695	20.1236	5.0847	20.1270
42	5.0697	20.1236	5.0851	20.1270
43	5.0699	20.1236	5.0854	20.1270
44	5.0702	20.1236	5.0859	20.1265
45	5.0705	20.1235	5.0862	20.1265
46	5.0707	20.1235	5.0866	20.1265
47	5.0711	20.1235	5.0869	20.1265
48	5.0712	20.1235	5.0874	20.1260
49	5.0714	20.1235	5.0876	20.1260
50	5.0716	20.1234	5.0879	20.1260

Fig. 6.

Pareto-frontier comparison with TCSC–case a.

Case b: Real power loss and capital cost of TCSC

Here MOGWO and MOPSO algorithms are applied to the test system, and the multiobjective function relating to real power loss and capital cost of TCSC is solved. The Pareto-optimal solution, thus generated, is presented in Table 4. The optimal trade-off solution is captured from the Pareto-optimal frontier by the fuzzy set technique. The optimal trade-off solution obtained from the Pareto-optimal frontier of the MOPSO algorithm is 5.0625 MW and 150.6561US$/KVar. The optimal trade-off solution obtained from the Pareto-optimal frontier of the MOGWO algorithm is 5.0596 MW and 149.2531US$/KVar. The reduction in real power losses when compared with the base case is 9.48% and 9.53% by MOPSO and MOGWO respectively. The MOGWO algorithm gave relatively better results. The comparative depiction of results from both algorithms after locating TCSC at its optimal site is presented in Fig. 7.

Table 4.

MOGWO and MOPSO comparison with TCSC–case b.

	MOGWO		MOPSO
Solution No	Real power losses (MW)	Capital cost of TCSC(US$/KVar)	Real power losses (MW)	The capital cost of TCSC (US$/KVar)
1	5.0590	149.7295	5.0623	150.8165
2	5.0591	149.7133	5.0623	150.8012
3	5.0591	149.6923	5.0623	150.7951
4	5.0591	149.6743	5.0623	150.7829
5	5.0592	149.6643	5.0623	150.7784
6	5.0592	149.6493	5.0624	150.7635
7	5.0592	149.6343	5.0624	150.7556
8	5.0593	149.6143	5.0624	150.7429
9	5.0593	149.5734	5.0625	150.7343
10	5.0593	149.5393	5.0625	150.7036
11	5.0594	149.4943	5.0625	150.6893
12	5.0594	149.4443	5.0625	150.6561
13	5.0595	149.3994	5.0663	150.6211
14	5.0596	149.3758	5.0688	150.5867
15	5.0596	149.3343	5.0708	150.5515
16	5.0596	149.3194	5.0739	150.4963
17	5.0596	149.2531	5.0751	150.4698
18	5.0624	149.2054	5.0764	150.4462
19	5.0636	149.1601	5.0797	150.4414
20	5.0661	149.1053	5.0813	150.4185
21	5.0681	149.0456	5.0828	150.3964
22	5.0706	148.9903	5.0843	150.3672
23	5.0726	148.9457	5.0861	150.3444
24	5.0751	148.8802	5.0886	150.2884
25	5.0781	148.8254	5.0898	150.2661
26	5.0805	148.7805	5.0915	150.2426
27	5.0835	148.7356	5.0947	150.1993
28	5.0855	148.6755	5.0965	150.1969
29	5.0891	148.6103	5.0981	150.1559
30	5.0909	148.5894	5.1003	150.1437
31	5.0921	148.5552	5.1038	150.1392
32	5.0956	148.5151	5.1053	150.1123
33	5.0969	148.4915	5.1067	150.0865
34	5.0986	148.4606	5.1083	150.0691
35	5.0998	148.4319	5.1091	150.0456
36	5.1012	148.4148	5.1100	150.0382
37	5.1024	148.3927	5.1118	150.0158
38	5.1033	148.3495	5.1131	150.0001
39	5.1057	148.3281	5.1143	149.9727
40	5.1068	148.2999	5.1156	149.9388
41	5.1089	148.2596	5.1160	149.9103
42	5.1114	148.2196	5.1168	149.8916
43	5.1119	148.1925	5.1182	149.8778
44	5.1126	148.1643	5.1186	149.8654
45	5.1139	148.1592	5.1192	149.8482
46	5.1143	148.1579	5.1201	149.8266
47	5.1154	148.1385	5.1216	149.7994
48	5.1173	148.1292	5.1233	149.7785
49	5.1180	148.1202	5.1246	149.7569
50	5.1186	148.1112	5.1268	149.7483

Fig. 7.

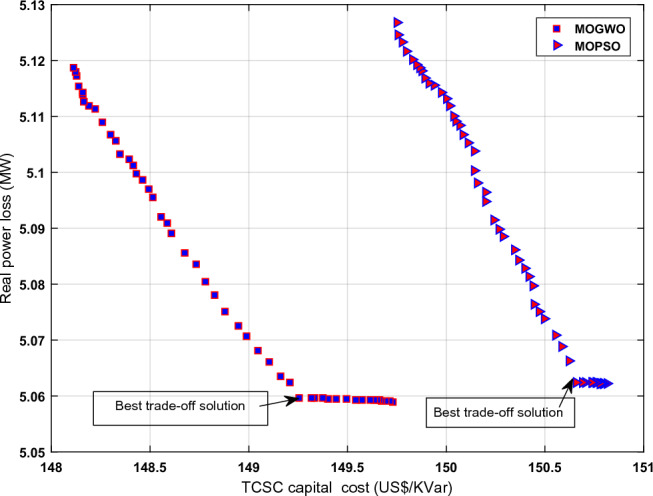
Pareto-frontier comparison with TCSC–case b.

The summary of the results obtained is presented in Table 5. It is worth noting that after the application of the optimization algorithms, the power losses got minimized. After installing TCSC at its optimal site, the power losses further reduced. The performance of the MOGWO algorithm in minimization of power losses is superior to that MOPSO algorithm in both the considered cases.

Table 5.

Summary of results with and without TCSC.

		Without TCSC				With TCSC (Case a)				With TCSC (Case b)
Base case		MOGWO		MOPSO		MOGWO		MOPSO		MOGWO		MOPSO
Real Power Loss (MW)	Reactive power loss (MVAR)	Real Power Loss (MW)	Reactive power loss (MVAR)	Real Power Loss (MW)	Reactive power loss (MVAR)	Real Power Loss (MW)	Reactive power loss (MVAR)	Real Power Loss (MW)	Reactive power loss (MVAR)	Real Power Loss (MW)	Capital Cost of TCSC (US$/KVar)	Real Power Loss (MW)	Capital Cost of TCSC (US$/KVar)
5.593	21.0658	5.2833	20.4436	5.3048	20.4656	5.0675	20.1246	5.0834	20.1323	5.0596	149.2531	5.0625	150.6561

Suggestion of multiple optimal trade-off solutions

From the above case studies it is evidient that optimal installation of TCSC can demnish the power losses. However, the fuzzy set approach employed could only provide one one optimal trade-off solution. In many cases, the solution provided may not be acceptable to all the utilities. Hence, it would be a better approach to put forward multiple solutions to serve a large range of utilities with diverse preferences to objectives. To this extent, the TOPSIS methodology is used and three solutions are suggested from the Pareto front, obtained from MOGWO algorithm for both case a and case b. The suggested solutions with respective objective preferences are presented in Table 6. Solution 1 in both cases represents the scenario where the utilities have a preference to the first objective i.e., real power losses in both cases. For selecting solution 2, equal preference is given to both objectives. At last, solution 3 represents the scenario where the utilities have a preference to the second objective i.e., reactive power losses in case a and capital cost of TCSC in case b.

Table 6.

Suggestion of multiple solutions using TOPSIS.

Case a
Objective preference	Real power losses (MW)	Reactive power losses (MVar)
Soultion 1—Preference to real power losses	5.0604	20.2880
Soultion 2—Equal preference to both objectives	5.0675	20.1246
Solution 3—Preference to reactive power losses	5.0716	20.1234

Case b
Objective preference	Real power losses (MW)	The capital cost of TCSC (US$/KVar)
Solution 1–Preference to real power losses	5.0590	149.7295
Solution 2–Equal preference to both objectives	5.0751	148.8802
Solution 3–Preference to Capital cost of TCSC	5.1186	148.1112

Conclusion

The work presented in this paper underscores on optimal placement of TCSC for power loss reduction. Real and reactive power loss minimization, real power, and capital cost of TCSC minimization are considered as the multiobjective optimization functions. In the proposed approach, MOGWO, an efficient multiobjective algorithm, is used to optimize the considered minimization problems. The task of generating the non-dominated solutions is fulfilled by the Pareto-optimal technique. The fuzzy set technique is applied to obtain a compromised solution and TOPSIS method has been applied to generate multiple compromised solutions. The study is performed on an IEEE 30 bus standard test system. To establish the worthiness of TCSC installation in the minimization of power loss, the multiobjective functions are solved before and after the location of TCSC. Simulation results suggest that the optimal siting of TCSC can help in the reduction of power losses. Alleviation of power losses can facilitate augmenting the utility of the system without increasing the generation volume. In addition, the multiobjective problem under study is also solved using MOPSO. MOGWO algorithm provided relatively superlative results than the MOPSO algorithm. The work proposed is limited to single type FACTS device i.e. TCSC. The incorporation of multi-type FACTS devices may be treated as a future scope of this work. Further, the proposed investigations can be carried out on a larger benchmark test systems.

Author contributions

All the authors have contributed equally to this article.

Funding

No funding was supported for this research work.

Data availability

The data used to support the findings of this study are included in the article.

Competing interests

The authors declare no competing interests.