Abstract
Fueled by the rapid advancement of nanofabrication, metasurface has provided unprecedented opportunities for 3D holography. Large depth 3D meta-holography not only greatly increases information storage capacity, but also enables distinguishing of the relative spatial relationship of 3D objects, which has important applications in fields like optical information storage and medical diagnosis. Although the methods based on Fresnel diffraction theory can reconstruct the real depth information of 3D objects, the maximum depth is only 2 mm. Here, we develop a 3D meta-holography based on angular spectrum diffraction theory to break through the depth limit. By developing the angular spectrum diffraction theory into meta-holography, the metasurface structure with independent polarization control is used to create a polarization multiplexing 3D meta-hologram. The fabricated amorphous silicon metasurface increases the depth range by 47.5 times and realizes 0.95 dm depth reconstruction for polarization independent and different color 3D meta-hologram in visible. Such polarization controlled large-depth color meta-holography is expected to open avenue for data storage, display, information security and virtual reality.
Subject terms: Metamaterials, Displays
The authors present an exciting 3D meta-holography based on angular spectrum diffraction theory that significantly improves depth limits. The showcased amorphous silicon metasurface with independent polarization control herein achieves a 47.5x depth increase and 0.95 dm depth reconstructions for polarization-independent and different color 3D meta-hologram.
Introduction
Holography provides a way to record and reconstruct complete wavefront information with both phase and amplitude, which is widely used in fields such as microscopic imaging, encryption, beam shaping and 3D reproduction1–6. Since Dennis Gabor invented the landmark 3D holographic technology, great efforts have been made to realize 3D holography with a large depth, wide viewing angle and abundant information7–10. Large-depth holography can greatly improve the depth information of 3D reconstructed images. For example, when large-depth holography is applied to the display field, it can bring viewers a better sense of immersion and experience, and this stunning effect is expected to be further applied in virtual and augmented reality and other fields. Additionally, in the field of industrial inspection, the large-depth holography enables detailed information of 3D objects to be reconstructed in a large depth range, which is critical for the calibration of component details. In traditional 3D holography, the phase and amplitude information of an object are dynamically regulated by a spatial light modulator (SLM) or digital mirror device (DMD)11–14. The pixel size of these modulators is usually larger than 3.7 µm15. Such large pixel size leads to narrow holographic viewing angle of around 8° limiting the application of 3D holography16. The emerging metasurface provides a unique opportunity for holography due to the sub-wavelength structures that can arbitrarily control the properties of light and also enable larger viewing angle reaching 22° 17,18. It has seen unprecedented development and has attracted tremendous attention because of the advantages of small pixel size and light weight19–25.
Although meta-holography provides sufficient viewing angle, the challenge of realizing large depth 3D imaging has not been overcome26–32. Large depth 3D meta-holography is essential to accurately identify the detailed information of objects, which is critical in the fields such as detection and medical research, where information storage capacity or relative spatial information of 3D scenes is the key. The traditional reconstruction based on Fourier holography requires Fourier transform of the lens, and the image position is limited by the lens’s focal length. Holography based on Fresnel diffraction is near-field diffraction, and the relationship between aliasing and depth needs to be balanced in the process of diffraction propagation. During holographic reconstruction, the depth is also affected by spatial frequency and pixel size. The farther the propagation distance is, the higher the spatial frequency of the object is, resulting in aliasing. Distortion-free 3D images have been demonstrated in the visible and near-infrared range through on-axis plasmonic holography33. This achievement is realized by using subwavelength pixelated plasmonic metasurfaces, which makes imaging with a depth of approximately 1.3 mm possible. It is reported that the maximum depth achieved by metasurface holography in the visible range is only 2 mm34. Although impressive, the imaging capability is still constrained to tiny objects, and it is difficult to perceive the stereoscopic effect for human eyes.
3D meta-holography with large depth and polarization function can increase spatial information capacity in a new dimension, which is critical for storage, structured light modulation and encryption35–41. In large depth polarization meta-holography, it is necessary to take into account the sampling limitation of depth and the sampling constraint in different polarization states, which pose new challenges to the coding method of hologram and the structural design of metasurface. To the best of our knowledge, realizing polarization independent 3D imaging with decimeter level depth has not been reported.
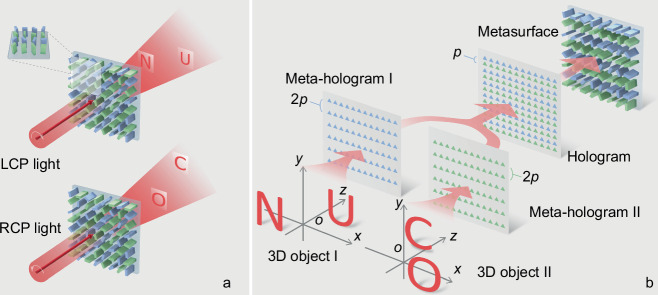
Here, we demonstrate large-depth and controllable polarization 3D meta-holography by using angular spectrum diffraction theory-based design method. By revealing the relationship between deep reconstruction and aliasing, the phase information can be optimized. Based on the established diffraction propagation conditions, the maximum depth reconstruction is achieved by reducing aliasing. This strategy represents a great advance in meta-holography for the following reasons. First, this approach is effective to realize large depth meta-hologram. As shown in Fig. 1a, when light irradiates the metasurface formed by rectangular amorphous silicon nanorods, the true depth reconstruction of 3D light field can be realized by angular spectrum diffraction theory. The spectrum aliasing relationship under the condition of angular spectrum diffraction propagation is revealed, and the depth is increased by reducing aliasing. The maximum depth is 0.95 dm. To our knowledge, this is not easy to show 3D meta-holography with such a large depth. Second, the proposed meta-holography solves the problem that the existing 3D meta-holography is difficult to realize both large depth imaging and polarization control. We use line-by-line insertion to synthesize two sub-holograms into a final hologram, thus obtaining the complex amplitude modulation information corresponding to the metasurface. The proposed meta-holography does not sacrifice the spatial dimension information of the light field. When left/right circularly polarized (LCP/RCP) light irradiates the metasurface, different 3D images can be seen, thus increasing the amount of spatial information. Third, the experiments also demonstrate the color meta-holography with different wavelengths. Holographic images with the same size and different colors can be reproduced, which is an important step to realize color meta-holography. In addition, due to the high-resolution unit structure of the metasurface, large viewing angle can be achieved, representing a further step towards wide-viewing-angle naked-eye 3D display. The proposed meta-holography is expected to find broad applications such as data storage, encryption and beam shaping.
Fig. 1. Concept of the proposed 3D meta-holography.
a Schematic diagram of the 3D meta-holographic reconstruction. b Design principle of the metasurface.
Results
Structure of the metasurface
The designed metasurface is based on the principle of geometric phase control to realize the independent control of light field phase for each unit cell. The unit cell of the metasurface consists of a rectangular amorphous silicon nanorod fabricated on a quartz substrate. The Pancharatnams-Berry (PB) phase is utilized for a broadband non-dispersive phase control by rotating the principle axis of the birefringent nanorod. The relationship between the PB phase shift φ and rotation angle θ satisfies φ = ±2θ, where the positive sign is taken when the polarization state of the incident light is LCP, and the negative sign is taken when the polarization state is RCP. The schematic illustration of the proposed metasurface for encoding the hologram and manipulating the corresponding polarization states simultaneously is shown in Fig. 1b. For two different 3D objects, the corresponding meta-holograms I and II are calculated based on the angular spectrum diffraction theory. The two meta-holograms correspond to the a pair of orthogonal circular polarization states respectively. The pixel spacings are p and 2p along x and y directions, respectively.
After merging the two meta-holograms, the pixel spacing is p along two directions, which is the same as the designed periodicity of the unit cells in the metasurface. In addition, the pixel number corresponding to different circular polarization is the same as that of the meta-hologram. In the previous work on polarization multiplexing holograms, two meta-holograms with pixel spacing of p were usually merged with a displacement vector of (p/2, p/2) or by extracting half of the pixels42,43. The former two approaches both led to degradation of the quality of reconstructed image because of the change of periodicity or pixel number. Our design effectively avoids the above problem and can obtain the optimal reconstructed image quality. Moreover, to reduce the interference between adjacent phases, we use line-by-line insertion to synthesize two sub-holograms into a final hologram, thus obtaining the complex amplitude modulation information corresponding to the metasurface. When LCP or RCP light irradiates the metasurface, holographic reconstruction of different 3D objects with large depth can be realized. This function is realized by the complex amplitude modulation of two orthogonal polarization bases provided by the metasurface, which is difficult to realize by using the SLM in the traditional optical systems.
Holographic angular spectrum diffraction principle based on metasurface
The traditional Gerchberg–Saxton (GS) algorithm uses Fourier transform to realize the convergence of light field in holographic reconstruction, which leads to the fundamental restriction of the focal length of a Fourier lens on the position and depth of reconstructed image. In addition, the size of the reconstructed image is different for different wavelengths of illumination light due to chromatic aberration. In contrast, angular spectrum diffraction is based on lensless diffraction imaging. The depth and position of the reconstructed image are set in advance, which is not determined by the lens in the optical path. We introduce the principle of angular spectrum diffraction into meta-holography to reconstruct the holographic image with large depth. In order to ensure the high quality of the reconstructed images with large depth, the phase of the meta-hologram is optimized to minimize speckle noise.
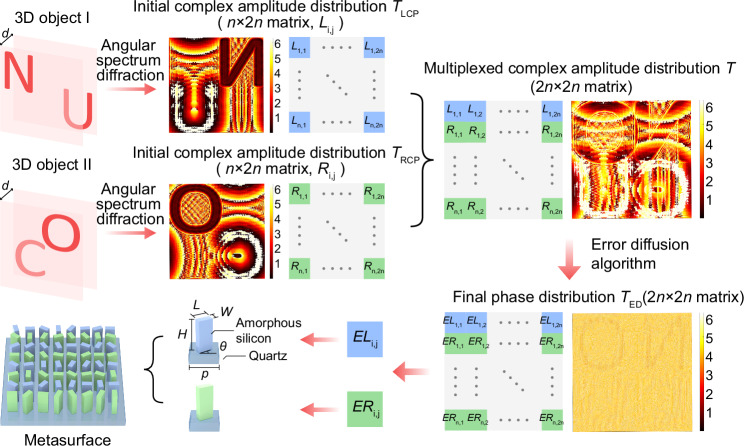
The generated meta-holograms based on the holographic angular spectrum diffraction principle44 are shown in Fig. 2. In Fourier optics, any light field can be decomposed into the superposition of wavelets with different spatial frequencies and amplitudes. Therefore, the complex amplitude distribution of the 3D object and the complex amplitude distribution of the holographic plane can be regarded as the integral of the spatial spectrum of the 3D object and the spatial spectrum of the holographic plane, respectively.
| 1 |
| 2 |
where T0 and T are the complex amplitude distributions of the 3D object and the holographic plane, respectively. x0 and y0 are the coordinates of the 3D object. j is the imaginary number, and z is the distance between the holographic plane and the 3D object. (fx, fy) is the spatial frequency of spatial light field in x direction and y direction, respectively. A0(fx, fy; d0) and A(fx, fy; z) are the spatial spectrum of the 3D object and the holographic plane, respectively.
Fig. 2.
Computation strategy of the meta-hologram.
Then Eqs. (3) and (4) can be obtained by solving the Helmholtz equation:
| 3 |
| 4 |
where is the transfer function and is the phase of the transfer function. λ is the wavelength. So, the complex amplitude distributions TLCP and TRCP of the holographic plane corresponding to the two polarization states can be obtained by calculating their respective corresponding initial light fields:
| 5 |
| 6 |
where represents Fourier transform, and represents inverse Fourier transform, T1(x, y; d0) and T2(x, y; d0) represent the complex amplitude distributions of 3D objects I and II, respectively. HLCP(fx, fy; z) and HRCP(fx, fy; z) represent the transfer function for different polarization states.
When calculating the hologram, all the light fields, spectra and transfer functions are discretely sampled with equal grids, and the Fourier transform and inverse transform of the continuous space involved in Eqs. (5) and (6) are also replaced by Fast Fourier transform and inverse Fast Fourier transform calculation, respectively. The under-sampling operation in the discrete sampling process causes errors, which will lead to spectrum aliasing, and finally the reconstructed light field of large depth holography will be seriously affected. The local signal frequency of the transfer function Mf can be expressed as follows:
| 7 |
In the sampling of the transfer function, the sampling frequency Δfx needs to satisfy the Nyquist sampling theorem to avoid the aliasing error:
| 8 |
However, in the calculation of meta-holography, the sampling frequency is usually determined by the following equation:
| 9 |
where N is the number of pixels in the x direction on the meta-hologram. Therefore, in order to achieve large depth meta-holography, the transfer function itself can only be band-limited to meet the requirements of Nyquist sampling theorem.
According to Eq. (8), the transfer function in the x direction should be constrained within the region:
| 10 |
| 11 |
where is the maximum frequency of the transfer function in the x direction. The bandwidth of the transfer function in the x direction is limited to the positive ellipse with the y axis as the long axis, as shown in Eq. (10). Similarly, the bandwidth in the y direction is limited to the positive ellipse with the x axis as the long axis. The overlapping region of the two represents the band-limited region of the transfer function. To ensure that the high-frequency information of 3D objects is not affected by the spectrum aliasing in the process of meta-holography reconstruction at ultra-large depth, it is necessary to limit the transfer function to this bandwidth-limited region. Since the transfer function itself does not contain the optical field information of the 3D objects, limiting the bandwidth of the transfer function will not impact the details and resolution of the reconstructed image in meta-holography. Conversely, if the bandwidth of the sampled transfer function is not restricted, the maximum depth of meta-holography will be only a few millimeters.
After the initial complex amplitude distributions TLCP and TRCP are acquired by using the angular spectrum diffraction principle, they are horizontally interleaved to obtain the multiplexed complex amplitude distribution denoted as T. In the calculation of angular spectrum diffraction, both TLCP and TRCP are quantized into matrices of size (n×2n). Therefore, the matrix of synthesized T is (2n × 2n). Because the designed metasurface is used to realize the phase modulation, if the amplitude information of the complex amplitude hologram is directly removed, each pixel will have an error, which will affect the quality of holographic reconstruction. In order to reduce this error, after obtaining the pure phase information, the pixel points are scanned one by one by using the error diffusion algorithm, and the error of each pixel point is diffused to the adjacent pixels that have not been scanned according to a certain weight. The final phase distribution TED is obtained by using iterative optimization, which leads to a significant improvement in the quality of holographic reconstruction (Supplementary Material S1). Then, the metasurface is designed, and the unit cell of the metasurface is consisted of a rectangular amorphous silicon nanorod fabricated on a quartz substrate. The length, width and height of amorphous silicon are L, W and H, respectively. The period is p, and the rotation angle relative to the x axis is θ.
Metasurface fabrication and optical characterization
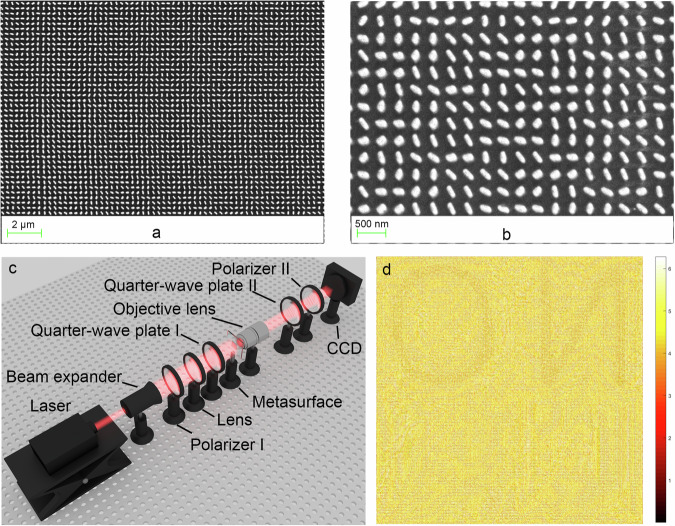
To verify the concept, a metasurface-based hologram consisting of 5000 × 5000 pixels is designed and fabricated. Based on the principle of angular spectrum diffraction, the light field distributions of 3D object I and 3D object II are calculated respectively, and meta-holograms I and II are generated accordingly. The resolution of the meta-holograms is 2500 × 5000, and the horizontal pixel spacing is 0.3 µm and the vertical pixel spacing is 0.6 µm. According to the line-by-line extraction method, two meta-holograms with different polarization information of 3D objects are superimposed together to generate the final hologram. The resolution of the final hologram is 5000 × 5000, and the pixel size is 0.3 µm. Finally, based on the hologram design, we experimentally fabricate the corresponding metasurface via nanofabrication process. The period, height, length and width of the nanorod are 300 nm, 400 nm, 210 nm and 90 nm, respectively. The scanning electron microscopy (SEM) images of the fabricated sample are shown in Fig. 3a, b, and the fabrication details can be found in the Materials and methods section.
Fig. 3. Experimental configuration and realization of 3D meta-holography.
a Top view SEM images of the metasurface (scalebar: 2 µm). b Top view SEM images of the metasurface (scalebar: 500 nm). c Experimental setup for the reconstruction process. d Phase diagram of the meta-hologram.
The schematic diagram of the experimental setup for holographic reproduction is shown in Fig. 3c. The meta-holographic reconstruction system includes a laser, a beam expander, two polarizers, two quarter-wave plates, a lens, a metasurface, and an objective lens. Among them, the laser and beam expander are used to generate uniform collimated incident light. Polarizer I and quarter-wave plate I are used to convert the incident linearly polarized light into circularly polarized. In order to increase the energy of the incident beam on the metasurface, the lens is used to condense the beam. The objective lens is placed behind the metasurface to enlarge the holographic image, so that the CCD can detect the holographic image conveniently. Polarizer II and quarter-wave plate II are used to filter out unconverted circularly polarized light. When circularly polarized light is used to illuminate the metasurface, the complex amplitude distribution of two orthogonal polarized light fields can be arbitrarily controlled. Therefore, holographic 3D reproduction with large depth can be realized in each polarization state (LCP and RCP).
The output power of the laser (MRL-III-671, @ 671 nm) is 50 mW and it can be adjusted. The designed wavelengths of quarter-wave plate I and quarter-wave plate II are both at 671 nm, and the focal length of the lens is 30 cm. The microscope objective is GCO-2101, with a magnification of 4×, a working distance of 35 mm and a numerical aperture of 0.1. The four letters ‘N’, ‘O’, ‘C’ and ‘U’ are selected as the recorded 3D objects in meta-holography, in which the letters ‘N’ and ‘U’ located at a depth of 3 mm and 70 mm, respectively, are recorded as 3D object I with LCP, and the letters ‘O’ and ‘C’ located at a depth of 3 mm and 70 mm, respectively, are recorded as 3D object II with RCP. The letters ‘N’ and ‘O’ are at the same depth (the reconstruction distance is 3 mm), and the letters ‘C’ and ‘U’ are at the same depth (the reconstruction distance is 70 mm). In the experiment, the diffraction distance and reconstruction depth of the reconstructed image are the same. The model of the CCD is CANON 77D.
Reconstruction process
To separate the reconstructed image from the zero-order light, a blazed grating with a suitable angle needs to be encoded in the meta-hologram, and then the interference of stray light can be eliminated. Because theoretical full-wave simulations require large memory, full-wave simulation of the large-scale metasurface is difficult. Before fabricating the metasurface structure, we use physical optics method to simulate the holographic phase, and verify the experiment of coding blazed grating based on an SLM, so as to acquire the appropriate angle of the blazed grating. The depth range of meta-holographic 3D reconstruction is also verified (Supplementary Material S2 and S3).
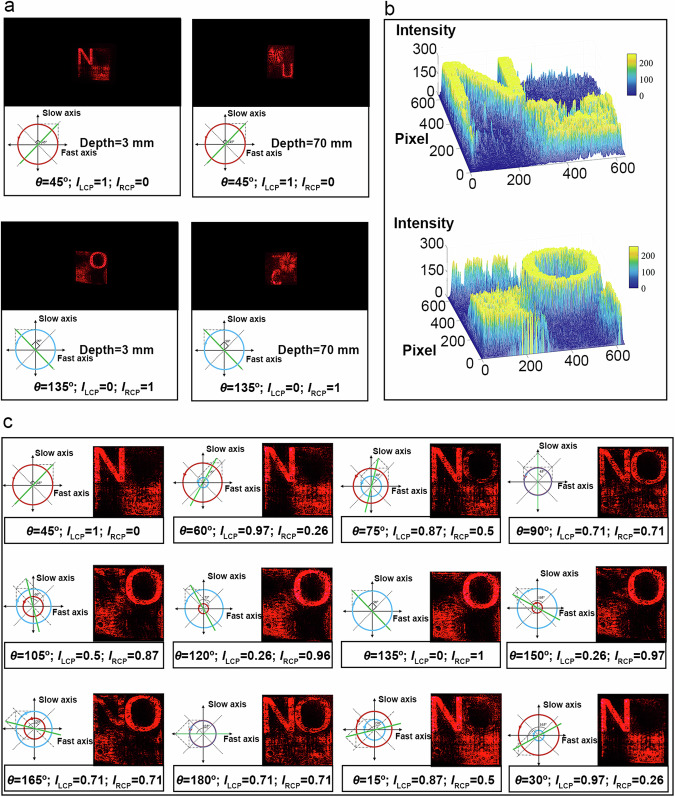
In holographic reproduction, polarizer I is kept unchanged. The angle between the fast axis direction of quarter-wave plate I and the polarization direction of polarizer I is set to be 45°. At this time, the light beam becomes left-handed circularly polarized after passing through quarter-wave plate I. As shown in Fig. 4a, when the diffraction distance is 3 mm, the holographic reconstructed image with the letter ‘N’ in focus can be seen on the CCD. When the diffraction distance is 70 mm, the holographic reconstructed image with the letter ‘U’ in focus can be seen on the CCD. When the included angle between the fast axis direction of quarter-wave plate I and the polarization direction of polarizer I is −45°, the light beam becomes right-handed circularly polarized after passing through quarter-wave plate I. At this time, the holographic reconstructed images of the letters ‘O’ and ‘C’ in focus can be obtained at the diffraction distances of 3 mm and 70 mm, respectively. It can be seen when light with different polarization states irradiates the metasurface, different 3D images with large depth can be reconstructed, which greatly increases the spatial information of meta-holography.
Fig. 4. Reconstructed results of the 3D meta-holography.
a Experimental results of large depth and controllable polarization meta-holography. b Intensity distributions of the optical field at a position 3 mm away from the meta-hologram under LCP/RCP irradiation. c Experimental results at a position 3 mm away from the meta-hologram when the relative angle between polarizer I and quarter-wave plate I is changed.
When the reconstructed image is obtained at a depth of 3 mm, the metasurface is located near the working distance of the microscopic objective. In this case, most of the energy of the holographic diffraction light field modulated by the metasurface can be efficiently received by the objective. However, when the reconstructed image is obtained at a depth of 70 mm, the metasurface is positioned far away from the working distance of the objective. In this case, only a small portion of the holographic diffraction light field modulated by the metasurface can be efficiently collected by the objective, thus significantly affecting the imaging quality. However, this is only the difference introduced during the optical reconstruction, it is not the intrinsic limitation of the approach. The simulation results demonstrate the high-quality reconstruction capability of the proposed method at a large-depth range.
Moreover, the zero-order light is completely separated from the reconstructed image when light irradiates the metasurface. Not only is the crosstalk of zero-order light eliminated, but also high-quality 3D reconstruction results of polarization meta-holography with large depth of field are obtained. The intensity distributions of the reconstructed image when the letters ‘N’ and ‘O’ are focused respectively are shown in Fig. 4b. It can be seen that the intensity distribution of the reconstructed image is uniform and the speckle noise is well suppressed. With the increase of diffraction distance, the energy of diffraction image decreases slightly, which is caused by the divergence of diffraction light. Since the pixel size of the designed metasurface is only 300 nm, the viewing angle of the 3D reconstructed image can reach 96° 28.
In order to verify the polarization characteristics, the reconstruction results with different polarization states of incident light are obtained by changing the fast axis direction of quarter-wave plate I, as shown in Fig. 4c. When the included angle between the fast axis of quarter-wave plate I and the polarization direction of polarizer I is θ = 45°, the incident light is LCP (the intensity of LCP incident on the metasurface ILCP = 1, and the intensity of RCP incident on the metasurface IRCP = 0). At this time, the CCD can only receive the holographic reconstructed image of ‘N’. With the change of θ, the intensity of LCP and RCP incident on the metasurface changes accordingly. The captured reconstruction results match the intensity of the corresponding incident circular polarization. With the increase of the included angle, the proportion of RCP gradually increases, CCD can receive the holographic reconstructed image of ‘O’ with a gradually increasing intensity. When the incident light is RCP, the CCD can only receive the holographic reconstructed image of ‘O’ (Video 1).
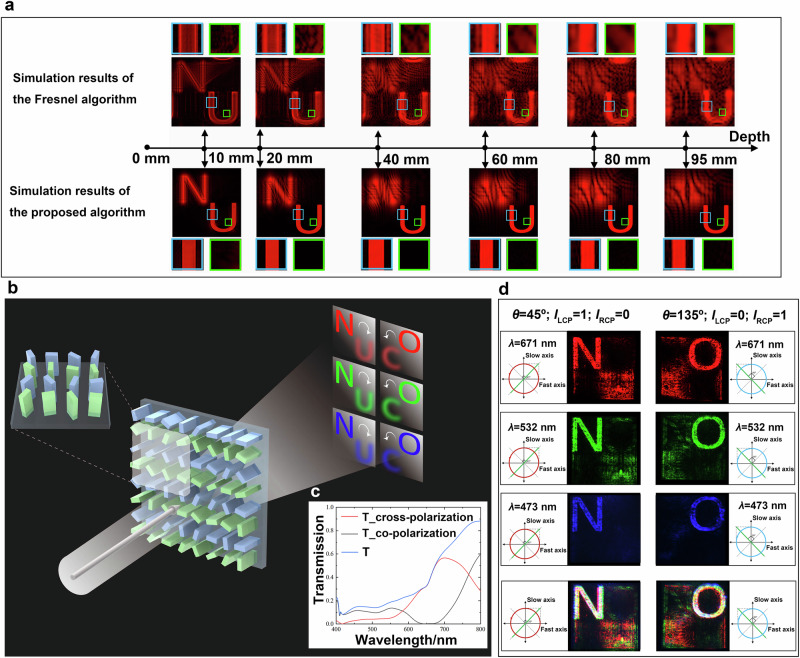
To verify the effectiveness of the proposed holographic angular spectrum diffraction method, the 3D reconstruction results by using different algorithms are simulated. The 3D object is composed of two letters ‘N’ and ‘U’ located at different depths, where the depth of ‘N’ is 3 mm. The Fresnel algorithm and the proposed method are used to calculate the meta-hologram respectively, and the holographic reconstruction results are shown in Fig. 5a. The scale on the coordinate axis is the depth value of the letter ‘U’, and the top row in Fig. 5a is the reconstruction results based on Fresnel algorithm. Affected by diffraction crosstalk, the reconstruction quality is poor and the intensity distribution of the reconstructed image is uneven. With the increase of depth, the reconstructed image of meta-hologram becomes blurred or even deformed under the influence of diffraction crosstalk. The depth range is limited to approximately 20 mm due to the crosstalk. In comparison, the reconstructed results based on the proposed holographic angular spectrum diffraction method (bottom row in Fig. 5a) show uniform brightness and no crosstalk even at a depth of 95 mm.
Fig. 5. Large depth and color 3D meta-holography.
a Large depth simulation results of the meta-hologram. b Schematic diagram of the color 3D meta-holography. c Transmittance of the metasurface with different wavelengths. d Experimental results of the meta-hologram with different wavelengths.
When the complex amplitude information is directly converted into pure phase information, conversion errors may occur. Different from the Fresnel method, the proposed method compensates the conversion errors by error diffusion algorithm, instead of directly extracting the phase from the complex amplitude information of the 3D object, thus circumventing the problem of uneven distribution of internal light field, as shown in the blue boxed areas in Fig. 5a. Besides, the under-sampling operation of meta-hologram in the discrete sampling process will introduce errors, leading to spectrum aliasing. The proposed method analyzes the mechanism of spectrum aliasing and realizes 3D reconstruction with ultra-large depth by constraining the frequency domain of the transfer function. As shown in the green boxed areas in Fig. 5a, with the increase of depth, the reconstructed image using the Fresnel method rapidly produces stray light in the central region of the letter “U”, which seriously affects the quality. In contrast, the corresponding regions by using the proposed method are almost unaffected by the depth.
Using the proposed method, we also verify the effect of color meta-holography at different wavelengths. Figure 5b is the schematic diagram of the color 3D meta-holography when light of different colors irradiates the metasurface. The transmittance of the metasurface under different wavelengths is shown in Fig. 5c. The left column of Fig. 5d shows the experimentally holographic reconstructed images when LCP light is used to irradiate the metasurface, in which ‘N’ is focused. The right column of Fig. 5d are the holographic reconstructed images when RCP light is used to irradiate the metasurface, in which ‘O’ is focused. High-quality holographic reconstruction has been achieved at different wavelengths with the highest transmittance of green light and the lowest transmittance of blue light. The intensity change of the reconstructed image is also consistent with the result of transmittance test. Thus, by using the proposed method, multi-color meta-holographic reconstruction in a single metasurface is achieved. The meta-hologram based on the angular spectrum diffraction can handle positional chromatic aberration and magnification chromatic aberration in holographic reconstruction. However, there is a challenge for it to handle axial chromatic aberration. When the meta-hologram is illuminated by RGB composite light sources, the gap between RGB holographic images with a depth of 3 mm is negligible, and white holographic reconstruction result can be obtained at this position. However, the gap between RGB holographic images with a depth of 70 mm becomes large, which makes it challenging to achieve high-quality white light holographic reconstruction (Supplementary Material S4). When the meta-hologram is irradiated with mismatched wavelengths laser, the axial displacement is directly proportional to the reconstruction distance and also depends on the ratio of wavelengths. Therefore, the proposed algorithm can realize white light holographic reconstruction at a close range.
To demonstrate the hologram density of the proposed method in 3D reconstruction more intuitively, nine objects located at different depths along the z direction are simulated, and the polarization states are set accordingly. As shown in Fig. 6, when LCP light is the incident light, the nine numbers “123456789” are reconstructed at nine different depths respectively. When RCP light is the incident light, the nine letters “ABCDEFGHI” are reconstructed at nine different depths respectively. The simulation results verify the feasibility of the proposed method in coding more dense holograms.
Fig. 6. 3D meta-holographic reconstruction results in different z-spaces.
a Reconstructed images at nine different depths under LCP irradiation. b Reconstructed images at nine different depths under RCP irradiation.
3D meta-holography with large depth and polarization function can increase the spatial information capacity in a new dimension, which has great application potential in the fields such as storage and encryption. Rapid advancement has been made in meta-holography with high information capacity36–38. Different from these methods, the proposed method develops a 3D meta-holography based on angular spectrum diffraction theory to break through the depth limitation. Combined with the proposed meta-hologram algorithm, more dense holograms with different ranges can be encoded in different z-spaces, and the depth is extended to the decimeter level. The proposed algorithm is unique, which realizes large depth reconstruction without sacrificing information in other dimensions such as polarization or wavelength. The fabricated metasurface structure is amorphous silicon based on geometric phase control. Our proposed method extends the angular spectrum diffraction theory to meta-holography, and uses the metasurface structure with independent polarization control to generate polarization-multiplexed 3D meta-hologram, thus realizing large-depth meta-holographic reconstruction in different polarization states.
Disscusion
In summary, we develop the angular spectrum diffraction theory into meta-holography, and use the metasurface structure with independent polarization control to create a unique methodology with large depth, high information capacity, and a polarization multiplexing capability. The fabricated amorphous silicon metasurface increases the depth range by 47.5 times and realizes 0.95 dm depth reconstruction for polarization independent and different color 3D meta-hologram in visible. These concurrent merits provide the proposed meta-holography a high potential for the realization of naked-eye 3D display, volumetric data storage, encryption and virtual and augmented reality.
Methods
Sample fabrication
Fabrication of the metasurface goes through the processes of silicon deposition, patterning, and etching. First, a 400-nm-thick amorphous silicon film is deposited on a 500-μm-thick quartz substrate with plasma enhanced chemical vapor deposition (PECVD). Then, after spin-coating a 100-nm-thick hydrogen silsesquioxane electron beam resist (HSQ, XR-1541) and a thin conductive protective coating (Electra 92, AR-PC 5092.02) on the silicon film, the desired pattern is imprinted on the resist via a standard electron beam lithography (Nanobeam Limited, NB5) and a development process in NMD-3 solution (concentration 2.38%) for 2 min. Finally, the sample is successfully obtained by transferring the pattern to the amorphous silicon film by inductively coupled plasma etching (ICP, Oxford Instruments, Oxford Plasma Pro 100 Cobra300) process.
Supplementary information
Acknowledgements
This work is supported by National Key Research and Development Program of China (2021YFB2802100), National Natural Science Foundation of China (62020106010, 62275009, U22A2079, 62175006), Strategic Priority Research Program of the Chinese Academy of Sciences (XDB0580000) and CAS Pioneer Hundred Talents Program.
Author contributions
D.W., R.N.J. and Q.H.W. conceived the project. D.W., Y.L.L. and R.N.J. proposed the idea, performed the simulations and conducted the experiments; X.R.Z., X.X., K.S., and S.W.W. fabricated the metasurface and analyzed the data; F.C.L., N.N.L., Z.J., C.L., Y.W.Z., W.L. and B.H.J. assisted in the verification experiments of meta-holography and manuscript revision. All authors discussed the results and commented on the paper.
Peer review
Peer review information
Nature Communications thanks Junsuk Rho and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
All key data that support the findings of this study are included in the article and its Supplementary Information. Additional datasets and raw measurements are available from the corresponding authors upon reasonable request.
Code availability
All relevant codes that support the findings of this work are available. And all have been uploaded to codeocean. https://codeocean.com/capsule/7666010/tree.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Di Wang, Yi-Long Li.
Contributor Information
Ruo-Nan Ji, Email: jiruonan@mail.sitp.ac.cn.
Qiong-Hua Wang, Email: qionghua@buaa.edu.cn.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-52267-9.
References
- 1.Rosen, J. et al. Non-scanning motionless fluorescence three-dimensional holographic microscopy. Nat. Photon.2, 190–195 (2008). [Google Scholar]
- 2.Hirayama, R. et al. A volumetric display for visual, tactile and audio presentation using acoustic trapping. Nature575, 320–323 (2019). [DOI] [PubMed] [Google Scholar]
- 3.Smalley, D. E. et al. A photophoretic-trap volumetric display. Nature553, 486–490 (2018). [DOI] [PubMed] [Google Scholar]
- 4.Fang, X. et al. Orbital angular momentum holography for high-security encryption. Nat. Photon.14, 102–108 (2020). [Google Scholar]
- 5.Wang, D. et al. Holographic capture and projection system of real object based on tunable zoom lens. PhotoniX1, 6 (2020). [Google Scholar]
- 6.Shi, L. et al. Towards real-time photorealistic 3D holography with deep neural networks. Nature591, 234–239 (2021). [DOI] [PubMed] [Google Scholar]
- 7.Blanche, P. A. et al. Holographic three-dimensional telepresence using large-area photorefractive polymer. Nature468, 80–83 (2010). [DOI] [PubMed] [Google Scholar]
- 8.Makey, G. et al. Breaking crosstalk limits to dynamic holography using orthogonality of high-dimensional random vectors. Nat. Photon.13, 251–256 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yu, H. et al. Ultrahigh-definition dynamic 3D holographic display by active control of volume speckle fields. Nat. Photon.11, 186–192 (2017). [Google Scholar]
- 10.Lee, J. et al. Time multiplexing technique of holographic view and Maxwellian view using a liquid lens in the optical see-through head mounted display. Opt. Express26, 2149–2159 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Sando, Y. et al. Holographic augmented reality display with conical holographic optical element for wide viewing zone. Light Adv. Manuf.3, 12 (2022). [Google Scholar]
- 12.Yaraş, F. et al. Circular holographic video display system. Opt. Express19, 9147–9156 (2011). [DOI] [PubMed] [Google Scholar]
- 13.Xiong, J. et al. Planar liquid crystal polarization optics for augmented reality and virtual reality: from fundamentals to applications. eLight1, 3 (2021). [Google Scholar]
- 14.Tay, S. et al. An updatable holographic three-dimensional display. Nature451, 694–698 (2008). [DOI] [PubMed] [Google Scholar]
- 15.Wang, D. et al. Large viewing angle holographic 3D display system based on maximum diffraction modulation. Light Adv. Manuf.4, 18 (2023). [Google Scholar]
- 16.Li, Y. L. et al. Tunable liquid crystal grating based holographic 3D display system with wide viewing angle and large size. Light Sci. Appl.11, 188 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Almeida, E. et al. Nonlinear metamaterials for holography. Nat. Commun.7, 12533 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li, S. Q. et al. Phase-only transmissive spatial light modulator based on tunable dielectric metasurface. Science364, 1087–1090 (2019). [DOI] [PubMed] [Google Scholar]
- 19.Li, L. et al. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun.8, 197 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kim, J. et al. Scalable manufacturing of high-index atomic layer-polymer hybrid metasurfaces for metaphotonics in the visible. Nat. Mater.22, 474–481 (2023). [DOI] [PubMed] [Google Scholar]
- 21.Kim, J. et al. A water-soluble label for food products prevents packaging waste and counterfeiting. Nat. Food5, 293–300 (2024). [DOI] [PubMed] [Google Scholar]
- 22.Kim, J. et al. One-step printable platform for high-efficiency metasurfaces down to the deep-ultraviolet region. Light Sci. Appl.12, 68 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kang, H. et al. Tailoring high-refractive-index nanocomposites for manufacturing of ultraviolet metasurfaces. Microsyst. Nanoeng.10, 53 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kim, J. et al. 8″ wafer-scale, centimeter-sized, high-efficiency metalenses in the ultraviolet. Mater. Today73, 9–15 (2024). [Google Scholar]
- 25.Moon, S. W. et al. Wafer‐scale manufacturing of near‐infrared metalenses. Laser Photonics Rev18, 2300929 (2024). [Google Scholar]
- 26.High, A. et al. Visible-frequency hyperbolic metasurface. Nature522, 192–196 (2015). [DOI] [PubMed] [Google Scholar]
- 27.Dorrah, A. H. et al. Metasurface optics for on-demand polarization transformations along the optical path. Nat. Photon.15, 287–296 (2021). [Google Scholar]
- 28.Zheng, G. et al. Metasurface holograms reaching 80% efficiency. Nat. Nano.10, 308–312 (2015). [DOI] [PubMed] [Google Scholar]
- 29.Jiang, Q. et al. When metasurface meets hologram: principle and advances. Adv. Opt. Photon.11, 518–576 (2019). [Google Scholar]
- 30.Bao, Y. et al. Full-colour nanoprint-hologram synchronous metasurface with arbitrary hue-saturation-brightness control. Light Sci. Appl.8, 95 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhang, X. et al. Polarization-independent broadband meta-holograms via polarization-dependent nanoholes. Nanoscale10, 9304–9931 (2018). [DOI] [PubMed] [Google Scholar]
- 32.Lin, R. et al. GaN metalens for pixel-level full-color routing at visible light. Nano Lett14, 764–781 (2021). [DOI] [PubMed] [Google Scholar]
- 33.Huang, L. L. et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun.4, 2808 (2013). [Google Scholar]
- 34.Gao, H. et al. Dynamic 3D meta-holography in visible range with large frame number and high frame rate. Sci. Adv.6, eaba8595 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.So, S. et al. Multicolor and 3D holography generated by inverse‐designed single‐cell metasurfaces. Adv. Mater.35, 2208520 (2023). [DOI] [PubMed] [Google Scholar]
- 36.Kim, J. et al. Dynamic hyperspectral holography enabled by inverse‐designed metasurfaces with oblique helicoidal cholesterics. Adv. Mater.36, 2311785 (2024). [DOI] [PubMed] [Google Scholar]
- 37.Xiong, B. et al. Breaking the limitation of polarization multiplexing in optical metasurfaces with engineered noise. Science379, 294–299 (2023). [DOI] [PubMed] [Google Scholar]
- 38.Kim, J. et al. Photonic encryption platform via dual-band vectorial metaholograms in the ultraviolet and visible. ACS Nano16, 3546–3553 (2022). [DOI] [PubMed] [Google Scholar]
- 39.Wu, P. C. et al. Versatile polarization generation with an aluminum plasmonic metasurface. Nano Lett17, 445–452 (2017). [DOI] [PubMed] [Google Scholar]
- 40.Huang, Y. W. et al. Aluminum plasmonic multicolor meta-hologram. Nano Lett15, 3122–3127 (2015). [DOI] [PubMed] [Google Scholar]
- 41.Chen, W. T. et al. High-efficiency broadband meta-hologram with polarization-controlled dual images. Nano Lett14, 225–230 (2014). [DOI] [PubMed] [Google Scholar]
- 42.Guo, X. et al. Full‐color holographic display and encryption with full‐polarization degree of freedom. Adv. Mater.34, 2103192 (2022). [DOI] [PubMed] [Google Scholar]
- 43.Wen, D. et al. Vectorial holograms with spatially continuous polarization distributions. Nano Lett21, 1735–1741 (2021). [DOI] [PubMed] [Google Scholar]
- 44.Matsushima, K. et al. Band-limited angular spectrum method for numerical simulation of free-space propagation in far and near fields. Opt. Express17, 19662–19673 (2009). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All key data that support the findings of this study are included in the article and its Supplementary Information. Additional datasets and raw measurements are available from the corresponding authors upon reasonable request.
All relevant codes that support the findings of this work are available. And all have been uploaded to codeocean. https://codeocean.com/capsule/7666010/tree.