Abstract
Host–pathogen coevolution is defined as the reciprocal evolutionary changes in both species due to genotype × genotype (G×G) interactions at the genetic level determining the outcome and severity of infection. While co-analyses of hosts and pathogen genomes (co-genome-wide association studies) allow us to pinpoint the interacting genes, these do not reveal which host genotype(s) is/are resistant to which pathogen genotype(s). The knowledge of this so-called infection matrix is important for agriculture and medicine. Building on established theories of host–pathogen interactions, we here derive four novel indices capturing the characteristics of the infection matrix. These indices can be computed from full genome polymorphism data of randomly sampled uninfected hosts, as well as infected hosts and their pathogen strains. We use these indices in an approximate Bayesian computation method to pinpoint loci with relevant G×G interactions and to infer their underlying interaction matrix. In a combined single nucleotide polymorphism dataset of 451 European humans and their infecting hepatitis C virus (HCV) strains and 503 uninfected individuals, we reveal a new human candidate gene for resistance to HCV and new virus mutations matching human genes. For two groups of significant human–HCV (G×G) associations, we infer a gene-for-gene infection matrix, which is commonly assumed to be typical of plant–pathogen interactions. Our model-based inference framework bridges theoretical models of G×G interactions with host and pathogen genomic data. It, therefore, paves the way for understanding the evolution of key G×G interactions underpinning HCV adaptation to the European human population after a recent expansion.
Keywords: population genomics, linkage disequilibrium, single nucleotide polymorphism, host–pathogen coevolution, G×G interactions
Introduction
Host–pathogen or host–parasite antagonistic interactions are pervasive in nature. Their relevance ranges from specific simple interactions underpinning devastating epidemics (Gilligan 2008; Tomley and Shirley 2009; Andreakos et al. 2022) up to the multitrophic interactions shaping ecosystems and microbiomes (Scanlan 2017). Coevolution is defined as the evolutionary change in one antagonist (host) in response to changes in the other antagonist (pathogen) and vice versa. At the genetic level, these changes are determined by genotype × genotype (G×G) interactions between a few (up to many) host and pathogen genes. Host genotypes differ in their resistance to pathogen strains which in turn differ in their infectivity (ability to infect and cause disease) on the given host genotypes. Host–pathogen G×G interactions are defined by their (i) genetic architecture (how many genes are involved?), (ii) specificity (which G×G interactions can yield a resistance phenotypic outcome?), and (iii) strength (what is the phenotypic outcome, full resistance up to severe infection?). Previous studies suggest that the number of loci involved varies between different host–pathogen systems and there are often epistatic interactions between loci (Dexter et al. 2023). Knowing the genetic architecture, specificity, and strength of G×G interactions is crucial for understanding and predicting the speed and outcome of coevolutionary dynamics (Gandon and Michalakis 2002; Boots et al. 2014; Tellier et al. 2014) and for disease management in agriculture and medicine.
The potentially devastating effects of infection prompted a wealth of genome-wide association studies (GWAS) to identify the genetic architecture (involved genes) of host–pathogen G×G interactions. Single-species GWAS are performed by associating genomic variants with a binary disease outcome: (i) infected versus noninfected hosts such as humans (Barreiro and Quintana-Murci 2010; Casanova and Abel 2021), invertebrates (Bento et al. 2017, 2020), and plants (Nemri et al. 2010; Pogoda et al. 2020; Demirjian et al. 2023), or (ii) infective/noninfective pathogens (Andras et al. 2020). With the growing availability of both host and pathogen genomic data, two types of joint GWAS (so-called co-GWAS) have been developed to identify significant G×G loci (Bartha et al. 2013; Bartoli and Roux 2017; Wang et al. 2018; Märkle et al. 2021). Experimental co-GWAS require a full experimental factorial design of reciprocal infections to assess the outcome of infection (phenotype) (Wang et al. 2018; Märkle et al. 2021). However, controlling for the genetic background and running controlled infection experiments is not feasible for human hosts and often difficult to achieve for nonmodel natural host–pathogen interactions. As an alternative, natural co-GWAS (Bartoli and Roux 2017; Märkle et al. 2021) jointly associate genome-wide polymorphism data of infected hosts with polymorphism data of their respective infecting pathogen strains (Bartha et al. 2013). Such natural co-GWAS have since been applied successfully to find associations between human genes and pathogen loci of HIV (Bartha et al. 2013), the hepatitis C virus (HCV) (Ansari et al. 2017), Streptococcus pneumoniae (Lees et al. 2019) and Plasmodium falciparum (Band et al. 2022) and to study interactions between Daphnia magna host and Pasteuria ramosa (Dexter et al. 2023).
Yet, deciphering the specificity and strength of the G×G interactions at the loci of interest has remained empirically out of reach for most host–pathogen systems. The specificity and strength of host–pathogen G×G interactions are classically summarized within the so-called infection matrix, which captures the extent to which each pathogen genotype successfully infects each host genotype (0 meaning full host resistance, and 1 meaning full host susceptibility, Fig. 1a,b). There is a wide range of possible infection matrices which differ in their levels of symmetry, specificity, and strength (Agrawal and Lively 2002; Gandon and Michalakis 2002; Boots et al. 2014). Throughout the article we will focus on five matrices of interest (Fig. 1b): (i) the generalist pathogen (P) infectivity/noninfectivity matrix () in which one pathogen genotype has a high infectivity on all host genotypes, (ii) the generalist host (H) resistance/susceptibility matrix () where one host genotype is highly resistant to all pathogen genotypes, (iii) the specific matching-alleles (MA) matrix () where each pathogen genotype is specialized to infect one host genotype as found in the D. magna–Pasteuria pathosystem (Luijckx et al. 2013), (iv) the specific gene-for-gene (GFG) matrix () were one host genotype is universally susceptible and one pathogen genotype is universally infective, and (v) a perfect inverse GFG matrix () where one host genotype is universally resistant and one pathogen genotype is universally noninfective (Fenton et al. 2009). GFG interactions have been mainly documented for plant–pathogen interactions (Thompson and Burdon 1992; Dybdahl et al. 2014). MA interactions have been long hypothesized to underlie the interactions between the human major histocompatibility complex (MHC) and mammalian immunity genes and corresponding pathogen genes (Hill et al. 1997; Dybdahl et al. 2014; Råberg 2023). Experimentally deciphering the infection matrix requires combinatorial infection assays of many host and pathogen genotypes (clones or isogenic lines with known allelic variants) in controlled conditions. Thus, it is prohibitive for most host–pathogen systems (but see Luijckx et al. 2013; Moury et al. 2021).
Fig. 1.
Schematic view of the principles of G×G interactions underlying host–pathogen coevolution and the characteristics of the sampling process. Our framework captures the effects of experimental and disease exposure sampling at a single time point of the coevolutionary dynamics. a) We assume an interaction between a biallelic host and a biallelic pathogen locus. b) The outcome of the interaction is summarized by a 2×2 infection matrix with host genotypes as rows and pathogen genotypes as columns. Some classic examples with extreme values are schematically depicted, namely the pathogen infectivity/noninfectivity (, yellow), matching-allele (, blue), inverse GFG (, dark green), host resistance/susceptibility (, light green), GFG (, purple), and neutral (, gray) matrix. c) Schematic representation of the infection process and the host’s status at the population level. In a homogeneous population, a proportion ϕ (the disease encounter rate) of hosts encounters pathogen infectious propagules at random, and a proportion does not (disease exposure sampling). Hosts with a solid outline (and circled in green) in the exposed class are resistant to the infection (appear as healthy) due to the specific form of the underlying infection matrix. d) Genomic studies are performed by taking a sample of healthy and infected hosts from the total population, generating a potential bias in sample allele frequencies compared to population allele frequencies (experimental sampling). On a population level, the frequencies of the host and pathogen alleles are determined by the coevolutionary process (coevolutionary sampling).
We propose and develop a framework that jointly uses genomic data of hosts and their pathogens from natural populations to detect the genes underpinning G×G interactions and infer the interactions’ specificity and strength. The model underlying our framework builds upon the classic theory of disease epidemiology and host–pathogen coevolution (Kermack and McKendrick 1927; Anderson and May 1982; May and Anderson 1983; Boots et al. 2009; Diekmann et al. 2013; Gandon et al. 2016; Buckingham and Ashby 2022) and explicitly accounts for three fundamental sampling processes in host and pathogen populations (Fig. 1c): (i) (co)evolutionary sampling (Dybdahl et al. 2014; MacPherson et al. 2018), (ii) disease exposure sampling, and (iii) experimental sampling. The first process is a result of coevolution itself, namely host and pathogen genotype frequencies fluctuate in space and time as a direct result of reciprocal selection (coevolution), genetic drift, mutations, and gene flow (Gandon and Michalakis 2002; Tellier et al. 2014). As a result, only a subset of all possible interactions between host and pathogen genotypes may be present at a given point in space and time (Fig. 1c) (Dybdahl et al. 2014; Tellier et al. 2014). Thus, the sampling of host and pathogen genotypes may be incomplete. This effect is a major hindrance for host (or pathogen) single-species GWAS as it decreases the statistical power when not accounting for the genetic heterogeneity of populations (MacPherson et al. 2018). Second, host genotypes need to encounter corresponding pathogen genotypes in order to get infected as a result of a specific G×G interaction. We refer to this process as disease exposure sampling. The likelihood of such encounters in natural populations is governed by the host and pathogen genotype frequencies (or densities), the host population size, and the disease transmission rate. These factors, in combination with the specific G×G matrix, determine the disease dynamics and the disease prevalence (that is, the number/proportion of infected hosts) at a given point in time. An observer cannot know if an uninfected host in a natural population had a pathogen exposure but is resistant, or if the host has never been in contact with pathogens (Fig. 1c,d). Third, sampling a limited number (subset) of host (infected and noninfected) and pathogen individuals (genotypes) from the entire population for experimental and genomic studies may further blur the true infection matrix (Fig. 1d), as the sampling may over- (or under)represent some G×G associations. The combination of these three sampling processes renders the inference of the underlying infection matrix a nontrivial task (Fig. 1). We argue that, so far, the consequences of these stochastic processes on the statistical power of natural co-GWAS are poorly understood. Specifically, we expect that these three processes generate variability in the sample allele frequencies. Thus, in addition to the previously reported effects of the coevolutionary dynamics and incomplete sampling of hosts and pathogen genotypes (MacPherson et al. 2018), the statistical power of GWAS and co-GWAS studies to detect G×G interactions would depend on the true (yet unknown) infection matrix, the probability of being exposed to potentially infective pathogens and the sampling scheme (infected and/or noninfected hosts).
In this study, we first derive four different indices based on host–pathogen coevolutionary theory which are jointly used to tackle the problem of inferring the significant G×G interactions and assess their infection matrices under the described stochastic processes. We aim to (i) pinpoint genes underlying G×G interactions, and (ii) infer the underlying infection matrix using these indices. The indices are incorporated as summary statistics into an approximate Bayesian computation (ABC) framework to jointly analyze genomes of noninfected hosts as well as infected hosts and their matching pathogens. We assess by stochastic simulations and via the power analysis of the ABC model choice procedure (leave-one-out cross-validation) if and how the statistical power of these indices to discriminate between different infection matrices is affected by the three mentioned sampling processes. We infer, as a proof of principle, the interaction matrices underpinning 535 biologically relevant G×G associations between human single nucleotide polymorphism (SNPs) and single amino acid polymorphisms (SAAPs) of HCV, using 451 infected individuals and the HCV sequences of the infecting strains (Ansari et al. 2017) complemented by 503 human genomes (The 1000 Genomes Project Consortium 2015). While our theoretical framework can be further refined, it encompasses the complexity of host–pathogen interactions and the relevant stochastic processes to be considered when designing and performing natural co-GWAS studies.
Results
Indices Capture Features of the Infection Matrices
We develop a simple theoretical model capturing the current state of an infection process in a host population of large size. The model underlying our framework builds upon the classic theory of disease epidemiology and coevolution (May and Anderson 1983; Gandon and Michalakis 2002; Boots et al. 2009, 2014; Buckingham and Ashby 2022), or population genetics host–pathogen coevolution models with frequency-dependent disease transmission (Leonard 1977; Tellier and Brown 2007; Tellier et al. 2014). It summarizes the outcome of various different types of infection processes as explicitly stated in (i) epidemiological models with density- or frequency-dependent disease transmission or (ii) population genetic models. We coin the term disease exposure sampling as the process by which only a fraction (<100%) of host individuals in the population is exposed to the disease. Our model is kept simple and does not account for (i) temporal epidemiological dynamics, or (ii) interactions between the host/pathogen allele frequencies and disease transmission dynamics (the so-called epidemiological feedback, May and Anderson 1983; Gandon and Michalakis 2002; Boots et al. 2009, 2014; Buckingham and Ashby 2022). The model focuses on the current state/outcome of an infection process at the time of sampling individuals for sequencing (see supplementary text S1, Supplementary Material online for a more detailed discussion). In other words, our disease exposure sampling does not refer to the process of epidemic development itself but to the stochastic inherent nature of disease transmission in a host population (with two types of hosts and two types of parasites/pathogens).
In short, the model assumes that biallelic hosts encounter biallelic pathogens at random (mass action principle) at a given disease encounter rate ϕ (supplementary table S1 and Supplementary text S1, Supplementary Material online) which we use as a proxy for disease exposure sampling. Thus, our model follows the assumption of the SI-type of models of disease contact being homogeneous and random (mean field approximation, May and Anderson 1983; Buckingham and Ashby 2022). We assume frequency-dependent disease transmission as we are only interested in the frequencies of the different alleles in the different infected and noninfected compartments. At the time of sampling host individuals for genomic analyses, the host population is split into two compartments, namely infected hosts (frequency ) and uninfected hosts (frequency ). The latter comprises hosts that either did not encounter pathogens or resisted infection when exposed to infectious propagules. Note, we implicitly assume here that hosts cannot encounter pathogens twice, and there is no immune memory present in the current population, i.e. from previous epidemics.
We denote the frequency of uninfected hosts of type i in the entire population as . Assuming biallelic host and pathogen genotypes, there is a maximum of four possible host–pathogen associations in the infected compartment. We denote the frequency of hosts with genotype i infected by pathogens genotype j in the entire population as and in the infected subpopulation as . These frequencies depend on the frequency of hosts of type i (), the initial frequencies of pathogen genotype j () before the disease exposure sampling, the infection matrix (α), and the rate ϕ at which hosts are exposed to the disease (for a summary and explanation of all parameters see supplementary table S1, Supplementary Material online).
We develop four indices that capture different aspects of a given G×G interaction matrix α (Fig. 1b). These indices combine information of host allele frequencies from infected hosts and their associated pathogen strains (pathogen allele frequencies) as in a natural co-GWAS (Bartha et al. 2013; Ansari et al. 2017; Bartoli and Roux 2017), as well as additional information of allele frequencies in a sample of noninfected hosts as in host GWAS (Barreiro and Quintana-Murci 2010; Nemri et al. 2010). Our first index, the cross-species association () index, is a cross-species analog of linkage disequilibrium (Fenton et al. 2009; Märkle et al. 2021) (also termed interlinkage Dexter et al. 2023). It assesses the association between the genotype of an infected host and the genotype of the pathogen strain infecting it. Thus, it is expected to capture information similar to that of natural co-GWAS. The host susceptibility () index compares allele frequencies in the infected versus noninfected host subsamples and is thus similar to host GWAS. The pathogen infectivity () assesses differences between pathogen allele frequencies (thus similar to pathogen GWAS). Finally, the host partitioning () index is designed to compare the allele frequency of one host genotype when infected by a particular pathogen genotype to its frequency in the noninfected part of the population. The index thus contains novel information (compared to co-GWAS and GWAS) on the asymmetry, specificity, and strength of the infection matrix. The four indices are defined as:
| (1) |
with:
| (2) |
Expressing these indices in terms of the population composition (supplementary table S1, Supplementary Material online) and the coefficients of an arbitrary 2×2 infection matrix we find (supplementary text S1, Supplementary Material online):
| (3) |
We first derive the population level values of these indices (Table 1, supplementary table S1, Supplementary Material online) for different infection matrices and initial host and pathogen allele frequencies. The frequencies provide us with a way to capture the performance of our indices for different unknown coevolutionary/epidemiological dynamics when genomic data have been only sampled at a single time point. This allows us to assess if the combination of these four indices is suitable to distinguish between different matrices. Note that our neutral matrix (all matrix elements 1, Fig. 1b) builds on the hypothesis that the G×G interaction of a given pair of host and pathogen loci is not relevant for the infection status. Studying the most extreme forms (all elements either 0 or 1) of these infection matrices we find that the behavior of the combination of our indices differs among infection matrices. For example, the index provides a clear distinction between the and matrix from all other matrices. Our results (Table 1) further highlight dependencies of the index values on the disease encounter rate (ϕ) and/or nonlinear relationships with pathogen allele frequencies prior to host exposure to pathogens (equation (3)). When we derive expressions of the index values for more general forms of the corresponding G×G matrices (supplementary table S1, Supplementary Material online) where infection matrix elements can deviate from 0 and 1, the expressions become more cumbersome (supplementary table S2, Supplementary Material online). These deviations reflect more quantitative disease resistance/susceptibility and account for the fact that the investigated matrices are expected to show some variation in natural systems. Yet, we still find that the combination of all four index values shows a differential behavior across the different infection matrices. Therefore, it appears that the combination of our four indices can be suitable to discriminate between different types of infection matrices. Extending these theoretical results, it is, in principle, possible to directly compute the values of the coefficients of the infection matrix () by simultaneously solving the set of all equations (equation (3)). However, this approach shows only reasonable results when the disease encounter rate is known and ∼50% and when population-level allele frequencies are known (which is in practice not the case because of the effect of the experimental sampling, Fig. 1d, supplementary text S1, Supplementary Material online).
Table 1.
Values of indices for different G×G matrices assuming host genotypes being fully susceptible to infection by pathogen genotype j when or fully resistant when . Note that the numerator of is zero for the , , and matrices with values 0/1. However, the normalization factor (denominator) also equals zero and invalidates the computations. These cases are not studied in natural co-GWAS because they correspond to either the host and/or the pathogen to be monomorphic.
| 0 | 0 | |||
| 0 | 1 | 0 | ||
| 0 | 0 | |||
| 0 | 0 | |||
| 0 | 0 |
Indices’ Behavior is Robust to Sampling Procedures
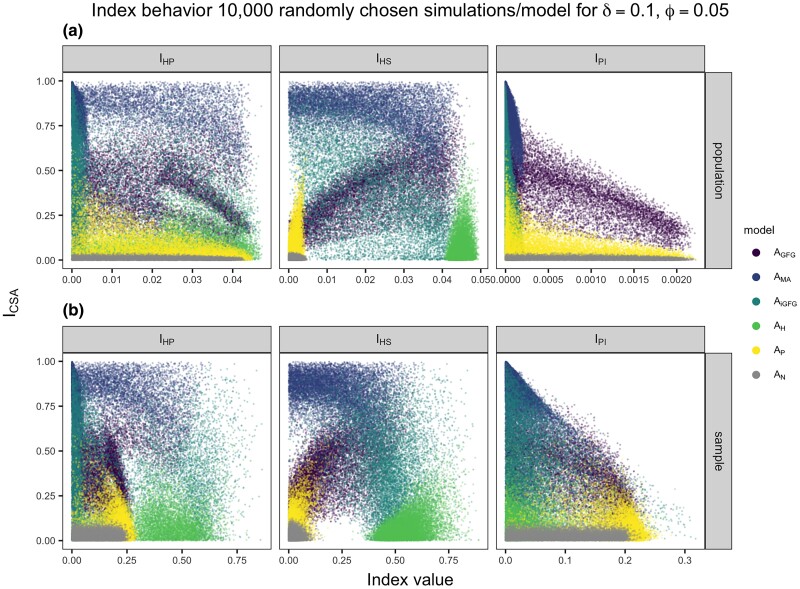
Our model accounts for the coevolutionary sampling via the interaction between allele frequencies and the infection matrix α, the disease exposure sampling via the disease encounter rate ϕ, and the experimental sampling via the sample size n. We can quantify the effect of the three above-mentioned sampling effects on the accuracy of inference using stochastic simulations. Also, we can assess if the joint behavior of the four developed indices allows for discriminating between different infection matrices under the combination of coevolutionary, experimental, and disease exposure sampling procedures (Fig. 1b,c) (for more details see Methods and supplementary text S1, Supplementary Material online). First, we explore the indices’ distributions over a wide range of minor allele frequencies ( between 0.05 and 0.5) and allow for random deviations of the matrix coefficients within a tolerance δ, which are reflective of coevolutionary sampling. These deviations are reflective of more quantitative forms of the investigated infection matrices and take into account their expected variability in host–pathogen interactions. Under coevolutionary sampling, the ranges of our , , and indices for the entire population are very small for small disease encounter rates. Yet, their combination still distinguishes well between different matrices (Fig. 2, top row). The distributions of the indices’ values become wider when taking a sample from the entire population with more or less equal amounts of noninfected and infected individuals (Fig. 2, bottom row). Encouragingly, the distributions of indices’ values differ between the different matrices for various disease encounter rates (Fig. 2) for population and experimental samples. More importantly, there is at least one combination of two or more indices (albeit not necessarily linear) for each G×G infection matrix, discriminating it from the neutral infection matrix (Fig. 2).
Fig. 2.
Distribution of values of indices’ pairs comprising (y axis) and one of the other indices , , or (x axis) for different infection matrices (, , , , , ) for a low disease encounter rate (). The population has size (population row) and a random sample of healthy and infected haploid individuals is taken (sample row). Results are shown for 10,000 simulations where , , and . The simulations are a randomly selected subset of the 50,000 simulations used in the ABC model choice.
We observe a strong dependency between the range of possible indices’ values and the disease encounter rate ϕ (compare Fig. 2, supplementary figs. S1 and S2, Supplementary Material online) which indicates the effect of the disease exposure sampling. Consistent with our theoretical results, the ranges of values for , , and are small for low disease encounter rates and increase with higher disease encounter rates (supplementary figs. S1 and S2, Supplementary Material online). Yet, for all three disease encounter rates the different matrices are distinguished by the combination of indices under the population sample. As for , we observe that taking a fixed sample from the entire population changes the range of observed index values in the sample compared to the population. This effect depends on the specific combination of (host and pathogen) sample sizes (Fig. 2, supplementary figs. S3 and S4, Supplementary Material online). When we consider a sampling scheme with 5% infected and 95% noninfected hosts (keeping the total number of samples to 951 hosts) for a disease encounter rate , the distribution of indices’ values becomes more narrow and more similar to that of the population sample. This potentially decreases the extent to which different matrices can be discriminated (supplementary fig. S4, Supplementary Material online). On the other hand, if we consider a sampling scheme with 95% infected and 5% noninfected hosts (keeping the total number of samples to 951 hosts) the range of indices’ values further broadens and becomes less similar to the population sample (supplementary fig. S3, Supplementary Material online). The difference in sample indices’ distributions reflects the effect of experimental sampling of infected hosts on top of the disease exposure sampling for a low disease encounter rate. Our results exemplify the, so far, largely ignored effects of the disease exposure and experimental sampling in natural co-GWAS and the importance of deriving optimal sampling schemes to overcome this interplay.
Increasing the infection matrix tolerance threshold (value of δ), and thus, allowing for a wider range of more quantitative forms of each infection matrix, increases the amount of overlap between the indices’ distributions. As a consequence, different matrices may be confounded (supplementary fig. S5, Supplementary Material online for δ varying between 0.1 and 0.3). In other words, choosing a low tolerance parameter generates a more stringent statistical test to disentangle between the neutral infection matrix and other matrices. This should decrease the rate of false positives (association and underlying matrices appearing to be biologically relevant, whereas these are, in fact, neutral).
An ABC Framework Allows to Infer the Infection Matrices
We then use these simulation results ( and ) in an ABC framework to infer the infection (G×G) matrix (neutral, MA, GFG,…) for a given association. Therefore, we use our four indices as ABC summary statistics. We consider the interaction between two loci to not be biologically relevant for a host–pathogen interaction if the ABC model choice procedure reveals the neutral matrix as the best (or equally best) model. We assess the statistical power of ABC model (matrix) choice by running a leave-one-out cross-validation (rejection algorithm, tolerance 0.05) based on randomly choosing 500 simulations from all simulations for a given infection matrix. For each of these simulations, we infer the best model using all simulations for all matrices (50,000 per matrix). We demonstrate that our ABC with our four indices as summary statistics can discriminate between all matrices (Table 2, supplementary tables S3 and S4, Supplementary Material online). It discriminates especially well between biologically relevant G×G matrices and the neutral matrix (under the most stringent threshold, supplementary tables S3 and S4, Supplementary Material online). The host resistance and the MA matrix can be well discriminated from all other matrices, whereas the pathogen infectivity and iGFG matrices may still be confounded with other matrices for some parts of the explored parameter space (Table 2). The pathogen infectivity matrix () is less distinguishable from the neutral matrix when the disease encounter rate (ϕ) is small. Here, one of the pathogen alleles exhibits a small frequency and, thus, a large bias in the disease exposure and empirical sampling. The inverse GFG matrix is hard to discern from other matrices when some of the host and pathogen allele frequencies are small. Then, up to three out of the four possible host–pathogen associations in the infected compartment are found in low proportions in the sample due to the specific structure of the matrix. Therefore, the variance in the frequency of these associations is higher than for other matrices, which in turn increases the likelihood that iGFG matrices appear like pathogen infectivity or resistance matrices.
Table 2.
Results of a leave-one-out ABC (rejection) cross-validation for 500 randomly chosen simulations per infection matrix under low disease encounter rate
| Inferred model | ||||||
|---|---|---|---|---|---|---|
| True model | ||||||
| 458 | 0 | 0 | 0 | 0 | 42 | |
| 16 | 361 | 24 | 46 | 6 | 47 | |
| 0 | 7 | 471 | 22 | 0 | 0 | |
| 2 | 52 | 63 | 244 | 138 | 1 | |
| 0 | 0 | 0 | 7 | 492 | 1 | |
| 114 | 39 | 0 | 0 | 0 | 347 | |
For each model 50,000 simulations are produced for , , , , , haploid, and haploid.
We conclude that explicitly accounting for various sampling effects within our ABC simulation framework by introducing corresponding parameter priors and given sample sizes allows us to disentangle between the different infection matrix models (Table 2, supplementary tables S3 and S4, Supplementary Material online). The statistical power of the ABC inference is thus determined by the combined effect of the sampling procedures yielding the indices’ values.
535 Biologically Relevant G×G Associations between Humans and HCV
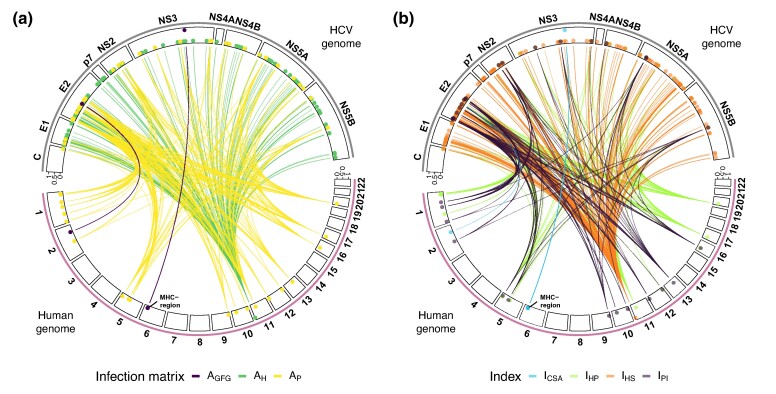
We now apply our ABC framework to a dataset of human diploid host sequences and their infecting HCV strains (Ansari et al. 2017) (the infected sample) and 503 diploid individuals of European ancestry from the 1,000 genomes project (Sudmant et al. 2015; The 1000 Genomes Project Consortium 2015) (the noninfected sample). In order to limit the confounding effects of population structure, we restrict our analysis of the HCV dataset to a subset of 451 individuals of European ancestry (PCA and fastSTRUCTURE analysis in supplementary figs. S6 and S7, Supplementary Material online, respectively, Ansari et al. 2017). As previously described (Ansari et al. 2017), we convert the viral nucleotide sequence data into single amino acid polymorphisms (biallelic SAAPs) data. We filter for a minor allele frequency (MAF) to maximize the power to disentangle between infection matrices. As highlighted above, below this frequency, several stochastic sampling effects significantly decrease the power to pinpoint relevant G×G associations. We compute our four indices for all possible pairwise associations between 326,520 human SNPs and 208 viral SAAPs. For the 800 top associations defined as exhibiting the highest values of our indices, we run the ABC model choice between the possible six infection matrices (, , , , , ). Our model choice results in 535 interactions, which differ from the neutral matrix based on a Bayes factor threshold of two () and for a matrix tolerance threshold (Fig. 3).
Fig. 3.
Genome-to-genome relevant associations from the ABC-model choice for all 535 associations ( to the neutral matrix). a) The 535 associations between host SNPs and pathogen SAAPs colored by the single best infection matrix. b) The 535 associations colored by the most informative index. The human chromosomes are shown on the bottom, and the virus contigs on the top. The second circle of lines indicates the number of closely linked sites sharing an association (most inner line, a single site, number of sites increasing to the outermost line). Infection matrices are color-coded as follows: , , . Indices are coded as , , , and .
We infer the most probable infection matrix (supplementary tables S5 to S8, Supplementary Material online) for each of the 535 associations and summarize the estimated infection matrices by index (Fig. 3, supplementary figs. S8 and S9, Supplementary Material online). We find two main groups of associations with an estimated GFG matrix (). One group includes associations between the viral HCV gene nonstructural protein 3 (NS3) and several SNPs on the human chromosome 6 falling into the MHC region. The second group consists of a single association between a SAAP on the HCV gene E2 and an SNP at the clathrin heavy chain linker domain containing 1 (CLHC1) gene on human chromosome 2. Furthermore, we find several associations with an estimated resistance matrix () between SAAPs at various viral genes and an SNP at the lymphocyte-specific protein 1 (LSP1) on chromosome 11. Finally, we also find several pathogen infectivity matrices () between 21 SNPs in the human genome and 45 SAAPs in the HCV genome. We also highlight that we do not find any associations which are indicative of a matching-allele () infection matrix, even when lowering the detection threshold (higher δ) and considering competing best models (supplementary tables S5 to S8, Supplementary Material online). Analyzing the details of these 535 biologically relevant G×G associations, we find few host sites (106), especially exhibiting GFG or resistance matrices, while pathogen SAAPs (221) exhibit chiefly infectivity matrices. We also compare our results to co-GWAS on the subset of 451 European infected individuals (and their 451 pathogen strains) following the previous analysis (Ansari et al. 2017) using plink. All tested associations with a high index are also picked up with our Bonferroni corrected co-GWAS (supplementary fig. S10, Supplementary Material online). In addition, 68 of these candidate associations also appear in the 104 top candidates from the Bonferroni corrected results obtained previously for the full dataset (supplementary fig. S11, Supplementary Material online, Ansari et al. 2017). We conclude that our ABC framework reveals relevant G×G associations but is more stringent than co-GWAS studies. Using our four indices, which capture different aspects of infection matrices, we are also able to reveal new associations which were not previously reported, especially potential human resistance alleles to HCV (under GFG and resistance matrices) and HCV infectivity alleles (under infectivity matrix).
Discussion
We derived four indices to tackle the problem of inferring the underlying infection matrix from host–pathogen association data. We developed some general predictions on the behavior of these indices, established their joint ability to discriminate between several infection matrices and used them successfully as summary statistics in an ABC framework to reveal infection matrices in a human host/HCV virus dataset. Our theoretical study is not only the first study attempting to establish the conceptual aspects of natural co-GWAS and the effect of various sampling procedures but also lays the ground for a methodological framework to infer the infection matrix using natural co-GWA set-ups. The predicted biologically relevant G×G interactions would need to be subsequently validated experimentally. Our theoretical model is based on and summarizes features of existing well-known models from epidemiological and coevolutionary theory (for example, Kermack and McKendrick 1927; Leonard 1977; Anderson and May 1982; May and Anderson 1983; Agrawal and Lively 2002; Gandon and Michalakis 2002; Boots et al. 2009, 2014; Diekmann et al. 2013 and reviews in Gandon et al. 2016; Ewald et al. 2020; Buckingham and Ashby 2022). The design of our indices allows us to draw inferences on the underlying infection matrix (Agrawal and Lively 2002; Boots et al. 2014; Dybdahl et al. 2014) and thus to optimally jointly analyze host and pathogen genomic interactions. In the following, we discuss the additional insights obtained in our proof of principle case study on the human–HCV interaction, present current limitations of the framework and its underlying model, and discuss future extensions along with general recommendations for conducting such studies in future.
Case Study: European Humans–HCV Interaction
As a proof of principle, we specifically present results on the interaction between European humans and HCV. Therefore, we tuned our method to study a sample size of 451 infected diploid humans (and their respective viral strains) and 503 noninfected European humans, and a known disease encounter rate of 0.05 (slightly higher than the disease prevalence of ∼3% previously reported Mohd Hanafiah et al. 2013; Petruzziello et al. 2016).
Inferred interaction matrices
We confirm a large number of associations between human and viral genes which were previously detected (Ansari et al. 2017). All observed associations at the MHC on chromosome 6 are associated with one viral site located at position 1,444 on the NS3 gene. Most likely, all these human sites are linked to alleles at the HLA genes as a result of high amount of linkage disequilibrium across the region (Bakker et al. 2006). HLA genes play a role in the adaptive immune response as they determine which viral peptides are presented to T cells. This process can drive viral evolution and result in the emergence of viral escape mutations, which have been previously identified for the NS3 gene (Merani et al. 2011; Ansari et al. 2017). We further detected a GFG interaction between the CLHC1 gene with an amino acid in the HCV gene E2. There is some empirical evidence that small interfering RNA-mediated clathrin heavy chain depletion affects endocytosis of HCV (Blanchard et al. 2006; Coller et al. 2009). Therefore, we speculate that the CLHC1 gene may be involved in such a process, and the inferred GFG-matrix might be a result of this process. Additionally, we found a putative resistance allele at the LSP1 gene, which is an F-actin-binding protein. This protein is involved in the regulation of various immune system functions, including lymphocyte activation, proliferation, and migration (Pulford et al. 1999). It also has been shown to play a role in endocytosis and transendothelial migration of leukocytes, allowing these to be recruited to the sites of inflammation (Liu et al. 2005; Walther et al. 2006). Studies demonstrating that the depletion of LSP1 significantly reduces the rate of endocytosis of HIV particles (Chauhan et al. 2014; Chauhan and Khandkar 2015) could suggest that this protein may also play a role in the endocytosis of HCV. On a side note, as for GWAS for host resistance, a significant allele association with the status of infection (infected versus uninfected) which would be inferred as a host resistance matrix, can also be interpreted as a locus significantly determining disease transmission (for example a locus enhancing the behavioral exposure to the disease). As mentioned above, empirical evidence for LSP1 rather points to a biological role of this gene in the infection mechanism of HCV.
Inferred matrices and HCV—European humans coevolution
Despite likely coevolving with humans over thousands of years in Africa, HCV has a very recent history of infection and spreading in the European human population (supplementary fig. S12, Supplementary Material online, Drummond et al. 2005; Ebranati et al. 2021). Therefore, the biologically most relevant SNP-SAAP associations should be interpreted in the light of the HCV virus adapting to existing standing genetic variation in the European population within the (approximately) last 150 years. Experimental results from a bacteria–phage coevolution interaction (Hall et al. 2011) indicate that initial coevolutionary dynamics are characterized by rapid fixation of advantageous alleles in hosts and pathogens (arms race dynamics Bergelson et al. 2001). The dynamics are then replaced by trench warfare dynamics (Stahl et al. 1999) with the maintenance of two or more alleles at the coevolving genes by balancing selection (Tellier et al. 2014). Our inferred asymmetric matrices (host resistance, pathogen infectivity, and GFG) likely indicate that we capture the initial dynamics of the interaction between humans and HCV in Europe. Asymmetric matrices are more likely to generate arms race dynamics, especially when population sizes are small (Agrawal and Lively 2002; Tellier and Brown 2007; Tellier et al. 2014). In this light, we interpret the finding of a resistance matrix at the LSP1 gene as an indication that resistance to HCV may be segregating in the human European population. Several mutations in the virus populations have likely been selected for overcoming this resistance allele (green lines in Fig. 3). In addition, several SAAPs with inferred infectivity matrices likely indicate that strains of HCV exhibit mutations allowing them to infect and match several host genes and alleles. In other words, there are virus strains with different infectivity ranges. Finally, the inferred GFG interactions indicate that the virus has evolved to overcome host recognition alleles at several MHC genes and at one gene on chromosome 2 (CLHC1). These human alleles likely provided initial resistance to HCV at the onset of the epidemics, which were overcome by subsequent mutations in the virus.
Current Limitations of Our Inference Framework
In the following, we discuss several main limitations of our current inference framework due to modeling assumptions: the choice of a simplified interaction model integrating over various types of epidemiological dynamics and focusing on the resulting pattern rather than the underlying process, the assumption of haploid hosts and pathogens, the sampling set-up, and allele frequencies at biallelic loci, and not accounting for epistatic interactions. We suggest that our results are rather conservative with a low rate of false negatives but likely missing possible relevant associations.
Disease exposure rate and the disease transmission process
We specifically focus on random disease transmission and low disease encounter rate which likely best describe HCV transmission dynamics in Europe (Mohd Hanafiah et al. 2013; Petruzziello et al. 2016). This allows us to account for the effect of the disease exposure sampling on the distribution of allele frequencies in the population and our experimental samples without specifying a corresponding wide prior for the disease encounter rate in the ABC. Our use of priors for host and pathogen allele frequencies considers that in empirical data the “true” allele frequencies prior to the infection process ( and in our model) are unknown. The observed sample allele frequencies represent the outcome of the joint interaction of disease encounter rate, the “true” but hidden allele frequencies and the infection matrix. We acknowledge that disease encounter rates might be less well-known for host–pathogen interactions involving nonmodel species. One way to tackle this limitation for nonmodel plant host–pathogen interactions would be to obtain estimates for the range of disease encounter rates from field data and include this range as an additional prior into the ABC simulations. However, based on our analytical results, we only expect this approach to be successful within our current framework if the corresponding estimated range of the disease encounter rate is relatively narrow.
Our simplified model summarizes the features of classic epidemiological (May and Anderson 1983; Gandon and Michalakis 2002; Boots et al. 2014; Buckingham and Ashby 2022) and coevolutionary (Leonard 1977; Tellier and Brown 2007; Tellier et al. 2014) models between biallelic hosts and biallelic pathogens at a single time point of the coevolutionary trajectory. Four main biological factors are not yet accounted for. First, additional epidemiological features more common to human diseases, such as large overlap between age classes and long-term immune memory, would decrease the statistical power of our ABC framework (similarly to decreasing the power of co-GWAS). Nonetheless, regarding the analysis of the HCV data, such bias is unlikely, as the incidence of the disease is rare, so only a few human individuals may exhibit such a memory effect. Second, we also acknowledge that our model is rather suited to study endemic diseases which do not present large variations of the disease encounter rate in time, as is likely the case for HCV. Third, our model does not suppose any interaction between the genetic composition of the host population (host allele frequencies) and the disease transmission, as we ignore the so-called epidemiological feedback (May and Anderson 1983; Boots et al. 2014; Buckingham and Ashby 2022). In an epidemiological setup, host and parasite allele frequencies do determine (in part) disease spread and the severity of an epidemic. As a result, some parts of our simulated parameter space may be unrealistic, and the efficiency of the ABC simulations could be improved by simulating a smaller parameter space with hyper-priors linking allele frequencies and disease encounter rate. However, the nature of the epidemiological feedback depends on the pathogen and host biology and genetics, and it is difficult to cover all cases in our proof of concept paper. Indeed, we suggest that for diseases with low disease incidence and peculiar transmission routes, such as HCV, the disease encounter rate is likely determined by biological (and environmental) factors largely independent of the host resistance composition (Tellier et al. 2014; Buckingham and Ashby 2022). Furthermore, there are numerous theoretical possibilities linking infection matrices and disease incidence, especially if we consider that several genes may be involved in determining host resistance to various parasite loci (epistasis) and loci can be multiallelic (more than biallelic). Thus, we conveniently (and to avoid bias) design our ABC framework (i.e. define priors) to be agnostic vis-à-vis the epidemiological dynamics. Fourth, we do not account for the possible host tolerance to infection or high parasite virulence of deadly diseases that kill hosts before these can be sampled. This latter case would present deviations from our model as the disease incidence does not reflect the true infection rates. The number of infected hosts would be underrepresented, thus biasing our indices and decreasing the statistical power of our ABC method. Note, however, that for some human diseases, pathogen strains can be sampled from dead bodies using ancient DNA techniques, which then would give information on the composition of the infected compartment. We are currently extending the modeling framework to study fast-changing devastating epidemics under a realistic epidemiological model.
Diploid host and dominance effect
A second critical point of our model is to assume the codominance of heterozygote alleles in the host with regard to the haploid pathogen genotype. We followed the previous haploid treatment of co-GWAS (Ansari et al. 2017) by duplicating the pathogen strain for each human diploid genome and performing all analyses on a haploid association model. This assumption simplifies our equations, avoids introducing a dominance parameter, and allows us to compare our results directly with those from previous co-GWAS. Nevertheless, the codominance assumption introduces noise in the statistical association between host and pathogen alleles and decreases the statistical power to discriminate neutral from nonneutral infection matrices. In other words, we may miss some relevant associations hidden by a host dominance effect for resistance or susceptibility.
Sample size and allele frequencies
We follow previous GWAS and co-GWAS approaches and assume sufficiently large sample sizes (several hundred individuals) to allow the detection of significant associations. As some of our indices rely on estimating the allele frequencies in the noninfected subsample and the infected subsample with comparatively small error, obtaining a sample that well reflects the population frequencies of genotypes/phenotypes in the entire population is crucial. Specifically, if the disease encounter rate is small, it is important to sample the infected part of the population well enough. Conversely, if the disease encounter rate is high, sufficient sampling of the noninfected part of the population becomes important. This emphasizes the importance of accounting for the interaction between sampling size and disease prevalence when devising sampling schemes in co-GWAS studies. Especially low sample sizes are very likely to produce biased allele and association frequencies in the sample and, hence, erroneous infection matrix estimates.
An inherent difficulty for any co-GWAS and our ABC is to confidentially detect associations which involve alleles with low frequencies. Therefore, we conservatively restricted our testing to loci with a MAF to avoid excess false positives. However, coevolutionary dynamics can transiently decrease allele frequencies or maintain alleles at low frequencies as a result of negative indirect frequency-dependent selection (Tellier and Brown 2007; Tellier et al. 2014; MacPherson et al. 2018). The chosen high MAF means that we also are less likely to detect genes under arms race dynamics with very high or very low allele frequencies, while we overrepresent alleles at intermediate frequencies (possibly under trench warfare dynamics or balancing selection). Therefore, we speculate that our ABC method can be further improved by incorporating sample allele frequencies as additional summary statistics and using association data from several time points. We expect the latter to help better track the allele frequency changes over time, which directly result from the coevolutionary dynamics and the underlying infection matrix.
Two further current limitations of our model (and all co-GWAS) are multilocus infection matrices and epistatic effects. We classify sites as being biallelic loci for convenience in building 2×2 interaction matrices and to allow comparison to previous co-GWAS results (Ansari et al. 2017). While theoretically, it is possible to include more than two alleles per site, the number of parameters of the infection matrix to be estimated may become prohibitive beyond a 3×3 matrix. We currently duplicate triallelic sites into different combinations of biallelic sites, which likely reduces the statistical power to detect an association if these alleles present different resistance/infectivity effects, especially under epistatic associations. Indeed, epistatic interactions between several loci have been shown to underlie disease resistance phenotypes in species such as Daphnia (Luijckx et al. 2013). By integrating such knowledge of epistatic interactions, the results of the co-GWAS could recently be improved, and additional genes of interactions discovered (Dexter et al. 2023). Integrating time-sampled data, additional summary statistics, and the effect of epistasis (for biallelic and triallelic sites) between host (and pathogen) loci into our framework constitute the topic of future work.
Future Extensions of the Current Framework
Time-series genomic data
We speculate that extending our inference framework to include data sampled from different time points can improve the accuracy to elucidate the speed and timing of coevolution and changes in the G×G interactions at the genetic level. One key prediction from coevolutionary theory is that due to various stochastic and selective processes, the number of genes under coevolution and the corresponding infection matrices are subject to change over time (Boots et al. 2014; Dybdahl et al. 2014) with varying degrees of asymmetry (Agrawal and Lively 2002; Gandon and Michalakis 2002). This, in turn, generates different coevolutionary dynamics in time (arms race and trench warfare dynamics, respectively, Gandon et al. 2008; Tellier et al. 2014). Having data from different time points at hand likely helps to track more accurately allele and association frequencies over time. We speculate that such temporally resolved genomic data help to better characterize the coevolutionary cycles over time and, thus, to narrow down the potential parameter space generating such dynamics and, ultimately, to identify potential shifts in the interaction matrices over time. In the long term, coevolution between HCV and other human populations, SNP × SAAP interactions may be characterized by infection matrices promoting trench warfare dynamics or balancing selection. These include (i) symmetric MA interactions, or (ii) asymmetric GFG interactions with the necessary, but not sufficient (Tellier and Brown 2007; Tellier et al. 2014) condition of costs of resistance and infectivity existing at these coevolving loci. Applying our inference framework to other diseases with a range of short to long-term coevolutionary histories would shed light on the speed of coevolution between humans and their viruses (Ghafari et al. 2021) and the underlying coevolutionary dynamics.
Accounting for population structure
It is well known from the GWAS literature that spatial structure in the host and pathogen samples can affect and distort the power to detect associations. Therefore, we restricted our analysis to a single population (European) without any obvious population substructure, especially between infected and noninfected hosts (supplementary figs. S6 and S7, Supplementary Material online). Our results align with and are more conservative than the previous co-GWAS (Ansari et al. 2017) on the same dataset (supplementary figs. S10 and S11, Supplementary Material online). Therefore, we are confident that our framework is conservative and stringent and exhibits a low rate of false positives. In addition, recent studies demonstrate the usefulness of using local population rather than widespread sampling in a GWAS setting (Gloss et al. 2022). Accounting for spatial structure covariates and kinship matrix in our ABC framework is the topic of future work.
In conclusion, we built an ABC integrative method based on four indices as summary statistics. These indices combine ideas from host or pathogen GWAS with those of host–pathogen co-GWAS and additional information from noninfected hosts. Our framework is based on a widely applicable theoretical infection model. It also considers various sampling procedures defining observed host and pathogen allele frequencies in empirical samples, which allows us to define a threshold for detecting biologically relevant G×G associations in a Bayesian framework. While the current framework is incomplete, it lays the foundation for a more theoretically motivated investigation of the limits and strengths of co-GWAS studies and tackles the long-standing problem of inferring the interaction matrix underlying host–pathogen interactions. In general, the ideas of our framework are not limited to studying host–pathogen interactions, but also applicable to other G×G interactions, such as between hosts and mutualistic symbionts or between chloroplasts/mitochondria × nuclear genes interactions.
Methods
Definition of Indices
The index is calculated based on the frequencies of host/pathogen genotype combinations in the infected subpopulation/sample. We define the frequency of host genotype i infected by pathogen genotype j among all infected individuals as (). The is, therefore, utilizing information which is contained in natural co-GWAS data.
| (4) |
By analogy with the linkage disequilibrium measure in population genetics, we normalize the index by the square root of the product of all infected host and pathogen allele frequencies.
| (5) |
We define the genotype frequencies of uninfected hosts of type i in the population/sample as . Individuals can be uninfected due to two reasons: (i) they have not been exposed to the pathogen , or (ii) they had a pathogen encounter but resisted infection . We lump these two frequencies into a single frequency as in a natural population it is usually impossible to tell apart the difference.
The , , and indices are defined as follows:
| (6) |
| (7) |
| (8) |
with
| (9) |
We derived expressions for these indices for a single point in time given the initial host genotype frequencies , pathogen genotype frequencies , a disease encounter rate ϕ, and a given infection matrix α (see supplementary text S1, Supplementary Material online).
Stochastic Simulations
Next, we assessed by stochastic simulations the effect of three types of stochastic processes on the behavior of the indices for all matrices in Table 1: (i) varying host and pathogen alleles frequencies and deviations of the matrix elements from the extreme values 0 and 1, (ii) random sampling of a fixed number healthy and infected individuals from a population of size N, and (iii) small (), intermediate () or large disease encounter rates (). The simulation scheme worked as follows. For a given matrix, we first randomly chose one of the possible assignments of α values (0 or 1) to the matrix elements (two possibilities for and four possibilities for , see supplementary text S1, Supplementary Material online). Second, after assigning 0s or 1s to the matrix elements, we replaced each element by randomly drawing a value from a corresponding uniform distribution . Equally, we replaced each element by drawing from a uniform distribution (supplementary text S1, Supplementary Material online). The initial host frequencies and pathogen for each simulation are both independently drawn from a uniform distribution . Based on the resulting matrix and initial host and pathogen frequencies, we calculated the frequencies of all possible infected and healthy host phenotypes in the entire population and the respective subpopulation ( for infected, for healthy) (equations in supplementary table S2, Supplementary Material online). We then randomly picked a sample of haploid infected individuals (drawn from a multinomial distribution ) and a sample haploid healthy individuals (drawn from a binomial distribution ). These sample sizes have been chosen to reflect the sample sizes for our empirical dataset. Based on recommendations for ABC simulation of a multidimensional parameter space (Csillery et al. 2012) of dimension six (frequency of host allele 1, frequency of pathogen allele 1, and the four infection matrix coefficients with priors values constrained by the matrix type and the value of δ), we then generated 50,000 simulations for each matrix for all possible combinations of and .
ABC Leave-One-Out Cross-Validation for Model Selection
We first run a leave-one-out cross-validation to test the suitability of ABC model choice, using our four indices as summary statistics, to distinguish between different infection matrices. Leave-one-out cross-validation was run separately for each combination of ϕ and δ for a cross-validation sample of size 500 using the function cv4postpr in the R-package abc (rejection algorithm, ) (Csillery et al. 2012). Note that the ABC tolerance is here the threshold for accepting simulations in the ABC framework, and is not related to the parameter δ which accounts for more quantitative forms of the investigated infection matrices. As the parameters were tuned for the HCV dataset, we then reused this simulated dataset for inference from real data.
Application to Human Data
In the next step, we combined two existing human datasets to apply and test our framework. For the infected sample, we used human genome-wide genotype data and HCV whole-genome sequence data from Ansari et al. (2017). These data were collected from a total of 541 patients infected by HCV genotypes 2 and 3. We only used a subset of 451 humans of European ancestry to prevent confounding effects of population structure. For the pathogen genome information, we used the viral (nucleotide and protein) data from Ansari et al. (2017) from NCBI GenBank (accessions KY620313-KY620880). Following Ansari et al. (2017), we generated whole-genome viral consensus sequences (nucleotide and protein) for each patient using MAFFT (v.7.429) (Katoh et al. 2002). Future details of how we processed the virus data for our analysis are given in supplementary text S1, Supplementary Material online. For the noninfected sample, we used genotype data from the 1,000 Genomes Project Phase 3 (The 1000 Genomes Project Consortium 2015). We used the 503 samples from five subpopulations of European ancestry and therefore, retrieved vcf-data from 91 individuals from England and Scotland (GBR), 99 Finnish individuals (FIN), 99 Utah residents with Northern and Western European ancestry (CEU), 107 Spanish individuals (IBS), and 107 Italian individuals (TSI) for a total of 503 genomes (details in supplementary text S1, Supplementary Material online). In order to check for population stratification in the infected and uninfected European human sample, a fastSTRUCTURE analysis was conducted using default options (Raj et al. 2014).
Co-GWAS
We run a natural co-GWAS with PLINK2 (Purcell et al. 2007; Chang et al. 2015) on the data using a logistic regression with the firth-fallback option. This analysis assumes an additive genetic model, excluding dominance effects. For each regression, we used the presence of a particular amino acid at a given position in the viral alignment as a response variable and the genotype at a given human SNP as the genotype. To account for multiple testing, we calculated several P-value adjustments using the --adjust option of PLINK2. We incorporated sex, human PC1–PC3 and virus PC1–PC10 as covariates in the PLINK co-GWAS.
Index Calculation with Application to the HCV Data
We obtained frequencies for each host–virus association from the infected human dataset using PLINK2 and vcftools v0.1.17 (Danecek et al. 2011). We also extracted the frequencies of alleles in the noninfected human subsample. Combining these frequencies, we calculated all of our four indices using equations (4), (6), (7), and (8) with customized R-scripts. After that, we retrieved a summary table with the top outlier associations for each index.
Model Choice for the Top Association Candidates
We selected the associations with the 200 highest values for each of our indices from the human/HCV dataset. For each of these 800 associations, we run ABC model choice using the function postpr(…,tol=0.05, method=“rejection”) from the R-package abc v.2.2.1 (Csillery et al. 2012) and using all matrix simulations for , and for a sample of healthy and infected individuals. Based on the model choice results we assigned a nonneutral matrix to a given association whenever the model with the highest Bayes factor was a single nonneutral model/matrix, and the Bayes factor compared to the neutral matrix was larger than 2.
Supplementary Material
Acknowledgments
The authors thank Joy Bergelson, Dieter Ebert, and Lars Raberg for comments on an earlier version of the manuscript.
Contributor Information
Hanna Märkle, Population Genetics, Department of Life Science Systems, School of Life Sciences, Technical University of Munich, Freising 85354 Germany; Center for Genomics and Systems Biology, New York University, New York, NY 10003, USA.
Sona John, Population Genetics, Department of Life Science Systems, School of Life Sciences, Technical University of Munich, Freising 85354 Germany.
Lukas Metzger, Population Genetics, Department of Life Science Systems, School of Life Sciences, Technical University of Munich, Freising 85354 Germany.
STOP-HCV Consortium, Nuffield Department of Medicine, Peter Medawar Building for Pathogen Research, University of Oxford, Oxford, UK.
M Azim Ansari, Nuffield Department of Medicine, Peter Medawar Building for Pathogen Research, University of Oxford, Oxford, UK.
Vincent Pedergnana, Laboratoire MIVEGEC (UMR CNRS 5290, UR IRD 224, UM), Montpellier, France.
Aurélien Tellier, Population Genetics, Department of Life Science Systems, School of Life Sciences, Technical University of Munich, Freising 85354 Germany.
STOP-HCV Consortium:
Eleanor Barnes, Emma Hudson, Paul Klenerman, Peter Simmonds, Chris Holmes, Graham Cooke, Geoffrey Dusheiko, John McLauchlan, Mark Harris, William Irving, Philip Troke, Diana Brainard, John McHutchinson, Charles Gore, Rachel Halford, Graham R Foster, and Cham Herath
Supplementary Material
Supplementary material is available at Molecular Biology and Evolution online.
Author Contributions
H.M., S.J., and A.T. designed the project; H.M., S.J., and A.T. developed the model; H.M., S.J., and L.M. performed the simulations, L.M. performed the data analysis; H.M., S.J., and L.M. wrote the manuscript with support from A.T. STOP-HCV consortium, M.A.A., and V.P. obtained and preprocessed the sequence data before making them available.
Funding
AT acknowledges support from the Deutsche Forschungsgemeinschaft project numbers 274542535 (TE809/3) and 221691301 (TE809/6) within the Priority Program SPP1819 “Rapid adaptation”. The data acquisition was funded by a grant from the Medical Research Council (MRC) (MR/K01532X/1; to the STOP-HCV Consortium). E.B. is funded by the NIHR Oxford BRC. M.A.A. is jointly supported by the Royal Society and the Wellcome Trust (Sir Henry Dale Fellowship, 220171/Z/20/Z).
STOP-HCV Consortium
List of members and affiliations: Eleanor Barnes, Emma Hudson, Paul Klenerman, and Peter Simmonds (Nuffield Department of Medicine and the NIHR Oxford BRC, Peter Medawar Building for Pathogen Research, University of Oxford, Oxford, UK); Chris Holmes (Department of Statistics, University of Oxford, Oxford, UK); Graham Cooke (Wright-Fleming Institute, Imperial College London, London, UK); Geoffrey Dusheiko (Institute of Liver Studies, King’s College Hospital NHS Foundation Trust, London, UK); John McLauchlan (MRC-University of Glasgow Centre for Virus Research, Glasgow, UK); Mark Harris (School of Molecular and Cellular Biology, Faculty of Biological Sciences and Astbury Centre for Structural Molecular Biology, University of Leeds, Leeds, UK); William Irving (University of Nottingham, Queen’s Medical Centre, Nottingham, UK); Philip Troke (Gilead Sciences Ltd., London, UK); Diana Brainard and John McHutchinson (Gilead Sciences, Foster City, CA, USA); Charles Gore and Rachel Halford (Hepatitis C Trust, London, UK); Graham R. Foster (Queen Mary University of London, London, UK); Cham Herath (Gilead Sciences, Middlesex, UK).
Data availability
The scripts underlying this article are available in the GitLab repository https://gitlab.lrz.de/population_genetics/cogenomics_method. The genomic data can be obtained upon request to the STOP-HCV consortium (https://www.expmedndm.ox.ac.uk/stop-hcv). The viral (nucleotide and protein) data are available from NCBI GenBank (accessions KY620313-KY620880). Data from the 1,000 Genomes Project Phase 3 are available from the project webpage: https://www.internationalgenome.org/category/phase-3/.
References
- Agrawal A, Lively CM. Infection genetics: gene-for-gene versus matching-alleles models and all points in between. Evol Ecol Res. 2002:4(1):91–107. [Google Scholar]
- Anderson RM, May RM. Coevolution of hosts and parasites. Parasitology. 1982:85(2):411–426. 10.1017/S0031182000055360. [DOI] [PubMed] [Google Scholar]
- Andras JP, Fields PD, Du Pasquier L, Fredericksen M, Ebert D. Genome-wide association analysis identifies a genetic basis of infectivity in a model bacterial pathogen. Mol Biol Evol. 2020:37(12):3439–3452. 10.1093/molbev/msaa173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andreakos E, Abel L, Vinh DC, Kaja E, Drolet BA, Zhang Q, O’farrelly C, Novelli G, Rodríguez-Gallego C, Haerynck F, et al. A global effort to dissect the human genetic basis of resistance to SARS-CoV-2 infection. Nat Immunol. 2022:23(2):159–164. 10.1038/s41590-021-01030-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ansari MA, Pedergnana V, LC Ip C, Magri A, Von Delft A, Bonsall D, Chaturvedi N, Bartha I, Smith D, Nicholson G, et al. Genome-to-genome analysis highlights the effect of the human innate and adaptive immune systems on the hepatitis C virus. Nat Genet. 2017:49(5):666–673. 10.1038/ng.3835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakker P, McVean G, Sabeti P, Miretti M, Green T, Marchini J, Ke X, Wijmenga-Monsuur A, Whittaker P, Delgado M, et al. A high-resolution HLA and SNP haplotype map for disease association studies in the extended human MHC. Nat Genet. 2006:38(10):1166–1172. 10.1038/ng1885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Band G, Leffler EM, Jallow M, Sisay-Joof F, Ndila CM, Macharia AW, Hubbart C, Jeffreys AE, Rowlands K, Nguyen T, et al. Malaria protection due to sickle haemoglobin depends on parasite genotype. Nature. 2022:602(7895):106–111. 10.1038/s41586-021-04288-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barreiro LB, Quintana-Murci L. From evolutionary genetics to human immunology: how selection shapes host defence genes. Nat Rev Genet. 2010:11(1):17–30. 10.1038/nrg2698. [DOI] [PubMed] [Google Scholar]
- Bartha I, Carlson JM, Brumme CJ, McLaren PJ, Brumme ZL, John M, Haas DW, Martinez-Picado J, Dalmau J, López-Galíndez C, et al. A genome-to-genome analysis of associations between human genetic variation, HIV-1 sequence diversity, and viral control. eLife. 2013:2:e01123. 10.7554/eLife.01123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartoli C, Roux F. Genome-wide association studies in plant pathosystems: toward an ecological genomics approach. Front Plant Sci. 2017:8:763. 10.3389/fpls.2017.00763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bento G, Fields PD, Duneau D, Ebert D. An alternative route of bacterial infection associated with a novel resistance locus in the Daphnia–Pasteuria host–parasite system. Heredity. 2020:125(4):173–183. 10.1038/s41437-020-0332-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bento G, Routtu J, Fields PD, Bourgeois Y, Du Pasquier L, Ebert D. The genetic basis of resistance and matching-allele interactions of a host-parasite system: the Daphnia magna-Pasteuria ramosa model. PLoS Genet. 2017:13(2):e1006596. 10.1371/journal.pgen.1006596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergelson J, Kreitman M, Stahl EA, Tian D. Evolutionary dynamics of plant R-genes. Science. 2001:292(5525):2281–2285. 10.1126/science.1061337. [DOI] [PubMed] [Google Scholar]
- Blanchard E, Belouzard S, Goueslain L, Wakita T, Dubuisson J, Wychowski C, Rouillé Y. Hepatitis C virus entry depends on clathrin-mediated endocytosis. J Virol. 2006:80(14):6964–6972. 10.1128/JVI.00024-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boots M, Best A, Miller MR, White A. The role of ecological feedbacks in the evolution of host defence: what does theory tell us?. Phil Trans R Soc B. 2009:364(1513):27–36. 10.1098/rstb.2008.0160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boots M, White A, Best A, Bowers R. How specificity and epidemiology drive the coevolution of static trait diversity in hosts and parasites. Evolution. 2014:68(6):1594–1606. 10.1111/evo.2014.68.issue-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckingham LJ, Ashby B. Coevolutionary theory of hosts and parasites. J Evol Biol. 2022:35(2):205–224. 10.1111/jeb.v35.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casanova J-L, Abel L. Lethal infectious diseases as inborn errors of immunity: toward a synthesis of the germ and genetic theories. Annu Rev Pathol. 2021:16(1):23–50. 10.1146/pathmechdis.2021.16.issue-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang CC, Chow CC, Tellier LC, Vattikuti S, Purcell SM, Lee JJ. Second-generation PLINK: rising to the challenge of larger and richer datasets. GigaScience. 2015:4(1):7. 10.1186/s13742-015-0047-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chauhan A, Khandkar M. Endocytosis of human immunodeficiency virus 1 (HIV-1) in astrocytes: a fiery path to its destination. Microb Pathog. 2015:78:1–6. 10.1016/j.micpath.2014.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chauhan A, Mehla R, Vijayakumar TS, Handy I. Endocytosis-mediated HIV-1 entry and its significance in the elusive behavior of the virus in astrocytes. Virology. 2014:456–457:1–19. 10.1016/j.virol.2014.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coller KE, Berger KL, Heaton NS, Cooper JD, Yoon R, Randall G. RNA interference and single particle tracking analysis of hepatitis C virus endocytosis. PLoS Pathog. 2009:5(12):e1000702. 10.1371/journal.ppat.1000702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csillery K, François O, Blum MGB. abc: an R package for approximate Bayesian computation (ABC). Methods Ecol Evol. 2012:3(3):475–479. 10.1111/j.2041-210X.2011.00179.x. [DOI] [Google Scholar]
- Danecek P, Auton A, Abecasis G, Albers CA, Banks E, DePristo MA, Handsaker RE, Lunter G, Marth GT, Sherry ST. The variant call format and VCFtools. Bioinformatics. 2011:27(15):2156–2158. 10.1093/bioinformatics/btr330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demirjian C, Vailleau F, Berthomé R, Roux F. Genome-wide association studies in plant pathosystems: success or failure? Trends Plant Sci. 2023:28(4):471–485. 10.1016/j.tplants.2022.11.006. [DOI] [PubMed] [Google Scholar]
- Dexter E, Fields PD, Ebert D. Uncovering the genomic basis of infection through co-genomic sequencing of hosts and parasites. Mol Biol Evol. 2023:40(7):msad145. 10.1093/molbev/msad145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diekmann O, Heesterbeek H, Britton T. Mathematical tools for understanding infectious disease dynamics. 7. Princeton, USA: Princeton University Press; 2013. [Google Scholar]
- Drummond AJ, Rambaut A, Shapiro B, Pybus OG. Bayesian coalescent inference of past population dynamics from molecular sequences. Mol Biol Evol. 2005:22(5):1185–1192. 10.1093/molbev/msi103. [DOI] [PubMed] [Google Scholar]
- Dybdahl MF, Jenkins CE, Nuismer SL. Identifying the molecular basis of host-parasite coevolution: merging models and mechanisms. Am Nat. 2014:184(1):1–13. 10.1086/676591. [DOI] [PubMed] [Google Scholar]
- Ebranati E, Mancon A, Airoldi M, Renica S, Shkjezi R, Dragusha P, Della Ventura C, Ciccaglione AR, Ciccozzi M, Bino S, et al. Time and mode of epidemic HCV-2 subtypes spreading in Europe: phylodynamics in Italy and Albania. Diagnostics. 2021:11(2):327. 10.3390/diagnostics11020327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewald J, Sieber P, Garde R, Lang SN, Schuster S, Ibrahim B. Trends in mathematical modeling of host–pathogen interactions. Cell Mol Life Sci. 2020:77(3):467–480. 10.1007/s00018-019-03382-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenton A, Antonovics J, Brockhurst MA. Inverse-gene-for-gene infection genetics and coevolutionary dynamics. Am Nat. 2009:174(6):E230–E242. 10.1086/645087. [DOI] [PubMed] [Google Scholar]
- Gandon S, Buckling A, Decaestecker E, Day T. Host–parasite coevolution and patterns of adaptation across time and space. J Evol Biol. 2008:21(6):1861–1866. 10.1111/jeb.2008.21.issue-6. [DOI] [PubMed] [Google Scholar]
- Gandon S, Day T, Metcalf CJE, Grenfell BT. Forecasting epidemiological and evolutionary dynamics of infectious diseases. Trends Ecol Evol. 2016:31(10):776–788. 10.1016/j.tree.2016.07.010. [DOI] [PubMed] [Google Scholar]
- Gandon S, Michalakis Y. Local adaptation, evolutionary potential and host–parasite coevolution: interactions between migration, mutation, population size and generation time. J Evol Biol. 2002:15(3):451–462. 10.1046/j.1420-9101.2002.00402.x. [DOI] [Google Scholar]
- Ghafari M, Simmonds P, Pybus OG, Katzourakis A. A mechanistic evolutionary model explains the time-dependent pattern of substitution rates in viruses. Curr Biol. 2021:31(21):4689–4696. 10.1016/j.cub.2021.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilligan CA. Sustainable agriculture and plant diseases: an epidemiological perspective. Phil Trans R Soc B. 2008:363(1492):741–759. 10.1098/rstb.2007.2181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gloss AD, Vergnol A, Morton TC, Laurin PJ, Roux F, Bergelson J. Genome-wide association mapping within a local Arabidopsis thaliana population more fully reveals the genetic architecture for defensive metabolite diversity. Phil Trans R Soc B. 2022:377(1855):20200512. 10.1098/rstb.2020.0512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall AR, Scanlan PD, Morgan AD, Buckling A. Host–parasite coevolutionary arms races give way to fluctuating selection. Ecol Lett. 2011:14(7):635–642. 10.1111/ele.2011.14.issue-7. [DOI] [PubMed] [Google Scholar]
- Hill AV, Jepson A, Plebanski M, Gilbert SC. Genetic analysis of host–parasite coevolution in human malaria. Phil Trans R Soc B. 1997:352(1359):1317–1325. 10.1098/rstb.1997.0116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katoh K, Misawa K, Kuma K, Miyata T. MAFFT: a novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic Acids Res. 2002:30(14):3059–3066. 10.1093/nar/gkf436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc A. 1927:115(772):700–721. [Google Scholar]
- Lees JA, Ferwerda B, Kremer PH, Wheeler NE, Serón MV, Croucher NJ, Gladstone RA, Bootsma HJ, Rots NY, Wijmega-Monsuur AJ, et al. Joint sequencing of human and pathogen genomes reveals the genetics of pneumococcal meningitis. Nat Commun. 2019:10(1):2176. 10.1038/s41467-019-09976-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leonard K. Selection pressures and plant pathogens. Ann N Y Acad Sci. 1977:287(1):207–222. 10.1111/nyas.1977.287.issue-1. [DOI] [Google Scholar]
- Liu L, Cara DC, Kaur J, Raharjo E, Mullaly SC, Jongstra-Bilen J, Jongstra J, Kubes P. LSP1 is an endothelial gatekeeper of leukocyte transendothelial migration. J Exp Med. 2005:201(3):409–418. 10.1084/jem.20040830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luijckx P, Fienberg H, Duneau D, Ebert D. A matching-allele model explains host resistance to parasites. Curr Biol. 2013:23(12):1085–1088. 10.1016/j.cub.2013.04.064. [DOI] [PubMed] [Google Scholar]
- MacPherson A, Otto SP, Nuismer SL. Keeping pace with the red queen: identifying the genetic basis of susceptibility to infectious disease. Genetics. 2018:208(2):779–789. 10.1534/genetics.117.300481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Märkle H, John S, Cornille A, Fields PD, Tellier A. Novel genomic approaches to study antagonistic coevolution between hosts and parasites. Mol Ecol. 2021:30(15):3660–3676. 10.1111/mec.v30.15. [DOI] [PubMed] [Google Scholar]
- May RM, Anderson RM. Epidemiology and genetics in the coevolution of parasites and hosts. Proc R Soc B. 1983:219(1216):281–313. 10.1098/rspb.1983.0075. [DOI] [PubMed] [Google Scholar]
- Merani S, Petrovic D, James I, Chopra A, Cooper D, Freitas E, Rauch A, di Iulio J, John M, Lucas M, et al. Effect of immune pressure on hepatitis C virus evolution: insights from a single-source outbreak. Hepatology. 2011:53(2):396–405. 10.1002/hep.24076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohd Hanafiah K, Groeger J, Flaxman AD, Wiersma ST. Global epidemiology of hepatitis C virus infection: new estimates of age-specific antibody to HCV seroprevalence. Hepatology. 2013:57(4):1333–1342. 10.1002/hep.26141. [DOI] [PubMed] [Google Scholar]
- Moury B, Audergon J-M, Baudracco-Arnas S, Ben Krima S, Bertrand F, Boissot N, Buisson M, Caffier V, Cantet M, Chanéac S. The quasi-universality of nestedness in the structure of quantitative plant-parasite interactions. Peer Community J. 2021:1:e44. 10.24072/pcjournal.51. [DOI] [Google Scholar]
- Nemri A, Atwell S, Tarone AM, Huang YS, Zhao K, Studholme DJ, Nordborg M, Jones JD. Genome-wide survey of Arabidopsis natural variation in downy mildew resistance using combined association and linkage mapping. Proc Natl Acad Sci USA. 2010:107(22):10302–10307. 10.1073/pnas.0913160107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petruzziello A, Samantha M, Loquercio G, Cozzolino A, Cacciapuoti C. Global epidemiology of hepatitis C virus infection: an up-date of the distribution and circulation of hepatitis C virus genotypes. World J Gastroenterol. 2016:22(34):7824. 10.3748/wjg.v22.i34.7824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pogoda M, Liu F, Douchkov D, Djamei A, Reif JC, Schweizer P, Schulthess AW. Identification of novel genetic factors underlying the host-pathogen interaction between barley (Hordeum vulgare L.) and powdery mildew (Blumeria graminis f. sp. hordei). PLoS One. 2020:15(7):e0235565. 10.1371/journal.pone.0235565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pulford K, Jones M, Banham A, Haralambieva E, Mason D. Lymphocyte-specific protein 1: a specific marker of human leucocytes. Immunology. 1999:96(2):262–271. 10.1046/j.1365-2567.1999.00677.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira M, Bender D, Maller J, Sklar P, Bakker P, Daly M, et al. Plink: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007:81(3):559–575. 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Råberg L. Human and pathogen genotype-by-genotype interactions in the light of coevolution theory. PLoS Genet. 2023:19(4):1–17. 10.1371/journal.pgen.1010685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj A, Stephens M, Pritchard JK. fastSTRUCTURE: variational inference of population structure in large SNP data sets. Genetics. 2014:197(2):573–589. 10.1534/genetics.114.164350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scanlan PD. Bacteria–bacteriophage coevolution in the human gut: implications for microbial diversity and functionality. Trends Microbiol. 2017:25(8):614–623. 10.1016/j.tim.2017.02.012. [DOI] [PubMed] [Google Scholar]
- Stahl EA, Dwyer G, Mauricio R, Kreitman M, Bergelson J. Dynamics of disease resistance polymorphism at the Rpm1 locus of Arabidopsis. Nature. 1999:400(6745):667–671. 10.1038/23260. [DOI] [PubMed] [Google Scholar]
- Sudmant P, Rausch T, Gardner E, Handsaker R, Abyzov A, Huddleston J, Zhang Y, Ye K, Jun G, Fritz M, et al. An integrated map of structural variation in 2,504 human genomes. Nature. 2015:526(7571):75–81. 10.1038/nature15394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tellier A, Brown JK. Stability of genetic polymorphism in host–parasite interactions. Proc R Soc B. 2007:274(1611):809–817. 10.1098/rspb.2006.0281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tellier A, Moreno-Gámez S, Stephan W. Speed of adaptation and genomic footprints of host–parasite coevolution under arms race and trench warfare dynamics. Evolution. 2014:68(8):2211–2224. 10.1111/evo.12427. [DOI] [PubMed] [Google Scholar]
- The 1000 Genomes Project Consortium . A global reference for human genetic variation. Nature. 2015:526(7571):68–74. 10.1038/nature15393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson JN, Burdon JJ. Gene-for-gene coevolution between plants and parasites. Nature. 1992:360(6400):121–125. 10.1038/360121a0. [DOI] [Google Scholar]
- Tomley FM, Shirley MW. Livestock infectious diseases and zoonoses. Phil Trans R Soc B. 2009:364(1530):2637–2642. 10.1098/rstb.2009.0133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walther T, Brickner J, Aguilar P, Bernales S, Pantoja C, Walter P. Eisosomes mark static sites of endocytosis. Nature. 2006:439(7079):998–1003. 10.1038/nature04472. [DOI] [PubMed] [Google Scholar]
- Wang M, Roux F, Bartoli C, Huard-Chauveau C, Meyer C, Lee H, Roby D, McPeek MS, Bergelson J. Two-way mixed-effects methods for joint association analysis using both host and pathogen genomes. Proc Natl Acad Sci USA. 2018:115(24):E5440–E5449. 10.1073/pnas.1710980115. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The scripts underlying this article are available in the GitLab repository https://gitlab.lrz.de/population_genetics/cogenomics_method. The genomic data can be obtained upon request to the STOP-HCV consortium (https://www.expmedndm.ox.ac.uk/stop-hcv). The viral (nucleotide and protein) data are available from NCBI GenBank (accessions KY620313-KY620880). Data from the 1,000 Genomes Project Phase 3 are available from the project webpage: https://www.internationalgenome.org/category/phase-3/.