Abstract
We present a higher-order space-time adaptive method for the numerical solution of the Richards equation that describes a flow motion through variably saturated media. The discretization is based on the space-time discontinuous Galerkin method, which provides high stability and accuracy and can naturally handle varying meshes. We derive reliable and efficient a posteriori error estimates in the residual-based norm. The estimates use well-balanced spatial and temporal flux reconstructions which are constructed locally over space-time elements or space-time patches. The accuracy of the estimates is verified by numerical experiments. Moreover, we develop the hp-adaptive method and demonstrate its efficiency and usefulness on a practically relevant example.
Keywords: Space-time discontinuous Galerkin method, Richards equation, A posteriori error estimate, hp-mesh adaptation
Introduction
Fluid flows in variably saturated porous media are usually described by the Richards equation [33], which is expressed in the form
| 1 |
where denotes the derivative with respect to time, and are the divergence and gradient operators, respectively, is the sought pressure head (= normalized pressure), z is the vertical coordinate, is the water content function, is the hydraulic conductivity tensor and g is the source term. In addition, the active pore volume is related to by the following relation
| 2 |
where are material parameters. The hydraulic conductivity satisfies , where is the saturated conductivity tensor, and is the relative saturation. The functions and are given by constitutive relations, e.g., by van Genuchten’s law [27] and by Mualem’s law [31], respectively.
The Richards equation belongs to the nonlinear parabolic problems, and it can degenerate, in particular or . Due to the degeneracy, the numerical solution is challenging, and various techniques have been developed for its solution in the last decades, see [25] for a survey.
In [14], we presented the adaptive space-time discontinuous Galerkin (STDG) method for the numerical solution of (1). This technique is based on a piecewise polynomial discontinuous approximation with respect to both the spatial and temporal coordinates. The resulting scheme is sufficiently stable, provides high accuracy, and is suitable for the hp-mesh adaptation. This is an important property, since the weak solution of the Richards equation is (only) piecewise regular and exhibits singularities along the material interfaces and the unsaturated/saturated zone (when ). Therefore, an adaptive method that allows different meshes at different time levels, can achieve an accurate approximation with a relatively small number of degrees of freedom.
The numerical experiments presented in [14] showed the potential of the adaptive STDG method. However, the mesh adaptation used is based on interpolation error estimates that do not guarantee an upper error bound. The aim of this work is to overcome this bottleneck, derive a posteriori error estimates, and use them in the hp-mesh adaptation framework.
A posteriori error estimates for the numerical solution of the Richards equation have been treated in many papers for different numerical methods. We mention the finite volume framework with multistep time discretization in [5], the mixed finite element method in [6], the two-point finite volume discretization in [8], the lowest-order discretization on polytopal meshes in [38], finite element techniques in [30] and the references cited therein.
Guaranteed error estimates without unknown constants are usually obtained by measuring the error in a dual norm of the residual. Introducing reconstructed fluxes from the space , the upper bound can then be obtained directly. In [18], we developed this approach to the higher-order STDG method for nonlinear parabolic problems, where the temporal discontinuities were treated by temporal flux reconstructions considering the time jumps.
In this paper, we extend the approach [18] to the Richards equation (1). Although the definition of the temporal and spatial flux reconstructions as well as the derivation of the upper bounds is straightforward, the proof of the lower bound (efficiency) is rather tricky since the term in the time derivative is not a polynomial function for a polynomial . In contrary to [18], the proof of efficiency requires the additional oscillatory data terms. We construct spatial fluxes by solving local Neumann problems defined on space-time patches that generalize the approach from [22]. Moreover, we provide numerical experiments verifying derived error estimates. Compared to [18], the resulting effectivity indices are much closer to one. This is the first novelty of this paper.
Secondly, we deal with the errors arising due to iterative solution of nonlinear algebraic systems. We introduce a cheap stopping criterion for iterative solvers and justify it by numerical experiments. Thirdly, we introduce a space-time adaptive algorithm that employs the anisotropic hp-mesh adaptation technique [15]. The algorithm admits local adaptation of size and shape of mesh elements and the local adaptation of degrees of polynomial approximation with respect to space. However, the size of the time step can vary globally, and the degree of polynomial approximation with respect to time is fixed. Using the equidistribution principle, the algorithm gives an approximate solution with the error estimate under the given tolerance. The performance of the adaptive algorithm is demonstrated numerically, including a practically relevant example.
The rest of the paper is organized as follows. In Sect. 2, we introduce the problem considered, its STDG discretization is briefly described in Sect. 3. The main theoretical results are derived in Sect. 4, where the upper and lower bounds are proved. Two possible spatial reconstructions are discussed in Sect. 5 together with the stopping criteria of iterative solvers. The numerical verification of the error estimates is given in Sect. 6. Furthermore, we present the resulting hp-mesh adaptation algorithm in Sect. 7 and demonstrate its performance by numerical examples. Finally, we conclude with some remarks in Sect. 8.
Problem Formulation
Let () be the domain occupied by a porous medium and the physical time to be reached. For simplicity, we assume that is polygonal. By , we denote the boundary of which consists of two disjoint parts: the Dirichlet boundary and the Neumann boundary . We write the Richards equation (1) in a different form, which is more suitable for the analysis. We seek a function , which represents a hydraulic head (with the physical unit ). The quantity is related to the pressure head by . The Richards equation (1) reads
| 3 |
where represents a source term if g is positive or a sink term if g is negative, denotes the dimensionless active pore volume, and is the hydraulic conductivity with the physical unit (L = length, T = time). Moreover, is a trace of a function on , and . We note that with respect to (1), we should write and , however, we skip this notation for simplicity. We assume that the function is non-negative, non-decreasing and Lipschitz continuous. Moreover, the tensor is symmetric, positively semi-definite, and Lipschitz continuous.
In order to introduce the weak solution, we set and define the spaces
| 4 |
where denotes the time derivative (in the weak sense). Obviously, if then . In order to shorten the notation, we set the physical flux
| 5 |
Definition 1
We say that is the weak solution of (3) if and
| 6 |
where and .
The existence and uniqueness of the Richards equation is studied in [2], see also the later works [3, 28].
Space-time discretization
We briefly describe the discretization of (6) by the space-time discontinuous Galerkin (STDG) method, for more details, see [13, 14]. Let be a partition of the time interval (0, T) and set and . For each , we consider a simplicial mesh covering . For simplicity, we assume that , are conforming, i.e., neighbouring elements share an entire edge or face. However, this assumption can be relaxed by the technique from [12].
For each element , we denote by its boundary, its unit outer normal and its diameter. In order to shorten the notation, we write . By the generic symbol , we denote an edge () or a face () of and denotes its diameter. In the following, we speak only about edges, but we mean faces for . We assume that
, are shape regular, i.e., for all , where is the radius of the largest d-dimensional ball inscribed in K and constant C does not depend on for , .
, are locally quasi-uniform, i.e., for any pair of two neighbouring elements K and , where the constant C does not depend on , .
Let be an integer denoting the degree of polynomial approximation on , and be the corresponding space of polynomial functions on K. Let
| 7 |
denote the spaces of discontinuous piecewise polynomial functions on with possibly varying polynomial approximation degrees. Furthermore, we consider the space of space-time discontinuous piecewise polynomial functions
| 8 |
where denotes the time polynomial approximation degree and is the Bochner space, i.e., can be written as , , .
For , we define the one-sided limits and time jumps by
| 9 |
where is the initial condition. In the following, we use the notation
| 10 |
where M is either element or its (part of) boundary . The corresponding norms are denoted by and , respectively. By , we denote the sum over all space-time elements , where and .
Moreover, we define the jumps and mean values of on edges by
| 11 |
where and denote the traces of v on from interior and exterior of K, respectively, and comes from the Dirichlet boundary condition. For vector-valued , we set for and similarly for boundary edges.
For each space-time element , , , we define the forms
| 12 |
where is a sufficiently large penalization parameter () and corresponds to the choice of the variants of the interior penalty discretization (SIPG with , IIPG with and NIPG with ), see, e.g., [13, Chapter 2].
We introduce the space-time discontinuous Galerkin discretization of (3).
Definition 2
The function is called the approximate solution of (6) obtained by the space-time discontinuous Galerkin method (STDGM), if
| 13 |
where
| 14 |
Remark 1
We note that is discontinuous with respect to time at . The solution between and is stuck together by the “time-penalty” term which also makes sense for u and v belonging to different finite element spaces.
Finally, we derive some identities that will be used later. Let denote the set of all interior edges of mesh and the set of boundary edges of lying on . Then, the identity
| 15 |
holds for a piecewise smooth vector-valued function w and a piecewise smooth scalar function z.
Using identity (15) and the following obvious formulas valid for interior edges , , , , we gain
| 16 |
Consequently, from (12) and (16), we obtain the identity
| 17 |
A Posteriori Error Analysis
Error Measures
In order to proceed to the derivation of error estimators, we define the spaces of piecewise continuous functions with respect to time by
| 18 |
Obviously, and . Moreover, we have the following result.
Lemma 1
Let be the weak solution of (6). Then it satisfies
| 19 |
where
| 20 |
with given by (12) and the time jump defined by (9). Moreover, there exists a unique solution such that and satisfies (19).
Proof
The proof follows directly by comparing formulas (19)–(20) with (6) and the fact that for . For the proof of uniqueness, we employ the fact that is dense in , i.e., there exists a sequence for any such that as , cf. [34, Theorem 3.14]. We apply in (19), where the spatial component tends to as and the time component is given as 0 outside the interval and on , i.e., tends to 0 as . Therefore, all the terms containing time integrals in (19) tend to 0 when tends to 0. Since , the remaining jump term tends to as tends to 0. From this it follows that . Then it is possible to see that any solution of (19) satisfies the original weak formulation (6). Since the weak problem (6) has a unique solution, cf. [2], the extended problem (19) has a unique solution as well.
In virtue of [11, § 2.3.1], we define a parameter associated with the space-time element , , . The parameter represents a user-dependent weight, typically with physical units so that the error measure has the same physical unit as the energy norm. In this paper, we use two choices
| 21a |
| 21b |
where . We note that the following error analysis is independent of the choice of . Moreover, we define the norm in the space (cf. (18)) by
| 22 |
In virtue of (19), we introduce the error measure as a dual norm of the residual
| 23 |
where is given by (20). The residual represents a natural error measure for , cf. [11, Remark 2.3]. In Sect. 4, we estimate for being the solution of (13).
Since the approximate solution belongs to the space of discontinuous function , we introduce the second building block measuring the nonconformity of the solution in spatial variables. Therefore, similarly to [18], we define the form
| 24 |
where . The scaling factors are chosen such that has the same physical unit as .
We note that measures also the violation of the Dirichlet boundary condition since contains the term , cf. (11).
The final error measure is then defined by
| 25 |
Lemma 2
The error measure if and only if is the weak solution given by (6).
Proof
Obviously, if , then and due to (19). On the other hand, if , then and . Moreover, and the uniqueness of (19) imply that is the weak solution (6).
Temporal and Spatial Flux Reconstructions
Similarly as in [18], we define a temporal reconstruction as a continuous function with respect to time that mimics , . Let be the right Radau polynomial on , i.e., and , and is orthogonal to with respect to the inner product. Then we set
| 26 |
where is given by (9). The temporal flux reconstruction is continuous in time, namely and it satisfies the initial condition due to
| 27 |
Moreover, by the integration by parts and the properties , , we obtain
| 28 |
which together with definition (26) implies
| 29 |
Finally, using the orthogonality of to , we obtain from (28), the formula
| 30 |
Consequently, if is the approximate solution given by (13), then it satisfies
| 31 |
Obviously, the reconstruction is local and explicit, so its computation is fast and easy to implement.
The spatial flux reconstruction needs to define a function which mimics the flux , cf. (5). In particular, where
| 32 |
is the Raviart-Thomas-Nedelec finite elements, cf. [7] for more details. We assume that the reconstructed flux has to be equilibrated with the temporal flux
| 33 |
and with the Neumann boundary condition
| 34 |
In Sect. 5 we present two possible constructions of including the choice of the spatial polynomial degree p in (32).
Auxiliary Results
In the forthcoming numerical analysis, we need several technical tools. We will employ the scaled space-time Poincarè inequality, cf. [11, Lemma 2.2]: Let be the -orthogonal projection of onto a constant in each space-time element , , . Then,
| 35 |
where is the Poincarè constant equal to for simplicial elements and the last equality follows from (22).
Moreover, we introduce the space-time trace inequality
Lemma 3
Let be the -orthogonal projection of onto a constant on each , where is an edge of . Then there exists a constant such that
| 36 |
where , is from (35) and is the constant from the (space) trace inequality.
Proof
The proof is straightforward, we present it for completeness. Let and, for all , set . Observing that and are -orthogonal, we have
| 37 |
Using the standard trace inequality (e.g., [21, Lemma 3.32]), we have
| 38 |
where is a constant whose values can be set relatively precisely, see the discussion in [37, Section 4.6]. Hence, integrating the square of (38) over and using the fact that , , we estimate the first term on the right-hand side of (37) as
| 39 |
Using the fact that , the one-dimensional Poincarè inequality on and the Cauchy–Schwarz inequality yield
| 40 |
Collecting bounds (37), (39), (40) and the definition of the norm (22) yields (36).
Reliability
We presented the upper bound of , cf. (23).
Theorem 1
Let be the weak solution of (6) and be the approximate solution given by (13). Let be the temporal reconstruction given by (26) and be the spatial reconstruction satisfying (33). Then
| 41 |
where is the constant from Poincarè inequality (35), is the constant from the trace inequality (36) and the estimators , , , and are given by
| 42a |
| 42b |
| 42c |
| 42d |
The proof of Theorem 1 can be found in [19] for the case of the homogeneous Dirichlet boundary condition. For completeness, we present its modification including mixed Dirichlet-Neumann boundary conditions.
Proof
Starting from (20), adding the terms and , and using the integration by parts, we obtain
| 43 |
The terms , are estimated separately.
Let be the piecewise constant projection of given by the identity . Using the Cauchy–Schwarz inequality, assumption (33), the Poincarè inequality (35), and (22), we have
| 44 |
Furthermore, by the Cauchy–Schwarz inequality and (22), we obtain
| 45 |
The use of (29), and a similar manipulations as in (45), give
| 46 |
Hence, estimates (45)–(46), the Cauchy inequality and (22) imply
| 47 |
Furthermore, let , be the -orthogonal projection from Lemma 3. Then using assumption (34), the Cauchy inequality and the space-time trace inequality (36), we have
| 48 |
The particular estimates (44), (47), and (48), together with the discrete Cauchy–Schwarz inequality, imply (41).
Remark 2
Obviously, if , then .
Efficiency
The aim is to show that the local individual error estimators , and from (41)–(42) are locally efficient, i.e., they provide local lower bounds to the error measure up to a generic constant which is independent of u, , h and , but may depend on data problems and the degrees of polynomial approximation p and q. A dependence of the estimate up to this generic constant we will denote by .
In order to derive the local variants of the error measure, we denote by the set of elements sharing at least a vertex with , i.e.,
| 49 |
Moreover, we define the functional sub-spaces for any set (cf. (18)) and the corresponding error measures (cf. (23))
| 50 |
Obviously, the definition of and together with the shape regularity implies
| 51 |
Moreover, for each space-time element , , , we introduce the -projection of the non-polynomial functions, namely
| 52 |
Finally, for each vertex a of the mesh , we denote by a patch of elements that share this vertex. By we denote the maximal polynomial degree on . Then, for each a of , we define a vector-valued function (cf. (32)) by
| 53 |
where denotes the mean value on and is a continuous piecewise linear function such that and it vanishes at the other vertices of K. Finally, we set .
The proof of the local efficiency of the error estimates presented is based on the choice of a suitable test function in (23). We set
| 54 |
where is the standard bubble function on K, is the Legendre polynomial of degree on (and vanishing outside) and is the -projection weighted by given by
| 55 |
We note that
| 56 |
in general, compare with (52).
Using the inverse inequality, the polynomial function w given by (54) can be estimated as
| 57 |
Similarly as in [11] or [18], we introduce the oscillation terms
| 58 |
The goal is to prove the lower bounds of the proposed error estimates, namely to estimate , and by and the oscillation terms (58), , .
Theorem 2
Let , , be the error estimates given by (42), then
| 59 |
where are the local error measures defined by (49)–(50) and the oscillation terms , and are given by (58).
Proof
We start the proof by the putting function w from (54) as the test function in (50), i.e.
| 60 |
since , cf. (54). Then, using (20) and the fact that w vanishes on , we have
| 61 |
The functions , and are polynomials of degree q in time whereas w and are the (Legendre) polynomial of degree in time, cf. (54). Due to the -orthogonality of the Legendre polynomials, we have , since
| 62 |
Moreover, using inequality (57), relations (54)-(55) and the equivalence of norms on finite dimensional spaces,
we obtain
| 63 |
Furthermore, let be the mean value of w on the space-time element . Due to (52), the Cauchy–Schwarz inequality and (35), we have
| 64 |
and
| 65 |
Similarly, the Cauchy–Schwarz inequality and (22) imply
| 66 |
| 67 |
Moreover, using (42c), (26), integration by parts, the boundedness of the Radau polynomials, the triangle inequality and (58), we have
| 68 |
| 69 |
which proves the theorem.
Theorem 3
Let and , , be the error estimates given by (42), then
| 70 |
| 71 |
where is the local error measures defined by (49)–(50) and the oscillation terms , and are given by (58).
Proof
The proof is in principle identical with the proof [18, Lemmas 7-9], we present the main step for completeness. Let and be the projection given by (52) and (53). Using the triangle inequality, the inverse inequality and (58), we obtain
| 72 |
The first term on the right-hand side of (72) can be estimated as in [36, Theorem 4.10] by
| 73 |
where the resulting oscillation terms are estimated with the aid (58). Moreover, the last term on the right-hand side of (72) together with (42b) and assumption (58), reads
| 74 |
which proves (70).
The proof of (71) is based on the decomposition
| 75 |
While the second term on the right-hand side of (75) can be estimated by assumption (58), the estimate of the first term is somewhat more technical. It depends on the flux reconstruction used. For the flux reconstruction in Sect. 5.2, the proof is identical to the proof of [18, Lemma 9], which mimics the stationary variant [24, Theorem 3.12]. On the other hand, using the flux reconstruction from Sect. 5.1, it is possible to apply the technique from [11, Lemma 7.5], where the final relation has to be integrated over .
Spatial Flux Reconstructions and Stopping Criteria
We present two ways of reconstructing the spatial flux that satisfies the assumptions (33)–(34). The first one, proposed in [19] for the case of homogeneous Dirichlet boundary condition, is defined by the volume and edge momenta of the Raviart-Thomas-Nedelec (RTN) elements, cf. [7], and is easy to compute. The second approach is based on the solution of local Neumann problems on patches associated with each vertex of the mesh. This idea comes from, e.g., [24], its space-time variant was proposed in [18] for nonlinear convection-diffusion equations. Finally, in Sect. 5.3, we discuss the errors arising from the solution of algebraic systems and introduce a stopping criterion for the appropriate iterative solver.
Element-Wise Variant
We denote by the maximum polynomial degree over the element K and its neighbours that share the entire edge with K and the maximum polynomial degree on neighbouring elements having a common edge . Let be the space of RTN finite elements of order for element , cf. (32), and be the approximate solution. The spatial reconstruction is defined element-wise: for each , find with such that
| 76 |
The edge momenta in (76) are uniquely defined and since , in (76) is well defined as well. Here, the numerical flux is conservative on interior edges, which implies that are the same on each interior edge and therefore the resulting reconstruction globally.
Obviously, the first relation in (76) with directly implies assumption (34). Moreover, using the Green theorem, (76), (12), (31) and , we obtain
| 77 |
which justifies the assumption (33).
Patch-Wise Variant
For each vertex a of the mesh , we denote by a patch of elements sharing this vertex. By we denote the maximal polynomial degree on . Let be the space of piecewise polynomial discontinuous functions of degree on with mean value zero for . We define the space
| 78 |
We set the local problems on patches for all vertices a: find and such that
| 79 |
where
| 80 |
with
| 81 |
and is the lifting operator defined by
| 82 |
Then the final reconstructed flux is obtained by summing up on each element that contains vertex a, i.e.,
| 83 |
The assumption (34) follows directly from (78) and . Inserting the hat function for and in (17), using (5), (82) and omitting the zero terms, we have
| 84 |
Applying (13) and (31), we gain for and
| 85 |
From this it follows that the second relation in (79) holds element-wise, i.e.
| 86 |
Then (33) follows from
| 87 |
and from .
Stopping Criteria for Iterative Solvers
The space-time discretization (13) leads to a system of nonlinear algebraic equations for each time level . These systems have to be solved iteratively by a suitable solver, e.g., the Picard method, the Newton method or their variants. Therefore, it is necessary to set a suitable stopping criterion for the iterative solvers so that, on the one hand, the algebraic errors do not affect the quality of the approximate solution and, on the other hand, an excessive number of algebraic iterations is avoided.
However, the error estimates presented in Sect. 4 do not take into account errors arising from the inaccurate solution of these systems. Indeed, the aforementioned reconstructions fulfill assumption (33) only if the systems given by (13) are solved exactly. The full a posteriori error analysis including algebraic errors has been treated, e.g., in [8, 23, 29]. These error estimators are based on additional flux reconstructions that need to be evaluated at each iteration, and therefore, the overall computational time is increased.
To speed up the computations and control the algebraic errors, we adopt the technique of [17]. This approach offers (i) the measurement of algebraic errors by a quantity similar to the error measure (23), (ii) the setting of the stopping criterion for iterative solvers with one parameter corresponding to the relative error, and (iii) a fast evaluation of the required quantities.
For each , we define the estimators (cf. (23))
| 88 |
where the norm is given by (22),
| 89 |
The space is an enrichment space of by polynomials of the space degree and the time degree for each , , . Finally, we define the global in time quantities
| 90 |
Obviously, if fulfills (13) exactly, then for all . Moreover, if is the weak solution (6) then for all . Comparing (88) with (23), the quantity exhibits a variant of the error measure . Nevertheless, is neither lower nor upper bound of since and .
The quantities (88) can be evaluated very fast since the suprema (maxima) are the sum of the suprema (maxima) for all space-time elements , , , which are computable separately, cf. [17] for details. Hence, we prescribe the stopping criterion for the corresponding iterative solver as
| 91 |
where is the user-dependent constant. The justification of this approach and the influence of algebraic errors on the error estimates are studied numerically in Sect. 6.1.1.
Numerical Experiments
We present numerical experiments that justify the a posteriori error estimates (41)–(42). Since the error measure (23) is the dual norm of the residual, it is not possible to evaluate the error even if the exact solution is known. Therefore, similarly to [18], we approximate the error by solving the dual problem given for each time interval : Find ,
| 92 |
| 93 |
Then we have . We solve (92) for each by linear conforming finite element on a global refinement of the space-time mesh which is proportional to the space and time polynomial approximation degrees. We denote this quantity by . The second error contribution given by (24) is computable, so the total error (cf. (25)) is approximated by .
Remark 3
Sometimes, this approximate evaluation of the (exact) error is not sufficiently accurate for fine grids and high polynomial approximation degrees. In this case, very fine global refinement is required and then the resulting algebraic systems are too large to be solved in a reasonable time.
All numerical experiments were carried out using the patch-wise reconstruction from Sect. 5.2 using the in-house code ADGFEM [10]. The arising nonlinear algebraic systems are solved iteratively by a Newton-like method, we refer to [14] for details. Each Newton-line iteration leads to a linear algebraic system that is solved by GMRES method with block ILU(0) preconditioner.
Barenblatt Problems
We consider two nonlinear variants of (3) following from the Barenblatt problem [4] where the analytical solution exists. The first variant reads
| 94 |
where the analytical solution is
| 95 |
Using the substitution , we have the second variant
| 96 |
having the solution
| 97 |
For both problems ((94)–(95) and (96)–(97)), the computational domain is and the Dirichlet boundary condition is prescribed on all boundaries by (95) or (97). The final time is .
We carried out computation using a sequence of uniform triangular grids (having 288, 1152, 4608 and 18432 triangles) with several combinations of polynomial approximation degrees with respect to space (p) and time (q). The time step has been chosen constant . Besides the error quantities ( and ) and its estimators , , and , we evaluate the effectivity indices
| 98 |
In addition, we present the experimental order of convergence (EoC) of the errors and the estimators for each pair of successive meshes.
Tables 1–4 show the results for both Barenblatt problems ((94)–(95) with and (96)–(97) with ) with two variants of the scaling parameter , , given by (21a) and (21b). The quantity represents the number of degrees of freedom in the space, that is, , . We observe a good correspondence between and , the effectivity index varies between 1 and 2.5 for all tested values of p and q and both variants of ((21a) and (21b)).
Table 1.
Barenblatt problem (94)–(95), , scaling parameter given by (21a), approximation of the error and the error estimators, EOC in parenthesis
| h | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| & | |||||||||
| 1.41 | 864 | 1.73 | 1.13 | ||||||
| 0.71 | 3456 | 1.76 | 1.13 | ||||||
| (0.20) | (0.18) | (0.12) | (0.00) | (0.07) | (0.56) | ||||
| 0.35 | 13824 | 2.09 | 1.16 | ||||||
| (0.55) | (0.30) | (0.33) | (0.16) | (0.18) | (1.80) | ||||
| 0.18 | 55296 | 2.31 | 1.18 | ||||||
| (0.18) | (0.04) | (0.07) | (0.07) | (0.02) | (2.26) | ||||
| & | |||||||||
| 1.41 | 1728 | 1.70 | 1.09 | ||||||
| 0.71 | 6912 | 1.60 | 1.08 | ||||||
| (0.82) | (0.91) | (0.74) | (3.61) | (0.86) | (1.14) | ||||
| 0.35 | 27648 | 1.34 | 1.04 | ||||||
| (0.84) | (1.10) | (0.87) | (0.25) | (1.02) | (2.20) | ||||
| 0.18 | 110592 | 1.23 | 1.03 | ||||||
| (0.89) | (1.00) | (0.92) | (0.26) | (0.99) | (2.56) | ||||
| & | |||||||||
| 1.41 | 2880 | 1.83 | 1.12 | ||||||
| 0.71 | 11520 | 1.49 | 1.06 | ||||||
| (1.64) | (1.94) | (1.37) | (0.33) | (1.73) | (2.66) | ||||
| 0.35 | 46080 | 1.41 | 1.05 | ||||||
| (1.81) | (1.89) | (1.81) | (0.61) | (1.81) | (3.17) | ||||
| 0.18 | 184320 | 1.55 | 1.07 | ||||||
| (2.10) | (1.97) | (2.12) | (0.30) | (1.98) | (3.82) | ||||
Table 4.
Barenblatt problem (96)–(97), , scaling parameter given by (21b), approximation of the error and the error estimators, EOC in parenthesis
| h | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| & | |||||||||
| 1.41 | 864 | 1.59 | 1.72 | 1.13 | |||||
| 0.71 | 3456 | 1.87 | 1.16 | ||||||
| (1.97) | (1.85) | (2.05) | (1.13) | (1.74) | (2.09) | ||||
| 0.35 | 13824 | 2.07 | 1.21 | ||||||
| (1.64) | (1.49) | (1.75) | (1.29) | (1.34) | (2.29) | ||||
| 0.18 | 55296 | 2.22 | 1.25 | ||||||
| (1.25) | (1.15) | (1.34) | (1.40) | (1.09) | (2.47) | ||||
| 0.09 | 221184 | 2.29 | 1.27 | ||||||
| (1.06) | (1.02) | (1.09) | (1.48) | (1.01) | (2.32) | ||||
| & | |||||||||
| 1.41 | 1728 | 2.00 | 1.12 | ||||||
| 0.71 | 6912 | 1.84 | 1.11 | ||||||
| (1.96) | (2.08) | (2.04) | (1.28) | (2.04) | (2.14) | ||||
| 0.35 | 27648 | 1.57 | 1.08 | ||||||
| (1.77) | (2.00) | (1.90) | (1.40) | (1.85) | (2.33) | ||||
| 0.18 | 110592 | 1.39 | 1.06 | ||||||
| (1.63) | (1.80) | (1.70) | (1.46) | (1.67) | (2.48) | ||||
| & | |||||||||
| 1.41 | 2880 | 2.20 | 1.14 | ||||||
| 0.71 | 11520 | 1.79 | 1.10 | ||||||
| (1.77) | (2.06) | (1.91) | (1.54) | (1.84) | (2.30) | ||||
| 0.35 | 46080 | 1.50 | 1.06 | ||||||
| (1.59) | (1.85) | (1.66) | (1.50) | (1.63) | (2.33) | ||||
| 0.18 | 184320 | 1.36 | 1.05 | ||||||
| (1.53) | (1.67) | (1.57) | (1.50) | (1.55) | (2.48) | ||||
Finally, we note that the experimental orders of convergence EoC in Tables 1–4) of the error and its estimate are for the choice (21b) of the scaling parameter but only for the choice (21a). This follows from the fact that for the computations of the Barenblatt problem and then the dominant part of is , cf. (21a), which implies that (the time step is the same for all computations). The dominant part of the error estimator is , hence if then , cf. (42b). Nevertheless, comparing the pairs of Tables 1–2 and Tables 3–4, we found that the effectivity indexes are practically independent of the choice of .
Table 2.
Barenblatt problem (94)–(95), , scaling parameter given by (21b), approximation of the error and the error estimators, EOC in parenthesis
| h | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| & | |||||||||
| 1.41 | 864 | 1.12 | 1.73 | 1.13 | |||||
| 0.71 | 3456 | 1.76 | 1.13 | ||||||
| (1.20) | (1.18) | (1.12) | (1.00) | (1.07) | (1.56) | ||||
| 0.35 | 13824 | 2.09 | 1.16 | ||||||
| (1.55) | (1.30) | (1.33) | (0.84) | (1.18) | (2.80) | ||||
| 0.18 | 55296 | 2.31 | 1.18 | ||||||
| (1.18) | (1.04) | (1.07) | (0.93) | (1.02) | (3.26) | ||||
| 0.09 | 221184 | 2.31 | 1.18 | ||||||
| (1.01) | (1.00) | (1.01) | (0.98) | (1.00) | (2.97) | ||||
| & | |||||||||
| 1.41 | 1728 | 1.70 | 1.09 | ||||||
| 0.71 | 6912 | 1.60 | 1.08 | ||||||
| (1.82) | (1.91) | (1.74) | (4.61) | (1.86) | (2.14) | ||||
| 0.35 | 27648 | 1.34 | 1.04 | ||||||
| (1.84) | (2.10) | (1.87) | (0.75) | (2.02) | (3.20) | ||||
| 0.18 | 110292 | 1.23 | 1.03 | ||||||
| (1.89) | (2.00) | (1.92) | (0.74) | (1.99) | (3.55) | ||||
| & | |||||||||
| 1.41 | 2880 | 1.83 | 1.12 | ||||||
| 0.71 | 11520 | 1.49 | 1.06 | ||||||
| (2.64) | (2.94) | (2.37) | (1.33) | (2.73) | (3.66) | ||||
| 0.35 | 46080 | 1.29 | 1.04 | ||||||
| (2.68) | (2.89) | (2.81) | (0.39) | (2.81) | (4.17) | ||||
| 0.18 | 184320 | 1.55 | 1.07 | ||||||
| (3.23) | (2.97) | (3.12) | (0.70) | (2.98) | (4.82) | ||||
Table 3.
Barenblatt problem (96)–(97), , scaling parameter given by (21a), approximation of the error and the error estimators, EOC in parenthesis
| h | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| & | |||||||||
| 1.41 | 864 | 1.72 | 1.13 | ||||||
| 0.71 | 3456 | 1.87 | 1.16 | ||||||
| (0.97) | (0.85) | (1.05) | (0.13) | (0.74) | (1.09) | ||||
| 0.35 | 13824 | 2.07 | 1.21 | ||||||
| (0.64) | (0.49) | (0.75) | (0.29) | (0.34) | (1.29) | ||||
| 0.18 | 55296 | 2.22 | 1.25 | ||||||
| (0.26) | (0.15) | (0.34) | (0.41) | (0.10) | (1.48) | ||||
| & | |||||||||
| 1.41 | 1728 | 2.00 | 1.12 | ||||||
| 0.71 | 6912 | 1.84 | 1.11 | ||||||
| (0.96) | (1.08) | (1.04) | (0.28) | (1.04) | (1.14) | ||||
| 0.35 | 27648 | 1.57 | 1.08 | ||||||
| (0.77) | (1.00) | (0.91) | (0.40) | (0.85) | (1.33) | ||||
| 0.18 | 110592 | 1.39 | 1.06 | ||||||
| (0.63) | (0.81) | (0.71) | (0.47) | (0.68) | (1.48) | ||||
| & | |||||||||
| 1.41 | 2880 | 2.20 | 1.14 | ||||||
| 0.71 | 11520 | 1.79 | 1.10 | ||||||
| (0.77) | (1.06) | (0.91) | (0.54) | (0.84) | (1.30) | ||||
| 0.35 | 46080 | 1.50 | 1.06 | ||||||
| (0.59) | (0.85) | (0.66) | (0.50) | (0.63) | (1.33) | ||||
| 0.18 | 184320 | 1.35 | 1.05 | ||||||
| (0.53) | (0.68) | (0.58) | (0.51) | (0.56) | (1.49) | ||||
Justification of the Algebraic Stopping Criterion (91)
We present the numerical study of the stopping criterion (91) which is used in the iterative solution of algebraic systems given by (13). We consider again the Barenblatt problem (94)–(95) with and (96)–(97) with . The user-dependent constant in (91) has been chosen as , , and . Tables 5 and 6 show the estimators , , and , cf. (90), for selected meshes and polynomial approximation degrees and the scaling parameter chosen by (21a).
Table 5.
Barenblatt problem (94)–(95), , scaling parameter given by (21a), numerical study of the algebraic stopping criterion (91)
| time(s) | |||||||
|---|---|---|---|---|---|---|---|
| , & , | |||||||
| 202 | 14148 | 422.1 | |||||
| 362 | 21589 | 606.8 | |||||
| 529 | 26545 | 693.6 | |||||
| 579 | 27766 | 705.1 | |||||
| , & , | |||||||
| 406 | 10581 | 1968.3 | |||||
| 536 | 12059 | 2119.4 | |||||
| 576 | 12541 | 2030.1 | |||||
| 618 | 13580 | 2132.1 | |||||
| , & , | |||||||
| 534 | 10480 | 6610.2 | |||||
| 602 | 11479 | 6998.3 | |||||
| 636 | 12288 | 7181.7 | |||||
| 668 | 13178 | 7566.5 | |||||
Table 6.
Barenblatt problem (96)–(97), , scaling parameter given by (21a), numerical study of the algebraic stopping criterion (91)
| time(s) | |||||||
|---|---|---|---|---|---|---|---|
| , & , | |||||||
| 100 | 2199 | 224.6 | |||||
| 200 | 4957 | 284.5 | |||||
| 299 | 7715 | 352.6 | |||||
| 378 | 9790 | 413.7 | |||||
| , & , | |||||||
| 201 | 4065 | 1535.3 | |||||
| 286 | 5820 | 1675.9 | |||||
| 393 | 7803 | 1759.7 | |||||
| 529 | 10172 | 1984.6 | |||||
| , & , | |||||||
| 202 | 4222 | 5539.6 | |||||
| 316 | 6538 | 6068.2 | |||||
| 453 | 8880 | 6615.7 | |||||
| 591 | 11150 | 7101.3 | |||||
Additionally, we present the total number of steps of the Newton-like solver , the total number of GMRES iterations and the computational time in seconds. The computational time has only an informative character.
We observe that the error estimators , and also converge to the limit values for decreasing in (91) which mimic the case when the algebraic errors are negligible. Moreover, the relative differences between the actual values and and their limits correspond more or less to the value of . Obviously, smaller values of cause prolongation of the computational time, due to a higher number of iterations, with a negligible effect on accuracy. Thus, the choice seems to be optimal in order to balance accuracy and efficiency.
The presented numerical experiments indicate that the estimator gives an upper bound of , however, this observation is not supported by the theory. The quantity is used only in the stopping criterion (91).
Tracy Problem
Tracy problem represents a standard benchmark, where the analytical solutions of the Richards equation are available [35]. We consider the Gardners constitutive relations [26]
| 99 |
where is the pressure head, z is the vertical coordinate and the material parameters , , , and are the isotropic conductivity, saturated water content, residual water content, and the soil index parameter related to the pore-size distribution, respectively.
The computational domain is , the initial condition is set in where corresponds to the hydraulic head when the porous medium is dry. On the top part of the boundary , we prescribe the boundary condition
| 100 |
and on the rest of boundary we set . We note that this benchmark poses an inconsistency between the initial and boundary conditions on . Hence, the most challenging part is the computation close to . In order to avoid the singularity at , we investigate the error only on the interval with the fixed time step is .
We perform a computation using a sequence of uniform triangular grids with several combinations of polynomial approximation degrees and the choice (21b), the results are shown in Table 7. We observe reasonable values of the effectivity indices except for the finest grids and the higher degrees of polynomial approximation, where the effectivity indices are below 1. Based on the values of EoC, we suppose that below 1 is not caused by the failure of the error estimator but due to an inaccurate approximation of the exact error; see Remark 3.
Table 7.
Tracy problem scaling parameter given by (21b), approximation of the error and the error estimators, EOC in parenthesis
| h | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| & | |||||||||
| 0.18 | 384 | 1.22 | 1.00 | ||||||
| 0.09 | 1536 | 1.35 | 1.00 | ||||||
| (1.47 ) | (1.32) | (1.43) | (1.18) | (1.40) | (0.15) | ||||
| 0.04 | 6144 | 1.67 | 1.00 | ||||||
| (2.55) | (2.24) | (2.40) | (2.90) | (2.20) | (2.58) | ||||
| 0.02 | 24576 | 1.66 | 1.00 | ||||||
| (1.03) | (1.04) | (1.05) | (0.71) | (0.99) | (1.98) | ||||
| & | |||||||||
| 0.18 | 768 | 1.27 | 1.00 | ||||||
| 0.09 | 3072 | 1.13 | 1.00 | ||||||
| (1.48) | (1.65) | (1.67) | (4.54) | (1.63) | (1.86) | ||||
| 0.04 | 12288 | 1.12 | 1.00 | ||||||
| (1.64) | (1.65) | (1.64) | (1.62) | (1.68) | (1.11) | ||||
| 0.02 | 49,152 | 4.37 | 0.70 | 1.00 | |||||
| (1.56) | (2.24) | (2.15) | (0.96) | (2.21) | (3.06) | ||||
| & | |||||||||
| 0.18 | 1280 | 1.18 | 1.00 | ||||||
| 0.09 | 5120 | 1.27 | 1.00 | ||||||
| (1.84) | (1.74) | (1.79) | (1.00) | (1.87) | (0.37) | ||||
| 0.04 | 20480 | 1.63 | 0.33 | 1.00 | |||||
| (2.16) | (4.11) | (4.08) | (2.08) | (3.99) | (5.29) | ||||
| 0.02 | 81920 | 0.06 | 1.00 | ||||||
| (0.03) | (2.38) | (2.41) | (0.28) | (2.39) | (3.03) | ||||
Mesh Adaptive Algorithm
We introduce the mesh adaptive algorithm which is based on the a posteriori error estimates , cf. (41). Let be the given tolerance, the goal of the algorithm is to define the sequence of time steps , meshes and spaces , such that the corresponding approximate solution given by (13) satisfies the condition
| 101 |
Another possibility is to require , then the following considerations have to be modified appropriately.
The mesh adaptation strategy is built on the equi-distribution principle, namely the sequences should be generated such that
| 102a |
| 102b |
where is the error estimate corresponding to the time interval , and denotes the number of elements of . Obviously, if all the conditions in (102) are valid, then the criterion (101) is achieved.
Algorithm 1.
Space-time mesh adaptive algorithm.
Based on (101)–(102), we introduce the abstract Algorithm 1. The size of , (step 8 of the algorithm) are chosen to equilibrate estimates of the spatial and temporal reconstruction, and , cf. (42). Particularly, we set the new time step according to the formula
| 103 |
where is the security factor and is the polynomial degree with respect to time. Therefore, corresponds to the temporal order of convergence.
The construction of the new mesh (step 11 in Algorithm 1) is based on the modification of the anisotropic hp-mesh adaptation method from [15, 20]. Having the actual mesh , for each we set the new volume of K according the formula
| 104 |
where is the local tolerance from (102b), |K| is the volume of |K| and is a suitable increasing function such that . For particular variants of , we refer to [15, 20].
When the new volume of mesh elements is established by (104), the new shape of K and a new polynomial approximation degree are optimized by minimizing the interpolation error. This optimization is done locally for each mesh element. In one adaptation level, we admit the increase or decrease of by one. Setting the new area, shape, and polynomial approximation degree for each element of the current mesh, we define the continuous mesh model [16] and carry out a remeshing using the code ANGENER [9].
The generated meshes are completely non-nested and non-matching, hence the evaluation of the time-penalty term (cf. Remark 1) is delicate. We refer to [20] where this aspect is described in detail and numerically verified. The presented numerical analysis takes into account the errors arising from the re-meshing in the temporal reconstruction , which contains term , cf. (26). The following numerical experiments show that the error estimator is under the control also after each remeshing.
Barenblatt Problem
We apply Algorithm 1 to the Barenblatt problem (96) with . Table 8 shows the error estimators obtained by adaptive computation for three different tolerances . Compared with the error estimators from Table 4, we observe that the adaptive computations achieve significantly smaller error estimates using a significantly smaller number of degrees of freedom. We note that we are not able to present the quantity (cf. (92)–(93)) approximating the error since the finite element code used for the evaluation of supports only uniform grids.
Table 8.
Barenblatt problem (96)–(97), scaling parameter given by (21b), the error estimators obtained by the adaptive computations using Algorithm 1
| hp adaptation | ||||||
|---|---|---|---|---|---|---|
| 2.0E−03 | 4 543 | |||||
| 1.0E−03 | 6 244 | |||||
| 5.0E−04 | 9 071 | |||||
The quantity is the average number of space degrees of freedom per one time step
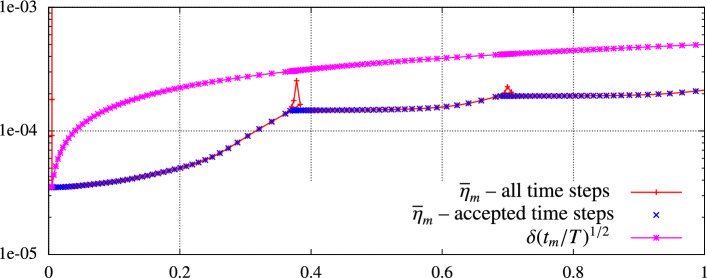
Figure 1 shows the performance of Algorithm 1, where each dot corresponds to one time step . We plot the values of the accumulated estimators for all . The red nodes correspond to all computed time steps, including the rejected ones (steps 11–12 of Algorithm 1) whereas the blue nodes mark only the accepted time steps. The rejected time steps indicate the re-meshing. Moreover, we plot the “accumulated” tolerance , cf. (101) and (102a). We observe that the resulting estimator at is below the tolerance by a factor of approximately 2.5 since conditions (102) are stronger than (101).
Fig. 1.
Barenblatt problem, (96)–(97), , performance of Algorithm 1, accumulated error estimator and the “accumulated” tolerance for
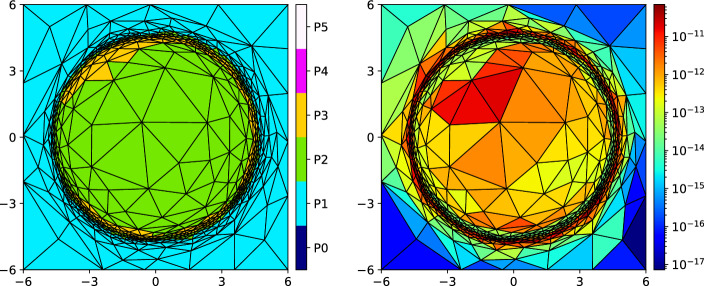
Figure 2, left, shows the hp-mesh obtained by Algorithm 1 at the final time , each triangle is highlighted by a color corresponding to the polynomial degree used , . We observe a strong anisotropic refinement about the circular singularity of the solution when , see the analytical formula (97). Outside of this circle, large triangles with the smallest polynomial degree () are generated. On the other hand, due to the regularity of the solution in the interior of the circle, the polynomial degrees or are generated.
Fig. 2.
Barenblatt problem, hp-mesh obtained by Algorithm 1 (left) and the error estimators , at
Moreover, Fig. 2, right, shows the error estimator , at . The elements in the exterior of the circle have small values of – due to a constant solution and negligible errors. On the other hand, the values of for the rest of elements are in the range – due to the equidistant principle used.
Single Ring Infiltration
We deal with the numerical solution of the single ring infiltration experiment, which is frequently used for the identification of saturated hydraulic conductivity, cf. [32, 39] for example. We consider the Richards equation (3) where the active pore volume is given by (2), the water content function is given by the van Genuchten’s law [27] and the conductivity is given by the Mualem function [31], namely
| 105 |
where is the pressure head, z is the vertical coordinate and the material parameters , , , , , and (cf. (2)).
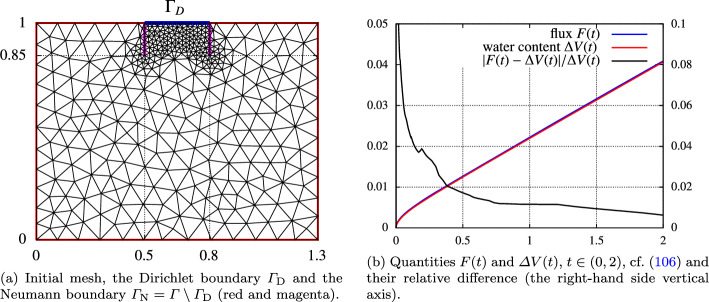
The computational domain together with the boundary parts is sketched in Fig. 3a. On the boundary part we set the Dirichlet boundary condition , and on we consider the homogeneous Neumann boundary condition. The smaller “magenta” vertical lines starting at belong to . At , a dry medium with is prescribed. We carried out the computation until the physical time . The inconsistency of the initial and boundary condition on makes the computation quite difficult for .
Fig. 3.
Single ring infiltration problem
Figure 3b verifies the conservativity of the adaptive method. We plot the quantities
| 106 |
where F(t) is the total flux of the water through the boundary till time t and is the changes of the water content in the domain between times 0 and t. From equation (3) and the Stokes theorem, we have the conservation law for all . Therefore, we also show the relative difference between these quantities for in Fig. 3b the vertical label on the right. We observe that, except for the time close to zero, where the inconsistency between initial and boundary conditions is problematic, the relative difference is at the level of several percent.
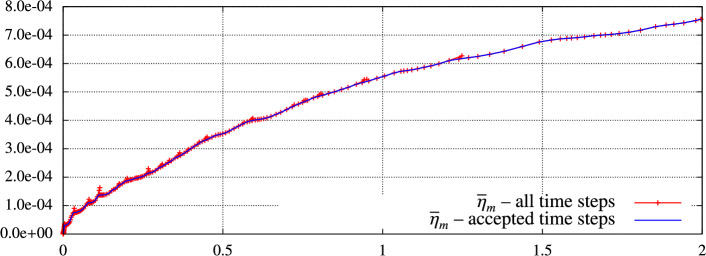
Furthermore, Fig. 4 shows the accumulated estimators for time levels , . The red nodes correspond to all computed time steps, including the rejected steps whereas the blue line connects only the accepted time steps. The rejected time steps are followed by the remeshing which is carried out namely for small t. We observe that the elimination of the rejected time steps causes that the errors arising from the remeshing do not essentially affect the total error estimate .
Fig. 4.
Single ring infiltration, performance of Algorithm 1, accumulated error estimator with respect to ,
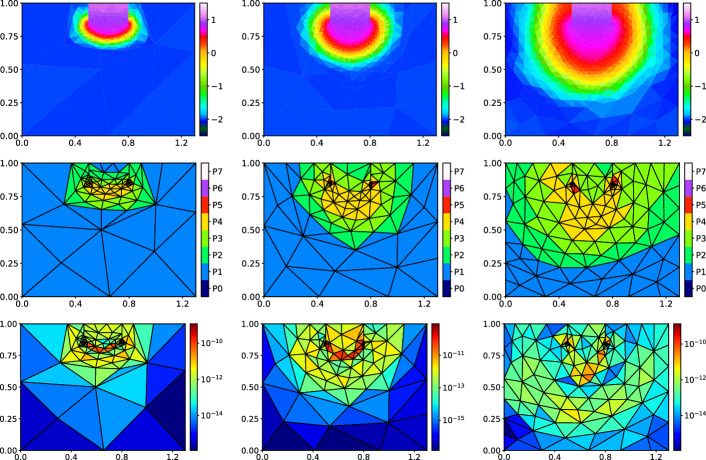
Moreover, Fig. 5 shows the hp-meshes, the hydraulic head and the error estimator , at selected time levels obtained from Algorithm 1 with . We observe the mesh adaptation namely at the (not sharp) interface between the saturated and non-saturated medium and also in the vicinity of the domain singularities. The error estimators , indicate an equi-distribution of the error.
Fig. 5.
Single ring infiltration, hydraulic head (top ), the corresponding hp-meshes obtained by Algorithm 1 (center) and the error estimators , (bottom) at , and (from left to right)
Conclusion
We derived reliable and efficient a posteriori error estimates in the residual-based norm for the Richards equation discretized by the space-time discontinuous Galerkin method. The numerical verification indicates the effectivity indexes between 1 and 2.5 for the tested examples. Moreover, we introduced the hp-mesh adaptive method handling varying non-nested and non-matching meshes and demonstrated its efficiency for simple test benchmark and its applicability for the numerical solution of the single ring infiltration experiment.
It will be possible to generalize the presented approach to genuinely space-time hp-adaptive method, where the (local) polynomial order q in time is varied as well. However, the question is of potential benefit. Based on our experience, the setting gives sufficiently accurate approximation for the majority of tested problems.
On the other hand, the choice would be sufficient only in subdomains of where the solution is almost constant in time. Therefore, we suppose that the benefit of local varying of polynomial order in time will be low.
Although the presented numerical examples are two-dimensional, it would be possible to apply the presented error estimates and mesh adaptation to three-dimensional problems as well. We refer, e.g., to [1] and the references therein, where the anisotropic mesh adaptation techniques are developed for time-dependent 3D problems.
Funding
Open access publishing supported by the National Technical Library in Prague. This work has been supported by the Czech Science Foundation Grant No. 20-01074 S (V.D.), the Charles University grant SVV-2023-260711, and the Grant Agency of Charles University Project No. 28122 (H.S.), European Development Fund-Project “Center for Advanced Aplied Science” No. CZ.02.1.01/0.0/0.0./16 019/0000778 (M.V.). V.D. acknowledges the membership in the Nečas Center for Mathematical Modeling ncmm.karlin.mff.cuni.cz.
Data Availability
No datasets were generated or analysed during the current study.
Declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Alauzet, F., Loseille, A., Olivier, G.: Time-accurate multi-scale anisotropic mesh adaptation for unsteady flows in CFD. J. Comput. Phys. 373, 28–63 (2018) [Google Scholar]
- 2.Alt, H.W., Luckhaus, S.: Quasilinear elliptic-parabolic differential equations. Math. Z. 183(3), 311–341 (1983) [Google Scholar]
- 3.Baradi, M., Difonzo, F.V.: Strong solutions for Richards’ equation with Cauchy conditions and constant pressure. Environ. Fluid Mech. 20, 165–174 (2020) [Google Scholar]
- 4.Barenblatt, G.I.: On some unsteady motions of a liquid and gas in a porous medium. Akad. Nauk SSSR. Prikl. Mat. Meh. 16, 67–78 (1952) [Google Scholar]
- 5.Baron, V., Coudière, Y., Sochala, P.: Adaptive multistep time discretization and linearization based on a posteriori error estimates for the Richards equation. Appl. Numer. Math. 112, 104–125 (2017) [Google Scholar]
- 6.Bernardi, C., El Alaoui, L., Mghazli, Z.: A posteriori analysis of a space and time discretization of a nonlinear model for the flow in partially saturated porous media. IMA J. Numer. Anal. 34(3), 1002–1036 (2014) [Google Scholar]
- 7.Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods, Springer Series in Computational Mathematics, vol. 15. Springer, New York (1991) [Google Scholar]
- 8.Di Pietro, D.A., Vohralík, M., Yousef, S.: An a posteriori-based, fully adaptive algorithm with adaptive stopping criteria and mesh refinement for thermal multiphase compositional flows in porous media. Compu. Math. Appl. 68(12, Part B), 2331–2347 (2014) [Google Scholar]
- 9.Dolejší, V.: ANGENER – Anisotropic mesh generator, in-house code. Charles University, Prague, Faculty of Mathematics and Physics (2000). https://msekce.karlin.mff.cuni.cz/~dolejsi/angen/
- 10.Dolejší, V.: ADGFEM – Adaptive discontinuous Galerkin finite element method, in-house code. Charles University, Prague, Faculty of Mathematics and Physics (2020). https://msekce.karlin.mff.cuni.cz/~dolejsi/adgfem/
- 11.Dolejší, V., Ern, A., Vohralík, M.: A framework for robust a posteriori error control in unsteady nonlinear advection-diffusion problems. SIAM J. Numer. Anal. 51(2), 773–793 (2013) [Google Scholar]
-
12.Dolejší, V., Ern, A., Vohralík, M.:
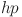 -adaptation driven by polynomial-degree-robust a posteriori error estimates for elliptic problems. SIAM J. Sci. Comput. 38(5), A3220–A3246 (2016) [Google Scholar]
-adaptation driven by polynomial-degree-robust a posteriori error estimates for elliptic problems. SIAM J. Sci. Comput. 38(5), A3220–A3246 (2016) [Google Scholar] - 13.Dolejší, V., Feistauer, M.: Discontinuous Galerkin Method: Analysis and Applications to Compressible Flow. Springer Series in Computational Mathematics, vol. 48. Springer, Cham (2015) [Google Scholar]
- 14.Dolejší, V., Kuráž, M., Solin, P.: Adaptive higher-order space-time discontinuous Galerkin method for the computer simulation of variably-saturated porous media flows. Appl. Math. Model. 72, 276–305 (2019) [Google Scholar]
-
15.Dolejší, V., May, G.: Anisotropic
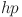 -Mesh Adaptation Methods. Birkhäuser, Cham (2022) [Google Scholar]
-Mesh Adaptation Methods. Birkhäuser, Cham (2022) [Google Scholar] -
16.Dolejší, V., May, G., Rangarajan, A.: A continuous
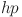 -mesh model for adaptive discontinuous Galerkin schemes. Appl. Numer. Math. 124, 1–21 (2018) [Google Scholar]
-mesh model for adaptive discontinuous Galerkin schemes. Appl. Numer. Math. 124, 1–21 (2018) [Google Scholar] - 17.Dolejší, V., Roskovec, F., Vlasák, M.: Residual based error estimates for the space-time discontinuous Galerkin method applied to the compressible flows. Comput. Fluids 117, 304–324 (2015) [Google Scholar]
- 18.Dolejší, V., Roskovec, F., Vlasák, M.: A posteriori error estimates for higher order space-time Galerkin discretizations of nonlinear parabolic problems. SIAM J. Numer. Anal. 59(3), 1486–1509 (2021) [Google Scholar]
- 19.Dolejší, V., Shin, H.G.: A posteriori error estimate and mesh adaptation for the numerical solution of the richards equation. In: J.M. Melenk, et al. (eds.) Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2020+1, Lecture Notes in Computational Science and Engineering 137 (2023)
-
20.Dolejší, V., May, G.: An anisotropic
 -mesh adaptation method for time-dependent problems based on interpolation error control. J. Sci. Comput. 95(2) (2023)
-mesh adaptation method for time-dependent problems based on interpolation error control. J. Sci. Comput. 95(2) (2023)
- 21.Ern, A., Guermond, J.L.: Theory and Practice of Finite Elements. Springer, Berlin (2004) [Google Scholar]
- 22.Ern, A., Smears, I., Vohralík, M.: Guaranteed, locally space-time efficient, and polynomial-degree robust a posteriori error estimates for high-order discretizations of parabolic problems. SIAM J. Numer. Anal. 55(6), 2811–2834 (2017) [Google Scholar]
- 23.Ern, A., Vohralík, M.: Adaptive inexact Newton methods with a posteriori stopping criteria for nonlinear diffusion PDEs. SIAM J. Sci. Comput. 35(4), A1761–A1791 (2013) [Google Scholar]
- 24.Ern, A., Vohralík, M.: Polynomial-degree-robust a posteriori estimates in a unified setting for conforming, nonconforming, discontinuous Galerkin, and mixed discretizations. SIAM J. Numer. Anal. 53(2), 1058–1081 (2015) [Google Scholar]
- 25.Farthing, M., Ogden, F.: Numerical solution of Richards’ equation: a review of advances and challenges. Soil Sci. Soc. Am. J. 81(6), 1257–1269 (2017) [Google Scholar]
- 26.Gardner, W.R.: Some steady state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 85, 228–232 (1958) [Google Scholar]
- 27.van Genuchten, M.T.: Closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44(5), 892–898 (1980) [Google Scholar]
- 28.Kim, I.C., Požár, N.: Nonlinear elliptic-parabolic problems. Arch. Ration. Mech. Anal. 210, 975–1020 (2013) [Google Scholar]
- 29.Mallik, G., Vohralík, M., Yousef, S.: Goal-oriented a posteriori error estimation for conforming and nonconforming approximations with inexact solvers. J. Comput. Appl. Math. 366 (2020)
- 30.Mitra, K., Vohralík, M.: A posteriori error estimates for the Richards equation. Tech. Rep. hal-03328944v2, INRIA (2022)
- 31.Mualem, Y.: A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 12(3), 513–522 (1976) [Google Scholar]
-
32.Nakhaei, M., Šim
 nek, J.: Parameter estimation of soil hydraulic and thermal property functions for unsaturated porous media using the hydrus-2d code. J. Hydrol. Hydromech. 62(1) (2014)
nek, J.: Parameter estimation of soil hydraulic and thermal property functions for unsaturated porous media using the hydrus-2d code. J. Hydrol. Hydromech. 62(1) (2014)
- 33.Richards, L.A.: Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1(5), 318–333 (1931) [Google Scholar]
- 34.Rudin, W.: Real and Complex Analysis, 3rd edn. McGraw-Hill, New York (1987) [Google Scholar]
- 35.Tracy, F.T.: Clean two- and three-dimensional analytical solutions of Richards equation for testing numerical solvers. Water Resour Res 42(8) (2006)
- 36.Verfürth, R.: A Posteriori Error Estimation Techniques for Finite Element Methods. Numerical Mathematics and Scientific Computation. Oxford University Press, Oxford (2013) [Google Scholar]
- 37.Vohralík, M.: A posteriori error estimates for efficiency and error control in numerical simulations. Universite Pierre et Marie Curie – Paris 6 (2018). Lecture notes Course NM497
- 38.Vohralík, M., Yousef, S.: A simple a posteriori estimate on general polytopal meshes with applications to complex porous media flows. Comput. Methods Appl. Mech. Eng. 331, 728–760 (2018) [Google Scholar]
- 39.Xu, X., Lewis, C., Liu, W., Albertson, J., Kiely, G.: Analysis of single-ring infiltrometer data for soil hydraulic properties estimation: comparison of BEST and Wu methods. Agric. Water Manag. 107, 34–41 (2012) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No datasets were generated or analysed during the current study.