Abstract
During the last few years, Bike Sharing Systems (BSS) have become a popular means of transportation in several cities across the world, owing to their low costs and associated advantages. Citizens have adopted these systems as they help improve their health and contribute to creating more sustainable cities. However, customer satisfaction and the willingness to use the systems are directly affected by the ease of access to the docking stations and finding available bikes or slots. Therefore, system operators and managers' major responsibilities focus on urban and transport planning by improving the rebalancing operations of their BSS. Many approaches can be considered to overcome the unbalanced station problem, but predicting the number of arrivals and departures at the docking stations has been proven to be one of the most efficient. In this paper, we study the features that influence the prediction of bikes' arrivals and departures in Barcelona BSS, using a Random Forest model and a one-year data period. We considered features related to the weather, the stations' characteristics, and the facilities available within a 200-meter diameter of each station, called spatial features. The results indicate that features related to specific months, as well as temperature, pressure, altitude, and holidays, have a strong influence on the model, while spatial features have a small impact on the prediction results.
Keywords: Feature importance, Bike demand forecasting, Bike Sharing Systems
1. Introduction
Several cities around the world have adopted Bike Sharing Systems (BSS) as a new and alternative mode of transportation. Their adoption has helped enhance urban mobility and contributed to a more sustainable traffic model, creating a greener and healthier society. However, there are several challenges that supervisors of the system need to overcome, not only in terms of vandalism or lack of respect for shared property but also in how they provide equitable access and optimize rebalancing operations. Several authors have studied how the lack of available bikes or docks, especially during rush hours, can lead to a reduction in service reliability and customer satisfaction [1], [2].
Different methods have been adopted by BSS system operators to redistribute the bikes between stations, for example based on their experience, using customers' reports or travelling around the city in trucks and checking the status of the docking stations. Nevertheless, these methods could lead to unnecessary waste of resources and inconveniences for users if there are no bikes or available docks in the stations. Therefore, an accurate prediction of the available bikes and docks in each station is important for the optimization of the re-balancing process as well as for the users of the system. The research in the stations' balancing field has increased in the latest years, numerous studies focus on optimizations of vehicles routes or bikes inventory management [3], [4], [5]. However, a more dynamic approach, which consist in providing an accurate forecast of BSS status (arrivals and departures) to system managers, has become a popular and effective method to overcome the challenges of unbalanced stations. By using this information, BSS operators can improve the system management and create more efficient balancing truck routes and bike re-balancing strategies. Similarly, customers can also benefit of this information, by planning their trips ahead of time and choosing different stations to borrow or drop off bikes according to future availability forecast. Most studies have mainly focused on evaluating different prediction algorithms or creating alternative prediction models to enhance the accuracy of the forecasted bike demand. However, few studies focus on identifying and studying other potential features that could help improve model performance and prediction accuracy.
1.1. Hypothesis and contributions
This paper builds on the study conducted by Cortez et al., where five prediction algorithms were analyzed when forecasting short-term station level arrivals and departures in three BSS: small BBS in Logroño (Spain), medium BSS in Barcelona (Spain) and Large BSS in New York (US) [6]. In this study, external features (station-related and weather features) were used to train and evaluate the models. These features have been extensively studied by several authors [7], [8], [9], and have been proven to have some effect on BSS demand. However, as mentioned before, the effect of other external variables such as the business population, presence of educational centers, available transport connections, and other facilities has been barely studied. Similarly, other temporal variables, such as holidays, have not been considered in BSS forecast models. In this investigation, we seek to bridge that gap in the existing literature by analyzing several weather, stations' characteristics, stations' usage, and spatial features and studying their correlation and effect on BSS demand forecast.
Given the data availability of the different BSS, we focused on Bicing which is the public bike sharing system in Barcelona. The hypotheses of this study are cited as follows:
-
•
H1: Weather features have a strong influence in Bicing arrivals and departures. This hypothesis is based on the contributions of different authors [10], [11], [12], [13].
-
•
H2: Spatial features, such as build facilities in a 200-meter radius of each docking station, are among the most influential features in Bicing system. This hypothesis is based on several studies [14], [10], [15]. However, there is no consensus on the influence of these variables in bike demand, as it depends on each BSS characteristics. More details are given in Section 2.
-
•
H3: Holidays and other temporal variables influence Bicing demand. This hypothesis is supported by findings in different studies [14], [10]
The particular characteristics of each BSS require a different analysis of the features that can contribute to the improvement of the forecast accuracy. Consequently, this study makes two key contributions:
-
•
An analysis of several weather, spatial, stations' characteristics and stations' usage related features for Barcelona BSS.
-
•
A feature importance analysis of the attributes that affect Bicing arrivals and departures forecast.
Most of the data has been collected from Open Data BCN webpage, using a one-year period. Two reasons have influenced this decision: i) the data availability, and ii) the need to study long-term patterns and understand the effect of weather and monthly patterns on the BSS demand. Later, the collected data has been used to train the Random Forest model, which was the model that showed better performance in [6]. Then, a feature analysis was performed to understand the influence of each feature on Bicing arrivals and departures prediction.
The results obtained in this study can help improve the accuracy of arrivals and departures prediction in Barcelona BSS and be leveraged by system managers to create policies to improve this BSS and promote its use. However, these results cannot be directly extended to other medium-sized systems, as the particular characteristics of each BSS need to be studied to decide which features should be collected. For example, Bicing is a system designed for Barcelona residents and cannot be used by tourists or temporary visitors. Therefore, the effect of features related to tourism, such as the most touristic places around a station, will have a small effect on Bicing demand; but the number of universities or educational centers could have a bigger effect.
The rest of the paper is organized as follows: Section 2 describes related work. Details about the data collection and processing are given in Section 3. In Section 4, we describe the analysis of the features and the collected data. Additionally, Section 5 provides an overview of the prediction model and error metrics employed. Section 6, presents the model results. Section 7 discusses the main findings. Finally, the main conclusions and suggestions for future investigation are given in Section 8.
2. Previous work
The worldwide deployment of Bike Sharing Systems has significantly increased recently, extending beyond major cities as well as medium and small-sized cities. BSS is considered a means to achieve more sustainable cities and provides many benefits, such as convenient, low-cost, and environmentally friendly transportation. It also improves citizens' health and reduces pollution, among other advantages [16], [17], [18], [19]. BSS popularity among citizens is undeniable. They offer a practical solution for avoiding traffic congestion and alleviate many of the burdens related with acquiring a personal bicycle, such as maintenance, possible theft, and bike storage. However, challenges remain, including issues associated with civic behavior, unique city characteristics (e.g., elevation) [20], ensuring equitable access [21], and optimizing re-balancing operations, which have also caught the attention of the political entities.
Notable efforts have been conducted lately to analyze how BSS are being used and to predict the rental demand for bikes. An accurate forecast, especially at peak hours when the system tends to be irregular, will help BSS users to plan their trips in advance [22]. From the point of view of system operators and managers, it could help with re-balancing operations, the proposal of efficient vehicle routes [3], [23] or smart traffic control [24]. Many authors have focused on the study of weather [25], [11], calendar events [11], [26], [27] or important events [12] and their influence in bike use. Other areas of investigation are the characteristics of trips [28], [29], [30], destination preferences [13], [31], traffic flows [32], [12], [33] or the impact of urban configuration [34], [35] in bike usage trends. We share with these authors the aim to identify the diverse sociodemographic or meteorological factors that could influence bike sharing flows. However, our analysis is extended to identify the impact of these features in the station-level prediction models.
The massive data generated by these systems and the fact that many cities have this information publicly available have promoted the study of forecasting models with different approaches in mind. While some authors have predicted the trip destination and duration [36], others focused on the application of different machine learning models for bike demand forecasting [32], [37], [38], [36]. Graph structural information [39] has also been used to improve the results of machine learning models, while deep learning techniques [40] and Recurrent Neural Networks [41] have also been employed. Another area of interest has been clustering using metrics like the “activity score” [42], patterns in trip behavior [43], availability levels [22], or classifications by time interval (day or month) [44]. Likewise, demand forecast at cluster-level has drawn the attention of several authors like Li et al. [45] who predicted bike demand in New York and Washington at station cluster level using a Gradient Boosting Regression Tree. In contrast to these authors, in this study, we focus on the prediction of bike demand at the station level and the improvement of this prediction using different features.
Several studies also investigate machine learning algorithms to forecast demand at the station level. For instance, using a Graph Convolutional Neural Network and data from New York, Lin et al. [7] predicted hourly demand for each station, while Chen et al. [46] utilized a Recurrent Neural Network (RNN). In San Francisco, Random Forest and Least-Squares Boosting have been used by Ashqar et al. [47]. Moreover, smaller BSS has also been studied, Lozano et al. [48] have tested predictive models in Salamanca (Spain) BSS, which has fewer than 50 docking stations. In this paper, we focus on Barcelona, a medium-size BSS with around 500 stations. Unlike the above-mentioned studies, we also explore which features are more important in predicting bike demand in Barcelona.
Moreover, different authors have analyzed Bicing, Barcelona BSS, data. For instance, Froehlich et al. [42] analyzed 13 weeks of Bicing data. They clustered the stations based on their activity and tested four predictive models (Last Value, Historic Mean, Historic Trend, and Bayesian Network) to check the impact of factors that could affect the prediction: the amount of historical data, the time of the day, the prediction window, and station's clusters. Unlike them, we will focus on prediction at the station level and test other sociodemographic and meteorological factors that could influence the system. Dias et al. [49] forecasted the status of Barcelona's BSS system, categorizing stations as completely full, almost full, bikes and slots available, almost empty, and completely empty. Using Random Forest and information about holidays and weather, their predictions were accurate nearly half of the time. We also employ Random Forest, but we will test other variables and how they influence the model. Besides, our goal is to predict the number of arrivals and departures at each station, rather than the status.
Many authors have compared the performance of various prediction algorithms using data from the same city. Cortez and Vázquez [50] developed a visual tool to evaluate and compare four prediction models using data from Barcelona (Spain). However, their focus is on the improvement of visual tools for results comparison rather than on the improvement of model accuracy. Data from Washington, D.C.'s BSS has been used by Yin et al. [51] and Feng et al. [52] to compare the performance of several forecast algorithms. Feng et al. [52] found that the Random Forest model exceeded a traditional Multiple Linear Regression, while Wang and Kim study [8], observed no significant difference in accuracy between Random Forest, GRU, and LSTM when applied to data from the Suzhou (China) BSS. However, Xu et al. study [9] reported that LSTM resulted in more accurate estimations for the Nanjing (China) BSS. Hulot et al. [53] tested Gradient Boosted Tree, Random Forest, and MLP with data from Montreal's system. They concluded that the Gradient Boosted Tree achieved better scores. Li et al. [54] developed five prediction models and an irregular convolutional LSTM model to predict BSS in Chicago, Washington, D.C., New York, and London. We have also compared different prediction algorithms for three BSS in [6]. This paper is a follow-up study where the goal is not to compare different prediction algorithms; rather, our efforts will be focused on identifying how different features can influence the demand forecast using data from Barcelona's BSS.
Multiple studies have attempted to understand and define the factors that determine bicycle usage. Eren and Uz [14] worked on a literature review and compiled different articles that study the factors affecting bike-sharing demand. They divided these factors into six categories: weather, built environment and land use, public transportation, station level, socio-demographic effect and temporal factors, and safety. For them, there are no clear factors that affect demand except for rainy weather, which negatively affects demand in almost all studies. Scott and Ciuro [10] examined the effects of different weather, temporal, and hub attributes on Hamilton's system. They predicted daily arrivals and departures and confirmed that weather and temporal variables are statistically significant. Other variables, such as social and built environments measured at a 200-meter buffer around stations, are insignificant. They were not sure if the chosen distance of 200 meter influenced the significance of the features. El-Assi et al. [11] studied Toronto's BSS and its sociodemographic factors, land use, and built environment attributes to understand bike demand. As in previous studies, they concluded that temperature has a significant correlation with bike use. Faghig-Imani and Eluru [31] have used a Multinomial Logit Model and data from Chicago's system to test the impact of travel distance, land use, built environment, and access to public transportation infrastructure on users' destination preferences. Gao et al. [55] used synthetic data and field data from Shanghai, China, of a dockless BSS to analyze the nonlinear and interactive effects of different built environment factors. However, their focus was the comparison of two methods: the Partial Dependence Analysis (PDA) and the Accumulated Local Effect (ALE) when dealing with correlated features. Data from Seoul, Korea, have been used by Choi et al. [15] to test the influence of different features on bike-sharing demand. They found that the number of bike stations, holders, and climate factors had a significant impact on the prediction. Rixey [56] conducted a regression analysis to determine the most influential features for predicting station-level demand across three U.S. cities. The author found that population density, retail job density, bike lanes, and transit commuters, days of precipitation, and proximity to other bike stations have statistically significant correlations with station-level bike-sharing ridership.
Summarizing, the impact of different features (weather, temporal, environmental attributes, transportation infrastructure) has been analyzed by several authors. It is difficult to generalize which are the most influential features, as each BSS and city has its own characteristics. However, many authors agree that weather features influence BSS demand. Moreover, these studies have focused mainly on cities with larger BSS, and no similar study has been performed using data from medium-sized systems such as Barcelona's BSS. We use the insights provided by these studies regarding the features that could determine bike demand, and test other features related to specific Barcelona characteristics. We especially focus on the facilities (public transportation means, shops, entertainment, cultural, or educational centers, etc.) that are close to the docking stations and the effect they have on Barcelona's BSS demand.
3. Data preparation
Processing, cleaning, and preparing data were carried out using R, as well as model training and evaluation. A Windows 10 machine equipped with an Intel Core i5-6200U CPU running at 2.30 GHz and 16GB of RAM was used.
3.1. Data collection
The information available for this type of study differs among public BSSs. Therefore, we concentrate on Barcelona's BSS, called Bicing. All data, except for weather information, was sourced from Open Data BCN [57], an open data service provided by Barcelona city government. For model training and evaluation, we focused on data spanning from June 1, 2021, to June 7, 2022. Having a period of at least one year is useful to understand how weather, seasons, holidays, and other temporal variables can affect bike demand. Besides, information from previous years was not used for the following reasons:
-
•
The company that provided the bike service in Barcelona was gradually changed during 2019, so there is a lack of continuity in the information during that year.
-
•
The COVID-19 pandemic and associated travel limitations altered user behavior. During several months in 2020, data was unavailable because the system was closed due to lockdown measures.
-
•
Most of the COVID-19 mobility limitations were gradually eased throughout the first half of 2021. Therefore, we consider that data from summer 2021 and onwards could be useful to train and evaluate models as it can capture the new Bicing usage patterns.
After analyzing Bicing, the characteristics of Barcelona, and the previous literature in this area [14], [10], [11], [55], [15], [56], we chose several features that we considered to have an effect on the demand forecast and that were publicly available. A description of the features considered is presented in the following subsections.
3.1.1. Station-characteristics features
Monthly information about the characteristics of the station is provided in Open Data BCN. Most of the given information is static, such as the latitude and longitude. Other data, such as the number of docks, new working stations, or closed stations, also appear in the monthly data. The features collected are listed in Table 1.
Table 1.
Collected features describing Bicing stations' characteristics.
| Features Collected by station |
|---|
| Date and hour |
| Station ID |
| Station Name |
| Station address |
| Station postcode |
| Station bike type (electrical, mechanical or both) |
| Station latitude |
| Station longitude |
| Station altitude |
| Station capacity (total number of docks) |
The timestamp, station ID, and capacity are used to clean the data. To train and evaluate the models, only information about the capacity and altitude is used, as we are not interested in forecasting station usage according to its location; our focus is to predict usage based on station characteristics.
3.1.2. Station-use features
At the start of each month, bike usage data from the prior month is made available to Open Data BCN. Each month, this data can exceed 4 million records, with information collected approximately every 5 minutes. The collected features are detailed in Table 2.
Table 2.
Collected features describing Bicing stations' usage.
| Features Collected by station |
|---|
| Station ID |
| Number of bikes available (mechanical and electrical) |
| Available Mechanical bikes |
| Available Electrical bikes |
| Number of docks available |
| Date and hour |
| Can power electrical bikes (1 or 0) |
| Is properly installed (1 or 0) |
| Provide bikes without problems (1 or 0) |
| Bikes can be returned to the station (1 or 0) |
| Station status (Closed/In service) |
To train and test the forecasting algorithm, only the date and hour, station ID, and total number of available bikes and docks were used as input features. However, to clean the dataset, the last 5 features (Table 2) were used.
3.1.3. Weather features
Weather data was sourced from the website of Time and Date, which provides hourly data for the relevant features used in this investigation. The selected features are detailed in Table 3.
Table 3.
Weather features collected.
| Features Collected |
|---|
| Atmospheric pressure (unit: mbar) |
| Humidity (unit: %) |
| Temperature (unit: Celsius) |
| Visibility (unit: numerical) |
| Weather type (text) |
| Wind (unit: km/h) |
More than 80% of the data for the feature ‘Visibility’ is missing, so we did not use this feature.
3.1.4. Spatial features
This information can also be found at the Open Data BCN website [57]. All the features have geolocation information (latitude and longitude). The frequency of update of each feature varies; some are updated monthly, weekly, or depending on the needs of surveys or censuses. None of the features have historical information available, except for ‘Economic Activities.’ The features collected are described as follows:
-
•
Economic Activities: Corresponds to a census from 2019 of ground-floor economic activities in the city of Barcelona.
-
•
Music and drink spaces: This dataset contains a list of all music bars, pubs, cocktails, discotheques, karaokes, nightclubs, ballrooms, flamenco tablaos, and any other music and drink venues registered in Barcelona.
-
•
Parks and gardens
-
•
Culture spaces: A list of all libraries, cinemas, bookshops, museums, viewing points, theaters, concert halls, and auditoriums.
-
•
Education facilities: Educational centers located in Barcelona of different types: infants, primary, secondary, professional training, special education, adult lifelong learning. For this study, data from infant, primary, and secondary centers have been removed.
-
•
Sports spaces: Information about sports clubs, federations, and sports facilities is included.
-
•
Markets: markets and shopping centers in Barcelona.
-
•
Health facilities: This dataset includes primary care centers, hospitals, private medical centers, pharmacies, ambulance services, mental health and drug addiction treatment centers, and clinical analysis laboratories.
-
•
Religious services: Information about different religious service centers.
-
•
Beaches
-
•
Restaurants
-
•
Car Parking
-
•
Taxi stops
-
•
Public transports: Metro, RENFE, FGC, funicular, cable car, tramcar, and other public transport facilities except for buses.
-
•
Bus stops: It contains day, night, and airport bus stops in Barcelona city.
3.2. Data cleaning and processing
3.2.1. Data cleaning
Data cleaning has been performed separately for features related to the stations' usage (arrivals and departures) and weather information. Spatial features were already cleaned. For the first group, data cleaning involved removing those stations that, despite appearing in the original dataset, were not being used. Additionally, stations that remained unused throughout the entire one-year period were removed from the dataset, along with those that were malfunctioning or designated as test stations (around 3%). Moreover, erroneous data, including dates outside the analyzed range (June 2021 to June 2022) and negative bike availability figures, were removed from the dataset. Missing data were imputed only for those stations with less than 10% of missing information and when missing data were not sequential, i.e., when the missing data points were random within the dataset and did not span an entire period (day or week). In this case, 9 stations were deleted, which represents less than 1% of the total data. Given that data were available every 5 minutes, linear interpolation was used to impute the missing data, as simpler methods usually give good results [58], [59].
A similar procedure was applied to the weather data, with missing values being imputed through linear interpolation. However, the feature ‘variability’ was not used as it had more than 80% of missing data. The ‘weather type’ feature has text information of the weather and has variations due to misspellings and punctuation. We grouped these categories into five weather types: snow, heavy rain, light rain, cloudy and sunny.
3.2.2. Data processing
Following the data cleaning process, bike usage and weather datasets were merged and grouped into time intervals. The same four periods computed in [6] have been considered:
-
•
night: from 01:00 to 06:59
-
•
morning: from 07:00 to 12:59
-
•
afternoon: from 13:00 to 18:59
-
•
evening: from 19:00 to 00:59
As in [6], supplementary information was computed as it was required for model training, such as day of the week (Monday to Sunday), season (spring, summer, autumn, winter), month, time interval, holiday (1 if the given day is a holiday in Barcelona and 0 if it is a normal day), and total arrivals and departures by station and time interval. Later, the altitude and capacity of each station were added. In addition, for each station, their spatial characteristics, i.e., the number of other docking stations, bus stops, restaurants and other facilities that are close to the given station in a 200 meters ratio, were calculated using the Haversine formula. Moreover, the Usage Ratio was also computed:
Usage Ratio
The ratio computed in [60] has been calculated as it facilitates the identification of the more frequently used stations. It was derived from the frequency of pickups (departures) and drop-offs (arrivals). Its calculation is shown in equation (1).
| (1) |
Where i = StationID, j = day, k= hour interval
To improve interpretation, we normalized the ratio so that all values fall between 0 and 1, creating a uniform scale, as it is shown in equation (2)
| (2) |
Where i = StationID, j = day, k= hour interval
Finally, the dataset was split into training and testing subsets. The training data comprised the period from June 1, 2021, to May 31, 2022, while the testing set covered the first week of June 2022, from June 1 to June 7, and was used for model evaluation and feature importance analysis. The features employed to train and evaluate the Random Forest model are summarized in Table 4.
Table 4.
Description of features for training and evaluating the Random Forest Model.
| Category | Feature | Type |
|---|---|---|
| Time | Date | DateTime |
| Day (Mon-Sun) | Categorical | |
| Holiday (1 or 0) | Categorical | |
| Month (Jan-Dec) | Categorical | |
| Season (1-4) | Categorical | |
| Time Interval (1-4) | Categorical | |
| Weather (t-1) | Humidity | Real Value |
| Pressure | Real Value | |
| Temperature | Real Value | |
| Weather Type (1-5) | Categorical | |
| Wind | Real Value | |
| Station characteristics | # arrivals | Real Value |
| # departures | Real Value | |
| Station altitude | Real Value | |
| Station Capacity | Real Value | |
| Spatial features | Economic Activities | Real Value |
| Bus stops | Real Value | |
| Music Drink spaces | Real Value | |
| Parks Gardens | Real Value | |
| Cultural spaces | Real Value | |
| Education facilities | Real Value | |
| Sport spaces | Real Value | |
| Markets | Real Value | |
| Health facilities | Real Value | |
| Religious services | Real Value | |
| Beaches | Real Value | |
| Restaurants | Real Value | |
| Car parkings | Real Value | |
| Taxi Stops | Real Value | |
| Public transports | Real Value | |
| Bike stations | Real Value | |
4. Data analysis
In this section, we explore the features collected and their correlations. Besides, an analysis of the usage patterns is presented.
4.1. Time-dependent features
The time-dependent features vary over time, but are constant for all the stations in the Bicing system. In this case, all the weather features meet this condition. A short summary of the numerical weather features is displayed in Table 5. By analyzing this table, we could say that Barcelona has Mediterranean weather with mild conditions throughout the year, which can favor the riding conditions for citizens.
Table 5.
Summary of the numerical weather features.
| Min | 1st Qu. | Median | Mean | 3rd Qu. | Max | |
|---|---|---|---|---|---|---|
| Temperature | 2 | 12 | 19 | 18 | 24 | 30 |
| Wind | 1 | 3 | 4 | 4.78 | 6 | 37 |
| Humidity | 15 | 64 | 73 | 71.51 | 80 | 100 |
| Pressure | 997 | 1014 | 1017 | 1017 | 1021 | 1035 |
4.2. Space-dependent features
The space-dependent features are constant over time but vary by station in the Bicing system according to their geographical location. In this case, all the spatial features have these characteristics, plus the altitude and station capacity (total number of docks), which describe the station's own attributes. It is important to highlight that these features could change over the period considered, but these changes are small, contrary to the weather features, which varied in each time interval. Table 6 displays the statistical summary of these features. As it is shown, each station had on average less than 10 facilities of each type within a 200-meter radius. However, the economic activities reach an average of 204 for each station and a maximum of 817 for some docking stations.
Table 6.
Summary of the features that vary over the space and are constant during the period considered.
| Min | 1st Qu. | Median | Mean | 3rd Qu. | Max | |
|---|---|---|---|---|---|---|
| Altitude | 2 | 9 | 25 | 35.5 | 53 | 166 |
| Total docks | 12 | 24 | 27 | 27.09 | 29 | 54 |
| Beaches | 0 | 0 | 0 | 0.19 | 0 | 2 |
| Parks & Gardens | 0 | 0 | 0 | 0.87 | 1 | 7 |
| Markets | 0 | 0 | 0 | 0.43 | 1 | 7 |
| Religious services | 0 | 0 | 1 | 2.1 | 3 | 24 |
| Music & Drink spaces | 0 | 0 | 0 | 1.84 | 2 | 30 |
| Education facilities | 0 | 1 | 3 | 3.28 | 4 | 29 |
| Health facilities | 0 | 3 | 5 | 5.79 | 8 | 26 |
| Cultural Spaces | 0 | 3 | 5 | 6.75 | 9 | 36 |
| Sport spaces | 0 | 2 | 5 | 8.65 | 12 | 54 |
| Restaurants | 0 | 1 | 4 | 7.81 | 12 | 57 |
| Economic Activities | 0 | 95.25 | 127 | 204.91 | 292 | 817 |
| Bus stops | 0 | 4 | 6 | 6.39 | 9 | 29 |
| Public transports | 0 | 0 | 0 | 1.55 | 3 | 17 |
| Bike stations | 0 | 0 | 0 | 0.7 | 1 | 4 |
| Taxi stops | 0 | 0 | 0 | 0.836 | 1 | 7 |
| Car parkings | 0 | 0 | 1 | 1.61 | 3 | 8 |
4.3. Correlation analysis
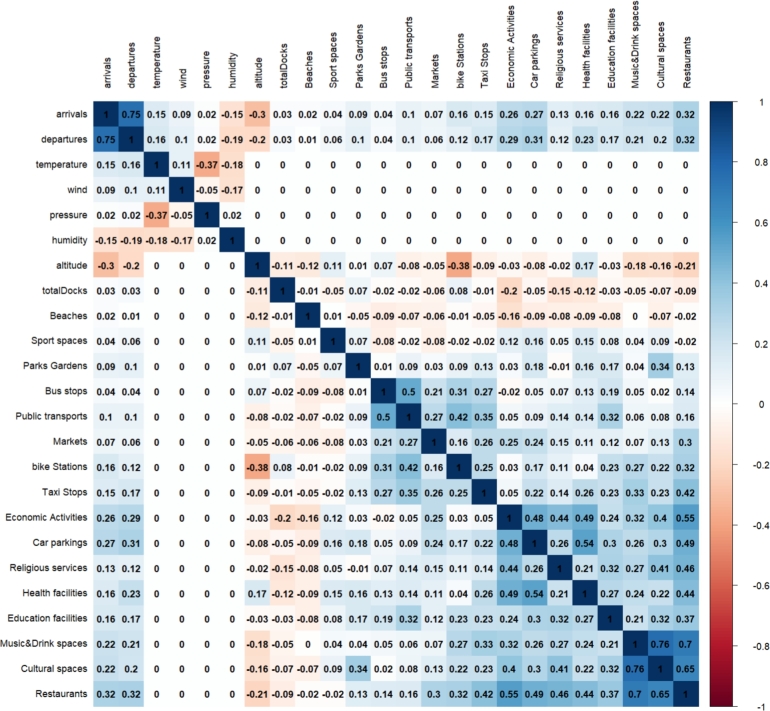
The relationship between the numerical features displayed in Table 4 has been analyzed using the Pearson correlation coefficient. Fig. 1 shows the correlation of arrivals and departures with the other numerical features in the first two columns (or rows). The correlation between arrivals and departures is equal to 0.75. This strong positive correlation can be explained from the perspective of usage behavior. When a station has more (or less) bikes arriving, there will be more (or less) bikes available to be picked up by customers. Both arrivals and departures have similar correlation values and do not show any strong correlation with any of the features considered. The features Restaurants, car parking, and economic activities are the only ones with a positive correlation greater than 0.25 with arrivals and departures, while the station's altitude has a negative correlation (-0.3). This can be explained by the citizens' preferences for using bikes to go downhill [20]; to avoid sweating and tiredness when going uphill, they might use alternative transport methods such as the metro, buses, or moped and scooter sharing services, which have increased in popularity recently [61], [62].
Figure 1.
Correlation between arrivals, departures, and the other numerical features considered for the feature importance analysis using the Random Forest method. The correlation between arrivals and departures is strong and positive (0.76). However, there is no significant correlation with the other features considered. The weather-related features are only correlated with the target features (negative for humidity and positive for the others), and they have a value of 0, indicating no correlation, with the other features. Finally, features like music and drink, cultural spaces, and restaurants, have strong positive correlations among themselves.
Another interesting insight that was found is the lack of correlation between the weather-related features (humidity, pressure, temperature, and wind) with all the other numerical features, except for the arrivals and departures. As shown in Fig. 1, we see a value of 0 in the corresponding cells of the correlation matrix. This is caused by the nature of the spatial features, the altitude, and stations' capacity. These values are static and barely change over the considered period. However, the arrivals, departures, and weather features vary over time. Moreover, there are strong correlations between the station characteristics features. For instance, the ‘Culture spaces’ and ‘Music and Drink spaces’ features have a correlation of 0.76, which can be interpreted as an increase in the number of Music and Drink venues around a bike station when there are Cultural spaces. Similarly, ‘Restaurants’ and ‘Music and Drinks’ facilities also have a significant correlation of 0.7. Features like ‘Markets’, ‘Sports’ and ‘Education facilities’, ‘Parks and Gardens’, and ‘Taxi stops’ do not have a strong correlation with any other feature. In the case of the feature ‘Beach’, the correlation is generally negative, but the values are close to zero. Therefore, we cannot consider this correlation significant.
Finally, we can conclude that even though we do not observe a strong correlation between arrivals, departures, and the other numerical features, it is well known that significant correlation does not imply causation. Besides, we have based the selection of features on the previous literature [14], [10], [11], [55], [15], [56] as well as the information available for Barcelona through Open Data BCN.
4.4. Usage analysis
Barcelona is a city with an elevation above sea level that varies between 0 m to 516 m in the highest part of the city (Tibidabo). However, most of the city, as well as the docking stations of this BSS, are located up to 130 meters above sea level. This altitude variation, together with other variables that influence usage, makes some stations more or less dynamic. In fact, stations situated around the center of the city exhibit a higher Usage Ratio, as demonstrated in [6].
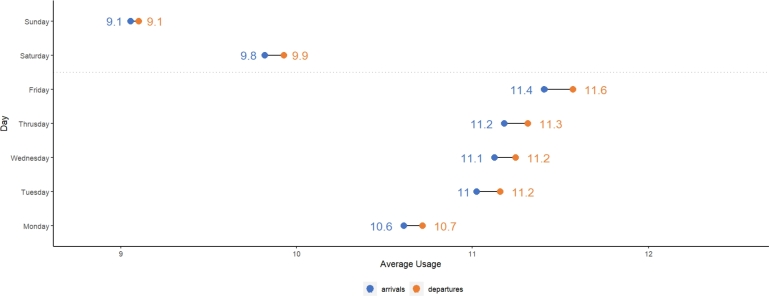
Fig. 2 contains the average usage by day of the week (Monday to Sunday). Departures are higher than arrivals by a small margin, but they remain at similar levels. Moreover, there is a clear pattern of usage: The Bicing system is actively used during weekdays. Its arrivals and departures slightly increase as the working days progress, with Friday being the day with the highest usage (arrivals and departures). During the weekends, both arrivals and departures decrease. Therefore, we can hypothesize that the Bicing system is mainly used for work- and study-related activities. However, to test this hypothesis and gain insights into customer usage preferences, a more detailed study using customer surveys will be necessary, similar to the approach taken in Alonso et al.'s research [63]. Furthermore, when checking the usage by the time intervals defined in the Data Cleaning section, the first interval (from 1:00 to 06:59) is the least dynamic, while the third interval (from 13:00 to 18:59) is the most dynamic, as shown in Table 8.
Figure 2.
Usage average by day. Departures exceed arrivals by a small margin. The Bicing system is used more frequently during workdays, with usage peaking on Friday. On Saturday and Sunday, usage decreases.
Table 8.
Error metrics and average usage by hour interval. The error is bigger during the first interval for arrivals and departures, when the Usage Ratio is the lowest.
| Arrivals |
Departures |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | nRMSE | RMSLE | Usage Ratio | RMSE | nRMSE | RMSLE | Usage ratio | ||
| Interval 1 | 01:00-06:59 | 3.27 | 0.95 | 0.53 | 4.02 | 3.47 | 1.15 | 0.58 | 3.69 |
| Interval 2 | 07:00-12:59 | 4.46 | 0.45 | 0.39 | 11.20 | 4.71 | 0.44 | 0.39 | 12.15 |
| Interval 3 | 13:00-18:59 | 4.18 | 0.31 | 0.32 | 14.35 | 4.55 | 0.32 | 0.33 | 14.99 |
| Interval 4 | 19:00-00:59 | 4.37 | 0.35 | 0.34 | 12.85 | 4.22 | 0.36 | 0.36 | 12.06 |
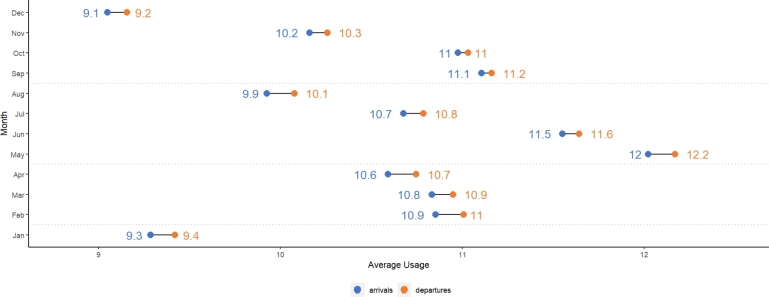
Monthly usage also presents patterns that are similar for arrivals and departures. Even though the weather variation in Barcelona is not extreme, we can relate the weather to the usage patterns displayed in Fig. 3. May has the largest number of arrivals and departures, but these metrics begin to decrease and reach a lower point in August. We can assume that Bicing usage declines when the temperature increases as summer arrives. August in Barcelona is characterized by higher temperatures (around 29 °C) and high humidity levels, which make it unpleasant to use a means of transportation that requires physical effort. Also, July and August are a holiday period when many people take a break and numerous work and study activities are suspended. During September, arrivals and departures increase again, but not to the same levels as in May. Following this peak, usage decreases towards December. However, September and October have similar levels of arrivals and departures. During these months, the temperature varies between 17 and 21 °C, which could promote bike usage. During November, December, and January, temperatures are often below 10 °C. Nevertheless, usage during December is the lowest of the year. In addition to the weather, another reason for its low use may be the Christmas vacation period in December. The final usage pattern can be seen during February, March, and April. As before, usage increases in February and then slowly decreases towards April. The average temperature during these months varies between 10 and 14 °C.
Figure 3.
Usage average by month. Between May and August, the usage average is higher, and the system is more dynamic. This could be related to temperature. Similarly, during the autumn and winter months, usage decreases progressively. From February to April, levels of usage slightly vary.
5. Prediction model and error metrics used
Considering the results provided by Cortez et al. study [6], which showed that Random Forest is the model that generally outperforms other predictive algorithms for the Barcelona BSS, we chose it to evaluate the influence of the described features on bike arrivals and departures' forecasting.
5.1. Random Forest (RF)
The Random Forest algorithm is a powerful tree learning technique in Machine Learning. It creates an uncorrelated forest of decision trees by using bagging and feature randomness. Each of these Decision Trees are constructed using a random subset of the dataset to measure a random subset of features in each partition. This randomness introduces variability among individual trees, reducing the risk of overfitting and improving overall prediction performance. However, due to the large number of trees, the algorithm can be computationally intensive. Additional information is available in [64].
5.2. Root Mean Square Error
Root Mean Square Error (RMSE) quantifies the discrepancy between model predictions and actual observed values. It is calculated as the square root of the average of squared errors. In fact, RMSE is sensitive to outliers because each error's impact is proportional to the squared error's magnitude. Moreover, while a lower Root Mean Square Error (RMSE) is generally preferable, it's essential to consider the context as this metric is sensitive to the data scale used. Therefore, comparing RMSE values in different scales or data types would be inappropriate. It can be computed as it is shown in equation (3):
| (3) |
Where are the predicted values, are the observed values, and n is the number of observations.
5.3. Normalized Root Mean Square Error
It is also known as nRMSE. It is an error metric that enables comparisons between models with different scales. Therefore, the key distinction between RMSE and nRMSE lies in the absence of units for nRMSE, allowing it to be interpreted as a relative measure. To normalize RMSE, various methods can be employed, including using the mean, interquartile range, standard deviation, or the difference between maximum and minimum values. In this study, we followed the approach used by [6], which utilizes the mean. Equation (4) summarizes its calculation:
| (4) |
Where is the observed values' mean.
5.4. Root Mean Square Logarithmic Error
Root Mean Square Logarithmic Error or RMSLE is a commonly used error metric in BSS demand prediction, particularly in Kaggle competitions. Its robustness to outliers makes it popular. The formula for RMSLE involves taking the logarithm of the predicted and actual values, which effectively reduces the impact of outliers. RMSLE is usually considered as the relative error between predictions and real values because of its unitless nature. It is computed as shown in equation (5):
| (5) |
Where are the predicted values, are the observed values, and n is the number of observations.
6. Results
6.1. Overall results
Table 7 contains the error metrics. The RMSE is 4.10 for arrivals and 4.27 for departures. This means that on average, the difference between the real and predicted values is 4 bikes. Moreover, the percentage error nRMSE is 0.34 for arrivals and 0.35 for departures. Similarly, the RMSLE for arrivals is equal to 0.40 and for departures is 0.43. As we can see, the error metrics are slightly higher for departures forecast than for arrivals.
Table 7.
Error metrics for the Random Forest algorithm. The forecasting error for arrivals is slightly lower than for departures. There is a prediction error for arrivals and departures of around 4 bikes. The percentage error is around 30%.
| Metric | Arrivals | Departures |
|---|---|---|
| RMSE | 4.10 | 4.27 |
| nRMSE | 0.34 | 0.35 |
| RMSLE | 0.40 | 0.43 |
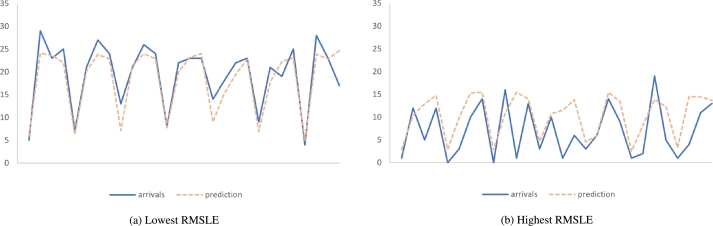
The predicted, and real arrivals for the stations with the largest and the lowest RMSLE are displayed in Fig. 4. On the left side (Fig. 4-(a)) readers can see the station with the lowest RMSLE where the prediction is quite accurate. The estimated values for arrivals closely follow the trend, particularly during peak usage periods. On the right (Fig. 4-(b)), data for the docking station exhibiting the largest error metrics is shown. We can observe that Random Forest is failing to estimate the values when the usage of the station is low, similar to what was found in [6].
Figure 4.
Arrivals predicted and real values for the stations with the lowest (a) and highest (b) RMSLE using Random Forest. The left side of the figure shows that arrivals are being predicted more accurately. The right side of the figure displays that Random Forest is failing to capture the trend when the usage levels are low.
6.2. Impact of Usage Ratio
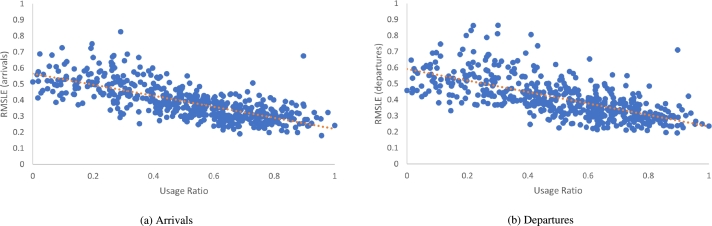
The Usage Ratio (refer to section 3.2) and error metrics were computed for all Bicing docking stations. Their relationship is shown in Fig. 5-(a) for arrivals and Fig. 5-(b) for departures, which illustrates a strong linear correlation between these variables. This correlation is negative, indicating that as the Usage Ratio decreases, the error metric increases. A similar relationship was also found in [6].
Figure 5.
Error metric and Usage Ratio in Barcelona. In Barcelona, the error metric and Usage Ratio exhibit a negative linear relationship, indicating that as one metric increases, the other decreases.
6.3. Error temporal distribution
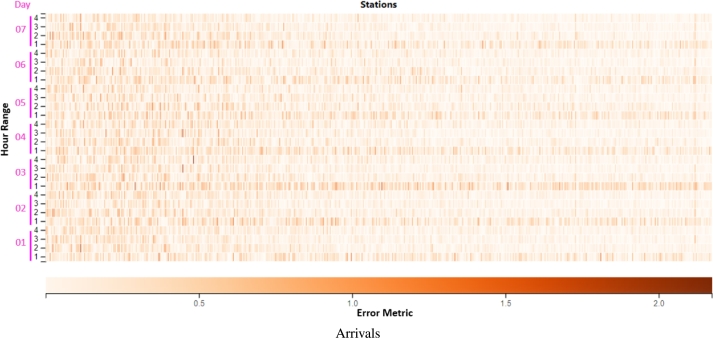
Error metrics were also calculated by station, interval, and date within the test subset, which covers the first week of June 2022. Fig. 6 illustrates a heatmap for the arrivals, where the orange color is used to represent the error metric (RMSLE) scale. The docking stations have been ordered ascending from left to right using the Usage Ratio. As we can see, the inverse relationship between the error metric and the Usage Ratio in Barcelona is again clear: the color tone is darker on the left, where the error is higher, and it becomes lighter as we move to the right, where the Usage Ratio increases. Moreover, errors are higher (darker color) for the first time interval (from 01:00 to 06:59) of each day. This happens because the prediction error has a strong negative relationship with the station's Usage Ratio. Error metrics increase when the station is less used, including daily early hours when there are few or no movements at the stations. A similar pattern was found in [6].
Figure 6.
The heatmap shows the information of bike stations on the X-axis, ordered by Usage Ratio. The vertical axis shows the predicted days, subdivided into time intervals throughout the day. The error metric variation is depicted in orange tones and shows a clear pattern. The first interval (from 01:00 to 06:59), usually has a bigger error. Additionally, the negative relationship between the error metric and Usage Ratio in Barcelona is again clear, as the stations with lower Usage Ratio also have a greater error (the orange tones are darker for stations on the left).
6.4. Feature importance analysis
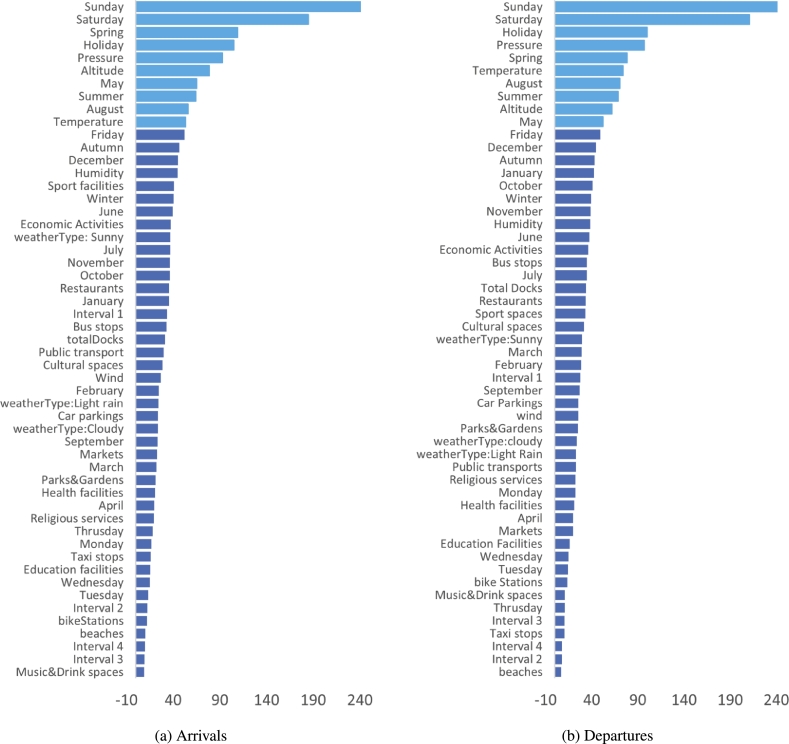
A key piece to getting accurate predictions when building good machine learning models is the selection of the appropriate features. Given that the Random Forest package in R also provides feature importance measures, we have used it to analyze the results. The R package provides two measures: %IncMSE and IncNodePurity [65]. We will use the %IncMSE measure as it is the most robust and informative. In this case, we can interpret that the higher the metric is, the more important the feature is. Fig. 7 displays the features in descending order, considering the %IncMSE metric for both arrivals and departures. We can see that the features in departures have a slightly larger value for this metric. Nevertheless, to make a proper analysis, it is important to consider that the feature importance analysis provided by Random Forest cannot be interpreted as the level or direction (negative or positive) of how features are influencing the model. The feature importance only provides information about the relevance of the variables to the model.
Figure 7.
There are 53 features used to train the Random Forest Model for arrivals and departures. Some specific days, months, or weather seasons have bigger effect in the prediction model.
Initially, 30 features were used to train the models for arrivals and departures (see Table 4), of which 6 features are categorical: Season, Month, day, time interval, holiday, and weather type. After dealing with these features using one-hot encoding, the models were fed with 53 variables, which are shown in Fig. 7. This way, we can analyze the impact of each category on the model. For example, we can see that some specific days, months, or seasons have a greater effect on the model.
A closer look at the 10 most important features, displayed in light-blue in Fig. 7, shows that Sunday and Saturday are the features with the largest impact on arrivals and departures using the Random Forest model. Considering that during weekends, the usage decreases (Fig. 2), and that in Barcelona, when a station is less dynamic, the prediction error increases, as shown in Fig. 5, we can assume that those features, Saturday and Sunday, negatively affect the prediction. However, as mentioned in the previous paragraph, the Random Forest feature importance analysis does not provide a “direction” of how features influence the model. The direction of the influence can be inferred by analyzing the results in depth.
Holiday and the spring season features are also relevant in the arrivals model and slightly less important in the departures model. Summer also contributes to the prediction model, as well as the temperature. In fact, for both arrivals and departures, the seasons and months are related to the temperature. For example, May (spring season) has a pleasant temperature that can contribute to bike usage, similar to late August (late summer). As explained in the 4, May is the month with the highest number of arrivals and departures for all bike stations during the analyzed period. A surprising factor is the pressure feature, which also plays an important role in the forecasting models. Conversely, the altitude was an expected important feature, and it has a negative correlation with both arrivals and departures. According to the results, none of the facilities within a 200-meter radius of each station (spatial features) plays an important role or influences the prediction model significantly. This could be related to the constant nature of these variables over time. Most of these facilities require time to be built, and even when the databases are updated weekly or monthly, the number of facilities barely changes. These results align with the findings of previous studies summarized in [14].
Finally, there are some minor differences between the feature importance analysis for arrivals (Fig. 7-(a)) and departures (Fig. 7-(b)). These differences could be in the magnitude of the %IncMSE metric or the order of the features. However, as mentioned before, the magnitude cannot be interpreted as the level of ‘importance’ of the feature. On the other hand, the different order of the variables can be explained by the random nature of the prediction model used (Random Forest), as each tree is built by randomly selecting features.
7. Discussion
This paper is a follow-up study of [6], where the objective was to compare different models' performance for three BSS with different characteristics and size during the same period and using the same features. For this reason, the date range was restricted to be sure that the required data was available for the three cities selected in [6]. In this new study, we have used a different and longer period, from June 2021 to May 2022, to train the models and the first week of June 2022 to evaluate them. We have used a one-year period with the objective of capturing the seasonal trends present in the data that were not possible to study with a shorter period. Moreover, it also allows the evaluation of features that are relevant only when at least one year's data is considered, such as holidays, seasons, and months. During data cleaning, we removed some incorrect data and imputed missing values, which represents around 1% of the total dataset. Their removal caused any bias.
Given that the date range differs in [6] and this study, we cannot directly compare the results obtained in both investigations, as the dataset used is different. Even though the error metrics are not comparable, we can identify some similarities. For example, the correlation between the Usage Ratio and the error is linear and negative, even when the data period used is different. This is the same relationship found in [6] for Barcelona. Additionally, the temporal distribution of the error found in [6] matches with the pattern shown in Fig. 6. It means the error is more significant during the first interval of each day in the test set. Table 8 displays the error metrics by time interval as an average for all stations. We can see that RMSLE is larger for the first time interval when the Usage Ratio is the lowest. This occurs due to the low number of arrivals and departures between 01:00 and 06:59 AM.
As was mentioned in the previous paragraph, when the Usage Ratio increases, the prediction becomes more accurate. For instance, if a station experiences low usage behavior with one bike arriving during the first time interval, a prediction of two arrivals represents an error of 100%. However, if during any other time interval the same station has 5 arrivals and the prediction is 6, even though the RMSE error will be the same (1 bike), the percentage error will be only 20%. This example also helps to underscore the importance of selecting the appropriate error metric to interpret the results. In fact, when analyzing the RMSE metric in Table 8, during the first interval, this metric is lower than in other intervals. However, as mentioned before, an error of 3 bikes during this interval can represent an error of almost 100%, while for other intervals, an error of 4 bikes might represent a deviation of around 30%.
The usage analysis by day and month also revealed interesting patterns. For instance, during weekends, the usage decreases (see Fig. 2). Furthermore, months with less favorable weather conditions, such as winter or early spring, also have lower usage (see Fig. 3). From May to August, the usage is high compared to other months, which could be attributed to the pleasant spring and summer weather in Barcelona. Feature importance analysis indicates that the months of May and August play a significant role in the prediction model, similar to the weekend days: Saturday and Sunday. However, the feature importance metrics provided by the Random Forest model do not indicate the magnitude and direction (decrease or increase) of the influence of these factors. Given the linear and negative relationship between the error and the Usage Ratio, we can formulate two hypotheses:
-
•
The categorical features that indicate the weekend days (Saturday and Sunday), where the Usage Ratio is lower, negatively influence the prediction accuracy, and the error metrics will likely increase.
-
•
The categorical features of the months May, August, and the seasons of spring and summer, where the Usage Ratio increases, positively influence the prediction accuracy, and the error metrics will likely decrease.
Nevertheless, these hypotheses need to be tested with more data.
The temperature and air pressure were among the most important features, as well as other features related to weather such as summer, spring, and the months of May and August. Previous studies [10], [11], [15] also found that weather-related features play a significant role in explaining bike demand; however, it depends on each city under analysis. For example, for some BSS, winter and rainy days are more influential, but this is not the case in Barcelona, where most days during the period under analysis were sunny, and the weather is generally pleasant. Additionally, a surprising finding is that none of the spatial features considered (facilities within a radius of 200 meters for each station) were among the most important features for both arrivals and departures. In fact, these features are among the least important. This result can be related to the fact that spatial features are static, while the others change over time. Unfortunately, not enough historical information is available to include possible variations of these features in the dataset; even if enough historical information were available, the results would likely be similar, as most of these facilities take time to be built, so their numbers will remain stable over time. Similar to our results, Scoot and Ciuro [10] found that the built environment within a 200-meter radius was not significant for bike demand prediction. However, Rixey study [56] found that features like population density, retail job density, bike lanes, and proximity to other bike stations have a significant correlation with bike-sharing ridership. Unfortunately, data on job or population density and bike lanes were not available for Barcelona, so we could not test these features. The feature that represents the number of bike stations within a 200-meter radius was not significant for Barcelona's BSS. This highlights once again the variation in each BSS and the challenges in generalizing the features that influence bike demand across all BSS, as it depends on the characteristics of each system.
For arrivals and departures, the analysis of the first 10 most important features shows that they are the same in both scenarios. However, the ranking of the features in terms of importance is different. This may be attributed to the Random Forest algorithm's method, which involves selecting a random subset of features for each decision tree.
The results of feature importance given by Random Forest have certain limitations. The most relevant is that the calculation is performed using an impurity-based method, which evaluates how much a feature contributes to reducing impurity in each tree. Therefore, the importance assigned to features with high cardinality can be inflated and may not accurately reflect their real impact, since this method tends to favor features with many unique values. Considering this, it will be important to contrast the results against other feature importance techniques like Shapley values or LIME (Local Interpretable Model-Agnostic Explanations). Different studies show some similarities but also differences among the feature importance results of different techniques [58]. We aim to perform a comparison of these techniques in future research.
Finally, K-fold cross-validation is a recommended method used for evaluating the robustness of the model. However, the time series data used in this dissertation does not allow its direct application because each observation in the time series dataset is not independent; they are strongly correlated with their previous and future observations. Moreover, cross-validation methods are not suitable for directly assessing feature importance. The main reason is that, due to the random splitting of the data, cross-validation may not include all the relevant information needed to assess the importance of a feature. This can lead to assigning similar weights to different features, even if one of them is more important than the others, resulting in an inaccurate assessment of feature importance. [66].
8. Conclusions
Considering that the factors influencing bike demand can vary across different BSS, we focused on the Barcelona BSS known as Bicing for a more detailed analysis. This study is a follow-up of [6], where the Random Forest model had the best performance for Barcelona data. Therefore, a Random Forest model was trained using data from June 2021 to May 2022 and tested using the first week of June 2022. During the selected period, all restrictions resulting from the COVID-19 pandemic were lifted, allowing us to assume that Bicing had a “new-normal” behavior. We used a one-year period (from June 2021 to June 2022) to study the features that define the characteristics of all the stations in the Barcelona BSS. This facilitated understanding the effects of weather, seasons, holidays, and other temporal variables on bike demand. In addition to these features, we also included the stations' altitude and capacity, as well as other spatial features used to describe the facilities close to each docking station. These features are described in Table 4.
After the models for arrivals and departures were trained and tested, we found an RMSE of around 4 bikes and the percentage error (nRMSE) of around 30% for both scenarios. We also investigated the association between Usage Ratio and the error metric, discovering a distinct linear negative correlation: as the Usage Ratio increases, the error metric decreases. The analysis of error metrics by hour intervals also shows a larger error during the first time interval (from 01:00 to 06:59) when the usage dynamic is the lowest. These results are similar to the ones found in Cortez et al. study [6].
Feature importance was provided directly by Random Forest. Weekend days are the most important features, as well as two months: May and August, which are related to the spring and summer seasons that are also part of the 10 most important features. Temperature, pressure, altitude, and holidays also have a significant influence. For both arrivals and departures, the 10 most important features are similar but ranked differently. This could be explained by the random selection of features in each tree of the Random Forest. Moreover, the coefficient of %IncMSE cannot be interpreted as the contribution of the feature to the model. This value only shows the influence that features have, but not the magnitude nor the direction (increase, decrease). A surprising factor is that none of the spatial features considered in this analysis are among the most important features. In fact, music, and drink spaces, beaches, and bike stations within a 200-meter radius are among the least important features for arrivals and departures. These results are in line with the studies performed by different authors and summarized in [14]. The outcomes of this study can help as a reference to improve Bicing demand, establish policies to improve the Bicing service, optimize it, and promote its use among Barcelona residents.
8.1. Limitations and future research
As mentioned in the discussion section, there are some limitations to this study. The first one is related to the data availability. Unfortunately, we were unable to test certain desirable features, such as job and population density, due to their unavailability. Moreover, due to COVID-19 mobility restrictions, changes in the Bicing operator, and data availability on the Open Data platform, the period under analysis is restricted to one year. However, a one-year period is enough to understand the seasonal patterns present in the data. The analysis of COVID-19's impact on Bicing mobility can be found in [67].
Another limitation of this study is the restricted insight provided by the feature importance results from the Random Forest model, as previously discussed. However, these initial findings serve as a valuable foundation for a more in-depth analysis. As future work, exploring other feature importance techniques, such as Shapley values or LIME (Local Interpretable Model-Agnostic Explanations), can be helpful to evaluate the obtained results.
We have also considered analyzing and improving model predictions for stations with a high Usage Ratio, as these stations can be particularly busy or empty during peak hours, which has a significant impact on system optimization and customer satisfaction. Another research direction we are exploring is predicting station status (empty, normal, or full) instead of the number of arrivals and departures. This can help us test other forecasting algorithms and analyze their performance, as well as the differences between classification and regression models in BSS. Finally, we are also interested in studying events that can affect bike usage, such as football matches, concerts, and other situations that temporarily increase or decrease bike usage. Capturing the information about these events can assist in improving prediction algorithms.
CRediT authorship contribution statement
Alexandra Cortez-Ordoñez: Writing – review & editing, Writing – original draft, Visualization, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Pere-Pau Vázquez: Writing – review & editing, Supervision, Methodology, Conceptualization. Jose Antonio Sanchez-Espigares: Writing – review & editing, Supervision, Methodology, Conceptualization.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This project has been supported by PID2021-122136OB-C21 from the Ministerio de Ciencia e Innovación, by 839 FEDER (EU) funds and 2021SGR00613-(ADBD) by Generalitat de Cataluña.
Contributor Information
Alexandra Cortez-Ordoñez, Email: alexandra.cortez@upc.edu.
Pere-Pau Vázquez, Email: pere.pau.vazquez@upc.edu.
Jose Antonio Sanchez-Espigares, Email: josep.a.sanchez@upc.edu.
Data availability statement
The datasets used and analyzed in this study are property of Open Data Barcelona. The authors do not have permission to share data.
References
- 1.Fishman E. Bikeshare. A review of recent literature. Transp. Rev. 2016;36(1):92–113. [Google Scholar]
- 2.O'Brien O., Cheshire J., Batty M. Mining bicycle sharing data for generating insights into sustainable transport systems. J. Transp. Geogr. 2014;34:262–273. doi: 10.1016/j.jtrangeo.2013.06.007. [DOI] [Google Scholar]
- 3.Raidl G.R., Hu B., Rainer-Harbach M., Papazek P. International Workshop on Hybrid Metaheuristics. Springer; 2013. Balancing bicycle sharing systems: improving a vns by efficiently determining optimal loading operations; pp. 130–143. [DOI] [Google Scholar]
- 4.Rainer-Harbach M., Papazek P., Hu B., Raidl G.R. European Conference on Evolutionary Computation in Combinatorial Optimization. Springer; 2013. Balancing bicycle sharing systems: a variable neighborhood search approach; pp. 121–132. [DOI] [Google Scholar]
- 5.Kloimüllner C., Papazek P., Hu B., Raidl G.R. European Conference on Evolutionary Computation in Combinatorial Optimization. Springer; 2014. Balancing bicycle sharing systems: an approach for the dynamic case; pp. 73–84. [DOI] [Google Scholar]
- 6.Cortez-Ordoñez A., Vázquez P.P., Sanchez-Espigares J.A. Scalability evaluation of forecasting methods applied to bicycle sharing systems. 2023. https://doi.org/10.1016/j.heliyon.2023.e20129 p. e20129. [DOI] [PMC free article] [PubMed]
- 7.Lin L., He Z., Peeta S. Predicting station-level hourly demand in a large-scale bike-sharing network: a graph convolutional neural network approach. Transp. Res., Part C, Emerg. Technol. 2018;97:258–276. doi: 10.1016/j.trc.2018.10.011. [DOI] [Google Scholar]
- 8.Wang B., Kim I. Short-term prediction for bike-sharing service using machine learning. International Symposium of Transport Simulation (ISTS'18) and the International Workshop on Traffic Data Collection and Its Standardization (IWTDCS'18) Emerging Transport Technologies for Next Generation MobilityTransp. Res. Proc. 2018;34:171–178. doi: 10.1016/j.trpro.2018.11.029. [DOI] [Google Scholar]
- 9.Xu C., Ji J., Liu P. The station-free sharing bike demand forecasting with a deep learning approach and large-scale datasets. Transp. Res., Part C, Emerg. Technol. 2018;95:47–60. doi: 10.1016/j.trc.2018.07.013. [DOI] [Google Scholar]
- 10.Scott D.M., Ciuro C. What factors influence bike share ridership? An investigation of Hamilton, Ontario's bike share hubs. Travel Behav. Soc. 2019;16:50–58. doi: 10.1016/j.tbs.2019.04.003. [DOI] [Google Scholar]
- 11.El-Assi W., Mahmoud M.S., Habib K.N. Effects of built environment and weather on bike sharing demand: a station level analysis of commercial bike sharing in Toronto. Transportation. 2017;44(3):589–613. doi: 10.1007/s11116-015-9669-z. [DOI] [Google Scholar]
- 12.Xie X.F., Wang Z. Examining travel patterns and characteristics in a bikesharing network and implications for data-driven decision supports: case study in the Washington DC area. J. Transp. Geogr. 2018;71:84–102. doi: 10.1016/j.jtrangeo.2018.07.010. [DOI] [Google Scholar]
- 13.Faghih-Imani A., Eluru N., El-Geneidy A.M., Rabbat M., Haq U. How land-use and urban form impact bicycle flows: evidence from the bicycle-sharing system (BIXI) in Montreal. J. Transp. Geogr. 2014;41:306–314. doi: 10.1016/j.jtrangeo.2014.01.013. [DOI] [Google Scholar]
- 14.Eren E., Uz V.E. A review on bike-sharing: the factors affecting bike-sharing demand. Sustain. Cities Soc. 2020:54. doi: 10.1016/j.scs.2019.101882. [DOI] [Google Scholar]
- 15.Choi S.J., Jiao J., Lee H.K., Farahi A. Combatting the mismatch: modeling bike-sharing rental and return machine learning classification forecast in Seoul, South Korea. J. Transp. Geogr. 2023;109 doi: 10.1016/j.jtrangeo.2023.103587. [DOI] [Google Scholar]
- 16.Fuller D., Gauvin L., Kestens Y., Daniel M., Fournier M., Morency P., et al. Use of a new public bicycle share program in Montreal, Canada. Am. J. Prev. Med. 2011;41(1):80–83. doi: 10.1016/j.amepre.2011.03.002. [DOI] [PubMed] [Google Scholar]
- 17.Woodcock J., Tainio M., Cheshire J., O'Brien O., Goodman A. Health effects of the London bicycle sharing system: health impact modelling study. BMJ. 2014:348. doi: 10.1136/bmj.g425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen Y., Zhang Y., Coffman D., Mi Z. An environmental benefit analysis of bike sharing in New York city. Cities. 2022;121 doi: 10.1016/j.cities.2021.103475. [DOI] [Google Scholar]
- 19.Filipe Teixeira João, Silva C., e Sá F.M. Empirical evidence on the impacts of bikesharing: a literature review. Transp. Rev. 2021;41(3):329–351. doi: 10.1080/01441647.2020.1841328. [DOI] [Google Scholar]
- 20.Midgley P. Bicycle-sharing schemes: enhancing sustainable mobility in urban areas. U.N. Dep. Econ. Soc. Aff. 2011;8:1–12. [Google Scholar]
- 21.Ricci M. Bike sharing: a review of evidence on impacts and processes of implementation and operation. Res. Transp. Bus. Manag. 2015;15:28–38. doi: 10.1016/j.rtbm.2015.03.003. [DOI] [Google Scholar]
- 22.Cortez A., Vázquez P.P. Computer Science Research Notes, Proceedings of WSCG. 2021. Advanced visual interaction with public bicycle sharing systems; pp. 207–216. [DOI] [Google Scholar]
- 23.Shu J., Chou M.C., Liu Q., Teo C.P., Wang I.L. Models for effective deployment and redistribution of bicycles within public bicycle-sharing systems. Oper. Res. 2013;61(6):1346–1359. doi: 10.1287/opre.2013.1215. [DOI] [Google Scholar]
- 24.Xie X.F., Wang Z. Combining physical and participatory sensing in urban mobility networks. 2014. https://doi.org/10.13140/RG.2.1.4349.4887
- 25.Gebhart K., Noland R. The impact of weather conditions on bikeshare trips in Washington, DC. Transportation. 2014;41:1205–1225. doi: 10.1007/s11116-014-9540-7. [DOI] [Google Scholar]
- 26.Kim K. Investigation on the effects of weather and calendar events on bike-sharing according to the trip patterns of bike rentals of stations. J. Transp. Geogr. 2018;66:309–320. doi: 10.1016/j.jtrangeo.2018.01.001. [DOI] [Google Scholar]
- 27.Younes H., Zou Z., Wu J., Baiocchi G. Comparing the temporal determinants of dockless scooter-share and station-based bike-share in Washington, DC. Transp. Res., Part A, Policy Pract. 2020;134:308–320. doi: 10.1016/j.tra.2020.02.021. [DOI] [Google Scholar]
- 28.Borgnat P., Fleury É., Robardet C., Scherrer A. ECCS'09. Complex Systems Society; 2009. Spatial analysis of dynamic movements of Vélo'v, Lyon's shared bicycle program. [Google Scholar]
- 29.Borgnat P., Abry P., Flandrin P., Robardet C., Rouquier J.B., Fleury E. Shared bicycles in a city: a signal processing and data analysis perspective. Adv. Complex Syst. 2011;14(03):415–438. doi: 10.1142/S0219525911002950. [DOI] [Google Scholar]
- 30.Zhang Y., Brussel M.J., Thomas T., van Maarseveen M.F. Mining bike-sharing travel behavior data: an investigation into trip chains and transition activities. Comput. Environ. Urban Syst. 2018;69:39–50. [Google Scholar]
- 31.Faghih-Imani A., Eluru N. Analysing bicycle-sharing system user destination choice preferences: Chicago's divvy system. J. Transp. Geogr. 2015;44:53–64. doi: 10.1016/j.jtrangeo.2015.03.005. [DOI] [Google Scholar]
- 32.Bhat C.R., Astroza S., Hamdi A.S. A spatial generalized ordered-response model with skew normal kernel error terms with an application to bicycling frequency. Transp. Res., Part B, Methodol. 2017;95:126–148. doi: 10.1016/j.trb.2016.10.014. [DOI] [Google Scholar]
- 33.Talavera-Garcia R., Romanillos G., Arias Molinares D. Examining spatio-temporal mobility patterns of bike-sharing systems: the case of bicimad (Madrid) J. Maps. 2021:17. doi: 10.1080/17445647.2020.1866697. [DOI] [Google Scholar]
- 34.Kim I., Pelechrinis K., Lee A.J. The anatomy of the daily usage of bike sharing systems: elevation, distance and seasonality. ACM SIGKDD Workshop Urban Comput. 2020 https://par.nsf.gov/biblio/10205854 [Google Scholar]
- 35.Frade I., Ribeiro A. Bicycle sharing systems demand. Transportation: Can We do More with Less Resources? – 16th Meeting of the Euro Working Group on Transportation – Porto 2013Proc., Soc. Behav. Sci. 2014;111:518–527. doi: 10.1016/j.sbspro.2014.01.085. [DOI] [Google Scholar]
- 36.Zhang J., Pan X., Li M., Philip S.Y. 2016 17th IEEE international conference on mobile data management (MDM) vol. 1. IEEE; 2016. Bicycle-sharing system analysis and trip prediction; pp. 174–179. [DOI] [Google Scholar]
- 37.Holmgren J., Aspegren S., Dahlströma J. Prediction of bicycle counter data using regression. Proc. Comput. Sci. 2017;113:502–507. doi: 10.1016/j.procs.2017.08.312. [DOI] [Google Scholar]
- 38.Holmgren J., Moltubakk G., O'Neill J. Regression-based evaluation of bicycle flow trend estimates. Proc. Comput. Sci. 2018;130:518–525. doi: 10.1016/j.procs.2018.04.073. [DOI] [Google Scholar]
- 39.Yang Y., Heppenstall A., Turner A., Comber A. Using graph structural information about flows to enhance short-term demand prediction in bike-sharing systems. Comput. Environ. Urban Syst. 2020;83 doi: 10.1016/j.compenvurbsys.2020.101521. [DOI] [Google Scholar]
- 40.Collini E., Nesi P., Pantaleo G. Deep learning for short-term prediction of available bikes on bike-sharing stations. IEEE Access. 2021;9:124337–124347. doi: 10.1109/ACCESS.2021.3110794. [DOI] [Google Scholar]
- 41.Chen P.C., Hsieh H.Y., Su K.W., Sigalingging X.K., Chen Y.R., Leu J.S. Predicting station level demand in a bike-sharing system using recurrent neural networks. IET Intell. Transp. Syst. 2020;14(6):554–561. doi: 10.1049/iet-its.2019.0007. [DOI] [Google Scholar]
- 42.Froehlich J.E., Neumann J., Oliver N. Twenty-First International Joint Conference on Artificial Intelligence. 2009. Sensing and predicting the pulse of the city through shared bicycling. [Google Scholar]
- 43.Shi X., Wang Y., Lv F., Liu W., Seng D., Lin F. Finding communities in bicycle sharing system. J. Vis. 2019;22(6):1177–1192. doi: 10.1007/s12650-019-00587-0. [DOI] [Google Scholar]
- 44.Noussan M., Carioni G., Sanvito F.D., Colombo E. Urban mobility demand profiles: time series for cars and bike-sharing use as a resource for transport and energy modeling. Data. 2019;4(3):108. doi: 10.3390/data4030108. [DOI] [Google Scholar]
- 45.Li Y., Zheng Y., Zhang H., Chen L. Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems. SIGSPATIAL '15. Association for Computing Machinery; New York, NY, USA: 2015. Traffic prediction in a bike-sharing system. [DOI] [Google Scholar]
- 46.Chen P.C., Hsieh H.Y., Sigalingging X.K., Chen Y.R., Leu J.S. 2017 IEEE 85th Vehicular Technology Conference. VTC Spring; 2017. Prediction of station level demand in a bike sharing system using recurrent neural networks; pp. 1–5. [DOI] [Google Scholar]
- 47.Ashqar Huthaifa I., Elhenawy Mohammed, Rakha Hesham A., Almannaa Mohammed, House Leanna. Network and station-level bike-sharing system prediction: a San Francisco bay area case study. J. Intell. Transp. Syst. 2022;26(5):602–612. doi: 10.1080/15472450.2021.1948412. [DOI] [Google Scholar]
- 48.Lozano Murciego Á., De Paz J., Villarrubia G., Hernández de la Iglesia D., Bajo J. Multi-agent system for demand prediction and trip visualization in bike sharing systems. Appl. Sci. 2018;8:67. doi: 10.3390/app8010067. [DOI] [Google Scholar]
- 49.Dias G.M., Bellalta B., Oechsner S. IntelliSys 2015 - Proceedings of 2015 SAI Intelligent Systems Conference. 2015. Predicting occupancy trends in Barcelona's bicycle service stations using open data; pp. 439–445. [DOI] [Google Scholar]
- 50.Cortez Ordoñez A.P., Vázquez Alcocer P.P. International Conference on Computer Graphics, Visualization, Computer Vision and Image Processing (CGVCVIP2021), Connected Smart Cities (CSC2021), and Big Data Analytics, Data Mining and Computational Intelligence (BIGDACI 2021): Held at the 15th Multi-Conference on Computer Science and Information Systems (MCCSIS 2021): Online, 20-23 July 2021. Curran Associates; 2021. Analysis and visual exploration of prediction algorithms for public bicycle sharing systems; pp. 61–70. [Google Scholar]
- 51.Yin Y.C., Lee C.S., Wong Y.P. Demand prediction of bicycle sharing systems. 2012. https://cs229.stanford.edu/proj2014/Yu-chun%20Yin,%20Chi-Shuen%20Lee,%20Yu-Po%20Wong,%20Demand%20Prediction%20of%20Bicycle%20Sharing%20Systems.pdf
- 52.Feng Y., Wang S. A forecast for bicycle rental demand based on random forests and multiple linear regression. In: Zhu G., Yao S., Cui X., Xu S., editors. 16th IEEE/ACIS International Conference on Computer and Information Science; ICIS 2017, Wuhan, China, May 24-26, 2017; IEEE Computer Society; 2017. pp. 101–105. [DOI] [Google Scholar]
- 53.Hulot P, Aloise D, Jena SD. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. KDD '18. Association for Computing Machinery; New York, NY, USA: 2018. Towards station-level demand prediction for effective rebalancing in bike-sharing systems; pp. 378–386. [DOI] [Google Scholar]
- 54.Li X., Xu Y., Zhang X., Shi W., Yue Y., Li Q. Improving short-term bike sharing demand forecast through an irregular convolutional neural network. Transp. Res., Part C, Emerg. Technol. 2023;147 doi: 10.1016/j.trc.2022.103984. [DOI] [Google Scholar]
- 55.Gao K., Yang Y., Gil J., Qu X. Data-driven interpretation on interactive and nonlinear effects of the correlated built environment on shared mobility. J. Transp. Geogr. 2023;110 doi: 10.1016/j.jtrangeo.2023.103604. [DOI] [Google Scholar]
- 56.Rixey R.A. Station-level forecasting of bikesharing ridership: station network effects in three U.S. systems. Transp. Res. Rec. 2013;2387(1):46–55. doi: 10.3141/2387-06. [DOI] [Google Scholar]
- 57.Barcelona City Hall, B. Open data bcn. 2022. https://opendata-ajuntament.barcelona.cat/en/open-data-bcn
- 58.Ribeiro S.M., de Castro C.L. Missing data in time series: a review of imputation methods and case study. Special Issue: Time Series Analysis and Forecasting Using Computational IntelligenceLearn. Nonlinear Models, Rev. Soc. Bras. Redes Neurais. 2021;19(2) [Google Scholar]
- 59.Wijesekara W.M.L.K.N., Liyanage L. In: Advances in Information and Communication. Arai K., Kapoor S., Bhatia R., editors. Springer International Publishing; Cham: 2020. Comparison of imputation methods for missing values in air pollution data: case study on Sydney air quality index; pp. 257–269. [Google Scholar]
- 60.Cortez-Ordoñez A., Sanchez-Espigares J.A., Vázquez P.P. A visual tool for the analysis of usage trends of small and medium bicycle sharing systems. 2022;109:30–41. doi: 10.1016/j.cag.2022.09.009. [DOI] [Google Scholar]
- 61.Aguilera-García Á., Gomez J., Sobrino N., Vinagre Díaz J.J. Moped scooter sharing: citizens' perceptions, users' behavior, and implications for urban mobility. Sustainability. 2021;13(12) doi: 10.3390/su13126886. [DOI] [Google Scholar]
- 62.Bach X., Marquet O., Miralles-Guasch C. Assessing social and spatial access equity in regulatory frameworks for moped-style scooter sharing services. Transp. Policy. 2023;132:154–162. doi: 10.1016/j.tranpol.2023.01.002. [DOI] [Google Scholar]
- 63.Alonso F., Faus M., Esteban C., Useche S.A. Who wants to change their transport habits to help reduce air pollution? A nationwide study in the Caribbean. J. Transp. Health. 2023;33 doi: 10.1016/j.jth.2023.101703. [DOI] [Google Scholar]
- 64.Ho T.K. Proceedings of the Third International Conference on Document Analysis and Recognition (Volume 1) - Volume 1. ICDAR '95. IEEE Computer Society; USA: 1995. Random decision forests; p. 278. [Google Scholar]
- 65.Liaw A., Wiener M. Classification and regression by randomforest. R News. 2002;2(3):18–22. https://CRAN.R-project.org/doc/Rnews/ [Google Scholar]
- 66.Adler A.I., Painsky A. Feature importance in gradient boosting trees with cross-validation feature selection. Entropy. 2022;24(5):687. doi: 10.3390/e24050687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Cortez-Ordoñez A., Tulcanaza-Prieto A.B. Are we back to normal? A bike sharing systems mobility analysis in the post-covid-19 era. Sustainability. 2024;16(14) doi: 10.3390/su16146209. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and analyzed in this study are property of Open Data Barcelona. The authors do not have permission to share data.