Ventricular Ectopic Beat Detection Using a Wavelet Transform and a Convolutional Neural Network

Abstract

Objective:

Ventricular contractions in healthy individuals normally follow the contractions of atria to facilitate more efficient pump action and cardiac output. With a ventricular ectopic beat (VEB), volume within the ventricles are pumped to the body’s vessels before receiving blood from atria, thus causing inefficient blood circulation. VEBs tend to cause perturbations in the instantaneous heart rate time series, making the analysis of heart rate variability inappropriate around such events, or requiring special treatment (such as signal averaging). Moreover, VEB frequency can be indicative of life-threatening problems. However, VEBs can often mimic artifacts both in morphology and timing. Identification of VEBs is therefore an important unsolved problem. The aim of this study is to introduce a method of wavelet transform in combination with deep learning network for the classification of VEBs.

Approach:

We proposed a method to automatically discriminate VEB beats from other beats and artifacts with the use of wavelet transform of the electrocardiogram (ECG) and a convolutional neural network (CNN). Three types of wavelets (Morlet wavelet, Paul wavelet and Gaussian Derivative) were used to transform segments of single channel (1-D) ECG waveforms to 2-D time-frequency ‘images’. The 2-D time-frequency images were then passed into a CNN to optimize the convolutional filters and classification. Ten-fold cross validation was used to evaluate the approach on the MIT-BIH arrhythmia database (MIT-BIH). The American Heart Association (AHA) database was then used as an independent dataset to evaluate the trained network.

Main results:

Ten-fold cross validation results on MIT-BIH showed that the proposed algorithm with Paul wavelet achieved an overall F1 score of 84.94% and accuracy of 97.96% on out of sample validation. Independent test on AHA resulted in an F1 score of 84.96% and accuracy of 97.36%.

Significance:

The trained network possessed exceptional transferability across databases and generalization to unseen data.

1. Introduction

Although electrocardiogram (ECG) arrhythmia classification techniques have been studied and used for many decades, automatic processing and accurate diagnosis of pathological ECG signals remains a challenge (Clifford et al. (2006), Oster et al. (2015)). Ventricular ectopic beat (VEB) is a common abnormal heart rhythm to be detected by automatic algorithms. Although single VEBs do not usually pose a danger and can be asymptomatic in healthy individuals, frequent or certain patterns of VEBs may be at increased risk of developing serious arrhythmia, cardiomyopathy or even sudden cardiac death.

As recommended by ANSI-AAMI (1998), the VEBs include premature ventricular contraction (PVC), R-on-T PVC and ventricular escape beats. There have been extensive researches on VEBs or PVCs. Almendral et al. (1995) suggested that there exists a strong correlation of VEBs with left ventricular hypertrophy in hypertensive patients, and that individuals with left ventricular hypertrophy carried a significant risk of mortality and sudden death. Baman et al. (2010) evaluated the PVC burdens in 174 patients where 57 (33%) patients had left ventricular dysfunction and discovered a mean PVC burden of 33% ± 13% was present in those with a decreased left ventricular ejection fraction (LVEF) as compared with a mean PVC burden of 13% ± 12% with normal left ventricular function. The authors came to the conclusion that “A PVC burden of >24% was independently associated with PVC-induced cardiomyopathy.” Dukes et al. (2015) studied 1,139 participants and found that those in the upper quartile of PVC frequency possessed 3-fold greater odds of a 5-year decrease in LVEF, a 48% increased risk of incident congestive heart failure and a 31% increased risk of death compared to the lowest quartile.

The common VEB detection approaches include two important steps, 1) feature extraction, 2) pattern classification. Beat detection is the basis for feature extraction. Two open-source physiologic signal processing toolboxes, ECG-kit and PhysioNet Cardiovascular Signal Toolbox (Vest et al. (2018)), provided by physionet.org (Goldberger et al. (2000)), integrated some classical beat detectors such as Pan & Tompkins (Pan and Tompkins (1985)), EP-Limited (Hamilton and Tompkins (1986)), gqrs, wqrs (Zong et al. (2003)), ecgpuwave, wavedet (Martínez et al. (2004)) as well as the state-of-the-art one, jqrs (Behar et al. (2014), Johnson et al. (2014)). The extracted features are usually related to ECG morphologies (Shadmand and Mashoufi (2016)), cardiac rhythms or heartbeat intervals (Raj and Ray (2017)) and wavelet-based features (Elhaj et al. (2016)). De Chazal et al. (2004) extracted four inter-beat (RR) interval features (pre-RR interval, post-RR interval, average RR interval and local average RR interval), three heartbeat interval features (QRS duration, T-wave duration and P wave flag) and eight groups of ECG morphology features which contained amplitude values of the ECG signal and then combined them into eight feature sets to examine the classification performance. The current challenge is how to select relevant features for next classification (Saeys et al. (2007)).

A variety of machine learning approaches have previously been used for VEB pattern classification, including linear discriminant analysis (LDA) (De Chazal et al. (2004), De Chazal and Reilly (2006), Llamedo and Martnez (2011)), artificial neural networks (ANN), (Dokur and Ö lmez (2001), Inan et al. (2006), Mar et al. (2011)) and support vector machine (SVM) approaches (Zhang et al. (2014)). Many researcher selected LDA since it is easy to develop the model and it is a convenient modeling form when nominal classes are considered, however, the discriminant function is always linear (Zopounidis and Doumpos (2002)), therefore not fitting for complex non-linear problems. Due to the nonlinearity of the activation function of ANN, the decision boundary can be nonlinear, making the ANN model more flexible and can lead to an improved classification accuracy (Dreiseitl and Ohno-Machado (2002)).

Novel methods were applied on VEB detection and showed enhanced performance. Sayadi et al. (2010) proposed a model-based dynamic algorithm for tracking the ECG characteristic waveforms using an extended Kalman filter. A polar representation of the ECG signal, constructed using the Bayesian estimations of the state variables, and a measure of signal fidelity by monitoring the covariance matrix of the innovation signals from the extended Kalman filter were introduced. VEBs were detected by simultaneously tracking the signal fidelity and the polar envelope. The algorithm showed an accuracy of 99.10%, sensitivity of 98.77% and positive predictivity of 97.47% on the MIT-BIH arrhythmia database (MIT-BIH). The drawback of the method is the dependency of the results on the initial estimations for the state vector as well as the selection of the covariance matrices of the process and the measurement noise, so it may be unsuitable for ECG signals with pathological rhythms. Oster et al. (2015) proposed a state-of-the-art PVC detection algorithm based on switching Kalman filters. The switching Kalman filter could automatically select the most likely mode (beat type), normal beat or ventricular beat, while concurrently filter the ECG signal using appropriate prior knowledge. For certain heartbeats that could not be clustered into expected morphologies of ventricular or normal beats, either due to their rarity or due to the amount of noise distorting the apparent morphology, they were classified as a new mode (X-factor). An F1 scores of 98.6%, sensitivity of 97.3% and positive predictivity of 99.96% were reported on the MIT-BIH when 3.2% of the heartbeats were discarded as X-factor. However, this approach was semi-supervised and relied on trained cardiologist to assign every beat cluster to normal or ventricular classes. It is therefore inappropriate for analysis of large datasets or continuous recordings.

We also note that VEB detection is equivalent to classification in a two class VEB / not VEB problem. Historically, PVC / VEB detection has been implemented using heuristics or optimized thresholds on hand crafted features, such as the relative change in the RR interval compared to adjacent RR intervals and/or QRS duration and amplitude. In particular we note that Geddes and Warner (1971) designed a logic-based program that measured RR interval, duration and shape of QRS complexes to find the optimum combination of parameters to detect PVCs while rejecting muscle artifacts. Oliver et al. (1971) adopted a similar approach that followed a rigidly defined protocol, consisted of artifact detection, shape classification and prematurity test for the detection of PVCs. Laguna et al. (1991) used an adaptive Hermite model and extracted the b parameter for the width of QRS complex and compared the b parameter with a threshold for PVC detection. Clifford et al. (2002) demonstrated that RR interval-based thresholds were highly sensitive to the threshold and quantified the trade-off between misclassifying noise as ectopy or sinus beats. A threshold of 15% was shown to be optimal, although by no means sufficient for accurate PVC detection.

Convolutional neural network (CNN) architectures have been successfully used over the last several decades in image recognition (Lawrence et al. (1997)), audio and video analysis (Karpathy et al. (2014)) and many other domains (Shashikumar et al. (2017)) due to their high accuracy, low error rate and fast learning rate. To motivate the use of the CNN, we note that a CNN can eliminate the feature design and extraction process required in other approaches, identifying the network connections to reproduce the representation of the VEB at an autoassociative node. Clifford et al. (2001) and Tarassenko et al. (2001) first demonstrated this for a one-dimensional (1-D) representation of normal ECG beats and PVCs. That work was limited by the lack of data and computational power to fully train a network over a large population, thereby learning generalized morphologies. These authors also showed that, in the limit, with a linear activation function, the approach mapped to the Karhunen-Love transform, first reported for PVC classification in 1989 by Moody and Mark (1989). In this work we extend these earlier works to the time-scale domain and apply further deep CNN layers to map these time-scale images to beat classes. In order to take advantage of the success of CNN in the domain of image processing, we converted the 1-D ECG signals to two-dimensional (2-D) images by a continuous wavelet transform. By offering a simultaneous localization in time and frequency domain, the wavelet transform provides a clear time-frequency characteristic of the PVC (Sifuzzaman et al. (2009)). The convolutional transformation converts a set of amplitude or energy measurements (pixels in an image) into feature maps. The spatial dependence of the pixels is exploited by local connectivity on neurons on adjacent layers (Affonso et al. (2017)). The CNN automatically learns features when the network is tuned by the stochastic gradient descent algorithm. Moreover, a CNN is capable of learning translationally (and under specific circumstances, rotationally) invariant features from a vast amount of trained data (Cha et al. (2017)). Since the VEB morphology can change based on the respiratory cycle, sympathovagal balance, heart rate and other movements, it is important to identify subtle changes in the beat that are relatively invariant to such changes. The CNN allows us to automatically select such invariant spatio-temporal correlations in the image. We note that other authors, such as Kiranyaz et al. (2016) and Acharya et al. (2017), have attempted to classify beats using a CNN-based approach, but used a 1-D CNN instead. While, in theory, the CNN could learn a time-scale representation of the beat as a preliminary filter, it is unlikely that these exact basis function would be learned. In that sense, one can think of this as analogous to whitening a neural network with principal component analysis. We also note that there has been much interest in classifying rhythms (rather than beats) from the recent Computing in Cardiology (CinC) Challenge 2017 (Clifford et al. (2017)). In particular Acharya et al. (2017), Kamaleswaran et al. (2018), Parvaneh et al. (2018), Xiong et al. (2018) and Plesinger et al. (2018) used 1-D CNN approaches to classify arrhythmias. None use a time-scale representation as detailed in this work, or on a beat-by-beat level.

In this study we propose a systematic approach for training, validating and testing a CNN model for VEB classification. The method section introduces the datasets we used, a validation and test design as well as a wavelet transform to convert the 1-D ECG signals to 2-D images and the CNN structure. Results section shows the performance of the algorithm, followed by discussion, where we compare the proposed method with the state of the art algorithms for VEB detection.

2. Method

2.1. Dataset

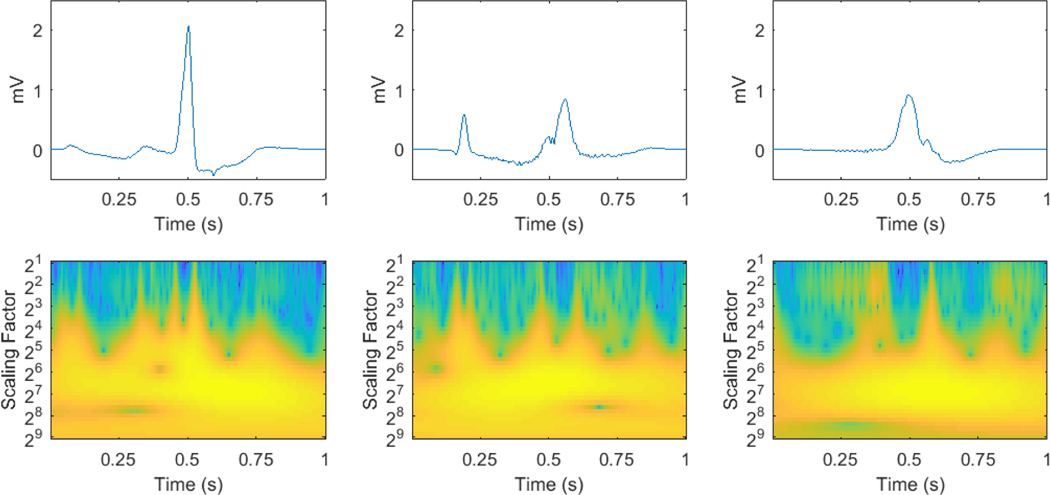
The MIT-BIH arrhythmia database was used for algorithm training, validation and testing. The American Heart Association database (AHA) was also used as a separate dataset for further testing. The MIT-BIH consists of 48 two-channel recordings, each lasts 30 minutes, obtained from 47 subjects. Each beat is annotated by at least two expert cardiologists independently and all disagreements have been resolved. The ECG signals are sampled at 360 Hz. In this study, ECG signals from the first channel were used, mostly collected by the modified limb lead II (MLII) and on 3 occasions (record number 102, 104 and 114) by V5. The AHA includes 80 two-channel recordings, each lasts 35 minutes. The final 30 minutes of each recording are annotated beat-by-beat. The sampling frequency is 250 Hz. These 80 recordings are divided into eight classes of ten recordings each, according to the highest level of ventricular ectopy present: class 1, no ventricular ectopy; class 2, isolated unifocal PVCs; class 3, isolated multifocal PVCs; class 4, ventricular bigeminy and trigeminy; class 5, R-on-T PVCs; class 6, ventricular couplets; class 7, ventricular tachycardia; class 8, ventricular flutter/fibrillation. Since recordings in class 8 are used for ventricular flutter and fibrillation detection and some ECG waveforms at the beginning of the ventricular flutter segments are annotated as PVC beats, where similar segments in MIT-BIH are annotated as ventricular flutter instead, the ten recordings in class 8 were excluded from this study for consistency. As recommended by ANSI-AAMI (1998), the recordings with paced beats, 4 (102, 104, 107 and 217) out of 48 from MIT-BIH and 2 (2202 and 8205) out of 80 from AHA, were also excluded from this study. The reference annotation files the databases provided were used as the gold standard. Since we focus on two-type classification, VEB (V) or non-VEB (N), any beat that does not fall into the V category is set to type N. Examples of VEBs and their corresponding time-scale images are shown in Figure 1.

Figure 1:

Examples of PVC, R-on-T PVC and ventricular escape beats from left to right and their time-scale images.

In order to find an appropriate window length for beat classification by CNN, we extracted each beat of the ECG signal at different window lengths, varying from 0.5 seconds to 6 seconds at 0.5-second intervals, with the annotation placed at the center of the window. This annotation then marks the beat type of the window. As the sampling frequency of MIT-BIH is 360 Hz, a range of 180-point to 2160-point windows were generated. The beats in the first and last 3 seconds of ECG were excluded in all 44 recordings (of the MIT-BIH) in order to keep the total number of beats consistent across all window lengths, resulting in a total of 100372 beats in which 6990 were V. The 69 AHA records were resampled to 360 Hz and a total number of 163802 beats including 14735 V were extracted in the same manner.

2.2. Wavelet transform

Wavelet transform is a spectral analysis technique where signals can be expressed as linear combinations of shifted and dilated versions of a base wavelet. Time-frequency representations of these signal can then be constructed, offering good time and frequency localization.

Sahambi et al. (1997) used the first derivative of a Gaussian to characterize ECG in real-time. The quadratic spline wavelet originally proposed by Mallat and Zhong (1992) was used to characterize the local shape of irregular structures. Martínez et al. (2004) adopted this wavelet in their ECG delineator to determine the QRS complexes and P and T wave peaks. Li et al. (1995) and Bahoura et al. (1997) also used this wavelet to detect the characteristic points and waveforms of ECG. While wavelet transforms have been adopted in the past for detecting ECG waveforms, in this paper, we used an improved algorithm to increase efficiency by fast convolution via the fast Fourier transform (FFT), explained in detail by Montejo and Suarez (2013). We used the common nonorthogonal wavelet functions: complex wavelets Morlet and Paul, and real valued wavelets Derivative of Gaussian (DOG) (Torrence and Compo (1998)), which are suitable for input to the continuous wavelet transform for time series analysis (Farge (1992)).

We converted each extracted 1-D ECG beat to a 2-D time-scale image in this way. The toolbox “A cross wavelet and wavelet coherence toolbox” was used to perform this conversion (https://github.com/grinsted/wavelet-coherence). The mathematics behind the wavelet analysis is well documented by Grinsted et al. (2004). The converted image consists of information with the wavelet scaling factor as vertical axis ranging from 2¹ to 2⁹ at 2^0.2 intervals and time as horizontal axis. The processed data with different window lengths were resampled to a fixed number of points of 45 for consistency. All the images were normalized to scale [0,1]. In this way, the resulting 2-D images all possess the same size of 41×45 and scale, standardized for further processing.

The toolbox supports three types of wavelets for transformation: Morlet wavelet, Paul wavelet and DOG wavelet. All three were adopted to compare the effects of different wavelet types when convoluted with the extracted ECG beats.

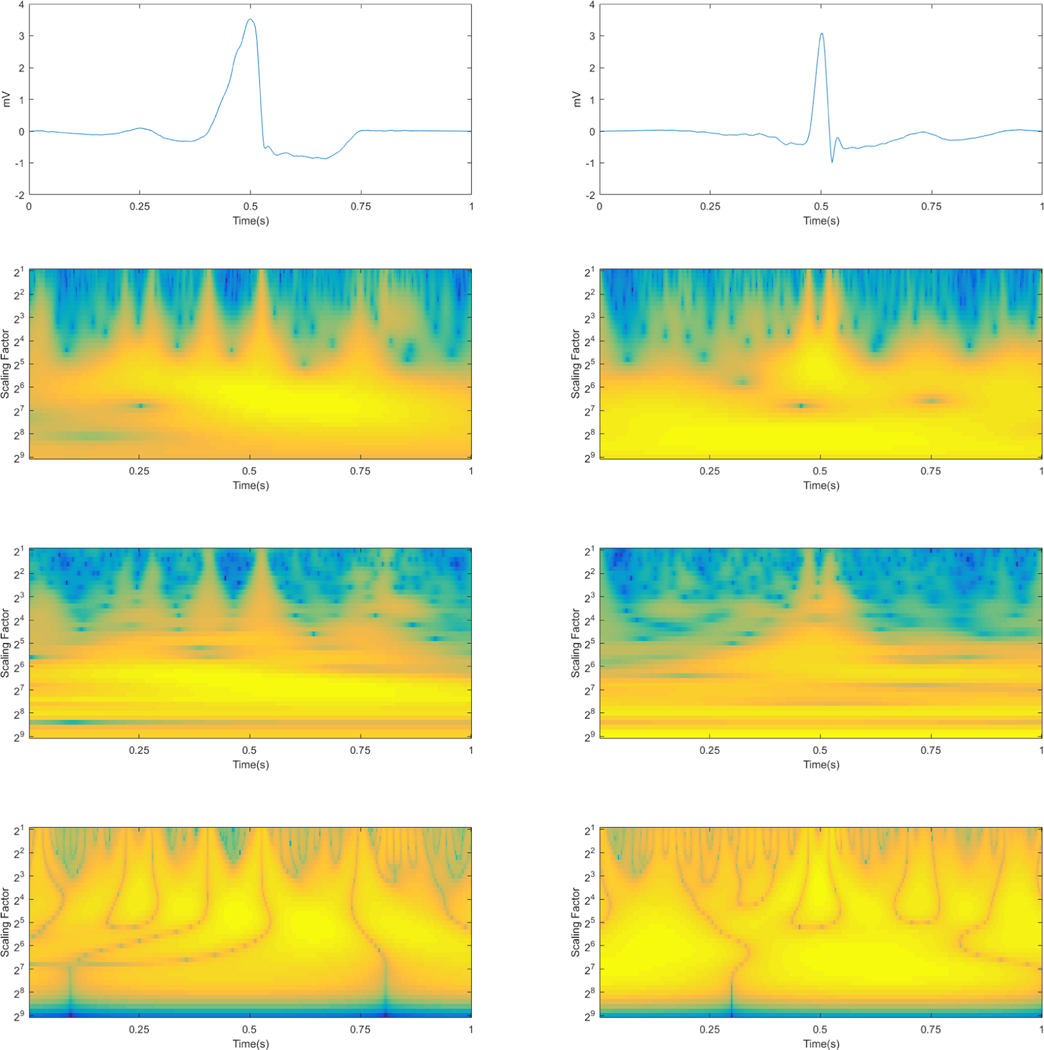
Figure 2 gives an illustration of a VEB beat and a non-VEB beat in their ECGs forms and the results after wavelet transform by each type of wavelet. The left shows a VEB beat with a broadened irregularly-shaped QRS complex in its ECG and multiple wider warm-colored peaks in its processed images whereas the right shows a non-VEB beat with a normal QRS complex in its ECG and two main narrower peaks at the centers of both images processed by the Morlet wavelet and the Paul wavelet. There are discernible differences in the outcomes of the two beat types processed by the DOG wavelet as well.

Figure 2:

The original ECGs (first row) and their results after wavelet transform with three types of wavelets of the two beat types (VEB on the left and non-VEB on the right). The second row represents the outcomes with the Paul wavelet, the third the Morlet wavelet and the last the DOG wavelet.

2.3. Convolutional neural network

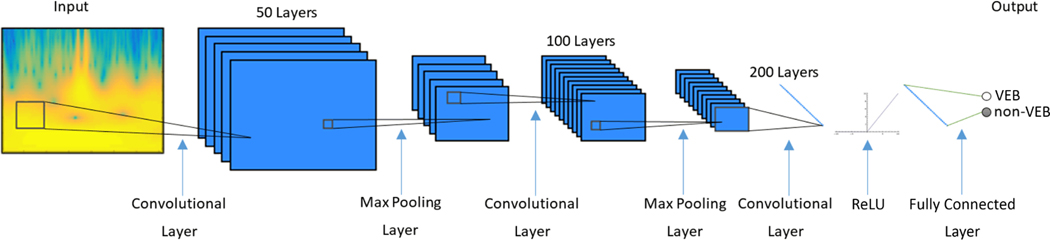
Since we have converted the ECG beats to wavelet power spectra in a 2-D space, we then used CNN to study relevant information from the power spectra and achieve classification. The input to the CNN was the wavelet power spectrum computed from each exacted ECG beat. Our CNN architecture consists of three convolutional layers, two max pooling layers (implemented after the first and the second convolutional layer), a rectified linear unit (ReLU) layer and finally a fully connected layer. The CNN was implemented using the MatConvNet toolkit in Matlab (Vedaldi and Lenc (2015)).

In the convolutional layer, a n-by-m sized filter is convoluted with the input image with a stride of 1 along both directions, resulting in an output with n-1 x m-1 reduction in size from the input. The size of filters used for each convolutional layer are 4×4, 4×6 and 8×8, and the number of filters are 50, 100 and 200 respectively. The 2×2 max pooling layer with a stride of 2 downsamples the input by a factor of 2 in both directions, dropping 75% of data size while retaining most discernible features for classification. The final layer of convolution computes the input into a single value, which after increasing nonlinear properties by the ReLU layer, is passed into the fully connected layer thereby producing a final classification result. The weights of the CNN model were randomly initialized from uniform distribution. Stochastic gradient descent (SGD) algorithm was chosen to optimize the weights of the model. A learn rate of 0.001 was used. Figure 3 shows the structure of the CNN.

Figure 3:

Convolutional neural network structure

2.4. Training, validation and test

The 44 recordings of MIT-BIH were randomly allocated into ten subsets (folds) of data. Random grouping was done by recording numbers rather than the total heartbeats, so that the data of one recording would not appear in both the training dataset and the testing set to avoid bias and overfitting. Note that records 201 and 202, which are from the same patient, are put to one subset mandatorily as well.

To train the CNN model, nine folds of the dataset were used for training and the remaining fold for testing. The heartbeats in the training set were further randomly divided into two subsets during the training procedure, where 5/6 heartbeats were used to train the model directly and 1/6 heartbeats were used for validation during the learning process to optimize the model parameters and avoid overfitting. Finally the trained model was tested on the remaining fold. This process was repeated ten times so that each of the ten folds was tested and the results on each fold were combined.

See Table A1 in appendix for details of the randomly generated K-fold set up we adopted in this evaluation.

After we obtained the ten-fold cross validation models, we tested the ten models on the AHA database. The classification result was acquired by averaging the ten probability output of each model. A separate CNN model trained on all heartbeats of MIT-BIH was tested on AHA as well. To test the transferability of our model further, we used all heartbeats of the AHA database to train a new model and performed a final testing back on MIT-BIH.

2.5. Evaluation method

We used accuracy (Acc), sensitivity (Se), specificity (Sp), positive predictive value (PPV, or +P) and F1 score (F1) to evaluate the performance of the algorithm. For each test fold in MIT-BIH, after we acquired the results of TP (V beats correctly identified as V), FN (V beats incorrectly identified as N), FP (N beats incorrectly identified as V) and TN (N beats correctly identified as N), we calculated the statistical measures as below.

$$\text{Acc}=(\text{TP}+\text{TN})/(\text{TP}+\text{FN}+\text{TN}+\text{FP})$$

$$\text{Se}=\text{TP}/(\text{TP}+\text{FN})$$

$$\text{Sp}=\text{TN}/(\text{TN}+\text{FP})$$

$$\text{PPV}=\text{TP}/(\text{TP}+\text{FP})$$

$$\text{F1}=2\text{TP}/(2\text{TP}+\text{FN}+\text{FP})$$

To combine the ten test folds results into an overall statistics, two types of aggregate statistics were used (ANSI-AAMI (1998)): gross statistics, in which each beat was given equal weight, and average statistics, in which the measures of ten folds were averaged and stored along with their standard deviations.

3. Results

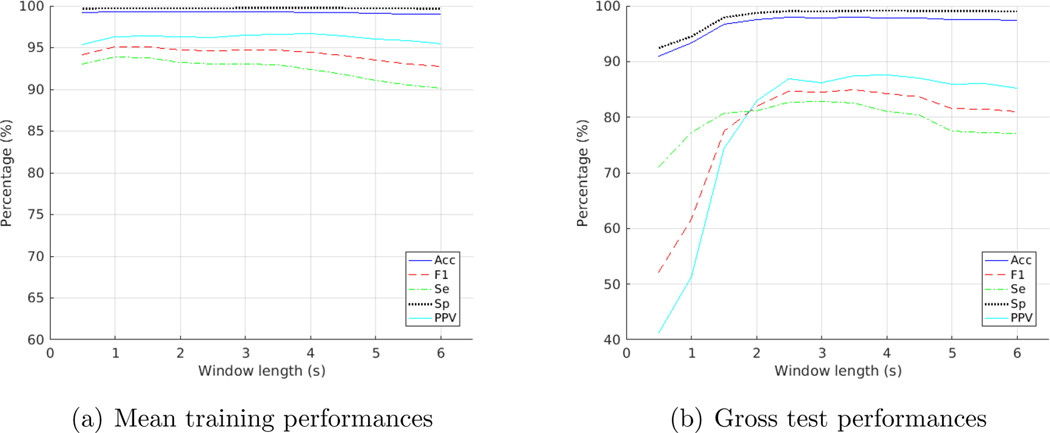
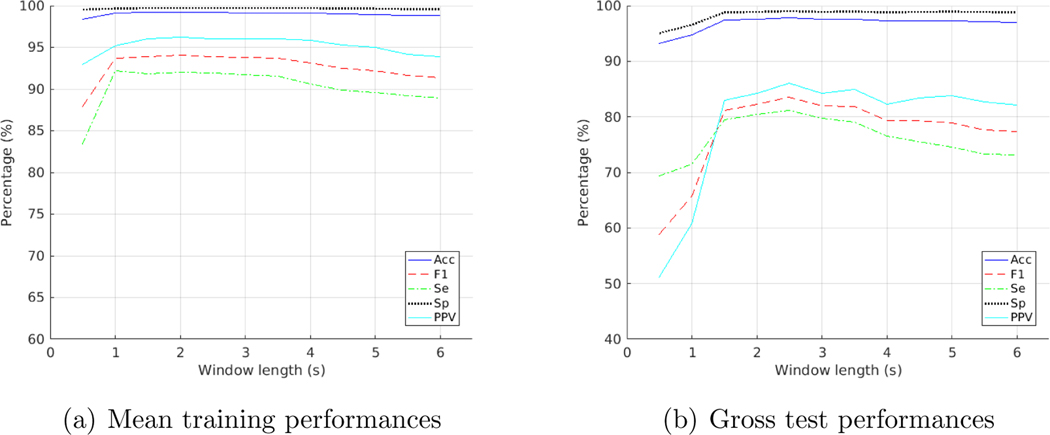
Table 1 illustrated the gross results on the test folds of MIT-BIH. What we obtained with the Paul wavelet at different window lengths for test folds was that the F1 score was at its highest with a 3.5-second window, as shown in Figure 4(b). Results for training folds however, showed a highest F1 score for a 1.5-second window, as shown in Figure 4(a). Amongst the three wavelets, Paul wavelet provided the best test performance. An Acc of 97.96%, an Se of 82.60%, an Sp of 99.11%, a PPV of 87.42% and an F1 of 84.94% were achieved as the gross result on the test folds of MIT-BIH with Paul wavelet on a 3.5-second window.

Table 1:

Gross results on the test folds of the MIT-BIH database

Wavelet	Window(s)	Acc(%)	Se(%)	Sp(%)	PPV(%)	F1(%)
Paul	0.5	90.94	71.03	92.43	41.24	52.19
Paul	1	93.29	77.22	94.50	51.23	61.60
Paul	1.5	96.73	80.72	97.92	74.42	77.44
Paul	2	97.52	81.20	98.75	82.90	82.04
Paul	2.5	97.92	82.62	99.07	86.92	84.71
Paul	3	97.88	82.78	99.01	86.23	84.47
Paul	3.5	97.96	82.60	99.11	87.42	84.94
Paul	4	97.88	80.96	99.15	87.65	84.17
Paul	4.5	97.80	80.47	99.10	87.02	83.62
Paul	5	97.55	77.57	99.05	85.90	81.52
Paul	5.5	97.54	77.18	99.06	86.04	81.37
Paul	6	97.48	77.07	99.00	85.26	80.96
Morlet	0.5	93.24	69.33	95.03	51.10	58.83
Morlet	1	94.80	71.42	96.55	60.78	65.67
Morlet	1.5	97.43	79.46	98.77	82.91	81.15
Morlet	2	97.59	80.46	98.87	84.25	82.31
Morlet	2.5	97.77	81.14	99.01	86.04	83.52
Morlet	3	97.55	79.74	98.88	84.21	81.92
Morlet	3.5	97.56	79.01	98.95	84.93	81.86
Morlet	4	97.22	76.57	98.77	82.30	79.33
Morlet	4.5	97.25	75.51	98.88	83.45	79.28
Morlet	5	97.23	74.62	98.92	83.85	78.96
Morlet	5.5	97.07	73.28	98.85	82.69	77.70
Morlet	6	97.02	73.16	98.81	82.11	77.38
DOG	0.5	93.42	49.60	96.70	52.91	51.20
DOG	1	91.90	65.24	93.89	44.44	52.86
DOG	1.5	96.90	77.63	98.34	77.79	77.71
DOG	2	97.74	78.98	99.15	87.41	82.99
DOG	2.5	97.74	78.80	99.16	87.51	82.93
DOG	3	97.74	77.93	99.22	88.20	82.74
DOG	3.5	97.80	78.03	99.28	88.99	83.15
DOG	4	97.81	77.27	99.35	89.91	83.11
DOG	4.5	97.76	76.74	99.33	89.56	82.66
DOG	5	97.66	75.11	99.35	89.65	81.74
DOG	5.5	97.36	73.43	99.15	86.56	79.46
DOG	6	97.33	72.76	99.17	86.79	79.16

Figure 4:

Training and test performances on the MIT-BIH database with Paul wavelet at varying window lengths

For the training folds, we achieved the best training performance with Paul wavelet on a 1.5-second window an Acc of 99.32% and an F1 score of 95.08%. Please see Table A2 in appendix for details of the average results on the training folds. Details of the average results on the test folds can also be found in Table A3.

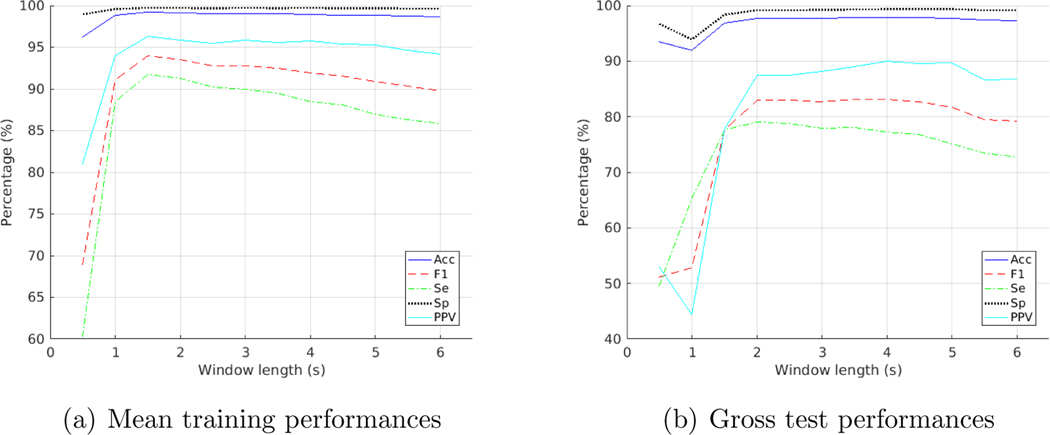
For the Morlet wavelet, a 2.5-second window achieved the highest F1 score for the testing folds and a 2-second window for training folds. DOG wavelet performed the best with a 3.5-second window on testing folds and a 1.5-second window on training folds. See Figure A1 and A2 in appendix for details.

The performances on individual test fold and individual recording with Paul wavelet at 3.5-second window length were shown in Table 2 and Table 3 respectively.

Table 2:

Test performances on individual fold of the MIT-BIH database with Paul wavelet at 3.5-second window size

K-th fold	TP	FP	FN	TN	Acc(%)	Se(%)	Sp(%)	PPV(%)	F1(%)
1	406	193	247	8278	95.18	62.17	97.72	67.78	64.86
2	278	70	39	7350	98.59	87.70	99.06	79.89	83.61
3	807	44	131	9960	98.40	86.03	99.56	94.83	90.22
4	368	12	122	10634	98.80	75.10	99.89	96.84	84.60
5	542	9	47	8365	99.38	92.02	99.89	98.37	95.09
6	755	2	72	8480	99.21	91.29	99.98	99.74	95.33
7	527	195	315	13641	96.53	62.59	98.59	72.99	67.39
8	578	9	153	7811	98.11	79.07	99.88	98.47	87.71
9	958	235	30	7884	97.09	96.96	97.11	80.30	87.85
10	555	62	60	10148	98.87	90.24	99.39	89.95	90.10

Table 3:

Test performances on individual records of the MIT-BIH database with Paul wavelet at 3.5-second window size

Record	TP	FP	FN	TN	Acc(%)	Se(%)	Sp(%)	PPV(%)	F1(%)
100	1	0	0	2263	100	100	100	100	100
101	0	0	0	1858	100	-	100	-	-
103	0	0	0	2077	100	-	100	-	-
105	28	29	13	2493	98.36	68.29	98.85	49.12	57.14
106	483	9	35	1494	97.82	93.24	99.40	98.17	95.64
108	11	38	6	1701	97.49	64.71	97.81	22.45	33.33
109	19	0	19	2485	99.25	50.00	100	100	66.67
111	0	1	1	2115	99.91	0	99.95	0	0
112	0	0	0	2530	100	-	100	-	-
113	0	3	0	1785	99.83	-	99.83	0	0
114	38	5	5	1824	99.47	88.37	99.73	88.37	88.37
115	0	0	0	1946	100	-	100	-	-
116	107	2	2	2293	99.83	98.17	99.91	98.17	98.17
117	0	0	0	1529	100	-	100	-	-
118	12	3	4	2251	99.69	75.00	99.87	80.00	77.42
119	442	0	1	1537	99.95	99.77	100	100	99.89
121	1	3	0	1852	99.84	100	99.84	25.00	40.00
122	0	0	0	2466	100	-	100	-	-
123	3	0	0	1508	100	100	100	100	100
124	40	0	7	1567	99.57	85.11	100	100	91.95
200	752	2	72	1766	97.15	91.26	99.89	99.73	95.31
201	3	98	195	1661	85.03	1.52	94.43	2.97	2.01
202	6	20	13	2091	98.45	31.58	99.05	23.08	26.67
203	277	132	167	2395	89.94	62.39	94.78	67.73	64.95
205	35	0	36	2576	98.64	49.30	100	100	66.04
207	128	45	80	1596	93.24	61.54	97.26	73.99	67.19
208	958	111	30	1846	95.21	96.96	94.33	89.62	93.15
209	1	6	0	2989	99.80	100	99.80	14.29	25.00
210	149	5	44	2442	98.14	77.20	99.80	96.75	85.88
212	0	0	0	2740	100	-	100	-	-
213	180	45	40	2974	97.38	81.82	98.51	80.00	80.90
214	228	24	28	1973	97.69	89.06	98.80	90.48	89.76
215	53	0	111	3188	96.69	32.32	100	100	48.85
219	59	62	4	2021	96.92	93.65	97.02	48.76	64.13
220	0	16	0	2024	99.22	-	99.22	0	0
221	393	0	2	2023	99.92	99.49	100	100	99.75
222	0	30	0	2444	98.79	-	98.79	0	0
223	356	6	117	2117	95.26	75.26	99.72	98.34	85.27
228	307	0	54	1684	97.36	85.04	100	100	91.92
230	0	3	1	2243	99.82	0	99.87	0	0
231	2	0	0	1562	100	100	100	100	100
232	0	124	0	1650	93.01	-	93.01	0	0
233	699	6	129	2234	95.60	84.42	99.73	99.15	91.19
234	3	3	0	2738	99.89	100	99.89	50.00	66.67

On the AHA database, we reached an Acc of 97.36%, an Se of 82.83%, an Sp of 98.80%, a PPV of 87.20% and an F1 of 84.96% when a model was trained on all heartbeats in MIT-BIH database with Paul wavelet at 3.5-second window length. The averaged results from the ten probability outputs of each model obtained from ten-fold cross validation classification of MIT-BIH were also similar. The performance of the two models is shown in Table 4.

Table 4:

Test results on AHA database by the model(s) trained on MIT-BIH database with Paul wavelet at 3.5-second window size

Model	TP	FP	FN	TN	Acc(%)	Se(%)	Sp(%)	PPV(%)	F1(%)
trained on MIT	12205	1792	2530	147275	97.36	82.83	98.80	87.20	84.96
average of 10	12004	1736	2731	147331	97.27	81.47	98.84	87.37	84.31

When we trained the model on AHA database and tested back on MIT-BIH, we obtained an Acc of 97.56%, an Se of 82.55%, an Sp of 98.68%, a PPV of 82.39% and an F1 of 82.47%, as shown in Table 5.

Table 5:

Test results on MIT-BIH database by the model trained on AHA database with Paul wavelet at 3.5-second window size

Model	TP	FP	FN	TN	Acc(%)	Se(%)	Sp(%)	PPV(%)	F1(%)
trained on AHA	5770	1233	1220	92149	97.56	82.55	98.68	82.39	82.47

4. Discussion

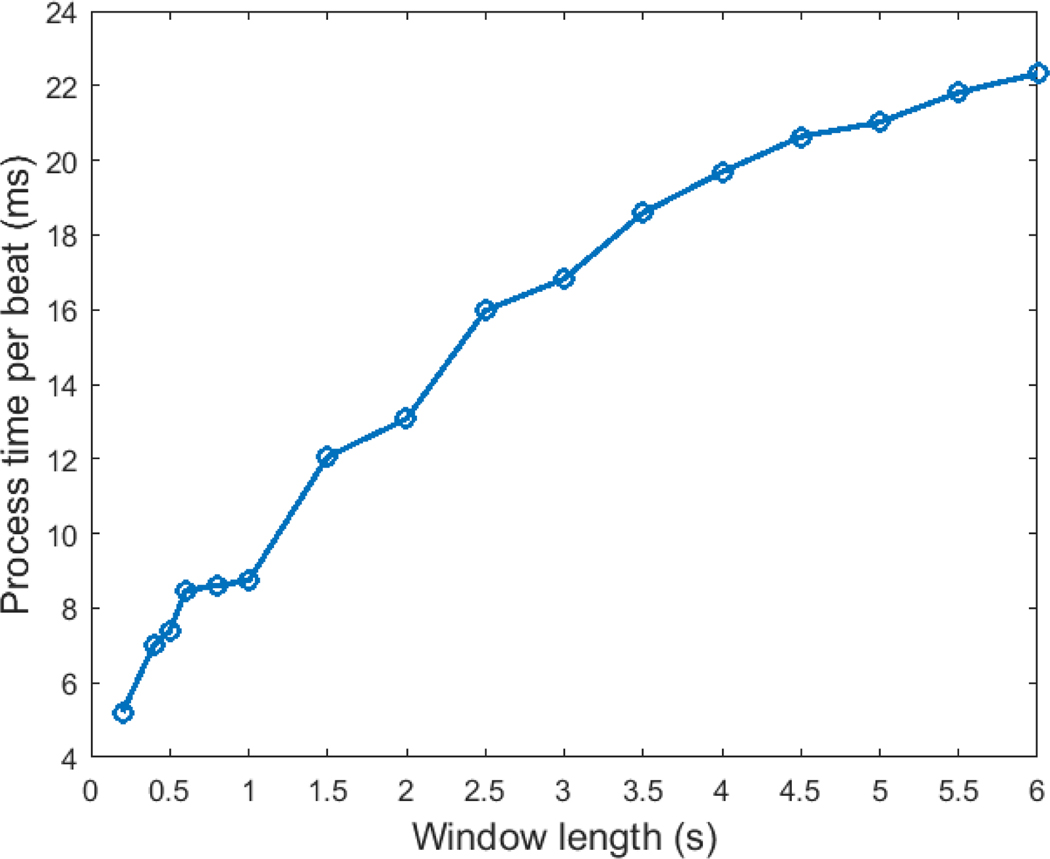
In this work we presented a novel deep learning neural network approach to distinguish VEBs from all other types of ECG beats, using a CNN with continuous wavelet transform of the ECG signal as input. The proposed approach is not highly computationally intensive due to the relatively simple kernels that were utilized in the CNN. We tested the computational time using the trained CNN model for prediction on MIT-BIH database on an Intel Xeon E5–2660 2.2GHz CPU and a Linux platform. The total process time for generating the time-scale images on a 3.5 s window using Paul wavelet and classifying the beat using the trained CNN model was 1866 s for 100372 beats, which is equivalent to 18.6 ms per beat. Figure A3 (in the appendix) illustrates the timing for various window lengths. We have also tested the process time for several open source algorithms published as part of the Physionet / CinC Challenge 2017 (focused on atrial fibrillation detection) as a comparison. Results are shown for windows sizes from 10 seconds to 60 seconds in Table A4. We note that our new algorithm is over 100 times faster per unit time/window than our previously reported algorithm and approximately 1000 times faster than the other algorithms from the Physionet / CinC Challenge 2017.

It was shown that the Paul wavelet displayed the best performance among the three types of wavelets tested. This could be due to the closer resemblance of Paul wavelet to the shape of a standard ECG wave compared to the other two wavelet types tested.

The 3.5-second window exhibited the highest accuracy (97.96%) and F1 score (84.94%) using the Paul wavelet. We speculate that this is because the 3.5-second window contained at least one heartbeat before the VEB and one heartbeat after it, so the window captures the dynamic of the premature contraction and the following compensatory pause. A relatively shorter window length (3-second for Paul) provided the highest sensitivity (82.78%), and on the other hand a relatively longer window length (4-second for DOG) exhibited the highest specificity (99.35%) and PPV (89.91%).

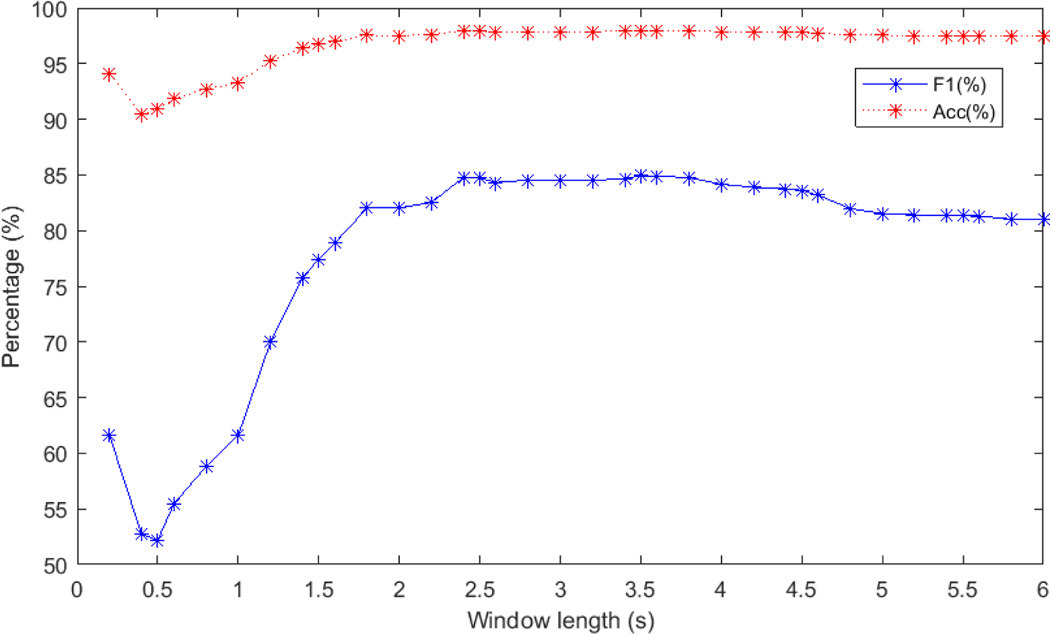
We repeated our algorithms at 0.2-second intervals and obtained the following results (illustrated in Figure A4). A window length of 3.5 second provided the best accuracy and F1 score. The performance on the 0.2-second windows is notably impressive, given that it encompasses only the ventricular period and provides no context on prematurity. Conversely, longer windows provide information of the relative prematurity or retardation of the beat compared to adjacent beats.

Table 4 showed that the performance of the model using all heartbeats in MIT-BIH database is slightly better than that of the average of ten-fold models on the AHA database. The independent test on a separate database showed almost the same performance with that on the original database (for F1 score, 84.96% for AHA compared with 84.94% for MIT-BIH, for accuracy, 97.36% for AHA compared with 97.96% for MIT-BIH), indicating an generalization ability of the trained CNN model on a separate database.

Comparing to other studies (Table 6), we reported ten-fold cross validation results and an independent test on a separate database. In contrast to this, other studies divided 44 recordings of MIT-BIH (after the removal of 4 recordings containing paced beats) into two subsets and used half the recordings (DS1) for training and the other half (DS2) for testing (De Chazal et al. (2004), Mar et al. (2011), Oster et al. (2015)). A sensitivity of 77.7%, positive predictivity of 81.9% and false positive rate of 1.2% were reported for VEB class on DS2 by De Chazal et al. (2004). Note when compared to K-fold cross validation, arbitrary subset-splitting could cause bias since only half of the data were used for testing. In addition, records 201 and 202, two records of the same patient, belonged to subsets DS1 and DS2 separately, causing the heartbeats of the same patient appear in both training and test sets. The conventional methods have some disadvantages, for instance, 1) features were extracted from raw ECG data and then fed into the classifier, therefore performance relied on the quality of feature extraction; 2) classification models trained and tested following the above procedure suffer from overfitting and show lower performances when validated on a separate dataset (Acharya et al. (2017)). Since the morphologies of VEBs can vary enormously from patient to patient, if patients are not stratified (completely held out of training) there may be an optimistic bias in reporting. As shown in Table 2, we achieved a superior result on one fold (fold 6) with an Acc of 99.21%, an Se of 91.29%, an Sp of 99.98%, a PPV of 99.74% and an F1 of 95.33%, but an inferior result on another fold (fold 1) with an Acc of 95.18%, an Se of 62.17%, an Sp of 97.72%, a PPV of 67.78% and an F1 of 64.86%.

Table 6:

Performance comparison with reference studies

Algorithm	records	validation	Acc (%)	Se (%)	Sp (%)	PPV (%)	F1 (%)	separate testset	semi/auto
De Chazal et al. (2004)	44	DS2	97.4	77.7	98.8	81.9	79.7	No	auto
Mar et al. (2011)	44	DS2	97.3	86.8	-	75.9	81.0	No	auto
Oster et al. (2015)	44	DS2	98.87	87.61	99.75	96.43	91.81	Yes	semi
Proposed in this study	44	ten-fold	97.96	82.60	99.11	87.42	84.94	Yes	auto

On the other hand, Acharya et al. (2017) also trained a CNN model and adopted a ten-fold cross validation in order to classify heartbeats and achieved accuracies of 94.03% and 93.47% in original and noise free ECGs of the MIT-BIH database, respectively. In that approach, a balanced database was constructed by replicating the beats of classes with a lower beat count to match the majority (class N). For instance, V beats were oversampled 12.5 times (i.e. increasing them from 7235 to 90592). After which, the repeated beats were randomly partitioned into ten equal folds by beats instead of by records. As a result, the same VEBs can be found in both training folds as well as validation fold violating the basic principles of cross validation. It is far more realistic to evaluate an algorithm’s performance with proper K-fold cross validation with stratification of patients across folds.

5. Conclusion

A highly generalizable VEB classification algorithm that utilizes continuous wavelet transform and CNN was developed. ECG data can be analyzed rapidly (at 18.6 ms per beat on a standard processor). It was shown that the algorithm retained its high performance when tested on a separate database.

Appendix

Figure A1:

Appendix - Training and test performances on the MIT-BIH database with Morlet wavelet at varying window lengths

Figure A2:

Appendix - Training and test performances on the MIT-BIH database with DOG wavelet at varying window lengths

Figure A3:

Appendix - Process time per beat with varying window sizes

Figure A4:

Appendix - Test performance on the MIT-BIH database with Paul wavelet at 0.2-second and 0.5-second intervals

Figure A5:

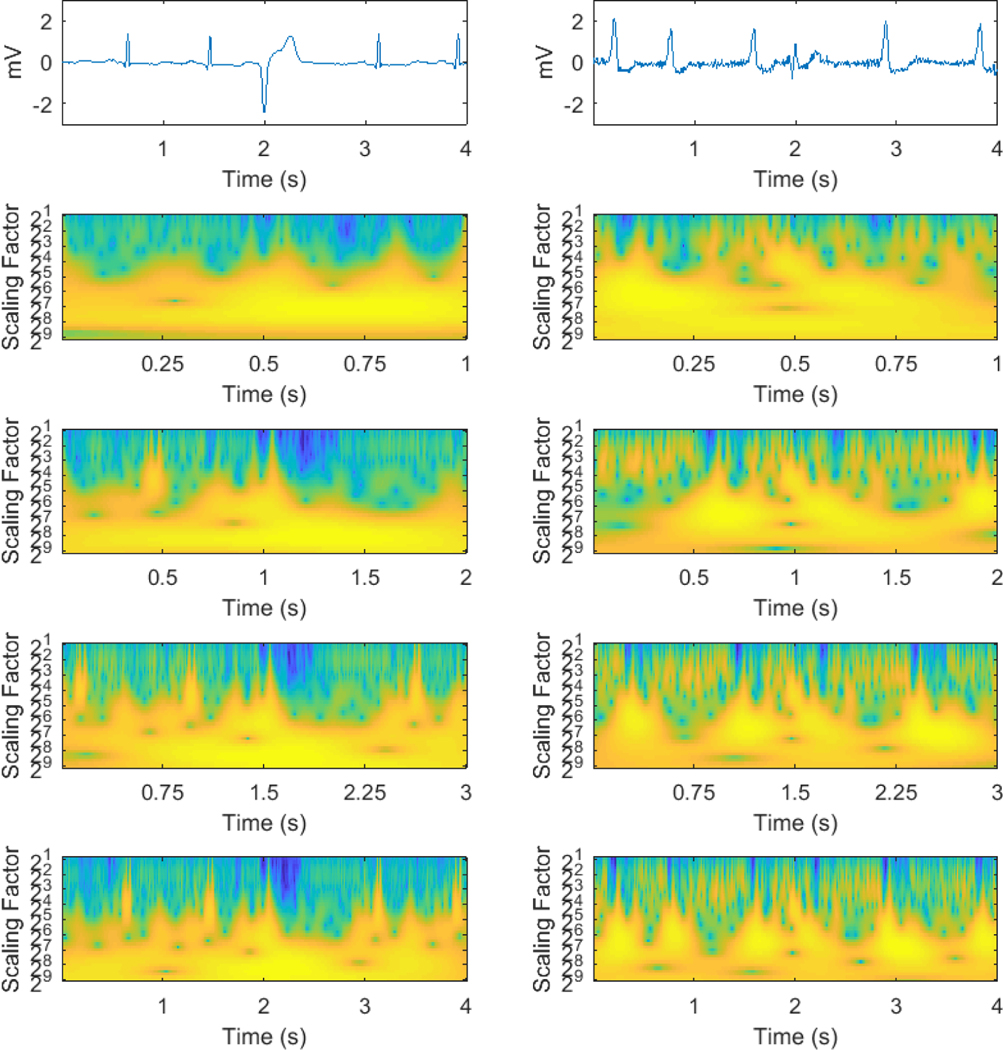
Appendix - Example of a successful detection of VEB (left) versus a failed detection (right). Top to bottom: original ECG and time-scale images of window length: 1 s, 2 s, 3 s, 4 s

Table A1:

Appendix - The randomly generated K-fold set up adopted

K-fold	Record Number	VEB beats	non-VEB beats	Total	K-fold	Record Number	VEB beats	non-VEB beats	Total
1	100	1	2263	2264	6	122	0	2466	2466
1	203	444	2527	2971	6	123	3	1508	1511
1	207	208	1641	1849	6	200	824	1768	2592
1	220	0	2040	2040	6	212	0	2740	2740
	Total	653	8471	9124		Total	827	8482	9309
2	108	17	1739	1756	7	105	41	2522	2563
2	114	43	1829	1872	7	201	198	1759	1957
2	121	1	1855	1856	7	202	19	2111	2130
2	214	256	1997	2253	7	213	220	3019	3239
					7	228	361	1684	2045
					7	234	3	2741	2744
	Total	317	7420	7737		Total	842	13836	14678
3	116	109	2295	2404	8	106	518	1503	2021
3	209	1	2995	2996	8	124	47	1567	1614
3	222	0	2474	2474	8	215	164	3188	3352
3	233	828	2240	3068	8	231	2	1562	1564
	Total	938	10004	10942		Total	731	7820	8551
4	103	0	2077	2077	9	101	0	1858	1858
4	115	0	1946	1946	9	112	0	2530	2530
4	118	16	2254	2270	9	208	988	1957	2945
4	223	473	2123	2596	9	232	0	1774	1774
4	230	1	2246	2247
	Total	490	10646	11136		Total	988	8119	9107
5	111	1	2116	2117	10	109	38	2485	2523
5	113	0	1788	1788	10	117	0	1529	1529
5	210	193	2447	2640	10	119	443	1537	1980
5	221	395	2023	2418	10	205	71	2576	2647
					10	219	63	2083	2146
	Total	589	8374	8963		Total	615	10210	10825
							Total VEB beats	Total non-VEB beats	Total beats
							6990	93382	100372

Table A2:

Appendix - Average results on training folds of the MIT-BIH database

Wavelet	Window(s)	Acc(%)	Se(%)	Sp(%)	PPV(%)	F1(%)
Paul	0.5	99.20±0.06	92.99±1.28	99.66±0.09	95.42±1.06	94.18±0.48
Paul	1	99.32±0.04	93.86±0.76	99.73±0.07	96.35±0.90	95.08±0.31
Paul	1.5	99.32±0.04	93.79±1.05	99.74±0.04	96.40±0.52	95.08±0.37
Paul	2	99.28±0.05	93.23±1.03	99.73±0.07	96.34±0.78	94.75±0.38
Paul	2.5	99.26±0.06	93.02±0.87	99.73±0.06	96.26±0.73	94.61±0.41
Paul	3	99.28±0.06	93.08±0.96	99.74±0.06	96.49±0.75	94.75±0.44
Paul	3.5	99.28±0.05	92.94±0.96	99.75±0.06	96.58±0.79	94.72±0.38
Paul	4	99.25±0.05	92.39±1.20	99.76±0.06	96.68±0.71	94.47±0.46
Paul	4.5	99.19±0.06	91.79±1.38	99.74±0.08	96.43±0.92	94.04±0.54
Paul	5	99.12±0.06	91.03±1.49	99.72±0.07	96.07±0.74	93.47±0.57
Paul	5.5	99.06±0.07	90.52±1.56	99.70±0.07	95.80±0.75	93.08±0.66
Paul	6	99.02±0.07	90.13±1.38	99.68±0.07	95.48±0.71	92.72±0.62
Morlet	0.5	98.41±0.17	83.40±2.61	99.53±0.08	92.98±1.02	87.9±1.53
Morlet	1	99.13±0.06	92.20±0.87	99.65±0.09	95.23±1.13	93.68±0.48
Morlet	1.5	99.16±0.07	91.81±1.57	99.71±0.07	96.01±0.86	93.85±0.57
Morlet	2	99.20±0.06	92.04±1.11	99.73±0.04	96.25±0.45	94.09±0.50
Morlet	2.5	99.17±0.06	91.92±1.34	99.71±0.06	96.02±0.75	93.92±0.51
Morlet	3	99.16±0.05	91.70±1.11	99.71±0.06	95.99±0.62	93.79±0.46
Morlet	3.5	99.14±0.05	91.50±1.00	99.72±0.06	96.03±0.77	93.71±0.43
Morlet	4	99.07±0.06	90.61±0.96	99.70±0.05	95.81±0.58	93.14±0.52
Morlet	4.5	98.98±0.07	89.85±1.41	99.66±0.07	95.25±0.88	92.46±0.61
Morlet	5	98.95±0.07	89.62±1.40	99.65±0.06	95.03±0.60	92.24±0.66
Morlet	5.5	98.86±0.08	89.23±1.23	99.58±0.06	94.14±0.71	91.61±0.67
Morlet	6	98.83±0.07	88.93±1.20	99.57±0.06	93.89±0.69	91.33±0.64
DOG	0.5	96.26±0.34	60.34±6.98	98.94±0.17	80.95±1.91	68.95±4.95
DOG	1	98.80±0.12	88.41±1.92	99.57±0.10	93.97±1.19	91.09±0.98
DOG	1.5	99.18±0.07	91.73±1.76	99.74±0.08	96.33±0.94	93.96±0.57
DOG	2	99.11±0.09	91.23±1.64	99.70±0.11	95.86±1.25	93.47±0.62
DOG	2.5	99.02±0.09	90.26±1.53	99.68±0.07	95.51±0.76	92.80±0.66
DOG	3	99.03±0.10	89.97±1.81	99.70±0.09	95.82±1.00	92.79±0.79
DOG	3.5	98.98±0.10	89.51±1.55	99.69±0.07	95.60±0.82	92.45±0.77
DOG	4	98.92±0.10	88.47±2.01	99.70±0.06	95.72±0.69	91.94±0.94
DOG	4.5	98.87±0.10	88.05±2.15	99.68±0.09	95.37±1.00	91.54±0.93
DOG	5	98.79±0.10	86.98±2.04	99.68±0.08	95.29±1.09	90.92±0.95
DOG	5.5	98.71±0.12	86.34±2.33	99.63±0.09	94.67±1.12	90.29±1.11
DOG	6	98.65±0.13	85.83±2.29	99.60±0.08	94.19±1.05	89.80±1.21

Table A3:

Appendix - Average results on the test folds of the MIT-BIH database

Wavelet	Window(s)	Acc(%)	Se(%)	Sp(%)	PPV(%)	F1(%)
Paul	0.5	90.55±8.54	70.46±22.99	92.07±9.19	55.39±31.14	54.86±25.74
Paul	1	92.87±8.51	77.19±19.74	94.12±9.34	70.14±31.80	66.69±25.34
Paul	1.5	96.53±3.04	80.34±15.62	97.66±3.21	78.55±23.75	76.86±17.68
Paul	2	97.50±2.15	80.95±13.13	98.65±1.87	84.64±17.64	81.85±13.28
Paul	2.5	97.94±1.61	82.03±11.25	99.05±1.16	87.39±13.23	84.41±11.36
Paul	3	97.92±1.49	82.83±11.27	98.98±1.25	87.09±13.51	84.44±10.46
Paul	3.5	98.01±1.34	82.32±12.26	99.11±1.00	87.92±11.75	84.67±10.51
Paul	4	97.95±1.31	80.70±13.06	99.15±0.96	88.14±11.62	83.87±10.86
Paul	4.5	97.85±1.33	80.06±12.78	99.10±1.14	87.73±12.12	83.24±10.61
Paul	5	97.60±1.26	76.68±14.45	99.03±1.20	86.58±13.13	80.52±11.23
Paul	5.5	97.58±1.23	76.00±15.28	99.05±1.16	86.78±13.69	80.00±11.76
Paul	6	97.51±1.32	75.89±15.38	98.97±1.29	86.14±14.18	79.59±12.15
Morlet	0.5	92.87±8.46	68.12±26.31	94.70±9.17	70.23±31.80	61.52±28.95
Morlet	1	94.43±5.96	71.16±22.57	96.18±6.46	71.73±27.35	65.98±23.76
Morlet	1.5	97.31±2.24	78.97±15.95	98.63±2.17	83.82±20.36	79.37±16.25
Morlet	2	97.56±1.60	80.17±13.33	98.80±1.32	84.37±16.87	81.19±12.66
Morlet	2.5	97.84±1.31	80.54±11.69	99.04±0.86	86.32±12.08	83.01±10.40
Morlet	3	97.59±1.12	79.26±13.19	98.88±0.98	84.30±13.97	80.77±10.44
Morlet	3.5	97.63±1.10	78.35±14.30	98.96±0.90	85.48±11.95	80.86±10.13
Morlet	4	97.32±1.31	75.55±15.96	98.82±1.04	83.51±13.10	78.32±11.75
Morlet	4.5	97.31±1.28	74.26±16.14	98.89±1.02	83.96±13.15	77.81±12.33
Morlet	5	97.28±1.23	73.35±16.42	98.92±1.00	84.13±13.46	77.28±12.42
Morlet	5.5	97.10±1.25	72.07±16.55	98.84±1.20	83.45±14.66	76.06±12.47
Morlet	6	97.03±1.31	71.72±16.85	98.78±1.20	82.45±15.45	75.42±13.33
DOG	0.5	92.94±7.27	49.32±31.44	96.12±8.10	73.83±30.63	49.55±28.05
DOG	1	91.53±9.23	64.35±21.28	93.57±9.84	66.76±34.97	58.63±26.46
DOG	1.5	96.82±2.92	77.46±15.09	98.19±2.78	80.84±23.52	77.12±17.62
DOG	2	97.74±1.70	78.78±14.02	99.11±1.10	87.27±14.62	82.25±12.75
DOG	2.5	97.76±1.60	78.04±12.62	99.14±1.08	87.88±13.55	82.34±11.83
DOG	3	97.77±1.42	77.63±15.32	99.19±0.92	87.81±13.86	81.63±12.51
DOG	3.5	97.84±1.45	77.6±15.70	99.26±0.76	88.32±12.45	82.02±12.72
DOG	4	97.87±1.47	76.55±15.81	99.35±0.66	89.27±11.63	81.97±13.09
DOG	4.5	97.79±1.36	76.18±15.15	99.32±0.64	88.70±11.36	81.52±12.61
DOG	5	97.71±1.31	74.11±16.55	99.35±0.57	88.42±11.85	80.00±13.77
DOG	5.5	97.38±1.38	71.89±19.17	99.12±1.00	86.21±16.28	76.76±16.17
DOG	6	97.36±1.32	71.09±19.81	99.15±0.88	86.31±14.60	76.30±16.21

Table A4:

Appendix - Process time in ms of open source algorithms in the Physionet CinC Challenge 2017 on each ECG.

	Process time of algorithms on each ECG (ms)
	Window length (s)
Algorithms	10	15	20	25	30	35	40	45	50	55	60
Li et al. (2016), Vest et al. (2018)	2437	2441	2529	2670	2830	3544	3770	4037	4551	4702	4941
Datta et al. (2017)	33663	33860	34290	34723	35158	35432	35624	35798	36031	36245	36472
Bin et al. (2017)	10295	10302	10306	10326	10338	10354	10405	10456	10473	10508	10512
Zabihi et al. (2017)	77259	77277	77323	77343	77363	77422	77465	77467	77478	77503	77569
Plesinger et al. (2018)	45803	45988	49059	50666	52037	56895	57222	57574	57590	57613	57701