Data-driven determination of ¹H-MRS basis set composition

Abstract

Purpose

Metabolite amplitude estimates derived from linear combination modeling of MR spectra depend upon the precise list of constituent metabolite basis functions used (the “basis set”). The absence of clear consensus on the “ideal” composition or objective criteria to determine the suitability of a particular basis set contributes to the poor reproducibility of MRS. In this proof-of-concept study, we demonstrate a novel, data-driven approach for deciding the basis-set composition using Bayesian information criteria (BIC).

Methods

We have developed an algorithm that iteratively adds metabolites to the basis set using iterative modeling, informed by BIC scores. We investigated two quantitative “stopping conditions”, referred to as max-BIC and zero-amplitude, and whether to optimize the selection of basis set on a per-spectrum basis or at the group level. The algorithm was tested using two groups of synthetic in-vivo-like spectra representing healthy brain and tumor spectra, respectively, and the derived basis sets (and metabolite amplitude estimates) were compared to the ground truth.

Results

All derived basis sets correctly identified high-concentration metabolites and provided reasonable fits of the spectra. At the single-spectrum level, the two stopping conditions derived the underlying basis set with 77–87% accuracy. When optimizing across a group, basis set determination accuracy improved to 84–92%.

Conclusion

Data-driven determination of the basis set composition is feasible. With refinement, this approach could provide a valuable data-driven way to derive or refine basis sets, reducing the operator bias of MRS analyses, enhancing the objectivity of quantitative analyses, and increasing the clinical viability of MRS.

1. Introduction

In vivo proton magnetic resonance spectroscopy (MRS) is a non-invasive method for estimating the concentrations of approximately 20 metabolites in the human brain. Levels of neurotransmitters and antioxidants, for example, may serve as biomarkers of function and pathology, but also general indicators of neuronal health and cell proliferation. Extracting metabolite concentrations from the in vivo spectrum depends on reliably resolving the contributions of constituent signals. For this task, expert consensus recommends^1,2 linear-combination modeling (LCM), a well-established method that uses a weighted sum of simulated signals—basis functions—to approximate the measured spectrum.

To achieve optimal precision and accuracy, the basis set included in LCM should be selected without bias. Poor spectral dispersion at clinical field strengths causes overlap between metabolite signals, preventing them from being estimated independently. Furthermore, many potentially MRS-detectable compounds are present below the threshold of detection in the healthy brain, only reaching detectable levels in pathology (e.g., 2-hydroxyglutarate in primary brain tumors with isocitrate dehydrogenase mutations³).

In practice, the choice of which metabolites to include in the LCM basis set is delicate because many different basis set compositions are admissible, i.e., they could be considered reasonable choices. Several fundamental challenges arise from this problem:

1. Wrongly in- or ex-cluding basis functions can lead to substantial biases of^4–8 and interactions between^9,10 metabolite amplitude estimates. Beyond these studies, the effects of basis set composition have received surprisingly little attention.

2. There is no consensus on the ideal basis set composition even for the healthy brain, let alone in pathology. This has resulted in significant analytic variability between research groups.

3. The definition of the basis-set composition currently requires a-priori knowledge (e.g., an external brain tumor diagnosis is necessary to adequately model a brain tumor spectrum), limiting the clinical application of MRS.

4. The number of metabolites that can be modeled with reasonable accuracy and precision depends strongly on the quality of the data. High-SNR, well-resolved spectra allow the modeling of metabolites that might otherwise have simply led to the overfitting of lower-quality data.

5. Finally, no objective criteria exist to determine the ideal basis-set composition. Current methods do not assess whether a specific basis set will overfit, underfit, or appropriately model a spectrum.

To address these challenges, we investigated the feasibility of determining the appropriate basis set composition directly from the spectrum itself using model selection. Model selection is the process of determining the most suitable model from a list of potential candidates informed by a quantitative information criterion (IC). There are several specific definitions of ICs^11–14, but generally, they attempt to “score” candidate models, balancing goodness-of-fit and model complexity in a single value^15,16. Higher IC scores are interpreted as a proxy measure of model parsimony, i.e., the “cost-effectiveness” of particular candidate models; ICs have previously been used in MRS to derive optimal baseline model parameters¹⁷.

In this study, we demonstrate an automated data-driven procedure—using iterative fitting of the spectra and informed by IC scores—to determine the appropriate composition of the basis set. We developed two variations of this algorithm: the first determines the optimal basis set for a single spectrum, and the second for a group of spectra. We also designed two different stopping conditions: the first stops adding metabolites to the basis set after reaching the maximum IC score, and the second keeps adding metabolites beyond this point until they no longer contribute any signal to the fit. We then tested the performance of the different algorithms with two classes of in-vivo-like simulated spectra, representing healthy brain and low-grade glioma. The glioma data included two oncometabolites that were not present in the healthy brain data. To establish the effectiveness of our new approach, we quantified how well the basis sets selected by the different algorithms overlapped with the ground-truth basis sets from which spectra were generated.

2. Materials & methods

2.1. Synthetic in-vivo-like data generation

We first simulated realistic in-vivo-like spectra to establish a known ground truth. We generated two datasets of 100 spectra, each with distinct spectral characteristics, reflecting healthy-appearing brain spectra and those typically seen in low-grade glioma, respectively. We chose the latter case as low-grade glioma spectra very commonly feature metabolites that are effectively absent from healthy brain tissue (namely, cystathionine^18,19 and 2-hydroxyglutarate²⁰) and exhibit markedly different amplitudes of major metabolites like NAA, choline, myo-inositol, and lactate.

Synthetic spectra were derived from a “library set” of metabolite basis functions, simulated using the density-matrix formalism of a 2D-localized 101 x 101 spatial grid (field of view 50% larger than the voxel) implemented in MRSCloud²¹, which is based on FID-A²². We synthesized 3T sLASER spectra to reflect a typical acquisition used to measure 2HG (TE = 97 ms with TE1/2 = 32/65 ms; 8192 complex points; spectral width 4000 Hz).

In total, we simulated 32 metabolite basis functions: Acetoacetate, AcAc; acetate, Ace; alanine, Ala; ascorbate, Asc; aspartate, Asp; citrate, Cit; creatine, Cr; creatine methylene, CrCH2; cystathionine, Cystat; ethanolamine, EA; ethanol, EtOH; γ-aminobutyric acid, GABA; Glycerophosphocholine, GPC; glutathione, GSH; glucose, Glc; glutamine, Gln; glutamate, Glu; glycine, Gly; myo-inositol, mI; lactate, Lac; N-acetylaspartate, NAA; N-acetylaspartylglutamate, NAAG; phosphocholine, PCh; phosphocreatine, PCr; phosphoethanolamine, PE; phenylalanine, Phenyl; scyllo-inositol, sI; serine, Ser; taurine, Tau; tyrosine, Tyros; β-hydroxybutyrate, bHB; and 2-hydroxyglutarate, 2HG. We also simulated basis functions for 5 macromolecular (MM09, MM12, MM14, MM17, MM20) and 3 lipid resonances (Lip09, Lip13, Lip20) and added them to this basis set. Out of the full set of 40 basis functions, we selected 26 to assemble the synthetic healthy ground-truth spectra: Asc; Asp; Cr; CrCH2; GABA; GPC; GSH; Gln; Glu; mI; Lac; NAA; NAAG; PCh; PCr; PE; sI; Tau; MM09; MM12; MM14; MM17; MM20; Lip09; Lip13; and Lip20. The locations, widths, and relative amplitudes of the parameterized lipid and MM resonances are reported in Supplementary Table 1 and the full library of basis functions is visualized in Supplementary Figure 1.

For the tumor spectra, we added additional contributions from 2HG and Cystat for a total of 28 basis functions in the tumor ground-truth basis set. The metabolite basis functions were combined into realistic spectra using the “OspreyGenerateSpectra” function in Osprey²³. The data generator combined the individual simulated profiles with metabolite-specific amplitudes, Gaussian and Lorentzian linebroadening terms, and white noise, taken from Gaussian distributions. Crucially, each group was defined with distinct model parameter ranges, which were informed by previously modeled in vivo data^7,24. Briefly, besides the additional 2HG and Cystat contributions, the tumor spectra also had higher tCho (100%), lower tNAA (60%), higher mI (30%), lower Glu (25%), higher Lac (1000%), higher lip09 (550%), and higher Lip20 (550%). The means and standard deviations of the parameters for each group are fully reported in Supplementary Table 2 and the two groups of resulting spectra are visualized in Supplementary Figure 2.

2.2. Basis set determination algorithm

Our proposed algorithm uses IC scores to build the basis set in an iterative process. Introducing more basis functions to the model reduces fit residuals but will also increase the number of model parameters (i.e. more metabolite-specific amplitudes, frequency shifts, and lineshape parameters). Determining the IC scores for each potential basis set composition allows us to counterbalance these two competing modeling aspects to arrive at a parsimonious compromise, i.e., to maximize the goodness-of-fit without overfitting.

2.2.1. Information criteria

The Akaike IC (AIC), corrected AIC (AICc), and Bayesian IC (BIC), only differ in how they regularize goodness-of-fit against model complexity and are linearly offset from one another for our purposes. We elected to proceed using the BIC as the sole model performance metric in the algorithm, defined:

$$BIC=-2\cdot n\cdot ln\left(\sigma \right)-ln\left(n\right)\cdot p$$

where $n$ is the number of points, $p$ is the total number of model parameters, and $\sigma ={}^2\sqrt{\sum \left(residual{s}^2\right)}$, the root sum square of the fit residual.

2.2.2. Algorithm implementation

We designed an algorithm to determine which of the library set of 40 basis functions (32 metabolites plus 8 MM/Lips) merits inclusion in the “selected set”. The selected set (which is initially empty) is built up one basis function at a time—the function added in each round of the algorithm is chosen from among the remaining candidates in the library set, based upon which model had the highest BIC. Thus, the algorithm consists of two nested loops: the outer loop (of rounds) to determine which is the next candidate to add to the selected set, and the inner loop (of steps) which consists of modeling the data with the current selected set plus one additional candidate function.

Both loops fill the selected basis set iteratively until a certain stopping condition is triggered. The algorithm is illustrated in Figure 1A, and further demonstrated in a Supplementary Video, with the specific steps as follows:

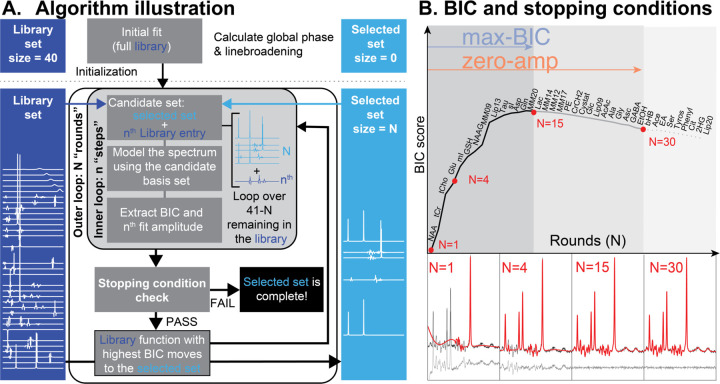
Figure 1.

Basis set selection algorithm. A. A visualization of the algorithm. Metabolites are iteratively moved from a library set (dark blue) to a selected set (light blue) using BIC scores. The basis function that yields the best BIC score is moved to the selected set (unless a stopping condition is triggered). B. A visualization of the evolution of BIC scores as the basis set is optimized. The two stopping conditions are represented by the colored arrows and shaded regions. 4 example fits are shown in the panels below (corresponding to red points on the curve).

1. Initialize an empty selected set and a full library set.

2. Perform a preliminary fit using the full library set to estimate global lineshape and phase parameters which are then fixed during subsequent model calls.

3. Round 1:

   1. Step 1 consists of modeling the spectrum with a candidate set containing only the first library basis function.
   2. The remaining 39 steps of Round 1 consist of modeling the spectrum with a candidate set consisting of each library basis function. The BIC is calculated for each model.
   3. Round 1 concludes by moving the candidate function that resulted in the model with the highest BIC into the selected basis set.
4. The $N$-th Round then steps over the $\left(41-N\right)$ remaining library functions, thus:

   1. Form the candidate basis set from the current selected set and the $n^{\text{th}}$ basis function from those remaining in the library set.
   2. Model the data with the candidate set.
   3. Calculate the BIC and note the amplitude of the $n^{\text{th}}$ basis function within the model.

5. Check whether the stopping condition has been met (as described below).

6. If the stopping condition is not met, move the candidate basis function with the highest BIC score from the library set to the selected set and return to step 4.

We investigated two domains of selection, i.e. whether to select a basis set for each spectrum individually or to select one basis set at the group level for a set of spectra. For each domain, we also investigated two stopping conditions, i.e when to stop adding basis functions to the selected set, see Figure 1B. The optimization domains are referred to as:

1. “Single-spectrum”: Executes the algorithm on each spectrum in isolation. Candidate basis functions are added based on the BIC scores derived from that spectrum alone, resulting in a spectrum-specific selected set.

2. “Group-level”: Executes the algorithm as described, but aggregates BIC scores across a group of spectra. At each step, we fit all spectra within a group with the candidate set and then use the median BIC score across the cohort as the metric to decide which metabolite is selected for that round. This procedure results in a single basis set for the entire group.

The two stopping conditions were:

1. “Max-BIC”: The algorithm stops adding metabolites to the selected set once the BIC is decreased by the inclusion of the next basis function. For the group-level optimization, it stops once the median BIC across all datasets decreases.

2. “Zero amplitude”: The algorithm keeps adding metabolites beyond the maximum BIC until the round when no candidate functions are modeled with non-zero amplitude. For the group-level optimization, it stops once all potential candidate functions are estimated with a median amplitude of zero across all datasets.

To stabilize the procedure, we instructed the algorithm to “link” certain pairs of practically indistinguishable basis functions, i.e., add both of them to the temporary candidate basis set as a single step, and, if selected, to add both to the selected basis set. Specifically, we linked Cr and PCr (referred to as the tCr step) and PCho and GPC (the tCho step).

2.2.3. MRS modeling

All MRS modeling steps were performed using Osprey’s²⁴ general LCM algorithm²³, introduced in our recent work^23,25. Aside from the Gaussian and zero-order phase parameters—which were fixed following the initial modeling step—the model was defined using our default in vivo parameters, naïve to the composition of the simulated spectra. We performed optimization over the range of 0.5–4.2 ppm and included a non-regularized spline baseline with knot spacing of 0.5 ppm. Metabolite-specific Lorentzian linewidth and frequency shift parameters were regularized (as described in the original LCModel publication²⁶) with expectation and standard deviation values of 2.75 ± 1.5 and 0 ± 3 Hz, respectively.

2.3. Statistical analysis

The algorithm's performance was primarily judged by its ability to correctly identify the metabolite signals that were present in the synthetic spectra. This was assessed using three related metrics to compare each derived basis set to the ground truth set:

1. False positives: The number of basis functions selected for inclusion by the algorithm that were not present in the synthetic spectra (incorrectly included).

2. False negatives: The number of basis functions not selected for inclusion by the algorithm that were present in the synthetic spectra (incorrectly omitted).

3. The Sorensen-Dice coefficient (SDC): The SDC was used as a measure of overlap with the ground truth basis set, defined:

   $$SDC=\frac{2\cdot \text{TruePositive}}{2\cdot \text{TruePositive}+\text{FalsePositive}+\text{FalseNegative}}.$$

Finally, we investigated the effect that the derived basis set composition had on metabolite amplitude estimates. Amplitude deviations from the ground truth are reported as percentage changes relative to the known ground-truth value that entered the simulation. We also compared the amplitudes derived from each basis set to those derived from a fit using the correct ground truth basis set, i.e. modeling the data with only the metabolites we know to be present in the simulation. Distributions were compared using paired t-tests. All statistical analyses were conducted in Matlab 2022a.

The algorithm implementation, specific Osprey version, and other code used to generate the results of this manuscript have been made available online (DOI: 10.17605/OSF.IO/P2USJ).

3. Results

3.1. Algorithmic trends of BIC scores

As the algorithm added basis functions to the selected set, BIC scores tended to follow a characteristic trajectory. High-concentration singlet resonances were initially prioritized by the algorithm, and their inclusion in the basis set rapidly reduced model residuals and, consequently, increased the BIC score. After this—as diminishing contributions are added to the spectrum—the rapid ascent of the BIC scores tapered off before reaching a maximum (which triggers the max-BIC stopping condition). According to the interpretation of BIC scores, this point is considered to be optimally parsimonious, and while additional basis functions do continue to reduce the residuals, they do not reduce them sufficiently to warrant the additional model parameters. This ascent of the BIC scores reliably identified the high-concentration metabolites that were present in the simulation.

Beyond the peak, we noted a gradual decrease in the BIC scores as relatively smaller spectral contributions lowered the cost-effectiveness of the overall model. Eventually, the candidate metabolite basis functions contribute an amplitude of zero when added to the model. In other words, it costs model parameters to include the candidate but provides no benefit to the model residual (this triggers the 2^nd stopping condition: zero-amplitude). After the zero-amplitude point, we observed a continued decline as the remaining basis functions were added. Importantly, in most cases, ground-truth metabolites (those present in the synthetic spectra) tended to be included before the algorithm reached this final zone. Typical BIC score trajectories across rounds of the algorithm are illustrated in Figure 2.

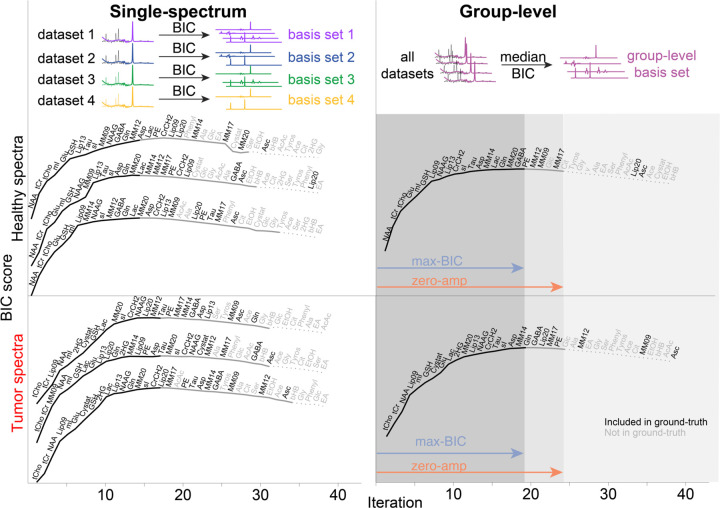
Figure 2.

BIC scores as a function of algorithm round. The top row shows a conceptual visualization of the difference between the two optimization methods. The lower two rows show the results for the healthy spectra (middle row) and tumor spectra (bottom row). The left column shows 3 (out of 100) example BIC curves for the single-subject optimizations, and the right column shows the group-level optimization (median BIC). Text labels indicate the basis function added at each round, with label color reflecting the presence/absence (black/grey) of that metabolite in the ground-truth simulation. Line style is used to illustrate the extent of the derived basis sets in each stopping condition: included in both stopping conditions (solid black line), included only in the zero-amplitude condition (grey line), or included in neither (light-grey dotted line).

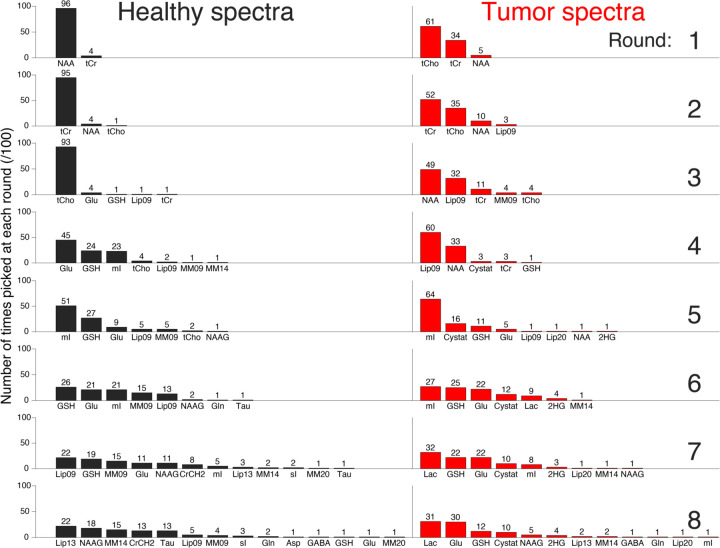
The single-spectrum results in Figure 2 illustrate the between-spectrum variation of the basis set composition. Whilst it is cumbersome to visualize all 200 single-spectrum optimization curves, we have attempted to illustrate the initial algorithmic trends of the single-spectrum optimization in Figure 3. For healthy spectra, there is a clear prioritization of NAA, tCr, and tCho, in that order. The tumor spectra have a less clearly defined hierarchy of signals. The lower NAA and higher tCho amplitudes lead to a less unanimous prioritization of the singlets, and the larger lipid signals are prioritized as early as the 2^nd round. Beyond the 5^th round, both groups of spectra had a diverse set of metabolites selected. A visualization summarizing the prioritization of basis functions across the full optimization process is shown in Supplementary Figure 3.

Figure 3.

Histograms of the frequency with which particular metabolites were picked at each round of the algorithm. Rows represent the different rounds (increasing from top-to-bottom), and the two columns represent the two groups of spectra.

3.2. Overlap with the ground-truth basis set

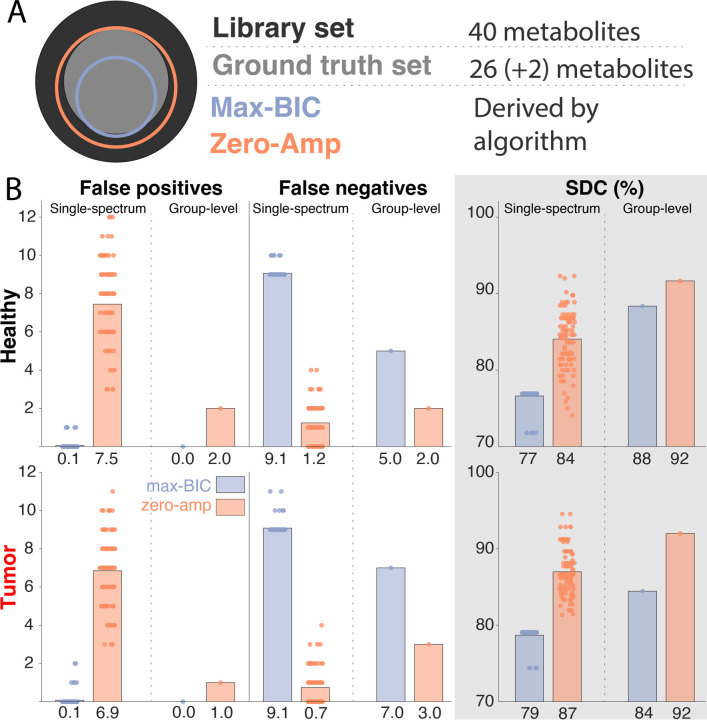
For the single-spectrum optimization, we found that the max-BIC stopping condition tended to be too conservative (few false positives, many false negatives) whereas the zero-amplitude condition tended to be too aggressive (few false negatives, many false positives). Bar plots showing the false positives, false negatives, and SDC are shown in Figure 4. Overall, the zero-amplitude condition exhibited a better overlap with the ground-truth set, as evidenced by the SDC for both healthy-appearing spectra (mean difference = 7%, p < 0.005) and tumor spectra (mean difference = 8%, p < 0.005).

Figure 4.

A. Conceptual Venn diagram showing the ground truth, library, and both derived basis sets. B. Overlap of the derived basis sets compared to the ground truth for the healthy spectra (top) and tumor spectra (bottom). From left to right, columns show the number of false positives, the number of false negatives, and the Sorensen-Dice coefficient (SDC) reported as a percentage. Within each panel, the left half shows the 100 single-spectrum results, and the right half shows the sole result of the group-wise optimization. Stopping conditions are color-coded: Max-BIC (purple) and zero-Amp (orange). Below each bar, the mean value is reported.

When the optimization was performed at the group level, a similar trend was present, but with greater overall fidelity to the ground truth. Across both datasets and both stopping conditions, the group-level optimization outperformed the single-spectrum optimization in all metrics with one exception (zero-amplitude stopping condition, false negatives for the tumor spectra). This better performance of the group-level approach is most clearly summarized in the SDC plots, with the ground-truth overlap increasing by 11% for the max-BIC (from 77% to 88%) and 8% for the zero-amplitude stopping conditions (from 84% to 92%) in the healthy spectra, and both stopping conditions increasing by 5% for the tumor spectra.

3.3. Inclusion of 2HG and Cystat

For the single-spectrum optimization, the inclusion or omission of Cystat and 2HG depended on the stopping condition used, with neither providing perfect results. The zero-amplitude condition included the oncometabolites in 97% of the tumor spectra (n_Cystat = 100; n_2HG = 94) but also provided a large number of false positives for these same metabolites in healthy spectra (n_Cystat = 54; n_2HG = 42). The situation is reversed for the max-BIC stopping condition. It does better at omitting Cystat and 2HG from healthy spectra (n_Cystat = 0; n_2HG = 2), but incorrectly omits these metabolites from most tumor spectra (n_Cystat = 89; n_2HG = 85).

For group-level optimization, the results are encouraging and definitive. Cystat and 2HG were correctly omitted from the basis set of the healthy spectra and correctly included in the tumor spectra for both stopping conditions.

3.4. Effect on metabolite amplitudes

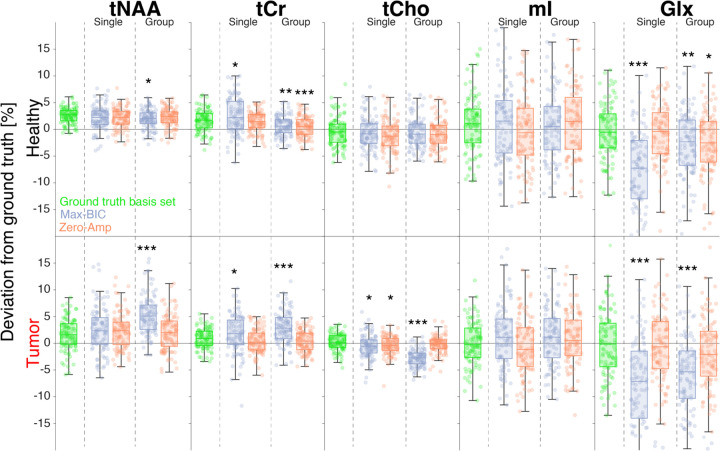
Metabolite amplitude errors depended on the underlying ground truth amplitude, with larger relative error for low-concentration metabolites. Figure 5 shows the percentage deviation of metabolite amplitude estimates from the ground truth for 5 metabolite measures commonly reported in the MRS literature: tNAA (NAA + NAAG), tCr (Cr + PCr), tCho (GPC + PCho), mI, and Glx (Glu + Gln).

Figure 5.

Boxplots of the percentage deviation of amplitude estimates from the simulated ground truth for 5 commonly reported metabolites (tNAA, tCr, tCho, mI, and Glx). Results for the healthy spectra are shown in the top row and tumor spectra in the bottom. The results using the ground truth basis set (i.e. including only the metabolites present in the simulation) are shown in green. The two stopping conditions—max-BIC (purple) and zero-Amp (orange)—are shown in each panel, for the single-spectrum optimization (left) and group-level optimization (right). Significant deviations from the estimates derived using the ground-truth basis set are marked with asterisks: “*” (0.005 ≤ p < 0.05), “**” (0.0005 ≤ p < 0.005), and “***” (p < 0.0005). Note that the plot limits exclude Glx outliers for comparability.

Across both groups and all derived basis set compositions, absolute amplitude errors were typically below 15% for these 5 metabolites but with some negative Glx outliers as large as – 37%, namely for max-BIC-derived basis sets. For the major singlet resonances (tNAA, tCr, and tCho), absolute amplitude errors were < 16% overall, and ≤ 11 % for the healthy-appearing spectra, specifically.

As reported in section 3.2, the max-BIC stopping condition included too few metabolites, and this underprescription of the basis set results in larger mean amplitude errors (4.6% for single-spectrum optimization and 3.9% group-wise) than for the zero-amplitude stopping condition (3.2% for both single-spectrum and group-wise optimization). The best-performing optimization method (as measured by SDC; group-wise & zero-amplitude) only deviated from the ground truth amplitude estimates in healthy spectra for Glx (mean difference = 2.1%, p = 0.0071) and tCr (mean difference = 1.2%, p < 0.0005).

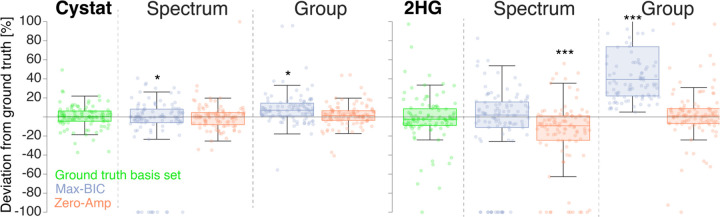
The deviation of amplitude estimates from ground truth is shown in Figure 6 for Cystat and 2HG in the tumor spectra. Note that an estimated amplitude of zero is assumed for single-spectrum-optimized basis sets which omitted that particular metabolite. This resulted in a cluster of data points at –100%. However, 4/10 of these points for the single-spectrum, zero-amplitude basis sets were true zero-amplitude estimates of 2HG when it was present in the derived basis set.

Figure 6.

Boxplots of the percentage deviation of amplitude estimates from the simulated ground truth for Cystat and 2HG in the tumor spectra. The results using the ground truth basis set (i.e. including only the metabolites present in the simulation) are shown in green. The two stopping conditions—max-BIC (purple) and zero-Amp (orange)—are shown in each panel, for the single-spectrum optimization (left) and group-level optimization (right). Significant deviations from the estimates of the ground-truth basis set are marked with asterisks: “*” (0.005 ≤ p < 0.05), “**” (0.0005 ≤ p < 0.005), and “***” (p < 0.0005).

The max-BIC stopping condition again exhibited the largest mean amplitude errors for both Cystat (19% for single-spectrum, and 16% for group-level optimization) and 2HG (28% for single-spectrum, and 73% for group-level optimization).

4. Discussion

A key challenge for in vivo MRS is that a ‘true’ model of the in vivo MR spectrum cannot be known, since the processes that shape it—the interplay of concentrations, microstructure, microscopic particle motion, macroscopic subject motion, temperature, pH, etc.—are too complex. In practice, all conventional ¹H-MRS modeling methods therefore focus on the most relevant macroscopic quantities, i.e., signal amplitudes for key metabolites, and must simplify other aspects. This epistemic uncertainty has provided a fertile environment in which a multitude of model functions, algorithms, software tools, and fitting strategies have grown over the last thirty years. Unsurprisingly, the different models and strategies do not agree very well with each other^27–29. This analytic variability has contributed to the overall poor reproducibility and comparability of metabolite estimates reported in the MRS literature³⁰.

“If we have several options to model our data, which should we pick?” is a common question across the sciences. If there are multiple suitable ways to model in vivo MRS data, we posit that modeling procedures should not only traverse the parameter space within a single model definition (via non-linear least-squares optimization) but also search across model spaces, i.e., explore the breadth of reasonably admissible model definitions. Quantitative model selection methods provide a formal, rigorous framework to do this—exemplified by the ABfit algorithm, which uses model selection to pick the one from many admissible baseline spline models that afford just enough flexibility to approximate the data, but not more¹⁷.

The composition of the basis set is another prime example of the range of reasonably admissible models, having been at the sole discretion of individual researchers since the inception of LCM for in vivo MRS. The surprisingly limited number of studies that have investigated the impact of this modeling decision highlights the potential for operator bias, with changes to the basis set composition substantially affecting metabolite estimates^4–10. In this proof-of-concept study, we therefore demonstrate the use of model selection for determining basis set composition directly from the spectra.

Across all procedural variations we considered, the algorithm was able to derive reasonable basis sets and consistently produced fits with flat residuals. High-concentration metabolites were correctly included in the algorithm-derived basis sets, without exception. The algorithm’s ability to correctly identify lower-concentration metabolites was more varied and depended decidedly on the choice of stopping condition and single-vs-group analysis. We found that group-level basis set estimation with the ‘zero-amplitude’ stopping condition minimized the number of false positives and negatives, correctly recognized 2HG and Cystat in the tumor group, and provided metabolite estimates close to those estimated with the ground-truth basis set. This is an encouraging starting point, although further investigation is required.

4.1. Choice of Stopping condition

We initially designed the algorithm to select the basis set that simply maximized the BIC—certainly the most intuitive choice, as it is purported to provide the optimal balance between goodness-of-fit and the number of model parameters. In practice, the “max-BIC” condition is too conservative: the least-squares model was flexible enough to reasonably mimic the signal of metabolites (particularly J-coupled, low-concentration ones) through some combination of baseline bumps, lineshape distortions, and overlapping metabolites already present in the basis set. This—according to raw BIC scores—is more parsimonious than bringing in a new basis function, which would be penalized for the additional model parameters.

Adding further metabolites (beyond the maximum BIC) until all remaining basis functions are fit with zero amplitude alleviated these problems, albeit at the expense of including more false positives. Despite this, quantitative overlap with the ground truth and amplitude estimation was still better than for the max-BIC stopping condition. Together, the two stopping conditions delineated a “Goldilocks” region that provided reliable upper and lower bounds on the ground truth basis set.

4.2. Group-wise or single-spectrum

Further improvement in basis set estimation was achieved by optimizing across an entire group of spectra. This approach counteracted the challenges of reliably discerning the contributions of lower-concentration metabolites at the single-spectrum levels. We hypothesize that the aggregation of BIC scores across many spectra reduces the impact of noise and individual amplitude variations, allowing the algorithm to better prioritize signals that we are less able to consistently model on a per-spectrum basis. Still, there are some notable omissions, particularly from mutually overlapping lipids and MMs. Asc is also omitted from both group-wise optimizations. We ascribe this to Asc having a very small amplitude in the ground truth spectra (0.36 ± 0.28, and 0.42 ± 0.31) to begin with, and, for the chosen fit range of 0.5–4.2 ppm, Asc only has resonances in the 3.6–4.1 ppm region, in which it heavily overlaps with other metabolites it can be easily mistaken for—see Supplementary Figure 1. Future avenues of study may benefit from incorporating additional information into the decision-making process to tackle issues of strong overlap. These may include Cramer-Rao lower bounds, metabolite amplitude correlation matrices derived from the Fisher information matrix, or a modification to the IC metric.

It is important to note that the two groups of spectra generated for this study are fairly homogeneous, and crucially, group-wise optimization removes our ability to adapt to individual outlier spectra that may be present in heterogeneous in vivo samples. The correct inclusion of 2HG and Cystat in the tumor cohort (and simultaneous exclusion in the healthy cohort) illustrates that the selection process might even deem two different models to be most appropriate if two cohorts exhibit markedly different spectral characteristics. This is, in general, of course desirable! For example, healthy tissue does not produce detectable levels of 2HG^31(p2), and model selection for a set of healthy spectra should select a model that does not contain a 2HG basis function because fewer degrees of freedom will reduce the variance in estimating signals like Glu/Gln that overlap with 2HG. However, the idea of running one model for healthy spectra and another for tumor spectra does raise challenging questions in terms of model bias and hypothesis testing.

4.3. Limitations

Our synthetic data are somewhat idealized since they omitted some common characteristics of in vivo MRS data. For example, we did not introduce phase alterations, frequency shifts, correlated noise, baseline components, or artifacts like lipids, residual water, or spurious echoes. Broad resonances underlying the metabolite signals, in particular, significantly impact the accuracy of MRS modeling^8,28. Modeling of the baseline would also be further complicated by the frequent omission of MM and lipid models from the optimized basis sets, as we saw in our data. The algorithm tended to capture some of the—admittedly small—MM signals using the spline baseline rather than a specific basis function. While this did reduce the number of model parameters, it compromised the validity of our baseline model. Future work could include some algorithm penalty term for baseline amplitudes, or perhaps this issue is best solved by including an experimentally acquired MM basis function, as recommended by expert consensus³² and our previous investigations^28,33.

Lastly, the repeated modeling required for this method obviously takes longer to complete than traditional single-model analysis with a single pre-defined basis set. For a library set of size $N$, our algorithm requires $\frac{1}{2}N\left(N+1\right)$ model calls to complete the full IC curves, like those shown in Figure 2. That said, with an initial fit to fix global model parameters, small basis set compositions in the early stages, and stopping conditions avoiding the latter algorithm steps, computation time, fortunately, does not scale linearly with the number of model calls for this algorithm. A computationally cost-effective compromise of our approach could be to use this algorithm as a refinement of some predefined basis set. Specifically, an expert-recommended starting basis set could be modulated, using the iterative process described here to add (or subtract) appropriate metabolites.

4.4. Perspectives

Model selection can, in principle, be applied to any aspect of modeling, not just baseline estimation¹⁷ or basis set composition. Information criteria may be useful to determine optimal lineshape representations, e.g., deciding whether simple Voigtian parametrization suffices, or whether a more generalized convolution kernel (with more model parameters) is required to adequately fit lineshape irregularities resulting from B₀ inhomogeneities. They may also help decide whether metabolite-specific frequency shifts are warranted by the data or whether a single, global, shift parameter suffices.

Parameter regularization may provide an alternative to model selection. This usually involves additional terms in the model expression that penalize the deviation of model parameters from certain expectation values or impose constraints on, e.g., smoothness.

This often-overlooked injection of prior knowledge is widely considered to be the “secret ingredient” of LCModel. Apart from baseline regularization, the effects of regularization on metabolite estimates are not well studied. Future work should therefore explore whether this approach can complement model selection. For example, instead of excluding certain metabolites like 2HG from a basis altogether, it might be wiser to simply set their amplitude expectation values to zero. This would incentivize the model to only assign signal to 2HG when it is strongly warranted by the data. Of course, choosing the nature and strength of the regularization terms is, yet again, a form of operator bias.

Finally, the best solution to the epistemic uncertainty problem may be to not even try to select a single model but to synthesize the evidence from multiple models. So-called multiverse analyses^34–38 have been pioneered to integrate multiple statistical models in psychology and have recently been applied to resting-state fMRI analysis. It has further been proposed to weigh different models by their Akaike information criterion scores^39–41 to emphasize the evidence from more parsimonious models, conceptually similar to CRLB weighting to improve statistical inference across multiple spectra⁴².

Conclusion

Data-driven determination of the basis set composition is feasible with single-spectrum and group-level optimization. With refinement, this method could provide a valuable data-driven way to derive or refine basis sets, reduce the operator bias of MRS analyses, enhance the objectivity of quantitative analyses, and increase the clinical viability of MRS.

Funding Statement

This work was supported by National Institutes of Health Grants R01 EB035529, R21 EB033516, R00 AG062230, R01 EB016089, R01 EB023963, K99 AG080084, and P41 EB031771. SA was funded by the Mildred Scheel Career Center Frankfurt (Deutsche Krebshilfe).