“Hydridic Hydrogen-Bond Donors” Are Not Hydrogen-Bond Donors

Abstract

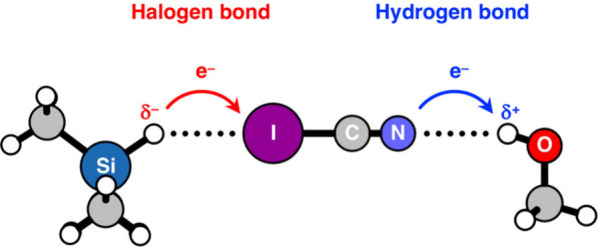
Herein, we dismiss a recent proposal by Civiš, Hobza, and co-workers to modify the IUPAC definition of hydrogen bonds in order to expand the scope from protonic Y–H^δ+ to hydridic Y–H^δ− hydrogen-bond donor fragments [J. Am. Chem. Soc.2023, 145, 8550]. Based on accurate Kohn–Sham molecular orbital (KS-MO) analyses, we falsify the conclusion that interactions involving protonic and hydridic hydrogens are both hydrogen bonds; they are not. Instead, our quantitative KS-MO, energy decomposition, and Voronoi deformation density analyses reveal two fundamentally different bonding mechanisms for protonic Y–H^δ+ and hydridic Y–H^δ− fragments which go with charge transfer in opposite directions. On one hand, we confirm the IUPAC definition for regular hydrogen bonds in the case of protonic Y–H^δ+ fragments. On the other hand, complexes involving Y–H^δ− fragments are, in fact, acceptors in other well-known families of Lewis-acid/base interactions, such as halogen bonds, chalcogen bonds, and pnictogen bonds. These mechanisms lead to the same spectroscopic phenomenon in both the Y–H^δ+ and Y–H^δ− fragments, that is, the redshift in the Y–H stretching frequency, which is, thus, not an exclusive indicator for hydrogen bonding.

Introduction

The hydrogen bond is a key chemical interaction in biological, supramolecular, and organic chemistry.¹ IUPAC defines the hydrogen bond (HB) as an attractive interaction between a hydrogen atom from a molecule or a molecular fragment Y–H, in which Y is more electronegative than H, and an atom or group of atoms (Z), in which there is evidence of bond formation (i.e., a Y–H···Z hydrogen-bonded complex).² According to molecular orbital (MO) theory, the reason behind the stability of the HB is twofold: (i) the electrostatic attraction between the protonic hydrogen in the Y–H^δ+ fragment and Z; and (ii) the covalent donor–acceptor interaction stemming from the charge transfer from the HOMO of Z into the empty σ* Y–H antibonding orbital.³ The covalency of HB is manifested in the characteristic Y–H bond elongation and a decrease, i.e., redshift, in the vibrational frequency associated with the Y–H bond stretching mode.^3b,4

Hydridic hydrogens are also known to engage in intramolecular interactions that do not fit the IUPAC definition of the HB. For example, in the case of the charge inverted hydrogen bonds (CIHB),⁵ a designation coined by Jabłoński to cover systems of the type Y–H^δ−···Z, in which Y is less electronegative than H and Z is an electron-deficient fragment. In this point of view, hydrogen bonding refers to all interactions involving a hydrogen atom that can either be protonic, forming a regular HB, or hydridic, forming a CIHB. Recently, Civiš, Hobza, and co-workers proposed a generalization of the IUPAC definition of HB in order to cover both the protonic and hydridic forms within the same definition.⁶ According to the authors, CIHBs still hold many important features of the HB, such as the donation of charge into the σ* Y–H^δ− antibonding orbital and the elongation, i.e., redshift, of the Y–H^δ− bond. This implies that, in CIHB, hydridic hydrogens behave as Lewis acids and the electron-deficient Z fragment behaves as a Lewis base; thus, the bonding mechanism of HB and CIHB would be the same.

In this work, we challenge the idea that hydridic hydrogen bonds involve only an inversely polarized H-bond donor but otherwise are, in essence, electronically similar to protonic hydrogen bonds. To this end, we analyze the bonding mechanism of a series of Me_mYH···NH₃, Me_mYH···NCI, and Me_mYH···ICN complexes (Y = C, Si, Ge, N, P, As, O, S, Se; m = 3, 2, 1), using Kohn–Sham molecular orbital (KS-MO) theory (Scheme 1). Our model systems feature Y–H groups with protonic and hydridic hydrogens and allow for a systematic and quantitative comparison of how bonding mechanisms change in nature along the series. We show that true hydrogen bonds, i.e., in which the H-bond acts as a Lewis acid accepting charge in its σ* Y–H LUMO, can only be formed with protonic hydrogens. On the contrary, complexes involving hydridic hydrogens lead to a completely different bonding mechanism in which the molecular fragment containing the hydrogen atom acts as a Lewis base, not as a Lewis acid.⁷ Thus, CIHB is not a correct designation for interactions involving hydridic hydrogens, and hence, there is no need to change the IUPAC definition of the hydrogen bond.

Scheme 1. Schematic Me_mYH···NH₃, Me_mYH···NCI, and Me_mYH···NCI Model Complexes (Y = C, Si, Ge, N, P, As, O, S, Se; m = 3, 2, 1).

Results and Discussion

The Me_mYH Fragments

We start by analyzing the protonic or hydridic character of the H atom of the studied model Me_mYH fragments, in which Y is an element belonging to groups 14, 15, and 16 and periods 2, 3, and 4 of the periodic table (Y = C, Si, Ge, N, P, As, O, S, Se, and m = 3, 2, and 1). For this purpose, we analyze the Voronoi deformation density (VDD) charge on the H atom (Q_H) directly bound to atom Y (see Theoretical Methods). In general, we find that Y atoms with an electronegativity higher than H (χ_H = 2.20)⁸ cause a charge depletion on H, i.e., a positive VDD charge on H, whereas Y atoms with an electronegativity lower than H result in an accumulation of charge on H, i.e., a negative VDD charge on H. For example, Q_H is +154 milli-electrons for MeOH and −92 milli-electrons for Me₃SiH, where the electronegativity of O and Si are χ_O = 3.44 and χ_Si = 1.90, respectively (Figure 1). Thus, the nature of atom Y greatly influences the charge of the H atom in the Me_mYH monomer, making them either protonic or hydridic.

Figure 1.

Equilibrium geometries, Voronoi deformation density charges (in milli-electrons) on the indicated hydrogen atom, and the electronegativity of Y on the Pauling scale⁷ (χ_Y; in gray) of the Me_mYH fragments (Y = C, Si, Ge, N, P, As, O, S, Se; m = 3, 2, 1). The electronegativity of H is χ_H = 2.20.⁸ Computed at ZORA-BLYP-D3(BJ)/TZ2P.

We recall that, according to the IUPAC definition,² a hydrogen bond is only formed when the Y atom is more electronegative than H. In other words, the Me₃SiH, Me₃GeH, Me₂PH, and Me₂AsH fragments with hydridic H should be unable to engage in a hydrogen bond with an electron-rich fragment, i.e., a Lewis base (Figure 1). In the following section, we quantify this statement and explain why hydrogen bonds involving a hydric hydrogen can indeed not be formed.

On the Nonexistence of Hydridic Hydrogen Bonds

To evaluate the ability of protonic and hydridic hydrogens to engage in hydrogen bonding, we study the interaction between the Me_mYH fragments and NH₃, a well-known Lewis base and hydrogen-bond acceptor, to form complexes of the type Me_mYH···NH₃ (see Scheme 1a). The equilibrium geometries, electronic bond energies ΔE, and the charge depletion on the NH₃ fragment are reported in Figure 2 (see Table S1 for additional data). We find that Me_mYH···NH₃ complexes exist only for the Me_mYH fragments with protonic or close to neutral hydrogens, namely, for Y = C, N, O, S, and Se, in which the most stable and shortest is MeOH···NH₃, with ΔE = −7.2 kcal mol^–1 and r_H···N = 1.93 Å, and the least stable and longest is Me₃CH···NH₃, with ΔE = −1.0 kcal mol^–1 and r_H···N = 2.68 Å (Figure 2). The fragments with hydridic hydrogens (Y = Si, Ge, P, As), but also the slightly protonic Me₃CH, form structurally completely different bonding motifs of the type Me₃YH···HNH₂, which are less stable, ranging from Me₂AsH···HNH₂, with ΔE = −2.6 kcal mol^–1, to Me₃CH···HNH₂, with ΔE = −1.4 kcal mol^–1 (Figure 2).

Figure 2.

Equilibrium geometries (in Å), electronic bond energies (in kcal mol^–1; in brackets), and the charge depletion on the NH₃ fragment (ΔQ_NH3; in milli-electrons; in blue) of the Me_mYH···NH₃ hydrogen-bonded complexes (Y = C, N, O, S, Se) and the Me_mYH···HNH₂ complexes (Y = C, Si, Ge, P, As). Computed at ZORA-BLYP-D3(BJ)/TZ2P.

The different bonding motifs in protonic Me_mYH···NH₃ versus those in hydridic Me_mYH···HNH₂ are accompanied by different bonding mechanisms. In Me_mYH···NH₃, we find a depletion of charge on NH₃ upon binding, i.e., positive ΔQ_NH3, that is, there is charge transfer from NH₃ into the Me_mYH fragment (see Figure 2). The charge transfer mechanism from NH₃ to Me_mYH is the characteristic covalent component of the hydrogen bond, where the lone pair orbital of NH₃ (LP_N) donates charge into the empty σ* Y–H antibonding orbital of Me_mYH (σ*_Y–H; see Scheme 2).³ As the σ*_Y–H becomes more populated, the Y–H bond elongates (see Table S1), resulting in the characteristic redshift in the vibrational frequency associated with the Y–H bond stretching mode. In contrast, there is no charge transfer in the Me_mYH···HNH₂ bonding motif involving a hydridic hydrogen, that is, there is no charge depletion or accumulation on NH₃ and, hence, no hydrogen bond in these complexes (see Figure 2). Next, we explain why hydridic fragments cannot form Me_mYH···NH₃ hydrogen-bonded complexes.

Scheme 2. Schematic Molecular Orbital Diagram for the Attractive (Green) and Repulsive (Red) Orbital Interactions in Me_mYH···NH₃ (Y = C, N, O, S, Se).

Stable hydrogen-bonded complexes are formed because the electrostatic attraction between Y–H^δ+ and the electron-rich bond acceptor, together with the covalent, charge transfer interaction, overcomes the destabilizing Pauli repulsion between the occupied σ Y–H bonding orbital (σ_Y–H) and the occupied orbitals of the bond acceptor (see Scheme 2).³ Protonic hydrogens are depleted of electron density, which exposes their positively charged nucleus to the electron density of an incoming electron-rich fragment, resulting in a stronger electrostatic attraction. On the other hand, hydridic hydrogens have an excess of electron density that: (i) screens their positively charged nucleus, causing a weaker electrostatic attraction between Y–H^δ− and the hydrogen-bond acceptor; and (ii) increases the size of σ_Y–H on the H atom, resulting in a more destabilizing Pauli repulsion between σ_Y–H and the occupied orbitals of the bond acceptor. As a result, hydrogen-bonded complexes involving a hydridic hydrogen are not formed because the attractive electrostatic and charge transfer interactions are not strong enough to overcome the repulsive wall arising from the Pauli repulsion. These findings emerge from our energy decomposition and quantitative KS-MO analyses that will be explained in detail in the next section.

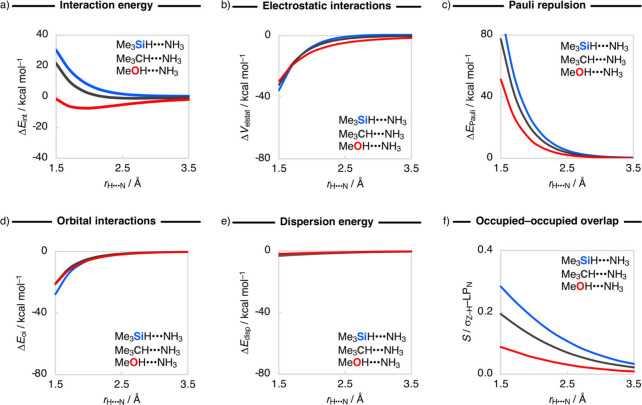
First, we analyze the bonding mechanism of the representative MeOH···NH₃, Me₃CH···NH₃, and Me₃SiH···NH₃ hydrogen-bonded complexes using our canonical energy decomposition analysis (EDA)⁹ as a function of the H···N bond distance (r_H···N), while keeping the geometries of the fragments frozen to the equilibrium geometries of the complexes (Figure 3; see Theoretical Methods). The Me₃SiH···NH₃ complex is unbound; therefore, in this case, we have the Me₃SiH and NH₃ fragments approach each other along the r_H···N in their respective equilibrium geometries.

Figure 3.

Energy decomposition analysis (in kcal mol^–1) and the repulsive occupied–occupied overlap (S) as a function of the H···N bond distance for the representative Me₃SiH···NH₃, Me₃CH···NH₃, and MeOH···NH₃ complexes. Computed at ZORA-BLYP-D3(BJ)/TZ2P.

The interaction energy curve, ΔE_int(r_H···N), goes from stabilizing, i.e., binding, for MeOH···NH₃ to weakly stabilizing for Me₃CH···NH₃ to destabilizing, i.e, unbound, for Me₃SiH···NH₃, reflecting the trends in hydrogen-bond stability of the complexes (Figure 3a). This trend is a direct result of the Pauli repulsion, ΔE_Pauli(r_H···N), which becomes significantly more destabilizing from MeOH···NH₃ to Me₃CH···NH₃ to Me₃SiH···NH₃ (Figure 3c). Along this series, Y becomes less electronegative than H, which significantly affects the size of the occupied σ_Y–H orbital on the H atom. The orbital amplitude on the H atom substantially increases along MeOH to Me₃CH to Me₃SiH (see Figure 4), causing the repulsive orbital overlap between the σ_Y–H orbital of Me_mYH and the LP_N orbital of NH₃ to increase along MeOH···NH₃, Me₃CH···NH₃, and Me₃SiH···NH₃ and, thus, leading to more build-up of Pauli repulsion upon bond formation (see Figure 3f). Note that the reduced Pauli repulsion is also the reason why MeOH···NH₃ can form a shorter hydrogen bond compared to the other complexes (Figure 3). In addition, the electrostatic interactions curve, ΔV_elstat(r_H···N), also becomes less stabilizing along MeOH···NH₃, Me₃CH···NH₃, and Me₃SiH···NH₃, especially around the equilibrium hydrogen-bond bond length (Figure 3b). This is a direct consequence of the decreasing electronegativity of Y along O, C, and Si, which makes the donating H atom less positively (or more negatively) charged along the same series, leading to a weaker electrostatic attraction between Me_mYH and the electron-rich NH₃ fragment. In summary, a hydridic hydrogen atom causes the Me_mYH···NH₃ complexes to experience a substantial build-up in steric repulsion and a weakening of electrostatic attraction, resulting in the nonexistence of hydridic hydrogen bonds in Me_mYH···NH₃.

Figure 4.

Electron density, occupied σ Y–H bonding orbital, and empty σ* Y–H antibonding orbital (contour plots from 0.9 to 0.03 au) for the representative Me₃SiH, Me₃CH, and MeOH fragments. Computed at ZORA-BLYP-D3(BJ)/TZ2P.

Hydridic Hydrogens as Bond Acceptors

We have shown that hydridic hydrogens are unable to engage in hydrogen bonds with electron-rich molecules like NH₃. In this section, we address the question: can hydrogen bonding be the most dominant interaction when a hydridic hydrogen engages in an intermolecular interaction with electron-poor halogen-bond donors as proposed by Civiš, Hobza, and co-workers?⁶ To answer this question, we study the bonding mechanism for the interaction between Me_mYH and ICN, where ICN can form a hydrogen bond with the nitrogen side and a halogen bond with the iodine side,¹⁰ according to the IUPAC definitions of hydrogen bonds² and halogen bonds^10a (see Scheme 1). The equilibrium geometries, electronic bond energies ΔE, and the charge rearrangement in the ICN fragment are reported in Figure 5.

Figure 5.

Equilibrium geometries (in Å), electronic bond energies (in kcal mol^–1; in brackets), and the charge accumulation (red) and depletion (blue) on the ICN fragment (in milli-electrons) of the Me_mYH···NCI complexes (Y = C, N, O, S, Se) and Me_mYH···ICN (Y = C, Si, Ge, P, As). Computed at ZORA-BLYP-D3(BJ)/TZ2P.

Similar to Me_mYH···NH₃, the Me_mYH fragments involving protonic and close to neutral hydrogens (Y = C, N, O, S, Se) form regular Y–H^δ+···N^δ− hydrogen bonds, in which charge flows into the hydrogen-bond donor Me_mY–H, i.e., positive ΔQ_ICN (Figure 5). This bond has a strength of up to 4.6 kcal mol^–1 for MeOH···NCI (Figure 5). On the other hand, the Me_mYH fragments involving a hydridic hydrogen (Y = Si, Ge, P, As) form regular H^δ−···I^δ+–C halogen bonds, in which charge flows out of the halogen-bond acceptor Me_mY–H into the halogen-bond donor I–CN, i.e., negative ΔQ_ICN (Figure 5). There is one intermediate situation, namely, the Me₃CH fragment, which shows both Me₃CH···NCI and Me₃CH···ICN bonding modes. As will become clear, this change in bonding mode occurs because we go from protonic Me_mYH···NCI hydrogen bonds to Me_mYH···ICN halogen bonds, not hydridic Me_mYH···ICN hydrogen bonds, in line with the current IUPAC definitions of hydrogen bonds² and halogen bonds.^10a

The bonding mechanism in Me_mYH···NCI involves a regular Y–H^δ+···N^δ− hydrogen bond and hence is similar to that of the Me_mYH···NH₃ complexes (vide supra). The ICN fragment acts as a hydrogen-bond acceptor on the N side through which the LP_N orbital of the ICN fragment donates charge into the empty σ*_Y–H orbital of Me_mYH fragments involving protonic hydrogens (Scheme 3, right side). However, as explained in the previous section, this donor–acceptor interaction is not strong enough to overcome the buildup of steric repulsion when involving Me_mYH fragments with hydridic hydrogens and, thus, Me_mYH···NCI complexes cannot be found for Y = Si, Ge, P, and As.

Scheme 3. Schematic Molecular Orbital Diagram (Contour Plots from 0.9 to 0.03 a.u.) for the Attractive (Green) and Repulsive (Red) Orbital Interactions in the Halogen-Bonded Me_mYH···ICN and Hydrogen-Bonded Me_mYH···NCI Complexes (Computed at ZORA-BLYP-D3(BJ)/TZ2P).

The hydridic Me_mYH···ICN complexes are constructed via a different bonding mechanism, namely, a halogen-bond,^3b,11 which is characterized by the covalent, donor–acceptor interaction between the occupied σ_Y–H orbital of Me_mYH and the empty σ* I–C antibonding orbital of ICN (σ*_I–C) (Scheme 3, left side). Consequently, upon binding, the charge flows from Me_mYH into the ICN fragment, as indicated by the negative ΔQ_ICN (see Figure 5). Note that the hydrogen-bonding and halogen bonding mechanisms go with charge transfer in opposite directions; that is, ΔQ_ICN is positive for the former and negative for the latter. Therefore, the negative ΔQ_ICN is clear evidence that there is no hydrogen-bonding mechanism that is able to overcome the halogen bond in the Me_mYH···ICN complexes. This is because ICN is a poor hydrogen-bond acceptor, i.e., weak Lewis base, on the I side due to its very low-lying I lone-pair (LP_I) orbital (see Scheme 3).

The magnitude of the various pairwise donor–acceptor orbital interactions is approximately proportional to their orbital overlap squared (S²) divided by the orbital energy gap (Δε). For Me₃SiH···ICN, the S and Δε for the σ_Y–H → σ*_I–C halogen-bond interaction are 0.19 and 4.0 eV, respectively, and its associated S²/Δε is 9.4 × 10³ (see Figure 6 and Table S5 for all the Me_mYH···ICN complexes). The LP_I orbital of ICN has a large amplitude on the I side and overlaps with the empty σ*_Y–H of Me₃SiH, in which S is 0.15 (Figure 6). However, this σ*_Y–H ← LP_I hydrogen-bond interaction is significantly weaker due to a large Δε of 13.3 eV, leading to an S²/Δε of only 1.7 × 10³, which is about five times weaker than that of the σ_Y–H → σ*_I–C halogen-bond interaction (Figure 6). Therefore, the magnitude of the hydrogen-bonding mechanism is negligible and dominated by the halogen bond in Me₃SiH···ICN. For this reason, Me₃SiH···ICN and the other Me_mYH···ICN complexes involving hydridic hydrogens should be seen as halogen-bonded, not hydridic hydrogen-bonded, complexes.

Figure 6.

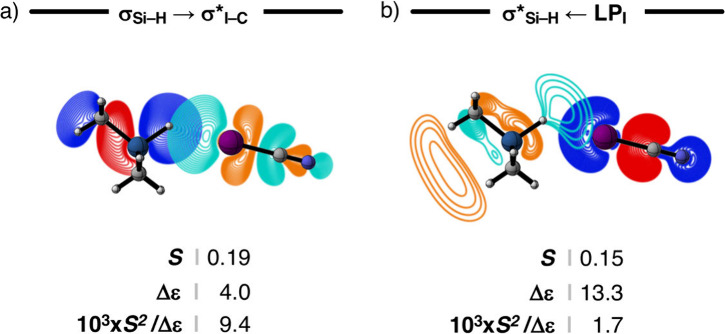
Donor–acceptor orbital overlap (S), energy gap (Δε, in eV), and the orbital stabilization for a) the σ_Si–H → σ*_I–C halogen bond and b) the σ*_Si–H ← LP_I hydrogen bond in the representative Me₃SiH···ICN complex (contour plots from 0.9 to 0.03 au). Computed at ZORA-BLYP-D3(BJ)/TZ2P.

The Redshift

The analyzed Me_mYH···NH₃ hydrogen-bonded systems feature the characteristic Y–H bond elongation and, thus, the redshift in the Y–H bond stretching frequency. For example, in the series of MeOH···NH₃, MeSH···NH₃, and MeSeH···NH₃, the Y–H bond elongates by 0.016 Å, 0.010 Å, and 0.012 Å, and the symmetric Y–H bond stretching frequency in the complexes decreases by −316 cm^–1, −125 cm^–1, and −134 cm^–1, respectively, in respect to the isolated Me_mYH monomers (Table 1). The Y–H bond elongation in hydrogen-bond donors is the manifestation of the covalent nature of hydrogen bonds, that is, it is caused by the donation of charge into the empty σ*_Y–H orbital via donor–acceptor interactions.^3b,4 In the series of MeOH···NH₃, MeSH···NH₃, and MeSeH···NH₃, there is a depletion of charge in the NH₃ fragment, i.e., positive ΔQ_NH3, while the population in empty σ*_Y–H orbital increases to 0.04 0.03, and 0.03 electrons along the same series.

Table 1. Y–H Bond Elongation (in Å), Change in the Y–H Stretching Frequency (in cm^–1), Charge in the Voronoi Deformation Density Charge on the NH₃ or ICN Fragments (in Milli-electrons), and Populations in the Filled σ_Y–H and Empty σ*_Y–H Orbitals for Representative Me_mYH···NH₃ (Y = O, S, Se) and Me_mYH···ICN (Y = C, Si, Ge) Complexes (Computed at ZORA-BLYP-D3(BJ)/TZ2P^a).

Complex	ΔrY–H	ΔυY–H	ΔQNH3/ICN	Pop.σY–H	Pop.σ*Y–H
MeOH···NH3	0.016	–316	+41	2.00	0.04
MeSH···NH3	0.010	–125	+28	2.00	0.03
MeSeH···NH3	0.012	–134	+34	2.00	0.03
Me3CH···ICN	0.003	–47	–11	1.99	0.00
Me3SiH···ICN	0.014	–87	–35	1.94	0.00
Me3GeH···ICN	0.019	–98	–39	1.93	0.01

^aSee complete data in Tables S1–S4 in the Supporting Information.

In the halogen-bonded Me_mYH···ICN complexes, we find that the Y–H bond also elongates and, thus, the Y–H bond stretching frequency redshifts. For example, in the series of Me₃CH···ICN, Me₃SiH···ICN, and Me₃GeH···ICN, the Y–H bond elongates by 0.003 Å, 0.014 Å, and 0.019 Å, and the symmetric Y–H bond stretching frequency in the halogen-bond acceptors decreases by −47 cm^–1, −87 cm^–1, and −98 cm^–1, respectively (Table 1). However, since the hydrogen-bonding mechanism is negligible in the Me_mYH···ICN complexes (vide supra), the population in the empty σ*_Y–H orbital does not significantly change and, therefore, cannot be responsible for the Y–H bond elongation in these complexes (Table 1). In fact, the redshift in the Me_mYH halogen-bond acceptors is a consequence of their Lewis basicity. In the previous section, we showed that the halogen-bond donor–acceptor mechanism in the Me_mYH···ICN complexes is the donation of charge from the filled σ_Y–H orbital of Me_mYH into the empty σ*_I–C orbital of ICN. For example, in the series of Me₃CH···ICN, Me₃SiH···ICN, and Me₃GeH···ICN, the population in the filled σ_Y–H orbital is reduced to 1.99 electrons, 1.94 electrons, and 1.94 electrons respectively, while there is charge accumulation in the ICN fragment, i.e., negative ΔQ_ICN (Table 1). Consequently, the Y–H bond becomes longer and, thus, redshifts, as the σ_Y–H bonding orbital loses electrons due to the halogen bond. Therefore, the redshift in the Y–H bond stretching frequency should also be expected in situations when hydridic Y–H^δ− fragments behave as a Lewis base and hence is not an exclusive feature of hydrogen-bond donors.

A similar phenomenon is found when the hydridic hydrogen of Me₃SiH engages in a stabilizing intermolecular interaction with the different electron-poor molecules studied by Civiš, Hobza, and co-workers,⁶ that is, ICF₃, BrCN, S(CN)₂, P(CN)₃, and K⁺. In all these complexes, the Si–H bond elongates and redshifts upon complex formation. However, this is not because Me₃SiH behaves a hydrogen-bond donor, but as a bond acceptor. We find that there is charge transfer from Me₃SiH into the electron-poor fragments and the population in the filled σ Si–H bonding orbital is reduced, which, in fact, characterizes different intermolecular interactions, e.g., halogen bonds, chalcogen bonds, and pnictogen-bonds¹¹ (see Table S6; see addition analyses on palladium hydride, boron hydride, beryllium hydride, and lithium hydride in Tables S7 and S8). A bonding motif in which a hydridic hydrogen acts as the acceptor of a hydrogen bond exists in the particular form of dihydrogen bonds (DHB); this has been described elsewhere.⁷ Thus, we have presented clear evidence that the interaction between the hydridic hydrogen of Me₃YH and an electron-poor molecule should not be seen as any kind of hydrogen bonding but instead as a different intermolecular interaction named after the nature of the electron-poor bond donor.

Conclusions

We have quantum chemically analyzed the bonding mechanism of a series of Me_mYH···NH₃ and Me_mYH···ICN complexes, in which Y = C, Si, Ge, N, P, As, O, S, Se and m = 3, 2, 1, using quantitative Kohn–Sham molecular orbital (KS-MO) theory. We showed that Me_mY–H^δ+ fragments involving protonic hydrogens (i.e., Y = C, N, O, S, Se) form regular Y–H^δ+···N^δ− hydrogen bonds, whose stability is due to the H^δ+···N^δ− electrostatic attraction and the charge transfer from the hydrogen-bond acceptor NH₃ into the hydrogen-bond donor Me_mY–H^δ+. The Me_mY–H^δ− fragments involving hydridic hydrogens (i.e., Y = Si, Ge, P, As) are unable to act as hydrogen-bond donors and, instead, behave as Lewis bases, donating charge into electron-poor fragments, such as ICN, forming a H^δ−···I^δ+–C halogen bond. Therefore, our findings do not support the proposal to change the IUPAC definition of hydrogen bonds to include molecules with partially negatively charged H as hydrogen-bond donors.⁶

Regular hydrogen bonds, as in Me_mY–H^δ+···NH₃, involve charge transfer into the empty σ* Y–H antibonding orbital of the hydrogen-bond donor fragment. This hydrogen-bond donor–acceptor interaction is negligible in the Me_mY–H^δ−···ICN complexes, and the charge transfer goes in the opposite direction from the occupied σ Y–H bonding orbital into the ICN fragment. This is because ICN is a poor electron donor on the I side, which leads to a weaker hydrogen-bond donor–acceptor interaction in Me_mY–H^δ−···ICN. In turn, the covalent component in Me_mY–H^δ−···ICN is dominated by the halogen-bond donor–acceptor interaction between the occupied σ Y–H bonding orbital and the empty σ* I–C antibonding orbital of ICN. Therefore, the Me_mY–H^δ− fragments are halogen-bond acceptors, not hydrogen-bond donors.

The accumulation of charge in the empty σ* Y–H antibonding orbital causes the Y–H bond elongation and, thus, the typical redshift in the of the Y–H stretching frequency for regular Me_mY–H^δ+···NH₃ hydrogen bonds. However, the elongation the Y–H bond can also be caused by other factors, e.g., the depletion of charge in the occupied σ Y–H bonding orbital in halogen-bonded Me_mY–H^δ−···ICN complexes. Therefore, the redshift in the Y–H stretching frequency should not be used as the unique but as one of the diagnostics to characterize hydrogen bonds.

Theoretical Methods

Computational Details

All calculations were carried out using the Amsterdam Density Functional (ADF) 2023.101 program.¹² All stationary points and energies were obtained using relativistic, dispersion-corrected density functional theory at ZORA-BLYP-D3(BJ)/TZ2P (see Tables S9, S10, and S11 in the Supporting Information for the Cartesian coordinates). This approach comprises the BLYP level of the generalized gradient approximation (GGA); the exchange functional developed by Becke (B), and the GGA correlation functional developed by Lee, Yang, and Parr (LYP).¹³ The empirical DFT-D3(BJ) correction developed by Grimme and co-workers,¹⁴ which contains the damping function proposed by Becke and Johnson,¹⁵ is used to account for nonlocal dispersion interactions. Scalar relativistic effects are accounted for using the zeroth-order regular approximation (ZORA).¹⁶ This level has been proven to accurately describe weak interactions.¹⁷ Molecular orbitals (MO) were expanded into a large, uncontracted set of Slater-type orbitals (STOs) containing diffuse functions: TZ2P.¹⁸ The basis set is of triple-ζ quality augmented with polarization functions, i.e., one 2p and one 3d set on H; one 3d and one 4f set on C, N, O, Si, P, S; one 4d and one 4f set on Ge, As, Se; one 5d and one 4f set on I. All electrons were included in the variational process; i.e., no frozen core approximation was applied. The accuracies of both the Zlm fitting scheme^19a and the Becke integration grid^19b were set to ‘EXCELLENT’.

Bond Analyses

Insight into the bonding mechanism is obtained by analyzing the intermolecular interaction between Me_mYH (Y = C, Si, Ge, N, P, As, O, S, Se) and the NH₃ or ICN fragments using the activation strain model,⁹ which is a fragment-based approach to understanding the energy profile associated with a chemical process in terms of the original reactants. Thus, the total bond energy ΔE is decomposed into the strain energy ΔE_strain, which is associated with the geometrical deformation of the individual reactants as the process takes place, plus the actual interaction energy ΔE_int between the deformed reactants (eq 4).

4

The interaction energy ΔE_int between the deformed reactants is further analyzed in the conceptual framework provided by the quantitative Kohn–Sham MO model.⁹ To this end, it is decomposed into physically meaningful terms, using a quantitative energy decomposition analysis (EDA) as implemented in ADF (eq 5).⁹ The analyses are done as a function of the H···N (r_H···N) or H···I (r_H···I) bond distances along the range of 1.5 to 3.5 Å. Since ΔE_strain is negligible (see Tables S1 and S3), we performed the analyses starting from the equilibrium geometry of the complex while keeping all other geometrical parameters frozen. Values in the equilibrium geometries are shown in Tables S2 and S4.

5

ΔV_elstat is the classical Coulomb interaction between the unperturbed charge distributions of the deformed reactants which is usually stabilizing and comprises four components: (i) the electron–electron electrostatic repulsion between the electron densities of fragments 1 and 2, ΔV_{elstat,ρ1ρ2}; (ii) the nuclei–electron electrostatic attraction between the nuclei of fragment 1 and the electron density of fragment 2, ΔV_elstat,n1ρ2; (iii) the electron–nuclei electrostatic attraction between the electron density of fragment 1 and the nuclei of fragment 2, ΔV_elstat,ρ1n2; and (iv) the nuclei–nuclei electrostatic repulsion between the nuclei of fragments 1 and 2, ΔV_elstat,n1n2.

The Pauli repulsion energy (ΔE_Pauli) comprises the destabilizing interactions between occupied orbitals on either fragment (more precisely, between same-spin occupied spinorbitals on either fragment) and arises from the antisymmetrization of the Hartree wave function due to the Pauli principle. The orbital-interaction energy (ΔE_oi) accounts for charge transfer, that is, the interaction between occupied orbitals of one fragment with unoccupied orbitals of the other fragment, including the interactions of the highest occupied and lowest unoccupied MOs (HOMO–LUMO), and polarization, that is, empty–occupied orbital mixing on one fragment, due to the presence of another fragment. ΔE_disp accounts for the empirical dispersion corrections as introduced by Grimme et al.¹⁴ To facilitate the analyses, the ASM and EDA were performed using the PyFrag 2019 program.²⁰

Voronoi Deformation Density (VDD) Charge Analysis

The Voronoi Deformation Density (VDD) charge analysis allows for the quantification of the flow of electronic charge as a consequence of chemical-bond formation.²¹ In our model Me_mYH fragments, the VDD atomic charge of atom H directly bound to Y (Q_H) is computed by the spatial integration of the deformation density over the Voronoi cell of atom H, which is the space defined by the bond midplanes on and perpendicular to all bond axes between atom H and its neighboring atoms (eq 1).

1

Herein, the deformation density Δρ(r) = [ρ(r) – ∑_iρ_i(r)] is the density change going from a superposition of the original atomic densities at the positions of the molecule to the actual density of that molecule. This atomic or so-called promolecular density is defined as the sum of the (spherically averaged) ground-state atomic densities ∑_iρ_i(r). This is the fictitious state in which the charge density has not been affected by chemical bonding and in which all atoms have zero charge. Then, Q_H represents the amount of charge that, due to chemical bonding, flows from a position closer to another nucleus to a position closer to the nucleus of H (Q_H < 0), or from a position closer to the nucleus of H to a position closer to another nucleus (Q_H > 0).

Besides the above regular VDD atomic charges relative to noninteracting neutral atoms, the VDD method allows for the analysis of changes in atomic charges (ΔQ), i.e., charge-density rearrangements, caused by interactions between molecular fragments (eq 2).

2

Equation 2 defines the charge rearrangements in an atom A of a fragment i (ΔQ_A) in the final density of the overall complex ρ_complex(r) relative to the sum of the initial molecular fragment densities ∑_fragment,iρ_i(r)_i. This reveals how the interactions between the molecular fragments affect the electron density distribution in atom A of fragment i. The sum of the ΔQ_A of all atoms in a fragment i gives the amount of charge transfer into (ΔQ_fragment,i < 0) or out of (ΔQ_fragment,i > 0) the Voronoi cell of a fragment i due to the interaction between the molecular fragments (eq 3).

3

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.4c07821.

• Activation strain, energy decomposition, and VDD analyses; and Cartesian coordinates of all stationary points. (PDF)

The authors declare no competing financial interest.