Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Sep 5;128(37):7879–7888. doi: 10.1021/acs.jpca.4c04990

Temperature-Dependent Kinetics of the Reactions of the Criegee Intermediate CH2OO with Aliphatic Aldehydes

Jonas J Enders †, Zachary A Cornwell †, Aaron W Harrison ‡, Craig Murray †,*
PMCID: PMC11421089  PMID: 39233465

Abstract

graphic file with name jp4c04990_0007.jpg

Criegee intermediates, formed by alkene ozonolysis in the troposphere, can react with volatile organic compounds (VOCs). The temperature-dependent kinetics of the reactions between the Criegee intermediate CH2OO and three aliphatic aldehydes, RCHO where R = H, CH3, and C2H5 (formaldehyde, acetaldehyde, and propionaldehyde, respectively), have been studied using a laser flash-photolysis transient absorption spectroscopy technique. The experimental measurements are supported by ab initio calculations at various composite levels of theory that characterize stationary points on the reaction potential and free energy surfaces. As with other reactions of CH2OO with organic carbonyls, the mechanisms involve 1,3-dipolar cycloaddition at the C=O group, over submerged barriers, leading to the formation of 1,2,4-trioxolane secondary ozonides. The bimolecular rate constants of all three reactions decrease with increasing temperature over the range 275–335 K and are characterized by equations of Arrhenius form: k(T) = (7.1 ± 1.5) × 10–14exp((1160 ± 60)/T), (8.9 ± 1.7) × 10–15exp((1530 ± 60)/T), and (5.3 ± 1.3) × 10–14exp((1210 ± 70)/T) cm3 s–1 for HCHO, CH3CHO, and C2H5CHO, respectively. Based on estimated concentrations of CH2OO, the reactions with aldehydes are unlikely to play a significant role in the atmosphere.

Introduction

Aldehydes (RCHO) are found in the atmosphere as a result of direct anthropogenic and biogenic emissions and are formed as secondary products of alkane and alkene oxidation.1 Anthropogenic aldehyde emissions are centered around urban areas, but biogenic emissions and secondary production create an even distribution across the atmosphere, with global average mixing ratios in the parts per billion range.2−4 The two most common aldehydes found in the atmosphere are formaldehyde and acetaldehyde.5 The ability of aldehydes to form diols in the aqueous phase leads to large Henry’s law coefficients, implying that the scavenging of aldehydes from the gas phase by aqueous droplets is important.6,7 Atmospheric lifetimes of gas phase aldehydes are determined by photolysis and reaction with OH.3 Photolytic lifetimes under typical tropospheric conditions range from 10–20 h,8−10 while reaction with OH radicals are similar, ranging from 5–30 h, depending on the aldehyde.11 The reactive pathway leads ultimately to an increase in tropospheric O3, volatile organic compounds (VOCs), and secondary organic aerosol (SOA) in the atmosphere.3 Another potential sink for aldehydes in the atmosphere, also leading to the formation of SOAs and less volatile VOCs, is reaction with Criegee intermediates (CIs), which is the subject of this work.

CIs are reactive carbonyl oxides (R1R2COO) formed as products of alkene ozonolysis.12−14 Extensive recent work has probed their spectroscopy,15,16 unimolecular decay mechanisms,17 and reactivity toward trace atmospheric trace gases.18−21 The most prevalent CI in the atmosphere is thought to be formaldehyde oxide (CH2OO),22 and its reactions with various RCHO species have been studied experimentally23−31 and computationally.25,30,32−35 Recently, Luo et al. have used mid-infrared frequency combs to measure a room temperature rate constant of (4.11 ± 0.25) × 10–12 cm3 s–1 for the reaction of CH2OO with formaldehyde (HCHO), and showed that it could lead to enhanced production of formic acid (HCOOH) in the upper troposphere. The reaction of CH2OO with acetaldehyde (CH3CHO) has been studied using time-resolved photoionization mass spectrometry (PIMS), UV absorption spectroscopy, and LIF detection of secondary OH, finding room temperature rate constants of (0.95 ± 0.07) × 10–12, (1.3 ± 0.2) × 10–12 cm3 s–1, and (2.16 ± 0.39) × 10–12, respectively.23,25,31 Indirect measurements of HCHO production using laser-induced fluorescence (LIF) suggest a high-pressure limit room temperature rate constant of 1.7 × 10–12 cm3 s–1.24 Reactions involving larger aliphatic aldehydes have been studied more extensively. Using a technique based on OH laser-induced fluorescence(LIF),36 Dong and co-workers have quantified the kinetics of reactions of CH2OO with propionaldehyde (C2H5CHO), linear n-butyraldehyde (n-C3H7CHO), and branched iso-butyraldehyde (iso-C3H7CHO), reporting high-pressure limit room temperature rate constants of (3.23 ± 0.49) × 10–12, (2.97 ± 0.53) × 10–12, and (3.99 ± 0.72) × 10–12 cm3 s–1, respectively.26−28 Cavity ring-down spectroscopy (CRDS) measurements by Debnath and Rajakumar on the CH2OO + n-C3H7CHO and iso-C3H7CHO reactions resulted in slightly smaller room temperature rate constants of (2.63 ± 0.14) × 10–12 and (2.20 ± 0.21) × 10–12 cm3 s–1.30 Weak negative temperature dependences have been observed for all CH2OO + RHCO reactions, with typical −Ea/R values of approximately 1000 K (Ea = −1.9 kcal mol–1), independent of the identity of the substituent.25−28,30

Recently, we have embarked on a series of kinetics studies exploring the effects of different carbonyl substituents on the reactivity of CH2OO with organic carbonyls (R1R2CO),37−39 and have observed a strong correlation between bimolecular rate constants and energies of frontier molecular orbitals (FMOs).40−42 The primary interaction controlling reactivity is between the occupied n(pC-pO) orbital of CH2OO and the lowest unoccupied π* orbital of the R1R2CO reactant. Groups with electron-withdrawing character, loosely quantified by Hammett substituent constants, lower the π* orbital energy and increase reactivity, while electron-donating groups have the opposite effect. The FMO picture can be used to explain observed reactivity trends for CH2OO with a range of organic carbonyls and quantitatively predict rate constants. Alkyl substituents are electron-donating and deactivate the carbonyl, hence ketones react with CH2OO relatively slowly (rate constants of order 10–13 cm3 s–1).23,25,37,38,43−45 Hydroxyketones react with CH2OO with a similar rate to acetaldehyde,39 while carbonyls with electron-withdrawing groups, such as α-dicarbonyls or hexafluoracetone, tend to react even faster.23,36−38 A preliminary correlation between bimolecular rate constants and the π* orbital energies allowed us to predict a room temperature rate constant for the reaction of CH2OO with HCHO that was subsequently confirmed by the measurements of Luo et al.29,37

Here we examine the reactions of CH2OO with a series of aldehydes (RCHO, where R = H, CH3, and C2H5). Temperature-dependent bimolecular rate constants for all three reactions are measured over the range 275–335 K using a laser flash photolysis transient absorption spectroscopy technique. The experimental results are paired with complementary ab initio calculations that map out the reaction pathways and explain reactivity trends resulting from different substituents within the framework of FMO theory. The potential atmospheric implications of the CH2OO + RCHO reactions will be briefly discussed.

Experimental and Computational Methods

Experimental Methods

Experiments were carried out in a laser flash photolysis transient absorption spectroscopy apparatus that has been described in detail previously.38 CH2OO is produced in a temperature-controlled flow reactor by laser photolysis of diiodomethane (CH2I2) in the presence of excess O2. Absolute time-dependent concentrations of CH2OO were determined from transient absorption spectra acquired at various time delays after photolysis by dispersing the transmitted output of pulsed UV LEDs in a spectrograph. Each transient spectrum was obtained from the accumulation of 400 reference I0(λ) spectra at Δt = tLED – tlaser < 0 and 400 signal spectra I(λ)at each Δt > 0. Spectra were acquired at 15 delays, acquired by cycling (typically four times) over the delays to minimize any systematic errors. Kinetics measurements were made under pseudo-first-order conditions, using aldehyde concentrations that were at least 2 orders of magnitude greater than that of CH2OO.

Liquid reactants, acetaldehyde (CH3CHO) and propionaldehyde (C2H5CHO), were placed in smog bubblers and carried into the reactor by a flow of N2, with total reactant flow rates controlled using a series of choked-flow orifices.37−39 The bubblers were held in an ice/water slush at 273 K to ensure the vapor pressures of the aldehydes remained constant (316.8 Torr for acetaldehyde and 98.8 Torr for propionaldehyde).46 CH2I2 was photolyzed using the 355 nm output of an Nd:YAG laser with a typical fluence of approximately 28 mJ cm–2. The photolysis laser beam was steered through the cell using dichroic mirrors, which, in conjunction with long-pass filters that protect the LED driver from residual laser light, limit detection to λ > 363 nm. Transient absorption spectra were recorded in the range 363–390 nm using the counter-propagating output of a 365 nm LED, which captures both CH2OO and the IO byproduct, as shown in Figure 1.47−51 Separate absorption spectroscopy measurements in the range 270–295 nm using a 280 nm UV LED were made to quantify the CH3CHO and C2H5CHO concentrations achieved with each choked-flow orifice using their first UV absorption bands (see Figure 1),51,52 under conditions that were otherwise identical to those used during kinetics experiments.

Figure 1.

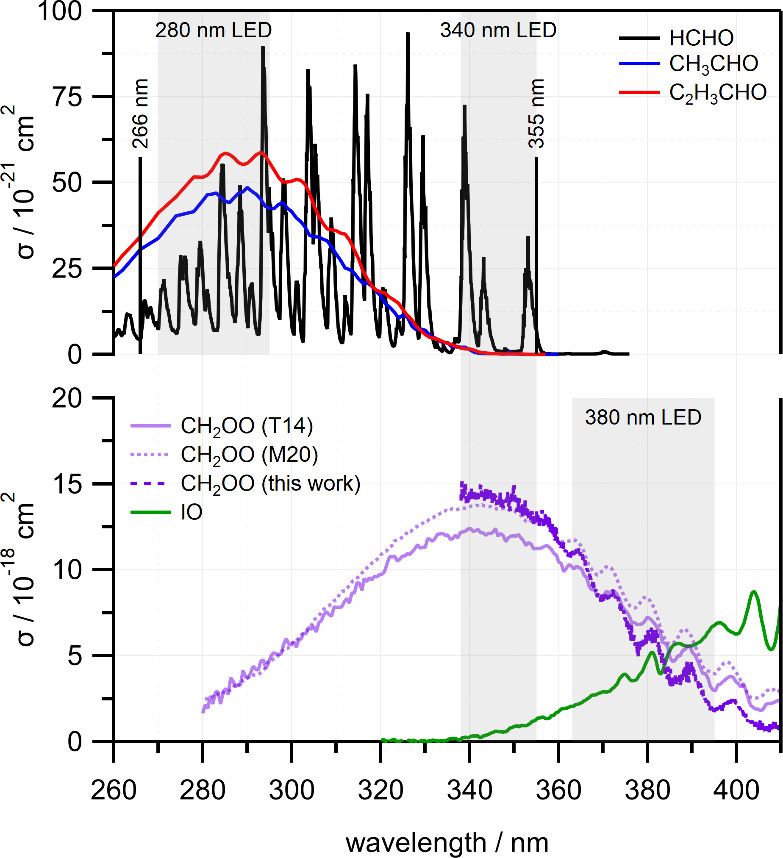
Figure 1

Open in a new tab

Absorption spectra of (top panel) RCHO reactants (HCHO, CH3CHO, and C2H5CHO) and (lower panel) transient species CH2OO and IO, obtained from various sources, as discussed in the text. The gray shaded boxes represent the wavelength regions covered by each probe UV LED. Probe wavelength ranges are restricted to λ ≥ 315 nm for 266 nm photolysis and λ ≥ 363 nm for 355 nm photolysis.

The experimental approach was modified for experiments with formaldehyde (HCHO). First, gaseous HCHO was produced through thermal decomposition of paraformaldehdye (PFA). Solid PFA was packed in a stainless-steel sample holder (Swagelok) and held in place with glass wool. A band heater (MPI Morheat) was used to heat the sample holder to temperatures in the range 360–380 K, and gaseous HCHO was carried into the reactor by a flow of N2. Experiments with HCHO used a shorter photolysis wavelength of 266 nm, which allowed for the use of long-pass dichroic mirrors and filters that extended the detection window to λ > 315 nm. A 340 nm UV LED was used to measure transient absorption spectra in the range 338–355 nm, which spans the CH2OO absorption maximum, while minimizing the contribution of the IO byproduct. The first three vibronic bands of the S0 → S1(nπ*) transition of HCHO also fall within this wavelength range as shown in Figure 1, allowing its concentration to be monitored in situ throughout the kinetics measurements.52−54 Consequently, we did not attempt to directly control [HCHO] in the flow reactor, as we did for the other aldehydes. Rather, the observed [HCHO] depended on the sample temperature and decayed slowly with time, allowing access to a range of concentrations. The absorption cross section of CH2I2 is around five times higher at 266 nm than at 355 nm,55,56 so lower fluences of approximately 5 mJ cm–2 were used to ensure that a comparable fraction of CH2I2 was photolyzed.

Experiments were typically performed at a total pressure of 73–76 Torr, with the gas mixture comprising [CH2I2] = 1 × 1015 cm–3, [O2] = 2 × 1017 cm–3, [RCHO] = (0.1–7) × 1016 cm–3, and balance [N2] ≈ 2 × 1018 cm–3. The flow reactor temperature was varied over the range 275–335 K, with a precision of better than 1 K, as measured on two thermocouples. All chemicals were used as supplied: O2 (Airgas, UHP 4.4), N2 (Airgas, industrial grade), CH2I2 (Sigma-Aldrich, 99%), paraformaldehyde (Fisher Scientific, 100%), CH3CHO (Sigma-Aldrich, 99%), and C2H5CHO (Sigma-Aldrich, 97%).

Computational Methods

Unimolecular reaction intermediates and energies involved in the cycloaddition reaction of CH2OO to HCHO, CH3CHO, and C2H5CHO were characterized with the Gaussian 16 software package.57 Equilibrium and transition state structures were calculated with the CBS-QB3 composite method. Transition states and minima were confirmed by frequency analysis. Images and Cartesian coordinates of the optimized geometries of the entrance channel complexes, transition states, and secondary ozonide (SOZ) products for each aldehyde can be found in the Supporting Information.

Results

The reactions of CH2OO with RCHO (R = H, CH3, C2H5) were studied over the temperature range 275–335 K and at a total pressure of 73–76 Torr. CH2OO was generated by the rapid reaction of CH2I, produced by the laser photolysis of CH2I2 at either 355 or 266 nm, with O2. Time-dependent concentrations [CH2OO]t were determined from transient absorption spectra recorded at ∼15 time delays after photolysis, as discussed below. Peak concentrations ([CH2OO]0 = (6–8) × 1012 cm–3) were reached ∼20 μs after photolysis, indicating that <1% of the CH2I2 precursor was photolyzed on each laser pulse, independent of photolysis wavelength. Following the initial fast formation as a product of the CH2I + O2 reaction, CH2OO is lost on a time scale of ∼2 ms by bimolecular self-reaction and background loss processes, such as reaction with I atoms.58 The presence of excess aldehydes with [RCHO]/[CH2OO]0 ≥ 102 provides an additional pseudo-1st order loss that shortens the CH2OO lifetime. The kinetic model accounting for these CH2OO loss processes has been described previously,37−39 and results in the following integrated rate equation, which is used to fit the [CH2OO]t concentration–time profiles:

graphic file with name jp4c04990_m001.jpg 1

The value of kself is held fixed at the temperature-independent value of 7.8 × 10–11 cm3 s–1as discussed in previous work.38 The pseudo-first-order rate constant kloss = kbgd + kRCHO[RCHO], where the background loss rate in the absence of RCHO at room temperature is typically kbgd ≈ 1500 s–1. Bimolecular rate constants kRCHO are determined as the gradients of linear fits of the observed loss CH2OO rates kloss plotted as a function of aldehyde concentration [RCHO].

Kinetics of the Reactions of CH2OO with CH3CHO and C2H5CHO

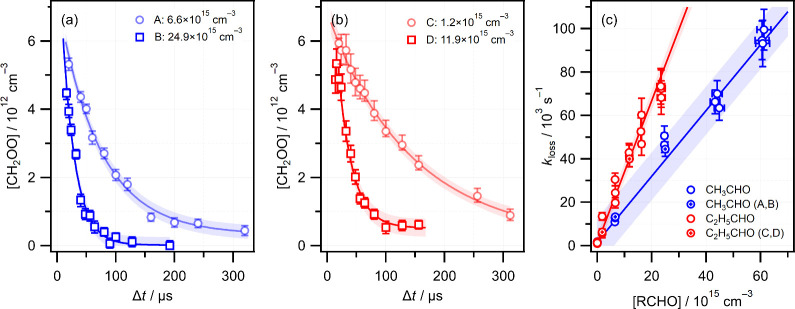
Kinetics measurements of the CH3HCO and C2H5CHO reactions followed the same approach used previously.38,39 Following photolysis of CH2I2 at 355 nm, transient absorption spectra were acquired in the range 363–390 nm, capturing contributions from both CH2OO and IO, at fixed flow reactor temperature and [RCHO] concentration. Time-dependent concentrations [CH2OO]t (and [IO]t) were determined by decomposing the transient spectra into their respective contributions using known wavelength-dependent absorption cross sections,47−50 which are shown in Figure 1. Examples of [CH2OO]t profiles in the presence of different concentrations of CH3CHO and C2H5CHO obtained at 295 K are shown in Figure 2a,b, respectively. The CH2OO lifetime decreases in the presence of higher concentrations of RCHO and loss rates kloss are obtained from fitting the [CH2OO]t time profiles to eq E1. The aldehyde concentrations present in the flow reactor during kinetics measurements were varied using a range of choked-flow orifices, with concentration calibration determined from absorption spectra in the range 270–295 nm using a 280 nm UV LED (see Figure 1) under otherwise identical conditions. The calibration method has been described previously and is summarized in the Supporting Information.38,39

Figure 2.

Figure 2

Open in a new tab

(a) Typical [CH2OO]t time profiles in the presence of different concentrations of CH3CHO (blue) (labeled A and B) at 295 K; (b) as (a) but different concentrations of C2H5CHO (red) (labeled C and D). Error bars are 1σ uncertainties in the concentrations derived from fitting the transient absorption spectra. Solid lines are fits to the integrated rate equation, and shaded areas represent 1σ prediction bands. (c) Pseudo-first-order plot of kloss against [RCHO] at 295 K. The specific data points corresponding to time profiles A–D in panels (a) and (b) are highlighted. Vertical and horizontal error bars represent the 1σ statistical uncertainty in fitting CH2OO concentration profiles and uncertainty arising from aldehyde concentration calibration measurements, respectively. Solid lines are linear fits and shaded areas represent 1σ prediction bands.

Figure 2c shows the complete set of CH2OO loss rates measured at different CH3CHO and C2H5CHO concentrations at room temperature (295 K). The plots of kloss against [RCHO] are linear, as expected for pseudo-first-order kinetics in which RCHO is present in excess. Bimolecular rate constants are obtained by performing a global fit to the complete data sets. At room temperature, the rate constant for the reaction of CH2OO with CH3CHO is kCH3CHO = (1.61 ± 0.14) × 10–12 cm3 s–1 while the C2H5CHO reaction is faster with a rate constant kC2H5CHO = (3.29 ± 0.29) × 10–12 cm3 s–1. The quoted error limits are 1σ statistical uncertainties from linear fits, which were weighted by the uncertainties in both kloss and [RCHO]. The results of temperature-dependent measurements are described below.

Kinetics of the Reaction of CH2OO with HCHO

Experiments with HCHO required a departure from the experimental methods used for CH3CHO and C2H5CHO. A shorter photolysis wavelength of 266 nm was used to dissociate CH2I2, which allowed transient spectra in the range 338–355 nm to be acquired using a 340 nm UV LED. The shorter-wavelength probe window spans the maximum of the CH2OO absorption,47,49 and is less sensitive to the byproduct IO,50 which was neglected in the analysis of the transient absorption spectra. It also allows in situ detection of HCHO, as it spans the 210410, 430, and 410 bands associated with excitation to the S1 state that lie at 339.0, 343.2, and 353.2 nm,53 for which absorption cross sections are well-known.54 The relevant absorption spectra and the 340 nm LED wavelength range are shown in Figure 1. We note that the peak absorption cross section of the transient CH2OO is around 300 times greater than of HCHO, leading to similar order of magnitude absorbances under pseudo-first-order conditions.

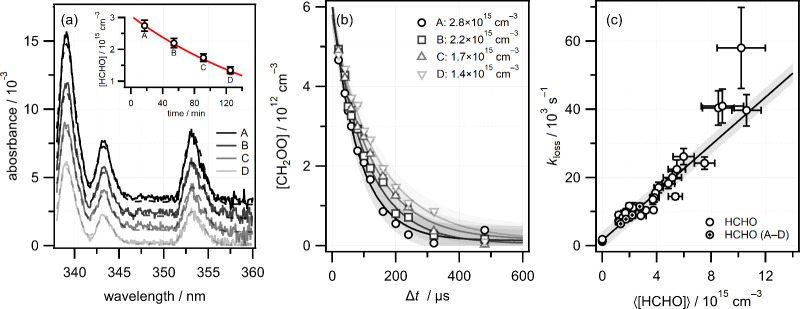
Gaseous HCHO was produced by thermal decomposition of PFA in a sample holder, which was held at a constant temperature in the range 360–380 K. HCHO absorption spectra were obtained by using appropriate combinations of reference and signal spectra from the usual data acquisition procedure. The reference spectra are provided by blank runs ([HCHO] = 0) acquired to determine background CH2OO loss rates in the absence of aldehyde, while the “signal” spectra are provided by the transient reference spectra that are acquired during reaction runs ([HCHO] ≠ 0, Δt < 0), for which the flow of gases other than HCHO are identical. Since the data acquisition cycles over the delay sets, the HCHO “signal” spectra are acquired at fixed intervals during each kinetics measurement. The absorption spectra are analyzed to determine the average HCHO concentration ⟨[HCHO]⟩ that was present in the flow reactor during the measurement.

Figure 3a shows an example of four consecutive HCHO absorption spectra, labeled A–D, that were obtained in back-to-back kinetics measurements (each stepping over 15 photolysis-probe delays) with the PFA sample holder held at 375 K and the flow reactor at 295 K. The inset shows that ⟨[HCHO]⟩ derived from the spectra decreased monotonically with time, by about a factor of 2 over the course of four successive kinetics measurements, and is well-described by an exponential decay. The uncertainty in the HCHO concentration was estimated from the fit and represents the standard deviation in the average concentration observed during the measurements. The effect of the decreasing HCHO concentration is reflected in the steadily decreasing CH2OO loss rates shown in Figure 3b. The complete set of kloss values obtained at 295 K from fitting each [CH2OO]t time profile to eq E1 are plotted against ⟨[HCHO]⟩ in Figure 3c. A linear fit yields a room temperature bimolecular rate constant for the CH2OO + HCHO reaction of kHCHO = (3.50 ± 0.35) × 10–12 cm3 s–1, where the error represents a 1σ statistical uncertainty from the fit, weighted by the uncertainties in kloss and ⟨[HCHO]⟩.

Figure 3.

Figure 3

Open in a new tab

(a) Average HCHO absorption spectra (solid lines) obtained over the course of four kinetics runs (labeled A–D) at 295 K, along with fits (dashed lines). The spectra have been offset vertically 1 × 10–3 for clarity. The inset shows the decrease in [HCHO] over the course of the experiment. An exponential decay (red) is used to model the decline in [HCHO] and estimate the uncertainties in the average value as described in the text. (b) [CH2OO]t time profiles for each average ⟨[HCHO]⟩, along with fits. (c) Pseudo-first-order plot of kloss against ⟨[HCHO]⟩. Vertical and horizontal error bars represent the statistical uncertainty in fitting CH2OO concentration profiles and the statistical uncertainty determined from the variation in HCHO concentrations, respectively. The specific data points corresponding to time profiles A–D in panel (b) are highlighted. The solid line is a linear fit to the experimental data, and the shaded area represents 1σ prediction bands.

Temperature and Pressure Dependence

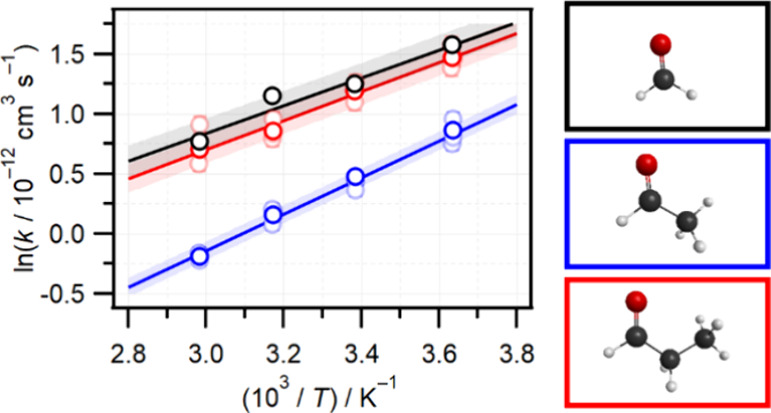
Kinetics measurements for all three CH2OO + RCHO reactions were made at temperatures of 275, 295, 315, and 335 K, and at a total pressure of ∼78 Torr. The complete set of pseudo-first order plots at all four experimental temperatures in the range 275–335 K are shown in Figures S4–S6 of the Supporting Information. The bimolecular rate constants measured for each reaction at each temperature are summarized in Table 1. All three reactions display negative temperature dependencies. The Arrhenius plots shown in Figure 4 are linear over the 275–335 K range and the temperature-dependent bimolecular rate constants are well-characterized by equations of Arrhenius form: kHCHO(T) = (7.1 ± 1.5) × 10–14exp((1160 ± 60)/T), kCH3CHO(T) = (8.9 ± 1.7) × 10–15exp((1530 ± 60)/T), and kC2H5CHO(T) = (5.3 ± 1.3) × 10–14exp((1210 ± 70)/T) cm3 s–1. The Arrhenius pre-exponential factors A and activation energies Ea are compiled in Table 2. Both A and Ea values are similar for the HCHO and C2H5CHO reactions, while for the CH3CHO reaction the A factor is an order of magnitude smaller, but a stronger T dependence (more negative Ea) is found.

Table 1. Bimolecular Rate Constants for the Reactions of CH2OO with HCHO, CH3CHO, and C2H5CHO across the Temperature Range 275–335 Ka.

  kRCHO / 10–12 cm3 s–1
T / K HCHO CH3CHO C2H5CHO
275 4.84 ± 0.41 2.37 ± 0.21 4.35 ± 0.38
295 3.50 ± 0.35 1.61 ± 0.14 3.29 ± 0.29
315 3.16 ± 0.28 1.17 ± 0.10 2.36 ± 0.20
335 2.16 ± 0.19 0.83 ± 0.07 2.03 ± 0.18
Open in a new tab
a

Errors are 1σ statistical uncertainties from the fits.

Figure 4.

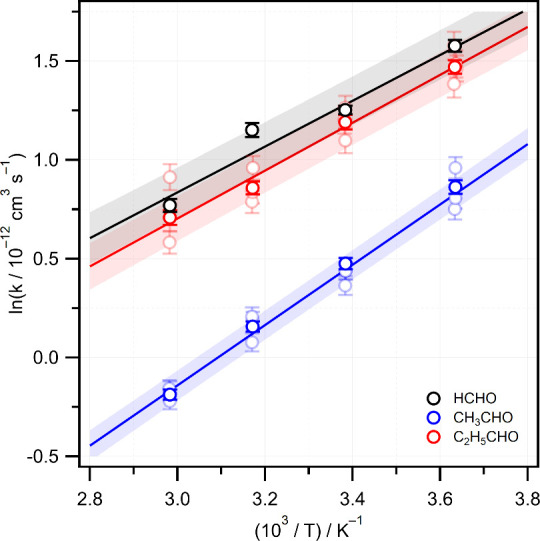
Figure 4

Open in a new tab

Arrhenius plots for the reactions of CH2OO with HCHO (black), CH3CHO (blue), and C2H5CHO (red). Solid lines are linear fits with shaded areas representing 1σ prediction bands.

Table 2. Arrhenius Parameters and Derived Thermodynamic Propertiesa.

  HCHO CH3CHO C2H5CHO
A / 10–15 cm3 s–1 71 ± 15 8.9 ± 1.7 53 ± 13
–(Ea/R) / K 1160 ± 60 1530 ± 60 1210 ± 70
Ea / kcal mol–1 –2.30 ± 0.13 –3.03 ± 0.11 –2.41 ± 0.14
Δ‡S° / cal K–1 mol–1 –33.9 ± 0.2 –38.1 ± 0.2 –34.5 ± 0.2
Δ‡H° / kcal mol–1 –3.5 ± 0.1 –4.2 ± 0.1 –3.6 ± 0.1
Δ‡G° / kcal mol–1 +6.6 ± 0.1 +7.1 ± 0.1 +6.7 ± 0.2
Open in a new tab
a

Standard Gibbs energy of activation is evaluated at 298 K, assuming no T dependence in the standard enthalpies and entropies of activation.

The standard entropy of activation Δ‡S° and the standard enthalpy of activation Δ‡H° for each reaction can be found from the Arrhenius parameters using the relations

graphic file with name jp4c04990_m002.jpg 2

and

graphic file with name jp4c04990_m003.jpg 3

where the T-dependent rate constant is described by the thermodynamic formulation of canonical transition state theory (CTST) for a bimolecular reaction.59 The values derived for T = 298 K and standard pressure p° = 1 bar are summarized in Table 2. The values of Δ‡H° and Δ‡S° are similar for the HCHO and C2H5CHO reactions at around −3.5 kcal mol–1 and −34 cal K–1 mol–1, respectively, while those for the CH3CHO reaction are more negative at −4.2 kcal mol–1 and −38 cal K–1 mol–1. The standard Gibbs energies of activation Δ‡G° at 298 K span a range of only 0.5 kcal mol–1, which is sufficient to cause a factor of 2 variation in the calculated rate constants.

A limited set of pressure-dependent measurements was performed with constant CH3CHO and C2H5CHO concentrations to confirm that the primary reactions were likely studied at the high-P limit, as expected.25,26 CH2OO loss rates were measured at constant [RCHO], while the flow rate of N2 buffer gas was varied to change the total pressure Ptot across the range 40–100 Torr. All other gas flows were held constant. The average kloss values were constant across the pressure range at as shown in Figure S7 in the Supporting Information. The absence of any significant change in kloss with pressure is consistent with the high-P limit having been reached at Ptot < 40 Torr.

Computational Results

The cycloaddition reaction pathways of CH2OO with each aldehyde were investigated using the CBS-QB3 composite method. This 1,3-cycloaddition involves the initial formation of a reactive van der Waals (vdW) complex, which then passes over the transition state (TS) to yield the secondary ozonide (SOZ). For the asymmetric aldehydes acetaldehyde and propionaldehyde, the cycloaddition can occur in two ways depending on the orientation of CH2OO. Structures with the central O atom of the CI oriented toward the aldehydic H atom are labeled as exo, and those oriented toward the alkyl group are labeled endo. The TS energy barriers for endo vs exo approach are nearly identical for acetaldehyde (the exo pathway being lower in energy or free energy by ∼0.3 kcal mol–1) but the endo pathway causes a more significant distortion of propionaldehyde in which there is rotation about the α-CC bond, converting the methyl group from a syn to a gauche arrangement with respect to the O atom (see TS structures in Figure 5). This distortion results in a TS barrier that is ∼0.7 kcal mol–1 higher for endo attack. As such, we focused on the exo addition path for both acetaldehyde and propionaldehyde. These findings are presented in Table 3; the results for the endo pathways are in Table S1 in Supporting Information. Overall, the TS free energy barriers at 298 K determined from the CBS-QB3 calculations order them as formaldehyde (+3.6 kcal mol–1) < acetaldehyde (+5.1 kcal mol–1) ∼ propionaldehyde (+5.2 kcal mol–1). We have not carried out an extensive search to identify various conformers of the SOZ products, but energy differences are expected to be small relative to the exoergicity of the reactions.

Figure 5.

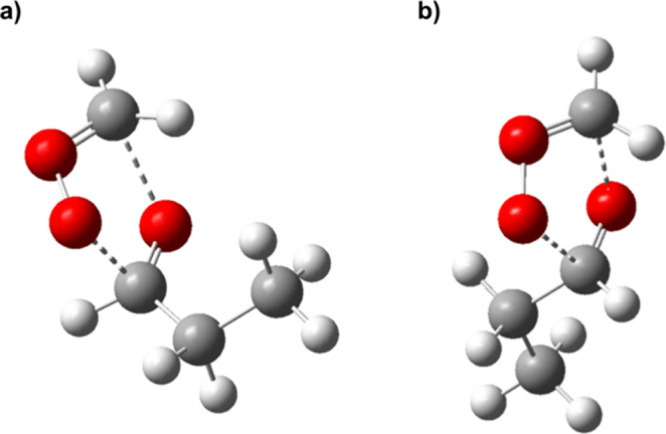
Figure 5

Open in a new tab

Transition state structures calculated at the CBS-QB3 level for the cycloaddition reaction between CH2OO and C2H5CHO in the (a) exo and (b) endo configurations.

Table 3. Relative Energies, including Zero-Point Contributions, Δ(E+ZPE) at 0 K, Standard Enthalpies ΔH° at 298 K, and Standard Free Energies ΔG° at 298 K Calculated at the CBS-QB3 Levels for the SOZ exo Pathway for Reactions of CH2OO with Formaldehyde, Acetaldehyde, and Propionaldehydea.

  Δ(E+ZPE) {ΔH°} [ΔG°] / kcal mol–1
  HCHO CH3CHO C2H5CHO
vdW –7.1 {−7.5} [+2.5] –7.8 {−7.8} [+2.3] –8.2 {−8.1} [+2.1]
TSSOZ –6.7 {−7.7} [+3.6] –6.4 {−7.3} [+5.1] –6.4 {−7.2} [+5.2]
SOZ –51.4 {−53.2} [−40.2] –50.9 {−52.4} [−38.5] –50.8 {−51.6} [−37.5]
Open in a new tab
a

All energies are reported in kcal mol–1.

Discussion

The experimental rate constants measured in this work generally agree with previously reported values. Luo et al.29 found a room temperature rate constant for the CH2OO + HCHO reaction of (4.11 ± 0.25) × 10–12 cm3 s–1, with which our value of (3.5 ± 0.35) × 10–12 cm3 s–1 agrees within the mutual (1σ) uncertainties. We note that both reported experimental values also fall comfortably within the range (1.9–6.4) × 10–12 cm3 s–1 predicted by Cornwell et al.37 based on an inverse correlation between ln k and the energy gap between FMOs (evaluated at the M06-2X/aug-cc-pVTZ level) of the Criegee intermediate and various organic carbonyl reactants. The experimental activation energies (−Ea/R = 910 ± 20 K measured by Luo et al. and 1160 ± 60 K measured in this work) are also in reasonably good agreement.

The CH2OO + CH3CHO reaction has been studied more extensively experimentally. Initial PIMS measurements by Taatjes et al.23 at a total pressure of 4 Torr found a room temperature rate constant of (0.95 ± 0.07) × 10–12 cm3 s–1, while Elsamra et al.25 used a UV absorption technique to measure a value of (1.3 ± 0.2) × 10–12 cm3 s–1 at 50 Torr and observed a slight positive pressure dependence. Jiang et al.31 found a room temperature rate constant of (2.16 ± 0.39) × 10–12 cm3 s–1 at 50 Torr using LIF detection of OH produced by CH2OO decomposition. Our value of (1.61 ± 0.14) × 10–12 cm3 s–1, measured at ∼80 Torr, falls between the higher pressure measurements and is also in excellent agreement with the estimated high-pressure limit value of 1.7 × 10–12 cm3 s–1 estimated by Stone et al.,24 based on indirect measurements using LIF detection of HCHO secondary products. Since we additionally do not observe any change in CH2OO loss rate with total pressure, we expect that our measurements were made at the high-pressure limit. The discrepancy between our results and the earlier measurements is likely a consequence of different total pressure and choice of buffer gas (He in the earlier work and N2 in this work). The temperature dependence of the acetaldehyde reaction was also investigated by Elsamra et al. and Jiang et al.,25,31 who found values of – Ea/R = 1090 ± 170 and 870 ± 156 K, respectively, both of which are smaller than the value of 1530 ± 60 K found in the current work. In general, the T-dependent rate constants reported by Jiang et al. are systematically larger than those of Elsamra et al., while our values are in excellent agreement with the latter the high end and with the former at the low end of our experimental temperature range, leading to a steeper Arrhenius plot. The origin of the discrepancy is not clear.

Finally, the room temperature rate constant of (3.29 ± 0.29) × 10–12 cm3 s–1 measured for the CH2OO + C2H5CHO reaction is in excellent agreement with the value (3.2 ± 0.2) × 10–12 cm3 determined by Liu et al.26 using an OH LIF technique. The experimental propionaldehyde reaction rate constants were both made under conditions that correspond to the high-P limit. The activation energies are also in reasonably good agreement: Liu et al. reported a value – Ea/R = 1000 ± 120 K, while we find a value of 1210 ± 70 K. In general, aldehydes with alkyl substituents larger than methyl, tend to show greater reactivity toward CH2OO than acetaldehyde does.27,28,30

The reactions of CH2OO with formaldehyde and acetaldehyde have been the subject of previous computational studies at the CCSD(T)-F12 level of theory.32,35 The Δ(E+ZPE) energies of the vdW, TS, and SOZ reported here at the CBS-QB3 level are in general within ∼1 kcal mol–1. The biggest discrepancy is the TS energy of −5.1 kcal mol–1 reported by Zhang et al., which is higher than the value of −6.7 kcal mol–1 determined here. The TS energy may be underestimated at the CBS-QB3 level of theory. The calculated free energies for the vdW complex and TS for acetaldehyde were also reported by Wei et al. at the CCSD(T)/aug-cc-pVTZ//B3LYP/6-311++G(2d,2p) level of theory to be +3.4 and +7.2 kcal mol–1, respectively,60 which is another indication that CBS-QB3 is possibly overbinding the complex and transition state. However, CBS-QB3 compares favorably to the higher correlation methods in general and is expected to perform reasonably well for larger aldehydes such as propionaldehyde. The calculated free energy barriers at the CBS-QB3 level of theory (Table 3) show the following trend: ΔG°(HCHO) < ΔG°(CH3CHO) ∼ ΔG°(C2H5CHO). While formaldehyde reacts faster than acetaldehyde, consistent with the calculations, propionaldehyde, by contrast, has a measured rate constant similar to formaldehyde. Comparison of the experimental and thermodynamics data shown in Table 2 and Table 3, respectively, shows that calculated free energies and enthalpies of activation are systematically lower than those derived from the Arrhenius analysis of the experimental data.

In previous work,37−39 we have explored relationships between the room temperature rate constants of 1,3-dipolar cycloaddition reactions of CH2OO with R1R2CO species and the electron-donating or electron-withdrawing effects of the R1 and R2 substituents. Hammett substituent constants (σm or σp)$ describe the electron-donating or electron-withdrawing nature of a given substituent relative to hydrogen, which is defined as zero (σm = σp = 0).61 Electron-donating alkyl groups such as CH3 (σm = −0.07, σp = −0.17) and C2H5 (σm = −0.07, σp = −0.15) are expected to be deactivating, as they tend to increase the magnitude of the energy gap |ΔES| between the occupied npC – pO nonbonding orbital of CH2OO and the unoccupied π* orbital on RCHO, which destabilizes the transition state. The nearly identical Hammett substituent constants for CH3 and C2H5 suggest that they should be similarly deactivating, and consequently the rate constants for the acetaldehyde and propionaldehyde reactions should also be similar and smaller than that of the formaldehyde reaction. Experimentally, however, the room temperature rate constant for the acetaldehyde reaction is smallest, while formaldehyde and propionaldehyde show very similar reactivity. A similar effect is observed for the reactions of ketones, as acetone (R1 = R2 = CH3)23,25,37,38,43,44 reacts with a smaller rate constant than methylethylketone (R1 = CH3, R2 = C2H5).45

Figure 6 shows the effect of carbonyl substituents on reactivity of ketones and aldehydes in the form of semilog plot of room temperature rate constants against the FMO energy gap |ΔES|, defined above. A linear fit to the data provides a simple structure-activity relationship (SAR) that can be used to predict rate constants. The FMO energies have been calculated at the B3LYP/cc-pVDZ level of theory and the rate constants are the weighted average of results from a range of sources;23−31,36,38,43−45 the data set has been expanded to include more aliphatic aldehydes–our previous correlation diagram included only HCHO and CH3CHO.39 A linear fit to the complete data set comprising both ketones and aldehydes yields the relationship

graphic file with name jp4c04990_m004.jpg

However, the aldehydes all lie above line, with the ≥ C3 aldehydes lying beyond the 1σ prediction bands. For contrast, Figure 6 also shows a fit to only the ketone data, which is better determined, yielding

graphic file with name jp4c04990_m005.jpg

Figure 6.

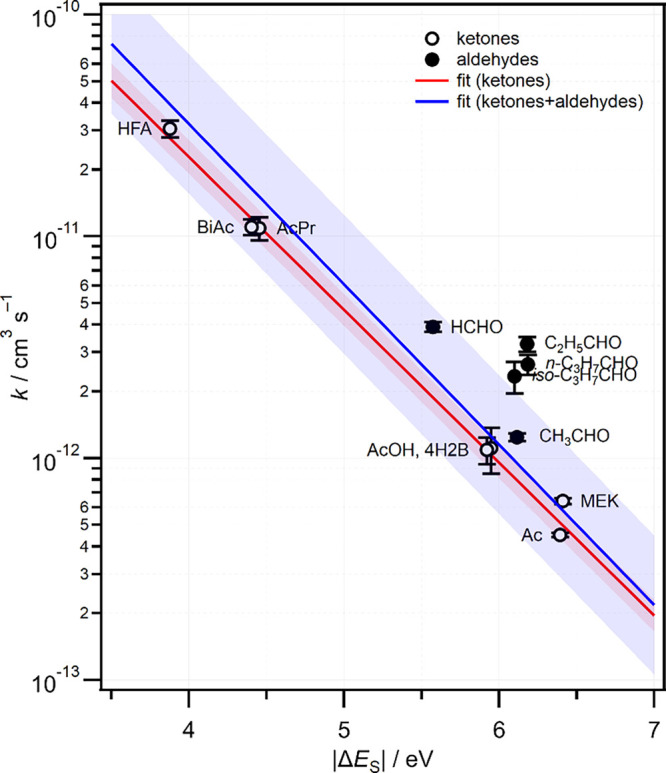
Figure 6

Open in a new tab

Correlation between experimental rate constants and FMO orbital energy gaps. Room temperature rate constants for various CH2OO + organic carbonyl reactions were compiled from various sources (see text), while |ΔES| values were calculated at the B3LYP/cc-pVDZ level. Linear fits are shown for ketones only (red) and for ketones + aldehydes (blue). The shaded areas represent 1σ prediction bands.

The calculated |ΔES| values are very similar for all the RCHO species where R ≠ H, consistent with the similar values of the Hammett substituent constants across a range of alkyl groups. The greater reactivity of propionaldehyde and butyraldehyde relative to acetaldehyde is not captured by the oversimplified model. One possible explanation could be the presence of higher-energy conformers for the longer alkyl chains. For example, propionaldehyde has a gauche conformer that lies only ∼1.0 kcal mol–1 higher in energy (CBS-QB3) than the most stable syn conformer, as defined by rotation about the αC–C bond. However, the effect on the π* orbital energy is only ∼0.1 eV, which is too small to explain the greater reactivity observed, within the limits of the proposed SAR. Alternative reaction pathways to cycloaddition may be possible for the carbonyls with longer alkyl chains accounting for the enhanced reactivity. A computational study to further explore the reactivity trends observed in CI + R1R2CO cycloaddition reactions is underway and will be the subject of a forthcoming publication.

Luo et al. have suggested that the CH2OO + HCHO reaction could contribute to formic acid (HCOOH) production in the atmosphere.29 While our measurements are blind to the reaction products, our kinetics measurements are in good agreement and dissociation of the SOZ primary product is feasible, given the large exothermicity. The dominant atmospheric loss processes for aldehydes are photolysis and reaction with OH, both of which result in lifetimes that depend on the particular aldehyde but are typically on the order of a day or less.8−11 In contrast, if we use the room temperature rate constants and an estimated concentration of 2 × 104 cm–3 for CH2OO,19,62 the atmospheric lifetimes with respect to reaction with CH2OO are approximately six months for HCHO and C2H5CHO and around a year for CH3CHO. While these lifetimes will decrease at lower temperatures as the CH2OO + RCHO rate constants increase, reaction with CH2OO is never competitive with OH, for which the rate constants are almost an order of magnitude larger and weakly (negatively) temperature dependent.52 The reactions of CH2OO with aldehydes are likely to be of minor significance in the atmosphere.

Conclusions

We have measured the temperature-dependent rate constants for the reactions of the Criegee intermediate CH2OO with formaldehyde, acetaldehyde, and propionaldehyde (RCHO where R = H, CH3, C2H5) over the range 275–335 K. At room temperature, the rate constants fall in the range (1–4) × 10–12 cm3 s–1. All three reactions show negative temperature dependences, which is typical of 1,3-dipolar cycloaddition reactions between CIs and organic carbonyls. Ab initio calculations were performed to characterize stationary points on the reaction potential energy surfaces. For all three reactions studied, the reactions proceed via entrance channel van der Waals complexes that lead to cycloaddition TSs that are submerged relative to the reactants, to form cyclic SOZs. Based on estimated typical CH2OO concentrations in the atmosphere, the reactions are unlikely to be significant reactive sinks for aldehydes.

Acknowledgments

This material is based upon work supported by the National Science Foundation under grant no. ECS-1905364. A.W.H. is supported by the Welch Foundation (grant no. AD-0007).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.4c04990.

  • Description of the calibration procedure; global pseudo-first-order plots; pressure dependence of CH2OO loss rates; CBS-QB3 Cartesian coordinates and energies of the reactants, complexes, TSs, and products; relative energies, standard enthalpies, and standard free energies of endo pathways (PDF)

The authors declare no competing financial interest.

Footnotes

$

Hammett substituent constants are defined based on their effects on the acid dissociation constant of substituted benzoic acid (C6H5COOH). Values depend on whether the substituent is in the meta (σm) or para (σp) position relative to the carboxylic acid group.

Supplementary Material

jp4c04990_si_001.pdf (1.9MB, pdf)

References

  1. Lary D. J.; Shallcross D. E. Central Role of Carbonyl Compounds in Atmospheric Chemistry. J. Geophys. Res. 2000, 105 (D15), 19771–19778. 10.1029/1999JD901184. [DOI] [Google Scholar]
  2. Nguyen H. T.-H.; Takenaka N.; Bandow H.; Maeda Y.; de Oliva S. T.; Botelho M. M. F.; Tavares T. M. Atmospheric Alcohols and Aldehydes Concentrations Measured in Osaka, Japan and in Sao Paulo. Brazil. Atmos. Environ. 2001, 35 (18), 3075–3083. 10.1016/S1352-2310(01)00136-4. [DOI] [Google Scholar]
  3. Liu Q.; Gao Y.; Huang W.; Ling Z.; Wang Z.; Wang X. Carbonyl Compounds in the Atmosphere: A Review of Abundance, Source and Their Contributions to O3 and SOA Formation. Atmos. Res. 2022, 274, 106184 10.1016/j.atmosres.2022.106184. [DOI] [Google Scholar]
  4. Luecken D. J.; Hutzell W. T.; Strum M. L.; Pouliot G. A. Regional Sources of Atmospheric Formaldehyde and Acetaldehyde, and Implications for Atmospheric Modeling. Atmos. Environ. 2012, 47, 477–490. 10.1016/j.atmosenv.2011.10.005. [DOI] [Google Scholar]
  5. Kamal M. S.; Razzak S. A.; Hossain M. M. Catalytic Oxidation of Volatile Organic Compounds (VOCs) – A Review. Atmos. Environ. 2016, 140, 117–134. 10.1016/j.atmosenv.2016.05.031. [DOI] [Google Scholar]
  6. Ervens B.; Wang Y.; Eagar J.; Leaitch W. R.; Macdonald A. M.; Valsaraj K. T.; Herckes P. Dissolved Organic Carbon (DOC) and Select Aldehydes in Cloud and Fog Water: The Role of the Aqueous Phase in Impacting Trace Gas Budgets. Atmos. Chem. Phys. 2013, 13 (10), 5117–5135. 10.5194/acp-13-5117-2013. [DOI] [Google Scholar]
  7. Seinfeld J. H.; Pandis S. N.. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change; Wiley, 2012. [Google Scholar]
  8. Pope F. D.; Smith C. A.; Davis P. R.; Shallcross D. E.; Ashfold M. N. R.; Orr-Ewing A. J. Photochemistry of Formaldehyde under Tropospheric Conditions. Faraday Discuss. 2005, 130, 59. 10.1039/b419227c. [DOI] [PubMed] [Google Scholar]
  9. Zhu L.; Tang Y.; Chen Y.; Cronin T. Wavelength-Dependent Photolysis of C3-C7 Aldehydes in the 280–330 nm Region. Spectrosc. Lett. 2009, 42 (8), 467–478. 10.1080/00387010903267195. [DOI] [Google Scholar]
  10. Martinez R. D.; Buitrago A. A.; Howell N. W.; Hearn C. H.; Joens J. A. The near U.V. Absorption Spectra of Several Aliphatic Aldehydes and Ketones at 300 K. Atmos. Environ. 1992, 26 (5), 785–792. 10.1016/0960-1686(92)90238-G. [DOI] [Google Scholar]
  11. Atkinson R.; Arey J. Atmospheric Degradation of Volatile Organic Compounds. Chem. Rev. 2003, 103 (12), 4605–4638. 10.1021/cr0206420. [DOI] [PubMed] [Google Scholar]
  12. Criegee R. Mechanism of Ozonolysis. Angew. Chem., Int. Ed. Engl. 1975, 14 (11), 745–752. 10.1002/anie.197507451. [DOI] [Google Scholar]
  13. Johnson D.; Marston G. The Gas-Phase Ozonolysis of Unsaturated Volatile Organic Compounds in the Troposphere. Chem. Soc. Rev. 2008, 37 (4), 699–716. 10.1039/b704260b. [DOI] [PubMed] [Google Scholar]
  14. Donahue N. M.; Drozd G. T.; Epstein S. A.; Presto A. A.; Kroll J. H. Adventures in Ozoneland: Down the Rabbit-Hole. Phys. Chem. Chem. Phys. 2011, 13 (23), 10848–10857. 10.1039/c0cp02564j. [DOI] [PubMed] [Google Scholar]
  15. Osborn D. L.; Taatjes C. A. The Physical Chemistry of Criegee Intermediates in the Gas Phase. Int. Rev. Phys. Chem. 2015, 34 (3), 309–360. 10.1080/0144235X.2015.1055676. [DOI] [Google Scholar]
  16. Cabezas C.; Nakajima M.; Endo Y. Criegee Intermediates Meet Rotational Spectroscopy. Int. Rev. Phys. Chem. 2020, 39 (3), 351–384. 10.1080/0144235X.2020.1782651. [DOI] [Google Scholar]
  17. Stephenson T. A.; Lester M. I. Unimolecular Decay Dynamics of Criegee Intermediates: Energy-Resolved Rates, Thermal Rates, and Their Atmospheric Impact. Int. Rev. Phys. Chem. 2020, 39 (1), 1–33. 10.1080/0144235X.2020.1688530. [DOI] [Google Scholar]
  18. Taatjes C. A.; Shallcross D. E.; Percival C. J. Research Frontiers in the Chemistry of Criegee Intermediates and Tropospheric Ozonolysis. Phys. Chem. Chem. Phys. 2014, 16 (5), 1704–1718. 10.1039/c3cp52842a. [DOI] [PubMed] [Google Scholar]
  19. Khan M. A. H.; Percival C. J.; Caravan R. L.; Taatjes C. A.; Shallcross D. E. Criegee Intermediates and Their Impacts on the Troposphere. Environ. Sci.: Processes Impacts 2018, 20 (3), 437–453. 10.1039/C7EM00585G. [DOI] [PubMed] [Google Scholar]
  20. Chhantyal-Pun R.; Khan M. A. H.; Taatjes C. A.; Percival C. J.; Orr-Ewing A. J.; Shallcross D. E. Criegee Intermediates: Production, Detection and Reactivity. Int. Rev. Phys. Chem. 2020, 39 (3), 385–424. 10.1080/0144235X.2020.1792104. [DOI] [Google Scholar]
  21. Cox R. A.; Ammann M.; Crowley J. N.; Herrmann H.; Jenkin M. E.; McNeill V. F.; Mellouki A.; Troe J.; Wallington T. J. Evaluated Kinetic and Photochemical Data for Atmospheric Chemistry: Volume VII – Criegee Intermediates. Atmos. Chem. Phys. 2020, 20 (21), 13497–13519. 10.5194/acp-20-13497-2020. [DOI] [Google Scholar]
  22. Stone D.; Au K.; Sime S.; Medeiros D. J.; Blitz M.; Seakins P. W.; Decker Z.; Sheps L. Unimolecular Decomposition Kinetics of the Stabilised Criegee Intermediates CH2OO and CD2OO. Phys. Chem. Chem. Phys. 2018, 20 (38), 24940–24954. 10.1039/C8CP05332D. [DOI] [PubMed] [Google Scholar]
  23. Taatjes C. A.; Welz O.; Eskola A. J.; Savee J. D.; Osborn D. L.; Lee E. P. F.; Dyke J. M.; Mok D. W. K.; Shallcross D. E.; Percival C. J. Direct Measurement of Criegee Intermediate (CH2OO) Reactions with Acetone, Acetaldehyde, and Hexafluoroacetone. Phys. Chem. Chem. Phys. 2012, 14 (30), 10391–10400. 10.1039/c2cp40294g. [DOI] [PubMed] [Google Scholar]
  24. Stone D.; Blitz M.; Daubney L.; Howes N. U. M.; Seakins P. Kinetics of CH2OO Reactions with SO2, NO2, NO, H2O and CH3CHO as a Function of Pressure. Phys. Chem. Chem. Phys. 2014, 16 (3), 1139–1149. 10.1039/C3CP54391A. [DOI] [PubMed] [Google Scholar]
  25. Elsamra R. M. I.; Jalan A.; Buras Z. J.; Middaugh J. E.; Green W. H. Temperature- and Pressure-Dependent Kinetics of CH2OO + CH3COCH3 and CH2OO + CH3CHO: Direct Measurements and Theoretical Analysis. Int. J. Chem. Kinet. 2016, 48 (8), 474–488. 10.1002/kin.21007. [DOI] [Google Scholar]
  26. Liu Y.; Zhou X.; Chen Y.; Chen M.; Xiao C.; Dong W.; Yang X. Temperature- and Pressure-Dependent Rate Coefficient Measurement for the Reaction of CH2OO with CH3CH2CHO. Phys. Chem. Chem. Phys. 2020, 22 (44), 25869–25875. 10.1039/D0CP04316H. [DOI] [PubMed] [Google Scholar]
  27. Liu S.; Chen Y.; Jiang H.; Shi J.; Ding H.; Yang X.; Dong W. Kinetics for the Reaction of Criegee Intermediate CH2OO with n-Butyraldehyde and Its Atmospheric Implications. Atmos. Environ. 2023, 311, 120012 10.1016/j.atmosenv.2023.120012. [DOI] [Google Scholar]
  28. Liu S.; Chen Y.; Jiang H.; Shi J.; Ding H.; Yang X.; Dong W. Reaction between Criegee Intermediate CH2OO and Isobutyraldehyde: Kinetics and Atmospheric Implications. ChemistrySelect 2023, 8 (47), e202303129 10.1002/slct.202303129. [DOI] [Google Scholar]
  29. Luo P.-L.; Chen I.-Y.; Khan M. A. H.; Shallcross D. E. Direct Gas-Phase Formation of Formic Acid through Reaction of Criegee Intermediates with Formaldehyde. Commun. Chem. 2023, 6 (1), 1–10. 10.1038/s42004-023-00933-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Debnath A.; Rajakumar B. Experimental and Theoretical Study of Criegee Intermediate (CH2OO) Reactions with n-Butyraldehyde and Isobutyraldehyde: Kinetics, Implications and Atmospheric Fate. Phys. Chem. Chem. Phys. 2024, 26 (8), 6872–6884. 10.1039/D3CP05482A. [DOI] [PubMed] [Google Scholar]
  31. Jiang H.; Liu Y.; Xiao C.; Yang X.; Dong W. Reaction Kinetics of CH2OO and syn-CH3CHOO Criegee Intermediates with Acetaldehyde. J. Phys. Chem. A 2024, 128 (25), 4956–4965. 10.1021/acs.jpca.4c01374. [DOI] [PubMed] [Google Scholar]
  32. Jalan A.; Allen J. W.; Green W. H. Chemically Activated Formation of Organic Acids in Reactions of the Criegee Intermediate with Aldehydes and Ketones. Phys. Chem. Chem. Phys. 2013, 15 (39), 16841–16852. 10.1039/c3cp52598h. [DOI] [PubMed] [Google Scholar]
  33. Kaipara R.; Rajakumar B. Temperature-Dependent Kinetics of the Reaction of a Criegee Intermediate with Propionaldehyde: A Computational Investigation. J. Phys. Chem. A 2018, 122 (43), 8433–8445. 10.1021/acs.jpca.8b06603. [DOI] [PubMed] [Google Scholar]
  34. Wang P.-B.; Truhlar D. G.; Xia Y.; Long B. Temperature-Dependent Kinetics of the Atmospheric Reaction between CH2OO and Acetone. Phys. Chem. Chem. Phys. 2022, 24 (21), 13066–13073. 10.1039/D2CP01118B. [DOI] [PubMed] [Google Scholar]
  35. Zhang T.; Wen M.; Ding C.; Zhang Y.; Ma X.; Wang Z.; Lily M.; Liu J.; Wang R. Multiple Evaluations of Atmospheric Behavior between Criegee Intermediates and HCHO: Gas-Phase and Air-Water Interface Reaction. J. Environ. Sci. 2023, 127, 308–319. 10.1016/j.jes.2022.06.004. [DOI] [PubMed] [Google Scholar]
  36. Liu Y.; Bayes K. D.; Sander S. P. Measuring Rate Constants for Reactions of the Simplest Criegee Intermediate (CH2OO) by Monitoring the OH Radical. J. Phys. Chem. A 2014, 118 (4), 741–747. 10.1021/jp407058b. [DOI] [PubMed] [Google Scholar]
  37. Cornwell Z. A.; Harrison A. W.; Murray C. Kinetics of the Reactions of CH2OO with Acetone, α-Diketones, and β-Diketones. J. Phys. Chem. A 2021, 125 (39), 8557–8571. 10.1021/acs.jpca.1c05280. [DOI] [PubMed] [Google Scholar]
  38. Cornwell Z. A.; Enders J. J.; Harrison A. W.; Murray C. Temperature-Dependent Kinetics of the Reactions of CH2OO with Acetone, Biacetyl, and Acetylacetone. Int. J. Chem. Kinet. 2023, 55 (3), 154–166. 10.1002/kin.21625. [DOI] [Google Scholar]
  39. Cornwell Z. A.; Enders J. J.; Harrison A. W.; Murray C. Temperature-Dependent Kinetics of the Reactions of the Criegee Intermediate CH2OO with Hydroxyketones. J. Phys. Chem. A 2024, 128 (10), 1880–1891. 10.1021/acs.jpca.4c00156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Sustmann R. A Simple Model for Substituent Effects in Cycloaddition Reactions. I. 1,3-Dipolar Cycloadditions. Tetrahedron Lett. 1971, 12 (29), 2717–2720. 10.1016/S0040-4039(01)96961-8. [DOI] [Google Scholar]
  41. Houk K. N. Frontier Molecular Orbital Theory of Cycloaddition Reactions. Acc. Chem. Res. 1975, 8 (11), 361–369. 10.1021/ar50095a001. [DOI] [Google Scholar]
  42. Fukui K. Role of Frontier Orbitals in Chemical Reactions. Science 1982, 218 (4574), 747–754. 10.1126/science.218.4574.747. [DOI] [PubMed] [Google Scholar]
  43. Berndt T.; Kaethner R.; Voigtländer J.; Stratmann F.; Pfeifle M.; Reichle P.; Sipilä M.; Kulmala M.; Olzmann M. Kinetics of the Unimolecular Reaction of CH2OO and the Bimolecular Reactions with the Water Monomer, Acetaldehyde and Acetone under Atmospheric Conditions. Phys. Chem. Chem. Phys. 2015, 17 (30), 19862–19873. 10.1039/C5CP02224J. [DOI] [PubMed] [Google Scholar]
  44. Chhantyal-Pun R.; Khan M. A. H.; Martin R.; Zachhuber N.; Buras Z. J.; Percival C. J.; Shallcross D. E.; Orr-Ewing A. J. Direct Kinetic and Atmospheric Modeling Studies of Criegee Intermediate Reactions with Acetone. ACS Earth Space Chem. 2019, 3 (10), 2363–2371. 10.1021/acsearthspacechem.9b00213. [DOI] [Google Scholar]
  45. Debnath A.; Rajakumar B. Investigation of Kinetics and Mechanistic Insights of the Reaction of Criegee Intermediate (CH2OO) with Methyl-Ethyl Ketone (MEK) under Tropospherically Relevant Conditions. Chemosphere 2023, 312, 137217 10.1016/j.chemosphere.2022.137217. [DOI] [PubMed] [Google Scholar]
  46. Yaws C. L.The Yaws Handbook of Vapor Pressure; Elsevier, 2015. 10.1016/C2014-0-03590-3. [DOI] [Google Scholar]
  47. Ting W.-L.; Chen Y.-H.; Chao W.; Smith M. C.; Lin J. J.-M. The UV Absorption Spectrum of the Simplest Criegee Intermediate CH2OO. Phys. Chem. Chem. Phys. 2014, 16 (22), 10438–10443. 10.1039/C4CP00877D. [DOI] [PubMed] [Google Scholar]
  48. Foreman E. S.; Kapnas K. M.; Jou Y.; Kalinowski J.; Feng D.; Gerber R. B.; Murray C. High Resolution Absolute Absorption Cross Sections of the B̃1A′–X̃1A′ Transition of the CH2OO Biradical. Phys. Chem. Chem. Phys. 2015, 17 (48), 32539–32546. 10.1039/C5CP04977F. [DOI] [PubMed] [Google Scholar]
  49. Mir Z. S.; Lewis T. R.; Onel L.; Blitz M. A.; Seakins P. W.; Stone D. CH2OO Criegee Intermediate UV Absorption Cross-Sections and Kinetics of CH2OO + CH2OO and CH2OO + I as a Function of Pressure. Phys. Chem. Chem. Phys. 2020, 22 (17), 9448–9459. 10.1039/D0CP00988A. [DOI] [PubMed] [Google Scholar]
  50. Spietz P.; Gómez Martín J. C.; Burrows J. P. Spectroscopic Studies of the I2/O3 Photochemistry: Part 2. Improved Spectra of Iodine Oxides and Analysis of the IO Absorption Spectrum. J. Photochem. Photobio. A 2005, 176 (1–3), 50–67. 10.1016/j.jphotochem.2005.08.023. [DOI] [Google Scholar]
  51. Keller-Rudek H.; Moortgat G. K.; Sander R.; Sörensen R. The MPI-Mainz UV/VIS Spectral Atlas of Gaseous Molecules of Atmospheric Interest. Earth Syst. Sci. Data 2013, 5, 365–373. 10.5194/essd-5-365-2013. [DOI] [Google Scholar]
  52. Burkholder J. B.; Sander S. P.; Abbatt J.; Barker J. R.; Cappa C.; Crounse J. D.; Dibble T. S.; Huie R. E.; Kolb C. E.; Kurylo M. J.; Orkin V. L.; Percival C. J.; Wilmouth D. M.; Wine P. H.. Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 19,” JPL Publication 19–5; Jet Propulsion Laboratory: Pasadena, 2019http://jpldataeval.jpl.nasa.gov. [Google Scholar]
  53. Clouthier D. J.; Ramsay D. A. The Spectroscopy of Formaldehyde and Thioformaldehyde. Annu. Rev. Phys. Chem. 1983, 34 (1), 31–58. 10.1146/annurev.pc.34.100183.000335. [DOI] [Google Scholar]
  54. Meller R.; Moortgat G. K. Temperature Dependence of the Absorption Cross Sections of Formaldehyde between 223 and 323 K in the Wavelength Range 225–375 nm. J. Geophys. Res. 2000, 105 (D6), 7089–7101. 10.1029/1999JD901074. [DOI] [Google Scholar]
  55. Roehl C. M.; Burkholder J. B.; Moortgat G. K.; Ravishankara A. R.; Crutzen P. J. Temperature Dependence of UV Absorption Cross Sections and Atmospheric Implications of Several Alkyl Iodides. J. Geophys. Res. 1997, 102 (D11), 12819–12829. 10.1029/97JD00530. [DOI] [Google Scholar]
  56. Mössinger J. C.; Shallcross D. E.; Anthony Cox R. UV-VIS Absorption Cross-Sections and Atmospheric Lifetimes of CH2Br2, CH2I2 and CH2BrI. J. Chem. Soc., Faraday Trans. 1998, 94 (10), 1391–1396. 10.1039/a709160e. [DOI] [Google Scholar]
  57. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.. et al. Gaussian 16, Revision B.01; Gaussian, Inc.: Wallingford CT, 2016. [Google Scholar]
  58. Ting W.-L.; Chang C.-H.; Lee Y.-F.; Matsui H.; Lee Y.-P.; Lin J. J.-M. Detailed Mechanism of the CH2I + O2 Reaction: Yield and Self-Reaction of the Simplest Criegee Intermediate CH2OO. J. Chem. Phys. 2014, 141 (10), 104308. 10.1063/1.4894405. [DOI] [PubMed] [Google Scholar]
  59. Laidler K. J.Chemical Kinetics, 3rd ed.; Harper & Row: New York, 1987. [Google Scholar]
  60. Wei W.; Yang X.; Zheng R.; Qin Y.; Wu Y.; Yang F. Theoretical Studies on the Reactions of the Simplest Criegee Intermediate CH2OO with CH3CHO. Comput. Theor. Chem. 2015, 1074, 142–149. 10.1016/j.comptc.2015.10.013. [DOI] [Google Scholar]
  61. Hansch C.; Leo A.; Taft R. W. A Survey of Hammett Substituent Constants and Resonance and Field Parameters. Chem. Rev. 1991, 91 (2), 165–195. 10.1021/cr00002a004. [DOI] [Google Scholar]
  62. Novelli A.; Hens K.; Tatum Ernest C.; Martinez M.; Nölscher A. C.; Sinha V.; Paasonen P.; Petäjä T.; Sipilä M.; Elste T.; et al. Estimating the Atmospheric Concentration of Criegee Intermediates and Their Possible Interference in a FAGE-LIF Instrument. Atmos. Chem. Phys. 2017, 17 (12), 7807–7826. 10.5194/acp-17-7807-2017. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp4c04990_si_001.pdf (1.9MB, pdf)

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES