Improving effort-aware just-in-time defect prediction with weighted code churn and multi-objective slime mold algorithm

Abstract

Effort-aware just-in-time software defect prediction (JIT-SDP) aims to effectively utilize the limited resources of software quality assurance (SQA) to detect more software defects. This improves the efficiency of SQA work and the quality of the software. However, there is disagreement regarding the representation of the key feature variable, SQA effort, in the field of effort-aware JIT-SDP. Additionally, the most recent metaheuristic optimization algorithms (MOAs) have not yet been effectively integrated with multi-objective effort-aware JIT-SDP tasks. These deficiencies, in both feature representation and model optimization (MO), result in a significant disparity between the performance of effort-aware JIT-SDP techniques and the expectations of the industry. In this study, we present a novel method called weighted code churn (CC) and improved multi-objective slime mold algorithm (SMA) (WCMS) for effort-aware JIT-SDP. It comprises two stages: feature improvement (FI) and MO. In the FI phase, we normalize the two feature variables: number of modified files (NF) and distribution of modified code across each file (Entropy). We then use an exponential function to quantify the level of difficulty of the change. The equation is as follows: DD = NF^Entropy, where DD is an acronym for the degree of difficulty, NF denotes the base number, and Entropy denotes the index. We define change effort as the product of the difficulty degree in implementing the change and CC, with weighted CC representing the change effort. During the MO stage, we improve the SMA by incorporating multi-objective handling capabilities and devising mechanisms for multi-objective synchronization and conflict resolution. We develop a multi-objective optimization algorithm for hyperparameter optimization (HPO) of the JIT-SDP model in WCMS. To evaluate the performance of our method, we conducted experiments using six well-known open-source projects and employed two effort-aware performance evaluation metrics. We evaluated our method based on three scenarios: cross-validation, time-wise cross-validation, and across-project prediction. The experimental results indicate that the proposed method outperforms the benchmark method. Furthermore, the proposed method demonstrates greater scalability and generalization capabilities.

1. Introduction

The relationship between software defects and software is similar to that between diseases and people. If left unchanged over time, these issues can lead to substantial economic losses or other unforeseen consequences [1]. The number of defects present is directly related to software quality. A higher quantity of defects reduces the quality of the software, leading to increased maintenance costs. Software defect prediction (SDP) aims to predict the likelihood of a software module containing faults before it undergoes testing. This prediction helps to allocate limited resources effectively for software quality assurance (SQA). The early identification of defects allows software developers and testers to reduce the scope of troubleshooting and allocate testing resources optimally [2]. Consequently, SDP techniques have gained significant attention from researchers. Numerous studies have explored SDP models at various levels, including methods [3], files [4], and subsystems [5]. These studies have also examined the software metrics used to construct these models [[6], [7], [8]].

In certain cases, module-level SDP techniques have proven useful [9]. However, these techniques have drawbacks, such as coarse graining, delayed prediction results, and the inability to quickly allocate SQA resources. To overcome these limitations, researchers have proposed software change-based SDP [6,10]. SDP based on software changes offers the advantages of greater granularity and the ability to predict fault-proneness for changes in particular. This approach is commonly known as just-in-time defect prediction [11]. Just-in-time software defect prediction (JIT-SDP) focuses on identifying changes that induce defects at the developer level. Because the change is just committed, developers have a fresh memory of it, making it easier to apply the suggested predictions. In traditional module-level SDP, it is often assumed that the effort required for SQA activities is the same for each module [12]. However, different changes may require different efforts in the JIT-SDP.

Kamei et al. first proposed using lines of code (LOC) to represent effort in the first model of JIT-SDP [11]. Liu et al. highlighted the significance of code churn (CC) as a metric for constructing an unsupervised model [13]. Chen et al. emphasized that effort representation should consider LOC and a combination of four metrics (LOC, Entropy, NDEV, and EXP) that are involved in change modification; they proposed a new approach for representing effort [14]. To enhance the performance of SDP, researchers have proposed several methods, including CC based unsupervised model (CCUM) [13], OneWay [15], classify before sorting plus (CBS+) [16], multi-objective optimization based supervised method (MULTI) [17], and differential evolution algorithm for effort-aware JIT-SDP (DEJIT) [18].

However, there is disagreement regarding the representation of the key feature variable, SQA effort, in the field of effort-aware JIT-SDP. Additionally, the most recent metaheuristic optimization algorithms (MOAs) have not yet been effectively integrated with multi-objective effort-aware JIT-SDP tasks. There is still room for further improvement in this area. In this study, we aim to enhance the performance of effort-aware JIT-SDP by improving both the features and models concurrently. To better represent the effort of change for feature improvement (FI), we introduce a weighted CC metric. Additionally, we improve the single-objective optimization algorithm slime mold algorithm (SMA) to support multi-objective optimization. This enhanced multi-objective SMA is then utilized to optimize the model structure and further enhance the performance of the model. Therefore, the methodology employed in this study involves using weighted CC and the improved multi-objective SMA (WCMS) to enhance the performance of the effort-aware JIT-SDP.

To validate the effectiveness of using weighted CC to represent change effort for FI and the multi-objective SMA for model optimization (MO), we selected six well-known open-source projects: Bugzilla (BUG), Columba (COL), Jdt (JDT), Platform (PLA), Mozilla (MOZ), and Postgres (POS). These projects involve Java and C/C++ technologies and comprise a total of 207,697 changes, of which 27,866 are defective. In this study, we utilized two evaluation metrics, ACC and Popt, and employed three decision tree-based ensemble learning algorithms, namely Random Forest (RF), eXtreme Gradient Boosting (XGB), and LightGBM (LGBM), to construct SDP models. These models were then validated using cross-validation, time-wise cross-validation, and across-project prediction scenarios. The results demonstrate that our approach surpasses the average performance of the current benchmark methods and achieves superior results in most tasks compared with the best available benchmark methods.

The contributions of this paper are as follows.

• (1)This study proposes a novel approach for representing change effort by multiplying CC with the degree of difficulty (DD). Normalization techniques are applied to the feature variables “number of modified files” (NF) and “distribution of modified code across each file” (Entropy). An exponential function is then used to represent the level of difficulty.
• (2)This study enhances SMA by integrating multi-objective processing capabilities and developing mechanisms for multi-objective synchronization and conflict resolution.
• (3)This study proposes using an improved SMA for the hyperparameter optimization (HPO) of decision tree-based ensemble learning models in effort-aware JIT-SDP. The goal is to improve the performance of the JIT-SDP. This is the first attempt to apply this algorithm to HPO in the field of machine learning.

The rest of this paper is structured as follows. Section II provides an overview of previous studies conducted on effort-aware JIT-SDP. Section III presents a detailed explanation of the methodology used in this study. Section IV outlines the experimental setup and the research questions addressed in this study. Section V presents the detailed findings and results of the experiments. Section VI discusses the implications and significance of the obtained results. Section VII analyzes the validity of the study. Finally, Section VIII concludes the study and provides recommendations for future research.

2. Background and related work

2.1. Background

2.1.1. Effort-aware JIT-SDP

SDP involves analyzing the intrinsic features of a software system instead of running the system to make predictions about module fault-proneness. First, an SDP model is created by analyzing historical data from a known project that includes information about the product, development process, and defects. This model is then applied to predict the fault-proneness of an unknown software project [19]. Software change refers to the difference between two versions of software in a software configuration management (SCM) system [20]. The JIT-SDP model is constructed by establishing the relationship between software change features and labels.

Different changes may require different efforts in JIT-SDP. Even if two changes have the same CC, their required efforts can vary significantly. For instance, Changes A and B may have the same amount of CC, but Change A has five files, while Change B has only one file. In general, the process of locating, fixing, reviewing, and verifying Change A is significantly more challenging than that of Change B. Consequently, the effort required for Change A can generally be greater than that required for Change B. It is of utmost importance to consider effort when devising an effort-aware JIT-SDP model, as the performance of the model in real-world applications may be compromised without such consideration. Therefore, effort is an important metric, and effectively representing effort plays a vital role in the performance of the model.

Current studies on representing essential feature effort metrics have two main issues: (1) omitting the process and focusing only on the results. For instance, let us consider two changes, A and B, which fix different defects, D₁ and D₂, respectively. Both changes have a CC of 10. However, the changes in code for A are distributed across five files, while the changes for B are in only one file. If we consider only the results, the efforts for both changes are deemed equal. From a process perspective, fixing a defect involves several steps, including defect localization, code fixing, reviewing, and verification. Because defect D₁ is distributed across five files, it is evident that the effort required for Change A is generally greater than that for Change B. (2) Another problem in previous studies is the lack of standardization in change efforts. For instance, when handling Change A, which has a CC of 10, an experienced SQA person may take a day to complete the task. However, an inexperienced SQA person may take at least two days to complete the same task. Because software SQA teams typically comprise individuals with varying levels of expertise, comparing change efforts without standardization can result in inaccuracies.

Effort-aware JIT-SDP extensively uses logistic regression models [11,17,18]. Other regression models, such as logistic forests [14], support vector machines [14], and deep neural networks [21] have also demonstrated promising results. Several studies have employed metaheuristic optimization algorithms (MOAs) to optimize the hyperparameters of the models [17,18]. Despite the variations among different effort-aware JIT-SDP techniques, they share a similar structure, which can be summarized as follows:

$$P=F\ast M\text{.}$$ (1)

The current focus of research is to improve the performance of JIT-SDP techniques, which is represented by P, by enhancing existing features (F) or refining models (M).

2.1.2. Slime mold algorithm

SMA is a novel MOA designed by Li et al., in 2020 [22]. The algorithm is inspired by the oscillation patterns observed during the natural foraging process of the slime mold. It uses a unique mathematical model and adaptive weights to simulate the positive and negative feedback processes of the slime mold propagation waves. This allows for the formation of an optimal path that connects food sources while exhibiting excellent exploratory capabilities and development tendencies. It has been validated that the algorithm possesses strong optimization capabilities and achieves a fast convergence speed.

SMA has been successfully applied to engineering constraint design optimization problems, such as welding beams, pressure vessels, cantilever beams, and I-beams. These are typical single-objective optimization problems. In classification and regression prediction tasks, decision tree-based ensemble learning algorithms have several advantages in terms of high accuracy, strong interpretability, robustness, and scalability. However, these algorithms have multiple hyperparameters, and different combinations of these hyperparameters can significantly affect algorithm performance. To optimize the model structure of these algorithms, this study explores the applications of SMA for HPO in effort-aware JIT-SDP models.

2.2. Related work

2.2.1. Just-in-time defect prediction

Change-level defect prediction was first proposed by Mockus and Weiss, who utilized change history information to construct a statistical model for forecasting the likelihood of faults in new changes [23]. This study provides an important foundation for future studies on change-level SDP. Next, Graves et al. used historical software changes to predict the defect incidence [6]. They developed several statistical models and evaluated the factors contributing to numerous defects in the subsequent software development process. Moser et al. conducted a comparative analysis of the predictive power of metrics used for defect prediction [24]. They proved that product-related process metrics are more effective than code metrics. Kamei et al. summarized the advantages of change-level SDP and refined the features of software changes based on previous studies [11]. They divided the 14 features into 5 dimensions: Diffusion, Size, Purpose, History, and Experience. They used these characteristics to develop a change-level SDP model and validated its effectiveness on six open-source and five commercial datasets. The model identified 35 % of the changes that induce defects and used only 20 % of the total effort. This study also provides six open-source datasets that can be used as benchmarks for future studies in this field. Subsequently, Kamei et al. conducted a study on JIT-SDP across-project models [25]. Yang et al. were the first to introduce deep learning techniques in this field [26]. They constructed an SDP model called Deeper using a deep belief network algorithm. Yang et al. proposed an approach called two-layer ensemble learning (TLEL) [27]. Hoang et al. proposed deep learning framework for JIT-SDP (DeepJIT), an end-to-end deep learning framework that automatically extracts features from commits and code changes to identify defects [28]. Pascarell et al. investigate partially defective commits and propose a fine-grained just-in-time defect prediction model [29]. This model accurately predicts defective files and reduces the effort required for defect diagnosis. Zhou et al. utilized ensemble learning and deep learning techniques to develop an SDP model called defect prediction using deep forest (DPDF) [30], which incorporates a deep forest model. The model converts an RF classifier into a layered structure and employs a cascading strategy to identify the most significant defect features. Pornprasit et al. propose JITLine, a JIT-SDP approach that provides accurate identification of defect-introducing commits and the corresponding defective lines [31]. Zhao et al. proposed a simplified deep forest SDP model by modifying the state-of-the-art deep forest model SDF and applying it to JIT-SDP for Android mobile applications [32]. Cabral and Minku analyzed the problem of conceptual drift in software change features and proposed constructing defect classifiers using predictive information from unlabeled software changes to address this issue [33]. Falessi et al. present and validate the defectiveness prediction of methods and classes can been enhanced by JIT [34].

Previous studies have laid the foundation for this study. To enhance the performance of the JIT-SDP model, this study aims to improve both the features and the model. In terms of features, we modify the representation of the change effort. For this model, we employ an improved SMA to optimize the structure of the JIT-SDP model.

2.2.2. Effort-aware defect prediction

Mende and Koschke first introduced the concept of effort-aware in the field of SDP [12,35,36]. They proposed a new performance evaluation metric called comparing a prediction model with an optimal mode (Popt). In a subsequent study, Kamei et al. validated the results of two types of common SDP from previous studies using effort-aware models [37]. They found that process metrics, such as change history, outperformed product metrics, such as LOC. Kamei et al. were the first to apply the effort-aware model to JIT-SDP and propose the first model of effort-aware linear regression (EALR) [11]. Several studies in this field have used LOC as a measure of effort, as investigated by Shihab et al. [38]. Through their analysis of four open-source projects, they discovered that complexity metrics demonstrated the strongest correlation with effort. Moreover, they found that a combination of three metrics (complexity, size, and CC) was more effective in representing effort than using only LOC. In a subsequent study, Yang et al. investigated the predictive power of unsupervised models in the context of effort-aware JIT-SDP [39]. They developed a simple unsupervised model called lines of code in a file before the current change (LT), which utilizes common change metrics. They compared this model with state-of-the-art supervised models in three scenarios: cross-validation, time-wise cross-validation, and across-project prediction. The results revealed that several basic unsupervised models performed better than the current state-of-the-art supervised models. Based on the study by Yang et al., Liu et al. developed the first unsupervised model, CCUM, which is based on CC. The performance of CCUM was evaluated on six open-source projects. The results indicate that CCUM outperforms all the previous supervised and unsupervised models. In a similar study conducted by Huang et al. [16], new insights were presented. First, it was observed that LT requires developers to check for more changes within the same timeframe, resulting in more context switches. Second, although LT can identify more defect-inducing changes, many of the top-ranked changes are false positives. Finally, when considering the harmonic mean (F1-score) of the accuracy and recall, LT is not superior to EALR. Additionally, Huang et al. proposed an improved supervised model called CBS + [16]. Compared to the EALR model, CBS + demonstrated the ability to identify approximately 15%–26 % more defect-inducing changes while reducing the number of context switches and false alarms to a level similar to EALR. Moreover, compared with the LT model, CBS + achieved a similar number of detected defect-inducing changes but significantly reduced context switching and false alarms before the first success. Guo et al. investigated the effect of effort on the classification performance of the SDP model [40]. They observed that this issue arose from the imbalanced distribution of the change sizes. To address this problem, they proposed trimming as a practical solution. Li et al. introduced a semi-supervised model called effort-aware tri-training (EATT) [22], which employs a greedy strategy to effectively rank changes. Chen et al. proposed a novel effort representation called multi-metric joint calculation (MMJC) [14], which integrates four metrics, including LOC, Entropy, NDEV, and EXP, of the changes. Çarka et al. propose that normalizing PofBs enhances the realism of results, improves classifier utility, and promotes the practical adoption of prediction models in the industry [41]. Xu et al. addressed the issue of frequent update iterations in mobile applications and the lack of timely labeled data by proposing a cross-triad deep feature embedding method known as cross-triad deep feature embedding (CDFE) [21].

Effort-aware JIT-SDP research aims to utilize limited SQA resources effectively by identifying and fixing software defects to improve software quality. Previous studies have primarily focused on effort representation, change ordering, and effort-aware SDP models, providing valuable insights for this study. However, most of these studies considered only the outcome and overlooked the process of representing effort, thereby failing to standardize the measurement of effort. Consequently, this study introduces a novel method for representing effort by incorporating weighted CC. By assigning weights, the effect of CC on the overall effort can be accurately represented.

2.2.3. Single-objective and multi-objective MOAs

When confronted with complex combinatorial optimization problems, traditional optimization methods often exhibit inefficiency and are unable to satisfy the required criteria. To address this issue, researchers have developed MOAs, such as the genetic algorithm [42], differential evolution (DE) algorithm [43], and ant colony optimization algorithm [44]. These algorithms are based on heuristic strategies and can be applied regardless of the specific problem conditions. However, most of these MOAs consider only a single optimization objective. To address multi-objective optimization problems, researchers have proposed various algorithms, including non-dominated sorting genetic algorithm II (NSGA-II) [45] and multi-objective evolutionary algorithm based on decomposition (MOEA/D) [46]. To improve the effectiveness of MOEA/D, it is important to adjust the neighborhood size (NS) parameter. The ensemble method ensemble multi-objective evolutionary algorithm based on decomposition (ENS-MOEA/D) was proposed with online self-adaptation using various NSs [47]. Zhang et al. successfully applied this method to optimize hyperparameters in variational model decomposition, thereby demonstrating improved results [48]. In recent years, MOAs have become a popular topic in academic research, leading to the development of various new algorithms. Some notable examples include the Golden Sine Algorithm [49], Grasshopper Optimization Algorithm [50], Seagull Optimization Algorithm [51], Butterfly Optimization Algorithm [52], Sparrow Search Algorithm [53], SMA [22], and Multi-Objective Simulated Annealing (MOSA) algorithm [54]. These MOAs are extensively used in industry [55,56].

In this study, we focus on two performance metrics for the effort-aware JIT-SDP model: ACC and Popt. To enhance the performance of the model, our goal is to optimize both metrics as the objectives of optimization simultaneously. Because the SMA is a single-objective optimization algorithm, we first transform it into a multi-objective version and apply it to optimize the structure of the effort-aware JIT-SDP model.

2.2.4. HPO for defect prediction

With default settings, the SDP model tends to exhibit poor performance [57]. To address this issue, Tantithamthavorn et al. explored the effects of HPO on SDP models [58]. They discovered that by investing a small amount of computational time, HPO can significantly improve the area under the curve (AUC) performance of the model. However, it also resulted in significant changes in the ranking of variable importance while maintaining the stability of the model. Chen et al. proposed a supervised learning-based multi-objective optimization model called MULTI [17]. In this model, the problem was transformed into a multi-objective optimization problem with two objectives: maximizing the number of identified defect-inducing changes and minimizing the effort. They used a logistic regression algorithm to build the model and employed the NSGA-II algorithm to calculate the coefficients of the logistic regression model. Although the MULTI method exhibits better average performance, it still produces numerous suboptimal solutions with poor performance. Additionally, to enhance the performance of JIT-SDP, Yang et al. proposed a supervised model called DEJIT, which is based on differential evolution [18]. They used the density-percentile average as the optimization objective for the training set and employed logistic regression to design an SDP model. Notably, the researchers utilized the differential evolution algorithm to calculate the coefficients of the logistic regression model.

In this study, three decision tree-based ensemble learning algorithms, namely RF, XGB, and LGBM, are employed to construct the effort-aware JIT-SDP model. Furthermore, the structure of the SDP model is optimized using an improved SMA.

3. Methodology

This section defines the overall aim of our study, motivates our research questions and outlines our proposed approach.

3.1. Research questions

The objective of this study is to enhance the performance of effort-aware JIT-SDP by improving both the features and models concurrently. Our work is structured around two key questions. The first addresses how to enhance the performance of effort-aware JIT-SDP by improving the features of software changes during the FI phase. The second focuses on optimizing multiple performance indicators of effort-aware JIT-SDP simultaneously during the MO phase. The entire process comprises two stages: FI and MO. The results of these stages allow us to identify the optimal values for the performance indicators.

RQ1

Which method can be employed to represent the change effort during the FI phase to enhance the performance of effort-aware JIT-SDP?

The level of effort required for different changes may vary significantly in the context of software development. The level of effort needed for a change is not only determined by the complexity and extent of the modifications but also impacts the overall effectiveness of the models. It is crucial to accurately represent change effort to ensure an effort-aware JIT-SDP. The main goal of this study is to develop an effective method for depicting change effort during the FI phase. The aim is to improve the efficiency of effort-aware JIT-SDP by refining this depiction, enabling more precise predictions and better resource allocation. This study introduces a new approach to quantify and represent change effort by integrating historical data analysis with machine learning techniques. This method involves analyzing past changes to extract informative features that capture the nuances of change effort. Incorporating this new representation in the FI phase is expected to enhance the efficiency of effort-aware JIT-SDP and optimize the effectiveness of subsequent modeling efforts in the JIT-SDP process, ultimately leading to improved performance across various metrics.

RQ2

What methods can be employed to optimize multiple performance indicators simultaneously during the MO phase to enhance the performance of effort-aware JIT-SDP?

The efficacy of a model depends on various factors, such as the specific project at hand and the evaluation metrics used. Additionally, the hyperparameters of the machine learning model significantly impact the model's overall performance. Therefore, optimizing the model is crucial for achieving improved performance in JIT-SDP. The effort-aware JIT-SDP process requires the use of multiple performance metrics, necessitating the simultaneous optimization of these metrics. This study aims to investigate effective strategies for optimizing multiple performance indicators concurrently during the MO phase. The goal is to enhance the overall performance of JIT-SDP and maintain a balance among different performance metrics. This challenge is reframed as a multi-objective optimization problem with the aim of improving effort-aware JIT-SDP performance. The study presents a new multi-objective optimization approach to address this issue.

3.2. Proposed approach

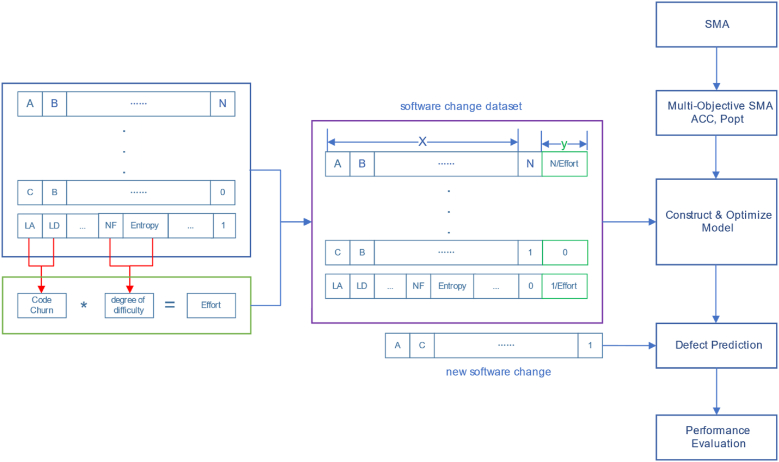
Our proposed WCMS method is illustrated in Fig. 1. The WCMS approach comprises two stages. In the FI phase, we use the sum of Lines of Code Added (LA) and Lines of Code Deleted (LD) to represent the CC and calculate the difficulty level of the changes by combining NF and Entropy. The change in effort is then measured by multiplying these two factors. During the MO stage, we enhance the SMA to optimize both ACC and Popt simultaneously. This enhancement enables the concurrent optimization of multiple objectives. Subsequently, we utilize the improved SMA to optimize the structure of the effort-aware JIT-SDP model to attain the optimal values of ACC and Popt.

Fig. 1.

Overall architecture diagram of the proposed approach.

3.2.1. Use weighted CC for measuring change effort in FI

It is reasonable to use CC as a measure of change effort. However, it may not accurately capture the effort required for changes in many application scenarios. This is because it is influenced by the number of LOC, specific programming techniques, code distribution, and problem complexity [16,38]. Research and practice have shown that the amount of effort required for change is not always directly proportional to the number of LOC [16]. To address this issue, this study proposes using weighted CC as a measure of change effort. The specific calculation steps for weighted CC are as follows.

• (1)The CC for each change is calculated as the sum of LA and LD for that change. The formula is as follows:

$$CC=LA+LD\text{.}$$ (2)

• (2)The DD of the change can be determined by calculating NF and Entropy. The specific steps for the calculation are as follows.
• i)NF is normalized using the min–max normalization method:

$$N{F}_{\text{norm}}=\left(NF-N{F}_{\min }\right)/\left(N{F}_{\max }-N{F}_{\min }\right)\text{,}$$ (3)

where NF_min denotes the minimum value of NF and NF_max denotes the maximum value of NF. NF denotes the original value, while NF_norm denotes the normalized result, which ranges from 0 to 1.

• ii)The Shannon entropy of the distribution of the modification files for changes is calculated.

$$H_n\left(P\right)=-{\sum }_{k=1}^n(p_k\ast {\log }_2{p}_k)\text{,}$$ (4)

where P _k denotes the probability of document k appearing, with P _k ≥ 0, and $\sum _{k=1}^n{P}_k=1$.

• iii)Logarithmic normalization of Shannon's entropy is utilized to compare the entropy of different changes in various projects.

$$Entropy=\frac{1}{{\log }_{2}n}\ast H_n\left(P\right)\text{.}$$ (5)

The normalized result falls in the interval of [0, 1], meaning that 0 ≤ Entropy ≤1. A higher value of Entropy indicates a broader distribution of the modified change files.

• iv)The DD for changes in the SQA stage is primarily determined by NF and Entropy, which exhibit an exponential relationship. Therefore, we can use an exponential function to quantify the DD for changes, where NF denotes the base and Entropy denotes the exponent:

$$DD=N{F_{norm}}^{Entropy}\text{.}$$ (6)

• v)The effort required for changes during the SQA stage is influenced by both the CC and complexity of the changes. Thus, we can represent the change effort by multiplying the DD by CC.

$$Effort=DD\ast CC\text{.}$$ (7)

3.2.2. Improve SMA for ACC and popt concurrent optimization in MO

In this study, we use the maximum values of both ACC and Popt as optimization objectives to obtain optimal results. However, because SMA is suitable only for single-objective optimization tasks, we need to improve its capability to optimize multiple objective tasks. The specific steps for implementation are as follows.

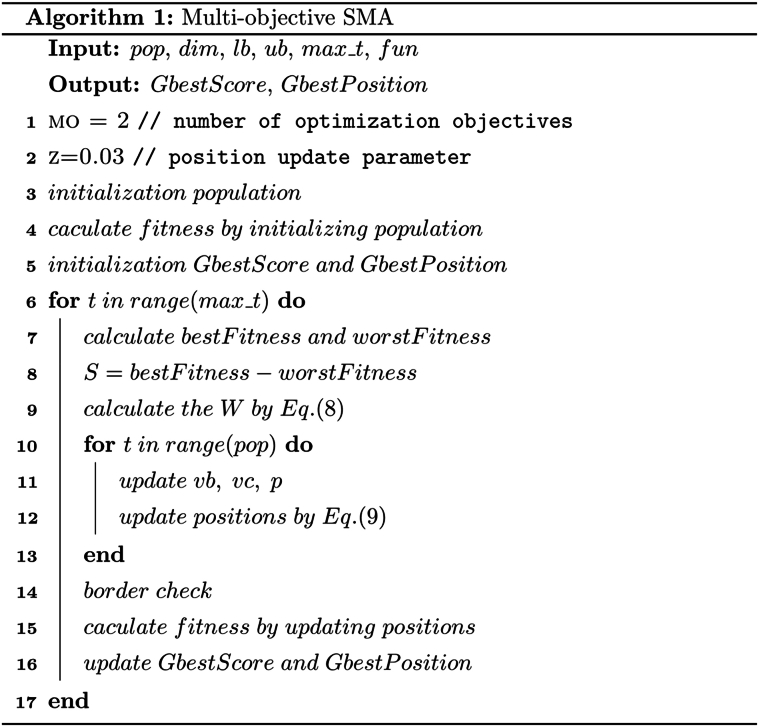
• (1)Develop a multi-objective mechanism to synchronize and resolve conflicts in SMA. During this stage, the slime mold is active and vibrant. Its organic matter actively finds food, surrounds it, and secretes enzymes to digest it. The mathematical model of the SMA primarily simulates the two processes of slime mold approaching, surrounding, and capturing food. The pseudocode for the multi-objective SMA is shown in Algorithm 1.

• i)Approaching Food

$$W\left(SortIndex\left(i\right)\right)=\{\begin{array}{l}\mathit{max}\left(1+r\times \mathit{log}\left(\frac{bF\left(j\right)-S\left(i\right)\left(j\right)}{bF\left(j\right)-wF\left(j\right)}+1\right)\right),condition\\ \mathit{min}\left(1-r\times \mathit{log}\left(\frac{bF\left(j\right)-S\left(i\right)\left(j\right)}{bF\left(j\right)-wF\left(j\right)}+1\right)\right),others\end{array}$$ (8)

where “condition” denotes slime mold individuals with fitness values ranking in the first half of the population, while “others” denotes slime mold individuals with fitness values ranking in the second half of the population. The variable “r" denotes a random number between 0 and 1. This allows slime mold individuals to create search vectors at any angle and search in any direction within the solution space. Consequently, their chances of finding the optimal solution increase. bF(j) denotes the best fitness value obtained for the j-th optimization objective during the current iteration process. wF(j) denotes the worst fitness value obtained for the j-th optimization objective during the current iteration process.

In this study, ACC and Popt denote two different slime mold individuals. After each iteration, ACC and Popt have different fitness values. To achieve synchronized optimization, different slime mold individuals must update their positions with a consistent oscillation frequency. Therefore, when the slime mold detects a high-quality food source, it can approach it faster while moving slowly toward areas with lower food concentrations. To standardize the weight parameter W, we implemented the following approach: we chose the highest value of the weight parameter among different slime mold individuals in the first half of the population, and the lowest value in the second half of the population.

• ii)Surrounding the food and capturing it

This process emulates the contraction of the vein network in the slime mold during the search. The biological oscillators produce stronger waves and increase cytoplasmic flow when a vein encounters a higher concentration of food. Equation (8) represents the interdependent relationship between the width of the vein and the concentration of the food being explored. The random variable “r" denotes the uncertainty in the pattern of vein contractions. The logarithm function is used to decrease the rate of change in values, thereby stabilizing the frequency of the contractions. The simulation demonstrates how the slime mold adjusts its search pattern based on the quality of the food. When the food concentration increases, the weight in its vicinity increases. However, if the food concentration is low, the weights in that area decrease, which causes a shift in the search direction and prompts the exploration of other regions. The formula for updating the position based on this principle is as follows:

$$X^{\ast }=\{\begin{array}{l}rand\times \left(ub-lb\right)+lb,rand<z\\ \underset{\forall c\in p}{X_b\left(t\right)+vb\left(W\times X_A\left(t\right)-X_B\left(t\right)\right)},r<c\\ \underset{\forall c\in p}{vc\times X\left(t\right)},r\ge c\end{array}$$ (9)

where “rand” and “r" denote arbitrary values generated between 0 and 1, and “ub” and “lb” denote the upper and lower boundaries of the search space, respectively. The parameter z denotes the position update parameter, which functions as a step size but is used for comparing random numbers instead of indicating the magnitude of each shift. In the context of multi-objective optimization tasks, “p" denotes a set. The second equation in the formula indicates that “r" is smaller than any value in the set.

• (2)Define the configuration space for hyperparameters and design the objective function to incorporate the capability to handle multiple objectives. In this study, maximizing the performance metrics ACC and Popt corresponds to the two optimization objectives. Taking the example of 10-fold cross-validation using an RF regressor, the pseudocode for the objective function is shown in Algorithm 2.

4. Experiment setup

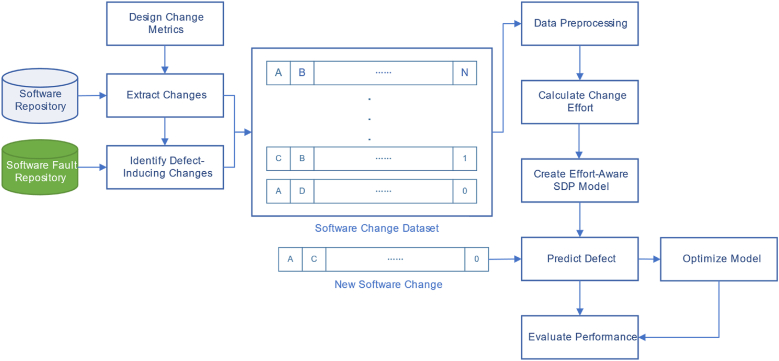
Fig. 2 illustrates the flowchart of the experimental process, which comprises the following six steps: constructing the change dataset, preprocessing the data, calculating change effort, constructing and optimizing the effort-aware JIT-SDP model, and evaluating performance.

Fig. 2.

Flowchart of the experimental process.

4.1. Studied projects and datasets

To create the change dataset, the first step is to formulate the change metrics. Subsequently, changes are derived from SCM using

change metrics, followed by identifying defects in the changes. The change metrics comprise product and process metrics that include.

14 features categorized into five dimensions: Diffusion, Size, Purpose, History, and Experience. Please refer to Table 1 (see Appendix for Table 1) for further information.

Table 1.

Summary of change measures ([11]).

Dimension	Name	Definition
Diffusion	NS	Number of modified subsystems
	ND	Number of modified directories
	NF	Number of modified files
	Entropy	Distribution of modified code across each file
Size	LA	Lines of code added
	LD	Lines of code deleted
	LT	Lines of code in a file before the change
Purpose	FIX	Whether or not the change is a defect fix
History	NDEV	The number of developers that changed the modified files
	AGE	The average time interval between the last and current change
	NUC	The number of unique changes to the modified files
Experience	EXP	Developer experience
	REXP	Recent developer experience
	SEXP	Developer experience on a subsystem

There are two types of change extraction depending on whether the SCM system supports transaction processing. For widely used SCM, such as Subversion and Git, which support transaction processing, all modifications are consolidated into a single transaction before submission. These changes can be directly extracted using the transaction ID. For older SCMs that do not support transaction processing, such as concurrent versions system (CVS), developers can submit only one file at a time. In these instances, we utilize the

method suggested by Zimmermann and Weiβgerber [59], which employs commonly used heuristic techniques to cluster interconnected single-file submissions into a change [10]. More precisely, we identify the activities performed by the same developer with identical log messages and within the same time frame as parts of the same change.

To detect whether changes induce defects, we employed the SZZ algorithm proposed by Śliwerski, Zimmermann, and Zeller and its variants [[60], [61], [62], [63]]. We used the datasets provided by Kamei et al. [11] and applied the SZZ algorithm for analysis. The SZZ algorithm and its variants typically involve four steps to determine whether changes induce defects: (1) Identifying potential defect-fixing.

changes by analyzing commit logs to determine if the change includes identifiers associated with defects and checking whether these identifiers are defined as defects in the bug tracking system. (2) Identifying faulty LOC. Different variants of SZZ employ different mapping strategies. The SZZ algorithm identifies all modified lines in defect-fixing changes as faulty lines. However, the meta-change aware SZZ (MA-SZZ) and refactoring aware SZZ (RA-SZZ) algorithms exclude nonsemantic lines, such as blank lines, comment lines, and lines that involve only code formatting modifications. They also exclude lines that involve code refactoring. (3) Confirming potential defect-inducing changes. When examining the history of changes, a search strategy is applied to identify potential defect-inducing changes. (4) Filtering out incorrectly identified changes. We adopted the filtering strategy proposed by Kim et al. [62], which excludes defect-inducing changes created after the defect report date. As suggested by Fan et al., suitable algorithms must be selected for various projects [18]. The statistical data for our research project are shown in Table 2 (see Appendix for Table 2).

Table 2.

Statistics of the studied projects.

Project	Clean Number	Bug Number	Average LOC/Change	Modified Files/Change
BUG	2924	1696	591.38	2.29
COL	3094	1361	114.24	6.2
JDT	30297	5089	437.72	3.87
PLA	54798	9452	354.7	3.76
MOZ	93126	5149	970.59	3.7
POS	15312	5119	853.34	4.46

4.2. Data preprocessing

To enhance the quality of the data, model performance, and generalizability, we applied the following data preprocessing techniques to all datasets.

• (1)Data cleaning: Data cleaning is the process of identifying and rectifying errors, missing values, outliers, and duplicates in a dataset. For the software change datasets, we used deletion methods to address these problems.
• (2)Handling data collinearity: Collinearity can lead to model instability and decrease interpretability. For the open-source datasets, we utilized the variance inflation factor method to detect collinearity and implement stepwise variable selection.
• (3)Skewness handling: Because most variables have highly skewed distributions, except for the “FIX” (Boolean variable), we applied a logarithmic transformation to the variables with high skewness. This was done to reduce skewness and minimize the influence of outliers.
• (4)Data normalization: To facilitate the comparison of SQA effort across various projects, we normalized the two feature variables (NF and Entropy) used to calculate the change in effort.
• (5)Handling data imbalance: Software change datasets often exhibit data imbalance, with a significantly smaller number of defect-inducing changes than clean changes. Imbalanced data can reduce the model performance [64,65]. To address this issue, we employed undersampling by randomly removing a specific number of instances of clean changes. This was done to balance the number of clean changes with changes that could introduce defects.

4.3. Regression model

RF, XGB, and LGBM are all ensemble learning algorithms based on decision trees. They share the following common features: (1) High accuracy and strong adaptability. (2) Robustness to outliers and missing values. (3) Learning and capturing nonlinear relationships between feature variables automatically make them suitable for analyzing complex data structures. (4) Parallel computing capabilities ensure high training efficiency when working with large-scale datasets. (5) Reducing the risks of overfitting and improving generalization capabilities by integrating multiple tree models. These features make them well suited for addressing JIT-SDP problems, such as handling highly imbalanced datasets, high-dimensional feature spaces, and complex nonlinear relationships. In addition to these shared characteristics, each algorithm also offers unique advantages. This study selects three algorithms to construct an effort-aware JIT-SDP model, providing valuable insights for both academic and industrial purposes.

4.4. Parameter settings

The hyperparameter settings for RF, XGB, LGBM, and multi-objective SMA are presented in Table 3 (see Appendix for Table 3).

Table 3.

Parameter settings.

Model	Name	Type	Range
RF	n_estimators	discrete	[10,300]
	max_depth	discrete	[5,20]
	max_features	discrete	[1,14]
	min_samples_split	discrete	[2,11]
	min_samples_leaf	discrete	[1,11]
	criterion	categorical	['squared_error’, ‘absolute_error']
XGB	n_estimators	discrete	[10,300]
	max_depth	discrete	[5,20]
	learning_rate	discrete	[0.01,0.3]
	subsample	discrete	[0.5,1]
	colsample_bytree	discrete	[0.5,1]
	gamma	discrete	[0,10]
	reg_alpha	discrete	[0,1]
	reg_lambda	discrete	[0,1]
LGBM	n_estimators	discrete	[10,300]
	max_depth	discrete	[5,20]
	learning_rate	discrete	[0.01,0.3]
	num_leaves	discrete	[20,100]
	min_data_in_leaf	discrete	[10,100]
	feature_fraction	discrete	[0.5,1]
	reg_alpha	discrete	[0,1]
	reg_lambda	discrete	[0,1]
Multi-Objective SMA	pop	discrete	[10,300]
	max_t	discrete	[10,200]

4.5. Performance evaluation metrics

Similar to previous studies [11,[14], [15], [16], [17], [18]], this study selects ACC and Popt as the performance evaluation metrics for the effort-aware JIT-SDP model. When calculating the ACC and Popt metrics, Kamei et al. used CC as a measure of change effort [11]. Subsequent studies have also employed this method [[15], [16], [17], [18]]. In contrast to this approach, this study adopts a weighted CC to quantify the effort required for changes. In addition to using ACC and Popt as evaluation metrics, we also consider the tuning time to assess the effectiveness of the multi-objective SMA.

ACC represents the proportion of defect-inducing changes that can be identified using only 20 % of the total effort. The calculation steps are as follows: (1) Calculate the effort of each defect change using weighted CC (the effort of clean changes is 0). (2) Take the reciprocal of the change effort as the target variable and divide the change dataset into training and testing sets. Train a new regressor, NR, using the training set. (3) Use NR to predict the testing set and obtain the prediction results R. (4) Sort the results in descending order. (5) Calculate the total effort of defect-inducing changes in sorted R, and determine the threshold point at which the cumulative effort represents 20 % of the total effort. Count the number of defect-inducing changes (n) and the total number of changes (m) within the threshold point that causes defects. The formula for calculating ACC is as follows: $\text{ACC}=n/m$.

The Popt is the metric used to evaluate the performance of the effort-aware JIT-SDP model by quantifying the gap between the current prediction model and the optimal model. As depicted in Fig. 3, the three curves represent the optimal, current prediction, and the worst models. The x-axis represents the ratio of current cumulative effort to total effort, while the y-axis represents the ratio of detected defect-inducing changes to total defect-inducing changes. When calculating Popt, the target variable (the inverse of change effort) plays a crucial role. Changes in the optimal and current prediction model curves are sorted in descending order based on this variable, whereas changes in the worst model curve are sorted in ascending order. Similar to Kamei et al.'s study [11,37], the formula for calculating Popt is as follows:

$$Popt\left(actual\right)=\frac{AUC\left(actual\right)-AUC\left(worst\right)}{AUC\left(optimal\right)-AUC\left(worst\right)}\text{,}$$ (10)

where AUC (optimal) denotes the area under the curve of the optimal model, AUC (worst) denotes the area under the curve of the worst model, AUC (actual) denotes the area under the curve of the current prediction model, and Popt(actual) denotes the calculated result, which ranges from 0 to 1.

Fig. 3.

Performance evaluation indicator Popt.

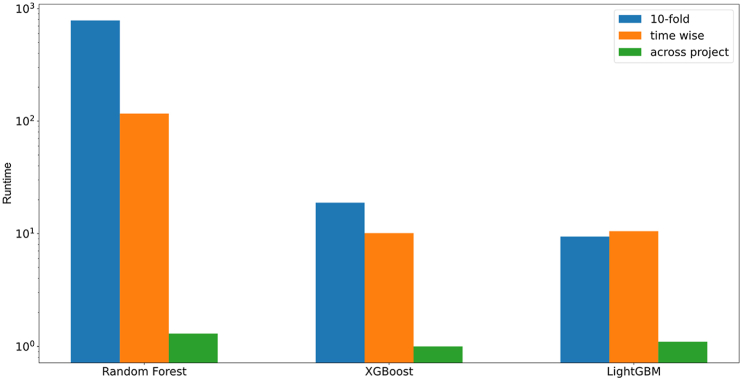
Model tuning time refers to the time spent by the optimization algorithms in finding the optimal combination of hyperparameters for a model under identical conditions. The tuning time is influenced by several factors, including the size of the dataset, the number of parameters, the parameter search space, the available computational resources, and the tuning strategies employed.

To comprehensively assess the performance differences of the three decision tree-based ensemble learning regression models after FI, we not only consider ACC and Popt but also incorporate model running time as an evaluation metric. Model running time refers

to the total time required to calculate ACC and Popt for various projects under different evaluation scenarios.

4.6. Model performance evaluation scenarios

Based on previous studies [11,[14], [15], [16], [17], [18]], we conducted performance evaluations of the WCMS method under three scenarios: 10 times 10-fold cross-validation, time-wise cross-validation, and across-project prediction. The WCMS method is divided into two stages. The first stage involves feature improvement, where we utilize weighted CC to estimate change effort, labeled as “FI.” The second stage focuses on optimizing the model structure using multi-objective SMA for hyperparameter tuning, labeled “MO.” We executed both stages for each project in each validation scenario to align with the WCMS approach.

10 times 10-fold cross-validation is a technique used for cross-validation within a single project. It randomly divides the dataset into 10 equal-sized subsets, with nine subsets used for training and one subset used for testing. This process is repeated ten times, with

each experiment selecting a different subset as the test set and the remaining subsets as the training set. In each experiment, the model is first trained on the training set and then used to make predictions on the test set. This process is repeated ten times, resulting in 100

predictions for each model. Finally, the predictions of the models are averaged. To expedite the optimization speed during the MO

phase, we directly partitioned the project dataset into training and testing sets. This partition was randomly done in a ratio of 9:1 based on the objective function of the multi-objective SMA. The model in question is fitted using the training set and then tested using the testing set for validation.

Time-wise cross-validation, which considers the chronological order of changes, is another method for conducting cross-validation within the same project. For each project, the changes are first sorted in chronological order based on their submission dates. All changes submitted within the same year and month are then grouped together. Assuming that there are n groups in the project, we use the following approach for prediction. Because the open-source datasets used span a considerable timeframe, we must ensure that the training set contains a sufficient number of instances. To achieve this, we construct model M using data from six consecutive months and then utilize model M to predict data for the seventh month. The open-source datasets used in this study are all large software projects with development cycles that exceed six months. This makes the approach more relevant to real-world scenarios.

Across-project prediction is a validation method used across various projects. We use a model trained on one project (i.e., the training set) to predict data from another project (i.e., the testing set). Assuming that we have n projects, each project is used as a training set to construct the model. For each project, we use this model to predict the remaining n-1 projects. Therefore, each stage produces n × (n-1) prediction results. In this study, the result is 2 × 6 × (6 − 1) = 60 predicted values.

4.7. Baseline methods

We compared the WCMS approach with two categories of state-of-the-art effort-aware JIT-SDP methods: supervised and unsupervised models. We evaluated their performance using ACC and Popt as the metrics. The supervised models included EALR [11], MULTI [17], and DEJIT [18]. For unsupervised models, we utilized LT and AGE, which were the best-performing methods in the study by Yang et al. [11], along with CCUM [13]. We excluded OneWay [15], CBS + [16], MMJC [14], and EATT [22] from the benchmark methods because they have different research objectives, methods, and evaluation metrics.

To evaluate the effectiveness of the multi-objective SMA, we compared it with state-of-the-art multi-objective optimization algorithms, namely MOSA [54] and ENS-MOEA/D [47]. Performance evaluation metrics included ACC, Popt, and model tuning time.

4.8. Research questions

To validate the effectiveness of the WCMS, we formulated the following four research questions.

• (1)How does WCMS perform compared with the baseline methods in the cross-validation scenario?
• (2)How does WCMS perform compared with the baseline methods in the time-wise cross-validation scenario?
• (3)How does WCMS perform compared with the baseline methods in the across-project prediction scenario?
• (4)How does our proposed multi-objective SMA perform in solving the effort-aware JIT-SDP problem compared with the baseline methods?

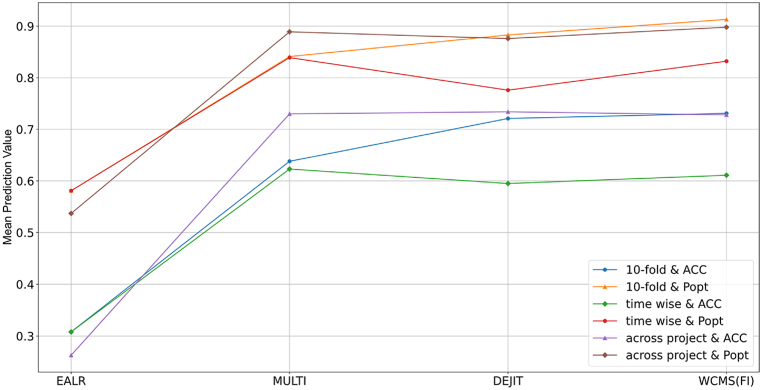
In this study, we improved the feature variables and SDP model for JIT-SDP to enhance its performance. We compare the results of the two aspects separately.

4.9. Statistical test

The Scott-Knot Effect Size Difference (SK-ESD) test is a mean comparison approach [66]. It is an alternative approach to the Scott-Knott test [67], which identifies the magnitude of the difference between each mean within a group and between groups. The SK-ESD test ranks and clusters the methods into significantly different groups, where the methods in the same group have no significant differences whereas those in distinct groups have significant differences. The advantage of the SK-ESD test is that it results in completely distinct groups without overlapping.

In this study, we apply the SK-ESD test to determine the magnitude difference between the proposed method and baseline methods. The SK-ESD test is employed to cluster the methods into distinct groups at the significance level of 0.05 using the hierarchical clustering algorithm. Cohen's d is used to measure effect size. The methods in the same rank have no statistically significant differences, whereas the methods in different ranks have statistically significant differences.

5. ExperimenTal results

In this section, we address our research questions and present the experimental results.

RQ1

How does WCMS perform compared with the baseline methods in the cross-validation scenario?

To provide a comprehensive evaluation, we conducted 10 iterations of 10-fold cross-validation to compare WCMS with state-of-the-art benchmark methods. This approach enabled us to obtain more accurate results. The results of the comparisons for ACC are presented in Table 4 (see Appendix for Table 4), while the results for Popt are presented in Table 5 (see Appendix for Table 5). The best values for each row are highlighted in bold.

Table 4.

WCMS vs. State-of-the-Art Methods in a 10-fold Cross-Validation Scenario (ACC).

Project	Baseline Methods						RF		XGB		LGBM
	EALR	MULTI	DEJIT	LT	AGE	CCUM	FI	MO	FI	MO	FI	MO
BUG	0.286	0.696	0.769	0.477	0.413	0.785	0.618	0.639	0.553	0.619	0.518	0.619
COL	0.400	0.696	0.786	0.626	0.687	0.812	0.745	0.798	0.592	0.761	0.498	0.771
JDT	0.323	0.626	0.715	0.523	0.476	0.745	0.735	0.762	0.531	0.760	0.536	0.708
PLA	0.305	0.684	0.605	0.459	0.385	0.765	0.716	0.781	0.526	0.769	0.575	0.747
MOZ	0.180	0.511	0.748	0.375	0.244	0.605	0.817	0.832	0.541	0.859	0.475	0.821
POS	0.356	0.613	0.700	0.519	0.464	0.705	0.756	0.808	0.590	0.785	0.614	0.812
MEAN	0.308	0.638	0.721	0.497	0.445	0.736	0.731	0.770	0.556	0.759	0.536	0.746

Table 5.

WCMS vs. State-of-the-Art Methods in a 10-fold Cross-Validation Scenario (Popt).

Project	Baseline Methods						RF		XGB		LGBM
	EALR	MULTI	DEJIT	LT	AGE	CCUM	FI	MO	FI	MO	FI	MO
BUG	0.594	0.883	0.924	0.754	0.748	0.929	0.887	0.897	0.828	0.846	0.813	0.868
COL	0.619	0.880	0.909	0.842	0.856	0.937	0.918	0.944	0.773	0.943	0.727	0.929
JDT	0.590	0.829	0.874	0.781	0.747	0.885	0.905	0.922	0.745	0.919	0.781	0.899
PLA	0.583	0.853	0.812	0.748	0.707	0.893	0.908	0.937	0.743	0.927	0.813	0.919
MOZ	0.498	0.757	0.886	0.644	0.621	0.812	0.932	0.952	0.774	0.958	0.787	0.929
POS	0.6	0.843	0.892	0.805	0.768	0.902	0.930	0.948	0.778	0.939	0.820	0.948
MEAN	0.581	0.841	0.883	0.762	0.741	0.893	0.913	0.933	0.774	0.922	0.790	0.915

Table 4 shows that the WCMS method performs better than the current state-of-the-art methods during the MO phase regarding the average ACC value. Furthermore, when the RF regression model is utilized, the average value of the FI phase surpasses that of the LT, AGE, EALR, and DEJIT methods and corresponds to the CCUM method. Although XGB and LGBM outcompete LT, AGE, and EALR, their performances are lower than those of the DEJIT and CCUM methods. The WCMS method is optimal for JDT, PLA, MOZ, and POS projects with the best results. The COL project produced results comparable to those of the DEJIT and CCUM methods. However, it did not achieve the best performance of the DEJIT and CCUM methods in the BUG project. During the FI phase, RF outperformed XGB and LGBM, while they demonstrated similar results during the MO phase.

According to the results presented in Table 5, the WCMS method outperforms the state-of-the-art methods in terms of achieving higher average Popt values during the MO phase. Additionally, when using the RF regression model, it outperforms the state-of-the-art methods in terms of the average values during the FI phase. Although XGB and LGBM outperform the LT, AGE, and EALR methods in the FI phase, they lag slightly behind the top-performing DEJIT and CCUM methods. The WCMS method yields optimal

results in the COL, JDT, PLA, MOZ, and POS projects. Moreover, the BUG project performs comparably with the MULTI method but lags slightly behind the top-performing DEJIT and CCUM methods. However, it surpasses the EALR, LT, and AGE methods. The RF model outperforms the XGB and LGBM models during the FI phase, while the XGB and LGBM models consistently produce similar results throughout this phase.

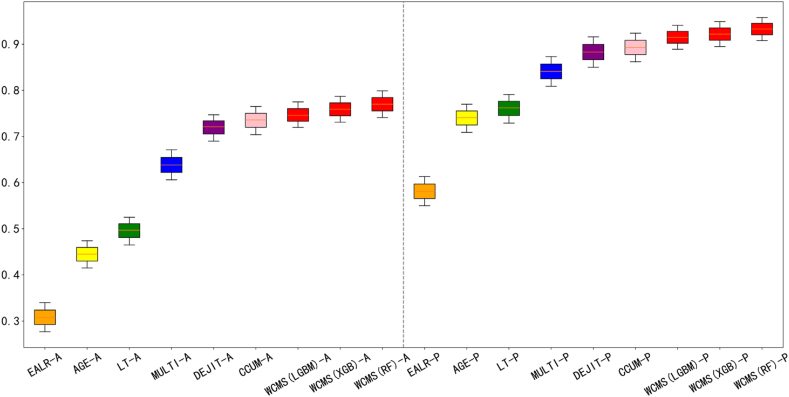
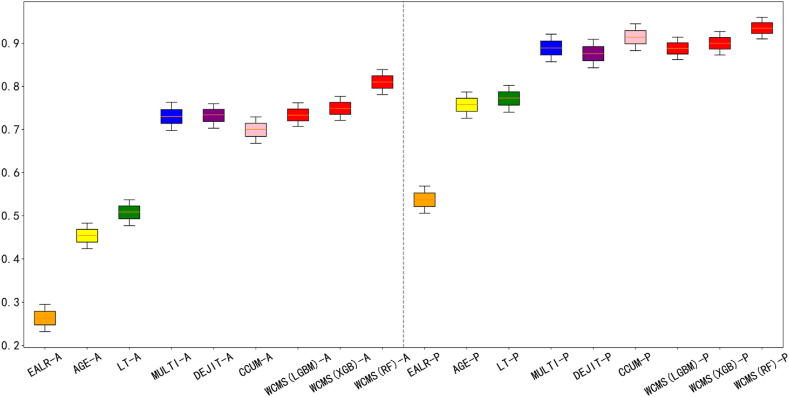
To better evaluate the performance of different methods in the 10-fold cross-validation scenario, we conducted an SK-ESD test using the experimental results. The comparison results are shown in Fig. 4. The figure is divided into two parts, with the left side representing the ACC indicator and the right side representing the Popt indicator. Different methods are depicted in various colors, with our method shown in red. The ACC and Popt indicators are arranged in descending order on the chart. Consequently, the methods are listed in descending order based on their ACC and Popt indicator values as follows: WCMS(RF), WCMS(XGB), WCMS(LGBM), CCUM, DEJIT, MULTI, LT, AGE, and EALR. The results in the chart show that in both scenarios, the proposed methods achieved the highest average ranking. This suggests that in the cross-validation application scenario, the performance of the proposed methods exceeds that of the baseline methods. Among the proposed methods, RF demonstrated the most promising performance, followed by XGB, while LGBM showed the least promising performance.

RQ2

How does WCMS perform compared with the baseline methods in the time-wise cross-validation scenario?

Fig. 4.

SK-ESD test for 10 times 10-fold cross-validation.

To address this question, we conducted a comparison between the WCMS and state-of-the-art benchmark methods using time-wise cross-validation. The comparison results for ACC are presented in Table 6 (see Appendix for Table 6), and those for Popt are shown in Table 7 (see Appendix for Table 7). The best values for each row are highlighted in bold.

Table 6.

WCMS vs. State-of-the-Art Methods in Time-Wise Cross-Validation Scenario (ACC).

Project	Baseline Methods						RF		XGB		LGBM
	EALR	MULTI	DEJIT	LT	AGE	CCUM	FI	MO	FI	MO	FI	MO
BUG	0.286	0.598	0.552	0.449	0.375	0.697	0.475	0.871	0.446	0.574	0.417	0.962
COL	0.400	0.686	0.636	0.440	0.568	0.720	0.584	0.840	0.551	0.778	0.444	0.909
JDT	0.323	0.625	0.592	0.452	0.408	0.637	0.642	0.804	0.573	0.763	0.443	0.750
PLA	0.305	0.688	0.684	0.432	0.429	0.704	0.659	0.806	0.550	0.700	0.429	0.748
MOZ	0.180	0.549	0.545	0.363	0.280	0.582	0.696	0.816	0.605	0.713	0.361	0.833
POS	0.356	0.592	0.560	0.432	0.426	0.615	0.609	0.929	0.611	0.780	0.428	0.824
MEAN	0.308	0.623	0.595	0.428	0.414	0.659	0.611	0.844	0.556	0.718	0.420	0.838

Table 7.

WCMS vs. State-of-the-Art Methods in Time-Wise Cross-Validation Scenario (Popt).

Project	Baseline Methods						RF		XGB		LGBM
	EALR	MULTI	DEJIT	LT	AGE	CCUM	FI	MO	FI	MO	FI	MO
BUG	0.594	0.838	0.709	0.721	0.661	0.909	0.771	0.988	0.756	0.841	0.737	0.986
COL	0.619	0.885	0.825	0.732	0.786	0.907	0.824	0.929	0.785	0.863	0.727	0.975
JDT	0.590	0.828	0.782	0.709	0.685	0.837	0.842	0.923	0.778	0.865	0.691	0.861
PLA	0.583	0.859	0.835	0.717	0.709	0.868	0.860	0.931	0.772	0.869	0.695	0.841
MOZ	0.498	0.786	0.737	0.651	0.638	0.802	0.866	0.926	0.796	0.882	0.675	0.949
POS	0.600	0.837	0.768	0.742	0.731	0.866	0.828	0.977	0.809	0.888	0.688	0.919
MEAN	0.581	0.839	0.776	0.712	0.702	0.865	0.832	0.946	0.783	0.868	0.702	0.922

Based on the results in Table 6, the WCMS method has a higher average ACC during the MO phase than the state-of-the-art methods. During the FI phase, the RF method has slightly lower average values than the top-performing CCUM and MULTI methods but performs better than the EALR, DEJIT, LT, and AGE methods. XGB has slightly lower average values than the MULTI, DEJIT, and CCUM methods but performs better than the LT, AGE, and EALR methods. LGBM has higher average values than the AGE and EALR methods, which is similar to the LT method, but slightly lower than the DEJIT and CCUM methods. During the MO phase, RF and LGBM achieve the best results among the six projects, while XGB performs the best in the COL, JDT, MOZ, and POS projects. In the BUG project, XGB performs slightly worse than the CCUM method, similar to the MULTI method, but better than

the EALR, DEJIT, LT, and AGE methods. In the PLA project, XGB performs similarly to the CCUM method but outperforms the other methods. RF performs the best during the FI phase, followed by XGB, with LGBM performing the worst.

Based on the results in Table 7, the WCMS method demonstrates a higher average Popt value during the MO phase compared to the state-of-the-art methods. During the FI phase, RF performs slightly worse than the CCUM method, but it is comparable to the MULTI method and superior to the AGE, DEJIT, EALR, and LT methods. The average value of XGB is lower than that of the CCUM and MULTI methods but higher than that of the AGE, DEJIT, EALR, and LT methods. LGBM yields a higher average value compared to the EALR approach and performs similarly to the AGE and LT methods. However, it is inferior to the CCUM, MULTI, and DEJIT methods. During the MO phase, RF produces the most optimal outcomes for all six projects. XGB performs most effectively in the JDT, PLA, MOZ, and POS projects, while LGBM yields the best results in the remaining five projects, except for PLA. RF leads during the FI phase, followed by XGB, with LGBM performing the worst.

To better evaluate the performance of the various methods under the time-wise cross-validation scenario, we conducted an SK-ESD test based on the experimental results. The comparison results are shown in Fig. 5. The figure is divided into two parts, with the left side representing the ACC indicator and the right side representing the Popt indicator. Different methods are depicted in various colors, with our method shown in red. The ACC and Popt indicators are arranged in descending order on the chart. Consequently, the methods are listed in descending order based on their ACC and Popt indicator values as follows: WCMS(RF), WCMS(XGB), WCMS(LGBM), CCUM, DEJIT, MULTI, LT, AGE, and EALR. The results depicted in the chart show that in both scenarios, the proposed methods attained the highest average ranking. This implies that in the time-wise cross-validation application scenario, the performance of the proposed methods surpasses that of the baseline methods. Among the proposed methods, RF demonstrated the most promising performance, whereas LGBM and XGB exhibited the least promising performance.

RQ3

How does WCMS perform compared to the baseline methods in the across-project prediction scenario?

Fig. 5.

SK-ESD test for time-wise cross-validation.

To address this question, we conducted a comparison between WCMS and state-of-the-art baseline methods in the context of across-project predictions. The comparison results for ACC are presented in Table 8 (see Appendix for Table 8), while the comparison results

Table 8.

WCMS vs. State-of-the-Art Methods Across Project Scenarios (ACC).

Train	Test	Baseline Methods						RF		XGB		LGBM
		EALR	MULTI	DEJIT	LT	AGE	CCUM	FI	MO	FI	MO	FI	MO
BUG	COL	0.497	0.716	0.661	0.641	0.702	0.836	0.737	0.851	0.526	0.779	0.577	0.730
	JDT	0.281	0.773	0.698	0.582	0.490	0.761	0.691	0.782	0.422	0.691	0.442	0.712
	PLA	0.429	0.772	0.768	0.494	0.427	0.774	0.684	0.793	0.489	0.721	0.423	0.675
	MOZ	0.219	0.763	0.605	0.367	0.240	0.605	0.728	0.775	0.515	0.681	0.393	0.641
	POS	0.349	0.765	0.726	0.533	0.432	0.726	0.761	0.786	0.399	0.549	0.393	0.731
COL	BUG	0.336	0.821	0.790	0.435	0.432	0.790	0.535	0.823	0.438	0.657	0.376	0.684
	JDT	0.113	0.828	0.760	0.582	0.490	0.761	0.688	0.836	0.502	0.731	0.539	0.772
	PLA	0.239	0.824	0.770	0.494	0.427	0.774	0.681	0.832	0.540	0.749	0.478	0.641
	MOZ	0.148	0.830	0.591	0.367	0.240	0.605	0.800	0.851	0.640	0.819	0.436	0.749
	POS	0.167	0.825	0.726	0.533	0.432	0.726	0.672	0.836	0.589	0.77	0.481	0.725
JDT	BUG	0.376	0.757	0.789	0.435	0.432	0.790	0.561	0.822	0.428	0.584	0.469	0.673
	COL	0.378	0.721	0.833	0.641	0.702	0.836	0.779	0.853	0.503	0.775	0.594	0.761
	PLA	0.277	0.733	0.775	0.494	0.427	0.774	0.716	0.796	0.524	0.725	0.556	0.754
	MOZ	0.168	0.740	0.605	0.367	0.240	0.605	0.815	0.817	0.352	0.755	0.637	0.796
	POS	0.299	0.749	0.727	0.533	0.432	0.726	0.754	0.763	0.332	0.659	0.639	0.804
PLA	BUG	0.367	0.768	0.787	0.435	0.432	0.790	0.532	0.792	0.428	0.641	0.351	0.715
	COL	0.363	0.763	0.760	0.641	0.702	0.836	0.778	0.863	0.479	0.636	0.514	0.784
	JDT	0.152	0.772	0.760	0.582	0.490	0.761	0.719	0.852	0.422	0.672	0.490	0.737
	MOZ	0.168	0.780	0.605	0.367	0.240	0.605	0.811	0.814	0.425	0.709	0.521	0.794
	POS	0.230	0.780	0.719	0.533	0.432	0.726	0.515	0.812	0.432	0.571	0.312	0.685
MOZ	BUG	0.350	0.592	0.790	0.435	0.432	0.790	0.534	0.833	0.522	0.644	0.473	0.694
	COL	0.247	0.572	0.836	0.641	0.702	0.836	0.742	0.852	0.528	0.739	0.499	0.745
	JDT	0.057	0.587	0.696	0.582	0.490	0.761	0.704	0.786	0.486	0.646	0.512	0.785
	PLA	0.173	0.580	0.770	0.494	0.427	0.774	0.69	0.783	0.502	0.724	0.515	0.750
	POS	0.135	0.584	0.726	0.533	0.432	0.726	0.722	0.767	0.467	0.723	0.474	0.794
POS	BUG	0.351	0.711	0.782	0.435	0.432	0.790	0.556	0.822	0.423	0.687	0.385	0.711
	COL	0.439	0.690	0.828	0.641	0.702	0.836	0.748	0.865	0.578	0.703	0.451	0.701
	JDT	0.159	0.703	0.762	0.582	0.490	0.761	0.699	0.786	0.466	0.742	0.472	0.719
	PLA	0.261	0.700	0.774	0.494	0.427	0.774	0.677	0.781	0.562	0.752	0.508	0.745
	MOZ	0.159	0.706	0.598	0.367	0.240	0.605	0.793	0.815	0.597	0.780	0.565	0.790
	MEAN	0.263	0.73	0.734	0.509	0.454	0.749	0.694	0.810	0.484	0.700	0.483	0.733

for Popt are shown in Table 9 (see Appendix for Table 9). The best values for each row are highlighted in bold.

Table 9.

WCMS vs. State-of-the-Art Methods Across Project Scenarios (Popt).

Train	Test	Baseline Methods						RF		XGB		LGBM
		EALR	MULTI	DEJIT	LT	AGE	CCUM	FI	MO	FI	MO	FI	MO
BUG	COL	0.701	0.894	0.737	0.858	0.868	0.948	0.903	0.956	0.774	0.943	0.754	0.805
	JDT	0.592	0.923	0.823	0.815	0.769	0.897	0.888	0.933	0.678	0.935	0.687	0.920
	PLA	0.695	0.922	0.884	0.770	0.740	0.899	0.883	0.928	0.739	0.893	0.714	0.804
	MOZ	0.563	0.918	0.813	0.660	0.622	0.813	0.897	0.935	0.713	0.935	0.607	0.754
	POS	0.603	0.918	0.907	0.810	0.762	0.908	0.925	0.929	0.682	0.828	0.636	0.805
COL	BUG	0.633	0.945	0.932	0.726	0.758	0.932	0.871	0.962	0.749	0.962	0.714	0.845
	JDT	0.418	0.945	0.882	0.815	0.769	0.897	0.877	0.951	0.741	0.882	0.753	0.905
	PLA	0.506	0.944	0.878	0.770	0.740	0.899	0.881	0.963	0.736	0.926	0.712	0.838
	MOZ	0.476	0.946	0.768	0.660	0.622	0.813	0.926	0.959	0.777	0.887	0.720	0.903
	POS	0.426	0.943	0.876	0.810	0.762	0.908	0.881	0.947	0.774	0.901	0.681	0.888
JDT	BUG	0.674	0.895	0.925	0.726	0.758	0.932	0.862	0.944	0.677	0.867	0.812	0.972
	COL	0.564	0.876	0.937	0.858	0.868	0.948	0.927	0.956	0.711	0.959	0.766	0.860
	PLA	0.555	0.883	0.899	0.770	0.740	0.899	0.903	0.904	0.745	0.921	0.802	0.957
	MOZ	0.502	0.885	0.814	0.660	0.622	0.813	0.925	0.927	0.658	0.879	0.800	0.941
	POS	0.514	0.891	0.906	0.810	0.762	0.908	0.93	0.930	0.696	0.900	0.83	0.984
PLA	BUG	0.685	0.895	0.929	0.726	0.758	0.932	0.892	0.952	0.777	0.941	0.764	0.986
	COL	0.564	0.889	0.857	0.858	0.868	0.948	0.931	0.955	0.700	0.866	0.791	0.963
	JDT	0.458	0.897	0.896	0.815	0.769	0.897	0.908	0.909	0.720	0.862	0.789	0.943
	MOZ	0.498	0.899	0.814	0.660	0.622	0.813	0.936	0.937	0.688	0.893	0.717	0.903
	POS	0.478	0.899	0.898	0.810	0.762	0.908	0.879	0.913	0.691	0.895	0.755	0.933
MOZ	BUG	0.619	0.806	0.932	0.726	0.758	0.932	0.885	0.939	0.789	0.963	0.791	0.879
	COL	0.482	0.793	0.948	0.858	0.868	0.948	0.905	0.963	0.708	0.939	0.682	0.838
	JDT	0.367	0.803	0.807	0.815	0.769	0.897	0.892	0.906	0.713	0.875	0.743	0.895
	PLA	0.414	0.799	0.889	0.770	0.740	0.899	0.895	0.911	0.734	0.960	0.757	0.840
	POS	0.382	0.800	0.908	0.810	0.762	0.908	0.919	0.925	0.759	0.953	0.806	0.935
POS	BUG	0.629	0.902	0.913	0.726	0.758	0.932	0.847	0.942	0.727	0.964	0.718	0.846
	COL	0.617	0.884	0.929	0.858	0.868	0.948	0.905	0.965	0.742	0.948	0.700	0.866
	JDT	0.459	0.897	0.888	0.815	0.769	0.897	0.889	0.912	0.760	0.957	0.740	0.869
	PLA	0.544	0.894	0.897	0.770	0.740	0.813	0.885	0.899	0.767	0.895	0.760	0.866
	MOZ	0.497	0.898	0.785	0.660	0.753	0.899	0.916	0.923	0.762	0.892	0.753	0.894
	MEAN	0.537	0.889	0.876	0.773	0.758	0.900	0.899	0.935	0.730	0.914	0.742	0.888

Based on the findings presented in Table 8, RF demonstrates superior ACC performance during the MO phase compared with all other benchmark methods. Moreover, XGB displays better average performance than LT, AGE, and EALR. However, it is slightly less effective than the DEJIT, MULTI, and CCUM methods. LGBM performs better than the LT, AGE, and EALR methods on average, and it performs similarly to the DEJIT, MULTI, and CCUM methods. Furthermore, the performance of the RF method was comparable to those of the DEJIT, MULTI, and CCUM methods during the FI phase, but it outperformed the LT, AGE, and EALR methods in the same phase. During both the FI and MO phases, RF outperforms XGB and LGBM.

Based on the results in Table 9, during the MO phase, RF demonstrates the best performance in terms of the Popt value, surpassing all the benchmark methods. Additionally, the average Popt value of XGB and LGBM outperforms those of the LT, AGE, EALR, and DEJIT methods and is comparable to those of the MULTI and CCUM methods. During the FI phase, the average performance of RF

is comparable to that of the CCUM method but better than those of the other methods. RF outperforms XGB and LGBM during both the FI and MO phases.

To better evaluate the performance of the different methods in the across-project prediction scenario, we conducted an SK-ESD test based on the experimental results. The comparison results are shown in Fig. 6. The figure is divided into two parts, with the left side representing the ACC indicator and the right side representing the Popt indicator. Different methods are depicted in various colors, with our method shown in red. The results depicted in the chart show that in both scenarios, the RF of the proposed methods attained the highest average ranking. However, the XGB and LGBM of the proposed methods exhibited slightly lower performance than CCUM. This implies that in the across-project prediction application scenario, the performance of the proposed methods surpasses those of most baseline methods. Among the proposed methods, RF demonstrated the most promising performance, whereas LGBM and XGB demonstrated the least promising performance.

RQ4

How does our proposed multi-objective SMA perform while solving the effort-aware JIT-SDP problem compared with the baseline methods?

Fig. 6.

SK-ESD test under across-project prediction.

To address this question, we applied the XGB and LGBM methods and conducted experiments using a 10-fold cross-validation approach. First, we measured the experimental results (ACC and Popt) of both models during the FI phase. Then, we employed multi-objective SMA, MOSA, and ENS-MOEA/D to optimize the hyperparameters of the models. We evaluated the experimental results during the MO phase and recorded the tuning duration for each optimization algorithm.

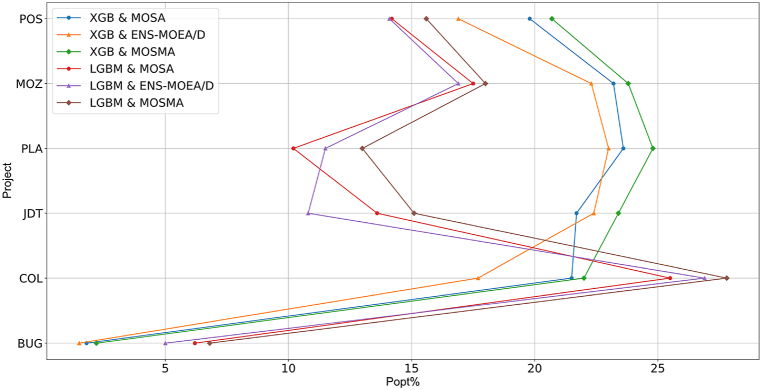
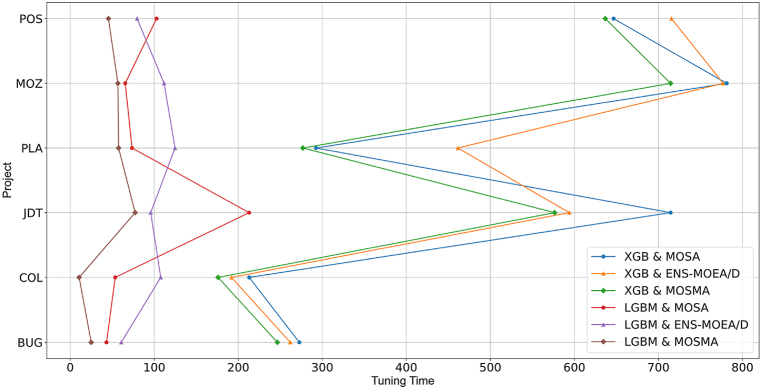
To compare the performance of the three optimization algorithms, we selected three performance metrics: the improvement rate of ACC (ACC%), the improvement rate of Popt (Popt%), and the tuning time (in seconds). The calculation formula for ACC% is $ACC\%=\left(AC{C}_{MO}-AC{C}_{FI}\right)/AC{C}_{FI}$, and the calculation formula for Popt% is $Popt\%=\left(Pop{t}_{MO}-Pop{t}_{FI}\right)/Pop{t}_{FI}$. The performance metrics are calculated based on the average values of six projects. The results of the experimental comparison are shown in Table 10 (see Appendix for Table 10). From the table, we can observe that the multi-objective SMA demonstrates superior performance in terms of the improvement rate of ACC, Popt, and tuning time under a 10-fold cross-validation scenario.

Table 10.

MOSMA vs. MOSA and ENS-MOEA/D on HPO in a 10-fold Cross-Validation Scenario.

	XGB									LGBM
	MOSA			ENS-MOEA/D			MOSMA			MOSA			ENS-MOEA/D			MOSMA
Project	ACC%	Popt%	TT	ACC%	Popt%	TT	ACC%	Popt%	TT	ACC%	Popt%	TT	ACC%	Popt%	TT	ACC%	Popt%	TT
BUG	3	1.8	273	2.6	1.5	262	11.9	2.2	247	18.7	6.2	43	18.5	5	61	19.5	6.8	25
COL	27.2	21.5	213	27.7	17.7	192	28.5	22	176	52.9	25.5	54	45.2	26.9	108	54.8	27.8	11
JDT	39.9	21.7	715	34.9	22.4	594	43.1	23.4	577	31.6	13.6	213	28.2	10.8	96	32.1	15.1	77
PLA	44.7	23.6	293	42.6	23	461	46.2	24.8	277	29.8	10.2	74	29.6	11.5	127	29.9	13	58
MOZ	58.1	23.2	781	58.5	22.3	777	58.8	23.8	716	67.5	17.5	66	63.5	16.9	112	72.8	18	57
POS	29.2	19.8	647	29.3	16.9	716	33.1	20.7	636	27.3	14.2	102.7	23.6	14.1	80	32.2	15.6	46
MEAN	33.7	18.6	487	32.6	17.3	500	36.9	19.5	438	38	14.5	91.9	34.8	14.2	97	40.2	16.1	46

6. Discussions

6.1. Evaluating the performance of weighted code churn as a representation of the SQA effort for changes

Kamei et al. were the first to introduce effort metrics in the field of JIT-SDP [11]. The purpose of introducing these metrics is to identify more defect-inducing changes within limited resources. Koru and Menzies et al. found that the relationship between module size and defect count is not linear but logarithmic [68,69]. As the module size increases, the rate of growth in fault proneness decreases. However, smaller modules are more likely to have defects and should be checked first. Inspired by the research, Kamei et al. transferred this idea to the field of JIT-SDP [11]. To construct the EALR model, they represented the CC of defect-inducing changes as effort and used its reciprocal (defect density) as the target variable. The optimal results were obtained when the predicted outcomes were sorted in descending order of defect density, and the worst results were obtained when sorted in ascending order of defect density.

Research and practice have shown that effort is not always proportional to LOC. Therefore, representing effort with CC is not scientifically sound. To standardize change efforts, this study developed a weighted CC approach. When identifying, verifying, and resolving changes that cause defects, the effort is primarily associated with feature variables, such as CC, NF, and Entropy. This study determined that the variables NF and Entropy significantly affect the complexity of tasks, such as change detection, verification, and correction. Therefore, we use two feature variables to represent the level of difficulty of changes, which are comprehensively outlined in Subsection 3.1.

Based on the statistical analysis presented in Section V, the statistical information of the prediction results of our method (RF) is shown in Table 11 (see Appendix for Table 11). Based on the results in Table 11, we found that our method can detect an average of 67.9 % of defect-inducing changes and has an average value of 88.1 % for Popt when 20 % of the effort is used. Furthermore, the results are consistent. Our method holds a high reference value for both academic and industry domains.

Table 11.

Statistical information of prediction results of WSMS (FI).

	10-Fold		Time Wise		Across Project		Total
	ACC	Popt	ACC	Popt	ACC	Popt	ACC	Popt
Max	0.817	0.932	0.696	0.866	0.815	0.936	0.817	0.937
Min	0.618	0.887	0.475	0.771	0.515	0.847	0.475	0.771
Mean	0.731	0.913	0.611	0.832	0.694	0.899	0.679	0.881
STD	0.065	0.017	0.077	0.034	0.087	0.022	0.076	0.024

To further evaluate the performance of our method, we investigated the correlation between the project size, the number of clean changes, the number of defect-inducing changes, the defect rate, and the predicted results (RF) within the project. The results are shown in Table 12 (see Appendix for Table 12).

Table 12.

Correlation analysis of prediction results of WSMS(FI).

	10-Fold		Time Wise
	ACC	Popt	ACC	Popt
Project Size	0.612	0.48	0.827	0.803
Clean Num	0.603	0.46	0.81	0.792
Bug Num	1	0.202	0.684	0.717
Bug Ratio	−0.673	−0.51	−0.938	−0.909

Based on the results presented in Table 12, we observed a positive correlation between ACC and Popt with project size, the number of clean changes, and the number of defect-inducing changes in both 10-fold cross-validation and time-wise cross-validation scenarios. However, there was a negative correlation with the defect rate. Moreover, the positive and negative correlations of Popt were not statistically significant in the 10-fold cross-validation scenario. This can be attributed to the relatively high average Popt value of 0.913 across the six projects. These results indicate that our method performs better as the size of the project dataset increases. Furthermore, this proves that our method has a better generalization ability.

To evaluate the performance of our method, we compared it with three benchmark-supervised methods: EALR, MULTI, and DEJIT. We used the RF regression model to compare the average predicted values of these methods in three scenarios: 10-fold cross-validation, time-wise cross-validation, and across-project prediction. The comparison results are presented in Fig. 7. The figure illustrates the comparison results of the WSMS (FI) method with the baseline methods. As depicted in the figure, the WCWS method consistently outperforms the other methods in terms of ACC and Popt when evaluated using the 10-fold cross-validation scenario. Furthermore, in the time-wise cross-validation scenario, the WCWS method performs similarly to the MULTI method but outperforms the EALR and DEJIT methods. In the across-project prediction scenario, the WCWS method demonstrates comparable ACC performance to those of the MULTI and DEJIT methods while showing superior Popt performance compared with other methods. Overall, our WCWS method outperforms the supervised methods and is recommended as a benchmark for future studies.

Fig. 7.

Comparison of predictive results for WSMS (FI) with baseline methods.

We observed the unusual performance of the BUG project across the three validation scenarios. In both the 10-fold cross-validation and time-wise cross-validation scenarios, the ACC and Popt showed the worst performance. The prediction results were also the worst when the BUG project was used as the testing project in the across-project prediction scenario. Upon analyzing the dataset of this project, we found that it had a small size and a high defect rate. It comprised a total of 4620 changes with a defect rate of 37 %.

Compared with other projects, this dataset showed a smaller size and a higher defect rate. Based on the findings of the previous correlation analysis, these two factors could be the primary causes of this outcome. Additionally, we speculate that the BUG dataset might contain noise or mislabeled data.

6.2. Evaluating the performance of multi-objective SMA for HPO

Slime mold possesses numerous remarkable survival and adaptive abilities, including locomotion, aggregation, learning, memory, cooperation, and collaboration. These unique features have attracted significant interest from the academic community, leading to the widespread use of slime mold as a model organism in various research areas, such as animal behavior, collective intelligence, and complex adaptation [[70], [71], [72]]. Taking advantage of these capabilities, Li et al. introduced SMA in 2020 [22]. This algorithm has undergone extensive validation of various benchmark problems across various search domains. It has been compared to high-performing MOAs, such as particle swarm optimization (PSO) [73] and differential evolution (DE) [74], as well as recent algorithms, such as whale optimization algorithm (WOA) [75] and adaptive genetic algorithm (AGA) [76]. SMA has consistently demonstrated exceptional performance in optimization by effectively avoiding local optima and converging rapidly. However, it is important to note that SMA is currently limited to single-objective optimization problems and cannot address multi-objective optimization problems simultaneously.

To enhance the efficiency of effort-aware JIT-SDP, we set the objective of maximizing both ACC and Popt simultaneously during the MO phase. To achieve this goal, we initially enhanced SMA to enable it to optimize multiple objectives. Subsection 3.2 presents the specific procedures for enhancement. We subsequently implemented the improved multi-objective SMA to optimize the model structure.

Based on the experimental results in Section V, the improvement rates of ACC and Popt optimization using multi-objective SMA are shown in Table 13 (see Appendix for Table 13). From the results in Table 13, two critical key points can be observed. First, the multi-objective SMA illustrates robust HPO capabilities when incorporated with three ensemble learning regression models: RF, XGB, and LGBM. The efficacy of the algorithm is indicated by an average improvement rate of 28.3 % for both ACC and Popt. Second, ACC exhibits a superior percentage improvement rate compared with Popt across all three cross-validation scenarios. This indicates that ACC has a wider optimal range, while Popt maintains a consistent average value above 0.9, implying a narrower optimal range.

Table 13.

ACC% and Popt% of MOSMA for HPO.

	ACC%			Popt%
	RF	XGB	LGBM	RF	XGB	LGBM	Mean
10-Fold	5.3	36.9	40.2	2.2	19.5	16.1	20
Time Wise	40.7	29.3	100.4	13.9	10.9	31.3	37.6
Across Project	16.7	44.6	51.8	4	25.2	19.7	27
Mean	20.9	36.9	64.1	6.7	18.5	22.4	28.3

This demonstrates the superior optimization capabilities of the enhanced multi-objective SMA, which achieves effective exploration of the search space.

To further analyze the performance of the multi-objective SMA, we studied its convergence. We used multi-objective SMA to optimize the LGBM regression model and generated a convergence curve (as illustrated in Fig. 8) in a 10-fold cross-validation scenario. From the graph, it is evident that the convergence curve reduces rapidly at the start and quickly approaches the global optimum. This suggests that the multi-objective SMA has a powerful search capability and excellent global convergence performance. As the number of iterations increases, the curve gradually stabilizes, indicating the strength of the optimization algorithm in the local search. We also noted that the convergence curves for both ACC and Popt share similar shapes, implying the potential of the algorithm to achieve a

Fig. 8.

Convergence curve of multi-objective SMA in a 10-fold cross-validation scenario.

balance point between different objectives and to demonstrate equilibrium. Based on these observations, it can be inferred that multi-objective SMA exhibits outstanding performance and convergence properties in the context of hyperparameter tuning.

Based on the experimental results in Section V, we compared the optimization results of three algorithms: multi-objective SMA, MOSA, and ENS-MOEA/D. We also plotted line graphs to compare the improvement rates of ACC optimization (Fig. 9), Popt optimization (Fig. 10), and the tuning time (Fig. 11). Based on the results shown in Fig. 9, the multi-objective SMA performs the best in terms of the improvement rate of ACC, followed by MOSA, whereas ENS-MOEA/D performs the worst. As illustrated in Fig. 10, the multi-objective SMA also exhibits the highest improvement rate in Popt. For XGB, MOSA achieves a higher improvement rate in Popt than ENS-MOEA/D. However, for LGBM, both MOSA and ENS-MOEA/D demonstrate similar performance. As illustrated in Fig. 11, it can be concluded that the multi-objective SMA performs the best in terms of tuning time, while MOSA and ENS-MOEA/D have similar tuning times. In summary, based on the experimental results and comparison graphs, it can be concluded that the multi-objective SMA demonstrates the best optimization performance across multiple metrics.

Fig. 9.

ACC% comparison of model optimization.

Fig. 10.

Popt% comparison of model optimization.

Fig. 11.

Tuning time comparison of model optimization.

6.3. Comparison with the CCUM method

Unsupervised learning can uncover hidden patterns and structures from feature variables without predefined labels. Constructing unsupervised models incurs lower costs than supervised models. To fully utilize the benefits of unsupervised models, Yang et al.

proposed a method that utilizes common change metrics to construct simple unsupervised models [39]. Based on this, Liu et al. utilized CC metrics to construct the CCUM method [13]. In the three typical validation scenarios, the CCUM method exhibited excellent performance.

Huang et al. replicated the study by Yang et al. [16]. and identified three issues. First, under the same inspection budget, LT requires developers to inspect numerous changes, thereby increasing context switching. Second, although LT can detect more defect-inducing changes, many of the highly ranked changes are false positives. Finally, when considering the harmonic mean of recall and precision (F1-score), LT is not superior to EALR. Because the CCUM method follows the same approach as that of Yang et al., it was found that these issues still exist in the CCUM method after verification. Based on the experimental results presented in Section V, the WCMS method outperforms the CCUM method in terms of average prediction results in 10-fold cross-validation, time-wise cross-validation, and across-project prediction scenarios. This is demonstrated by the results of the RF regression model. Additionally, the prediction results of the WCMS method are more stable.

To further compare the CCUM method with our method, we conducted a correlation analysis for the 10-fold cross-validation and time-wise cross-validation scenarios. We investigated the correlation between the project size, the number of clean changes, the number of defect-inducing changes, the defect rate, and the prediction results of the CCUM method. The results are shown in Table 14 (see Appendix for Table 14). Based on the analysis, the prediction results of the CCUM method are negatively correlated with the project size, the number of clean changes, and the number of defect-inducing changes, whereas they are positively correlated with the defect rate. Compared with our method, the CCUM method performs poorly in terms of scalability and generalization. Overall, our method outperforms the CCUM method in terms of performance, scalability, and generalization.

Table 14.

Correlation analysis of prediction results of CCUM.

	10-Fold		Time Wise
	ACC	Popt	ACC	Popt
Project Size	−0.789	−0.931	−0.575	−0.857
Clean Num	−0.805	−0.943	−0.588	−0.861
Bug Num	−0.305	−0.443	−0.202	−0.491
Bug Ratio	0.744	0.903	0.648	0.942

6.4. Comparison with MULTI and DEJIT methods

Both MULTI [17] and DEJIT [18] methods utilize logistic regression models to construct effort-aware JIT-SDP models. They optimize the coefficient vector of the logistic regression model using optimization algorithms. In our study, we use a multi-objective SMA approach to optimize the hyperparameters of three ensemble learning decision tree-based regression models. The difference between these two methods depends on their optimization approaches. MULTI employs a multi-objective optimization strategy, whereas DEJIT uses a single-objective optimization approach. Based on the experimental results in Section V, the WCMS method outperforms the MULTI and DEJIT methods in terms of average prediction results under the 10-fold cross-validation, time-wise cross-validation, and across-project prediction scenarios. Additionally, the prediction results obtained using the WCMS method show higher stability.

To further compare the MULTI and DEJIT methods with our approach, we conducted a correlation analysis for the 10-fold cross-validation and time-wise cross-validation scenarios. We investigated the correlations between project size, the number of clean changes, the number of defect-inducing changes, the defect rate, and the prediction results of the MULTI and DEJIT methods. The results are shown in Table 15 (see Appendix for Table 15).

Table 15.

Correlation analysis of prediction results of MULTI and DEJIT.

	MULTI				DEJIT
	10-Fold		Time Wise		10-Fold		Time Wise
	ACC	Popt	ACC	Popt	ACC	Popt	ACC	Popt
Project Size	−0.741	−0.873	−0.341	−0.672	−0.399	−0.563	0.001	−0.009
Clean Num	−0.762	−0.889	−0.372	−0.693	−0.349	−0.512	−0.038	−0.044
Bug Num	−0.21	−0.355	0.158	−0.174	−0.953	−0.954	0.465	0.416
Bug Ratio	0.758	0.881	0.269	0.63	0.422	0.6	−0.0398	−0.132

Based on the analysis results, the MULTI method shows a negative correlation between the project size and the number of clean changes. However, the correlation between the number of changes inducing defects and the defect rate is uncertain. Similarly, the correlations between the DEJIT method and the project size, the number of clean changes, the number of defect-inducing changes, and the defect rate are unclear. Compared with our approach, both the MULTI and DEJIT methods perform poorly in terms of scalability and generalization. Overall, our method outperforms the MULTI and DEJIT methods in terms of performance, scalability, and generalization.

6.5. RF vs. XGB vs. LGBM for effort-aware JITDP

We compare the performance of three decision tree-based ensemble learning regression models, namely RF, XGB, and LGBM, in effort-aware JIT-SDP from three aspects.

• (1)ACC and Popt in the FI phase: Based on the experimental results in Section V, the RF algorithm consistently performs the best in 10-fold cross-validation, time-wise cross-validation, and across-project prediction scenarios, while the XGB and LGBM algorithms yield similar results. This indicates that RF performs the best among the three regression models when weighted CC is used to represent effort in the field of effort-aware JIT-SDP. RF is the best choice when considering only the performance of the SDP.
• (2)Runtime during the FI phase: We compared the runtimes of the RF, XGB, and LGBM under the same conditions. To account for the varying durations of runtime in both the 10-fold cross-validation and time-wise cross-validation scenarios, we displayed the results on a logarithmic scale (as depicted in Fig. 12). Based on the results in the graph, we found that in both the 10-fold cross-validation and time-wise cross-validation scenarios, RF consistently exhibited the longest runtime, surpassing those of XGB and LGBM by a significant margin. However, XGB and LGBM exhibited similar runtimes. In the across-project prediction scenario, XGB and LGBM still exhibited similar runtimes, while RF exhibited the longest average runtime. When the size of the test set was small, the runtime of the model was similar to that of XGB and LGBM. This suggests that XGB or LGBM may be a better option when using weighted CC to represent effort and considering runtime as a performance evaluation metric.
• (3)ACC and Popt in the MO phase: In the FI and MO phases, we compare the results of XGB and LGBM with those of RF. The comparison results are shown in Table 16 (see Appendix for Table 16), where the bold numbers indicate the maximum values in each row. For example, when comparing RF and XGB in a 10-fold cross-validation scenario in the FI phase, the average ACC of RF is 0.731 (referred to as ACC1), while the average ACC of XGB is 0.556 (referred to as ACC2); $R=\left(ACC1-ACC2\right)/ACC2\ast 100$ = 31.5. R indicates that the prediction results of RF are 31.5 % higher than those of XGB, corresponding to the value in the top left corner of the table.

Fig. 12.

Runtime comparison of RF, XGB and LGBM.

Table 16.

Comparison of Prediction Results of RF vs. XGB and LGBM.

	RF vs. XGB				RF vs. LGBM
	FI		MO		FI		MO
	ACC	Popt	ACC	Popt	ACC	Popt	ACC	Popt
10-Fold	31.5	18	1.4	1.2	36.4	15.6	3.2	2
Time Wise	9.9	6.3	17.5	9	45.5	18.5	0.7	2.6
Across Project	43.4	23.2	15.7	2.3	43.7	21.2	10.5	5.3
Mean	28.3	15.8	11.5	4.2	41.9	18.4	4.8	3.3

From Table 16, we can observe a significant difference in the FI phase in the 10-fold cross-validation scenario between XGB and LGBM compared with RF. However, after optimizing with the multi-objective SMA, the results of XGB and LGBM approached those of RF. In the time-wise cross-validation scenario, XGB and LGBM still showed a significant difference compared with RF in the FI phase. However, after optimizing with the multi-objective SMA, the results of LGBM approached those of RF, while the results

of XGB were less satisfactory. In the across-project prediction scenario, XGB and LGBM showed a significant difference compared with RF in the FI phase. However, after optimizing with the multi-objective SMA, the gap decreased. Considering the overall assessment, RF still performed the best in the MO phase, but the results of LGBM approached those of RF. RF is the optimal choice if runtime is not considered a performance evaluation metric. LGBM is the preferred option when considering runtime.

7. Threats to validity

7.1. Internal validity

Internal validity is primarily associated with three factors.

• (1)Accuracy and reliability of the experimental code: Measures such as standardized coding, team pair programming, and code reviews were implemented in this study to ensure the accuracy of the experimental code. Regarding the experimental results, the average values were obtained from 10 runs to improve the reliability of the results.
• (2)Parameter settings for the multi-objective SMA: After conducting several experimental comparisons, we determined the optimal parameter configurations to enhance the performance of the algorithm. These configurations include a population size that is five times larger than the number of hyperparameters, 100 iterations, and a position update parameter of 0.03.
• (3)The configuration space of the hyperparameters for the regression model. Initially, default hyperparameter settings were used as the baseline model for training. Then, the performance of the model was optimized by gradually narrowing the search space or exploring new search spaces when necessary. After conducting multiple experimental comparisons, the optimal configuration space for the hyperparameters was determined.

In summary, reasonable measures were taken in this study to ensure internal validity, and there were no threats to it.

7.2. External validity

External validity is primarily associated with two factors.

• (1)Constructing a change dataset involves two main steps: measuring the change metrics and identifying the changes that cause defects. Measuring change metrics requires the use of counting, statistical, and other methods, while identifying defect-inducing changes involves using the SZZ algorithm or its variants. Both aspects may introduce errors that pose threats to external validity.
• (2)The experimental implementation of this research applied Python technology, which offers excellent flexibility and openness. Our approach can be easily applied to other projects, but it is necessary to verify whether the prediction results align with those of our study.

Overall, external validity poses certain risks that must be validated and scrutinized on a project-by-project basis.

7.3. Construct validity

Construct validity is closely related to the appropriateness of the performance evaluation metrics that we selected. In the field of effort-aware JIT-SDP, ACC and Popt are commonly used to evaluate the model performance. During the FI and MO phases, we use ACC and Popt to assess the performance of our method. To compare the running speed of the three ensemble learning regression models (RF, XGB, and LGBM) during the FI phase, we selected the running time as the performance evaluation metric. When evaluating the effectiveness of the multi-objective SMA, we considered not only ACC and Popt but also tuning time as an additional performance evaluation metric. Thus, this study thoroughly considers construct validity and carefully selects the appropriate performance evaluation metrics.

7.4. Conclusion validity

The SK-ESD test was conducted using nonparametric bootstrap sampling and considering Cohen's d effect size to prevent making conclusions about a disparity in predictive performance that may be insignificant owing to a small effect size.

8. Conclusion and future work

This study proposes a novel effort-aware JIT-SDP method called WCMS, which enhances the performance of SDP during the FI and MO phases. During the FI phase, we used weighted CC to measure the effort required for change, thus standardizing the measurement of the change effort. In the MO phase, we enhanced the SMA by incorporating multi-objective handling functionality and developed a mechanism for multi-objective synchronization and conflict resolution. Based on the FI phase, we utilized the multi-objective SMA to optimize the hyperparameters of the decision tree-based ensemble learning regression model. We conducted experiments on six large, well-known open-source projects using the following three decision tree-based ensemble learning algorithms: RF, XGB, and LGBM. The results showed that our method outperformed the current best-supervised methods in the FI phase and surpassed all the best methods (including both supervised and unsupervised methods) in the MO phase. This demonstrates improved scalability and generalization capabilities. To assess the effectiveness of multi-objective SMA, we conducted a comparison with baseline methods. The results showed that the multi-objective SMA outperformed the baseline methods in terms of ACC, Popt, and tuning time. Additionally, we compared the applications of RF, XGB, and LGBM in the field of effort-aware JIT-SDP. RF performed the best in both the FI and MO phases, while XGB and LGBM exhibited a significant gap compared to RF in the FI phase. However, after optimizing with multi-objective SMA, the performance of LGBM approached that of RF and demonstrated a faster execution speed.

In the future, we will continue to enhance the performance of effort-aware JIT-SDP by implementing FIs and optimizing the model. To improve features, we will analyze the significant changes by utilizing both commercial software and the latest open-source software as datasets. In the MO stage, we will integrate deep learning techniques to enhance performance. Additionally, we intend to apply multi-objective SMA to other domains to further enhance its optimization capabilities.

Data availability statement

The databases and Python scripts used for this study are available for download at the following link: https://zenodo.org/records/12805239.

CRediT authorship contribution statement

Hongming Dai: Writing – review & editing, Formal analysis, Conceptualization, Writing – original draft, Visualization, Validation, Software, Methodology, Investigation, Data curation, Conceptualization. Jianqing Xi: Writing – review & editing, Supervision, Resources, Project administration, Funding acquisition, Conceptualization. Hong-Liang Dai: Conceptualization, Formal analysis, Writing – Review & Editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.