Cooperative binding of bivalent ligands yields new insights into the guanidine-II riboswitch

Abstract

Riboswitches are involved in regulating the gene expression in bacteria. They are located within the untranslated regions of bacterial messenger RNA and function as switches by adjusting their shape, depending on the presence or absence of specific ligands. To decipher the fundamental aspects of bacterial gene control, it is therefore important to understand the mechanisms that underlie these conformational switches. To this end, a combination of an experimental binding study, molecular simulations and machine learning has been employed to obtain insights into the conformational changes and structural dynamics of the guanidine-II riboswitch. By exploiting the design of a bivalent ligand, we were able to study ligand binding in the aptamer dimer at the molecular level. Spontaneous ligand-binding events, which are usually difficult to simulate, were observed and the contributing factors are described. These findings were further confirmed by in vivo experiments, where the cooperative binding effects of the bivalent ligands resulted in increased binding affinity compared to the native guanidinium ligand. Beyond ligand binding itself, the simulations revealed a novel, ligand-dependent base-stacking interaction outside of the binding pocket that stabilizes the riboswitch.

Graphical Abstract

Graphical Abstract.

Introduction

Riboswitches are control structures that are located within the untranslated regions of bacterial messenger RNA. They are able to bind small molecules directly and—upon ligand binding—undergo structural rearrangement, thereby altering the expression of the adjacent genes (1). The ability to control gene expression by utilizing a small molecule trigger offers many applications ranging from synthetic biology, functional genomics and pharmaceutical target validation, to prospects in gene therapy (2–5). Recently, four different riboswitch classes have been characterized as guanidine-responsive riboswitches (6–10). These riboswitches control genes that allow bacteria to use guanidine as a nitrogen source (11–16). The source of guanidine in biological systems remains mostly elusive (7,17), but given the widespread occurrence of RNA sensors for this metabolite, a fundamental and possibly archaic role in metabolism is anticipated (18). In the present study, we focus on the guanidine-II riboswitch (6,19–23). Its ligand-binding region, which is called an aptamer, comprises two hairpins that are separated by an unstructured non-conserved stretch of seven or more nucleotides. The two hairpins form two distinct binding pockets within their loop regions where two guanidinium (Gdm⁺) ions can bind cooperatively (see Figure 1A). The loops contain a conserved ACGA (less frequent ACGG) loop sequence that is involved in both ligand binding and dimer formation between the two hairpins (6).

Figure 1.

Depiction of the guanidine-II aptamer dimer and the set of bivalent ligands investigated experimentally and in silico and schematic representation of the computational workflow. (A) Illustration of the sequence and arrangement of the two aptamers. Solid lines indicate base pairs in the stem and dotted lines indicate H-bonds between the opposing C9 and G10 nucleobases. Additional hairpin–hairpin interactions are present between nucleobases highlighted by colored symbols: G7–A8 (triangles) and A11–A11 (stars). (B) Depiction of the native ligand, guanidinium and the diguanidines used in this work in skeletal representations. In-vivo and in-vitro studies were conducted with all compounds shown, whereas molecular simulations focused on C4-diguanidine (brackets). (C–F) Illustration of the dimerized aptamers with fully bound C4-diguanidine (C, D) and bound only on one side (E, F). Dotted circles illustrate the location of the binding pockets. (G) Conceptualized workflow followed in this work; for a detailed description see the ‘Materials and methods’ section.

The structural characterization of guanidine-responsive (and other) riboswitches is often complemented by molecular simulations that help to shed light on structure dynamics and interactions of these ligand–RNA systems not easily accessible by experimental methods (22,24–29). For the guanidine-II riboswitch, we have explored the conformational states that a single aptamer adopts in a previous simulation study. Ligand binding in the monomer follows a conformational selection mechanism and the ligand-bound aptamer assumes a conformation where the nucleotides involved in the dimer interface are optimally exposed to the respective other monomer (25). These results suggest that ligand binding and dimerization are coupled. However, the simulations that were focused on ligand binding to the aptamer monomer leave several important questions unanswered. For example, does ligand binding necessarily precede dimerization, or can ligand binding/unbinding occur after the riboswitch dimer has formed? To address these open questions, the present study is focused on the aptamer dimer using a carefully designed, bivalent ligand.

The two incorporated Gdm⁺ ions in the dimerized state are in close proximity (see Figure 1 for a structural depiction of the aptamer dimer). To investigate ligand binding in the dimerized state, a bivalent ligand would be ideally suited since it has the potential to simultaneously, and cooperatively, bind to both binding sites. Analyzing the distance between the two binding sites revealed that bivalent diguanidines connected by an alkyl linker of three to five carbon atoms are suitable candidates.

Huang et al. analyzed such bivalent diguanidines and reported an up to 10-fold increase in the binding affinity compared to Gdm⁺ and solved the corresponding crystal structures (30). Complementary to the study by Huang et al., we investigated whether those non-natural compounds were able to maintain their bioactivity and performed reporter assays to determine their potential as artificial high-affinity ligands for the guanidine-II riboswitch. We studied the affinity and bioactivity of the C3–C5 bridged diguanidine compounds (see Figure 1B) against the guanidine-II riboswitch of Escherichia coli that regulates the expression of a guanidinium exporter (15). Of those compounds, arcaine (from here on referred to as C4-diguanidine) and audouine (C5-diguanidine) had been studied as pharmaceutically active compounds before (31,32).

The C4-diguanidine (see Figure 1C) is the bivalent ligand where the length of the alkyl linker best corresponds to the geometry of the riboswitch dimer. It is also the ligand that was recognized by the riboswitch with the highest binding affinity (30). This positions C4-diguanidine as a particularly promising tool to better understand the mechanism of ligand binding and the interconnection between ligand binding and dimerization. The fact that the bivalent ligands form a bridge between the dimerized aptamers suggests that here, at least for the second Gdm⁺ group, dimerization precedes binding. While ligand binding in the monomer seems probable (25), it is not known whether the fully formed dimer structure also allows a ligand to slip in or out of one of the binding pockets. In principle, ligand binding and dimerization could follow a more complex, concerted choreography of opening and closing of the pocket. Thus, we decided to investigate the binding of C4-diguanidine to the aptamer dimer by atomistic molecular dynamics (MD) simulations.

The odds of observing spontaneous ligand binding of freely diffusing ligands in an MD simulation are usually extremely low, in particular in the case of a rather closed-off binding pocket. However, a half-bound bivalent ligand effectively tethers the free Gdm⁺ group near the empty pocket, therefore, creating a system with an increased likelihood for ligand binding. Simulations with the C4-ligand bound only on one side to the dimerized aptamers were performed to see if spontaneous binding events are observed in this entropically favored situation. As a supplement, simulations of the dimerized aptamers with fully bound C4-guanidine, without ligand, and with Gdm⁺, were carried out. A machine learning-based analysis workflow to characterize the so-obtained conformational ensemble with a focus on the immediate binding pocket and nucleotides involved in the dimer interface was implemented (see Figure 1G). A detailed description of the workflow is given in the ‘Materials and methods’ section. With the combination of this custom-tailored set of simulations and data analysis, we shed light on the ligand-binding process and identified factors that contribute to the stability of the dimeric form of the aptamer.

Materials and methods

Experiments

Synthesis of C3- to C5-diguanidine

The synthesis of the bivalent diguanidine ligands was adapted from Böttcher et al. (33). The diamino-alkanes were converted with S-methylisothiourea to yield the corresponding diguanidines. For details, see Supplementary Information.

Cloning

The guanidine-II riboswitch of E. coli (see Supplementary Figure S1A), which resides in front of the Gdx sequence, was cloned into a constitutively expressing lacZ reporter vector. The guanidine-II motif was amplified from genomic DNA by primer MS095 5’-GAATACTAGTCCCCTGCCACCTGGCAAA-3’ and MS96 5’-CTTACCATGGCTCCGGAGAATTGGGGCCGTCC -3’. The polymerase chain reaction product and vector pQE31-J06-lacZ were cut with SpeI and NcoI (NEB) according to the manufacturer’s protocol. Products were ligated and transformed into E. coli K-12 BW25113. Plasmid integrity was checked by Sanger sequencing (GATC Biotech).

Growth conditions

Escherichia coli K-12 BW25113 harboring the guanidine-II riboswitch reporter construct was grown in lysogeny broth (LB) medium with carbenicillin and Gdm⁺ or diguanidine as annotated, diluted 10 times 1:2 from 10 mM. Cells were grown in a 96-deep well plate overnight at 37°C with 200 rpm. The next day OD600 and β-galactosidase activity were measured.

β-galactosidase assay

A simplified Miller assay was performed based on a protocol from Zhang and Bremer (34). OD600 of 150 μl in a 96-well plate was measured; 20 μl of the outgrown cell culture were lysed in 80 μl permeabilization solution (100 mM Na₂HPO₄, 20 mM KCl, 2 mM MgSO₄, 0.8 mg/ml hexadecyltrimethylammonium bromide, 0.4 mg/ml sodium deoxycholate, 5.4 μl/ml β-mercaptoethanol); 600 μl of substrate solution [60 mM Na₂HPO₄, 40 mM NaH₂PO₄, 1 mg/ml o-nitrophenyl-β-D-Galactoside (ONPG), 2.7 μl/ml β-mercaptoethanol] were added. The reaction was stopped after a yellow color developed by the addition of 700 μl 1 M Na₂CO₃. The reaction time (rt) was recorded. Cell debris was removed by centrifugation. The chromophore amount was determined in a Tecan reader while 150 μl of the reaction solution was transferred into a 96-well plate and absorbance was measured at 420 nm. β-galactosidase activity was calculated as arbitrary Miller Units:

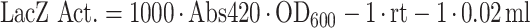Means of quadruplicates were plotted against the compound concentration. Half-maximal induction was determined by fitting curves with a sigmoidal model (HYPNOS GraphPad Prism).

Computational details

Force field and simulation parameters

Simulation setup and parameters were chosen identical to our earlier study of the guanidine-II monomer (25). For all simulations, the GROMACS 2020.4 software package (35) was used in combination with the DESRES force field developed by the D.E. Shaw research group (36). It was used as implemented by Giovanni Bussi, Stefano Piana and Sandro Bottaro at https://github.com/srnas/ff/tree/desres in combination with TIP4PD, a reparameterized version of the TIP4P water model (37) and a salt concentration of 0.15 mol/l Na⁺ and Cl⁻ ions. The total number of solvent molecules for each simulation is shown in Table 1. Parameters of the bivalent C4-diguanidine ligand were derived from the arginine parameters in the DESRES force field. More precisely, parameters for the guanidine group (CZ, NH1, NH2, NE and all connected hydrogens) in adenine were used for the two guanidine moieties in C4-diguanidine (C1, N1, N2, N3 and all connected hydrogens, and C6, N4, N5 and all connected hydrogens). Furthermore, parameters of the CD and CG methylene groups of adenine were used for the respective C2/C5 and C3/C4 methylene groups in the C4-diguanidine linker.

Table 1.

Overview of dimer simulations with different ligands

	Ligand(s)	PDBa	Comment	Solventb	Trajectory length	Simulation IDsc
Half-boundd
	C4-diguanidine	6HBT		10 000	3 × 10 μs	1–3
	C4-diguanidine	6HBT		10 000	3 × 10 μs	4–6
	C4-diguanidine	6HBT		10 000	3 × 10 μs	7–9
Fully bound
	C4-diguanidine	6HBT	Crystal structure	10 000	3 × 10 μs	10–12
	C4-diguanidine	6HBT	Inverted ligande	10 000	3 × 10 μs	13–15
Other
	None	6HBT		10 000	3 × 10 μs	16–18
	Gdm+	5NDIf		20 000	3 × 2 μs	19–21
	None	5NDIf		20 000	3 × 2 μs	22–24

^aProtein Data Bank structure identifier, indicating the aptamer structure the simulations are based on. ^bThe total number of solvent molecules initially present in each simulation during setup. Water molecules were subsequently replaced by ions for charge neutralization purposes and to adjust for a salt concentration of 0.15 mol/l Na⁺ and Cl⁻ ions. ^cThe simulation IDs listed here will be used throughout this manuscript to distinguish individual trajectories. ^dFor the three sets of half-bound C4-diguanidine simulations, one Gdm⁺ group was positioned outside the binding pocket pointing in three different spatial directions. The three half-bound starting structures are shown in Supplementary Figure S2A–C. ^eFor this structure with both Gdm⁺ groups bound, the position of one Gdm⁺ was rotated inside the binding pocket of chain B by hand compared to the orientation in the crystal structure—in order to account for different binding poses. This results in the hydrogen atom H9 of the ligand facing toward the pocket entrance. The fully bound starting structures are shown in Supplementary Figure S2D and E. ^fFor the 5NDI-based structures, RNA chains A and B were used.

Electrostatic interactions were calculated using the particle mesh Ewald method (38,39), with real space and van der Waals cutoff distances of both 1 nm. All MD simulations were performed using an integration timestep of 2 fs in the isothermal-isobaric (NpT) ensemble at 300 K and 1 bar. The velocity-rescale algorithm (40) was used for temperature coupling and the Parrinello–Rahman algorithm (41) with a damping constant of 2.0 ps for pressure coupling.

Simulated systems

All simulations of the guanidine-II riboswitch dimer with C4-diguanidine were based on the 6HBT PDB structure. Simulations were started from the crystal structure, i.e. with both Gdm⁺ groups bound, and from a structure where the ligand was initially bound to the riboswitch only at one end. In that case, the position of the RNA atoms as well as those of the bound Gdm⁺ group is the same as in the 6HBT structure, and the atoms of the second Gdm⁺ group and the linker atoms were adjusted. To reduce the risk of introducing a bias due to the initial structure, three different starting structures were set up manually, with the free end of the ligand positioned in three different directions (Supplementary Figure S2). For each initial structure, three simulations were run for 10 μs, resulting in a total of 30 μs of simulation data for the fully bound ligand and 90 μs for the system with the half-bound ligand. Additionally, simulations with two (unlinked) Gdm⁺ ions in the binding pockets and of the dimer without ligand based on the 5NDI PDB structure were included in some of the analyses. Table 1 lists all simulations that are part of this work, including information on how they will be referred to (‘IDs’). If not noted otherwise, analyses were performed on snapshots every 100 ps for all trajectories.

Analysis of simulation data

For the analysis of the large, high-dimensional datasets from the MD simulations of the aptamer-ligand systems, a workflow was established as illustrated in Figure 1G. First, we have identified a set of features, e.g. internal distances of the binding pocket, which is well suited to describe and distinguish important conformational changes in the system. A dimensionality reduction method was applied to the data in this still high-dimensional feature space. The so-obtained 2D projection represents the conformational landscape of the system and was used to identify characteristic states with a clustering algorithm.

Feature selection

We aimed to describe the simulations of the half-bound C4-diguanidine concerning the binding of the loose end of the ligand. For this, a set of descriptors was developed based on the pairwise distances between the four heavy atoms of the unbound Gdm⁺ group (C1, N1, N2 and N3) and the heavy atoms of residues 7, 8, 9, 10 and 12 of both chains. From these pairwise distances, only those that correspond to RNA atoms that come into proximity (here defined as closer than 3 Å) to unbound Gdm⁺ throughout the analyzed simulations were selected, thereby further reducing the number of pairwise distances while ensuring no substantial loss of information. The final reduced set consisted of 112 pairwise distances (Supplementary Figure S3).

Dimensionality reduction with EncoderMap

The simulation data in feature space were projected to two dimensions by using EncoderMap (EM) (42,43), a dimensionality reduction algorithm that relies on a combination of a neural network autoencoder with a multidimensional scaling type metric. The resulting 2D projections of the high-dimensional input data will be referred to as maps. Due to the non-linearity of the dimensionality reduction, the two axes of the maps do not have an immediate physical meaning and are therefore unlabeled. The EM python package was used as available on github.com (version 1, https://github.com/AG-Peter/encodermap). The EM default weights for the autoencoder cost function (ka = 500) and the sketch map cost function (ks = 1) were used. Each EM autoencoder was trained for 5000 steps. The parameters for training the EM autoencoder were adjusted to the respective set of pairwise distances by hand. Likewise, the parameters of the sigmoid function used in EM were adjusted for each set of pairwise descriptors individually. The learning rate and the l2 regularization parameter were adjusted to produce a low-dimensional representation of the input data by visual inspection. A Jupyter-Notebook containing the code needed to reproduce the EM-based dimensionality reduction can be found in the data repository for this publication.

Clustering with HDBSCAN

To identify densely populated regions in the low-dimensional projection, the hierarchical density-based spatial clustering of applications with noise (HDBSCAN) algorithm (44) was used. As each point in the 2D projection corresponds to a molecular structure observed in the MD simulations, the identified clusters can be understood as the prevalent, conformationally homogeneous states of the ligand–RNA construct. This clustering algorithm can identify clusters of varying density and shape while requiring few input parameters (and being quite robust to their selection). The HDBSCAN python implementation (version 0.8.19) (44) was used with a minimum cluster size of 5 × 10⁴ structures and the minimum number of clusters set to 2. While HDBSCAN allows for efficient clustering of the input data, it does not provide cluster centers (centroids) by design. The conformation corresponding to the data point closest to the geometric center of all data points on the map that are assigned to the respective cluster was retrieved as a reference structure for visualization of the cluster.

Analysis of a11 base stacking

To obtain an understanding of the interactions between the two nucleobases A11 (the respective second adenine residues in the two ACGA loops of the opposing RNA chains, marked by red stars in Figure 1A), the angle between the two nucleobase rings was monitored. Here, the gmx gangle function included in the GROMACS software package was used. The plane of RNA nucleotide bases was defined by three heavy atoms (N3, C6 and C8) in the aromatic system. The angle of this plane (represented by its normal vector) to the z-axis of the RNA was calculated (the latter was obtained after aligning the simulated structure to a reference structure). A good descriptor denoting the parallel arrangement of the A11 nucleobases was the difference between the two angles relative to the RNA z-axis.

Results and discussion

As discussed above, diguanidines are promising candidates to be used as high-affinity triggers for controlling gene expression. Their functional relevance in the context of the coupling of ligand binding and dimerization (i.e. RNA switching) in the guanidine-II riboswitch system motivated us to investigate their binding affinity, bioactivity as well as the ligand-binding process by a combination of experimental and computational methods.

Diguanidines are high-affinity ligands

An in-line probing assay revealed the binding affinities for the three different diguanidines (Supplementary Figure S1). C4-diguanidine was bound with the lowest apparent K_d to the riboswitch (100 ± 5 nM). C5-diguanidine was bound with an apparent K_d of 400 ± 60 nM. This is still 10-fold lower than the C3-diguanidine (4.3 ± 0.3 μM) and almost 100-fold lower than the natural ligand Gdm⁺ (20 μM), corroborating that the C4-diguanidine in particular is a great fit for the guanidine-II aptamer. Hill-coefficients for C3-diguanidine and Gdm⁺ are greater than 1, whereas they are equal to 1 for C4-diguanidine and C5-diguanidine. This indicates a shift from the binding of multiple molecules of Gdm⁺ for the native ligand and C3-diguanidine to the simultaneous binding of a single molecule to both distinct binding sites of the riboswitch for C4-diguanidine and C5-diguanidine. The nucleotides affected in the in-line probing assay are the same as for Gdm⁺. This confirms the results reported by Huang et al. (30).

To assess the bioactivity of the diguanidines, guanidine-II riboswitch of E. coli was cloned in front of the reporter gene β-galactosidase. The guanidine-II riboswitch of E. coli regulates the Gdx sequence, which is coding for a guanidinium exporter (15) and is a genetic ON-switch (6). Cells were grown in LB medium in the presence of Gdm⁺ and the C3-, C4- and C5-bridged diguanidines. Reporter activity was monitored qualitatively with X-Gal or quantitatively with an ONPG assay (Figure 2). The reporter was induced by all compounds at high concentrations. However, quantitative measurements revealed that the half-maximal induction differed between the studied compounds. The half-maximum in the case of C4-diguanidine was reached already at 400 ± 60 μM, for C5-guanidine at 1. ± 0.2 mM, whereas for Gdm⁺ it was only reached at 3.8 ± 0.4 mM. Thus, the bioactivity reflects the results from the in-line probing experiments. The apparent difference between in vitro and in vivo effector concentrations is likely due to the poor cell permeability of the charged (di-)guanidines. Thus, the concentration of the compounds in the cells is expected to be lower than outside. C3-diguanidine-treated cells only showed little reporter activity, despite its binding with lower K_d to the riboswitch in vitro. This result fits well with the aforementioned observation that multiple C3 molecules are bound per riboswitch and underlines the importance of a sufficiently long C-linker between the Gdm⁺ moieties.

Figure 2.

Bioactivity of diguanidines. LacZ activity of the guanidine-II riboswitch lacZ reporter construct. Escherichia coli transformed with the reporter was grown in the presence of C3-diguanidine (dots), C4-diguanidine (diamonds), C5-diguanidine (triangles) or Gdm⁺ (circles). LacZ activity was determined in a Miller assay with the conversion of ONPG. Data points represent means of quadruplicates and were fitted with a sigmoidal model to determine half-maximal induction.

Molecular dynamics simulations of C4-diguanidine exhibit spontaneous ligand binding

The experimental results show that the diguanidines, the C4-diguanidine ligand in particular, are promising candidates to be used as high-affinity triggers for controlling gene expression. These bivalent ligands also offer the opportunity to study ligand binding in the guanidine-II riboswitch at the molecular level by creating a setup that entropically increases the likelihood of ligand-binding events. For this, a set of nine independent simulations of 10 μs length each of the dimers with half-bound C4-diguanidine were carried out. Monitoring the distance between the central carbon of the unbound Gdm⁺ group and the center of mass (COM) of the heavy atoms of all pocket residues allows for a quick assessment of the status of the free end of the ligand (Figure 3A shows an illustration of this distance). Figure 3C shows the ‘typical’ behavior of the half-bound system as seen in one of the simulations (simulation 1). The free end of the ligand does not enter the pocket and maintains a distance to the pocket center that fluctuates around 9 Å with occasional, short-lived periods at slightly shorter or longer distances. This behavior is observed in seven out of the nine simulations (see Supplementary Figure S4). In two simulations, however, the free Gdm⁺ group does enter the initially empty binding pocket. In simulation 4, ligand binding occurs after 9.25 μs (Figure 3C, simulation 4 and Supplementary Movie S1), as can be seen by a stepwise decrease of the monitored distance to first 4 Å and then 2 Å, which corresponds to the bound state. In simulation 7, binding happens earlier in the course of the simulation at 3.96 μs (Figure 3C, simulation 7 and Supplementary Movie S2).

Figure 3.

Ligand-binding events are observed in simulations with half-bound C4-diguanidine. (A) Illustration of the distance (solid line) defined to monitor ligand binding between the center of the unbound Gdm⁺ group and the center of the unoccupied binding pocket (depicted as a sphere) of RNA chain A. The approximate location of the binding pocket is indicated by dashed half-circles for the two RNA chains. (B) EM projections of internal distance data of all nine half-bound simulations (see Table 1), shown as a 2D histogram. Low values indicate more densely populated regions. (C) Plotting the distance defined in (A) against time reveals ligand-binding events in simulations 4 and 7. Simulation 1, where no binding occurs, is shown for comparison (for time series of all half-bound simulations, see Supplementary Figure S4). Coloring according to simulation time. The running average is shown for a sliding window of 100 frames as a solid line. (D) The EM projection of individual trajectories reveals a ligand-binding pathway in the upper left corner of the map for simulations 4 and 7. Apart from this binding pathway, the simulations visit the same regions of the map and, thus, the same range of conformations. The trajectories of selected simulations 1, 4 and 7 are plotted on top of the full projection. Coloring of the data points was done according to time and follows the color of the respective time series in panel (C).

While the distance between the Gdm⁺ group and the pocket center is very well suited to monitor the overall behavior, the time traces also show that a more thorough conformational analysis of both unbound and bound states is warranted. For the unbound state, the mentioned brief instances of shorter and longer distances compared to the average of 9 Å indicate the existence of metastable states while Gdm⁺ is outside the binding pocket. The decrease in fluctuations of the ligand–pocket distance observed at around 6 μs in simulation 7 (Figure 3C), i.e. 2 μs after the actual binding event, indicates that in the fully bound state further conformational substates also exist (that will be analysed later).

Interpretation of ligand binding guided by a low-dimensional representation

To better characterize the conformations of the pocket and the ligand, and to describe what happens during the binding events, a 2D representation (‘map’) of the simulation data was generated. This map is based on the distances between the Gdm⁺ group and the residues of the riboswitch lining the pocket and the pocket entrance (for more details, see the ‘Materials and methods’ section). Figure 3B shows a logarithmic density representation of the resulting EM projection, i.e. dark areas can be interpreted as free energy minima, i.e. conformational states. Clustering of this detailed landscape with the HDBSCAN algorithm yields 13 distinct clusters (Figure 4). A dominant cluster (cluster 12) is surrounded by several less densely populated, smaller clusters (Supplementary Figure S5A). Most of the clusters are visited by all nine simulations (Figure 3 and Supplementary Figure S5B). This conclusion that most regions of the landscape are visited by all simulations is confirmed by projecting the individual simulations separately into the map (Supplementary Figure S6).

Figure 4.

Identification of conformational states using the HDBSCAN clustering algorithm on the EM projection of pairwise distance data between the (initially) half-bound Gdm⁺ group and the binding pocket. Data points in the EM projection are colored according to the cluster they are assigned to, while data points not assigned to a cluster are shown in the background. The corresponding cluster IDs are shown in filled circles at the location of the cluster centers. Representative structures (cluster centroids) are shown in boxes and arrows indicate the cluster of origin. Ligand-binding poses are shown in more detail for the two observed bound states, clusters 0 and 2. These two states are differentiated by the position/orientation of a hydrogen (highlighted) of the NH group, which is connected to the alkyl chain in the C4 linker. Chain and nucleobase identity are labeled for state 0. Possible hydrogen bonds are indicated by dashed lines.

A notable exception is the region that corresponds to clusters 0, 1 and 2. These three clusters are located in the upper left part of the map and are only visited in simulation 4 (clusters 0 and 1) and simulation 7 (clusters 1 and 2) (Supplementary Figure S5B) and are the result of the two spontaneous binding events of the initially free Gdm⁺ group. By coloring the map according to the distance between the free Gdm⁺ group and the binding pocket, insights into the progression of ligand binding can be obtained (Supplementary Figure S7A). The regions with the lowest distances (∼ 4 Å) are centered around clusters 0 and 2, which correspond to the bound states. A steady decrease of the ligand–pocket distance from cluster 3 via cluster 1 to the bound states suggests that this part of the map corresponds to a transition region in the binding process. Visualization of the two binding trajectories in the EM projection (Supplementary Figure S8) shows that the two binding events indeed follow this pathway through clusters 3 and 1 before they diverge and end up in the region of either cluster 0 (simulation 4) or cluster 2 (simulation 7). Interestingly, while cluster 3 is visited occasionally throughout all simulations (Supplementary Figures S5B and S6), the pre-bound cluster 1 is only visited by the two binding simulations. This suggests that the transition from cluster 3 to cluster 1 is a crucial event required to initiate ligand binding.

For a more detailed structural interpretation, representative cluster centroids are visualized in Figure 4. Clusters 0 and 2 correspond to two different orientations of the Gdm⁺ group inside the binding pocket characterized by the position/orientation of the hydrogen of the NH group that is connected to the alkyl chain in the C4 linker (Figure 4, upper two panels). Cluster 2 corresponds to the experimentally reported structure. In cluster 1, which was already described above as a ‘pre-bound’ state, the Gdm⁺ group is positioned at the pocket entrance; it is aligned with the binding pocket and forms hydrogen bonds to two oxygen atoms flanking both sides of the binding pocket (Supplementary Figure S9A and B). This observation in combination with the relevance of cluster 1 for both binding events suggested a closer investigation of this oxygen–oxygen distance. It indeed appears to be a meaningful descriptor that allows monitoring of the opening that is required for the ligand to enter into the pocket (for more details, see Supplementary Figure S9C, which shows that in both simulations 4 and 7 the actual binding is preceded by significant changes in this oxygen–oxygen distance, a widening of the pocket entrance, and a transition from cluster 3 to cluster 1). Cluster 3 represents another conformational state that is passed through before the ligand binds. Different from cluster 1, though, it is regularly visited in all nine simulations and not only in the two where the ligand enters the pocket (see Supplementary Figures S5B and S6). Here, the free Gdm⁺ group is directed into the solvent-exposed groove that lies between the two binding pockets, which forces the C4 linker into a bent shape (see state 3 in Figure 4 and Supplementary Figure S7B). In the binding simulations, we found in cluster 3 a water molecule positioned at the pocket entrance, between the two previously identified oxygen atoms that guard the binding pocket (see Supplementary Figure S9D). The actual binding, i.e. the passing from cluster 3 to cluster 1 and ultimately to either cluster 0 or 2 requires a displacement of said water molecule.

The remainder of the conformational landscape (clusters 4–12) corresponds to states where the free Gdm⁺ group forms transient interactions via hydrogen bonds with different regions (e.g. phosphate groups) on the RNA surface in the vicinity of the pocket entrance (Figure 4). The arrangement of the states in the 2D map follows a clockwise rotation in which the unbound Gdm⁺ group gradually closes in on the binding pocket with the actual ligand-binding pathway—as described already—in the upper left corner of the map. The analysis of the map presented so far clearly indicates that the EM-dimensionality reduction produces a meaningful map. This can be further corroborated by comparison with principal component analysis (PCA), a frequently used, linear dimensionality reduction algorithm. Supplementary Figure S10 shows in detail that qualitatively the two dimensionality reduction methods agree very well. The linear PCA algorithm allows for the quantification that the first two principal components of the PCA already account for 86.79% of the conformational variance of the input data. Since the (non-linear) EM-based map represents the conformational states in a qualitatively similar but structurally more clearly defined manner compared to PCA (the latter e.g. not being able to distinguish between the two bound states), we conclude that indeed the EM yields a meaningful 2D representation of the conformational space of half-bound and fully bound C4-diguanidine.

In summary, the free MD simulations with the bivalent ligand show that ligand binding is indeed possible in the dimeric state of the aptamer. The conformational analysis of the simulations of the half-bound C4-diguanidine and the spontaneous binding events give important clues about how the ligand actually slips into the binding pocket. Interestingly, though, the conformational analysis does reveal even more insights into the inner workings of the guanidine-II riboswitch, as highlighted in the next section.

Ligand-dependent stabilization of the aptamer dimer through a novel conformational state

Coming back to simulation 7, it is worthwhile setting the focus on the aforementioned conformational change happening approximately 2 μs after the actual binding event. The rather drastic and lasting reduction of what can be interpreted as positional fluctuations of the ligand in the pocket (Figure 3C, simulation 7) suggests the occurrence of a structural change that has a stabilizing effect on the dimerized aptamers. Inspection of the simulation trajectory during the relevant time segment of simulation 7 reveals a base-stacking interaction between the two aptamers via the two A11 nucleobases (Figure 5B and Supplementary Movies S3 and S4). These two A11 nucleobases are the respective second adenine residues in the two ACGA loops and located at the backside of the binding pockets, close to the dimerization interface. As soon as this ‘handshake’ conformation was adopted, an increase in stability and stiffness of the dimerized aptamers was observed, both visually (see Supplementary Movies S3 and S4) and in root mean square deviation (RMSD) fluctuations of all pocket residues (not shown). This particular base-stacking interaction is not present in the crystal structure of the riboswitch and has not been described before. While in the crystal structure, the two A11 bases interact in such a way that they both remain, to some extent, solvent-exposed (Figure 5A), the new state is characterized by the base stacking of the two A11 nucleobases, with the adenine of one hairpin ending up tucked in between the two chains (Figure 5B). The other A11 nucleobase is stacked upon it towards the solvent-exposed side. The A11 nucleobase that is positioned inside comes into close proximity to the binding pocket of the same chain, which potentially allows for it to be impacted by the presence or absence of a ligand in the respective binding pocket. Since the two RNA chains of the dimer are identical in sequence and the dimer structure is symmetrical, two equivalent conformations of this base-stacking interaction exist. Here, either the A11 base of chain A or the one of chain B is tucked in while the respective other one is solvent exposed (see Figure 5C). Since this handshake conformation is an interesting, potentially stabilizing factor in the dimer, we investigated whether it is in any way connected to the presence of the ligand in one or both of the binding pockets. To this end, a larger number of simulations was analyzed, namely all previously examined half-bound C4-diguanidine simulations, simulations with a fully bound ligand (in two ligand orientations) and simulations without ligands (for details, see Table 1). In order to identify the handshake interaction, we monitored for all these simulations the alignment of the two A11 nucleobases (via the difference between the orientations of the nucleobases relative to the RNA z-axis; for details, see the ‘Materials and methods’ section) and the distances between the COM of each A11 nucleobase to the respective binding pocket center of the same chain (for illustration, see the blowup panel in Figure 5B). Time series for these angle- and distance-descriptors are shown for four representative simulations in Figure 5D and E. One sees that for longer periods (up to several microseconds) the angle descriptor ceases to fluctuate and stays close to zero, indicating that the nucleobases adopt a parallel arrangement, while at the same time, one of the two distances drops to a value of below 0.5 nm. This nicely illustrates that the handshake conformations are adopted in several simulations, notably only in those where C4-diguanidine is bound to at least one of the binding pockets. In simulation 13 (a simulation with a fully bound ligand) we even observe an exchange between the two mirror conformations. A full analysis of these distance and angle descriptors for the complete set of simulations can be found in Supplementary Figures S11 and S12, as well as a further EM-based analysis with an expanded set of pairwise distance features (Supplementary Figures S13 and S14). The data show that for simulations in which the ligand is half-bound to pocket B, only instances of base stacking are found in which the A11 base of RNA chain B is folded onto the RNA structure. For fully bound simulations, both conformations of the stacking interaction are observed. Notably, after ligand binding of the free end of the ligand to the binding pocket of chain A, simulation 7 can be considered a fully bound simulation, and the handshake conformation with A11 chain A inside is observed, which is not found in any other half-bound simulation.

Figure 5.

Two adenine residues from the opposing RNA chains form a ‘handshake’ interaction, a base-stacking interaction stabilizing the dimer if a suitable ligand is present. The stacking interactions of the two A11 nucleobases (highlighted nucleotides) reported for (A) the crystal structure are distinct from the conformations (B) identified in this work. Blowup panel: Illustration of distances between the COMs of the A11 nucleobases and the COM of the binding pocket that was used to monitor the two possible handshake conformations. COMs are depicted as spheres and distances as solid lines between them. (C) The alignment of the A11 bases, illustrated as discs, was used to identify the handshake conformations (see ‘Materials and methods’ section). Depending on which nucleobase is solvent-protected and positioned towards the binding pocket, the two conformations are called ‘A11 chain B inside’ and ‘A11 chain A inside’. (D, E) Angle differences (‘alignment’) and distances between A11 nucleobase and respective ligand-binding pocket showcase the formation of the two handshake conformations for representative simulations. This includes simulation 1 (half-bound, single handshake event), simulation 7 (ligand binding at ∼4 μs, handshake ∼2 μs later), simulation 13 (fully-bound, switch between the two handshake conformations) and simulation 16 (no ligand, no handshake). All simulations are shown in Supplementary Figures S11 and S12. The identity of the stacking interaction is annotated according to the illustration in panel (C). Line colors in panel (E) follow the distances shown in panel (B).

Combining the results for half-bound, fully bound and no-ligand simulations, we conclude that the formation of the handshake interaction requires at least one occupied binding pocket and the A11 base that is positioned inside requires the binding pocket of the same chain to be occupied. Thus, in summary, a pair of novel, locked states of the dimerized aptamers that so far had eluded experimental characterization were identified. This new interaction is insofar quite remarkable since it potentially stabilizes the dimeric state of the riboswitch while being linked to ligand binding.

Conclusion

We synthesized C3 to C5 linked diguanidines and assessed these compounds as bivalent ligands for the guanidine-II riboswitch of E. coli. Thereby, we could confirm the results of Huang et al. and additionally demonstrate that the diguanidines are also biologically active. The C4-diguanidine ligand binds the riboswitch with two orders of magnitude lower apparent K_d than the natural ligand Gdm⁺. Furthermore, C4-diguanidine and C5-diguanidine maintained the bioactivity of the natural ligand. C4-diguanidine reached the half-maximal induction of the guanidine-II reporter construct at a 10-fold lower concentration than Gdm⁺.

Building on this experimental groundwork, a combination of MD simulations with dimensionality reduction and clustering methods allowed us to characterize the conformational landscape of the guanidine-II dimer in the presence of C4-diguanidine. By setting up simulations with the bivalent linker bound only on one side, we created a model system ideally suited to study unbiased ligand binding and investigate the conformational states of the Gdm⁺ group close to the binding pocket. Two spontaneous binding events of the half-bound Gdm⁺ group to the guanidine-II dimer were observed, i.e. showing that ligand binding to the pocket in the dimer state is indeed possible, in spite of obstacles due to steric hindrances and increased stiffness of the pocket compared to the aptamer monomer that had been investigated earlier (25). The resulting, stable bound states agree in principle with the crystal structure but reveal a so-far-unrecognized structural variability due to two possible orientations of the Gdm⁺ group inside the binding pocket. In both binding events, an intermediate state was observed, where the Gdm⁺ group is located close to the entrance of the binding pocket in a pre-aligned conformation to the bound state. From this pre-bound state, a brief opening of the residues flanking both sides of the binding pocket allows for ligand binding, followed by a recovery of the initial conformation of the pocket entrance. During binding, the aliphatic linker of the C4-diguanidine had to (intermittently) assume a tense, bent conformation. While in our previous work we had investigated ligand binding to a single guanidine-II hairpin, the findings presented here clarify that ligand binding in the dimerized aptamer is not only feasible but—at least for the second binding event—also likely. As the aliphatic linker in the bivalent ligand is solvent-exposed and sterically unhindered, it appears to be a promising target for the future development of novel C4-diguanidine derivatives to control bacterial gene expression, for example, by decreasing its hydrophobicity. Our results suggest that the space for such modifications is limited, as they should account for the flexibility of the linker, which is crucial for successful ligand binding. Furthermore, the peak in binding affinity for the C4-diguanidine compared to the C3- and C5-variants implies that the linker length in the C4-diguanidine is close to optimal. In addition to the structural and mechanistic insights into the actual ligand binding, the simulations also revealed the ligand-dependent formation of a novel type of base-stacking interaction between the two hairpins that stabilizes the dimerized aptamer. If at least one of the binding pockets is occupied, the two solvent-exposed A11 nucleobases located at the back of the binding pocket were observed to rearrange into a persistent base-stacking interaction. This conformation had so far not been observed in the experimentally reported structures and constitutes a novel mechanism of ligand recognition in the guanidine-II riboswitch. A full characterization of the ligand-dependent interactions between the two adenine residues and how they stabilize the dimerized conformation is desirable and will be addressed in the future.

Our present and previous findings regarding the conformational states of the aptamer with and without ligands, on the ligand binding and unbinding pathways in both the aptamer monomer and dimer, and on structural features that potentially play a relevant role in describing the binding transition path, will be important ingredients in setting up an approach (such as transition path sampling) to statistically meaningfully characterize the ligand binding pathway. Given that the dimerization and switching transition takes place on very long timescales [the rate constants for transitions between the conformational states reported in the study of Fuks et al. (22) lie between 0.6 and 4.6 s⁻¹], simulating the coupling of ligand binding and dimerization constitutes a veritable challenge. Our results regarding the influence of the ligand’s presence on the dimerization interface (25) and on stabilizing interactions, such as the A11 base stacking, will be essential in devising a suitable enhanced sampling approach and/or coarse grained model.

Data availability

Simulation protocols, Jupyter Notebook and simulation data underlying this article are freely available from https://dx.doi.org/10.48606/fTBvhsaGfoDmhOTV.

Supplementary data

Supplementary Data are available at NARGAB Online.

Funding

The state of Baden-Württemberg through the bwHPC project, the German Research Foundation (DFG) (grant INST no. 35/1134-1 FUGG); and the Publication Fund of the University of Konstanz (open access publication).

Conflict of interest statement. None declared.