Consequences of Pore Polarity and Solvent Structure on Epoxide Ring-Opening in Lewis and Brønsted Acid Zeolites

Abstract

The structure of solvent molecules within zeolite pores influences the rates and selectivities of catalytic reactions by altering the free energies of reactive species. Here, we examine the consequences of these effects on the kinetics and thermodynamics of 1,2-epoxybutane (C₄H₈O) ring-opening with methanol (CH₃OH) in acetonitrile (CH₃CN) cosolvent over Lewis acidic (Zr-BEA) and Brønsted acidic (Al-BEA) zeolites of varying (SiOH)_x density. Despite ostensibly identical reaction mechanisms across materials, turnover rates depend differently on (SiOH)_x density between acid types. (SiOH)_x-rich Zr-BEA (Zr-BEA-OH) provides ∼10 times greater rates than a (SiOH)_x-poor material (Zr-BEA-F), while Al-BEA-OH and Al-BEA-F give turnover rates within a factor of 2. Zr-BEA-OH shows more positive activation enthalpies and entropies than Zr-BEA-F across the range of [CH₃OH], which reflect the displacement of solvent molecules and lead to greater rates in Zr-BEA-OH due to the dominant role of entropic gains. Measurements of the density and composition of solvent within the pores show that the (SiOH)_x nests within Zr-BEA-OH promote hydrogen-bonded solvent structures distinct from Zr-BEA-F, while the Brønsted acid sites confer interactions similar to (SiOH)_x nests and give solvent structures within Al-BEA-F that resemble those within Al-BEA-OH. Correlations between apparent activation enthalpies and C₄H₈O adsorption enthalpies show that interactions with solvent molecules give proportional changes to both C₄H₈O adsorption and ring-opening transition state formation. The differences in intrapore environment carry consequences for both rates and regioselectivities of epoxide ring-opening, as demonstrated by product regioselectivities that increase by a factor of 3 in response to changes in solvent composition and the type of acid site in the *BEA structure (i.e., Lewis or Brønsted). These results demonstrate the ability to control rates, regioselectivities, and adsorption thermodynamics relevant for industrially relevant liquid-phase reactions through the design of noncovalent interactions among solvating molecules, reactive species, and (SiOH)_x functions.

1. Introduction

Zeolites serve as useful materials for catalysis and adsorption because the subnanometer pores within zeolites can stabilize guest molecules of selected shapes and sizes.^1,2 The zeolite pore walls stabilize these adsorbate molecules through nonspecific van der Waals interactions.^3,4 The introduction of a condensed intrapore phase adds further complexity to systems due to specific interactions (e.g., hydrogen bonds) between reactants, spectator molecules (e.g., solvent), and pore functions.⁵⁻⁸ These interactions introduce thermodynamic nonidealities that alter the excess free energies (G^ε) of adsorbates and transition states.⁹ Altering the surface functions within zeolite pores leads to differences in the arrangement of solvent and reactant molecules near active sites, which provides an opportunity to influence the rates and selectivities of catalytic and separation processes.

The presence of intrapore silanol ((SiOH)_x) functions strongly affects both adsorption and catalysis in zeolites. Vega-Vila and Gounder demonstrated that hydrophobic Sn-incorporated zeolites stabilize 2–5 times greater densities of methanol molecules than hydrophilic materials, which contain (SiOH)_x groups that promote extended hydrogen-bonded structures of methanol (CH₃OH) that pack the pores less densely.¹⁰ In other reports, hydrophilic zeolites adsorb 5 to 100-fold more water (H₂O) than hydrophobic zeolites because (SiOH)_x groups stabilize networks of H₂O molecules.¹¹⁻¹⁴ Pore polarity can also influence the selectivity of adsorption from binary mixtures, as Zhang et al. found that the selectivity for ethanol adsorption from ethanol and H₂O mixtures within hydrophobic pores exceeds that of hydrophilic pores by 5 times.¹⁵ The differences in the structure of intrapore liquids between (SiOH)_x-rich and (SiOH)_x-poor materials also affect rates and selectivities of zeolite-catalyzed reactions. For example, hydrophilic Ti- and Sn-BEA zeolites give 5–10 times lower turnover rates than the hydrophobic variants for aqueous-phase glucose isomerization.^{10,14,16−18} Measured activation enthalpies and entropies suggest that the H₂O networks in hydrophilic pores provide a significant entropic destabilization to the hydrophilic transition state for isomerization, which exceeds the corresponding enthalpic stabilization and leads to lower rates. Conversely, hydrophilic Ti-incorporated zeolites provide greater turnover rates than hydrophobic materials for alkene epoxidations with aqueous hydrogen peroxide (H₂O₂) in acetonitrile (CH₃CN),^{11,13,19−22} CH₃OH,^11,19,20,23 and gamma-butyrolactone¹¹ (C₄H₆O₂) solvents. Trends of rates and activation barriers indicate that the hydrophobic alkyl tail of the epoxidation transition state disrupts hydrogen bonds between H₂O molecules within hydrophilic pores, leading to entropic gains that increase turnover rates. The examples discussed here demonstrate that solvent molecules influence catalysis and adsorption in zeolites through changes in the excess free energy of adsorbates (G^ε).

Beyond epoxidation, manipulating the intrapore solvent environment in zeolites provides opportunities to influence the rates and regioselectivities of the subsequent epoxide ring-opening reaction (Scheme 1). An early study found that ion-exchanged FAU zeolites show greater selectivities but lower turnover rates to secondary alcohols (from ²C attack) in polar solvents compared to nonpolar solvents for the reaction between 1,2-epoxyoctane and sodium azide (NaN₃), although the authors do not provide clear hypotheses for these trends.²⁴ Brunelli and co-workers found that the postsynthetic fluoride treatment of Sn-BEA increases the rate of epichlorohydrin ring-opening with CH₃OH by a factor of 2 compared to an untreated Sn-BEA material.²⁵ They attributed the rate increases to a decrease in the density of (SiOH)_x groups that leads to entropic gains for ring-opening. More recent work used site quantification, rate measurements, and ¹⁵N NMR of adsorbed pyridine to show that Sn sites adjacent to (SiOH)_x nests provide greater turnover rates for epoxide ring-opening than Sn sites adjacent to a point SiOH defect.²⁶ These findings indicate that the (SiOH)_x structure near Sn atoms influences ring-opening kinetics, which may stem from differences in local solvent structure. Inspired by these findings, our group examined the mechanism of ring-opening 1,2-epoxybutane (C₄H₈O) with CH₃OH over hydrophilic M-BEA zeolites and demonstrated that addition of an aprotic cosolvent (CH₃CN) increases the preference to form the terminal ether product (from ¹C attack).²⁷ Measurements of activation barriers provide evidence that differences in regioselectivity arise from differences in the solvent composition near active sites that affect the stability of transition states for each regioisomers to different extents. To summarize, the acid site and (SiOH)_x density significantly influence epoxide ring-opening and other liquid-phase chemistries. While industrial ring-opening processes commonly utilize Brønsted²⁸⁻³⁰ and Lewis³¹⁻³³ acid catalysts, the literature lacks comparisons of how these different acid types affect the solvent environment during liquid-phase catalysis. The ability of Brønsted acidic protons (H⁺) to detach from the zeolite framework and form ionic solvent clusters intuitively leads to different solvent structures near catalytic active sites than for Lewis acidic metal atoms that remain bound to the framework.^5,13,34 Still, the effect of the interplay between (SiOH)_x functions and Lewis and Brønsted acid sites on the intrapore solvent environment in zeolites remains unclear. The strong influence of the choice of solvent and zeolite hydrophilicity shown in previous ring-opening studies underscores the importance of establishing these connections.

Scheme 1. Primary Reaction Products Formed by Epoxide Ring-Opening with a CH₃OH Nucleophile.

The nucleophile can attack at the primary (¹C) or secondary (²C) carbon on the epoxide ring.

Here, we reveal the impact of varying the (SiOH)_x density of Lewis acidic Zr- and Brønsted acidic Al-BEA zeolites on the intrapore solvent environment and, consequently, rates and regioselectivities of C₄H₈O ring-opening with CH₃OH in CH₃CN cosolvent. Despite apparently identical reaction mechanisms, turnover rates over (SiOH)_x-rich Zr-BEA (Zr-BEA-OH) exceed those over a (SiOH)_x-poor material (Zr-BEA-F) by ∼10 times. In contrast, turnover rates over Al-BEA-OH and Al-BEA-F materials differ by less than two times. Measurements of liquid and vapor solvent uptake provide evidence that Zr-BEA-OH adsorbs greater quantities of CH₃OH and promotes greater intrapore ratios of CH₃OH to CH₃CN than Zr-BEA-F, while Al-BEA-OH and Al-BEA-F show more similar solvent uptakes. The Al-BEA materials show nearly identical activation enthalpies and entropies for ring-opening and adsorption enthalpies for C₄H₈O, which likely lead to similar rates between the catalysts. In contrast, Zr-BEA-OH shows more positive activation enthalpy, entropy, and C₄H₈O adsorption enthalpy values than Zr-BEA-F. This trend provides strong evidence that the entropic gain from the disruption of hydrogen-bonded solvent molecules in the Zr-BEA-OH pores leads to greater ring-opening rates than Zr-BEA-F. Reaction regioselectivities depend strongly on the active metal choice and solvent composition but weakly on (SiOH)_x density, demonstrating that pore polarity influences rates and regioselectivities differently. Cumulatively, these findings show that the intrapore solvent structure depends intimately on the (SiOH)_x density and active site structure within the *BEA pores, which provides opportunities to control the kinetics and thermodynamics of catalytic reactions (i.e., epoxide ring-opening).

2. Methods and Materials

2.1. Catalyst Synthesis

M-BEA-OH (M = Al, Zr) were prepared by postsynthetic modification of a commercial Al-BEA material (TOSOH, lot no. 94HA6X02Y; Si/Al = 20). For Zr-BEA-OH, the commercial Al-BEA was treated in refluxing HNO₃ (Macron Chemicals, 68–70 wt %, 20 cm³ g^–1) at 433 K for ∼24 h to remove Al atoms from the *BEA framework by forming aqueous (AlNO₃)₃ complexes. The HNO₃ treatment was repeated three times to give a thoroughly dealuminated material denoted Si-BEA-OH (Si:Al > 1200 from EDXRF, >3500 from ICP-OES, vide infra). Between acid treatments, the catalyst sample was washed with deionized H₂O (18.2 MΩ cm, Elga Purelab Flex 2, 50 cm³ g_zeolite^–1) and recovered with vacuum filtration. For Al-BEA-OH, the parent Al-BEA material was treated in dilute HNO₃ (1 M) for ∼3 h to partially remove Al atoms from the framework. After the acid treatments, the dealuminated *BEA materials were loaded into quartz boats and placed in a three-zone furnace (Applied Test Systems, 3210), which was heated to 823 K (5 K min^–1) in flowing air (200 cm³ min^–1; Airgas, Ultra Zero grade) and held at 823 K for 6 h to remove organic residues. The heat treatment resulted in white powder Al-BEA-OH and Si-BEA-OH samples.

Zr-BEA-OH was synthesized by the liquid-phase incorporation of Zr atoms into the Si-BEA-OH material, based on previously reported procedures.^13,35 Si-BEA-OH was first heated in a round-bottom flask under vacuum (<5 Pa, 473 K) for 2 h to create a moisture-free environment. A rubber seal was then removed from the side arm of the flask, and isopropanol solvent (C₂H₇OH, Fisher Chemicals, 20 cm³ g_zeolite^–1) was poured into the flask under a high flow of Ar (500 cm³ min^–1) to minimize the adsorption of moisture from the air. Zr atoms were incorporated by then adding solid ZrCl₄ powder (Sigma-Aldrich, ≥99.9% trace metals basis) to the Si-BEA-OH and solvent mixture under flowing Ar (500 cm³ min^–1). The rubber seal was placed back onto the flask side arm, and the mixture was then heated and left overnight under an inert atmosphere (373 K, refluxing solvent, ∼16 h, 50 cm³ min^–1 Ar, Airgas, Ultra High Purity). The resulting material was recovered by vacuum filtration and was heated to 823 K (5 K min^–1) in flowing air (200 cm³ min^–1) and held at 823 K for 6 h, resulting in a white powder Zr-BEA-OH sample.

M-BEA-F (M = Al, Zr) were synthesized by adapting previously published procedures for hydrothermal synthesis of Ti-BEA-F materials.^16,36 For each M-BEA-F, 20 g of tetraethylammonium fluoride hydrate (TEAF, Sigma-Aldrich, 98%) was dissolved in 32.1 cm³ of deionized H₂O (18.2 MΩ cm, Elga Purelab Flex 2) in a polypropylene container. Next, 47.4 cm³ of tetraethylorthosilicate (TEOS, Sigma-Aldrich, >98 wt %) was added, and the mixture was stirred for 30 min at room temperature. Either 0.455 g of aluminum(III) isopropoxide (Al[OCH(CH₃)₂]₃, AIPO, Sigma-Aldrich, ≥98%) or 0.921 cm³ of zirconium(IV) n-propoxide in n-propanol (Zr[OCH(CH₃)₂]₄, ZrPO, Alfa Aesar, 70 wt % in n-propanol) was added, and the solutions were covered and stirred for an additional 16 h to produce white, opaque homogeneous solutions. The covers were removed, and the mixtures were stirred for 12–24 h to evaporate the alcohols formed from the hydrolysis of AIPO or ZrPO (isopropanol or n-propanol) and TEOS (ethanol). The mass of alcohols formed was estimated by assuming complete and stoichiometric hydrolysis of all AIPO, ZrPO, and TEOS added. The solutions were left uncovered to allow the alcohols to evaporate until the mass of the solutions decreased by an amount equal to ∼115% of the calculated mass of the alcohols to increase the likelihood of complete evaporation of these alcohols. The alcohols are assumed to evaporate preferentially before water based on their greater volatility. A mass of deionized H₂O equivalent to the difference between the total mass evaporated (42–47 g) and the calculated mass of alcohols formed (40–41 g) was added to account for the H₂O lost during evaporation. The evaporation procedure yielded gels with an approximate molar composition of 1 Si:0.006 Al or Zr:0.56 TEAF:8.89 H₂O. The gels were subsequently transferred to Teflon liners (Parr Instruments, 125 cm³, Model 4748). A small amount of Si-BEA-OH seeds (3% by mass relative to SiO₂ in the synthesis gel) from a previous synthesis was added to each gel to promote crystallization. The Teflon liners were loaded into a stainless-steel autoclave (Parr Instruments, 125 cm³, Model 4748) and heated to 413 K at dynamic conditions (60 rpm) in a convection oven (Yamato, DKN602C) for 22 days. The resulting materials were recovered by centrifugation, washed with H₂O, and dried in an oven for 12 h at 343 K. The dried solids were heated at 5 K min^–1 to 823 K in flowing air (200 cm³ min^–1) and held at 823 K for 6 h to produce white powder Al-BEA-F and Zr-BEA-F samples.

2.2. Catalyst Characterization

The crystallinities of the M-BEA materials were confirmed with an X-ray diffractometer (Bruker, D8 Advance) with Cu Kα radiation under ambient conditions. The M-BEA powders were loaded into a polypropylene sample holder. Metal oxide samples were purchased commercially and used as received: γ-Al₂O₃ (US Research Nanomaterials, Inc., 20 nm, 99%) and ZrO₂ (Sigma-Aldrich, 5 μm 99% trace metals basis). The diffractograms of M-BEA-OH (Figure S1a) and M-BEA-F (Figure S1b) match previously reported diffraction patterns for *BEA,³⁷ supporting that all M-BEA possess the *BEA framework. Furthermore, the patterns for M-BEA do not possess strong features in the characteristic peak locations for the respective metal oxides (Figure S1c), supporting that negligible quantities of each incorporated metal exist in metal oxide form.

The metal contents of the M-BEA samples were calculated with inductively coupled plasma optical emission spectroscopy (ICP-OES, PerkinElmer, Optima 8300) measurements carried out by staff scientists at the Microanalysis Laboratory at the University of Illinois. The measurements confirm that Zr-BEA-OH and Zr-BEA-F contain negligible quantities of Al (Si:Al ∼4000). Each Zr-BEA possesses similar Si:Zr values (131 for Zr-BEA-OH, 103 for Zr-BEA-F), and each Al-BEA shows a similar Si:Al ratio (69 for Al-BEA-OH, 61 for Al-BEA-F). Reported turnover rates are calculated by normalizing rates with the metal loadings determined by ICP-OES. Metal loadings and Si:Al ratios for each zeolite are shown in Table 1. The M-BEA-F materials were also tested for residual fluorine content using the ion-selective electrode (ISE) method (Orion, Thermo Scientific). No fluorine is detected in these materials from the ISE method, which has a detection limit of 0.01 ppm. This indicates that the M-BEA-F catalysts contain no (or sub ppm) levels of fluorine after hydrothermal synthesis, which does not impact the catalytic and thermodynamic measurements presented below.

Table 1. Characterization of the Chemical, Physical, and Electronic Properties of Synthesized M-BEA.

catalyst	M wt %a	Si:Ma	Si:Ala	band gap (eV)b	ΦIRc	BET surface area (m2 g–1)d	micropore volume (cm3 g–1)e	active metal (%)f
Al-BEA-OH	0.63	69	69		1.44	602 ± 11	0.145	97 ± 4
Al-BEA-F	0.72	61	61		0.19	516 ± 13	0.172	92 ± 3
Zr-BEA-OH	1.03	131	3980	5.8	1.41	536 ± 12	0.142	104 ± 7
Zr-BEA-F	1.44	103	4090	5.7	0.21	522 ± 13	0.170	96 ± 2

^aMeasured with ICP-OES.

^bExtracted from leading edge of Tauc plot from DRUV–vis.

^cCalculated from infrared transmission spectra of dehydrated M-BEA samples.

^dDetermined from Ar physisorption.

^eCalculated using the t-plots from Ar physisorption.

^fMeasured from in situ 1,2-diphenylethylenediamine site titrations.

The dispersity of the M atoms in the M-BEA catalysts was probed with diffuse reflectance UV–visible (DRUV–vis) spectroscopy. M-BEA were mixed and finely ground with magnesium oxide (MgO, Sigma-Aldrich, 99.9995%) at a MgO:M-BEA mass ratio of 10:1. MgO was used as a background for measurements. The total reflectance sample spectra were obtained with a UV–vis spectrophotometer (Varian, Cary 5G) under ambient conditions. γ-Al₂O₃ and ZrO₂ were again used as received. The band gap energies (Table 1) were determined by extrapolating the linear portion of the Tauc plots [F(R)·hv]^1/2) to the horizontal axis to determine the minimum energy of photons adsorbed (eV) (Figure S2). The band gap of ZrO₂ was measured in a similar manner as the M-BEA materials (Figure S2). Each Zr-BEA shows a greater band gap than ZrO₂, supporting that the Zr atoms are substituted within the framework at dispersed locations. Both Al-BEA materials and Al₂O₃ show very weak or no reflectance features, likely because the band gap of each material exceeds the scan range of the spectrophotometer. Nevertheless, the low weight loadings of each Al-BEA (Si:Al ∼60–70) and the unfavorable nature of Al–O–Al pairs (Loewenstein’s rule³⁸) support that Al atoms are well dispersed within the *BEA framework.

The coordination of metal atoms within M-BEA was examined using Raman spectroscopy. Ex situ Raman spectra were measured at ambient conditions on pressed catalyst pellets with a Raman spectrometer (Renishaw, InVia) equipped with a 532 nm laser. The accumulation time was 20 s per scan, and each Raman spectra was calculated by averaging 10 scans. The power density at the sample was approximately 2 mW μm^–2 (Gentec-EO, PRONTO-SI). The Raman spectra for each M-BEA-OH (Figure S3) and M-BEA-F (Figure S4) lack discernible features in the regions where the respective metal oxides show strong features, indicating the absence of M-O-M bonds. Together with the high band gap energies (Table 1), these spectra support that the M atoms in each material predominantly reside in tetrahedral positions within *BEA.

The relative density of (SiOH)_x groups within M-BEA was measured with infrared spectroscopy. A background spectrum was first taken with an empty transmission cell configured with CaF₂ windows. The cell was loaded into a Fourier transform infrared spectrometer (Bruker, Vertex 70) equipped with a liquid N₂-cooled HgCdTe detector, as described previously.³⁹ The cell was connected to a temperature controller and gas manifold, then heated to 573 K (∼5 K min^–1) and held for 2 h in flowing Ar (50 cm³ min^–1, 99.997%, Airgas) to desorb volatile compounds and H₂O. The background spectrum was then collected at 573 K (128 scans, 4 cm^–1). Each M-BEA was pressed into a pellet and loaded into the transmission cell. The cell was loaded into the spectrometer, and the spectra for M-BEA (Figure S5) were obtained in the same manner as the background measurement. The vibrational features of the infrared spectra at 1800–2100 and 3300–3750 cm^–1 represent the Si–O–Si overtones⁴⁰ of the *BEA framework and v(O–H) of (SiOH)_x groups,^41,42 respectively. The broad features from 3300 to 3700 cm^–1 arise from SiOH defects containing multiple hydroxyl moieties within (SiOH)_x groups. The sharper feature at ∼3750 cm^–1 represents isolated SiOH defects that do not interact with other SiOH.^41,42 The ratio of the areas for v(O–H) and v(Si–O–Si) at 1865 and 2000 cm^–1 gives a relative measure of SiOH density defined as Φ_IR (eq 1) in each M-BEA. The isolated SiOH feature is excluded from A_ν(O–H) in eq 1. The v(O–H) region was deconvoluted into multiple peaks (see Figure S6), and the isolated SiOH peak area was subtracted from the combined area of the v(O–H) region.

1

Values of Φ_IR (Table 1) indicate that the M-BEA-OH materials contain greater densities of (SiOH)_x groups than M-BEA-F. Calculation estimates based on the quantity of Al removed and M incorporated indicate that the M-BEA-OH materials contain 2.1–2.6 (SiOH)_x (unit cell)⁻¹ (see Section S1.5). M-BEA-F were synthesized hydrothermally without Al present, so we cannot make the same calculation of (SiOH)_x (unit cell)⁻¹. However, previously established trends⁴³ between Φ_IR and (SiOH)_x suggest that the M-BEA-F samples synthesized for this work (Φ_IR ∼0.20, Table 1) contain fewer than 0.1 (SiOH)_x per unit cell.

The presence of Lewis and Brønsted acid sites in M-BEA was characterized by infrared spectra of adsorbed pyridine (C₅H₅N, Sigma-Aldrich, >99%) and deuterated acetonitrile (CD₃CN, Cambridge Isotope Laboratories, 99.8% D atom). The catalysts were pelletized, loaded into the spectrometer, and pretreated at 573 K, as described above. The cell was then cooled to either 393 K (C₅H₅N) or 303 K (CD₃CN). A background spectrum was taken before flowing the adsorbates. C₅H₅N or CD₃CN were then introduced with a syringe pump (KD Scientific, Legato) and vaporized into a stream of flowing Ar (20 cm³ min^–1) within the heated gas-transfer lines. Reported spectra were collected after the absorbance features had reached a steady state. Section S1.6 presents the spectra and a detailed analysis of the results.

The structure of Al atoms within the Al-BEA materials was also examined with ex situ ²⁷Al NMR spectroscopy (Bruker AVIII 400, 10 kHz spin speed). The Al-BEA samples were loaded into a zirconia-based rotor (Bruker, 4 mm, kel-f cap). The rotor was then loaded into the NMR spectrometer, where spectra were collected at ambient temperature. The spectra were referenced to aqueous Al³⁺ at 0.24 ppm. The reported spectra are an average of 1024 scans, with a 0.6 μs pulse time and 1 s relaxation time. Figures S9 and S10 report the ²⁷Al NMR spectra for the bare Al-BEA samples and Al-BEA impregnated with C₅H₅N. These spectra provide insight into the structure of Al atoms with and without adventitious H₂O present.

The morphology of the M-BEA materials was examined with scanning electron microscopy (SEM). The samples were dispersed on double-sided carbon tape attached to an SEM holder. A sputter coater (Emitech, K575) was then used to coat the materials with an Au–Pd alloy. Au–Pd provides a conductive surface layer that inhibits surface charging and improves the SEM signal quality. The sample holder was loaded into the microscope (Hitachi-S 4800) and degassed before taking images. The micrographs were obtained at a working distance of 10 mm with an accelerating voltage of 5 kV. The SEM measurements reveal that M-BEA-F materials show larger particle sizes than M-BEA-OH. The SEM images for all M-BEA materials are displayed in Figure S11.

The surface area and micropore volumes of each M-BEA were determined using gas-phase adsorption isotherms of Ar (87 K) on a volumetric adsorption instrument (Micromeritics, 3Flex). The M-BEA samples were pelletized and sieved to retain particles from 100–250 μm in diameter. The samples were degassed under dynamic vacuum prior to adsorption (<7 × 10^–4 Pa, 673 K, 3 h). The surface area shown in Table 1 was calculated using the Rouquerol-modified Brunauer–Emmett–Teller (BET) method,⁴⁴ while the micropore volume was determined from the t-plot method.⁴⁵Figure S12 shows the Ar isotherms, and Table S4 presents the total and external surface area obtained from the Ar isotherms for each M-BEA. The surface area and pore volumes differ by less than 1.25 times between M-BEA-OH and M-BEA-F in each case but external surface area, in which M-BEA-OH materials show ∼2 times greater area than M-BEA-F. The similarities in these values suggest that differences in accessible pore volume and surface area do not contribute significantly to changes in epoxide ring-opening rates discussed in Section 3 (vide infra).

Collectively, the characterization of the M-BEA materials gives strong evidence that each material possesses a crystalline *BEA framework containing similar densities of (SiOH)_x. All M-BEA lack spectroscopically detectable quantities of the respective metal oxides and plausibly contain atomically dispersed metal atoms incorporated at framework positions.

2.3. Epoxide Ring-Opening Turnover Rate Measurements

Turnover rates for 1,2-epoxybutane (C₄H₈O, TCI Chemicals, >99.0%) ring-opening with methanol (CH₃OH, Sigma-Aldrich, ≥99.9%) in acetonitrile (CH₃CN, Fisher Chemical, HPLC grade) solvent were measured in three-necked round-bottom flasks with magnetic stirring (700 rpm). Benzene (Sigma-Aldrich, thiophene-free, >99%) was included in the reaction mixture as an internal standard. The flasks were submerged in a temperature-controlled bath containing either H₂O (298–318 K) or silicone oil (Sigma-Aldrich, viscosity 100 cSt) (323–328 K) on a hot plate (Corning, PC-420D). The flasks were also connected to reflux condensers to prevent evaporative losses. The reaction mixture was stirred for 0.5 h at the reaction temperature before taking an initial aliquot (∼0.5 cm³) to determine the initial concentration of C₄H₈O and the ring-opening products, 1-methoxy-2-butanol (C₅H₁₂O₂, 1M2B) and 2-methoxy-2-butanol (C₅H₁₂O₂, 2M1B). M-BEA (∼15–60 mg) was then added to initiate the reaction, and aliquots were taken as a function of time with a syringe equipped with a polypropylene filter (Tisch Scientific, 0.22 μm) to separate the sample solution from the catalyst. The concentrations of C₄H₈O, benzene, and ring-opening products were quantified as a function of time with a gas chromatograph (GC) (Agilent, 6850) equipped with a liquid autosampler, flame ionization detector, and polysiloxane column (HP-1, Agilent, 19091Z-115E). Elution times and sensitivity factors were determined using commercially obtained samples of C₄H₈O, CH₃OH, benzene, 1M2B (TCI Chemicals, >93.0%), and 2M1B (TCI Chemicals, >98.0%) (Section S2).

Reagents and solvents were used as received (i.e., not dried) prior to their use in rate measurements. Previous works demonstrate that H₂O may reversibly bind to Lewis^12,16 or Brønsted^34,46 acid sites in zeolites and influence reaction turnover rates for chemistries including alkene epoxidation.^11,13 Here, we exclude significant contributions from H₂O on ring-opening rates and thermodynamics for two reasons. First, ¹H NMR of the CH₃OH and CH₃CN do not contain detectable features corresponding to H₂O, which indicates these solvents contain less than 5 mM H₂O based on measured detection limits.¹¹ Second, we do not observe detectable quantities of 1,2-butanediol during reactions, which demonstrates that C₄H₈O does not undergo nucleophilic attack by H₂O.

Turnover rates were measured in CH₃CN cosolvent to allow for control of both C₄H₈O and CH₃OH concentrations ([C₄H₈O], [CH₃OH], where [x] denotes the concentration of species x). Measurements were also made in neat CH₃OH (24.7 M CH₃OH). The reaction yields two possible products, 1-methoxy-2-butanol (1M2B, a terminal ether) or 2-methoxy-1-butanol (2M1B, a terminal alcohol) (see Scheme 1 above). Initial turnover rate values were calculated by fitting turnover numbers (moles of product per moles of active metal) as a function of time to a second-order polynomial with the turnover rate fixed at zero at time equal to zero, then determining the derivative at time equal to zero. All reported turnover rates were measured at differential conversion (<10%) with an uncertainty of ∼10%, as demonstrated with replicated measurements. The carbon balance closes within 90–110% for all reported measurements. Furthermore, the carbon selectivity to the desired 1M2B and 2M1B products exceeds 90% across all measurements. Two minor peaks appear at similar GC retention times to the ring-opening products. While these products have not been identified, we excluded many likely species that may form by side reactions of C₄H₈O, including butanone, 1-butanol, 2-butanol, butyraldehyde, crotonaldehyde, crotyl alcohol, 1,2-butanediol, and dibutyl ether (Section S2). In addition, the unknown peaks evolve in the absence of CH₃OH, which demonstrates these do not form by secondary reaction of either ring-opening product with CH₃OH or C₄H₈O. Consequently, we conclude these peaks signify the reactions between C₄H₈O and other species present, such as atmospheric CO₂ to form 1,2-butylene carbonate (C₅H₈O₃) or CH₃CN^47,48 to form C₆H₁₀ON.

Hot filtration experiments were conducted to determine if the metal atoms or catalytic H⁺ sites leach from the *BEA framework during reactions and form homogeneous complexes active for ring-opening. A large aliquot (∼4 cm³) was taken ∼600–900 s after adding the catalyst, filtered with a polypropylene filter (Tisch Scientific, 0.05 μm) to separate the catalyst, then transferred into a scintillation vial (20 cm³, Trident Technology). The vial was transferred to a hot plate, which was preheated to 308 K and stirred at 700 rpm. Aliquots (∼0.5 cm³) were taken from the vial as a function of time. Figure S16 in Section S3 shows that the product concentrations change negligibly after filtering out the solid catalyst but continue to increase in the presence of the catalyst. Furthermore, a dealuminated *BEA material (Si-BEA-OH) shows product formation rates per gram of catalyst at least 13 times less than all M-BEA materials (Table S7), demonstrating that (SiOH)_x and Si–O–Si functions do not contribute significantly to the measured ring-opening turnover rates over M-BEA. These experiments provide strong evidence that the ring-opening of C₄H₈O with CH₃OH proceeds solely at active sites within the *BEA framework.

Mass transfer constraints prevent the measurement of intrinsic kinetic behavior, thus corrupting comparisons between catalysts and convoluting the interpretation of apparent rate measurements.⁴⁹ Therefore, we conducted experimental measurements to detect these potential artifacts and select optimal reaction conditions using methods recently described.⁵⁰ The conditions used for rate measurements here avoid internal and external mass transfer constraints because turnover rates do not depend on the loading of metal atoms for all materials within the range of loadings studied (Figure S17 in Section S3). These measurements demonstrate that all M-BEA materials satisfy the Madon–Boudart criterion⁴⁹ and are free of mass transfer artifacts. In addition, turnover rates exhibit combinations of first- and zero-order dependencies on the concentrations of C₄H₈O and CH₃OH at limiting conditions (Section 3.1).⁵¹ A mass-transfer limited material would show a sublinear dependence on reactant concentrations because the mean concentration of the reactants throughout the pores would not depend linearly on the fluid phase reactant concentrations.

The percentage of active metal atoms within each M-BEA was probed using in situ site titration experiments with (1R,2R)-(+)-1,2-diphenylethylenediamine (DPED, Sigma-Aldrich, 97%). Briefly, DPED was added to a mixture of CH₃CN, benzene, CH₃OH, and M-BEA at a ratio of DPED to metal atoms ranging from 0 to 1.5. The reaction flask was stirred for 0.5 h at 308 K to allow DPED to bind to the active sites before reaction. The reaction was then initiated by adding C₄H₈O, after which an aliquot was quickly taken at ∼0.004 h. Further aliquots were then taken as a function of time. The number of active sites in the materials was quantified by fitting a line to the linear portion of the titration curves shown in Section S4. All materials contain more than 90% active metal atoms, as shown in Table 1.

The DPED titration measurements for Zr-BEA-F suggest that a minor fraction (<5%) of Zr sites may be inactive for C₄H₈O ring-opening. While no extraframework Zr features (i.e., ZrO₂) are observed by Raman or DRUV–vis, we cannot exclude the possibility that a small percentage of ZrO₂ may exist in Zr-BEA-F and do not catalyze C₄H₈O ring-opening. The intensities of the ZrO₂ features may simply fall below the detection limit of the Raman and DRUV–vis spectrometers. Alternatively, Zr-BEA-F may contain a small number of tetrahedrally incorporated Zr atoms located in close proximity such that the bulky DPED titrant cannot titrate the sites individually,^52,53 which would cause the DPED titration method to slightly underestimate active metal content. In contrast, the minor fraction of inactive Al sites observed in the titrations for Al-BEA-OH and Al-BEA-F aligns with octahedral Al features present in the ²⁷Al NMR spectra (Figures S9 and S10). Based on the peak area ratios of tetrahedral to octahedral Al in the presence of C₅H₅N, the ²⁷Al NMR spectra predict 4% and 10% of Al atoms exist as octahedral species in Al-BEA-OH and Al-BEA-F, respectively. Adding C₅H₅N removes residual H₂O that forms hydrated octahedral Al species, which provides a more accurate report of the structure of Al atoms than ²⁷Al NMR spectra of the bare zeolites (see Section S1.7). The greater intensity of the octahedral NMR feature and the presence of a Lewis acid Al feature in the CD₃CN FTIR spectra for Al-BEA-F also both agree with the lower active metal percentage in Al-BEA-F (92%) than Al-BEA–OH (97%). These three techniques provide strong evidence that each Al-BEA material contains a minor fraction of extraframework, octahedral, Lewis acidic Al species that do not catalyze C₄H₈O ring-opening. We do not believe the presence of these extraframework species convolutes the kinetics in this manuscript because they comprise <10% of metal sites in all materials. Reported rates are normalized by the number of active metal atoms calculated from the DPED titrations.

2.4. Liquid-Phase and Gas-Phase Adsorption Measurements

The mole fraction of CH₃OH in the pores of M-BEA was estimated via liquid-phase uptake measurements from CH₃CN. The intrapore solvent compositions, shown in Figure 4, were estimated from the amount of solution absorbed by M-BEA and the difference in the liquid phase composition before and after mixing the solution with the catalyst.

Figure 4.

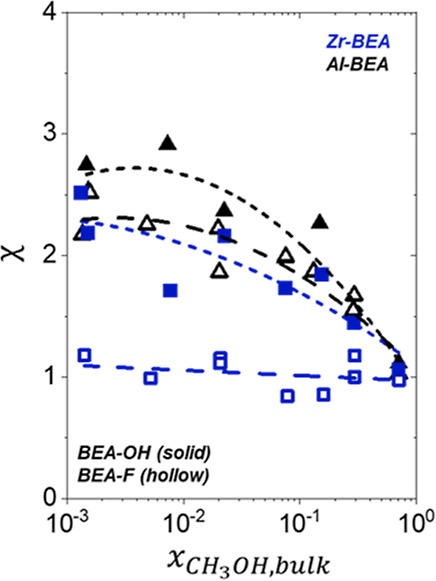
Preferential absorption of CH₃OH within zeolite pores expressed as values of χ as a function of x_CH3OH,bulk at 308 K in a mixture of CH₃OH and CH₃CN over hydrophilic (solid) and hydrophilic (hollow) Al- (black) and Zr-BEA (blue) materials.

The effect of (SiOH)_x density on gaseous CH₃OH (293 K) and CH₃CN (296 K) uptake was determined from gas-phase adsorption isotherms (Micromeritics, 3Flex). The M-BEA samples were pelletized and sieved to retain particles from 100–250 μm in diameter. The CH₃OH and CH₃CN used here were HPLC grade (Sigma-Aldrich) and were degassed under three freeze–pump–thaw cycles to ensure that the vapors were contamination free. The samples were degassed under dynamic vacuum prior to adsorption (<7 × 10^–4 Pa, 673 K, 3 h). The isotherms are presented in Figure 5.

Figure 5.

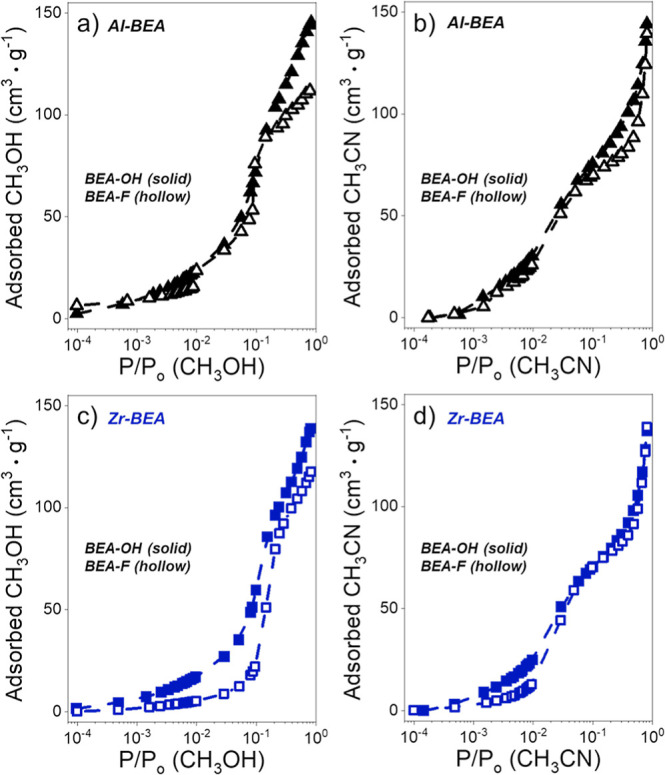
(a) CH₃OH (293 K) and (b) CH₃CN (296 K) adsorption isotherms over hydrophilic (solid) and hydrophilic (hollow) Al- (black) and Zr-BEA (blue) materials.

2.5. Liquid-Phase Adsorption Enthalpies for Reactants

The heat released upon adsorption of C₄H₈O and CH₃OH was measured with an isothermal titration calorimeter (ITC) (TA Instruments, NanoITC) equipped with sample and reference cells. A brief cleaning procedure was performed to prepare the sample and reference cells for each experiment. First, 500 cm³ of a cleaning solution consisting of 2 volume % detergent in DI H₂O (18.2 MΩ cm, Elga Purelab Flex 2) was flowed through the cell at room temperature. The sample cell was then rinsed with 1000 cm³ of DI H₂O. The sample cell and reference cell were then filled with 350 μL of H₂O (maximum cell volumes are 500 μL). A 50 μL ITC syringe was filled with H₂O, then loaded into the instrument. A subsequent electrical calibration used sequential pulses to determine the heat released from a calibrated Pt resistor. Finally, pure DI H₂O was injected into DI H₂O to ensure the sample cell was clean enough to begin experiments. The cell was assumed to be clean when the H₂O–H₂O injection released negligible amounts of heat (±3 μJ for each injection of 1 μL). The cleaning procedure was repeated if the H₂O–H₂O injection did not give sufficiently low heat rates.

In a typical experiment, a slurry of M-BEA (20–40 mg) in CH₃CN or CH₃OH was titrated by C₄H₈O (0.005 M) or CH₃OH (0.1 M) diluted in the same solvent used for the slurry. The mass of M-BEA in the sample cell was calculated by taking the difference between the mass added to the slurry and the mass remaining upon evaporation of the residual slurry after loading the cell. The titrations were carried out at 308 K with a stirring rate of 250 rpm. The sample cell was filled with 350 μL of M-BEA and solvent, while the reference cell was filled with 350 μL of solvent. The enthalpies of adsorption were calculated by averaging the integrated heats released upon adsorption of the titrant molecules to M-BEA sites from a 1 μL injection of titrant at low coverages (<0.25 mol titrant (mol M)⁻¹). The heat released in this regime remains approximately constant, suggesting that the calculated enthalpies represent the isosteric adsorption enthalpies for each titrant.⁴³

3. Results and Discussion

3.1. Brønsted and Lewis Acid Zeolites Show Distinct Ring-Opening Rate Dependences on Reactant Concentrations and (SiOH)_x Density

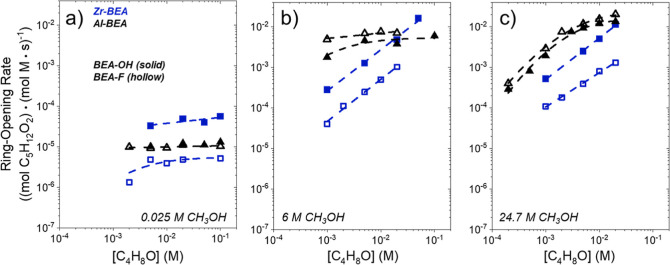
Turnover rates for C₄H₈O ring-opening depend on the concentrations of the reactants and products present, which determine the coverages of species on the active sites within M-BEA. Figures 1 and 2 show that rates depend differently on [CH₃OH], [C₄H₈O], and (SiOH)_x density between Al-BEA and Zr-BEA materials. The (SiOH)_x-dense Brønsted acid (Al-BEA-OH) shows nearly identical turnover rates to the (SiOH)_x-poor analog (Al-BEA-F) at all conditions. In contrast, ring-opening turnover rates over Zr-BEA-OH exceed rates over Zr-BEA-F by approximately an order of magnitude across the range of [CH₃OH] and [C₄H₈O] examined. Despite Zr-BEA and Al-BEA providing different rate dependences on (SiOH)_x density, turnover rates over each acid type exhibit nearly identical dependences on reactant concentrations among (SiOH)_x-rich and (SiOH)_x-poor materials. All M-BEA show linear rate dependences on [CH₃OH] (Figure 1) and a nearly zero-order dependence on [C₄H₈O] (Figure 2) at molar ratios of [CH₃OH] to [C₄H₈O] less than 50. These dependencies hold over Al-BEA catalysts up to ratios of [CH₃OH] to [C₄H₈O] around 1200. Turnover rates approach a near zero-order dependence on [CH₃OH] and linear dependence on [C₄H₈O] when ratios of [CH₃OH] to [C₄H₈O] exceed 5000 over Al-BEA materials. However, rates transition to the regime of strong dependence on [C₄H₈O] and weak dependence on [CH₃OH] over the Zr-BEA materials at much lower ratios of [CH₃OH] to [C₄H₈O] (>500). To summarize, the measurements in Figures 1 and 2 demonstrate that the (SiOH)_x density influences epoxide ring-opening rates over Lewis acid zeolites (Zr-BEA) but do not significantly affect rates over Brønsted acid zeolites (Al-BEA). The (SiOH)_x density does not influence the dependence of rates on reactant concentrations over either class of materials, with either C₄H₈O- or CH₃OH-derived species saturating the active sites within (SiOH)_x-rich and (SiOH)_x-poor M-BEA materials during C₄H₈O ring-opening.

Figure 1.

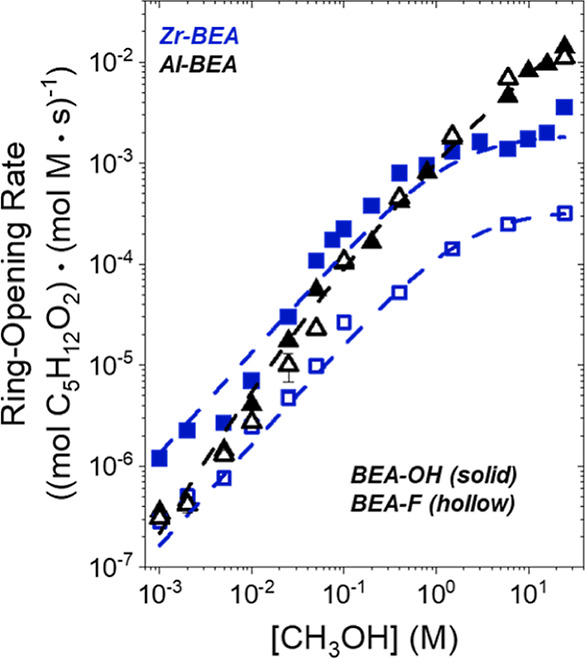
Turnover rates for C₄H₈O ring-opening with CH₃OH as functions of CH₃OH concentration over hydrophilic (solid points) and hydrophobic (hollow) Zr- (blue) and Al-BEA (black) materials (0.005 M C₄H₈O, CH₃CN solvent, 308 K).

Figure 2.

Turnover rates for C₄H₈O ring-opening with CH₃OH as functions of C₄H₈O concentration at (a) 0.025 M CH₃OH, (b) 6 M CH₃OH, or c) neat (24.7 M) CH₃OH (CH₃CN solvent, 308 K) over hydrophilic (solid points) and hydrophobic (hollow) Zr- (blue) and Al-BEA (black) materials.

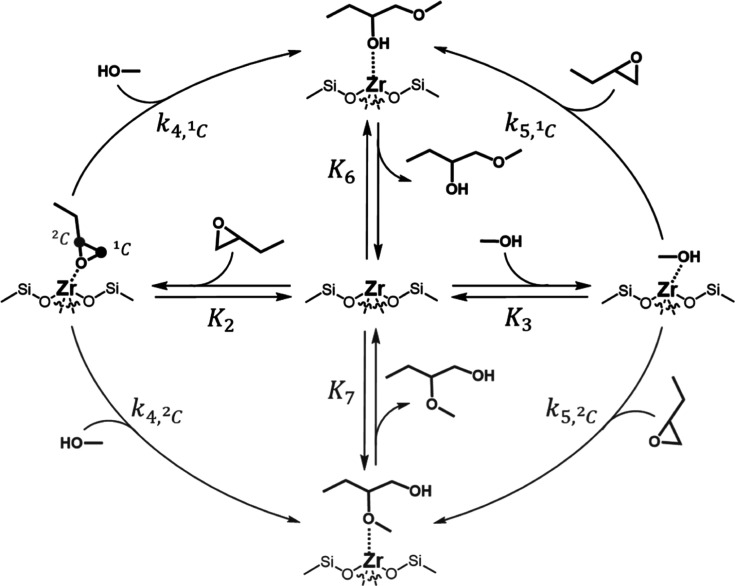
Scheme 2 presents a plausible system of elementary steps that explain the rate dependencies in Figures 1 and 2 over Zr-BEA materials (analogous set of steps for Al-BEA shown in Scheme S1). The cycle begins with the reversible adsorption of CH₃CN (step 1, not shown for clarity), C₄H₈O (step 2), or CH₃OH (step 3) to the active sites. The epoxide ring may open by the nucleophilic attack of bound C₄H₈O by CH₃OH (step 4) or the reaction of bound CH₃OH and a liquid phase C₄H₈O molecule (step 5). The distinct ring-opening products (C₅H₁₂O₂—1M2B and 2M1B) desorb to complete the catalytic cycle (steps 6 and 7). Here, steps with a ¹C subscript represent nucleophilic attack at the primary carbon in the C₄H₈O ring to form 1M2B, while a ²C subscript signifies attack at the secondary carbon to form 2M1B. 1M2B and 2M1B may form through either adsorbed intermediate by similar elementary steps that possess distinct rate constants (e.g., k_4,¹C, k_4,²C) and transition state structures that drive changes in regioselectivity. The formation rates of 1M2B and 2M1B show very similar dependencies on [CH₃OH] and [C₄H₈O] (see Section S5), supporting that the products form from common intermediates.

Scheme 2. Proposed Catalytic Cycle for C₄H₈O Ring-Opening with CH₃OH in CH₃CN Solvent Over Zr-BEA Zeolites.

We expect an identical set of steps over the Al-BEA materials, although the structure of the intermediates differs due to proton transfer to the reactive species. All adsorption steps are currently assumed as reversible. Steps to form 1M2B and 2M1B are denoted as ¹C or ²C, to signify nucleophilic attack on the primary and secondary carbons in the epoxide ring, respectively. For brevity, we do not show the reversible adsorption of CH₃CN molecules (step 1) in this cycle. We portray only reactions with molecularly adsorbed CH₃OH and C₄H₈O and not dissociatively bound oxygenates, although we expect each scenario may occur.

Rates for ring-opening (r_RO) equal the sum of the rates of total product formation through bound C₄H₈O- (r₄) or CH₃OH-derived intermediates (r₅)

2

where k₄ and k₅ represent the sum of the rate constants to form 1M2B and 2M1B in steps 4 (k_4,¹C, k_4,²C) and 5 (k_5,¹C, k_4,²C) in Scheme 2. [C₄H₈O*] and [CH₃OH*] represent the number of adsorbed C₄H₈O and CH₃OH intermediates, respectively. Applying the pseudo steady state hypothesis to the bound intermediates and deriving a site balance yields a turnover rate expression that accounts for reactions through bound C₄H₈O or CH₃OH intermediates

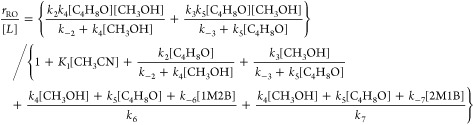3

Section S6 provides a full derivation and discussion of the necessary assumptions to simplify the rate expression under conditions where C₄H₈O- or CH₃OH-derived species saturate active sites and act as the most abundant reactive intermediate (MARI). Briefly, we utilize adsorption enthalpy measurements of C₄H₈O and CH₃OH and the molar ratios of [CH₃OH] to [C₄H₈O] to simplify eq 3 to yield the following rate expressions under conditions of C₄H₈O- (eq 4) and CH₃OH-derived (eq 5) MARI species

4

5

Equation 4 describes the rate trends in Figures 1 and 2 at lower molar ratios of [CH₃OH] to [C₄H₈O] (<50 over Zr-BEA, <1200 over Al-BEA), while eq 5 matches trends at higher [CH₃OH] to [C₄H₈O] ratios (>500 over Zr-BEA, >5000 over Al-BEA). The trends hold for both (SiOH)_x-rich and (SiOH)_x-poor materials, suggesting that each M-BEA material shares common reaction mechanisms and surface intermediates. Rate differences between materials instead likely stem from changes in the rate constants of the kinetically relevant nucleophilic attacks (k₄ and k₅).

Previous studies show that epoxide ring-opening rates and regioselectivities over zeolites depend strongly on the active metal and intrapore solvent structure. These variables likely drive the differences in k₄ and k₅ over Al-BEA and Zr-BEA materials through changes in the stability of reactive species. We postulate that turnover rate differences between Zr-BEA-OH and Zr-BEA-F reflect differences in noncovalent interactions with surrounding solvent molecules due to differences in (SiOH)_x density. Differences in k₄ and k₅ between Al-BEA and Zr-BEA likely stem from both the different charge transfer mechanisms of Lewis and Brønsted acid sites and the solvent environment surrounding these active sites. The following section quantitively examines the effect of these interactions on the stability of reactive species through activation barrier measurements.

3.2. Active Site Structure and Solvent Environment Drive Changes in Activation Barriers

The turnover rates for C₄H₈O ring-opening in Figures 1 and 2 depend on both the (SiOH)_x density of the *BEA framework and the active metal substituted within *BEA, stemming from changes in the values of k₄ and k₅ from the kinetically relevant steps shown in Scheme 2. The rate constants depend on the activation free energies (ΔG^‡) and corresponding activation enthalpies (ΔH^‡) and entropies (ΔS^‡), according to transition state theory

6

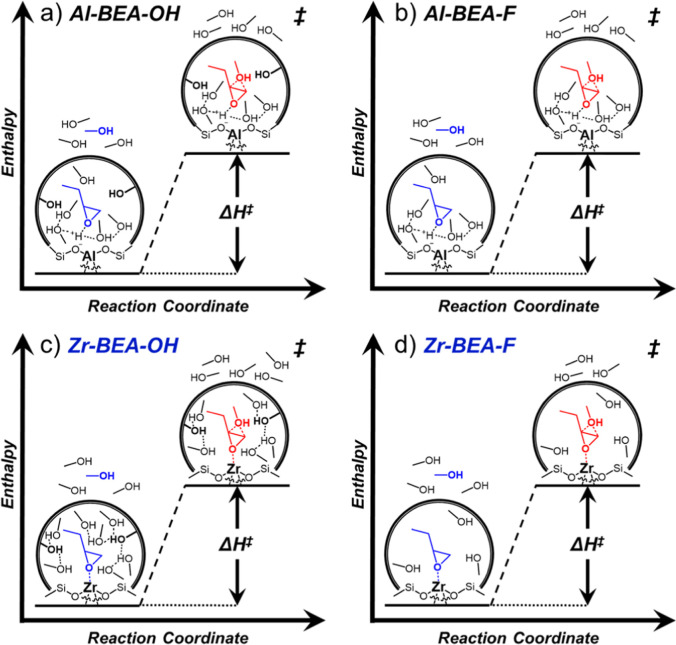
Scheme 3 depicts the proposed reaction coordinates for C₄H₈O ring-opening over (SiOH)_x-rich and (SiOH)_x-poor Zr-BEA and Al-BEA materials under a C₄H₈O-derived MARI. Values of ΔH^‡ and ΔS^‡ represent the difference between the energy of the transition state for nucleophilic attack and the sum of the energies of liquid-phase CH₃OH and the bound C₄H₈O intermediate (C₄H₈O*)

7

8

Scheme 3. Proposed Reaction Coordinate Diagrams for C₄H₈O Ring-Opening with CH₃OH in CH₃CN Solvent under Conditions of a MARI Species Derived From C₄H₈O Over (a) Al-BEA-OH, (b) Al-BEA-F, (c) Zr-BEA-OH, and (d) Zr-BEA-F.

CH₃OH adsorbs to react with C₄H₈O* and form the product, which desorbs to complete the reaction.

The activation parameters represent the total formation rate of both products. Both parameters consist of standard state (H⁰, S⁰) and excess (H^ε, S^ε) contributions

9

10

H⁰ and S⁰ values represent the covalent interactions stemming from the coordinate covalent bonds between Lewis acidic Zr sites and reactive species and the ionic interactions between the zeolite anion and protonated intermediates and transition states in the Brønsted acid material. H^ε and S^ε values encompass noncovalent interactions of the transition state or reactive intermediates with surrounding solvent molecules and the pore walls of the zeolite.^5,9

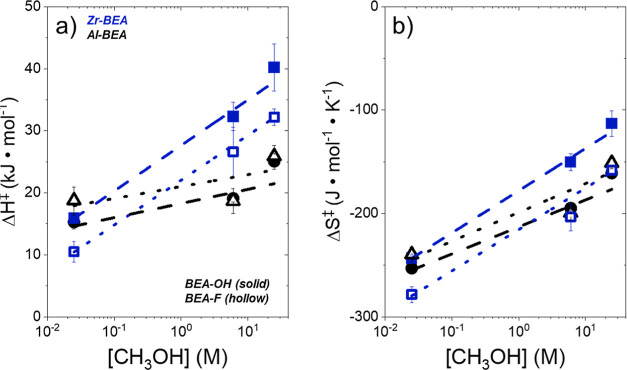
Figure 3 presents ΔH^‡ and ΔS^‡ values as a function of [CH₃OH] under conditions of a C₄H₈O-derived MARI species, corresponding to the rate expression described in eq 4. For all M-BEA, ΔH^‡ and ΔS^‡ values increase as a function of [CH₃OH]. The value of H_CH3OH⁰ does not vary as a function of [CH₃OH] over a given M-BEA material, while calculated H_CH3OH^ε values span a range of less than 3 kJ mol^–1 across the range of [CH₃OH] (see Section S7). Therefore, changes in the stability of reactive species within the zeolite pores (i.e., C₄H₈O*, transition state) drive the activation barrier differences with [CH₃OH] in Figure 3. Increasingly positive ΔH^‡ and ΔS^‡ values at higher [CH₃OH] suggest that the displacement of CH₃OH molecules from the *BEA pores during transition state formation leads to a greater enthalpic cost and corresponding entropic gain than the displacement of CH₃CN, consistent with our previous interpretations of epoxide ring-opening²⁷ and alkene epoxidation¹¹ activation barriers over M-BEA materials.

Figure 3.

Activation (a) enthalpies and (b) entropies for C₄H₈O ring-opening with CH₃OH (solid points −0.005 M C₄H₈O, 0.025 M CH₃OH in CH₃CN; half solid points −0.25 M C₄H₈O, 6 M CH₃OH in CH₃CN; hollow points −1 M C₄H₈O in neat (24.7 M) CH₃OH), 298–323 K) over hydrophilic (solid points, dashed lines) and hydrophobic (hollow points, dotted lines) Zr- (blue) and Al-BEA (black) materials. Turnover rates obtained at additional concentrations (0.25 and 1 M C₄H₈O) are provided in Section S9.

As [CH₃OH] increases from 0.025 to 24.7 M CH₃OH, the Al-BEA materials show less significant increases in ΔH^‡ (7–10 kJ mol^–1) and ΔS^‡ (88–92 J mol^–1 K^–1) than the Zr-BEA materials (22–25 kJ mol^–1, 120–130 J mol^–1 K^–1). The different dependences of these energies on [CH₃OH] stem from both standard state and excess contributions. The protonation of the transition state and adsorbed C₄H₈O in Al-BEA likely influences ΔH^‡,0 and ΔS^‡,0 values, leading to differences between Al- and Zr-BEA materials. Furthermore, the proton that comprises the active site within Al-BEA delocalizes across clusters of CH₃OH molecules⁵⁴⁻⁵⁶ at higher [CH₃OH] values (24.7 M and possibly 6 M, illustrated in Scheme 3). The delocalization and solvation of the proton may lower ΔH^‡ through either an enthalpic stabilization of the transition state (increasing H^‡ in eq 7) or an enthalpic destabilization of C₄H₈O* (increasing H_C4H8O*). We hypothesize that the delocalization of the active site increases H_C4H8O* but leads to a corresponding increase in S_C4H8O* by increasing the mobility of this adsorbed intermediate, as supported by more endothermic C₄H₈O adsorption enthalpies in CH₃OH than CH₃OH (see Section 3.4). These changes may arise from a combination of covalent and noncovalent interactions. Despite the convoluting effects of active site solvation in Al-BEA, the increasing trends of ΔH^‡ and ΔS^‡ with [CH₃OH] for all M-BEA shows the strong effect of noncovalent interactions on the activation barriers through changes in ΔH^‡,ε and ΔS^‡,ε.

The (SiOH)_x density of M-BEA can also influence ΔH^‡ and ΔS^‡ values for C₄H₈O ring-opening. Al-BEA-OH and Al-BEA-F provide similar values of ΔH^‡ (within 1–4 kJ mol^–1) and ΔS^‡ (within 5–10 J mol^–1 K^–1) at each [CH₃OH] value. The differences in ΔH^‡ and ΔS^‡ largely compensate to provide very similar rates over Al-BEA-OH and Al-BEA-F (Figures 1 and 2), as ΔG^‡ values at 308 K fall within 1 kJ mol^–1 at each [CH₃OH] for these materials. In contrast, Zr-BEA-OH shows more positive ΔH^‡ and ΔS^‡ values than Zr-BEA-F by 5–8 kJ mol^–1 and 35–55 J mol^–1 K^–1, respectively. Zr-BEA-OH provides ΔG^‡ values 5–6 kJ mol^–1 less than Zr-BEA-F (308 K), demonstrating that entropic gains lead to greater turnover rates in Zr-BEA-OH. The presence of (SiOH)_x groups plausibly alters ΔH^‡,ε and ΔS^‡,ε through changes in the solvent structure surrounding the active sites, as illustrated in Scheme 3. The H⁺ sites in the Al-BEA materials likely govern the solvent structure surrounding C₄H₈O* and the ring-opening transition state, leading to similar solvent configurations around the active sites in Al-BEA-OH (Scheme 3a) and Al-BEA-F (Scheme 3b). Therefore, the H⁺ sites may lessen the effect of (SiOH)_x on the solvent environment near active sites, giving similar ΔH^‡ and ΔS^‡ between Al-BEA-OH and Al-BEA-F. In comparison, the stronger influence of (SiOH)_x on ΔH^‡ and ΔS^‡ for Zr-BEA materials implies a more significant role of (SiOH)_x on the solvent structure surrounding the Zr sites. Zr-BEA-OH likely adsorbs greater quantities of CH₃OH and CH₃CN that form hydrogen bond networks within the pores (Scheme 3c), while the pores of Zr-BEA-F primarily contain weakly interacting CH₃OH and CH₃CN molecules (Scheme 3d). These hypotheses align with previous proposals for the structural differences of H₂O,^12,14,57 CH₃CN,^57,58 and alcohol^10,11,59 molecules within hydrophilic and hydrophobic Lewis acid zeolites. The formation of the ring-opening transition state likely requires the disruption of hydrogen bonds between solvent molecules within Zr-BEA-OH that leads to greater ΔH^‡ and ΔS^‡ values compared to Zr-BEA-F at all [CH₃OH]. The entropic gains exceed the enthalpic penalty, leading to greater rates for ring-opening in Zr-BEA-OH than Zr-BEA-F. These trends align with previous observations for alkene epoxidation with H₂O₂ in organic solvents (CH₃OH, CH₃CN) containing H₂O over Ti-BEA-OH and Ti-BEA-F,^{11,13,19,20,57,58} providing evidence that the intrapore solvent structure influences alkene epoxidation and the secondary epoxide ring-opening process in similar ways.

Figure 3 shows that differences in metal identity, solvent composition, and (SiOH)_x density lead to differences in rate constants for epoxide ring-opening through changes in ΔH^‡ and ΔS^‡, which stem from changes in the stability of reactive species in the zeolite pores. The distinct dependences of ΔH^‡ and ΔS^‡ on (SiOH)_x density over Al-BEA and Zr-BEA materials imply that different contributions govern the intrapore solvent structure within these Brønsted and Lewis acid materials. The following section establishes the differences in solvent structure among M-BEA-OH and M-BEA-F that drive rate differences for ring-opening.

3.3. Solvent Environment Governed by Different Functions in Brønsted and Lewis Acid Zeolites

Recent studies show that the intrapore composition of binary liquid mixtures in zeolites depends on the liquid solvent composition,^11,60−62 (SiOH)_x density within Lewis acid¹¹ and siliceous zeolites,^15,63,64 and the density of H⁺ sites within Brønsted acids.^15,34,65 We hypothesize that differences in the intrapore solvent composition will correlate strongly with observed trends in rates and activation barriers described above.

Figure 4 demonstrates that the solvent composition within M-BEA depends on the active metal identity, (SiOH)_x density, and mole fraction of CH₃OH within CH₃CN in the bulk solvent (x_CH3OH,bulk). Here, χ represents the ratio of the estimated mole fractions of CH₃OH in the zeolite pores (x_CH3OH,pore) and x_CH3OH,bulk at equilibrium (full experiment and calculation details provided in Section S10)

11

The M-BEA-OH materials in Figure 4 consistently show higher χ values than the corresponding M-BEA-F material, suggesting that (SiOH)_x groups facilitate CH₃OH adsorption relative to CH₃CN. CH₃OH contains a greater sum of hydrogen bond donors and acceptors (3) than CH₃CN (1), meaning that CH₃CN molecules contain fewer functions to coordinate with (SiOH)_x groups or form hydrogen-bonding networks with other molecules. Values of χ generally decrease with increasing x_CH3OH,bulk over each M-BEA material, with the M-BEA-OH and M-BEA-F materials collapsing to more similar values at higher x_CH3OH,bulk. These trends suggest that (SiOH)_x functions influence CH₃OH uptake more strongly at lower x_CH3OH,bulk, when lower quantities of CH₃OH reside in the pores. This interpretation appears consistent with previous observations in which H₂O uptake within hydrophilic zeolites from mixtures with ethanol^66,67 and acetic acid⁶⁸ depend more strongly on x_H2O,bulk at lower x_H2O,bulk values. At higher mole fractions, CH₃OH molecules can likely associate with preadsorbed CH₃OH within the pores, leading to a weaker influence of the (SiOH)_x density or active site structure on CH₃OH adsorption.

Interestingly, Al-BEA-OH and Al-BEA-F show more similar χ values than Zr-BEA-OH and Zr-BEA-F across the range of x_CH3OH,bulk. The greater dependence of χ values on (SiOH)_x density over Zr-BEA materials provides strong evidence that (SiOH)_x groups carry a greater influence on the intrapore solvent structure within Zr-BEA than Al-BEA materials. While Al-BEA-OH generally shows greater χ than Al-BEA-F, the similar trends and magnitudes of χ across x_CH3OH,bulk for these materials suggest that the H⁺ sites within Al-BEA impact the intrapore solvent structure more strongly than the framework Zr active sites in Zr-BEA. This explanation agrees with previous works that examined H₂O adsorption over Brønsted acid materials, which found that H₂O preferentially coordinates at H⁺ at lower coverages before binding to (SiOH)_x groups after saturating the H⁺ sites.^34,46,65 CH₃OH molecules may show a similar binding preference to the H⁺ sites in Al-BEA materials here. The observations from Figure 4 align with the interpretations of ΔH^‡ and ΔS^‡ values discussed in the previous section and the hypothesized differences in solvent structure among M-BEA illustrated in Scheme 3 above. The active sites in Al-BEA-OH and Al-BEA-F likely promote similar surrounding configurations of solvent molecules, while the difference in density of (SiOH)_x groups between Zr-BEA-OH and Zr-BEA-F leads to dissimilar solvent structures around the active sites. The distinct solvent structures within these materials likely drive the rate and activation barrier differences described in the previous sections.

While the χ values shown in Figure 4 give insight into the intrapore solvent compositions in M-BEA during C₄H₈O ring-opening, these data do not probe the absolute density of solvent within the pores. Figure 5 presents single-component vapor adsorption isotherms for CH₃OH and CH₃CN over M-BEA, revealing that the (SiOH)_x density and active site structure influence the density of solvent molecules within each M-BEA material. The ratios of uptakes between Al-BEA-OH and Al-BEA-F vary from 0.9 to 1.2 for CH₃CN and 1.0 to 1.5 for CH₃OH at relative pressures (P/P₀) less than 0.05. In contrast, Zr-BEA-OH uptakes differ significantly, ranging from 1.5 to 2.4 times more CH₃CN and 2.7 to 5.1 times more CH₃OH than Zr-BEA-F when P/P₀ falls below 0.05. The similar uptakes of both adsorbates for the Al-BEA materials support that CH₃CN and CH₃OH bind preferentially to H⁺ sites. The greater uptakes over Zr-BEA-OH than Zr-BEA-F indicate that the adsorbates coordinate to different framework locations; CH₃CN and CH₃OH likely bind preferentially to the (SiOH)_x nests within Zr-BEA-OH, while CH₃CN and CH₃OH should primarily bind to framework Zr atoms or Si–O–Si linkages within Zr-BEA-F.

As P/P₀ values surpass 0.05 and the pores begin to fill, the M-BEA-OH and M-BEA-F materials reach more similar uptakes of CH₃OH and CH₃CN regardless of acid type. For example, when P/P₀ equals 0.8, M-BEA-OH and M-BEA-F adsorb nearly identical quantities of CH₃CN, while the M-BEA-OH materials adsorb 1.3 times more CH₃OH than M-BEA-F. Comparisons between Zr-BEA and Al-BEA materials of similar (SiOH)_x density show the total uptake differs by less than 10% at P/P₀ of 0.8. These similarities suggest that as the adsorbates coordinate to less favorable binding sites and begin to form extended networks within the pore, the M-BEA materials reach similar densities of CH₃OH and CH₃CN regardless of the intrapore (SiOH)_x density or active site character.

Nevertheless, the differences in vapor uptake at the lowest P/P₀ values (i.e., P/P₀ < 0.05; Figure 5) show that the solvent environments surrounding the Brønsted acid sites depend weakly on nearby (SiOH)_x groups. In contrast, the (SiOH)_x nests within Zr-BEA-OH promote hydrogen-bonding structures of CH₃CN and CH₃OH near Zr active sites that do not appear within Zr-BEA-F pores. Furthermore, M-BEA-OH and M-BEA-F materials show greater differences in CH₃OH than CH₃CN uptake across the full range of P/P₀, demonstrating that (SiOH)_x nests carry a greater influence on the adsorption of CH₃OH. These findings agree with the interpretation of χ values in Figure 4. Overall, the comparisons of single-component vapor uptakes (Figure 5) further indicate that the H⁺ sites structure solvent similarly within Al-BEA-OH and Al-BEA-F, while the difference in (SiOH)_x density leads to differences in the solvent structure surrounding the catalytic active sites in Zr-BEA-OH and Zr-BEA-F.

Figures 4 and 5 give strong evidence that Lewis and Brønsted acid zeolites promote distinct intrapore solvent structures that depend differently on the (SiOH)_x density of the zeolite pores. Tuning the liquid solvent composition, active site structure, and (SiOH)_x density provides opportunities to control the solvent composition and density within porous catalysts. The solvent environment within M-BEA pores significantly influences C₄H₈O ring-opening rates and likely impacts the thermodynamics and selectivities of these processes, as highlighted in the following sections.

3.4. Enthalpies of 1,2-Epoxybutane Adsorption and Correlations to Apparent Barriers Show Influence of Intrapore Environment on Stability of Reactive Species

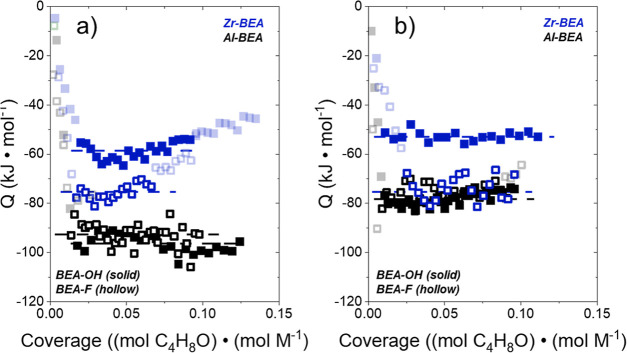
The Brønsted–Evans–Polanyi model proposes that the enthalpy of reaction for an elementary step scales linearly with the intrinsic activation energy of the same step, therefore establishing a connection between the intrinsic kinetics and thermodynamics of a reaction.⁶⁹⁻⁷¹ Hammond later explained this connection by postulating that the transition state for a reaction resembles the stable state (i.e., reactant or product) most similar in energy.^72,73 Recent studies demonstrate that the liquid-phase adsorption enthalpies for epoxide molecules over *BEA zeolites correlate positively with ΔH^‡ values for alkene epoxidation as a function of the active metal,³⁵ (SiOH)_x density,^43,57 and solvent composition.¹¹ More recently, we established linear correlations between epoxide adsorption enthalpies (ΔH_ads,C4H8O) and ΔH^‡ values for C₄H₈O ring-opening over M-BEA materials, implicating a transition state for ring-opening that resembles the adsorbed C₄H₈O reactant.²⁷ The measurement of ΔH_ads,C4H8O can provide insight into the differences in ring-opening transition state stability over M-BEA-OH and M-BEA-F materials.

Figure 6 reveals that ΔH_ads,C4H8O measured by isothermal titration calorimetry (ITC) depends on the active metal identity, solvent choice, and density of (SiOH)_x groups within M-BEA. The Al-BEA materials show more exothermic ΔH_ads,C4H8O values than the Zr-BEA materials in a CH₃CN-rich solvent, suggesting that C₄H₈O adsorbs more strongly to the Brønsted acid sites than to Zr framework sites. This trend corresponds with the weaker dependence of rates on [C₄H₈O] in Al-BEA than Zr-BEA materials (Figure 2) and gives insight into why C₄H₈O saturates sites on Al-BEA across nearly all conditions examined. ΔH_ads,C4H8O values over Zr-BEA-OH and Zr-BEA-F change negligibly upon changing the solvent from CH₃CN and CH₃OH, while CH₃OH provides ΔH_ads,C4H8O values ∼15 kJ mol^–1 more endothermic than CH₃CN over both Al-BEA-OH and Al-BEA-F. The more endothermic ΔH_ads,C4H8O for Al-BEA in CH₃OH may stem from the solvation of H⁺ by CH₃OH, which could influence the binding enthalpy of C₄H₈O to the H⁺ sites. However, we also cannot exclude that the reaction of C₄H₈O and CH₃OH may contribute to the measured ΔH_ads,C4H8O in CH₃OH over both Zr-BEA and Al-BEA materials.

Figure 6.

Heat released upon C₄H₈O adsorption in (a) CH₃CN and (b) CH₃OH as a function of C₄H₈O to metal ratio over hydrophilic (solid) and hydrophilic (hollow) Al- (black) and Zr-BEA (blue) materials (0.005 M C₄H₈O, 308 K). Transparent points are omitted from the adsorption enthalpy calculation, denoted by the dashed line. Section S11 includes adsorption enthalpy calculation details, raw data for the ITC experiments from Figure 6, and further ITC measurements, including CH₃OH adsorption over each M-BEA.

In both CH₃CN and CH₃OH, ΔH_ads,C4H8O values vary by less than 5 kJ mol^–1 between Al-BEA-OH and Al-BEA-F. In contrast, Zr-BEA-OH shows a more endothermic ΔH_ads,C4H8O than Zr-BEA-F by 17–21 kJ mol^–1 in both solvents. The similar ΔH_ads,C4H8O for the Al-BEA materials suggests that C₄H₈O similarly reorganizes the solvent surrounding the H⁺ sites in Al-BEA-OH and Al-BEA-F during adsorption. This observation provides strong evidence that the Al-BEA materials stabilize similar solvent structures around the H⁺ active sites, which leads to similar behavior between Al-BEA-OH and Al-BEA-F during C₄H₈O ring-opening, solvent adsorption, and C₄H₈O adsorption. The more endothermic ΔH_ads,C4H8O for Zr-BEA-OH compared to Zr-BEA-F likely originates from the disruption of hydrogen-bonded solvent molecules (CH₃OH or CH₃CN) by adsorbing C₄H₈O within the pores of Zr-BEA-OH. The displacement of weakly interacting solvent molecules within Zr-BEA-F requires a smaller enthalpic penalty and gives more exothermic ΔH_ads,C4H8O values.

Figure 7 shows that ΔH^‡ and ΔH_ads,C4H8O values correlate linearly for Al-BEA and Zr-BEA materials as a function of (SiOH)_x density at a given solvent composition. Interestingly, the Al-BEA and Zr-BEA materials do not fall on the same trendline. These differences likely originate from the proton transfer to the C₄H₈O* and ring-opening transition state or the delocalization of H⁺ by CH₃OH, which may convolute the comparisons between Brønsted and Lewis acids. Furthermore, changing the solvent from CH₃CN-rich to neat CH₃OH leads to a discontinuity in the trend for the Zr-BEA materials but not for the Al-BEA materials in Figure 7. We postulate that the enthalpy of reaction between C₄H₈O and CH₃OH may contribute to ΔH_ads,C4H8O and contribute to the discontinuity of the Zr-BEA materials (i.e., following adsorption of C₄H₈O, the adsorbed epoxide ring opens by reaction with CH₃OH in the calorimeter). The solvation of H⁺ by CH₃OH in Al-BEA apparently prevents or offsets this reaction contribution and leads to a consistent trend across all points. Section S12 includes a modified version of the enthalpy relationship from Figure 7 that accounts for the possible contribution of the enthalpy of reaction to ΔH_ads,C4H8O. Regardless of the reaction potentially convoluting ΔH_ads,C4H8O contributions between CH₃CN and CH₃OH, the linear correlations between ΔH^‡ and ΔH_ads,C4H8O over Zr-BEA and Al-BEA at a given solvent composition provide strong evidence that the adsorption of C₄H₈O and the formation of the C₄H₈O ring-opening transition state depend similarly on the surrounding solvent structure.

Figure 7.

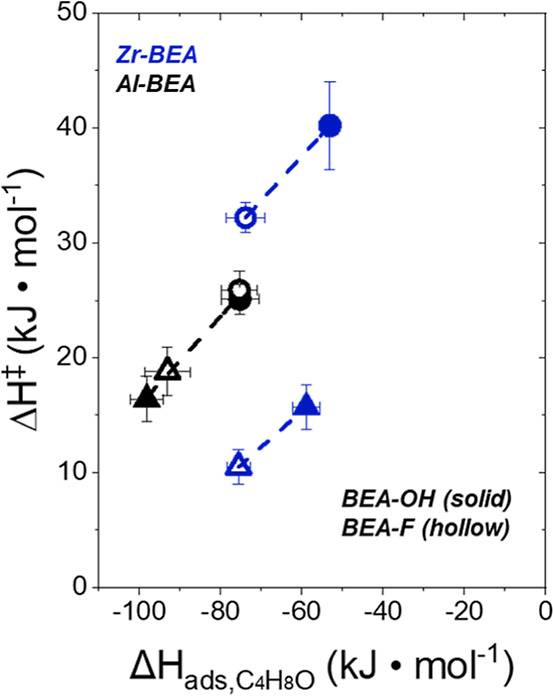
ΔH^‡ values for C₄H₈O ring-opening (from Figure 3, 0.025 M CH₃OH in CH₃CN (triangles) or 24.7 M CH₃OH (circles)) as a function of ΔH_ads for C₄H₈O over hydrophilic (solid) and hydrophilic (hollow) Al- (black) and Zr-BEA (blue) materials.

Al-BEA-OH and Al-BEA-F show very similar ΔH^‡ and ΔH_ads,C4H8O within both solvent compositions, giving further evidence that the difference in (SiOH)_x density between these materials does not yield differences in the intrapore solvent structure that drive differences in catalysis or adsorption. The more endothermic values of each enthalpy at a higher [CH₃OH] likely originate from a greater disruption of hydrogen-bonding solvent molecules during the formation of the ring-opening transition state and the adsorption of C₄H₈O within CH₃OH-rich solvents. ΔH_C4H8O^ε values vary by less than 3 kJ mol^–1 across the range of [CH₃OH] studied (Section S7), demonstrating that changes in ΔH_ads,C4H8O between solvents in Figure 7 result from changes in the stability of C₄H₈O* rather than liquid-phase C₄H₈O. Significantly, the enthalpic penalty for forming the transition state in Scheme 3a,b must exceed that for C₄H₈O adsorption to cause an increase in ΔH^‡ with [CH₃OH]; in other words, the excess enthalpy increases for the transition state (H^‡,ε) must exceed that of the reference state for ring-opening (H^ε_C4H8O*) (eq 9). The transition state likely occupies more space than the C₄H₈O* intermediate and requires a more significant displacement of surrounding solvent molecules, which may yield a more significant excess enthalpic penalty.

The disruption of hydrogen-bonded solvent also appears to impart a greater enthalpic penalty to the larger transition state in the Zr-BEA materials. However, Zr-BEA-OH shows more endothermic ΔH^‡ and ΔH_ads,C4H8O values than Zr-BEA-F in both CH₃CN-rich and neat CH₃OH solvents. The inability of solvent molecules to form hydrogen-bonding networks in the pores of Zr-BEA-F likely lessens the enthalpic cost required to form the ring-opening transition state or adsorb C₄H₈O to the Zr sites. Notably, the slope of the correlation between Zr-BEA materials in Figure 7 becomes more positive in neat CH₃OH compared to a CH₃CN-rich solvent. The steeper slope of the Zr-BEA correlations in neat CH₃OH likely occurs because H^‡,ε depends more strongly on the (SiOH)_x density within Zr-BEA than H^ε_C4H8O* in the presence of CH₃OH than CH₃CN. Specifically, the difference in enthalpic penalties provided to the larger transition state and smaller C₄H₈O* becomes more significant when the pores of Zr-BEA-OH contain hydrogen-bonded CH₃OH compared to hydrogen-bonded CH₃CN. Overall, the different dependences of ΔH^‡ and ΔH_ads,C4H8O on (SiOH)_x density between Al-BEA and Zr-BEA materials reinforces that the solvent structure within the *BEA pores depends on different functions within Brønsted and Lewis acid zeolites. The H⁺ sites likely govern the solvent environment surrounding active sites within Al-BEA-OH and Al-BEA-F, while the higher density of (SiOH)_x groups within Zr-BEA-OH likely leads to a significantly different solvent environment around the Zr active sites than in Zr-BEA-F.

The solvent structure within M-BEA pores appears to drive differences in ring-opening turnover rates and activation barriers through changes in the excess energies of reactive species, as described above. The following section examines the consequences of these excess interactions and the covalent interactions between the reactive species and active sites on the regioselectivities of C₄H₈O ring-opening.

3.5. Active Site Structure and Solvation Drive Changes in Ring-Opening Regioselectivity

The interactions between transition states and intermediates with active and interactions with surrounding solvent molecules within zeolites influence rates and barriers for epoxide ring-opening. The distribution of regioisomers for C₄H₈O ring-opening with CH₃OH over M-BEA (see Scheme 1 above) also depends on these intrapore interactions, as shown in our previous work.²⁷ The regioselectivities are quantified with a rate ratio defined as β

12

where r_1M2B and r_2M1B represent the formation rates of 1M2B and 2M1B, respectively. The formation rates depend on the reactant concentrations and product-specific rate constants for the kinetically relevant steps (k_4,¹C, k_4,²C, k_5,¹C, k_5,²C) (Scheme 2). The expression for β simplifies if we assume the products form from identical surface intermediates and fluid-phase reactants upon the same set of active sites and we consider only conditions of C₄H₈O*-covered active sites (full derivation and discussion of assumptions in Section S6). In this case, β solely depends on the difference between the free energies of the transition states for the individual products (i.e., G^‡_1M2B and G^‡_2M1B)

13

Figure 8 presents β values as a function of reactant concentrations under conditions of C₄H₈O*-covered active sites, which depend on the liquid solvent composition and the active metal and (SiOH)_x density within the *BEA pores. β values decrease at greater [CH₃OH] for the Zr-BEA materials (Figure 8a), with β values approaching 3–3.5 at the lowest [CH₃OH] (<0.1 M CH₃OH) and β values of 1–1.5 in CH₃OH-rich solvents. The β values over Al-BEA-OH and Al-BEA-F change less strongly with [CH₃OH], with values between 0.75 and 1.5 across the range of [CH₃OH]. Figure 8b shows that β values increase slightly with increasing [C₄H₈O] across each M-BEA at several values of [CH₃OH] (0.025, 6, and 24.7 M). The generally greater regioselectivities to the terminal ether (1M2B) compared to the terminal alcohol (2M1B) in Figure 8 aligns with prior studies, which commonly attribute the difficulty of forming the terminal alcohol to the steric hindrance for nucleophilic attack at the more substituted C-atom of the oxirane ring.⁷⁴⁻⁷⁷ However, Figure 8 also reveals that increasing the number of hydrogen bond donors and acceptors within the solvent by increasing [CH₃OH] leads to a greater preference to form 2M1B, which agrees with a recent report showing that intentionally adding hydrogen-bonding acceptors to the system (e.g., diols) leads to greater selectivity to terminal alcohols during epoxide ring-opening with alcohols over homogeneous borane catalysts.⁷⁸ CH₃OH molecules may preferentially stabilize the 2M1B transition state relative to 1M2B through hydrogen-bonding interactions within M-BEA, as evidenced by the increasing enthalpic preference to form 2M1B at higher [CH₃OH] that corresponds to lower β values (see Section S8 for comparisons of the activation barriers to form the products). At lower [CH₃OH] values, CH₃CN molecules likely interrupt CH₃OH from forming hydrogen bonds, thus contributing to the greater preference toward the TE product.

Figure 8.

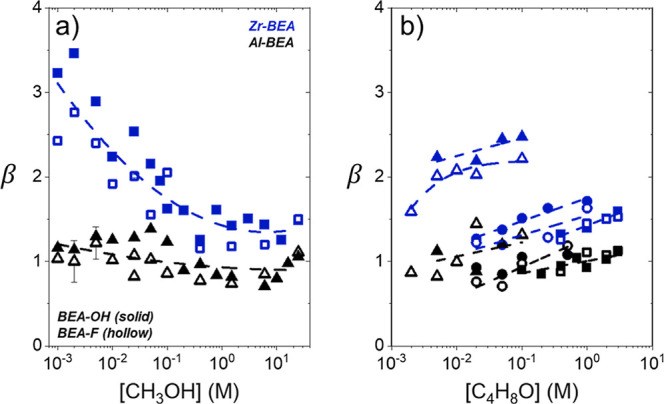
Measures of regioselectivity quantified by values of β for C₄H₈O ring-opening with CH₃OH as a function of (a) CH₃OH concentration (0.005–1 M C₄H₈O, [CH₃OH]/[CH₃CN] = 0.2–100, CH₃CN solvent, 308 K), and (b) C₄H₈O concentration at 0.025 M (triangles), 6 M (circles), or 24.7 M CH₃OH (squares) (CH₃CN, 308 K) over hydrophilic (solid) and hydrophilic (hollow) Al- (black) and Zr-BEA (blue). All measurements were made under C₄H₈O*-covered active sites.

The weaker dependence of β values on reaction composition over Al-BEA compared to Zr-BEA materials in Figure 8 suggests that the intrapore solvent environment plays a lesser role in regioselectivity trends over the Brønsted acids. Instead, the covalent interactions between the H⁺ sites and reactive species appear to drive the distribution of regioisomers over Al-BEA. At an equivalent reaction composition, the Al-BEA materials consistently show lower β values than the Zr-BEA materials. Recent quantum chemical calculations reveal that protonation of the epoxide causes elongation of the weaker C–O bond between the more substituted carbon and epoxide oxygen atom,⁷⁹ thereby facilitating the nucleophilic attack at this carbon to form the terminal alcohol.⁷⁹⁻⁸² These interactions between the epoxide ring, H⁺ site, and the attacking CH₃OH molecule likely lead to β values near unity in all conditions. A previous study reported β values from 0.8 to 1.3 for C₄H₈O ring-opening in neat CH₃OH catalyzed by sulfuric acid and Brønsted acid zeolites of varying pore size, agreeing with the span of values for Al-BEA in Figure 8.⁸³ Homogeneous (i.e., aluminum triflate)^84,85 and heterogeneous Lewis acids (i.e., Hf-, Sn-, Zr-BEA)⁷⁵ previously achieved β values between 1.2 and 1.4 for C₄H₈O ring-opening in neat CH₃OH. Figure 8 demonstrates that introducing an organic cosolvent (i.e., CH₃CN) provides opportunities to extend to higher β values over Lewis acidic materials.

The (SiOH)_x density of the M-BEA materials only slightly affects β values, in contrast to the strong effect of the active metal choice and solvent composition. The weak influence of (SiOH)_x on regioselectivity aligns with previous observations for 1,2-epoxyhexane ring-opening over Sn-BEA catalysts.²⁵ While this trend corresponds with the weak dependence of rates, activation barriers, and intrapore solvent composition on the (SiOH)_x density of Al-BEA (vide supra), which differ from the persistent differences between the Zr-BEA-OH and Zr-BEA-F materials in previous sections. The explanation for this dissimilarity also remains unclear, but we postulate that the differences in solvent structure between Zr-BEA-OH and Zr-BEA-F do not influence β values as strongly as rates or activation barriers. The solvent environment surrounding the epoxide ring, where the nucleophilic attack occurs (i.e., near the active site), may sense the influence of (SiOH)_x groups less significantly than the extended solvent structure near the hydrophobic alkyl tail of the transition state (i.e., further from the active site) (see Scheme 4). In other words, the disruption of hydrogen-bonded solvent molecules by the alkyl tail of the transition state likely facilitates greater rates in Zr-BEA-OH over Zr-BEA-F, but does not contribute significantly to regioselectivity trends. To summarize, the observations from Figure 8 indicate that changing the active metal and solvent composition leads to differences in regioselectivities by altering the stability of transition states to form the ring-opening products, and the contributions from differences in (SiOH)_x density only weakly influence the regioselectivity for a given form of active site.

Scheme 4. Proposed Origins of Differences between Zr-BEA-OH and Zr-BEA-F.

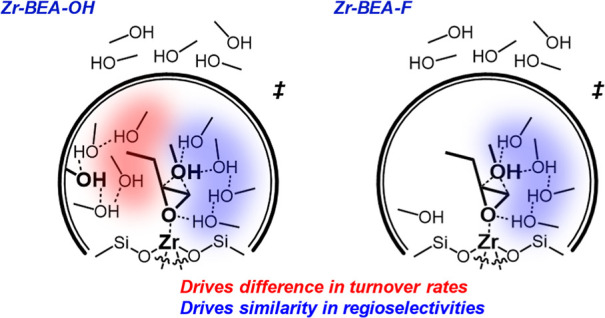
The disruption of hydrogen bonded-solvent by the alkyl tail of the transition state drives greater rates in Zr-BEA–OH, while the similar solvent structure surrounding the epoxide ring leads to similar regioselectivities among the materials.

Industrial liquid-phase epoxide ring-opening processes commonly utilize homogeneous catalysts^31−33,86 and ion-exchange resins,⁸⁷⁻⁸⁹ which provide high rates but suffer from issues with deactivation, regeneration, and separation. Microporous silicates (i.e., zeolites) offer a more stable and sustainable alternative that allows for precise control of the density and structure of intrapore liquids through changes in the active site character and (SiOH)_x density. While shown here for epoxide ring-opening, manipulating the properties of zeolite catalysts provides opportunities to control rates and selectivities of liquid-phase processes in general.

4. Conclusions

Rates and regioselectivities for epoxide ring-opening reactions depend intimately on the structure of solvent molecules, type of acid site (Lewis or Brønsted), and quantity of (SiOH)_x groups confined within zeolite pores. Introducing a high density of (SiOH)_x defects to the Lewis acidic zeolite (i.e., Zr-BEA-OH) facilitates C₄H₈O ring-opening rates by ∼10 times compared to the low density (SiOH)_x counterpart (i.e., Zr-BEA-F). Measurements of activation barriers, C₄H₈O adsorption enthalpies, and intrapore solvent compositions provide evidence that the disruption of networked solvent molecules within Zr-BEA-OH confers entropic gains to the transition state for ring-opening. This strong effect of (SiOH)_x nests on turnover rates over Lewis acidic zeolites corresponds to previous reports for alkene epoxidation^{11,13,19−23} and glucose isomerization,^{10,14,16−18} where (SiOH)_x groups stabilize hydrogen-bonded solvent structures that increase and decrease rates, respectively.

In contrast to the Lewis acids, Al-BEA-OH and Al-BEA-F show similar ring-opening rates (within a factor of 2), activation barriers, and solvent compositions across all conditions examined. These trends align with previous studies that Brønsted acid zeolites of different (SiOH)_x density provide rate constants for ethanol dehydration⁶⁵ and rates for glucose acetalization⁹⁰ within a factor of 2 in a condensed phase. Taking this work together with previous studies, the interactions between solvent molecules and (SiOH)_x nests in zeolites can strongly influence the kinetics of a variety of liquid phase catalytic reactions over Lewis acid sites but generally have a weak effect on kinetics over Brønsted acid sites. The H⁺ sites in the Brønsted acids likely lessen the effect of (SiOH)_x on the solvent environment near active sites, while the density of (SiOH)_x groups likely governs differences in solvent structure among the Zr-BEA materials. Interestingly, regioselectivities depend weakly on (SiOH)_x density for Al- and Zr-BEA, instead showing strong dependences on the acid type and reaction solvent composition. Therefore, different combinations of variables drive changes in rates and regioselectivities for ring-opening, providing opportunities to control these important reaction parameters independently. Evidently, the choices of zeolite acid type, intrapore (SiOH)_x density, and solvent carry strong consequences and warrant consideration during the design of catalysis and adsorption processes at zeolite–liquid interfaces.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.4c00398.

• X-ray diffraction, diffuse-reflectance UV–vis, ex situ Raman spectroscopy, transmission total-reflectance FT-infrared spectroscopy, ex situ solid-state ²⁷Al NMR spectroscopy, scanning electron microscopy, Ar physisorption, GC sensitivity factors, hot filtrations, Madon–Boudart tests, 1,2-diphenyl-1,2-ethylene diamine active site titrations, supplemental epoxide ring-opening kinetics, rate expression derivation, excess enthalpies and free energies, supplemental activation barriers and equations, intrapore solvent uptakes, supplemental ITC thermograms, and supplemental adsorption enthalpies (PDF)

Author Contributions

D.S.P. synthesized the zeolites and performed kinetic, thermodynamic, spectroscopic, and catalyst characterization experiments. J.K.K. performed catalyst characterization, kinetic measurements, and assisted with zeolite synthesis. M.A.J. performed the vapor physisorption experiments. H.L. performed the ²⁷Al NMR spectroscopy experiment and assisted with zeolite synthesis. D.S.P. and D.W.F. planned the project and conceptualized the manuscript. The manuscript was written by D.S.P. with input from all the authors. All authors have given approval to the final version of the manuscript.

This work was supported by the Department of Energy (DE-SC0020224). D.S.P. acknowledges the National Science Foundation Graduate Research Fellowship program (DGE-1746047).

The authors declare no competing financial interest.