Abstract
We analyze the global structure of the worldwide air transportation network, a critical infrastructure with an enormous impact on local, national, and international economies. We find that the worldwide air transportation network is a scale-free small-world network. In contrast to the prediction of scale-free network models, however, we find that the most connected cities are not necessarily the most central, resulting in anomalous values of the centrality. We demonstrate that these anomalies arise because of the multicommunity structure of the network. We identify the communities in the air transportation network and show that the community structure cannot be explained solely based on geographical constraints and that geopolitical considerations have to be taken into account. We identify each city's global role based on its pattern of intercommunity and intracommunity connections, which enables us to obtain scale-specific representations of the network.
Keywords: complex networks, betweenness centrality, critical infrastructures
Like other critical infrastructures, the air transportation network has enormous impact on local, national, and international economies. It is thus natural that airports and national airline companies are often times associated with the image a country or region wants to project (1–4).
The air transportation system is also responsible, indirectly, for the propagation of diseases such as influenza and, recently, severe acute respiratory syndrome (SARS). The air transportation network thus plays for certain diseases a role that is analogous to that of the web of human sexual contacts (5) for the propagation of AIDS and other sexually transmitted infections (6, 7).
The worldwide air transportation network is responsible for the mobility of millions of people every day. Almost 700 million passengers fly each year, maintaining the air transportation system ever so close to the brink of failure. For example, U.S. and foreign airlines schedule ≈2,700 daily flights in and out of O'Hare International Airport (Chicago) alone, >10% of the total commercial flights in the continental U.S. and more than the airport could handle even during a perfect “blue-sky” day. Low clouds, for example, can lower landing rates at O'Hare from 100 per hour to just 72 per hour, resulting in delays and flight cancellations across the country. The failures and inefficiencies of the air transportation system have large economic costs; flight delays cost European countries 150 billion to 200 billion Euro in 1999 alone (8).
These facts prompt several questions. What has led the system to this point? Why can't we design a better system? To answer these questions, it is crucial to characterize the structure of the worldwide air transportation network and the mechanisms responsible for its evolution. The solution to this problem is, however, far from simple. The structure of the air transportation network is mostly determined by the concurrent actions of airline companies, both private and national, that try, in principle, to maximize their immediate profit. However, the structure of the network is also the outcome of numerous historical “accidents” arising from geographical, political, and economic factors.
Much research has been conducted on the definition of models and algorithms that enable one to solve problems of optimal network design (9, 10). However, a worldwide, “system” level analysis of the structure of the air transportation network is still lacking. However, just as one cannot fully understand the complex dynamics of ecosystems by looking at simple food chains (11) or the complex behavior in cells by studying isolated biochemical pathways (12, 13), one cannot fully understand the dynamics of the air transportation system without a “holistic” perspective. Modern “network analysis” (14–18) provides an ideal framework within which to pursue such a study.
We analyze here the worldwide air transportation network. We build a network of 3,883 locales, villages, towns, and cities with at least one airport and establish links between pairs of locales that are connected by nonstop passenger flights. We find that the worldwide air transportation network is a small-world network (19) for which (i) the number of nonstop connections from a given city and (ii) the number of shortest paths going through a given city have distributions that are scale-free. In contrast to the prediction of scale-free network models, we find that the most-connected cities are not necessarily the most “central,” that is, the cities through which most shortest paths go. We show that this surprising result can be explained by the existence of several distinct “communities” within the air transportation network. We identify these communities by using algorithms recently developed for the study of complex networks and show that the structure of the communities cannot be explained solely based on geographical constraints and that geopolitical considerations also must be taken into account. The existence of communities leads us to the definition of each city's global role, based on its pattern of intercommunity and intracommunity connections.
Data
Many measures, including total number of passengers, number of flights, or amount of cargo, quantifying the importance of the world airports were compiled and publicized (20). We study here the oag max database (http://oagdata.com/solutions/max.aspx), which comprises flight schedule data of >800 of the world's airlines for the period November 1, 2000, to October 31, 2001. This database is compiled by OAG Worldwide (Downers Grove, IL), and includes all scheduled flights and scheduled charter flights, both for big aircrafts (air carriers) and small aircrafts (air taxis).
We focused our analysis on a network of cities, not of airports; for example, Newark Liberty International Airport, John F. Kennedy International Airport, and LaGuardia Airport are all assigned to New York City. We further restricted our analysis to passenger flights operating in the time period November 1, 2000, to November 7, 2000. Even though these data are >4 years old, the resulting worldwide airport network is virtually indistinguishable from the network one would obtain if using data collected today. The reason is that air traffic patterns are strongly correlated with (i) socioeconomic factors, such as population density and economic development; and (ii) geopolitical factors, such as the distribution of the continents over the surface of the Earth and the locations of borders between states (21). Clearly, the time scales associated to changes in these factors are much longer than the lag in the data we analyzed here.
During the period considered, there were 531,574 unique nonstop passenger flights, or flight segments, operating between 3,883 distinct cities. We identified 27,051 distinct city pairs having nonstop connections. The fact that the database is highly redundant, that is, that most connections between pairs of cities are represented by more than one flight, adds reliability to our analysis. Specifically, the fact that unscheduled flights are not considered does not mean, in general, that the corresponding link between a certain pair of cities is missing in the network, because analogous scheduled flights may still operate between them. Similarly, even if some airlines have canceled their flights between a pair of cities since November 2000, it is highly unlikely that all of them have.
We created the corresponding adjacency matrix for this network, which turns out to be almost symmetrical. The very minor asymmetry stems from the fact that a small number of flights follow a “circular” pattern, i.e., a flight might go from A to B to C and then back to A. To simplify the analysis, we symmetrized the adjacency matrix.
Further, we built regional networks for different geographic regions (Table 1). Specifically, we generated 21 regional networks at different aggregation levels. At the highest-aggregation level, we generated six networks; one each for Africa, Asia and Middle East, Europe, Latin America, North America, and Oceania. For each of these regions, except for North America and Oceania, we generated between two and five subnetworks. For instance, the Asia and Middle East network was further subdivided into South Asia, Central Asia, Southeast Asia, Northeast Asia, and Middle East.
Table 1. Number of locations with airports by major geographic region.
| Region | No. of locations |
|---|---|
| Africa | 364 |
| Asia and Middle East | 719 |
| Europe | 691 |
| Latin America | 523 |
| North America | 1,064 |
| Oceania | 522 |
Large-Scale Structure of the Air Transportation Network
A ubiquitous characteristic of complex networks is the so-called “small-world” property (22). In a small-world network, pairs of nodes are connected by short paths as one expects for a random graph (23). Crucially, nodes in small-world networks also have a high degree of cliquishness, as one finds in low-dimensional lattices but not in random graphs.
In the air transportation network, the average shortest path length d is the average minimum number of flights that one needs to take to get from any city to any other city in the world. We found that for the 719 cities in the Asia and Middle East network, d = 3.5 and that the average shortest path length between the 3,663 cities in the giant component of the worldwide network is only approximately one step greater, d = 4.4. Actually, most pairs of cities (56%) are connected by four steps or less. More generally, we found that d grows logarithmically with the number S of cities in the network, d ≈ log S. This behavior is consistent with both random graphs and small-world networks but not with low-dimensional networks, for which d grows more rapidly with S.
Still, some pairs of cities are considerably further away from each other than the average. The farthest cities in the network are Mount Pleasant in the Falkland Islands and Wasu, Papua New Guinea: To get from one city to the other, one needs to take 15 different flights. From Mount Pleasant, one can fly to Punta Arenas, Chile, and from there fly to some hubs in Latin America. At the other end of the path, from Wasu one needs to fly to Port Moresby (Papua New Guinea), which requires a unique sequence of eight flights. In the center of the path, between Punta Arenas and Port Moresby, six different flights are needed. In contrast to what happens the ends of the path, in the central region of the path there are hundreds of different flight combinations, all of them connecting Punta Arenas and Port Moresby in six steps.
The clustering coefficient C, which quantifies the local cliquishness of a network, is defined as the probability that two cities that are directly connected to a third city also are directly connected to each other. We find that C is typically larger for the air transportation network than for a random graph and that it increases with size. These results are consistent with the expectations for a small-world network but not with those for a random graph. For the worldwide network, we find that C = 0.62, whereas its randomization yields C = 0.049. Therefore, we conclude that the air transportation network is, as expected, a small-world network (19).
Another fundamental aspect in which real-world networks often deviate from the random graphs typically considered in mathematical analysis (23) is the degree distribution, that is, the distribution of the number of links of the nodes (15, 19, 24). In binomial random graphs, all nodes have similar degrees, whereas many real-world networks have some nodes that are significantly more connected than others. Specifically, many complex networks, termed “scale-free,” have degree distributions that decay as a power law. A plausible mechanism for such a phenomenon is preferential attachment (19, 24), that is, the tendency to connect preferentially to nodes with already high degrees.
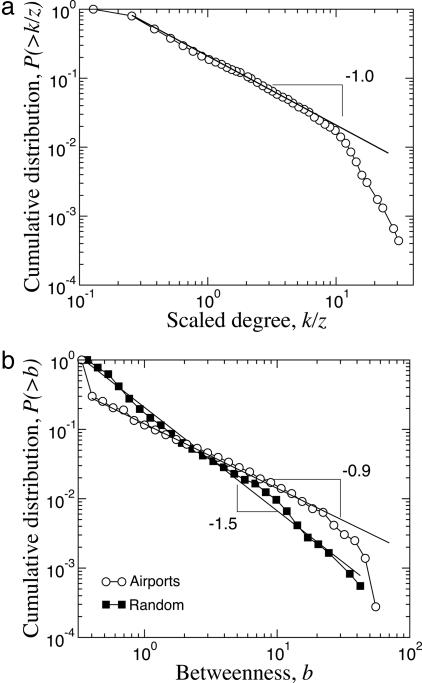
To gain greater insight into the structure and evolution of the air transportation network, we calculated the degree distribution of the cities. The degree of a city is the number of other cities to which it is connected by a nonstop flight. In Fig. 1a, we show the cumulative degree distribution¶ for the worldwide air transportation network. The data suggest that P(> k) has a truncated power-law decaying tail (19, 24)
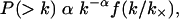 |
[1] |
where α = 1.0 ± 0.1 is the power law exponent, f(u) is a truncation function, and k× is a crossover value that depends on the size of the network. The measured value of the exponent α would imply that, as one increases the size of the network, the average degree of the cities also is expected to increase (15).
Fig. 1.
Degree and betweenness distributions of the worldwide air transportation network. (a) Cumulative degree distribution plotted in double-logarithmic scale. The degree k is scaled by the average degree z of the network. The distribution displays a truncated power-law behavior with exponent α = 1.0 ± 0.1. (b) Cumulative distribution of normalized betweennesses plotted in double-logarithmic scale. The distribution displays a truncated power-law behavior with exponent ν = 0.9 ± 0.1. For a randomized network with exactly the same degree distribution as the original air transportation network, the betweenness distribution decays with an exponent ν = 1.5 ± 0.1. A comparison of the two cases clearly shows the existence of an excessive number of large betweenness values in the air transportation network.
The degree of a node is a source of information on its importance. However, the degree does not provide complete information on the role of the node in the network. To start to address this issue, we considered the “betweenness centrality” of the cities comprising the worldwide air transportation network. The betweenness Bi of city i is defined as the number of shortest paths connecting any two cities that involve a transfer at city i (25–27). We define the normalized betweenness as bi = Bi/〈B〉, where 〈B〉 represents the average betweenness for the network. We plot in Fig. 1b the cumulative distribution P(> b) of the normalized betweenness for the worldwide air transportation network. Our results suggest that the distribution of betweennesses for the air transportation network obeys the functional form
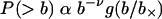 |
[2] |
where ν = 0.9 ± 0.1 is the power law exponent, g(u) is a truncation function, and b× is a crossover value that depends on the size of the network.
A question prompted by the previous results regarding the degree and the centrality of cities is: “Are the most connected cities also the most central?” To answer this question, we analyzed first the network obtained by randomizing the worldwide air transportation network (Fig. 1b). We found that the distribution of betweennesses still decays as a power law but, in this case, with a much larger exponent value, ν = 1.5 ± 0.1. This finding indicates the existence of anomalously large betweenness centralities in the air transportation network.
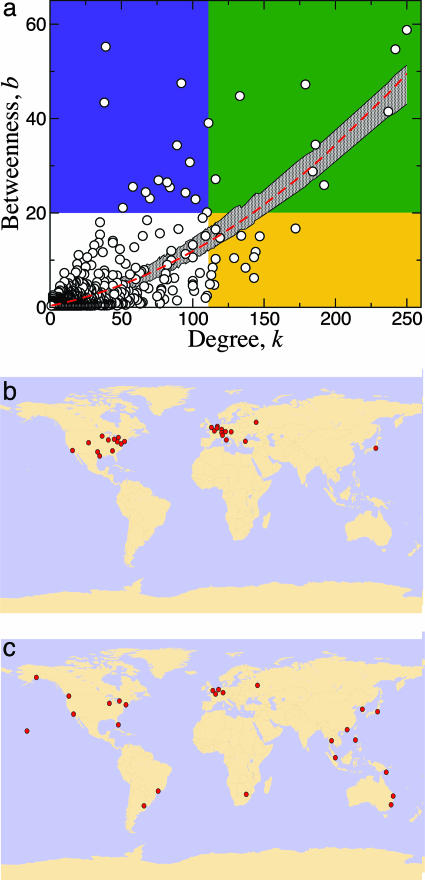
For the randomized network, the degree of a node and its betweenness centrality are strongly correlated; i.e., highly connected nodes are also the most central (Fig. 2a). In contrast, for the worldwide air transportation network, it turns out that there are cities that are not hubs, i.e., have small degrees but that nonetheless have very large betweennesses (Fig. 2a).
Fig. 2.
Most-connected versus most-central cities in the worldwide air transportation network. (a) Betweenness as a function of the degree for the cities in the worldwide air transportation network (circles). For the randomized network, the betweenness is well described as a quadratic function of the degree (dashed line) with 95% of all data falling inside the gray region. In contrast to the strong correlation between degree and betweenness found for randomized networks, the air transportation network comprises many cities that are highly connected but have small betweenness and, conversely, many cities with small degree and large betweenness. We define a blue region containing the 25 most central cities in the world and a yellow region containing the 25 most connected cities. Surprisingly, we find there are only a few cities with large betweenness and degree (green region, which is the intersection of the blue and yellow regions). (b) The 25 most connected cities in the world. (c) The 25 most central cities in the world.
To better illustrate this finding, we plotted the 25 most connected cities and contrasted such a plot with another of the 25 most central cities according to their betweenness (Fig. 2 b and c). Although the most connected cities are located mostly in Western Europe and North America, the most central cities are distributed uniformly across all of the continents. Significantly, each continent has at least one central city, which is typically highly connected when compared with other cities in the continent, i.e., Johannesburg in Africa or Buenos Aires and São Paulo, Brazil, in South America. Interestingly, besides these cities with relatively large degree, there are others, such as Anchorage (AK) and Port Moresby (Papua New Guinea), that, despite having small degrees, are among the most central in the network (Table 2).
Table 2. The 25 most central cities in the worldwide air transportation network.
| Rank | City | b | b/bran | Degree |
|---|---|---|---|---|
| 1 | Paris | 58.8 | 1.2 | 250 |
| 2 | Anchorage* | 55.2 | 16.7 | 39 |
| 3 | London | 54.7 | 1.2 | 242 |
| 4 | Singapore* | 47.5 | 4.3 | 92 |
| 5 | New York | 47.2 | 1.6 | 179 |
| 6 | Los Angeles | 44.8 | 2.3 | 133 |
| 7 | Port Moresby* | 43.4 | 13.6 | 38 |
| 8 | Frankfurt | 41.5 | 0.9 | 237 |
| 9 | Tokyo | 39.1 | 2.7 | 111 |
| 10 | Moscow | 34.5 | 1.1 | 186 |
| 11 | Seattle* | 34.3 | 3.3 | 89 |
| 12 | Hong Kong* | 30.8 | 2.6 | 98 |
| 13 | Chicago | 28.8 | 1.0 | 184 |
| 14 | Toronto | 27.1 | 1.8 | 116 |
| 15 | Buenos Aires* | 26.9 | 3.2 | 76 |
| 16 | São Paulo* | 26.5 | 2.8 | 82 |
| 17 | Amsterdam | 25.9 | 0.8 | 192 |
| 18 | Melbourne* | 25.5 | 4.5 | 58 |
| 19 | Johannesburg* | 25.4 | 2.6 | 84 |
| 20 | Manila* | 24.4 | 3.5 | 67 |
| 21 | Seoul* | 24.3 | 2.1 | 95 |
| 22 | Sydney* | 23.1 | 3.2 | 70 |
| 23 | Bangkok* | 22.9 | 1.8 | 102 |
| 24 | Honolulu* | 21.1 | 4.4 | 51 |
| 25 | Miami* | 20.1 | 1.4 | 110 |
Cities are ordered according to their normalized betweenness. We also show the ratio of the actual betweenness of the cities to the betweenness that they have after randomizing the network.
These cities are not among the 25 most connected.
Degree-Betweenness Anomalies and Multicommunity Networks
Nodes with small degree and large centrality can be regarded as anomalies. Other complex networks that have been described in the literature, like the Internet (28), do not display such a behavior, and nodes with the highest degree are also those with the highest betweenness (29). It is, in principle, easy to construct a network in which a node has small degree and large centrality; think, for example, of a network formed by two communities that are connected to one another through a single node with only two links. The relevant question is, however, “what general and plausible mechanism would give rise to scale-free networks with the obtained anomalous distribution of betweenness centralities?”
To answer this question, it is useful to consider a region such as Alaska. Alaska is a sparsely populated, isolated region with a disproportionately large, for its population size, number of airports. Most Alaskan airports have connections only to other Alaskan airports. This fact makes sense geographically. However, distance-wise, it also would make sense for some Alaskan airports to be connected to airports in Canada's Northern Territories. These connections are, however, absent. Instead, a few Alaskan airports, singularly Anchorage, are connected to the continental U.S. The reason is clear: the Alaskan population needs to be connected to the political centers, which are located in the continental U.S., whereas there are political constraints making it difficult to have connections to cities in Canada, even to ones that are close geographically (21). It is now obvious why Anchorage's centrality is so large. Indeed, the existence of nodes with anomalous centrality is related to the existence of regions with a high density of airports but few connections to the outside. The degree-betweenness anomaly is therefore ultimately related to the existence of communities in the network.
The unexpected finding of central nodes with low degree is a very important one because central nodes play a key role in phenomena such as diffusion and congestion (30) and in the cohesiveness of complex networks (31). Therefore, our finding of anomalous centralities points to the need to (i) identify the communities in the air transportation network and (ii) establish new ways to characterize the role of each city based on its pattern of intracommunity and intercommunity connections and not merely on its degree.
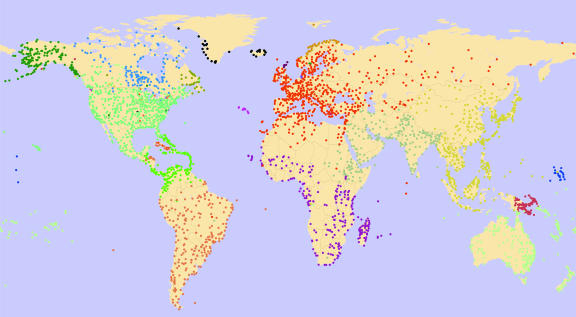
Community Structure. To identify communities in the air transportation network, we used the definition of modularity introduced in refs. 32 and 33. The modularity of a given partition of the nodes into groups is maximum when nodes that are densely connected among them are grouped together and separated from the other nodes in the network. To find the partition that maximizes the modularity, we used simulated annealing (34–37). We display in Fig. 3 the communities identified by our algorithm in the worldwide air transportation network.∥
Fig. 3.
Communities in the giant component of the worldwide air transportation network. Each node represents a location, and each color corresponds to a community.
As we surmised, both Alaska and Papua New Guinea form separate communities.** This fact explains the large betweenness centrality of Anchorage and Port Moresby, because they provide the main links to the outside world for the other cities in their communities.
Another significant result is that even though geographical distance plays a clear role in the definition of the communities, the composition of some of the communities cannot be explained by purely geographical considerations. For example, the community that contains most cities in Europe also contains most airports in Asian Russia. Similarly, Chinese and Japanese cities are mostly grouped with cities in the other countries in Southeast Asia, but India is mostly grouped with the Arabic Peninsula countries and with countries in Northeastern Africa. These facts are consistent with the important role of political factors in determining community structure (21).
Global Role of Cities. We characterized the role of each city in the air transportation network based on its pattern of intracommunity and intercommunity connections. We first distinguished nodes that play the role of hubs in their communities from those that are nonhubs. Note that cities like Anchorage are hubs in their communities, but they are not hubs if one considers all of the nodes in the network. Thus, we define the within-community degree of a node. If κi is the number of links of node i to other nodes in its community si, 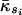 is the average of κ over all of the nodes in si, and σκs is the standard deviation of κ in si, then
is the average of κ over all of the nodes in si, and σκs is the standard deviation of κ in si, then
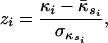 |
[3] |
is the so-called z-score. The within-community degree z-score measures how “well-connected” node i is to other nodes in the community.
We then distinguished nodes based on their connections to nodes in communities other than their own. For example, two nodes with the same z-score will play different roles if one of them is connected to several nodes in other communities and the other is not. We define the participation coefficient Pi of node i as
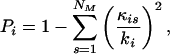 |
[4] |
where κis is the number of links of node i to nodes in community s, and ki is the total degree of node i. The participation coefficient of a node is therefore close to one if its links are uniformly distributed among all of the communities and zero if all its links are within its own community.
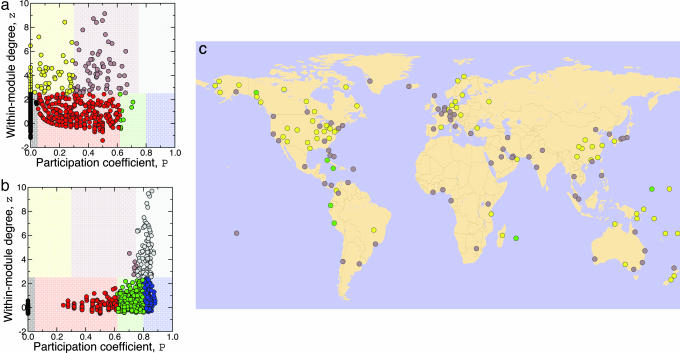
We hypothesized that the role of a node can be determined, to a great extent, by its within-module degree and its participation coefficient (36, 37). We defined heuristically seven different “universal roles,” each one corresponding to a different region in the zP phase-space. According to the within-module degree, we classified nodes with z ≥ 2.5 as module hubs and nodes z < 2.5 as nonhubs. Both hub and nonhub nodes are then more finely characterized by using the values of the participation coefficient (36, 37).
We divided nonhub nodes into four different roles as follows: (R1) “ultraperipheral nodes,” i.e., nodes with all their links within their module (P ≤ 0.05); (R2) “peripheral nodes,” i.e., nodes with most links within their module (0.05 < P ≤ 0.62); (R3) “nonhub connector nodes,” i.e., nodes with many links to other modules (0.62 < P ≤ 0.80); and (R4) “nonhub kinless nodes,” i.e., nodes with links homogeneously distributed among all modules (P > 0.80).
We divided hub nodes into three different roles as follows: (R5) “provincial hubs,” i.e., hub nodes with the vast majority of links within their module (P ≤ 0.30); (R6) “connector hubs,” i.e., hubs with many links to most of the other modules (0.30 < P ≤ 0.75); and (R7) “kinless hubs,” i.e., hubs with links homogeneously distributed among all modules (P > 0.75).
For each city in the worldwide air transportation network, we calculated its within-community degree zi and its participation coefficient Pi. Then, we assigned each city a role according to the definitions above (Fig. 4 a and c). Significantly, 95.4% of the cities in the worldwide air transportation network are classified as either peripheral or ultra-peripheral. Additionally, there is a small fraction of nonhub connectors (0.5%). These results suggest that cities that are not hubs in their respective communities rarely have links to many other communities in the air transportation network. This situation is in stark contrast to what happens in some biological networks, in which nonhub connectors seem to be relatively frequent and play an important role (36).
Fig. 4.
Toward a scale-specific representation of the worldwide air transportation network. (a) Each point in the zP phase-space corresponds to a city, and different colors indicate different roles. Most cities are classified as ultraperipheral (black) or peripheral (red) nodes. A small number of nonhub nodes play the role of connectors (green). We find approximately equal fractions of provincial (yellow) and connector (brown) hubs. (b) Same as a but for a randomization of the air transportation network. The absence of communities manifests itself in that most hubs become kinless hubs (gray) and in the appearance of kinless nonhubs (blue). (c) Nonhub connectors (green), provincial hubs (yellow), and connector hubs (brown) in the worldwide air transportation network.
The remaining 4.1% of the nodes are hubs. We found approximately equal fractions of provincial and connector hubs. The former include cities that, for historical, political, or geographical reasons, are comparatively not well-connected to other communities. Examples are Denver, Philadelphia, and Detroit in North America; Stuttgart, Copenhagen, Istanbul (Turkey), and Barcelona in the community formed by Europe, North Africa, and the former Soviet Union; Adelaide (Australia) and Christchurch (New Zealand) in Oceania; Brasília (Brazil) in South America; Fairbanks and Juneau in Alaska; and the already-discussed case of Port Moresby. Connector hubs include the most recognizable airport hubs in the world: Chicago, New York, Los Angeles, and Mexico City in North America; Frankfurt, London, Paris, and Rome in Europe; Beijing, Tokyo, and Seoul in the Southeastern Asian community; Delhi, Abu Dhabi (United Arab Emirates), and Kuwait in the community comprising India, the Arabic Peninsula, and Northeastern Africa; Buenos Aires, Santiago, and São Paulo in South America; Melbourne, Auckland, and Sydney in Oceania; and Anchorage in Alaska.
The fractions of cities with each role in the worldwide air transportation network contrast with the corresponding fractions in a randomization of the network (Fig. 4b). In this case, the community identification algorithm still yields certain communities, but the network lacks “real” community structure. The identification of roles enables one to realize that these communities are somehow artificial. Indeed, many cities are either kinless hubs or kinless nonhubs because of the absence of a real community structure, and the network contains essentially no provincial or connector hubs.
Discussion
We carried out a “systems” analysis of the structure of the worldwide air transportation network. The study enables us to unveil a number of significant results. The worldwide air transportation network is a small-world network in which (i) the number of nonstop connections from a given city and (ii) the number of shortest paths going through a given city have distributions that are scale-free. Surprisingly, the nodes with more connections are not always the most central in the network. We hypothesize that the origin of such a behavior is the multicommunity structure of the network. We find the communities in the network and demonstrate that their structure can only be understood in terms of both geographical and political considerations.
Our analysis of the community structure of the air transportation network is important for two additional reasons. First, it allows us to identify the most efficient ways to engineer the structure of the network. Specifically, having identified the communities, one can identify which ones are poorly connected and the ways to minimize that problem. Second, cities that connect different communities play a disproportionate role in important dynamic processes such as the propagation of infections such as severe acute respiratory syndrome. As we described, finding the communities is the first step toward identifying these cities.
The existence of communities and the understanding that different cities may have very different impacts on the global behavior of the air transportation system call for the definition of the role of each city. We addressed this issue by classifying cities into seven roles, according to their patterns of intercommunity and intracommunity connections. We found that most of the nodes (95%) are peripheral; that is, the vast majority of their connections are within their own communities. We also found that nodes that connect different communities are typically hubs within their own community, although not necessarily global hubs. This finding is in stark contrast with the behavior observed in certain biological networks, in which nonhub connectors are more frequent (36).
The fact that different networks seem to be formed by nodes with network-specific roles points to the more general question of what evolutionary constraints and pressures determine the topology of complex networks and how the presence or absence of specific roles affects the performance of these networks.
Acknowledgments
We thank A. Arenas, A. Barrat, M. Barthélémy, A. Díaz-Guilera, A. A. Moreira, R. Pastor-Satorras, M. Sales-Pardo, D. Stouffer, and A. Vespignani for stimulating discussions and helpful suggestions. We also thank OAG for providing their electronic database of airline flights and Landings. com for providing the geographical coordinates of the world airports.
Author contributions: R.G. and L.A.N.A. designed research; R.G., S.M., and L.A.N.A. performed research; R.G., S.M., A.T., and L.A.N.A. analyzed data; and R.G. and L.A.N.A. wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Footnotes
The cumulative degree distribution P(> k) gives the probability that a city has k or more connections to other cities and is defined as 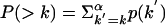 , where p(k) is the probability density function.
, where p(k) is the probability density function.
We do not know the geographical coordinates of ≈10% of the 3,663 cities in the giant component of the worldwide air transportation network. Those cities are not plotted in the map. Also, some small cities may be misplaced because of duplications in the three-letter code of the corresponding airport.
Alaska and Papua New Guinea are small communities compared with most of the others, which confirms the idea that these are very well defined communities; otherwise, they would be incorporated in a larger community. This fact is particularly important taking into consideration that the community identification algorithm does not take into account the betweenness of the nodes at all.
References
- 1.Bisseur, A. & Alamdari, F. (1998) Transportation 25, 331–355. [Google Scholar]
- 2.Dana, L. P. & Vignali, D. (1999) Int. Marketing Rev. 16, 278–290. [Google Scholar]
- 3.Turton, B. J. & Mutambirwa, C. C. (1996) Tourism Manage. 17, 453–462. [Google Scholar]
- 4.Raguraman, K. (1998) Tourism Manage. 19, 533–543. [Google Scholar]
- 5.Liljeros, F., Edling, C. R., Amaral, L. A. N., Stanley, H. E. & Aberg, Y. (2001) Nature 411, 907–908. [DOI] [PubMed] [Google Scholar]
- 6.Liljeros, F., Edling, C. R. & Amaral, L. A. N. (2003) Microbes Infect. 5, 189–196. [DOI] [PubMed] [Google Scholar]
- 7.Pastor-Satorras, R. & Vespignani, A. (2001) Phys. Rev. Lett. 86, 3200–3203. [DOI] [PubMed] [Google Scholar]
- 8.European Organisation for the Safety of Air Navigation (2000) Cost of Air Transportation Delay in Europe, Technical Report (European Organisation for the Safety of Air Navigation, Brussels).
- 9.Magnanti, T. L. & Wong, R. T. (1984) Transportation Sci. 18, 1–55. [Google Scholar]
- 10.Minoux, M. (1989) Networks 19, 313–360. [Google Scholar]
- 11.Camacho, J., Guimerà, R. & Amaral, L. A. N. (2002) Phys. Rev. Lett. 88, 228102. [DOI] [PubMed] [Google Scholar]
- 12.Kitano, H. (2002) Science 295, 1662–1664. [DOI] [PubMed] [Google Scholar]
- 13.Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N. & Barabási, A. L. (2000) Nature 407, 651–654. [DOI] [PubMed] [Google Scholar]
- 14.Strogatz, S. H. (2001) Nature 410, 268–276. [DOI] [PubMed] [Google Scholar]
- 15.Albert, R. & Barabási, A.-L. (2002) Rev. Mod. Phys. 74, 47–97. [Google Scholar]
- 16.Dorogovtsev, S. N. & Mendes, J. F. F. (2002) Adv. Phys. 51, 1079–1187. [Google Scholar]
- 17.Newman, M. E. J. (2003) SIAM Rev. 45, 167–256. [Google Scholar]
- 18.Amaral, L. A. N. & Ottino, J. (2004) Eur. Phys. J. B 38, 147–162. [Google Scholar]
- 19.Amaral, L. A. N., Scala, A., Barthélémy, M. & Stanley, H. E. (2000) Proc. Natl. Acad. Sci. USA 97, 11149–11152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Airport Council International (1999) 1999 Annual Worldwide Airport Traffic Report (Airport Council International, Geneva).
- 21.Guimerà, R. & Amaral, L. A. N. (2004) Eur. Phys. J. B 38, 381–385. [Google Scholar]
- 22.Watts, D. J. & Strogatz, S. H. (1998) Nature 393, 440–442. [DOI] [PubMed] [Google Scholar]
- 23.Bollobás, B. (2001) Random Graphs (Cambridge Univ. Press, Cambridge, U.K.), 2nd Ed.
- 24.Barabási, A.-L. & Albert, R. (1999) Science 286, 509–512. [DOI] [PubMed] [Google Scholar]
- 25.Freeman, L. C. (1977) Sociometry 40, 35–41. [Google Scholar]
- 26.Newman, M. E. J. (2001) Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 64, 016131. [DOI] [PubMed] [Google Scholar]
- 27.Newman, M. E. J. (2001) Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 64, 016132. [DOI] [PubMed] [Google Scholar]
- 28.Vázquez, A., Pastor-Satorras, R. & Vespignani, A. (2002) Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 65, 066130. [DOI] [PubMed] [Google Scholar]
- 29.Goh, K.-I., Oh, E., Kahng, B. & Kim, D. (2003) Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 67, 017101. [DOI] [PubMed] [Google Scholar]
- 30.Guimerà, R., Díaz-Guilera, A., Vega-Redondo, F., Cabrales, A. & Arenas, A. (2002) Phys. Rev. Lett. 89, 248701. [DOI] [PubMed] [Google Scholar]
- 31.Holme, P. & Kim, B. J. (2002) Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 65, 056109. [DOI] [PubMed] [Google Scholar]
- 32.Newman, M. E. J. & Girvan, M. (2004) Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 69, 026113. [DOI] [PubMed] [Google Scholar]
- 33.Newman, M. E. J. (2004) Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 69, 066133. [DOI] [PubMed] [Google Scholar]
- 34.Kirkpatrick, S. Gelatt, C. D. & Vecchi, M. P. (1983) Science 220, 671–680. [DOI] [PubMed] [Google Scholar]
- 35.Guimerà, R., Sales-Pardo, M. & Amaral, L. A. N. (2004) Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 70, 025101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Guimerà, R. & Amaral, L. A. N. (2005) Nature 433, 895–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Guimerà, R. & Amaral, L. A. N. (2005) J. Stat. Mech. Theor. Exp., P02001. [DOI] [PMC free article] [PubMed]