Theoretical model of prion propagation: A misfolded protein induces misfolding

Abstract

There is a hypothesis that dangerous diseases such as bovine spongiform encephalopathy, Creutzfeldt-Jakob, Alzheimer's, fatal familial insomnia, and several others are induced by propagation of wrong or misfolded conformations of some vital proteins. If for some reason the misfolded conformations were acquired by many such protein molecules it might lead to a “conformational” disease of the organism. Here, a theoretical model of the molecular mechanism of such a conformational disease is proposed, in which a metastable (or misfolded) form of a protein induces a similar misfolding of another protein molecule (conformational autocatalysis). First, a number of amino acid sequences composed of 32 aa have been designed that fold rapidly into a well defined native-like α-helical conformation. From a large number of such sequences a subset of 14 had a specific feature of their energy landscape, a well defined local energy minimum (higher than the global minimum for the α-helical fold) corresponding to β-type structure. Only one of these 14 sequences exhibited a strong autocatalytic tendency to form a β-sheet dimer capable of further propagation of protofibril-like structure. Simulations were done by using a reduced, although of high resolution, protein model and the replica exchange Monte Carlo sampling procedure.

The biological function of a protein can be performed only if the protein molecules adopt a precisely folded conformation (the native structure). A deviation from that structure, i.e., a misfolded conformation of a particular protein molecule either makes it inactive or active in another direction, in many cases (however, not always) harmful or even destructive for the host organism. Alternative folding or refolding (1, 2), frequently followed by a large-scale aggregation (3) of proteins may lead to bovine spongiform encephalopathy, Creutzfeldt-Jakob (4), Alzheimer's, fatal familial insomnia, and several other dangerous diseases (5, 6). The misfolded structures that are associated with the prion diseases contain a larger fraction of a β-type structure than the native structure does (7, 8). The β-rich fragments of such proteins easily associate and subsequently form the amyloid fibrils (9). Interestingly, it appears that under extreme conditions of pH (9–11), solvent composition, high pressure (12), etc. almost all globular proteins can be converted into the amyloid form (8, 13, 14). Fortunately, at physiological conditions such aggregation is relatively rare. Experimental data indicate that the internal part of amyloid fibrils is highly ordered, although the detailed structure is not known. The leading hypothesis is that the fibrils are composed from protofibrils that have regular β-sheet type structure (8, 9). Alternative molecular models postulate a β-helical structure (8, 15).

Numerous computational studies, especially when combined with known experimental facts (11, 16), provided valuable insights into the structure and mechanism of formation of amyloids (17). These studies used various modeling techniques and various levels of representation of the protein conformational space. Studies of highly idealized simple lattice models (18, 19) have demonstrated that association observed for some protein-like models can lead to significant change of the single-chain conformation, as compared with the ground-state conformation of an isolated chain. Detailed, atomistic simulations are computationally too demanding for modeling a large-scale molecular rearrangement necessary for protein refolding and aggregation into a fibril-like form. Nevertheless, detailed molecular dynamics simulations allow estimation of relative stability and flexibility (20) of the native structure of proteins (21), their amyloid-like model structures, and possible intermediates of the aggregation process (22, 23). Efficient Monte Carlo technique applied to an all-atom model enabled modeling of autocatalytic transition of a short peptide from its ground-state helical conformation to a β-sheet-type structure, when a part of the model chain was forced to stay in an extended conformation (24). Recently, it was possible to perform molecular dynamics simulations of the transition of the prion protein into its scrapie form. Subsequently, the resulting structure was used as a building block in molecular docking, leading to a plausible model of a fragment of the fibril structure (9).

In the present work we designed a number of de novo short protein sequences that fold into well defined helical “native conformation” and can also assume metastable β-type structures. The helical structure corresponds to the global (free) energy minima and the metastable structure to a higher-energy local minimum of the energy landscape (25). Then, a long series of simulations enabled us to select a single sequence that exhibited strong autocatalytic effect, leading to spontaneous formation of the amyloid protofibrils, provided the process was initiated by freezing one of the molecules in the β-type metastable conformation. Simulations were performed by using a high-resolution reduced representation of protein conformational space, the refiner model (26, 27), and replica exchange Monte Carlo method (28) as an effective sampling scheme. The model uses united atom representation and continuous space conformational updating. The force field consists of a carefully designed (29) and optimized set of knowledge-based potentials (30) derived from a statistical analysis of structural regularities seen in known crystallographic structures of globular proteins (31). Thus it could be postulated that the model of interactions mimics “averaged” physiological conditions.

Methods

Protein Model and Simulation Technique. Protein is represented as a chain of Cα atoms in continuous space (26, 27). The idea of the reduced representation of polypeptide conformational space in the refiner model is illustrated in Fig. 1. Subsequent Cα atoms are connected by a virtual Cα-Cα bond with a constant distance of 3.8 Å. The protein chain is terminated by dummy united atoms mimicking the C- and N-terminal caps and enabling proper definition of the side chains for the end residues. The side chains are represented by one or two united atoms depending on their size. In the case of glycine the entire residue is represented by a Cα atom only. Conformations of the side chains were read from the database and stored in a rotamer library. The rotamers were divided into three groups according to three classes of the main-chain local geometry. During the simulation the rotamers were randomly selected from the library.

Fig. 1.

Explanation of the refiner representation of polypeptides conformational space. A schematic drawing of a short fragment of a polypeptide chain (Top), definition of the α-carbon trace reduced representation of the main chain (Middle), and the grouping of the side chains into united atoms (Bottom). In refiner reduced representation the dummy atoms on the chain ends provide the reference frame for the definition of the terminal side-chain orientations.

The force field contains a number of terms simulating various physical interactions in proteins with the solvent treated as an effective medium. The short-range potentials control local geometry of the model chain and depend on distances between ith and i + 3, ith and i + 4, ith and i + 5Cα atoms, torsional angles, and the identity of the involved residues. Predicted secondary structure can be used to introduce a bias, which could be treated as an averaged multibody contribution to the short-range potentials. In this work, such predictions of secondary structure were ignored. Thus the folding of model sequences has been solely controlled by the refiner generic force field. The long-range interactions are modeled by two types of potentials. The first one is the contact-type potential for the side-chain united atoms. The strength of interaction for a given pair depends on mutual orientation of the interacting chain fragments. There are three types of contacts: parallel, intermediate, and antiparallel. The second type of long-range interactions is the main-chain hydrogen bond. This term awards those arrangements of Cα atoms that correspond to the geometry of hydrogen-bonded residues. The details of the design and derivation of the potentials are very similar to the design of force field for analogous high-resolution lattice model (29, 32). The refiner modeling tool had been previously tested during the CASP5 experiment (26) and in a benchmark of de novo prediction of protein fragments (27), which demonstrated better performance (accuracy and reproducibility) than was possible with standard molecular modeling tools. During the last round of the community-wide protein structure prediction experiment (CASP6) the refiner model and its force field produced several very good predictions, especially in the new fold category.

In all simulations the model molecules were placed within a sphere with soft repulsive surface. The radius of the sphere (at which the model molecules start to feel the walls) in the initial set of simulations was three times larger than the radius of the folded structures. As a result, the approximate effective molar fraction of proteins was equal to 0.00091, 0.00086, and 0.00075 for one-molecule, two-molecule and three-molecule systems, respectively. Obviously, similar values of the molar fractions in various systems do not mean similar effective concentrations. The effective concentration for the one-molecule system is equal to zero, because the multibody interactions between molecules are a priori excluded. With an increasing number of molecules the effective concentration increases, although the precise values cannot be specified for so small a number of molecules in a fixed volume. To further elucidate the concentration effects more diluted systems of three molecules were subsequently simulated.

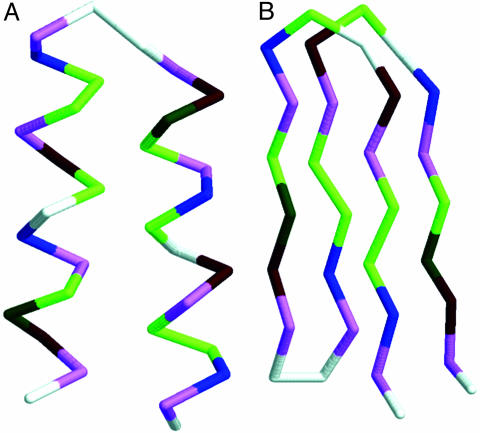
Design of Sequences. The first purpose was to design sequences for which the target “native” α-hairpin conformation corresponds to the lowest (free) energy. In reality, a protein molecule usually has a manifold of the native-like conformations, the so-called native basin. A number of sequences that are rich with helix-forming amino acids, arranged in a characteristic for helices pattern of polar and hydrophobic residues, and with a flexible fragment for the putative loop, can satisfy the requirements for a well defined ground state of our simple target motif. In the past we designed in silico a number of such simple and more complex folds (33). Such “hypothetical” proteins are usually “overdesigned” and are, at least in the context of the model's force field, more stable than the corresponding motifs of real proteins. Besides the native basin the protein molecule might exhibit a metastable basin, in which the conformations may differ widely (by their 3D structure) from those of the native basin and are of a little higher energy. Both basins are separated by a barrier of conformational energy. To ensure the existence of these two basins, the starting helical sequences were modified step by step, introducing small elements of β-type patterns. This goal has been accomplished by a knowledge-driven trial-and-error procedure. The resulting sequences contain characteristic signatures of both types of secondary structure motifs. They are rich with helix-forming alanine and have a helical-type pattern of Lys-Glu-charged residues. On the other hand, a high content of the β-sheet forming valine and elements of amphipathic β-type pattern of hydrophobic/polar residues provide a possibility of sheet formation. The length of the designed sequences also plays some role. For short helical bundles the fraction of unsaturated hydrogen bonds on the ends of helices is similar to the number of unsaturated bonds on the edges of small sheets. A large number of designed sequences was subject to test simulations in a relatively wide range of temperatures, and the trajectories were inspected for the appearance of the two types of structures. As a result of such processes, 14 sequences, each consisting of 32 aa, were selected. The sequences are listed in Table 1. For each of the designed sequences the native conformation corresponded to the structure of a simple α-helical motif (Fig. 2A), whereas the metastable structure adopted a β-motif (Fig. 2B). Both motifs represent the main building blocks of all proteins. For the sake of clarity all snapshots of the chain conformations show only the Cα traces. The side groups are omitted.

Table 1. Designed helical sequences with metastable β-type conformations.

1	GVEIAVKGAEVAAKVGGVEIAVKAGEVAAKVG
2	GVEIAVKGGEVAAKVGGVEIAVKGGEVAAKVG
3	GVEIAIKGGEIAAKVGGVEIAVKGGEVAAKVG
4	GVEIAVKAGEVAAKVGGVEIAVKAGEVAAKVG
5	GVEIAIKGGEIAAKVGGVEIAVKGGEIAAKVG
6	GVEIAVKGGEVAAKVGGVEIAVKGGEIAAKVG
7	IKVAIEVGGVKAAVEGGKVAIEVGGVKAAVEI
8	IKVAIEVAGVKAAVEGGKVAIEVAGVKAAVEI
9	IKVAIEVAGVKAAVEGGKVAIEVGAVKAAVEI
10	IKVAIEIGGVKAAVEGGKVAIEVGGVKAAVEI
11	IKVAIEVGGIKAAVEGGKVAIEVGGVKAAVEI
12	IKVAIEVGGIKAAVEGGKVAIEIGGVKAAVEI
13	IKVAIEVAGVKGAVEGGKVAIEVGGVKAAVEI
14	IKVAIEVAGVKAAVEGGKVAIEVAGVKAAIEI

Fig. 2.

The native α-helical conformation (A) and the metastable β-conformation (B) of the amino acid sequence GVEIAVKGAEVAAKVGGVEIAVKAGEVAAKVG.

Results

All designed sequences possess the features of their energy landscape we sought. Namely, each of them folds into a well defined two-helical bundle with relatively well pronounced hydrophobic interface. Moreover, each of the designs has a very well defined metastable structure of the four-member β-barrel arranged in two minimal, two-stranded sheets. Fig. 2 shows these two distinct structures for the first sequence from Table 1. The conformational energies of these structures are –85.3 and –78.6, respectively, in dimensionless k_BT units. The resulting sequence contains hydrophobic residues valine, isoleucine, and alanine and polar residues glutamic acid and lysine. Glycine marks the flexible loop region and the chain ends. The sequence contains strongly helix-forming alanine and β-forming valine.

To elucidate a putative mechanism of the prion propagation we designed three types of complementary folding simulations. First, a single protein study has been performed that included >100 runs (for all sequences investigated) of the replica exchange Monte Carlo method with 10 replicas (uniformly distributed around the folding temperature), each run consisting of the 1,000,000 Monte Carlo steps. A huge number of intermediate structures have been observed along the folding pathway. For the sufficiently wide temperature range considered, the most stable conformation was always the two-helix bundle, independent of the starting structures. With low-temperature range and the β-form as the initial conformation, the system remained in the β-form, confirming its metastable character.

Then, a system of two interacting protein molecules has been considered. One of the molecules has been frozen in the metastable β-form, whereas the other one was free to fold in the neighborhood of the first one. Whatever the reason for the freezing might be, it may happen in real system as well (14). Here the behavior of the first sequence differed qualitatively from the behavior of the remaining sequences, for which the freezing of one molecule did not influence qualitatively the folding of the second molecule. For the first sequence, because of the interaction between the protein molecules instead of folding to the native α-helical form, the second molecule folded to the β-form. This folding occurred independently of the starting conformation used in >80 runs. In particular, two tests have been crucial. In the first test, the starting conformation of the mobile chain was the metastable β-form. The molecule unfolded and then folded again to the β-form, which proves that the misfolded β-form is stable in the presence of the already misfolded β-form. The most interesting, however, were folding simulations with the α-helical form (the native one for the single protein molecule) as the starting conformation. The α-helical form first unfolded and then in the presence of the misfolded β-form folded to the β-form as well, assembling into a larger dimer-type structure with a perfect overall β-type geometry (Fig. 3). There are clearly favorable interactions between the two β-type molecules; the energy of the dimer was between –195.47 and –200.39 (depending on particular run, because of slightly different structural details of the resulting dimers), i.e., significantly lower than twice of the single-helical or single β-type molecule. An additional type of computational experiments has been performed, where the β-type dimer was used as a starting conformation and both molecules were allowed to change their geometries. It remained stable over very long runs, proving that upon association the dimer structure becomes a very long-living complex. Energy of the free dimer (i.e., both chains are allowed to move) is very close, although lower, to that of two isolated helical structures. This fact indicates that the (free) energy barrier between the two states must be very high. There is one additional reason for the above statement. Very long simulations performed by us that started from two unfolded or helical structures never resulted with β-type dimer. Consequently, a spontaneous transition from the native to the propagating “scrapie” form of the protein designed here must be a very rare event.

Fig. 3.

A model of prion disease propagation. The correct (helical) form of a protein misfolds to a β-structure in the presence of the stiff misfolded β-structure form.

Dimerization in the β-form could be considered as an initiation event for a further propagation of an amyloid form. To check this possibility we performed simulations of three molecules with various starting conditions. These are outlined below.

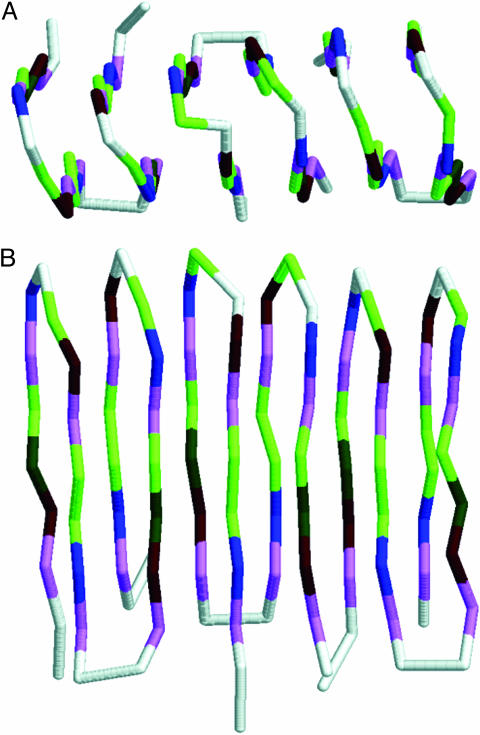
1. One molecule was frozen in the β-form with the two remaining, freely moving, either both helical or one helical and one β-type. In all cases the resulting structure for the first sequence was a very regular trimer, composed of two three-member β-sheets (Fig. 4), although the mutual orientation of strands (parallel versus antiparallel) varied between simulations. The stabilization energy of such protofibrils (as compared with the energy of three separated molecules) was significantly higher than the corresponding quantity for the dimer (as compared with the energy of two separated chains), both quantities calculated per single chain. This result suggests that formation of a dimer could be considered as a well defined initiation step for the amyloid aggregation.

2. Free (not frozen) β-type dimer and a helical structure represented the second starting point. Like the experiment with starting condition i the resulting structure was the β-trimer, with only slightly higher conformational energy, probably because of structural fluctuations of the entire structure.

3. Two helical hairpins and one β-barrel, all free, were considered as the third starting point. Here, only in about half of the simulations the resulting structure was the β-type trimer. The remaining simulations led to mixed conformations.

Fig. 4.

Structures of model amyloid protofibrils obtained in simulations of three molecules. (A) Top view. (B) Side view.

To further elucidate the concentration effects two additional sets of simulations were performed for the “prion” sequence and other designed sequences. In all cases the simulations started from the β-type trimers. In the first set of simulations the volume accessible for model system was increased by 50% (mole fraction equal to 0.00047) and 125% (mole fraction equal to 0.00030) in the second set. In all cases the protofibril formed by the first sequence remained stable. Also the trimer with the second sequence remained stable, whereas the starting structures for other sequences dissociated and the particular chains folded into separate, predominantly helical structures. This result proves that the concentration may influence the kinetics of amyloid formation, and for some sequences (sequence 2) also the ability of aggregation. Indeed, at various concentrations the first sequence had stable amyloid structure, the second sequence was stable as a trimer, although it did not undergo spontaneous aggregation, whereas the remaining sequences did not form stable aggregates at any of the studied conditions. Obviously, for the prion sequences (sequence 1) the concentration has to be large enough to allow a dimer formation (a trimer for sequence 2), provided that one of the molecules finds itself in a close vicinity of another molecule (two molecules for sequence 2), which for some reason adopted for a while the metastable β-type structure.

The difference between the results of simulations of the two free molecules and the three free molecules is very suggestive. It appears that autocatalytic effect is much stronger (more cooperative) when larger number of prion-like molecules is present in the system.

Discussion

Several computational studies of prions were published recently and brought valuable insights into our understanding of the problem on a molecular level. These studies fall roughly into two categories: detailed molecular mechanics studies of local conformational properties and studies of highly idealized protein-like models. The present work seem to go further, a reduced (however, realistic) model is used, which allows for a reconstruction of all atomic details (34) and the entire folding pathways. The prion-type conformational rearrangements were simulated in detail, providing a putative picture of prion self-propagation. Obviously, we have used a reduced representation of the conformational space and relatively simple, although nontrivial, models of protein sequences. The interaction potential takes into account all important contributions such as steric repulsion, hydrogen bonds, hydrophobic interactions, etc. The particular interactions have some weights that can be derived from the analysis of the structural regularities (statistical potentials) encountered in the Protein Data Bank. The effect of solvent is accounted for in an implicit averaged effect in the hydrophobic contribution to the pairwise interactions of the side groups. The force-field of the model has proven to be successful in correctly predicting an extended set of the test protein structures. Because of an efficient sampling technique and the reduced representation of the conformational space the method finds rapidly global energy minima of small proteins. In particular, we have used the replica exchange Monte Carlo method, in which many Monte Carlo simulations (for a series of different temperatures) are simultaneously under way and the generalized Metropolis criterion enables one to accept conformations also computed for different temperatures. The details of this modeling tool can be found in our recent publications (26, 27).

This work demonstrates by in silico folding experiments that a misfolded conformation of the protein is able to induce the unfolding of the correctly folded native structure and its refolding into the misfolded conformation, the same one that induces the conformational change. This model may be considered as a plausible model of conformational disease propagation just by contact of the correct (i.e., native) form with the misfolded form of a molecule.

Several conclusions could be derived from the sequence design process described here. First, it was relatively easy to design a number of model sequences that in addition to a well defined, ground-state native conformation can adopt a completely different metastable structure corresponding to a deep local energy minimum. It seems to be a rather common property of proteins. However, only one of these designed sequences was capable of autocatalytic transition from helical to β-type dimeric form. This sequence differed only slightly from several other sequences. Why then can this sequence aggregate (sequence 2 is also capable of aggregation, provided a trimer β-type structure somehow is formed), whereas the others do not? Certainly, it is not because of the relative energy differences between the native and metastable states; some of the remaining sequences exhibit higher and some of them exhibit lower differences. What is characteristic for the first sequence is that upon dimerization the side groups form a large number of energetically favorable contacts. Upon aggregation additional main-chain hydrogen bonds can be formed. This ability to extend the regular β-sheet type pattern of hydrogen bonds was suggested before as a possible factor facilitating formation of protofibrils (9). This effect is generic and should apply to all studied sequences. However, only one of them forms the stable protofibril upon formation of a dimer. Only one more (sequence 2) is prone to further aggregation upon formation of a trimer. Here, the complete saturation of the hydrogen-bond network for the central unit of the trimer is certainly an important factor of stability. However, this stabilizing effect is not strong enough for the remaining 12 sequences studied. It again proves the importance of various interactions and subtle sequence features leading to the spontaneous aggregation. Thus, for the time being one cannot pinpoint a single particular feature responsible for nonaggregating.

Simulations of multiple chain systems show a strong effect of protein concentration on the aggregation process. In the two-chain system (sequence 1) the β-type aggregate was obtained only when one of the molecules has been frozen in the β-conformation. Apparently, in the system of freely moving molecules the lifetime of the β-form is too short for frequent autocatalytic transitions. This effect must be kinetic, because when starting from the dimer, the system remains in this state for a very long time, exhibiting only small conformational fluctuations. In contrast, the freely moving three-chain system (a higher concentration) undergoes fast spontaneous transition into the protofibril structure, provided the starting conformation contains a considerable fraction of the β-type structure in one or more molecules. From a practical point of view, the true nucleus of the amyloid protofibril propagation for the designed aggregating sequence 1 is its dimeric form. At sufficiently high concentration the β-type dimer formation and amyloid propagation is spontaneous. At low concentrations (systems of two molecules) the dimer formed only when one of the molecules was artificially frozen in the β-structure. Because even at low concentration the dimeric form is stable a word of caution needs to be made. It cannot be excluded that even despite the short lifetime of the β-type monomer in very long simulations the dimerization may eventually occur. This event, however, would be very rare, perhaps insignificant for its hypothetical biological context.

Simulations at various concentrations show that the amyloid form of sequence 1 is stable, regardless of the concentrations, whereas the other sequences do not form aggregates even at relatively high concentrations. The exception is sequence 2, for which the trimer, but no dimer, is stable. The remaining 12 nonaggregating sequences dissolve and refold into helices from artificially forced starting amyloid-type structures.

The observed mode of amyloid propagation supports the hypothesis that the amyloid fibrils are built from β-sheets, with the strands running approximately orthogonally to the fibril axis and the β-sheet network of hydrogen bonds running parallel to the axis. The relative orientation of the associating strands (parallel or antiparallel) may change from case to case, at least in the initial stages of the amyloid propagation and seems to depend on the mode of initiation (a frozen, structurally ideal monomer versus spontaneously assembled dimer). The small β-type structures, monomers and dimers, exhibit significant structural fluctuations. The fluctuations may influence the mechanisms of the next steps of the association, which is in qualitative agreement with recent findings by Dima and Thirumalai (35). Obviously, the design of our sequences, especially relatively short β-strands in the resulting structures, introduce some bias toward the β-sheet structure of the aggregates. Thus, the present simulations cannot falsify the β-helix hypothesis for the amyloid structure. Nevertheless, the results of this work and the results of previous experimental and computational studies (7–9, 17) strongly support the β-sheet structure.