Stress release drives symmetry breaking for actin-based movement

Abstract

By using a simple assay composed of purified proteins, we studied the spontaneous polarization of actin networks polymerizing on spherical beads, which subsequently undergo movement. We show evidence that this symmetry breaking is based on the release of elastic energy, analogous to the fracture of polymer gels. The dynamics of this process and the thickness at which it occurs depend on the growth rate and mechanical properties of the actin gel. We explain our experimental results with a model based on elasticity theory and fracture mechanics.

Actin polymerization-based movement is a fascinating process in which monomer assembly at a surface generates the force that is necessary for displacement. This phenomenon drives lamellipodia protrusion in cells, where polymerization of actin is nucleated at the plasma membrane and modulated by crosslinking, capping, and depolymerizing proteins that are present in the cytoplasm. The actin machinery can be triggered by an external chemical signal, leading to cell polarization and directional movement. However, oriented displacement can also occur in the absence of external cues by spontaneous symmetry breaking (1). Moreover, polarization followed by actin-based motility is displayed by simple objects like bacteria, liposomes, endosomes, soft droplets, or solid beads in cells or cytosol (2–4). Understanding how directional movement arises in these systems could lead to comprehension of how symmetry breaking occurs in cells.

One broadly studied nucleator of actin polymerization is the Arp2/3 complex that is activated near the plasma membrane by WASP (Wiskott–Aldrich syndrome protein) family proteins (5) or near the surface of the bacteria Listeria monocytogenes by the protein ActA (6). When it is associated with an actin filament, activated Arp2/3 complex nucleates a new filament by initiating a branch, thus organizing a dendritic actin network (7). Capping proteins, actin depolymerizing factor (ADF)/cofilin and profilin, regulate the rate of polymerization and depolymerization of actin filaments and cooperate to ensure a high concentration of actin monomers (8). Crosslinking proteins change the mechanical properties of actin networks in vitro (9–13) and have an important role in motility (for example, in the protrusion of filopodia) (14).

The motility of Listeria can be reproduced in a medium containing a minimum set of purified proteins that can also support the movement of solid beads coated with activating factors of actin polymerization (4, 15, 16). Except in cases of preexisting asymmetry, the initial actin gel that grows around the beads is homogeneous and must undergo symmetry breaking to generate a comet that can push forward (3, 4, 17–19). In this article, we examine how symmetry breaking arises on beads coated with verprolin/cofilin/acidic domain (VCA) (an Arp2/3 activator derived from WASP) in a mix of commercially available proteins. We varied the composition of the motility medium and added actin filament crosslinking agents to obtain a precise description of the physical and biochemical parameters that govern the growth of actin gels and the characteristics of symmetry breaking. We show experimental evidence that symmetry breaking occurs through a release of elastic energy in the actin gel, which can be triggered locally by disrupting the region of accumulated stress. This process is reminiscent of the fracture observed in brittle solids or gels. We propose a theoretical model based on elasticity and fracture mechanics to explain the experimental results.

Materials and Methods

Proteins. Actin, Arp2/3, gelsolin, ADF/cofilin, profilin, α-actinin, VCA, and biotinylated actin were purchased from Cytoskeleton (Denver), and used without further purification. Protein concentrations were determined by SDS/PAGE using a BSA standard. Alexa Fluor 594- and Alexa Fluor 488-labeled actin were obtained from Molecular Probes, and streptavidin was obtained from Perbio Science (Brebières, France). Fascin was purified as described (20). Human filamin A was a gift from Fumi Nakamura and Thomas Stossel (Brigham and Women's Hospital, Boston).

Bead Preparation. Polystyrene beads (Polysciences) with radii of 0.9, 1.4, 2.3, 2.9, 4.8, and 7.9 μm were incubated for 1 h at 4 °C with 5 μM VCA solution at a total bead surface area of 15 m²/liter that was kept constant when changing bead sizes. The density of VCA on the bead surface was estimated by measuring the VCA remaining in solution by a Bradford assay, and it was 0.10 ± 0.015 μmol/m², corresponding to an average distance between VCA molecules of 4.0 ± 0.3 nm, similar to reported values (4). By varying the VCA concentration in the incubation, we verified that this density corresponded to complete saturation of the bead surface. Beads were stored in a storage buffer (10 mM Hepes, pH 7.5/0.1 M KCl/1 mM MgCl₂/0.1 mM CaCl₂/1 mg/ml BSA) for up to 1 week at a total bead surface area of 15 m²/liter.

Gel Growth and Motility Assay. Unless otherwise indicated, the motility medium contained 10 mM Hepes (pH 7.5), 0.1 M KCl, 1 mM MgCl₂, 0.15 mM CaCl₂, 1.8 mM Mg·ATP, 6 mM DTT, 0.13 mM diazabicyclo[2.2.2]octane (Dabco; an antiphotobleaching agent), 7.44 μM F-actin (10% labeled with Alexa Fluor 594 or Alexa Fluor 488 for confocal microscopy), 0.05 μM Arp2/3, 0.2 μM gelsolin, 3 μM ADF/cofilin, 0.3 μM profilin, and 10 mg/ml BSA. At time 0, a small volume of bead suspension was diluted 30 times in motility medium and mixed gently with a pipette. (Note that the same results were obtained for twice the amount of beads.) The sample was placed between a glass slide and coverslip (18 × 18 mm) sealed with Vaseline/lanolin/paraffin (1:1:1). The total volume of sample was such that the spacing between slide and coverslip was at least three times the bead diameter (5 μl for beads with radii of R = 1, 1.4, and 2.3 μm; 6 μl for beads with a radius of R = 3 μm; 10 μl for beads with a radius of R = 5 μm; and 16 μl for beads with a radius of R = 8 μm).

Bead Observation and Data Processing. Fluorescence microscopy was performed by using an Olympus inverted microscope with a ×100 oil-immersion objective. Measurement of the thickness of the actin gel (the edge of the gel was taken as the point at which the fluorescence intensity decayed to half the maximum intensity) and the bead velocity were performed by using meta-morph software (Universal Imaging). We either followed one single bead for a certain time or took pictures of many different, randomly chosen beads. Both methods gave the same results for the thickness as a function of time (see Fig. 5, which is published as supporting information on the PNAS web site). Confocal microscopy experiments were carried out with a Zeiss confocal microscope with a ×63 (1.40 numerical aperture) oil-immersion objective and controlled by lsm 510 meta software. Actin–Alexa Fluor 488 was observed with an ion–argon 25-mW laser (488 nm). To limit convective flux, 0.5–1 μM α-actinin was added. Surface-rendered 3D reconstructions of confocal slices were performed by using volumej software (21) with filtered images (metamorph, Median Filter) and enhanced contrast. Photodamage was achieved by local illumination of a sample containing 5% Alexa Fluor 594-labeled actin and 5% Alexa Fluor 488-labeled actin with a helium–neon 1-mW laser (543 nm) iterated 200–400 times (corresponding to a few seconds).

Results

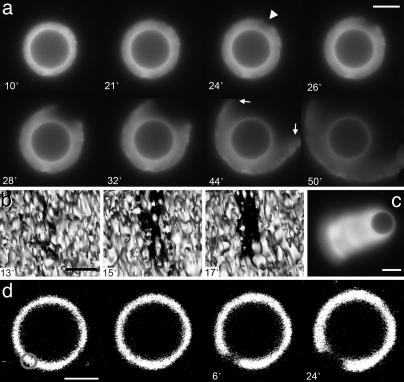
Growth and Symmetry Breaking of Actin Gels Around Spherical Beads. In motility medium, actin assembles at the surface of VCA-coated beads and pushes away the already assembled gel, as shown by two-color fluorescent marking (see Fig. 6, which is published as supporting information on the PNAS web site). First, the actin halo is spatially homogeneous, and its thickness grows with an initial rate of a few tenths of a micrometer per minute (Fig. 1a). Eventually, the spherical symmetry is broken; a notch appears at the external surface of the actin gel (arrowhead in Fig. 1a), which grows inward and expands laterally with a velocity of a few micrometers per minute. As shown in Fig. 1b, the shape of the hole in the gel is elongated rather than circular (see Movies 1–3, which are published as supporting information on the PNAS web site, for other examples). After several minutes, the hole is big enough for the bead to escape from the gel, and the bead starts to move, trailing an actin comet (Fig. 1c). Strikingly, symmetry breaking can be triggered by a local disruption of the actin gel. Taking advantage of our observation that Alexa Fluor 594-labeled actin is damaged by prolonged exposure to green light, we locally damage the actin gel by illuminating a small region with a 543-nm laser (see Materials and Methods) and, thus, induce symmetry breaking (Fig. 1d and Movie 4, which is published as supporting information on the PNAS web site).

Fig. 1.

Spontaneous and induced symmetry breaking around beads. VCA-coated beads were placed in a medium containing 7.44 μM F-actin (10% labeled with Alexa Fluor 594), 0.05 μM Arp2/3, 0.2 μM gelsolin, and 3 μM ADF/cofilin. Time after mixing is indicated in minutes (except for in d). (a) Fluorescence microscopy images for a bead with a radius of 7 μm. The arrowhead at 24 min indicates the appearance of a notch at the outer surface of the gel. At 44 min, the gel straightens near the edges of the hole (arrows). (Scale bar, 10 μm.) (b) Surface-rendered 3D reconstructions from confocal slices of a hole opening in the actin gel on a bead with a radius of 5 μm. The granular aspect is due to the reconstruction software (see Materials and Methods). (Scale bar, 2 μm.) (c) Fluorescence microscopy image of a comet attached to a bead of 3 μm radius moving at a velocity of 0.3 μm/min. (Scale bar, 5 μm.) (d) Symmetry breaking can be triggered locally by photodamage of the region indicated by the circle. The first two images were taken just before and just after photodamage. A few minutes after photodamage, a hole appeared. Time after photodamage is indicated in minutes. (Scale bar, 5 μm.)

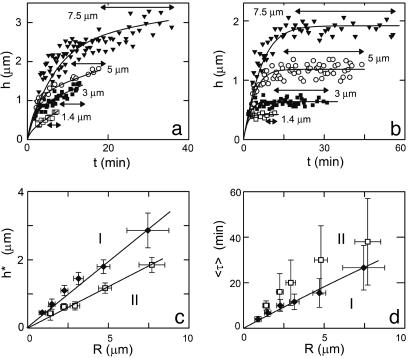
For spontaneous symmetry breaking, we define the moment of symmetry breaking as the first appearance of the notch in the actin gel. We denote the symmetry breaking time τ as the interval between the addition of the beads to the motility medium and the moment of symmetry breaking, and we define h* as the actin gel thickness at time τ. The values of τ and h* depend on the size of the beads, the medium composition, and the presence of crosslinkers, as described below. Depending on the exact composition of the motility medium, two different symmetry-breaking scenarios can be observed, as shown in Fig. 2 a and b. In case I (Fig. 2a), the actin gel grows continuously until the symmetry breaks spontaneously. No steady-state thickness is reached in this case. In contrast, in case II (Fig. 2b), symmetry breaking is preceded by a plateau in gel thickness. The average time of symmetry breaking, 〈τ〉, is usually longer in case II and could reach infinity, whereas the distribution of τ (double-headed arrows in Fig. 2 a and b) is wider (Δτ/〈τ〉 can be up to 70% for case II, whereas it is typically 20–40% for case I). The occurrence of case I or II does not depend on the size of the beads. For both cases, h* increases linearly with increasing bead radius (Fig. 2c). The average time 〈τ〉 also increases with the bead radius (Fig. 2d), and its increase is approximately linear in R, in agreement with earlier observations (4).

Fig. 2.

Symmetry breaking scenario is independent of bead size. Actin gel thickness of randomly chosen beads as a function of time for beads of different radii in a medium containing 7.44 μM F-actin (10% labeled with Alexa Fluor 594), 0.05 μM Arp2/3, 3 μM ADF/cofilin, and 0.25 (a; case I) and 0.05 (b; case II) μM gelsolin. Symmetry breaking occurs before h reaches a plateau in case I (a) and after h reaches a plateau in case II (b). Double-headed arrows indicate the intervals where symmetry breaking occurs. (c) The thickness at which symmetry breaks as a function of the bead radius for case I (a) and II (b). (d) The average time after which symmetry breaking starts as a function of the bead radius for both cases. The vertical error bars correspond with the double-headed arrows in a and b. Errors in the bead radii are provided by the manufacturer.

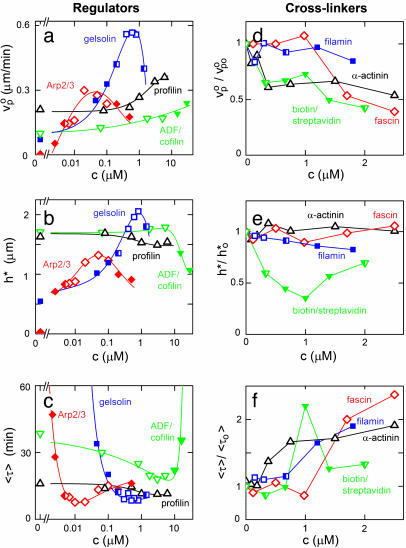
Effect of the Composition of the Medium. The only protein, besides actin and VCA, that is required for the accumulation of actin at the bead surface is Arp2/3. Gelsolin is not required for the growth of the actin gel, but without gelsolin, no symmetry breaking is observed, even after 8 h (see Fig. 7b, which is published as supporting information on the PNAS web site), and the actin gel at steady state is approximately four times thinner than at the optimal gelsolin concentration (Fig. 3b). Symmetry breaking is observed for Arp2/3 concentrations >0.002 μM and gelsolin concentrations of >0.03 μM. The initial growth rate of the gel has an optimum at ≈0.05 μM Arp2/3 and 0.7 μM gelsolin (Fig. 3a), where the gel thickness is highest (Fig. 3b) and the time of symmetry breaking is, within experimental error, at a minimum (≈8 min for 3-μm radius beads; see Fig. 3c). Varying Arp2/3 and gelsolin concentrations leads to a transition from case I to II (as indicated in Fig. 3, see also Fig. 7 a and b).

Fig. 3.

Effect of actin-regulating proteins and crosslinkers on gel growth and symmetry breaking. Beads with a radius of 3 μm were incubated in a medium containing 7.44 μM F-actin (10% labeled with Alexa Fluor 594) and, if not varied, 0.05 μM Arp2/3, 3 μM ADF/cofilin, and 0.2 μM gelsolin. (a–c) The effect of the concentrations of Arp2/3 (red), gelsolin (blue), ADF/cofilin (green), and profilin (black) on the initial growth velocity 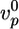of the actin gel (a), the gel thickness h*(b), and the average time 〈τ〉 at which symmetry breaking starts (c) is shown. Lines are shown as guides to assist viewing. (d–f) The effect of the concentrations of fascin (red), α-actinin (black), filamin (blue), and streptavidin (in the presence of 1.8 μM biotinylated actin) (green) on 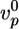(d), h*(e), and 〈τ〉 (f). Values were normalized with respect to the values in the absence of crosslinkers (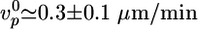, 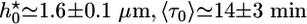) to make trends more apparent. In all images, open symbols correspond with case I, filled symbols correspond with case II, and half-filled symbols are intermediate. Each point is an average of at least 10 measurements. The variance was 10–20% for h* and 20–40% for 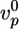and 〈τ〉 in case I, and it could be up to 70% for 〈τ〉 in case II because of the nature of symmetry breaking under these conditions (see Discussion). Plots of h as a function of time for several different concentrations of all proteins are shown in Figs. 7 and 8.

Contrary to earlier observations on Listeria (15), we found that ADF/cofilin is not essential for symmetry breaking and motility, although it enhances gel growth and symmetry breaking (Fig. 3 a and c) at concentrations of <10 μM. However, increasing the ADF/cofilin concentration from 10 to 25 μM shifts the behavior from case I to II (see also Fig. 7c), decreases the steady-state gel thickness (Fig. 3b), and increases the time of symmetry breaking (Fig. 3c). At >25 μM, no symmetry breaking is observed. Profilin is not essential and has a smaller effect than the other proteins. It speeds up polymerization and slightly enhances symmetry breaking (Figs. 3 a and c and 7d).

After the symmetry is broken, the beads develop an actin comet and start moving with a speed that depends on the concentrations of the actin-binding proteins in a comparable fashion as for Listeria (15). We found that the optimal conditions for motility (highest velocity) are approximately the same as those for symmetry breaking (shortest time 〈τ〉). The optimal mix is ≈0.05 μM Arp2/3, 0.7 μM gelsolin, 5 μM ADF/cofilin, and 0.8 μM profilin, which gives an average velocity ≈0.5 μm/min for 3-μm radius beads, similar to values reported before for beads (4) and Listeria (15).

Effect of Crosslinkers. To investigate the influence of the elastic properties of the actin gel, the following crosslinkers were tested: the native actin crosslinkers α-actinin, fascin, and filamin, and the nonphysiological crosslinker streptavidin used in combination with biotinylated actin (24% of total actin). At sufficiently high crosslinker concentrations (>1 μM), we could see actin bundles throughout the sample for all four crosslinkers. As expected (11), the bundles were the most obvious for fascin and the least obvious for filamin. The thickness of the actin gel at which symmetry breaking occurs, h*, is hardly affected by fascin and α-actinin (Fig. 3e) and the system is in case I for all concentrations (see also Fig. 8 a and b, which is published as supporting information on the PNAS web site). However, with increasing concentrations of fascin or α-actinin, the initial growth velocity of the actin gel decreases (Fig. 3d) and the time of symmetry breaking increases (Fig. 3f). The presence of filamin slightly decreases h* (Fig. 3e) and causes a transition from case I to II (see also Fig. 8c). Interestingly, this effect is much more pronounced for biotin/streptavidin crosslinking, which also causes a transition to case II (see also Fig. 8d) and gives a minimum gel thickness and a maximum time 〈τ〉 at a streptavidin/biotin–actin ratio of ≈1:2 (Fig. 3 e and f).

Discussion

Symmetry Breaking Is Due to Stress Release. As shown in Fig. 1a, symmetry breaking starts as a notch at the external surface of the actin gel (arrowhead at 24 min). The hole has an elongated shape, like a crack (Fig. 1b), and grows inward and expands laterally, rupturing near the bead surface. As indicated by the arrows in Fig. 1 at 44 min, the gel straightens near the edges of the hole to reduce its curvature. Together, these observations strongly suggest that symmetry breaking is driven by the release of elastic energy (4, 19) stored in the actin cloud, which is gel-like because of the action of Arp2/3 and crosslinkers (22–24). A piece of gel that is polymerized and crosslinked at the bead surface is stretched as it moves outward (see Fig. 6), resulting in the build-up of a tensile stress, which is maximum at the exterior surface (19). The elastic energy stored in the gel may be released by a fracture of the gel (4, 19), and this breakage of crosslinks or filaments leads to polarization of the actin gel. Alternatively, symmetry breaking may result from an enhancement of depolymerization at the exterior of the gel by the tensile stress, which renders the symmetric gel unstable toward inhomogeneous fluctuations in the gel thickness (18). In both cases, symmetry breaking starts at the exterior of the gel where the tensile stress is largest. Although it is not excluded that the first event generating the notch could be based on unstable small-scale fluctuations (18), the process that follows is more reminiscent of the fracture of a brittle elastic material or a gel, than of a depolymerization phenomenon. Furthermore, our observations do not favor a stochastic mechanism based on fluctuations in polymerization and depolymerization rates, which predicts that symmetry breaking should start at the bead surface (17). Next, we focus on the initial stages of the fracture event and analyze the data in terms of an elastic model for gel growth and fracture. The variables and parameters used in the model are summarized in Table 1, which is published as supporting information on the PNAS web site.

Growth of an Actin Gel Around a Bead. First, we consider the growth of a homogeneous crosslinked actin gel around a bead. Polymerization occurs at the surface of the bead (Fig. 6), whereas depolymerization occurs at the pointed ends that are assumed to be mostly situated near the exterior of the gel (18, 19). Thus, the growth velocity of the gel can be described as follows:

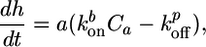[1]

where 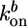and 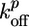are the rate constants for monomer addition at the inner surface (barbed ends) and monomer loss at the outer surface (pointed ends), respectively, C_a is the concentration of G-actin available for polymerization, and a ≃ 2.7 nm is the gained filament length per monomer (25). The rate parameters 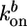and 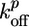depend on the stress in the gel, because forces pushing or pulling on a filament can change the rate constants (26). However, in the early stages of gel growth, the stresses in the gel are still small, and the rate constants are approximately equal to those of free barbed and pointed ends. We find experimentally that the optimum initial polymerization rate 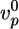is ≈0.6 μm/min, in accordance with an estimate of Eq. 1 using reported values for the rate constants (27): 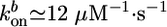, , 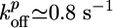and C_a ≃ 0.6 μM (close to the critical concentration of pointed ends, because all barbed ends are capped by Note gelsolin). Note that 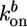, , 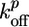and thus 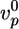, depend on the concentrations of the various actin binding proteins (see Fig. 3 a and d).

After several minutes, the growth velocity of the gel decreases, because the stress in the gel increases with increasing thickness. If the symmetry does not break, the gel thickness reaches a steady state, where polymerization at the bead surface balances depolymerization at the external surface (19). The steady-state thickness is either stress-limited, in which case it is proportional to the bead radius R, or diffusion-limited and independent of R (19, 28). For case II, in which a steady state is indeed reached, we are in the stress-limited regime, because h^s is proportional to R (Fig. 2c). The following equation then applies (19):

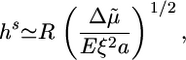[2]

where 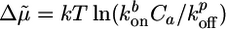is a measure for the chemical energy of the polymerization process, ξ is the mesh size of the actin network, and E is the elastic modulus of the gel, which depends on ξ and on the density of crosslinks (9).

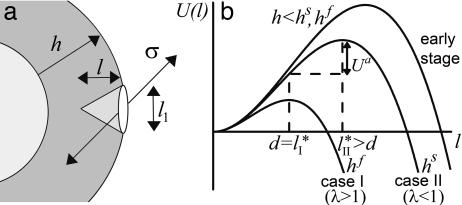
Symmetry Breaking and Fracture. As suggested by Griffith (29), the resistance of a material to fracture can be estimated by considering the contributions of the fracture energy that is needed for breaking bonds (U_br) and the elastic energy that is released when a crack is formed (U_el). Fig. 1b and Movies 1–3 show that the crack has an elongated shape. An elongated crack is more likely to grow than a circular one, because the stresses are higher at the tip of a narrow, elongated hole than around a circular hole (30). Therefore, let us consider an elongated crack at the exterior of the spherical gel with a depth l and a length l₁ along the contour of the gel (Fig. 4a). We assume that initially l and l₁ are of the same order of magnitude (31) and that the crack is much smaller than the gel thickness h. The tensile stress can then be considered as constant along the crack: σ ≃ σ_θθ(h) ≃ Eh/R (19). The amount of elastic energy released by the presence of the crack is on the order of U_el ≃ (σ ²/E)l³ ≃ El³h²/R² (29, 31). (Note that we neglect all geometrical prefactors that depend on the exact shape of the crack.) The energy required for breaking bonds is U_br ≃ Γl², where Γ is the fracture energy per unit area (29). It can be estimated as 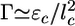, where ε_c is the energy needed to break one crosslink and 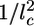is the average number of crosslinks per unit area (with l_c being the average distance between crosslinks). The total energy change due to the crack U(l) = U_br – U_el is maximal for a value l* ≃ EΓ/σ ² (Fig. 4b). For small cracks with l < l*, crack growth is energetically unfavorable, but for l ≥ l*, crack growth is spontaneous because the energy decreases with increasing l. As the gel thickness and the tensile stress increase, the critical crack length l* decreases (Fig. 4b). Assuming that fracture starts as soon as the critical crack size l* equals the typical size d of a flaw or a preexisting crack present in the material (29), spontaneous fracture occurs at a critical stress σ ^f ≃ (EΓ/d)^1/2 or at the following critical thickness:

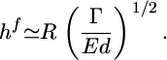[3]

When the stress is smaller than the critical stress σ ^f, fracture can still be triggered by an external perturbation, as shown by damaging a small region in the actin gel (Fig. 1d and Movie 4).

Fig. 4.

Griffith model for gel fracture. (a) Schematic representation of a bead supporting a spherical actin gel of thickness h with a crack of depth l and length l₁ at the exterior of the gel. The tensile stress σ is indicated. (b) The total energy change U(l) between the homogeneous gel and the gel with a crack as a function of the crack size l. The critical crack size l* and the energy barrier to spontaneous fracture decrease as the gel thickness grows. For case I, the gel grows until h = h^f, where 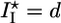and spontaneous fracture occurs, because the total energy decreases as l increases. For case II, the gel stops growing when h = h^s and 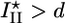. In this case, there is an energy barrier Ua for the preexisting crack of length d to grow to the critical length 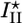, and crack growth and symmetry breaking are delayed.

Two Scenarios for Spontaneous Fracture: Cases I and II. The presence of a plateau in the h(t) curves depends on the relative magnitude of the homogeneous steady-state thickness (Eq. 2) and the critical fracture thickness (Eq. 3). We define a dimensionless parameter λ as follows:

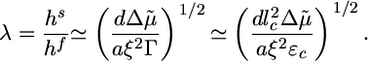[4]

Case I corresponds to λ > 1, because the critical stress for fracture is reached before the thickness reaches its homogeneous steady-state value. Thus, the gel grows until h = h^f, where l* = d and the gel ruptures spontaneously (Fig. 4b). Case II corresponds to λ < 1, because the gel thickness reaches a steady-state value h^s before the critical stress is reached, so that l* > d (Fig. 4b). Note that both h^s and h^f are proportional to R (Eqs. 2 and 3), in agreement with our experimental results (Fig. 2c). Let us estimate orders of magnitude for h^s and h^f and compare with the experimental results. For case I, h^f/R (the slope in Fig. 2c) is ≈0.4. With Eq. 3, and an energy per crosslink ε_c of order 10 kT (similar to the strength of a bond between actin monomers; ref. 32), a distance between crosslinks l_c of ≈50 nm (28) and an elastic modulus E of 10³–10⁴ Pa (22, 23), we find a typical flaw size d of order a tenth of a micrometer, which is reasonable. Note that ε_c is not expected to depend strongly on the type of crosslink because rupture can occur also on an actin filament next to the crosslink. A lower estimate for the average time of symmetry breaking is 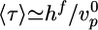, which neglects the decrease of the growth velocity as the gel thickness increases. Taking 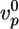as independent of R, we find that 〈τ〉 is proportional to R, in agreement with Fig. 2d (case I). By using 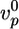≃ 0.3 μm/min, as obtained from Fig. 2a, and h^f/R ≃ 0.4, as obtained from Fig. 2c, we find 〈τ〉/R ≃ 1.3 min/μm, just below the slope in Fig. 2d. For case II, the slope h^s/R in Fig. 2c is ≈0.3, of the same order as an estimate of Eq. 3 using (see above) 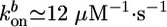, , 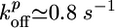C_a ≃ 0.6 μM, E ≃ 10³ – 10⁴ Pa, and ξ ≃ 50 nm. Note that the two characteristic thicknesses h^s and h^f are of the same order of magnitude, so that a transition between the two regimes can be observed by a slight variation of the parameters. The parameter λ is independent of R, so that the transition from case I to II does not depend on R, in agreement with our experimental results (Fig. 2). Note also that λ is independent of the elastic modulus E but does depend on the mesh size ξ and the fracture energy Γ.

In case II, there is a delay between reaching the steady state and the start of fracture, which can range from several minutes to infinity. This delay could be explained by the following two different effects: an energy barrier for fracture nucleation that is overcome by thermal fluctuations (31) or the time needed for a thickness fluctuation to grow until it generates sufficient tensile stress to produce a crack (18). The first mechanism introduces a nucleation rate k_n ∼ exp(–U^a/kT), where U^a is an energy barrier to go from the preexisting crack of length d to a crack of length l*: U^a = U(l*) – U(d) (Fig. 4b). For d « l* (corresponding to h^s « h^f), we get U^a ≃ U(l*) ≃ E²Γ³/σ⁴, which becomes the following at h = h^s (with σ = Eh^s/R and Eq. 2):

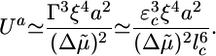[5]

The average time of symmetry breaking in this regime can be estimated as the time needed to reach steady state plus the average delay before a crack is nucleated: 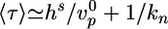. This nucleation mechanism explains our observation that the distribution of τ is wider in case II than in case I (Fig. 2d). The second effect involves a characteristic time that is much larger than the time needed to reach a steady state (18) and could come into play in our case II observations in which the time of symmetry breaking largely exceeds the time necessary to reach the steady state. In this situation, symmetry breaking might start as a fluctuation in the gel thickness, which is amplified because of enhanced depolymerization and results in a fracture as soon as the amplitude of the perturbation becomes of order l*. Thus, this mechanism would greatly enhance symmetry breaking in conditions in which the thermal nucleation rate k_n is small.

Note that we did not take into account stress dissipation by rearrangement of crosslinks, which could become relevant especially if the gel growth is slow and would increase the symmetry breaking time.

The Effect of Actin-Binding Proteins. As shown in Fig. 3, the various actin-binding proteins have a large effect on the growth of actin gels and the kinetics of symmetry breaking. Next, we discuss these effects in the light of the known functions of these proteins and compare these results to the predictions of the model described above. Arp2/3, activated by VCA, is essential for gel growth around the beads and enhances polymerization (7) (as shown in Fig. 3a) and, thus, increases 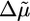. Because Arp2/3 induces branching of actin filaments, it reduces the mesh size ξ and the distance between crosslinks l_c, and decreases the typical flaw size d (24). If we assume that Arp2/3 affects the mesh size and the crosslink density in the same way (l_c ∼ ξ) and that ε_c is not affected by Arp2/3, we find from Eq. 4 that 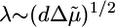. We observe a transition from case II to I when the Arp2/3 concentration increases from 0.0025 to 0.02 μM (Figs. 3 and 7a), which indicates that λ increases and that the increase in 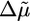is stronger than the decrease in d. At >0.05 μM, we see a decrease of the polymerization rate, probably because the large number of nucleated barbed ends depletes the pool of G-actin. As a result, 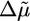and, thus, λ decrease and the behavior corresponds again to case II (Fig. 3). As expected, the time of symmetry breaking is smallest in the concentration range that corresponds to case I.

Gelsolin caps barbed ends and prevents them from elongating (8, 33). As a result, the concentration C_a of G-actin in the medium increases with increasing gelsolin concentration and polymerization is enhanced according to Eq. 1, in agreement with our observations (Fig. 3a). Furthermore, the capping activity of gelsolin also decreases the number of growing barbed ends, so that the density of the gel decreases (34), leading to an increase in ξ, l_c, and in the typical flaw size d (inhomogeneities become more important with decreasing density). Assuming again that 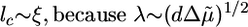, we find that an increase in the gelsolin concentration leads to an increase in the parameter λ (Eq. 4) and a transition from case II to I, as observed experimentally (Figs. 3 and 7b). Note that without gelsolin, no symmetry breaking could be observed, indicating that the energy barrier for crack nucleation (Eq. 5) is too large. As expected, the time of symmetry breaking is again smallest for concentrations corresponding to case I. Note that at the present concentration of calcium symmetry breaking could also be enhanced by the severing activity of gelsolin (33).

ADF/cofilin is known to increase the depolymerization rate at the pointed ends 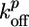, which results in a further increase in the concentration C_a of G-actin (8, 35) and, therefore, in an increase in the polymerization velocity, as observed (Fig. 3a). At low concentrations, in which the behavior corresponds to case I, symmetry breaking is enhanced by this increased polymerization velocity (Fig. 3c), whereas the fracture thickness h^f (Eq. 3) is hardly affected by ADF. The transition to case II at 10 μM ADF/cofilin can be explained by the enhanced depolymerization rate, which causes a decrease of 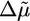and, thus, λ. The steady-state thickness h^s decreases with increasing ADF concentration (Fig. 3b) in accordance with Eq. 2, whereas the time of symmetry breaking increases and becomes virtually infinite at very high concentrations (Fig. 3c).

Last, profilin is known to enhance polymerization (see Fig. 3a), because it provides G-actin for polymerization and catalyzes nucleotide exchange (ADP to ATP) on actin monomers (8). As a result, symmetry breaking is slightly enhanced (Fig. 3c). Because λ > 1 in the absence of profilin and 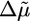increases in the presence of profilin, λ increases and the system remains in case I.

Effect of Crosslinkers. The four different crosslinkers have different effects on the characteristics of symmetry breaking. α-Actinin and fascin are dynamic crosslinkers that favor the formation of actin bundles (10, 13). This bundling may be the reason for the decreased polymerization velocity upon addition of crosslinkers (Fig. 3d), because bundling could stabilize actin filaments, leaving less actin available for polymerization (36). The final thickness of the actin gel (Fig. 3e) and the scenario of symmetry breaking are hardly affected by these crosslinkers and the increase in the time 〈τ〉 (Fig. 3f) can be attributed completely to the decreased gel growth rate. For all fascin and α-actinin concentrations, we are in case I, so that the time of symmetry breaking is equal to the time needed for the gel to reach its critical thickness: 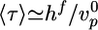. For α-actinin, 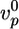decreases by approximately a factor of two, whereas 〈τ〉 increases by the same factor. For fascin, a 2.5-fold decrease in 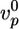is mirrored by a 2.5-fold increase in 〈τ〉. These results suggest that α-actinin and fascin affect the structure and the elastic properties of the gel only weakly, perhaps because the Arp2/3-nucleated array is not appropriate for binding of these proteins.

Filamin crosslinks actin filaments into 3D networks that are stiffer and more solid-like than those formed by fascin and α-actinin (11, 12). With increasing amounts of filamin, a transition from case I to II can be observed (see also Fig. 8c), which indicates that the parameter λ (Eq. 4) decreases when crosslinks are added. This decrease in λ can be explained by an increase in the fracture energy Γ (or a decrease in the average distance between crosslinks l_c) and a decrease in the flaw size d. The mesh size ξ can be assumed to be unaffected by crosslinkers because it is determined by the density of the actin gel (9). The time 〈τ〉 increases significantly with increasing filamin concentration (Fig. 3f) because of an increase in the fracture delay time (Eq. 5; see also Fig. 8c). Contrary to fascin and α-actinin, it cannot be explained by the polymerization rate, which is almost unaffected by filamin (Fig. 3d), in agreement with the observation that fewer bundles could be observed in the medium for filamin than for the other crosslinkers. The steady-state thickness is affected only slightly by filamin.

Interestingly, the effect on h* and 〈τ〉 is much more pronounced for biotin/streptavidin, which is a much stronger crosslinker than fascin, α-actinin, and filamin (10). We see a clear transition from case I to II after addition of streptavidin (see also Fig. 8d), and h* decreases to a minimum and 〈τ〉 increases to a maximum at a ratio of 1:2 between streptavidin and biotin (Fig. 3 e and f). This ratio corresponds to the optimum ratio for crosslinking, because every crosslink is composed of two biotin–actin monomers and one streptavidin. At higher streptavidin concentrations, crosslinking is less efficient so that h* increases again and 〈τ〉 decreases. An explanation for why streptavidin has a larger effect on h* than filamin is that the polymerization velocity decreases more strongly for streptavidin than for filamin (Fig. 3d), which leads to a larger decrease in 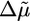and, thus, h^s (Eq. 2). Moreover, the dynamics of biotin/streptavidin crosslinks are much slower than for filamin. The lifetime of a filamin crosslink is in the order of seconds (37), so that a crosslink formed by filamin at the bead surface just after polymerization is dissociated long before it reaches the outer regions of the gel. Hence, a filamin crosslink only slightly contributes to the stress, so that the steady-state gel thickness h^s (Eq. 2) is only weakly affected. Biotin/streptavidin crosslinks, on the contrary, are virtually irreversible (10), so that they do increase the stress and decrease the steady-state thickness.

Concluding Remarks. By using VCA-coated beads in a mix of purified proteins, we have shown that fracture of an elastic actin gel can drive symmetry breaking. Moreover, our results suggest an explanation for why symmetry breaking on beads in cell extracts is more difficult to obtain than in the purified protein mix (under optimal conditions) (3, 4); the abundance of crosslinkers in cell extracts slows down fracture nucleation. More generally, the mechanism we describe here might be relevant in cells for polarization in the absence of external cues.