Development of interpretable machine learning models to predict in‐hospital prognosis of acute heart failure patients

Abstract

Aims

In recent years, there has been remarkable development in machine learning (ML) models, showing a trend towards high prediction performance. ML models with high prediction performance often become structurally complex and are frequently perceived as black boxes, hindering intuitive interpretation of the prediction results. We aimed to develop ML models with high prediction performance, interpretability, and superior risk stratification to predict in‐hospital mortality and worsening heart failure (WHF) in patients with acute heart failure (AHF).

Methods and results

Based on the Kyoto Congestive Heart Failure registry, which enrolled 4056 patients with AHF, we developed prediction models for in‐hospital mortality and WHF using information obtained on the first day of admission (demographics, physical examination, blood test results, etc.). After excluding 16 patients who died on the first or second day of admission, the original dataset (n = 4040) was split 4:1 into training (n = 3232) and test datasets (n = 808). Based on the training dataset, we developed three types of prediction models: (i) the classification and regression trees (CART) model; (ii) the random forest (RF) model; and (iii) the extreme gradient boosting (XGBoost) model. The performance of each model was evaluated using the test dataset, based on metrics including sensitivity, specificity, area under the receiver operating characteristic curve (AUC), Brier score, and calibration slope. For the complex structure of the XGBoost model, we performed SHapley Additive exPlanations (SHAP) analysis, classifying patients into interpretable clusters. In the original dataset, the proportion of females was 44.8% (1809/4040), and the average age was 77.9 ± 12.0. The in‐hospital mortality rate was 6.3% (255/4040) and the WHF rate was 22.3% (900/4040) in the total study population. In the in‐hospital mortality prediction, the AUC for the XGBoost model was 0.816 [95% confidence interval (CI): 0.815–0.818], surpassing the AUC values for the CART model (0.683, 95% CI: 0.680–0.685) and the RF model (0.755, 95% CI: 0.753–0.757). Similarly, in the WHF prediction, the AUC for the XGBoost model was 0.766 (95% CI: 0.765–0.768), outperforming the AUC values for the CART model (0.688, 95% CI: 0.686–0.689) and the RF model (0.713, 95% CI: 0.711–0.714). In the XGBoost model, interpretable clusters were formed, and the rates of in‐hospital mortality and WHF were similar among each cluster in both the training and test datasets.

Conclusions

The XGBoost models with SHAP analysis provide high prediction performance, interpretability, and reproducible risk stratification for in‐hospital mortality and WHF for patients with AHF.

Introduction

Heart failure (HF) is a major public health issue worldwide. ¹ With an aging population, the proportion of patients with HF is rapidly increasing in Japan. ² Consistent with the rise in the number of patients with HF, the number of patients admitted for acute heart failure (AHF) has also increased. Therefore, there is a need to develop models for stratifying the prognosis of patients with AHF based on the disease's life‐threatening status and high in‐hospital mortality. ³ , ⁴ , ⁵ Researchers in various regions have reported models that can predict the long‐term prognosis of patients with AHF. ⁶ , ⁷ , ⁸ Short‐term prognosis models have also been developed for in‐hospital mortality and worsening heart failure (WHF). ³ , ⁴ , ⁵ , ⁹ In the analysis of the ADHERE registry, a simple decision tree model based on three parameters [levels of blood urea nitrogen (BUN), levels of serum creatinine, and systolic blood pressure (SBP)] divided patients into five groups with in‐hospital mortality rates ranging from 2.1% to 21.9%. ³ A decision tree model is a classical machine learning (ML) model developed through a recursive partitioning process based on the values of input variables. It can capture non‐linear relationships between explanatory and objective variables. ¹⁰ , ¹¹ , ¹² It is simple to interpret and suitable for clinical decisions.

On the other hand, patients with AHF constitute a diverse population with variations across regions and countries. ¹³ , ¹⁴ Therefore, to accurately predict the short‐term prognosis of Japanese patients with AHF in the form of a decision tree, we found it necessary to develop a decision tree model for predicting the short‐term prognosis using the registry of patients with AHF in Japan and to validate its performance. Furthermore, with the remarkable advancement of ML analysis in recent years, there have been reports of ML prediction models that may outperform decision tree models. ¹⁵ , ¹⁶ , ¹⁷ Especially, the emergence of ensemble learning has played a significant role in the advancement of ML analysis. Ensemble learning is a technique that combines multiple decision tree models to develop a robust, unified model. By integrating diverse learners, the strengths of individual decision tree models are leveraged and overfitting is minimized, leading to an overall improvement in performance. Despite the evolution of these ML analyses leading to improved prediction performance, another aspect of ML has become problematic. With the advances in ML models, the structure of ML models has become more complex, and ML models have become black boxes, making them difficult for people to interpret intuitively. ¹⁸ , ¹⁹ However, SHapley Additive exPlanations (SHAP), proposed by Lundberg and Lee, may have the potential to address this issue. SHAP is an explainable artificial intelligence (XAI) that scales all variables as SHAP values ²⁰ and shows the contribution of each variable to the prediction outcome, effectively clarifying and explaining the rationale for the complex ML model's predictions. For example, there is a report applying SHAP to prediction models for 3 year all‐cause mortality among HF patients due to coronary heart disease. ²¹ In addition, clustering SHAP values can classify a target dataset into explainable clusters. ²² , ²³ , ²⁴

In this study, we aimed to develop various ML prediction models for in‐hospital mortality and WHF in patients with AHF. From the information collected on the first day of admission (including demographics, physical examination, and blood test results), we developed various ML prediction models. In complex ML models, we utilized SHAP to enhance interpretability and performed SHAP clustering for risk stratification. Finally, we visualized the prediction performance of each model and highlighted clinically significant features for predicting in‐hospital mortality and WHF.

Methods

Study population

The Kyoto Congestive Heart Failure (KCHF) registry study is a Japanese prospective, observational, multicentre cohort study that enrolled consecutive patients who were first admitted for AHF between October 2014 and March 2016. ²⁵ All patients with AHF, as defined by the modified Framingham criteria, who were admitted to a participating facility and treated for AHF within 24 h of hospital arrival were enrolled in the KCHF registry. ²⁵ Patients who died within 1 day after admission were considered to have an extremely high likelihood of being unlikely to survive hospitalization. Predicting in‐hospital mortality or WHF for these patients was deemed to have little practical benefit. Therefore, they were excluded from the analysis, focusing on identifying patients who experienced acute changes leading to in‐hospital mortality or WHF after admission. Of the 4056 patients enrolled, 4 who died on the first day of admission and 12 who died the day after admission were excluded. The final study population thus consisted of 4040 patients. This study adhered to the principles outlined in the Declaration of Helsinki. The study protocol was approved by the Ethics Committee of the Kyoto University Hospital (local identifier: E2311) and each participating hospital. In addition, the Institutional Review Boards of Kyoto University Hospital and each participating institution waived the need for written informed consent, as this study met the conditions outlined in the ‘Ethical Guidelines for Medical and Health Care Research Involving Human Subjects’.

Definitions

In‐hospital mortality was defined as in‐hospital death within 24 h after admission. WHF was defined as the use of additional diuretics and inotropic drugs, mechanical support (such as intra‐aortic balloon pumping and percutaneous cardiopulmonary support), respiratory management (i.e. non‐invasive positive pressure ventilation or intubation), or continuous haemodiafiltration 24 h after admission.

Data preprocessing

Missing values were completed using multivariate feature imputation, which is a method of imputation using all other variables as well as those with missing values. ²⁶ We used only explanatory variables with missing values below 20% for developing the prediction model. All explanatory variables were imputed for missing values and standardized before being used in the development of all prediction models.

Development of prediction models

Based on the KCHF registry, prediction models for in‐hospital mortality and WHF were developed using information obtained on the first day of admission.

Specifically, demographic information, physical examinations, and blood tests commonly performed on patients with AHF were used as explanatory variables.

In addition, variables such as New York Heart Association (NYHA) classifications at admission, the presence of acute coronary syndromes at admission, and the presence of atrial fibrillation at admission are included as explanatory variables. These factors have a significant impact on the prognosis of patients with AHF. The original dataset (n = 4040) was randomly split 4:1 into training (n = 3232) and test datasets (n = 808) in such a way that the rates of in‐hospital mortality and WHF were consistent between the training and test datasets. The same training and test datasets were used for all prediction models.

The hyperparameters of all the models were optimized using Bayesian optimization with stratified 10‐fold cross‐validation (CV). Bayesian optimization is widely utilized as an automated technique for tuning hyperparameters in ML models. ²⁷ All prediction models were developed exclusively with the training dataset, and their performance was assessed using the test dataset (Figure  1 ).

Figure 1.

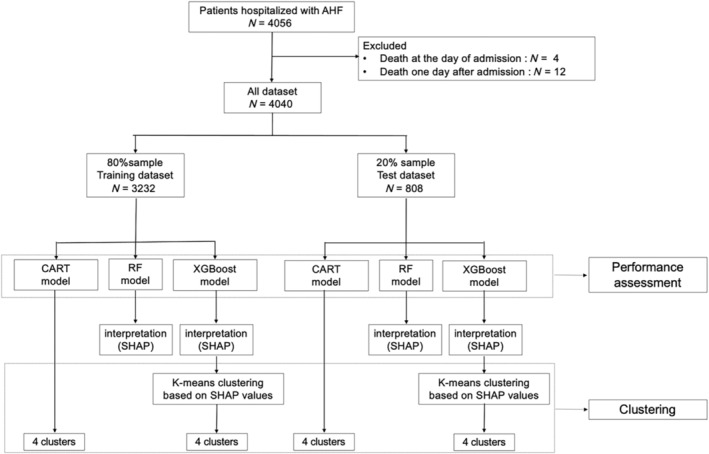
Study flowchart for the development and evaluation of models. AHF, acute heart failure; CART, classification and regression trees; RF, random forest; SHAP, SHapley Additive exPlanations; XGBoost, extreme gradient boosting.

Development of the classification and regression trees model

The classification and regression trees (CART) model is one of the representative decision tree models. In the CART model, the tree construction involves using the Gini impurity to split nodes. ³ The Gini impurity represents the impurity of the probabilities of different classes within a node. In this study, we aimed to maximize the reduction in the Gini impurity by selecting the most effective splits at each node. Additionally, to prevent overfitting, pruning based on the maximum tree depth was performed, ensuring that the tree does not become excessively complex. The training and test datasets were divided into four groups each using the CART model (Figure  1 ).

Development of the random forest model

The random forest (RF) model is a type of ensemble learning that combines multiple decision trees to achieve high prediction performance. ²⁸ , ²⁹ In the RF model, it initiates the process by randomly sampling from the original dataset and then proceeds to construct multiple decision trees. The model then employs a technique known as bagging to aggregate the predictions of these trees through a majority vote. This process enhances the prediction performance of the model and mitigates the risk of overfitting.

Development of the extreme gradient boosting model

Extreme gradient boosting (XGBoost) is an ensemble learning method that uses multiple decision trees, similar to RF. Yet, the significant distinction lies in the sequential construction of each tree. ²¹ , ³⁰ Once one tree is built, the subsequent trees concentrate on minimizing the prediction errors of the preceding tree. In other words, each successive tree corrects the inaccuracies of the previous ones, contributing to an overall more potent prediction model.

Development of the multivariable logistic regression model

We also developed the multivariable logistic regression (MLR) model as a comparison to multiple ML models. Using a stepwise backward selection algorithm based on the Akaike information criterion, we selected explanatory variables from the significant predictors through the univariate analysis shown in Table 1 and developed the model.

Table 1.

Baseline characteristics (in‐hospital mortality and worsening heart failure)

Dataset for in‐hospital mortality	Survival discharge	In‐hospital death	P value	Number of missing values
	N = 3785	N = 255
Demographics
Age, years	77.7 ± 12.0	81.8 ± 11.0	<0.001	0
Women	1696 (44.8%)	114 (44.7%)	0.98	0
Body mass index, kg/m2	22.8 ± 4.5	21.7 ± 4.5	<0.001	583
Vital signs
Systolic blood pressure, mmHg	148.4 ± 35.0	130.5 ± 34.6	<0.001	14
Diastolic blood pressure, mmHg	85.1 ± 23.9	75.4 ± 22.4	<0.001	23
Heart rate, b.p.m.	95.9 ± 27.7	96.6 ± 25.6	0.70	30
Saturation of percutaneous oxygen, %	93.5 ± 6.3	91.9 ± 8.1	<0.001	40
Body temperature, degrees	36.5 ± 0.6	36.5 ± 0.8	0.92	188
Blood test
Brain natriuretic peptide, pg/mL	986.2 ± 1012.0	1396.1 ± 1357.2	<0.001	464
Haemoglobin, g/L	11.6 ± 2.4	11.1 ± 2.2	0.004	7
White blood cell, μL	7973.1 ± 3593.3	8694.7 ± 4441.3	0.002	8
Platelet, 104 μL	20.0 ± 8.3	17.6 ± 8.9	<0.001	23
Aspartate aminotransferase, U/L	54.1 ± 174.5	163.8 ± 528.2	<0.001	12
Total bilirubin, μmol/L	0.9 ± 2.2	1.1 ± 0.8	0.37	109
Alkaline phosphatase, g/L	294.6 ± 164.0	311.6 ± 163.5	0.14	594
Gamma‐glutamyl transpeptidase, IU/L	61.7 ± 74.1	61.9 ± 73.5	0.96	578
Albumin, g/dL	3.5 ± 0.5	3.2 ± 0.6	<0.001	117
Creatine kinase, U/L	177.1 ± 334.0	318.3 ± 844.9	<0.001	184
Sodium, mmol/L	139.1 ± 4.2	137.4 ± 5.3	<0.001	13
Potassium, mmol/L	4.2 ± 0.7	4.5 ± 0.8	<0.001	13
Blood urea nitrogen, mg/dL	28.4 ± 16.2	41.6 ± 22.7	<0.001	11
Creatinine, μmol/L	1.5 ± 1.3	1.8 ± 1.2	<0.001	7
Uric acid, mmol/L	6.9 ± 2.2	8.1 ± 3.1	<0.001	695
C‐reactive protein, mg/dL	2.0 ± 3.6	3.9 ± 5.0	<0.001	95
Blood glucose, mg/dL	154.1 ± 70.1	157.7 ± 76.1	0.48	610
Others
New York Heart Association Class IV	1769 (46.7%)	164 (65.1%)	<0.001	20
Acute coronary syndrome	210 (5.5%)	28 (11.0%)	0.001	0
Atrial fibrillation rhythm	1370 (36.2%)	84 (32.9%)	0.292	0

Dataset for WHF	No WHF	WHF	P value	Number of missing values
	N = 3140	N = 900
Demographics
Age, years	78.2 ± 12.0	76.7 ± 12.1	0.001	0
Women	1457 (46.4%)	352 (39.1%)	<0.001	0
Body mass index, kg/m2	22.8 ± 4.4	23.0 ± 4.8	0.15	583
Vital signs
Systolic blood pressure, mmHg	147.8 ± 34.3	145.3 ± 38.2	0.06	14
Diastolic blood pressure, mmHg	84.6 ± 23.6	83.9 ± 25.0	0.39	23
Heart rate, b.p.m.	95.1 ± 27.4	99.0 ± 27.7	<0.001	30
Saturation of percutaneous oxygen, %	93.7 ± 6.1	92.6 ± 7.6	<0.001	40
Body temperature, degrees	36.5 ± 0.6	36.5 ± 0.7	0.43	188
Blood test
Brain natriuretic peptide, pg/mL	934.4 ± 890.1	1276.6 ± 1413.1	<0.001	464
Haemoglobin, g/L	11.5 ± 2.3	11.6 ± 2.4	0.23	7
White blood cell, μL	7706.3 ± 3483.4	9110.8 ± 4020.8	<0.001	8
Platelet, 104 μL	19.8 ± 8.3	20.1 ± 8.6	0.31	23
Aspartate aminotransferase, U/L	47.5 ± 112.2	108.2 ± 404.2	<0.001	12
Total bilirubin, μmol/L	0.9 ± 2.4	0.9 ± 0.7	0.50	109
Alkaline phosphatase, g/L	292.9 ± 148.6	306.0 ± 211.7	0.06	594
Gamma‐glutamyl transpeptidase, IU/L	60.9 ± 72.0	64.5 ± 80.5	0.22	578
Albumin, g/dL	3.5 ± 0.5	3.4 ± 0.5	<0.001	117
Creatine kinase, U/L	153.5 ± 221.8	298.9 ± 697.8	<0.001	184
Sodium, mmol/L	139.2 ± 4.1	138.3 ± 4.8	<0.001	13
Potassium, mmol/L	4.2 ± 0.6	4.4 ± 0.8	<0.001	13
Blood urea nitrogen, mg/dL	27.7 ± 15.7	34.6 ± 20.0	<0.001	11
Creatinine, μmol/L	1.3 ± 0.9	2.1 ± 2.0	<0.001	7
Uric acid, mmol/L	6.9 ± 2.2	7.3 ± 2.5	<0.001	695
C‐reactive protein, mg/dL	1.9 ± 3.4	3.1 ± 4.5	<0.001	95
Blood glucose, mg/dL	149.8 ± 66.1	170.6 ± 82.2	<0.001	610
Others
New York Heart Association Class IV	1364 (43.7%)	569 (63.4%)	<0.001	20
Acute coronary syndrome	116 (3.7%)	122 (13.6%)	<0.001	0
Atrial fibrillation rhythm	1203 (38.3%)	251 (27.9%)	<0.001	0

WHF, worsening heart failure.

Categorical variables were presented as numbers and percentages and were compared using the χ ² test. Continuous variables were presented as mean ± standard deviation and were compared using the univariate t‐test according to their distributions.

SHapley Additive exPlanations analysis in the random forest model and the extreme gradient boosting model

To get insight into why the complicated RF models and XGBoost models make accurate predictions, additional analyses were performed using SHAP, ²⁰ which is a unified framework for interpreting ML predictions. The absolute SHAP values for the relevant variables represent the magnitude of their influence on the prediction outcome. SHAP values can be negative or positive. A higher positive SHAP value indicates a greater positive impact on the prediction outcome, while a higher negative SHAP value indicates a greater negative impact on the prediction outcome. ²⁰ In this study, SHAP values were calculated to visualize the impact of each variable on the in‐hospital mortality model and the WHF model.

Visualization of SHapley Additive exPlanations in the random forest model and the extreme gradient boosting model

In the feature plots, the length of each bar represents the mean absolute SHAP value of the 20 most important variables in the model. The feature ranking (Y‐axis) indicates which variables are important for the prediction outcome, and the SHAP value (X‐axis) is a unifying indicator of the influence of each variable on the model. Each variable is indicated by differently coloured dots for the attribution of all patients to the prediction outcome. For numerical variables, low actual values are represented by blue dots, while high actual values are represented by red dots. For categorical variables processed with one‐hot encoding, blue and red dots represent 0 and 1, respectively.

Visualization of the average SHapley Additive exPlanations values for each cluster in the extreme gradient boosting model

Using the K‐means clustering method based on the SHAP values, the patients were classified into four clusters (Figure  1 ). The K‐means clustering method divides each dataset point into a specified number of clusters by calculating the shortest distance between the cluster centre point and the data points. ³¹ We analysed average event incidence rates and average SHAP values for each cluster formed by clustering based on SHAP values.

Statistical analysis

Categorical variables were presented as numbers and percentages and were compared using the χ ² test. Continuous variables were presented as means ± standard deviations and were compared using the t‐test according to their distributions. To assess the performance of the prediction models, we employed the bootstrap method on the test dataset. Utilizing 1000 bootstrap resamples obtained from the test dataset, we determined the 95% confidence intervals (CIs) for each performance metric. Multiple metrics based on sensitivity, specificity, area under the receiver operating characteristic (ROC) curve (AUC), Brier score, and calibration slope were used to evaluate the performance of the prediction models. The optimal cut‐off value was defined using the highest Youden index, and based on the optimal cut‐off value, sensitivity and specificity were calculated. Calibration measures how well the predicted probabilities of models align with the actual probabilities of events. ³² In clinical fields where precise predictions are essential, evaluating calibration is a vital tool to assess the practicality and reliability of prediction models. The closer the Brier score is to 0 and the calibration slope is to 1, the more ideal the model's performance is.

All P values were two‐tailed, and statistical significance was set at P < 0.05 in comparing the characteristics of clinical information on the admission.

Package for analysis

Pandas (1.4.2) and Sklearn (1.0.2) on Python (3.8.13) were used to develop the decision tree model. Pandas (1.4.2), NumPy (1.21.5), Sklearn (1.0.2), XGBoost (1.5.1), Scipy (1.7.3), and SHAP (0.40.0) on Python (3.8.13) were used to develop the ML model. The χ ² test and the t‐test were conducted using JMP Version 17 (SAS Institute Inc., Cary, NC, USA).

Results

Characteristics of the explanatory variable concerning in‐hospital mortality and worsening heart failure

In the original dataset, the proportion of females was 44.8% (1809/4040), and the average age was 77.9 ± 12.0. The in‐hospital mortality rate was 6.3% (255/4040) and the WHF rate was 22.3% (900/4040) in eligible patients. Univariate analysis results for each explanatory variable concerning the outcome variables of in‐hospital mortality and WHF are presented (Table  1 ).

Performance of the prediction models

Performance of the prediction models for in‐hospital mortality

For the CART model predicting in‐hospital mortality, the AUC on the test dataset was 0.683 (95% CI: 0.680–0.685), and the sensitivity was low at 0.401 (95% CI: 0.393–0.409). However, the model demonstrated good calibration results with a Brier score of 0.057 (95% CI: 0.057–0.058) and a calibration slope of 0.795 (95% CI: 0.777–0.814). In contrast, the RF model for in‐hospital mortality had a relatively high AUC of 0.755 (95% CI: 0.753–0.757) and sensitivity of 0.655 (95% CI: 0.648–0.662) on the test dataset. Nevertheless, the calibration slope was 0.495 (95% CI: 0.491–0.500), indicating poor calibration results. The XGBoost model for in‐hospital mortality exhibited a high AUC of 0.816 (95% CI: 0.815–0.818) and sensitivity of 0.762 (95% CI: 0.757–0.767) on the test dataset. Additionally, the XGBoost model showed good calibration with a Brier score of 0.054 (95% CI: 0.053–0.054) and a calibration slope of 0.894 (95% CI: 0.866–0.923) (Table  2 ). The ROC curves in the models for in‐hospital mortality are shown in Figure 2 A . The calibration plots are shown in Supporting Information, Figure S1 , and the hyperparameters of prediction models are shown in Supporting Information, Table S1 . Furthermore, the MLR model, a non‐ML model, demonstrated a relatively high AUC, but it did not achieve the level of the XGBoost model (Supporting Information, Table S2 ).

Table 2.

Performance of the prediction model for in‐hospital mortality and worsening heart failure

	CART model	RF model	XGBoost model
In‐hospital mortality
Sensitivity	0.401 (0.393–0.409)	0.655 (0.648–0.662)	0.762 (0.757–0.767)
Specificity	0.810 (0.804–0.815)	0.737 (0.729–0.744)	0.736 (0.730–0.742)
AUC	0.683 (0.680–0.685)	0.755 (0.753–0.757)	0.816 (0.815–0.818)
Brier score	0.057 (0.057–0.058)	0.057 (0.057–0.058)	0.054 (0.053–0.054)
Calibration slope	0.795 (0.777–0.814)	0.495 (0.491–0.500)	0.894 (0.866–0.923)
WHF
Sensitivity	0.440 (0.435–0.446)	0.564 (0.558–0.569)	0.598 (0.594–0.603)
Specificity	0.823 (0.820–0.827)	0.759 (0.753–0.764)	0.815 (0.811–0.820)
AUC	0.688 (0.686–0.689)	0.713 (0.711–0.714)	0.766 (0.765–0.768)
Brier score	0.158 (0.158–0.159)	0.168 (0.168–0.169)	0.139 (0.138–0.139)
Calibration slope	1.344 (1.332–1.355)	5.217 (5.174–5.259)	1.435 (1.427–1.444)

AUC, area under the receiver operating characteristic curve; CART, classification and regression trees; RF, random forest; WHF, worsening heart failure; XGBoost, extreme gradient boosting.

In various models (CART model, RF model, and XGBoost model), the prediction results for in‐hospital mortality and WHF are shown. In order to evaluate the performance of the models, sensitivity, specificity, AUC, Brier score, and calibration slope are calculated. The sensitivity and specificity were determined using the optimal cut‐off value, which is the point on the receiver operating characteristic curve where the Youden index is maximized.

Figure 2.

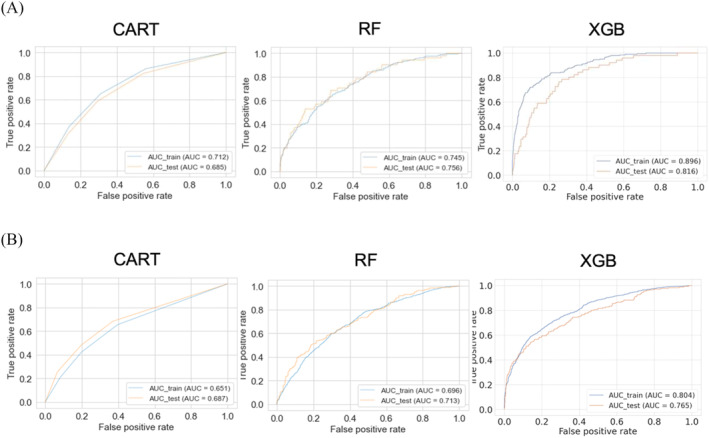
(A) The receiver operating characteristic (ROC) curves in the various models (the CART model, the RF model, and the XGBoost model) for in‐hospital mortality. (B) The ROC curves in the various models (the CART model, the RF model, and the XGBoost model) for worsening heart failure. AUC, area under the ROC curve; CART, classification and regression trees; RF, random forest; XGB, extreme gradient boosting.

Performance of the prediction models for worsening heart failure

For the CART model predicting WHF, the AUC on the test dataset was 0.688 (95% CI: 0.686–0.689), and the sensitivity was low at 0.440 (95% CI: 0.435–0.446). However, the model demonstrated good calibration results with a Brier score of 0.158 (95% CI: 0.158–0.159) and a calibration slope of 1.344 (95% CI: 1.332–1.355). In contrast, the RF model for WHF had a relatively high AUC of 0.713 (95% CI: 0.711–0.714) and sensitivity of 0.564 (95% CI: 0.558–0.569) on the test dataset. Nevertheless, the calibration slope was 5.217 (95% CI: 5.174–5.259), indicating poor calibration results. The XGBoost model for WHF exhibited a high AUC of 0.766 (95% CI: 0.765–0.768) and sensitivity of 0.598 (95% CI: 0.594–0.603) on the test dataset. Additionally, the XGBoost model showed good calibration with a Brier score of 0.139 (95% CI: 0.138–0.139) and a calibration slope of 1.435 (95% CI: 1.427–1.444) (Table  2 ). The ROC curves in the models for WHF are shown in Figure 2 B . The calibration plots are shown in Supporting Information, Figure S2 , and the hyperparameters of prediction models are shown in Supporting Information, Table S3 . Furthermore, the MLR model demonstrated a relatively high AUC, but it did not achieve the level of the XGBoost model (Supporting Information, Table S2 ).

Visualization of the prediction models

Visualization of the prediction models for in‐hospital mortality

In the CART model, patients were initially split based on BUN levels, then further divided based on C‐reactive protein (CRP) levels, and finally split based on SBP, resulting in a total of four groups. The respective raw cut‐off values were 45.0 mg/dL for BUN, 2.5 mg/dL for CRP, and 135.5 mmHg for SBP (Figure  3 ). The standardized cut‐off values for these explanatory variables and the Gini impurity for each node are presented in Supporting Information, Figure S3 . The in‐hospital mortality rates for the four groups in the training and test datasets are shown (Figure  3 ). In the training dataset, the in‐hospital mortality rates were 5.4% in Group 1, 2.1% in Group 2, 9.7% in Group 3, and 15.4% in Group 4. In the test dataset, the in‐hospital mortality rates were 5.9% in Group 1, 2.6% in Group 2, 10.3% in Group 3, and 13.7% in Group 4. In the CART model, the in‐hospital mortality rates between the four groups were similar between the training and test datasets.

Figure 3.

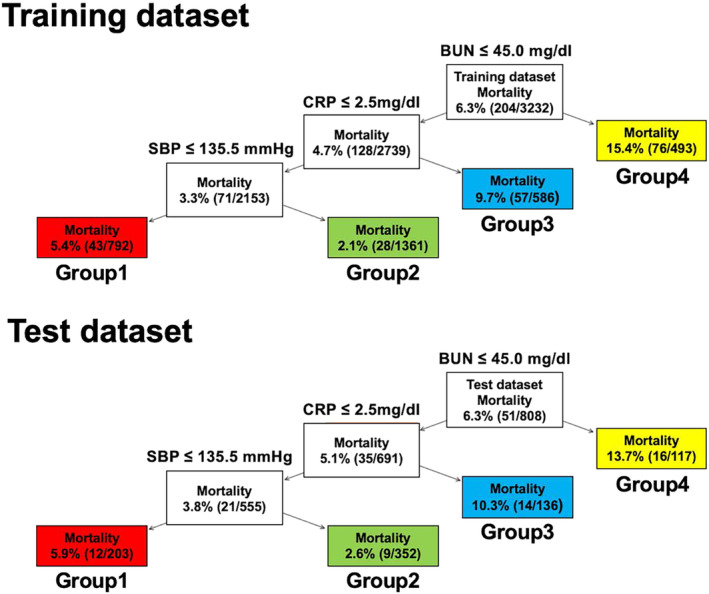
The classification and regression trees model of worsening heart failure prediction in the training and test datasets. Patients were initially split based on BUN levels, then further divided based on CRP levels, and finally split based on SBP, resulting in a total of four groups. BUN, blood urea nitrogen; CRP, C‐reactive protein; SBP, systolic blood pressure.

In the RF model, the feature plots showed the important variables in the in‐hospital mortality prediction model (Supporting Information, Figure S4A,B ). BUN level, SBP, and sodium level were the most important variables for predicting in‐hospital mortality.

In the XGBoost model, the feature plots showed the important variables in the in‐hospital mortality prediction model (Figure 4 A,B ). Sodium level, BUN level, and age were the most important variables for predicting in‐hospital mortality. Next, the average SHAP values for each variable and the average in‐hospital mortality rate in the XGBoost model were analysed. All patients were divided into four clusters as follows: Cluster 1 with low SHAP values for all variables; Cluster 2 with high SHAP values for age; Cluster 3 with high SHAP values for low sodium levels; and Cluster 4 with high SHAP values for high BUN levels (Figure 4 C ). In the training dataset, the in‐hospital mortality rates were 1.3% in Cluster 1, 6.9% in Cluster 2, 9.0% in Cluster 3, and 14.3% in Cluster 4. In the test dataset, the in‐hospital mortality rates were 1.7% in Cluster 1, 5.5% in Cluster 2, 8.5% in Cluster 3, and 16.8% in Cluster 4 (Figure 4 C ). As in the CART model results, the in‐hospital mortality rate was higher in the group with higher BUN levels. Also, in the XGBoost model, the in‐hospital mortality rates between the four groups were similar between the training and test datasets.

Figure 4.

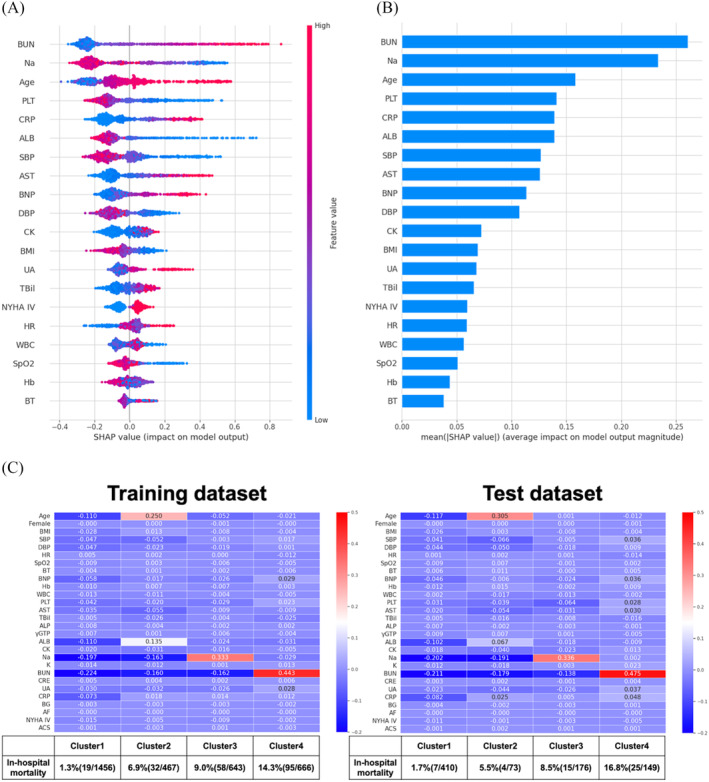
(A, B) The interpretation of the extreme gradient boosting (XGBoost) model for in‐hospital mortality prediction. (A) The importance ranking of the top 20 variables according to the collective absolute SHapley Additive exPlanations (SHAP) values. (B) SHAP value plots of the top 20 variables with a strong impact on the XGBoost model. The positive and negative contributions to in‐hospital mortality prediction are demonstrated as their respective positive and negative SHAP values, and the magnitude of the absolute SHAP values indicates the degree of influence on the prediction outcome. (C) The results of clustering the training and test datasets based on SHAP values in the XGBoost model for predicting in‐hospital mortality. The average in‐hospital mortality rates and the average SHAP values for each cluster. ACS, acute coronary syndrome at admission; AF, atrial fibrillation at admission; ALB, albumin; ALP, alkaline phosphatase; AST, aspartate aminotransferase; BG, blood glucose; BMI, body mass index; BNP, brain natriuretic peptide; BT, body temperature at hospitalization; BUN, blood urea nitrogen; CK, creatine kinase; CRE, creatinine; CRP, C‐reactive protein; DBP, diastolic blood pressure at hospitalization; Hb, haemoglobin; HR, heart rate at hospitalization; NYHA, New York Heart Association; PLT, platelet; SBP, systolic blood pressure at hospitalization; SpO₂, saturation of percutaneous oxygen; TBil, total bilirubin; UA, uric acid; WBC, white blood cell; γGTP, gamma‐glutamyl transpeptidase.

Visualization of the prediction models for worsening heart failure

In the CART model, patients were initially split based on creatinine levels, then further divided based on white blood cell (WBC) count, and finally split based on CRP levels, resulting in a total of four groups. The respective raw cut‐off values were 2.4 mg/dL for creatinine, 11 000 mg/μL for WBC count, and 1.5 mg/dL for CRP (Figure  5 ). The standardized cut‐off values for these explanatory variables and the Gini impurity for each node are presented in Supporting Information, Figure S5 . The in‐hospital mortality rates for the four groups in the training and test datasets are shown (Figure  5 ). In the training dataset, the WHF rates were 14.1% in Group 1, 25.2% in Group 2, 34.4% in Group 3, and 42.0% in Group 4. In the test dataset, the WHF rates were 12.6% in Group 1, 25.0% in Group 2, 33.1% in Group 3, and 52.3% in Group 4. In the CART model, the WHF rates between the four groups in the XGBoost model were similar between the training and test datasets.

Figure 5.

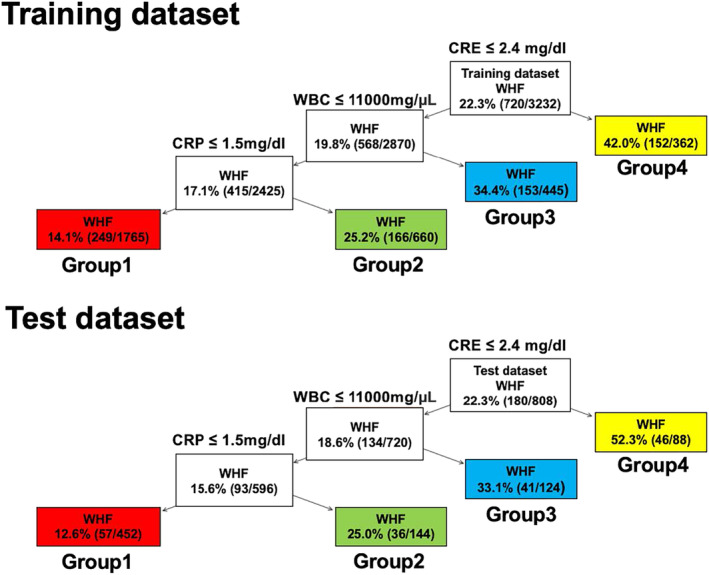
The classification and regression trees model of WHF prediction in the training and test datasets. Patients were initially split based on creatinine levels, then further divided based on WBC count, and finally split based on CRP levels, resulting in a total of four groups. CRE, creatinine; CRP, C‐reactive protein; WBC, white blood cell; WHF, worsening heart failure.

In the RF model, the feature plots showed the important variables in the WHF prediction model (Supporting Information, Figure S6A,B ). WBC count, CRP level, and NYHA Class IV were the most important variables for predicting WHF.

In the XGBoost model, the feature plots showed the important variables in the WHF prediction model (Figure 6 A,B ). Creatinine level, CRP level, and NYHA Class IV were the most important variables for predicting WHF. Next, the average SHAP values for each variable and the average WHF rate in the XGBoost model were analysed. All patients were divided into four clusters as follows: Cluster 1 with low SHAP values for all variables; Cluster 2 with high SHAP values for NYHA Class IV; Cluster 3 with high SHAP values for high CRP levels; and Cluster 4 with high SHAP values for high creatinine levels (Figure 6 C ). In the training dataset, the WHF rates were 11.6% in Cluster 1, 22.2% in Cluster 2, 30.6% in Cluster 3, and 56.6% in Cluster 4. In the test dataset, the WHF rates were 11.9% in Cluster 1, 20.4% in Cluster 2, 30.3% in Cluster 3, and 68.8% in Cluster 4 (Figure 6 C ). As in the CART model results, the WHF rate was higher in the group with higher creatinine levels. Also, in the XGBoost model, the WHF rates between the four groups were similar between the training and test datasets.

Figure 6.

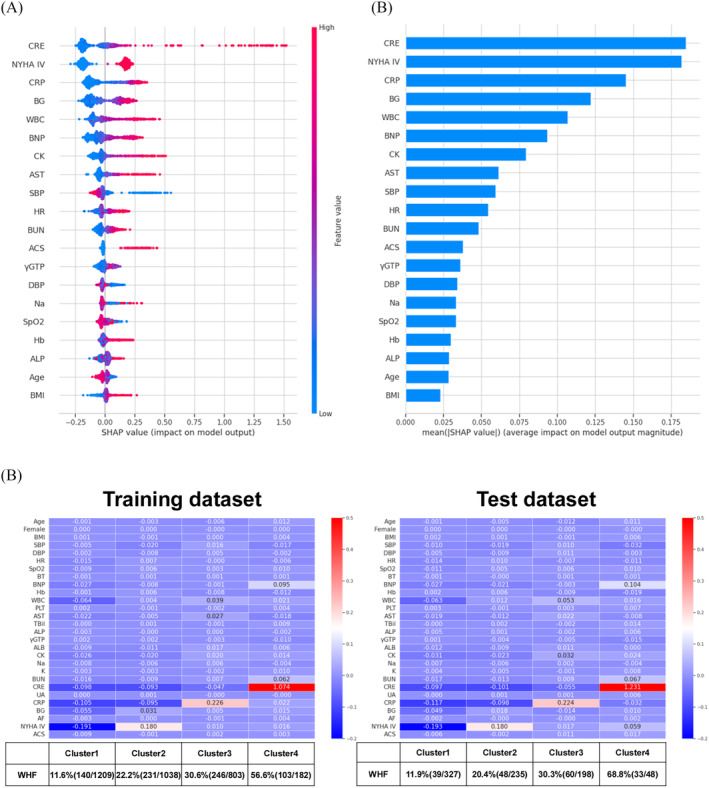
(A, B) The interpretation of the extreme gradient boosting (XGBoost) model for worsening heart failure (WHF) prediction. (A) The importance ranking of the top 20 variables according to the collective absolute SHapley Additive exPlanations (SHAP) values. (B) SHAP value plots of the top 20 variables with a strong impact on the XGBoost model. (C) The results of clustering the training and test datasets based on SHAP values in the XGBoost model for predicting WHF. The average WHF rates and the average SHAP values for each cluster. ACS, acute coronary syndrome at admission; AF, atrial fibrillation at admission; ALB, albumin; ALP, alkaline phosphatase; AST, aspartate aminotransferase; BG, blood glucose; BMI, body mass index; BNP, brain natriuretic peptide; BT, body temperature at hospitalization; BUN, blood urea nitrogen; CK, creatine kinase; CRE, creatinine; CRP, C‐reactive protein; DBP, diastolic blood pressure at hospitalization; Hb, haemoglobin; HR, heart rate at hospitalization; NYHA, New York Heart Association; PLT, platelet; SBP, systolic blood pressure at hospitalization; SpO₂, saturation of percutaneous oxygen; TBil, total bilirubin; UA, uric acid; WBC, white blood cell; γGTP, gamma‐glutamyl transpeptidase.

Discussions

We developed various ML models to predict in‐hospital mortality and WHF in patients with AHF. The goal was to anticipate acute changes in patients with AHF, enable early intervention, and improve the short‐term prognosis. The CART model has a simple algorithm that is intuitive, easy to understand, and suitable for clinical applications. However, even after implementing automatic adjustment of hyperparameters, it could not demonstrate superior performance in terms of AUC and sensitivity. While the CART model is particularly notable for its interpretability, previous reports have also indicated its limited performance, with an AUC of approximately 0.7. ³ Therefore, applying the CART model to identify high‐risk patients with AHF might not be suitable due to its performance limitations. The RF model exhibited superior AUC and sensitivity compared with the CART model, but calibration was inadequate. This discrepancy arises from the RF model being either over‐calibrated (overpredicting probabilities) or under‐calibrated (underpredicting probabilities). Even if AUC and sensitivity are high, the RF model's inability to accurately predict patient risk introduces uncertainty in the selection of treatment strategies, leading to a decrease in its reliability. ³¹ The XGBoost model demonstrated high AUC and sensitivity, along with good calibration. This indicates a low likelihood of missing patients experiencing acute changes, such as in‐hospital mortality or WHF, among patients with AHF. Moreover, the predicted risks align well with the actual occurrence rates, highlighting the XGBoost model as an accurate and reliable prediction model.

Some prediction models that show comparable performance to our XGBoost model have been reported. ³³ , ³⁴ , ³⁵ However, it is significant that such high performance was achieved on the KCHF registry, a relatively small Japanese registry dataset of 4040 individuals (3232 in the training dataset and 808 in the test dataset). In general, the performance of prediction models tends to improve as the number of target data increases. On the other hand, in improving the prognosis of patients with AHF, it is important to develop prediction models with high prediction performance even when the target dataset is relatively small, as shown in this study. This is because patients with AHF constitute a diverse population with variations across regions and countries. ¹³ , ¹⁴ Applying universally renowned prediction models to all patients with AHF in distinct regions may not be optimal. Therefore, even with a limited dataset, developing high‐performance prediction models based on patients with AHF in each region is crucial, contributing significantly to improving the prognosis of patients with AHF in each region.

However, as the prediction performance of ML models, such as the XGBoost model, improves, the structure of the model becomes more complex, and the issue of the model's black‐box nature arises. In this study, SHAP analysis was used to visualize the XGBoost model, providing a clear interpretation for clinicians. Additionally, SHAP clustering, based on SHAP values, classified patients into four clusters. The event rates for each cluster were similar in both the training and test datasets, demonstrating good reproducibility in risk stratification. Thus, through the implementation of SHAP analysis and SHAP clustering, it is possible to preserve interpretability that might be compromised with the enhanced performance. SHAP analysis and SHAP clustering have been reported to enable the development of prediction models with interpretable clusters in various clinical scenarios, including emergency departments and cases involving COVID‐19 infection. ²² , ²³ , ²⁴ Using SHAP analysis and SHAP clustering, high‐performance and complex ML models like the XGBoost model can be applied in clinical settings. This study demonstrated the ability to accurately identify high‐risk AHF patients with an interpretable approach.

Many patients hospitalized with AHF are admitted urgently, often without scheduled admissions, which frequently limits the possibility of undergoing comprehensive testing at the time of admission. We decided to avoid using explanatory variables with extensive missing data, as it may compromise the accuracy and generalizability of the prediction model. Therefore, we utilized explanatory variables with minimal missing data that are easily available. Despite the limited set of explanatory variables, especially in the case of the XGBoost model, sufficient prediction performance was achieved. Regarding the prediction of in‐hospital mortality, the CART model identified BUN, CRP, and SBP as important, while the XGBoost model highlighted the significance of BUN, sodium, and age. In both models, BUN was the most crucial explanatory variable. For predicting WHF, the CART model identified creatinine, WBC count, and CRP as important, while the XGBoost model highlighted the significance of creatinine, CRP, and NYHA classification. In both models, creatinine was the most important explanatory variable. These explanatory variables are consistent with previous reports, demonstrating the validity of our study. Particularly, BUN and creatinine have been reported as the most crucial explanatory variables in predicting in‐hospital mortality and WHF in the ADHERE registry, ³ , ⁹ consistent with our study. Inflammation‐related markers such as CRP have been shown to be clinically important in the prognosis of patients with AHF, as reported previously. ³⁶ Our study further demonstrated the importance of these inflammatory markers as crucial explanatory variables in developing short‐term prognosis prediction models for patients with AHF.

Limitations

This study had several limitations. First, the KCHF registry has a low occurrence rate of in‐hospital mortality and WHF in patients with AHF, resulting in an imbalanced dataset with low event rates. Imbalanced data can lead to biased learning, where there is a strong tendency for prediction models to favour the majority class. As a consequence, the minority class can be overlooked, resulting in diminished prediction performance for the minority class. Second, the selected explanatory variables for the ML model development in this study were limited to those with few missing data and easy data collection based on clinical use. As a result, the prediction performance of the ML models may be slightly inferior compared with prediction models that utilize a larger number of explanatory variables. Finally, the data from the KCHF registry represent only facilities in Japan and may not be representative of patients with AHF in other regions worldwide. In the future, it will be necessary to validate the ML models using independent external data that include patients from different regions and hospitals.

Conclusions

The XGBoost models with SHAP clustering provide high prediction performance, interpretability, and reproducible risk stratification for in‐hospital mortality and WHF for patients with AHF, making them potentially applicable in clinical settings.

Conflict of interest

None declared.

Funding

This study was supported by grant 18059186 from the Japan Agency for Medical Research and Development (Drs T. Kato, K. Kuwahara, and N. Ozasa).

Supporting information

Figure S1. Calibration plots in the models for in‐hospital mortality.

Figure S2. Calibration plots in the models for WHF.

Figure S3. In the CART model, we aimed to maximize the reduction in the Gini coefficient, selecting the most effective splits at each node. The Gini coefficient and in‐hospital mortality rate are indicated for each node. The standardized cutoff values for explanatory variables are also shown. Gini, Gini impurity.

Figure S4. The interpretation of the Random Forest model for in‐hospital mortality prediction. The importance ranking of the top 20 variables according to SHAP values.

Figure S5. In the CART model, we aimed to maximize the reduction in the Gini coefficient, selecting the most effective splits at each node. The Gini coefficient and WHF rate are indicated for each node. The standardized cutoff values for explanatory variables are also shown. Gini, Gini impurity.

Figure S6. The interpretation of the Random Forest model for WHF prediction. The importance ranking of the top 20 variables according to SHAP values.

Table S1. The hyperparameters of the prediction models for in‐hospital mortality were optimized using Bayesian Optimization with stratified 10‐fold cross‐validation.

Table S2. In the multivariable logistic regression (MLR model), the prediction results for in‐hospital mortality and WHF are shown. In order to evaluate the performance of the models, sensitivity, specificity, AUC, Brier Score, calibration slope are calculated. The sensitivity and specificity were determined using the optimal cutoff value, which is the point on the ROC curve where the Youden index is maximized.

Table S3. The hyperparameters of the prediction models for WHF were optimized using Bayesian Optimization with stratified 10‐fold cross‐validation.

Tanaka, M. , Kohjitani, H. , Yamamoto, E. , Morimoto, T. , Kato, T. , Yaku, H. , Inuzuka, Y. , Tamaki, Y. , Ozasa, N. , Seko, Y. , Shiba, M. , Yoshikawa, Y. , Yamashita, Y. , Kitai, T. , Taniguchi, R. , Iguchi, M. , Nagao, K. , Kawai, T. , Komasa, A. , Kawase, Y. , Morinaga, T. , Toyofuku, M. , Furukawa, Y. , Ando, K. , Kadota, K. , Sato, Y. , Kuwahara, K. , Okuno, Y. , Kimura, T. , Ono, K. , and the KCHF Study Investigators (2024) Development of interpretable machine learning models to predict in‐hospital prognosis of acute heart failure patients. ESC Heart Failure, 11: 2798–2812. 10.1002/ehf2.14834.