Discovering regulatory binding-site modules using rule-based learning

Abstract

Transcription factors regulate expression by binding selectively to sequence sites in cis-regulatory regions of genes. It is therefore reasonable to assume that genes regulated by the same transcription factors should all contain the corresponding binding sites in their regulatory regions and exhibit similar expression profiles as measured by, for example, microarray technology. We have used this assumption to analyze genome-wide yeast binding-site and microarray expression data to reveal the combinatorial nature of gene regulation. We obtained IF-THEN rules linking binding-site combinations (binding-site modules) to genes with particular expression profiles, and thereby provided testable hypotheses on the combinatorial coregulation of gene expression. We showed that genes associated with such rules have a significantly higher probability of being bound by the same transcription factors, as indicated by a genome-wide location analysis, than genes associated with only common binding sites or similar expression. Furthermore, we also found that such genes were significantly more often biologically related in terms of Gene Ontology annotations than genes only associated with common binding sites or similar expression. We analyzed expression data collected under different sets of stress conditions and found many binding-site modules that are conserved over several of these condition sets, as well as modules that are specific to particular biological responses. Our results on the reoccurrence of binding sites in different modules provide specific data on how binding sites may be combined to allow a large number of expression outcomes using relatively few transcription factors.

One of the major challenges faced by molecular biology is to dissect the regulatory circuitry of living cells. Knowing the precise role of regulatory proteins such as transcription factors is key to understanding transcriptional regulation of genes (Holstege et al. 1998). The ability of these proteins to selectively bind specific DNA motifs (i.e., transcription factor binding sites) in the regulatory regions of genes is essential for the complex regulation observed in living organisms. As the amount of available sequence data is increasing, it has become possible to analyze the regulatory regions of DNA in search for putative regulatory motifs (e.g., Brazma et al. 1998; Vilo et al. 2000). Currently the most common approach involves searching for statistically overrepresented sequence motifs (e.g., Roth et al. 1998; Liu et al. 2001; Thompson et al. 2003). Many approaches have assumed that the influence of different transcription factors on gene expression is additive, leading to simple analytical models of gene regulation (Bussemaker et al. 2001; Liu et al. 2001). However, other studies have indicated that the synergistic effect of several transcription factors affecting regulation of a gene is nonadditive (e.g., GuhaThakurta and Stormo 2001). Therefore, algorithms have been developed based only on the assumption that genes regulated by the same transcription factors (i.e., coregulated) also exhibit similar expression profiles obtained, for example, by the microarray technology (i.e., coexpressed). This includes algorithms that cluster genes into classes of coexpressed genes and then mine their sequences for common motifs (DeRisi et al. 1997; Roth et al. 1998; Vilo et al. 2000; Berman et al. 2002; Gasch and Eisen 2002).

Pilpel et al. (2001) found that genes sharing pairs of binding sites are significantly more likely to be coexpressed than genes with only single binding sites in common. This result is in agreement with the hypothesis that a limited number of transcription factors combine in various ways in order to respond to a much larger number of environmental conditions or stress factors. Segal et al. (2003a,b) and recently Beer and Tavazoie (2004) further developed this idea to find combinations of regulatory mechanisms that best explain expression data. We present an alternative approach using “rule learning” to perform a comprehensive analysis of the combinatorial nature of gene regulation by constructing rules that identify sets of binding sites (i.e., binding-site modules) associated with particular gene expression profiles. It is important to note that the only assumption required for this approach is that genes that are regulated by the same transcription factors should contain common binding sites and exhibit similar expression. However, this is a very powerful assumption that allows investigation of coregulation through genome-wide sequence and expression data analysis.

The rough set theory (Pawlak 1991) and Boolean reasoning (Brown 1990) constitute a mathematical framework for inducing rules from examples. We used this framework, as implemented in the Rosetta system (Komorowski et al. 2002), for the analysis of sequence motif and expression data with the objective of elucidating the combinatorial nature of coregulation in yeast. The method extracts IF-THEN rules of minimal binding-site combinations (IF-part) shared by genes with a common expression profile (THEN-part) (see Table 1 for an example). The rules hence describe general, underlying relationships in an easily understandable format, providing hypotheses on combinatorial coregulation that may later be experimentally validated.

Table 1.

Example of an induced rule: a rule combining binding sites RAP1, SWI5, and MCM1′

RULE: IF RAP1 and SWI5 and MCM1′ THEN similar expression in cell cycle, sporulation, diauxic shift, heat and cold shock, and DNA-damaging agents (see Fig. 2)
Gene symbol	Biological process	Molecular function	Cellular component	Possible transcription factors (P < 0.01)
RPL16B	Protein biosynthesis	RNA binding, structural constituent of ribosome	Cytosolic ribosome (sensu Eukarya), large ribosomal subunit	FHL1, GAT3, PDR1, RAP1, RGM1, YAP5
RPL26A	Protein biosynthesis	RNA binding, structural constituent of ribosome	Cytosolic ribosome (sensu Eukarya), large ribosomal subunit	FHL1, RAP1
RPS18A	Protein biosynthesis	Structural constituent of ribosome	Cytosolic ribosome (sensu Eukarya), eukaryotic 43S pre-initiation complex, eukaryotic 48S initiation complex, mall ribosomal subunit	FHL1, GAT3, HIR2, RAP1, RGM1, YAP5
RPL30	Protein biosynthesis, rRNA processing, mRNA splicing, regulation of translation	Structural constituent of ribosome	Cytosolic ribosome (sensu Eukarya), cytoplasm, large ribosomal subunit	FHL1, GAT3, RAP1, SFP1
RPL18A	Protein biosynthesis	Structural constituent of ribosome	Cytosolic ribosome (sensu Eukarya), large ribosomal subunit	FHL1, MAL13, RAP1, YAP5
RPL14A	Protein biosynthesis	RNA binding, structural constituent of ribosome	Cytosolic ribosome (sensu Eukarya), large ribosomal subunit	FHL1, GAT3, GRF10(Pho2), GTS1, RAP1
SST2	Signal transduction, adaptation to pheromone during conjugation with cellular fusion	GTPase activator activity	Plasma membrane	DIG1, FHL1, RAP1, STE12
RPS24A	Protein biosynthesis	Structural constituent of ribosome	Cytosolic ribosome (sensu Eukarya), eukaryotic 43S pre-initiation complex, eukaryotic 48S initiation complex, small ribosomal subunit	FHL1, GAT3, PDR1, RAP1, RGM1, SMP1, YAP5

The rule was found in five of the six gene expression data sets. All genes containing the three binding sites in their promoter regions are listed in the table together with their annotations as to the Gene Ontology biological process, molecular function, and cellular component, and the transcription factors they bind according to Lee et al. (2002) (P-value < 0.01). The gene expression profiles for all genes in this table are shown in Figure 2. All the induced rules and their evaluation with Gene Ontology and binding data can be found at our Web site.

To test the methodology, we used the binding-site database previously analyzed by Pilpel et al. (2001) containing information on 43 known binding sites (see Fig. 4 below) and 313 putative motifs and their occurrences in the promoters of all genes in the yeast genome. These known and putative binding sites have been identified by Hughes et al. (2000) as overrepresented motifs in DNA sequences using a Gibbs sampling algorithm, and these data were used in this paper without further processing. We also used expression profiles of yeast genes under six different sets of conditions: cell cycle (Cho et al. 1998), sporulation (Chu et al. 1998), diauxic shift (DeRisi et al. 1997), heat and cold shock (Eisen et al. 1998), pheromone (Roberts et al. 2000), and DNA-damaging agents (Jelinsky et al. 2000). Our results demonstrate that we are indeed able to find binding-site combinations associated with several coexpressed genes. Furthermore, these binding-site modules are to a large degree in agreement with experimental binding data published by Lee et al. (2002). We also find evidence for functional binding-site modules by evaluating our results using annotations from Gene Ontology (Ashburner et al. 2000). The extensive reoccurrence of binding sites in the discovered modules indicates the combinatorial nature of gene regulation as a response to the studied stress conditions.

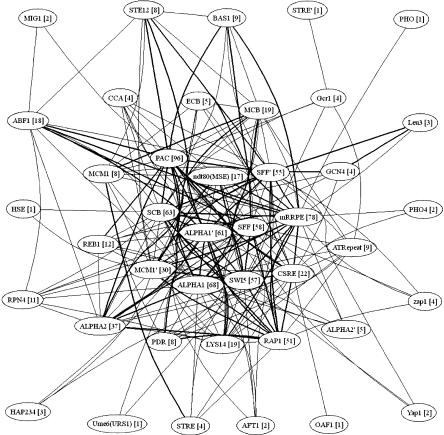
Figure 4.

Graph showing which binding-site pairs participate in the same binding-site modules as hypothesized by our rules. Nodes are the binding sites, and there is an edge between any two binding sites if they appear in the same rule (the number of rules including a particular binding site is given in brackets). Bold edges indicate that the two binding sites appear in a rule that was induced from more than one expression data set. The graph includes 41 of the 43 known binding sites. GAL and MET31-32 were not found in any rule. Corresponding graphs constructed using only significant rules according to each part of Gene Ontology and the binding data by Lee et al. (2002) may be found at http://www.lcb.uu.se/~vidsten/binding_sites/.

Results

Discovering potential regulatory modules

We used a framework for rule induction to investigate the relationship between binding sites and expression profiles in yeast. For each gene we found minimal sets of binding sites that were highly discriminatory of that particular gene and any other gene with a similar expression profile (see Fig. 1 and Methods). Identical rules found from several different genes were removed prior to evaluation. In the present study we placed no restriction on the order of or distance between individual binding sites in such binding-site modules. As an example, we will use the following rule induced from the cell cycle data set (see Table 1 for specifics on this rule and our Web site for all rules):

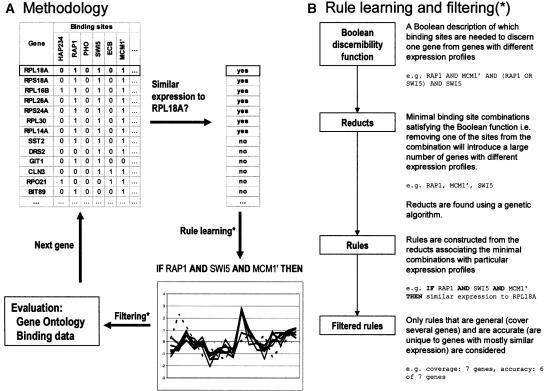
Figure 1.

A schematic description of the method and the rule learning algorithm. (A) Rules are induced from one gene at a time by first identifying similarly expressed genes and then by learning minimal binding-site combinations unique to these coexpressed genes. Filtered rules are finally evaluated using Gene Ontology and binding data by Lee et al. (2002). (B) The rule learning algorithm starts by building a Boolean function describing which binding sites are needed to discern one gene from genes with different expression profiles. This discernibility function is then simplified using a genetic algorithm in order to find minimal binding-site combinations (reducts) satisfying the function. Rules are constructed from the minimal combinations and filtered using accuracy and coverage. The examples given in B are constructed from the small table in A. The obtained reduct (RAP1, MCM1′, SWI5) is the minimal combination needed to discern RPL18A from genes with a different expression. Note that the set of similarly expressed genes in A is indiscernible from the differentially expressed gene SST2 with respect to the binding-site data. The set is thus said to be rough, and the resulting rule has an accuracy that is <1.

IF RAP1 AND SWI5 AND MCM1′ THEN expression similar to RPL18A

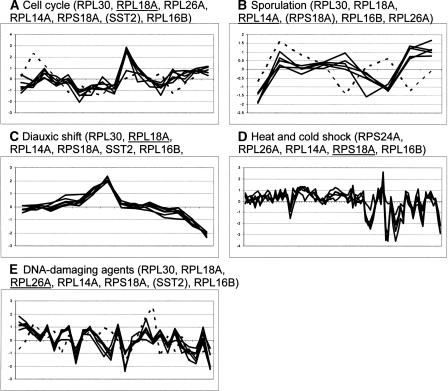
Figure 2A shows the expression profiles of RPL18A and all the other six genes containing the three binding sites RAP1, SWI5, and MCM1′ in the cell cycle expression data. (Table 1 lists eight genes containing these three binding sites, but the expression profile for one of them was not available from the cell cycle data set.) We evaluated rules using the concept of coverage and accuracy. Coverage indicates the generality of the rules (i.e., the number of genes with similar expression to RPL18A and containing binding sites RAP1, SWI5, and MCM1′), while accuracy indicates the exactness of the rule (i.e., the fraction of genes that contain the specified binding sites RAP1, SWI5, and MCM1′ that, in fact, have similar expression). Since one of the seven genes in Figure 2A has an expression profile that differs from that of RPL18A, coverage is 6 and accuracy is 6/7. Obviously, rule induction may produce a large number of very specific rules (i.e., rules with low coverage), indicating that no general relationship could be found between binding-site occurrences and expression data for these genes. Other rules will cover many genes with a large diversity in their expression profiles (i.e., rules with low accuracy), violating the assumption that genes regulated by the same transcription factors through common binding sites should be coexpressed. Only when we find binding-site combinations common to several genes with similar expression may we expect a high probability for actual coregulation.

Figure 2.

Expression profiles for the genes containing the three binding sites RAP1, SWI5, and MCM1′. The rule linking these binding sites to the expression profiles shown was induced from five expression data sets (i.e., all except pheromone). Each set of graphs is labeled with the expression condition set and with the list of genes for which expression profiles were available. Table 1 lists all eight genes with Gene Ontology annotations and transcription factor bindings. Each graph shows how the expression level of one gene varies over different measurement points. In A, B, and C, these measurement points correspond to time points, while in D and E, they also correspond to other relevant conditions: see individual publications for details. The central genes (i.e., genes for which a rule was induced) are underlined. Genes that did not satisfy the similarity criterion are written in parentheses, and their expression profiles are plotted with a dashed line.

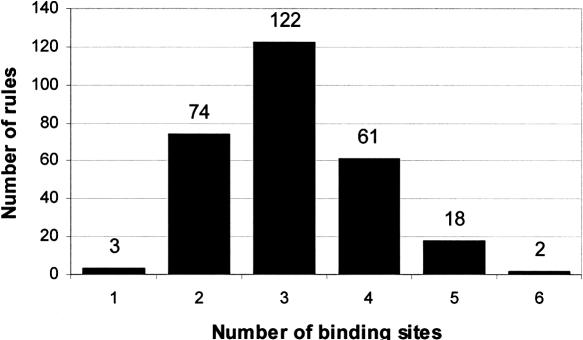
In order to get a good estimate of our ability to discover biologically interesting binding-site modules, we induced rules using only the 43 known transcription factor binding sites in yeast (Pilpel et al. 2001). The number of rules induced from each expression data set is given in column 3 in Table 2. Figure 3 shows the distribution of the number of binding sites in rules induced from all expression data sets. The fact that our rule-learning algorithm finds minimal binding-site combinations is attractive in general (i.e., the principle of Occam's razor stating that the simplest model explaining the data should always be chosen) and may be particularly relevant in biology, where, for example, energy-expensive solutions would not be favored by evolution. Our data indicate that typically between two and four binding sites are sufficient to ensure coexpression in yeast, and that combinations of more than five are very rare. These findings are in good agreement with Segal et al. (2003b) and Beer and Tavazoie (2004).

Table 2.

Evaluation of the induced rules using the binding data from Lee et al. (2002)

			Binding data evaluation (significant fractions P < 0.01)
				Random tests
Expression data	Expression similarity thresholds	No. rules unique/all	Rules (P-value)	Similar expression	Common motifs	Random
Cell cycle	0.250	39/109	0.54 (0.000)	0.11	0.17	0.02
Sporulation	0.250	45/81	0.13 (0.708)	0.09	0.18	0.02
Diauxic shift	0.200	150/428	0.29 (0.000)	0.06	0.18	0.02
Heat and cold shock	0.125	52/123	0.52 (0.000)	0.18	0.18	0.02
Pheromone	0.150	53/91	0.39 (0.001)	0.14	0.17	0.02
DNA-damaging agents	0.200	59/116	0.35 (0.000)	0.10	0.17	0.02

A rule is said to be significant if at least one transcription factor binding any of the matching genes obtained a Bonferroni-corrected P-value of <0.01 (only experimental bindings at P < 0.01 from Lee et al. 2002 were considered). The table gives the fraction of significant rules for each data set, and compares these values to what is observed when randomly selecting corresponding sets of genes with only similar expression, common binding sites, or neither. All three random tests produce a P-value that is the probability of observing a higher value than the one reported for the rules. We show the highest of these P-values in parentheses and mark the corresponding random test in bold if this P-value is >0. The table also gives the Euclidean distance threshold (normalized by the number of measurement points) used to define similar expression profiles and the number of rules induced for each expression data set (number of rules unique to that data set/all rules derived for that data set). Additional statistics on the standard deviation of the random test scores and comparisons to a new binding data set (Harbison et al. 2004) may be found at our Web site.

Figure 3.

The figure shows how the rules induced from all expression data sets distribute over the number of binding sites included in the rules. The results indicate that most often three binding sites are required to obtain coexpression.

Evaluation using experimental binding interactions and Gene Ontology

With the current knowledge of combinatorial coregulation there is little information allowing us to validate potential regulatory modules directly. However, Lee et al. (2002) experimentally identified binding between 106 known transcription factors and promoters in yeast. We evaluated whether genes containing binding sites specified by a rule (i.e., genes matching a rule) also seem to be bound by the same transcription factors according to this study. Also, genes that are coregulated may to some degree be related by the biological roles they play. Therefore, we used Gene Ontology (Ashburner et al. 2000) to evaluate whether the potential coregulated genes discovered by our method actually have a significant relationship in terms of known annotations to biological processes, cellular components, and molecular function. Haverty et al. (2004) recently used a similar evaluation scheme on yeast regulatory networks constructed using transcription factors found in the TRANSFAC library (Wingender et al. 2000).

We evaluated genes matching the same rule by only using binding interactions at P < 0.01 as reported by Lee et al. (2002). For each rule and each transcription factor, we used the hypergeometric distribution to calculate the probability of the transcription factor binding the observed or greater number of genes by chance (i.e., the P-value) (see Methods). As an example, all genes matching the rule in Table 1 seem to be bound by both transcription factors FHL1 and RAP1, while five of eight genes are bound by GAT3. The corresponding Bonferroni-corrected (see Methods) P-values in the cell cycle data set are 2.38^-10 for FHL1, 3.38^-8 for RAP1, and 2.96^-5 for GAT3 (it should be pointed out that only RAP1 has a clearly identified corresponding binding-site motif; see Case Studies for further discussion). Of course, it may be argued that one would expect genes with similar expression or genes associated with any arbitrarily chosen known binding site(s) to be bound by at least some of the same transcription factors. Hence, we selected a relatively strict significance level of P < 0.01 for defining a rule to be significant. Furthermore, we tested whether the fraction of significant rules extracted from each data set was significantly higher than what we observe when investigating corresponding sets of randomly selected genes with only similar expression profiles, common binding sites, or neither similar expression nor common binding sites (see Methods). Hence, we obtained P-values both for the individual rules (available at http://www.lcb.uu.se/~hvidsten/binding_sites/) and for the whole set of rules extracted from each data set (Table 2).

Table 2 indicates that the fraction of significant rules, as defined using the binding data by Lee et al. (2002), are significantly higher than what is observed in any randomization test (P < 0.001) for all expression data sets except sporulation. It is interesting to note that the randomization test selecting genes with common binding sites produced significant results considerably more often than the test with similarly expressed genes. Also, both these tests produced significant results much more often than genes selected randomly without any further requirements. However, the obtained significance levels for genes with common binding sites have to be considered as relatively low when taking into account that we investigated only known sites. This indicates that the occurrence of sequence motifs in promoter regions, even those corresponding to known binding sites, is not sufficient to conclude that these sites are in fact involved in regulation, at least not under the specific expression conditions investigated here. However, when the requirement of coexpression is added (rules we derive require both common binding sites and similar expression), the experimental evidence for coregulation is significantly higher. The most notable example is that of the rules induced from the cell cycle expression data. Of these rules, 54% are significant, which is considerably higher than for most other expression conditions and more than three times higher than that of randomly selected binding-site combinations. In this context it is interesting to notice that Lee et al. (2002) did not include any stress conditions in their chromatin immunoprecipitation (ChIP)-based binding experiments. Hence, some of the regulatory mechanisms related to, for example, sporulation may not have been registered in this study, explaining at least some of the differences in scores between the different expression data sets.

By providing an organized controlled vocabulary for describing gene and protein roles in terms of their molecular function, biological process, and cellular component (Ashburner et al. 2000), Gene Ontology lends itself as means for evaluating the rules we derive. For each rule and each Gene Ontology term, we used the hypergeometric distribution to calculate the probability of the term being used to annotate the observed or greater number of genes by chance (i.e., P-value) (see Methods). Using the rule in Table 1 as an example, only SST2 does not share common annotations with all the other genes matching this rule. For the cell cycle data set, the Bonferroni-corrected (see Methods) P-values associated with observing this are 2.35^-4 for the biological process protein biosynthesis, 2.36^-6 for the molecular function structural constituent of ribosome, and 5.66^-7 for the cellular component cytosolic ribosome (sensu Eukarya). Again, we might suspect that any genes containing common known binding sites or having similar expression profiles might also share biological roles. Consequently, we designate a rule as significant if at least one Gene Ontology term obtains P < 0.01 and compare the fraction of significant rules from each data set with what was observed for randomly selecting genes with similar expression profiles, common binding sites, or neither similar expression nor common binding sites (see Methods).

Table 3 indicates a significant relationship (the corresponding P-values are smaller than 0.006) with the Gene Ontology annotations for all expression data sets and in all three parts of Gene Ontology (i.e., molecular function, biological process, and cellular component). Expression studies show that coexpressed genes correlate more strongly with broad biological goals (i.e., biological process in Gene Ontology) than with tasks performed by individual gene products (i.e., molecular function in Gene Ontology) (Brown et al. 2000). In agreement with these findings, our results (Table 3) in general show higher scores for biological process than for molecular function and cellular component. Furthermore, the randomization tests show that genes with similar expression or common binding sites more often are significantly coannotated with a biological process than is the case for molecular function and cellular component. In fact, for molecular function and cellular component, these two tests perform only marginally better than the test selecting genes randomly without further restrictions, while for biological process they perform considerably better. Hence, Table 3 provides further evidence for the intuitive assumption that coregulated genes more often participate in the same biological process than they perform the same molecular function or are active in the same location (i.e., cellular component). Most importantly, none of the randomization tests performs as well as the rules. It is by combining the requirements of similar expression profile and common binding sites that the truly significant results are observed. Using the two data sources in combination hence seems to be the best approach to discover biologically important regulatory binding-site modules, confirming similar findings by other groups (Pilpel et al. 2001; Segal et al. 2003b; Beer and Tavazoie 2004).

Table 3.

Evaluation of the induced rules using annotations from the three parts of Gene Ontology

	Gene Ontology evaluation (significant fractions P < 0.01)
	Rule (P-values)			Random tests Similar expression/common motifs/random
Expression data	Molecular function	Biological process	Cellular component	Molecular function			Biological process			Cellular component
Cell cycle	0.31 (0.000)	0.46 (0.000)	0.41 (0.000)	0.05	0.04	0.01	0.13	0.18	0.03	0.03	0.04	0.00
Sporulation	0.26 (0.000)	0.54 (0.000)	0.44 (0.000)	0.08	0.04	0.01	0.19	0.17	0.02	0.05	0.03	0.00
Diauxic shift	0.30 (0.000)	0.43 (0.000)	0.44 (0.000)	0.04	0.05	0.02	0.11	0.17	0.03	0.02	0.03	0.00
Heat and cold shock	0.54 (0.000)	0.64 (0.006)	0.60 (0.000)	0.24	0.06	0.03	0.46	0.24	0.05	0.17	0.04	0.01
Pheromone	0.51 (0.000)	0.67 (0.000)	0.60 (0.000)	0.10	0.05	0.01	0.25	0.16	0.02	0.08	0.03	0.00
DNA-damaging agents	0.39 (0.000)	0.64 (0.000)	0.61 (0.000)	0.09	0.05	0.01	0.19	0.17	0.03	0.07	0.04	0.00

A rule is said to be significant if at least one Gene Ontology term used to annotate the matching genes obtained a Bonferroni-corrected P-value of <0.01. The table gives the fraction of significant rules for each data set and each part of Gene Ontology, and compares these values to what is observed when randomly selecting corresponding sets of genes with only similar expression, common binding sites, or neither. All three random tests produce a P-value that is the probability of observing a higher value than the one reported for the rules. We show the highest of these P-values in parentheses and mark the corresponding random test in bold if this P-value is >0. Additional statistics on the standard deviation of the random tests may be found at our Web site.

Rule-related tightness of expression—comparison to single binding sites

A legitimate question to ask is whether the discovered binding-site modules that are often composed of more than one binding site, are associated with tighter expression profiles than the single sites in the modules. To answer this question, we computed the average Euclidean distance between the central gene from which each rule is induced and all the other genes matching that rule. We then compared this expression tightness to what we observed by sampling sets of genes from all genes containing each of the single binding sites in the rule. For example, the seven genes associated with the three binding sites RAP1, MCM1′, and SWI5 in the running example had an expression tightness of 0.19 in the cell cycle data set. The probability (P-value) of sampling seven genes with an equal or tighter expression similarity, considering only one of these sites, was 0.030 for RAP1 and 0.000 for MCM1′ and SWI5 (we performed 1000 samplings for each binding site). In fact, 72% of the rules induced from the cell cycle data set had a significant increase in expression tightness (P < 0.05) compared to any of the individual binding sites in the rule. Corresponding numbers were 58% for sporulation, 53% for diauxic shift, 46% for heat and cold shock, 96% for pheromone, and 73% for DNA-damaging agents (P-values for all rules may be found at http://www.lcb.uu.se/~hvidsten/binding_sites/). These results show that it is very unlikely that the discovered binding-site modules are simply binding sites occurring together by chance.

Reoccurrence of binding sites in identified modules

We obtained binding-site combinations by inducing rules starting from each gene in each expression data set. Many of the 948 obtained binding-site combinations were identified for several different genes and in several different expression data sets. Removing repeating occurrences of such modules within specific expression data sets reduces the number of combinations to 398, while removing repeats over all expression data sets further reduces this number to 280 unique binding-site combinations. Hence, most of the rediscovery was done inside data sets (reduction from 948 to 398 rules) by finding the same combinations starting from several different genes. However, the same binding-site combinations were also found under several different gene expression conditions (reduction from 398 to 280 rules). The expression data sets represent biological responses to different environmental changes (e.g., heat and cold shock), and it seems natural that these stress conditions result in different regulatory modules being activated. On the other hand, a substantial fraction of gene regulation may remain the same independent of these external changes. Table 4 lists the binding-site combinations identified under several different sets of expression conditions, and hence possibly reflecting binding modules important in all these biological settings. In total, 68 rules were found in more than one expression data set, while the rest (212) were found only in one. The second combination in Table 4 is our running example from Table 1 including binding sites RAP1, SWI5, and MCM1′; this module was associated with coexpressed genes under five different expression conditions. Such combinations may be of particular interest because of the large amount of evidence accumulated from several expression studies conducted under different biological conditions.

Table 4.

Rediscovering potential binding-site modules from several expression data sets

Binding-site combination
PAC AND mRRPE
MCM1′ AND RAP1 AND SWI5
MCM1′ AND PAC AND mRRPE
LYS14 AND PAC AND mRRPE
MCM1′ AND RAP1
The table shows binding-site combinations found in five of six gene expression data sets (no combination was found in all six data sets). Frequently occurring binding sites in combinations found in several expression data sets are PAC (polymerase A and C-box), mRRPE (ribosomal RNA processing element), and RAP1 (repressor activator protein). These binding sites were much less frequent in combinations found in one or two expression data sets. An extension of the table listing all combinations and the information from which expression data sets they were induced may be found at our Web site.

Another interesting case involves individual binding sites that are members of binding-site combinations. Most binding sites occur in several different modules (i.e., rules) and hence seem to combine with binding sites for several different transcription factors. Figure 4 illustrates which two binding sites occur together in at least one rule and to how many different combinations each binding site is predicted to belong. It is worth emphasizing that this graph only shows pairs of binding sites operating in the same binding-site modules and does not illustrate a regulatory network. The graph also highlights binding-site pairs from modules that were found under more than one set of expression conditions. The graph indicates the existence of a certain core of binding sites that are particularly frequently used and are involved in a large number of different binding-site combinations found for different biological responses. These might be the underlying regulatory combinations making the cell work under normal conditions (i.e., the cell cycle), while the more peripheral combinations are activated as a response to particular environmental changes (as given by the other five sets of expression conditions). It is also interesting to observe the topology of the graph in Figure 4. The fact that the graph does not contain subparts with high intraconnectivity and low interconnectivity suggests that the regulatory system to a large degree combines different binding sites in order to allow a relatively small number of transcription factors to govern a much larger number of expression outcomes.

Including putative binding sites

The method used for the experimentally tested transcription factor binding sites may also be used for an extended binding-site library containing both the known binding sites and the 313 putative motifs. Inducing rules from the cell cycle data resulted in 1055 combinations (of which 656 were unique) including most of the rules found using the set of known sites (78 of 109)6 and 323 rules with at least two known binding sites also occurring together in the previously found rules. The latter may be of special interest in discovering new regulatory modules. Again using the rule in Table 1 as an example (binding sites RAP1, SWI5, and MCM1′), we found two new overlapping modules:

MCM1′ AND RAP1 AND m_g-proteins_orfnum2SD_n12

MCM1′ AND SWI5 AND m_metal_ion_transporters_orfnum2SD_ n17

The first module is associated with five genes (RPL11B, RPP1B, RPL30, RPL14A, and RPL26A). Although only three of them are found in Table 1, all of them have the same biological roles as the genes in that table (biological process: protein biosynthesis; molecular function: structural constituent of ribosome; and cellular component: cytosolic ribosome) and are possibly bound by one of the same transcription factors (FHL1). This might be considered as strong evidence that the sequence motif m_g-proteins_ orfnum2SD_n12 is involved in a regulatory module together with MCM1′ and RAP1. The second module is associated with a totally different set of genes (MDJ1, SSQ1, VPS4, TFS1, ORT1) with a less clear interpretation in terms of Gene Ontology annotations (biological process: protein metabolism, three genes; molecular function: chaperone activity, two genes; and cellular component: cytoplasm, four genes), and with no common transcription factors according to Lee et al. (2002). Although this combination might be more difficult to interpret, it illustrates the power of (re-)combining binding sites to address a completely different set of genes.

Evaluating all rules induced from known and putative motifs, 26%, 30%, and 26% of the rules were significant according to Gene Ontology annotations to molecular function, biological process, and cellular component, respectively, while 20% were significant according to the binding data (significance level 0.01 as before). These scores are considerably lower than the scores obtained using only known binding sites, but still compare favorably to results obtained from randomly selected genes and genes with only similar expression profiles or only common known binding sites (see Tables 2 and 3). The fact that rules induced from known binding sites score better may be considered as a further confirmation that these known binding sites actually are active, and moreover, that the set of putative motifs includes a considerable number of false positives. Furthermore, 90% of the rules induced from known and putative motifs had a significant increase in expression tightness (P < 0.05) compared to any of the individual motifs in the rules.

Case studies

Although in this work we focused on a statistical evaluation of our method, we now look more closely at the biology behind two of the discovered combinations. The following discussion is based on the information available in the Saccharomyces Genome Database (SGD) and the relevant literature.

The running example suggests a connection between RAP1, MCM1′, and SWI5. The transcription factor RAP1 targets several genes that encode ribosomal proteins and that have an extremely high expression in rapidly growing yeast cells. However, RAP1 is also known to be required for the transcription of several nonribosomal proteins, which hints at the need for a combinatorial regulatory mechanism to separate these activities. The fact that the transcription factors MCM1 and SWI5 are related to cell cycle regulation suggests that one way for RAP1 to specifically target ribosomal proteins in growing yeast cells is to require the presence of MCM1 and SWI5. This is also supported by the Gene Ontology annotations in Table 1, which suggests that the genes associated with the binding sites RAP1, MCM1′, and SWI5 are involved in ribosomal activity. The combination is also supported in literature: Gray and Fassler (1993) published data suggesting that in Ty1 elements RAP1 forms a complex with MCM1, while Lydall et al. (1991) showed that MCM1 and SWI5 are responsible for the cell-cycle-restricted transcription of SW15.

Another example is the rule associating STRE′ and GCR1 with the group of genes ENO1, ZWF1, TDH1, ALD4, and BMH1. Since zinc finger proteins MSN2 and MSN4 bind to the STRE′ binding site (Herrero et al. 1999), and the transcription factor GCR1 binds to the binding site of the same name, the rule suggests a connection between stress response (STRE) and control of glycolysis (GCR1). Indeed, Herrero et al. (1999) showed that GCR1 is needed for constitutive expression of the GLK1 gene, while the STRE element is needed for induction/de-repression of the same gene in the presence of ethanol (or rather absence of glucose).7 A logical explanation is that the absence of glucose may be regarded as one form of stress (nutrient stress or starvation). The glucose level does affect cAMP signaling, which, in turn, regulates MSN2/4 activity, and hence a mechanism is also available. The rule indicates a possibility that the matching genes may be involved in the primary carbon metabolism in a way similar to GLK1. This applies to the five genes, four of which fit this assumption (ENO1, ZWF1, TDH1, and ALD4 are annotated with alcohol metabolism) and one that possibly does not (BMH1 is involved in MAP kinase signaling).

Discussion

We have presented a novel method to discover potential regulatory binding-site modules from a library of sequence motifs and gene expression data. We have selected binding-site combinations for which the occurrence of several genes with a common expression profile indicates a likely relationship between these binding sites and gene expression. These combinations represent strong evidence for actual coregulation, in particular, when the same combinations are found in several sets of expression conditions (e.g., Table 1 and Fig. 2).

Since literature-based validation of combinatorial regulation appears not to provide any significant number of cases, we resorted to validation using experimental data on transcription factor binding to specific yeast promoters (Lee et al. 2002), and separately, using Gene Ontology to test for common biological roles among putatively coregulated genes. Both of these external sources showed a statistically significant result for genes hypothesized to be coregulated through binding-site modules discovered with our method. It is particularly interesting to notice that an organism-independent source of knowledge such as Gene Ontology confirmed the biological relationship between many genes associated with common potential regulatory module for all three aspects of the cellular roles of genes (i.e., biological process, molecular function, and cellular component). Also, we observed that adding noise to the set of binding sites used in the calculations (in terms of putative motifs) decreased the scores of both binding data and Gene Ontology, suggesting that, in fact, the known binding sites are, indeed, involved in regulation. Finally, we also see a relationship between these external validation methods and the parameters in the learning framework (data available at http://www.lcb.uu.se/~hvidsten/binding_sites/). Specifically, it is clear that rules of higher quality either in terms of accuracy/coverage or in terms of expression tightness obtain higher scores with respect to both the binding data and Gene Ontology.

Several other studies investigating the combinatorial nature of gene regulation in yeast have been published. Pilpel et al. (2001) provided evidence for the existence of combinatorial interaction between transcription factors by observing a significant increase in expression similarity between genes sharing one common transcription factor binding site and genes sharing a pair of binding sites. Expression similarity was measured based on Euclidean distance, and the study provided a simple, yet effective, method for proving the combinatorial nature of gene regulation in yeast. Segal et al. (2003b) used an expectation maximization (EM) algorithm to obtain sets of genes that are coregulated (gene modules) through a combination of sequence motifs. The algorithm first clusters expression data into gene modules and then selects motif combinations for each module. It then iteratively moves genes between modules to optimize the degree to which selected motifs explain the expression profiles in the modules. Segal et al. (2003a) used the same methodology to build gene module networks using gene expression data and candidate regulators such as known transcription factors or signaling proteins. Beer and Tavazoie (2004) built similar networks using expression data and sequence motifs. We have used a rule-based approach based on finding minimal binding-site combinations associated with coexpressed genes. Segal et al. (2003a,b) and, to some degree, Beer and Tavazoie (2004) aim at explaining coregulation as a set of broad nonoverlapping gene clusters. Our aim is rather to explore a large number of overlapping groups in search for binding-site modules associated with an often relatively small set of genes. We then select instances where substantial evidence for coregulation exists. In this way we discover binding-site combinations that are more often significant than the findings reported by the previous studies. These comparisons are made in terms of Gene Ontology annotations and in terms of binding data by Lee et al. (2002) (data comparing different published approaches available at http://www.lcb.uu.se/~hvidsten/binding_sites/). We also observed that genes with similar expression or common binding-site motifs are more often annotated with the same biological process, compared to randomly selected genes, than with the same molecular function or cellular component. This is in agreement with assumptions and previous observations of other authors (e.g., Brown et al. 2000).

As more and more genomes are sequenced, the efforts in molecular biology turn to functional genomics; understanding gene regulation and the cellular roles of gene products. The automated processing of thousands of genes and gene products with respect to measured data and available knowledge is necessary in order for progress to be made in this field. Gene Ontology provides one approach to formalizing biological knowledge, and using Gene Ontology annotations we have shown that genes with common binding sites and common expression profiles exhibit a significantly higher probability for being functionally related than genes matching any of these criteria alone. This shows the power of combining the sequence data (static code) and the expression data (dynamic execution) in the pursuit of understanding both regulation and function, and in particular in the discovery of functional regulatory modules.

The binding-site modules we have predicted here may be interpreted as complex nodes in a gene regulation network similar to what was proposed by Segal et al. (2003a). Two nodes would be connected by an edge if one of the transcription factors binding to one of the sites specified by the child node was coded by one of the genes associated with the parent node. The fact that modules discovered here correspond reasonably well with the experimental binding data demonstrates the viability of building such regulatory networks. However, we also see several other extensions within the framework of the present work leading to better understanding of the regulatory mechanisms. Since some transcription factors are only active at certain times or under certain conditions, a more advanced definition of coexpression which, for instance, takes into account correlation over subsets of expression time points might be advantageous (see Lægreid et al. 2003). Another current research issue involves repeating the grouping of expression profiles and rule induction in a feedback loop. It would allow refining of both the groups and the set of rules in an iterative procedure using groups of coexpressed genes to induce rules and using rules to improve the groups. By doing so we could significantly improve the consistency of the resulting model and reduce the impact of both the intrinsic noise in the expression data and the large number of false positives among automatically inferred sequence motifs. We would also like to test this approach on different organisms. There are possibilities for applying it to higher organisms, for example, by using noncoding elements conserved between human and mouse as putative regulatory motifs. Another possible application is to use our method to analyze microbial data. As more and more microbial genomes become available and expression studies are conducted for these genomes, we could produce consistent rule-based models of transcriptional regulation.

Methods

Data material

Known and putative regulatory motifs and their occurrences in promoters in yeast genes were obtained from Pilpel et al. (2001). Gene expression data were downloaded from ExpressDB (Aach et al. 2000). Expression profiles were log-transformed and normalized individually to a unit standard deviation with a mean of zero. For genes where several expression profiles were available under the same conditions, we averaged them to form one profile. Profiles with missing values were removed completely since this only applied to a few genes in each data set.

We used Gene Ontology version 1.320. Annotations were downloaded from the Gene Ontology Web site.

Rough set-based rule induction

The rough set theory is a mathematical framework for analyzing tabular data. For the gene regulation analysis in this paper, we have constructed a table with genes as rows, binding sites as columns, and entries 1 or 0 depending on whether the binding site was present in the promoter region of the corresponding gene or not. The theory sees the data in terms of equivalence classes, in this case sets of genes that are indiscernible (indistinguishable) with respect to an arbitrary subset of binding sites. A “rough set” is a set of genes that cannot be uniquely represented by these basic classes. In practice, this means that a set is rough if it only partly overlaps with one of the equivalence classes. Sets of genes satisfying this requirement cannot be uniquely defined using the binding sites since at least one gene in the set is associated with the exact same binding sites as at least one gene not in the set.

We subsequently classified genes according to whether they were expressed similarly to one particular fixed gene or not. Such sets of similarly classified genes (i.e., coexpressed genes) are called “decision classes.” In particular, decision classes may be rough sets, in which case at least one gene with different expression cannot be discerned from the coexpressed genes using the binding sites. To obtain combinations of binding sites, we built a Boolean function (i.e., a function that evaluates to true or false) that is only true for the binding-site combinations needed to discern the fixed gene from genes not in the decision class. We then simplified this so-called discernibility function to obtain minimal combinations of binding sites discerning a sufficiently large fraction of genes (90% in this study) with different expression than those in the decision class of coexpressed genes. We used a genetic algorithm to search for such approximate solutions called approximate reducts. Finally, IF-THEN rules were constructed to obtain links between minimal combinations of binding sites (i.e., reducts) and particular expression profiles. The framework is implemented in our software system called the ROSETTA system, which is available on the Web.

Grouping gene expression and selecting important rules

We defined two genes to have similar expression profiles if the Euclidean distance, normalized by the number of measurement points, was shorter than a specified threshold distance. The threshold distances were in general chosen to be relatively loose (see column 2 in Table 2) allowing a broad search for potentially coregulated genes. Stricter thresholds in general resulted in fewer rules with better evaluation scores (see our Web site for data). Furthermore, we found that reasonable criteria for including a rule in our study were a coverage value of at least 5 and an accuracy value of at least 2/3. These values where chosen so that virtually no rules were selected during multiple rule induction from random gene expression groups.

Computing P-values for binding interactions and Gene Ontology

For each rule, we used the hypergeometric distribution to calculate P-values for each transcription factor using the binding interactions by Lee et al. (2002). The P-values were computed using the formula

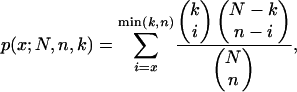where x is the number of genes matching the rule that were bound by the transcription factor, N is the number of genes in the data set, n is the number of genes matching the rule, and k is the number of genes in the data set bound by the transcription factor. Hence, the P-value is the probability of the transcription factor binding the observed or greater number of genes by chance. Since we calculated one P-value for each transcription factor, we multiplied the resulting P-values by the number of transcription factors binding to at least one gene matching the rule. This is called the Bonferroni correction for multiple hypotheses. We chose 0.01 as the significance level and considered a rule to be significant if at least one transcription factor had a Bonferroni-corrected P-value lower than this level. Correspondingly, we also calculated P-values for Gene Ontology annotations and considered a rule to be significant for one part of Gene Ontology if at least one annotation from this part had a Bonferroni-corrected P-value of <0.01.

In addition to reporting P-values for each rule, we also reported P-values for the fractions of significant rules induced from each data set. For this purpose, we conducted randomization tests in which sets of genes were drawn according to different requirements and an element of randomness was introduced (see a description of the three tests below). To ensure that the tests were directly comparable with the rules, we drew as many sets of genes as there were rules and calculated the fraction of significant sets. We then repeated this process 1000 times and counted the fraction of times we observed more significant sets than the number of significant rules in the original rule set. This fraction may be interpreted as a P-value, that is, the probability of observing at least that many significant rules under different randomization assumptions.

In the three randomization tests, we randomly sampled

1. genes with similar expression profiles, that is, we drew one gene randomly and added the closest genes in the expression space (using Euclidean distance);

2. genes with common binding sites, that is, we randomly sampled a set of binding sites and selected the set of genes with these sites in common; and

3. genes without any further restrictions.

Each randomly sampled set corresponded to a particular rule in the sense that we drew the same number of genes as found matching the rule (tests 1 and 3) or the same number of binding sites as in the rule (test 2).

Detailed results

All rules and their evaluation with binding data and Gene Ontology can be found in Supplemental material, which also includes standard deviation for the randomization tests in Table 2 and Table 3 and extended versions of Table 4 and Figure 4.