Prediction of solvent accessibility and sites of deleterious mutations from protein sequence

Abstract

Residues that form the hydrophobic core of a protein are critical for its stability. A number of approaches have been developed to classify residues as buried or exposed. In order to optimize the classification, we have refined a suite of five methods over a large dataset and proposed a metamethod based on an ensemble average of the individual methods, leading to a two-state classification accuracy of 80%. Many studies have suggested that hydrophobic core residues are likely sites of deleterious mutations, so we wanted to see to what extent these sites can be predicted from the putative buried residues. Residues that were most confidently classified as buried were proposed as sites of deleterious mutations. This proposition was tested on six proteins for which sites of deleterious mutations have previously been identified by stability measurement or functional assay. Of the total of 130 residues predicted as sites of deleterious mutations, 104 (or 80%) were correct.

INTRODUCTION

Knowledge of a protein's three-dimensional (3D) structure is essential for a full understanding of its functionality. However, only a small fraction of the enormous number of sequenced proteins have their structures determined. As large-scale gene sequencing projects continue to widen the sequence–structure gap, developing reliable and generally applicable structure prediction methods has become an urgent problem and one of the most important tasks of computational biology. Currently, reliable 3D prediction is still limited to the proteins with significant sequence identity to proteins with known 3D structures through homology modeling. Thus simplification of the problem, from 3D structure to 1D features, may be useful as a first-step. The prediction of secondary structure is the most familiar and well-defined aspect of the problem. The prediction of residue solvent accessibility, as either buried or exposed, is another aspect.

In the folded structure of a protein polar and charged side chains have higher solvent accessibility than non-polar side chains, suggesting that formation of a hydrophobic core is a strong driving force in protein folding (1). The prediction of residue solvent accessibility can aid in elucidating the relationship between sequence and structure. To that end various approaches have been developed, typically by examining a window of residues centered at the test residue and using either amino acid identity (single-sequence input) or a sequence profile (multiple-sequence input) as input attributes. These include neural network (2–5), Bayesian statistics (6), multiple linear regression (7), information theory (8) and support vector machine (9). Reported accuracies for two-state (buried or exposed) classification are ∼70–72% for single-sequence methods and ∼73–78% for multiple-sequence methods. Comparison of the methods was difficult due to the variety of datasets used and the difference in state definition. We have made a direct comparison of five classification methods on a single large dataset and using an identical state definition (10). The five methods were Bayesian statistics (BS), multiple linear regression (MLR), decision tree (DT), neural network (NN) and support vector machine (SVM). We then developed a metamethod based on an ensemble average of the five methods, leading to a two-state classification accuracy of 80%.

In addition to providing insight into the organization of 3D structure, prediction of residue solvent accessibility has many other applications. For example, it has been observed that the distribution of surface residues of a protein is correlated with its subcellular environments and using the information of surface residues has indeed led to improvement in the prediction of protein subcellular location (11). Solvent accessibility has also been used to predict sites of protein hydration, which might play a role in a protein's function (12). A related problem is the prediction of surface residues that become buried in an interface upon protein binding (13,14).

Many studies have found that, beyond the small number of residues directly involved in biological activity (e.g. active-site residues and residues involved in DNA binding), a large fraction of residues harboring deleterious mutations are located in the interior of a protein (15–19). The interior residues may be critical for protein stability (18,20). In an earlier study, residues predicted to be buried were proposed to be sites that give rise to temperature-sensitive mutations (21). Wang and Moult (22) found that the vast majority of disease mutations affected protein stability rather than function, and could be predicted using straightforward rules. Many of these rules centered on buried sites, such as replacing a buried non-polar residue by another that is also non-polar but is either too large or too small, or instead is charged. Similarly, Ramensky et al. (23) noted that, among structural characteristics, 'hydrophobic core stability parameters are the best predictors of disease mutations. While evolutionary information is very useful for predicting deleterious mutations (24), structural information can also contribute, and Saunders and Baker (25) found that the structural attribute that gave the most accurate predictions was a solvent-accessibility term.

Giving the mounting evidence indicating that hydrophobic core residues are likely sites of deleterious mutations, we wanted to see to what extent these sites can be predicted from putative buried residues. We modified the solvent-accessibility predictors to identify residues that were most confidently classified as buried. These were proposed as sites of deleterious mutations. This proposition was tested on six proteins for which sites of deleterious mutations have been identified by stability measurement or functional assay (15–20). Of the total 130 residues predicted as sites of deleterious mutations, 104 (or 80%) were correct.

DATASETS AND METHODS

Training and test data for solvent-accessibility classification methods

Non-homologous proteins (sequence identity <25%) were extracted from the FSSP database (release of October 30, 2001) (26). A total of 2148 protein chains with sequence lengths ≥90 were obtained (listed in Supplementary Table S1). The dataset consisted of 582 352 residues. Residue surface areas were calculated by the DSSP program (27). For each residue, the relative solvent accessibility was calculated by normalizing its accessible surface area by the maximum surface area of that type of residue (28). A cutoff of 20% was used to define the two states, buried or exposed. With this definition, the dataset was, roughly, evenly split between the two states. Sequence profiles used in multiple-sequence methods were extracted from the position-specific scoring matrices produced by PSI–BLAST (29). In implementing the solvent-accessibility classification methods, each sequence profile was transformed via the relation 1/(1 + e^−x) into a vector with components representing occurrence probabilities for the 20 types of amino acids.

Of the 2148 chains in the dataset, 886 had lengths between 90 and 200 residues, 883 had lengths between 200 and 440 residues, and the remaining 379 had lengths >440 residues. These three subsets are called small, medium and large proteins. A total of 464 chains were randomly selected as the test set, and the remaining 1684 chains were used for training the classification methods.

Proteins with known sites of deleterious mutations

Six proteins were the targets for predicting sites of deleterious mutations: λ repressor N-terminal domain (first 92 residues), HIV-1 protease (length of monomer at 99 residues), staphylococcal nuclease (149 residues), T4 lysozyme (164 residues), gene V protein (87 residues) and Lac repressor core protein (residues 61–329). For these proteins, stability measurements and functional assays identified a total of 316 sites of deleterious mutations. Because of the different experimental techniques used, the criteria for labeling a residue as a site of deleterious mutations were somewhat different. For λ repressor, a site was identified if any mutation led to sensitivity to infection by phage λ (15). Similarly, for HIV-1 protease, a site was identified if any mutation led to total loss of enzyme activity (16). For staphylococcal nuclease and gene V protein, a site was identified if any mutation led to a loss in stability by >2 kcal/mol (18,20). For T4 lysozyme, a site was labeled as deleterious if at least two mutations resulted in temperature sensitivity. For Lac repressor, the sites were classified by the authors (19) according to phenotypes.

For calculating solvent accessibility, the following Protein Data Bank (PDB) entries were used: 1lmb3 for λ repressor, 1nh0 for HIV-1 protease, 1snc for staphylococcal nuclease, 1l92 for T4 lysozyme, 1gvp for gene V protein and 1tlf for Lac repressor.

Bayesian statistics method

In the BS approach, one uses probability theory to manage uncertainty by explicitly representing the conditional dependencies between the different knowledge components. Specifically, Bayes' theorem allows one to express the conditional probability for the accessibility state s_i of residue i, given a stretch of amino acid sequence {A_j} centered at residue i, in terms of the conditional probability for the occurrence of sequence {A_j}, given that the central residue has accessibility state s_i:

$$P\left(s_i\right|\left\{A_j\right\})=P(\left\{A_j\right\}\left|s_i\right)P\left(s_i\right)/P\left(\right\{A_j\left\}\right).$$ 1

Because of the low occurrence probability for any specific stretch of residues in protein sequences, statistically significant results for the burial probability of a residue cannot be obtained from a strict application of Equation 1. Therefore approximations must be made. Thompson and Goldstein (6) proposed the simplest approximation: the probability for a type of residue to appear within a segment of accessibility states is independent of neighboring positions.

We adopted the BS method of Thompson and Goldstein for a multiple-sequence implementation. Based on the sequence profiles from PSI-BLAST in the training set, we first constructed a set of 28 amino acid substitution classes that were optimally predicative of solvent accessibility states. Each class was a vector with components representing occurrence probabilities for the 20 types of amino acids. Predictions were performed by matching each position in a window of 13 residues with one of the substitution classes instead of the amino acid identity A_j in Equation 1.

Multiple linear regression method

The goal of MLR is to obtain a least-squares equation to predict some response. For example, one may assume that the accessibility state can be predicted from a linear model of the sort:

$$I_i\left(\text{s}\right)={\displaystyle \sum _{j=i-n/2}^{i+n/2}}{\alpha }_j\left(\text{s}\right)·{\text{R}}_j+{\displaystyle \sum _{j=i-n/2}^{i+n/2}}{\displaystyle \sum _{k=i-n/2}^{i+n/2}}{\beta }_{jk}\left(\text{s}\right)p_j{p}_k,$$ 2

where s is either ‘b’ for buried or ‘e’ for exposed, n + 1 is the window size (=13), R_j is a vector representing the residue identity at position j (with 19 zero components and a single component of value 1), and p_j is the value of a physiochemical property (such as the transfer free energy) at position j (7). In an ideal model, if position i is known to be buried (or exposed), then I_i(b) = 1 and I_i(e) = 0 [or I_i(b) = 0 and I_i(e) = 1]. The regression coefficients α_j and β_jk have to be estimated from the training data. We extended the original method of Li and Pan to multiple-sequence input. Specifically, the residue-identity vector R_j was replaced by the sequence-profile vector. Following Li and Pan, two types of physiochemical properties were included: the free energy of transferring a residue from oil to water and the molecular mass of the side chain. The two sets of coefficients for the two accessibility states were determined by the training data separately. Predictions were then performed by using these coefficients in Equation 2. The state with a higher value of I_i(s) was chosen as the prediction.

Decision tree method

DT has been used on a wide range of applications. Those in bioinformatics include gene finding (30), pattern recognition in genome (31), prediction of protein cellular localization (32), prediction of secondary structure (33). In this approach, one recursively splits the datasets into different sub-trees based on the value of one or more attributes until nearly all the data points in the nodes are in the same category. In our case, the attributes were residue identities (single-sequence input) or sequence profiles (multiple-sequence input) of a stretch of 15 residues centered at the target position. The two categories were the accessibility states (buried or exposed). A main advantage of DT is that the rules derived are easy to understand. In our implementation for prediction of solvent accessibility, we used the C5.0 software of RuleQuest (http://www.rulequest.com) with either single-sequence or multiple-sequence input.

Neural network method

Many types of NN have been developed over the years, including back-propagation, the delta rule and Kohonen learning. We used a two-stage feed-forward, back-propagation NN proposed by Jones (34), with sequence profiles as input (35). The first network had 21 × 15 input nodes, in which the first quantity was the number (i.e. 20) of entries in a sequence profile plus an extra unit indicating whether the window spans either the N- or C-terminal of the protein chain, and the second quantity was the window size. Different numbers of hidden nodes were tested and a layer of 150 hidden nodes was selected. The output layer had two nodes (one for the buried state and the other for the exposed state). A second network was used to filter output values for consecutive positions from the first network. The input layer of the second network had 3 × 15 nodes, in which the first quantity consisted of the two output values of the first network plus an indicator of chain terminal, and the second quantity was again the window size. The second network was completed with 45 hidden nodes and 2 output nodes. The predictor was trained at different learning rate and momentum, and respective values of 0.001 and 0.9 were selected.

Support vector machine method

SVM, first proposed by Vapnik and co-workers (36) based on statistical learning theory, has quickly become one of the most popular classification and regression methods, due to its flexibility in choosing a similarity function, the ability to handle large feature spaces and accuracy. It has been used extensively in many areas, such as microarray data analysis (37) and protein structure prediction (38,39).

SVM maps the training samples into a higher-dimensional feature space, and then constructs an optimal hyper-plane that separates the positive from the negative examples. A kernel function, playing the role of dot product between the input vector and the support vectors in the feature space, allows a non-linear mapping of the input space to the feature space. The choice of a proper kernel function is an important issue for SVM training.

Here, we were interested in classifying a residue as exposed or buried from the 21 × 15 input data as used in NN. Each residue may be thought of a point in the 315-dimensional input space. Yuan et al. (9) implemented SVM^light (40) to predict solvent accessibility. We adopted Yuan and coworker's implementation with the kernel function

$$K(\text{v},\text{R})={(1+\text{v}·\text{R})}^4,$$ 3

where, v is a support vector and R is the input vector of a residue.

Metamethod

The individual methods have different emphasis on input attributes and different levels of accuracy. Therefore they may complement each other, and their combination may lead to improvement in accuracy. A simple rule of combination is that majority wins: if a majority of the methods predict buried, then the state of a residue is taken as buried. We devised a weighted-ensemble (WE) rule that accounts for both difference in accuracy among the methods and the confidence of predictions.

To define the confidence level of a prediction, the output values of a predictor and the corresponding known accessibility states for all the residues in the test set were sorted into bins. In each bin (say, bin n containing output values centered at v_n) the fraction, f_n, of exposed residues was calculated. The dependence of f_n on v_n was then fitted to a monotonically increasing function: f_n = F(v_n). This function was then used to assign the predicted state and the associated confidence. Specifically, if the output value was v, then the predicted state was exposed if F(v) ≥ 0.5 and buried otherwise, and the confidence for either predicted state was taken as |2F(v) − 1|. SVM had a single output (with values ranging from ∼−2.2 to ∼2.2), so the assignment of v was unambiguous. DT gave the predicted state (buried or exposed) and the probability (range from 0.5 to 1) for the prediction; v was set to the prediction probability if exposed was predicted or (1−the prediction probability) if buried was predicted. Though NN had two outputs, typically the sum of the two outputs was very close to 1, and v was simply taken as the value of the ‘exposed’ output node. BS and MLR each had two outputs, and v was taken as the difference between the ‘exposed’ output and the ‘buried’ output. The function F(v) was F(v) = v for DT and NN, and F(v) = 1/(1 + e^−av) for BS, MLR and SVM.

For a given residue, if s_i (=−1 for buried or +1 for exposed) was the prediction of the ith method, C_i was the corresponding prediction confidence and W_i was the weight assigned to this method, then the WE prediction was

$$s={\displaystyle \sum _{i=1}^5}{W}_i{C}_i{s}_i.$$ 4

If the resulting value of s was positive, then the residue was predicted as exposed, otherwise it was buried. Methods with higher accuracies were assigned higher weights. The weights for BS, MLR, DT, NN and SVM were 0.1, 0.2, 0.4, 0.9 and 1.0, respectively.

Prediction of sites of deleterious mutations

We proposed to identify as sites of deleterious mutations the residues that were most confidently predicted as buried. We therefore shifted the focus of accessibility prediction to those that were confidently predicted. This shift meant that residues that could not be confidently predicted were no longer of interest. Of course, we had to choose a reasonable level of confidence, because picking an extremely high confidence level meant that only a few predictions would be made.

Two other changes were also made. First, some of the methods with lower accuracy were no longer used. As will be seen later, SVM and NN had the highest accuracy levels and were retained. MLR was also retained because it had input attributes, i.e. physiochemical properties of residues, not present in the other methods, but BS and DT were not used. Second, a metamethod based on unanimity among SVM, NN and MLR was used as the final predictor for sites of deleterious mutations.

Assessment of predictions

Prediction accuracy was measured by the percentage of correctly predicted residues. For solvent-accessibility classification, every residue of a protein was given a prediction (corresponding to coverage of 1). If 75 residues of a 100-residue protein are classified correctly (e.g. as buried when relative solvent accessibility is actually <20%), then accuracy would be 75%. This definition of accuracy is also known as specificity. A complementary measure is the correlation coefficient between observed (o) and predicted (p) states, given by

$$\frac{N{\sum }_{j=1}^N{o}_j{p}_j-{\sum }_{j=1}^N{o}_j{\sum }_{j=1}^N{p}_j}{{\left[N{\sum }_{j=1}^N{o}_j^2-{\left({\sum }_{j=1}^N{o}_j\right)}^2\right]}^{1/2}{\left[N{\sum }_{j=1}^N{p}_j^2-{\left({\sum }_{j=1}^N{p}_j\right)}^2\right]}^{1/2}},$$ 5

where, N is the total number of residues in the test set. For the test set of 464 protein chains, N = 115 122.

Prediction of sites of deleterious mutations was measured by both accuracy and coverage. The former is the percentage of correctly predicted sites among all predictions, whereas the latter is the fraction of correctly predicted sites among all actual sites.

RESULTS AND DISCUSSION

Performance of the classification methods

Details of the prediction results for solvent accessibility on the test set of 464 protein chains and on the 52 targets from CASP5 have been presented previously (10). Here, we give a summary of the results in Table 1 to provide an indication of the accuracies of the different methods. It can be seen that, according to both accuracy and correlation, the methods were ranked as follows: BS < MLR < DT < NN ∼ SVM < WE. It is heartening that the metamethod indeed outperformed all the individual methods.

Table 1.

Accuracy (%) and correlation (in parentheses) of multiple-sequence predictions for solvent accessibility on a test set of 464 protein chains

Test set	Chains	BS	MLR	DT	NN	SVM	WE
Small	208	76.0 (0.48)	75.5 (0.46)	77.5 (0.52)	79.6 (0.56)	79.5 (0.56)	80.1 (0.57)
Medium	198	75.6 (0.51)	76.4 (0.53)	77.1 (0.54)	79.2 (0.58)	79.8 (0.60)	80.2 (0.60)
Large	58	74.7 (0.49)	75.5 (0.51)	76.3 (0.52)	78.4 (0.57)	78.9 (0.58)	79.4 (0.59)
All	464	75.5 (0.51)	76.0 (0.52)	77.0 (0.54)	79.1 (0.58)	79.5 (0.59)	80.0 (0.60)

Every protein residue was given a prediction, so the coverage was 1.

Given the large size of the test set, the results listed in Table 1 were very representative of what would be obtained by cross-validation. For example, when the 883 medium proteins in the dataset were equally divided into five groups, with any four of these for training and the remaining group for testing, NN had accuracy of 79.4% and correlation of 0.59, almost identical to the results found on the 464-protein test set (79.2% accuracy and 0.58 correlation; see Table 1).

The five individual methods and the WE metamethod were also applied to the 64 CASP6 targets (http://predictioncenter.llnl.gov/casp6). Domains of these targets have been labeled as CM (comparative modeling), FR(H) or FR(A) [fold recognition (homologous or analogous)] and NF (new fold), according to sequence and structure alignments with the PDB of summer 2004. The accessibility classification was done on the whole target chain instead of its domains separately. For easy reference, here each target is given the labeling of its largest domain, leading to 48 targets in the CM/FR(H) category and the remaining 16 in the FR(A)/NF category (Table 2). Performance of the six methods on the CASP6 targets tracked that on the 464-protein test set. Again, NN and SVM were the top performers among the five individual methods, and WE gave further improvement in accuracy. The results on the FR(A)/NF targets were slightly worse than those on the CM/FR(H) targets. The overall accuracy of WE was 79.2%.

Table 2.

Accuracy (%) and correlation (in parentheses) of accessibility classification methods on CASP6 targets

Test set	Chains	NN	SVM	WE	ROBETTA	PROFacc	SABLE	ACCpro
CM/FR(H)	48	78.6 (0.57)	78.9 (0.57)	79.4 (0.58)	74.5 (0.49)	76.7 (0.54)	78.4 (0.57)	78.9 (0.58)
FR(A)/NF	16	78.6 (0.56)	77.7 (0.54)	78.8 (0.56)	65.3 (0.26)	76.4 (0.52)	77.2 (0.54)	76.9 (0.53)
All	64	78.6 (0.57)	78.6 (0.57)	79.2 (0.58)	72.5 (0.44)	76.6 (0.54)	78.2 (0.57)	78.5 (0.57)

For comparison, classification results were also obtained by using three recently published NN based methods: ACCpro (http://www.igb.uci.edu/tools/scratch/) (3), SABLE (http://sable.cchmc.org/) (4) and PROFacc (http://cubic.bioc.columbia.edu/predictprotein/submit_adv.html) (5). For the CM/FR(H) targets, our NN was comparable in accuracy with SABLE and ACCpro, and better than PROFacc. For the FR(A)/NF targets, NN was better than the other three methods. It should be noted that ACCpro included a bypass to use the actual structure of a close homologue whenever available in the PDB. This bypass partly explains the relatively high accuracy of ACCpro for the CM/FR(H) targets. WE outperformed PROFacc, SABLE and ACCpro by 0.7–2.6% points in accuracy.

Another comparison on the CASP6 targets was made to the solvent accessibilities calculated from structure models built automatically by the ROBETTA server (available at http://predictioncenter.llnl.gov/casp6). Based on model 1 structures, the accuracy of ROBETTA was only 72.5% for residue solvent accessibilities of the 64 targets. This level of accuracy was easily surpassed by any of the classification methods, and in particular, was lower by 6.7% points than that of WE.

Relation between accuracy and coverage

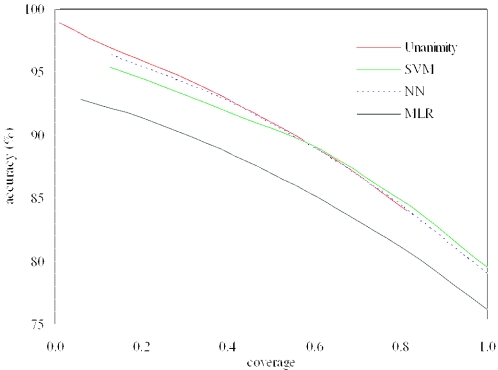
For the results shown in Tables 1 and 2, the accessibility state of each residue was given a prediction, regardless of the confidence. For predicting sites of deleterious mutations, only residues with high-confidence predictions are of interest. It is easy to see that, when confidence threshold is raised, accuracy should increase whereas coverage should decrease. Figure 1 shows the relation between accuracy and coverage for MLR, NN, SVM and the unanimity metamethod. At coverage <0.5, the metamethod outperformed all the three individual methods in accuracy. The metamethod that was used for predicting sites of deleterious mutations were built by taking the predictions of the three methods at confidence threshold of 0.5. For the 464-protein test set, the accuracy of the metamethod for solvent accessibility was 92.2% and the coverage was 0.44.

Figure 1.

Relation between accuracy and coverage, as found for the 464-protein test set. Values of accuracy at coverage of 1 are listed in Table 1. Coverage of MLR, NN and SVM was controlled by the confidence threshold (higher confidence corresponds to lower coverage). The unanimity metamethod was based on predictions of MLR, NN and SVM at the same confidence threshold.

Prediction on sites of deleterious mutations

According to the X-ray structures of the six target proteins, the fraction of buried residues among the 316 sites of deleterious mutations identified by experiments was 0.72. This large fraction strongly justifies the proposition of predicting sites of deleterious mutations by predicting buried residues. Table 3 presents the prediction results by the MLR, NN and SVM methods and the unanimity metamethod. Overall, the accuracy levels of the three individual methods stood at ∼75%. Accuracy was improved by the metamethod to 80%—of the 130 predicted sites of deleterious mutations, 104 were consistent with experiments. The latter covered a fraction of 0.33 of all the sites identified by experiments. These results are very encouraging, especially considering the fact that no data on deleterious mutations were ever used in training the predictors.

Table 3.

Statistics of proteins with identified sites of deleterious mutations

Protein	Real sites	Fraction buried	Predictions				Accuracy (%)
			MLR	NN	SVM	Una	MLR	NN	SVM	Una
λ Repressor	22	0.50	16	8	12	6	44	50	50	50
HIV-1	42	0.74	22	7	12	6	50	14	25	0
Snase	32	0.78	23	28	35	17	78	57	57	77
T4 lyso.	60	0.77	31	28	31	16	84	82	84	94
Gene V	15	0.47	10	5	5	4	70	100	100	100
LacI	145	0.75	89	101	125	81	83	81	50	85
Total	316	0.72	191	177	220	130	75	74	73	80

Una, unanimity metamethod. Results of MLR, NN and SVM were obtained from predictions with confidence threshold of 0.5.

The performance of the methods was not even among the six proteins. For four of these (staphylococcal nuclease, T4 lysozyme, gene V protein and Lac repressor), predictions were satisfactory, but for the remaining two (λ repressor and HIV-1 protease), accuracy was low. Perhaps the identifications of deleterious mutations by different experimental methods contributed to the uneven performance of the predictions. Pinpointing deficiencies of the predictions and method refinements with experimental data on a large set of proteins will likely help improve accuracy for predicting sites of deleterious mutations. It will also be possible to directly train the predictors on data for sites of deleterious mutations.

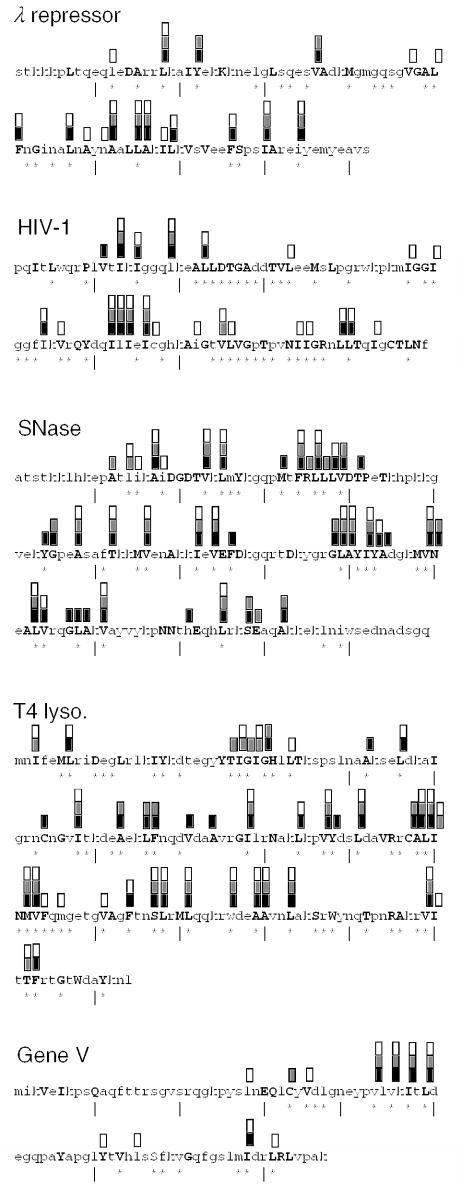
The details of the predictions are shown in Figure 2. Though most of the predicted positions are buried according to the X-ray structures, a significant fraction (e.g. 9% of the unanimity predictions) was exposed. Interestingly, accuracies of the predictions at exposed and buried positions were nearly the same. In particular, 8 of the 12 predictions of the unanimity metamethod at exposed positions were correct. A cutoff of 20% solvent accessibility for defining buried and exposed states is somewhat arbitrary. In addition, solvent accessibilities at corresponding positions among homologous proteins will vary somewhat. The results in Figure 2 suggest that the predictors were able to transcend such idiosyncrasy.

Figure 2.

Details of the predictions for sites of deleterious mutations. Upper-case letters in each sequence denote buried residues (as determined by solvent accessibility calculated on the X-ray structure). Asterisks below each sequence denote sites of deleterious mutations determined experimentally. Vertical lines below the sequence are positioned at every tenth residue (if not already occupied by an asterisk). Bars above the sequence denote predictions by MLR (white), NN (gray) and SVM (black). A prediction by the unanimity metamethod is signified by the simultaneous presence of all three types of bars.

In conclusion, we have refined a number of methods for predicting solvent accessibility. These methods have been found to be useful for predicting sites of deleterious mutations. The results presented here suggest that the methods can be the basis for accurate predictions of deleterious mutations.

Software for the methods presented here is available by email to zhou@sb.fsu.edu. A server will also be available.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.