Equivariant Neural Networks Utilizing Molecular Clusters for Accurate Molecular Crystal Lattice Energy Predictions

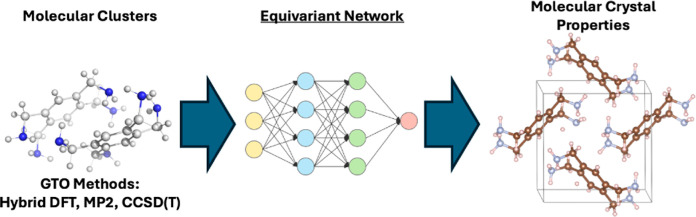
Abstract

Equivariant neural networks have emerged as prominent models in advancing the construction of interatomic potentials due to their remarkable data efficiency and generalization capabilities for out-of-distribution data. Here, we expand the utility of these networks to the prediction of crystal structures consisting of organic molecules. Traditional methods for computing crystal structure properties, such as plane-wave quantum chemical methods based on density functional theory (DFT), are prohibitively resource-intensive, often necessitating compromises in accuracy and the choice of exchange–correlation functional. We present an approach that leverages the efficiency, and transferability of equivariant neural networks, specifically Allegro, to predict molecular crystal structure energies at a reduced computational cost. Our neural network is trained on molecular clusters using a highly accurate Gaussian-type orbital (GTO)-based method as the target level of theory, eliminating the need for costly periodic DFT calculations, while providing access to all families of exchange–corelation functionals and post-Hartree–Fock methods. The trained model exhibits remarkable accuracy in predicting lattice energies, aligning closely with those computed by plane-wave based DFT methods, thus representing significant cost reductions. Furthermore, the Allegro network was seamlessly integrated with the USPEX framework, accelerating the discovery of low-energy crystal structures during crystal structure prediction.

1. Introduction

Molecular organic solids, characterized by their crystalline nature, are fundamental to a wide array of industries, including pharmaceuticals,¹⁻⁴ agrochemicals,⁵ defense,⁶ electronics,⁷⁻¹⁰ and semiconductors.¹¹ They also significantly contribute to processes such as gas separations,¹² as well as the purification and separation of organic molecules.¹³⁻¹⁸ Crucially, the properties of these organic solids are intimately linked to their crystal structure, underscoring the importance of understanding and controlling this aspect. Consequently, the development of crystal structure prediction (CSP) methods,¹⁹ employing computational techniques, has been gaining momentum.^20,21 These methods aim to identify the experimentally observed (or the most stable) crystalline polymorphs of a given organic molecule under ambient conditions, a crucial task given that approximately half of all organic molecular crystals are known to exhibit polymorphism.²²

The CSP protocol encompasses two primary steps. The first step involves the exploration of potential crystal structures, requiring an exhaustive search within the conformational and crystallographic space. The sheer number of feasible combinations for the crystal structures that arise from this high-dimensionality escalates the problem to an NP-hard level of complexity.²³ The second step involves the accurate ranking of these crystal structure polymorphs based on their relative energetic stability. Traditionally, this ranking is achieved by calculating the lattice or binding energy of the crystal structures at absolute zero temperature (0 K). However, recent advances in machine learning (ML) methods are opening up new possibilities for moving beyond zero Kelvin CSPs, with increasing interest in exploring binding free energy metrics for crystal structure ranking.²⁴ While this approach shows promise for more accurate and realistic predictions, it represents an exciting future direction that complements the primary focus of our current work.

During the ranking phase of the CSP process, the number of polymorphs can often range between 10⁴ and 10⁶,²⁵ which need to undergo energy minimization for structure refinement, to weed out duplicate or equivalent structures, and to filter out high-energy configurations. Given the magnitude of the task, leveraging cost-effective theoretical methods, such as force fields or semiempirical approaches, becomes essential. Invariably, the definitive ranking of these structures is predicated on lattice energy calculations, with a strong preference for dispersion-corrected density functional theory (DFT) methods to capture the van der Waals interactions that bind molecular fragments in the crystal phase. In this context, the application of periodic boundary conditions (PBC) is a concomitant procedure for computations on molecular solids. With plane-wave basis sets, the system is distinctly defined within a uniformly filled three-dimensional (3D) space, ensuring intrinsic periodicity in all dimensions. This inherent characteristic has long favored plane-wave (PW) based DFT methods for determining the energetic stability of crystal structures, leading to their widespread acceptance as the final ranking method in organic CSP blind tests.²⁰

While the PW approach offers distinct advantages, it comes with its own set of challenges. Primarily, for technical reasons, most PW DFT calculations use generalized gradient approximation (GGA) DFT. Attempts to employ more accurate hybrid functionals (and post-Hartree–Fock methods), which incorporate exact Hartree–Fock (HF) exchange, are met with substantial increases in computational costs, thereby limiting their mainstream adoption.²⁶⁻²⁸ Moreover, PWs predominantly describe only valence electrons, using pseudopotentials to capture the effects of core electrons. Yet, even when employing pseudopotentials, a PW calculation might require several hundred times more basis functions than Gaussian-type orbitals (GTOs) to reach a similar level of convergence with respect to the basis set limit.

In contrast, Gaussian-type basis sets, though less frequently employed in quantum chemical analyses of molecular solids, have a foundational role in molecular quantum chemistry, drawing upon decades of established techniques and insights. This includes recent breakthroughs in accelerating the computation of coulomb and exchange-type matrices using RIJCOSX^29,30 approximations, as well as the evolution of linear scaling correlated methods through tensor decomposition techniques, notably the domain-based local pair natural orbital³¹⁻³⁴ method. Hence, GTO-based methods have naturally found their application in computing crystal structure lattice energies, though in an implicit manner. Most notably, fragment-based energy methods—often expressed through many-body expansions such as the hybrid many-body interaction^35,36 approach—incorporate corrections from one- and two-body interactions (represented by monomers and dimers, respectively) employ accurate GTO methods.³⁷⁻³⁹ Moreover, the rapidly expanding field of ML has been instrumental in enhancing these many-body expansion methods, either through ΔML approaches or by offering a more efficient and accurate computation of the many-body terms.^40,41

In this study, we seek to bridge the gap between the PW and GTO based methods via ML. Our approach involves training an equivariant neural network on a data set of molecular clusters, derived from computationally efficient GTO-based methods. This is intended to craft a ML potential proficient at capturing both intra- and intermolecular interactions within our targeted systems. Once trained, this potential is equipped to predict lattice energies of periodic molecular crystal structures. In this context, it is noteworthy that Szalewicz and co-workers developed the autoPES method, an intermolecular potential based on symmetry-adapted perturbation theory, fitted to molecular cluster data, which has been utilized for lattice energy minimization of crystal structures.⁴²⁻⁴⁴ Their approach employs a distinct empirical potential for intramolecular interactions, which must align with the intermolecular potential for consistency. Our method differs by aiming to concurrently capture both inter- and intramolecular interactions within a unified framework through the application of an equivariant neural network.

Amine molecules serve as our primary testbed in this endeavor, selected for their scientific significance, especially for their pivotal role in capturing carbon dioxide.⁴⁵⁻⁴⁹ Historically, amines have been extensively researched for their ability to bind with CO₂, facilitating its capture under a range of conditions. Notable examples of this include amine-appended metal–organic frameworks (MOFs)⁵⁰ and cyanuric acid-stabilized melamine nanoporous networks⁵¹ capturing carbon dioxide through chemisorption. In the case of ethylenediamine-appended MOFs, amine molecules engage in cooperative CO₂ capture to form ammonium carbamate chains reminiscent of the crystal structure of neat N-(2-ammoniumethyl)carbamate. Appreciable insight in periodic crystalline structure of polyamines more complex than ethylenediamine may rapidly accelerate the discovery of candidate polyamines suitable for CO₂ capture. Additionally, aqueous amines are employed in industrial settings, particularly due to their efficiency in selectively binding and removing carbon dioxide from flue gas.⁴⁸ In the solid state, these organic amines can manifest an array of crystalline structures. This diversity arises from the interplay of noncovalent intra- and intermolecular interactions, resulting in a range of crystal structures. While this study emphasizes amine structures, our proposed methodology possesses the flexibility and versatility to address crystal structures of any organic molecule. To demonstrate the broader applicability of our method, we predict crystal structures of two organic molecules with complex intermolecular interactions, illustrating its potential beyond amine structures.

2. Methods

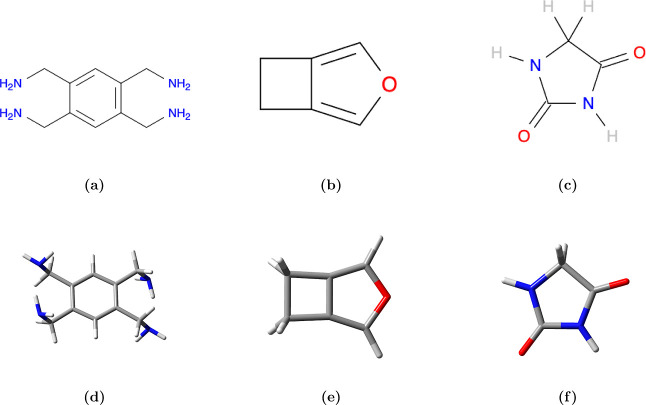
An aromatic tetraamine (benzene-1,2,4,5-tetrayltetramethanamine⁵²) (Figure 1a) was selected as a representative molecule for designing the ML protocol. Its high symmetry, coupled with multiple amine groups and conformationally flexible substituents, makes periodic packing predictions challenging. Furthermore, the numerous amine groups can facilitate a vast array of periodic hydrogen bonding structures, adding to its complexity and making it an intriguing test case.

Figure 1.

(a) 2D and (d) 3D structures of benzene-1,2,4,5-tetrayltetramethanamine. (b) 2D and (e) 3D structures of 3-oxabicyclo[3.2.0]hepta-1,4-diene. (c) 2D and (f) 3D structures of Hydantoin.

To further validate our protocol, Section 3.4 discusses 3-oxabicyclo[3.2.0]hepta-1,4-diene (Figure 1b) and hydantoin (Figure 1c) molecules, test cases from the Cambridge Crystallographic Data Centre CSP challenges, encompassing a broader spectrum of noncovalent interactions between molecules.^53,54

2.1. Molecular Cluster Data Set

To develop a robust ML model for predicting properties in periodic systems, we curated a comprehensive data set of molecular clusters. These clusters, including monomers, dimers, trimers, and higher-order aggregates, aim to capture the full spectrum of intramolecular, intermolecular, and multibody interactions characteristic of the target system. While ML methods often require large data sets, recent advances in equivariant neural networks (e.g., NequIP,⁵⁵ Allegro,⁵⁶ MACE^57,58) have demonstrated data efficiency by leveraging molecular symmetries to reduce data requirements by up to 3 orders of magnitude while maintaining accuracy.⁵⁵⁻⁵⁸ Nevertheless, a reasonably sized data set is still necessary to avoid underfitting. To further explore the data efficiency of equivariant neural networks in the context of CSP, we aim to utilize a similar number of data points (typically, on the order of 10³) for model training as in other data-efficient methods for CSP, such as AutoPES^43,44 and Gaussian Process Regression.⁴¹ Additionally, we build the data set sequentially, progressing from simpler (smaller) body terms to more complex higher-body terms, effectively minimizing both data generation costs and computational resources required for model training.

To accurately predict energies of molecular crystal structures with diverse molecular conformations and orientations, our training data set fundamentally requires monomers and dimers in various configurations. This captures intra- and intermolecular interactions, providing a baseline representation of the system. To enhance data set diversity, we employ an energy window parameter, controlling the range of generated conformers relative to the lowest energy conformation. Broader energy windows typically yield more varied conformations, increasing the data set size and diversity. While an energy window of 12 kcal mol^–1 (50.2 kJ mol^–1) is typically sufficient for systems with moderate conformational flexibility,⁵⁹ achieving a large and diverse data set size may necessitate enlarging this window to include higher-energy conformers. However, it is important to note that simply widening the energy window does not guarantee increased diversity, particularly for molecules with limited intermolecular interactions. In such cases, higher-energy conformations may predominantly consist of disjointed monomers, i.e., configurations where the interaction energy between the constituent molecules is negligible (typically, less than 0.1 kcal mol^–1). These noninteracting monomers offer no additional information beyond what is already captured in the monomer data set. Therefore, we refined our data sets by removing such structures, ensuring the relevance of each configuration to potential crystal packing. When monomers and dimers alone fail to yield a sufficiently large data set (on the order of 10³ data points), particularly for conformationally rigid molecules, we systematically incorporate higher-order many-body configurations, starting with trimers and progressing to more complex configurations (e.g., tetramers, etc.) as necessary to ensure comprehensive representation of molecular interactions. This approach expands the data set’s scope and scale, capturing a wider range of intermolecular interactions relevant to crystal packing and potentially improving both the model’s performance and its ability to generalize to unseen data, albeit at an increased computational cost. In summary, we utilize two tunable parameters—cluster aggregate size and conformer energy window—to control the data set’s size and diversity, striking a balance between computational cost and model performance.

Utilizing the aforementioned protocol, we constructed cluster data sets for the molecules in this study. The Conformer Rotamer Ensemble Sampling Tool (CREST)⁶⁰ was employed to generate cluster conformations using the non-covalent interactions mode at the GFN2-xTB^61,62 level of theory. Given the high conformational flexibility of tetramine, we focused on the simplest data model, generating only monomer and dimer conformers within a 12 kcal mol^–1 energy window. This process yielded a diverse data set of 548 monomers and 4995 dimers, aligning with the target data set size. For the conformationally rigid molecule 3-oxabicyclo[3.2.0]hepta-1,4-diene, our initial protocol yielded only one monomer configuration (due to the absence of rotatable bonds) and 119 dimer structures, insufficient for robust ML model training. Attempting to expand the data set by widening the energy window was not effective, as it predominantly resulted in disjointed monomers rather than more diverse conformations. Consequently, to augment the diversity and size of our data set—and to better capture a broader spectrum of molecular orientations—we generated trimer conformers for 3-oxabicyclo[3.2.0]hepta-1,4-diene using the CREST protocol and maintained a 12 kcal mol^–1 energy window. This approach generated 600 trimer configurations, bringing the total data set size to a level suitable for effective ML model training. For hydantoin, we applied the same protocol to generate the cluster data set. However, due to its conformationally restrictive nature—characterized by no rotatable bonds—we obtained only 29 dimer and 368 trimer configurations. Given hydantoin’s multiple hydrogen bonding sites and the relatively small size of this initial data set, we expanded the scope to include tetramer configurations within a larger energy window of 24 kcal mol^–1. This aimed to comprehensively capture the complex intermolecular interactions facilitated by multiple hydrogen bonding sites. This expansion resulted in 1106 tetramer configurations, bringing the combined data set to a reasonable size suitable for robust ML model training.

Following conformer generation, we have the flexibility to perform single-point energy computations on these conformers using any highly accurate GTO-based method, such as DFT or various post-Hartree–Fock approaches, which then serves as the target level of theory for training our ML model. In this study, we selected the PBE-D3BJ^63,64 functional with the Karlsruhe triple-ζ basis set (def2-TZVP)^65,66 as the target level of theory. This choice facilitated direct comparison with the equivalent periodic PBE-D3BJ method applied to crystal structures. In Section 3.2, we present results obtained using other higher level quantum chemical methods, specifically the B3LYP-D4⁶⁷⁻⁷⁰ hybrid functional and DLPNO-MP2³¹⁻³⁴ correlated method. All single-point energy computations on molecular clusters were conducted using the Orca 5.0.3 software.⁷¹

2.2. Molecular Crystal Structure Data Set

To assess the efficacy of the trained ML model, we created a data set of molecular crystal structures for the tetraamine using the evolutionary algorithm (EA) within USPEX 10.5.0⁷² (Universal Structure Predictor: Evolutionary Xtallography). Given the computational expense of variable-cell relaxation processes during the structure refinement phase of CSP, we utilized the cost-effective xTB⁶² method, compatible with periodic boundary conditions, integrated within the DFTB+⁷³ program package via the tblite project. We used a two-step variable-cell relaxation protocol, starting with the GFN1-xTB⁷⁴ method until the maximum absolute force element reduced to 10^–3 Ha Bohr^–1, followed by the GFN2-xTB method with the corresponding convergence criterion of 10^–4 Ha Bohr^–1. The application of a “k-point resolution” value of 0.06 × 2π Å^–1 in USPEX automatically generated an on-grid k-point mesh for DFTB+, allowing simulations to be conducted beyond the Γ-point. The structure evolutions were conducted over 25 generations with two molecules per unit cell (Z), utilizing heredity, random generation from prespecified space groups, topology-based structure generation,⁷⁵ and rotational mutation strategies.⁷⁶ The search space for molecular crystals was confined to the 22 most frequently encountered space groups in the Cambridge Structural Database, with group numbers: 14, 2, 15, 19, 4, 61, 33, 9, 62, 1, 5, 60, 148, 29, 13, 12, 11, 7, 18, 88, 56, and 43. The EA within USPEX navigates the crystal structure landscape based on fitness evaluations derived from crystal structure energies. Our methodology enhances these evaluations by integrating a ML model (viz., Allegro), providing energy predictions with a higher level of theoretical accuracy than achievable with the GFN2-xTB method alone.

To obtain accurate electronic energies (and hence, lattice energies), the xTB-relaxed molecular crystal structures were subjected to single-point energy calculations using the plane wave projector-augmented-wave (PAW)⁷⁷ DFT methodology. In particular, we utilized the PBE functional augmented by Grimme’s D3⁶⁴ dispersion correction with Becke–Johnson (BJ) damping, a crucial aspect for accounting for van der Waals dispersion interactions in organic molecular crystals. All calculations were performed using the Quantum ESPRESSO v.7.0 program suite.^78,79 To strike a balance between computation time and accuracy, we employed an energy cutoff of 80 Ry for wave functions, and 480 Ry for charge density. We used a Monkhorst–Pack⁸⁰k-point grid with a spacing of 0.06 × 2π Å^–1 to ensure higher precision in the calculations. Core electrons were accounted for using PAW pseudopotentials from the pslibrary version 1.0.0.⁸¹

Building on the calculated DFT energies, the lattice or binding energy (per molecule) of the molecular crystals within the periodic boundary condition (PBC) formalism can then be computed using the following equation

1

where E_cell represents the total energy of the crystal unit cell, Z is the number of molecules within the unit cell, and E_molecule denotes the total energy of an isolated molecule in the gas phase computed within a cubic unit cell with dimensions 20 Å.

2.3. Model Architecture and Training

In this study, we utilize the Allegro⁵⁶ architecture, a prime example of an equivariant deep neural network^55,82 designed for accurate molecular property predictions. Allegro utilizes a unique approach that eliminates the need for atom-centered message passing,⁸²⁻⁸⁶ thus achieving scalability on par with strictly local ML models (viz., Behler–Parinello neural networks,⁸⁷ ACE,⁸⁸ GAP,⁸⁹ SNAP,⁹⁰ DeepMD,⁹¹ Moment Tensor Potentials⁹²) while retaining the accuracy and transferability characteristic of equivariant atom-centered message passing neural networks. Allegro, an equivariant neural network, is explicitly constructed from equivariant operations, ensuring the preservation of known transformation properties of physical systems under coordinate changes, thereby inherently enhancing its data efficiency. In fact, Allegro surpasses existing models by requiring up to 3 orders of magnitude fewer training data.⁵⁵ This superior data efficiency paves the way for the creation of accurate models using high-order quantum chemical theory as a reference, enabling high-fidelity property predictions for larger systems, thus making Allegro an optimal choice, particularly in scenarios with limited data availability.

As demonstrated in various studies employing Allegro, a modest radial cutoff of 4–6 Å has proven effective across a wide range of chemical systems, including large biomolecules, irrespective of molecular size, shape, or flexibility.^56,93−95 Therefore, in the process of constructing the Allegro models, radial cutoffs of 6.0 Å was judiciously chosen, which ensures the comprehensive capture of neighboring π–π interactions, as well as other extended noncovalent interactions between molecules.^56,93 A significant consideration during this process was balancing complexity and transferability. Specifically, a deeper architectural configuration with three layers was employed to improve the model’s transferability to molecular crystal structures. At the same time, it was critical to keep the number of model weights within a modest range to mitigate overfitting to the molecular cluster data. To this end, and to avoid proliferation of trainable parameters, we crafted the Allegro model employing a modest, singular feature for both odd and even irreducible representations of O(3) group and l_max = 1. The 2-body latent multilayer perceptron (MLP) is composed of four hidden layers of dimensions [8, 16, 32, 64], utilizing Sigmoid Linear Unit (SiLU)⁹⁶ nonlinearities. The latent MLP, in turn, consists of four hidden layers with identical dimensionality [8, 16, 32, 64], also employing SiLU nonlinearity. The embedding weight projection was implemented via a single matrix multiplication, with no additional hidden layer or nonlinearity. The final edge energy MLP comprises one hidden layer of dimension 16, with no nonlinearity as well. All four MLPs were initialized in accordance with a uniform distribution. The basis encoding was accomplished using eight trainable Bessel functions, complemented by a polynomial envelope function with an exponent of 6. For a detailed overview of the Allegro architecture, please refer Musaelian et al.⁵⁶

Each Allegro model⁵⁶ was trained on a curated molecular cluster data set, partitioned into a 90–10% split for the training and validation sets respectively, and reshuffled after each epoch. The training was carried out on a single NVIDIA GeForce GTX 1080 Ti GPU with a batch size of four. Employing a joint loss function for energies and forces, we utilized the mean absolute error (MAE or L1Loss) as the loss function, with both energy and force terms receiving an equal weight of 1. Optimization of the model parameters was performed using the Adam⁹⁷ algorithm in PyTorch,⁹⁸ with default parameters of β₁ = 0.9, β₂ = 0.999, and ϵ = 10^–8 without weight decay. We initiated the optimization process with a starting learning rate of 0.01, which was subsequently adjusted via a ReduceLROnPlateau schedule. This scheme reduced the learning rate by a factor of 0.75 whenever the training loss plateaued within a user-specified threshold of 2.5 × 10^–5 Ha. We employed an exponential moving average with a weight of 0.99 to evaluate the validation set and for determining the final model. Training was concluded when one of the following conditions was met: a maximum of 1500 epochs were reached, or the learning rate dropped below 10^–5. Training and validation errors for the tested models are provided in Table S1 of the Supporting Information.

3. Results and Discussion

Given the divergence in the theoretical and mathematical foundations of PW basis set-based DFT and atom-centered basis set DFT—which uses GTOs—these can be considered somewhat different levels of theory. This distinction means that the absolute electronic energies for the molecular crystals computed using PW PBE-D3BJ cannot be directly compared with those predicted by the ML model trained on PBE-D3BJ/def2-TZVP data. Yet, it is possible to make qualitative, and, to some extent, quantitative comparisons between the lattice energies of the crystal structures derived from these two approaches. These lattice energies, indicative of the strength of intermolecular and intramolecular interactions within the crystal structures, allow for such comparisons due to the cancellation of systematic differences in their calculation. Therefore, we adopted the correlation between the ML-predicted and the PW DFT-derived lattice energies of the crystal structures as one of the metrics for evaluating the performance of the ML model on the crystal structure data set. The molecular crystal structure data for benzene-1,2,4,5-tetrayltetramethanamine was generated adhering to the protocol delineated in Section 2.3 and consists of 641 structures, inclusive of the isolated molecule (or monomer) necessary for lattice energy computation using eq 1. The lattice energies of these structures, spanning a broad range, reflect diverse molecular orientations and configurations, affirming the structural diversity of the crystal structure data set (see Figure 2). Furthermore, the crystal energy landscape showcases a wide spectrum of densities, highlighting the comprehensiveness of the data set.

Figure 2.

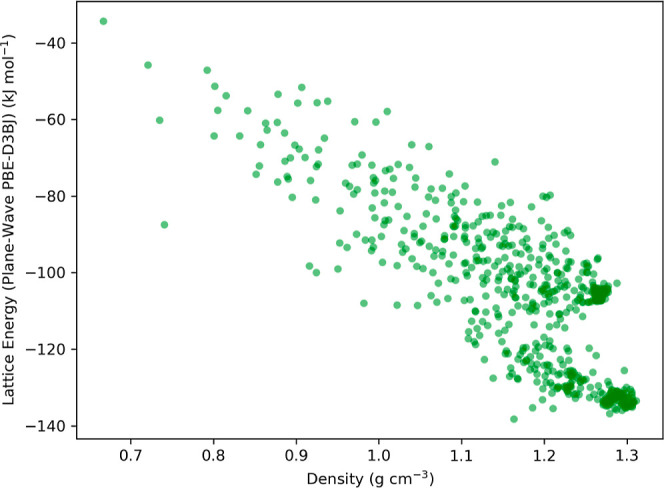
Crystal energy landscape of molecular crystal structures for benzene-1,2,4,5-tetrayltetramethanamine curated using the USPEX protocol, as detailed in Section 2.2, forming a diverse data set. The displayed lattice energies of the crystal structures were calculated employing the PW PBE-D3BJ functional.

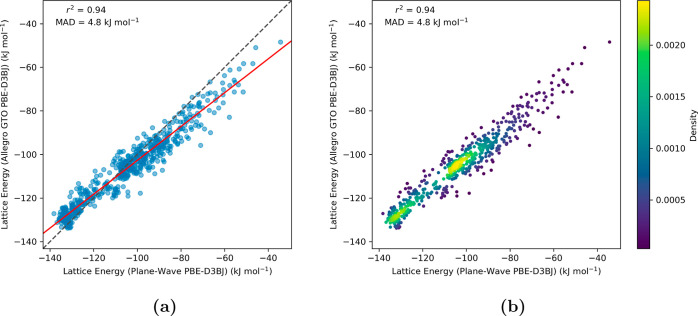
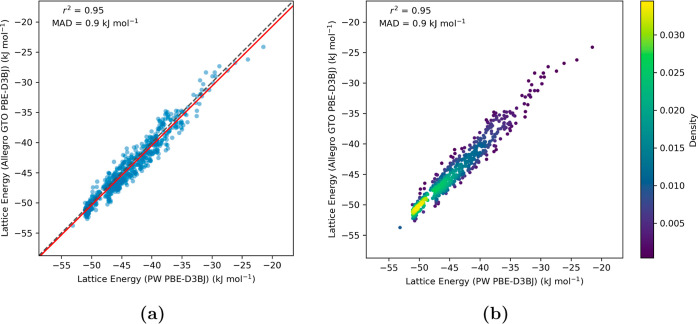
We utilized the Allegro models, which were trained on molecular cluster data, to predict single point absolute energies of periodic molecular crystal structures. This approach leverages Allegro’s atom-centric architecture, enabling compatibility with both periodic and nonperiodic structures. Allegro computes molecular energies by summing per-atom contributions, each decomposed into pairwise interactions with neighboring atoms within a specified cutoff radius, thus effectively capturing the local chemical environment. Subsequently, these predicted energies were employed to compute the corresponding lattice energies via eq 1. A graphical comparison of the lattice energies computed with the PW approach and those predicted by the Allegro model [with a radial cutoff (r_cutoff) of 6.0 Å] is displayed in the parity plots of Figure 3. Upon evaluating the performance of the Allegro model, we found substantial agreement between the PW computed and Allegro predicted lattice energies. We quantified the model’s accuracy by computing the square of Pearson correlation coefficient (r²), 0.94. Additionally, a mean absolute deviation (MAD) of 4.8 kJ mol^–1 further underscore the reliable predictive performance of the Allegro model in comparison to the PW approach.

Figure 3.

Parity plots evaluating the Allegro model’s accuracy (r_cutoff = 6.0 Å) in estimating the lattice energies of molecular crystal structures for benzene-1,2,4,5-tetrayltetramethanamine. The y-axis, labeled “Lattice Energy (Allegro GTO PBE-D3BJ)”, represents lattice energies calculated from crystal structures’ absolute energies as predicted by the Allegro model, which was trained using GTO PBE-D3BJ molecular cluster data. The x-axis, labeled “Lattice Energy (Plane-Wave PBE-D3BJ)”, corresponds to values derived using the periodic PBE-D3BJ functional. Subfigure (a) illustrates the correlation between PW DFT and Allegro computed lattice energies, highlighted by the best-fit line in red. Subfigure (b) shows the density distribution of the data points, with a notable concentration near the identity line, indicating close agreement for the majority of data points.

3.1. Lattice Energy Predictions through Δ-ML

Owing to its design, the Allegro model features an inherently local structure, preventing the explicit incorporation of long-range energy terms or interactions during its construction. This design feature enables Allegro to distinguish between short- and long-range energy terms, an advantage that nonetheless may limit its predictive accuracy in cases where system properties are significantly influenced by long-range interactions. Specifically, neglecting these interactions could notably skew the quantitative assessment of lattice energies within molecular crystal structures. A consideration of the optimal ways to include these interactions within the framework of local models like Allegro is, therefore, crucial.

To remedy this, we implemented a Δ-machine learning (Δ-ML) scheme to account for the long-range interactions in the molecular solid. In this scheme, the long-range interactions are approximated by calculating the energy of the molecular crystal structure at a more cost-effective baseline level of theory. The Δ-ML strategy is primarily aimed at learning the energy difference between a high-cost target level of theory and a lower-cost baseline level. This approach capitalizes on the systematic nature of the error between the two theoretical methods. Hence, with the energy determined at the baseline theory, the energy at the high-cost level can be derived by adding an ML-learned correction term. In this study, the baseline level of theory is represented by the semiempirical GFN2-xTB method and the high-cost target level of theory is chosen as a DFT method. In terms of computational efficiency, while a typical GGA periodic DFT method demands approximately 3000 CPU-minutes, the GFN2-xTB approach requires only around 0.1 CPU-minutes for a single energy (and force) computation for a tetraamine crystal structure. This difference starkly highlights the advantage of utilizing GFN2-xTB within the Δ-ML scheme, especially when considering computational resource allocation and time. Specifically, within the Δ-ML framework, the energy (E_ΔML-DFT) of a molecular crystal structure at a high level of theory (DFT in this case) can be computed as follows

2

where

3

Here, E_PBC-GFN2-xTB is the energy of the molecular crystal structure computed using periodic GFN2-xTB in DFTB+, following the settings outlined in Section 2.2 to account for long-range interactions. The term Δ_ML signifies the “delta” energy of the crystal structure as predicted by a ML model trained on the energy differences between canonical GFN2-xTB and the target level GTO-based DFT method for a molecular cluster data set. In the context of the present study, the same monomer and dimer data set was used to train the Allegro model, with the aim of learning the energy differences between GTO PBE-D3BJ and GFN2-xTB. While the Δ-ML scheme shown employs DFT method for the sake of consistency, any GTO-based method, such as MP2, CCSD(T), etc., could be utilized in principle. This trained ML model can then be deployed to make energy predictions on the data set comprised of molecular crystal structures to obtain the Δ_ML energy term in eq 2. With the long-range corrected absolute energies derived from eq 2, the corresponding lattice energy of the crystal structure can be computed using eq 1.

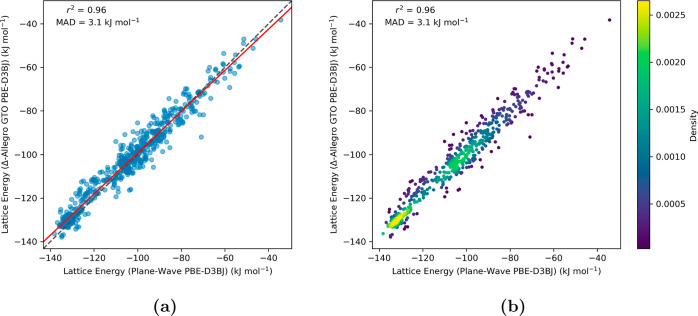
The lattice energies for benzene-1,2,4,5-tetrayltetramethanamine crystal structures were computed employing the same Allegro architecture to quantify the improvements gained through the Δ-ML scheme. For r_cutoff = 6.0 Å Allegro model (Figure 4), the inclusion of long-range corrections via the Δ-ML approach enhanced both performance metrics, most notably reducing the MAD to a mere 3.1 kJ mol^–1 while simultaneously boosting the correlation coefficient r² to 0.96. Moreover, the best-fit line, closely parallel to the identity line, now demonstrates a robust alignment with the ground truth.

Figure 4.

Parity plots assessing the Δ-ML (or Δ-Allegro) model’s performance (r_cutoff = 6.0 Å) in predicting the lattice energies of molecular crystal structures for benzene-1,2,4,5-tetrayltetramethanamine. The y-axis, labeled “Lattice Energy (Δ-Allegro GTO PBE-D3BJ)”, displays lattice energies derived from the absolute energies of crystal structures as computed by the Δ-ML method, utilizing eq 2. For this model, training involved the use of energy differences between the GTO PBE-D3BJ and GFN2-xTB methods on molecular cluster data. On the x-axis, “Lattice Energy (Plane-Wave PBE-D3BJ)” represents lattice energies obtained using the periodic PBE-D3BJ functional. Subfigure (a) portrays the relationship between the lattice energies computed by PW DFT and those estimated by the Δ-Allegro scheme, with a best-fit line in red closely aligning with the identity line (r² = 0.96). Subfigure (b) depicts the data points’ density distribution, demonstrating that the majority are clustered near the identity line, indicating strong agreement between the two methods.

3.2. Lattice Energy Predictions at Higher Levels of Theory

In earlier discussions, we emphasized the use of molecular clusters computed using GTO methods for training our Allegro-based ML models. Building upon this foundation, we now integrate more sophisticated theoretical methods as the training target for the ML model. This subsection outlines the training of Allegro architectures using the monomer and dimer molecular cluster data set, as introduced in Section 2.1, but recalculated with more advanced theoretical methods, specifically B3LYP-D4 and DLPNO-MP2, employing the triple-ζ basis set def2-TZVP. The hybrid DFT functional B3LYP, enhanced with Grimme’s D4⁷⁰ dispersion model, was selected for its enhanced accuracy in electronic structure calculations, especially for noncovalent interactions, which are crucial for the accurate representation of molecular systems. DLPNO-MP2, recognized for balancing accuracy with computational efficiency, is particularly adept at capturing hydrogen bond interactions and long-range dispersion forces, which are sometimes inadequately addressed by density functionals lacking nonlocal orbital contributions. Consequently, our ML framework benefits from the flexibility to select learning targets across a spectrum of accuracy levels, enabling tailored approaches to specific interaction types.

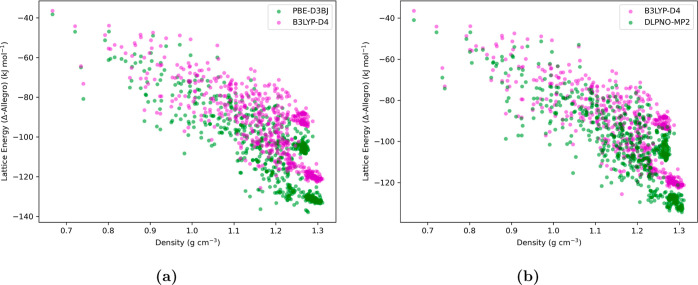
Employing the Δ-Allegro model with the radial cutoff, r_cutoff = 6.0 Å, previously established as one of our most effective models (see Section 3.1), we generated lattice energy predictions for molecular crystal structures at B3LYP-D4 level of theory. These predictions exhibited a high degree of correlation (r² = 0.98) with those derived from the PBE-D3BJ functional using the same Allegro model (Figure S1 in the Supporting Information). This reflects a consistent energy ranking of the crystal structures by both DFT functionals. Additionally, Figure 5a presents the crystal energy landscape, illustrating the lattice energy predictions for the test set of crystal structures at both B3LYP-D4 and PBE-D3BJ levels of theory. Importantly, the lattice energies computed using B3LYP were characteristically lower in magnitude, aligning with the literature that reports B3LYP’s tendency to underestimate hydrogen bond strengths compared to the PBE functional; however, B3LYP offers more accurate estimations of relative hydrogen bond energies.⁹⁹ In addition, we also present lattice energy predictions using the same Δ-Allegro model, but applying DLPNO-MP2 theory, in Figure 5b. The results show a slight overestimation of lattice energies relative to those obtained with the B3LYP-D4 functional. This outcome aligns with documented behavior of the MP2 method for molecular systems, which is known to accurately predict hydrogen bonding interactions but tends to overestimate other long-range noncovalent interactions, particularly π-stacking energies.^100,101 Thus, the Allegro model adeptly mirrored the characteristic energy profile of the B3LYP and DLPNO-MP2 methods, affirming its capability to capture and reproduce the intrinsic theoretical properties of advanced electronic structure methods. This divergence in predicted lattice energies highlights the critical need for careful selection of reference methods in the training of ML models, to ensure fidelity in the replication of nuanced quantum mechanical effects.

Figure 5.

Crystal energy landscape of molecular crystal structures for benzene-1,2,4,5-tetrayltetramethanamine, as predicted by the Δ-ML (or Δ-Allegro model) with a cutoff radius of r_cutoff = 6.0 Å. The y-axis, labeled “Lattice Energy (Δ-Allegro)”, represents lattice energies derived from the absolute energies of crystal structures as predicted by the Δ-ML scheme, employing eq 2. The Allegro model’s training utilized energy and force differences between a GTO and the GFN2-xTB methods on the molecular cluster data set. (a) The Δ-ML predictions are shown for PBE-D3BJ (green dots) and B3LYP-D4 (magenta dots) functionals as the target levels of theory. The observed minor divergence between the predicted lattice energies with Δ-Allegro PBE-D3BJ and Δ-Allegro B3LYP-D4 models are consistent with the literature, which notes a slight overestimation of hydrogen bond energies by the PBE functional in comparison to B3LYP, which has been reported to provide a more accurate estimation of relative energies between molecular crystal structures. (b) The Δ-ML predictions are shown for DLPNO-MP2 (green dots) method and B3LYP-D4 (magenta dots) functional as the target levels of theory. The minor divergence observed in the lattice energy predictions between Δ-Allegro DLPNO-MP2 and Δ-Allegro B3LYP-D4 models aligns with literature findings, which attribute a slight overestimation of lattice energies by the MP2 method, particularly for π–π interactions.

3.3. Enhancing CSP with Allegro Model Integration in USPEX

In our pursuit to advance the application of ML in CSP, we have deployed trained Allegro models for energy evaluations directly into the USPEX workflow. Specifically, Allegro’s inference engine, while not directly applicable for energy and force computations within USPEX, is designed to be conducive to integration with LAMMPS.¹⁰² This integration not only enables the seamless incorporation of Allegro into the USPEX framework but also leverages LAMMPS’ capabilities for molecular dynamics simulations, and structure minimizations, consequently enhancing the speed and accuracy of crystal structure predictions and facilitating advanced computational operations within USPEX. Consistent with the protocol delineated in Section 2.2 for crystal structure generation and prediction, a tertiary computational phase has been introduced to the energy evaluation process. Following structural relaxation via xTB methods, the Allegro model—specifically, the Δ-Allegro model trained on B3LYP-D4 molecular cluster data—calculates the crystal’s energy. Utilizing eqs 1 and 2, Allegro predicted absolute energy is converted into lattice energy, which then informs the EA within USPEX to optimize the search for low-energy crystal structures. Further insights drawn from the crystal energy landscape presented in Figure 2 revealed a propensity for the tetraamine to stabilize in configurations with lower energies at higher densities. Prompted by this observation, we embarked on a strategy to discover even lower energy structures. We opted for a more compact conformation of the tetraamine, illustrated in Figure S2 of the Supporting Information, as the initial geometry for USPEX-driven crystal structure predictions. This strategic choice is predicated on the hypothesis that a constricted molecular conformation could foster more efficient stacking of the rings. Such an arrangement is likely to reinforce π–π interactions, potentially giving rise to crystal structures with both higher symmetry and density, thereby navigating us toward the energy minima with greater precision. Notably, the identified lowest-energy crystal structure closely matched the target reference structure, with a root-mean-square deviation (rmsd₁₅) of only 0.11 Å.

In the resultant crystal energy landscape, depicted in Figure 6, we observe a nearly linear relationship between the predicted lattice energies by Allegro and the crystal density in regions of higher density. This trend resonates with the physical principles governing these structures: as density escalates, unit cell volume diminishes, leading to increased molecular symmetry and packing efficiency. Consequently, this denotes heightened intermolecular noncovalent interactions and, therefore, increased lattice energy. Moreover, at lower unit cell volume, the crystal’s potential to adopt a variety of configurations is markedly limited due to reduced spatial degrees of freedom, which is reflected in the sparse distribution of crystal structures in the areas of the plot characterized by very high crystal density.

Figure 6.

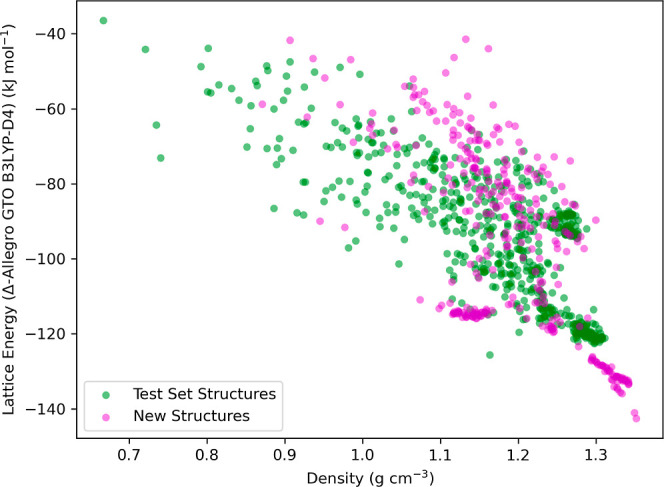
Crystal energy landscape of molecular crystal structures for benzene-1,2,4,5-tetrayltetramethanamine, including those obtained using the Allegro-enhanced USPEX protocol with the B3LYP-D4 functional as the target level of theory. Crystal structures, discussed in Section 2.2, are marked with green dots, while magenta dots represent newly generated crystal structures, which were derived using the conformation from Figure S2 as the starting point within the USPEX-based CSP framework. The y-axis, labeled “Lattice Energy (Δ-Allegro GTO B3LYP-D4)”, represents lattice energies derived from the absolute energies of crystal structures as predicted by the Δ-ML method, employing eq 2. The Allegro model’s training utilized energy and force differences between the GTO B3LYP-D4 and GFN2-xTB methods on molecular cluster data.

3.4. Lattice Energy Predictions of 3-Oxabicyclo[3.2.0]hepta-1,4-diene and Hydantoin Crystal Structures

In curating the training data set for 3-oxabicyclo[3.2.0]hepta-1,4-diene and hydantoin clusters, we adhered to the protocol outlined in Section 2.1, with adaptations to accommodate the conformationally rigid nature of these molecules. These data set sizes are comparable to those utilized in constructing the autoPES potentials for these molecules, demonstrating the data efficiency of the equivariant neural network approach.⁴⁴ Following the methodology described in Section 2.2, we then generated crystal structures, with four and eight molecules per unit cell for 3-oxabicyclo[3.2.0]hepta-1,4-diene and hydantoin, respectively.

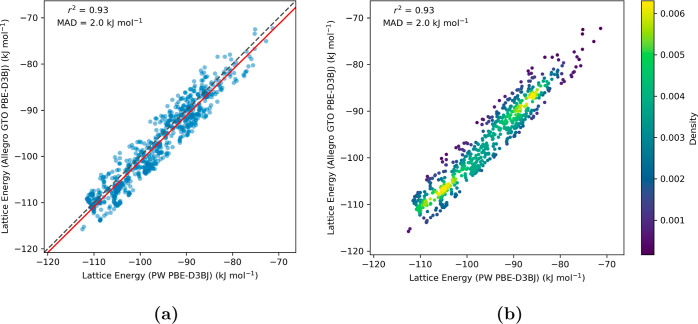
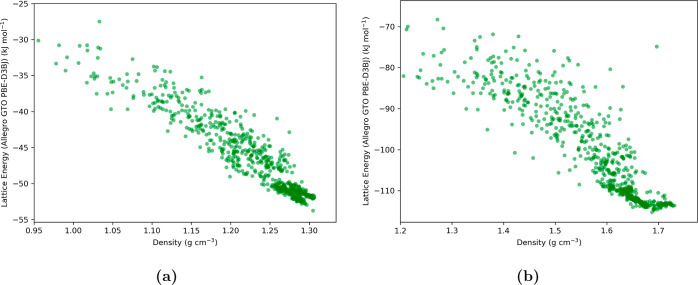
For the 3-oxabicyclo[3.2.0]hepta-1,4-diene clusters, we opted for a more compact Allegro model architecture, incorporating two layers, to align with the data set’s comparatively smaller size. This model effectively predicted the crystal structure lattice energies, achieving a low error margin of just 0.9 kJ mol^–1 alongside a robust correlation coefficient (r²) of 0.95 (Figure 7). Given the smaller magnitude and range of lattice energies observed for this molecule, relative to the tetramine, maintaining a minimal MAD is crucial for accurately differentiating between different crystal structures. For hydantoin, a deeper architecture consisting of four layers was utilized to adequately learn the wider variety of hydrogen bonding interactions between the molecules. The lattice energy predictions from the ML model demonstrated a high correlation (r² = 0.93) with an MAD of approximately 2 kJ mol^–1 with respect to the PW DFT method (Figure 8).

Figure 7.

Parity plots evaluating the Allegro model’s accuracy (r_cutoff = 6.0 Å) in estimating the lattice energies of molecular crystal structures of 3-oxabicyclo(3.2.0)hepta-1,4-diene. The y-axis, labeled “Lattice Energy (Allegro GTO PBE-D3BJ)”, represents lattice energies calculated from crystal structures’ absolute energies as predicted by the Allegro model, which was trained using GTO PBE-D3BJ molecular cluster data. The x-axis, labeled “Lattice Energy (PW PBE-D3BJ)”, corresponds to values derived using the periodic PBE-D3BJ functional. Subfigure (a) illustrates the correlation between PW DFT and Allegro computed lattice energies, highlighted by the best-fit line in red. Subfigure (b) shows the density distribution of the data points, with a notable concentration near the identity line, indicating close agreement for the majority of data points.

Figure 8.

Parity plots evaluating the Allegro model’s accuracy (r_cutoff = 6.0 Å) in estimating the lattice energies of molecular crystal structures of hydantoin. The y-axis, labeled “Lattice Energy (Allegro GTO PBE-D3BJ)”, represents lattice energies calculated from crystal structures’ absolute energies as predicted by the Allegro model, which was trained using GTO PBE-D3BJ molecular cluster data. The x-axis, labeled “Lattice Energy (PW PBE-D3BJ)”, corresponds to values derived using the periodic PBE-D3BJ functional. Subfigure (a) illustrates the correlation between PW DFT and Allegro computed lattice energies, highlighted by the best-fit line in red. Subfigure (b) shows the density distribution of the data points, with a notable concentration near the identity line, indicating close agreement for the majority of data points.

We seamlessly integrated the trained ML models with USPEX to enhance our ability to efficiently search for low-energy crystal structures, as detailed in Section 3.3. This integration resulted in a denser population of crystal structures in regions of low energy and high crystal density (Figure 9), with some structures approaching the experimental structures within 1 kJ mol^–1, even using modest USPEX search criteria (Section 2.2). Employing more stringent search parameters (50 generations), although computationally demanding, explored a broader range of low-energy regions within the crystal structure landscape. For hydantoin, the lowest-energy structure obtained exhibited an rmsd₁₅ of 0.52 Å compared to the experimental structure (Figure 10), as calculated using the Crystal Packing Similarity module in Mercury software. This result demonstrates the effectiveness of our protocol in correctly predicting the experimental crystal structure. In the case of 3-oxabicyclo[3.2.0]hepta-1,4-diene, an extended USPEX search did not initially yield a polymorph resembling the experimental structure. However, when we provided the experimental structure as a starting point to the USPEX search algorithm, it was confirmed as the lowest-energy structure (−53.04 kJ mol^–1) within the search space. This validation underscores the ML model’s ability to correctly rank the relative energies of the discovered polymorphs, including the experimental crystal structure. Given the inherent stochasticity of the USPEX EA, further fine-tuning of search parameters may be necessary for efficient identification of the experimental crystal structure for 3-oxabicyclo[3.2.0]hepta-1,4-diene. Nevertheless, our Allegro ML models, being independent of the specific search algorithm or package, can be readily integrated with more advanced software for crystal structure exploration.

Figure 9.

Crystal energy landscape of molecular crystal structures for (a) 3-oxabicyclo(3.2.0)hepta-1,4-diene, and (b) hydantoin, obtained using the Allegro-enhanced USPEX protocol with the PBE-D3BJ functional as the target level of theory. The y-axis, labeled “Lattice Energy (Allegro GTO PBE-D3BJ)”, represents lattice energies derived from the absolute energies of crystal structures as predicted by the ML model, employing eq 1. The Allegro model’s training utilized energies and forces from the GTO PBE-D3BJ method on molecular cluster data.

Figure 10.

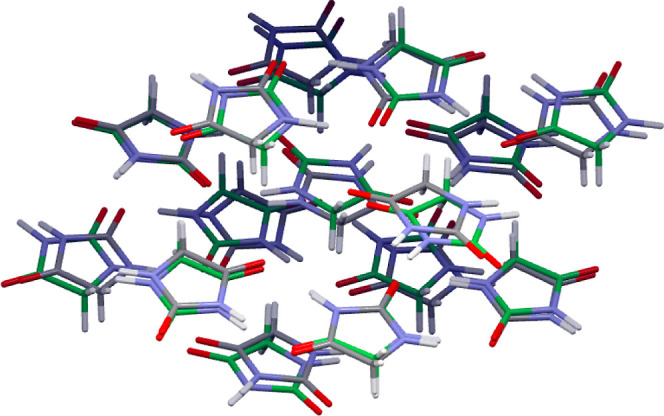
Overlay of the experimental (element-specific colors) and lowest-energy predicted (green) crystal structures for hydantoin. The predicted structure, obtained using the Allegro model integrated with the USPEX crystal structure search algorithm, exhibits an RMSD₁₅ of 0.52 Å relative to the experimental structure.

4. Conclusions

In this study, we demonstrated the applicability of an equivariant neural network, Allegro, for predicting lattice energies of molecular crystal structures—a novel endeavor considering the model’s development without any a priori knowledge of the crystal structures. The efficacy of Allegro was not only showcased in bridging PW and GTO-based DFT methods with ML but was also extended to higher levels of theory, particularly B3LYP-D4 and DLPNO-MP2, for lattice energy predictions. This marked a significant stride in enhancing the model’s predictive accuracy, bringing it closer to the sophistication required for real-world applications. Through rigorous training on a carefully curated data set of molecular clusters, calculated using GTO-based methods, we accurately predicted the lattice energies of crystal structures, involving the complex interplay of inter- and intramolecular interactions. The significant correlation achieved between our model predictions and plane-wave DFT lattice energies affirm the robustness of our approach. Furthermore, our use of the Δ-ML scheme to capture long-range interactions led to a notable enhancement in predictive accuracy, aligning closely with the lattice energy trends observed between GTO and PW methods.

Our efforts resulted in the successful integration of the Allegro model within the USPEX framework, advancing the use of ML in CSP. By integrating Allegro with LAMMPS, we leveraged the model’s predictive power to rapidly and accurately calculate energies, thereby guiding the search for low-energy crystal structures with improved efficiency and precision. This approach ultimately facilitated convergence toward the experimentally determined crystal structure. We also show that although our proposed methodology was demonstrated using DFT methods, our ML protocol is readily adaptable to Post-Hartree–Fock methods as the target level of theory, which promises greater predictive precision and reliability. Looking ahead, our work sets the stage for developing a sophisticated protocol based on equivariant neural networks to facilitate relaxations of molecular crystal structures during CSP, reducing our reliance on comparatively rudimentary methods like force fields and semiempirical approaches. Furthermore, we aim to evolve our approach by creating neural networks capable of predicting higher-order energy derivatives, which will enable us to calculate lattice free energies, offering a more reliable metric for energy rankings of crystal structures and enriching our understanding of their stability under realistic conditions. Additionally, with the advent of chemical foundation models, we anticipate achieving heightened accuracy for CSP tasks while requiring minimal training data for fine-tuning these models.¹⁰³ Such an integrated approach paves the way for transformative changes in how computational chemists and materials scientists approach the design and discovery of novel crystalline materials.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c07434.

• Parity plot comparing the lattice energy predictions from Δ-ML using PBE-D3BJ and B3LYP-D4 methods. Illustration of a more compact conformation of the tetraamine molecule. Table detailing the training and validation errors for the Allegro models tested (PDF)

Author Present Address

^⊥ University of California Irvine, Irvine, CA 92697

The authors declare no competing financial interest.