Cross-wavelength calibrating method for real-time imaging of tissue optical properties using frequency-domain diffuse optical spectroscopy

Abstract

Frequency-domain diffuse optical spectroscopy (FD-DOS) is a powerful non-invasive technique for assessing tissue optical properties, with applications ranging from basic research to clinical diagnosis. In this study, we introduce and validate a novel approach termed the cross-wavelength calibrating (CWC) method within the framework of TrackDOSI, a real-time FD-DOS imaging system for tissue characterization. The CWC method aims to mitigate the effects of changing optical coupling and motion artifacts encountered during probe scanning, thus enhancing the accuracy and reliability of optical property measurements. Notably, the CWC method also allows for a simpler geometry with fewer sources than traditional self-calibrating (SC) methods, reducing instrumental complexity and cost while maintaining robustness in estimating optical properties. We first validate the CWC method on solid silicone phantoms, demonstrating strong agreement with the gold standard SC method with an error of -10% and 1% for absorption and reduced scattering coefficients, respectively. Furthermore, experiments on phantom and human tissue reveal the CWC approach's ability to suppress motion artifacts and optical coupling variations, thereby improving measurement repeatability, signal fidelity, and artifact correction in dynamic imaging scenarios. Our findings underscore the potential of the CWC method to enhance the clinical utility of DOSI techniques by enabling real-time artifact correction and improving the accuracy of tissue optical property measurements.

1. Introduction

Frequency-domain diffuse optical spectroscopy (FD-DOS), also called as frequency-domain near infrared spectroscopy (FD-NIRS), is a noninvasive optical method for monitoring regional tissue chromophore concentrations, including oxy-hemoglobin, deoxy-hemoglobin, water, lipid, as well as optical scattering properties within tissue up to a few centimeters below the surface [1–5]. Employing light sources modulated at frequencies of the order of 100 MHz, FD-DOS enables separate quantification of absolute tissue optical properties, namely absorption coefficient (µ_a) and reduced scattering coefficient (µ_s′) [6]. By conducting FD-DOS measurements across multiple light source wavelengths, typically within the range of ∼600-1000 nm, tissue chromophore concentrations can be determined [7–9] along with insights into tissue cell morphology [10]. Over the span of several decades, FD-DOS has found widespread applications in clinical settings [7,11–14]. Our group has recently engineered a novel diffuse optical spectroscopy imaging (DOSI) instrument, expanding the imaging capabilities of FD-DOS [15]. This advancement enables the real-time generation of two-dimensional images depicting local tissue chromophore concentrations and optical scattering properties while the optical probe scans across the tissue surface. Referred to as Track-DOSI, this technology incorporates automatic probe tracking capabilities, thereby enabling real-time optical data visualization. Track-DOSI minimizes the time and effort typically associated with manual DOSI scans. Moreover, the potential for real-time feedback during data acquisition enhances usability by enabling users to retake measurements as needed. Although promising, further advancements are necessary to enhance the practicality of Track-DOSI for clinical applications, particularly in addressing challenges such as motion artifacts and variations in optical coupling encountered during probe scanning over tissue surfaces.

At a given modulation frequency, optical signals acquired via FD-DOS or Track-DOSI consist of amplitude intensity (I) and phase (ϕ) components, represented as complex reflectance $(\tilde{R}=I{e}^{i\varphi })$ [6]. Decoupling µ_a and µ_s′ is typically achieved using a single-distance (SD) method, which involves measuring $\tilde{R}$ at a specific source-detector distance (ρ) [11,16–18]. However, this method often requires initial calibration using an optical phantom with known optical properties, under the assumption that the optical coupling factors on the phantom remain consistent during data acquisition on tissue samples. This dependence on off-phantom calibration introduces practical limitations and may lead to errors in absolute optical property extraction, particularly noteworthy in Track-DOSI where the calibration factors are more prone to variation as the probe is maneuvered and scanned across the tissue surface. To solve these calibration-related issues, a so-called self-calibrating (SC) method was introduced in the 1990s [19]. This method utilizes symmetrical sets of light sources and detectors to mitigate motion artifacts, optical coupling, and instrumental factors. For each wavelength utilized, the SC approach requires two laser sources at the same wavelength symmetrically positioned about the midline of two detectors. Consequently, for n wavelengths, the method requires 2n laser sources, imposing expense burdens and instrumental complexity and thereby limiting the number of wavelengths used as well as the practicability of the SC method.

In this paper, a novel method termed cross-wavelength calibrating (CWC) approach is introduced. This method leverages self-calibrated optical signal at one wavelength to extend calibration across other wavelengths. This CWC approach is based on the notion that the emitted and detected light from tissue sample at different wavelengths are delivered and collected using the same source and detector system, thus minimizing wavelength-dependent variations in instrumental and optical coupling factors during data acquisition. For n wavelengths, the proposed CWC approach requires only $n+1$ laser sources (comprising 2 laser sources at the same wavelength positioned at two separate locations for the SC approach and $n-1$ laser sources at the same location), representing a reduction of $n-1$ laser sources compared to the SC approach. At the same time, the CWC approach retains the advantages of the SC method, demonstrating reduced sensitivity to changes in instrumental and optical coupling factors compared to the SD method.

This study presents the introduction of the CWC approach and explores its potential applications within Track-DOSI to mitigate the impacts of fluctuating optical coupling and motion artifacts during probe scanning. Subsequent sections detail the development and validation of the novel CWC method through measurements of absolute absorption and reduced scattering properties in highly scattering media (i.e., optical phantoms). Additionally, this method is characterized to showcase its improved repeatability in estimated optical properties as well as resilience to alterations in optical probe pressures and optical coupling changes during the process of probe scanning during TrackDOSI data acquisition.

2. Methods

2.1. Theory

A simplified schematic of a linear geometry employed in the CWC approach is shown in Fig. 1, showcasing a configuration with three laser sources and two wavelengths (λ and λ’). Within this setup, two laser sources emitting at wavelengths λ and λ’ are positioned at source 1. This arrangement features two source locations and two detectors, symmetrically placed about the midline between the two sources, featuring two pairs of short and long source-detector distances (ρ_S and ρ_L, respectively).

Fig. 1.

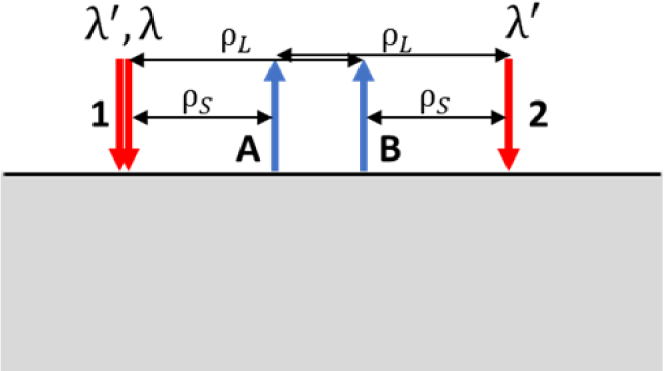
A simplified example of a linear source-detector arrangement for the CWC approach with two source locations (1 and 2) and two detectors (A and B). Source 1 includes two co-localized laser sources at two wavelengths λ’ and λ; source 2 includes one laser at wavelength λ’. The probe geometry features two sets of source-detector distances ρ_S and ρ_L.

In the depicted configuration, considering source 1 and detector B for source-detector distance ρ_L, the measured complex reflectance quantity ${\tilde{R}}_{1B}$ can be expressed as:

$${\tilde{R}}_{1B}={\tilde{C}}_{1B}\tilde{R}({\rho }_L).$$ (1)

Here, ${\tilde{C}}_{1B}={\tilde{C}}_1{\tilde{C}}_B$ where ${\tilde{C}}_1$ and ${\tilde{C}}_B$ are complex factors accounting for optical couplings originating from random or systematic temporal fluctuations, drifts in source 1 or detector B characteristics, displacement of the optical probe, etc., and $\tilde{R}({\rho }_L)$ denotes the theoretical complex reflectance value that would be measured at source-detector distance ρ_L in the absence of noise or experimental confounds [19,20]. Our goal is to compute $\tilde{R}({\rho }_L)$ from ${\tilde{R}}_{1B}$ measurements to extract optical properties µ_a and µ_s′ at all wavelengths. In this study, we employed a Monte Carlo look-up table (MC-LUT) method as an inverse model to extract optical properties, as detailed in Section 2.4.

The single-distance (SD) approach involves measuring the calibration factor ${\tilde{C}}_{1B}$ from an optical phantom with known optical properties and assumes that ${\tilde{C}}_{1B}$ remains constant when moving the probe onto the tissue surface [16]. While this assumption may not hold true due to varying optical probe pressure or contact on the tissue surface causing changing in ${\tilde{C}}_{1B}$ , we anticipate the wavelength-dependent variations in ${\tilde{C}}_{1B}$ to remain consistent. That is, the ratio ${\tilde{C}}_{1B}^{{\lambda }^{\mathrm{\prime }}}/{\tilde{C}}_{1B}^{\lambda }$ between wavelengths λ’ vs λ is expected to remain unchanged regardless of measurement schemes and can also be obtained from measurements on an optical phantom with known optical properties (calibration phantom). In other words, ${\tilde{C}}_{1B}^{{\lambda }^{\mathrm{\prime }}}/{\tilde{C}}_{1B}^{\lambda }={\tilde{C}}_{1B,p}^{{\lambda }^{\mathrm{\prime }}}/{\tilde{C}}_{1B,p}^{\lambda }$ where ${\tilde{C}}_{1B,p}^{{\lambda }^{\mathrm{\prime }}}/{\tilde{C}}_{1B,p}^{\lambda }$ values are measured on the calibration phantom p. This is because the emitted and detected light at all wavelengths are delivered and measured using the same delivery and collection system. The main idea of our proposed CWC approach is to compute ${\tilde{C}}_{1B}^{\lambda }$ at any wavelength λ based on the known ${\tilde{C}}_{1B}^{{\lambda }^{\mathrm{\prime }}}/{\tilde{C}}_{1B}^{\lambda }$ ratio and ${\tilde{C}}_{1B}^{{\lambda }^{\mathrm{\prime }}}$ at wavelength λ’ obtained from SC approach (as explained in the next paragraph). The overall data processing pipeline of the CWC approach is summarized in Fig. 2. By continuously measuring ${\tilde{C}}_{1B}^{{\lambda }^{\mathrm{\prime }}}$ and ${\tilde{C}}_{1B}^{\lambda }$ during data collection with our CWC approach, we aim to capture any variations in the confounding effects arising from changes in optical couplings, instrumental drifts, probe pressure on tissue surface, etc., in real time. Our hypothesis is that the CWC approach will yield more accurate measurements of optical properties that are less susceptible to changes in optical coupling compared to traditional off-phantom calibration with SD approach.

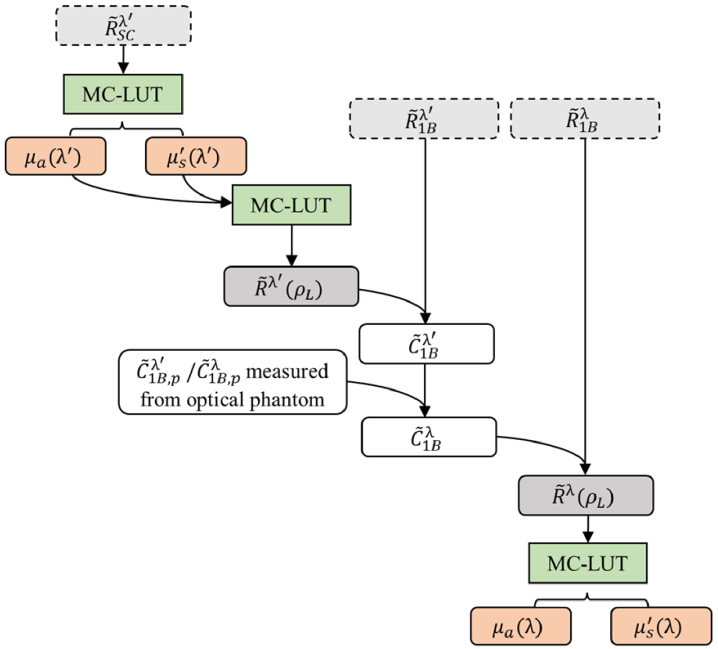
Fig. 2.

Flowchart depicting the data processing steps for the CWC approach. Light gray boxes with dashed lines indicate direct measurement quantities at wavelengths λ’ and λ, including self-calibrated complex reflectance ${\tilde{R}}_{SC}$ , complex reflectance measured at source 1-detector B ${\tilde{R}}_{1B}$ . Dark gray boxes indicate theoretical complex reflectance values $\tilde{R}$ for long source-detector distance ρ_L, $\tilde{R}({\rho }_L)$ . White boxes indicate calibration factors ${\tilde{C}}_{1B}$ . Subscript “p” indicates values measured from a calibration phantom with known optical properties. Green boxes indicate Monte Carlo look-up table (MC-LUT) method as an inverse or forward model. Red boxes indicate absorption and scattering optical properties (µ_a and µ_s′, respectively) extracted from theoretical $\tilde{R}$ using MC-LUT.

By combining the measurements from two sources (1, 2) and two detectors (A, B) at wavelength λ’, the SC measurement ${\tilde{R}}_{SC}$ should theoretically be immune to coupling effects from sources and detectors [19]. That is expressed as:

$${\tilde{R}}_{SC}=\sqrt{\frac{{\tilde{R}}_{1B}{\tilde{R}}_{2A}}{{\tilde{R}}_{1A}{\tilde{R}}_{2B}}}=\frac{\tilde{R}({\rho }_L)}{\tilde{R}({\rho }_S)}.$$ (2)

Thus, we obtained an ${\tilde{R}}_{SC}$ measurement quantity representing only the ratio between theoretical complex reflectance values at two source-detector distances ρ_S and ρ_L. The optical properties at λ’, µ_a(λ’) and µ_s′(λ’), can be extracted from ${\tilde{R}}_{SC}^{{\lambda }^{\mathrm{\prime }}}$ by using the MC-LUT as an inverse model. Assuming a homogeneous medium, the theoretical complex reflectance value $\tilde{R}({\rho }_L)$ can be computed using the optical properties µ_a(λ’) and µ_s′(λ’) (calculated from ${\tilde{R}}_{SC}^{{\lambda }^{\mathrm{\prime }}}$ ) and MC-LUT as a forward model. Finally, the calibration factor ${\tilde{C}}_{1B}^{{\lambda }^{\mathrm{\prime }}}$ for the CWC approach can be obtained as ${\tilde{C}}_{1B}^{{\lambda }^{\mathrm{\prime }}}={\tilde{R}}_{1B}^{{\lambda }^{\mathrm{\prime }}}/{\tilde{R}}^{{\lambda }^{\mathrm{\prime }}}({\rho }_L)$ , where ${\tilde{R}}_{1B}^{{\lambda }^{\mathrm{\prime }}}$ is the measured complex reflectance value from source 1 and detector B pair.

2.2. TrackDOSI instrument

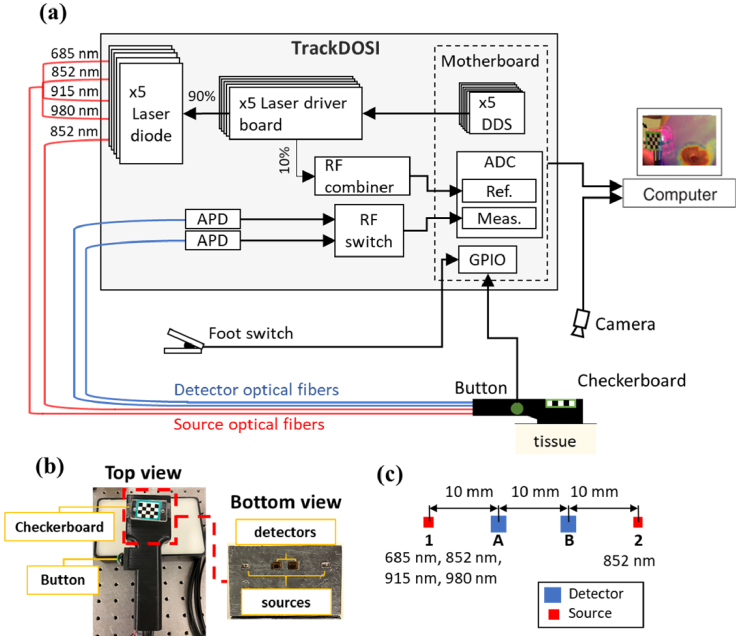
In this study, we employed a custom-built frequency-domain diffuse optical spectroscopy imaging (FD-DOSI) system equipped with real-time probe tracking and data visualization, namely Track-DOSI. The system architecture is summarized in Fig. 3(a) and has been described in detail elsewhere [15,21]. Briefly, this system used six direct digital synthesis (DDS) boards to simultaneously modulate six fiber coupled laser diodes at different modulation frequencies. For this study, we utilized five laser diodes emitting wavelengths at 685 nm, 852 nm (two laser diodes), 915 nm, and 980 nm (FMXL685-025SFOB BlueSky, LP852-SF30 Thorlabs, LP915-SF40 Thorlabs, and FMXL980-025SFOB BlueSky). These lasers were modulated at modulation frequencies of 127 MHz, 137 MHz, 147 MHz, 157 MHz, 177 MHz, respectively. Note that there were two laser diodes at 852 nm wavelength to generate SC measurements for the purpose of the CWC approach. The system includes two detector fiber bundles, each of which was connected to a 3 mm diameter avalanche photodiode (APD) (S8890-30, Hamamatsu Photonics) to convert optical signals into analog voltage. A radio frequency (RF) switch (HRF-SW1030, Honeywell) was used to alternate the signal from each APD to a two channel 250 MHz analog-to-digital converter (ADC) for digital processing. Amplitude and phase computations were performed on a Zynq system-on-chip (SoC) with an integrated field-programmable gate array (FPGA) using the Goertzel Algorithm [11,15]. To achieve real-time high-speed Track-DOSI measurements across unrestricted locations of the tissue surface, we implemented a two-step monocular probe pose estimation technique [22]. This method involved real-time processing of images captured by a monocular camera (FLIR BlackFly BFS-U3-13Y3C-C, 1.3 MP, Teledyne FLIR) focused on the optical probe and tissue surface. A checkerboard pattern outlined with a green border was affixed to the probe surface (Fig. 3(b)) to aid in pose estimation. The optical probe itself was 3D-printed with a handle and a trigger button to facilitate easy data collection. Data acquisition was initiated by pressing and holding the button. A foot switch was used to terminate data collection upon completion of the measurement. Both the foot switch and trigger button signals were monitored via the general-purpose input/output (GPIO) interface. Data collection protocols were programmed in Python, and image processing as well as pose estimation were conducted using the open computer vision (OpenCV) library.

Fig. 3.

(a) Schematic diagram of the track-DOSI system. Real-time probe tracking is facilitated by a camera. Key components include direct digital synthesis DDS boards, avalanche photodiode APD, analog to digital converter ADC, general-purpose input/output GPIO interface. (b) Probe featuring a checkerboard pattern. Inset: Dielectric-coated right-angle prisms terminate two detectors and two source optical fiber bundles, enabling parallel alignment of the optical fibers with the tissue surface. (c) Schematic of the optical probe. The sources are labeled in numbers (1 and 2), and the detectors are labeled in letters (A and B). The probe has: two measurements at 10 mm (1A and 2B) and two measurements at 20 mm (1B and 2A).

For the CWC approach, we utilized an optical probe comprising a linear array of two source optical fibers (1, 2) and two detector fiber bundles (A, B), symmetrically positioned about the midline between the two sources (Fig. 3(c)). At each source location, an eight-in-one source fiber bundle (400 µM core diameter for each source fiber) was used deliver light to the sample. At each detector location, a 2.3 mm fiber bundle was used for light detection. Both the source and detector optical fibers were custom-made (Fiberoptic Systems, Simi Valley, CA) and were terminated with right-angle prisms to ensure a flat probe surface contact with the tissue. The probe configuration featured two source-detector pairs (1A, 2B) at 10 mm distances and two source-detector pairs (1B, 2A) at 20 mm distances. Two laser diodes emitting at 852 nm were employed for SC calculations, with the 137 MHz diode positioned at source 1 and the 147 MHz diode positioned at source 2. A detailed summary of the CWC method processing steps for source 1 and detector B measurements is provided in the Appendix (Table 3).

2.3. Experiments

2.3.1. Validation and characterization of the cross-wavelength self-calibrating (CWC) approach

We first assessed the accuracy of CWC method by conducting a comparative analysis with the gold standard SC method on nine solid tissue-mimicking homogeneous silicone optical phantoms. These phantoms were fabricated with different amounts of nigrosine and titanium dioxide powder to have a physiologically relevant range of absorption and scattering properties [23]. During the experiment, detectors A and B were positioned at fixed locations, 10 mm apart from each other, on the phantom surface. An optical fiber bundle containing four co-localized source fibers emitting at wavelengths of 685 nm, 852 nm, 915 nm, and 980 nm was sequentially placed at the locations of source 1 (10 mm from detector A and 20 mm from detector B) and source 2 (10 mm from detector B and 20 mm from detector A). This arrangement facilitated the acquisition of measurements of ${\tilde{R}}_{1A}$ , ${\tilde{R}}_{1B}$ , ${\tilde{R}}_{2A}$ , and ${\tilde{R}}_{2B}$ at all wavelengths for the SC approach, serving as ground-truth data for the phantom optical properties. Simultaneously, using the CWC approach, we computed the calibrated ${\tilde{R}}_{1B}$ , i.e., theoretical $\tilde{R}$ at source-detector distance 20 mm, at 685 nm, 915 nm, and 980 nm based on SC measurements at 852 nm. Pearson’s correlation coefficient (r) and Lin’s concordance correlation coefficient (CCC) [24] were employed to evaluate the relationship between the CWC and SC methods. Bland-Altman analysis [25] was also conducted. Values were reported with 95% confidence interval (CI).

In a subsequent experiment, we investigated the sensitivity of the CWC approach to variations in optical coupling by manipulating the probe pressure on the surface of an optical phantom. Here, we used a flexible silicone-based phantom to replicate the characteristics of soft tissue surfaces [26,27]. Throughout the experiment, we intermittently applied pressure to the probe surface, inducing deformation of the phantom surface and resulting in alterations in probe contact with the phantom surface. Additionally, we compared the performance of the CWC approach against that of the off-phantom calibration with SD approach to highlight the advantages of the CWC approach in mitigating the effects of changes in optical coupling.

Finally, we tested the variability and repeatability of CWC approach when applied to in vivo human tissue measurements. One subject (female, 30 years old) participated in this study and provided informed consent in accordance with a protocol approved by Boston University’s Institutional Review Board. During this experiment, we held the probe on the subject’s front leg muscle (tibialis anterior) for 5 s, then removed it and repeated the measurements again for five times. The variability of the measured optical properties from these five repeated measurements was evaluated to assess the repeatability of different measurement approaches.

2.3.2. TrackDOSI with CWC approach

As the optical probe traversed the tissue surface, we anticipated fluctuations in optical coupling arising from changes in probe contact and pressure exerted on the tissue. Our hypothesis predicted that the proposed CWC approach could effectively mitigate optical coupling artifacts from the collected optical signals during real-time Track-DOSI data acquisition and visualization. To validate this hypothesis, we conducted Track-DOSI scanning on a homogeneous silicone phantom. We anticipated that the observed variations in optical properties obtained through the CWC approach would be notably reduced compared to those obtained from the SD approach using off-phantom calibration.

2.4. Optical property extraction and visualization

A Monte Carlo based look-up table (MC-LUT) for a homogeneous medium with semi-infinite geometry was built to translate optical properties µ_a and µ_s′ to theoretical complex reflectance data (forward model) and vice versa (inverse model). The construction of MC-LUT was described in detail in our previous work [11]. Briefly, white Monte Carlo (MC) simulations were performed at various µ_s′ values [28]. For each MC simulation, photon paths and corresponding time-of-flight values were recorded to construct different photon time-of-flight distributions at different absorption weights. Subsequently, FD complex reflectance values at different modulation frequencies at different optical property pairs were computed from the photon time-of-flight distributions. In this study, we constructed the LUT from the resulting FD reflectance values for µ_a ranging from 0.0001 mm^-1 to 0.03 mm^-1 with a step of 0.0001 mm^-1 and µ_s′ ranging from 0.01 mm^-1 to 3 mm^-1 with a step of 0.01 mm^-1, assuming a refractive index of 1.4 and an anisotropy value of 0.9. We note that for the range of wavelengths used by the Track-DOSI instrument in this study, the inverse model based on the MC-LUT produced results comparable to those derived from the diffusion equation [15]. Our use of the MC-LUT is intended for potential future extensions of the instrument to wavelengths above 1000 nm. At wavelengths greater than 1000 nm, tissue absorption is generally high (due to increased water and fat absorptions) while scattering is low, making the diffusion equation less accurate than the MC-LUT approach.

Absorption properties obtained from Track-DOSI measurements were then displayed by using a visualization method that weighted µ_a at each measurement location by a spatially dependent sensitivity function and then linearly combined them to generate a final 2D absorption image. Specifically, by considering a set of N scanning locations, the resulting 2D image of µ_a at coordinate (x, y) can be obtained as:

$${\mu }_a(x,y)=\frac{{\sum }_{i=1}^N{S}_{{\mu }_a}^{(i)}(x,y){\mu }_a^{(i)}}{{\sum }_{i=1}^N{S}_{{\mu }_a}^{(i)}(x,y)}.$$ (3)

Here, µ_a⁽ⁱ⁾ is the absorption measured at the i-th location. The 2D sensitivity matrix of µ_a, $S_{{\mu }_a}^{(i)}(x,y)$ , was obtained from a Monte-Carlo simulation for a source-detector distance of 20 mm [15]. At each measurement location, the sensitivity matrix was rotated based on the known rotation of the probe such that the simulated source and detector locations matched with the apparent locations of the source and detector.

3. Results

3.1. Validation of the self-calibrating (CWC) approach on solid silicone phantoms

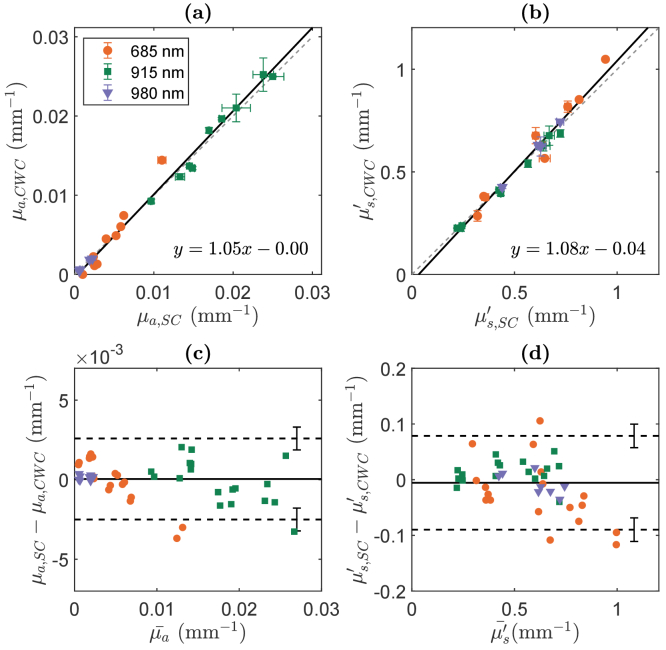
The estimated µ_a and µ_s′ of the nine optical phantoms using the CWC approach exhibited strong agreement with the expected values obtained through the self-calibrating (SC) approach (Fig. 4). We note that data from five phantoms at 980 nm were excluded due to exceedingly low µ_a values. Across all phantoms at wavelengths of 685 nm, 915 nm, and 980 nm, we observed robust linear correlations between the SC and CWC values for µ_a (slope = 1.05 [CI: 1.00 - 1.10], intercept = −4 × 10⁻⁴ [CI: −9 - 2 × 10⁻⁴], r = 0.990, p < 0.001, CCC = 0.988 [CI: 0.979 - 0.993]) and µ_s′ (slope = 1.08 [CI: 1.01 - 1.14], intercept = −0.04 [CI: −0.07 - 0.002], r = 0.982, p < 0.001, CCC = 0.977 [CI: 0.961 - 0.987]), as shown in Fig. 4 (a) and (b). The error between the two systems was −10 ± 4% in µ_a and 1 ± 1% in µ_s′. In the Bland-Altman analysis, the mean differences between measured and expected µ_a and µ_s′ are close to zero (0.00004 mm^-1 for µ_a, −0.006 mm^-1 for µ_s′, Fig. 4(c) and (d)). The 10% error in absorption and ∼1% error in scattering is associated with a discrepancy between the two methods, SC and CWC, of about 10% in amplitude and less than 1 degree in phase measurements.

Fig. 4.

(a, b): Optical properties µ_a (a) and µ_s′ (b) measured by cross-wavelength calibrating (CWC) approach at 20 mm source-detector distance plotted against self-calibrating (SC) approach in nine optical phantoms. Dashed lines represent the line of unity. Solid lines indicate the linear best fit. Error bars indicate the standard deviation of two repeated measurements on each phantom. (c, d): Bland-Altman plots of the difference between µ_a (c) and µ_s′ (d) measured between CWC and SC versus the mean of these two methods. The solid horizontal lines indicate the mean difference between the two methods. The dashed horizontal lines indicate estimates of the limits of agreement. Error bars on those lines indicate uncertainty of those estimates. The average difference between CWC and SC was in µ_a and in µ_s′. The limits of agreement in µ_a were 0.0026 and −0.0024 ± 0.0007 mm^-1 and in µ_s′ was 0.08 and −0.09 ± 0.02 mm^-1.

3.2. Insensitivity to optical couplings

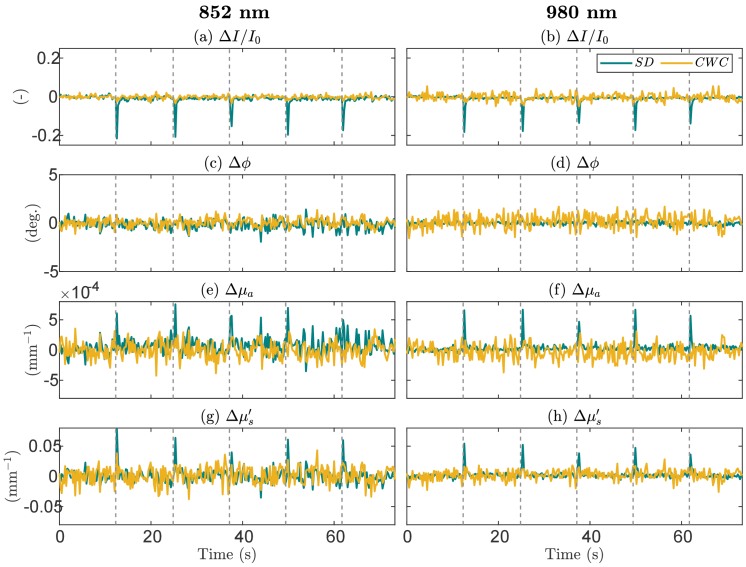
The time traces of relative changes in amplitude intensity (ΔI/I₀, where I₀ is average baseline I), phase (Δϕ), absorption (Δµ_a), and scattering (Δµ_s′) at 852 nm and 980 nm for measurements obtained from the SD 1B and CWC 1B measurements are displayed in Fig. 5. Measurements were subtracted or normalized to average values of the first 5-second baseline. We note that the CWC measurements at 852 nm were technically identical to the SC measurements at this wavelength. Throughout the measurements, pressure was intermittently applied to the optical probe, as denoted by dashed lines in the figures. These pressure variations on the tissue surface led to fluctuations in optical coupling, resulting in spike-like distortions in intensity, absorption, and scattering signals recorded at SD measurements. Phase signals were notably unaffected by these pressure changes. In the examples of CWC measurements at 852 nm and 980 nm, the spike features observed in raw and optical property signals were effectively removed. By detecting outliers in the data (values > 1.5 times of interquartile range), we found a greater number of outliers observed in the SD data, attributed to spike-like distortions in the optical property signals. Specifically, at 852 nm, Δµ_a showed that ∼3% of the SD data are outliers, compared to ∼0.7% in the CWC data; Δµ_s′ showed that ∼2% of the SD data are outliers, compared to no outlier found in the CWC data. At 980 nm, Δµ_a showed that ∼3% of the SD data are outliers, compared to less than 0.3% in the CWC data; Δµ_s′ showed that ∼4% of the SD data are outliers, compared to ∼2% in the CWC data.

Fig. 5.

Time traces of normalized amplitudes (ΔI/I₀, a, b), phase differences (Δϕ, c, d), relative absorption (Δµ_a, e, f) and reduced scattering coefficients (Δµ_s′, g, h) for single-distance (SD) and cross-wavelength calibrating (CWC) measurements with source 1 and detector B. Measurements were subtracted or normalized to first 5-second baseline data and were shown for wavelengths 852 nm and 980 nm. Vertical dashed lines indicate when pressure was applied on the probe. Spike-like distortion in the signals are observed in the SD signals.

3.3. Repeatability of CWC measurements on human tissue

We performed multiple measurements by removing and replacing the probe on the human front calf. This experiment allowed us to assess the repeatability of optical property estimations using the SD and CWC methods in vivo. These results are reported in Table 1. Overall, the deviation among different measurements is low for both methods. The coefficients of variation (CV, calculated as the percentage ratio between standard deviation and mean) are lower for the CWC method compared to the SD method for both µ_aand µ_s′ at most wavelengths. The maximum CV values for CWC are ∼8% for µ_a and ∼2.5% µ_s′.

Table 1. Optical properties from repeated measurements on human tissue at different wavelengths for SD and CWC methods. Values are reported as means, standard deviations (std), and coefficients of variation (CV).

		µa		µs′
		Mean ± std (mm-1)	CV (%)	Mean ± std (mm-1)	CV (%)
685 nm	SD	0.0055 ± 0.0005	9.7	0.67 ± 0.02	2.3
	CWC	0.0055 ± 0.0004	7.8	0.56 ± 0.01	2.4
852 nm	SD	0.0064 ± 0.0003	4.3	0.53 ± 0.01	1.0
	CWC	0.0067 ± 0.0001	1.1	0.433 ± 0.004	0.8
915 nm	SD	0.0068 ± 0.0004	6.0	0.61 ± 0.01	1.3
	CWC	0.0068 ± 0.0002	3.3	0.510 ± 0.004	0.8
980 nm	SD	0.0137 ± 0.0003	2.4	0.52 ± 0.01	1.1
	CWC	0.0147 ± 0.0002	1.7	0.423 ± 0.002	0.6

3.4. Track-DOSI with CWC on a homogeneous phantom

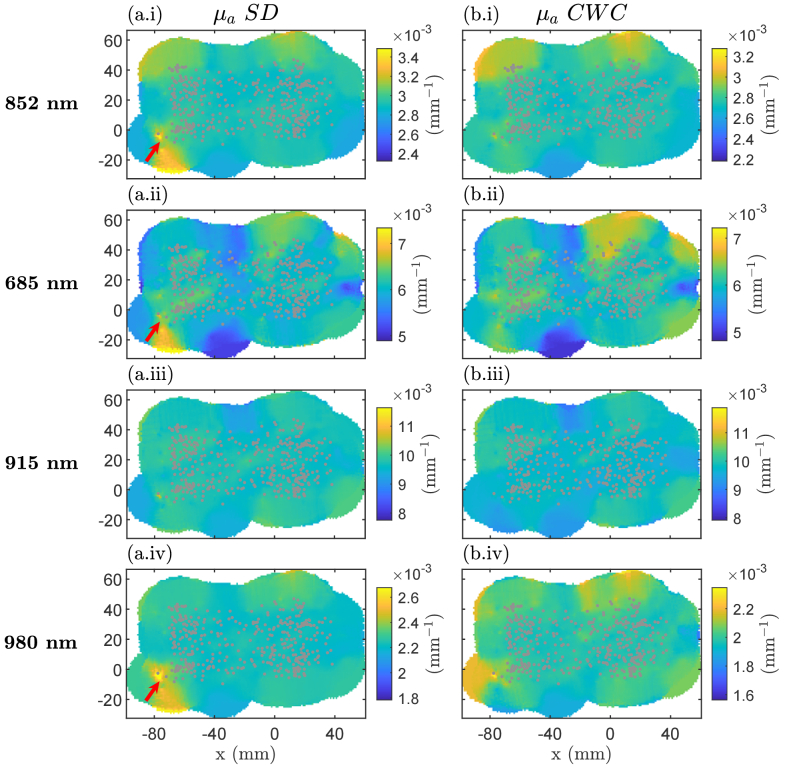
In this experiment, we explored the application of the CWC approach at 1B in Track-DOSI by scanning the probe across a solid optical phantom with homogeneous optical properties. We visualized the estimated µ_a derived from SD measurements at 1B and compared them with those obtained using the CWC method. We note that the CWC measurements at 852 nm were technically identical to the SC measurements at this wavelength. The 2D maps of estimated µ_a obtained from SD and CWC approaches are shown in Fig. 6. We observed changes in optical coupling resulting from motion artifacts induced by probe movement on the phantom surface for SD 1B measurements at three out of four wavelengths (852 nm, 685 nm, and 980 nm). These motion artifact features were primarily observed near the phantom’s edge. However, in the µ_a signal obtained from CWC method for 852 nm, 685 nm, and 980 nm, the motion artifact features were mitigated or disappeared entirely. Table 2 summarizes the number of outliers and maximum values of outliers detected in SD and CWC µ_a data. The number of outliers is greater in SD compared to CWC for µ_a at 852 nm, 915 nm, and 980 nm. Additionally, the maximum of outlier values relative to the medians are also higher in SD compared to CWC at these wavelengths. The outliers are attributed to motion artifacts induced by probe movement on the phantom surface.

Fig. 6.

Two-dimensional images of estimated absorption coefficients (µ_a) from a homogeneous phantom. Data are displayed using weighted average-based visualization for (a) single distance (SD and for (b) cross-wavelength calibrating (CWC) measurements at source 1-detector B. Gray circles indicate the location of each measurement. Arrows indicate where the artifacts occurred during measurements at 852 nm, 915 nm, and 980 nm. Color bars are scaled between median value ± 20%.

Table 2. Comparison of outliers and maximum outlier values between SD and CWC absorption measurements using Track-DOSI on a homogeneous phantom.

Wavelengths	Number of outliers (%)		Maximum outlier values (w.r.t median values) (mm-1)
	SD	CWC	SD	CWC
685 nm	2.6	2.8	0.002	0.002
852 nm	3.1	2.8	0.002	0.0006
915 nm	1.5	1.3	0.003	0.002
980 nm	2.2	1.3	0.002	0.0008

3.5. CWC measurements from heterogeneous media

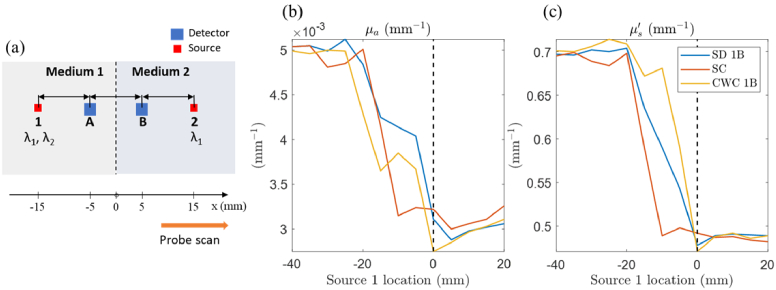
In this section, we simulated the application of the CWC method on a heterogeneous medium. The same optical probe geometry as shown in Fig. 3 was used, with source-detector distance pairs of 10 mm and 20 mm. The heterogeneous medium consisted of two separate semi-infinite homogeneous media with different optical properties at two wavelengths λ₁ and λ₂. Specifically, medium 1 has µ_a(λ₁) = 0.01 mm^-1, µ_s′(λ₁) = 1 mm^-1, µ_a(λ₂) = 0.005 mm^-1, µ_s′(λ₂) = 0.7 mm^-1; medium 2 has µ_a(λ₁) = 0.007 mm^-1, µ_s′(λ₁) = 1.3 mm^-1, µ_a(λ₂) = 0.003 mm^-1, µ_s′(λ₂) = 0.5 mm^-1. The probe was moved horizontally from medium 1 to 2 (Fig. 7(a)) from source 1 location of −40 mm to 20 mm, in steps of 5 mm, with respect to the medium midpoint. At each step, Monte Carlo simulations were performed to generate simulated FD complex reflectance values for all source-detector pairs ${\tilde{R}}_{1A},{\tilde{R}}_{1B},{\tilde{R}}_{2A}$ , and ${\tilde{R}}_{2B}$ at two wavelengths λ₁ and λ₂. We first computed optical properties using the SC approach for wavelength λ₁. Then, the calibration factor ${\tilde{C}}_{1B}^{\lambda 1}$ was obtained from the simulated ${\tilde{R}}_{1B}^{\lambda 1}$ value and the theoretical reflectance value based on self-calibrated optical properties. Note that this calibration factor does not account for any real experimental or instrumental coupling confounds but rather addresses the discrepancies in the sensitivity of the two approaches, SC vs SD, on the two different medium optical properties. Next, we performed the CWC approach on ${\tilde{R}}_{1B}^{\lambda 2}$ by using the assumption ${\tilde{C}}_{1B}^{\lambda 2}={\tilde{C}}_{1B}^{\lambda 1}$ . All the recovered optical properties were obtained using the MC-LUT inverse model on a homogeneous medium. Figures 7(b) and (c) showed the recovered µ_a and µ_s′ at λ₂ obtained from SD, SC, and CWC approaches. As the probe moved towards medium 2, all approaches displayed similar transitions from the optical properties of medium 1 to those of medium 2. Notably, the SC approach exhibited earlier changes in optical properties (at source 1 location of -20 mm) compared to the other two techniques.

Fig. 7.

(a) Schematic diagram of a heterogeneous medium used for Monte Carlo simulation. The probe is shown positioned at the midpoint of the heterogeneous medium, which is the boundary of two separate homogeneous media. The sources are numbered (1 and 2), and the detectors are labeled with letters (A and B). Wavelength λ₁ is used at both source 1 and 2 positions to calculate the cross-wavelength calibration factor for λ₂. (b) and (c): Recovered optical properties µ_a and µ_s′ at wavelength λ₂ obtained from three methods (single distance SD, self-calibration SC, and cross-wavelength calibration CWC), plotted relative to the source 1 locations with respect to the medium midline when moving the probe horizontally on the medium surface. The dashed line indicates the medium midline. SD and CWC methods were performed using measurements from source 1 and detector B.

4. Discussion

Diffuse optical spectroscopy imaging (DOSI) techniques offer valuable insights into tissue optical properties, enabling the non-invasive assessment of physiological parameters such as chromophore concentrations and scattering properties. In this study, we introduced and validated a novel method known as the cross-wavelength calibrating (CWC) approach within the framework of Track-DOSI, a real-time imaging system for tissue characterization and active feedback at the point-of-care. The development of tracking DOSI systems, including Track-DOSI developed in our group, has recently gained traction as a promising research area with potential relevance to various clinical applications [18,22,29]. Our findings underscore the effectiveness of the CWC method in mitigating changing optical coupling and motion artifacts encountered during probe scanning in these systems.

Validation of the CWC method on solid silicone phantoms showcased robust agreement between the estimated optical properties using CWC and those derived from the gold standard self-calibrating (SC) method [19]. Across all wavelengths, strong correlations were observed with r = 0.99, CCC = 0.99 for µ_a; r = 0.98, CCC = 0.97 for µ_s′. This agreement persisted at individual wavelength: at 685 nm, r = 0.99, CCC = 0.91 for µ_a and r = 0.97, CCC = 0.96 for µ_s′; at 915 nm, R = 0.97, CCC = 0.96 for µ_a and R = 0.99, CCC = 0.98 for µ_s′; at 980 nm, r = 0.98, CCC = 0.95 for µ_a and r = 0.93, CCC = 0.93 for µ_s′. Previous studies have illustrated that the SC method exhibited smaller deviations against light intensity drifts and achieved high reproducibility in tissue oxygen saturation measurements [19,30,31]. Here, we demonstrated that the CWC approach maintains the advantages of the SC method, displaying reduced susceptibility to alterations in instrumental and optical coupling factors compared to the single-distance (SD) method. Additionally, we emphasize that one advantage of the CWC method over the SC method is its capacity to reduce the number of required laser sources, thereby minimizing instrumental complexity and cost while retaining robustness in estimating optical properties.

Our experiments on homogeneous phantoms also highlighted the CWC approach's capability to reduce motion artifacts and optical coupling variations during probe scanning on tissue surfaces. By comparing SD measurements with those obtained using CWC or SC methods, we observed significant improvements in signal fidelity and artifact suppression. Our probe-repositioning test on human tissue demonstrated that the CWC method resulted in higher reproducibility than the SD geometry. These results underscore the practical utility of the CWC method in enhancing the quality and reliability of optical property measurements in dynamic tissue imaging scenarios. Future works will focus on evaluating the robustness and reproductivity of CWC method when applied with Track-DOSI on human tissues in vivo.

While CWC measurements exhibited reduced sensitivity to motion artifacts and fluctuations in optical coupling, they displayed higher levels of noise compared to SD measurements of absolute optical properties (see 980 nm optical properties in Fig. 5). This noise stemmed from the inclusion of signals from other wavelengths (852 nm) and from other source-detector distances in CWC measurements. Nevertheless, the real-time removal of motion artifacts remains a valuable advantage, particularly for data acquisition and the immediate visualization of optical properties using Track-DOSI. Additionally, it’s worth noting that the CWC method could be utilized to derive relative absorption measurements from amplitude intensity data using a modified Beer-Lambert law [32]. We expect that relative µ_a measurements would be less susceptible to high noise compared to absolute measurements, yet still benefit from the CWC method to reduce sensitivity to motion artifacts and changes in optical coupling.

We highlight the potential extension of the CWC method to broadband absorption spectroscopy, which integrates frequency-domain (FD) with broadband continuous-wave (CW) techniques. Broadband µ_a measurements offer enhanced precision in determining tissue chromophore concentrations [7,16,17,33]. This can be achieved by combining SC measurements at two wavelengths (using two symmetrical FD sources and two FD detectors) with broadband CW measurements (utilizing a lamp for broadband light source and a spectrometer co-localized at the same positions as the FD light source and detector, respectively). SC measurements are utilized to obtain cross-wavelength calibration factors for the broadband CW SD measurements as well as scattering parameters. Subsequently, these calibration factors, along with the scattering parameters, are applied to the broadband measurements to provide absolute broadband absorption data. It’s worth noting that SC method has previously been employed for broadband measurements [34]. This system requires two lamps and one spectrometer with an optical switch to alternate the detection at two different locations. Our proposed system aims to streamline instrumental complexity by reducing the requirement for two lamps and two detector locations to just one lamp and one detector location. Additionally, removing the optical switch will enhance the system’s detection speed.

Several limitations and avenues for future research in the CWC method warrant further exploration. While the present study focused on solid silicone phantoms, additional validation on biological tissues is imperative to evaluate the method's efficacy in vivo to obtain tissue chromophore concentrations and tissue oxygenation. Further investigations are required to optimize its performance across diverse physiological conditions and tissue types. One limitation of CWC is its assumption of a homogeneous medium beneath the probe region, which typically exceeds that of the SD method. In our simulations presented in this paper, we have shown that both CWC and SD approaches showed similar optical property values when measuring a heterogeneous medium (see Section 3.5). We also demonstrated that the CWC approach provided more accurate transitions in optical properties compared to the SC approach when scanning the optical probe across media with optical properties. This is because the SC approach has a more extended optical probe geometry than the SD and CWC approaches (i.e., 2 sources and 2 detectors geometry vs 1 source and 1 detector geometry). Although the CWC approach relies on the SC approach at one wavelength, it applies to SD measurements at the remaining wavelengths, thereby offering better measurements on heterogeneous medium than the SC approach. Finally, one disadvantage of the CWC approach compared to the SC method is that it still relies on initial calibration using an optical phantom with known optical properties.

In summary, the CWC method stands as a notable advancement in diffuse optical spectroscopy imaging, offering heightened accuracy, resilience, and real-time artifact correction. However, further investigation is needed to thoroughly assess its accuracy, particularly regarding sample inhomogeneities. Future research will concentrate on exploring the potential of CWC in determining tissue chromophore concentrations and enabling long-term monitoring. Real-time visualization and correction of optical property measurements can be invaluable in clinical settings, where accurate and timely assessment of tissue properties is critical for diagnosis and treatment monitoring. Furthermore, the reduced sensitivity to motion artifacts and optical coupling variations enhances the robustness and applicability of Track-DOSI in diverse clinical scenarios.

Appendix: Summary of CWC processing steps for Track-DOSI

Table 3. CWC processing steps for different wavelengths used in the Track-DOSI system. Source and detector arrangement is illustrated in Fig. 3(c).

Step #	Medium	Measured reflectance values	Computed reflectance $\tilde{R}$ b and calibration factor $\tilde{C}$ values	Computed µa and µs′ using MC-LUT
1	Calibration phantom a with known optical properties µa,p and µ′s,p	$\begin{array}{c}{\tilde{R}}_{1B,p}^{685\text{nm}},\\ {\tilde{R}}_{1B,p}^{852\text{nm}},\\ {\tilde{R}}_{1B,p}^{\text{915nm}},\\ {\tilde{R}}_{1B,p}^{\text{980nm}}.\end{array}$	Compute calibration factors from measurements on calibration phantom: $\begin{array}{l}{\tilde{C}}_{1B,p}^{685\text{nm}}={\tilde{R}}_{1B,p}^{\text{685nm}}/{\tilde{R}}_p^{\text{685nm}}({\rho }_L),\\ {\tilde{C}}_{1B,p}^{685\text{nm}}={\tilde{R}}_{1B,p}^{\text{685nm}}/{\tilde{R}}_p^{\text{685nm}}({\rho }_L),\\ {\tilde{C}}_{1B,p}^{685\text{nm}}={\tilde{R}}_{1B,p}^{\text{685nm}}/{\tilde{R}}_p^{\text{685nm}}({\rho }_L),\\ {\tilde{C}}_{1B,p}^{685\text{nm}}={\tilde{R}}_{1B,p}^{\text{685nm}}/{\tilde{R}}_p^{\text{685nm}}({\rho }_L).\end{array}$	-
2	Tissue or phantom with unknown µa and µs′	$\begin{array}{c}{\tilde{R}}_{1A}^{852\text{nm}},\\ {\tilde{R}}_{1B}^{852\text{nm}},\\ {\tilde{R}}_{2A}^{852\text{nm}},\\ {\tilde{R}}_{2B}^{852\text{nm}}.\end{array}$	Apply SC approach to find optical properties at 852 nm: $\begin{array}{l}{\tilde{R}}_{SC}^{852\text{nm}}=\sqrt{\frac{{\tilde{R}}_{1B}^{852\text{nm}}{\tilde{R}}_{2A}^{852\text{nm}}}{{\tilde{R}}_{1A}^{852\text{nm}}{\tilde{R}}_{2B}^{852\text{nm}}}}\\ ={\tilde{R}}^{852\text{nm}}({\rho }_L)/{\tilde{R}}^{852\text{nm}}({\rho }_S)\end{array}$	${\mu }_a(852\text{nm})$ and ${\mu }_s^{\mathrm{\prime }}(852\text{nm})$ from $\frac{{\tilde{R}}^{852\text{nm}}({\rho }_L)}{{\tilde{R}}^{852\text{nm}}({\rho }_S)}$
3		${\tilde{R}}_{1B}^{852\text{nm}}$	Apply CWC approach and values from step 1 to find calibration factors at all wavelengths: $\begin{array}{l}{\tilde{C}}_{1B}^{852\text{nm}}={\tilde{R}}_{1B}^{852\text{nm}}/{\tilde{R}}^{852\text{nm}}({\rho }_L),\\ {\tilde{C}}_{1B}^{685\text{nm}}={\tilde{C}}_{1B}^{852\text{nm}}/({\tilde{C}}_{1B,p}^{852\text{nm}}/{\tilde{C}}_{1B,p}^{685\text{nm}}),\\ {\tilde{C}}_{1B}^{915\text{nm}}={\tilde{C}}_{1B}^{852\text{nm}}/({\tilde{C}}_{1B,p}^{852\text{nm}}/{\tilde{C}}_{1B,p}^{915\text{nm}}),\\ {\tilde{C}}_{1B}^{\text{980nm}}={\tilde{C}}_{1B}^{852\text{nm}}/({\tilde{C}}_{1B,p}^{852\text{nm}}/{\tilde{C}}_{1B,p}^{\text{980nm}}).\end{array}$	-
4		$\begin{array}{c}{\tilde{R}}_{1B}^{\text{685nm}},\\ {\tilde{R}}_{1B}^{\text{852nm}},\\ {\tilde{R}}_{1B}^{\text{915nm}},\\ {\tilde{R}}_{1B}^{\text{980nm}}.\end{array}$	Compute CWC calibrated reflectance for 1B using calibration factors from step 3: $\begin{array}{l}{\tilde{R}}^{685\text{nm}}({\rho }_L)={\tilde{R}}_{1B}^{\text{685nm}}/{\tilde{C}}_{1B}^{\text{685nm}},\\ {\tilde{R}}^{852\text{nm}}({\rho }_L)={\tilde{R}}_{1B}^{852\text{nm}}/{\tilde{C}}_{1B}^{852\text{nm}},\\ {\tilde{R}}^{\text{915nm}}({\rho }_L)={\tilde{R}}_{1B}^{\text{915nm}}/{\tilde{C}}_{1B}^{\text{915nm}},\\ {\tilde{R}}^{\text{980nm}}({\rho }_L)={\tilde{R}}_{1B}^{\text{980nm}}/{\tilde{C}}_{1B}^{\text{980nm}}.\end{array}$	${\mu }_a$ and ${\mu }_s^{\mathrm{\prime }}$ from $\tilde{R}({\rho }_L)$ for all wavelengths 685 nm, 852 nm, 915 nm, and 980 nm.

^a Subscript “p” indicates quantities measured on the calibration phantom with known optical properties µ_a,p and µ′_s,p.

^b The notation ${\tilde{R}}^{\lambda }({\rho }_L)$ indicates a theoretical complex reflectance as a function of µ_a(λ) and µ_s′(λ) for source-detector distance ρ_L.

Funding

U.S. Department of Defense10.13039/100000005 (W81XWH2110832).

Disclosures

The authors declare no conflicts of interest.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.