Stability and Dynamics of Zeolite-Confined Gold Nanoclusters

Abstract

Nanoengineered metal@zeolite materials have recently emerged as a promising class of catalysts for several industrially relevant reactions. These materials, which consist of small transition metal nanoclusters confined within three-dimensional zeolite pores, are interesting because they show higher stability and better sintering resistance under reaction conditions. While several such hybrid catalysts have been reported experimentally, key questions such as the impact of the zeolite frameworks on the properties of the metal clusters are not well understood. To address such knowledge gaps, in this study, we report a robust and transferable machine learning-based potential (MLP) that is capable of describing the structure, stability, and dynamics of zeolite-confined gold nanoclusters. Specifically, we show that the resulting MLP maintains ab initio accuracy across a range of temperatures (300–1000 K) and can be used to investigate time scales (>10 ns), length scales (ca. 10,000 atoms), and phenomena (e.g., ensemble-averaged stability and diffusivity) that are typically inaccessible using density functional theory (DFT). Taken together, this study represents an important step in enabling the rational theory-guided design of metal@zeolite catalysts.

Introduction

Nanoengineered hybrid materials, consisting of small metal clusters confined within three-dimensional porous frameworks,¹⁻⁴ have recently emerged as promising materials for several different applications.^2,5,6 For instance, when compared to their larger supported metal analogues, subnanometric transition metal (TM) nanoclusters often show unique and desirable catalytic properties. These phenomena are exemplified by gold (Au), which is often considered to be the noblest of all metals.⁷ Specifically, seminal studies by Haruta,⁸⁻¹⁰ Hutchings,¹¹⁻¹³ and more recent work by Corma^14,15 and Iglesia¹⁶⁻¹⁸ have shown that Au clusters smaller than 1 nm are catalytically active for several reactions. These include CO oxidation,^8,19−21 propylene epoxidation,¹⁰ partial oxidation of methane,²²⁻²⁵ and others. Indeed, the unique size-dependent catalytic activity of transition metals is well-established in the literature.²⁶

However, a key challenge with using these hybrid materials as catalysts is their limited stability, which often results in irreversible deactivation under reaction conditions.²⁷ While several strategies such as confinement using nanoporous scaffolds (e.g., zeolites²⁸) have been used to address this challenge, the underlying physicochemical phenomena responsible for sintering are not well understood. Thus, notwithstanding the recent advances in synthesis and characterization of TM@zeolite catalysts,³ progress in this emerging domain has been limited by the lack of rational design principles that can be used to create catalytically active materials that are also stable under reaction conditions. A key limitation, and one that we seek to overcome in this study, is the inability of the current computational methods to predict the properties of these intriguing hybrid materials.

Density functional theory (DFT) is now routinely used to elucidate reaction mechanisms and to screen large catalyst libraries. However, the widely used slab approximation cannot capture the stability and dynamics of confined metal nanoclusters. Moreover, while several distinct force fields have been reported for nanoporous materials,²⁹ these classical methods are not well-suited to study reactive processes. Barring a few recent examples,^30,31 the inability of the current computational methods to describe the size, shape, stability, dynamics, and reactivity of zeolite-confined metal nanoclusters remains a major bottleneck. Thus, novel computational methods that can simultaneously overcome the challenges of both DFT and force-field-based approaches have now become necessary to enable the theory-guided design of metal@zeolite catalysts.

As a step toward addressing this method gap, here, we present an active learning workflow that uses DFT-based machine learning potentials (MLPs) to obtain quantitative trends related to the stability and diffusivity of Au nanoclusters confined within pores of several all-silica zeolites (denoted as Au@zeolites). Specifically, we combine conventional molecular dynamics (MD) simulations and metadynamics³² to develop an MLP that is transferable across different metal nuclearities and zeolite topologies. Importantly, we show that the resulting model maintains DFT accuracy at a range of temperatures (300–1000 K) and can be used to explore time scales (>10 ns) and length scales (∼10,000 atoms) that are typically inaccessible using DFT. This ability allows us, for the first time, to define and compute important physicochemical characteristics (i.e., ensemble-averaged stabilization energy, self-diffusivity, diffusion-free energy landscapes) that can potentially serve as descriptors to predict the stability and reactivity of Au@zeolite catalysts. More broadly, we anticipate that the methods and analyses reported in this study can be generalized to other hybrid materials consisting of metal clusters confined within nanoporous frameworks.³³

Methods

All DFT calculations were performed using the Vienna ab initio simulation package (VASP)³⁴ using the projector-augmented wave formalism. Similar to our previous work,³⁵ we used the RPBE functional³⁶ with a 400 eV plane wave energy cutoff. The initial DFT training data set was obtained using multiple short (2 ps, 0.5 fs time step) ab initio molecular dynamics (AIMD)³⁷ simulations. Specifically, we used 10 different zeolite topologies (AEI, BEA, CHA, LTA, MAZ, MFI, MOR, MWW, RHO, and SOD) and 15 metal nuclearities ranging from Au₁ to Au₁₅ for these simulations. The zeolite frameworks were selected to include several common materials across different pore sizes, shapes, and ring topologies.^{16−18,20,22−24,38} Due to the large size of the metal@zeolite unit cell, all DFT calculations for the zeolites are performed using the Γ-point. A 6 × 6 × 6 k-point sampling was used for the bulk Au, which serves as a reference for confinement energy calculations discussed later. The initial structures were obtained from the International Zeolite Association database (for the zeolites)³⁹ and the Materials Project (for the bulk Au).^40,41

We used the polarizable atom interaction neural network (PaiNN)^42,43 and the neuroevolution potential (NEP)⁴⁴ as the MLP architectures for model development. Initial MLP training, which relied on conventional molecular dynamics simulations (MLP/MD), was performed using PaiNN. However, due to technical limitations in combining PaiNN with graphical processing unit (GPU) accelerated codes (e.g., LAMMPS⁴⁵), we use the NEP available in GPUMD⁴⁶ for further model refinement and production runs. Details of these training protocols are presented in Supporting Information (SI).

Normal metadynamics with adaptive Gaussian^32,47,48 simulations (MLP/MTD) with the diffusion-based scheme (ADAPTIVE = DIFF in the input script) were then used to sample new configurations iteratively to investigate the diffusion of Au_n clusters. These simulations were performed in the NVT ensemble with a stochastic rescaling thermostat⁴⁹ using the PLUMED (version 2.9.0) interface⁵⁰⁻⁵² to GPUMD (version 3.8). We used two different temperatures (300 and 500 K) for Au@LTA. Analogous simulations at 300 K for four other zeolites (i.e., CHA, RHO, MFI, BEA) were used to improve the transferability of our LTA model to other zeolite topologies. As shown in eq 1, the distance between the center of mass (COM) of the Au nanocluster and the main zeolite cavity was used as the collective variable (CV).

1

A history-dependent bias (applied to the CV) was used to drive the interpore diffusion of Au nanoclusters. Depending on the cluster size, zeolite topology, and the simulation temperature, a Gaussian biasing potential of 0.004–0.03 eV (height) was used. These potentials were added every 25 fs. Since adaptive Gaussians are used, the width of the Gaussian hills was updated to cover the space of 20 time steps in collective variables (SIGMA = 20 in input script). Concomitant with the improving model performance over successive iterations, a variable simulation time, ranging from 10 ps (first iteration) to 500 ps (final iteration), was used to improve the diversity of the sampled configurations and accelerate the convergence of the model. All MLP-based MD simulations used a time step of 0.5 fs.

As shown in eq 2, the diffusion coefficient of Au nanoclusters was calculated using the dynamically correlated transition state theory (dcTST)^53,54

2

Here, λ is the pore-to-pore distance in the zeolite and k_A→B is the hopping rate between states A and B. The latter quantity is calculated using eq 3 as

3

where κ is the correction factor for state recrossing, m is the mass of the diffusing Au nanocluster, and q* is the reaction coordinate corresponding to the transition state. As high barriers are observed, we assumed a low recrossing probability (i.e., κ = 1.0) in our calculations. The CV defined in eq 1 is used as the reaction coordinate (i.e., q).

Results

Model Development and Model Performance

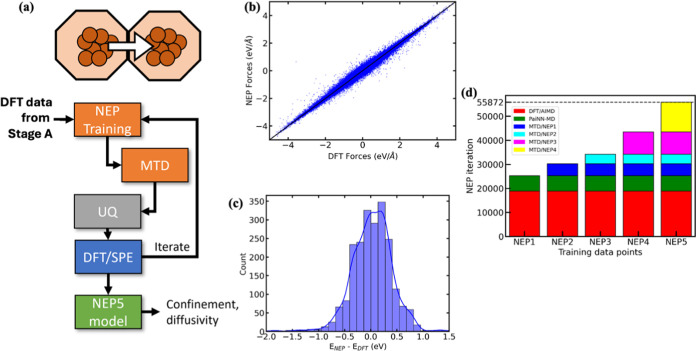
Figure 1a summarizes our two-stage MLP development protocol for describing the interactions between the Au, Si, and O atoms in our system. In stage A, we used 4 AIMD-based iterations to develop the PaiNN model. A random sampling strategy was used to select the configurations for DFT/SPEs. A total of 17,000 DFT-derived data points across 10 zeolites for Au₁–Au₁₀ clusters were used. This model shows a mean absolute error (MAE) of 0.01 eV (energies) and 0.007 eV/Å (forces). The details of the PainNN training process are presented in SI, and the model performance is summarized in Figures S1 and S2.

Figure 1.

(a) Overview of the active learning curriculum used to develop NEP-based MLPs for Au@zeolites. The associated (b) force parity plots and (c) energy error histograms for the final NEP5 model. The blue boxes in (a) refer to DFT calculations, orange to MLP-based simulations, and UQ to uncertainty quantification using the σ_f metric. (d) The progression of the data set used for different iterations of the NEP model.

Using the DFT data generated in stage A, in the second stage (stage B), our workflow uses adaptive Gaussian metadynamics to progressively explore new configurations that are relevant for interpore diffusion of Au nanoclusters. A subset of these configurations, based on their predicted model uncertainty, is selected for DFT/SPEs. These DFT/SPEs serve as training data for the next iteration of the model. The first stage B model (i.e., NEP1) is trained using the DFT data obtained from stage A. The next iteration, denoted as NEP2, is trained using 10 ps adaptive Gaussian metadynamics (i.e., NEP1/MTD) for Au₁–Au₁₀@LTA at 300 K. Subsequent models are trained using higher simulation temperatures (i.e., 100 ps NEP2/MTD at 500 K to obtain NEP3) and by expanding our training set to four additional zeolite types (i.e., BEA, CHA, MFI, and RHO using 200 ps NEP3/MTD at 300 K to obtain NEP4). Taken together, the final model, denoted as NEP5, has been trained using 55,872 DFT configurations that span different temperatures (i.e., 300–1000 K), metal nuclearities (Au₁–Au₁₀), and 10 different zeolite topologies (see Figure 1d for the data added in each training iteration). Details of the training procedure (Tables S1–S4 and Figure S3) and transferability across different temperatures (Table S5 and Figure S5) and zeolite topologies (Table S6 and Figure S6) are summarized in the SI.

Figure 1b,c summarizes the performance of the NEP5 model for our test data set. The test data set consists of configurations (5% of total) that were set aside during model training. As shown by the parity plots in Figure 1b,c, the observed MAEs for forces (<0.05 eV/Å) and energies (<0.3 eV) demonstrate the efficacy of our training procedure. Note that the energy MAE is calculated by directly comparing the raw NEP5-predicted and DFT-calculated values; an error analysis of relative energies is presented later.

A key advantage of the above iterative training curriculum is the ability to quantify and interpret the impact of each training step on the performance of the model. For instance, we can use σ_f as a metric of the model uncertainty (eq 4).

4

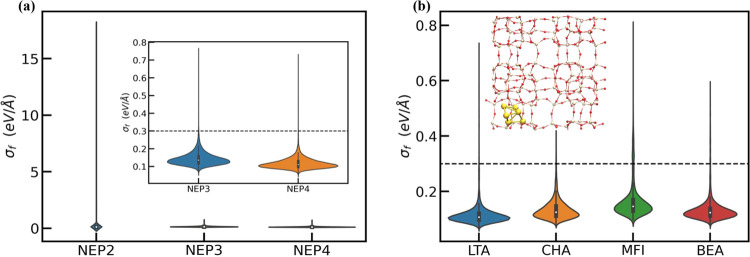
Here, σ_i for each atom indexed by i along each x–y–z Cartesian direction measures the model variance computed across the committee models. Using this metric, Figure 2a shows how the model performance improves across several stage B iterations. Specifically, while the distribution of σ_f for NEP2 shows a long tail, the high uncertainties associated with these configurations are dramatically reduced for NEP3 and NEP4 due to our active learning protocol. Further analysis across the individual Au_n@LTA systems (Figure S4 in SI) shows that the performance enhancement observed in Figure 2a arises due to an improved description of the Au₁₀@LTA system by the latter NEP models.

Figure 2.

(a) σ_f uncertainty estimation for the 2nd to 4th iterations of the NEP model. (Inset: a zoomed-in comparison of NEP3 and NEP4.) (b) The σ_f uncertainty estimation for four different zeolites using the NEP4 model. (Inset is the structure that has the highest uncertainty, Au₆@MFI.) Dashed line in the graph is the maximum preferred σ_f = 0.3 eV/Å.

Similar improvements in the model performance are observed for other zeolite topologies. For instance, Figure 2b shows that σ_f for Au₃@CHA, MFI, and BEA zeolites are comparable to those of the Au₃LTA system.

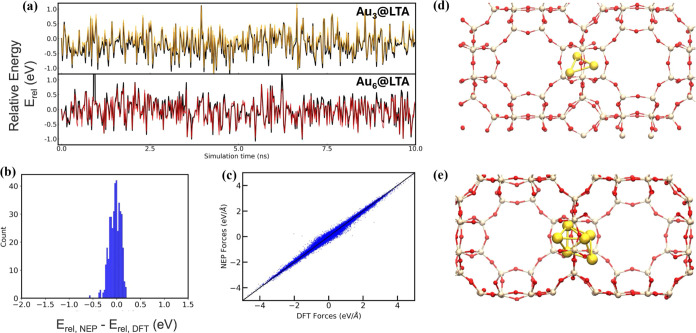
Beyond the analyses described above, we conducted several other assessments to confirm the predictive capabilities of NEP5 over extended time scales. Specifically, we performed a 10 ns well-tempered metadynamics (WTmetaD)⁵⁵ simulation to model the diffusion of Au₃ and Au₆@LTA at 300 K using the final NEP5 model. These results, plotted as a temporal evolution of relative energies (Figure 3a), relative energy error histograms (Figure 3b, MAE = 0.11 eV), and force parity plots (Figure 3c, MAE = 0.04 eV/Å) for Au₆@LTA, show that NEP5 reliably reproduces the dynamics of the system over time scales (i.e., 10 ns) that are much longer than those used during model development (e.g., 500 ps). Here, we use relative energies, defined as E_rel(t) = E(t) – E(t = 0), to circumvent the known limitations of MLPs in reproducing raw DFT energies.⁵⁶ Compared to the higher MAEs observed previously in Figure 1c, this analysis further evidences the ability of the MLP to model the energetics of nanocluster diffusion at DFT accuracy.

Figure 3.

(a) Comparing the temporal evolution of NEP5- and DFT-calculated (black) relative energies for a 10 ns WTmetaD simulation of Au₃@LTA (orange) and Au₆@LTA (red). (b) Relative energy error histogram and (c) force parity plots for the Au₆@LTA system. Representative configurations from the transition state region for the diffusion of (d) Au₃ and (e) Au₆ nanoclusters across the LTA eight-membered ring (8MR) window.

The above simulations employed a high bias factor (γ = 300), which determines the rate of decay of Gaussian hills, to drive the diffusion of Au clusters across the LTA eight-membered ring (8MR) windows. Representative configurations from these interpore transitions are shown in Figure 3d,e for Au₃@LTA and Au₆@LTA, respectively.

Redispersion Penalty and Confinement Stabilization

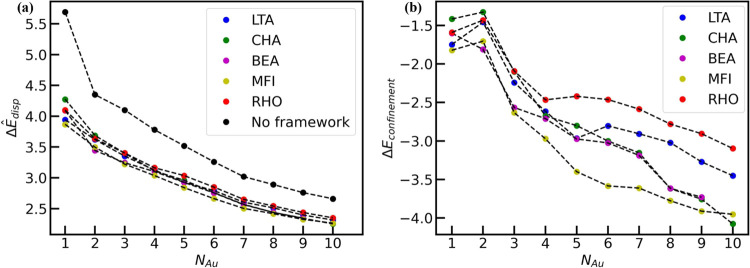
Based on the impressive performance of NEP5 across different cluster nuclearities and zeolite topologies, we now focus on calculating ensemble-averaged properties that are typically inaccessible using traditional DFT-based AIMD simulations. Specifically, using a series of conventional MD simulations with the NEP5 model (denoted as NEP5/MD), Figure 4a shows the trends in redispersion energy penalty (ΔÊ_disp) calculated for various Au@zeolite systems. As shown in eq 5, ΔÊ_disp measures the energy cost associated with the formation of small metal nanoclusters from the bulk metal.

5

Here, E̅_Au@zeolite, E̅_zeolite, and Ê_Aubulk represent the ensemble-averaged energies of the Au@zeolite, the empty framework, and the per atom energy of the bulk Au, respectively, and n_Au refers to the number of Au atoms in the cluster. E̅_Au@zeolite and E̅_zeolite are obtained using 1 ns NEP5/MD and 100 ps NEP5/MD simulations, respectively. Ê_Aubulk is calculated using DFT. We use ^ to denote quantities that are averaged by the number of metal atoms and ® to denote energy averages obtained from MD simulations.

Figure 4.

(a) Trend of ΔÊ_disp for Au₁–Au₁₀ in a vacuum and five zeolite topologies. (b) The trend of ΔE_confinement for five different zeolite topologies.

Figure 4a shows the dependence of the redispersion energy penalty on the size of the Au clusters. Unsurprisingly, we observe that smaller undercoordinated Au clusters are less stable than their larger analogues. Indeed, in the absence of the zeolite framework, this quantity (i.e., ΔÊ^vac_disp) is simply the gas phase formation energy of Au nanoclusters.

However, similar calculations across different zeolite topologies show interesting trends. Specifically, while it is clear that the three-dimensional environment of the framework stabilizes the Au nanoclusters (i.e., smaller ΔÊ^zeolite_disp), Figure 4b shows that the extent of stabilization depends on the properties of the zeolite framework. To quantify this effect, we define a new quantity called the framework-induced stabilization energy (denoted as ΔE_confinement) that measures the impact of the confining zeolite environment on the formation energy of the metal nanoclusters. Specifically, ΔE_confinement is defined as

6

Figure 4b shows the dependence of the stabilization energy across different frameworks and cluster sizes. In general, we observe two types of trends. While large channel-type zeolites such as BEA (pink) show a linear monotonic decrease in the confinement energy, several other frameworks (e.g., RHO (red), LTA (blue), and MFI (yellow)) show two distinct regimes. For these zeolites, the stabilization energy changes dramatically for smaller cluster sizes, but a weaker dependence is observed beyond a critical size threshold (n_threshold). In our preliminary analysis of the crystalline surface, we determined that the critical size threshold is correlated with the size and shape of the zeolite pore with MFI (n_threshold = 6) > LTA (5) > RHO (4).

Interestingly, CHA shows intermediate behavior that lies between the two regimes discussed above. Specifically, the stabilization energy for CHA (green) is similar to those of LTA and RHO for smaller clusters. However, for clusters larger than Au₄, our CHA results are almost identical to BEA (pink). Thus, while Au_1–3 is highly unstable in CHA, Au₁₀@CHA is slightly more stable than Au₁₀@MFI. This suggests that in addition to the pore size and zeolite topology (i.e., channel vs pore/window), the relative sizes of the zeolite pore and the window are also key contributing factors for stabilizing the Au nanoclusters. While a detailed investigation of these effects is beyond the scope of this study, their impact on the diffusion properties of Au nanoclusters in zeolites is discussed later.

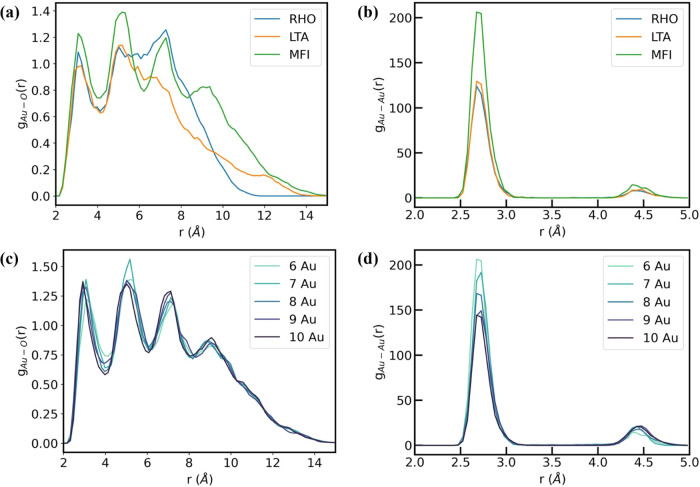
In general, we observe that MFI provides the most favorable confining environment among the zeolites considered here. We hypothesize that these trends arise due to the trade-offs between Au–Au and Au-framework interactions. For instance, comparing Au₆ clusters across different frameworks in Figure 4, we observe that Au₆@MFI is ca. 1 eV more stable than Au₆@RHO. Detailed analyses of Au–O radial distribution functions (RDF) in Figure 5 show the formation of distinct peaks for Au₆@MFI. In contrast, the Au–O RDF for Au₆@RHO and Au₆@LTA shows broader peaks, which suggests a higher degree of ordering induced by the MFI framework. Analogous analyses for other frameworks, Au nuclearities, and Au–Au RDF (Figures S7 and S8) are shown in the SI. Figure 5 further highlights the importance of Au–O RDF (rather than Au–Au interactions) in rationalizing the confinement energy trends observed previously in Figure 4. Similarly, the plateauing of ΔE_confinement at larger cluster sizes implies a decreasing role of Au-framework interactions, which can be inferred from the negligible changes in the Au–O RDF for larger clusters (Figure 5c,d).

Figure 5.

Trends in the (a) Au–O and (b) Au–Au radial distribution functions (RDFs) obtained from the dynamics of Au₆ nanoclusters confined within RHO, LTA, and MFI zeolites. Similar analysis of the (c) Au–O and (d) Au–Au RDFs for Au_6–10@MFI.

Diffusivity Trends

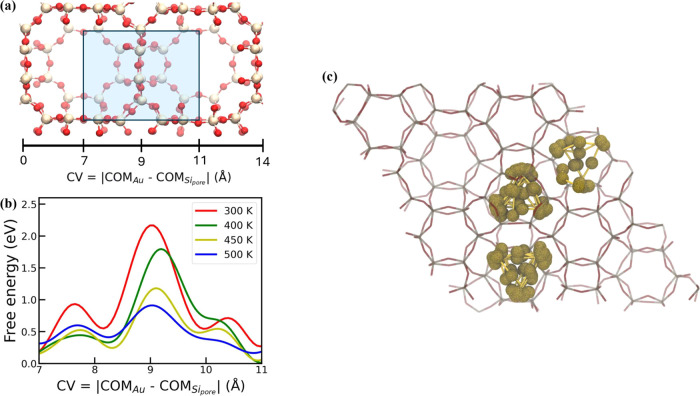
The previous section demonstrates how the pore size and topology of the framework impact the shape and size of zeolite-confined Au nanoclusters. Building on these results, we used the NEP5 model to investigate the kinetics of interpore diffusion. As no diffusion events were observed using conventional NEP5/MD (10 ns for Au₃@LTA), we used well-tempered metadynamics (WTmetaD)⁵⁵ simulations to obtain the free energy surfaces (FES) at four different temperatures (300, 400, 450, and 500 K). The CV used for all the WTmetaD simulations is the same as the one defined in eq 1.

Specifically, the FES for each temperature is obtained from three independent WTmetaD simulations (Figure S9). A starting hill height of 0.1 eV, width of 0.4 Å, and bias factors of 100 for 300 K, 60 for 400 K, 50 for 450 K, and 40 for 500 K were used to simulate a 10 ns WTmetaD in a 2 × 1 × 1 unit cell (two pores in the x-direction) as shown in Figure 6a. Harmonic wall potentials were added in the y and z directions to ensure that the pore-to-pore transition only occurs in the x-direction.

Figure 6.

(a) Positions of Au₃@LTA zeolite in the CV space (the CV is defined in eq 1). The blue region shows the region where free energy surface was estimated. (b) The free energy surfaces (FES) of Au₃@LTA at 300, 400, 450, and 500 K, respectively. (c) The pores occupied by an Au₃ nanocluster in a CHA zeolite from a 10 ns MD simulation conducted at 500 K.

The averaged free energy curve for each temperature is plotted in Figure 6b as a function of the CV. Figure 6b shows a peak near the CV value of 9 Å, corresponding to the window between the two pores. The averaged diffusion energy barrier is estimated as 2.04 ± 0.38 eV at 300 K, 1.78 ± 0.14 eV at 400 K, 1.13 ± 0.17 eV at 450 K, and 0.86 ± 0.12 eV at 500 K, respectively. The diffusion coefficient estimated from dcTST were 5.21 × 10^–19 m²/s at 450 K and 5.17 × 10^–15 m²/s at 500 K. The diffusion time scale determined by the relation

7

where L is the length scale of diffusion and D is the diffusion coefficient, gives t_450 K to be on the order of 10^–1 s and t_500 K on the order of 10^–5 s. This stark difference in the free energy barrier shows that while the Au₃ nanocluster remains kinetically trapped at 300 and 400 K, significantly higher mobility is expected at higher temperatures. Interestingly, analogous calculations for Au₅@LTA did not show any diffusion even at 500 K (Figure S10).

In contrast to Au₃@LTA, conventional MD simulations (10 ns, 500 K) using the NEP5 model showed facile diffusion of the Au nanocluster (Figure 6c). From the analysis of mean square displacements, we obtain a diffusion coefficient of 1.58 × 10^–11 m²/s for Au₃@CHA—-which is ca. 4 orders of magnitude higher than the corresponding value for Au₃@LTA. These results show how seemingly similar stabilization energies (i.e., −2.10 eV for Au₃@CHA and −2.24 eV for Au₃@LTA) can result in significantly different diffusivities. Although preliminary analysis shows that this phenomenon arises due to the differences in the shape of the confined nanocluster, detailed analysis and applications to other deactivation mechanisms (e.g., Ostwald ripening) are beyond the scope of this work. A similar comparison of Au₅@LTA and Au₅@CHA is shown in the SI (Figures S10 and S11)

Before proceeding further, it is useful to compare our predictions to other related studies in the field. For instance, Bukowski et al.³⁰ have investigated the diffusion of Au_1–4 across the sinusoidal and straight channels of the MFI framework (TS-1) at 473 K using a combination of AIMD, ab initio metadynamics, and nudged elastic band calculations.⁵⁷ Their reported diffusivities (i.e., 4 × 10^–15 m²/s), although obtained at significantly smaller simulation times (i.e., 200 ps, 2 fs time step), are comparable to our predictions obtained using longer simulations (i.e., 10 ns, 0.5 fs time step) and at much lower computational costs. Similarly, we note that the previous work by Heard et al.⁵⁸ has used analogous approaches (i.e., umbrella sampling to obtain barriers using SchNetPack-based models) to investigate several Pt/zeolite systems. Their work also highlights the impact of physical confinement by the cage on the diffusion properties of Pt_1–5 nanoclusters. Similarly, Ma and Liu⁵⁹ used the LASP code⁶⁰ to perform MLP/MD and stochastic surface walking (SSW)⁶¹ to study the formation of PtSnO_x clusters in an MFI zeolite.

Model Scalability

The analysis presented above uses computational models with Au weight loadings (e.g., 17.03 wt % for Figure 3d) that are much higher than those used experimentally.¹⁷ As an example of experimentally relevant materials, we summarize the results of Otto et al.¹⁷ Specifically, using a 1.1 wt % Au@NaLTA material, the authors show that sintering began at 773 K, with significant catalyst deactivation observed at temperatures higher than 823 K. Describing systems with such low metal loadings is computationally intractable using DFT due to system size limitations.

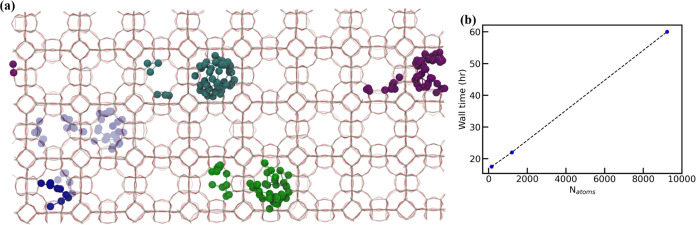
However, these types of simulations can now be readily accessed by using MLPs. For instance, Figure 7a shows the results of a 4 ns NEP5/MD simulation of 1.26 wt % Au@LTA material (Au₁₂Si₃₀₇₂O₆₁₄₄) containing 128 LTA unit cells. This simulation required 60 h on a single NVIDIA RTX A4000 GPU. Consistent with the metadynamics data presented previously, we observed facile diffusion of Au₃ across multiple unit cells. While no sintering events were observed in this specific simulation, the scalability plot in Figure 7b demonstrates the ability to investigate related diffusion and deactivation phenomena at DFT accuracies for a much lower computational cost.

Figure 7.

(a) Pores occupied by each Au₃ nanocluster in an LTA zeolite from a 4 ns MD simulation conducted at 700 K. The system comprises 9228 atoms (128 zeolite pores) of which 12 are Au atoms, which corresponds to a near experimental catalyst weight of 1.26 wt %. (b) A plot showing the wall time required on a single NVIDIA RTX A4000 GPU to run a 10 ns MD simulation of different system sizes in terms of the number of atoms.

Conclusions

In conclusion, this work demonstrates the development and application of a transferable active learning workflow using DFT-based MLPs to describe the stability and dynamics of zeolite-confined Au nanoclusters. The resulting MLP (denoted as NEP5) shows high accuracy for energies and forces and can be used to explore properties that are typically inaccessible by using conventional DFT simulations. Specifically, the NEP5 model has been used to compute ensemble-averaged redispersion penalties (ΔÊ_disp) and framework-induced confinement energies (ΔE_confinement) across a range of Au_n@zeolite materials. Although not explored here, we anticipate that ΔÊ_disp and ΔE_confinement, which are strongly influenced by the size and shape of the zeolite pores, may serve as descriptors to predict the catalytic performance of metal@zeolite catalysts.

We further utilized the NEP5 model to explore the dynamics and diffusion properties of Au nanoclusters within LTA and CHA zeolites. The free energy surfaces and diffusion coefficients, obtained by using well-tempered metadynamics simulations, provide valuable insights into the interplay between the stability and mobility of metal nanoclusters within confined nanoporous environments. We believe these computational workflows can be applicable to study other nanoengineered hybrid materials.

Data Availability Statement

All the data, models, and input files are available via. GitHub: https://github.com/Sonti974948/Data_Au_Zeo_Diffusion.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.4c00978.

• Parity plots comparing energies predicted using polarizable atom interaction neural network (PaiNN) model with corresponding DFT-calculated references (Figure S1); parity plots comparing forces predicted using polarizable atom interaction neural network (PaiNN) model with corresponding DFT-calculated references (Figure S2); progression of loss function for per hundred generations (Figure S3); σ_f uncertainty estimation for the 2nd to 4th iterations of NEP in Au_1–10@LTA (Figure S4); comparison of the parity between NEP and DFT predictions (Figures S5 and S6); Au–Au RDF of Au_1–10 (Figure S7); Au–O RDF of Au_1–10 (Figure S8); averaged free energy surfaces over three independent runs of Au₃@LTA (Figure S9); positions occupied by an Au₅ nanocluster in CHA and LTA zeolites (Figure S10); variations of center of mass of Au₅ in CHA (red) and LTA (blue) as a function of simulation time in (a) x-direction, (b) y-direction, and (c) z-direction (Figure S11); NEP hyperparameters optimization study part I (Table S1); NEP hyperparameters optimization study part II (Table S2); optimal hyperparameters for the NEP potential used for Au@zeolite systems (Table S3); details of the data involved in training different NEP iterations (Table S4); summary of MAEs of energy and force norm for transferability of Au@LTA systems across different temperatures (Table S5); summary of MAEs of energy and force norm for scalability of the NEP MLP across different purely silicious zeolite topologies (Table S6) (PDF)

Author Contributions

^⊥ S.S. and C.S. contributed equally to this work.

The authors declare no competing financial interest.