Abstract
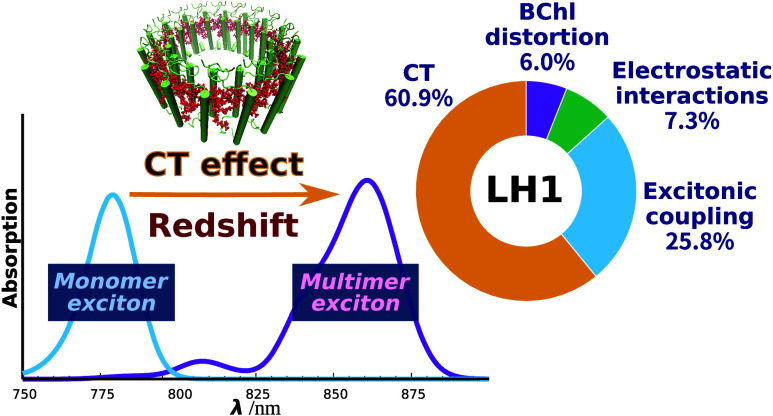
Purple bacteria possess two ring-shaped protein complexes, light-harvesting 1 (LH1) and 2 (LH2), both of which function as antennas for solar energy utilization for photosynthesis but exhibit distinct absorption properties. The two antennas have differing amounts of bacteriochlorophyll (BChl) a; however, their significance in spectral tuning remains elusive. Here, we report a high-precision evaluation of the physicochemical factors contributing to the variation in absorption maxima between LH1 and LH2, namely, BChl a structural distortion, protein electrostatic interaction, excitonic coupling, and charge transfer (CT) effects, as derived from detailed spectral calculations using an extended version of the exciton model, in the model purple bacterium Rhodospirillum rubrum. Spectral analysis confirmed that the electronic structure of the excited state in LH1 extended to the BChl a 16-mer. Further analysis revealed that the LH1-specific redshift (∼61% in energy) is predominantly accounted for by the CT effect resulting from the closer inter-BChl distance in LH1 than in LH2. Our analysis explains how LH1 and LH2, both with chemically identical BChl a chromophores, use distinct physicochemical effects to achieve a progressive redshift from LH2 to LH1, ensuring efficient energy transfer to the reaction center special pair.
Keywords: photosynthesis, light-harvesting antenna, exciton, charge transfer, quantum chemistry
1. Introduction
Photosynthetic reactions are fundamental photochemical processes that transform solar energy into chemical energy, and are the foundation of all biological activity.1 The initiation of photosynthetic reactions is facilitated through an interplay of light absorption by diverse pigments intricately bound to light-harvesting antenna proteins.2 The absorbed solar energy activates a cascading sequence of events leading to charge separation at the photosystem reaction center, a multicomponent membrane-protein complex that is deeply embedded in the photosynthetic membrane.3
The light-harvesting antenna system can be categorized into two distinct subgroups: core antennas, which are directly linked to the reaction center, and peripheral antennas, which pass energy to the core antenna rather than directly to the reaction center.4−6 Within this elaborate system, both core and peripheral antennas contain several chromophores, including bacteriochlorophyll (BChl) and carotenoids in the case of phototrophic bacteria.7,8 The interplay between the core and peripheral antennas enables the rapid transfer of absorbed solar energy from the light-harvesting antenna to the reaction center.9−11 The absorbed solar energy is then transported to two reaction center BChl molecules called the special pair, which functions as the driving force behind the charge separation reaction.5
The effective gain of solar energy is a pivotal requirement for photosynthetic reactions, enabling their fundamental role in biology.12,13 To achieve this, it is essential that phototrophic organisms absorb light across a broad spectrum of wavelengths to ensure the passage of solar energy to the special pair with minimal dissipation.8 Phototrophic organisms have accomplished this task by evolving a variety of unique light-harvesting antenna structures best adapted to the available wavelengths of light in their habitat.
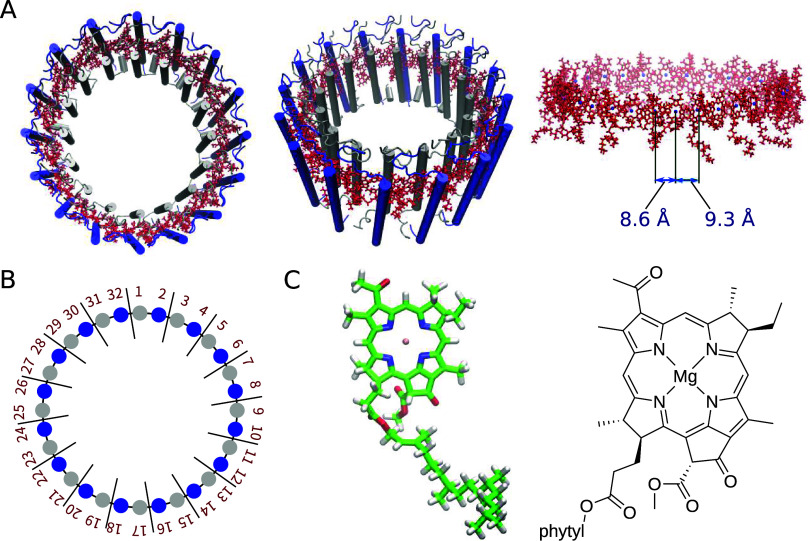
Many purple bacteria possess two light-harvesting complexes, light-harvesting 1 (LH1) and 2 (LH2), which work in concert to transfer captured solar energy to the reaction center (some species of purple bacteria contain only LH1).1,5 Structurally, both LH1 and LH2 typically form ring-shaped protein assemblies with differing radii. Several open ring LH1 structures have also been reported,14−18 but will not be discussed in this study. In Rhodospirillum rubrum, a species that contains only LH1, the LH1 complex comprises a single type of ring assembly of 32 BChl a molecules (Figure 1).19 In contrast, LH2 generally comprises two types of BChl a ring assemblies, namely B800 and B850, with B800 containing 7–9 BChl a molecules and B850 containing 14–18 BChl a molecules.20,21 The formation of these ring assemblies brings about notable alterations in the optical properties of the individual BChl a monomers, resulting in a redshift in the absorption wavelength: in LH2, B800 and B850 exhibit absorption maxima at 800 and 850 nm,1 respectively, and the structure in LH1 exhibits an absorption maximum at 871 nm.22 In the photosynthetic reactions, this difference in absorption maxima induces a stepwise energy transfer, first from LH2 to LH1 and from LH1 to the reaction center.5
Figure 1.
Structures of the LH1 protein complex and the BChl a chromophore. (A) Optimized structure of LH1. The BChl a structures are shown in red. Top view (left), oblique view (center), and side view (right). (B) Schematic of the LH1 ring, which consists of 32 BChl a molecules. (C) Chemical structures of BChl a.
In recent years, numerous structures of LH1 complexes have been determined by X-ray crystallography and cryo-electron microscopy (cryo-EM).19,23−27 These findings have enabled us to investigate the molecular mechanisms underlying the photosynthetic antenna system and to gain deep insights at the atomic level into the fundamental mechanisms and quantum processes of photosynthetic reactions. Collectively, these data provide a more detailed picture of energy transfer from a computational chemistry perspective.
The change in optical properties associated with the formation of cyclic molecular aggregates signifies the impact of intermolecular interactions on the excited states of BChl a.5 Thus, to precisely characterize the excited states of light-harvesting antennas, it is essential that we carry out quantitative calculations for the entire antenna rather than for individual BChl a units. However, light-harvesting antennas such as LH1 and LH2 are extremely large protein complexes, making it impractical to perform comprehensive excited-state calculations based on general quantum chemistry methodologies.
By contrast, the exciton model presents a highly effective approach for performing excited-state calculations on large-scale systems,28 while taking into account both computational accuracy and cost. This model reconstructs the electronic states determined for individual fragments, as demonstrated in previous studies.29,30 Notably, calculations conducted on retinal proteins31 and molecular crystals30 by employing the exciton model have yielded exceptional results in reproducing experimental absorption spectra with remarkable precision. Furthermore, we have successfully applied the exciton model to the calculations of absorption spectra of B800 and B850 within an LH2 antenna, demonstrating its ability to accurately reproduce the absorption spectra and examine the underlying physicochemical factors governing the spectral tuning mechanism.32
The present study aimed to determine the physicochemical origin of the spectral tuning mechanism in LH1. Many research groups have dedicated significant effort to computational studies on the spectral tuning in LH2.5,33−40 As a result, it has been established that the spectral redshift of B850 in LH2 arises primarily from electronic contributions, namely, excitonic coupling and charge transfer (CT) effects. The pioneering works of Hu et al.5 and Alden et al.34 of applying the exciton model to large-scale systems paved the way for further advancements. Building on this foundation, Scholes et al.35 emphasized the crucial role of excitonic coupling in the LH2 spectrum, which they demonstrated through precise calculations using the transition density cube method.41 Additionally, Li et al.,42 Cuppellini et al.,43 and Nottoli et al.44 applied ab initio exciton models to LH2, thereby elucidating the significant CT effects within its spectrum. Furthermore, we successfully quantified the contributions of excitonic coupling and CT effects to the total redshift observed in LH2.32 In contrast to LH2, investigations into the absorption spectrum of LH1 have remained scarce,45−47 leaving the intricate details of its spectral tuning mechanism largely unexplored. This was partly due to computational difficulties for the much larger LH1 complex and partly due to the lack of a relatively high-resolution structure of a typical LH1. The recent determination of several LH1 structures using cryo-EM provides opportunities for further exploration.19
Our previous study on LH2 demonstrated that the absorption spectrum of B850 cannot be replicated by the conventional exciton model (referred to as the monomer exciton model in this paper).32 To address this issue, we developed a dimer exciton model, wherein the BChl a dimer was treated as a unified fragment.32 This modification allowed for the incorporation of the crucial CT effect in the BChl a dimer, thereby enabling a more faithful representation of the spectrum. The present study focuses on the absorption spectrum of R. rubrum LH1,19 the most widely used representative model of bacterial LH1 complexes. The R. rubrum LH1 is characterized by a larger number of BChl a units and a smaller interchromophoric distance than LH2, which prompted us to use an extended version of the dimer exciton model, referred to as the multimer exciton model, to calculate the spectra. By employing this model and analyzing the resulting absorption spectrum, we explored the physicochemical factors associated with the spectral tuning mechanism in LH1.
2. Methods
2.1. Structural Optimization Using the ONIOM Method
The atomic coordinates of LH1 were obtained from the three-dimensional structure determined by cryo-EM (PDB code: 7EQD(19)). Structural optimization was performed using the ONIOM (short for “our own n-layered integrated molecular orbital and molecular mechanics”) method48 to refine the experimental structure, where the entire protein system was partitioned into quantum mechanical (QM) and molecular mechanical (MM) layers described by density functional theory (DFT) at the B3LYP-GD3BJ/6-31G* level49 and by the AMBER99 force field,50 respectively. To avoid the high computational demand of treating all 32 BChl a molecules in an antenna system as a single QM layer, the task was divided into several monomer-based structural optimizations. All 32 BChl a molecules were individually optimized using the ONIOM strategy, where one BChl a molecule was optimized at the QM level while the remaining BChl a molecules were treated at the MM level without relaxation. These structural optimizations using the ONIOM method were carried out using the Gaussian16 program package.51
2.2. Absorption Spectrum Calculation Using the Exciton Model
The absorption spectra of the optimized structure were calculated using the exciton model.28−31 In this model, we used the direct product of the electronic states of the N molecules as a basis (eq 1).
| 1 |
where φka represents the k state (k = ground state (g) or excited state (e)) of molecule a. To maintain clarity, here we focus on two electronic states that involve only molecules a and b:
| 2 |
For the actual calculations, 32 bases were used for LH1. Equation 2 allows for the Hamiltonian matrix to be expressed as
| 3 |
where the diagonal element Ei represents the electronic excitation energy of molecule i, while the off-diagonal element Vab represents the excitonic coupling between molecules a and b. The excitation energies of BChl a molecules were calculated using time-dependent DFT (TDDFT) at the ωB97X/6-31G* level,52 and the excitonic couplings between BChl a molecules were determined using the transition charge from electrostatic potential (TrESP) method.53,54 Electrostatic effects from the protein environment were incorporated into the calculation by assigning point charges using the AMBER99 force field.50 The numerical diagonalization of eq 3 results in the determination of the excited states of the entire system, which are the exciton states. These states are expressed as eigenstates of the Hamiltonian matrix, with the K-th exciton state represented as a linear combination of eq 2:
| 4 |
where ClK represents the expansion coefficient determined by the diagonalization of eq 3. The eigenvalues associated with the excited states of the system serve as exciton energies E′K. The coefficient ClK is used to convert the transition dipole moment of the noninteracting subsystem μl to that of the interacting system μ′K as follows:
| 5 |
Equation 6 was used to obtain the oscillator strength for the K-th exciton state, fK, with the transition dipole moment μ′K and exciton energy E′K.
| 6 |
Finally, the absorption spectrum ε(E) is obtained using eq 7.
| 7 |
where σ is the standard deviation of the Gaussian distribution, which was set to 0.0012 au (0.033 eV).
All the examined BChl a molecules exhibited π–π* excitations with large oscillator strengths. The excitation energies, transition dipole moments, and transition charges for each BChl a molecule were calculated using the Gaussian16 program package.51 Using a Ryzen threadripper pro 5995wx 64-core CPU, the TDDFT calculation for the BChl a 16-mer required 5.97 × 107 s of CPU time.
2.3. Multimer Exciton Model
In this study, we introduced an extended exciton model, named the multimer exciton model, that allows for the inclusion of CT-type excitations in the description of exciton states. The conventional exciton model, which is based on monomeric local excitations, is labeled as the monomer exciton model to distinguish it from the multimer exciton model.
The monomer exciton model straightforwardly uses eq 1 to describe the exciton state as a combination of direct products of N local electronic states associated with N monomeric units. As each BChl a molecule in LH1 serves as a local unit, the 32 local excitations that arise from the 32 BChl a molecules constitute the 32 basis states for the modeling of LH1 assembly (N = 32). Using these bases, the Hamiltonian matrix is written as
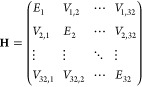 |
8 |
where the subscript of the matrix element indicates the index of the BChl a monomers.
The multimer exciton model replaces monomeric electronic states with multimeric states as the basic building blocks. To simplify the discussion, we consider the dimer exciton model,32 where the BChl a dimer serves as a single unit. In this case, an N-monomer system is considered an aggregate of N/2 dimers. If the first and second excited states of each of the 16 BChl a dimers in LH1 are incorporated into the basis, then the dimension of the Hamiltonian matrix of the dimer exciton model is 32, equal to that of the monomer exciton model. The Hamiltonian matrix of the dimer exciton model, using the redefined elements, is as follows:
 |
9 |
where E(i)Xdenotes the i-th excited state of dimer X (X = 1, 2, ···, 16) and V(i,i′)X,X′ represents the excitonic coupling between the i-th excited state of dimer X and the i′-th excited state of dimer X′. Notably, the off-diagonal elements associated with the identical BChl a dimer are assigned a value of zero, i.e., V(i,i′)X,X = 0 (i ≠ i′).
The multimer exciton model is a simple extension of the dimer exciton model: instead of dimer, the model is constructed with M-mer. We suppose that all N molecules in the system are divided into p M-mers (p = N/M) and the first to s-th states of each M-mer are considered. Then, the Hamiltonian matrix of the multimer exciton model is expressed as follows:
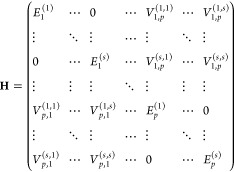 |
10 |
As in the dimer exciton model, the off-diagonal elements associated with the same BChl a multimer are assigned a value of zero.
3. Results and Discussion
3.1. Dependence of Absorption Energy on the Number of BChl a Molecules
Our previous studies revealed how incorporating the CT characteristics of LH2 (B850) BChl a dimers into the exciton model is vital in accurately reproducing the absorption energies.32 Given that the intermolecular Mg–Mg distances between BChl a molecules are smaller in LH1 (∼8.6 Å) than in LH2 (B800: ∼22 Å, B850: ∼9.3 Å), it will be helpful to consider CT involving a larger number of BChl a units in LH1 than the dimers used in LH2 in successfully reproducing the experimental absorption spectra. We therefore explored how varying the number of BChl a molecules in the 32-mer influences the magnitude of the absorption energy, using TDDFT at the ωB97X/6-31G* level.52 In our previous work,32 we showed that TDDFT with the ωB97X functional can accurately yield absorption energy predictions. This was verified by comparing with the results obtained from the complete active space second-order perturbation theory (CASPT2)55 calculations using density matrix renormalization group (DMRG)56 references. Arrangements of varying truncated multimer were constructed by systematically attaching LH1 BChl a molecules one by one in accordance with the structure of LH1, and TDDFT calculations were performed on each resulting arrangement. It should be noted that no exciton model was involved in these calculations. As shown in Figure 2, the absorption energies underwent a remarkable transition from 1.741 eV (712 nm) for the monomer to 1.431 eV (866 nm) for the 17-mer, indicating a redshift as the number of BChl a units increased. Additionally, the values of absorption energies of the 16- and 17-mers were almost indistinguishable, suggesting that the redshift associated with the increasing number of BChl a units reached a saturation point by the 16-mer stage (1.431 eV). Such progressive redshifts followed by saturation are in good agreement with the results of simulation47 and experimental observations.57,58
Figure 2.
Calculated BChl a absorption energies as a function of the number of BChl a molecules; TDDFT at the ωB97X/6-31G* level was employed. The BChl a arrangement considered in the multimer calculations was derived using the LH1 structure as a template. The exciton model was not applied in these calculations.
3.2. Absorption Spectra Calculated Using the Exciton Model
Based on the findings from the TDDFT calculations (Figure 2), we conducted LH1 spectrum computations using a multimer exciton model wherein a BChl a 16-mer was incorporated into a single fragment (referred to as the 16-mer exciton model). The total of 32 BChl a molecules in LH1 were thus considered as two 16-mer fragments. The calculated absorption spectrum of LH1, as depicted in Figure 3, exhibits an absorption peak at 858 nm (1.445 eV), successfully reproducing the experimental value (871 nm, 1.423 eV)22 with a deviation of only 0.022 eV. Furthermore, the shape of the calculated spectrum closely resembled that of the experimental spectrum. These findings strongly suggest that the 16-mer exciton model can accurately compute the absorption spectrum of LH1. The results computed using the 16-mer exciton model therefore served as the foundation for the analysis conducted in this study. It should be noted that Figure 2 illustrates the calculated absorption energy of a single excited state of the BChl a multimer, whereas the absorption peak observed in the calculated spectrum arises from the convolution of the respective intensities from many exciton states. In addition, because the spectrum in Figure 3 (purple line) is calculated using the exciton model, it includes the effects of interactions between the two 16-mer fragments, which are not considered in Figure 2. For these reasons, there is a slight discrepancy between the absorption energy at the 16-mer in Figure 2 and the absorption peak obtained with the 16-mer exciton model in Figure 3.
Figure 3.
Theoretical absorption spectra of LH1 calculated with the multimer (16-mer) exciton model (shown in purple). For comparison, the absorption spectra calculated with the monomer and dimer exciton models are shown in light blue and green, respectively. The experimental spectrum taken from ref (19) is shown in orange.
The absorption spectrum calculated with the 16-mer exciton model was compared with the spectra obtained with the monomer and dimer exciton models. This monomer exciton model corresponds to the conventional exciton model, and treats the BChl a monomer as a building block and accounts for the environmental effects of BChl a aggregation, including the excitonic Coulomb coupling59 between BChl a molecules. The dimer exciton model, on the other hand, treats the BChl a dimer as a building block, incorporating the CT effect within the BChl a dimer as well as the excitonic Coulomb coupling. However, the CT effect involving three or more BChl a molecules is not considered in the dimer exciton model. For the monomer and dimer exciton models, the exciton states were calculated using 32 BChl a monomers and 16 BChl a dimers, respectively. The absorption spectra calculated using the monomer and dimer exciton models exhibited absorption maxima at 777 nm (1.596 eV) and 827 nm (1.499 eV), respectively, as shown in Figure 3. The absorption peak obtained from the dimer exciton model was more red-shifted than that of the monomer exciton model; however, it deviated significantly from the experimental value (871 nm, 1.423 eV). These findings demonstrate the inadequacy of the dimer exciton model in accurately reproducing experimental spectra and underscore the effectiveness of the multimer exciton model.
3.3. Electronic Structure Analysis of Excited States of the BChl a 16-mer
To further confirm the validity of using the BChl a 16-mer as a building block in the exciton model, a detailed analysis was carried out on the electronic structure derived from the TDDFT calculations. It should be noted that this analysis focuses on the excited states of the building blocks used in the exciton model, rather than the exciton states obtained by applying the exciton model.34,60 Here, the localized Kohn–Sham orbitals, obtained through the unitary transformation of the canonical orbitals, were employed for the analysis of the singly excited configuration interaction (CI) coefficients CIA from the localized occupied orbital I to the localized virtual orbital A, as follows:
| 11 |
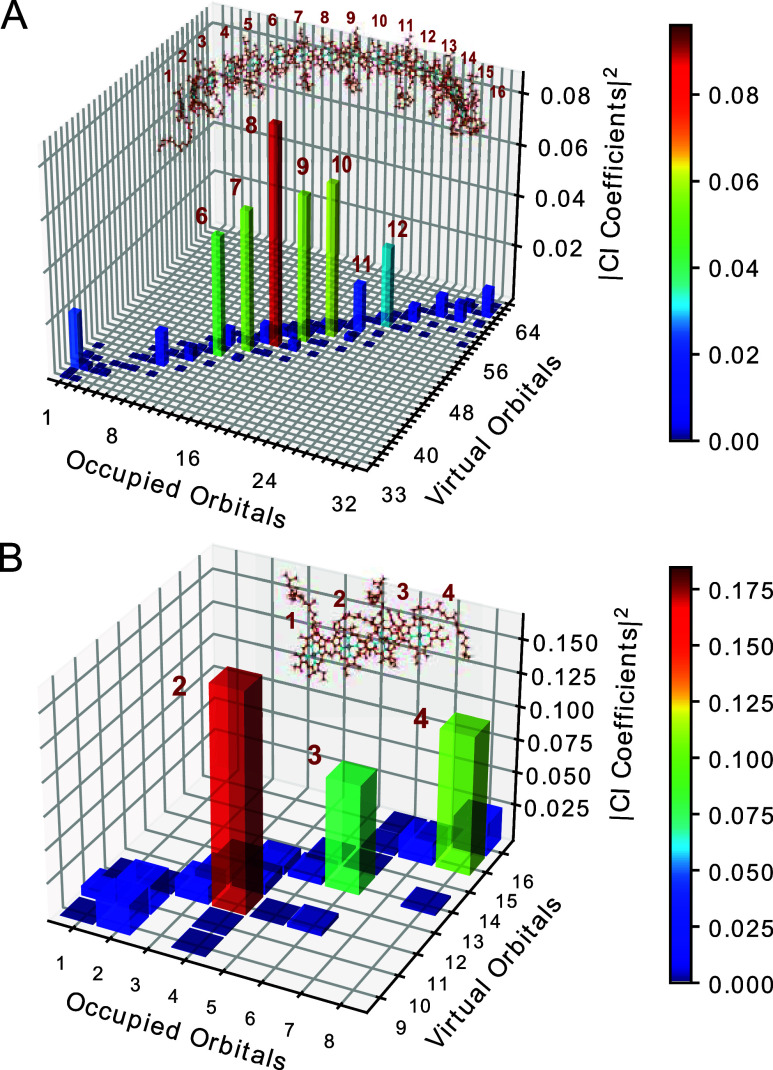
where UOcciI and UViraA denote the unitary matrices for canonical occupied orbital i and virtual orbital a, respectively, and Cia represents the CI coefficient offered by the TDDFT calculation with the canonical orbitals. For simplicity, the excited states in the localized orbital basis were constructed by superposing only the transitions from the highest occupied molecular orbital (HOMO) and HOMO–1 to the lowest unoccupied molecular orbital (LUMO) and LUMO+1 within each BChl a unit. Isosurface plots of the canonical and localized Kohn–Sham orbitals considered are shown in Figures S1 and S2, respectively. The unitary matrices were calculated using Pipek–Mezey localization algorithm61 to maximize the sum of the fragment-based partial charges. This approach revealed the distinctive contributions of individual BChl a molecules, enhancing our understanding of LH1 features. Figure 4A depicts the square of the transformed CI coefficients CIA for the excited state with the largest oscillator strength. The CI coefficients of the canonical orbitals are shown in Figure S3. Notably, the CI coefficients of the diagonal components, which correspond to local excitations in each molecule, peaked at the center of the 16-mer and gradually decayed toward the ends of the 16-mer. In contrast, for the BChl a tetramer, the CI coefficient values remained substantial, even at one of the ends of the tetramer (Figure 4B). These results suggest convergence in the spreading of the electronic structure of the 16-mer, resulting in the observed saturation of the absorption energy, as illustrated in Figure 2. We believe that this finding serves as important evidence supporting the validity of the 16-mer exciton model used in this study.
Figure 4.
Plots of the CI coefficients of the excited state with the largest oscillator strength for (A) BChl a 16-mer and (B) BChl a 4-mer obtained using localized Kohn–Sham orbitals.
3.4. Mechanism of Spectral Tuning
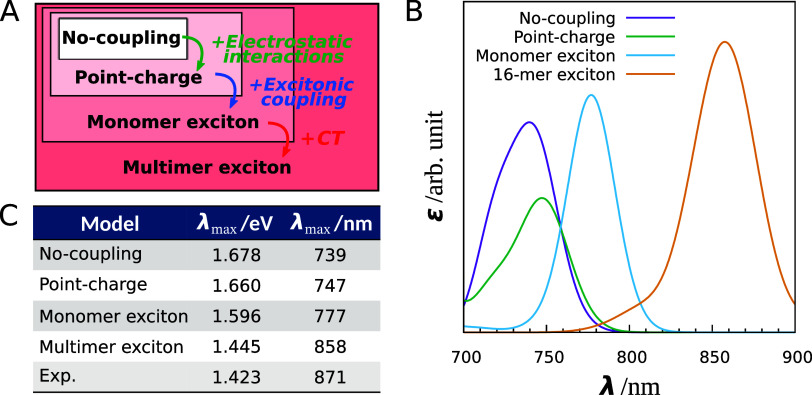
Our exciton model has proven to be reliable in reproducing the absorption wavelengths observed in the experimental spectrum of LH1 and in accurately capturing the redshift feature, which means that our spectrum simulation provides a meaningful approach for understanding the mechanisms behind spectral tuning. We subsequently performed a comprehensive analysis of the spectral redshift in LH1 to determine the contributions of various factors, including electrostatic interaction, excitonic coupling, and CT effects. To achieve this, we conducted additional spectrum calculations using the no-coupling, point-charge, and monomer exciton models, each applied separately to the ONIOM-optimized structure of LH1. Figure 5A illustrates the hierarchical relationships between the four computational models.
Figure 5.
Absorption spectrum analysis using four computational models (the no-coupling, point-charge, monomer exciton, and multimer (16-mer) exciton models). (A) Hierarchy of the four computational models. (B) Theoretical absorption spectra of LH1 calculated with the computational models. (C) Absorption maxima of the calculated spectra.
The no-coupling model can be considered as a Hamiltonian matrix comprising solely diagonal elements and employing the absorption energies of the BChl a monomers in the gas phase. The point-charge model introduces electrostatic effects from the protein environment into diagonal elements, and is an extension of the no-coupling model. Comparing the spectra simulated using the no-coupling and point-charge models allows us to evaluate the influence of electrostatic interactions on the observed redshift. The monomer exciton model accounts for the environmental effect of BChl a aggregation; thus, the differences between the point-charge and monomer exciton models sheds light on the effect of excitonic coupling. By comparing the outcomes of the monomer exciton model and of the multimer exciton model, we can observe the CT effect.
Figure 5B depicts the spectra of LH1 simulated using the four computational models, and Figure 5C shows the absorption peaks for the four models and the corresponding experimental values. The peaks calculated for LH1 under the no-coupling, point-charge, monomer exciton, and multimer exciton models were 1.678 eV (739 nm), 1.660 eV (747 nm), 1.596 eV (777 nm), and 1.445 eV (858 nm), respectively. As the models became more sophisticated, the absorption maxima gradually approached the experimental value of 1.423 eV (871 nm). In particular, the absorption maxima exhibited a remarkable shift in magnitude when the model was changed from the monomer exciton model to the multimer exciton model, highlighting the pronounced impact of the CT effect on the significant redshift observed in LH1.
The initial reference point for the spectral shift in LH1 was established by considering the absorption energy of the fully relaxed geometry of the BChl a monomer in the gas phase (1.693 eV, 732 nm). Accordingly, the redshift observed in the absorption wavelengths of the no-coupling model relative to this reference point can be ascribed to distortion of the molecular structure of BChl a. As shown in Table S5, an absorption energy of 1.630 eV (761 nm) was obtained from the excited-state calculations of the BChl a monomer in acetone, which closely matches the experimental value of 1.606 eV (772 nm).1 While the absorption energy in acetone could be used as a reference point, we chose the absorption energy in the gas phase as our reference point to directly assess the impact of proteins on the spectral shift.
In order to further examine the redshift in LH1 quantitatively, we performed additional physical treatments to simulate the absorption energies. By calculating the differences between the simulated absorption energies, we successfully decomposed the redshift into four factors: structural distortion, electrostatic interactions, excitonic coupling, and CT effects. A graphical representation of the results is shown in Figure 6. We can see that the CT effect has a dominant influence, corresponding to a redshift of 0.151 eV. This effect accounted for approximately 61% of the total redshift energy (0.248 eV). Similarly, the excitonic coupling effect corresponds to a redshift of 0.064 eV, contributing approximately 26% to the overall shift. The CT effect and the excitonic coupling effect together accounted for more than 86% of the observed redshift, emphasizing the importance of intermolecular electronic interactions, as elucidated through quantum mechanical methods, in understanding the spectral redshift of LH1. In contrast, the BChl distortion played the smallest role in the spectral tuning among the four factors analyzed. This finding is consistent with previous reports on water-soluble chlorophyll-binding proteins.62
Figure 6.
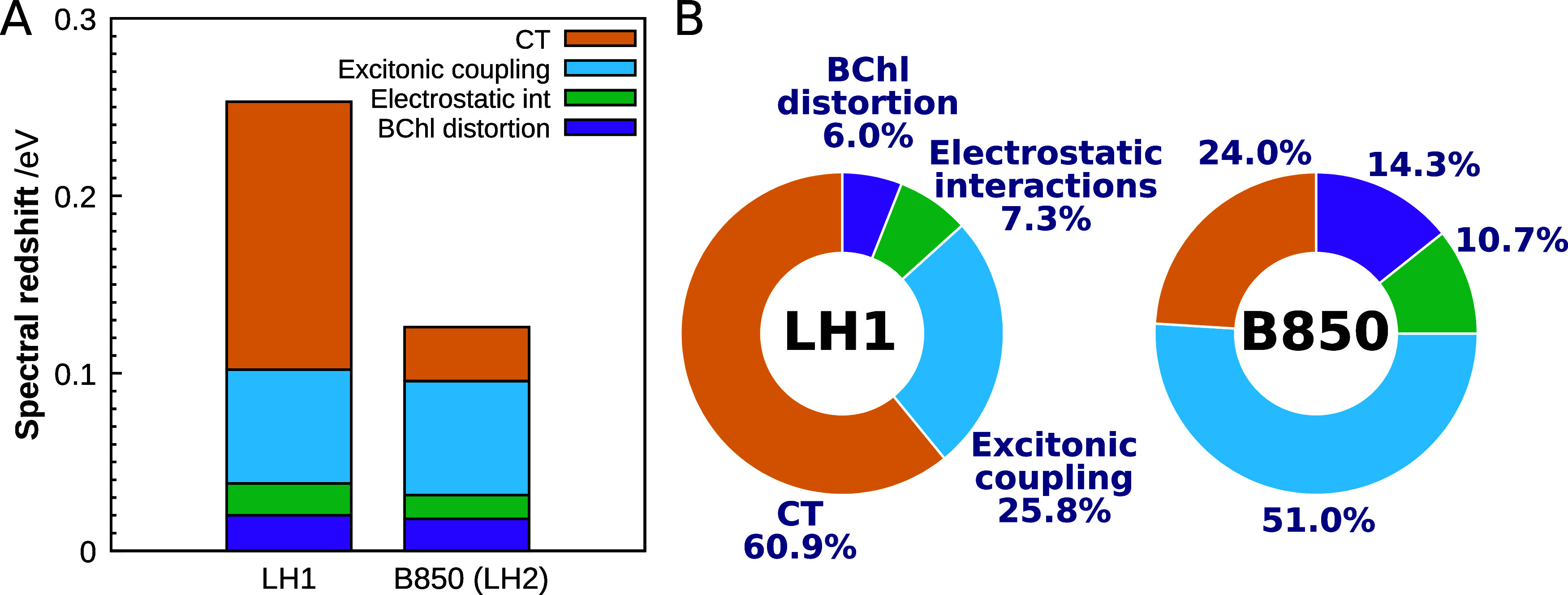
Analysis of spectral tuning. (A) Overall spectral redshift for LH1 and B850 (LH2) decomposed into the BChl a conformational distortion, protein electrostatic interaction, excitonic coupling, and CT effects. (B) Percentage of contribution to the overall redshift by factor in LH1 and B850. The absorption energy used as the reference is of the BChl a monomer with a fully relaxed molecular geometry in the gas phase.
For small intermolecular distances, the Dexter exchange term may play a substantial role in the total excitonic coupling.63 To explore the impact of this term, we employed the transition-density-fragment interaction (TDFI)64,65 method. The calculations revealed that even for the most adjacent pairs of BChl a comprising the ring, the magnitude of the exchange term is relatively small, ranging from 1.07 to 6.77 cm–1 (1.33 × 10–4 to 8.39 × 10–4 eV). This suggests that although the molecules are in close proximity, the exchange term is not the primary factor responsible for the excitonic coupling in this system.
The calculated percentages of contribution of the four factors to the spectral shift observed in LH1 were compared with the results for B850 in LH2. The right chart in Figure 6B illustrates the percentages of contribution to the spectral shift in B850 determined at the same DFT level; the hexamer exciton model was employed for this B850 analysis because the redshift associated with the increasing number of BChl a units reached a saturation point by the hexamer stage (Figure S6). In B850, the excitonic coupling is the dominant contributor to the redshift, followed by the CT effect. This finding is consistent with our previous results obtained using the dimer exciton model,32 suggesting that most of the CT contribution in B850 can be effectively described by using the BChl a dimer as a minimal building block. Notably, the current LH1 calculations reveal a much more significant impact of the CT effect than that observed in B850. It is evident that, despite having similar ring-shaped BChl a assemblies, B850 and LH1 employ distinct physicochemical factors in their spectral tunings (Figure 6B).
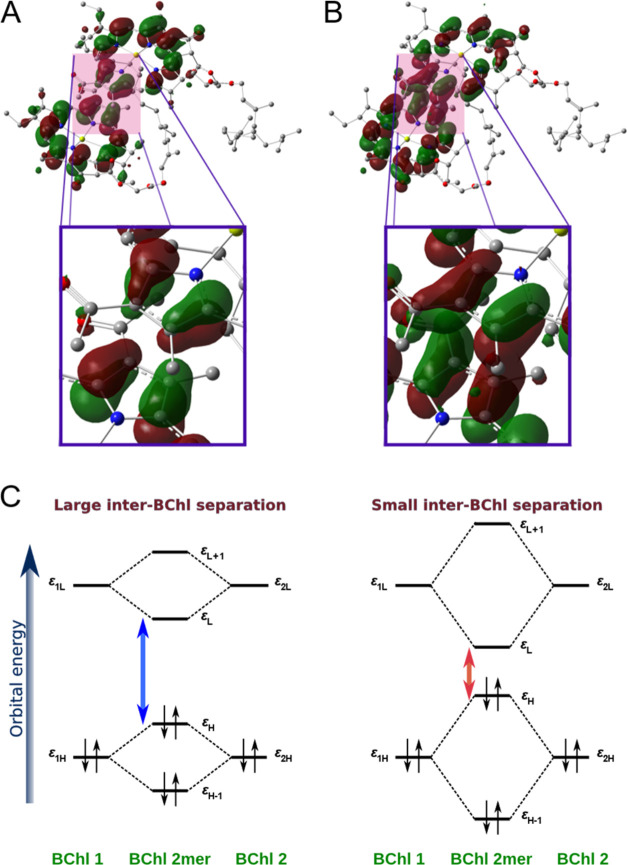
3.5. Intermolecular Orbital Interaction
To gain deeper insights into the CT effect in LH1, we analyzed the Kohn–Sham orbitals and their corresponding energies. To simplify our discussion, we specifically focused on the structure of the BChl a dimer within LH1. As depicted in Figure 7A, the HOMO of the BChl a dimer was observed to have an antibonding character, with the distribution of π orbitals on each molecular plane facing each other in opposite phases. Conversely, the distribution of the LUMO demonstrated a bonding character, as shown in Figure 7B, where the π orbitals on each molecular plane faced each other in the same phases. It is essential to note that molecular orbitals with antibonding character undergo destabilization, whereas orbitals with bonding character experience stabilization.66 By comparing the orbital energies of the monomer and the dimer, we can quantitatively evaluate the influence of these intermolecular orbital interactions (Figure 7C). As summarized in Table S7, the HOMO–LUMO gaps for the monomer and dimer of LH1 were ∼4.375 and 4.185 eV, respectively. Hence, the intermolecular orbital interactions resulted in a reduction of approximately 0.190 eV in the HOMO–LUMO gap of the dimer.
Figure 7.
Analysis of intermolecular orbital interaction. (A) HOMO and (B) LUMO distribution of the BChl a dimer in LH1. At the boundary between two BChl a molecules, the HOMO and LUMO exhibit different color overlap (antibonding character) and same color overlap (bonding characters), respectively. The isovalue of the molecular orbital is set to 0.02. All hydrogen atoms are omitted for clarity. (C) Schematic illustration of the inter-BChl orbital interaction. The HOMO–LUMO gap is large for large inter-BChl distances (left) and small for small inter-BChl distances (right).
A similar analysis was performed for B800 and B850 in LH2. As listed in Table S7, the reductions in the HOMO–LUMO gap due to intermolecular orbital interactions were ∼0.089 and ∼0.117 eV for B800 and B850, respectively. Notably, these values are much smaller than those observed for LH1 (∼0.190 eV), indicating that the order of magnitude of the intermolecular orbital interactions is as follows: LH1 > B850 > B800.
As mentioned earlier, the intermolecular Mg–Mg distances between BChl a molecules in LH1 (∼8.6 Å) are smaller than those in LH2 (B850: ∼9.3 Å, B800: ∼22 Å). The smaller intermolecular distance led to more pronounced intermolecular orbital interactions in LH1, which resulted in a smaller HOMO–LUMO gap (Figure 7C). This notable property contributes to the significant spectral redshift observed in LH1. These findings suggest that the predominant contribution of the CT effect, as shown in Figure 6, originates from large intermolecular orbital interactions.
4. Conclusions
This study aimed to elucidate the spectral tuning mechanism of the BChl a assembly in LH1 using an innovative expansion of the exciton model, which builds on the 16-mer fragmentation of the BChl a assembly. Through our simulations, we successfully reproduced the experimental absorption spectrum of LH1 in the Qy region, including the redshift effect, with an impressive accuracy of 0.022 eV. To the best of our knowledge, our simulated spectrum represents a pioneering demonstration of the necessity of treating the BChl a 16-mer as a single quantum mechanical fragment in accurately reproducing the absorption spectrum of LH1. Based on the calculated absorption maximum, we explored the spectral tuning mechanism within LH1 and examined the spectral shift in relation to the BChl a monomer absorption energy. This analysis encompassed the influence of BChl a structural distortion, electrostatic interactions, excitonic coupling, and CT effects. Remarkably, our findings highlight the indispensable role of the CT effects between BChl a molecules in driving the spectral redshift observed in LH1.
Our previous investigation focused on elucidating the spectral tuning mechanisms of B800 and B850 in LH2.32 We discovered that the primary factor responsible for the redshift in B800 was the electrostatic effect arising from the surrounding protein environment, whereas in B850, it was the result of excitonic coupling among BChl a molecules (Figure 6B). Although the CT effect played a notable role in B850, its influence was small compared with the profound impact of excitonic coupling. In contrast, our current work demonstrates that the spectral tuning observed in LH1 can be predominantly attributed to the extent of CT rather than to excitonic coupling.
Our calculations demonstrate a progressive redshift from LH2 to LH1, facilitating the efficient transfer of absorbed solar energy to the special pair. Although these antenna systems consist of chemically identical chromophores (BChl a), our analysis revealed that LH1 and LH2 achieve precise spectral tuning by exploiting distinct physicochemical effects.
Acknowledgments
This study was supported by JSPS KAKENHI (grant no. 20K05430 to K.J.F. and JPJSBP120237705, JPJSBP120229601, 21H01881 and 22K21346 to T.Y.), JST CREST (grant no. JPMJCR21O5 to K.J.F.), MEXT Promotion of Development of a Joint Usage/Research System Project CURE (grant no. JPMXP1323015482), and for the CPU time grant from the Research Center for Computational Science, Okazaki, Japan (23-IMS-C087). The authors thank Professor M. T. Madigan and C. Ushiro for their helpful comments on the manuscript.
Glossary
Abbreviations
- LH1
light-harvesting 1
- LH2
light-harvesting 2
- BChl
bacteriochlorophyll
- CT
charge transfer
- cryo-EM
cryo-electron microscopy
- ONIOM
our own n-layered integrated molecular orbital and molecular mechanics
- QM
quantum mechanical
- MM
molecular mechanical
- DFT
density functional theory
- TDDFT
time-dependent density functional theory
- TrESP
transition charge from electrostatic potential
- CASPT2
complete active space second-order perturbation theory
- DMRG
density matrix renormalization group
- CI
configuration interaction
- HOMO
highest occupied molecular orbital
- LUMO
lowest unoccupied molecular orbital
- TDFI
transition-density-fragment interaction
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphyschemau.4c00022.
CI coefficients (Cia) of the excited state for the BChl a 4-mer/16-mer obtained using canonical/localized Kohn–Sham orbitals; absorption energies of BChl a calculated using TDDFT; calculated absorption energies of BChl a in LH1; HOMO–LUMO gaps of the BChl a monomer and dimer in LH1, B850, and B800; excitonic couplings (|V|) between adjacent BChl a in LH1/B850; plots of canonical/localized Kohn–Sham orbitals for the BChl a 4-mer/16-mer considered in the CI coefficient analysis; plots of the CI coefficients of the excited states for the BChl a 4-mer/16-mer obtained using canonical Kohn–Sham orbitals; calculated B850 BChl a absorption energies as a function of the number of BChl a molecules; differences in absorption energy between BChl a multimers; theoretical absorption spectra of LH1 calculated with the octamer exciton model; and atomic coordinates of the optimized BChl a molecules (PDF)
Author Contributions
K.J.F. and Z.-Y.W.-O. designed the project. R.T., K.J.F., and T.Y. performed computations and data analysis. K.J.F. wrote the original draft. T.Y. and Z.-Y.W.-O. edited the manuscript. CRediT: Kazuhiro J. Fujimoto conceptualization, data curation, formal analysis, investigation, writing-original draft; Rio Tsuji data curation, investigation; Zheng-Yu Wang-Otomo conceptualization, writing-review & editing; Takeshi Yanai formal analysis, investigation, writing-review & editing.
The authors declare no competing financial interest.
Supplementary Material
References
- Cogdell R. J.; Gall A.; Köhler J. The architecture and function of the light-harvesting apparatus of purple bacteria: from single molecules to in vivo membranes. Q. Rev. Biophys. 2006, 39, 227–324. 10.1017/S0033583506004434. [DOI] [PubMed] [Google Scholar]
- Scholes G. D.; Fleming G. R.; Olaya-Castro A.; van Grondelle R. Lessons from nature about solar light harvesting. Nat. Chem. 2011, 3, 763–774. 10.1038/nchem.1145. [DOI] [PubMed] [Google Scholar]
- Shen J.-R. The structure of photosystem II and the mechanism of water oxidation in photosynthesis. Annu. Rev. Plant Biol. 2015, 66, 23–48. 10.1146/annurev-arplant-050312-120129. [DOI] [PubMed] [Google Scholar]
- Cheng Y.-C.; Fleming G. R. Dynamics of Light Harvesting in Photosynthesis. Annu. Rev. Phys. Chem. 2009, 60, 241–262. 10.1146/annurev.physchem.040808.090259. [DOI] [PubMed] [Google Scholar]
- Hu X.; Damjanović A.; Ritz T.; Schulten K. Architecture and mechanism of the light-harvesting apparatus of purple bacteria. Proc. Natl. Acad. Sci. U.S.A. 1998, 95, 5935–5941. 10.1073/pnas.95.11.5935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krauß N.; Schubert W.-D.; Klukas O.; Fromme P.; Witt H. T.; Saenger W. Photosystem I at 4 Å resolution represents the first structural model of a joint photosynthetic reaction centre and core antenna system. Nat. Struct. Biol. 1996, 3, 965–973. 10.1038/nsb1196-965. [DOI] [PubMed] [Google Scholar]
- Scholes G. D. Quantum-Coherent Electronic Energy Transfer: Did Nature Think of It First?. J. Phys. Chem. Lett. 2010, 1, 2–8. 10.1021/jz900062f. [DOI] [Google Scholar]
- Croce R.; van Amerongen H. Light harvesting in oxygenic photosynthesis: Structural biology meets spectroscopy. Science 2020, 369, eaay2058 10.1126/science.aay2058. [DOI] [PubMed] [Google Scholar]
- Sundström V.; Pullerits T.; van Grondelle R. Photosynthetic Light-Harvesting: Reconciling Dynamics and Structure of Purple Bacterial LH2 Reveals Function of Photosynthetic Unit. J. Phys. Chem. B 1999, 103, 2327–2346. 10.1021/jp983722+. [DOI] [Google Scholar]
- Wang D.; Fiebig O. C.; Harris D.; Toporik H.; Ji Y.; Chuang C.; Nairat M.; Tong A. L.; Ogren J. I.; Hart S. M.; et al. Elucidating interprotein energy transfer dynamics within the antenna network from purple bacteria. Proc. Natl. Acad. Sci. U.S.A. 2023, 120, e2220477120 10.1073/pnas.2220477120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q.; Orcutt K.; Cook R. L.; Sabines-Chesterking J.; Tong A. L.; Schlau-Cohen G. S.; Zhang X.; Fleming G. R.; Whaley K. B. Single-photon absorption and emission from a natural photosynthetic complex. Nature 2023, 619, 300–304. 10.1038/s41586-023-06121-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris M. A.; Jiang J.; Niedzwiedzki D. M.; Jiao J.; Taniguchi M.; Kirmaier C.; Loach P. A.; Bocian D. F.; Lindsey J. S.; Holten D.; Parkes-Loach P. S. Versatile design of biohybrid light-harvesting architectures to tune location, density, and spectral coverage of attached synthetic chromophores for enhanced energy capture. Photosynth. Res. 2014, 121, 35–48. 10.1007/s11120-014-9993-8. [DOI] [PubMed] [Google Scholar]
- Yoneda Y.; Noji T.; Katayama T.; Mizutani N.; Komori D.; Nango M.; Miyasaka H.; Itoh S.; Nagasawa Y.; Dewa T. Extension of Light-Harvesting Ability of Photosynthetic Light-Harvesting Complex 2 (LH2) through Ultrafast Energy Transfer from Covalently Attached Artificial Chromophores. J. Am. Chem. Soc. 2015, 137, 13121–13129. 10.1021/jacs.5b08508. [DOI] [PubMed] [Google Scholar]
- Cao P.; Bracun L.; Yamagata A.; Christianson B. M.; Negami T.; Zou B.; Terada T.; Canniffe D. P.; Shirouzu M.; Li M.; Liu L. N. Structural basis for the assembly and quinone transport mechanisms of the dimeric photosynthetic RC–LH1 supercomplex. Nat. Commun. 2022, 13, 1977 10.1038/s41467-022-29563-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swainsbury D. J. K.; Qian P.; Jackson P. J.; Faries K. M.; Niedzwiedzki D. M.; Martin E. C.; Farmer D. A.; Malone L. A.; Thompson R. F.; Ranson N. A.; et al. Structures of Rhodopseudomonas palustris RC-LH1 complexes with open or closed quinone channels. Sci. Adv. 2021, 7, eabe2631 10.1126/sciadv.abe2631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swainsbury D. J. K.; Qian P.; Hitchcock A.; Hunter C. N. The structure and assembly of reaction centre-light-harvesting 1 complexes in photosynthetic bacteria. Biosci. Rep. 2023, 43, BSR20220089 10.1042/BSR20220089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L.-N.; Bracun L.; Li M. Structural diversity and modularity of photosynthetic RC–LH1 complexes. Trends Microbiol. 2024, 32, 38–52. 10.1016/j.tim.2023.06.002. [DOI] [PubMed] [Google Scholar]
- Kimura Y.; Tani K.; Madigan M. T.; Wang-Otomo Z.-Y. Advances in the Spectroscopic and Structural Characterization of Core Light-Harvesting Complexes from Purple Phototrophic Bacteria.. J. Phys. Chem. B 2023, 127, 6–17. 10.1021/acs.jpcb.2c06638. [DOI] [PubMed] [Google Scholar]
- Tani K.; Kanno R.; Ji X.-C.; Hall M.; Yu L.-J.; Kimura Y.; Madigan M. T.; Mizoguchi A.; Humbel B. M.; Wang-Otomo Z.-Y. Cryo-EM Structure of the Photosynthetic LH1-RC Complex from Rhodospirillum rubrum. Biochemistry 2021, 60, 2483–2491. 10.1021/acs.biochem.1c00360. [DOI] [PubMed] [Google Scholar]
- Papiz M. Z.; Prince S. M.; Howard T.; Cogdell R. J.; Isaacs N. W. The Structure and Thermal Motion of the B800–850 LH2 Complex from Rps. acidophila at 2.0 Å Resolution and 100 K: New Structural Features and Functionally Relevant Motions. J. Mol. Biol. 2003, 326, 1523–1538. 10.1016/S0022-2836(03)00024-X. [DOI] [PubMed] [Google Scholar]
- Gardiner A. T.; Naydenova K.; Castro-Hartmann P.; Nguyen-Phan T. C.; Russo C. J.; Sader K.; Hunter C. N.; Cogdell R. J.; Qian P. The 2.4 Å cryo-EM structure of a heptameric light-harvesting 2 complex reveals two carotenoid energy transfer pathways. Sci. Adv. 2021, 7, eabe4650 10.1126/sciadv.abe4650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satoh I.; Gotou K.; Nagatsuma S.; Nagashima K. V. P.; Kobayashi M.; Yu L.-J.; Madigan M. T.; Kimura Y.; Wang-Otomo Z.-Y. Selective expression of light-harvesting complexes alters phospholipid composition in the intracytoplasmic membrane and core complex of purple phototrophic bacteria. Biochim. Biophys. Acta, Bioenerg. 2023, 1864, 149001 10.1016/j.bbabio.2023.149001. [DOI] [PubMed] [Google Scholar]
- Gisriel C. J.; Wang J.; Liu J.; Flesher D. A.; Reiss K. M.; Huang H.-L.; Yang K. R.; Armstrong W. H.; Gunner M. R.; Batista V. S.; et al. High-resolution cryo-electron microscopy structure of photosystem II from the mesophilic cyanobacterium, Synechocystis sp. PCC 6803. Proc. Natl. Acad. Sci. U.S.A. 2022, 119, e2116765118 10.1073/pnas.2116765118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheng X.; Watanabe A.; Li A.; Kim E.; Song C.; Murata K.; Song D.; Minagawa J.; Liu Z. Structural insight into light harvesting for photosystem II in green algae. Nat. Plants 2019, 5, 1320–1330. 10.1038/s41477-019-0543-4. [DOI] [PubMed] [Google Scholar]
- Pi X.; Tian L.; Dai H.-E.; Qin X.; Cheng L.; Kuang T.; Sui S.-F.; Shen J.-R. Unique organization of photosystem I–light-harvesting supercomplex revealed by cryo-EM from a red alga. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, 4423–4428. 10.1073/pnas.1722482115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su X.; Ma J.; Wei X.; Cao P.; Zhu D.; Chang W.; Liu Z.; Zhang X.; Li M. Structure and assembly mechanism of plant C2S2M2-type PSII-LHCII supercomplex. Science 2017, 357, 815–820. 10.1126/science.aan0327. [DOI] [PubMed] [Google Scholar]
- Roszak A. W.; Howard T. D.; Southall J.; Gardiner A. T.; Law C. J.; Isaacs N. W.; Cogdell R. J. Crystal structure of the RC-LH1 core complex from Rhodopseudomonas palustris. Science 2003, 302, 1969–1972. 10.1126/science.1088892. [DOI] [PubMed] [Google Scholar]
- Frenkel J. On the transformation of light into heat in solids. I. Phys. Rev. 1931, 37, 17 10.1103/PhysRev.37.17. [DOI] [Google Scholar]
- Fujimoto K. J. Transition-density-fragment interaction approach for exciton-coupled circular dichroism spectra. J. Chem. Phys. 2010, 133, 124101 10.1063/1.3480015. [DOI] [PubMed] [Google Scholar]
- Fujimoto K. J.; Kitamura C. A theoretical study of crystallochromy: Spectral tuning of solid-state tetracenes. J. Chem. Phys. 2013, 139, 084511 10.1063/1.4819133. [DOI] [PubMed] [Google Scholar]
- Fujimoto K. J.; Balashov S. P. Vibronic coupling effect on circular dichroism spectrum: Carotenoid–retinal interaction in xanthorhodopsin. J. Chem. Phys. 2017, 146, 095101 10.1063/1.4977045. [DOI] [Google Scholar]
- Fujimoto K. J.; Minoda T.; Yanai T. Spectral tuning mechanism of photosynthetic light-harvesting complex II revealed by ab initio dimer exciton model. J. Phys. Chem. B 2021, 125, 10459–10470. 10.1021/acs.jpcb.1c04457. [DOI] [PubMed] [Google Scholar]
- Curutchet C.; Mennucci B. Quantum Chemical Studies of Light Harvesting. Chem. Rev. 2017, 117, 294–343. 10.1021/acs.chemrev.5b00700. [DOI] [PubMed] [Google Scholar]
- Alden R. G.; Johnson E.; Nagarajan V.; Parson W. W.; Law C. J.; Cogdell R. G. Calculations of Spectroscopic Properties of the LH2 Bacteriochlorophyll-Protein Antenna Complex from Rhodopseudomonas acidophila. J. Phys. Chem. B 1997, 101, 4667–4680. 10.1021/jp970005r. [DOI] [Google Scholar]
- Scholes G. D.; Gould I. R.; Cogdell R. J.; Fleming G. R. Ab Initio Molecular Orbital Calculations of Electronic Couplings in the LH2 BacterialLight-Harvesting Complex of Rps. Acidophila. J. Phys. Chem. B 1999, 103, 2543–2553. 10.1021/jp9839753. [DOI] [Google Scholar]
- Linnanto J.; Freiberg A.; Korppi-Tommola J. Quantum Chemical Simulations of Excited-State Absorption Spectra of Photosynthetic Bacterial Reaction Center and Antenna Complexes. J. Phys. Chem. B 2011, 115, 5536–5544. 10.1021/jp111340w. [DOI] [PubMed] [Google Scholar]
- van der Vegte C. P.; Prajapati J. D.; Kleinekathöfer U.; Knoester J.; Jansen T. L. C. Atomistic Modeling of Two-Dimensional Electronic Spectra and Excited-State Dynamics for a Light Harvesting 2 Complex. J. Phys. Chem. B 2015, 119, 1302–1313. 10.1021/jp509247p. [DOI] [PubMed] [Google Scholar]
- Segatta F.; Cupellini L.; Jurinovich S.; Mukamel S.; Dapor M.; Taioli S.; Garavelli M.; Mennucci B. A Quantum Chemical Interpretation of Two-Dimensional Electronic Spectroscopy of Light-Harvesting Complexes. J. Am. Chem. Soc. 2017, 139, 7558–7567. 10.1021/jacs.7b02130. [DOI] [PubMed] [Google Scholar]
- Cupellini L.; Caprasecca S.; Guido C. A.; Müh F.; Renger T.; Mennucci B. Coupling to Charge Transfer States is the Key to Modulate the Optical Bands for Efficient Light Harvesting in Purple Bacteria. J. Phys. Chem. Lett. 2018, 9, 6892–6899. 10.1021/acs.jpclett.8b03233. [DOI] [PubMed] [Google Scholar]
- Bold B. M.; Sokolov M.; Maity S.; Wanko M.; Dohmen P. M.; Kranz J. J.; Kleinekathöfer U.; Höfener S.; Elstner M. Benchmark and performance of long-rangecorrected time-dependent density functional tight binding (LC-TD-DFTB) on rhodopsins and light-harvesting complexes. Phys. Chem. Chem. Phys. 2020, 22, 10500–10518. 10.1039/C9CP05753F. [DOI] [PubMed] [Google Scholar]
- Krueger B. P.; Scholes G. D.; Fleming G. R. Calculation of Couplings and Energy-Transfer Pathways between the Pigments of LH2 by the ab Initio Transition Density Cube Method. J. Phys. Chem. B 1998, 102, 5378–5386. 10.1021/jp9811171. [DOI] [Google Scholar]
- Li X.; Parrish R. M.; Liu F.; Schumacher S. I. L. K.; Martínez T. J. An Ab Initio Exciton Model Including Charge-Transfer Excited States. J. Chem. Theory Comput. 2017, 13, 3493–3504. 10.1021/acs.jctc.7b00171. [DOI] [PubMed] [Google Scholar]
- Cupellini L.; Jurinovich S.; Campetella M.; Caprasecca S.; Guido C. A.; Kelly S. M.; Gardiner A. T.; Cogdell R.; Mennucci B. An Ab Initio Description of the Excitonic Properties of LH2 and Their Temperature Dependence. J. Phys. Chem. B 2016, 120, 11348–11359. 10.1021/acs.jpcb.6b06585. [DOI] [PubMed] [Google Scholar]
- Nottoli M.; Jurinovich S.; Cupellini L.; Gardiner A. T.; Cogdell R.; Mennucci B. The role of charge-transfer states in the spectral tuning of antenna complexes of purple bacteria. Photosynth. Res. 2018, 137, 215–226. 10.1007/s11120-018-0492-1. [DOI] [PubMed] [Google Scholar]
- Kozlov M. I.; Poddubnyy V. V.; Glebov I. O.; Belov A. S.; Khokhlov D. V. Ab initio calculation of excitonic Hamiltonian of light-harvesting complex LH1 of Thermochromatium tepidum. Chem. Phys. Lett. 2016, 645, 48–52. 10.1016/j.cplett.2015.12.031. [DOI] [Google Scholar]
- Kozlov M. I.; Poddubnyy V. V.; Glebov I. O. Calculation of the Excited States Properties of LH1 Complex of Thermochromatium tepidum. J. Comput. Chem. 2018, 39, 1599–1606. 10.1002/jcc.25232. [DOI] [PubMed] [Google Scholar]
- Westerhuis W. H. J.; Hunter C. N.; van Grondelle R.; Niederman R. A. Modeling of Oligomeric-State Dependent Spectral Heterogeneity in the B875 Light-Harvesting Complex of Rhodobacter sphaeroides by Numerical Simulation. J. Phys. Chem. B 1999, 103, 7733–7742. 10.1021/jp991816t. [DOI] [Google Scholar]
- Svensson M.; Humbel S.; Froese R. D. J.; Matsubara T.; Sieber S.; Morokuma K. ONIOM: A Multilayered Integrated MO+MM Method for Geometry Optimizations and Single Point Energy Predictions. A Test for Diels-Alder Reactions and Pt(P(t-Bu)3)2+H2 Oxidative Addition. J. Phys. Chem. A 1996, 100, 19357–19363. 10.1021/jp962071j. [DOI] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Wang J.; Cieplak P.; Kollman P. A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules?. J. Comput. Chem. 2000, 21, 1049–1074. . [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.. et al. Gaussian 16, Rev. C.01; Gaussian, Inc.: Wallingford, CT, 2019.
- Chai J.-D.; Head-Gordon M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106 10.1063/1.2834918. [DOI] [PubMed] [Google Scholar]
- Madjet M. E.; Abdurahman A.; Renger T. Intermolecular Coulomb Couplings from Ab Initio Electrostatic Potentials: Application to Optical Transitions of Strongly Coupled Pigments in Photosynthetic Antennae and Reaction Centers. J. Phys. Chem. B 2006, 110, 17268–17281. 10.1021/jp0615398. [DOI] [PubMed] [Google Scholar]
- Fujimoto K. J. Electronic coupling calculations with transition charges, dipoles, and quadrupoles derived from electrostatic potential fitting. J. Chem. Phys. 2014, 141, 214105 10.1063/1.4902758. [DOI] [PubMed] [Google Scholar]
- Andersson K.; Malmqvist P. A.; Roos B. O.; Sadlej A. J.; Wolinski K. Second-order perturbation theory with a casscf reference function. J. Phys. Chem. A 1990, 94, 5483–5488. 10.1021/j100377a012. [DOI] [Google Scholar]
- Yanai T.; Saitow M.; Xiong X.-G.; Chalupský J.; Kurashige Y.; Guo S.; Sharma S. Multistate Complete-Active-Space Second-Order Perturbation Theory Based on Density Matrix Renormalization Group Reference States. J. Chem. Theory Comput. 2017, 13, 4829–4840. 10.1021/acs.jctc.7b00735. [DOI] [PubMed] [Google Scholar]
- Pandit A.; Visschers R. W.; van Stokkum I. H. M.; Kraayenhof R.; van Grondelle R. Oligomerization of Light-Harvesting I Antenna Peptides of Rhodospirillum rubrum. Biochemistry 2001, 40, 12913–12924. 10.1021/bi010163f. [DOI] [PubMed] [Google Scholar]
- Westerhuis W. H. J.; Sturgis J. N.; Ratcliffe E. C.; Hunter C. N.; Niederman R. A. Isolation, Size Estimates, and Spectral Heterogeneity of an Oligomeric Series of Light-Harvesting 1 Complexes from Rhodobacter sphaeroides. Biochemistry 2002, 41, 8698–8707. 10.1021/bi011663b. [DOI] [PubMed] [Google Scholar]
- Förster T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. Phys. 1948, 437, 55–75. 10.1002/andp.19484370105. [DOI] [Google Scholar]
- Kramer B.; MacKinnon A. Localization: theory and experiment. Rep. Prog. Phys. 1993, 56, 1469 10.1088/0034-4885/56/12/001. [DOI] [Google Scholar]
- Pipek J.; Mezey P. G. A fast intrinsic localization procedure applicable for ab initio and semiempirical linear combination of atomic orbital wave functions. J. Chem. Phys. 1989, 90, 4916–4926. 10.1063/1.456588. [DOI] [Google Scholar]
- Lahav Y.; Noy D.; Schapiro I. Spectral tuning of chlorophylls in proteins – electrostatics vs. ring deformation. Phys. Chem. Chem. Phys. 2021, 23, 6544–6551. 10.1039/D0CP06582J. [DOI] [PubMed] [Google Scholar]
- Dexter D. L. A Theory of Sensitized Luminescence in Solids. J. Chem. Phys. 1953, 21, 836–850. 10.1063/1.1699044. [DOI] [Google Scholar]
- Fujimoto K. J.; Hayashi S. Electronic Coulombic Coupling of Excitation-Energy Transfer in Xanthorhodopsin. J. Am. Chem. Soc. 2009, 131, 14152–14153. 10.1021/ja905697n. [DOI] [PubMed] [Google Scholar]
- Fujimoto K. J. Transition-density-fragment interaction combined with transfer integral approach for excitation-energy transfer via charge-transfer states. J. Chem. Phys. 2012, 137, 034101 10.1063/1.4733669. [DOI] [PubMed] [Google Scholar]
- Kazmaier P. M.; Hoffmann R. A Theoretical Study of Crystallochromy. Quantum Interference Effects in the Spectra of Perylene Pigments. J. Am. Chem. Soc. 1994, 116, 9684–9691. 10.1021/ja00100a038. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.