Abstract
Background
There is a growing trend to include non-randomised studies of interventions (NRSIs) in rare events meta-analyses of randomised controlled trials (RCTs) to complement the evidence from the latter. An important consideration when combining RCTs and NRSIs is how to address potential bias and down-weighting of NRSIs in the pooled estimates. The aim of this study is to explore the use of a power prior approach in a Bayesian framework for integrating RCTs and NRSIs to assess the effect of rare events.
Methods
We proposed a method of specifying the down-weighting factor based on judgments of the relative magnitude (no information, and low, moderate, serious and critical risk of bias) of the overall risk of bias for each NRSI using the ROBINS-I tool. The methods were illustrated using two meta-analyses, with particular interest in the risk of diabetic ketoacidosis (DKA) in patients using sodium/glucose cotransporter-2 (SGLT-2) inhibitors compared with active comparators, and the association between low-dose methotrexate exposure and melanoma.
Results
No significant results were observed for these two analyses when the data from RCTs only were pooled (risk of DKA: OR = 0.82, 95% confidence interval (CI): 0.25–2.69; risk of melanoma: OR = 1.94, 95%CI: 0.72–5.27). When RCTs and NRSIs were directly combined without distinction in the same meta-analysis, both meta-analyses showed significant results (risk of DKA: OR = 1.50, 95%CI: 1.11–2.03; risk of melanoma: OR = 1.16, 95%CI: 1.08–1.24). Using Bayesian analysis to account for NRSI bias, there was a 90% probability of an increased risk of DKA in users receiving SGLT-2 inhibitors and an 91% probability of an increased risk of melanoma in patients using low-dose methotrexate.
Conclusions
Our study showed that including NRSIs in a meta-analysis of RCTs for rare events could increase the certainty and comprehensiveness of the evidence. The estimates obtained from NRSIs are generally considered to be biased, and the possible influence of NRSIs on the certainty of the combined evidence needs to be carefully investigated.
Supplementary Information
The online version contains supplementary material available at 10.1186/s12874-024-02347-7.
Keywords: Meta-analysis, Rare events, Non-randomized studies of interventions, Risk of bias
Introduction
Evidence from high-quality randomized controlled trials (RCTs) is considered the gold standard for assessing the relative effects of health interventions [1]. However, RCTs have a strictly experimental setting and their inclusion criteria may limit their generalizability to real-world clinical practice [2]. Meta-analyses often ignore evidence from non-randomized studies of interventions (NRSIs) because their estimates of relative effects are more likely to be biased, especially if bias has not been adequately addressed. In recent years, there has been considerable development in the methods used in NRSIs, with a particular focus on causal inference [3]. NRSIs could complement the evidence provided by RCTs and potentially address some of their limitations, especially in cases where an RCT may be impossible to conduct (e.g., rare diseases), inadequate (e.g., lower external validity), or inappropriate (e.g., when studying rare adverse or long-term events) [4].
The study of rare events is one scenario in which evidence from NRSIs complements that from RCTs [4]. Rare events often occur when investigating rare adverse effects of health interventions. The results of RCTs may be very sparse due to smaller sample sizes and short follow-up periods [5], with some trials not observing any events at all, resulting in low statistical power [6]. NRSIs are important for studying rare adverse events because of the larger sample size and longer follow-up up [7]. NRSIs are increasingly included in systematic reviews and meta-analyses of rare adverse events evaluations to complement the evidence from RCTs [8]. Several tools, frameworks and guidelines exist to facilitate the combination of evidence from RCTs and NRSIs [4, 9–11]. However, the inclusion of NRSIs in a meta-analysis of RCTs is a complex challenge because estimates derived from NRSIs should be interpreted with caution [12].
Bun et al. [8] reviewed meta-analyses that included both RCTs and NRSIs published between 2014 and 2018 in five leading journals and the Cochrane Database of Systematic Reviews. They found that 53% of studies combined RCTs and NRSIs in the same meta-analysis without distinction. However, there are fundamental differences between RCTs and NRSIs in design, conduct, data collection, analysis, etc [4]. These differences may raise questions about potential bias and conflicting evidence between studies. Therefore, combining results and ignoring design types may lead to misleading conclusions [13]. Statistical methods for generalized evidence synthesis approaches have been proposed to combine evidence from RCTs and NRSIs [13–15]. Verde and Ohmann [14] have provided a comprehensive review of the methods and applications of combining the evidence from NRSIs and RCTs over the last two decades. They categorized statistical approaches into four main groups: the confidence profile method [16], cross-design synthesis [17], direct likelihood bias modelling, and Bayesian hierarchical modelling [18]. Bayesian methods are gaining increasing attention because of their outstanding flexibility in combining information from multiple sources. Verde [15] recently proposed a bias-corrected meta-analysis model for combining studies of different types and quality. Yao et al. [13] conducted an extensive simulation study to evaluate an array of alternative Bayesian methods for incorporating NRSIs into rare events meta-analysis of RCT, and found that the bias-corrected meta-analysis model yielded favorable results.
Most methods are based on normal approximations for both RCTs and NRSIs studies, because the aggregated data, i.e. the treatment effect estimates with the corresponding standard errors, are usually available for NRSIs. Most of these methods use RCTs as anchors and adjust for bias in NRSIs to ultimately obtain a pooled estimate [19]. However, there are dangers in using a normal distribution for rare events meta-analysis of RCTs [20]. If there are problems in modelling the RCT anchor, this would affect the final pooled result. In the context of rare events meta-analysis of RCTs, many studies have confirmed that the use of exact likelihoods, such as the binomial-normal hierarchical model for RCTs, may be preferable [21].
In order to account for the differences in study design between RCTs and NRSIs, a power prior approach is a good potential option [22]. This approach allows down-weighting of the NRSIs, so that the data from this type of study contribute less than the data from RCTs when they have the same precision before down-weighting. In this study, we used exact likelihoods for RCTs as an anchor, and an informative prior distribution on the treatment effect parameter is derived from NRSIs through a power prior method [23]. Compared with prior methods, this method does not depend on normal approximations, and the results may be more accurate. An important consideration for the power prior approach is how to set the values of the down-weighting factor to account for the potential bias in the pooled estimates [4]. The common approach is to elicit expert opinion regarding the range of plausible values for the bias parameters [24, 25]. However, this process is time consuming and it can be difficult to pool opinions from different experts [26].
Therefore, the aim of this study was to explore the use of a power prior within a Bayesian framework to integrate RCTs and NRSIs [27]. This approach did not adjust for the possible bias in the point estimates and only took into account the down-weighting of the NRSIs in the pooled estimates, with an uncertainty reflected in the down-weighting factor. We also proposed a way of specifying the down-weighting factor based on judgments of the relative magnitude (no information, and low, moderate, serious and critical risk of bias ) of the overall risk of bias for each NRSI using the ROBINS-I tool [28], leading to transparent probabilities and therefore more informed decision making.
Methods
For this study, we re-analyzed the two recently published meta-analyses of the risk of diabetic ketoacidosis (DKA) in patients using sodium/glucose cotransporter 2 (SGLT-2) inhibitors compared with active comparators [29], and the association between low-dose methotrexate exposure and melanoma [30]. Our study did not require ethics committee approval or patients consent, as it is a secondary analysis of the publicly available datasets.
Data
The first meta-analysis was conducted by Alkabbani et al. [29]. This study used evidence from RCTs and NRSIs to investigate the risk of DKA associated with one or more individual SGLT-2 inhibitors. The meta-analysis included twelve placebo-controlled RCTs, seven active-comparator RCTs, and seven observational studies. All the NRSIs were retrospective, propensity score-matched cohort studies. Our primary concern was whether SGLT-2 inhibitors increased the risk of DKA compared with the active comparator. We included all studies in the initial analysis, then we performed a sensitivity analysis by excluding one NRSI because its control was not an active comparator [31]. The second meta-analysis was done by Yan et al. [30]. This meta-analysis included six RCTs and six NRSIs for the primary analysis. For the NRSIs, two case-control studies and four cohort studies were included.
Assessment of the risk of bias
The risk of bias is assessed at the outcome-level and not study-level, if a study includes multiple outcomes, multiple risk of bias assessments should be performed. For the outcome from both RCTs and NRSIs, there are widely available tools that can be used to assess the risk of bias [32, 33]. For the both two meta-analyses, the first originally assessed the quality of both RCTs and NRSIs using the checklist proposed by Downs et al. [34], the second used the Cochrane risk-of-bias tool [35] for RCTs and the Joanna Briggs Institute checklist [36] for NRSIs. In this study, we reassessed the risk of bias for each study included in the two meta-analyses. The Cochrane risk-of-bias tool (RoB 2) was used for RCTs [35], as this is already an established practice for assessing the quality of RCTs. The RoB 2 table takes into account the following domains: bias arising from the randomization process, bias due to deviations from intended interventions, bias in missing outcome data, bias in the measurement of the outcome, and bias in the selection of the reported result [35]. Each domain is classified into three categories: “low risk of bias,” “some concerns,” or “high risk of bias.” [35]. The response options for an overall risk-of-bias judgment are the same as for individual domains.
The choice of assessment tool for NRSIs is therefore a critical consideration, as it may affect the selection of NRSIs for quantitative analysis and the credibility of subsequent meta-analysis results. For NRSIs, we used the ROBINS-I tool. This tool covers most of the issues commonly encountered in NRSIs [9] and assesses the risk of bias of NRSIs in relation to an ideal (or target) RCT as the standard of reference [28]. In other words, an NRSI that is judged to have a low risk of bias - using ROBINS-I - is comparable to a well-conducted RCT [37]. The ROBINS-I tool takes into account the following domains: pre-intervention (bias due to confounding, bias in the selection of participants into the study), at intervention (bias in classification of interventions), post-intervention (bias due to deviations from intended interventions, bias due to missing data, bias in measurement of outcomes, bias in selection of the reported result). Each domain is classified into five categories: “Low risk of bias” or “Moderate risk of bias” or “Serious risk of bias” or “Critical risk of bias” or “No information”. The“No Information” category should be used only when insufficient data are reported to permit a judgment of bias. The response options for an overall risk of bias judgement are also the same as for individual domains.
In the Bayesian analysis section, we showed how to specify the down-weighting factor based on judgments of the relative magnitude (i.e. no information, and low, moderate, serious and critical risk of bias) of the overall risk of bias for each NRSI using the ROBINS-I tool.
The conventional random effects model
The pooled odds ratio (OR) was calculated for the both two meta-analyses using the conventional random-effects model, also known as the naïve data synthesis method. A random-effects model was employed to account for potential heterogeneity between-studies. This method was also the most commonly used in the empirical analysis [8]. Between-study variance was estimated using restricted maximum likelihood estimation. The level of variability due to heterogeneity rather than chance was assessed using the I2 statistic, and subgroup analyses were conducted by type of study design (RCTs vs. NRSIs). We used of continuity correction (adding 0.5) for zero-event trials. All analyses were performed with R software (version 4.1.1, R Foundation for Statistical Computing, Vienna, Austria) using the meta package (version 4.19-0) [38].
Bayesian analysis
We used the power prior method to combine the data from RCTs and NRSIs, which combines the likelihood contribution of the NRSI, raised to the power parameter of alpha (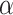
), with the likelihood of the RCT data [22]. The power prior approach allows to down-weigh the NRSI, thus making the data from this type of studies contribute less compared to data obtained from the RCTs. The power prior is constructed as the product of an initial prior and the likelihood of the NRSIs’ data with a down-weighting factor 
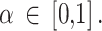[22] Defined as: 
, 
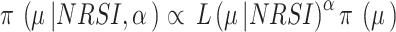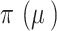is the initial prior before the NRSIs’ data is observed. 
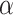with zero meaning that NRSI is entirely discounted, and with one indicating that NRSI is considered at ‘face-value’. 
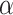is fixed and often specified based on the confidence to be placed in the NRSIs or determined based on data from the NRSIs and the RCTs in a dynamic way [39]. Here, we treated the 
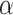as random to be estimated by using the full Bayesian methodology. For multiple NRSIs, we assign different independent down-weighting factors 
for each of the NRSI’s data [40], 
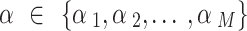. We assumed M NRSIs and K RCTs, the overall joint posterior distribution is given by [41]:
 |
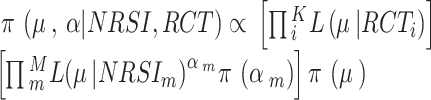where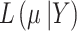 
is the likelihood of 
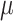given data Y, data are split into the part obtained from RCTs and part from NRSIs to form separate likelihood contributions and then combined (with the down-weighting factor for NRSIs’ data) to give the overall posterior distribution.
The likelihood of non-randomized studies of interventions
The NRSIs’ is modelled using the normal-normal hierarchical random effects meta-analysis model with a weight indexed by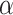 
. The model can be written as:
 |
 |
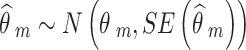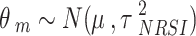Where m = 1, 2, …, M denotes NRSI m.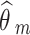 
and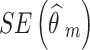 
are the observed relative treatment effect and the corresponding standard error for study m, respectively. Both the treatment effect (
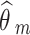) and standard error (
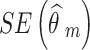) are calculated on the log OR scale. 
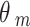denotes the true treatment effect for study m. 
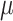represents the overall combined effect and 
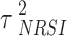is the between-study variance. We assign a weakly informative prior (WIP) to the treatment effect and the heterogeneity parameter, which is a normal prior with mean 0 and standard deviation 2.82 for the treatment effect 
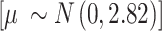[42] and a half-normal prior with scale of 0.5 for the heterogeneity parameter 
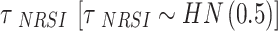[43]. The WIP of the treatment effect has two advantages. First, the normal prior is symmetric and the OR is constrained from 1/250 to 250 with a 95% probability. Second, it was consistent with effect estimates obtained from 37,773 meta-analysis datasets published in the Cochrane Database of Systematic Reviews [42].
The likelihood of randomized controlled trials
We consider a set of k RCTs with a binary outcome. In each trial 
, 
(
), 
(
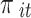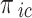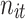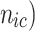, and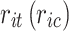 
denote the probability of the event, number of subjects, and event counts in the treatment (control) group, respectively. The number of events is modeled to follow a binomial distribution: 
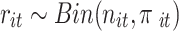and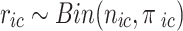 
. Under a random-effects assumption, a commonly-used Bayesian binomial-normal hierarchical model can be written as follows [44, 45]:
 |
 |
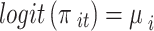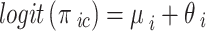Where the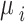 
are the fixed effects describing the baseline risks of the event in study i, 
,
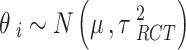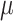is the mean treatment effect and 
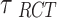measures the heterogeneity of treatment effects across RCTs.
To ensure full Bayesian inference, we need to specify the prior distributions for the parameters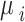 
and
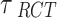. For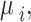 
we assume a vague normal prior 
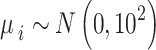. A weakly informative prior (WIP) is assigned for the heterogeneity parameter 
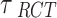, that is, a half-normal prior with scale of 0.5 
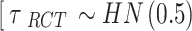] [46].
Down-weighting factor
The down-weighting factor can be interpreted as the quality of the study, we could set its magnitude according to the risk of bias of each NRSI [47, 48]. This approach follows standard health technology assessment methods, where the risk of bias is assessed at the individual outcome level. In ROBINS-I, a NRSI was classified as “Low risk of bias” or “Moderate risk of bias” or “Serious risk of bias” or “Critical risk of bias” or “No information” based on the risk of bias assessment. If a NRSI was assessed as having a “Low risk of bias,” we set the down-weighting factor to 1. This is because a low risk of bias in a NRSI, as assessed by ROBINS-I, indicates that the quality of the study is comparable to that of a well-conducted RCT [37].
For the other categories, we consider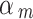 
as scale random variables and we model it as beta distribution.
 |
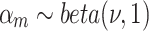To elicit a value of 𝜈, we can use the prior mean [15], which is
 |
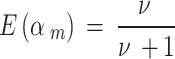If we take 𝜈 = 0.5, which corresponds to down-weighting in average 1-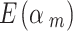
= 0.67 for the low-quality studies.
We set the down-weighting factor for the NRSI as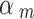 
~ beta (4, 1) if it was assessed as having a “Moderate risk of bias”, which corresponds to a down-weighting in the average 1-E(
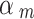) = 0.2; or 
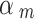~ beta (1.5, 1) if it was assessed as “Serious risk of bias”, which corresponds to a down-weighting in the average 1-E(
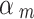) = 0.4, or 
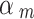~ beta (0.25, 1) if it was assessed as “Critical risk of bias”, which corresponds to a down-weighting in the average 1-E(
) = 0.8 [49]. If a study was rated as “No information” we handled this case as a “Critical risk of bias” from a conservative perspective.
Sensitivity analysis
Spiegelhalter and Best [50] proposed to give a set of fixed values (i.e. 0.1, 0.2, 0.3, 0.4) to discount low-quality studies and to perform a sensitivity analysis. Efthimiou et al. [51] set the down-weighting factor with a uniform distribution, e.g. uniform (0, 0.3), uniform (0.3, 0.7), and uniform (0.7, 1) represent places of low, medium and high confidence in the quality of the evidence. Therefore, we performed a sensitivity analysis to compare the results of our method with those of the Spiegelhalter and Best [50] and Efthimiou et al. [51]. For the method proposed by Spiegelhalter and Best [50], we provided a set of results using different values (i.e. 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1). For the method used by Efthimiou et al. [51], we set the down-weighting factor for the NRSI as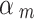 
~ uniform (0, 0.3), 
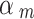~ uniform (0.3, 0.7), and 
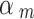~ uniform (0.7, 1) if a NRSI was assessed to have a “Critical risk of bias”, “Serious risk of bias”, and “Moderate risk of bias”, respectively.
Model implementation
All point estimates (OR) are presented with 95% credible interval (CrI). In addition, we calculated the posterior probabilities of any risk (OR > 1) and of meaningful clinical association (defined as OR > 1.15, i.e., at least 15% odds increase in outcomes) [52]. We assessed the posterior distribution of the between-study standard deviation (τ, a proxy for heterogeneity) by calculating the posterior probabilities of “small [τ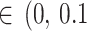
)]” “reasonable [τ
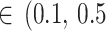)]” “fairly high [τ
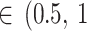)]” and “fairly extreme [τ
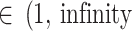)]” heterogeneity [53].
We performed Bayesian analysis using the RStan package (version 2.21.3). We fitted four chains for each model, each with 5,000 iterations. In each chain, we took the first 2,500 iterations as a warm-up and thinned the remaining 2,500 iterations by one. We performed convergence checks; convergence was judged to have occurred when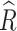 
(the potential scale reduction factor) was no greater than 1.1 for all parameters [54]. Overall, convergence was achieved.
Results
Study characteristics
Tables 1 and 2 show the basic characteristics of the included RCTs and NRSIs for the first and second meta-analyses, respectively. In the first meta-analysis, the majority of subjects were men, with a mean age of 46.0 to 74.2 years. Length of follow-up ranged from 0.54 to 2 years for the RCTs and from 0.5 years to 12 years for the NRSIs. A total of 8 DKA outcomes were reported in all RCTs, which included 8,100 patients, resulting in an incidence rate of 0.1%. For all NRSIs, we observed 2,693 DKA events in 1,311,868 patients, for an incidence rate of 0.2%.
Table 1.
Characteristics of studies included in the meta-analysis conducted by Alkabbani et al. [29] for the risk of diabetic ketoacidosis among patients using sodium/glucose cotransporter 2 inhibitors compared with active comparators
| First author (Year) | Design | Cases/ Participants |
Duration of study | Mean Age (years) | Female (No, %) | SGLT-2 Inhibitor or Exposure Group | Comparator |
|---|---|---|---|---|---|---|---|
| Lavalle-González (2013) | RCT | 1/1284 | 1 year | 55.4 | 52.9 | Canagliflozin | Placebo/sitagliptin |
| Roden (2015) | RCT | 1/680 | 1.46 years | 55.0 | 38.7 | Empagliflozin | Placebo/sitagliptin |
| Haering (2015) | RCT | 2/2702 | 1.46 years | 57.1 | 49.1 | Metformin + sulfonylureas + empagliflozin | Metformin + sulfonylureas |
| Frías (2016) | RCT | 1/463 | 0.54 years | 54.2 | 52.1 | Dapagliflozin | Exenatide |
| Hollander (2018) | RCT | 1/1361 | 1 year | 58.2 | 51.5 | Ertugliflozin | Glimepiride |
| Pratley (2018) | RCT | 1/1232 | 1 year | 55.1 | 46.1 | Ertugliflozin | Sitagliptin |
| Gallo (2019) | RCT | 1/414 | 2 years | 56.6 | 53.6 | Ertugliflozin | Placebo/glimepiride |
| Fralick (2017) | Cohort study | 81/76,090 | 0.5 years | 54.6 | 47.3 | SGLT-2i | DPP-4i |
| Wang (2017) | Cohort study | 55/60,932 | 1.5 years | 53.8 | NA | SGLT-2i | Non-SGLT-2i AHAs |
| Kim (2018) | Cohort study | 63/112,650 | 3.5 years | 53.2 | 44.8 | SGLT-2i | DPP-4i |
| Ueda (2018) | Cohort study | 30/34,426 | 3.5 years | 61.0 | 39.0 | SGLT-2i | GLP-1 |
| McGurnaghan (2019) | Cohort study | 677/238,876 | 12 years | 65.8 | 43.5 | Dapagliflozin | No-user for dapagliflozin |
| Douros (2020) | Cohort study | 505/404,372 | 5 years | 63.9 | 41.5 | SGLT-2i | DPP-4i |
| Wang-CCAE (2019) | Cohort study | 668/220,504 | 4.6 years | 46.9 | 49.1 | SGLT-2i | Insulinotropic AHAs† |
| Wang-MDCD (2019) | Cohort study | 155/20,532 | 4.7 years | 46.0 | 65.8 | SGLT-2i | Insulinotropic AHAs† |
| Wang-MDCR (2019) | Cohort study | 80/27,764 | 4.7 years | 74.2 | 54.0 | SGLT-2i | Insulinotropic AHAs† |
| Wang-Optum (2019) | Cohort study | 379/115,722 | 4.5 years | 58.8 | 49.3 | SGLT-2i | Insulinotropic AHAs† |
†Includes DPP-4 inhibitors, GLP-1 receptor agonists, SU, nateglinide, and repaglinide
Table 2.
Characteristics of studies included in the meta-analysis conducted by Yan et al. [30] for the association of low-dose methotrexate exposure and melanoma
| First author (Year) | Design | Cases/ Participants |
Duration of study | Mean Age (years) | Female (No, %) | Methotrexate | Comparator |
|---|---|---|---|---|---|---|---|
| Breedveld (2006) | RCT | 1/531 | 24 months | NA | 74.5 | Methotrexate | Adalimumab |
| Klareskog (2004) | RCT | 1/340 | 12 months | 53.0 | 77.0 | Methotrexate | Etanercept |
| Puéchal (2016) | RCT | 1/115 | 12 months | 59.8 | 51.6 | Methotrexate | Azathioprine |
| Vanni (2020) | RCT | 9/3676 | 27.6 months | 65.5 | 18.8 | Methotrexate | Unspecified |
| Van Vollenhoven (2020) | RCT | 1/945 | 6 months | 53.7 | 76.0 | Methotrexate | Upadacitinib |
| Westhovens (2021) | RCT | 1/626 | 12 months | 53.0 | 77.0 | Methotrexate | Filgotinib |
| Berge (2020) | Case-control study | 12,106/130,670 | NA | NA | NA | Methotrexate | Unspecified |
| Polesie (2020) | Case-control study | 395/4345 | NA | NA | 55.2 | Methotrexate | Unspecified |
| Chaparro (2017) | Cohort study | 10/5577 | 16.4 months | NA | 47.3 | Methotrexate | Thiopurine |
| Polesie (2017) | Cohort study | 3097/606,259 | 6 months | 57.4 | 62.8 | Methotrexate | Unspecified |
| Polesie (2017) | Cohort study | 654/7911 | 6 months | 59.3 | 63.7 | Methotrexate | Unspecified |
| Yan (2021) | Cohort study | 366/19,114 | NA | 74.0 | 56 | Methotrexate | Unspecified |
In the second meta-analysis, the majority of subjects were women, with a mean age of 53.0 to 74.0 years. Length of follow-up ranged from 6 to 27.6 months for RCTs and from 6 to 16.4 months for NRSIs. A total of 21 melanoma outcomes were reported in six RCTs involving 11,810 patients, giving an incidence rate of 0.2%. In all NRSIs, 16,628 melanoma outcomes were observed in 773,876 patients, for an incidence rate of 2.1%.
Risk of Bias Assessment
The risk of bias assessment for the included studies in the two meta-analyses is detailed in Tables S1-S4 in the Supplementary. In the first meta-analysis, 4 RCTs were assessed as ‘some concern’, 2 as ‘low risk’ and 1 as ‘high risk’; 5 NRSIs were assessed as ‘moderate risk of bias’ and 2 as ‘serious risk of bias’. In the second meta-analysis, 4 RCTs were assessed as ‘some concern’ and 2 as ‘low risk of bias’; for NRSIs, 2 as ‘moderate risk of bias’ and 4 as ‘serious risk of bias’.
The results of the conventional random effects model
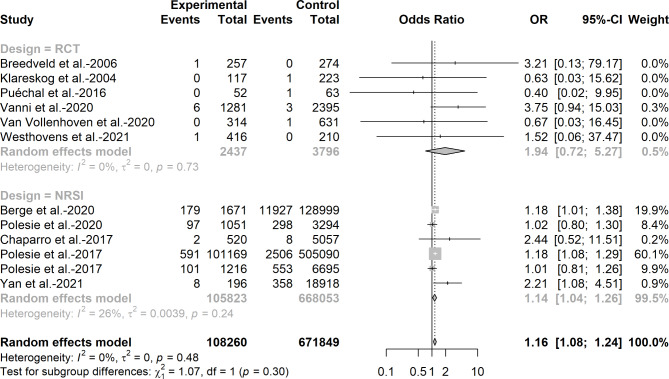
Figures 1 and 2 show the combined results of RCTs and NRSIs using the conventional random effects model for the first and second meta-analyses. For the risk of DKA among users receiving SGLT-2 inhibitors versus active comparators, we observed an increased risk of DKA when data from RCTs and NRSIs were pooled directly (OR = 1.50, 95%CI: 1. 11–2.03, I2 = 82%) and from NRSIs alone (OR = 1.56, 95%CI: 1.13–2.15, I2 = 90%), whereas no significant effect was observed when results from RCTs were pooled (OR = 0.82, 95%CI: 0.25–2.69, I2 = 0%). We found that the weight of RCTs in the total body of evidence is only 6.1%.
Fig. 1.
Odds ratio of diabetic ketoacidosis among patients receiving sodium-glucose co-transporter-2 inhibitors versus active comparators in randomized control trials and non-randomized studies of intervention
Fig. 2.
Odds ratio of melanoma among patients with low-dose methotrexate exposure in randomized control trials and non-randomized studies of intervention
For the association between low-dose methotrexate exposure and melanoma, we also observed an increased risk of melanoma when data were pooled directly from RCTs and NRSIs (OR = 1.16, 95%CI: 1.08–1.24, I2 = 0%) and from NRSIs alone (OR = 1. 14, 95%CI: 1.04–1.26, I2 = 0%), while no significant effect was observed when the results were pooled from RCTs only (OR = 1.94, 95%CI: 0.72–5.27, I2 = 0%).
The results of the Bayesian analysis
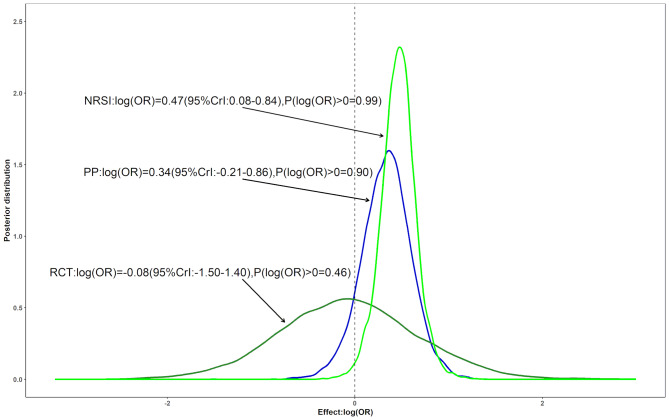
The estimated risk of DKA in users receiving SGLT-2 inhibitors versus active comparators is shown in Fig. 3 using Bayesian analysis. The point estimate from Bayesian analysis was much closer to the estimate from conventional random effects model [exp(0.34) = 1.40], while the interval from Bayesian analysis was much wider than the estimate from conventional random effects model. Despite the down-weighting of NRSIs, which increased the posterior variance, there was a near 90% probability of an increased risk and a 40% probability of a > 15% increased risk. There was reasonable heterogeneity based on the point estimate (τ = 0.33, not shown). When we excluded the study that its control is not an active comparator [31], there was a 97% probability of an increased risk and a 68% probability of a > 15% increased risk (Figure S1). There was also a reasonable heterogeneity based on the point estimate (τ = 0.32, not shown).
Fig. 3.
Three posterior distributions for the pooled log (OR) assessing the risk of diabetic ketoacidosis among patients using sodium/glucose cotransporter 2 inhibitors compared with active comparators: The dark green and the green lines correspond to Bayesian meta-analyses including only RCTs or NRSIs, respectively. The blue line is a posterior distribution combined by a power prior approach
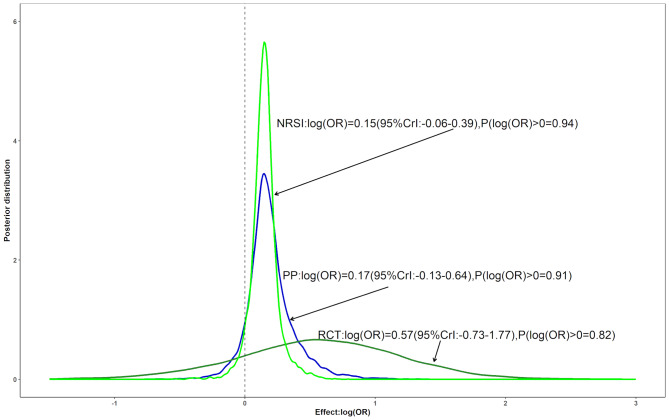
Figure 4 shows the Bayesian estimates of the association between low-dose methotrexate exposure and melanoma. The Bayesian analysis showed significant differences compared with the conventional random effects model. Although the point estimate from the Bayesian analysis was also close to the estimate from the conventional random effects model [exp (0.17) = 1.19], it did not indicate an increased risk of melanoma. Furthermore, the Bayesian analysis showed only an 91% probability of an increased risk and a 9.5% probability of a > 15% increased risk. There was also reasonable heterogeneity based on the point estimate (τ = 0.37, not shown).
Fig. 4.
Three posterior distributions for the pooled log (OR) assessing the association of low-dose methotrexate exposure and melanoma: The dark green and the green lines correspond to Bayesian meta-analyses including only RCTs or NRSIs, respectively. The blue line is a posterior distribution combined by a power prior approach
Sensitivity analysis
Figures S2 and S3 show the results for Case 1 and Case 2 when we use different fixed values for the down-weighting factors. For both studies, as we reduce the weight of NRSI, the posterior distribution shows a decrease in the probability of increasing risk. When we assign extremely low weights to NRSIs (α = 0.01), we observed a 52% probability of an increased risk of DKA in users receiving SGLT-2 inhibitors, while an 82% probability of an increased risk of melanoma in patients using low-dose methotrexate.
Figures S4 and S5 show the results for Case 1 and Case 2 when we assign a uniform distribution to the down-weighting factors. For both studies, the results are much closer to the results when we assign a beta distribution to the down-weighting factors.
Discussion
In this study, we discussed the use of power priors to discount NRSIs and apply this method to incorporate NRSIs in a rare events meta-analysis of RCTs. We demonstrate how to set the down-weighting factor based on judgments of the relative magnitude of the overall risk of bias for each NRSI outcome using the ROBINS-I tool. The methods were illustrated using two recently published meta-analyses, focusing on the risk of DKA in patients using SGLT-2 inhibitors compared with active comparators, and the association between low-dose methotrexate exposure and melanoma. There were no significant results for either meta-analysis when data from RCTs only were pooled. However, significant results were observed when data from NRSIs were pooled. When RCTs and NRSIs were combined directly in the same meta-analysis without distinction, both meta-analyses showed significant results. However, when the bias of the NRSIs was taken into account, there was a 90% probability of an increased risk of DKA in users receiving SGLT-2 inhibitors and an 91% probability of an increased risk of melanoma in patients using low-dose methotrexate.
Our study suggested that including NRSIs during the evidence synthesis process may increase the certainty of the estimates when rare events meta-analyses of RCTs cannot provide sufficient evidence. A previous meta-analysis concluded that the risk of DKA was not increased in users of SGLT-2 inhibitors compared with active comparators, possibly because of the small number of outcomes in all included RCTs [55]. However, in our study, we found that the sample size, number of DKA cases, and length of follow-up of the RCTs were much smaller than those of the NRSIs, and the range of mean ages in the NRSIs was wider than in the RCTs. There were 8 events in 8,100 patients in all the RCTs, and the pooled result was also not significant. The same results were observed for the risk between low-dose methotrexate exposure and melanoma. In an extensive simulation study, Yao et al. [13] found that the power of the rare events meta-analysis of RCTs was much lower. In addition, Jia et al. [6] found that many rare events meta-analyses are underpowered by evaluating the 4,177 rare events meta-analyses obtained from the Cochrane Database of Systematic Reviews. Our study showed that the precision of the relative treatment effect estimates for both meta-analyses increased when we included NRSIs and RCTs. All these results suggest that systematic reviews and meta-analyses of rare events should include evidence from both RCTs and NRSIs.
We do not recommend using the conventional approach as the primary method of the empirical analysis. Two recent meta-epidemiological studies have shown that many meta-analyses directly incorporate NRSIs using the conventional approach [8, 56]. The bias of relative treatment effect estimates from NRSIs can be reduced by some post-hoc adjustment techniques, such as propensity score analysis, but cannot be completely eliminated [12]. The conventional approach ignores differences in study design and is unable to account for the potential bias of NRSIs [49, 51]. Therefore, by including NRSIs in a rare events meta-analysis of RCTs using the conventional approach, we are not only combining results of interest, but also combining multiple biases. In addition, compared with RCTs, the results of NRSIs often have a small confidence interval because the events and the sample size are usually much larger [29]. This would give greater weight than that of RCTs, leading to NRSIs dominating the conclusions. Our two illustrative examples also confirm this. However, confidence intervals for effect estimates from NRSI are less likely to represent the true uncertainty of the observed effect than are the confidence intervals for RCTs [57]. The conventional approach may be used to assess the compatibility of evidence from NRSIs and RCTs by comparing changes in heterogeneity and inconsistency before and after the inclusion of NRSIs [51].
Estimates from NRSIs are generally considered to be biased, and it is difficult to quantify potential bias in empirical analysis [58, 59]. There are three commonly used methods to assess the direction or magnitude of potential bias in empirical analysis. The first method involves assessing the impact of NRSIs on combined estimates by varying the level of confidence placed in the NRSIs [41]. The second method treats bias parameters as random variables (i.e. a non-informative prior) to allow the combined estimates to be influenced by the agreement between sources of evidence [51]. The third approach is to seek expert opinion on the range of plausible values for bias parameters [24, 25]. Our study was the first to relate bias to study quality, with the direction or magnitude of possible bias determined by the risk of bias of each NRSI. Although tools to critically appraise NRSIs are widely available [33], they vary considerably in their content and the quality of the topics covered. We chose the ROBINS-I because it covers most of the issues commonly encountered in NRSIs [9] and assesses the risk of bias in relation to an ideal (or target) RCT as a standard of reference [28]. In this study, we did not down-weight of NRSI if it was assessed as having a “Low risk of bias,“, because an NRSI judged as having low risk of bias will be comparable to a well-conducted RCT [37]. However, one reviewer pointed out that an NRSI with low risk of bias as determined by ROBINS-I is likely to be of lower quality than an RCT with low risk of bias using the Cochrane tool. In the empirical analysis, we recommend using sensitivity analysis to explore the impact of reducing or not reducing the weight of low risk of bias NRSI on the estimates. The down-weighting factor for an NRSI with low risk of bias may be relatively large at this time, for example setting v = 0.1 or assuming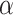 
= 0.9 or 
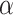~ uniform (0.9,1).
The choice of the prior distribution for the down-weighting factor is subjective. In this study, we set the down-weighting factors as scale random variables and modelled them as beta distributions. We grouped the studies according to different categories of risk of bias. We used the prior mean to determine the values of the parameter of the beta distribution and then set the values based on the results of the quality assessment of each literature. The values also represent a quantification of the confidence to be placed in each study. In practice, the prior can be informed by external information, such as using the empirical information from meta-epidemiological studies in combination with expert consensus to derive the prior.
The impact of the risk of bias of the RCT on the estimation was not considered in this study. Only a few methodological studies have considered the bias of both NRSIs and RCTs simultaneously. Turner et al. [24] proposed a method to construct prior distributions to represent the internal and external biases at the individual study level using expert elicitation, followed by synthesizing the estimates across multiple design types of studies. Schnell-Inderst et al. [26] simplify the methods by Tuner et al. and used the case of total hip replacement prosthesis to illustrate how to integrate evidence from RCT and NRSI. Verde et al. [15] proposed a bias-corrected meta-analysis model that combines different types of studies in a meta-analysis, with internal validity bias adjusted. This model is based on a mixture of two random effect distributions, where the first component corresponds to the model of interest and the second component corresponds to the hidden bias structure. In our framework, the likelihood function of RCT can be extended to explain its own bias, for example, using the robust Bayesian bias adjustment random effects model proposed by Cruz et al. [47] However, more in-depth studies need to explore how to assign a rational parameter for the risk of bias in RCTs [60].
There were some limitations to this study that need to be recognized. First, the bias of point estimates of NRSIs was not considered in the method. Bias in estimates of relative effects from NRSIs could depend on the method used to obtain them. Different methods used to estimate relative treatment effects from an NRSI could produce different results. Therefore, it may be difficult to predict the direction (and also the magnitude) of possible biases. The vast majority of empirical analyses reduce the NRSI weights in the pooled estimates, and this study follows a similar strategy. Second, only two illustrative examples were used in this study. More comprehensive analyses in further empirical or simulation studies are needed. Third, there are other methods for combining RCTs and NRSIs in a meta-analysis [14], but their performance compared to the current method was not investigated. Therefore, further evaluation of these methods in different scenarios, including the use of comprehensive simulation studies, is warranted. Fourth, although we used the OR as the effect measure, these methods can be applied to other measures of association commonly used in meta-analyses, including relative risk (e.g. using the Poisson regression for RCTs [21]), risk difference (e.g. using the beta-binomial model for RCTs [61]).
Conclusions
In summary, the inclusion of NRSIs in a rare events meta-analysis has the potential to corroborate findings from RCTs, increase precision, and improve the decision-making process. Our study provides an example of how to down-weight NRSIs by incorporating information from risk of bias assessments for each NRSI using the ROBINS-I tool.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
Not applicable.
Abbreviations
- CI
Confidence interval
- CrI
Credible interval
- DKA
Diabetic ketoacidosis
- NRSI
Non-randomised studies of interventions
- OR
Odds ratio
- RCT
Randomized Controlled Trial
- ROBINS-I
Risk of bias in non-randomised studies-of interventions
- SGLT-2
Sodium/glucose cotransporter-2
Author contributions
Y.Z, and M.Y., contributed equally as co-first authors. X.S., L.L., M.Y., and Y.Z., conceived and designed the study. X.S., M.Y., and L.L. acquired the funding. M.Y. drafted the manuscript. M.Y. conducted the data analysis. X.S., M.Y., L.L., F.M., Y.M., J.H., and K.Z. critically revised the article. X.S. is the guarantor.
Funding
We acknowledge support from the National Natural Science Foundation of China (Grant No. 72204173, 82274368, and 71904134), National Science Fund for Distinguished Young Scholars (Grant No. 82225049), special fund for traditional Chinese medicine of Sichuan Provincial Administration of Traditional Chinese Medicine (Grant No. 2024zd023), and 1.3.5 project for disciplines of excellence, West China Hospital, Sichuan University (Grant No. ZYGD23004).
Data availability
All data in this study have been taken from the published studies and no new data have been generated. Computing code for the two empirical examples can be accessed from the supplementary files.
Declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Yun Zhou and Minghong Yao contributed equally to this work as co-first authors.
Contributor Information
Ling Li, Email: liling@wchscu.cn.
Xin Sun, Email: sunxin@wchscu.cn.
References
- 1.Zabor EC, Kaizer AM, Hobbs BP. Randomized controlled trials chest. 2020;158(1s):S79–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rothwell PM. External validity of randomised controlled trials: to whom do the results of this trial apply? Lancet. 2005;365(9453):82–93. [DOI] [PubMed] [Google Scholar]
- 3.Hernán MA, Robins JM, editors. Causal inference: what if. Boca Raton, FL: Chapman & Hall/CRC; 2020. [Google Scholar]
- 4.Cuello-Garcia CA, Santesso N, Morgan RL, et al. GRADE guidance 24 optimizing the integration of randomized and non-randomized studies of interventions in evidence syntheses and health guidelines. J Clin Epidemiol. 2022;142:200–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hodkinson A, Kontopantelis E. Applications of simple and accessible methods for meta-analysis involving rare events: a simulation study. Stat Methods Med Res. 2021;30(7):1589–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jia P, Lin L, Kwong JSW, et al. Many meta-analyses of rare events in the Cochrane database of systematic reviews were underpowered. J Clin Epidemiol. 2021;131:113–22. [DOI] [PubMed] [Google Scholar]
- 7.Golder S, Loke YK, Bland M. Meta-analyses of adverse effects data derived from randomised controlled trials as compared to observational studies: methodological overview. PLoS Med. 2011;8(5):e1001026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bun RS, Scheer J, Guillo S, et al. Meta-analyses frequently pooled different study types together: a meta-epidemiological study. J Clin Epidemiol. 2020;118:18–28. [DOI] [PubMed] [Google Scholar]
- 9.Sarri G, Patorno E, Yuan H, et al. Framework for the synthesis of non-randomised studies and randomised controlled trials: a guidance on conducting a systematic review and meta-analysis for healthcare decision making. BMJ Evid Based Med. 2022;27(2):109–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Munn Z, Barker TH, Aromataris E, et al. Including nonrandomized studies of interventions in systematic reviews: principles and practicalities. J Clin Epidemiol. 2022;152:314–5. [DOI] [PubMed] [Google Scholar]
- 11.Saldanha IJ, Adam GP, Bañez LL, et al. Inclusion of nonrandomized studies of interventions in systematic reviews of interventions: updated guidance from the agency for health care research and quality effective health care program. J Clin Epidemiol. 2022;152:300–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sherman RE, Anderson SA, Dal Pan GJ, et al. Real-world evidence - what is it and what can it tell us? N Engl J Med. 2016;375(23):2293–7. [DOI] [PubMed] [Google Scholar]
- 13.Yao M, Wang Y, Ren Y, et al. Comparison of statistical methods for integrating real-world evidence in a rare events meta-analysis of randomized controlled trials. Res Synth Methods. 2023;14(5):689–706. [DOI] [PubMed] [Google Scholar]
- 14.Verde PE, Ohmann C. Combining randomized and non-randomized evidence in clinical research: a review of methods and applications. Res Synth Methods. 2015;6(1):45–62. [DOI] [PubMed] [Google Scholar]
- 15.Verde PE. A bias-corrected meta-analysis model for combining, studies of different types and quality. Biom J. 2021;63(2):406–22. [DOI] [PubMed] [Google Scholar]
- 16.Eddy DM, Hasselblad V, Shachter R. Meta-analysis by the confidence profile method: the statistical synthesis of evidence. San Diego,CA: Academic; 1992. [Google Scholar]
- 17.Droitcour J, Silberman G, Chelimsky E. A new form of meta-analysis for combining results from randomized clinical trials and medical-practice databases. Int J Technol Assess Health Care. 1993;9(3):440–9. [DOI] [PubMed] [Google Scholar]
- 18.Verde PE, Ohmann C, Morbach S, Icks A. Bayesian evidence synthesis for exploring generalizability of treatment effects: a case study of combining randomized and non-randomized results in diabetes. Stat Med. 2016;35(10):1654–75. [DOI] [PubMed] [Google Scholar]
- 19.Schmitz S, Adams R, Walsh C. Incorporating data from various trial designs into a mixed treatment comparison model. Stat Med. 2013;32(17):2935–49. [DOI] [PubMed] [Google Scholar]
- 20.Jackson D, White IR. When should meta-analysis avoid making hidden normality assumptions? Biom J. 2018;60(6):1040–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kuss O. Statistical methods for meta-analyses including information from studies without any events-add nothing to nothing and succeed nevertheless. Stat Med. 2015;34(7):1097–116. [DOI] [PubMed] [Google Scholar]
- 22.Ibrahim JG, Chen M-H. Power prior distributions for regression models. Stat Sci. 2000;15(1):46–60. [Google Scholar]
- 23.Cook RJ, Farewell VT. The utility of mixed-form likelihoods. Biometrics. 1999;55(1):284–8. [DOI] [PubMed] [Google Scholar]
- 24.Turner RM, Spiegelhalter DJ, Smith GC, Thompson SG. Bias modelling in evidence synthesis. J R Stat Soc Ser Stat Soc. 2009;172(1):21–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Efthimiou O, Mavridis D, Cipriani A, Leucht S, Bagos P, Salanti G. An approach for modelling multiple correlated outcomes in a network of interventions using odds ratios. Stat Med. 2014;33(13):2275–87. [DOI] [PubMed] [Google Scholar]
- 26.Schnell-Inderst P, Iglesias CP, Arvandi M, Ciani O, Matteucci Gothe R, Peters J, Blom AW, Taylor RS, Siebert U. A bias-adjusted evidence synthesis of RCT and observational data: the case of total hip replacement. Health Econ. 2017;26(Suppl 1):46–69. [DOI] [PubMed] [Google Scholar]
- 27.Ibrahim JG, Chen MH, Gwon Y, Chen F. The power prior: theory and applications. Stat Med. 2015;34(28):3724–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sterne JA, Hernán MA, Reeves BC, Savović J, Berkman ND, Viswanathan M, Henry D, Altman DG, Ansari MT, Boutron I, et al. ROBINS-I: a tool for assessing risk of bias in non-randomised studies of interventions. BMJ. 2016;355:i4919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Alkabbani W, Pelletier R, Gamble JM. Sodium/Glucose cotransporter 2 inhibitors and the risk of diabetic ketoacidosis: an example of complementary evidence for rare adverse events. Am J Epidemiol. 2021;190(8):1572–81. [DOI] [PubMed] [Google Scholar]
- 30.Yan MK, Wang C, Wolfe R, Mar VJ, Wluka AE. Association between low-dose methotrexate exposure and melanoma: a systematic review and meta-analysis. JAMA Dermatol. 2022;158(10):1157–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McGurnaghan SJ, Brierley L, Caparrotta TM, McKeigue PM, Blackbourn LAK, Wild SH, Leese GP, McCrimmon RJ, McKnight JA, Pearson ER, et al. The effect of dapagliflozin on glycaemic control and other cardiovascular disease risk factors in type 2 diabetes mellitus: a real-world observational study. Diabetologia. 2019;62(4):621–32. [DOI] [PubMed] [Google Scholar]
- 32.Morton SC, Costlow MR, Graff JS, Dubois RW. Standards and guidelines for observational studies: quality is in the eye of the beholder. J Clin Epidemiol. 2016;71:3–10. [DOI] [PubMed] [Google Scholar]
- 33.Quigley JM, Thompson JC, Halfpenny NJ, Scott DA. Critical appraisal of nonrandomized studies-a review of recommended and commonly used tools. J Eval Clin Pract. 2019;25(1):44–52. [DOI] [PubMed] [Google Scholar]
- 34.Downs SH, Black N. The feasibility of creating a checklist for the assessment of the methodological quality both of randomised and non-randomised studies of health care interventions. J Epidemiol Community Health. 1998;52(6):377–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sterne JAC, Savović J, Page MJ, Elbers RG, Blencowe NS, Boutron I, Cates CJ, Cheng HY, Corbett MS, Eldridge SM, et al. RoB 2: a revised tool for assessing risk of bias in randomised trials. BMJ. 2019;366:l4898. [DOI] [PubMed] [Google Scholar]
- 36.Moola S, Munn Z, Tufanaru C et al. Chapter 7: systematic reviews of etiology and risk. In: Aromataris E, Munn Z, eds. JBI Manual for Evidence Synthesis. JBI; 2020. Accessed December 13, 2023. https://jbi-global-wiki.refined.site/space/MANUAL/ 4687372/Chapter + 7% 3A + Systematic + reviews + of + etiology + and + risk.
- 37.Cuello CA, Morgan RL, Brozek J, Verbeek J, Thayer K, Ansari MT, Guyatt G, Schünemann HJ. Case studies to explore the optimal use of randomized and nonrandomized studies in evidence syntheses that use GRADE. J Clin Epidemiol. 2022;152:56–69. [DOI] [PubMed] [Google Scholar]
- 38.Schwarzer G, Carpenter JR, Rücker G. Meta-Analysis with R. Springer international publishing, 2015. https://link.springer.com/book/10.1007/978-3-319-21416-0
- 39.Gravestock I, Held L. Adaptive power priors with empirical Bayes for clinical trials. Pharm Stat. 2017;16(5):349–60. [DOI] [PubMed] [Google Scholar]
- 40.Duan Y, Ye K, Smith EP. Evaluating water quality using power priors to incorporate historical information. Environmetrics. 2006;17(1):95–106. [Google Scholar]
- 41.Jenkins DA, Hussein H, Martina R, Dequen-O’Byrne P, Abrams KR, Bujkiewicz S. Methods for the inclusion of real-world evidence in network meta-analysis. BMC Med Res Methodol. 2021;21(1):207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Günhan BK, Röver C, Friede T. Random-effects meta-analysis of few studies involving rare events. Res Synth Methods. 2020;11(1):74–90. [DOI] [PubMed] [Google Scholar]
- 43.Friede T, Röver C, Wandel S, Neuenschwander B. Meta-analysis of two studies in the presence of heterogeneity with applications in rare diseases. Biom J. 2017;59(4):658–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bhaumik DK, Amatya A, Normand SL, Greenhouse J, Kaizar E, Neelon B, Gibbons RD. Meta-analysis of rare binary adverse event data. J Am Stat Assoc. 2012;107(498):555–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Yao M, Jia Y, Mei F, Wang Y, Zou K, Li L, Sun X. Comparing various Bayesian random-effects models for pooling randomized controlled trials with rare events. Pharm Stat. 2024. 10.1002/pst.2392 [DOI] [PubMed] [Google Scholar]
- 46.Friede T, Röver C, Wandel S, Neuenschwander B. Meta-analysis of few small studies in orphan diseases. Res Synth Methods. 2017;8(1):79–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Raices Cruz I, Troffaes MCM, Lindström J, Sahlin U. A robust Bayesian bias-adjusted random effects model for consideration of uncertainty about bias terms in evidence synthesis. Stat Med. 2022;41(17):3365–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Greenland S, O’Rourke K. On the bias produced by quality scores in meta-analysis, and a hierarchical view of proposed solutions. Biostatistics. 2001;2(4):463–71. [DOI] [PubMed] [Google Scholar]
- 49.Yao M, Wang Y, Mei F, Zou K, Li L, Sun X. Methods for the inclusion of real-world evidence in a rare events meta-analysis of randomized controlled trials. J Clin Med. 2023;12(4). [DOI] [PMC free article] [PubMed]
- 50.Spiegelhalter DJ, Best NG. Bayesian approaches to multiple sources of evidence and uncertainty in complex cost-effectiveness modelling. Stat Med. 2003;22(23):3687–709. [DOI] [PubMed] [Google Scholar]
- 51.Efthimiou O, Mavridis D, Debray TP, Samara M, Belger M, Siontis GC, Leucht S, Salanti G. Combining randomized and non-randomized evidence in network meta-analysis. Stat Med. 2017;36(8):1210–26. [DOI] [PubMed] [Google Scholar]
- 52.Nakhlé G, Brophy JM, Renoux C, Khairy P, Bélisle P, LeLorier J. Domperidone increases harmful cardiac events in Parkinson’s disease: a Bayesian re-analysis of an observational study. J Clin Epidemiol. 2021;140:93–100. [DOI] [PubMed] [Google Scholar]
- 53.Spiegelhalter DJ, Abrams KR, Myles JP. Bayesian approaches to clinical trials and health-care evaluation. Wiley; 2004.
- 54.Gelman A, Hill J. Data analysis using regression and multilevel/hierarchical models. New York, NY: Cambridge University Press; 2007. [Google Scholar]
- 55.Liu J, Li L, Li S, Wang Y, Qin X, Deng K, Liu Y, Zou K, Sun X. Sodium-glucose co-transporter-2 inhibitors and the risk of diabetic ketoacidosis in patients with type 2 diabetes: a systematic review and meta-analysis of randomized controlled trials. Diabetes Obes Metab. 2020;22(9):1619–27. [DOI] [PubMed] [Google Scholar]
- 56.Zhang K, Arora P, Sati N, Béliveau A, Troke N, Veroniki AA, Rodrigues M, Rios P, Zarin W, Tricco AC. Characteristics and methods of incorporating randomized and nonrandomized evidence in network meta-analyses: a scoping review. J Clin Epidemiol. 2019;113:1–10. [DOI] [PubMed] [Google Scholar]
- 57.Deeks JJ, Dinnes J, D’Amico R, Sowden AJ, Sakarovitch C, Song F, Petticrew M, Altman DG. Evaluating non-randomised intervention studies. Health Technol Assess. 2003;7(27):iii–x. [DOI] [PubMed] [Google Scholar]
- 58.Valentine JC, Thompson SG. Issues relating to confounding and meta-analysis when including non-randomized studies in systematic reviews on the effects of interventions. Res Synth Methods. 2013;4(1):26–35. [DOI] [PubMed] [Google Scholar]
- 59.Anglemyer A, Horvath HT, Bero L. Healthcare outcomes assessed with observational study designs compared with those assessed in randomized trials. Cochrane Database Syst Rev. 2014;2014(4):Mr000034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Yao M, Mei F, Zou K, Li L, Sun X. A Bayesian bias-adjusted random-effects model for synthesizing evidence from randomized controlled trials and nonrandomized studies of interventions. J Evid Based Med. 2024. 10.1111/jebm.12633 [DOI] [PubMed] [Google Scholar]
- 61.Tang Y, Tang Q, Yu Y, Wen S. A Bayesian meta-analysis method for estimating risk difference of rare events. J BioPharm Stat. 2018;28(3):550–61. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data in this study have been taken from the published studies and no new data have been generated. Computing code for the two empirical examples can be accessed from the supplementary files.