Abstract
Genetic similarity determines the extent to which two genotypes share common genetic material. It can be measured in various ways, such as by comparing DNA sequences, proteins, or other genetic markers. The significance of genetic similarity is multifaceted and encompasses various fields, including evolutionary biology, medicine, forensic science, animal and plant breeding, and anthropology. Genetic similarity is an important concept with wide application across different scientific disciplines. The research material included 21 rapeseed genotypes (ten interspecific Brassicaceae hybrids of F2 generation and 11 of their parental forms) and 146 alleles obtained using 21 ISSR molecular markers. In the presented study, six measures for calculating genetic similarity were compared: Euclidean, Jaccard, Kulczyński, Sokal and Michener, Nei, and Rogers. Genetic similarity values were estimated between all pairs of examined genotypes using the six measures proposed above. For each genetic similarity measure, the average, minimum, maximum values, and coefficient of variation were calculated. Correlation coefficients between the genetic similarity values obtained from each measure were determined. The obtained genetic similarity coefficients were used for the hierarchical clustering of objects using the unweighted pair group method with an arithmetic mean. A multiple regression model was written for each method, where the independent variables were the remaining methods. For each model, the coefficient of multiple determination was calculated. Genetic similarity values ranged from 0.486 to 0.993 (for the Euclidean method), from 0.157 to 0.986 (for the Jaccard method), from 0.275 to 0.993 (for the Kulczyński method), from 0.272 to 0.993 (for the Nei method), from 0.801 to 1.000 (for the Rogers method) and from 0.486 to 0.993 (for the Sokal and Michener method). The results indicate that the research material was divided into two identical groups using any of the proposed methods despite differences in the values of genetic similarity coefficients. Two of the presented measures of genetic similarity (the Sokal and Michener method and the Euclidean method) were the same.
Keywords: similarity measures, rapeseed, molecular markers, correlation, dendrogram
1. Introduction
Genetic diversity is the presence of different forms of genes found in all ecosystems [1,2]. This means that regardless of the type of environment in which specific species live, their population can exhibit variable genetic traits [3]. The essence of this diversity is that most of the variable gene forms are inherited from generation to generation [4]. The impact of genetic diversity directly affects the entire population [5,6,7]. It is crucial for the process of selection—a process in which some genotype variants have an advantage over others. Selection is an important mechanism that acts on animal and plant populations [8,9,10,11]. This effect can be observed both at the population level and at the individual level. The main factor driving selection is the availability of resources in a given environment [12,13]. Naturally, if only limited environmental resources are available, the only way to survive and thrive is to gain an advantage through a genotype that has greater suitability to the environment [14,15,16]. In the case of plants and animals, genetic diversity has a crucial impact on selection [17]. In the process of natural selection, the force of choice operates, where unfavorable traits are eliminated, and an individual with the most advantageous traits for a given environment has a greater chance of survival [18,19]. This natural mechanism favors variants that are best adapted to living in a particular environment [20,21].
As a result of genetic diversity, the selection process begins with the recurrent genetic components present in the population [22,23]. Over time, these become important factors driving the diverse selection process [24]. Existing adaptive capabilities, including genetic traits, determine a population’s ability to survive in challenging conditions and provide an advantage based on genetic components [25,26]. Consequently, a diverse genotype has a greater chance of survival and the ability to cope with environmental conditions through reproduction, leading to the emergence of new generations from this genotype [25]. Another factor influencing genotype selection is polymorphism, the phenomenon of genetic discontinuity manifested by the presence of different forms within a single species that differ functionally or structurally [27,28,29]. Polymorphism involves the formation of hierarchies and the division of functions within a population. It can occur at the phenotypic level or the genetic or molecular levels [30,31]. When the frequency of two (or more) variations in a given population is too high to be caused by mutation, the population is considered polymorphic. In general, greater genetic diversity in a population may result in a higher chance of gaining an advantage in genotype selection [30,32]. In reality, genetic diversity arising from the combination of environmental conditions and the influence of biological factors is crucial for the adaptation of a population to new conditions [33,34]. A high level of genetic diversity will help minimize the effects of changing environmental conditions, consequently increasing the chances of survival for an individual or population [2,35].
The results of genetic similarity (genetic variability) have great significance in making selection decisions, which is related to the choice of the method for calculating this characteristic [2]. The method of genetic similarity is used in genetics and zoology to determine the degree of relatedness between individuals [36,37,38]. It involves comparing the levels of concordance in the genome of a given species or gene or DNA sequences to determine the phylogenetic distance between individuals. This method is commonly used in studies of human genealogy, species phylogeny, and research on evolutionary mechanisms and the tracing of species origins [39,40]. The genetic similarity method contributes to evolutionary studies on the origins of species, their lineage, and migrations [41,42]. Along with other methods, it is used to assess the impact of environmental changes and biological processes on biodiversity. Due to the potentially multi-level analysis of all DNA sequences, this method is particularly useful in zoology and molecular biology.
Different measures of calculating genetic similarity represent a specific type of statistic that compares genetic data between individuals [43,44,45]. Each measure has its advantages and disadvantages and reflects a particular methodology. The commonly encountered measures of genetic similarity can be divided into four main categories: classical, contemporary, dendrographic, and index-based. Classical measures include standard units, mean components, and the inbreeding index [46]. The first is a measure of identity, while the other two reflect the genetic composition relative to a given subset or population. Contemporary measures of genetic similarity, such as jump length and interdependence level, reflect the relationship between individual data and general data [47]. These measures identify the tendencies to occur in groups and calculate the likelihood of specific objects appearing within a population. These measures are often used, particularly in studies of genetic authenticity and microorganism identity. Dendrographic measures are very similar to classical measures but reflect similarities and differences at the genetic level [48,49]. Dendrographic measures help in understanding the genetic relationships between populations and other groups or individuals [50]. Index-based measures are multidisciplinary measures that examine the data structure at the population level [51]. They utilize elements of previous measures, estimating levels of similarities and differences within a population. Among other things, they estimate the ratio of individuals sharing a common ancestor or provide a detailed view of kinship and mismatch levels within a population. The aim of this study was to compare six statistical measures (Euclidean, Jaccard, Kulczyński, Sokal and Michener, Nei, and Rogers) to assess the genetic similarities of 21 rapeseed objects (10 interspecific Brassicaceae hybrids of the F2 generation, and 11 of their parental forms) based on the observations of 146 alleles obtained using 21 ISSR molecular markers.
2. Materials and Methods
2.1. Plant Material
The plant material for the genetic similarity analysis consisted of twenty-one Brassicaceae genotypes, including ten various Brassicaceae F2 hybrids and eleven parental genotypes (Table 1). Interspecific hybrids of the F2 generation were developed at the Department of Genetics and Plant Breeding (Poznań University of Life Sciences) with the use of in vitro embryo cultures.
Table 1.
Plant material used in this study for the analysis of genetic similarity based on ISSR markers.
| Maternal Form | Paternal Forms | Hybrids of F2 Generation |
|---|---|---|
| Brassica napus (BN) | Brassica carinata (BC) | B. napus × B. carinata (BN × BC) |
| Brassica rapa ssp. trilocularis (BRt) | B. napus × B. rapa ssp. trilocularis (BN × BRt) | |
| Brassica rapa ssp. chinensis (BRc) | B. napusx × B. rapa ssp. chinensis (BN × BRc) | |
| Brassica fruticulosa (BF) | B. napus × B. fruticulosa (BN × BF) | |
| Brassica rapa ssp. pekinensis (BRp) | B. napus × B. rapa ssp. pekinensis (BN × BRp) | |
| Brassica nigra (BNI) | B. napus × B. nigra (BN × BNI) | |
| Brassica juncea (BJ) | B. napus × B. juncea (BN × BJ) | |
| Sinapis alba (SA) | B. napus × S. alba (BN × SA) | |
| Brassica tournefortii (BT) | B. napus × B. rapa ssp. tournefortii (BN × BT) | |
| Brassica oleracea var. alboglabra (BO) | B. napus × B. oleracea var. alboglabra (BN × BO) |
2.2. Molecular Analysis
Genomic DNA was extracted from young seedling leaves of the studied genotypes using the Genomic Mini AX Plant kit (A&ABiotechnology, Gdańsk, Poland) according to the manufacturer’s protocol. The DNA concentration and purity were determined using a DeNovix® DS-11 Spectrophotometer (Tokyo, Japan). Prior to the PCR analysis, DNA samples were diluted to 50 ng μL−1 using Tris buffer. PCR reactions were performed in a total volume of 13.05 µL (6.25 µL of DreamTaq PCR Master Mix, 0.25 µL of primer, 5.55 µL of H2O, and 1 µL of DNA template) under the conditions indicated in Table 2. The primer sequences and annealing temperatures are presented in Table 3.
Table 2.
PCR amplification profiles for tested primers.
| Reaction Profile | Primers | Parameters | Temperature | Number of Cycles | Source |
|---|---|---|---|---|---|
| 1 | mstg 1, mstg 4, mstg 12, mstg 13, mstg 38 | Initial denaturation | 94 °C 30 s | ×1 | [52] |
| Denaturation | 94 °C 30 s | ×40 | |||
| Primers annealing | 60 °C * 30 s | ||||
| Elongation | 72 °C 1 min | ||||
| Final elongation | 72 °C 5 min | ×1 | |||
| 2 | UBC812, UBC840, UBC845 | Initial denaturation | 95 °C 2 min | ×1 | [53] |
| Denaturation | 93 °C 20 s | ×40 | |||
| Primers annealing | 52 °C * 1 min | ||||
| Elongation | 72 °C 20 s | ||||
| Final elongation | 72 °C 6 min | ×1 | |||
| 3 | UBC891, ISSR-840, ISSR-856, ISSR-857, ISSR-887, ISSR-888, ISSR-889, ISSR-890, scm51, P1, P2, P4, P5 | Initial denaturation | 94 °C 5 min | ×1 | [54] |
| Denaturation | 94 °C 45 s | ×35 | |||
| Primers annealing | 50 °C * 45 s | ||||
| Elongation | 72 °C 90 s | ||||
| Final elongation | 72 °C 7 min | ×1 |
* Primer annealing temperature was modified for each PCR reaction (Table 3).
Table 3.
List of ISSR primers used in this study.
| ISSR Primer | Sequence 5′-3′ | Annealing Temperature [°C] |
|---|---|---|
| mstg 1 | (TA)3(TG)9 | 53.9 |
| mstg 4 | (TA)3(TG)10 | 60 |
| mstg 12 | (TG)7 | 54 |
| mstg 13 | (TG)7CG(TG)2 | 59.7 |
| mstg 38 | (TG)3TT(TG)5 | 53.9 |
| UBC835 | (AG)8YC | 51.5 |
| UBC843 | (CT)8RA | 48.1 |
| UBC889 | DBD(AC)7 | 51.5 |
| UBC891 | HVH(TG)7 | 51.5 |
| scm 51 | (AGG)5 | 52.8 |
| P1 | GAG(CAA)5 | 49.7 |
| P2 | CTG(GT)8 | 56.5 |
| P4 | (AG)8GTG | 52.8 |
| P5 | (GA)8ACC | 51.5 |
| ISSR-840 | (GA)8YT | 48.4 |
| ISSR-856 | (GA)8YA | 48.4 |
| ISSR-857 | (GA)8YG | 55.3 |
| ISSR-887 | DVD(TC)7 | 47.8 |
| ISSR-888 | BDB(CA)7 | 48.4 |
| ISSR-889 | DBD(AC)7 | 48.1 |
| ISSR-890 | VHV(GT)7 | 48.4 |
Separation of the amplification product was performed on 1.5% agarose gel stained with Midori Green Advance (6 µL per 100 mL) in 1× TBE buffer at 104 V. The gels were visualized using the BIO-RAD Molecular Imager® (Hercules, CA, USA) Gel DocTM XR+ with Image LabTM v. 5.1 Software.
2.3. Measures of Genetic Similarity
The following six measures, most commonly used in practical research, were used to estimate the genetic similarity (GS) of the genotypes studied.
Euclidean measure [55]:
| (1) |
where N represents the number of markers and () denotes the observation of the i-th allele of genotype A (genotype B).
The Jaccarda measure [56]:
| (2) |
where denotes the number of alleles present in genotype A, denotes the number of alleles present in genotype B, and denotes the number of alleles present in both genotype A and genotype B.
The Kulczyński measure [57]:
| (3) |
The Nei measure [58]:
| (4) |
The Rogers measure [59]:
| (5) |
where denotes the number of alleles present in genotype A and is simultaneously absent in genotype B and denotes the number of alleles present in genotype B and is simultaneously absent in genotype A.
The Sokal and Michener measure [60]:
| (6) |
where denotes the number of cases where the same alleles are simultaneously absent in genotypes A and B.
2.4. Statistical Analysis
Genetic similarity values were estimated between all pairs of examined genotypes using the six measures proposed above. For each genetic similarity measure, the average, minimum, maximum values, and coefficient of variation were calculated. Correlation coefficients between the genetic similarity values obtained from each measure were determined. The significance of correlation coefficients was tested at a level of α = 0.001. The obtained genetic similarity coefficients were used for the hierarchical clustering of objects using the unweighted pair group method with the arithmetic mean (UPGMA). The results of the clustering analyses were presented in the form of dendrograms for the respective measures. A multiple regression model was written for each method (Euclidean, Jaccard, Kulczynski, Sokal and Michener, Nei, and Rogers), where the independent variables were the remaining methods. For each model, the coefficient of multiple determination (R2) was calculated. All these analyses were conducted using the GenStat v. 23.1 statistical software package [61].
3. Results
The analyzed material was examined using 21 primers. The number of amplification products for individual primers ranged from four (for UBC889, ISSR856, ISSR857, and ISSR890) to 11 (for mstg13, UBC835, and UBC891). In total, 146 markers were obtained.
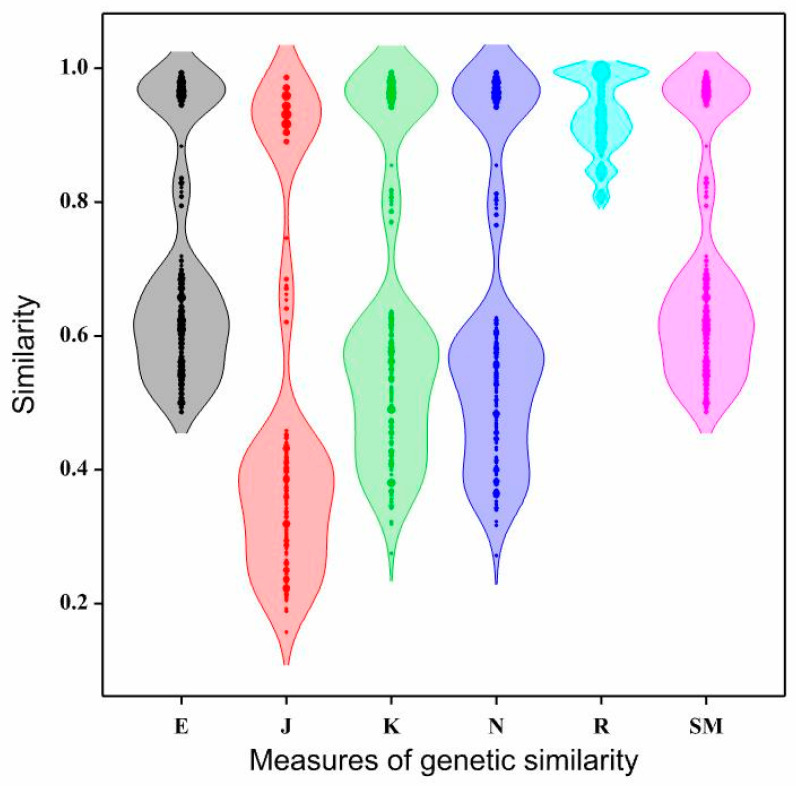
Table 4 presents the statistical characteristics of the genetic similarity coefficients obtained using six measures. The genetic similarity values estimated by the Euclidean method ranged from 0.486 (for two pairs of genotypes: SA-BN and SA-BJ) to 0.993 (for three pairs of genotypes: BN × BRc-BN × BJ, BN × SA-BN × BRc, and BN × BT-BN × SA) (Table 5), with an average of 0.709 (Table 4). The genetic similarity coefficients calculated using the Euclidean method exhibited moderate variability, with a coefficient of variation of 24.21% (Figure 1, Table 4).
Table 4.
Statistical characteristics of genetic similarity of interspecific Brassicaceae hybrids F2 generation and their parental forms.
| Genetic Similarity Measure | Minimal Value | Mean Value | Maximum Value | Coefficient of Variability [in %] |
|---|---|---|---|---|
| Euclidean | 0.486 | 0.709 | 0.993 | 24.21 |
| Jaccard | 0.157 | 0.508 | 0.986 | 54.15 |
| Kulczyński | 0.275 | 0.640 | 0.993 | 34.46 |
| Nei | 0.272 | 0.633 | 0.993 | 35.43 |
| Rogers | 0.801 | 0.929 | 1.000 | 6.14 |
| Sokal and Michener | 0.486 | 0.709 | 0.993 | 24.21 |
Table 5.
Genetic similarity coefficients between the examined genotypes calculated using the Euclidean measure (above diagonal) and Jaccard measure (below diagonal).
| Genotype | BN | BC | BRt | BJ | BNI | BO | BRc | SA | BRp | BF | BT | BN × BC | BN × BRt | BN × BJ | BN × BNI | BN × BO | BN × BRc | BN × SA | BN × BRp | BN × BF | BN × BT |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BN | 1.000 | 0.596 | 0.658 | 0.603 | 0.610 | 0.808 | 0.541 | 0.486 | 0.644 | 0.534 | 0.562 | 0.959 | 0.959 | 0.952 | 0.952 | 0.945 | 0.959 | 0.952 | 0.966 | 0.959 | 0.959 |
| BC | 0.359 | 1.000 | 0.582 | 0.692 | 0.699 | 0.610 | 0.658 | 0.548 | 0.637 | 0.637 | 0.500 | 0.637 | 0.637 | 0.603 | 0.603 | 0.596 | 0.596 | 0.603 | 0.616 | 0.610 | 0.610 |
| BRt | 0.419 | 0.282 | 1.000 | 0.685 | 0.706 | 0.644 | 0.555 | 0.555 | 0.712 | 0.589 | 0.521 | 0.671 | 0.671 | 0.678 | 0.678 | 0.671 | 0.685 | 0.692 | 0.664 | 0.658 | 0.685 |
| BJ | 0.370 | 0.430 | 0.410 | 1.000 | 0.884 | 0.616 | 0.623 | 0.486 | 0.712 | 0.630 | 0.589 | 0.616 | 0.616 | 0.637 | 0.623 | 0.644 | 0.630 | 0.623 | 0.623 | 0.616 | 0.630 |
| BNI | 0.387 | 0.450 | 0.449 | 0.746 | 1.000 | 0.610 | 0.658 | 0.521 | 0.719 | 0.623 | 0.582 | 0.610 | 0.623 | 0.630 | 0.603 | 0.610 | 0.623 | 0.616 | 0.616 | 0.610 | 0.623 |
| BO | 0.641 | 0.337 | 0.366 | 0.349 | 0.352 | 1.000 | 0.527 | 0.541 | 0.699 | 0.589 | 0.589 | 0.795 | 0.795 | 0.829 | 0.829 | 0.836 | 0.836 | 0.829 | 0.815 | 0.808 | 0.822 |
| BRc | 0.287 | 0.367 | 0.235 | 0.329 | 0.383 | 0.233 | 1.000 | 0.575 | 0.596 | 0.692 | 0.555 | 0.555 | 0.541 | 0.507 | 0.534 | 0.514 | 0.514 | 0.521 | 0.548 | 0.541 | 0.527 |
| SA | 0.211 | 0.214 | 0.207 | 0.157 | 0.205 | 0.221 | 0.225 | 1.000 | 0.569 | 0.651 | 0.527 | 0.500 | 0.500 | 0.493 | 0.507 | 0.500 | 0.500 | 0.507 | 0.493 | 0.514 | 0.500 |
| BRp | 0.381 | 0.321 | 0.409 | 0.425 | 0.446 | 0.413 | 0.253 | 0.192 | 1.000 | 0.671 | 0.658 | 0.658 | 0.671 | 0.678 | 0.678 | 0.685 | 0.685 | 0.692 | 0.664 | 0.658 | 0.685 |
| BF | 0.236 | 0.293 | 0.221 | 0.290 | 0.295 | 0.250 | 0.348 | 0.261 | 0.294 | 1.000 | 0.658 | 0.562 | 0.548 | 0.527 | 0.541 | 0.534 | 0.534 | 0.541 | 0.541 | 0.548 | 0.548 |
| BT | 0.319 | 0.207 | 0.214 | 0.302 | 0.307 | 0.310 | 0.244 | 0.188 | 0.342 | 0.315 | 1.000 | 0.548 | 0.562 | 0.555 | 0.582 | 0.575 | 0.562 | 0.569 | 0.569 | 0.562 | 0.562 |
| BN × BC | 0.917 | 0.405 | 0.435 | 0.385 | 0.387 | 0.620 | 0.301 | 0.223 | 0.398 | 0.264 | 0.305 | 1.000 | 0.973 | 0.952 | 0.966 | 0.945 | 0.959 | 0.966 | 0.980 | 0.959 | 0.973 |
| BN × BRt | 0.917 | 0.405 | 0.435 | 0.385 | 0.402 | 0.620 | 0.287 | 0.223 | 0.415 | 0.250 | 0.319 | 0.944 | 1.000 | 0.952 | 0.966 | 0.945 | 0.959 | 0.966 | 0.980 | 0.959 | 0.973 |
| BN × BJ | 0.904 | 0.370 | 0.447 | 0.411 | 0.413 | 0.675 | 0.258 | 0.221 | 0.427 | 0.233 | 0.316 | 0.904 | 0.904 | 1.000 | 0.973 | 0.980 | 0.993 | 0.986 | 0.959 | 0.966 | 0.980 |
| BN × BNI | 0.903 | 0.363 | 0.441 | 0.389 | 0.376 | 0.671 | 0.277 | 0.226 | 0.420 | 0.239 | 0.337 | 0.930 | 0.930 | 0.944 | 1.000 | 0.980 | 0.980 | 0.986 | 0.986 | 0.966 | 0.980 |
| BN × BO | 0.890 | 0.359 | 0.435 | 0.416 | 0.387 | 0.684 | 0.260 | 0.223 | 0.432 | 0.236 | 0.333 | 0.890 | 0.890 | 0.958 | 0.957 | 1.000 | 0.986 | 0.980 | 0.966 | 0.959 | 0.973 |
| BN × BRc | 0.917 | 0.359 | 0.452 | 0.400 | 0.402 | 0.684 | 0.260 | 0.223 | 0.432 | 0.236 | 0.319 | 0.917 | 0.917 | 0.986 | 0.957 | 0.971 | 1.000 | 0.993 | 0.966 | 0.973 | 0.986 |
| BN × SA | 0.903 | 0.363 | 0.458 | 0.389 | 0.391 | 0.671 | 0.263 | 0.226 | 0.438 | 0.239 | 0.323 | 0.930 | 0.930 | 0.971 | 0.971 | 0.957 | 0.986 | 1.000 | 0.973 | 0.966 | 0.993 |
| BN × BRp | 0.931 | 0.385 | 0.430 | 0.396 | 0.398 | 0.654 | 0.298 | 0.221 | 0.410 | 0.247 | 0.330 | 0.958 | 0.958 | 0.918 | 0.971 | 0.931 | 0.931 | 0.944 | 1.000 | 0.966 | 0.980 |
| BN × BF | 0.917 | 0.374 | 0.419 | 0.385 | 0.387 | 0.641 | 0.287 | 0.237 | 0.398 | 0.250 | 0.319 | 0.917 | 0.917 | 0.931 | 0.930 | 0.917 | 0.944 | 0.930 | 0.931 | 1.000 | 0.973 |
| BN × BT | 0.917 | 0.374 | 0.452 | 0.400 | 0.402 | 0.662 | 0.274 | 0.223 | 0.432 | 0.250 | 0.319 | 0.944 | 0.944 | 0.958 | 0.957 | 0.944 | 0.971 | 0.986 | 0.958 | 0.944 | 1.000 |
Figure 1.
Density plots of coefficients of genetic similarity of interspecific Brassicaceae hybrids and their parental forms using six measures of genetic similarity: E—Euclidean, J—Jaccard, K—Kulczyński, N—Nei, R—Rogers, SM—Sokal and Michener.
The smallest genetic similarity coefficients were obtained for the measure proposed by Jaccard (with an average of 0.508). These coefficients exhibited the highest variability (54.15%) among all measures used (Table 4, Figure 1). The lowest genetic similarity, according to Jaccard, was observed between the pair BJ-SA (0.157), while the highest was between the pair BN × BJ-BN × BRc (0.986) (Table 5).
Slightly larger genetic similarity coefficients were obtained for the measures proposed by Kulczyński and Nei compared to Jaccard. The results obtained with these two methods were similar in terms of both the values of genetic similarity coefficients (with average values of 0.640 and 0.633, respectively) (Table 4) and their variability (the coefficients of variation were 34.46% and 35.43%, respectively) (Table 4, Figure 1). The genetic similarity coefficients by Kulczyński ranged from 0.275 (between BJ and SA) to 0.993 (between BN × BJ and BN × BRc) (Table 6). Meanwhile, genetic similarity, calculated using the Nei method, ranged from 0.272 (between BJ and SA) to 0.993 (between BN × BJ and BN × BRc) (Table 6).
Table 6.
Genetic similarity coefficients between the examined genotypes were calculated using the Kulczyński measure (above diagonal) and Nei measure (below diagonal).
| Genotype | BN | BC | BRt | BJ | BNI | BO | BRc | SA | BRp | BF | BT | BN × BC | BN × BRt | BN × BJ | BN × BNI | BN × BO | BN × BRc | BN × SA | BN × BRp | BN × BF | BN × BT |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BN | 1.000 | 0.534 | 0.601 | 0.545 | 0.561 | 0.786 | 0.455 | 0.362 | 0.572 | 0.408 | 0.490 | 0.957 | 0.957 | 0.950 | 0.949 | 0.942 | 0.957 | 0.949 | 0.964 | 0.957 | 0.957 |
| BC | 0.528 | 1.000 | 0.441 | 0.602 | 0.621 | 0.505 | 0.538 | 0.356 | 0.489 | 0.465 | 0.342 | 0.582 | 0.582 | 0.546 | 0.537 | 0.534 | 0.534 | 0.537 | 0.563 | 0.550 | 0.550 |
| BRt | 0.590 | 0.440 | 1.000 | 0.583 | 0.622 | 0.537 | 0.381 | 0.345 | 0.582 | 0.368 | 0.352 | 0.617 | 0.617 | 0.630 | 0.621 | 0.617 | 0.634 | 0.638 | 0.613 | 0.601 | 0.634 |
| BJ | 0.540 | 0.602 | 0.582 | 1.000 | 0.855 | 0.517 | 0.497 | 0.275 | 0.602 | 0.461 | 0.464 | 0.561 | 0.561 | 0.589 | 0.564 | 0.593 | 0.577 | 0.564 | 0.573 | 0.561 | 0.577 |
| BNI | 0.558 | 0.621 | 0.620 | 0.855 | 1.000 | 0.521 | 0.556 | 0.346 | 0.626 | 0.472 | 0.471 | 0.561 | 0.576 | 0.588 | 0.549 | 0.561 | 0.576 | 0.565 | 0.573 | 0.561 | 0.576 |
| BO | 0.781 | 0.504 | 0.536 | 0.517 | 0.521 | 1.000 | 0.380 | 0.368 | 0.593 | 0.413 | 0.474 | 0.770 | 0.770 | 0.812 | 0.807 | 0.818 | 0.818 | 0.807 | 0.797 | 0.786 | 0.802 |
| BRc | 0.446 | 0.537 | 0.381 | 0.495 | 0.554 | 0.378 | 1.000 | 0.369 | 0.405 | 0.524 | 0.393 | 0.472 | 0.455 | 0.419 | 0.441 | 0.422 | 0.422 | 0.424 | 0.469 | 0.455 | 0.438 |
| SA | 0.348 | 0.353 | 0.343 | 0.272 | 0.340 | 0.362 | 0.367 | 1.000 | 0.323 | 0.415 | 0.319 | 0.380 | 0.380 | 0.378 | 0.383 | 0.380 | 0.380 | 0.383 | 0.378 | 0.399 | 0.380 |
| BRp | 0.552 | 0.485 | 0.580 | 0.596 | 0.617 | 0.585 | 0.404 | 0.323 | 1.000 | 0.457 | 0.513 | 0.590 | 0.608 | 0.622 | 0.612 | 0.626 | 0.626 | 0.630 | 0.605 | 0.590 | 0.626 |
| BF | 0.382 | 0.454 | 0.362 | 0.449 | 0.455 | 0.400 | 0.516 | 0.414 | 0.455 | 1.000 | 0.490 | 0.447 | 0.428 | 0.406 | 0.411 | 0.408 | 0.408 | 0.411 | 0.425 | 0.428 | 0.428 |
| BT | 0.484 | 0.342 | 0.352 | 0.464 | 0.470 | 0.474 | 0.393 | 0.317 | 0.510 | 0.479 | 1.000 | 0.474 | 0.490 | 0.487 | 0.510 | 0.507 | 0.490 | 0.493 | 0.503 | 0.490 | 0.490 |
| BN × BC | 0.957 | 0.576 | 0.607 | 0.556 | 0.558 | 0.766 | 0.463 | 0.365 | 0.569 | 0.418 | 0.468 | 1.000 | 0.971 | 0.950 | 0.964 | 0.942 | 0.957 | 0.964 | 0.979 | 0.957 | 0.971 |
| BN × BRt | 0.957 | 0.576 | 0.607 | 0.556 | 0.574 | 0.766 | 0.446 | 0.365 | 0.586 | 0.400 | 0.484 | 0.971 | 1.000 | 0.950 | 0.964 | 0.942 | 0.957 | 0.964 | 0.979 | 0.957 | 0.971 |
| BN × BJ | 0.950 | 0.540 | 0.618 | 0.583 | 0.585 | 0.806 | 0.410 | 0.362 | 0.598 | 0.378 | 0.480 | 0.950 | 0.950 | 1.000 | 0.971 | 0.979 | 0.993 | 0.986 | 0.957 | 0.964 | 0.979 |
| BN × BNI | 0.949 | 0.532 | 0.612 | 0.560 | 0.547 | 0.803 | 0.433 | 0.368 | 0.591 | 0.385 | 0.504 | 0.964 | 0.964 | 0.971 | 1.000 | 0.978 | 0.978 | 0.985 | 0.986 | 0.964 | 0.978 |
| BN × BO | 0.942 | 0.528 | 0.607 | 0.587 | 0.558 | 0.813 | 0.413 | 0.365 | 0.603 | 0.382 | 0.500 | 0.942 | 0.942 | 0.978 | 0.978 | 1.000 | 0.986 | 0.978 | 0.964 | 0.957 | 0.971 |
| BN × BRc | 0.957 | 0.528 | 0.623 | 0.571 | 0.574 | 0.813 | 0.413 | 0.365 | 0.603 | 0.382 | 0.484 | 0.957 | 0.957 | 0.993 | 0.978 | 0.986 | 1.000 | 0.993 | 0.964 | 0.971 | 0.986 |
| BN × SA | 0.949 | 0.532 | 0.628 | 0.560 | 0.563 | 0.803 | 0.417 | 0.368 | 0.609 | 0.385 | 0.488 | 0.964 | 0.964 | 0.986 | 0.985 | 0.978 | 0.993 | 1.000 | 0.971 | 0.964 | 0.993 |
| BN × BRp | 0.964 | 0.556 | 0.602 | 0.567 | 0.569 | 0.791 | 0.459 | 0.362 | 0.581 | 0.396 | 0.496 | 0.978 | 0.978 | 0.957 | 0.986 | 0.964 | 0.964 | 0.971 | 1.000 | 0.964 | 0.979 |
| BN × BF | 0.957 | 0.544 | 0.590 | 0.556 | 0.558 | 0.781 | 0.446 | 0.383 | 0.569 | 0.400 | 0.484 | 0.957 | 0.957 | 0.964 | 0.964 | 0.957 | 0.971 | 0.964 | 0.964 | 1.000 | 0.971 |
| BN × BT | 0.957 | 0.544 | 0.623 | 0.571 | 0.574 | 0.797 | 0.430 | 0.365 | 0.603 | 0.400 | 0.484 | 0.971 | 0.971 | 0.978 | 0.978 | 0.971 | 0.986 | 0.993 | 0.978 | 0.971 | 1.000 |
Significantly different results were obtained when using the Rogers measure (Table 4 and Table 7, Figure 1). The genetic similarity coefficients exhibited the lowest variability: 6.14% (Table 4) and ranged from 0.801 (for two genotype pairs: BF-BN × BJ and BF-BN × BRp) to 1.000 (for 23 genotype pairs) (Table 7). The average value of the Rogers coefficients was 0.929 (Table 4). The minimum value of the genetic similarity coefficients, estimated by this measure, was higher than the average values obtained for the other measures.
Table 7.
Genetic similarity coefficients between the examined genotypes were calculated using the Rogers measure (above diagonal) and the Sokal and Michener measure (below diagonal).
| Genotype | BN | BC | BRt | BJ | BNI | BO | BRc | SA | BRp | BF | BT | BN × BC | BN × BRt | BN × BJ | BN × BNI | BN × BO | BN × BRc | BN × SA | BN × BRp | BN × BF | BN × BT |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BN | 1.000 | 0.911 | 0.890 | 0.918 | 0.938 | 0.932 | 0.884 | 0.843 | 0.849 | 0.808 | 0.904 | 1.000 | 1.000 | 0.993 | 0.993 | 1.000 | 1.000 | 0.993 | 0.993 | 1.000 | 1.000 |
| BC | 0.596 | 1.000 | 0.980 | 0.993 | 0.973 | 0.980 | 0.973 | 0.932 | 0.938 | 0.897 | 0.993 | 0.911 | 0.911 | 0.904 | 0.918 | 0.911 | 0.911 | 0.918 | 0.904 | 0.911 | 0.911 |
| BRt | 0.658 | 0.582 | 1.000 | 0.973 | 0.952 | 0.959 | 0.993 | 0.952 | 0.959 | 0.918 | 0.986 | 0.890 | 0.890 | 0.884 | 0.897 | 0.890 | 0.890 | 0.897 | 0.884 | 0.890 | 0.890 |
| BJ | 0.603 | 0.692 | 0.685 | 1.000 | 0.980 | 0.986 | 0.966 | 0.925 | 0.932 | 0.890 | 0.986 | 0.918 | 0.918 | 0.911 | 0.925 | 0.918 | 0.918 | 0.925 | 0.911 | 0.918 | 0.918 |
| BNI | 0.610 | 0.699 | 0.706 | 0.884 | 1.000 | 0.993 | 0.945 | 0.904 | 0.911 | 0.870 | 0.966 | 0.938 | 0.938 | 0.932 | 0.945 | 0.938 | 0.938 | 0.945 | 0.932 | 0.938 | 0.938 |
| BO | 0.808 | 0.610 | 0.644 | 0.616 | 0.610 | 1.000 | 0.952 | 0.911 | 0.918 | 0.877 | 0.973 | 0.932 | 0.932 | 0.925 | 0.938 | 0.932 | 0.932 | 0.938 | 0.925 | 0.932 | 0.932 |
| BRc | 0.541 | 0.658 | 0.555 | 0.623 | 0.658 | 0.527 | 1.000 | 0.959 | 0.966 | 0.925 | 0.980 | 0.884 | 0.884 | 0.877 | 0.890 | 0.884 | 0.884 | 0.890 | 0.877 | 0.884 | 0.884 |
| SA | 0.486 | 0.548 | 0.555 | 0.486 | 0.521 | 0.541 | 0.575 | 1.000 | 0.993 | 0.966 | 0.938 | 0.843 | 0.843 | 0.836 | 0.849 | 0.843 | 0.843 | 0.849 | 0.836 | 0.843 | 0.843 |
| BRp | 0.644 | 0.637 | 0.712 | 0.712 | 0.719 | 0.699 | 0.596 | 0.569 | 1.000 | 0.959 | 0.945 | 0.849 | 0.849 | 0.843 | 0.856 | 0.849 | 0.849 | 0.856 | 0.843 | 0.849 | 0.849 |
| BF | 0.534 | 0.637 | 0.589 | 0.630 | 0.623 | 0.589 | 0.692 | 0.651 | 0.671 | 1.000 | 0.904 | 0.808 | 0.808 | 0.801 | 0.815 | 0.808 | 0.808 | 0.815 | 0.801 | 0.808 | 0.808 |
| BT | 0.562 | 0.500 | 0.521 | 0.589 | 0.582 | 0.589 | 0.555 | 0.527 | 0.658 | 0.658 | 1.000 | 0.904 | 0.904 | 0.897 | 0.911 | 0.904 | 0.904 | 0.911 | 0.897 | 0.904 | 0.904 |
| BN × BC | 0.959 | 0.637 | 0.671 | 0.616 | 0.610 | 0.795 | 0.555 | 0.500 | 0.658 | 0.562 | 0.548 | 1.000 | 1.000 | 0.993 | 0.993 | 1.000 | 1.000 | 0.993 | 0.993 | 1.000 | 1.000 |
| BN × BRt | 0.959 | 0.637 | 0.671 | 0.616 | 0.623 | 0.795 | 0.541 | 0.500 | 0.671 | 0.548 | 0.562 | 0.973 | 1.000 | 0.993 | 0.993 | 1.000 | 1.000 | 0.993 | 0.993 | 1.000 | 1.000 |
| BN × BJ | 0.952 | 0.603 | 0.678 | 0.637 | 0.630 | 0.829 | 0.507 | 0.493 | 0.678 | 0.527 | 0.555 | 0.952 | 0.952 | 1.000 | 0.986 | 0.993 | 0.993 | 0.986 | 1.000 | 0.993 | 0.993 |
| BN × BNI | 0.952 | 0.603 | 0.678 | 0.623 | 0.603 | 0.829 | 0.534 | 0.507 | 0.678 | 0.541 | 0.582 | 0.966 | 0.966 | 0.973 | 1.000 | 0.993 | 0.993 | 1.000 | 0.986 | 0.993 | 0.993 |
| BN × BO | 0.945 | 0.596 | 0.671 | 0.644 | 0.610 | 0.836 | 0.514 | 0.500 | 0.685 | 0.534 | 0.575 | 0.945 | 0.945 | 0.980 | 0.980 | 1.000 | 1.000 | 0.993 | 0.993 | 1.000 | 1.000 |
| BN × BRc | 0.959 | 0.596 | 0.685 | 0.630 | 0.623 | 0.836 | 0.514 | 0.500 | 0.685 | 0.534 | 0.562 | 0.959 | 0.959 | 0.993 | 0.980 | 0.986 | 1.000 | 0.993 | 0.993 | 1.000 | 1.000 |
| BN × SA | 0.952 | 0.603 | 0.692 | 0.623 | 0.616 | 0.829 | 0.521 | 0.507 | 0.692 | 0.541 | 0.569 | 0.966 | 0.966 | 0.986 | 0.986 | 0.980 | 0.993 | 1.000 | 0.986 | 0.993 | 0.993 |
| BN × BRp | 0.966 | 0.616 | 0.664 | 0.623 | 0.616 | 0.815 | 0.548 | 0.493 | 0.664 | 0.541 | 0.569 | 0.980 | 0.980 | 0.959 | 0.986 | 0.966 | 0.966 | 0.973 | 1.000 | 0.993 | 0.993 |
| BN × BF | 0.959 | 0.610 | 0.658 | 0.616 | 0.610 | 0.808 | 0.541 | 0.514 | 0.658 | 0.548 | 0.562 | 0.959 | 0.959 | 0.966 | 0.966 | 0.959 | 0.973 | 0.966 | 0.966 | 1.000 | 1.000 |
| BN × BT | 0.959 | 0.610 | 0.685 | 0.630 | 0.623 | 0.822 | 0.527 | 0.500 | 0.685 | 0.548 | 0.562 | 0.973 | 0.973 | 0.980 | 0.980 | 0.973 | 0.986 | 0.993 | 0.980 | 0.973 | 1.000 |
The genetic similarity coefficients calculated using the Sokal and Michener measure were identical to the coefficients calculated using the Euclidean method (Table 5 and Table 7). The minimum value was twice the minimum value obtained using the Kulczyński or Nei measures and four times when the Jaccard measure was used for comparison.
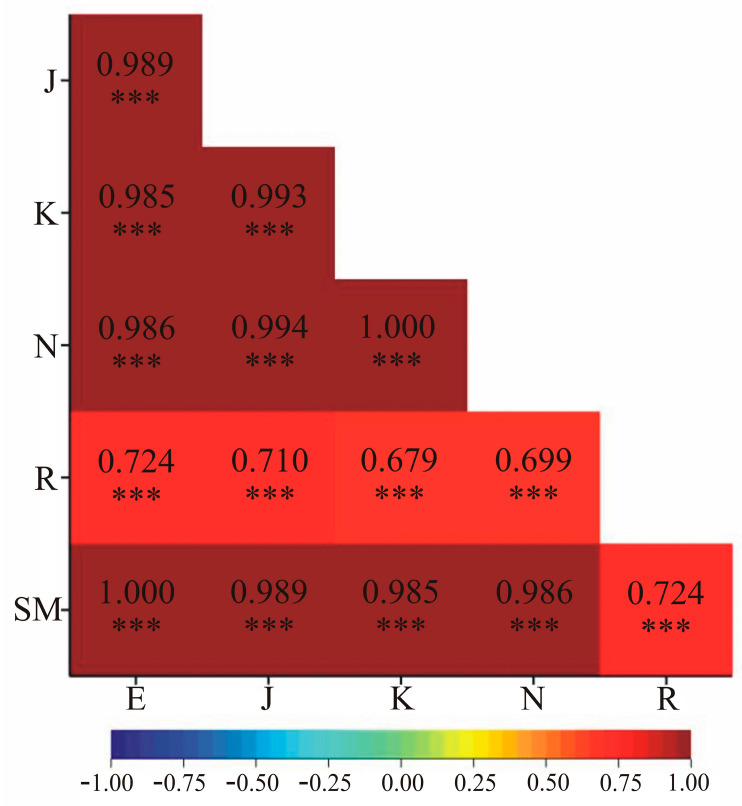
Figure 2 depicts the linear correlation coefficients between the genetic similarity values obtained using six measures. The results indicate statistically significant correlations between all applied genetic similarity measures (at α = 0.001 level). It is noteworthy that the genetic similarity coefficients calculated by the Kulczyński and Nei methods show perfect correlation (correlation coefficient was 1.000). A similar result was obtained for the Euclidean vs. the Sokal and Michener measures (Figure 2). However, this is due to the identical values obtained from these two methods.
Figure 2.
Linear correlation coefficients between pairs of measures of genetic similarity of the studied interspecific Brassicaceae hybrids and their parental forms: E—Euclidean, J—Jaccard, K—Kulczyński, N—Nei, R—Rogers, SM—Sokal and Michener. The coefficient of multiple determination (R2) for each method were equal: 1.00 (for Euclidean), 0.99 (for Jaccard), 1.00 (for Kulczyński), 1.00 (for Nei), 0.959 (for Rogers), and 1.00 (for Sokal and Michener). *** p < 0.001.
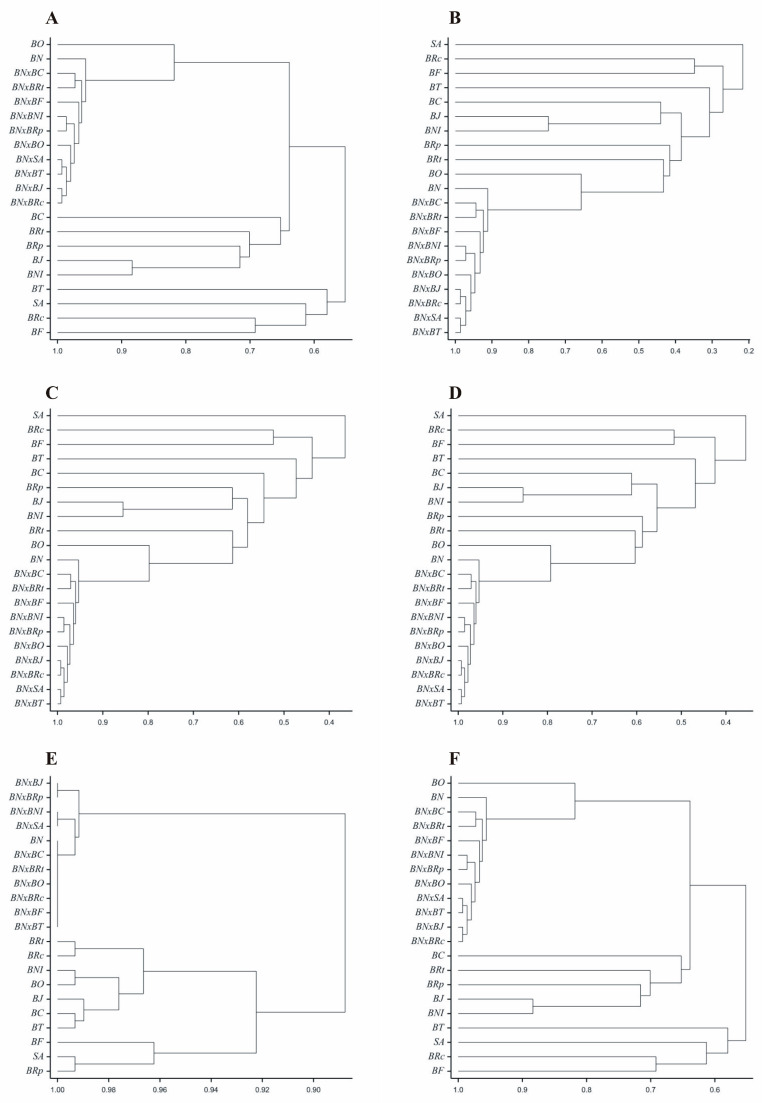
The obtained genetic similarity coefficients were used for the hierarchical clustering of objects using the average linkage method. The results of the clustering are presented in the form of dendrograms for the respective measures (Figure 3). The clustering of the genotypes based on the genetic similarity coefficients according to the Euclidean measure (Figure 3A) and Sokal and Michener measure (Figure 3F) was identical due to the identical similarity values obtained from these two methods. The clustering of the genotypes based on the genetic similarity coefficients according to the Kulczyński measure (Figure 3C) and Nei measure (Figure 3D) was nearly identical. A very similar clustering of objects to the aforementioned two measures was obtained based on Jaccard coefficients (Figure 3B). It is noteworthy that based on the genetic similarity coefficients estimated by all six measures, the examined rapeseed genotypes were clustered similarly into two clusters. One of these clusters comprised ten rapeseed hybrids, and the other comprised eleven parental forms.
Figure 3.
Dendrograms of genetic similarity of 21 Brassicaceae genotypes constructed using six measures based on 146 ISSR markers. (A)—Euclidean, (B)—Jaccard, (C)—Kulczyński, (D)—Nei, (E)—Rogers, (F)—Sokal and Michener.
4. Discussion
An important element in the accurate assessment of genetic similarity in plant material is the choice of molecular analysis technique, the number of molecular markers used in the study, and the appropriate statistical measure to estimate the relationships between studied genotypes [62]. Genetic variability among studied objects is defined based on the frequency of the DNA polymorphism obtained using different types of molecular markers. Various measures can be applied in estimating the genetic similarity/distance based on the results obtained from molecular markers. In studies of Brassica crops, the Nei and Li measure [63] has been most commonly used for Indian mustard (B. juncea) [64], cabbage (B. oleracea) [65], and rapeseed (B. napus) [66]. The Jaccard measure has been applied in studies on rapeseed [67] and cabbage [68,69], among others. To a lesser extent, in rapeseed studies, the Sokal and Michener measure has been utilized [70]. The Rogers measure has been used to assess the genetic variability in crops such as maize (Zea mays L.) [71,72] and sorghum (Sorghum bicolor L.) [73].
In the literature on the subject, little attention has been devoted to the theoretical comparisons of genetic similarity measures. Lamboy [74] compared the Nei and Jaccard measures, pointing out Nei’s measure as less biased for analyzing closely related organisms. Five of the genetic similarity measures used in the present study (excluding the Rogers measure) yielded very similar results. However, determining the best measure is not feasible. Nearly identical clustering of genotypes suggests that any of the proposed methods would be suitable for the overall characterization of the studied materials. Mohammadi and Prasanna [62] highlight Rogers’ genetic distance measure as useful for estimating genetic similarity based on the co-dominant molecular markers, where the amplification product can be equated with alleles. This is corroborated by Gauthier et al. [75] in their study of European maize populations, where both Rogers’ measure utilizing allele frequencies and Nei and Li’s measure based on a binary system (where 1 indicates allele presence and 0 is its absence) were applied. Similarly, Lombard et al. [76] demonstrated the utility of Rogers’ measure in assessing homogeneity within three rapeseed varieties, assuming the tested material was homozygous, and each marker was treated as a diallelic locus. Similar findings were reported by Lee et al. [77] and Dudley et al. [78] for homozygous maize breeding lines, as well as by Jordan et al. [73] for the sorghum lines analyzed using co-dominant markers.
The distinctly different similarity coefficient values obtained using the Rogers method stem from the fact that its calculation principle differs from the other proposed methods. Rogers’ method considers the number of alleles present only in one of the compared genotypes, whereas the other methods are based on the number of alleles present simultaneously in both compared genotypes. Previous studies on generated data [79] as well as real data [80] indicate a lack of significant correlation between Rogers’ genetic similarity measure and the other measures. The significant correlation obtained in this study may be a result of a large number of markers obtained, significantly exceeding the number of genotype observations considered in the aforementioned studies. Furthermore, it is noteworthy that each of the six applied measures yielded two identical clusters (hybrids and their parental forms) as a consequence of clustering using the UPGMA method. Rogers’ GS coefficients also distinguished these two groups despite the significantly different values compared to those obtained by the other methods. We performed clustering not only with the UPGMA method but also with other methods, such as maximum likelihood, neighbor-joining, minimum evolution, and maximum parsimony. The results we obtained were very similar, and some were identical.
Duarte et al. [81] obtained dendrograms for bean varieties with the same structure using UPGMA clustering based on Jaccard’s and Nei’s coefficients. Lombard et al. [70] applied the genetic similarity (GS) coefficients of Jaccard (J), Sokal and Michener (SM), and modified Sokal and Michener (MSM) to compare 83 spring and winter rapeseed varieties, whose diversity was assessed using AFLP. All of the tested similarity coefficients showed significant correlations (r = 0.96 for J and MSM, 0.97 for SM and MSM, and 0.98 for J and SM at the significance level of 0.001). The genetic similarity calculated using these three coefficients allowed for a very similar estimation of relationships among the studied varieties. A previous study [82] showed that the type of markers did not affect the evaluation of the genetic similarity coefficients of CMS ogura F1 hybrids of winter oilseed rape (B. napus L.) parental lines.
5. Conclusions
The purpose of this study was to compare six statistical measures (Euclidean, Jaccard, Kulczynski, Sokal and Michener, Nei, and Rogers) for assessing the genetic similarity of 21 rapeseed objects (10 interspecific hybrids of Brassicaceae of generation F2 and 11 of their parental forms) based on the observations of 146 alleles obtained using 21 ISSR molecular markers. All the mentioned measures define different categories of genetic similarity assessment and coexist with other techniques, such as gene sequencing and flora and fauna analyses. Choosing the appropriate type of measure requires a thorough understanding of its purpose and calculation technique to provide an assessment that is precise and comprehensive enough. Significantly different results were obtained when using the Rogers measure. The research material was divided into two identical groups using any of the methods despite differences in the genetic similarity coefficient values. Two of the presented genetic similarity measures (Sokal and Michener as well as Euclidean) were identical.
Author Contributions
Conceptualization, J.B.; methodology, J.B., J.N., A.J. and J.S.; software, J.B.; validation, J.B., J.N., A.J. and J.S.; formal analysis, J.B.; investigation, J.B. and J.N.; resources, J.B., J.N. and J.S.; data curation, J.N., A.J. and J.S.; writing—original draft preparation, J.B. and J.N.; writing—review and editing, J.B., J.N., A.J. and J.S.; visualization, J.B.; supervision, J.B.; project administration, J.B.; funding acquisition, J.B. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding Statement
This research received no external funding.
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Hoban S., Archer F.I., Bertola L.D., Bragg J.G., Breed M.F., Bruford M.W., Coleman M.A., Ekblom R., Funk W.C., Grueber C.E., et al. Global genetic diversity status and trends: Towards a suite of Essential Biodiversity Variables (EBVs) for genetic composition. Biol. Rev. 2022;97:1511–1538. doi: 10.1111/brv.12852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Salgotra R.K., Chauhan B.S. Genetic Diversity, Conservation, and Utilization of Plant Genetic Resources. Genes. 2023;14:174. doi: 10.3390/genes14010174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zeng C., Rowden A.A., Clark M.R., Gardner J.P.A. Species-specific genetic variation in response to deep-sea environmental variation amongst Vulnerable Marine Ecosystem indicator taxa. Sci. Rep. 2020;10:2844. doi: 10.1038/s41598-020-59210-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Singh H.P., Raigar O.P., Chahota R.K. Estimation of genetic diversity and its exploitation in plant breeding. Bot. Rev. 2022;88:413–435. doi: 10.1007/s12229-021-09274-y. [DOI] [Google Scholar]
- 5.Li C., Czyż E.A., Halitschke R., Baldwin I.T., Schaepman M.E., Schuman M.C. Evaluating potential of leaf reflectance spectra to monitor plant genetic variation. Plant Methods. 2023;19:108. doi: 10.1186/s13007-023-01089-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hoban S., Bruford M.W., da Silva J.M., Funk W.C., Frankham R., Gill M.J., Grueber C.E., Heuertz M., Hunter M.E., Kershaw F., et al. Genetic diversity goals and targets have improved, but remain insufficient for clear implementation of the post-2020 global biodiversity framework. Conserv. Genet. 2023;24:181–191. doi: 10.1007/s10592-022-01492-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Akbarzai D.K., Singh V., Yashveer S., Nimbal S., Kumar M., Dalal M.S., Mor V.S., Devi S. Evaluation of genetic diversity of wheat (Triticum aestivum) lines under terminal heat stress in the Hisar environment. Sci. Lett. 2023;11:59–66. doi: 10.47262/SL/11.2.132023800. [DOI] [Google Scholar]
- 8.Napier J.D., Heckman R.W., Juenger T.E. Gene-by-environment interactions in plants: Molecular mechanisms, environmental drivers, and adaptive plasticity. Plant Cell. 2023;35:109–124. doi: 10.1093/plcell/koac322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Castaneda-Barba S., Top E.M., Stalder T. Plasmids, a molecular cornerstone of antimicrobial resistance in the One Health era. Nat. Rev. Microbiol. 2024;22:18–32. doi: 10.1038/s41579-023-00926-x. [DOI] [PubMed] [Google Scholar]
- 10.Ashapkin V.V., Kutueva L.I., Aleksandrushkina N.I., Vanyushin B.F. Epigenetic Mechanisms of Plant Adaptation to Biotic and Abiotic Stresses. Int. J. Mol. Sci. 2020;21:7457. doi: 10.3390/ijms21207457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shaw A.K. Causes and consequences of individual variation in animal movement. Mov. Ecol. 2020;8:12. doi: 10.1186/s40462-020-0197-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Moktadir M.A., Kumar A., Ali S.M., Paul S.K., Sultana R., Rezaei J. Critical success factors for a circular economy: Implications for business strategy and the environment. Bus. Strategy Environ. 2020;29:3611–3635. doi: 10.1002/bse.2600. [DOI] [Google Scholar]
- 13.Garant D. Natural and human-induced environmental changes and their effects on adaptive potential of wild animal populations. Evol. Appl. 2020;13:1117–1127. doi: 10.1111/eva.12928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Renzi J.P., Coyne C.J., Berger J., von Wettberg E., Nelson M., Ureta S., Hernández F., Smýkal P., Brus J. How Could the Use of Crop Wild Relatives in Breeding Increase the Adaptation of Crops to Marginal Environments? Front. Plant Sci. 2022;13:886162. doi: 10.3389/fpls.2022.886162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Raboanatahiry N., Li H., Yu L., Li M. Rapeseed (Brassica napus): Processing, Utilization, and Genetic Improvement. Agronomy. 2021;11:1776. doi: 10.3390/agronomy11091776. [DOI] [Google Scholar]
- 16.Fokkema R.W., Korsten P., Schmoll T., Wilson A.J. Social competition as a driver of phenotype–environment correlations: Implications for ecology and evolution. Biol. Rev. 2021;96:2561–2572. doi: 10.1111/brv.12768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.De Kort H., Prunier J.G., Ducatez S., Honnay O., Baguette M., Stevens V.M., Blanchet S. Life history, climate and biogeography interactively affect worldwide genetic diversity of plant and animal populations. Nat. Commun. 2021;12:516. doi: 10.1038/s41467-021-20958-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bell D.A., Kovach R.P., Robinson Z.L., Whiteley A.R., Reed T.E. The ecological causes and consequences of hard and soft selection. Ecol. Lett. 2021;24:1505–1521. doi: 10.1111/ele.13754. [DOI] [PubMed] [Google Scholar]
- 19.Cohen I.R., Marron A. The evolution of universal adaptations of life is driven by universal properties of matter: Energy, entropy, and interaction. F1000Research. 2020;9:626. doi: 10.12688/f1000research.24447.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wani A.K., Akhtar N., Sher F., Navarrete A.A., Américo-Pinheiro J.H.P. Microbial adaptation to different environmental conditions: Molecular perspective of evolved genetic and cellular systems. Arch. Microbiol. 2022;204:144. doi: 10.1007/s00203-022-02757-5. [DOI] [PubMed] [Google Scholar]
- 21.Nguyen J., Lara-Gutiérrez J., Stocker R. Environmental fluctuations and their effects on microbial communities, populations and individuals. FEMS Microbiol. Rev. 2021;45:fuaa068. doi: 10.1093/femsre/fuaa068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Swarup S., Cargill E.J., Crosby K., Flagel L., Kniskern J., Glenn K.C. Genetic diversity is indispensable for plant breeding to improve crops. Crop Sci. 2021;61:839–852. doi: 10.1002/csc2.20377. [DOI] [Google Scholar]
- 23.Bernardo R. Reinventing quantitative genetics for plant breeding: Something old, something new, something borrowed, something BLUE. Heredity. 2020;125:375–385. doi: 10.1038/s41437-020-0312-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chen P.-J., Antonelli M. Conceptual Models of Food Choice: Influential Factors Related to Foods, Individual Differences, and Society. Foods. 2020;9:1898. doi: 10.3390/foods9121898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hoffmann A.A., Miller A.D., Weeks A.R. Genetic mixing for population management: From genetic rescue to provenancing. Evol. Appl. 2021;14:634–652. doi: 10.1111/eva.13154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Naciri Y., Linder H.P. The genetics of evolutionary radiations. Biol. Rev. 2020;95:1055–1072. doi: 10.1111/brv.12598. [DOI] [PubMed] [Google Scholar]
- 27.Tyulebaev S.D., Kadysheva M.D., Kosilov V.I., Gabidulin V.M. The state of polymorphism of genes affecting the meat quality in micropopulations of meat simmentals. IOP Conf. Ser. Earth Environ. Sci. 2021;624:012045. doi: 10.1088/1755-1315/624/1/012045. [DOI] [Google Scholar]
- 28.Hu J., Chen B., Zhao J., Zhang F., Xie T., Xu K., Gao G., Yan G., Li H., Li L., et al. Genomic selection and genetic architecture of agronomic traits during modern rapeseed breeding. Nat. Genet. 2022;54:694–704. doi: 10.1038/s41588-022-01055-6. [DOI] [PubMed] [Google Scholar]
- 29.Gritsenko D., Daurova A., Pozharskiy A., Nizamdinova G., Khusnitdinova M., Sapakhova Z., Daurov D., Zhapar K., Shamekova M., Kalendar R., et al. Investigation of mutation load and rate in androgenic mutant lines of rapeseed in early generations evaluated by high-density SNP genotyping. Helion. 2023;9:e14065. doi: 10.1016/j.heliyon.2023.e14065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bocianowski J., Nowosad K., Bujak H. Meta-Analysis of Influence of Diversity of Parental Forms on Heterosis and Specific Combining Ability of Their Hybrids. Appl. Sci. 2023;13:8704. doi: 10.3390/app13158704. [DOI] [Google Scholar]
- 31.Tomkowiak A., Bocianowski J., Kwiatek M., Kowalczewski P.Ł. Dependence of the heterosis effect on genetic distance, determined using various molecular markers. Open Life Sci. 2020;15:1–11. doi: 10.1515/biol-2020-0001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Demirel F., Yıldırım B., Eren B., Demirel S., Türkoğlu A., Haliloğlu K., Nowosad K., Bujak H., Bocianowski J. Revealing Genetic Diversity and Population Structure in Türkiye’s Wheat Germplasm Using iPBS-Retrotransposon Markers. Agronomy. 2024;14:300. doi: 10.3390/agronomy14020300. [DOI] [Google Scholar]
- 33.Bocianowski J., Liersch A. Multi-environmental evaluation of winter oilseed rape genotypic performance using mixed models. Euphytica. 2021;217:80. doi: 10.1007/s10681-020-02760-1. [DOI] [Google Scholar]
- 34.Pauls S.U., Nowak C., Bálint M., Pfenninger M. The impact of global climate change on genetic diversity within populations and species. Mol. Ecol. 2013;22:925–946. doi: 10.1111/mec.12152. [DOI] [PubMed] [Google Scholar]
- 35.Bernatchez L. On the maintenance of genetic variation and adaptation to environmental change: Considerations from population genomics in fishes. J. Fish. Biol. 2016;89:2519–2556. doi: 10.1111/jfb.13145. [DOI] [PubMed] [Google Scholar]
- 36.Jablonszky M., Canal D., Hegyi G., Herényi M., Laczi M., Markó G., Nagy G., Rosivall B., Szöllősi E., Török J., et al. The estimation of additive genetic variance of body size in a wild passerine is sensitive to the method used to estimate relatedness among the individuals. Ecol. Evol. 2024;14:e10981. doi: 10.1002/ece3.10981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ma Z., Li L., Zhang Y.P. Defining Individual-Level Genetic Diversity and Similarity Profiles. Sci. Rep. 2020;10:5805. doi: 10.1038/s41598-020-62362-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dubois A., Ohler A., Pyron R.A. New concepts and methods for phylogenetic taxonomy and nomenclature in zoology, exemplified by a new ranked cladonomy of recent amphibians (Lissamphibia) Megataxa. 2021;5:001–638. doi: 10.11646/megataxa.5.1.1. [DOI] [Google Scholar]
- 39.Padial J.M., De la Riva I. A paradigm shift in our view of species drives current trends in biological classification. Biol. Rev. 2021;96:731–751. doi: 10.1111/brv.12676. [DOI] [PubMed] [Google Scholar]
- 40.Kang J., Ismail A.M., Dehghan S., Rajaiya J., Allard M.W., Lim H.C., Dyer D.W., Chodosh J., Seto D. Genomics-based re-examination of the taxonomy and phylogeny of human and simian Mastadenoviruses: An evolving whole genomes approach, revealing putative zoonosis, anthroponosis, and amphizoonosis. Cladistics. 2020;36:358–373. doi: 10.1111/cla.12422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Alerstam T., Hedenström A., Åkesson S. Long-distance migration: Evolution and determinants. Oikos. 2003;103:247–260. doi: 10.1034/j.1600-0706.2003.12559.x. [DOI] [Google Scholar]
- 42.Gómez-Bahamón V., Márquez R.E., Jahn A.E., Miyaki C.Y., Tuero D.T., Laverde-R O., Restrepo S., Cadena C.D. Speciation Associated with Shifts in Migratory Behavior in an Avian Radiation. Curr. Biol. 2020;30:1312–1321.E6. doi: 10.1016/j.cub.2020.01.064. [DOI] [PubMed] [Google Scholar]
- 43.Queller D.C., Goodnight K.F. Estimating relatedness using genetic markers. Evolution. 1989;43:258–275. doi: 10.2307/2409206. [DOI] [PubMed] [Google Scholar]
- 44.Waples R.S., Gaggiotti O. INVITED REVIEW: What is a population? An empirical evaluation of some genetic methods for identifying the number of gene pools and their degree of connectivity. Mol. Ecol. 2006;15:1419–1439. doi: 10.1111/j.1365-294X.2006.02890.x. [DOI] [PubMed] [Google Scholar]
- 45.Heumos L., Schaar A.C., Lance C., Litinetskaya A., Drost F., Zappia L., Lücken M.D., Strobl D.C., Henao J., Curion F., et al. Best practices for single-cell analysis across modalities. Nat. Rev. Genet. 2023;24:550–572. doi: 10.1038/s41576-023-00586-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Makanjuola B.O., Maltecca C., Miglior F., Schenkel F.S., Baes C.F. Effect of recent and ancient inbreeding on production and fertility traits in Canadian Holsteins. BMC Genom. 2020;21:605. doi: 10.1186/s12864-020-07031-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Clarke M., Thomas G.H., Freckleton R.P. Trait Evolution in Adaptive Radiations: Modeling and Measuring Interspecific Competition on Phylogenies. Am. Nat. 2017;189:121–137. doi: 10.1086/689819. [DOI] [PubMed] [Google Scholar]
- 48.Vickery R.K., Jr., Wullstein B.M. Comparison of Six Approaches to the Classification of Mimulus Sect. Erythranthe (Scrophulariaceae) Syst. Bot. 1987;12:339–364. doi: 10.2307/2419258. [DOI] [Google Scholar]
- 49.Shor O., Yaniv-Rosenfeld A., Valevski A., Weizman A., Khrennikov A., Benninger F. EEG-based spatio-temporal relation signatures for the diagnosis of depression and schizophrenia. Sci. Rep. 2023;13:776. doi: 10.1038/s41598-023-28009-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Szathmary E.J.E., Ossenberg N.S., Clabeaux M.S., Cook D.C., Crawford M.H., Dumond D.E., Hall R.L., Harper A.B., Hurlich M.G., Jamison P.L., et al. Are the Biological Differences Between North American Indians and Eskimos Truly Profound? Curr. Anthropol. 1978;19:673–701. doi: 10.1086/202192. [DOI] [Google Scholar]
- 51.Kaalund K., Thoumi A., Bhavsar N.A., Labrador A., Cholera R. Assessment of Population-Level Disadvantage Indices to Inform Equitable Health Policy. Milbank Q. 2022;100:1028–1075. doi: 10.1111/1468-0009.12588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Tamura K., Nishioka M., Hayashi M., Zhang Z., Lian C., Hougetsu T., Harada K. Development of microsatellite markers by ISSR-suppression-PCR method in Brassica rapa. Breed. Sci. 2005;55:247–252. doi: 10.1270/jsbbs.55.247. [DOI] [Google Scholar]
- 53.Havlíčková L., Jozová E., Rychlá A., Klíma M., Kučera V., Čurn V. Genetic diversity assessment in winter oilseed rape (Brassica napus L.) collection using AFLP, ISSR and SSR markers. Czech J. Genet. Plant Breed. 2014;50:216–225. doi: 10.17221/220/2013-CJGPB. [DOI] [Google Scholar]
- 54.Huangfu C., Song X., Qiang S. ISSR variation within and among wild Brassica juncea populations: Implication for herbicide resistance evolution. Genet. Resour. Crop Evol. 2009;56:913–924. doi: 10.1007/s10722-009-9410-x. [DOI] [Google Scholar]
- 55.Gower J.C. A general coefficient of similarity and some of its properties. Biometrics. 1971;27:857–871. doi: 10.2307/2528823. [DOI] [Google Scholar]
- 56.Jaccard P. Nouvelles recherches sur la distribution florale. Bull. Soc. Vaud. Sci. Nat. 1908;44:223–270. [Google Scholar]
- 57.Kulczyński S. Die Pflanzenassoziationen der Pieninen. Bull. Int. L’Académie Pol. Sci. Lett. Cl. Sci. Math. Nat. Ser. B Supplément II. 1927;2:57–203. [Google Scholar]
- 58.Nei M. Genetic distance between populations. Am. Nat. 1972;106:283–292. doi: 10.1086/282771. [DOI] [Google Scholar]
- 59.Rogers J.S. Measures of genetic similarity and genetic distance. Stud. Genet. Univ. Tex. Publ. 1972;7213:145–153. [Google Scholar]
- 60.Sokal R.R., Michener C.D. A statistical method for evaluating systematic relationships. Univ. Kans. Sci. Bull. 1958;38:1409–1438. [Google Scholar]
- 61.VSN International . Genstat for Windows. 23rd ed. VSN International; Hemel Hempstead, UK: 2023. [Google Scholar]
- 62.Mohammadi S.A., Prasanna B.M. Analysis of genetic diversity in crop plants-salient statistical tools and considerations. Crop Sci. 2003;43:1235–1248. doi: 10.2135/cropsci2003.1235. [DOI] [Google Scholar]
- 63.Nei M., Li W. Mathematical model for studying genetic variation in terms of restriction endonucleases. Proc. Natl. Acad. Sci. USA. 1979;76:5256–5273. doi: 10.1073/pnas.76.10.5269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Liu J., Rana K., McKay J., Xiong Z., Yu F., Mei J., Qian W. Investigating genetic relationship of Brassica juncea with B. nigra via virtual allopolyploidy and hexaploidy strategy. Mol. Breed. 2021;41:5. doi: 10.1007/s11032-020-01197-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Morillo-Coronado Y., Rojas-González S., Morillo-Coronado A., Castaneda-Cardona C., Mendoza-Romero K., Marín-Colorado J. Genetic variability of wild palms Euterpe precatoria, Euterpe oleracea and Mauritia flexuosa with molecular markers ISSR. Rev. de Cienc. Agrícolas. 2023;40:e3212. doi: 10.22267/rcia.20234003.212. [DOI] [Google Scholar]
- 66.Framarzpour A., Abdoli-Nasab M., Rezvan Nezhad E., Baghizadeh A. Evaluation of Genetic Diversity of Rapeseed (Brassica napus L.) Cultivars Using SRAP Markers. [(accessed on 21 August 2024)];JAST. 2021 23:447–456. Available online: http://jast.modares.ac.ir/article-23-32588-en.html. [Google Scholar]
- 67.Kotwal S., Malode S.N. Protein stability study with respect to mutation in Brassica juncea, Brassica rapa and Brassica napus. J. Oilseed Brassica. 2023;14:129–134. [Google Scholar]
- 68.Poveda J., Zabalgogeazcoa I., Soengas P., Rodríguez V.M., Cartea M.E., Abilleira R., Velasco P. Brassica oleracea var. acephala (kale) improvement by biological activity of root endophytic fungi. Sci. Rep. 2020;10:20224. doi: 10.1038/s41598-020-77215-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Rana N., Sharma A., Rana R.S., Lata H., Bansuli, Thakur A., Singh V., Sood A. Morphological and molecular diversity in mid-late and late maturity genotypes of cauliflower. PLoS ONE. 2023;18:e0290495. doi: 10.1371/journal.pone.0290495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lombard V., Baril C.P., Dubreuil P., Blouet F., Zhang D. Genetic Relationships and Fingerprinting of Rapeseed Cultivars by AFLP: Consequences for Varietal Registration. Crop Sci. 2000;40:1417–1425. doi: 10.2135/cropsci2000.4051417x. [DOI] [Google Scholar]
- 71.Godshalk E.B., Lee M., Lamkey K.R. Relationship of restriction fragment length polymorphisms to single-cross hybrid performance of maize. Theor. Appl. Genet. 1990;80:273–280. doi: 10.1007/BF00224398. [DOI] [PubMed] [Google Scholar]
- 72.Benchimol L.L., de Souza C.L., Jr., Garcia A.A.F., Kono P.M.S., Mangolin C.A., Barbosa A.M.M., Coelho A.S.G., de Souza A.P. Genetic diversity in tropical maize inbred lines: Heterotic group assignment and hybrid performance determined by RFLP markers. Plant Breed. 2000;119:491–496. doi: 10.1046/j.1439-0523.2000.00539.x. [DOI] [Google Scholar]
- 73.Jordan D.R., Tao Y., Godwin I.D., Henzell R.G., Cooper M., McIntyre C.L. Prediction of hybrid performance in grain sorghum using RFLP markers. Theor. Appl. Genet. 2003;106:559–567. doi: 10.1007/s00122-002-1144-5. [DOI] [PubMed] [Google Scholar]
- 74.Lamboy W.F. The Accuracy of the Maximum Parsimony Method for Phylogeny Reconstruction with Morphological Characters. Syst. Bot. 1994;19:489–505. doi: 10.2307/2419773. [DOI] [Google Scholar]
- 75.Gauthier P., Gouesnard B., Dallard J., Redaelli R., Rebourg C., Charcosset A., Boyat A. RFLP diversity and relationships among traditional European maize populations. Theor. Appl. Genet. 2002;105:91–99. doi: 10.1007/s00122-002-0903-7. [DOI] [PubMed] [Google Scholar]
- 76.Lombard V., Tireau B., Blouet F., Zhang D., Baril C.P. Usefulness of AFLP markers to estimate varietal homogeneity of rapeseed inbred line varieties in the context of plant registration and protection. Euphytica. 2002;125:121–127. doi: 10.1023/A:1015755217589. [DOI] [Google Scholar]
- 77.Lee M., Godshalk E.B., Lamkey K.R., Woodman W.W. Association of Restriction Fragment Length Polymorphisms among maize inbreds with agronomic performance of their crosses. Crop Sci. 1989;29:1067–1071. doi: 10.2135/cropsci1989.0011183X002900040050x. [DOI] [Google Scholar]
- 78.Dudley J.W., Saghai Maroof M.A., Rufener G.K. Molecular markers and grouping of parents in maize breeding programs. Crop Sci. 1991;31:718–723. doi: 10.2135/cropsci1991.0011183X003100030036x. [DOI] [Google Scholar]
- 79.Bocianowski J. Przegląd statystycznych sposobów estymacji zróżnicowania genetycznego. Postępy Nauk. Rol. 2006;3:69–79. [Google Scholar]
- 80.Bocianowski J., Stępień Ł. Porównanie pięciu miar zróżnicowania genetycznego polskich odmian pszenicy ocenianych na podstawie danych z analiz markerów mikrosatelitarnych. Biul. IHAR. 2006;242:27–32. [Google Scholar]
- 81.Duarte J.M., dos Santos J.B., Melo L.C. Comparison of similarity coefficients based on RAPD markers in the common bean. Genet. Mol. Biol. 1999;22:427–432. doi: 10.1590/S1415-47571999000300024. [DOI] [Google Scholar]
- 82.Liersch A., Bocianowski J., Kozak M., Bartkowiak-Broda I. Comparison of isozyme, RAPD and AFLP markers in genetic similarity assessment of CMS ogura F1 hybrids of winter oilseed rape (Brassica napus L.) parental lines. Acta Biol. Cracov. Ser. Bot. 2013;55:49–57. doi: 10.2478/abcsb-2013-0001. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.