On-chip multifunctional metasurfaces with full-parametric multiplexed Jones matrix

Abstract

On-chip metasurface for guided wave radiation works as an upgrade of conventional grating couplers, enriching the interconnection between guided wave and free-space optical field. However, the number of controllable parameters in equivalent Jones matrix of on-chip metasurface is limited that restricts the channels for multiplexing. Here, a supercell design based on detour phase and geometric phase has been proposed to reach full-parametric modulation of Jones matrix. As proof of concept, four independent sets of amplitude-phase channels have been experimentally demonstrated through a single on-chip metasurface. Moreover, through joint modulation of three phase mechanisms including detour phase, geometric phase and propagation phase, the Jones matrix could be decoupled from forward- and backward-propagating guided waves for direction multiplexing. This work paves the way for guided wave radiation towards high-capacity multiplexing and may further extend its application in optical communications, optical displays and augmented/virtual reality.

The authors demonstrate an on-chip metasurface based on supercell scheme to enable full modulation of Jones matrix. The direction-multiplexed functionality has been implemented by joint control of detour phase, geometric phase and propagation phase, unlocking two independent sets of Jones matrices.

Introduction

Composed of artificial nanostructures, metasurface has emerged as a revolutionary flat optical device to manipulate the optical field at subwavelength scale, including amplitude, phase, polarization and so on^1–3. During the last decade, people have witnessed powerful optical meta-devices ranging from lens imaging, optical sensing, holographic display to quantum optics^4–11. Owing to the multi-dimensional modulation capability, metasurface has demonstrated unparalleled advantages in numerous multiplexing technologies^12–19. For polarization multiplexing, the optical response of metasurface could be described as a 2 × 2 equivalent Jones matrix, yet commonly with upper-limit of 6 independent parameters in free-space scenario^20,21. To expand the number of multiplexed channels, bilayer metasurface²² and noise engineering²³ were proposed from the perspective of spatial extension and algorithm optimization, which in turn usually need to sacrifice in fabrication convenience and signal-to-noise ratio (SNR) respectively.

On the other hand, photonic integrated circuit (PIC) promises a new information platform with more compact form with respect to the free space optical elements. Recently, metasurfaces have been incorporated with optical waveguides to elaborately tailor guided waves for extended functionalities and improved performance of photonic integrated devices^24–30. In particular, on-chip metasurface can flexibly modulate the extracted guided waves as a remarkable upgrade of traditional couplers to enhance the far-field beam engineering^31–35. Leveraging diverse phase modulation mechanisms, on-chip metasurface has been exploited in guided wave radiation to achieve beam focusing and deflection^36,37, orbital angular momentum (OAM) beams^38,39, holography^40,41, etc. Owing to the on-chip optical propagation scheme, such guided wave driven metasurfaces are featured with no zero-order diffraction, which is promising for high-quality images in augment reality (AR) projection and optical displays^42–44. In principle, resonant phase⁴⁵ and propagation phase^46,47 rely on the physical size of on-chip meta-atoms while geometric phase^36,48 depends on the rotation angle to manipulate guided wave radiation. By taking advantage of the position distribution of meta-atoms, detour phase also provides a feasible solution to on-chip phase modulation^49,50. Nevertheless, the limited degrees of freedom (DOFs) utilized in individual phase modulation mechanism inherently restrict the number of modulation channels. To address this issue, the combination of detour phase and geometric phase^51,52, harmonic strategy (complex superposition of multiple phase profiles)^48,53 and other mechanisms⁵⁴ were proposed and attempted to improve the multiplexing capability. Despite of above endeavors in on-chip metasurfaces, the number of controllable parameters in equivalent Jones matrix is no more than 4 (See Table S1 in Supplementary Note 1), which does not reach the maximum yet. In addition, the advent of lithium niobate on insulator (LNOI) has propelled PICs as a promising platform to efficiently manage multiple DOFs of light at high speeds^35,55,56.

Herein, we propose a strategy of on-chip metasurface design on LNOI platform to realize full-parametric modulation of Jones matrix for guided wave radiation. Through four-element supercell arrangement and combined modulation via detour phase and geometric phase, the symmetry and unitary of Jones matrix are broken and thus unlock the full four complex elements (i.e., 8 parameters). As an experimental demonstration, both the amplitude and phase of guided wave radiation under input guided waves propagating along x and y directions have been arbitrarily manipulated into four nano-printing and four holographic images in virtue of genetic algorithm optimization, as shown in Fig. 1. Moreover, to eliminate the conjugated effect induced in Jones matrices under two opposite propagating guided waves, propagation phase is additionally incorporated with detour phase and geometric phase to attain eight holographic images with respect to four illumination directions, resulting in two sets of direction-multiplexed Jones matrices in a single on-chip metasurface. On the basis of multiple phase modulation mechanisms, such on-chip metasurface design offers a platform for guided wave manipulation with high multiplexing capacity and may trigger broader applications in on-chip optical field manipulation.

Fig. 1. Conceptual illustration of guided wave radiation through on-chip metasurface composed of four-element supercells for full-parametric modulation of Jones matrix.

The generated nano-printing and holographic images under TE₀ guided wave illuminations along y (blue) and x (magenta) directions are featured with polarization properties indicated by white double arrows. The inset indicates the perspective view of the corresponding four-element supercell m₁, m₂, m₃ and m₄ based on detour phase and geometric phase.

Results

Design of on-chip metasurface

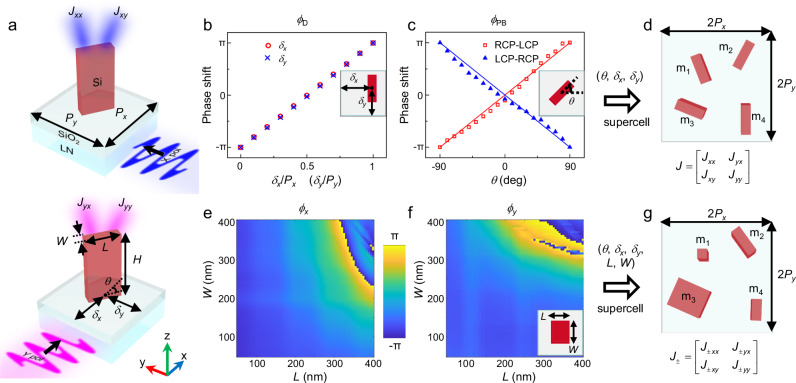
As depicted in Fig. 2a, the on-chip metasurface for guided wave radiation is comprised of silicon nanopillars arranged with periods of P_x and P_y along x and y directions on the substrate of x-cut LNOI. A 100 nm spacing layer of silicon dioxide is placed between LN waveguide and silicon metasurface to ensure weak interaction process. The variables of nanopillar include the two-dimensional position displacements δ_x and δ_y, rotation angle θ and geometric size of length L and width W (with a fixed height H of 1.2 μm). It should be noted that the definition of Jones matrix for on-chip metasurface is different from that for free-space metasurface. For on-chip scheme, guided wave illuminations along x and y directions could inherently introduce detour phase as two additional modulation DOFs, which breaks the limitation in modulation of Jones matrix. To this end, we define the input TE₀ modes propagating along y and x directions, which are equivalent to a pair of orthogonal polarization states, as two bases of Jones matrix for on-chip metasurface. Assuming that a TE₀ mode propagating y (x) direction with polarization ${\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \end{array}\right]}^T$(${\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \end{array}\right]}^T$) is excited in slab lithium niobate (LN) waveguide, the extracted radiation can be written as ${\left[\begin{array}{cc}\hfill J_{xx}\hfill & \hfill J_{xy}\hfill \end{array}\right]}^T$(${\left[\begin{array}{cc}\hfill J_{yx}\hfill & \hfill J_{yy}\hfill \end{array}\right]}^T$). Here, J_xx and J_xy (J_yx and J_yy) are the complex elements of equivalent Jones matrix J of on-chip metasurface described as follows

$$J=\left[\begin{array}{cc}\hfill J_{xx}\hfill & \hfill J_{yx}\hfill \\ \hfill J_{xy}\hfill & \hfill J_{yy}\hfill \end{array}\right].$$ 1

Fig. 2. The principle of on-chip metasurface for Jones matrix modulation.

a The schematic diagram of one nanopillar for Jones matrix modulation driven by guided waves along y (blue) and x (magenta) directions. The simulated detour phase ϕ_D and geometric phase ϕ_PB induced by (b) in-plane displacement δ_x, δ_y and c rotation angle θ of nanopillar. The solid lines represent the fitting lines. d The top view of the four-element supercell composed of m₁, m₂, m₃ and m₄ based on detour phase and geometric phase with period of 2P_x and 2P_y. e, f The phase responses ϕ_x and ϕ_y as a function of the length and width of nanopillar under guided waves propagating along y and x directions. g The illustration of the four-element supercell based on detour phase, geometric phase and propagation phase.

To modulate the parameters of Jones matrix, we first investigate the detour phase and geometric phase induced by on-chip metasurface through numerical simulations (See Methods). With P_y of 760 nm and P_x of 790 nm, equal to the effective wavelengths of TE₀ guided modes along y and x direction at 1550 nm, the phase shifts caused by detour phase ϕ_D linearly vary with the position displacements δ_x and δ_y of nanopillar for input guided modes along x and y directions (Fig. 2b). As shown in Fig. 2c, the phase shifts ϕ_PB of left-handed circularly polarized (LCP) and right-handed circularly polarized (RCP) radiations follow the relationship of ±2θ with rotation angle under input RCP and LCP guided modes. For such on-chip anisotropic nanopillars with C2-symmetry, individual detour phase contributes to a symmetric Jones matrix with only two independent elements J_xx and J_yy, and geometric phase for one element J_xx, see Eqs. (S2) and (S3). Through combining detour phase and geometric phase, the Jones matrix could be expressed as

$$J=\left[\begin{array}{cc}\hfill J_{xx}\hfill & \hfill J_{yx}\hfill \\ \hfill J_{xy}\hfill & \hfill J_{yy}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill e^{i2\pi \cdot \left({\delta }_y/P_y\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{i2\pi \cdot \left({\delta }_x/P_x\right)}\hfill \end{array}\right]R\left(\theta \right)\left[\begin{array}{cc}\hfill a_{x0}\cdot e^{i{\varphi }_{x0}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill a_{y0}\cdot e^{i{\varphi }_{y0}}\hfill \end{array}\right]R\left(-\theta \right).$$ 2

Here, a_x0, a_y0 and ϕ_x0, ϕ_y0 are the fixed amplitude and phase responses from nanopillar’s propagation phase with L = 300 nm and W = 100 nm under guided wave illuminations along y and x directions, R(±θ) is the rotation matrix. It should be noted that the above Jones matrix is asymmetric (J_xy≠J_yx) since the rotation symmetry within one pixel is broken by introducing position displacements (namely detour phase), which results in two non-diagonal terms decoupled. Nevertheless, the Jones matrix is nearly unitary (See Supplementary Note 2.1) and it leads to the four elements of Jones matrix interrelated, that is $J_{xx}\cdot J_{xy}^{*}+J_{yx}\cdot J_{yy}^{*}=0$ (* represents complex conjugation). Such unitary condition constraints the independent modulation channels no more than six. To construct a non-unitary Jones matrix, a practical way is to establish supercell design using interference effect of meta-atoms, which has been investigated in free-space metasurfaces^57–59. In view of this, a four-element supercell design with period of 2P_y = 1520 nm and 2P_x = 1580 nm presented in Fig. 2d is introduced for full-parametric modulation and the equivalent Jones matrix can be derived in summation of four matrices as below

$$J=\left[\begin{array}{cc}\hfill J_{xx}\hfill & \hfill J_{yx}\hfill \\ \hfill J_{xy}\hfill & \hfill J_{yy}\hfill \end{array}\right]={\sum }_{k=1}^4\left[\begin{array}{cc}\hfill e^{i2\pi \cdot \left({\delta }_{yk}/P_y\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{i2\pi \cdot \left({\delta }_{xk}/P_x\right)}\hfill \end{array}\right]R\left({\theta }_k\right)\left[\begin{array}{cc}\hfill a_{x0}\cdot e^{i{\varphi }_{x0}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill a_{y0}\cdot e^{i{\varphi }_{y0}}\hfill \end{array}\right]R\left(-{\theta }_k\right),$$ 3

where k is the sequence of the nanopillar in a four-element supercell. With coherent superposition of four unitary Jones matrices of single nanopillar expressed by Eq. (2), the above constructed Jones matrix of supercell turns into non-unitary (See Supplementary Note 2.1) and it means the full complex elements (J_xx, J_xy, J_yx and J_yy) are totally unlocked for full-parametric modulation. From the perspective of geometric arrangement, the asymmetric and non-unitary of Jones matrix arise from the induced C2-symmetry breaking and the interference effect by four-element supercell based on detour phase and geometric phase.

To map each parameter of Jones matrix into the physical model of on-chip metasurface, a group of complex equations are required to be solved according to Eq. (3). Hence, we establish eight complex equations to acquire four sets of amplitude-phase channels for full-parametric modulation of Jones matrix, shown in Eqs. (S7). It is worth mentioning that the separation between each nanopillar should be large enough to avoid spatial overlapping and strong coupling, a set of constraint conditions on spatial arrangement of nanopillars is assigned as inequalities S8 (See Supplementary Note 3). Herein, the variables of nanopillars in each supercell are determined by solving the complex equations using genetic algorithm optimization, as detailed in the flow chart in Fig. S2. Owing to the sufficient variables provided in the proposed four-element supercell design (12 variables for full-parametric modulation), the complex Eqs. (S7) are accessible to be solved for arbitrary desired parameters of Jones matrix. By means of the above optimization for all the supercells, four amplitude-phase images have been successfully reconstructed with negligible deviation shown in Fig. S5a. To validate the accuracy of the above theory expressed by Eq. (3), full-wave numerical simulations have been performed. The simulated results presented in Supplementary Note 4 are in agreement with the optimized results through genetic algorithm, which verifies the feasibility of full-parametric modulation based on supercell design.

Demonstration for full-parametric modulation of Jones matrix

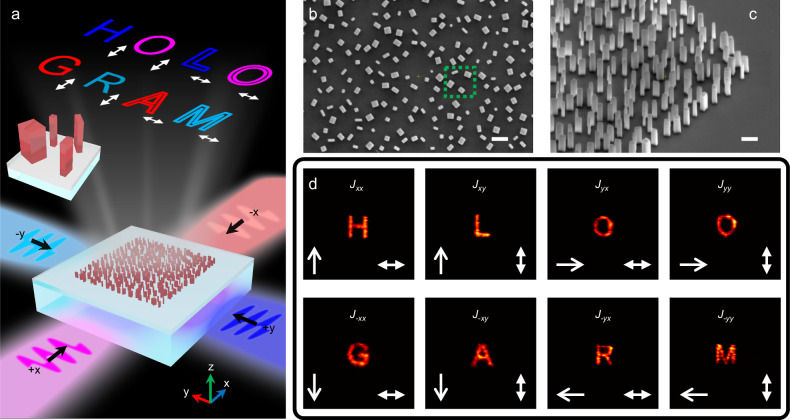
As experimental demonstrations, we fabricated the designed on-chip metasurface configuration through the preparation process detailed in Methods. Figures 3a, b display the optical microscope and scanning electron microscope (SEM) images of metasurface for full-parametric modulation, respectively. The green dashed box in Fig. 3b highlights one fabricated four-element supercell where each element is featured with the same geometric size of L = 300 nm and W = 100 nm. To excite the guided modes at 1550 nm along y and x directions in experiments, four silicon grating couplers surrounding the on-chip metasurface are prepared on top of LN slab waveguide with a silicon dioxide cladding layer. Once the on-chip metasurface is illuminated, the guided wave radiations are characterized by the measurement setup detailed in Supplementary Note 5. Figure 3c lists the four sets of nano-printing and holographic images recorded in the objective plane and Fourier plane respectively. As exhibited in the first column, the guided wave along y direction (input x-polarization) is extracted to display a nano-printing letter “χ” and a holographic image “C” after passing through x-polarization analyzer, corresponding to the complex element J_xx of Jones matrix. By rotating the analyzer to y-polarization, the nano-printing image shows another letter “β” while the holographic image turns into “A” in the second column, which represents the modulation of J_xy. When switching the propagation direction to x direction, another two nano-printing letters “η” and “ε” along with two holographic images “H” and “D” are presented in the third and fourth columns. The above eight independent channels verify the full-parametric Jones matrix modulation capability of single-layer on-chip metasurface. Here, the extraction efficiency of the on-chip metasurface, which is defined as the ratio of the power of the generated holographic images to the power of input guided waves, is experimentally measured to be ~6.5%. In addition, there is no constraint on the output polarization and an arbitrary set of two output polarization states has been achieved in Supplementary Note 6.

Fig. 3. Experimental demonstration of full-parametric modulation of Jones matrix.

a Optical microscope image of the fabricated silicon metasurface surrounded by four grating couplers (only three shown) on LNOI substrate. Scale bar: 200 μm. GC: grating coupler. MS: metasurface. b Scanning electron microscope image of the on-chip metasurface. The green dashed box outlines one supercell. Scale bar: 1 μm. c Measured four sets of nano-printing and holographic images related to four elements of Jones matrix J_xx, J_xy, J_yx and J_yy. The white arrows in the bottom left and right corner indicate the polarization states of input guided waves and output analyzers, respectively.

Direction-multiplexed modulation of Jones matrix

Although above supercell design based on detour phase and geometric phase has validated the feasibility of full-parametric modulation, the propagation direction of guided wave remains to be explored for multiplexing. According to the Eq. (3), the Jones matrix J₊ of on-chip metasurface for forward-propagating guided waves is a complex conjugate of J_- for backward-propagating guided waves, which disables the functionality of direction-multiplexed modulation. Such conjugated relation has been validated in Supplementary Note 7. To make a step further, we additionally introduce propagation phase to incorporate with detour phase and geometric phase to acquire direction-multiplexed modulation of Jones matrix, as illustrated in Fig. 4a. Figures 2e, f plot the simulated phase response maps ϕ_x and ϕ_y of extracted light with the length and width of single nanopillar for guided waves propagating along y and x directions, respectively (The amplitude response maps a_x and a_y can be obtained from the extracted efficiency T_x and T_y given in Fig. S1). As exhibited in Fig. 2g, based on three phase mechanisms, the on-chip metasurface featured with supercell design could demonstrate the following direction-multiplexed modulation of Jones matrices

$$J_{\pm }={\sum }_{k=1}^4\left[\begin{array}{cc}\hfill e^{\pm i2\pi \cdot \left({\delta }_{yk}/P_y\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{\pm i2\pi \cdot \left({\delta }_{xk}/P_x\right)}\hfill \end{array}\right]R\left({\theta }_k\right)\left[\begin{array}{cc}\hfill a_{xk}\cdot e^{i{\varphi }_{xk}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill a_{yk}\cdot e^{i{\varphi }_{yk}}\hfill \end{array}\right]R\left(-{\theta }_k\right).$$ 4

Fig. 4. Direction-multiplexed modulation of Jones matrix.

a Schematic of on-chip metasurface based on detour phase, geometric phase and propagation phase under guided wave illuminations along +x (magenta), +y (blue), -x (red) and –y (light blue) directions. The inset indicates the perspective view of the four-element supercell. b, c Top and side view of the fabricated on-chip metasurface. The green dashed box highlights one four-element supercell. Scale bars: 1 μm. d Measured eight holographic images under different propagation directions and polarization states of analyzers, corresponding to eight elements of J_±. The white one-way arrows represent the propagation directions of guided waves while the double arrows indicate the output polarization states.

Here, ± denotes the propagation direction of guided waves (+ for +x and +y directions while – for -x and -y directions). a_xk, a_yk and ϕ_xk, ϕ_yk are the amplitude and phase responses of induced propagation phase by the k-th naopillar in supercell. The introduction of propagation phase gives rise to the breaking of conjugated relation between J₊ and J_-, i.e., $J_{+}\ne J_{-}^{*}$ (See Eq. (S6) in Supplementary Note 2.2). Considering that the above direction-dependent Jones matrices are asymmetric and non-unitary, eight elements of two sets of Jones matrices (J_±xx, J_±xy, J_±yx, J_±yy) could be engineered at will. Based on Eq. (4), eight phase-only modulation channels are designed to confirm the direction-multiplexed modulation capability by selecting variables of four-element supercells through genetic algorithm optimization shown in Supplementary Note 3 with optimized results listed in Fig. S6a. The validity of such direction-multiplexed modulation design has been confirmed through numerical simulations, as plotted in Fig. S6b. Figures 4b, c showcase the top and side view of the fabricated sample, respectively. As captured in Fig. 4d, the holographic images exhibit four letters “HOLO” under input guided waves along y and x directions while another four different holographic images “GRAM” are demonstrated for guided waves along -y and -x directions when switching the polarization states of analyzer. The conjugacy of two equivalent Jones matrices J₊ and J_- has been totally broken and it contributes to the eight direction-multiplexed phase modulation channels.

Discussion

To conclude, an on-chip metasurface design strategy for multi-channel modulation of guided wave radiation has been proposed on the basis of joint phase modulation mechanism and supercell arrangement. By virtue of detour phase and geometric phase, such on-chip metasurface can perform full-parametric modulation of equivalent Jones matrix and the corresponding four sets of amplitude and phase channels have been experimentally demonstrated. Furthermore, attributed to the combination of detour phase, geometric phase and propagation phase, the equivalent Jones matrices under forward- and backward-propagating guided wave illuminations are decoupled for direction-multiplexed modulation. As an outlook, our approach for Jones matrix modulation is compatible with other strategies (e.g., harmonic strategy or phase optimization) to further increase the number of modulation channels and improve the multiplexing capability (See Supplementary Note 8). Also, since the on-chip metasurface is implemented on LNOI platform, a range of dynamic guided wave radiation device could be expected due to the distinctive electro-optic property of LN. Our work offers a compelling choice for on-chip information multiplexing and may inspire a plethora of intriguing multifunctional photonic integrated devices.

Methods

Numerical simulations

The phase response of nanopillar was investigated by numerical simulations via finite-difference time domain (FDTD) methods. For detour phase and propagation phase models, the silicon nanopillars were periodically arranged along y direction (x direction) with P_y = 760 nm (P_x = 790 nm) on top of a 20 μm-length x-cut LN waveguide with a 100 nm silicon dioxide cladding layer. The 1550 nm TE₀ mode source propagating along y direction (x direction) was excited in 600 nm-thick LN waveguide to illuminate nanopillars. Periodic boundary condition was applied along x direction (y direction) while perfectly matched layer (PML) conditions were utilized as boundary conditions along y and z directions (x and z directions). For geometric phase model, to synthesize in-plane LCP and RCP modes, two TE₀ mode sources propagating along y and x directions with phase difference of ±π/2 were simultaneously excited and all the boundary conditions were chosen to be PML. The refractive indexes of x-cut LN, silicon dioxide and silicon used in simulations were obtained from experimental samples measured by spectroscopic ellipsometer.

Device fabrication

The samples were fabricated on a commercial x-cut LNOI wafer with 600 nm thick LN layer and 2.0 μm thick buried silicon dioxide. As a first step, a 100 nm silicon dioxide layer and a α-Si layer with a thickness of 1.2 μm were successively deposited on top of LN substrate through plasma-enhanced chemical vapor deposition (PECVD). After spin-coating a 200 nm-thick electron beam resist (PMMA-A4) on α-Si layer, the patterns of on-chip metasurface and grating couplers were defined by Electron-beam lithography (EBL) system (ELS-F125, Elionix). Then, the generated patterns were transferred to an electron beam evaporated chromium layer after development, which served as a hard mask for the following dry etching process of α-Si layer in a mixture of C₄F₈ and SF₆ plasma (HSE200, Naura). At last, the remaining chromium mask was removed by ammonium cerium nitrate.

Author contributions

J.J., Z.W. and T.L. conceived the concept. J.J., X.L. and J.W. proposed the metasurface design and performed the numerical simulations; J.L. and J.S. fabricated the samples; J.J. performed the optical measurements with the help of J.W. and X.Y.; J.J., Z.W., B.F., C.C., T.L. and S.Z. discussed the results; J.J. and Z.W. wrote the manuscript; T.L. supervised the project.

Peer review

Peer review information

Nature Communications thanks Xian-Gang Luo and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data that support the findings of this study are provided in the Supplementary Information/ Source Data file. Source data are provided with this paper.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-52476-2.