Abstract
Electronic spins associated with the Nitrogen-Vacancy (NV) center in diamond offer an opportunity to study spin-related phenomena with extremely high sensitivity owing to their high degree of optical polarization. Here, we study both single- and double-quantum transitions (SQT and DQT) in NV centers between spin-mixed states, which arise from magnetic fields that are non-collinear to the NV axis. We demonstrate the amplification of the ESR signal from both these types of transition under laser illumination. We obtain hyperfine-resolved X-band ESR signal as a function of both excitation laser power and misalignment of static magnetic field with the NV axis. This, combined with our analysis using a seven-level model that incorporates thermal polarization and double quantum relaxation, allows us to comprehensively analyze the polarization of NV spins under off-axis fields. Such detailed understanding of spin-mixed states in NV centers under photo-excitation can help greatly in realizing NV-diamond platform’s potential in sensing correlated magnets and biological samples, as well as other emerging applications, such as masing and nuclear hyperpolarization.
Subject terms: Quantum physics, NMR spectroscopy
Introduction
The negatively charged NV center in diamond1 is a magneto-optically active defect that possesses an electronic spin-triplet (S = 1) with an exceptionally long spin lifetime2. A combination of properties make NV centers extremely promising for a wide range of applications such as magnetic sensing and imaging3–5, quantum communication6,7, lasing8, masing9 and nuclear hyperpolarization10–13.
A key feature enabling these is the optical polarization of the NV spins, which can be orders of magnitude greater than thermal polarization even at room temperature. While much of the work done with NV centers has used a static field collinear to the NV-axis to maximize the signal, to truly develop the NV spin as a universal magnetic sensor, we should be able to apply off-axis field, i.e., fields not collinear with the NV axis. Expanding the scope of NV research with off-axis fields opens up new possibilities for sensing magnetic fields from various directions relative to the NV axis, facilitating three-dimensional mapping of a magnetic field distribution. This is particularly significant in the study of correlated electron systems14,15. Similarly, biosensing with nanodiamonds5,16–18 may have off-axis fields given the challenges in controlling the orientation of nanodiamonds in biological samples. Understanding the dependence of polarization on field orientation may also be useful for NV-based amplifiers or masers9,19, aiding in tunability and performance comprehension.
An off-axis (static) field also enables a or double quantum transition (DQT) to be driven by ac magnetic/electric fields20, which is otherwise forbidden in aligned magnetic fields due to magnetic dipole selection rules. DQT offers increased sensitivity compared to conventional single quantum () transition (SQT). Furthermore, DQT exhibits more robustness against field misalignment (off-axis noise)21 and strain effect22. DQT, being magnetic-dipole-forbidden, can also selectively probe the magnetic and electric noise23. In the above context, studying the spin polarization of DQT under laser illumination while accounting for the extent of magnetic field misalignment provides an additional degree of freedom for NV-based diamond magnetometry.
Optically induced spin polarization of NV has been studied in literature9,19,24 using conventional inductively detected electron spin resonance (ESR) experiments. Such a measurement can specifically focus on the effect of the off-axis fields on the polarization process, without the complication of changes in optical spin-readout due to off-axis fields, as in an optically detected magnetic resonance experiment. Meanwhile, a comprehensive study analyzing the effect of both the knobs, off-axis field and laser intensity, is still lacking, especially for samples with low NV concentration ( ppm). Such samples, with extended spin lifetimes, are desirable for wide-field magnetic imaging applications.
In this work, we perform ESR spectroscopy on such a sample, studying the effects of varying laser intensity and magnetic field misalignment with the NV-axis. Our observations include both single and double quantum transitions. The experimental findings are interpreted within the theoretical framework of NV spin mixing in its seven-level electronic structure.
Spin mixing in NV centers
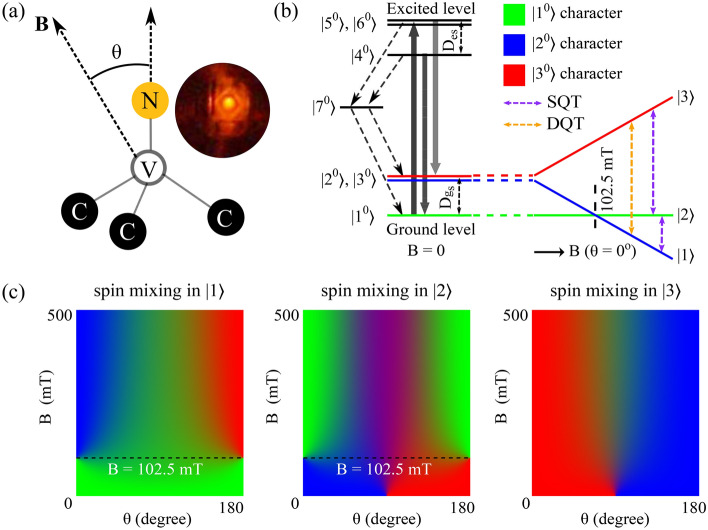
NV center is an atom-like defect in the diamond lattice (see Fig. 1a) with the property of getting spin-polarized by optical pumping with a green laser. This occurs because of its seven-level electronic structure (see Fig. 1b), where both the ground and excited states are spin triplets, and there is an additional singlet state (, the singlet state is being simplified to a single level for the purposes of this paper). The singlet state enables a non-radiative, spin-selective inter-system crossing, which play the central role in NV spin dynamics under laser illumination12,25,26. When optically excited, the preferentially decay in a spin-conserving radiative process, whereas also selectively populates ground state via singlet state (). This leads to the polarization of NV spins into the sublevel, even at room temperature, which is significantly higher than the polarization achievable through thermal equilibrium.
Fig. 1.
Mixing of Nitrogen Vacancy (NV) spin sub-levels in seven-level (kinetic) model used in this study. (a) Atomic configuration of the NV center with a substitutional nitrogen (N) atom in adjacent to a vacancy (V) defect in the diamond lattice. The line joining the two, called NV-axis, is used as reference for degree of NV defect misalignment (polar angle ) with the applied magnetic field B. Inset shows the real-time (red) fluorescence image of NV-containing diamond single crystal under (green) laser illumination. (b) Schematic seven-level electronic structure of the NV center, showing optical excitation, spin-conserving radiative decay (solid lines) and nonradiative, spin-selective intersystem crossing (dashed lines) via the metastable singlet state . The labels with a superscript 0 represent the seven zero-field eigenstates for each spin-pure sub-level (). For the simplest case of aligned magnetic fields, B(B, = 0), a Zeeman splitting of the ground state (degenerate) spin sub-levels is also shown, with possible SQT (violet) and DQT (orange dashed lines) between them under (resonant) microwave excitation. DQT is only weakly allowed in case under local strain effects. (c) The calculated spin-mixing of (ground-state) spin sub-levels as a function of B(B, ). Green, blue, and red represent the character or coefficients (see Eq. 2) respectively where is the given state.
The ground-state triplet, whose spin population/polarization will be measured in the experiment, is described by the Hamiltonian:
| 1 |
where, h is Plank’s constant, is the zero-field splitting, is the Land g-factor and is the Bohr magneton. are the applied magnetic field and spin vectors, respectively. The excited state is also described by a similar Hamiltonian with . The zero-field term accounts for the magnetic anisotropy in the system. This defines the spin quantization axis to be along the NV-axis (see Fig. 1a) which lies along one of the four crystallographic directions in a diamond lattice. The angle between the NV axis and the magnetic field is denoted by . The third term represents the hyperfine interaction between the NV electron and 14N nuclei spin. are the nuclear hyperfine tensor and nuclear spin vector, respectively. We have ignored other terms in the Hamiltonian that are not important for the current study.
In the absence of an external magnetic field, B = 0, the NV will have spin-pure states with and characters, in both the ground and excited states. We will denote these as (for ground state) and (for excited states) respectively, with the state being the lowest energy eigen state. When the magnetic field is precisely applied along the NV axis, i.e., B(B, ), the spin purity remains intact. However, for B > 102.5 mT (), the eigenvalue corresponding to the character state (as seen by its eigenvector) becomes the lowest energy state. To capture this, we denote the eigenstates as on the application of a field along the NV-axis. Please note that these are ordered by their energy rather than the spin character. For fields along the NV axis and < 102.5 mT, correspond to and for fields > 102.5 mT, they correspond to and respectively. Similar transformation also occurs for the levels in the excited state at B = 50.7 mT (). Any off-axis field, B(B, ) will result in mixing of the spin sub-levels. This spin mixing can be modeled by expressing each of the eigenstates as a linear combination of all the zero-field (spin-pure) eigenstates (see Fig. 1b), as follows27.
| 2 |
where, are the complex coefficients. These can be numerically computed for both the ground and excited states using and , respectively.
Figure 1c represents the evolution of spin-pure state for to a spin-mixed state in off-axis magnetic fields, B() as a function of both field magnitude (B) and its orientation (). The color indicates the proportion of the zero-field states. The strong spin-mixing, especially at fields and angles explored in this work, is clearly seen.
Results
Figure 2a depicts the schematic of our experiment utilizing a commercial ESR spectrometer, featuring the capability of photoexciting NV spins during measurements. We measure the ESR spectra of a diamond sample containing NV centers, varying their orientation () relative to the applied static magnetic field and laser illumination power. More details of the sample and experimental procedure are provided in “Methods”.
Fig. 2.
Schematic for ESR spectroscopy of NV spin-mixed states under photo-excitation. (a) The (100) diamond crystal was oriented at and glued to the quartz tube (yellow), which is inserted into a X-Band TE011 cylindrical cavity (blue). It can then be rotated about its axis to achieve the desired degree of NV defect misalignment () with external B (see Section “Methods” for details). The induced spin-mixed states is studied by applying (resonant) microwaves (in dashed lines) in dark and under laser illumination via the optical access of the cavity. (b) Representative ESR spectra demonstrating the inversion and amplification of NV single-quantum ESR () signal under photo-excitation.
Figure 2b displays the differential ESR spectra (top panel) acquired for the SQT for with the laser illumination on and off. The spectra are integrated, and a background is removed (bottom panel) prior to further analysis (see supplementary information for baseline correction in Fig. S1). The three peaks correspond to the hyperfine levels of this transition resulting from the coupling between the NV electron spin and the 14N nuclei spin (I = 1). The linewidth analysis of the hyperfine peaks gives an upper bound on of 5.6 μs , which is in close agreement with the value provided by the sample manufacturer.
The ESR spectrum obtained in the dark condition (with the laser turned off) represents the Boltzmann distribution of the spin population in thermal equilibrium. Conversely, the second spectrum acquired under laser illumination at a low intensity of 1 mW/ displays a notable increase in the signal, which signifies the polarization of (ground state) spins driven by photo-excitation. This optically-induced polarization also results in inversion of the peaks9, reflecting a population inversion (i.e. higher spin population in the higher energy spin sublevel) as expected for the transition above a field of 102.5 mT (see Fig. 1b). ESR results, along with the deduced degree of spin polarization (with comparison to theory), for this and another SQT () for and in off-axis magnetic fields (enabling DQT also) are described below.
Single quantum ESR spectroscopy
In Fig. 3a, the ESR spectra are shown for the experimental configuration with B pointing along one () of the four possible orientations of NV in diamond, under high-intensity laser illumination of 83 mW/. In such a case, the remaining NV centers in the sample lie at relative to B. The two outermost peaks in the ESR spectra represent the and SQTs for NVs at , while the inner pair of peaks correspond to the SQTs at . In addition to SQT at , the SQT at also show a population inversion (negative polarity), which is facilitated by spin-mixing in off-axis magnetic fields (see Fig. 1b) as explored in Section “Spin polarization”.
Fig. 3.
Single-quantum ESR spectroscopy of NV spin-mixed states under laser illumination. (a) (Integrated) single-quantum ESR spectra of NV centers after baseline correction (in blue symbols) measured under the maximum laser intensity of 83 mW/ at selected degrees ( and ) of NVs orientation relative to B (see supplementary information for ESR spectra at all in Fig. S3). The ESR intensity is analyzed by fitting to multiple Lorentzian peaks, associated with hyperfine splitting of the electronic transition. (b) The extracted resonant fields for the SQTs at all (in black and blue symbols) are compared to the theoretical values (in red lines) obtained by solving the ground state Hamiltonian (Eq. 1). The error bars for the experimental data are contained within the markers (within ).
Another feature to notice with higher laser powers is the unequal amplitudes of the hyperfine peaks at , which indicates dynamic nuclear polarization via the NV electron spin11. More spectra and clear power dependence of this polarisation is presented in Fig. S2 in the supplementary information. This hyperfine polarization is understood in the literature. In the main text, we focus on electron spin polarisation, calculated from the sum of the area under all the hyperfine transitions and its dependence on illumination intensity and spin mixing.
The picture becomes more complex in ESR signal measured for the case of . The and SQTs show a marked difference in intensity, which can be attributed to a significant change in microwave coupling for two SQTs at that angle (see Fig. S4 in the supplementary information). Furthermore, the hyperfine peaks for SQT tend to merge, while those for merge into a single broader peak. This may arise from the imperfect experimental configuration (1 resolution of the setup) in orientation of NVs at the intended in three (possible) different directions, considering the strong variation of the resonant field with field orientation at this angle. The electronic transition peak (for ) is accompanied by two additional peaks, which may originate from the forbidden double-quantum nuclear transitions or NV-P1 dipolar interactions28.
We next acquired the ESR data by rotating the sample for the desired degree () of misalignment of B() with the NVs in diamond, as described in Section “Methods”. The ESR data for both the SQTs at all (including ) is presented in Fig. S3 in the supplementary information. The ESR spectra are fitted to multiple Lorentzian peaks, with the constraint of equal magnitude for the hyperfine peaks (e.g., for and in Fig. 3a). The (average) resonant fields obtained by fitting the data at all are plotted in Fig. 3b, which agree well with the theoretically expected values by solving the Hamiltonian for NV spins in ground state (Eq. 1). This validates the Hamiltonian and subsequently spin-mixing calculations (see Fig. 1c), which provide the basis for the analysis of degree of spin polarization in Section “Spin polarization” as follows.
Spin polarization
We next focus on extracting the spin polarization, between any two spin sublevels with eigen states i, j, with being the population of state i. Using the ESR data, the degree of spin polarization under laser illumination (with optical pumping strength ) is calculated using the relation as follows.
| 3 |
For the specific transition (), represents the area under the peak (summed over all the hyperfine peaks) and accounts the change in microwave coupling at that relative to that for SQT at = 0, which can be found in Fig. S4 in the supplementary information. refers to the thermal spin polarization, which is calculated by quantifying the Boltzmann’s distribution of NV spins in two sublevels (, ) using ESR data acquired for SQT between them at = 0 in dark condition ( = 0), as presented in Fig. 2b. The optically-induced spin polarization thus calculated, using Eq. (3), for two SQTs are plotted in Fig. 4 with varying (at maximum laser intensity of 83 mW/) as well as the laser intensity (at specific ).
Fig. 4.
Optically-induced spin polarization of single-quantum transitions in NV centers. Spin polarization between the eigen-states of SQTs calculated from the ESR line intensities (in symbols) using Eq. (3) as a function of (a) the degree of magnetic field misalignment, under the highest laser intensity of 83 mW/ and (b) the laser intensity for selected = 0 and 70.5. The experimental values are compared to the spin polarization values (in red lines) calculated from the seven level kinetic model using Eq. (7) with parameters given in Table 1. The broken line represents thermal polarisation at room temperature . The error bars for the experimental data are contained within the markers (within ).
To make a quantitative understanding of optically-induced spin polarization in the framework of spin-mixing, we have also calculated it computationally using seven-level kinetic model (presented in Fig. 1b) by extracting the steady state populations for spin-mixed eigen states (i, j) from classical rate equation as follows.
| 4 |
Here, the optical transition rates, between spin-mixed states for the specific () transition can be obtained using the following relation:
| 5 |
The coefficients, are computed by solving the Hamiltonian (Eq. 1) at resonant fields for the respective transition (see Fig. S5 in the supplementary information). Here are the zero-field optical transition rates except where is the longitudinal spin relaxation rate. While zero-field optical decay rates, including the intersystem crossing, are measured experimentally in literature (see Table 1), the optical pumping rates can be calculated from the radiative decay rates () using the relation . Here is a dimensionless parameter related to the optical pumping rate as follows.
| 6 |
where is the absorption cross-section of NV centres under 532 nm laser illumination and is the laser frequency. A factor of 4 accounts the optical excitation of NVs in only one of the four possible orientations in diamond.
Table 1.
Parameters used in seven-level kinetic model for calculation of spin polarization values using using Eq. (7).
| Parameter | Value |
|---|---|
| 62.7 MHz | |
| 80 MHz | |
| 12.97 MHz | |
| 1.08 MHz | |
| 3.45 MHz | |
| 5.5 ms | |
Zero-field transition rates are taken from29.
In steady state, one of the classical rate equations becomes redundant and can be replaced with . In turn, this normalizes the solution with respect to the total NV concentration (as in the definition of spin polarization). To account for the thermal effect, Eq. (4) can be solved by expressing it in matrix form:
| 7 |
where is the matrix of transition rate coefficients, , while is a column matrix of unknown populations. At a given temperature i.e., room temperature in current study, another column matrix, can be calculated by setting to 0 (dark) in transition rate matrix A and replacing n with the dark state populations given by the Boltzmann’s distribution assuming that all the NV spins are in the ground state manifold at room temperature, thus .
Using the parameters provided in Table 1, the obtained spin polarization are plotted in Fig. 4. The 7-level energy model of NV centers successfully predicts the trend of angular and laser power dependence of spin polarization in experimental results.
The spin polarization reduces with increasing as shown in Fig. 4a since the selectivity of the inter-system crossing rates suffers due to spin-mixing of the ground state and excited state spin sub levels. The changing of the sign of the polarisation can also be understood for by looking at Fig. 1c. For example for the transition we see that for high , has more () character than . It is shown more clearly in Fig. S5 of the supplementary information ( for ). Similarly for transition, for , . The discrepancy at high theta, especially for the transition, may be due to differences in the microwave coupling constants from the expected values used in our simulation. It can be seen in Fig. S4 in the supplementary information that the microwave coupling constant for the is a stronger function of theta for high theta which is why the discrepancy is greater for transition.
The saturation of amplification with respect to the laser intensity, as shown in Fig. 4b, is related to the relaxation time. The relationship between laser power and spin polarization for SQTs is governed by two competing rates: the optical polarization rate, which is proportional to the pumping rate and spin selectivity, and the longitudinal relaxation rate of the NV centers, which determines how quickly the ground state depolarizes. Saturation occurs due to long lifetimes because, as the optical pumping rate increases, it becomes less effective at further polarizing the spins.
Double quantum transitions
In the ESR data acquired for experimental configuration with NV centers in off-axis B() under photo-excitation, we made a notable observation of emergence of the ESR signal corresponding to DQT. A representative spectra for is shown Fig. 5a. The side bands in the figure likely arise due to NV-P1 dipolar interactions28. This finding is confirmed by comparing the resonant fields extracted from the ESR signal for non-zero (through multipeak Lorentzian fits) with the values obtained by solving the Hamiltonian (Eq. 1). This has been presented in Fig. 5b. This is an intriguing finding because under perfect alignment (), this particular transition between and is not allowed. It is only under the strong spin-mixing regime (see Fig. 1c) that these transitions are allowed and are visible in the ESR spectra. Nevertheless, the observation of the DQT signal can provide valuable insights into the nature (angle) and strength of the misaligned magnetic fields relative to NV centers. This can help improve the performance of their various applications particularly quantum sensing, where precise information of the magnetic field is essential.
Fig. 5.
Double-quantum ESR spectroscopy of NV centers in off-axis magnetic fields. (a) (Integrated) ESR spectra under the laser illumination of , after baseline correction, of DQT between spin-mixed states at (in blue symbols), with fitting into multiple hyperfine peaks with a Lorentzian profile. (b) The extracted resonant fields at different are plotted against the theoretical values (in red line) derived from the ground state Hamiltonian (Eq. 1). (c) The experimentally calculated spin polarization (in symbols) using Eq. (3) for DQT at different are compared to the values obtained from the kinetic calculations using Eq. (7) with parameters given in Table 1. The broken line in (c) represents thermal polarisation at room temperature . The error bars for the experimental data are contained within the markers (within in (b) and in (c)).
We also calculated the optically-induced spin polarization, both experimentally from the ESR data (using Eq. 3) and computationally by solving the seven-level rate equation into matrix formalism (using Eq. 7). The extracted values are shown in Fig. 5c. A maximum (experimental) spin polarization is obtained within the range of 10–35°. While qualitatively, the trends of the experimental data (markers) and fits (solid lines) match well, we cannot obtain as good a quantitative fit for larger using the same parameters as the SQT case. This is likely because the ESR signal intensity depends on microwave-sample coupling in the EPR cavity. Exact coupling angles are crucial but altered by sample insertion, affecting DQT significantly more than SQT due to greater sensitivity of MW coupling with respect to angle (see Fig. S4 and Section I in supplementary information). This information is challenging to obtain, and the effect cannot be accounted for in our theory. Additionally, the DQT may have lower T compared to the SQTs30 which may also contribute to the discrepancy.
Discussion and conclusions
The commonly used seven-level kinetic model of NV centers was extended by27 to incorporate spin-mixing effects in off-axis magnetic fields. Authors primarily focus on the low magnetic field regime and specific angles. Further studies9,19 have investigated NV spin polarization under photo-excitation with seven-level model analysis at high fields, but specifically for aligned fields. In other work,24 examined the angular dependence of spin polarization in high off-axis magnetic fields. Their approach accounted for this by applying the Wigner rotation exclusively to the ground state Hamiltonian while considering equal population for levels and assuming a fixed polarization for the aligned case based on experimental data. In contrast, seven-level kinetic model, further incorporating thermal polarization, employed by us also derives the aligned case spin polarization from first principles and considers the differences in zero-field splittings ( and ) for the ground and excited states, which gives different spin mixing conditions. This is evident from the observation of DQT in our ESR data measured in off-axis field, demonstrating the distinct populations of sub-levels.
Moreover, none of the previous studies have investigated the amplification of double quantum transitions (DQT) under laser illumination for high off-axis field conditions. Our objective is to comprehensively explore the phase-space of these experimental parameters, enabling a more thorough understanding of the influence of laser illumination on ground state spins.
In this work, we conducted systematic ESR experiments on a diamond sample with a relatively lower NV concentration ( 0.2 ppm) compared to previous such studies ( 0.49 ppm in19 and 1.9 ppm in24). The lower concentration with long of 5.6 μs (vs 29 ns in19) gives rise to fully resolved N hyperfine levels in our ESR data. This longer is advantageous for magnetic sensing applications. In contrast, the higher NV density samples used in19,24 exhibited broader linewidths, which are more desirable for diamond maser applications, specifically to achieve the high bandwidth of operation, as highlighted by Sherman et al.19.
We compared our experimental results of optically-induced enhancement of spin polarization (vs thermal polarization) for case with previous works. Our data demonstrated a high amplification of 685 for SQTs at laser intensity of 83 mW/. This surpasses the maximum amplification of nearly 400 obtained Sherman et al.19 at similar illumination intensity for their lowest NV density (0.49 ppm) sample. The measured data in their study indicates a lowering of enhancement and as NV density increases in the sample. Subsequent kinetic model calculations, considering experimental values, clearly emphasize the noteworthy impact of on the spin polarization of the sample. Based on this analysis, the higher amplification in our low NV density sample compared to19 can be attributed to a relatively higher for our sample.
In other work, Drake et al.24 reported a saturation of amplification, reaching nearly 350 at a much lower laser intensity of about 30 mW/. While the above-stated works, including ours, are performed at room temperature, Degen and co-workers31 conducted ESR experiments at 200 K using a higher NV density sample (9 ppm). Their observations followed a similar trend as24, revealing a optical saturation effect at even lower laser intensity of about 10 mW/ and a maximum enhancement of 170. The team accounted this saturation effect in their kinetic model calculations by considering the NV (negatively charged neutral) charge state conversion processes, which are recognized to be stimulated by photo-excitation32,33.
In contrast to the findings in24,31, our experimental data, up to 83 mW/, does not exhibit any signs of saturation. This excludes a significant photo-ionization of (negatively charged) NV charge state in our sample. Conversely, our data reveals a higher experimental spin polarization for SQTs compared to that predicted by kinetic model calculations (even without considering photo-ionization processes) using typical values of different parameters reported in the literature, as discussed in Fig. S6 in the supplementary information.
Lastly, we analyze our experimental findings for both SQTs and DQT in the framework of seven-level kinetic model calculations. To start with, zero-field optical decay rates, including the intersystem crossing, for NV spin have been experimentally measured by different groups9,27,29,34,35. Specific values for different models are provided in Fig. S6a in supplementary information. A comprehensive analysis of the experimental results for different models is provided in Fig. S6 in the supplementary information. This reveals that the model 3, adapted from29, describes well the angular () dependence for SQTs. However, when model 3 is used for DQT, although calculated values show a similar trend to the experimental data, quantitatively, they tend to overestimate the spin polarization. The discrepancy could be due to lack of better data for microwave coupling in our measurements.
In summary, our comprehensive study of NV transitions under off-axis fields has significant implications for advancing NV sensing for a broad variety of emerging quantum materials based on correlated electron systems as well as biological samples. To our knowledge, this is the first experimental observation of the amplification of the double quantum transitions in NV centers, and we likely have also seen the amplification of the signal from the nuclear double quantum transitions as well. These findings can also offer valuable insights into nuclear hyperpolarization using NV centers.
Methods
The study employed a commercial continuous-wave Electron Spin Resonance (ESR) Spectrometer (JEOL JES-FA200) operating in the X-Band ( 9.43 GHz) with a cylindrical TE011 cavity. The (100)- single crystal diamond (DNV-B1 from Element Six, NV concentration: 200 ppb) was fixed to a quartz tube at and placed in the cavity such that the axis of the diamond crystal is parallel to the quartz tube. The quartz tube was then rotated about its axis (along the lab vertical) to change the orientation of the NV-axis with respect to the applied static field. This ensures that 2 of the 4 possible orientations of NV in diamond are always perpendicular to the microwave field and the applied magnetic field stays in the [110] plane. The angle was adjusted manually using a goniometer with resolution. The sample was illuminated by a 532 nm laser via an optical access to the cavity. All the ESR measurements were performed at room temperature and with a low microwave power of 10 μW, after verifying the linear response of the ESR signal at this power level.
Supplementary Information
Acknowledgements
This work was supported by DST, India, under QuST program vide sanction no. DST/ICPS/QuST/Theme-2/2019/General and IIT Madras via exploratory research and team research grants. The authors extend their thanks to the staff at Sophisticated Analytical Instruments Facility (SAIF), IIT Madras for making the EPR facility available for our use. The authors also thank Dr. Siddharth Dhomkar (IIT Madras) for fruitful discussions for interpreting dynamic nuclear polarisation in our measurements.
Author contributions
A.P. led the data collection, modeling, and analysis. Z.C. provided valuable assistance in both data collection and analysis. A.R. contributed significantly to the data analysis. VPB and A.Pr. conceptualized the problem. VPB and A. Pr contributed to securing funding. VPB was responsible for the overall project design and project supervision. All authors contributed to manuscript writing and proofreading.
Data availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-73118-z.
References
- 1.Schirhagl, R., Chang, K., Loretz, M. & Degen, C. L. Nitrogen-vacancy centers in diamond: Nanoscale sensors for physics and biology. Annu. Rev. Phys. Chem.65, 83–105 (2014). [DOI] [PubMed] [Google Scholar]
- 2.Herbschleb, E. et al. Ultra-long coherence times amongst room-temperature solid-state spins. Nat. Commun.10, 3766 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Degen, C. L. Scanning magnetic field microscope with a diamond single-spin sensor. Appl. Phys. Lett.92, 243111 (2008). [Google Scholar]
- 4.Taylor, J. M. et al. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys.4, 810–816 (2008). [Google Scholar]
- 5.Bhallamudi, V. P. & Hammel, P. C. Nanoscale MRI. Nat. Nanotechnol.10, 104–106 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Dutt, M. G. et al. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science316, 1312–1316 (2007). [DOI] [PubMed] [Google Scholar]
- 7.Neumann, P. et al. Quantum register based on coupled electron spins in a room-temperature solid. Nat. Phys.6, 249–253 (2010). [Google Scholar]
-
8.Savvin, A. et al. NV
 diamond laser. Nat. Commun.12, 1–8 (2021).
[DOI] [PMC free article] [PubMed] [Google Scholar]
diamond laser. Nat. Commun.12, 1–8 (2021).
[DOI] [PMC free article] [PubMed] [Google Scholar] - 9.Breeze, J. D., Salvadori, E., Sathian, J., Alford, N. M. & Kay, C. W. Continuous-wave room-temperature diamond maser. Nature555, 493–496 (2018). [DOI] [PubMed] [Google Scholar]
- 10.Jacques, V. et al. Dynamic polarization of single nuclear spins by optical pumping of nitrogen-vacancy color centers in diamond at room temperature. Phys. Rev. Lett.102, 057403 (2009). [DOI] [PubMed] [Google Scholar]
-
11.Busaite, L. et al. Dynamic
 nuclear spin polarization in nitrogen-vacancy centers in diamond. Phys. Rev. B102, 224101 (2020). [Google Scholar]
nuclear spin polarization in nitrogen-vacancy centers in diamond. Phys. Rev. B102, 224101 (2020). [Google Scholar] - 12.Duarte, H., Dinani, H. T., Jacques, V. & Maze, J. R. Effect of intersystem crossing rates and optical illumination on the polarization of nuclear spins close to nitrogen-vacancy centers. Phys. Rev. B103, 195443 (2021). [Google Scholar]
- 13.Poggiali, F., Cappellaro, P. & Fabbri, N. Measurement of the excited-state transverse hyperfine coupling in NV centers via dynamic nuclear polarization. Phys. Rev. B95, 195308 (2017). [Google Scholar]
- 14.Wolfe, C. S. et al. Off-resonant manipulation of spins in diamond via precessing magnetization of a proximal ferromagnet. Phys. Rev. B89, 180406 (2014). [Google Scholar]
- 15.McCullian, B. A. et al. Broadband multi-magnon relaxometry using a quantum spin sensor for high frequency ferromagnetic dynamics sensing. Nat. Commun.11, 5229 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Balasubramanian, G., Lazariev, A., Arumugam, S. R. & Wen Duan, D. Nitrogen-Vacancy color center in diamond-emerging nanoscale applications in bioimaging and biosensing. Curr. Opin. Chem. Biol.20, 69–77 (2014). [DOI] [PubMed] [Google Scholar]
- 17.Miller, B. S. et al. Spin-enhanced nanodiamond biosensing for ultrasensitive diagnostics. Nature587, 588–593 (2020). [DOI] [PubMed] [Google Scholar]
- 18.Teeling-Smith, R. et al. Electron paramagnetic resonance of a single NV nanodiamond attached to an individual biomolecule. Biophys. J .110, 2044–2052 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sherman, A., Buchbinder, L., Ding, S. & Blank, A. Performance analysis of diamond-based masers. J. Appl. Phys.129, 144503 (2021). [Google Scholar]
- 20.Klimov, P. V., Falk, A. L., Buckley, B. B. & Awschalom, D. D. Electrically driven spin resonance in silicon carbide color centers. Phys. Rev. Lett.112, 087601 (2014). [DOI] [PubMed] [Google Scholar]
-
21.Moussa, O., Hincks, I. & Cory, D. G. Preparing and preserving the double quantum coherence in NV
 centers in diamond at low fields. J. Magn. Reson.249, 24–31 (2014).
[DOI] [PubMed] [Google Scholar]
centers in diamond at low fields. J. Magn. Reson.249, 24–31 (2014).
[DOI] [PubMed] [Google Scholar] - 22.Felton, S. et al. Hyperfine interaction in the ground state of the negatively charged nitrogen vacancy center in diamond. Phys. Rev. B79, 075203 (2009). [Google Scholar]
- 23.Myers, B. A., Ariyaratne, A. & Jayich, A. C. B. Double-quantum spin-relaxation limits to coherence of near-surface nitrogen-vacancy centers. Phys. Rev. Lett.118, 197201 (2017). [DOI] [PubMed] [Google Scholar]
- 24.Drake, M., Scott, E. & Reimer, J. Influence of magnetic field alignment and defect concentration on nitrogen-vacancy polarization in diamond. New J. Phys.18, 013011 (2015). [Google Scholar]
- 25.Goldman, M. L. et al. State-selective intersystem crossing in nitrogen-vacancy centers. Phys. Rev. B91, 165201 (2015). [DOI] [PubMed] [Google Scholar]
- 26.Thiering, G. M. H. & Gali, A. Theory of the optical spin-polarization loop of the nitrogen-vacancy center in diamond. Phys. Rev. B98, 085207 (2018). [Google Scholar]
- 27.Tetienne, J. et al. Magnetic-field-dependent photodynamics of single NV defects in diamond: An application to qualitative all-optical magnetic imaging. New J. Phys.14, 103033 (2012). [Google Scholar]
- 28.Simanovskaia, M. et al. Sidebands in optically detected magnetic resonance signals of nitrogen vacancy centers in diamond. Phys. Rev. B87, 224106. 10.1103/PhysRevB.87.224106 (2013). [Google Scholar]
- 29.Robledo, L., Bernien, H., Van Der Sar, T. & Hanson, R. Spin dynamics in the optical cycle of single nitrogen-vacancy centres in diamond. New J. Phys.13, 025013 (2011). [Google Scholar]
- 30.Sangtawesin, S. et al. Origins of diamond surface noise probed by correlating single-spin measurements with surface spectroscopy. Phys. Rev. X9, 031052 (2019). [Google Scholar]
- 31.Loretz, M., Takahashi, H., Segawa, T. F., Boss, J. M. & Degen, C. L. Optical hyperpolarization of nitrogen donor spins in bulk diamond. Phys. Rev. B95, 064413 (2017). [Google Scholar]
- 32.Manson, N. & Harrison, J. Photo-ionization of the nitrogen-vacancy center in diamond. Diam. Relat. Mater.14, 1705–1710 (2005). [Google Scholar]
- 33.Siyushev, P. et al. Optically controlled switching of the charge state of a single nitrogen-vacancy center in diamond at cryogenic temperatures. Phys. Rev. Lett.110, 167402 (2013). [DOI] [PubMed] [Google Scholar]
- 34.Manson, N. B., Harrison, J. P. & Sellars, M. J. Nitrogen-vacancy center in diamond: Model of the electronic structure and associated dynamics. Phys. Rev. B74, 104303 (2006). [Google Scholar]
- 35.Gupta, A., Hacquebard, L. & Childress, L. Efficient signal processing for time-resolved fluorescence detection of nitrogen-vacancy spins in diamond. J. Opt. Soc. Am. B33, B28–B34 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.