Spike transmission failures in axons from cortical neurons in vivo

Summary

The propagation of action potentials along axons is traditionally considered reliable due to the high safety factor for axonal spike transmission. However, numerical simulations suggest that high-frequency spikes could fail to invade distal axonal branches. To explore this experimentally in vivo, we used an axonal-targeted calcium indicator to image action potentials at axonal terminal branches in the superficial layers of mouse somatosensory cortical neurons. We activated axons with an extracellular electrode, varying stimulation frequencies, and analyzed the images to computationally extract axonal morphologies and associated calcium responses. We found that axonal boutons have higher calcium accumulations than their axonal shafts, as was reported in vitro. However, contrary to previous in vitro results, our data reveal spike failures at high spike frequencies in a significant subset of branches as a function of branching geometry. These findings suggest that axonal morphologies could contribute to signal processing in the cortex.

Graphical abstract

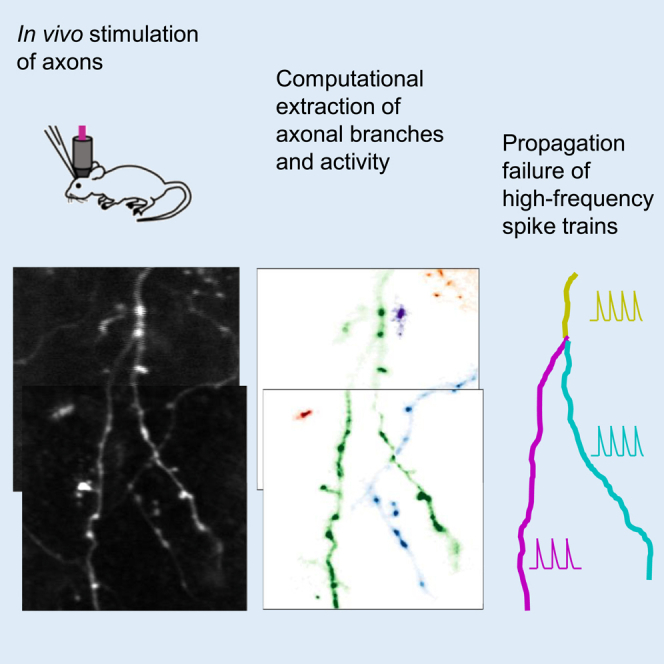
Highlights

• •Calcium accumulations are higher in axonal boutons than in axonal shafts
• •In most axons, action potentials propagate reliably across branch points
• •In some axons, higher frequency spike trains fail at branch points
• •Spike filtering correlates with the geometry of the axonal branch point

Neuroscience; Sensory neuroscience; Cell biology

Introduction

In the cerebral cortex, most neurons have long-range axons that can be very complex, including intrinsic collaterals with arbors in different cortical layers, extrinsic projections across cortical areas, and between brain regions and callosal connections.¹ Whether all action potentials propagate faithfully throughout these anatomically complex axonal arbors has long been debated.² Experiments in vitro have shown reliable transmission of individual spikes and spike trains through the axonal arbor of cortical pyramidal neurons.^3,4,5 However, theoretical simulations and cable analysis predict that geometrical heterogeneities, such as changes in axonal diameter or bifurcation points, may cause a delay or even a failure of an action potential propagation, due to different electrical impedance at these points.^6,7 Indeed, numerical simulations of action potential trains at branching points have shown differential propagation of firing patterns as a function of axonal branch diameters and spike frequency, suggesting differential neuronal information processing by specific axonal branches.^8,9 Thus, there is a discrepancy between experimental results and theoretical predictions. One possibility is that the reported fidelity of action potential propagation at branching points and in distal axons is ensured by non-uniform densities of sodium and potassium voltage-gated channels, which compensate for morphological changes.^10,11,12 However, given that these experimental data were obtained in vitro, it is possible that axonal propagation could differ in vivo, since many physiological factors may influence the reliability of propagation.

To measure spike propagation in vivo, we used two-photon imaging of action potentials with calcium indicators.¹³ In contrast to electrophysiology, this optical approach allows the measurement of signals throughout neuronal processes—including fine dendritic and axonal branches. Despite the relatively slow temporal resolution of calcium imaging, it can faithfully detect action potential activity in pyramidal cells at the single-spike level.^14,15 Although genetically encoded voltage indicators (GEVIs) are also capable of reporting axonal activity with single action potential resolution,^16,17 their application is still challenging due to the low signal-to-noise ratio and high-sampling rate required for imaging regions of interest (ROIs) along axonal branches. To specifically record action potential activity in axons, one can use axon-targeted GCaMP6s, characterized by a uniform expression and distribution, sufficient brightness, high signal-to-noise ratio, and photostability.¹⁸ To capture responses to dozens of spikes at high frequency, GCaMP6s actually outperforms the newer jGCaMP8, owing to its larger dynamic range with more linearity and less saturation.¹⁹ Because of this, to monitor activity across axonal branching points in response to high-frequency action potential trains in vivo, we imaged axon-targeted GCaMP6s expressed in superficial axonal branches from mouse primary somatosensory cortex, in response to extracellular electrical stimulation. We aimed to determine whether spikes originating from a parent axonal branch successfully reached the daughter branches. We found a heterogeneity of responses. In most axons (11 out of 17), spikes propagated from the parent branch into both daughter branches reliably, resulting in a similar response in all branches. However, in 6 axons, higher frequency spikes failed at the bifurcation point, leading to different responses in the daughter branches. Morphological analysis of these cases revealed a correlation between the geometrical ratio (GR) of the parent and daughter diameters and the reliability of spike transmission, which also decreased with the frequency of the action potential trains. Our results reveal that high-frequency action potentials fail to propagate in a significant number of axonal branches in mouse cortical neurons in vivo.

Results

We measured axonal calcium dynamics in 17 axonal branch points, likely belonging to 17 different neocortical neurons in the mouse primary somatosensory cortex, imaged in 5 different mice (Table 1). To study the propagation of action potential trains through these axonal branch points, we injected extracellular current pulses at various frequencies into the neighboring neuropil and examined axonal responses at branch bifurcations. Stimuli were designed to produce action potential trains at six different frequencies, between 40 and 140 Hz, with a duration of 200 ms. To express a calcium indicator in pyramidal axons, we utilized viral injections of axon-GCAMP6s into the cortex, driven by the human synapsin promoter.¹⁸ Although the expression is not specific for a cell type, these axons are likely to belong to pyramidal cells due to the higher fraction of pyramidal axons in the superficial layer²⁰ and the fact that long-range intracortical axonal projections are more frequent for pyramidal neurons compared to interneurons.²¹ The fluorescence of axons expressing axon-GCaMP6s was imaged using a custom-made two-photon microscope. We searched for axons where branches in the same focal plane responded to test pulses from the electrode and imaged their responses. To correct for differences in expression and focal plane, GCaMP6s fluorescence was normalized by mRuby3 fluorescence, which was bicistronically co-expressed (Figure 1). For each firing frequency, fluorescence signals of 7 trials were averaged, independently for each axonal branch—a “parent” and two “secondary” branches. The classification of branches into parent or secondary was based on their morphologies, whereby larger parent branches split into two smaller branches at an acute angle. We analyzed both the peak of the calcium signal and the area under the fluorescence curve, which respectively represent the peak current and the calcium ions charge injected. Peak signals were more sensitive to noise compared to areas, due to the sampling rate and the filters applied during the analysis.

Table 1.

Summary of experiments analyzed in the study

	Mouse 1	Mouse 2	Mouse 3	Mouse 4	Mouse 5	Total
Neurons	11	2	2	1	1	17
Propagation	9	0	0	1	1	11
Filtering	2	2	2	0	0	6

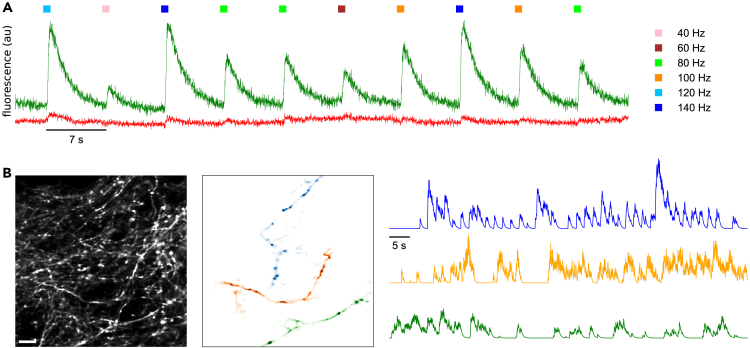
Figure 1.

Experimental design and spatiotemporal analysis of axonal branches

(A) Axonal calcium fluorescence responses to electrical stimulation of neuropil at different stimulation frequencies; axon-GCaMP6s, green trace and mRuby3, red trace.

(B) Computational segmentation and signal extraction process for axonal branches, automatically localizing individual axons and separating neuropil background based on calcium activity. Scale bar: 10 μm.

Axonal boutons generate increased calcium responses in vivo

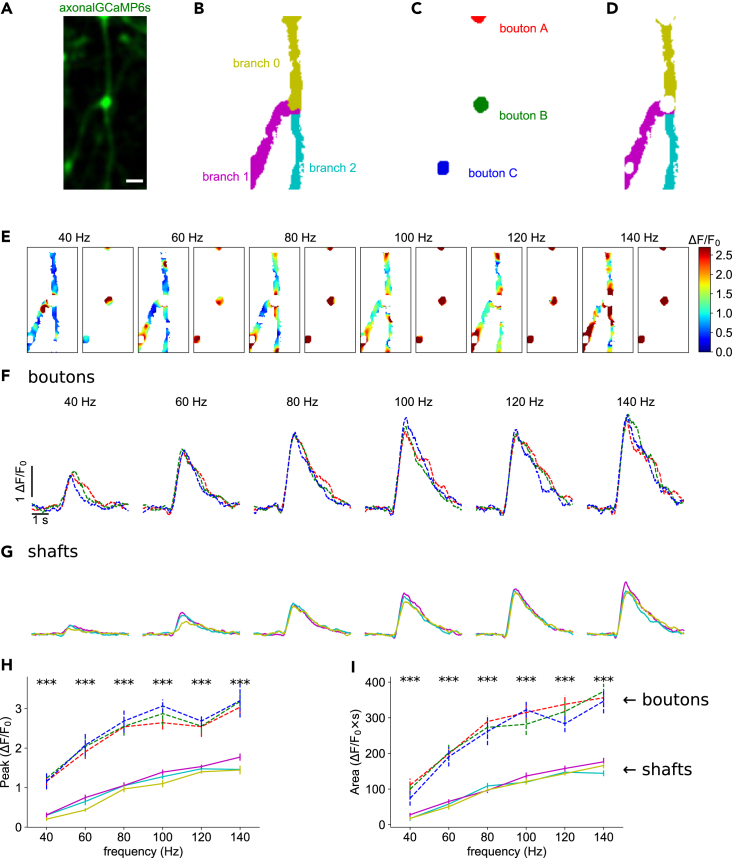
In our imaging data, we frequently observed axonal boutons, both en passant and terminal boutons (Figure 2A). Previous in vitro studies have reported that boutons have higher peak calcium accumulations than the shafts of the axonal branches.^3,4 To analyze this, we computationally extracted (STAR methods) these boutons in a pilot experiment and conducted separate analyses of signals from axonal boutons (Figure 2C) and axonal shafts (Figure 2D). In this experiment, the calcium signal intensity in axonal boutons was higher than those in axonal branches, as measured with peak amplitude (2.33 ± 0.71; mean ± SEM, all p values were less than 0.0004; Kruskal-Wallis H-test, Figure 2H) and area under the curve (2.75 ± 0.67; mean ± SEM, all p values were less than 0.0003; Kruskal-Wallis H-test, Figure 2I). Similar results were found in other experiments, with the bouton/axon shaft ratio of signal amplitudes being 3.46 ± 0.18 (mean ± SEM), and the area under the curve of 3.29 ± 0.16 (mean ± SEM, n = 19 boutons, 7 neurons, 3 mice). Altogether, in 6 out of 7 experiments, the differences in peaks and areas under the curve between boutons and branches were statistically significant across all stimulus frequencies (all p values were less than 0.04; Kruskal-Wallis H-test), while in one experiment, significant differences were only observed at frequencies above 100 Hz (all p values were less than 0.0003; Kruskal-Wallis H-test). The higher amplitude of the responses in axonal boutons (maximum of 3.18 ± 0.21 ΔF/F₀ compared to 1.77 ± 0.08 ΔF/F₀ at the axonal branch; Figure 2H) also indicated that the fluorescence signal at axonal branches was below the sensor’s saturation regime. We concluded that, in vivo, axonal boutons have increased calcium accumulations, as compared to axonal shafts, confirming previous in vitro results.^3,4

Figure 2.

Increased calcium responses of axonal boutons

(A) Time-averaged image of axon-GCaMP6s activity during electrical stimulation. Scale bar: 2 μm.

(B) Color map of the automatically identified parent (0) and the two secondary axonal branches (1 and 2).

(C) Masks of three axonal boutons (A, B, and C).

(D) Masks of axonal branches after removal of the boutons.

(E) Representative color maps depicting normalized calcium peak amplitudes for axonal branches and boutons at different firing frequencies.

(F) Normalized axon-GCaMP6s/mRuby3 signal for each bouton at different frequencies. Average of 7 trials per frequency. Traces are colored according to the boutons shown in C.

(G) Normalized axon-GCaMP6s/mRuby3 signal for each branch at different frequencies. Average of 7 trials per frequency. Traces are colored according to branches shown in D.

(H) Calcium peak amplitudes of signals from F and G as a function of firing frequency.

(I) Area under the curve of signals from F and G as a function of firing frequency. Data are represented as mean ± SEM. Asterisks indicate statistical significance difference between signals; Kruskal-Wallis H-test.

Reliable propagation of action potentials in most axonal branches

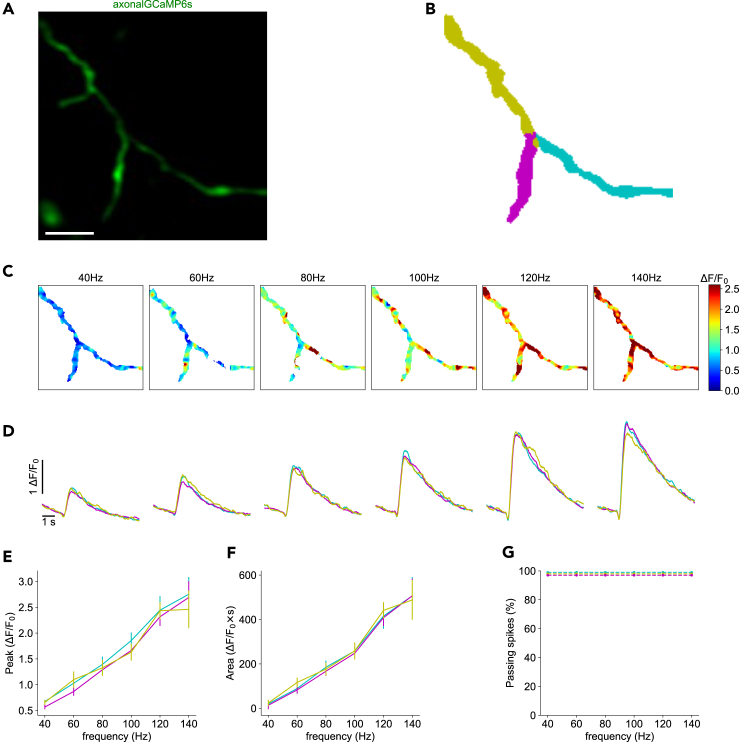
Due to variability in calcium signals between boutons and to avoid fluorescence contamination from the stronger signals of axonal boutons affecting the axonal shafts, for the remainder of the study boutons were computationally removed during the analysis process, and we only analyzed signals from axonal shafts. For 11/17 axonal bifurcations, we found similar responses in all axonal branches (Figure 3; Table 1; Figure S1). As the stimulation frequency increased (and presumably the number of propagated axonal spikes), the fluorescence response became stronger (Figures 3C and 3D). At each frequency, the peak amplitude and area under the curve of the calcium signals were similar across all parent and secondary branches (Figure 3D). There was no statistically significant difference between branches at any stimulation frequency, either in the peak amplitude of the signal (7 trials, 6 frequencies, all p values were greater than 0.18; Kruskal-Wallis H-test; Figure 3E) or area under the curve (7 trials, 6 frequencies, all p values were greater than 0.26; Kruskal-Wallis H-test; Figure 3F). These findings indicate that the same number of action potentials in the parent branch propagated into the two secondary branches, without transmission failures. We concluded that axonal propagation was reliable in the majority of cases (Figure 3G).

Figure 3.

Reliable propagation of action potentials at an axonal branching point

(A) Time-averaged image of axon-GCaMP6s activity during electrical stimulation. Scale bar: 5 μm.

(B) Color map showing the automatic segmentation of the parent branch and two secondary axonal branches.

(C) Representative color maps of normalized calcium peak amplitudes at the indicated firing frequencies.

(D) Normalized axon-GCaMP6s/mRuby3 signal for each branch at different firing frequencies. Average of 5 trials per frequency. Traces are colored according to the branches segmented in B.

(E) Peak amplitudes of calcium signals from D as a function of firing frequency.

(F) Area under the curve of signals from D as a function of firing frequency. Data are represented as mean ± SEM.

(G) Percentage of signals that propagate at each branch, as a function of firing frequency. See also Figure S1.

Differential action potential propagation at higher frequencies in axonal branches

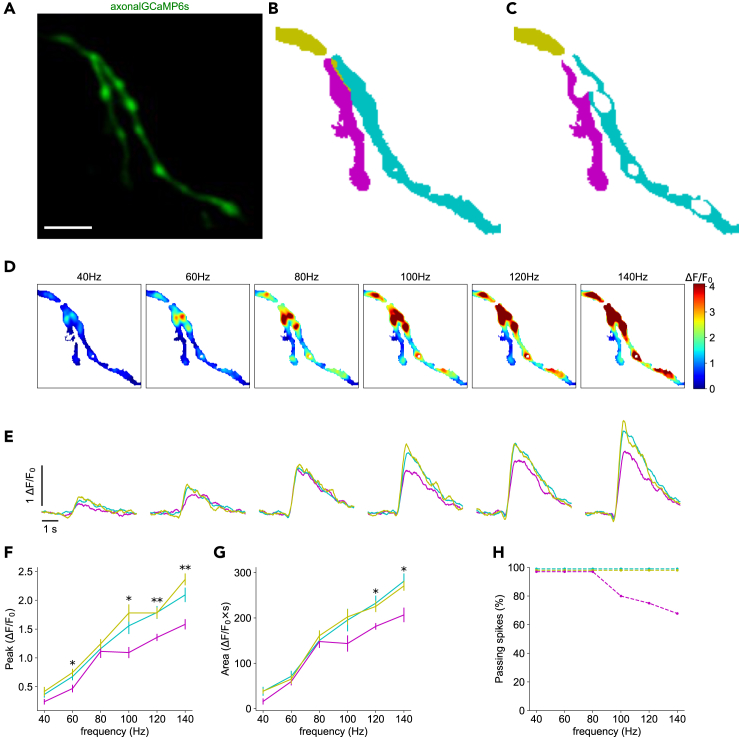
In 6 out of 17 axonal branches, we also observed that calcium signals differed between parent and secondary branches at particular frequencies (Figure 4; Table 1; Figure S2). To analyze this, the axon-GCaMP6s signal (Figure 4A) was normalized by the mRuby3 signal. Subsequently, branch segmentation and masks were spatially overlaid on time-series images (Figure 4B), and axonal boutons were removed (Figure 4C). At 40, 60, and 80 Hz, the fluorescence intensity was similar across all branches (n = 7, significant p value at a non-consecutive frequency in the peak signals; all p values were greater than 0.08 for the area under the signals; Kruskal-Wallis H-test). However, at 100, 120, and 140 Hz, some signals did not propagate into secondary branches (Figures 4D and 4E). In the example shown, the fluorescence response in the left secondary branch (cyan) was lower than that in the parent (yellow) and the right secondary branch (magenta). These differences in calcium peak signal amplitude were statistically significant above 100 Hz (p values were less than 0.05, Kruskal-Wallis H-test; Figure 4F), and the differences in the area under the curve of the signal were statistically significant above 120 Hz (p values were less than 0.05, Kruskal-Wallis H-test; Figure 4G). Variations in the expression of the axonal-enriched calcium indicator or z-plane between branches cannot explain these differences, as the responses in all branches were similar at lower firing frequencies. These observations suggest that, at this branching point, spike propagation at high frequencies may be impaired.

Figure 4.

Differential spike propagation in axonal branches

(A) Time-averaged image of axon-GCaMP6s activity during electrical stimulation. Scale bar: 5 μm.

(B) Color map showing the automatic segmentation of the parent branch and two secondary axonal branches.

(C) Color map of the parent and two secondary branches after removing the axonal boutons.

(D) Representative color maps of normalized calcium peak amplitudes at the indicated firing frequencies.

(E) Normalized axon-GCaMP6s/mRuby3 signal for each branch at different firing frequencies. Average of 7 trials per frequency. Traces are colored according to the branches segmented in C.

(F) Peak amplitudes of calcium signals from E as a function of firing frequency.

(G) Area under the curve of signals from E as a function of firing frequency. Data are represented as mean ± SEM. Asterisks indicate statistical significance differences between signals; Kruskal-Wallis H-test.

(H) Percentage of signals that propagate at each branch, as a function of frequency. See also Figure S2.

Frequency-dependent filtering of spike propagation

To better understand how spikes propagate or fail, we further analyzed the data, beginning with the example of the neuron presented in Figure 4. The ratio between the action potential train frequency and the calcium peak signal (Figure 4F) and the area under the curve (Figure 4G) was linear in both the parent branch (yellow) and the right secondary branch (cyan). This suggested that all spikes in the train propagated through these branches. Considering the nonlinear relationship between fluorescence and calcium concentration (see STAR methods), we inferred the number of spikes in the left secondary branch based on the fluorescence intensity in the parent branch.

We estimated the number of spikes that failed to propagate using the area under the curve graphs (Figure 4G), which was more robust to noise than the peak of calcium signals (Figure 4F). We found that in one of the secondary branches, the area under the curve was similar at 80 and 100 Hz (148 ± 13.13 ΔF/F₀·s and 143.58 ± 16.83 ΔF/F₀·s; flatness in the magenta curve in Figure 4G). We estimated that the same number of spikes—16—were propagated in both cases, but only 16 out of 20 spikes (80%) were propagated at 100 Hz. At 120 Hz, 18 out of 24 spikes (75%) propagated into the left daughter (magenta); and at 140 Hz, only 19 out of 28 spikes (67.8%) invaded the left branch (Figure 4H). In conclusion, based on the analysis of one neuron, whereas all spikes propagated into the two secondary branches at lower frequencies, the number of spikes that propagated decreased as the frequency of the action potential train increased.

Gradation of spike propagation failures in different neurons

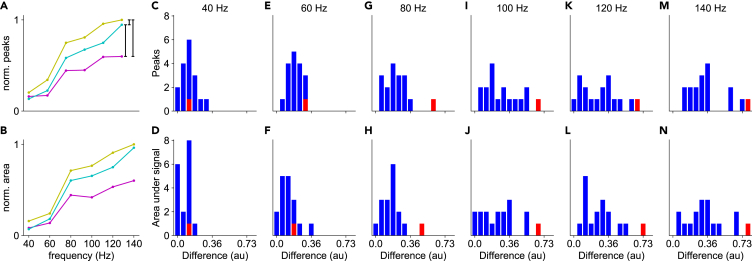
Thus, we found that spike propagation was effective for most axonal branches, but there were some cases of propagation failure at high frequencies. To assess the extent of these propagation failures across the entire population of axonal branching points, we quantified differences in peaks and areas under the curve of the calcium signals among branches, and designed criteria to classify whether propagation was effective or not (Figure 5). To achieve this, we calculated the cumulative differences in normalized signals between each pair formed by the parent branch and its two secondary branches (see Figure 5A). These differences became more pronounced at higher frequencies (see Figures 5C–5N). The distribution of signal differences across the 17 examined branch points was continuous, although at 140 Hz, we noted two distinguishable groups, one with low and one with high peak signal difference values (Figure 5M). The small number of samples (n = 17) did not allow statistical assessment of the potential bimodality of the distribution. Our findings also revealed a disparity in signal transmission between the two daughter branches, indicating that, on average, the number of action potentials invading each daughter branch differs, resulting in a gradation of responses.

Figure 5.

Comparison of calcium signal between axonal branches

(A) Example of the normalized calcium peak fluorescence as a function of stimulus frequency at a branch point; parent branch (yellow), and two secondary branches (cyan and magenta).

(B) Normalized integrated calcium fluorescence as a function of stimulus frequency.

(C–N) Pooled differences between normalized signals (black vertical lines in A), for peak (upper row) and area under the curve (bottom row) across different spike train frequencies (n = 17). Red bars indicate the difference values from the example shown in A and B.

Axonal branching point geometry correlates with spike propagation

To further understand the filtering properties of branching points, we compared axonal branch points with reliable propagation to those exhibiting filtering properties. For this purpose, we established statistical criteria to distinguish between “similar” and “different” responses in parent and secondary branches. A “different” response was defined as a statistically significant difference in calcium peak amplitude or area under the curve in at least two consecutive firing frequencies (see Figures 4F and 4G). Responses not showing this criterion were classified as “similar” (see Figures 3E and 3F). Using these criteria, we found similar responses across all axonal branches in 11 out of 17 axonal bifurcations analyzed. In contrast, the remaining 6 branch points, representing data from three different mice, showed different responses (Table 1).

Next, we measured the diameters of the axonal branches and calculated the geometrical ratio (GR) between the parent and secondary branches, defined as:

$$GR=\frac{{\sum }_j{d}_j^{3/2}}{d_a^{3/2}}$$ Equation 1

where d_a is the diameter of the parent branch, and d_j are the diameters of the secondary branches. According to cable theory, the GR reflects the electrical impedance at the branching point and is correlated with the diameters of the parent and secondary branches. For example, when all branches (parent and secondary) have the same diameter, GR = 2. Theoretical studies using cable theory have shown that when GR = 1, the propagation of the action potential is effective, whereas higher values of GR may lead to spike delays or failures.^6,7

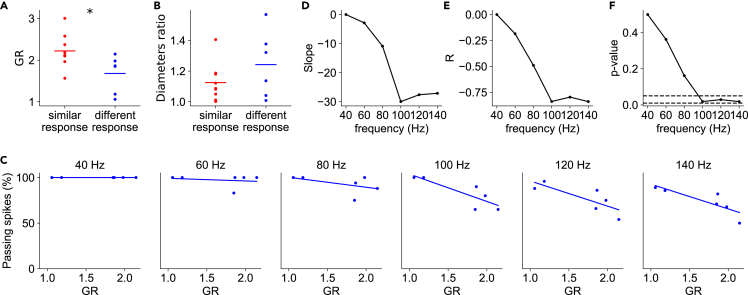
We found a significant difference in GR values between the group of branching points with similar or different responses (Figure 6A). We analyzed 15 branches from 5 mice, excluding 2 branches from our dataset: one due to failures in the parent branch and one for which we could not measure the axonal diameter with precision. Contrary to our expectations based on cable theory, GR values were lower (1.68 ± 0.41; mean ± SD, 1.86; median) in the “different” response group compared to the “similar” response group (2.22 ± 0.38; mean ± SD, 2.12; median; p < 0.05, t test). The ratio between the two secondary branches was higher in the “different” response group (1.24 ± 0.2; mean ± SD, 1.23 median) compared to the “similar” response group (1.13 ± 0.12; mean ± SD, 1.09; median), but the difference was not significant (p = 0.205, t test) (Figure 6B). We did not find a difference in the angle between the daughter branches in the branching points with and without filtering.

Figure 6.

Spike filtering correlates with axonal branch point geometrical ratio (GR)

(A) GR values of “similar” (n = 9) and “different” (n = 6) response branch points; t test two-sided.

(B) Ratio between diameters of the two secondary branches, “similar” in red and “different” in blue; t test two-sided. The horizontal lines represent the means.

(C) Percentage of propagating spikes as a function of GR for each spike train frequency. Lines represent linear fits to the data.

(D) Slope of the regression line as a function of action potential frequency.

(E) Pearson correlation coefficient (R) between the percentage of passing spikes and GR, as a function of action potential frequency.

(F) p value of the linear regression fitting as a function of the action potential frequency. Dashed lines indicate p values of 0.05 and 0.01.

We then analyzed the subgroup of axonal branch points with “different” responses and tested the correlation between the extent of filtering and GR value. At lower frequencies (40 and 60 Hz), there was no significant correlation (p > 0.4; Wald test). However, starting at 80 Hz, filtering significantly correlated with GR value, as one would expect from cable theory (Figures 6C–6E). Filtering increased with frequency, showing a statistically significant difference (p < 0.05; Wald test) at 100, 120, and 140 Hz (Figure 6F). We concluded that branch points with significant filtering of high-frequency action potential trains had lower GR, and within this population, the filtering was proportional to GR values.

Interestingly, we also noted that in 6 out of 17 branching points (5/9 cases in the “different” response group and 1/10 cases in the “similar” response group), a bouton was located precisely at the branching point, as shown in Figure 2A. This bouton location could potentially impact spike filtering at the branching point due to changes in GR or variations in ion channel densities and types in the bouton membrane.

Discussion

We demonstrate the existence of propagation failures of high-frequency action potential trains at axonal branch points in a significant number of cortical neurons in vivo. Axonal branch-specific activity could be important for neuronal information processing, similar to dendritic branch-specific activity.^22,23,24 Thus, the geometry of the axonal branches could modulate the firing pattern of action potential trains, and impact neuronal processing. Moreover, axons are also highly sensitive and vulnerable neuronal structures that are prone to damage, which can further impede spike propagation in cases of traumatic brain injury, stroke, and neurodegenerative diseases such as amyotrophic lateral sclerosis (ALS) or Parkinson’s disease.^25,26,27,28

Higher calcium concentration in axonal boutons in vivo

Our data demonstrate that axonal boutons in vivo have significantly higher calcium accumulations than axonal shafts. These differences cannot simply be attributed to differential targeting of the calcium indicator. While untargeted GCaMP6s-expressing axons displayed bright fluorescent varicosities, like boutons, axonal-targeted GCaMP6s had relatively homogenous basal fluorescence in both axonal shafts and varicosities.¹⁸ Our results extend to the in vivo setting previous in vitro findings. Bouton responses are variable, as when responses to a single action potential were measured across multiple axonal boutons in the same neuron, there was more than a 10-fold variation in the intensity of calcium transients.⁴ Thus, attempts to use data from individual axonal bouton to infer the firing rate of the presynaptic cell would be prone to error.²⁹ In our results, we observed a higher calcium concentration at axonal boutons compared to the axonal branches (Figure 2). Therefore, we masked and removed the boutons, enabling us to record the activity from axonal segments without the influence of calcium concentration at the boutons.

Differential propagation of high-frequency spike trains in axons

Importantly, and different from previous in vitro reports, we found two types of branch point propagation among neurons. In the first group (“similar” responses), all spikes reliably invaded all axonal branches. In the second group (“different” responses), there was a significant failure of spike propagation at high frequencies. Paradoxically with cable theory, GR values in the “different” response group were lower than GR values in the “similar” response group (Figure 6A). However, by independently sub-analyzing the “different” response group, we found a correlation between spike filtering and GR (Figure 6C), as expected by cable theory. So, in our results, there is evidence for and against cable theory. However, besides cable properties, additional mechanisms must be considered to elucidate the different phenomenology between axonal branch points that propagate or filter action potential trains. For example, the ratio between diameters in the secondary branches could differ between both groups, or, higher values of GR may be required to induce spike failures in the branching points of the “similar” response group. Importantly, since cable theory assumes passive electrical properties, variations in ion channel types and their respective densities could likely be at play. Finally, these two groups of axons may belong to different neuronal subtypes, with distinct membrane properties.

Comparison with previous studies

Previous studies conducted in brain slices have not reported spike failures in axonal bifurcations, using lower frequency trains. Our results are consistent with them, as most of the spike filtering we detected occurred at frequencies above 100 Hz. While the typical frequencies of spike trains in neocortical pyramidal neurons under physiological regime are below 50 Hz,^30,31 higher frequencies above 100 Hz have been observed in rodent pyramidal neurons.³² In particular, layer 5 pyramidal neurons have firing frequency distributions beyond 200 Hz and often have bursts of up to 6 spikes, above 100 Hz.³³

Importantly, previous in vitro studies examined branch points located in close proximity to the soma, typically within the first 300 μm,^5,34 often where the primary collaterals of the axon originate.³⁵ However, it is likely that spike failures might be more prevalent in more distal axonal arbors, such as the ones we studied. In our experiments, precise measurements of the distance between the branching point and the cell body were not feasible due to anatomical constraints. Nevertheless, the axonal branching points imaged were located at least 1 mm away from the electrode and the viral expression site. Furthermore, it is worth noting that axonal regions near the soma tend to have a higher degree of myelination,³⁶ which may prevent spike failures.³⁷ Our experimental setup does not enable us to observe the presence or absence of myelin sheath around the axons. Previous evidence shows that most neocortical axons are unmyelinated in distal regions. In the mouse somatosensory cortex, the amount of myelinated axons in layer 2/3 is around only 37%, lower than in layer 4 (56.7%) and layers 5/6 (63%).³⁶ In a reconstruction of the human temporal cortex, 40.6% of the volume consisted of unmyelinated axons and 7.6% of myelinated axons,³⁸ meaning that only ∼16% of the axons are myelinated. As a final difference with in vitro data, previous calcium measurements were mixed with axonal boutons,³ which typically exhibit higher and more variable calcium concentrations.

Potential factors affecting axonal propagation

Our results are consistent with the possibility that spike filtering cannot be simply explained by the electrical cable structure of the axon, which is influenced by its geometry (Figure 6). Besides geometrical factors of axonal bifurcations, other mechanisms, such as the presence of active conductance, can greatly influence spike propagation. In addition, inhibitory axons forming axo-axonic synapses onto the axonal tree may contribute to action potential failures and spike filtering. For example, cholinergic Kenyon cells in Drosophila have numerous axo-axonic connections that suppress signals in neighboring cells.³⁹ GABAergic neurons in the spinal cord of rodents and humans also form axo-axonic contacts with sensory axons, facilitating spike propagation by preventing spike failures at axon branch points.⁴⁰ Furthermore, excitatory synaptic inputs into dopaminergic axons were also identified in the mouse striatum, suggesting a physiological mechanism to regulate dopamine signaling.⁴¹

Other anatomical characteristics could influence spike propagation properties within the axonal tree. Along the axon, afferent synapses are closer to the soma than efferent synapses.³⁶ Additionally, presynaptic axonal boutons targeting inhibitory neurons are located more proximally along the axonal tree compared to those targeting excitatory neurons.⁴² Boutons within individual axons that innervate both motor and sensory areas of the cerebral cortex present significant area-specific differences in size.⁴³ Neurons with axons emerging from dendrites, rather than from the soma, have been suggested to facilitate information gating.⁴⁴ Finally, a neuron with two separate axons emerging from the soma was found in the human temporal cortex.³⁸

Dynamic morphological changes of axons

As we have demonstrated, the geometry of the axon, particularly the diameters at branching points, significantly influences spike filtering. Previous studies have shown activity-dependent plasticity of axonal diameters and bouton sizes, affecting action potential conduction velocity.^45,46 These dynamic changes in axonal dimensions may not only affect the velocity of action potential propagation but also the spike filtering properties. This dynamic spike filtering ability could have implications for learning and memory processes.

Limitations of the study

Our results provide proof of concept that spikes in high-frequency action potential trains can fail at axonal branching points in cortical neurons in vivo. One limitation of this study is the relatively small sample size (n = 17 axonal branches), due to the technical challenges of recording from branching points in thin cortical axons. While a larger dataset would enhance statistical power, the current sample size is adequate for this initial exploration of the physiology of the axonal compartment. Future investigations could also explore more natural scenarios of high-frequency spike trains using specific visual, auditory, or somatosensory stimuli. Additionally, higher temporal resolution, at the level of a single action potential, should be pursued in future studies, potentially utilizing newly engineered voltage sensors designed for recording axonal activity. Finally, the exact neuronal subtype of the axons studied should be ascertained.

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Netanel Ofer (netanelofer@gmail.com).

Materials availability

This study did not generate new materials.

Data and code availability

• •Videos of the activity at the branching points have been deposited at the Columbia University Academic Commons site and are publicly available as of the date of publication. DOIs are listed in the key resources table. https://doi.org/10.7916/y615-0e51
• •All original code has been deposited at Columbia University Neurotechnology Center’s GitHub page and the Jupyter notebooks of the Python code are publicly available as of the date of publication. DOIs are listed in the key resources table. https://github.com/NTCColumbia/Spike_transmission_failures_in_axons
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Acknowledgments

We would like to thank Yuriy Shymkiv and lab members for their support and helpful suggestions; This work was supported by NEI (R01EY035248), NIMH (R01MH115900), and NINDS (RM1NS132981) to R.Y. This work is dedicated to the memory of Roberto Araya.

Author contributions

All authors contributed to project conception, project design, and manuscript writing. V.C. performed the experiments and N.O. analyzed the results. R.Y. directed the project and secured resources and funding.

Declaration of interests

The authors declare no competing interests.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and virus strains
pAAV-hSynapsin1-axon-GCaMP6s (Plasmid #111262)	Addgene	RRID:Addgene_111262; https://www.addgene.org/111262/
Deposited data
Columbia University Academic Commons	Columbia University	https://doi.org/10.7916/y615-0e51
Custom Analysis Scripts	GitHub	RRID:SCR_002630; https://github.com/NTCColumbia/Spike_transmission_failures_in_axons
Experimental models: Organisms/strains
Mouse C57BL/6	In house breeding	–
Software and algorithms
Fiji/ImageJ (version 1.52a)	Fiji	RRID:SCR_003070; https://imagej.net/
Python (version 3.7.9)	Python Software Foundation	RRID:SCR_008394; https://www.python.org/
CaImAn	–	RRID:SCR_021152; https://caiman.readthedocs.io/

Experimental model and study participant details

Female and male wild-type C57BL/6 mice, aged 2–4 months, were used in this study. The mice were kept on a continuous 12-h light/dark cycle and had free access to food and water. All experimental procedures involving animals were approved by the Columbia University Institutional Animal Care and Use Committee (IACUC, protocol AC-AABN3562) in compliance with the National Institutes of Health guidelines for the care and use of laboratory animals.

Method details

Viral injections surgeries

Mice were anesthetized with 2% isoflurane and placed in a stereotaxic atop a heating pad maintained at 37°C. Enrofloxacin (5 mg/kg) and carprofen (5 mg/kg) were injected intraperitoneal and lidocaine (2 mg/kg) subcutaneously in the site of the skin incision over the midline of the scalp. A 0.5 mm hole was drilled in the skull over the anterior left portion of the somatosensory cortex. Virus pAAV-hSynapsin1-axon-GCaMP6s-P2A-mRuby3 (Addgene viral prep #1120050-AAV5) was injected into layer 2/3 of the primary somatosensory barrel (S1BF) cortex (3.2 mm lateral, 0.1 mm posterior and 1.6 mm down from the bregma) to target intra-cortical axons. 150 nL of the viral prep was injected at a rate of 50 nL/min, and 3 min wait period before needle withdrawal.

Head plate and cranial windows implantation

After 2–3 weeks of viral injection surgeries, mice were anesthetized with 2% isoflurane in the same stereotaxic rig, and a titanium head plate was attached to the skull using dental cement. A 3 mm round craniotomy was made over the primary somatosensory cortex, and the dura was removed. The upper tangent of the 3 mm round glass coverslip (Warner Instruments, CS-3R) was placed at the same site as the viral injection and fixed to the skull using cyanoacrylate.

Extracellular electrode stimulation and two-photon imaging

Immediately after head plate and cranial window implantation, the animal was moved to a two-photon microscope rig, and a concentric bipolar electrode of 200/50 μm diameter (outer/inner pole) (FHC, #30215) was placed at the same coordinates as the viral injection site in the somatosensory cortex. Stimulation was performed with a stimulus isolator (World Precision Instruments, A365) in bipolar mode. 1 ms pulses were generated using a Master-8 pulse generator (A.M.P.I.) to the isolator. Axonal branch searching was performed by giving a test pulse consisting of 5 pulses at 50 Hz, with the isolator set to 100 μA. Once target axonal branches were found, minimal stimulation was tested to observe significant responses, and the isolator was set in a range of 40–100 μA.

In vivo imaging was performed in layers 1 and 2/3 at 50–150 μm below the cortical surface of the exposed mouse cortex with a custom two-photon microscope (adapted from Prairie model, Bruker), with a 25×/1.05 N.A. water immersion objective (Olympus) and a tunable Ti-sapphire laser (Mai Tai eHP DS, Spectra-Physics). Animals expressing axon-GCAMP6s in the cortex were imaged with the two-photon system with the laser tuned at 940 nm and signals were collected with filters 510/20 nm for GCAMP6s and 605/15 for mRuby3. Axons were imaged at a resolution of 256 × 256 pixels to 10 or 12× zoom at ∼60 Hz (pixel size of 0.166 μm or 0.2 μm, accordingly). Imaging power laser at 940 nm was measured at the end of the objective and for regular imaging, 50–80 mW was used for all experiments.

Electrical stimulation

Six different series of electrical pulses with frequencies of 40, 60, 80, 100, 120, and 140 Hz were injected for a constant duration of 200 ms, which resulted in sequences of 8, 12, 16, 20, 24, and 28 pulses. The 1 ms pulses were designed in a way that each pulse led to a single action potential. The time interval between pulse series was 7 or 8 s to allow complete decay of the fluorescence before the next series of pulses. The stimulus for each frequency was repeated seven times in random order (Figure 1A). The stimulus was designed to account for the nonlinearity relationship between calcium concentration and the observed fluorescence. This nonlinearity is due to the properties of the indicator, which requires binding of four calcium ions for lighting, causing supralinear and sublinear regimes that can be approximated by the Hill equation.⁴⁷ To address the challenge of inferring the number of spikes from the fluorescence signal, we employed a strategy wherein the fluorescence signal from one branch at lower frequencies was used as a baseline to estimate the number of spikes that failed to propagate in another branch at higher frequencies.

Image analysis

Motion correction was applied on the GCaMP6s channel using CaImAn.⁴⁸ The same correction in X and Y that was conducted on the GCaMP6s channel was applied to the mRuby3 channel. Then, the GCaMP6s channel was normalized by the mRuby3 channel to correct axonal branches at a different distance from the focal plane. We used CaImAn to construct masks only for the axonal branched of the bifurcation points (Figure 1B). The ‘SparseNMF’ initialization strategy was used for quickly uncovering spatial structure in the imaging data, especially for neural processes such as dendrites or axons, where the degree of overlap between the different branches is higher.⁴⁹ Then, we dissected the ROIs of the parent and the two daughter branches (see Figure 2B).

Axonal boutons were identified and then removed using an automated and objective process. Detection was performed by applying a 2D convolution of the time-averaged activity image with a 6-pixel disk (∼1 μm radius), resulting in rounded areas of high fluorescence expression. Subsequent steps included creating a binary mask of the convolved image, followed by erosion and dilation steps to smooth the masks and remove noise. Finally, a connected component labeling algorithm was used to accurately delineate and isolate the boutons.

The fluorescence signals for the 7 trials were averaged separately for each branch and then were filtered with a Savitzky-Golay filter (filter length of 51; order of the polynomial was 3).

The ΔF/F₀ was calculated according to Equation 2. F₀ was calculated by averaging 100 frames (∼1.6 s) before the onset of each pulse series.

$$\Delta F/F_0=\frac{F-F_0}{F_0}$$ Equation 2

Measurement of axonal diameters

To measure the diameters of the axonal branches, we used ImageJ to draw a line (width of 10 pixels) perpendicular to the axon. The fluorescence intensity pattern was fitted to the Lorentzian function, and then the full width at half maximum (FWHM) was calculated. When possible, the axonal diameter measurements were done from the mRuby3 channel and not from the GCaMP6s channel, which may be affected by the axonal activity. For one branch (out of 17), measurements of the parent diameter were unreliable due to dense fluorescence in the neuropil background.

Quantification and statistical analysis

Statistical analysis

Data are expressed as mean ± SD or mean ± SEM, as detailed in the text for each case. A factorial non-parametric Kruskal-Wallis H-test or two-sided unpaired Student’s t test was applied. The correlation between parameters was examined by the Wald test with t-distribution of the test statistic. The two-sided p-value for a hypothesis test whose null hypothesis is that the slope is zero. The asterisks indicate statistical significance: n.s, not significant, ∗p < 0.05, ∗∗p < 0.01, ∗∗∗p < 0.001. The details of the specific test used in each case are provided in the text.

Published: September 5, 2024