Abstract
Photoacoustic tomography (PAT) is an innovative biomedical imaging technology, which has the capacity to obtain high-resolution images of biological tissue. In the extremely limited-view cases, traditional reconstruction methods for photoacoustic tomography frequently result in severe artifacts and distortion. Therefore, multiple diffusion models-enhanced reconstruction strategy for PAT is proposed in this study. Boosted by the multi-scale priors of the sinograms obtained in the full view and the limited-view case of 240°, the alternating iteration method is adopted to generate data for missing views in the sinogram domain. The strategy refines the image information from global to local, which improves the stability of the reconstruction process and promotes high-quality PAT reconstruction. The blood vessel simulation dataset and the in vivo experimental dataset were utilized to assess the performance of the proposed method. When applied to the in vivo experimental dataset in the limited-view case of 60°, the proposed method demonstrates a significant enhancement in peak signal-to-noise ratio and structural similarity by 23.08 % and 7.14 %, respectively, concurrently reducing mean squared error by 108.91 % compared to the traditional method. The results indicate that the proposed approach achieves superior reconstruction quality in extremely limited-view cases, when compared to other methods. This innovative approach offers a promising pathway for extremely limited-view PAT reconstruction, with potential implications for expanding its utility in clinical diagnostics.
Keywords: Photoacoustic tomography, Multiple diffusion models, Limited view, Multi-scale priors, Sinogram domain
1. Introduction
Photoacoustic tomography (PAT) is a non-invasive imaging technique used for imaging biological tissue structure, characterized by high contrast, high resolution, and deep penetration [1], [2], [3]. It has been widely applied in the biomedical field, such as cardiovascular detection [4], [5], functional brain mapping [6], [7], tumor diagnosis [8], [9], [10] and tissue imaging [11], [12]. It maximizes the efficiency of converting absorbed photon energy into heat by selecting lasers of appropriate wavelengths as the excitation source. The absorbed light energy is converted into heat energy, generating pressure waves, namely photoacoustic signals. Photoacoustic signals are received and converted into electrical signals by ultrasonic transducers. After appropriate processing of the collected signals, images are obtained using specific image reconstruction algorithms [13], [14]. However, traditional imaging methods such as universal back-projection (UBP) [15], delay-and-sum (DAS) [16] and filtered back-projection (FBP) [17], often result in poor image quality under limited views. In practical scenarios, due to constraints such as bandwidth and the quantity of ultrasonic transducers, ultrasonic transducers often can only scan within a limited angle in enclosed cavities. It is difficult to obtain complete photoacoustic signals. Thus, the reconstruction of images may be plagued by significant artifacts and distortion. The presence of blind spots, blurring and artifacts can diminish image contrast, obscure image structures and omit crucial information, posing significant impediments to practical diagnosis. Therefore, it is of paramount significance to address the challenges of distortion and artifacts in the limited-view PAT reconstruction.
Many studies have proposed hardware solutions to address the challenges. For example, Lawrence et al. developed a nearly full-view closed spherical system and achieved stereoscopic coverage of imaged objects by rotating and translating a circular transducer array [18]. The degree of match between the transducer response and the spectrum of the photoacoustic signal significantly impacts imaging quality [19]. Ku et al. developed a multi-transducer imaging system with varying center frequencies to enhance imaging accuracy in a broad spectrum range [20]. Huang et al. proposed improved transducer structures by adding a negative lens on the transducer surface or adding a 45° sound reflector array to achieve a larger signal reception angle [21], [22]. In addition, researchers from different teams, such as Yeh et al., improved the shape of the array, proposing spherical, cylindrical and other different shapes of detection arrays [18], [23]. However, due to the high cost of hardware improvements, it is difficult to promote in practical applications. Hardware improvements still have significant shortcomings in limited-angle reconstruction in PAT.
In recent years, an increasing number of studies have chosen to initiate from an algorithmic standpoint, aiming to enhance the quality of reconstructed images during the information processing phase. Tao et al. proposed a two-loop iteration (TLI) method, which involves approximating the physical model of PAT to reconstruct the photoacoustic source from measured photoacoustic signals, addressing the limited-view problem in PAT [24]. With the improvement of neural network training methods, deep learning techniques have been gradually applied to PAT reconstruction. A deep neural network based on a model iterative scheme was proposed, employing the network as a learnable regularization term for the PAT optimization model, achieving enhanced robustness [25]. Guan et al. introduced a pixel-wise deep learning (Pixel-DL) approach, employing pixel-wise interpolation and utilizing the convolutional neural network (CNN) to reconstruct images [26]. Tong et al. proposed a feature projection network (FPnet), establishing a domain transformation network to process collected photoacoustic signals [27]. Susmelj et al. introduced a signal domain adaptation network (SDAN), which extends the domain adaptation network (DAN) by incorporating a sides prediction network to compensate for limited angles and missing signals [28]. In recent years, generative models have become increasingly popular in imaging applications. Ho et al. proposed a denoising diffusion probabilistic model (DDPM), linking diffusion models and Langevin dynamics matching [29]. After that, diffusion models have made important contributions to image restoration [30], [31], [32], [33], [34], [35], [36], [37], [38], such as the inverse reconstruction of PAT [32], [33], [34], magnetic resonance imaging [35], computed tomography [36] and lensless imaging [37], [38]. Fei et al. proposed the generative diffusion prior for unified image restoration, using an unsupervised sampling method to model the posterior distribution to generate high-resolution images [30]. Xia et al. proposed the efficient diffusion model for image restoration (DiffIR) [31], leveraging the powerful mapping capabilities of the diffusion model to estimate a compact image prior representation for guiding image restoration. For PAT reconstruction, in 2023, Song et al. integrated model iteration with diffusion model and employed the gradient descent (GD) method for data consistency to tackle the challenge of PAT reconstruction under extremely sparse-view conditions [32]. Guo et al. (2024), from the same team, extended this method to further assess its effectiveness in limited-view PAT reconstruction [33]. Additionally, in 2024, Dey and his team proposed a measure-conditioning formula to address linear inverse problems and applied it to PAT reconstruction, demonstrating the effectiveness of the formula [34]. These approaches enhance the efficiency and stability of the diffusion model in image restoration by incorporating a structured prior representation.
Inspired by this, the paper proposes a multi-scale reconstruction strategy for PAT in the extremely limited view cases. The method driven by multi-scale priors employs two score-based diffusion models to learn the data distribution of sinograms in the full-view case and the limited-view case of 240°, respectively. Two sets of contrast experiments were conducted, one using the blood vessel simulation dataset to generate missing data on the sinogram in limited-view cases of 105°, 80°, 60° and 45°, respectively. and the other using the in vivo experimental dataset to generate missing data on the sinogram in limited-view cases of 120°, 105°, 80° and 60°, respectively. The experimental results show that this method can still achieve high-quality reconstruction for PAT in extremely limited-view cases.
2. Principles and methods
2.1. Optimization model of photoacoustic tomography
According to Green's function method, the photoacoustic signal that collected by ultrasonic transducers can be obtained [39] as Eq. (1):
| (1) |
The spatiotemporal representation for the photoacoustic signal delineates the forward process inherent in photoacoustic imaging. This equation can be streamlined into the linear process illustrated in Eq. (2) [40]:
| (2) |
where represents the photoacoustic signal detected by the ultrasonic transducer, denotes the linear operator for the forward process, which can be simulated using the k-Wave toolbox [41], and signifies the initial sound pressure.
The conversion of PAT fully-sampled sinograms to limited-view sinograms can be expressed as a linear process in Eq. (3):
| (3) |
where represents the full-view sinogram data, denotes the undersampled sinogram data, represents the subsampling mask for limited views.
When the DAS algorithm is used to directly solve the problem of limited-view PAT reconstruction, the resulting image often suffers from issues such as limited spatial resolution, severe artifacts and inconsistent brightness compared to the original image. Therefore, restoring full-view sinograms from limited-view sinograms can enhance the quality of the reconstructed image. To achieve this, the limited-view PAT reconstruction problem is formulated as an optimization problem, as shown in Eq. (4):
| (4) |
where is the data fidelity term, is the regularization term containing prior information, and is the balance factor between the two terms. The data fidelity term ensures that the limited-view sinograms is consistent with the estimated measured values obtained through the subsampling mask . The regularization term enhances the generalization ability of the model and improves the stability of the reconstruction process [42]. Common regularization methods include Tikhonov regularization [43], TV regularization [44], and l1 regularization [45].
2.2. Principle of alternating iterative reconstruction for PAT enhanced by multi-scale diffusion models
2.2.1. Diffusion model
Mainstream generative models are typically categorized into two types. One category is the implicit generative model, with the generative adversarial network (GAN) serving as a prominent example. GAN employs adversarial training, alternately optimizing the generator and discriminator to produce high-quality reconstructed images. However, if the real data exhibits multiple modes, the generator loss function becomes non-convex, making it susceptible to mode collapse. This phenomenon can lead to training failures [46]. The other class is the explicit generative model that directly fits the data distribution. Examples include variational autoencoders (VAE) [47], normalizing flow models [48], and deep Boltzmann machines [49]. In a generative model, each datum in the dataset is regarded as an independent and identically distributed random sample, whose distribution is treated as a probability distribution . This distribution is typically represented by a score function, where the score function corresponds to the gradient of the log-probability density function. The generative model employs the denoising score matching method to estimate the approximate score network of the data distribution . Subsequently, it utilizes the annealed Langevin Dynamics to randomly sample the image approximating data distribution .
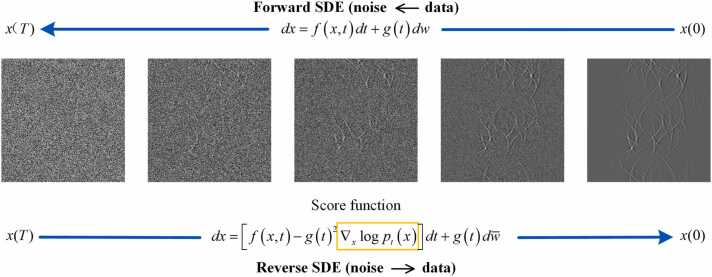
The diffusion model consists of forward diffusion process and reverse diffusion process. Forward diffusion process is a stochastic differential equation (SDE). As shown in Fig. 1, over successive time series , the forward diffusion process can be described by . , represents the original data distribution. , represents the data distribution after noise perturbation elapsed time, referred to as the prior distribution. Typically, during a forward process, by gradually introducing noise perturbations, the original data distribution transitions to an unstructured prior distribution . is independent of the original distribution. The forward diffusion process of the original image from to is illustrated in Eq. (5):
| (5) |
where is the drift coefficient, is the diffusion coefficient, and represents standard Brownian motion. Reverse SDE is a sampling process where the target distribution is derived by gradually sampling the noise-perturbed distribution through Langevin Dynamics [50]. The reverse diffusion process of the noise-perturbed image from to is illustrated in Eq. (6):
| (6) |
where represents the score function of , and is the inverse Brownian motion. The specific structure of SDE is defined by and . However, obtaining is challenging in practice, so the gradient is estimated by training a score-based network that is time-variant. Subsequently, can be sampled from the original distribution .
Fig. 1.
The forward diffusion and reverse diffusion processes.
To generate high-quality images, VE-SDE [51] is adopted in this paper, and the drift coefficient and diffusion coefficient are set as shown in Eq. (7):
| (7) |
where is a monotone increasing function of the noise scale.
In order to maximize the performance of the model, the training objective of the score model is illustrated in Eq. (8):
| (8) |
where is the positive weight function regulating the loss, is the gradient centered on Gaussian perturbation kernel, and is replaced by [52]. When condition is satisfied, it indicates that the score network has acquired ample prior information, and for all instances of , can be replaced by . The reverse diffusion process can then be reformulated as Eq. (9):
| (9) |
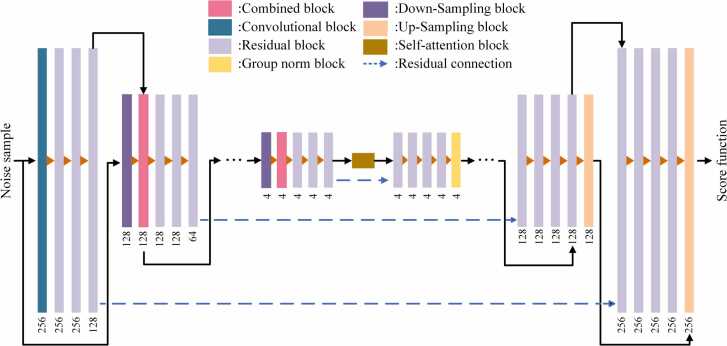
As shown in Fig. 2, the score network is implemented using the deformed U-Net architecture, which comprises two main components: the encoder and the decoder [53]. These components are interconnected by residual connections or self-attention modules. The residual connections are employed to reintroduce detailed features, while the self-attention modules are used to capture long-distance structural information within the image [54]. Notably, the incorporation of the self-attention mechanism helps the score network focus more effectively on important features, thereby improving the overall quality of the samples [55].
Fig. 2.
Structure of the score network. The number below the block represents the image size.
2.2.2. Alternating iterative PAT reconstruction enhanced by multi-scale diffusion models
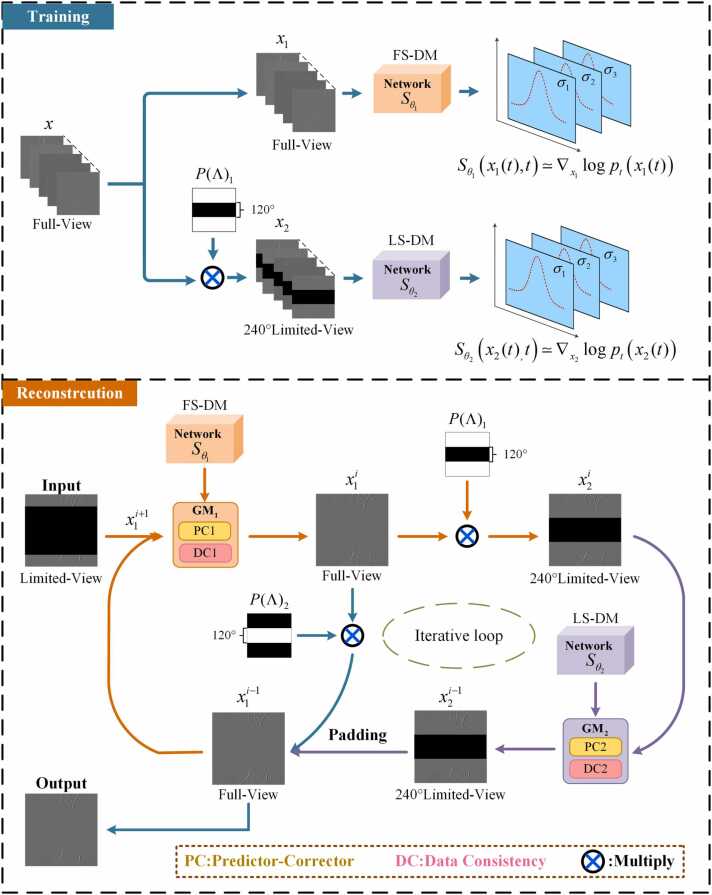
In this study, a novel multi-scale diffusion model strategy is proposed. Specifically, two different diffusion models are employed. As shown in Fig. 3, the full-view single diffusion model (FS-DM) can effectively learn global information, and the limited-view single diffusion model (LS-DM) uses masks to focus on learning specific local information. By integrating the strengths of both diffusion models, detailed information can be effectively refined while constructing the overall structure, enhancing the reconstruction efficacy of a single diffusion model and bolstering the stability of PAT reconstruction.
Fig. 3.
The multi-scale diffusion model strategy achieves the synthesis of global and local information. (a) FS-DM reconstructs images to capture global features, while (b) LS-DM focuses on reconstructing images for specific regions.
Prior learning: As shown in the training section of Fig. 4, the FS-DM and LS-DM models utilize fully-sampled sinogram data and undersampled sinogram data in the limited-view case of 240° as inputs, respectively. To acquire data distribution information at specific locations, masks are introduced to separate training data. The specific mask matrix operator is defined in Eq. (10):
| (10) |
where represents the fully-sampled sinogram, as illustrated in the training section of Fig. 4. is a binary matrix of size 512 × 512. The black rectangular region in the middle signifies that the data distribution of 120° within this region is disregarded. The information of 240° in the white region in the figure is extracted.
Fig. 4.
The pipeline for the training and iterative reconstruction processes. During the training process, is employed to extract the limited-sampled information of 240° indicated by the white part, while disregarding the information of the black. The reconstruction process comprises two reverse SDEs, involving the predictor-corrector (PC) and data consistency (DC). Similarly, is utilized to extract the limited-sampled information of 240° indicated by the white part, while ignoring the information of 120° indicated by the black part. Conversely, is used to extract the limited-sampled information of 120° indicated by the white part, disregarding the information of 240° indicated by the black part.
During training, the data distribution of the input sample is obtained through a gradual transformation from the structured raw data distribution to the unstructured prior distribution by slowly introducing noise perturbations. Through simulating the forward diffusion process, the target data distributions of FS-DM and LS-DM are estimated, respectively, leading to the achievement of the score networks for FS-DM and LS-DM.
Alternating iterative reconstruction: As shown in the reconstruction section of Fig. 4, two numerical inverse SDE solvers and data consistency operations are integrated into the reconstruction process to update the reconstructed image. The comprehensive framework of iterative reconstruction is presented in Eq. (11):
| (11) |
where GM1 represents the reconstruction process of the global information of the image, and GM2 represents the reconstruction process for the specific area of the image. and represent the output results of the network using different prior information corresponding to FS-DM and LS-DM, respectively. The variable denotes the number of reverse iterations. In the reconstruction segment of Fig. 4, both and represent 512 × 512 binary matrices. The black rectangular area in the indicates that the data distribution of 120° in this area is ignored. The information of 240° in the white part of the diagram is extracted. The expression for is analogous. Then, the extracted information is used to fill the sample reconstructed by the undersampled model.
Predictor-corrector (PC): During the reversal of SDE, the PC sampler is introduced. By removing the predicted noise, the predictor is utilized to generate the new sinogram data. Subsequently, the corrector calibrates the marginal distribution of the corresponding reconstructed sinograms using the annealed Langevin Dynamics. Both operations contribute to generating samples that adhere to the target distribution. The predictor can be expressed as Eq. (12):
| (12) |
where is the noise level, is the number of discretization steps (i.e., the number of iterations) of the reverse SDE, is the Gaussian disturbance of zero mean. Based on the discrepancy between output of the predictor and the target distribution, the corrector adjusts the output of predictor by using the Langevin Dynamics Markov chain Monte Carlo method [51], [56] to correct the gradient ascent direction. The correction process is shown in Eq. (13):
| (13) |
where is the noise iteration step. For , repeating the above equation, Langevin Dynamics guarantees that when , samples from under specified conditions.
Data consistency (DC): The limited-view reconstruction for PAT can be converted into solving an optimization problem. The optimization problem can be described as Eq. (14):
| (14) |
where represents the sinogram to be reconstructed, and represents the sinogram generated by score-based networks. Under the condition of first-order optimality, the solution of is realized, as shown in Eq. (15):
| (15) |
where represents the entries at the position in the data generated by the network, and represents the corresponding sampled positions when the sinograms in different limited-view cases are used as the inputs for reconstruction.
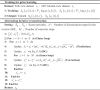
In summary, a limited-view PAT reconstruction algorithm based on multi-scale diffusion models is proposed, as shown in Algorithm 1. In the training stage, two diffusion models are trained by inputting different data samples to obtain sufficient prior information. The multiple prior information can impose stronger constraints on the solutions of optimization problems to mitigate ill-posedness during the iterative process, as regularization terms. In the reconstruction stage, through the alternating iteration operation, the multi-scale priors from two types of data distribution obtained during training are utilized. This achieves the transmission of information from the global to the local, thereby reconstructing more accurate details. At the same time, to ensure that the reconstructed sinogram data is generated in the correct direction, the fidelity method, as shown in Eq. (15), is adopted in each iteration after PC sampling. The data at sampled positions in the input sinogram is used to replace the data at corresponding positions of the sinogram matrix in the iteration process. In this way, high-quality reconstruction for PAT in extremely limited-view cases can be achieved by performing the alternating iteration operations.
Algorithm 1
Training for prior learning
 |
2.3. Dataset acquisition and network parameter setting
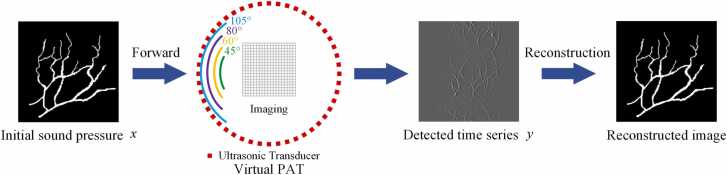
Dataset: This method utilized the blood vessel simulation dataset and the in vivo experimental dataset to assess the reconstruction effectiveness. (1) The blood vessel simulation dataset: To simulate the sinogram formed by forward propagation in photoacoustic imaging, this study constructed a virtual PAT platform using the k-Wave toolbox. The platform employs water as the medium, with a density of . As shown in Fig. 5, the simulation area of the platform is set at 50.1 mm × 50.1 mm and divided into a grid of 556 × 556 pixels, thereby discretizing the medium. Around the platform, the imaging object is positioned at the center with a radius of 18.5 mm, and the ultrasonic transducers used to receive ultrasonic signals are uniformly placed. Sinograms in different limited-view cases are obtained by varying the detection angles of ultrasonic transducers. The sinograms collected under the detection angle of 360° are used as the ground truths. The center frequency of the ultrasonic transducers is 2.25 MHz. The bandwidth is 100 %, and the sound speed is set to 1500 m/s. Publicly available retinal vessel datasets RAVIR and DRIVE [57], which are utilized in the experiment, are augmented through operations such as rotation and cropping. The training dataset comprises 1500 images. (2) The in vivo experimental dataset: This dataset is sourced from [58], which comprises reconstructed images from the full view of the mouse abdomen. These images are imported into the virtual PAT to obtain the sinograms. The simulation area of the platform is set at 50 mm × 50 mm and divided into a grid of 440 × 440 pixels. The ultrasonic transducers are positioned at a distance of 21.6 mm from the imaging object. Other parameters of the platform remain consistent with those of the vessel simulation experiment.
Fig. 5.
Process of simulated blood vessels reconstruction using virtual PAT.
Parameter setting: The size of input sinogram is 512×512. Adaptive moment estimation (Adam) is utilized as the optimizer to minimize the training loss (optimize the network), and the learning rate is set to 2×10−4. In the training phase, the noise range is from to , and the batch size is set to 1. The training process spans 200,000 iterations from the start of the training to its completion, while the reconstruction of a sinogram requires 999 iterations.
The experiment is conducted using the PyTorch framework and performed on an Ubuntu system equipped with two NVIDIA GeForce RTX 3060Ti GPUs.
2.4. Baseline methods
The comparison experiments include DAS, U-Net, GAN and FS-DM methods. Obtained from [59], the employed U-Net, which is an end-to-end network, uses an encoder and decoder to sample the input image and generate the target output from the extracted characteristics [60]. Similar to the traditional U-Net architecture, the encoder contains convolutional blocks and max pooling blocks, and the decoder contains upsampling blocks, convolutional blocks and concatenate blocks. As a variant of the GAN, CycleGAN is an unsupervised generative model that can map a source domain to a target domain without requiring a one-to-one correspondence between training datasets [61]. The FS-DM method signifies the iterative reconstruction method employing a diffusion model trained with fully-sampled sinograms.
3. Results
3.1. Reconstruction results of the blood vessel simulation dataset
As shown in Fig. 5, the augmented dataset is input into the virtual PAT platform for imaging. Corresponding photoacoustic signals are obtained by adjusting the detection angle of ultrasonic transducers, resulting in sinograms in different limited-view cases. Then, the limited-view sinograms are restored to full-view sinograms using the reconstruction algorithm. Finally, they are ultimately transitioned into the image domain.
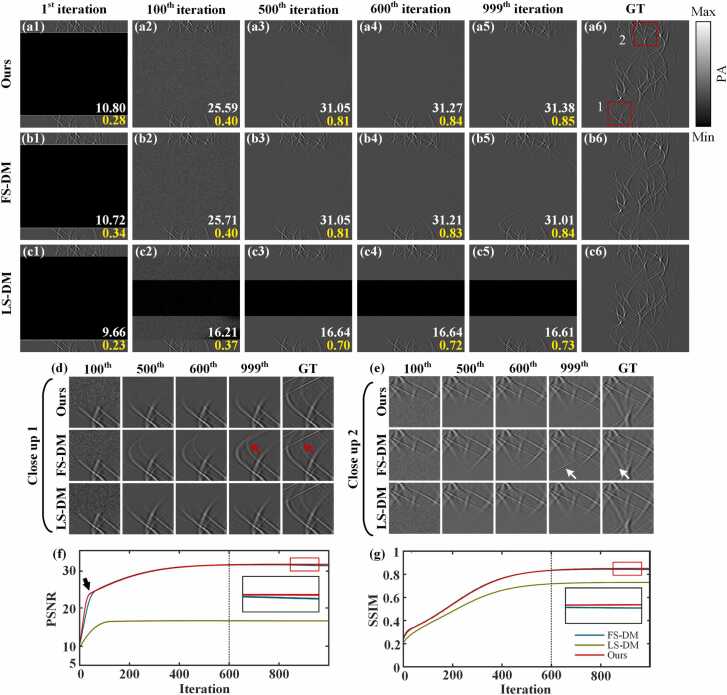
Fig. 6(a1)-(c5) show the iterative process of the proposed method, the FS-DM method and the LS-DM method in the limited-view case of 80°, respectively. The LS-DM method denotes the iterative reconstruction using a diffusion model trained with the sinograms in the limited-view case of 240°. The limited-view PAT reconstruction involves iteratively restoring undersampled photoacoustic data to fully-sampled photoacoustic data. In this process, the sinogram obtained in a limit-view case is taken as an input, and the unsampled signal distribution is ignored. With the increase in the number of iterations, the noise intensity gradually weakens, and the sinogram information close to the ground truth is gradually generated. Compared with the 10th iteration, the quality of the reconstructed sinogram improves significantly at the 100th iteration. At the 999th iteration, the peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) of the reconstructed sinogram based on the proposed method reach 31.38 dB and 0.85, respectively. Compared to FS-DM reconstruction, they are 0.37 dB and 0.01 higher, respectively. Additionally, they surpass those of the LS-DM reconstruction by 14.7 dB and 0.12.
Fig. 6.
Reconstruction of simulated blood vessels in the limited-view case of 80° using the proposed method. (a1)-(a5) depict the reconstruction results over iterations using the method proposed in this study, respectively. (b1)-(b5) represent the reconstruction results over iterations using FS-DM, respectively. (c1)-(c5) show the reconstruction results over iterations using LS-DM, respectively. (a6)-(c6) are the same ground truths. (d)-(e) represent the close-up images indicated by red rectangles 1 and 2 over iterations, respectively. (f)-(g) illustrate the changes of PSNR and SSIM over iterations, respectively. Ours, the approach utilizing multi-scale diffusion models; FS-DM, a diffusion model trained using the fully-sampled sinogram dataset; LS-DM, a diffusion model trained using the sinogram dataset in the limited-view case of 240°; GT, ground truth.
Fig. 6(d) and Fig. 6(e) represent close-up images indicated by red rectangles 1 and 2, respectively. It is evident that among the three methods, the LS-DM method reconstructs the least information. Additionally, at the position indicated by the red and white arrows, although the FS-DM method can reconstruct more information, it is evidently inconsistent with the information distribution of the corresponding position of the ground truth, which affects the quality of the reconstructed sinogram. However, the results of the proposed method not only ensure the generation of information but also conform to the data distribution of the corresponding position of the ground truth. Therefore, the method proposed in this study demonstrates excellent reconstruction effectiveness. Fig. 6(f) and Fig. 6(g) illustrate the changes in PSNR and SSIM over iterations. During the iterative process, both the PSNR and SSIM of the three methods exhibit a steady increase and eventually stabilize. In particular, the line resulting from the proposed method reaches a higher position precisely at the inflection point denoted by the black arrow. This observation suggests that the metric associated with the proposed method achieves stability more rapidly. Additionally, at the 500th iteration, the proposed method achieves PSNR and SSIM values of 31.05 dB and 0.81, respectively. Finally, during the iterative process, as indicated by the dashed line, the metrics of results obtained by the proposed method gradually tend to 31.38 dB and 0.85 from around the 600th iteration, respectively. Moreover, it can be observed from the lines enlarged in Fig. 6(f) and Fig. 6(g) that the PSNR and SSIM indices of the proposed method in this study are higher than those of the LS-DM and FS-DM methods. This indicates the effectiveness of the proposed method.
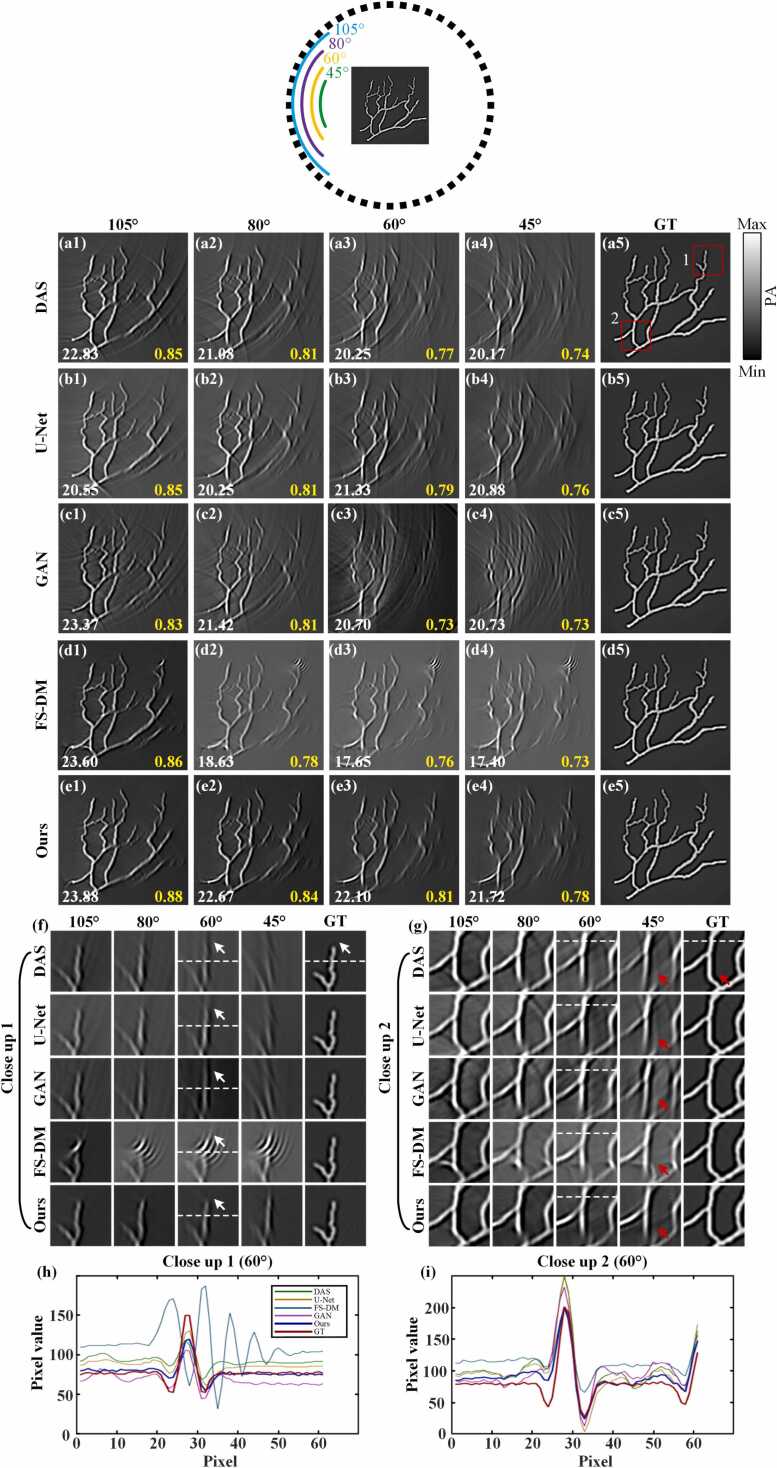
Fig. 7 illustrates the reconstruction results achieved by different methods on the blood vessel simulation dataset in limited-view cases of 105°, 80°, 60° and 45°, respectively. The white numbers in the figures represent PSNR, while the yellow numbers represent SSIM. Fig. 7(a5)-(e5) are the same ground truths. Fig. 7(a1)-(a4) exhibit the results obtained through the DAS method in limited-view cases of 105°, 80°, 60° and 45°, respectively. Fig. 7(b1)-(b4) show the reconstruction results achieved by the U-Net method in limited-view cases of 105°, 80°, 60° and 45°, respectively. It is worth noting that the U-Net method evidently exhibits significant limitations in the restoration of sinogram information. It is difficult to generate information corresponding to missing angles. Fig. 7(c1)-(c4) show the reconstruction results of the sinogram domain utilizing the GAN method in limited-view cases of 105°, 80°, 60° and 45°, respectively. The reconstruction results of the GAN method essentially do not generate new data, and the reconstructed image shown in Fig. 7(c3) exhibits notable artifacts. Fig. 7(d1)-(d4) show the reconstruction results of the sinogram domain utilizing the FS-DM method in limited-view cases of 105°, 80°, 60° and 45°, respectively. The disparity in recovery effectiveness becomes apparent when comparing it with the first two methods. As indicated by the white arrows, although the results obtained by applying this method produce new sinogram data. However, it is noticeable to generate several artifacts in the results as the angles decrease. These artifacts deviate from the sinogram information distribution of the ground truth, potentially compromising the quality of the reconstruction. Fig. 7(e1)-(e4) show the reconstruction results of the sinogram domain utilizing the proposed method in limited-view cases of 105°, 80°, 60° and 45°, respectively. It is noteworthy that the brightness of the reconstruction results from this method aligns closely with the ground truth. Notably, there is no conspicuous generation of artifacts, indicating a high-quality reconstruction. Specifically, in the limited-view case of 105°, the proposed method exhibits significant enhancements in PSNR and SSIM by 32.50 % and 1.15 %, respectively, compared to the U-Net method. Additionally, the proposed method outperforms the GAN method, achieving the increases in PSNR and SSIM of 35.37 % and 3.53 %, respectively. Furthermore, the PSNR attains 30.66 dB in the limited-view case of 45°, achieving improvements of 15.35 dB over the U-Net method and 0.36 dB over the FS-DM method. Similarly, the SSIM attains 0.85, with enhancements of 0.06 over the U-Net method and 0.01 over the FS-DM method, respectively. Overall, compared to other methods, the method proposed in this study demonstrates clear advantages, particularly in extremely limited-view cases (e.g., 45°-view). Additionally, the image quality surpasses that of other methods in each limited-view case, indicating the effectiveness of the proposed method in limited-view reconstruction for PAT.
Fig. 7.
The reconstruction results of the blood vessel simulation dataset on the sinogram domain under different limited imaging conditions. (a1)-(a4) depict the reconstructed sinograms using the DAS method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (b1)-(b4) show the reconstructed sinograms using the U-Net method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (c1)-(c4) show the reconstructed sinograms using the GAN method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (d1)-(d4) show the reconstructed sinograms using the FS-DM method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (e1)-(e4) represent the reconstructed sinograms using the method proposed in this study in limited-view cases of 105°, 80°, 60° and 45°, respectively. (a5)-(e5) are the same ground truths. Ours, the approach utilizing multi-scale diffusion models; FS-DM, a diffusion model trained using the fully-sampled sinogram dataset; GT, ground truth.
Fig. 8 depicts the reconstruction results of the blood vessel simulation dataset using different methods on the image domain in limited-view cases of 105°, 80°, 60° and 45°, respectively. Fig. 8(a5)-(e5) present the ground truths, which are the simulated blood vessel images reconstructed by the DAS method in the full-view case. The position indicated by the dotted circle approximates the location of the ultrasonic transducers. Less information is gleaned from positions farther away from the transducers. Therefore, as the detection angle decreases, the reconstructed area away from the transducers gradually becomes blurred. Fig. 8(a1)-(a4) depict the reconstruction results of the DAS method in limited-view cases of 105°, 80°, 60° and 45°. It is evident that numerous artifacts are present in the imaging in different limited-view cases. And the artifacts become increasingly pronounced as the angles decrease. Fig. 8(b1)-(b4) illustrate the reconstruction results of the U-Net method in limited-view cases of 105°, 80°, 60° and 45°, respectively. It is observable that, in each limited-view case, the results of the U-Net method still exhibit numerous artifacts. However, the structure information of reconstructed images is marginally improved compared to that of the DAS method. Fig. 8(c1)-(c4) exhibit the reconstruction results of the GAN method in limited-view cases of 105°, 80°, 60° and 45°, respectively. The reconstruction results of the GAN method exhibit a significant number of evident artifacts, and in extremely limited-view cases (e.g., 45°-view and 60°-view), new image information almost can not be reconstructed. Fig. 8(d1)-(d4) exhibit the reconstruction results of the FS-DM method in limited-view cases of 105°, 80°, 60° and 45°, respectively. The reconstruction results of this method appear relatively favorable, with fewer artifacts observed in the overall image. However, noticeable artifacts persist in certain areas. And the quality of reconstruction significantly diminishes when the detection angle is less than or equal to 80°. Fig. 8(e1)-(e4) depict the reconstruction results of the proposed method in limited-view cases of 105°, 80°, 60° and 45°, respectively. Notably, the brightness of the reconstructed images using this method is largely consistent with the ground truth. Moreover, the presence of artifacts in the reconstructed images is markedly reduced compared to other methods in each limited-view case.
Fig. 8.
The reconstruction results of the blood vessel simulation dataset in different limited-view cases. (a1)-(a4) exhibit the reconstruction results of the DAS method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (b1)-(b4) represent the reconstruction results of the U-Net method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (c1)-(c4) show the reconstruction results of the GAN method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (d1)-(d4) show the reconstruction results of the FS-DM method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (e1)-(e4) depict the reconstruction results of the method proposed in this study in limited-view cases of 105°, 80°, 60° and 45°, respectively. (a5)-(e5) are the ground truths. (f) and (g) represent close-up images indicated by the red rectangles 1 and 2, respectively. (h) and (i) exhibit the intensity distribution along the dashed lines in (f) and (g), respectively. Ours, the approach utilizing multi-scale diffusion models; FS-DM, a diffusion model trained using the fully-sampled sinogram dataset; GT, ground truth.
As shown in Fig. 8, from a quantitative standpoint, in the limited-view case of 60°, the reconstructed PSNR and SSIM using the proposed method reach 22.10 dB and 0.81, respectively. This represents a 9.14 % increase in PSNR and a 5.19 % increase in SSIM compared to the DAS method, while a 6.76 % increase in PSNR and a 10.96 % increase in SSIM compared to the GAN method. In the extremely limited-view case of 45°, the reconstructed PSNR and SSIM using the method proposed in this paper reach 21.72 dB and 0.78, respectively. This shows a 4.02 % increase in PSNR and a 2.62 % increase in SSIM compared to the U-Net method, and a substantial improvement of 24.83 % in PSNR and 6.85 % in SSIM compared to the FS-DM method. Fig. 8(f) and Fig. 8(g) show close-up images indicated by the red rectangles 1 and 2, respectively. It can be seen that in the limited-view case of 60° in Fig. 8(f), the close-up images of DAS, U-Net, GAN and FS-DM methods have obvious artifacts at the position indicated by the white arrows. These artifacts will affect the quality of the reconstructed image. In Fig. 8(g), in the limited-view case of 45°, the close-up images of DAS, U-Net, GAN and FS-DM methods also have obvious artifacts at the locations indicated by the red arrows. However, the reconstruction results of this method based on this study show no obvious artifacts in the positions indicated by these arrows, and the imaging quality is excellent. Fig. 8(h) and Fig. 8(i) depict the signal distribution along the dashed line. It can be found that the signal distribution of the proposed method is the closest to that of the ground truth. In general, compared with other methods, the method proposed in this study shows obvious advantages in extremely limited-view cases (e.g., 45°-view). The image quality of the proposed method is higher than other methods in different limited-view cases, demonstrating superior performance.
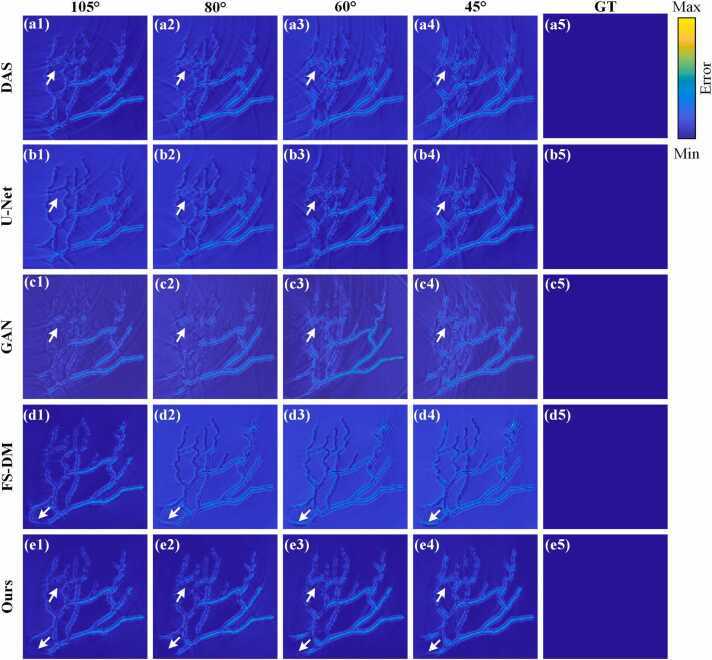
Fig. 9 shows the error maps obtained from the reconstruction results of the blood vessel simulation dataset. The error maps depicted in Fig. 9(a1)-(a4), Fig. 9(b1)-(b4) and Fig. 9(c1)-(c4) represent the performances of the DAS, U-Net and GAN methods, respectively, in limited-view cases of 105°, 80°, 60° and 45°. The artifacts are evident in regions marked by white arrows, resulting in increased deviation from the ground truth. Furthermore, Fig. 9(d1)-(d4) illustrate the error maps corresponding to the reconstruction results of the FS-DM method in limited-view cases of 105°, 80°, 60° and 45°, respectively. Prominent local artifacts are observed at the arrow-indicated positions, along with substantial discrepancies in brightness of the background compared to the ground truth. Fig. 9(e1)-(e4) present the error maps of the proposed method in limited-view cases of 105°, 80°, 60° and 45°, respectively. Fig. 9(a5)-(e5) are the same error maps corresponding to the same ground truths. There are no discernible artifacts at the positions indicated by the arrows, and the brightness corresponds closely to that of the ground truth. It is evident that the error between the method proposed in this study and the ground truth is minimal. Table 1 displays the mean values of PSNR, SSIM and mean square error (MSE) for the reconstruction results. In the limited-view case of 60°, the proposed method outperforms the FS-DM method with improvements of 7.47 % and 2.5 % in PSNR and SSIM, respectively, while reducing MSE by 63.95 %. Additionally, the proposed method demonstrates enhancements of 3.76 % and 9.33 % in PSNR and SSIM, alongside a decrease of 18.42 % in MSE, compared to the GAN method. Similarly, in the limited-view case of 45°, the mean PSNR, SSIM and MSE of the reconstruction results using the proposed method are 21.59 dB, 0.79 and 0.0067, respectively. The proposed method demonstrates enhancements of 5.01 % and 2.60 % in PSNR and SSIM, alongside a decrease of 17.28 % in MSE, compared to the U-Net method. Moreover, compared to the DAS method, the proposed method achieves increases of 8.82 % and 5.33 % in PSNR and SSIM, respectively, while decreasing MSE by 30.21 %. These findings further underscore the superiority and effectiveness of the proposed method for PAT reconstruction in limited-view cases.
Fig. 9.
The error maps derived from the reconstruction results of the blood vessel simulation dataset. (a1)-(a4) depict the error maps corresponding to the reconstruction results of the DAS method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (b1)-(b4) show the error maps corresponding to the reconstruction results of the U-Net method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (c1)-(c4) show the error maps corresponding to the reconstruction results of the GAN method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (d1)-(d4) represent the error maps corresponding to the reconstruction results of the FS-DM method in limited-view cases of 105°, 80°, 60° and 45°, respectively. (e1)-(e4) show the error maps corresponding to the reconstruction results of the proposed method in this study in limited-view cases of 105°, 80°, 60° and 45°, respectively. (a5)-(e5) represent the error maps corresponding to the same ground truths. Ours, the approach utilizing multi-scale diffusion models; FS-DM, a diffusion model trained using the fully-sampled sinogram dataset; GT, ground truth.
Table 1.
Average values of quantitative metrics PSNR/SSIM/MSE of the blood vessel simulated dataset.
| Limited -view | Method | PSNR(dB) | SSIM | MSE |
|---|---|---|---|---|
| DAS | 19.84 | 0.75 | 0.0096 | |
| U-Net | 20.56 | 0.77 | 0.0081 | |
| 45° | GAN | 20.65 | 0.73 | 0.0087 |
| FS-DM | 20.47 | 0.78 | 0.0181 | |
| Ours | 21.59 | 0.79 | 0.0067 | |
| DAS | 20.56 | 0.78 | 0.0094 | |
| U-Net | 20.69 | 0.79 | 0.0074 | |
| 60° | GAN | 21.23 | 0.75 | 0.0076 |
| FS-DM | 20.48 | 0.80 | 0.0172 | |
| Ours | 22.01 | 0.82 | 0.0062 | |
| DAS | 21.15 | 0.81 | 0.0078 | |
| U-Net | 21.28 | 0.82 | 0.0094 | |
| 80° | GAN | 21.93 | 0.79 | 0.0064 |
| FS-DM | 21.22 | 0.83 | 0.0137 | |
| Ours | 22.48 | 0.85 | 0.0054 | |
| DAS | 22.55 | 0.85 | 0.0052 | |
| U-Net | 21.65 | 0.86 | 0.0088 | |
| 105° | GAN | 22.92 | 0.82 | 0.0052 |
| FS-DM | 23.45 | 0.87 | 0.0044 | |
| Ours | 23.67 | 0.88 | 0.0040 |
3.2. Reconstruction results of the in vivo experimental dataset
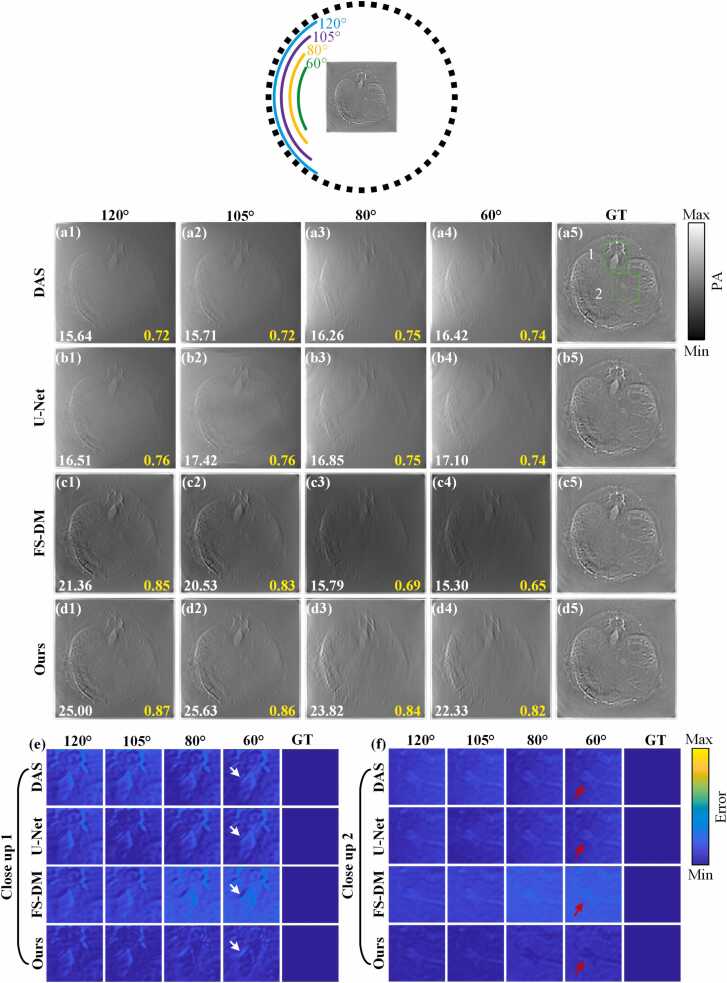
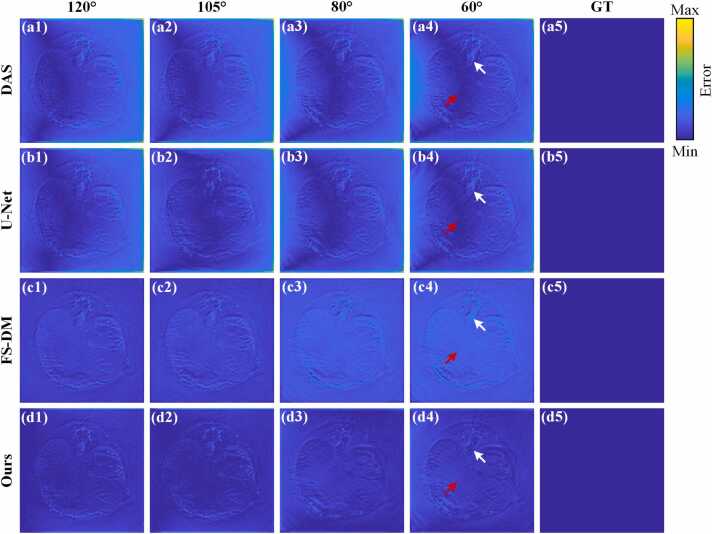
Fig. 10 presents the reconstruction results of the in vivo experimental dataset using different methods in limited-view cases of 120°, 105°, 80° and 60°, respectively. The dotted circle indicates the approximate position of the ultrasonic transducers. Fig. 10(a5)-(d5) represent the same ground truths. Fig. 10(a1)-(a4) depict the reconstruction results of the DAS method and the U-Net method in limited-view cases of 120°, 105°, 80° and 60°, respectively. For DAS and U-Net methods, it is evident that distortion is present in the reconstruction results, leading to poor reconstruction quality. Uneven brightness and significant artifacts are observed in the results, particularly in limited-view cases of 80° and 60°, which adversely affect the reconstruction quality. Fig. 10(c1)-(c4) illustrate the reconstruction results of the FS-DM method in limited-view cases of 120°, 105°, 80° and 60°, respectively. While the FS-DM method demonstrates commendable reconstruction performance with fewer artifacts, there remains a significant disparity in imaging brightness compared to the ground truth. Fig. 10(d1)-(d4) present the reconstruction results of the proposed method in limited-view cases of 120°, 105°, 80° and 60°, respectively. It is evident that, in comparison with other methods, the quality of the reconstructed images using this method is significantly superior in each limited-view case, even at 60°. In terms of quantitative comparison, in the limited-view case of 80°, the reconstruction results of the proposed method achieve PSNR and SSIM values of 23.82 dB and 0.84, respectively, which are 50.85 % and 21.74 % higher than those of the FS-DM method. Additionally, in the limited-view case of 60°, the reconstruction results of the proposed method achieve a PSNR of 22.33 dB and a SSIM of 0.82. These values represent a substantial improvement over the DAS method, with a 36.00 % increase in PSNR and a 10.81 % increase in SSIM. Likewise, compared to the U-Net method, there is a significant advancement, with a 30.58 % increase in PSNR and a 10.81 % increase in SSIM. Fig. 10(e) and Fig. 10(f) show error maps of close-up images indicated by the green rectangles. It can be observed that in the limited-view case of 60°, at positions indicated by the red and white arrows, the reconstruction results of the proposed method are closest to the ground truth and exhibit the fewest errors compared to other methods. This indicates that the proposed method shows outstanding performance.
Fig. 10.
The reconstruction results of in vivo experimental dataset under different limited imaging conditions. (a1)-(a4) are the reconstruction results of the DAS method in limited-view cases of 120°, 105°, 80° and 60°, respectively. (b1)-(b4) represent the reconstruction results of the U-Net method in limited-view cases of 120°, 105°, 80° and 60°, respectively. (c1)-(c4) are the reconstruction results of the FS-DM method in limited-view cases of 120°, 105°, 80° and 60°, respectively. (d1)-(d4) show the reconstruction results of the proposed method in this study in limited-view cases of 120°, 105°, 80° and 60°, respectively. (a5)-(d5) represent the ground truths. (e) and (f) show error maps of close-up images indicated by the green rectangles 1 and 2, respectively. Ours, the approach utilizing multi-scale diffusion models; FS-DM, a diffusion model trained using the fully-sampled sinogram dataset; GT, ground truth.
Fig. 11 illustrates the error maps of the in vivo experimental dataset when different methods are applied in limited-view cases of 120°, 105°, 80° and 60°, respectively. Fig. 11(a1)-(a4) and Fig. 11(b1)-(b4) show the error maps of the results reconstructed by DAS and U-Net methods in limited-view cases of 120°, 105°, 80° and 60°, respectively. The positions indicated by the red arrows indicate that the brightness distribution of the error maps is notably uneven, with obvious artifacts in the image background, leading to increased discrepancies with the ground truth. Fig. 11(c1)-(c4) show the error maps corresponding to the reconstruction results of the FS-DM method in limited-view cases of 120°, 105°, 80° and 60°, respectively. The positions indicated by the white arrows reveal imperfections in recovering information at a detailed level, with inconsistent brightness of the background compared to the ground truth. Fig. 11(d1)-(d4) depict the error maps corresponding to the reconstruction results of the proposed method in limited-view cases of 120°, 105°, 80° and 60°, respectively. In the limited-view case of 60°, the reconstruction results of this method exhibit a uniform brightness distribution at the position indicated by the red arrows, which closely matches the ground truth. Additionally, at the position indicated by the white arrows, the local reconstruction result of this method is most consistent with the ground truth. The difference between the ground truth and the reconstruction result is minimal, indicating excellent reconstruction performance.
Fig. 11.
Error maps of the reconstruction results of in vivo experimental dataset. (a1)-(a4) represent the error maps corresponding to the reconstruction results of the DAS method in limited-view cases of 120°, 105°, 80° and 60°, respectively. (b1)-(b4) are the error maps corresponding to the reconstruction results of the U-Net method in limited-view cases of 120°, 105°, 80° and 60°, respectively. (c1)-(c4) show the error maps corresponding to the reconstruction results of the FS-DM method in limited-view cases of 120°, 105°, 80° and 60°, respectively. (d1)-(d4) are the error maps corresponding to the reconstruction results of the proposed method in limited-view cases of 120°, 105°, 80° and 60°, respectively. (a5)-(d5) represent the error maps corresponding to the ground truth. Ours, the approach utilizing multi-scale diffusion models; FS-DM, a diffusion model trained using the fully-sampled sinogram dataset; GT, ground truth.
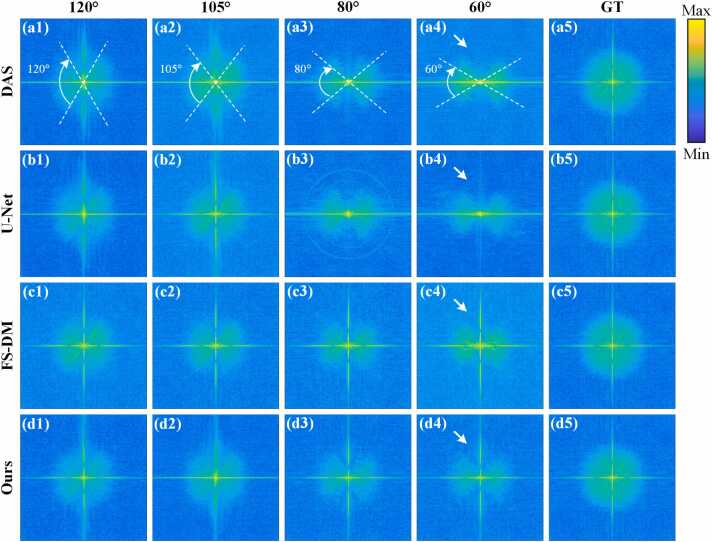
Fig. 12 illustrates the Fourier spectra of the in vivo experimental dataset through the Fourier transform when different methods are applied in limited-view cases of 120°, 105°, 80° and 60°, respectively. White dashed lines are used to indicate the distribution of information sampled in the Fourier spectra in different limited-view cases. Fig. 12(a5)-(d5) represent the ground truth in the frequency domain. Fig. 12(a1)-(a4) show the intensity maps on the frequency domain corresponding to the reconstruction results of the DAS method in limited-view cases of 120°, 105°, 80° and 60°, respectively. As indicated by the white arrows, the information deficiency of the results of the DAS method from the unsampled angle is obvious. Fig. 12(b1)-(b4) depict the intensity maps on the frequency domain corresponding to the reconstruction results of the U-Net method in limited-view cases of 120°, 105°, 80° and 60°, respectively. It can be observed that in the limited-view case of 60°, the reconstructed images contain little information outside the sampled view. Fig. 12(c1)-(c4) represent the intensity maps on the frequency domain corresponding to the reconstruction results of the FS-DM method in limited-view cases of 120°, 105°, 80° and 60°, respectively. As indicated by the white arrows, the information outside of the sampled view can be efficiently recovered using this method. However, the overall intensity distribution of FS-DM at high-frequency information is far from the ground truth. Fig. 12(d1)-(d4) depict the intensity maps corresponding to the reconstruction results of the proposed method in limited-view cases of 120°, 105°, 80° and 60°, respectively. As indicated by the white arrows, while recovering low-frequency information, the distribution of high-frequency information is also the closest to the ground truth. It can be observed that compared with other methods, the proposed method achieves the closest approximation to the ground truth in terms of overall and local information recovery, demonstrating excellent reconstruction performance. The Table 2 presents the mean values of PSNR, SSIM and MSE of the reconstruction results. Quantitative comparison further validates the superiority of the proposed method. In the limited-view case of 80°, the average PSNR, average SSIM and MSE of this method are 27.00 dB, 0.84 and 0.0021, respectively, which are 22.87 % and 14.49 % higher and 63.04 % lower than those of the FS-DM method. In the limited-view case of 80°, the average PSNR and SSIM of the reconstruction results of the proposed method reach 20.64 dB and 0.75, respectively, with the MSE being 0.0101. Compared with the U-Net method, the PSNR and SSIM are increased by 18.96 % and 7.14 %, respectively, and the MSE is decreased by 45.11 %. The experimental results demonstrate that the proposed method excel in uniformizing brightness and eliminating artifacts.
Fig. 12.
Frequency domain intensity maps of the reconstruction results of in vivo experimental dataset through Fourier transform. (a1)-(a4) are the frequency domain intensity maps corresponding to the reconstruction results of the DAS method in limited-view cases of 120°, 105°, 80° and 60°, respectively. (b1)-(b4) represent the frequency domain intensity maps corresponding to the reconstruction results of the U-Net method in limited-view cases of 120°, 105°, 80° and 60°, respectively. (c1)-(c4) show the frequency domain intensity maps corresponding to the reconstruction results of the FS-DM method in limited-view cases of 120°, 105°, 80° and 60°, respectively. (d1)-(d4) are the frequency domain intensity maps corresponding to the reconstruction results of the proposed method in this study in limited-view cases of 120°, 105°, 80° and 60°, respectively. (a5)-(d5) represent the frequency domain intensity maps corresponding to the ground truth. Ours, the approach utilizing multi-scale diffusion models; FS-DM, a diffusion model trained using the fully-sampled sinogram dataset; GT, ground truth.
Table 2.
Average values of quantitative metrics PSNR/SSIM/MSE of the in vivo experimental dataset.
| Limited-view | DAS | U-Net | FS-DM | Ours |
|---|---|---|---|---|
| 60° | 16.77/0.70/0.0211 | 17.35/0.70/0.0184 | 16.39/0.63/0.0235 | 20.64/0.75/0.0101 |
| 80° | 16.34/0.71/0.0232 | 17.23/0.72/0.0189 | 17.75/0.69/0.0184 | 21.81/0.79/0.0068 |
| 105° | 16.32/0.69/0.0234 | 17.72/0.72/0.0169 | 17.78/0.72/0.0174 | 26.61/0.82/0.0022 |
| 120° | 16.24/0.69/0.0238 | 17.07/0.73/0.0197 | 18.17/0.75/0.0161 | 27.00/0.84/0.0021 |
4. Conclusion and discussion
Currently, significant advancements have been made in PAT reconstruction. However, the challenge persists in reconstructing photoacoustic images in extremely limited-view cases. To address this issue, this study introduces multiple diffusion models-enhanced extremely limited-view reconstruction strategy for PAT boosted by multi-scale priors. The method trains two score-based diffusion models using both fully-sampled sinograms and sinograms in limited-view case of 240°, facilitating the capture of prior information. Then, the alternating iteration strategy is used to generate new sinogram data, aided by PC sampling and the fidelity term. Finally, while the overall distribution of the generated image remains aligned with the ground truth, local details are further refined. In this study, the blood vessel simulation dataset and the in vivo experimental dataset were utilized to assess the performance of the proposed method. Successively, comparisons were made with the DAS, U-Net and FS-DM methods. From a quantitative standpoint, in the case of the in vivo experimental dataset, the proposed method achieves a SSIM of 0.84 and a PSNR of 23.82 dB in the limited-view case of 80°. This represents an increase of 0.15 in SSIM and 8.03 dB in PSNR compared to the FS-DM method. Furthermore, in the extremely limited-view case of 60°, the SSIM and PSNR are 0.78 and 21.72 dB, respectively. These values demonstrate enhancements of 0.08 and 5.23 dB over the U-Net method, respectively. Similarly, they show improvements of 0.08 and 5.91 dB over the DAS method. From the reconstructed images, it is evident that the method proposed in this study exhibits exceptional performance in limited-view PAT reconstruction, compared to the U-Net, DAS and FS-DM methods.
In this study, each diffusion model does not require pairs of training samples and can effectively extract prior information from a limited number of training samples. Additionally, the score-based generative model focuses on the gradient of the logarithmic probability density as its primary research object. Compared to previous models such as GANs, this gradient-based approach offers greater numerical stability and controllability, resulting in a more stable training process [62]. However, GANs, which are a type of unsupervised networks that do not require paired datasets for training, typically demand large quantities of high-quality and diverse data to effectively support the training process [63]. Furthermore, in the traditional GAN training process, the adversarial competition between the generator and the discriminator can lead to training instability, resulting in issues such as convergence difficulties [64]. This instability makes it challenging to ensure that the model can stably and reliably generate high-quality samples in practical applications.
The method proposed in this study acquires prior information by gradually introducing Gaussian noise during the training phase. The training speed is contingent upon factors such as batch size, sinogram size, and GPU performance, etc. In our experiments, the batch size is set to 1, the sinogram size is 512×512, and the graphics card type is NVIDIA GeForce RTX 3060Ti. During the training of the model, one checkpoint is saved for every 1000 epochs, and each checkpoint requires approximately 1.2 h for generation. In total, 20 checkpoints are generated, amounting to approximately 24 h. During the reconstruction, the best model is firstly selected. The reconstruction process of each sinogram go through 999 iterations, each iteration takes about 1.8 s, and the total time is about 30 min. Finally, the sinograms are ultimately transitioned into the image domain. The DAS method can directly generate reconstructed images without necessitating training or iteration. U-Net is an end-to-end network that falls under the category of supervised methods. When dealing with different limited-view cases, the training of the network must use pairs of fully-sampled sinograms and undersampled sinograms. The training process requires 200 epochs and takes about 2.5 h. The reconstruction process of U-Net does not necessitate iteration, only taking 1 s to 2 s. Similarly, CycleGAN is an unsupervised generative model, but it still requires two data sets on different domains to train, and the training process also executes 200 epochs, which takes about 14 h. Its reconstruction process does not require iteration, only 1 s to 2 s. The reconstruction of the FS-DM method uses only one diffusion model trained by the dataset of fully-sampled sinogram, with a reconstruction time of approximately 15 min. During the reconstruction process, the proposed method requires alternating iteration, whereas other methods can directly convert from input to output. As a result, compared to these other methods, the proposed method exhibits a disadvantage in terms of time consumption during the reconstruction process.
In conclusion, to the best of our knowledge, this is the first implementation of applying multi-scale diffusion models directly to the sinogram domain for PAT reconstruction. In addition, this method addresses the limitation of traditional end-to-end networks that require paired data for training. The model obtained from one training can be broadly applied for PAT reconstruction in various limited-view cases without compromising reconstruction quality. Compared with the previous work [33], which only utilized a single diffusion model, the proposed method employs multi-scale priors, which can better constrain the erroneous generation of the model during the iteration and further refine the sinogram from global to local. Therefore, our approach significantly reduces the complexity of the PAT system, which in turn lowers the economic cost of constructing the physical system. The time required for model training is also descended. This breakthrough addresses the limitation of 45° imaging in extremely limited-view cases, offering a viable pathway for limited-view PAT reconstruction. The application of this technology holds immense potential in the domains of medical imaging diagnosis [7], [65], breast cancer detection [66], [67] and other related fields, thereby making significant contributions to the advancement of human health.
Funding
National Natural Science Foundation of China (62265011, 62122033); Jiangxi Provincial Natural Science Foundation (20224BAB212006, 20232BAB202038); National Key Research and Development Program of China (2023YFF1204302).
CRediT authorship contribution statement
Qiegen Liu: Writing – review & editing, Supervision, Funding acquisition, Conceptualization. Cheng Ma: Project administration, Resources, Supervision. Kangjun Guo: Writing – original draft. Kaixin Zeng: Writing – review & editing, Writing – original draft, Software, Methodology. Jiahong Li: Writing – original draft. Xianlin Song: Writing – review & editing, Writing – original draft, Supervision, Methodology, Data curation. Xueyang Zou: Writing – review & editing, Writing – original draft, Formal analysis, Data curation. Zilong Li: Writing – original draft. Zhiyuan Zheng: Writing – original draft. Shangkun Hou: Writing – original draft. Yuhua Wu: Writing – original draft.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors thanks Guijun Wang from School of Information Engineering, Nanchang University for helpful discussions.
Biographies

Xianlin Song received his PhD degree in Optical Engineering from Huazhong University of Science and Technology, China in 2019. He joined School of Information Engineering, Nanchang University as an assistant professor in Nov. 2019. He has published more than 20 publications and given more than 15 invited presentations at international conferences. His research topics include optical imaging, biomedical imaging and photoacoustic imaging.

Xueyang Zou is currently studying for bachelor degree in Computer Science and Technology in Nanchang University, Nanchang, China. Her research interests include image processing, deep learning and photoacoustic tomography.

Kaixin Zeng is currently studying for bachelor degree in Computer Science and Technology in Nanchang University, Nanchang, China. Her research interests include image processing, artificial intelligence and photoacoustic tomography.

Jiahong Li received the bachelor degree in Electronic Information Engineering from Yanshan University, Qinhuangdao, China. He is currently studying in Nanchang University for master’s degree in Electronic Information Engineering. His research interests include optical imaging, deep learning and photoacoustic tomography.

Shangkun Hou is currently studying for bachelor degree in Communication Engineering in Nanchang University, Nanchang, China. His research interests include image processing, artificial intelligence, photoacoustic tomography and holographic imaging.

Yuhua Wu is currently studying for bachelor degree in Materials Science and Engineering in Nanchang University, Nanchang, China. Her research interests include image processing, deep learning and photoacoustic tomography.

Zilong Li received the bachelor degree in Electronic Information Engineering from Guilin University of Electronic Technology, Guilin, China. He is currently studying in Nanchang University for master’s degree in Electronic Information Engineering. His research interests include optical imaging, deep learning and photoacoustic tomography.

Cheng Ma received his B.S. degree in Electronic Engineering from Tsinghua University, Beijing, China in 2004. He obtained his Ph. D. degree in Electrical Engineering from Virginia Tech, Blacksburg, VA, USA in 2012. From 2012–2016, he was a postdoctoral research associate in the Department of Biomedical Engineering at Washington University in St Louis, St. Louis, MO, USA. From May 2016 to present, he is an assistant professor in the Department of Electronic Engineering at Tsinghua University. His research interests include biophotonic imaging and sensing, in particular photoacoustic imaging and wavefront shaping.

Zhiyuan Zheng received the bachelor degree in Electronic Information Engineering from Nanchang University, Nanchang, China. He is currently studying in Nanchang University for master’s degree in Information and Communication Engineering. His research interests include deep learning, image processing and photoacoustic tomography.

Kangjun Guo is currently studying for bachelor degree in Automation Science in Nanchang University, Nanchang, China. His research interests include image processing, artificial intelligence and photoacoustic tomography.

Qiegen Liu received his PhD degree in Biomedical Engineering from Shanghai Jiao Tong University, Shanghai, China in 2012. Currently, he is a professor at Nanchang University. He is the winner of Excellent Young Scientists Fund. He has published more than 50 publications and serves as committee member of several international and domestic academic organizations. His research interests include artificial intelligence, computational imaging and image processing.
Data Availability
I've shared the link to my code in the manuscript file:https://github.com/yqx7150/MSDM-PAT.
References
- 1.Wang L.V. Multiscale photoacoustic microscopy and computed tomography. Nat. Photonics. 2009;3(9):503–509. doi: 10.1038/nphoton.2009.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhou Y., Yao J., Wang L.V. Tutorial on photoacoustic tomography. J. Biomed. Opt. 2016;21(6):61007. doi: 10.1117/1.JBO.21.6.061007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Beard P. Biomedical photoacoustic imaging. Interface Focus. 2011;1(4):602–631. doi: 10.1098/rsfs.2011.0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li M., Tang Y., Yao J. Photoacoustic tomography of blood oxygenation: a mini review. Photoacoustics. 2018;10:65–73. doi: 10.1016/j.pacs.2018.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang J., Yang S., Ji X., Zhou Q., Xing D. Characterization of lipid-rich aortic plaques by intravascular photoacoustic tomography: ex vivo and in vivo validation in a rabbit atherosclerosis model with histologic correlation. J. Am. Coll. Cardiol. 2014;64(4):385–390. doi: 10.1016/j.jacc.2014.04.053. [DOI] [PubMed] [Google Scholar]
- 6.Nasiriavanaki M., Xia J., Wan H., Bauer A.Q., Culver J.P., Wang L.V. High-resolution photoacoustic tomography of resting-state functional connectivity in the mouse brain. Proc. Natl. Acad. Sci. U. S. A. 2014;111(1):21–26. doi: 10.1073/pnas.1311868111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Na S., Russin J.J., Lin L., Yuan X., Hu P., Jann K.B., Yan L., Maslov K., Shi J., Wang D.J., Liu C.Y., Wang L.V. Massively parallel functional photoacoustic computed tomography of the human brain. Nat. Biomed. Eng. 2022;6(5):584–592. doi: 10.1038/s41551-021-00735-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wilson K.E., Wang T.Y., Willmann J.K. Acoustic and photoacoustic molecular imaging of cancer. J. Nucl. Med. 2013;54(11):1851–1854. doi: 10.2967/jnumed.112.115568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rao A.P., Bokde N., Sinha S. Photoacoustic imaging for management of breast cancer: a literature review and future perspectives. Appl. Sci. 2020;10(3):767. [Google Scholar]
- 10.Ye F., Yang S., Xing D. Three-dimensional photoacoustic imaging system in line confocal mode for breast cancer detection. Appl. Phys. Lett. 2010;97 [Google Scholar]
- 11.Wray P., Lin L., Hu P., Wang L.V. Photoacoustic computed tomography of human extremities. J. Biomed. Opt. 2019;24(2) doi: 10.1117/1.JBO.24.2.026003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.VanderLaan D., Karpiouk A.B., Yeager D., Emelianov S. Real-time intravascular ultrasound and photoacoustic imaging. IEEE Trans. Sonics Ultrason. 2017;64(1):141–149. doi: 10.1109/TUFFC.2016.2640952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang L.V. Prospects of photoacoustic tomography. Med. Phys. 2008;35(12):5758–5767. doi: 10.1118/1.3013698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Xia J., Yao J., Wang L.V. Photoacoustic tomography: principles and advances. Electromagn. Waves. 2014;147:1–22. doi: 10.2528/pier14032303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Xu M., Wang L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E. 2005;71(1) doi: 10.1103/PhysRevE.71.016706. [DOI] [PubMed] [Google Scholar]
- 16.Matrone G., Savoia A.S., Caliano G., Magenes G. The delay multiply and sum beamforming algorithm in ultrasound B-mode medical imaging. IEEE Trans. Med. Imag. 2015;34(4):940–949. doi: 10.1109/TMI.2014.2371235. [DOI] [PubMed] [Google Scholar]
- 17.Xu M., Wang L.V. Pulsed-microwave-induced thermoacoustic tomography: Filtered backprojection in a circular measurement configuration. Med. Phys. 2002;29(8):1661–1669. doi: 10.1118/1.1493778. [DOI] [PubMed] [Google Scholar]
- 18.Yip L.C.M., Omidi P., Raščevska E., Carson J.J.L. Approaching closed spherical, full-view detection for photoacoustic tomography. J. Biomed. Opt. 2022;27(8) doi: 10.1117/1.JBO.27.8.086004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gamelin J.K., Aguirre A., Maurudis A., Huang F., Castillo D., Wang L.V., Zhu Q. Curved array photoacoustic tomographic system for small animal imaging. J. Biomed. Opt. 2008;13(2) doi: 10.1117/1.2907157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ku G., Wang X., Stoica G., Wang L.V. Multiple-bandwidth photoacoustic tomography. Phys. Med. Biol. 2004;49(7):1329–1338. doi: 10.1088/0031-9155/49/7/018. [DOI] [PubMed] [Google Scholar]
- 21.Nie L., Chen X. Structural and functional photoacoustic molecular tomography aided by emerging contrast agents. Chem. Soc. Rev. 2014;43(20):7132–7170. doi: 10.1039/c4cs00086b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Huang B., Xia J., Maslov K.I., Wang L.V. Improving limited-view photoacoustic tomography with an acoustic reflector. J. Biomed. Opt. 2013;18(11) doi: 10.1117/1.JBO.18.11.110505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yeh C., Li L., Zhu L., Xia J., Li C., Chen W., Garcia-Uribe A., Maslov K.I., Wang L.V. Dry coupling for whole-body small-animal photoacoustic computed tomography. J. Biomed. Opt. 2017;22(4):41017. doi: 10.1117/1.JBO.22.4.041017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tao C., Liu X. Reconstruction of high quality photoacoustic tomography with a limited-view scanning. Opt. Express. 2010;18(3):2760–2766. doi: 10.1364/OE.18.002760. [DOI] [PubMed] [Google Scholar]
- 25.Hauptmann A., Lucka F., Betcke M., Huynh N., Adler J., Cox B., Beard P., Ourselin S., Arridge S. Model-based learning for accelerated, limited-view 3-D photoacoustic tomography. IEEE Trans. Med. Imag. 2018;37(6):1382–1393. doi: 10.1109/TMI.2018.2820382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Guan S., Khan A.A., Sikdar S., Chitnis P.V. Limited-view and sparse photoacoustic tomography for neuroimaging with deep learning. Sci. Rep. 2020;10(1) doi: 10.1038/s41598-020-65235-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tong T., Huang W., Wang K., He Z., Yin L., Yang X., Zhang S., Tian J. Domain transform network for photoacoustic tomography from limited-view and sparsely sampled data. Photoacoustics. 2020;19:2213–5979. doi: 10.1016/j.pacs.2020.100190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Susmelj A.K., Lafci B., Ozdemir F., Davoudi N., Deán-Ben X.L., Perez-Cruz F., Razansky D. Signal domain adaptation network for limited-view optoacoustic tomography. Med. Image Anal. 2023;91 doi: 10.1016/j.media.2023.103012. [DOI] [PubMed] [Google Scholar]
- 29.Ho J., Jain A., Abbeel P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020;33:6840–6851. [Google Scholar]
- 30.B. Fei, Z. Lyu, L. Pan, J. Zhang, W. Yang, T. Luo, B. Zhang, and B. Dai, Generative diffusion prior for unified image restoration and enhancement, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2023), pp. 9935–9946.
- 31.B. Xia, Y. Zhang, S. Wang, Y. Wang, X. Wu, Y. Tian, W. Yang, and L.V. Gool, DiffIR: Efficient diffusion model for image restoration, in Proceedings of the IEEE International Conference on Computer Vision (IEEE, 2023), pp. 13095-13105.
- 32.Song X., Wang G., Zhong W., Guo K., Li Z., Liu X., Dong J., Liu Q. Sparse-view reconstruction for photoacoustic tomography combining diffusion model with model-based iteration. Photoacoustics. 2023;33 doi: 10.1016/j.pacs.2023.100558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Guo K., Zheng Z., Zhong W., Li Z., Wang G., Li J., Cao Y., Wang Y., Lin J., Liu Q. Score-based generative model-assisted information compensation for high-quality limited-view reconstruction in photoacoustic tomography. Photoacoustics. 2024;38 doi: 10.1016/j.pacs.2024.100623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.S. Dey, S. Saha, B.T. Feng, M. Cui, L. Delisle, O. Leong, L.V. Wang, K.L. Bouman, Score-based diffusion models for photoacoustic tomography image reconstruction, in Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (IEEE, 2024), pp. 2470-2474.
- 35.Cao C., Cui Z., Wang Y., Liu S., Chen T., Zheng H., Liang D., Zhu Y. High-Frequency space diffusion model for accelerated MRI. IEEE Trans. Med. Imaging. 2024;43(5):1853–1865. doi: 10.1109/TMI.2024.3351702. [DOI] [PubMed] [Google Scholar]
- 36.Gao Q., Li Z., Zhang J., Zhang Y., Shan H. CoreDiff: Contextual error-modulated generalized diffusion model for low-dose CT denoising and generalization. IEEE Trans. Med. Imaging. 2023;43(2):745–759. doi: 10.1109/TMI.2023.3320812. [DOI] [PubMed] [Google Scholar]
- 37.Li H., Xu J., Wu X., Wan C., Xu W., Xiong J., Wan W., Liu Q. Dual-domain mean-reverting diffusion model-enhanced temporal compressive coherent diffraction imaging. Opt. Express. 2024;32(9):15243–15257. doi: 10.1364/OE.517567. [DOI] [PubMed] [Google Scholar]
- 38.Wan W., Ma H., Mei Z., Zhou H., Wang Y., Liu Q. Multi-phase FZA lensless imaging via diffusion model. Opt. Express. 2023;31(12):20595–20615. doi: 10.1364/OE.490140. [DOI] [PubMed] [Google Scholar]
- 39.Neprokin A., Broadway C., Myllyla T., Bykov A., Meglinski I. Photoacoustic imaging in biomedicine and life sciences. Life. 2022;12(4):588. doi: 10.3390/life12040588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wang T., He M., Shen K., Liu W., Tian C. Learned regularization for image reconstruction in sparse-view photoacoustic tomography. Biomed. Opt. Express. 2022;13(11):5721–5737. doi: 10.1364/BOE.469460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Treeby B.E., Cox B.T. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010;15(2) doi: 10.1117/1.3360308. [DOI] [PubMed] [Google Scholar]
- 42.Antholzer S., Haltmeier M. Discretization of learned NETT regularization for solving inverse problems. J. Imaging Sci. Technol. 2021;7(11):239. doi: 10.3390/jimaging7110239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hochstenbach M.E., Reichel L. Fractional Tikhonov regularization for linear discrete ill-posed problems. BIT Numer. Math. 2011;51(1):1572–9125. [Google Scholar]
- 44.Wang J., Wang Y. Photoacoustic imaging reconstruction using combined nonlocal patch and total-variation regularization for straight-line scanning Biomed. Eng. Online. 2018;17(1) doi: 10.1186/s12938-018-0537-x. , 1475-925X. , 1475-925X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kim H., Chen J., Wang A., Chuang C., Held M., Pouliot J. Non-local total-variation (NLTV) minimization combined with reweighted L1-norm for compressed sensing CT reconstruction. Phys. Med. Biol. 2016;61(18):6878–6891. doi: 10.1088/0031-9155/61/18/6878. [DOI] [PubMed] [Google Scholar]
- 46.Y. Luo and Z. Yang, DynGAN: Solving mode collapse in GANs with dynamic clustering, IEEE Trans. Pattern Anal. Mach. Intell. (to be published). [DOI] [PubMed]
- 47.D.P. Kingma and M. Welling, Auto-Encoding variational bayes, arXiv, arXiv:1312.6114 (2013).
- 48.Kobyzev I., Prince S.J.D., Brubaker M.A. Normalizing flows: an introduction and review of current methods. IEEE Trans. Pattern Anal. Mach. Intell. 2021;43(11):3964–3979. doi: 10.1109/TPAMI.2020.2992934. [DOI] [PubMed] [Google Scholar]
- 49.Salakhutdinov R., Hinton G. In: Deep boltzmann machines, in Proceedings of Machine Learning Research. van Dyk D., Welling M., editors. PMLR; 2009. pp. 448–455. [Google Scholar]
- 50.Y. Song and S. Ermon, Generative modeling by estimating gradients of the data distribution., arXiv, arXiv:1907.05600 (2019).
- 51.Y. Song, J. Sohl-Dickstein, D.P. Kingma, A. Kumar, S. Ermon and B. Poole, Score-based generative modeling through stochastic differential equations. arXiv, arXiv:2011.13456 (2020).
- 52.Vincent P. A connection between score matching and denoising autoencoders. Neural Comput. 2011;23(7):1661–1674. doi: 10.1162/NECO_a_00142. [DOI] [PubMed] [Google Scholar]
- 53.Sahli H., Slama A.B., Labidi S. U-net: A valuable encoder-decoder architecture for liver tumors segmentation in CT images. J. Xray Sci. Technol. 2022;30(1):45–56. doi: 10.3233/XST-210993. [DOI] [PubMed] [Google Scholar]
- 54.K. Han, Y. Wang, H. Chen, X. Chen, J. Guo, Z. Liu, Y., Tang, A. Xiao, C. Xu, Y. Xu, Z. Yang, Y. Zhang, D. Tao, A survey on visual transformer, in Proceedings of IEEE Transactions on Pattern Analysis and Machine Intelligence (IEEE, 2023), pp. 87-110. [DOI] [PubMed]
- 55.C. Saharia, W. Chan, H. Chang, C. Lee, J. Ho, T. Salimans, D. Fleet, M. Norouzi, Palette: Image-to-Image diffusion models, arXiv, arXiv: 2111.05826 (2022).
- 56.Parisi G. Correlation functions and computer simulations. Nucl. Phys. B. 1981;180(3):378–384. [Google Scholar]
- 57.Staal J., Abràmoff M.D., Niemeijer M., Viergever M.A., van Ginneken B. Ridge-based vessel segmentation in color images of the retina. IEEE Trans. Med. Imag. 2004;23(4):501–509. doi: 10.1109/TMI.2004.825627. [DOI] [PubMed] [Google Scholar]
- 58.Davoudi N., Deán-Ben X.L., Razansky D. Deep learning optoacoustic tomography with sparse data. Nat. Mach. Intell. 2019;1:453–460. [Google Scholar]
- 59.Davoudi N., Deán-Ben X., Razansky D. Deep learning optoacoustic tomography with sparse data. Nat. Mach. Intell. 2019;1(10):453–460. [Google Scholar]
- 60.Ronneberger O., Fischer P., Brox T. U-net: Convolutional networks for biomedical image segmentation. Lect. Notes Comput. Sci. 2015;9351:234–241. [Google Scholar]
- 61.Lu M., Liu X., Liu C., Liu C., Li B., Gu W., Jiang J., Ta D. Artifact removal in photoacoustic tomography with an unsupervised method. Biomed. Opt. Express. 2021;12(10):6284–6299. doi: 10.1364/BOE.434172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.P. Dhariwal, A. Nichol, Diffusion models beat gans on image synthesis, in Proceedings of Conference and Workshop on Neural Information Processing Systems 34, 8780-8794 (2021).
- 63.Lucic M., Kurach K., Michalski M., Gelly S., Bousquet O. Are gans created equal? a large-scale study. Adv. Condens. Matter Phys. 2018;31 [Google Scholar]
- 64.N. Kodali, J. Abernethy, J. Hays, and Z. Kira, On convergence and stability of GANs. arXiv, arXiv:1705.07215 (2017).
- 65.Kratkiewicz K., Pattyn A., Alijabbari N., Mehrmohammadi M. Ultrasound and photoacoustic imaging of breast cancer: clinical systems, challenges, and future outlook. J. Clin. Med. 2022;11(5):1165. doi: 10.3390/jcm11051165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lin L., Hu P., Shi J., Appleton C.M., Maslov K., Li L., Wang L.V. Single-breath-hold photoacoustic computed tomography of the breast. Nat. Commun. 2018;9(1):2352. doi: 10.1038/s41467-018-04576-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Tian C., Pei M., Shen K., Liu S., Hu Z., Feng T. Impact of system factors on the performance of photoacoustic tomography scanners. Phys. Rev. Appl. 2020;13(1) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
I've shared the link to my code in the manuscript file:https://github.com/yqx7150/MSDM-PAT.