Blood-wall fluttering instability as a physiomarker for the progression of thoracic aortic aneurysms

Abstract

The diagnosis of aneurysms is informed by empirically tracking their size and growth rate. Here, by analysing the growth of aortic aneurysms from first principles via linear stability analysis of flow through an elastic blood vessel, we show that abnormal aortic dilatation is associated with a transition from stable flow to unstable aortic fluttering. This transition to instability can be described by a critical threshold for a dimensionless number that depends on blood pressure, the size of the aorta, as well as the shear stress and stiffness of the aortic wall. By analysing data from four-dimensional flow magnetic resonance imaging for 117 patients who had undergone cardiothoracic imaging and for 100 healthy volunteers, we show that the dimensionless number is a physiomarker of the growth of thoracic ascending aortic aneurysms and that it can be used to accurately discriminate abnormal and natural growth. Further characterization of the transition to blood-wall fluttering instability may aid the understanding of the mechanisms underlying aneurysm progression in patients.

1. Introduction

Aneurysms are pathological, localized dilations of a blood vessel that may occur throughout the human body. Intracranial, thoracic aortic, and abdominal aortic aneurysms (IA, TAA, AAA) are each estimated to occur with a global prevalence of 2 – 5%^1;2;3. Rupture of an aneurysm induces a high rate of mortality and morbidity for the patient. Studies showed that over half of patients with ruptured TAAs or AAAs died before reaching a hospital, with overall mortality ranging from 80 to 100%^4;5. For patients with IA, between 10 to 30% died suddenly away from hospitals³, and of those admitted for treatment, 45% experienced an outcome categorized as either moderately disabled, severely disabled, vegetative survival, or death on the Glasgow Outcome Disability Scale. Surgical intervention can be performed to prevent rupture but also carries the risk of complications or death⁴. Thus, it is vital to accurately predict the risk of aneurysm formation and abnormal aortic growth to inform timely treatment.

1.1. Current standard of care.

The standard of care is to recommend elective treatment for aneurysms based on correlations between rupture risk and aneurysm dimensions. For TAAs, the chance of rupture increases from 2% for diameters between 4 and 4.9 cm to 7% for diameters above 6 cm⁶. The mean growth rate is approximately 0.1 cm/year¹⁷. This informs current clinical practice, which suggests surgical intervention for aneurysm diameters larger than a range between 5.5 to 6.0 cm or exhibiting growth rate larger than a range between 0.5 to 1 cm/year, depending on the aneurysm location and patient history^17;8. However, clinical assessment of growth requires comparison between images taken at two time points, typically between 2 to 5 years. Over this period, an aneurysm can grow substantially or rupture fatally. Conversely, an aneurysm which exceeds these statistical criteria may nonetheless remain stable. Thus, prevailing diagnostic guidelines are retrospective and apply population trends to individual patients. To improve predictive capability, the fundamental mechanism underlying aneurysm growth, dissection and rupture must be resolved.

1.2. Tissue mechanics associated with aneurysm progression.

A literature review of clinical observations on how aneurysm distensibility evolves during disease progression is provided in Table S3. As an aneurysm enlarges, the aortic wall degrades due to the loss of elastin and smooth muscle content (SMC)^9;10;11. This stage, sometimes also referred to as Stage 1, has been reported to be accompanied by intimal thickening¹⁶. Overall, the wall stiffness is found to decrease in this stage¹⁶.

In the subsequent stage (Stage 2), further decrease in elastin and SMC content has been reported along with the formation of a neo-adventitia layer from new collagen deposition on the outer walls. Wall stiffness has been reported to further decrease¹⁶.

Two possible developmental paths diverge after Stage 2. In Stage 3, either increasing collagen deposition stiffens the aortic wall to preclude further growth (a Type 1 aneurysm group), or the wall remodels to a weakened state due to a failure to lay down collagen, wall inflammation, and/or adipocyte accumulation (a Type 2 aneurysm group)¹⁶. This second branch triggers further growth and can lead to eventual dissection or rupture¹¹. It is noted that among all the stages of disease progression, listed above, stiffening of the wall is reported in the Stage 3, Type 1 aneurysm group, whereas wall stiffness is reported to decrease in all other stages.

While this important body of work explicates the tissue mechanics underlying growth, the invasive biopsy required to characterize aortic wall makeup preclude its use in clinical decision-making.

1.3. Prediction of aneurysm growth and rupture.

The pursuit of a causative relation between aneurysm progression and certain physical properties falling outside a normative range remains inconclusive. For instance, high blood pressure¹³, abnormal wall shear stress distribution¹⁴, large aortic size⁶, and high wall compliance¹⁶ have all been correlated with aneurysmal growth. However, it is uncertain how these factors interact to trigger abnormal aortic dilatation. For example, high shear stresses have been implicated in some scenarios while low shear stresses in other scenarios¹⁴.

Thus, the state-of-the-art to predict aneurysm growth is based on regression analyses for risk factors such as age or smoking history¹⁵; regression on morphologic features such as aneurysm diameter or undulation index¹⁶; machine learning approaches trained on imaging features such as aneurysm diameter or intraluminal thrombi thickness¹⁷. These methods are based on establishing a correlation between available clinical data and aneurysm growth rates. As with all regression techniques, the breadth of data used to train the model is the main determinant for performance; with a small training cohort relative to the disease population, the predictive capability of the model becomes extrapolative rather than interpolative.

1.4. A unifying hypothesis for aneurysm prediction.

Here, we introduce a unifying, ab initio hypothesis that elucidates the role of known physical factors – blood pressure, aortic size, wall shear stress, and pulse wave velocity – in the development of an aneurysm. The key ansatz is that when these interacting physiological variables fall outside of a normative range, they can trigger a fluid-structure instability that may lead to or signal the onset of abnormal aortic growth.

The dominant properties that destabilize the coupled fluid-structure motion within the aorta are the pressure gradient driving blood flow and the blood vessel diameter. They cause the vessel wall to ‘flutter’ under higher frequency, oscillatory modes of the heartbeat cycle. Concurrently, the viscosity dampens and the wall stiffness constrains these flutter perturbations to help stabilize the blood vessel. A first principles analysis of these competing factors yields a clinically measurable, dimensionless number that describes the transition from stable flow to unstable aortic fluttering. This is analogous to how the Reynolds number describes the transition from laminar to turbulent flow.

A physically intuitive analogy is the unstable fluttering of a banner in the wind, where the flow velocity, banner size, drag coefficient, and material elasticity take the place of blood pressure, aortic size, wall shear stress, and pulse wave velocity, respectively. Note that the pulse wave velocity, to be formally defined later in the paper, depends on material elasticity. Flutter in this mechanical context induces a substantial increase in stresses within the material due to large deformations. Analogously, we hypothesize that the instability that induces aortic wall fluttering may lead to or signal the necessary conditions for aneurysm growth and eventual rupture.

Pulsatile flow in a compliant channel has been studied prior^18;19;20;21, in which the walls of a 2D channel are modeled as spring and damper backed plates. The main instabilities resolved are boundary shear flow instabilities such as the Tollmien-Schlichting wave, which drives the transition to turbulence. Elastic wall deformation is obtained via a Kelvin-Helmholtz type shear instability driven by the Stokes layer near the wall.

In this work, our focus is on what mechanisms act on the aortic wall to trigger aneurysm development and progression. We therefore resolve a tubular 1D fluid-structure instability that depends on flow pulsatility, wall shear, blood pressure, and pulse wave velocity (wall stiffness). The wall fluttering stemming from this instability is primarily pressure mediated via the tube law describing the behavior of the elastic tube. We find that this instability appears strongly correlated with abnormal aortic dilatation.

1.5. Application of the instability-based aneurysm physiomarker.

This paper presents a theoretical analysis of the fluid-structure interaction that yields a critical threshold for the dimensionless number beyond which the instability occurs. This criticality condition is obtained from first principles and can be measured for each patient. Together, the dimensionless number minus the critical threshold encapsulates the instability onset potentially driving or signaling aneurysm progression. We further propose that this flutter instability parameter (dimensionless number minus critical threshold) can act as a aneurysm physiomarker to forecast abnormal aortic dilatation.

In a retrospective study of patients indicated for cardiac imaging with follow-up assessment of aortic dimensions available, we observed that the proposed aneurysm physiomarker is highly predictive of whether an aneurysm exhibits abnormal vs natural growth. The only input to calculate this aneurysm physiomarker for each patient is a single 4D flow magnetic resonance imaging (MRI) scan taken at an initial time point. This analytical determination was then compared with the clinical outcomes reported from a follow-up at least one year after the baseline MRI to evaluate its potential for predicting significant aortic dilation. As a binary predictor for abnormal growth and surgical intervention, the area under the curve (AUC) for a receiver operating characteristic analysis is 0.997. No training data is necessary to tune the calculation or performance of the aneurysm physiomarker.

The aneurysm physiomarker clarifies the exact interaction between physical properties like blood pressure and wall stiffness that trigger the instability and associated abnormal growth. Thus, it also reveals what physiological variables must be controlled to prevent this flutter instability. At a macro level, the dominant factor driving aneurysm progression is shown to vary depending on the patient’s aneurysm stage, which is useful for overall disease progression analysis. Patient-level differences are also captured explicitly by the aneurysm physiomarker, which can show the specific location along the aorta at highest risk for abnormal growth. Lastly, by binning participants according to age and sex, we also found that the proposed aneurysm physiomarker dominantly describes the clinically observed population traits of aneurysm development in both patient and normal participant cohorts.

1.6. Derivation of the ab initio aneurysm physiomarker.

Here, we derive the flutter instability parameter from first principles. A classical model for flow through a blood vessel consists of 1D conservation equations for mass and momentum from the Navier-Stokes equations, closed by a constitutive ‘tube law’ for the variation of pressure with the cross-sectional area^22;23 due to elasticity of the wall. The pressure gradient is chosen to vary periodically in time with frequency equal to that of the heartbeat cycle²⁴.

Following this problem formulation (Fig. 1), we conduct a linear stability analysis to determine a critical threshold beyond which the blood vessel area fluctuates unboundedly under infinitesimal perturbations. The blood vessel is assumed to be infinitely long along the axial direction to keep the theoretical analysis tractable. The base flow is chosen to be a periodic limit cycle following the pulsatile waveform of blood pressure over the cardiac cycle. The effect of perturbations at all higher order frequencies are resolved via the Floquet theory. We find that a single dimensionless number and its critical threshold describes the onset of the proposed instability which triggers the fluttering of the vessel wall.

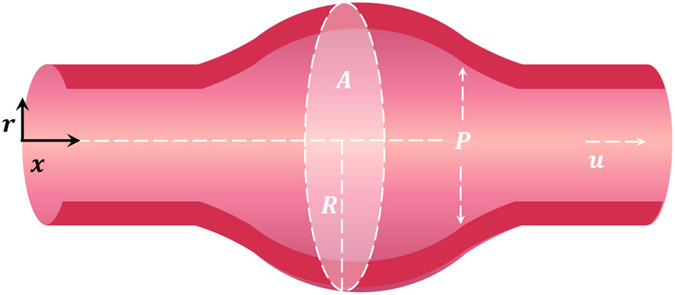
Figure 1.

The distensible blood vessel is modeled as a one-dimensional system with excess internal pressure $P$ (normalized by density) and velocity $u$ being averaged across the radial direction $r$, which is normal to the centerline coordinate $x$. The interior area $A=\pi R^2$ varies as a function of both space $x$ and time $t$.

1.7. Governing equations.

In 1D, the mass and momentum conservation equations are^22;23

$$\frac{\partial A}{\partial t}+\frac{\partial (uA)}{\partial x}=0,$$ (1)

$$A\frac{\partial u}{\partial t}+\widehat{\alpha }Au\frac{\partial u}{\partial x}=-A\frac{\partial P}{\partial x}+2\pi \frac{R}{\rho }{\tau }_w,$$ (2)

where $A[x,t]$ and $R[x,t]$ denote the cross-sectional area and radius, while the pressure $P[x,t]$ and velocity $u[x,t]$ represent values averaged over the radial profiles at each location $x$ and time $t$. Here, $P$ is the excess internal pressure inside the blood vessel normalized by the blood density $\rho$. The wall shear stress term is ${\tau }_w$ and $\widehat{\alpha }$ is a constant factor that arises from cross-sectional averaging of the non-linear convection term. Here, we take $\widehat{\alpha }=1$^22;23.

To close the problem, the tube law relating pressure to area is taken to be linear²⁵

$$P=\frac{K_e}{\rho }\left(\frac{A}{A_o}-1\right),$$ (3)

where $K_e$ is the blood vessel wall stiffness and $A_o$ is the relaxed area of the blood vessel corresponding to excess internal pressure $P=0$. In Supplementary S1.2, we show that the linear stability problem generalizes to any arbitrary tube law relating pressure to vessel area.

1.8. Base flow.

For pulsatile blood flow, the base equilibrium solutions for area $A_b$, pressure gradient $\frac{\mathrm{d}{P}_b}{\mathrm{d}x}$, and velocity $u_b$ can be written as

$$A_b=A_m+A_{\omega }[t]\simeq A_m,$$ (4)

$$u_b=u_m+u_{\omega }[t]=u_m+\frac{1}{2}({\overline{u}}_{\omega }{e}^{i\omega t}+{\overline{u}}_{\omega }^{\ast }{e}^{-i\omega t}),$$ (5)

$$-\frac{\partial P_b}{\partial x}={\varphi }_b={\varphi }_m+{\varphi }_{\omega }[t]={\varphi }_b+\frac{{\overline{\varphi }}_{\omega }}{2}(e^{i\omega t}+e^{-i\omega t}),$$ (6)

where $\omega$ is the angular frequency of the heartbeat cycle. $A_m$, $u_m$, and ${\varphi }_m$ are the temporal mean values of area, velocity, and pressure gradient, respectively. $u_{\omega }$ and ${\varphi }_{\omega }$ are the time dependent, oscillatory components. ${\overline{u}}_{\omega }$ is a complex amplitude associated with $u_{\omega }$ and superscript $\ast$ denotes the complex conjugate. The amplitude ${\overline{\varphi }}_{\omega }$ associated with ${\varphi }_{\omega }$ is taken to be real for simplicity since it is the driving term. Finally, note that for the given form of the driving pressure gradient $\frac{\partial P_b}{\partial x}$, the pressure $P_b$ and consequently the area $A_b$ (via the tube law) will vary along the axial ($x$) direction. Such variations in the base flow are typically on the order of 5% of the mean value as measured via transthoracic echocardiogram²⁶. Thus in this work, we assume for simplicity that the area is approximately constant in the base state; that is, $A_b\simeq A_m$.

The base flow is then described by the conservation equations

$$\frac{\partial u_b}{\partial x}=0,$$ (7)

$$A_m\frac{\partial u_{\omega }[t]}{\partial t}=A_m({\varphi }_m+{\varphi }_{\omega }[t])-{\beta }_m\pi \nu u_m-{\beta }_b\pi \nu u_{\omega }[t].$$ (8)

For constant forcing (as opposed to a pulsatile flow), a parabolic velocity profile generates a corresponding wall shear stress ${\tau }_{w,\text{parabolic}}=\frac{-4\rho \nu u}{R}$, where the kinematic viscosity of blood is given by $\nu$ and the negative sign indicates that the wall shear stress on the fluid is pointed in the direction opposite to that of $u$. For the constant mean flow $u_m$ we assume parabolic flow based mean shear stress which is equivalent to ${\beta }_m=8$ in equation (8). For the superposed oscillatory flow driven by the heartbeat cycle, the corresponding wall shear stress is obtained from a wall shear coefficient ${\beta }_b$ in the momentum equation via²²

$${\beta }_b[w_0]=8\frac{{\tau }_w}{{\tau }_{w,\text{parabolic}}}=-2w_0{i}^{3∕2}\left(\frac{J_1[w_0{i}^{3∕2}]}{J_0[w_0{i}^{3∕2}]}\right)\left(\frac{1}{1-2\frac{J_1[w_0{i}^{3∕2}]}{J_0[w_0{i}^{3∕2}]}∕(w_0{i}^{3∕2})}\right),$$ (9)

where $J_n$ denote Bessel functions of the first kind. The complex ${\beta }_b$ represents the ratio of wall shear stress (WSS) at a Womersley number ${\omega }_0=R\sqrt{\omega ∕\nu }\ge 0$ (pulsatile flow driven at angular frequency $\omega$) to the fully developed WSS associated with $w_0=0$ (constant forcing). The factor ${\beta }_b$ is determined via the functional dependence of the WSS ${\tau }_w$ on $w_0$ as derived by Womersley²⁷ (equation (9)) and displayed in Fig. S1. Finally, the mean terms ${\varphi }_m$ and $u_m$ are related through momentum conservation (equation (8)) via $u_m=\frac{{\varphi }_m{A}_m}{{\beta }_m\pi \nu }$. Analogously, the oscillatory flow components are related by

$${\overline{u}}_{\omega }=\frac{{\overline{\varphi }}_{\omega }{A}_m({\beta }_b\pi \nu -i\omega A_m)}{{({\beta }_b\pi \nu )}^2+{(\omega A_m)}^2}.$$ (10)

1.9. Linearized perturbation equations.

Next, the base solutions for the velocity, area, and pressure are perturbed by infinitesimal quantities $Y^{\prime }$ of the respective variables

$$Y=Y_b+Y^{\prime }=Y_b+\sum _{k=-\infty }^{\infty }{Y}_k^{\prime }[t]e^{ikx},$$ (11)

for $Y\in \{A,u,P\}$. The perturbations $Y^{\prime }$ are expressed as the sum of contributions from all wavenumbers $k$. After linearizing of the governing equations and subtracting the base solution, the equations for perturbation components $Y_k^{\prime }[t]$ corresponding to wavenumber $k$ are

$$\frac{\partial A_k^{\prime }}{\partial t}+A_{b}ik{u}_k^{\prime }+u_{b}ik{A}_k^{\prime }=0,$$ (12)

$$A_b\frac{\partial u_k^{\prime }}{\partial t}+A_k^{\prime }\frac{\partial u_b}{\partial t}+A_b{u}_{b}ik{u}_k^{\prime }=-A_{b}ik{P}_k^{\prime }-{\beta }_b\pi \nu u_k^{\prime }+{\varphi }_b{A}_k^{\prime },$$ (13)

$$P_k^{\prime }=\frac{K_e}{\rho }\frac{A_k^{\prime }}{A_o}.$$ (14)

We can combine the tube law (equation (14)) into the momentum equations (equation (13)) to express pressure $P_k^{\prime }$ in terms of area $A_k^{\prime }$ perturbations. The complex valued solution set tightens to ${\underset{¯}{X}}_k={[A_k^{\prime },u_k^{\prime }]}^T$.

The perturbation equations (12) and (13) can be written in matrix form as

$${\underset{¯}{\stackrel{.}{X}}}_k=H{\underset{¯}{X}}_k,$$ (15)

where ${\underset{¯}{\stackrel{.}{X}}}_k$ denotes the time derivative. The vector ${\underset{¯}{X}}_k\in C(\mathbb{R},M_{2,1}[\mathbb{C}])$, denoting a continuous, functional mapping from a real scalar in time to the complex vector space for ${[A_k^{\prime },u_k^{\prime }]}^T$. The coefficient matrix $\mathit{H}[t]\in C(\mathbb{R},M_{2,2}[\mathbb{C}])$ is periodic with associated frequency $\omega$. This class of periodic linear systems under parametric forcing admits solutions of the Floquet form.

1.10. Floquet solution.

The basis for all solutions to equation (15) can be expressed as the product of a periodic component, and an exponential term in time (Theorem 4.1 in Coddington et al.²⁸). That is, ${\mathit{X}}_k=\mathit{P}(t)e^{\mathit{R}t}$, where $\mathit{P}[t]$ is invertible, $\mathit{P}[t]=\mathit{P}[t+2\pi ∕\omega ]$, and $\mathit{P}[t]\in C(\mathbb{R},M_{2,2}[\mathbb{C}])$. ${\mathit{X}}_k[t]\in C(\mathbb{R},M_{2,2}[\mathbb{C}])$ is a complex valued matrix formed from the fundamental solution to equation (15). To assess the stability of the solutions ${\mathit{X}}_k$, we observe that the eigenvalues $\lambda$ of $\mathit{R}$ determine the stability of the system. Specifically, if there exist $\lambda =\mu +i\alpha \omega$ such that $\mu <0$ for all wavenumbers $k$, then the perturbations $A^{\prime }$ and $u^{\prime }$ decay in time. Otherwise if $\mu >0$ for any wavenumber $k$, the base solution is unstable, which according to our hypothesis may trigger aneurysm formation and abnormal growth²⁸.

To find $\lambda$, we see that each solution vector of the fundamental solution takes the form ${\underset{¯}{X}}_k=e^{\lambda t}\underset{¯}{P}[t]$, where $\underset{¯}{P}[t]$ is a vector polynomial with coefficients periodic in the associated frequency $\omega$ (Section 4.5 in Coddington et al.²⁸). This periodic function $\underset{¯}{P}[t]$ can therefore be written as the sum of temporal Fourier modes¹⁹, such that ${\underset{¯}{X}}_k$ becomes

$${\underset{¯}{X}}_k=\sum _{-\infty }^{\infty }{\underset{¯}{\widehat{X}}}_{k,n}{e}^{(u+i(n+\alpha )\omega )t},$$ (16)

$$\frac{\partial {\underset{¯}{X}}_k}{\partial t}=\sum _{-\infty }^{\infty }(\mu +i(n+\alpha )\omega ){\underset{¯}{\widehat{X}}}_{k,n}{e}^{(\mu +i(n+\alpha )\omega )t}.$$ (17)

Using this in the linearized perturbation equations (eqns. 12, 13), we obtain

$$(\mu +i(n+\alpha )\omega ){\widehat{A}}_{k,n}+A_{b}ik{\widehat{u}}_{k,n}+u_{b}ik{\widehat{A}}_{k,n}=0,$$ (18)

$$A_b(\mu +i(n+\alpha )\omega ){\widehat{u}}_{k,n}+{\widehat{A}}_{k,n}\frac{\partial u_b}{\partial t}+A_b{u}_{b}ik{\widehat{u}}_{k,n}=-A_{b}ik\frac{K_e}{\rho }\frac{{\widehat{A}}_{k,n}}{A_o}-{\beta }_b\pi \nu {\widehat{u}}_{k,n}+{\varphi }_b{\widehat{A}}_{k,n}.$$ (19)

Note that each equation corresponds to one temporal Fourier mode ($n\omega$, where $n\in \{-\infty ,\infty \}$) at a particular spatial wavenumber $k$. We substitute the base solutions (eqns. 5, 6) to obtain the final homogeneous equation for the Fourier coefficients ${\underset{¯}{\widehat{X}}}_{k,n}={[{\widehat{A}}_{k,n},{\widehat{u}}_{k,n}]}^T$.

$$(\mu +i(n+\alpha )\omega ){\widehat{A}}_{k,n}+A_{b}ik{\widehat{u}}_{k,n}+u_{m}ik{\widehat{A}}_{k,n}+\frac{1}{2}{\overline{u}}_{\omega }ik{\widehat{A}}_{k,n-1}+\frac{1}{2}{\overline{u}}_{\omega }^{\ast }ik{\widehat{A}}_{k,n+1}=0,$$ (20)

$$\begin{gathered} A_b(\mu +i(n+\alpha )\omega ){\widehat{u}}_{k,n}+{\overline{u}}_{\omega }\frac{i\omega }{2}{\widehat{A}}_{k,n-1}-{\overline{u}}_{\omega }^{\ast }\frac{i\omega }{2}{\widehat{A}}_{k,n+1} \\ +u_m{A}_{b}ik{\widehat{u}}_{k,n}+\frac{1}{2}{\overline{u}}_{\omega }{A}_{b}ik{\widehat{u}}_{k,n-1}+\frac{1}{2}{\overline{u}}_{\omega }^{\ast }{A}_{b}ik{\widehat{u}}_{k,n+1}= \\ -A_{b}ik\frac{K_e}{\rho }\frac{{\widehat{A}}_{k,n}}{A_o}-{\beta }_b\pi \nu {\widehat{u}}_{k,n}+{\varphi }_m{\widehat{A}}_{k,n}+\frac{{\overline{\varphi }}_{\omega }}{2}{\widehat{A}}_{k,n-1}+\frac{{\overline{\varphi }}_{\omega }}{2}{\widehat{A}}_{k,n+1}, \end{gathered}$$ (21)

1.11. Dimensionless groups.

To simplify the representation, we nondimensionalize the problem via Table S1. Using the dimensionless groups introduced, the nondimensional forms of the characteristic equations 20 and 21 are

mass conservation equation:

$$\begin{gathered} (\tilde{\mu }+i(n+\alpha )\tilde{\omega }){\tilde{A}}_{k,n}+i{k}^{″}{u}_{k,n}^{″}+\frac{1}{2}{N}_{m}i{k}^{″}{\tilde{A}}_{k,n}+\frac{1}{ph[{\beta }_b]}\frac{N_{\omega }}{2(2+i\tilde{\omega }∕(ph[{\beta }_b]))}i{k}^{″}{\tilde{A}}_{k,n-1} \\ +\frac{1}{ph[{\beta }_b]}\frac{N_{\omega }}{2(2-i\tilde{\omega }∕(ph[{\beta }_b]))}i{k}^{″}{\tilde{A}}_{k,n+1}=0, \end{gathered}$$ (22)

momentum conservation equation:

$$\begin{gathered} (\tilde{u}+i(n+\alpha )\tilde{\omega })u_{k,n}^{″}+\frac{1}{ph[{\beta }_b]}\frac{N_{\omega }}{2(2+i\tilde{\omega }∕(ph[{\beta }_b]))}i\tilde{\omega }{\tilde{A}}_{k,n-1}-\frac{1}{ph[{\beta }_b]}\frac{N_{\omega }}{2(2-i\tilde{\omega }∕(ph[{\beta }_b]))}i\tilde{\omega }{\tilde{A}}_{k,n+1} \\ +\frac{N_m}{2}i{k}^{″}{u}_{k,n}^{″}+\frac{1}{ph[{\beta }_b]}\frac{N_{\omega }}{2(2+i\tilde{\omega }∕(ph[{\beta }_b]))}i{k}^{″}{u}_{k,n-1}^{″}+\frac{1}{ph[{\beta }_b]}\frac{N_{\omega }}{2(2-i\tilde{\omega }∕(ph[{\beta }_b]))}i{k}^{″}{u}_{k,n+1}^{″}= \\ -i{k}^{″}{\tilde{A}}_{k,n}-2ph[{\beta }_b]u_{k,n}^{″}+N_m{\tilde{A}}_{k,n}\frac{{\beta }_m}{\mid {\beta }_b\mid }+\frac{N_{\omega }}{2}{\tilde{A}}_{k,n-1}+\frac{N_{\omega }}{2}{\tilde{A}}_{k,n+1}, \end{gathered}$$ (23)

where ${\beta }_b$ is the complex wall shear coefficient as defined earlier (equation (9)), and $ph[{\beta }_b]=\frac{{\beta }_b}{\mid {\beta }_b\mid }$ has only the phase information ${\beta }_b$ due to the normalization by the scalar amplitude $\mid {\beta }_b\mid$. Finally, $\tilde{\omega }$ is the dimensionless angular frequency of the cardiac cycle. The important parameters describing the oscillatory component of flow through the blood vessel — including wall shear coefficient ${\beta }_b$, vessel area $A_m$, pressure driven acceleration ${\overline{\varphi }}_{\omega }$, and wall stiffness $K_e$ — have been collected in a single dimensionless number

$$N_{\omega }=\frac{{\overline{\varphi }}_{\omega }{A}_m^{1∕2}}{(\frac{\mid {\beta }_b\mid }{2}\pi \nu )}\sqrt{\frac{\rho A_o}{K_e}}.$$ (24)

Akin to the role of the Reynolds number in describing the onset of turbulence, this dimensionless number $N_{\omega }$ tracks the inception of the flutter type instability at given values of the remaining variables. The other nondimensional number $N_m$ has similar definition as $N_{\omega }$ (see Table S1) with ${\varphi }_m$ replacing ${\overline{\varphi }}_{\omega }$. $N_m$ encapsulates the effect of mean flow and its value is typically smaller (0.05 – 0.7) compared to the values of $N_{\omega }(0.5-12)$ (0.5 – 12) for physiologic conditions. The dimensionless angular frequency $\tilde{\omega }$ takes values in the range of 12 – 34. Finally, the Womersley number $w_0$ has values in the range of 13 – 35.

The marginal stability curve $\tilde{\mu }=0$ marks the critical point above which $\tilde{\mu }>0$ perturbation amplitudes grow exponentially in time, and below which $\tilde{\mu }<0$ the base flow is stable under the decay of perturbation modes. To find the locus of points where $\tilde{\mu }=0$, we refer to the methodology proposed by Kumar et al¹⁹. That is, by fixing the values of $k^{″}$, $\tilde{\omega }$, $N_m$, and $w_0$ (and therefore of ${\beta }_b$) for a specific flow scenario, as well as presetting $\tilde{\mu }=0$ in eq. 22 and 23, we solve an eigenvalue problem for the critical $N_{\omega ,\text{crit}}$ on the marginal stability curve. This procedure is detailed in Supplementary S1.15.

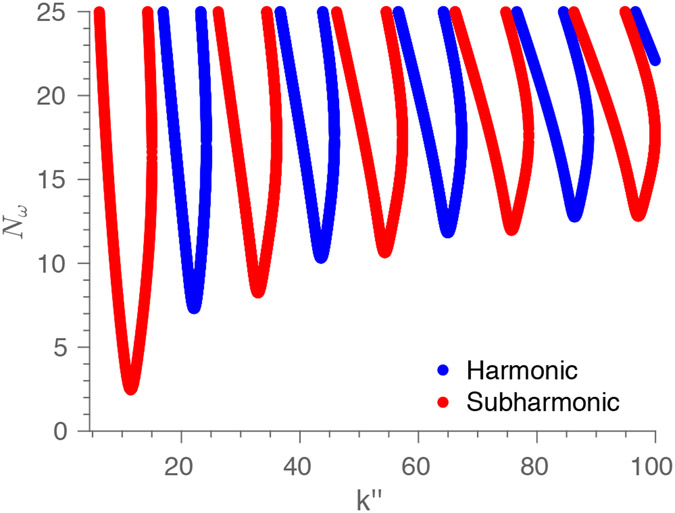
In Fig. 2, we plot the harmonic $\alpha =1$ and subharmonic $\alpha =1∕2$ “tongues” of instability¹⁹. The space of dimensionless wavenumber $k^{″}$ and dimensionless number $N_{\omega }$ is divided into tongue regions of instability, where perturbations to the flow grow in time, and outside zones of stability, where the base flow remains stable to perturbations. The harmonic response has the same frequency $\tilde{\omega }$ (and its multiples) as that of the driving pressure gradient in the base flow, whereas the subharmonic response has half the frequency $\tilde{\omega }$ (and its multiples). The subharmonic solution is excited first as $N_{\omega }$ increases past the lowest threshold value $N_{\omega ,\text{threshold}}$. This critical threshold value occurs at the bottom tip of the first subharmonic tongue. It is the global minimum of the critical dimensionless number on all tongues of marginal stability, $\text{min}(N_{\omega ,crit})=N_{\omega ,\text{threshold}}$ (see Fig. 2).

Figure 2.

The marginal stability curve $\tilde{\mu }=0$ as a function of the dimensionless wave number $k^{″}$ of the perturbation mode and the dimensionless number $N_{\omega }$. The dimensionless number $N_{\omega }$ encapsulates the blood viscosity, vessel diameter, pressure gradient (or flow acceleration), and viscous contribution under pulsatile waveform of the flow. For a specific value of $k^{″}$, $N_m$, and $\tilde{\omega }$, $N_{\omega }$ within the alternating tongues indicate that the system is unstable to perturbations and can grow unboundedly, whereas $N_{\omega }$ outside the tongues correspond to stable base flow. The figure uses representative values of the angular frequency $\tilde{\omega }=19.6$ and $N_m=1.7\times {10}^{-1}$ corresponding to human physiology.

If $N_{\omega }>N_{\omega ,\text{threshold}}$, the blood vessel will be unstable to a waveband of perturbation modes, whereas below this threshold, the base flow should remain stable. We hypothesize that the growth of perturbation modes will trigger or signal the permanent dilatation of a cross-sectional area of the blood vessel over time. We may test whether the dimensionless number is predictive of future aortic growth and potential aneurysm development by measuring the patient specific physiological properties comprising $N_{\omega }$ (e.g., through cardiac imaging) and validating this theoretical forecast against observed aortic dilatation at follow-up.

1.12. Pulse wave velocity.

To determine the flow stability for a specific patient, the above formulation requires information about the wall stiffness $K_e$ of the blood vessel. This physiological property can be found from the pulse wave velocity (PWV) measured from imaging techniques such as MRI scans and echocardiograms. The PWV is the propagation speed of the pulse wave in the aorta and is related to the elastic modulus or stiffness of the aortic wall. This relationship can be derived by transforming the set of simplified governing equations to the standard form of the wave equation¹. The precise steps are listed in Supplementary S1.2.

Although a linear tube law was used in the derivation of the dimensionless number, a general tube law is likewise permissible via $P=\frac{1}{\rho }G(A)$, where $G$ can be some nonlinear function of the local cross-sectional area. The function $G$ represents the full dependence of the excess internal pressure on the cross-sectional area and thus can encapsulate aortic wall properties such as elastic moduli, wall thickness, etc. in the most general case. The pulse wave velocity is then shown in Supplementary S1.2 to be

$$c_{pw}^2=\frac{1}{\rho }\frac{\mathrm{d}G}{\mathrm{d}A}A.$$ (25)

In the context of the dimensionless number derivation, the tube law term appears in the linearized perturbation equations. By expansion around the base pressure $P_b$ and area $A_m$,

$$P=P_b+P^{\prime }={\phantom{\mid }{P}_b+\frac{1}{\rho }\frac{\mathrm{d}G}{\mathrm{d}A}\mid }_b{A}^{\prime }=P_b+c_{pw}^2\frac{A^{\prime }}{A_m}.$$ (26)

We see that no matter which form the tube law $G(A)$ takes, the measured PWV can be used to quantify the blood vessel’s elastic properties. The key dimensionless number can be recast in terms of PWV as follows

$$N_{\omega }=\frac{{\overline{\varphi }}_{\omega }{A}_m^{1∕2}}{(\frac{\mid {\beta }_b\mid }{2}\pi \nu )}\sqrt{\frac{\rho A_o}{K_e}}=\frac{{\overline{\varphi }}_{\omega }{A}_m}{\frac{\mid {\beta }_b\mid }{2}\pi \nu c_{pw}}.$$ (27)

Using equation (27), $N_{\omega }$ can now be calculated explicitly from clinical imaging data for each cross-section along a blood vessel. The difference between this clinical patient specific value $N_{\omega }$ and the critical threshold $N_{\omega ,\text{threshold}}$ on the marginal stability curve produces an overall flutter instability parameter

$$N_{\omega ,\text{sp}}[N_m,\tilde{\omega },{\beta }_b[w_0]]=N_{\omega }-N_{\omega ,\text{threshold}}[N_m,\tilde{\omega },{\beta }_b[w_0]].$$ (28)

Eqns. 22 and 23 imply that $N_{\omega ,\text{threshold}}$ depends on $N_m$, $\tilde{\omega }$, and ${\beta }_b$. This is reflected in equation (28) from the functional dependence of $N_{\omega ,\text{threshold}}$ and by consequence of $N_{\omega ,\text{sp}}$ on these variables. Note that ${\beta }_b$ depends on the Womersley number $w_0$ (equation (9). All the independent variables ($N_m$, $\tilde{\omega }$, $w_0$) can be determined clinically.

If $N_{\omega ,\text{sp}}>0$, we hypothesize that the blood vessel cross-section is expected to grow due to the increase in perturbation amplitude. Otherwise for $N_{\omega ,\text{sp}}\le 0$, the blood vessel diameter should remain constant in time since all perturbation modes decay. Thus, the flutter instability parameter $N_{\omega ,\text{sp}}$ can serve as an aneurysm physiomarker that is predictive of abnormal aortic growth and is convenient to apply clinically.

In summary, we have developed an ab initio theoretical framework to predict the stability of an aortic section depending on a patient’s aorta diameter $A_m$, blood pressure gradient ${\overline{\varphi }}_{\omega }$ causing oscillatory acceleration, pulsatile contribution to wall shear ${\beta }_b$, blood viscosity $\nu$, and blood density $\rho$. These values can be extracted from 4D flow MRI or reference literature⁸.

2. Results

To gauge the performance of the proposed aneurysm physiomarker in analyzing aneurysm growth, a retrospective study was carried out for participants with and without existing aortopathies. For both the patient and healthy participant cohorts, the flutter instability parameter was calculated from each participant’s 4D flow MRI and used as an aneurysm physiomarker to gauge their disease state.

In a subcohort of patients with follow-up data, clinical outcomes were quantified for growth at the maximal-area ascending aorta (MAA) and the sinus of valsalva (SOV) through standardized imaging assessment. Surgical procedures were also noted for each patient. The flutter instability parameter was calculated from each patient’s first available 4D flow MRI at time 0 and used as an aneurysm physiomarker to forecast growth/surgical outcomes at follow-up. Further details are provided in Methods (5).

2.1. Patient aortic growth and $N_{\omega ,\mathbf{sp}}$ predictive performance.

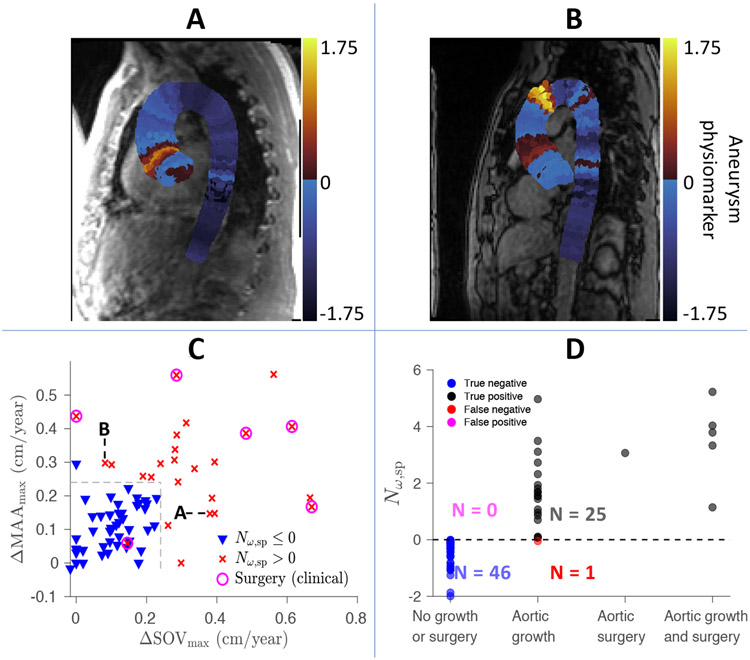
Since the flow velocities are resolved spatially through 4D flow MRI, the aneurysm physiomarker $N_{\omega ,\text{sp}}$ can be visualized based on location along the centerline of the aorta as a result of our 1D analysis (Fig. 3). The aneurysm physiomarker is calculated from the patient’s initial MRI taken at year 0 and can be evaluated against follow-up data that report SOV and MAA diameters. For instance, Fig. 3A shows that a patient’s SOV and MAA growth rates of 0.38 cm/year and 0.15 cm/year agree with their spatial aneurysm physiomarker distribution; $N_{\omega ,\text{sp}}>0$ is localized near the SOV rather than the MAA. Similarly, Fig. 3B demonstrates that a second patient’s SOV and MAA growth rates of 0.08 cm/year and 0.30 cm/year likewise matches their aneurysm physiomarker distribution; here, $N_{\omega ,\text{sp}}>0$ occurs at the MAA rather than the SOV. The growth rates in SOV and MAA vs their respective, locally measured aneurysm physiomarker are shown in Fig. S6.

Figure 3.

A) 1D spatial distribution of the aneurysm physiomarker $N_{\omega ,\text{sp}}$ along the central axis for one patient, calculated from their initial MRI taken at year 0. Each slice perpendicular to the centerline is colored the same to represent the value along the central axis. During clinical follow-up, the patient exhibited growth rates of 0.38 cm/year and 0.15 cm/year at their sinus of valsalva (SOV) and maximal-area ascending aorta (MAA). This agrees with the aneurysm physiomarker distribution, which shows $N_{\omega ,\text{sp}}>0$ localized near the SOV rather than the MAA. B) Spatial distribution of the aneurysm physiomarker for a second patient, who exhibited growth rates of 0.08 cm/year & 0.30 cm/year at the SOV & MAA. These rates likewise match the aneurysm physiomarker distribution, where $N_{\omega ,\text{sp}}>0$ at the MAA rather than the SOV. C) A prediction vs outcome diagram of all patients with follow-up imaging data. The maximum growth rate of their MAA and SOV (cm/year) measured from follow-up imaging data are visualized with respect to the theoretical prediction $N_{\omega ,\text{sp}}$, which are measured from a single MRI at time 0. If $N_{\omega ,\text{sp}}>0$, the patient’s marker is labeled by an $\mathrm{x}$. Otherwise, the data point is labeled by a downward pointing triangle. The circles indicate that the patient experienced a surgical intervention after their initial MRI at year 0. The growth boundary of 0.24 cm/year is labeled by black dotted lines. This boundary optimally discriminates between stable and unstable aneurysms predicted by the proposed aneurysm physiomarker and falls within the clinically observed range of abnormal growth (0.24 cm/year for small aneurysms to 0.31 cm/year for large aneurysms) that is associated with chronic dissection¹⁷. D) Each patient has been labeled according to whether $N_{\omega ,\text{sp}}>0$ accurately predicts a growth outcome (categorized as exhibiting a growth rate in SOV or MAA ≥ 0.24 cm/year), a surgical intervention, or both at follow-up.

Next, the per patient growth rates for the SOV and MAA are visualized in Fig. 3C and compared with our theoretical predictions. Each $\mathrm{x}$ in Fig. 3C denotes $N_{\omega ,\text{sp}}>0$, as calculated from the patient’s MRI image at year 0. This indicates that the ascending aorta is expected to grow due to the flutter type instability. Conversely, each downward pointing triangle represents $N_{\omega ,\text{sp}}\le 0$. Since all perturbation modes are damped in this case, the ascending aorta should not be subject to the identified instability. Data points for patients who experienced surgical intervention after their initial MRI are circled. All aneurysm physiomarker values $N_{\omega ,\text{sp}}$ were calculated from patient MRI at time zero, without reference to follow-up data.

Growth rates exceeding 0.2 cm/year lie outside the range of normal growth of the thoracic aorta¹⁷. When the stability of aneurysm measured at time zero via $N_{\omega ,\text{sp}}$ are plotted with respect to the growth rates measured from follow-up data, we find that a growth threshold of 0.24 cm/year optimally discriminates between stable and unstable aneurysms forecast by the proposed aneurysm physiomarker. This is an emergent division of the growth data based purely on the transition of $N_{\omega ,\text{sp}}$ from negative to positive- from natural aortic dilatation over time to abnormal growth driven by unstable flutter.

The proposed discriminating boundary of 0.24 cm/year falls within the clinically observed range of significantly higher growth rates (0.24 cm/year for smaller 4 cm aneurysms to 0.31 cm/year or larger 5.2 cm aneurysms) that is associated with chronic dissection in patients¹⁷. Growth between 0.2 to 0.3 cm/year thus appears to delineate a transition zone from low to high risk. For instance, the growth rate in a non-referral, low risk population of patients with ascending thoracic aneurysms (> 4 cm) ranged from 0.07 to 0.16 cm/year³²; meanwhile, European Society of Cardiology (ESC) guidelines³³ have suggested that growth exceeding 0.3 cm/year is a risk factor that can prompt surgical intervention for thoracic ascending aortic aneurysms.

This agreement between the emergent boundary based on the aneurysm physiomarker and the statistically significant growth rate that clinicians have independently deduced validates the aneurysm physiomarker as an unbiased, clinically valuable predictor of abnormal aneurysm growth. This boundary for abnormal growth has been visualized in Fig. 3C.

Fig. 3D shows that by using the aortic growth rate of 0.24 cm/year as an indicator of significant growth, the aneurysm physiomarker $N_{\omega ,\text{sp}}>0$ serves as a good binary predictor for the growth outcome of each patient. The accuracy, sensitivity, and specificity of this proposed aneurysm physiomarker in predicting abnormal growth in the thoracic aorta are 0.986, 0.962, and 1.000, respectively. The area under the curve (AUC) of a receiver operating characteristic (ROC) analysis (Fig. S7) is 0.997; an AUC above 0.9 is typically considered "outstanding" for the performance of a binary predictive diagnostic³⁴.

Additionally, the optimal operating point occurs at the minimum positive value for $N_{\omega ,\text{sp}}$ for patients with follow-up data, suggesting that the analytically derived threshold $N_{\omega ,\text{threshold}}$ accurately describes the onset of the underlying instability. No training data set was necessary to tune the calculation of the aneurysm physiomarker for each patient. If the more conservative threshold 0.31 cm/year is selected instead as a binary indicator of clinically significant growth, the accuracy, sensitivity, specificity, and AUC of this proposed aneurysm physiomarker become 0.875, 1.000, 0.8393, and 0.952 respectively. Its performance in classifying abnormal growth is therefore bounded from below in the "outstanding" category for typical clinical use cases ³⁴.

2.2. Cohort comparisons.

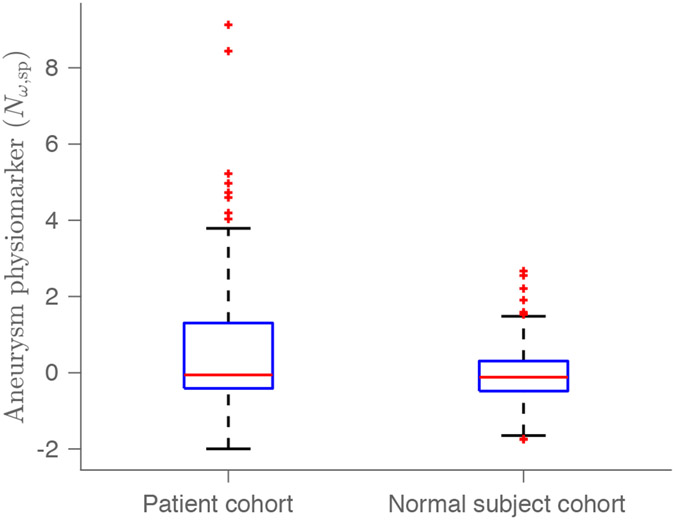
Next, the distributions of the aneurysm physiomarker $N_{\omega ,\text{sp}}$ in both the normal participant cohort and the patient cohort are examined. As seen in Fig. 4, the median aneurysm physiomarker value for the normal participant cohort is shown to be significantly (p= 0.0370) smaller than that for the patient cohort, via a one-tailed Wilcoxon rank sum test. This agrees with the inclusion criteria used to establish the patient and normal participant cohorts; Fig. S4 shows that the aneurysm physiomarker $N_{\omega }$ appears to trend with increased growth rates in the SOV and MAA. The sample size of both cohorts exceed 93, the value required to establish significance at a level of p<0.05 for the difference in their median values with 90% statistical power.

Figure 4.

A) The distribution of the aneurysm physiomarker $N_{\omega ,\text{sp}}$ in the patient (n=117) and normal participant (n=100) cohorts. The median aneurysm physiomarker value for the normal participant cohort is shown to be significantly (p=0.0370) smaller than that for the patient cohort, via a one-tailed Wilcoxon rank sum test. Patient cohort: {min, 25% quartile, median 75% quartile, max} = {−1.9961, −0.4107, −0.0561, 1.3035, 9.1285}. Normal participant cohort: {min, 25% quartile, median 75% quartile, max} = {−1.7499, −0.4807, −0.1180, 0.3061, 2.6680}

To neutralize potential bias in the statistics arising from lack of age or sex matching, we also binned the aneurysm physiomarker measured for patient and normal participant cohorts into different age and sex groups in Table S2. The female normal participants in the youngest age group (Age < 40) show a significantly smaller aneurysm physiomarker value compared to males in the same cohort. This could reflect population level observations that TAAs occur more commonly in males than in females, despite poorer outcomes in females³⁵. We also note that for the patient cohort, females exhibit systematically though not significantly higher $N_{\omega ,\text{sp}}$ than males across every age group. This sex disparity may mirror clinical observation that TAA growth is accelerated in females compared to males³⁵. Thus, the distribution of the aneurysm physiomarker among different sex and age groups in the two cohorts appear to agree with general population trends reported in the literature.

3. Discussion

3.1. Predictive power of the aneurysm physiomarker.

While the aneurysm physiomarker proves predictive of abnormal growth, we do not expect it to discriminate between no growth and any nonzero amount of aortic dilatation. After all, increase in aortic dimensions occurs with natural aging. Normal aortic growth, while complex in etiology, is generally understood to occur as a result of the repeated natural stresses induced by pressurized blood flow, which ultimately result in gradual loss of elastin fibers, remodeling of elastic lamellae, and ultimately increase of vessel diameter^36;37. Normative rates of increase in adults have been assessed at 0.11 cm/year in adults for both men and women, but several factors such as blood pressure and body surface area are associated with larger diameters. There is high variation in baseline aortic diameter at any given age range^38;39;37.

Instead of describing all modes of aortic dilatation, the aneurysm physiomarker identifies the specific presence of the flutter instability, which appears to signal subsequent abnormal growth for a substantial percentage of patients who eventually experience rates exceeding 0.24 cm/year. Thus, the aneurysm physiomarker’s ability to predict abnormal dilatation in contrast to natural growth is crucial for prompt clinical decision-making and accurate treatment¹⁷.

The aneurysm physiomarker may also expand aneurysm detection and prediction to aortic segments heretofore less commonly examined due to the effort and cost involved. Interestingly, the spatially resolved aneurysm physiomarker distribution in Fig. 3B displays a global maximum near the aortic arch as well as multiple pockets of instability $N_{\omega ,\text{sp}}>0$ along the descending aorta; this spatial variation in the aneurysm physiomarker is largely due to local change in the pressure driven acceleration ${\overline{\varphi }}_{\omega }$ and area $A_b$. This demonstrates that abnormal aortic dilatation is not necessarily confined near the SOV and MAA. More comprehensive imaging analysis motivated by predictive aneurysm physiomarker distributions may help detect "silent-until-rupture" aneurysms that evade screening at common sites¹⁴. It would be of strong interest to conduct a complete chart review showing whether such spatial aneurysm physiomarker predictions can be confirmed by follow-up imaging and clinical intervention; this procedure is out of the scope of the current work.

3.2. Aneurysm development in normal participants with respect to age.

Although age is not a direct input into the eigenvalue analysis that yields the aneurysm physiomarker $N_{\omega ,\text{sp}}$, many physiological properties vary systematically with age. For instance, both aortic diameter and wall stiffness are known to increase naturally in older, healthy participants. Less is known about how these age related variations affect aneurysm formation and growth. We elucidate important trends here.

Table 3 shows the breakdown of physiological properties that make up the aneurysm physiomarker $N_{\omega ,\text{sp}}$. This comparison occurs across three age groups. In the normal participant cohort, an unstable flow condition $N_{\omega ,\text{sp}}>0$ is induced on average by two significant factors relative to the stable $N_{\omega ,\text{sp}}\le 0$ normal participants – the larger pressure gradient ${\overline{\varphi }}_{\omega }$ that causes blood flow oscillatory acceleration as well as the smaller pulse wave velocity $c_{pw}$. $N_{\omega ,\text{sp}}$ becomes positive primarily because $N_{\omega }$ (equation (28)) increases for larger ${\overline{\varphi }}_{\omega }$ and smaller $c_{pw}$, while $N_{\omega ,\text{threshold}}$ decreases for larger ${\overline{\varphi }}_{\omega }$ and smaller $c_{pw}$.

Table 3.

Each physiological term that contributes to the aneurysm physiomarker $N_{\omega ,\text{sp}}$ is tabulated for both patients and normal participants in three age groups. This includes the aorta diameter $A_m$, blood pressure gradient ${\overline{\varphi }}_{\omega }$ causing oscillatory accelerations, pulsatile contribution to wall shear ${\beta }_b$, heartbeat angular frequency $\omega$, and pulse wave velocity $c_{pw}$. The one-tailed Wilcoxon rank sum test was used to determine whether the larger median of one population (e.g. patients, $N_{\omega ,\text{sp}}>0$) is significantly greater than the smaller median of the other (e.g. patients, $N_{\omega ,\text{sp}}\le 0$). The p-values comparing patient and normal participant cohorts as well as the p-values comparing $N_{\omega ,\text{sp}}>0$ and $N_{\omega ,\text{sp}}\le 0$ are presented. Rejection of the null hypothesis at the 5% level is in bold.

	$N_{\omega ,\text{sp}}>0$					$N_{\omega ,\text{sp}}\le 0$
	${\overline{\varphi }}_{\omega }$ m/s2	$c_{pw}$ m/s	$A_m$ cm2	${\beta }_b$ none	$\omega$ 1/s	${\overline{\varphi }}_{\omega }$ m/s2	$c_{pw}$ m/s	$A_m$ cm2	${\beta }_b$ none	$\omega$ 1/s
Patients (Age<40)
median	7.7377	5.2650	7.5719	42.0645	7.1400	7.7079	7.3322	5.8507	38.2583	8.3087
p-value between $N_{\omega ,sp}$	0.4699	0.0014	0.0168	0.13006	0.3706	-	-	-	-	-
p-value between cohorts	0.2648	0.4666	0.0358	0.1572	0.3144	0.0113	0.0113	0.3517	0.5218	0.4008
Normal participants
median	7.5684	5.0998	6.4396	39.7752	8.0143	6.2113	6.3452	5.6152	36.9418	8.4361
p-value between $N_{\omega ,sp}$	0.0081	5 × 10−6	0.0533	0.1054	0.4539	-	-	-	-	-
Patients (40 ≤ Age < 60)
median	7.1694	5.3235	9.0482	43.0926	8.1812	6.4033	7.8868	8.9853	44.5748	7.7121
p-value between $N_{\omega ,sp}$	0.1230	3 × 10−8	0.3522	0.17438	0.4378	-	-	-	-	-
p-value between cohorts	0.0966	0.0335	0.0526	0.1905	0.2701	0.2821	0.0528	0.0153	0.0018	0.5028
Normal participants
median	9.1976	6.0647	7.1551	40.2202	8.3585	7.2424	7.5973	7.7359	40.4069	7.8228
p-value between $N_{\omega ,sp}$	0.0092	0.0286	0.3518	0.4939	0.2515	-	-	-	-	-
Patients (Age ≥ 60)
median	6.6368	4.2547	10.2915	43.5787	7.5166	6.7577	8.5646	10.1875	43.5171	7.4592
p-value between $N_{\omega ,sp}$	0.3181	6 × 10−9	0.2232	0.3592	0.4268	-	-	-	-	-
p-value between cohorts	-	-	-	-	-	0.3190	0.2551	0.0039	0.0107	0.1911
Normal participants
median	-	-	-	-	-	6.9007	8.3760	8.5243	39.8121	7.7121
p-value between $N_{\omega ,sp}$	-	-	-	-	-	-	-	-	-	-

For the youngest age group (Age < 40), the dominant factor is larger (p = 0.0081) pressure gradient ${\overline{\varphi }}_{\omega }$. That is, normal participants with unstable aneurysm physiomarker $N_{\omega ,\text{sp}}>0$ exhibit larger ${\overline{\varphi }}_{\omega }$ compared to normal participants with a stable aneurysm physiomarker $N_{\omega ,\text{sp}}\le 0$ in a one-tailed Wilcoxon rank sum test. The role of greater blood flow acceleration is well established as a qualitative marker in aneurysm development; hypertension is well acknowledged as a risk factor in aneurysm formation and growth⁴¹ and has been implicated in modulating the morphology of unstable aneurysms⁴².

In the middle age group (40 ≤ Age < 60), the pressure gradient ${\overline{\varphi }}_{\omega }$ is likewise significantly higher for unstable aortic flow $N_{\omega ,\text{sp}}>0$. The second factor that appears is smaller (p = 0.029) pulse wave velocity $c_{pw}$, which indicates lower aortic stiffness. Compliant aortic walls distend farther and can sustain more unstable flutter modes under the same pressure gradient compared to stiffer aortas characterized by higher $c_{pw}$. Thus, the natural stiffening of the aorta with age for healthy participants serves to protect against further dilatation. This explains why the oldest age group (Age ≥ 60) has no normal participants exhibiting $N_{\omega ,\text{sp}}>0$.

3.3. Aneurysm development in patients with respect to age.

In the patient cohort (Table 3), flutter instability aneurysm physiomarker $N_{\omega ,\text{sp}}>0$ is mainly driven by a smaller pulse wave velocity $c_{pw}$ compared to patients experiencing stable flow $N_{\omega ,\text{sp}}\le 0$. In the youngest age group (Age < 40), we observe that aortic area $A_m$ is likewise significantly higher for patients with positive aneurysm physiomarker values. This matches clinical observations of increased dilatation risk with larger aneurysm size⁶. As before, $N_{\omega ,\text{sp}}$ becomes positive primarily because $N_{\omega }$ (equation (28)) increases and $N_{\omega ,\text{threshold}}$ decreases for smaller $c_{pw}$. Larger aortic area also leads to increased $N_{\omega }$ and, to a lesser extent, increased $N_{\omega ,\text{threshold}}$, such that the aneurysm physiomarker (equation (28)) increases overall.

In every age group for the patient cohort, the median pulse wave velocity is significantly lower for patients with unstable aortic flows $N_{\omega ,\text{sp}}>0$ compared to stable patients $N_{\omega ,\text{sp}}\le 0$. This suggests that greater wall distensibility plays a dominant role in facilitating growth of larger, developed aneurysms in the patient cohort. Permanent dilatation occurs when the aortic wall weakens and becomes less stiff. Such a process can form a self-perpetuating cycle, since thinning of the intimal and medial layers during aneurysm expansion increases aortic distensibility, which supports further dilation by increasing aortic wall susceptibility to unstable flutter modes.

A summary of clinical observations on how aneurysm distensibility evolves during disease progression is provided in Table S3. As noted earlier, the aortic wall degrades due to elastin and smooth muscle loss through aneurysm enlargement ^9;10;11. Hereafter, collagen deposition either stiffens the aortic wall (no further growth; Type 1), or the aortic wall weakens due to lack of collagen deposition, wall inflammation, and/or adipocyte accumulation (Type 2)¹⁶. The latter can lead to eventual dissection or rupture¹¹.

Our proposed aneurysm physiomarker provides support for these clinically observed pathways. Patients who exhibit stable flows $N_{\omega ,\text{sp}}\le 0$ have significantly larger pulse wave velocities and therefore fall within the Type 1 "stiff" aneurysm group. On the other hand, every patient age group with unstable aortic flows $N_{\omega ,\text{sp}}>0$ has significantly lower pulse wave velocity than stable patients in the same age group. Thus, patients whose compliant aortic walls fail to respond and lay down collagen remain vulnerable to growth driven by the flutter instability. This indicates that unstable patients possess Type 2 "soft/at-risk" aneurysms.

3.4. Cross cohort comparisons of aneurysm drivers.

Next, we compare different physiological properties driving aneurysm growth between the normal participant cohort and the patient cohort.

In the youngest age group (Age < 40), the stable $N_{\omega ,\text{sp}}\le 0$ patient cohort exhibits a significantly larger median pulse wave velocity than stable normal participants. This further reinforces the clinical observation that the branch of aneurysm progression toward the stable Type 1 aneurysm is marked by stiffening of the aortic wall that prevents additional dilatation. Similarly, the unstable $N_{\omega ,\text{sp}}>0$ patient cohort exhibits a significantly smaller median pulse wave velocity than stable (p=5 × 10⁻⁴) normal participants. Thus, unstable patients comprise the second trajectory of aneurysm development – the Type 2 aneurysm group for which increased wall distensibility triggers further growth.

As the age of normal participants increases through the three defined groups, we observe that the pulse wave velocity of stable normal participants $N_{\omega ,\text{sp}}\le 0$ increases significantly from (Age < 40) to (40 ≥ Age < 60) with (p =0.0011), as well as from (40 ≥ Age < 60) to (Age ≥ 60) with (p = 0.0011). This reflects the natural stiffening of the aorta with age and also serves to protect against unstable flutter. However, we note that the median pulse wave velocity of the youngest (Age < 40) stable normal participant cohort is still significantly larger than that of unstable patients of any age group. The Type 2 progression of aortic aneurysms therefore marks a diseased state in which distensibility increases abnormally above reference, healthy values due to wall remodeling. This disease trajectory is especially prominent in the oldest age group (Age ≥ 60), where the pulse wave velocity for the unstable patient cohort is significantly lower than that of the stable normal participant cohort (p =5 × 10⁻⁷). Natural stiffening of the aorta has entirely failed to kick in for the unstable patient cohort and is replaced by aneurysmal weakening of the wall. Thus, the trends obtained for our ab initio aneurysm physiomarker are in good agreement with observed tissue biology during aneurysm development and it provides a quantitative, noninvasive prediction of anticipated growth.

The aneurysm physiomarker trends also elucidate other physiological drivers that contribute to abnormal aortic dilatation. For instance, we observe that the initial growth of aneurysms in normal participants is driven mainly by a significantly larger pressure gradient ${\overline{\varphi }}_{\omega }$ for (Age < 40) and (40 ≥ Age < 60). Without the associated wall stiffening to constrain these unstable modes, due to a failure to remodel or insufficient response time relative to growth progression, abnormal aortic dilatation occurs. Meanwhile, the abnormal growth of aneurysm in the patient cohort for all age groups is driven primarily by lower pulse wave velocity, as we have already examined in depth. Thus, the fundamental physiology responsible for aneurysm progression varies significantly depending on whether the participant is in an earlier or later stage of the disease. Different treatment options and drug targets would then be necessary to address the root cause of abnormal growth for each patient depending on the dominant physiological property associated with or triggering the flutter instability. Quantitatively, this can be defined by measuring the sensitivity of $N_{\omega }$ to factors like pressure gradient ${\overline{\varphi }}_{\omega }$ associated with blood oscillatory acceleration and pulse wave velocity $c_{pw}$. For instance, if reducing ${\overline{\varphi }}_{\omega }$ to a manageable level would bring the aneurysm physiomarker $N_{\omega }$ below 0, indicating stable flow, then blood pressure management may be the preferred course of treatment for a patient.

Finally, we note that the median aortic area $A_m$ and oscillatory wall shear coefficient ${\beta }_b$ are both significantly larger for stable patients compared to stable normal participants in the age groups (40 ≥ Age < 60) to (Age ≥ 60). In the same age groups however, these two physiological properties are not significantly different between stable patients and unstable patients, nor for stable normal participants and unstable normal participants. This suggests that larger $A_m$ and ${\beta }_b$ accompany disease progression and may differentiate between participants who have already experienced aortic dilatation, but not necessarily drive further, abnormal growth on a consistent basis.

In existing literature, many ambiguous observations surround each of the individual physical properties examined in Table 3. For instance, a definite relationship between hypertension and aneurysm growth is not apparent¹³, especially since patients without hypertension can likewise experience both aneurysm growth and rupture⁴². High blood pressure is often interpreted as the mechanism driving increased shear stress along the aortic walls, but both high wall shear stress, low wall shear stress, and the spatio-temporal heterogeneity of wall shear stress have been implicated in wall remodeling and aneurysm growth^14;43. Similarly, larger aortic size is known to correlate with increasing risk of rupture⁶, but it is unclear why this is the case.

The aneurysm physiomarker presented in the current work explains not just how these properties trend at the cohort level, but also reveals the mechanism of how they interact explicitly in each patient. For instance, this aneurysm physiomarker framework suggests a future study to clearly delineate the role of shear stress in driving flutter at different parametric conditions. Under varying values of aortic area $A_m$, pulse wave velocity $c_{pw}$, and other physiological variables, wall shear can exhibit nonlinear, non-monotonic dependencies with $N_{\omega ,\text{sp}}$ that may account for the significant breadth of prior clinical observations.

The proposed aneurysm physiomarker clarifies the role of each physical property in driving the flutter type instability and delineates the threshold which separates stable aneurysms from unstable growth. These physiological properties cannot be used to predict abnormal dilatation on their own without knowing their relative, quantitative role in driving or inhibiting aneurysm growth for each patient – this, we propose, is the key problem resolved by the aneurysm physiomarker $N_{\omega ,\text{sp}}>0$.

3.5. Limitations.

While 4D flow MRI provides a resolved spatial view of flow variables and aneurysm dimensions, it is time limited to a window of one single heartbeat. The physiological variables measured in this interval may not necessarily be representative of a patient’s average daily hemodynamic flow conditions. Variability in physiological properties is not described.

3.6. Sensitivity analysis.

Thus, we gauge the local sensitivity of the aneurysm physiomarker toward uncertainty in the measurement of the input physiological properties. This analysis also estimates the error incurred by the constant kinematic viscosity value $\nu$ assumed for every participant; the finite spatial and temporal resolution of 4D flow MRI (S1.7); and retest variation⁴. Table 1 reports the resulting change in $N_{\omega ,\text{sp}}$ given an $ϵ\in [5,10,15]\%$ variation of the individual parameters around the measured values for the patient cohort. The aneurysm physiomarker proves most sensitive to the pulse wave velocity $c_{pw}$ and pressure driven acceleration ${\overline{\varphi }}_{\omega }$, both of which are measured algorithmically from the mean cross-sectional velocity calculated from 4D flow imaging (S1.8). The kinematic viscosity $\nu$ is of tertiary yet nonnegligible importance; a rigorous method to calculate blood viscosity and density through imaging or other non-invasive methods is therefore highly desirable, but out of the scope of the current work.

Table 1.

The fundamental physiological properties (e.g. pressure driven acceleration ${\overline{\varphi }}_{\omega }$) that contribute to evaluating the aneurysm physiomarker $N_{\omega ,\text{sp}}$ for 117 patients are varied by a total range of $2ϵ\%$ around either the measured value or the assumed constant value (kinematic viscosity) in a local sensitivity analysis (e.g. ${\overline{\varphi }}_{\omega }\pm (ϵ\%){\overline{\varphi }}_{\omega }$). $ϵ$ is varied from 5 to 15. The magnitude of the resulting change $\Delta N_{\omega ,\text{sp}}$ (e.g. $\mid N_{\omega ,\text{sp}}({\overline{\varphi }}_{\omega }+(ϵ\%){\overline{\varphi }}_{\omega })-N_{\omega ,\text{sp}}({\overline{\varphi }}_{\omega }-(ϵ\%){\varphi }_{\omega })\mid$) is reported as mean ± standard deviation.

	${\overline{\varphi }}_{\omega }\pm (ϵ\%){\overline{\varphi }}_{\omega }$ m/s2	$c_{pw}\pm (ϵ\%)c_{pw}$ m/s	$A_m\pm (ϵ\%)A_m$ cm2	$\nu \pm (ϵ\%)\nu$ m2/s	$\omega \pm (ϵ\%)\omega$ 1/s
$\Delta N_{\omega ,\text{sp}}(ϵ=5)$	0.31 ± 0.18	0.33 ± 0.19	0.17 ± 0.11	0.18 ± 0.11	0.15 ± 0.09
$\Delta N_{\omega ,\text{sp}}(ϵ=10)$	0.61 ± 0.36	0.66 ± 0.39	0.35 ± 0.22	0.35 ± 0.22	0.30 ± 0.17
$\Delta N_{\omega ,\text{sp}}(ϵ=15)$	0.92 ± 0.54	0.99 ± 0.59	0.52 ± 0.32	0.53 ± 0.33	0.46 ± 0.25

Fig. S5 shows that the resulting area under the curve (AUC) of the aneurysm physiomarker as a binary predictor for abnormal growth still exceeds 0.99 even for an $ϵ\%=5\%$ variation of the input parameters around their measured or assumed constant value (e.g. kinematic viscosity). The AUC drops to 0.98 for an $ϵ\%=10\%$ variation, and to 0.94 for $ϵ\%=15\%$. Given the maximum change in $\Delta N_{\omega ,\text{sp}}$ shown by Table 1 for $ϵ\%=5\%$, an uncertainty band of ±0.33 around the marginal stability case $N_{\omega ,\text{sp}}=0$ can be defined. That is, $N_{\omega ,\text{sp}}$ which fall in this band may swing between positive and negative values given natural deviation or measurement error of the physiological input parameters, such as pulse wave velocity $c_{p}w$. This uncertainty band occupies about 6% of the total range in measured aneurysm physiomarker values [−2.00, 9.13] within the patient cohort. The size of the uncertainty band increases to 12% for $ϵ=10$ and 18% for $ϵ=15$. Thus, uncertainty in the aneurysm physiomarker scales linearly with measurement error. In scenarios where $N_{\omega ,\text{sp}}\approx 0$ falls near the marginal stability state, repeat imaging and more frequent clinical follow-ups are therefore recommended to accurately quantify the physiomarker and predict future abnormal growth for the patient.

3.7. Imaging limitations.

Note that in this study, we have used clinical CT or MR measurements of aortic dimensions to asses growth over time. These measurements are subject to uncertainty due to need for manual selection of an oblique measurement plane, with intra- and inter-observer error rates around 5% in either modality^45;46. From the prognosis patient cohort, we have conducted a reproducibility analysis on the diameter measurement of SOV and MAA, finding a mean inter-observer error of 4.5% and 4.2% respectively over a set of 35 images each. This agrees with the inter-observer error of 5% reported in literature. Of the 35 SOV images, 5 were from CT; meanwhile, 4 of the 35 MAA images were from CT.

Additionally, there may be considerable discrepancy when different imaging modalities such as MRI or CT are used to measure patients’ SOV and MAA diameters at follow-up if measurement standards are not met⁴⁷. However, there appears to be no significant difference in maximum aortic root diameter, ascending aorta diameter, and aortic arch diameter measured using CT and MRI when the same techniques are used (e.g. inner lumen to inner lumen or outer lumen to outer lumen)⁴⁸. Since growth was tracked in this study only at the sinus of valsalva and maximal-area ascending aorta, the low mean differences between imaging modalities (0.2 mm for aortic root, 0.3 mm for the proximal ascending aorta)⁴⁸ suggests that growth rates > 0.2 cm can be meaningfully distinguished.

To test the effect of measurement error, we introduce 5% Gaussian noise (mean 0%, standard deviation 5%, truncated ±5%) to the diameter reported at every time point for all patients. The process was repeated 1000 times, yielding the mean 0.90 and standard deviation 0.02 for the AUC of the aneurysm physiomarker as a binary predictor of abnormal growth > 0.24 cm/year. The mean AUC increases to 0.92 when the threshold for abnormal growth is increased to 0.4 cm/year so that the signal threshold exceeds the average noise level. Thus, the performance of the aneurysm physiomarker is robust against the presence of aortic diameter measurement error in this comparative validation.

Note that adding this much random noise can effectively kill any robust measurement of growth through imaging. Even for a very conservative clinical intervention threshold of 0.5 cm/year, a potential intraobserver error of 0.2 cm means that an actual growth rate of 0.1 cm/year can be mistaken for 0.5 cm/year and vice versa. With the input of 5% error, the uncertainty band for direct diameter measurements via imaging is therefore 40% of the range of growth rates; the one order of magnitude lower 6% uncertainty of the aneurysm physiomarker suggests that it outperforms the current clinical standard in tracking abnormal aortic growth.

3.8. Modeling assumptions.

The prediction of flutter in this work is a linear approximation, in the sense that the aneurysm physiomarker measures whether flutter occurs given the patient’s current imaged physiological properties. It does not account for changes in physiological properties like blood pressure, aortic stiffness, aortic size, etc. from year to year. In essence, we are positing that observed flutter now is clinically indicative of abnormal growth in the future. This can be ameliorated by more frequent surveillance such as annual or bi-annual imaging for at-risk patients identified via $N_{\omega ,\text{sp}}>0$.

The data analyzed for this study have all originated from one site. Patients were selected without any precondition on inclusion that might explicitly bias the cohort composition in any way with respect to the aneurysm physiomarker; however, future work that investigates predictive performance from prospective data acquired across multiple sites would strengthen confidence for interpretation of our results.

We have conducted a linear stability analysis of a 1D blood vessel model. The immediate advantage is that the problem becomes tractable and yields a closed form solution. However, nonlinear damping or instability inducing effects may become important in certain flow conditions. Note additionally that the flutter instability examined in this work is primarily caused by pressure driven deformation of the aortic wall through the tube law. This flutter is therefore different from the shear induced destabilization of the channel walls induced by the Kelvin-Helmholtz type instability explored in prior literature¹⁸. Although we have shown that the pressure mediated flutter instability analyzed in this work is strongly associated with abnormal aneurysmal growth, a follow-up study of shear driven wall instabilities¹⁸ is of strong interest, though outside the scope of the current work.

Lastly, the asymmetry, curvature, and branching of the full 3D aortic geometry may also play a role. However, 1D models have in general been well validated against 3D clinical data⁴⁹;⁵⁰;^51;1. The reduced order 1D model we formulate from first principles preserves the key biomechanical features of the actual human aorta – flow pulsatility, wall elasticity, local blood acceleration and shear, etc. – while allowing the system to experience blood-wall interaction instability. The only factor missing is the complex 3D geometry of the system, but it would enter as higher order geometric correction terms to the core biomechanical mechanisms already described. That is, the underlying dimensionless number $N_{\omega }$ derived would not change because the core physics remain the same.

If the 1D model was not sufficient, then the critical threshold predicted by 1D model would not agree with clinical data. However, good agreement is observed. Experimentally, the 3D character of the actual system is injected in an average sense into our analysis via the actual area and pressure driven acceleration locally measured along the centerline through 4D flow MRI. These local flow values carry the effect of a complex 3D geometry as input into the 1D model. However, anatomical heterogeneity (lumen concavity, convexity, angulation, etc.) could undoubtedly impact the pressure-wall interaction beyond what the flow information can carry into the model. Additional data would be necessary to quantify how less axisymmetric anatomical domains influence generalization of $N_{\omega ,\text{sp}}$. This is a challenging task ripe for future work.

4. Conclusion

In this work we analyzed an instability-driven growth mechanism of aortic aneurysms from first principles through a linear stability analysis of flow through an elastic blood vessel. The perturbation equations around the base flow gives us a dispersion relation between the temporal growth rate of each flutter mode and its wave number. Floquet theory is used to account for the parametric effect of the heartbeat frequency—essentially, the oscillatory blood flow waveform.

The important parameters determining the onset of unstable flutter—including viscosity, vessel diameter, pressure gradient that drives acceleration, etc.—are collected in a single dimensionless number. Akin to the role of the critical Reynolds number in describing the onset of turbulence, the critical threshold of the dimensionless number tracks the transition of the system to the flutter type instability. If this flutter instability parameter (dimensionless number minus its critical threshold) exceeds zero at a local cross-section of the blood vessel, the growth of perturbation modes may trigger the abnormal dilatation of the local blood vessel. We therefore hypothesize that an aneurysm will form or grow at the site. Otherwise, perturbation amplitudes decay in time, and the location remains stable to this flutter mechanism.

Through follow-up analysis in a group of patients with suspected aortopathy, we’ve shown that the flutter instability parameter may serve as an aneurysm physiomarker to forecast aneurysm growth. The only input to calculate the aneurysm physiomarker for each patient was a baseline 4D flow magnetic resonance imaging scan taken during the initial visit. We found that this aneurysm physiomarker predicts abnormal aortic growth and/or surgical intervention at clinical follow-up with high accuracy, specificity, and sensitivity.

This ab initio aneurysm physiomarker has the potential to become a predictive diagnostic tool for aneurysm development. It captures the observed qualitative population trends in participants and clarifies the qualitative growth modes of nascent aortic dilation vs. the evolution of large, developed aneurysms. Here, we have presented a full derivation of the aneurysm physiomarker, tested its potential for diagnostic capability, and contextualized it as a fundamental mechanistic precursor to aneurysm formation and growth.

5. Methods

5.2. Overall patient cohort.

Patients were respectively identified from a database of patients who underwent a clinical cardiothoracic MRI exam, including 4D flow MRI, at Northwestern Memorial Hospital between 2011 and 2019. Inclusion criteria were referral for clinical imaging assessment of aortic dimensions and a normal tricuspid aortic valve (TAV). Exclusion criteria were presence of aortic valve stenosis (mild to severe), ejection fraction lower than 50%, or bicuspid aortic valve. In addition, patients with 4D flow MRI data that have not undergone dedicated analysis (eddy current and concomitant phase corrections, aortic 3D segmentation) were excluded. A summary of the selection process with inclusion and exclusion counts is given in Fig. S2.

A total of 125 patients were identified for inclusion in this study. Of these, 8 patients were excluded due to 4D flow MRI imaging artifacts, resulting in 117 patients for this study. All patients in this HIPAA compliant study were retrospectively included with approval from the Northwestern University Institutional Review Board (IRB) and IRB-approved waiver of consent. Records were de-identified prior to analysis.

5.3. Healthy participant cohort.

For comparison to the overall patient cohort, a total of 100 healthy control participants were included, evenly distributed across a wide range of ages and sexes (age range 19 years to 79 years, 50% female). The 100 healthy participants included were selected from a group of healthy participants who had been prospectively enrolled for research MRI exams under a separate IRB-approved protocol. Informed consent was provided by all study participants. The group of 100 healthy control participants selected for analysis was created by taking the first ten (chronological order) recruited participants of each sex, divided into the age ranges of 19-30, 31-40, 41-50, 51-60, and 61-79 years. The control cohort demographics are summarized in Table 2.

Table 2.

Characteristics of the study cohort are summarized as mean ± standard deviation and [minimum,maximum] of range or [percentage] values. Prognosis aortopathy patients had clinical follow-up data and were analyzed for growth rate validation of the aneurysm physiomarker; other patients did not have follow-up data. The p-values are reported for a Wilcoxon rank sum test between cohort statistics of healthy participants and all aortopathy patients.

	normal participants $(n=100)$	all aortopathy patients $(n=117)$	p-value	prognosis aortopathy patients $(n=72)$
age (years)	46.2±15.5 [19,79]	57.4±14.2 [22,86]	2 × 10−7	58.6±11.9 [29,79]
sex (female)	50 [50%]	35 [30%]	1.5 × 10−3	17 [24%]
height (m)	1.71±0.11 [1.30,1.96]	1.73±0.15 [1.14,2.03]	7.4 × 10−3	1.76±0.13 [1.40,2.03]
weight (kg)	79.2±17.9 [47.6,142.9]	84.8±18.1 [45.5,140.9]	3.5 × 10−2	86.5±19.2 [45.5,140.9]
follow-up (years)	-	-	-	5.86 ± 1.77 [1.13,8.67]

5.4. Subcohort for patient outcomes classification.

To evaluate the predictive performance of $N_{\omega ,\text{sp}}$, a subcohort (labeled prognosis aortopathy patients) was created for patients with follow-up measurement of aortic dimensions. The inclusion criterion was having magnetic resonance angiography (MRA) or computed tomography angiography (CTA) aortic dimensions assessment within five years of initial 4D flow imaging. Exclusion criteria for this subcohort were presence of genetic tissue disorders, congenital heart malformations, and history of aortic or mitral valve repair occurring before the 4D flow imaging analyzed (Fig. S2). Of the 117 patients, 25 patients lacked follow-up imaging, 3 had a history of dissection, 14 history of aortic repair, and 3 had Marfan syndrome. The final prognosis patient subcohort included 72 patients.

In this subcohort of patients, two outcomes were quantified: “growth” and “surgery”. The aortic diameter growth was assessed from radiological measurements taken with CT or MR angiography imaging, which included standardized assessment of the maximal-area ascending aorta (MAA) and the sinus of valsalva (SOV) diameters in double-oblique view. During the follow-up period, any intervention, such as valve repair or aortic graft placement, that occurred after the 4D flow imaging was used to categorize patients as having “surgery” outcomes. Additional details of image acquisition and processing are described in Supplementary S1.7 and S1.8, respectively.

As an illustration of how growth outcomes are calculated, the maximum of the SOV and MAA diameters recorded during each clinic visit (${\text{SOV}}_{\max }$ and ${\text{MAA}}_{\max }$ ) are presented in two time series after the initial MRI at year 0 (Fig. S4A, S4B). The growth rate was then calculated as the maximum rate of change over time between consecutive pairs of follow-up assessments. That is, the maximum SOV growth rate was characterized as $\Delta {\text{SOV}}_{\max }=\underset{\forall t}{\max }\left(\frac{d{\text{SOV}}_{\max }}{dt}\right)$, and the maximum MAA growth is characterized as $\Delta {\text{MAA}}_{\max }=\underset{\forall t}{\max }\left(\frac{d{\text{MAA}}_{\max }}{dt}\right)$. A diameter change in SOV or MAA of 0.24 cm/year or greater was then categorized as an abnormal “growth” outcome for the patient.

An example of a patient’s time-series is shown in Fig. S4A, where $\Delta {\text{SOV}}_{\max }=0.05$ cm/year due to a stepwise jump in measured ${\text{SOV}}_{\max }$ between years 2 to 3. This growth rate is defined analogously for the maximum MAA diameter; Fig. S4B gives $\Delta {\text{MAA}}_{\max }=0.14$ cm/year for the same patient. Since $\Delta {\text{MAA}}_{\max }<0.24$ cm/year, $\Delta {\text{SOV}}_{\max }<0.24$ cm/year, and this patient also did not undergo any surgery during follow-up, the classification "no growth or surgery" was applied.

Data Availability

The main data supporting the findings of this study are available within the paper and its Supplementary Information. The raw clinical data in the study are too large to be publicly shared, yet they are available for research purposes from the Markl group (co-author) on reasonable request.

Code availability

Codes for the collection and analysis of data are available on request.