Abstract
Hepatic glucose metabolism serves dual purposes: maintaining glucose homeostasis and converting glucose into energy sources; however, the underlying mechanisms are unclear. We quantitatively measured liver metabolites, gene expression, and phosphorylated insulin signaling molecules in mice orally administered varying doses of glucose, and constructed a transomic network. Rapid phosphorylation of insulin signaling molecules in response to glucose intake was observed, in contrast to the more gradual changes in gene expression. Glycolytic and gluconeogenic metabolites and expression of genes involved in glucose metabolism including glucose-6-phosphate, G6pc, and Pck1, demonstrated high glucose dose sensitivity. Whereas, glucokinase expression and glycogen accumulation showed low glucose dose sensitivity. During the early phase after glucose intake, metabolic flux was geared towards glucose homeostasis regardless of the glucose dose but shifted towards energy conversion during the late phase at higher glucose doses. Our research provides a comprehensive view of time- and dose-dependent selective glucose metabolism.
Subject terms: Dynamical systems, Dynamic networks, Time series
Introduction
Glucose is an important constituent of tissues and blood. Most cells utilize glucose as the principal and indispensable energy source1. Blood glucose level is tightly controlled in humans and mammals within a narrow range; this tight regulation is referred to as blood glucose homeostasis. Impaired glucose homeostasis can cause serious disorders including seizure or loss of consciousness in the case of hypoglycemia and diabetic ketoacidosis in the case of hyperglycemia2. The liver plays a key role in maintaining blood glucose homeostasis during both fasting and postprandial periods3–6. Hepatic glucose production is responsible for ∼90% of endogenous glucose production during fasting7. After dietary glucose intake, the liver buffers the blood glucose level to maintain glucose homeostasis and converts glucose into other energy sources such as glycogen, amino acids, and lipids8. These regulations collectively prevent either hypoglycemia or hyperglycemia and lead to the storage of energy in the body for future utilization.
Oral glucose administration, also known as the glucose challenge test, is clinically used to detect the efficiency of the body to dispose of glucose after an oral glucose load or meal9,10. Glucose administration triggers the release of insulin from the pancreas and a series of complex biological reactions to maintain glucose homeostasis through multiple organs including the liver11. One of the key mechanisms that regulate postprandial liver metabolism is the insulin signaling pathway. Insulin is an important hormone that triggers multiple metabolic changes in various organs including the liver. Insulin binds to the insulin receptor and causes tyrosine phosphorylation of intracellular substrate proteins known as insulin-responsive substrates (IRS). IRS bind to signaling molecules including phosphoinositide 3-kinase and thus activates insulin signaling12. The activation of insulin signaling in the liver promotes glycogenesis and suppresses gluconeogenesis through the activation of AKT and extracellular signal-regulated kinase (ERK)13,14. Insulin signaling also regulates protein abundance through transcriptional or translational regulation, including the expression of glucokinase (Gck) and phosphoenolpyruvate carboxykinase 1 (Pck1)15,16. In addition, altered metabolite concentrations after glucose administration also influence multiple metabolic pathways including glycolysis, gluconeogenesis, glycogenesis, amino acid metabolism, and lipid metabolism by regulating the abundance of substrates and products and the allosteric regulation of metabolic enzymes14,16–18.
Glucose metabolism involves the coordination of multiple processes including gene expression, protein synthesis, and substrate regulation. However, few studies have investigated the dose-dependent features of dynamic glucose metabolism including glucose dose sensitivity and response time after glucose administration in vivo across various types of metabolic regulation19,20. In this study, we investigated these features using transomic analysis. We previously proposed transomic analysis to construct a global regulatory network for metabolism with multi-omics datasets21–23. We used this method to investigate the dose-dependent regulatory metabolism after treatment of cell models with insulin and the construction of differential networks between obese and healthy subjects24–29. We previously showed that the stimulation of FAO cells derived from rat hepatoma with different doses of insulin led to selective responses with different insulin sensitivities including the regulation of induced and basal insulin stimulation across multiple omics24,30. Metabolic responses across omics after glucose administration have also been observed in mice25.
Here, we constructed a transomic network of glucose metabolism by integrating western blotting, transcriptomic, and metabolomics data of the mouse liver following multiple doses of glucose administration. We identified time- and dose-dependent glucose-responsive molecules. We found features of different types of metabolism in terms of their glucose responsiveness and proposed high glucose dose sensitivity as a potential indicator of glucose homeostasis, and low glucose dose sensitivity as a potential indicator of energy conversion. We also investigated the dose-dependent features of dynamic flux using a kinetic model of the transomic network. We examined the glucose responsiveness of fluxes and provided a potential mechanism for time- and dose-dependent glucose conversion. We found that metabolic flux was geared towards glucose homeostasis regardless of the glucose dose. However, during the late phase (60–240 min), the flux shifted towards energy conversion, but only at higher glucose doses. Thus, our kinetic transomic analysis provides insights into the possible dynamic mechanism of central carbohydrate metabolism in the liver.
Results
Overview of the study approach
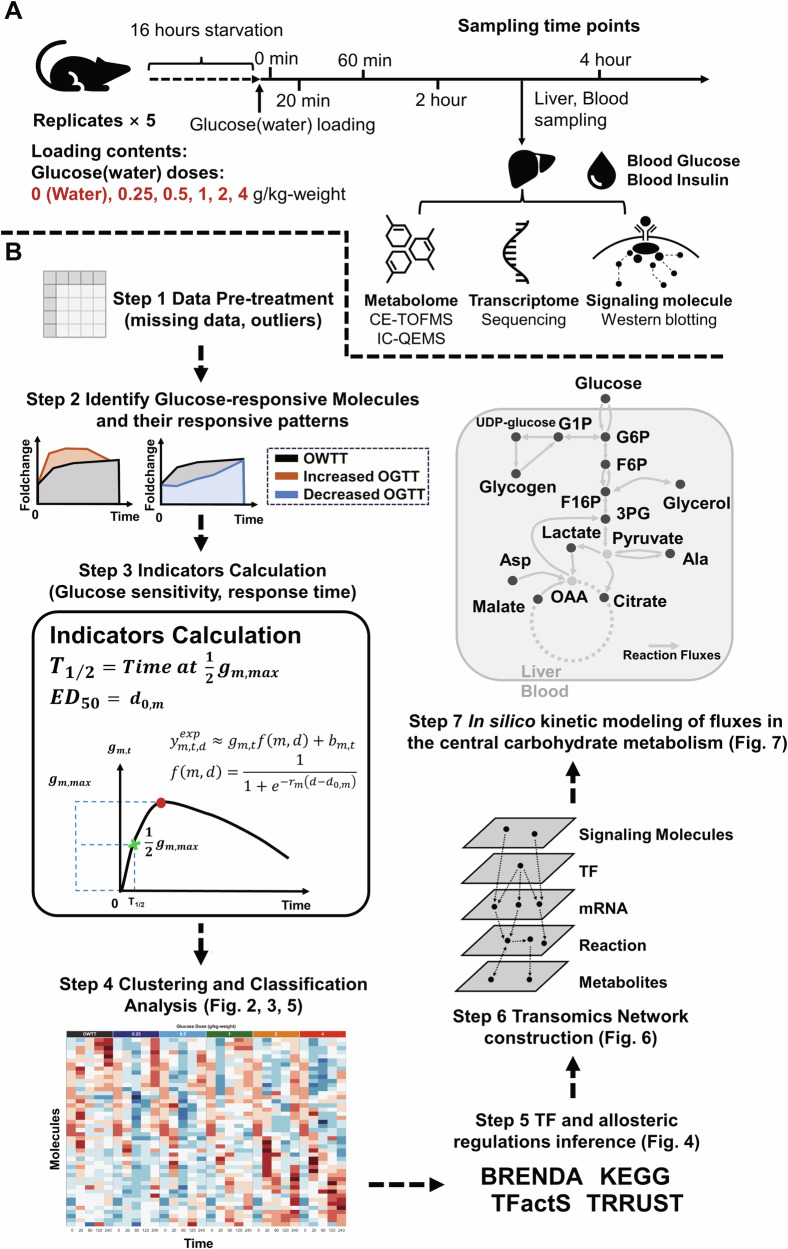
We fasted 10-week-old wild-type (WT) mice for 16 h and orally administered five different glucose doses (0.25, 0.5, 1, 2, 4 g/kg) or water. We collected the livers and blood samples at 0, 20, 60, 120, and 240 min after administration. We measured metabolite abundance (Metabolomics data, Supplementary Data 1), gene expression (Transcriptomic data, Supplementary Data 2), and total protein and phosphorylation levels of insulin signaling molecules (Phosphorylation data, Supplementary Data 3) in the liver samples; and blood insulin and glucose levels in the blood samples (Fig. 1A).
Fig. 1. Overview of the transomic analysis and kinetic modeling of dose-dependent glucose-responsive metabolism in the liver.
A We used WT mice and collected the liver and blood samples from 16 h-fasted mice after six doses of oral glucose administration. We measured the time series data of signaling molecules, gene expression, metabolites in the liver, glucose, and insulin in the blood. We used n = 5 as the mouse replicates for each time point in the analysis. B The seven steps for the analysis of time- and dose-dependent glucose metabolism in the transomic network in the liver.
We performed transomic analysis of dose-dependent glucose-responsive metabolism in the liver in seven successive steps (Fig. 1B). Among the measured omics data, we selected all molecules with at least three replicates for each time point in the analysis (Step 1). We excluded outliers of every molecule using the boxplot method31 (Supplementary Data 4). We defined molecules that responded both temporally and independently to water after glucose administration as glucose-responsive molecules (see “Methods” section). We identified the dose-dependent glucose-responsive molecules and their responsive patterns using the cleaned data (Supplementary Fig. 1; Step 2).
To understand the characteristics of the dose-dependent glucose-responsive molecules, we calculated the indicators of dose sensitivity and response time to glucose administration (Step 3; Supplementary Fig. 1). We evaluated the dose-dependent glucose responsiveness of molecules using two indicators: the dose required to achieve 50% of the maximal effect (ED50) and the half time to maximum response (T1/2). We also performed cluster and classification analyses of dose-dependent glucose-responsive metabolites and genes in terms of their time courses and glucose-responsiveness indicators (Step 4). We deduced the transcription factors (TFs) and allosteric modulation that regulate those glucose-responsive molecules using information from databases including Kyoto Encyclopedia of Genes and Genomes (KEGG) and BRaunschweig ENzyme DAtabase (BRENDA) (Step 5)32–34. Using the dose-dependent glucose-responsive metabolites, genes, phosphorylation level of insulin signaling molecules, TF, and allosteric regulation, we constructed a glucose-responsive transomic network of the mouse liver (Step 6).
Lastly, we conducted kinetic modeling of central carbohydrate metabolism of the transomic network and simulated the dynamic flux in the model after glucose administration (Step 7). Based on the simulated dynamic flux, we calculated the glucose responsiveness of the flux and dose sensitivities of their glucose responsiveness to modeling parameters. We also investigated whether glucose dose sensitivity can be an indicator of how glucose-responsive molecules and reactions are involved in energy conversion after glucose administration. Analyses of the glucose responsiveness of the simulated flux revealed time- and dose-dependent hepatic glucose metabolism for maintenance of glucose homeostasis and energy conversion.
Identification of dose-dependent glucose-responsive metabolites
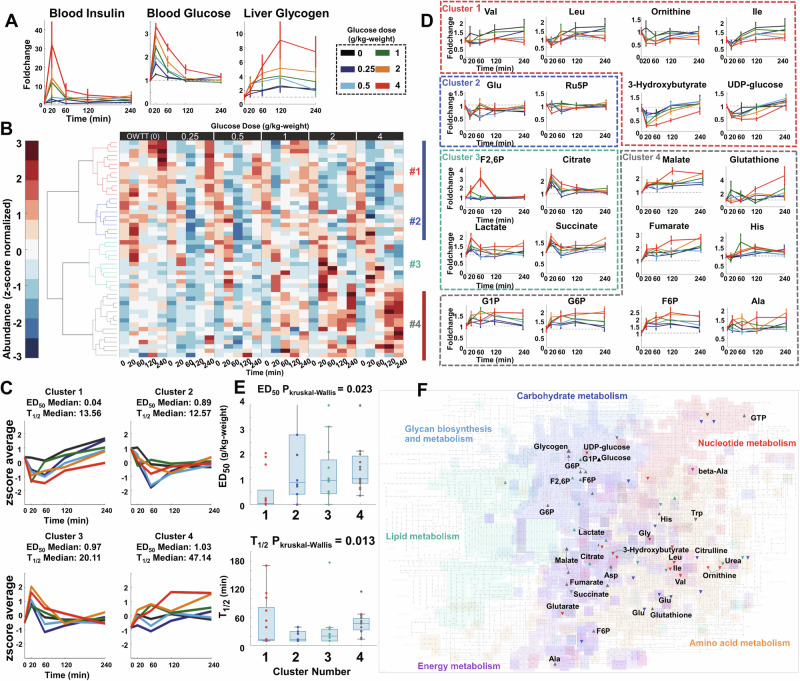
To construct the transomics network, we first identified dose-dependent glucose-responsive metabolites and calculate their glucose responsiveness for understanding the static responsive features of metabolome to glucose administration. After glucose administration, both the blood glucose and blood insulin level after all doses of glucose administration peaked at 20 min and decreased at about 120 min. By contrast, glycogen level gradually increased in the liver until at least 120 min (Fig. 2A).
Fig. 2. Identification of dose-dependent glucose-responsive metabolites.
A Time courses of blood insulin, blood glucose, and liver glycogen. B Hierarchical clustering of the time courses of dose-dependent glucose-responsive metabolites from the livers after administration of six doses of oral glucose (n = 5 mice per dose at all time points). Six-time courses for each metabolite were z-score normalized. Metabolites were ordered by hierarchical clustering using Euclidean distance and Ward’s method (Table 1, Supplementary Data 5). The colors of the dendrogram represent the clustering results (Red: Cluster 1, Blue: Cluster 2, Cyan: Cluster 3, Gray: Cluster 4). The color bar at the right of the heatmap represents their responsive patterns (Blue: Decrease, Red: Increase). C z-score average of time courses of metabolites in each cluster and the median ED50 and T1/2 of these clusters. This panel shared the same legend as Fig. 2A. D Examples of the time course of dose-dependent glucose-responsive metabolites in each cluster. The colors of the boxes show the clustering result of highlighted dose-dependent glucose-responsive metabolites. Data are shown as the mean and standard error of the mean (SEM) of five mice per dose. Metabolites are abbreviated as follows: Val valine, Leu leucine, Ile isoleucine, Trp tryptophan, Ser serine, F2,6P fructose 2,6-bisphosphate, G6P glucose-6-phosphate, F6P fructose 6-phosphate, G1P glucose 1-phosphate, Ala alanine. This panel shared the same legend as Fig. 2A. E Boxplot of ED50 (Top) and T1/2 (Bottom) for each cluster. Kruskal–Wallis tests for ED50 and T1/2 in each cluster were conducted to investigate whether there was statistical significance. The P values of Kruskal–Wallis tests are shown above the boxplot. F The dose-dependent glucose-responsive metabolites projected onto the KEGG metabolic pathways. The directions of the scatter marks represent their responsive patterns. The colors of the scatter marks represent the clustering result of these metabolites. Black scatter marks represent glucose or glycogen.
Among the 510 quantified liver metabolites, 119 had at least three replicates at each time point and were used for further quantitative analyses. Among the 119 metabolites, 50 were identified as dose-dependent glucose-responsive metabolites (Table 1, Supplementary Fig. 2, Supplementary Data 5) including 17 increased, 32 decreased metabolites and the liver glycogen.
Table 1.
Dose-dependent glucose-responsive metabolites
| Name | Pattern | Cluster | ED50 (g/kg-weight) | T1/2 (min) | Name | Pattern | Cluster | ED50 (g/kg-weight) | T1/2 (min) |
|---|---|---|---|---|---|---|---|---|---|
| 2-Hydroxybutyrate | Decrease | 1 | 0.00 | 10.81 | F2,6P | Increase | 3 | 3.98 | 23.12 |
| 3-Hydroxybutyrate | Decrease | 1 | 1.61 | 13.56 | Lactate | Increase | 3 | 1.01 | 10.00 |
| Glutarate | Decrease | 1 | 0.00 | 10.95 | Citrate | Increase | 3 | 0.44 | 10.00 |
| UDP-glucose | Decrease | 1 | 1.91 | 53.21 | Succinate | Decrease | 3 | 1.04 | 34.71 |
| Gly | Decrease | 1 | 2.07 | 39.29 | N-Acetylglutamate | Decrease | 3 | 3.12 | 10.00 |
| beta-Ala | Decrease | 1 | 0.00 | 10.00 | Taurocholate | Increase | 3 | 1.48 | 10.00 |
| 3-Aminoisobutyrate | Decrease | 1 | 0.00 | 10.00 | UDP-N-acetylglucosamine | Increase | 3 | 0.52 | 39.22 |
| 2AB | Decrease | 1 | 0.00 | 102.10 | Urea | Decrease | 3 | 0.00 | 35.52 |
| Val | Decrease | 1 | 0.16 | 11.38 | Hypotaurine | Decrease | 3 | 2.11 | 17.11 |
| Ile | Decrease | 1 | 0.24 | 74.79 | Pipecolate | Decrease | 3 | 0.00 | 24.74 |
| Leu | Decrease | 1 | 0.24 | 112.03 | Creatine | Decrease | 3 | 0.44 | 177.19 |
| Ornithine | Decrease | 1 | 0.00 | 10.00 | Phosphorylcholine | Increase | 3 | 0.93 | 10.00 |
| alpha-Aminoadipate | Decrease | 1 | 0.04 | 170.71 | G1P | Increase | 4 | 0.68 | 48.49 |
| Ru5P | Decrease | 2 | 2.80 | 10.00 | G6P | Increase | 4 | 0.86 | 47.14 |
| Sarcosine | Decrease | 2 | 0.97 | 25.26 | F6P | Increase | 4 | 0.85 | 52.66 |
| N,N-Dimethylglycine | Decrease | 2 | 4.14 | 10.00 | Fumarate | Increase | 4 | 1.71 | 52.47 |
| Hydroxyproline | Decrease | 2 | 0.00 | 10.00 | Malate | Increase | 4 | 2.03 | 63.80 |
| Glu | Decrease | 2 | 0.80 | 39.33 | S7P | Increase | 4 | 0.99 | 46.99 |
| Citrulline | Decrease | 2 | 0.73 | 10.00 | Mucate | Decrease | 4 | 1.52 | 16.63 |
| Adenosine | Decrease | 2 | 4.19 | 39.70 | Adenylosuccinate | Decrease | 4 | 4.04 | 67.25 |
| Inosine | Decrease | 2 | 0.00 | 30.14 | GTP | Increase | 4 | 0.36 | 39.18 |
| Saccharopine | Decrease | 2 | 1.99 | 13.39 | Ala | Increase | 4 | 1.03 | 13.78 |
| Ophthalmate | Decrease | 2 | 0.42 | 11.75 | Asp | Increase | 4 | 1.41 | 30.36 |
| Glucose | Increase | 1.26 | 10 | His | Increase | 4 | 0.62 | 39.10 | |
| Glycogen | Increase | 4 | 2.15 | 59.19 | Trp | Decrease | 4 | 0.92 | 31.54 |
| Glutathione(red) | Increase | 4 | 3.98 | 115.26 |
To classify these metabolites, we grouped them into four clusters using hierarchical cluster analysis, based on which had the largest silhouette value (Fig. 2B, Supplementary Figs. 2, 3). Metabolites in Clusters 1 and 2 both decreased until 20 or 60 min after glucose administration. After glucose administration, metabolites in Cluster 2 quickly recovered to water dose level after 120 min, whereas those in Cluster 1 did not (Fig. 2C). Metabolites in Cluster 1 include branched-chain amino acids (BCAAs, leucine [Leu] and valine [Val]), 3-hydroxybutyrate, and uridine diphosphate (UDP)-glucose while the Cluster 2 included metabolites such as citrulline and Glutamic acid [Glu] (Fig. 2D). The average time course of metabolites in Cluster 3 increased until 20 min after glucose administration, subsequently decreasing to the water dose level. These metabolites included citrate and succinate in the tricarboxylic acid cycle (TCA) cycle, as well as fructose 2,6-bisphosphate (F2,6BP) and lactate. Metabolites in Cluster 4 increased after glucose administration but did not recover. These metabolites included glucose-6-phosphate (G6P) in glycolysis; related molecules such as glucose 1-phosphate (G1P) and fructose 6-phosphate (F6P); glycogen in glycogenesis; fumarate and malate in the TCA cycle; and the amino acids alanine (Ala), histidine (His), and aspartate (Asp). Clusters 1 had low median ED50 and T1/2 values of less than 1 g/kg and 20 min, respectively, suggesting that metabolites in this cluster generally have high glucose dose sensitivity and a rapid response time to glucose administration. Cluster 2, on the hand, had higher median ED50 despite similar median T1/2 as Cluster 1. Metabolites in Cluster 3 responded to glucose with a slightly higher median T1/2 of 20.11 min, median ED50 of 0.91 g/kg. By contrast, metabolites in Cluster 4 had higher values of both median ED50 and T1/2 of 1.03 g/kg and 47.14 min, respectively, compared with other clusters. Median ED50 and T1/2 were significantly different among clusters (P < 0.05)35, indicating that glucose dose-responsive metabolites were characterized by different glucose dose sensitivities and response times (Fig. 2E). Metabolites in Clusters 1 had relatively higher glucose dose sensitivities to glucose administration than those in the other clusters, indicating that BCAAs, and 3-hydroxybutyrate have higher glucose dose sensitivities than the other metabolites. Metabolites in Cluster 4 had relatively slower response times with metabolites related with the central carbohydrate metabolism (Fig. 2F). These results indicate that the time course of metabolites after glucose administration reflects the features of their metabolic regulation. Metabolites, especially those related to carbohydrate and amino acid metabolism, responded differently in terms of their patterns and dose sensitivities to glucose administration.
Identification of dose-dependent glucose-responsive genes and insulin signaling molecules
As the transomics network also require layers for gene expressions and signaling molecules, we further identified dose-dependent glucose-responsive genes and insulin signaling molecules and calculate their glucose responsiveness to glucose administration. The expression of 55,487 genes or transcripts was measured, of which 6958 had at least three replicates for each time point and thus were used for further quantitative analyses. We identified 67 genes including 30 increased, 36 decreased, and 1 ambiguous (Rnf125) gene (Table 2, Supplementary Fig. 4, Supplementary Data 6). Our previous study identified 2420 (1369 increased and 1151 decreased) glucose-responsive genes in WT mice25. However, these results did not exclude the effects of water administration, and the pairwise test was used to compare the 0 min control with each time point rather than analysis of variance, which can detect a temporal change in the temporal dynamics of genes. Hence, the method we used in this study can better detect the dose-dependent features of glucose-responsive molecules.
Table 2.
Dose-dependent glucose-responsive genes
| Name | Pattern | Cluster | ED50 (g/kg-weight) | T1/2 (min) | Name | Pattern | Cluster | ED50 (g/kg-weight) | T1/2 (min) |
|---|---|---|---|---|---|---|---|---|---|
| G0s2 | Decrease | 1 | 1.57 | 106.9 | Cyp2a5 | Increase | 3 | 3.84 | 11.96 |
| Slc22a5 | Decrease | 1 | 0 | 89.67 | Slc16a10 | Decrease | 3 | 0 | 179.37 |
| Slc17a8 | Increase | 1 | 4.26 | 37.87 | Rtn4ip1 | Increase | 3 | 3.15 | 19.77 |
| Id2 | Decrease | 1 | 0.72 | 39.58 | Lpin1 | Increase | 3 | 1.94 | 73.11 |
| Arhgef3 | Decrease | 1 | 4.04 | 14.76 | Susd6 | Increase | 3 | 1.56 | 135.66 |
| Cdkn1a | Increase | 1 | 3.5 | 38.94 | Mtss1 | Increase | 3 | 4.28 | 39.79 |
| Ik | Decrease | 1 | 1.06 | 76.97 | Wdr12 | Decrease | 3 | 1.17 | 10 |
| Got1 | Increase | 1 | 2 | 140.4 | Upp2 | Increase | 3 | 0 | 10 |
| Rpf1 | Decrease | 1 | 4.16 | 17.06 | Pitpnm2 | Increase | 3 | 0.42 | 21 |
| Hnrnpdl | Decrease | 1 | 0.4 | 38.53 | Saa4 | Increase | 3 | 0.62 | 38.01 |
| Cfap20 | Decrease | 1 | 4.15 | 10 | Nrd1 | Decrease | 3 | 3.92 | 39.8 |
| Rnf125 | Decrease | 1 | Zfand2a | Increase | 3 | 1.05 | 88.83 | ||
| Hist1h1c | Decrease | 1 | 4.12 | 10 | Chd9 | Decrease | 3 | 0.44 | 120.7 |
| Tob1 | Increase | 1 | 2.17 | 88.46 | Saa2 | Decrease | 3 | 0.66 | 178.18 |
| Arhgap29 | Decrease | 1 | 0.3 | 71.16 | Kalrn | Decrease | 3 | 4.07 | 42.15 |
| Slc25a47 | Decrease | 1 | 0.91 | 31.11 | Saa1 | Increase | 3 | 1.96 | 59.01 |
| Ndst1 | ambiguous | 1 | 0.39 | 16.28 | Speer6-ps1 | Increase | 3 | 0 | 35.63 |
| Serpinb6a | Decrease | 1 | 1.01 | 39.33 | AY036118 | Increase | 3 | 0.29 | 131.35 |
| Acot1 | Decrease | 1 | 0.1 | 12.78 | Cela1 | Increase | 4 | 0.29 | 179.35 |
| Nlrp12 | Decrease | 1 | 1.32 | 20.76 | Amy2a5 | Increase | 4 | 0.79 | 10 |
| Gm12840 | Increase | 1 | 0.51 | 178.52 | Amy2b | Increase | 4 | 0.31 | 13.84 |
| Gm45551 | Decrease | 1 | 0.19 | 39.31 | Slc1a2 | Increase | 5 | 4.06 | 102.12 |
| Hipk1 | Decrease | 2 | 1.58 | 19.39 | Gcat | Decrease | 5 | 4.47 | 43.78 |
| Wsb1 | Decrease | 2 | 2.07 | 178.95 | Steap4 | Decrease | 5 | 1.46 | 55.17 |
| Igfbp1 | Decrease | 2 | 0.17 | 19.94 | Srek1ip1 | Increase | 5 | 1.02 | 39.5 |
| Gadd45g | Increase | 2 | 0.12 | 150.04 | Fubp1 | Increase | 5 | 0.47 | 10 |
| Slc25a25 | Increase | 2 | 1.09 | 80.83 | Eif3f | Increase | 5 | 4.07 | 43.66 |
| Pck1 | Decrease | 2 | 1.02 | 74.06 | Slco2a1 | Decrease | 5 | 0.21 | 10 |
| Mfsd2a | Decrease | 2 | 0.22 | 48.93 | Gck | Decrease | 5 | 1.65 | 54.5 |
| Alas1 | Decrease | 2 | 0 | 39.75 | Ppp1r3b | Increase | 5 | 1.65 | 41.09 |
| Txnip | Decrease | 2 | 0.92 | 10 | Nags | Increase | 5 | 1.11 | 87.15 |
| Zfp281 | Decrease | 2 | 3.21 | 47.91 | Atp6v1a | Increase | 5 | 3.12 | 87.42 |
| G6pc | Decrease | 2 | 0.63 | 55.99 | Gm10175 | Decrease | 5 | 1.55 | 10 |
| Arrdc3 | Increase | 5 | 0.31 | 39.69 |
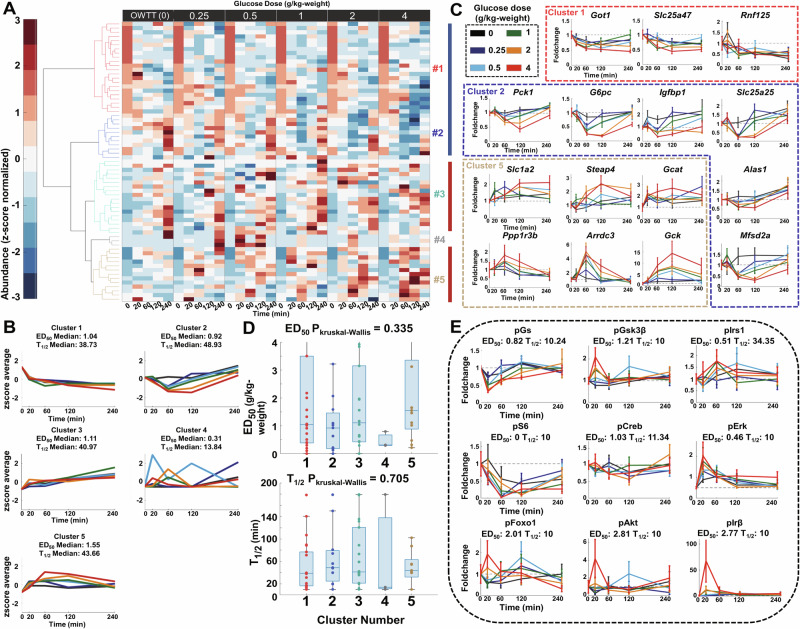
We grouped all of the identified glucose-responsive genes into five clusters using hierarchical cluster analysis, based on which had the largest silhouette value (Table 2, Fig. 3A, Supplementary Fig. 5). The expression of genes in Clusters 1 and 2 decreased after glucose administration until 60 min, whereas that in Cluster 2 gradually returned to water levels at 60 or 120 min after glucose administration (Fig. 3B). Cluster 2 included G6pase and Pck1 genes encoding PEPCK and G6Pase, respectively, which are important enzymes for gluconeogenesis (Fig. 3C). Clusters 3 and 5 consisted of increased metabolic enzyme genes such as Gck, but genes in Cluster 5 peaked at 60 min and recovered to equilibrium at 240 min after glucose administration. Cluster 4 included genes that significantly responded to particular doses, which were mainly those that were false positively identified as glucose-responsive with large responses to low glucose doses (0.25 and 0.5 g/kg) alone (Supplementary Data 5). All clusters of genes except Cluster 4 had a similar median ED50 and T1/2 of about 1 g/kg and 40 min, respectively, suggesting that this hierarchical cluster analysis grouped genes according to their response trends and overall temporal patterns rather than their indices of glucose dose sensitivities and response times after glucose administration (Fig. 3A, B).
Fig. 3. Identification of dose-dependent glucose-responsive genes and insulin signaling molecules.
A The time courses of dose-dependent glucose-responsive genes from the livers after administration of six doses of oral glucose (n = 5 mice per dose at all time points). Six-time courses for each gene were z-score normalized. Genes were ordered by hierarchical clustering using Euclidean distance and Ward’s method (Table 2, Supplementary Data 6). The colors of the dendrogram represent the clustering results (Red: Cluster 1, Blue: Cluster 2, Cyan: Cluster 3, Gray: Cluster 4, Gold: Cluster 5) B z-score the average of time courses of genes in each cluster and the median ED50 and T1/2 of these clusters. This panel shared the same legend as Fig. 3C. C Highlighted time courses of dose-dependent glucose-responsive genes in each cluster. The colors of the boxes show the clustering result of highlighted genes. Data are shown as the mean and SEM of five mice per dose. Genes are abbreviated as follows: Got1 glutamic-oxaloacetic transaminase, Slc25a47 solute carrier family 25 member 47, Rnf125 ring finger protein 125, Pck1 phosphoenolpyruvate carboxykinase 1, G6pc Glucose-6-phosphatase, Igfbp1 insulin-like growth factor binding protein 1, Slc25a25 solute carrier family 25 member 25, Alas1 5’-aminolevulinate synthase 1, Mfsd2a major facilitator superfamily domain-containing 2A, Slc1a2 solute carrier family 1 member 2, Steap4 six-transmembrane epithelial antigen of prostate 4, Gcat glycine C-acetyltransferase, Ppp1r3b protein phosphatase 1 regulatory subunit 3B, Arrdc3 arrestin domain-containing 3, Gck glucokinase, (Black: 0 g/kg [OWTT], Blue: 0.25 g/kg, Cyan: 0.5 g/kg, Green: 1 g/kg, Orange: 2 g/kg, Red: 4 g/kg). D Boxplot of ED50 (Left) and T1/2 (Right) for each cluster. Kruskal–Wallis tests for ED50 and T1/2 in each cluster were conducted to investigate whether there was statistical significance. The P values of the Kruskal–Wallis tests are shown above the boxplot. E Time courses, ED50 and T1/2 of dose-dependent glucose-responsive phosphorylation of insulin signaling molecules. Data are shown as the mean and SEM of five mice per dose. Insulin signaling molecules are abbreviated as follows: GS glycogen synthase, GSK3β glycogen synthase kinase 3 beta, IRS1 insulin receptor substrate 1, S6 ribosomal protein S6, CREB cAMP-response element-binding protein, ERK mitogen-activated protein kinase 1, FOXO1 forkhead box protein O1, AKT serine/threonine-specific protein kinase, IRβ insulin receptor β. This panel shared the same legend as (C).
Using dose-dependent analysis, we also found several dose-dependent glucose-responsive genes, including some that have not been described in studies on glucose metabolism36–38 (Fig. 3C). For example, arrestin domain-containing 3 (Arrdc3) in cluster 5, which is a member of the α-arrestin family, is an important regulator of insulin action and glucose metabolism in the liver36. Other identified dose-dependent glucose-responsive genes included glutamic-oxaloacetic transaminase 1 and solute carrier family 25 member 47 (Slc25a47) in cluster 1; insulin-like growth factor binding protein (Igfbp1), Slc25a25, 5′-aminolevulinate synthase 1, and major facilitator superfamily domain-containing 2A in cluster 2; and Slc1a2, six-transmembrane epithelial antigen of the prostate 4, glycine C-acetyltransferase, and protein phosphatase 1 regulatory subunit 3B in cluster 5. These results indicate that dose-dependent analysis may be a more powerful tool than single-dose analysis to identify unknown regulators in metabolism in terms of specificity. Unlike metabolites, genes in different clusters did not show statistical significance in ED50 or T1/2 (P > 0.05; Fig. 3D).
We also measured the phosphorylation and total protein levels of 13 insulin signaling molecules (glycogen synthase [GS], GS kinase 3 beta [GSK3β], IRS1, mammalian target of rapamycin, forkhead box protein O1 [FOXO1], Acc, AKT, ribosomal S6 kinase [S6], cAMP-response element-binding protein [CREB], eukaryotic translation initiation factor 4E, ERK, insulin receptor B) by western blotting, and quantified them after glucose or water administration. The phosphorylation level of insulin signaling molecules was determined by dividing their phosphorylation level by their total protein level. We identified nine glucose-responsive phosphorylated insulin signaling molecules including three with decreased phosphorylation (p-GS, p-S6, p-CREB) and six with increased phosphorylation (p-GSK3β, p-IRS1, p-FOXO1, p-AKT, p-ERK, p-IRB)14 (Fig. 3E, Supplementary Data 7). These molecules showed statistically significant temporal changes and response to glucose doses in their phosphorylation level at either 120 or 240 min. Nearly all of these signaling molecules, except p-IRS1, were rapidly phosphorylated (T1/2 < 20 min). However, their dose sensitivity responses to glucose were different after glucose administration. Molecules in the p-FOXO1 signaling pathway including insulin, p-AKT, p-IRB, and p-FOXO1 showed particularly lower dose sensitivity responses to glucose (ED50 > 2 g/kg), whereas others such as p-S6 and p-GS were relatively more dose-sensitive (ED50 < 0.5 g/kg), indicating that there were two different phosphorylation regulatory mechanisms with different dose sensitivities after glucose administration.
Inference of regulatory allosteric and TF regulation after glucose administration
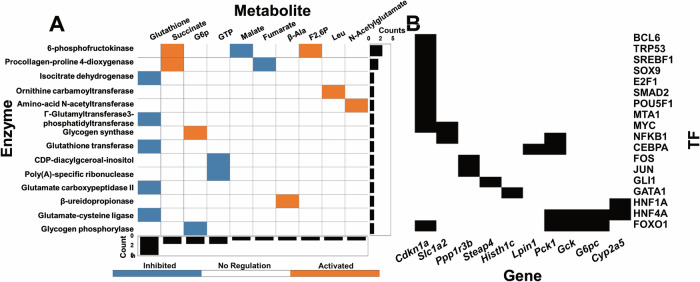
To clarify the regulatory mechanisms of glucose-responsive metabolites and genes, we determined the allosteric regulation of metabolic enzymes by the glucose-responsive metabolites (Fig. 4A) and the TFs that regulate gene expression (Fig. 4B, Supplementary Data 8). For allosteric regulations, we identified an allosteric regulation when a metabolite is served as the allosteric regulator of an enzyme. Allosteric regulatory connections were assigned according to the concentration of metabolites, Ki (inhibitory constant) values, and regulatory connections from the BRaunschweig ENzyme DAtabase (BRENDA) database(see Method)25. We also included some important literature-curated regulations (6-phosphofructokinase, Glycogen phosphorylase and Glycogen synthase) that are not included with quantitative Ki values in the BRENDA databases. We discovered a total of 17 regulatory allosteric regulations between 14 enzymes and 10 metabolites using a method that combined data from databases and the quantitative calculation of experimentally measured data Some of these allosteric regulations are well-known such as the allosteric regulation of 6-phosphofructokinase by succinate and F2,6P and glutathione transferase by glutathione. For TF regulation, we found 27 TF regulations between 18 TFs and 10 genes using a literature-curated method39 (Fig. 4B) including the TF regulation of FOXO1 and CCAAT/enhancer-binding protein alpha, consistent with our previous studies24,25 (Fig. 4B).
Fig. 4. Inference of regulatory allosteric and TF regulations after glucose administration.
A The inferred allosteric regulations of metabolic enzymes by the glucose-responsive metabolites. The metabolites serving as activators (orange) and inhibitors (blue) in the row labels regulate metabolic enzyme in the column labels. Bar charts on the left are the number of regulatory metabolites allosterically regulating each enzyme. The bar charts at the bottom are the number of enzymes allosterically regulated by each metabolite. B The inferred TF regulation of dose-dependent glucose-responsive genes by TFs using literature curations. The row labels are the dose-dependent glucose-responsive genes, regulated by the inferred TFs in the column label.
Classification of dose-dependent glucose-responsive molecules in the liver
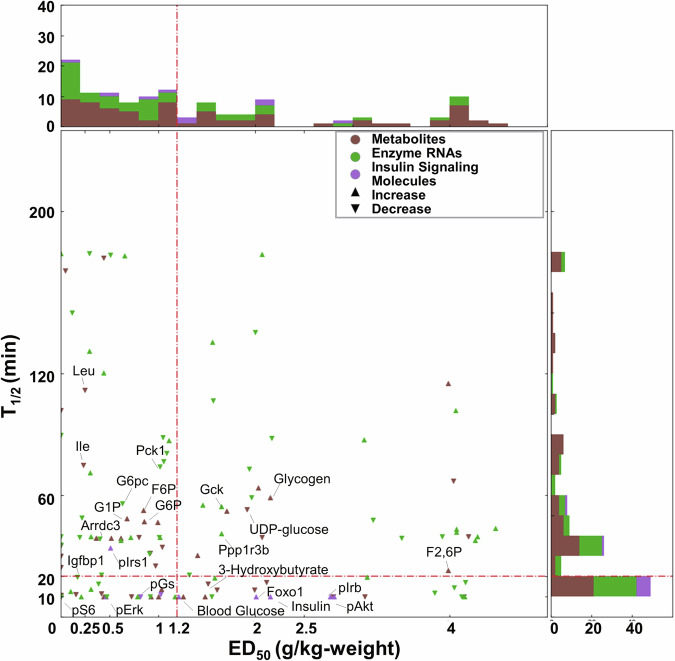
To understand glucose responsiveness in the liver across omics, we classified dose- and time-dependent glucose-responsive molecules into four different classifications according to their dose-responsiveness indicators: ED50 and T1/2. We set the threshold for each indicator using the triangle method40 and classified each identified dose- and time-dependent glucose-responsive molecule as high or low glucose dose sensitivity and rapid or slow response time. Molecules with ED50 > 1.2 g/kg and T1/2 > 20 min were considered to have lower glucose dose sensitivity and slower response time, respectively. By contrast, those with ED50 < 1.2 g/kg and T1/2 < 20 min were considered to have higher glucose dose sensitivity and more rapid response time, respectively (Fig. 5). The classification results are shown in Table 3.
Fig. 5. Classification of dose- and time-dependent glucose-responsive molecules in liver.
Distribution of ED50 (horizontal axis) and T1/2 (vertical axis) for dose- and time-dependent glucose-responsive molecules including metabolites (Brown), Enzyme RNAs (Green), and insulin signaling molecules (Purple). The directions of the scatter marks represented their responsive patterns (up: increase, down: decrease). Histograms of these indicators are on the right (T1/2) and upper (ED50) part of the scatter plot. Red dotted lines suggest the calculated threshold of ED50 (vertical, 1.2 g/kg) and T1/2 (horizontal, 20 min) using the triangle method.
Table 3.
Classification of molecules
| Rapid sensitive | Rapid insensitive | Slow sensitive | Slow insensitive | ||||
|---|---|---|---|---|---|---|---|
| Lactate | Metabolites | Ru5P | Metabolites | G1P | Metabolites | F2,6P | Metabolites |
| Citrate | 3-Hydroxybutyrate | G6P | Fumarate | ||||
| 2-Hydroxybutyrate | N-Acetylglutamate | F6P | Malate | ||||
| Glutarate | Mucate | Succinate | Adenylosuccinate | ||||
| beta-Ala | Taurocholate | S7P | UDP-glucose | ||||
| Ala | N,N-Dimethylglycine | GTP | Gly | ||||
| 3-Aminoisobutyrate | Hypotaurine | UDP-N-acetylglucosamine | Asp | ||||
| Val | Saccharopine | Urea | Adenosine | ||||
| Hydroxyproline | Glucose | Sarcosine | Glutathione(red) | ||||
| Ornithine | 2AB | Glycogen | |||||
| Citrulline | Pipecolate | ||||||
| Phosphorylcholine | Creatine | ||||||
| Ophthalmate | Ile | ||||||
| Leu | |||||||
| Glu | |||||||
| His | |||||||
| alpha-Aminoadipate | |||||||
| Trp | |||||||
| Inosine | |||||||
| pGs | Insulin signaling molecules | pGsk3b | Insulin signaling molecules | pIrs1 | Insulin signaling molecules | Insulin signaling molecules | |
| pS6 | pFoxo1 | ||||||
| pCreb | pAkt | ||||||
| pErk | pIrb | ||||||
| Insulin | |||||||
| Igfbp1 | Genes | Cyp2a5 | Genes | Slc22a5 | Genes | Slc1a2 | Genes |
| Wdr12 | Hipk1 | Slc16a10 | Gcat | ||||
| Upp2 | Rtn4ip1 | Id2 | G0s2 | ||||
| Fubp1 | Arhgef3 | Gadd45g | Steap4 | ||||
| Slco2a1 | Rpf1 | Srek1ip1 | Wsb1 | ||||
| Txnip | Cfap20 | Cela1 | Slc17a8 | ||||
| Ndst1 | Hist1h1c | Ik | Lpin1 | ||||
| Acot1 | Gm10175 | Slc25a25 | Susd6 | ||||
| Amy2a5 | Pck1 | Mtss1 | |||||
| Amy2b | Mfsd2a | Cdkn1a | |||||
| Hnrnpdl | Got1 | ||||||
| Pitpnm2 | Eif3f | ||||||
| Alas1 | Tob1 | ||||||
| Arhgap29 | Zfp281 | ||||||
| Saa4 | Gck | ||||||
| Nags | Ppp1r3b | ||||||
| Slc25a47 | Atp6v1a | ||||||
| Zfand2a | Nrd1 | ||||||
| Chd9 | Kalrn | ||||||
| Saa2 | Saa1 | ||||||
| Serpinb6a | Nlrp12 | ||||||
| Arrdc3 | |||||||
| G6pc | |||||||
| Gm12840 | |||||||
| Speer6-ps1 | |||||||
| AY036118 | |||||||
| Gm45551 | |||||||
With the classification of dose-dependent glucose-responsive molecules, the ED50 values of most molecules (74 of 127) fell into the glucose dose-sensitive group of lower than threshold ED50, but they generally had an even distribution in both classifications. By contrast, with the classification of time-dependent glucose-responsive molecules, the T1/2 values of most metabolites and insulin signaling molecules were within a very low time range (<10 min) (Fig. 5). The rapid response of metabolites and insulin signaling molecules to glucose administration was consistent with our previous study showing that the WT-specific regulation of metabolic reactions by glucose-responsive metabolites has the advantage of rapidness and is generally controlled by allosteric and phosphorylation regulations25,28,29.
Blood glucose (T1/2: 10.0 min, ED50: 1.26 g/kg) and insulin (T1/2: 10.0 min, ED50: 2.15 g/kg) had a more rapid response time and were less dose-sensitive to glucose administration (Fig. 5, Table 3). This is contrast to most metabolites in central carbon metabolism such as G1P (T1/2: 48.59 min, ED50: 0.68 g/kg) and G6P (T1/2: 47.14 min, ED50: 0.68 g/kg). Blood glucose and insulin also had similar responsiveness to the phosphorylation of upstream molecules in the insulin signaling pathway such as p-AKT (T1/2: 10.0 min, ED50: 2.81 g/kg), p-IRβ (T1/2: 10.0 min, ED50: 2.77 g/kg), p-FOXO1 (T1/2: 10.0 min, ED50: 2.01 g/kg), and insulin (T1/2: 10.0 min, ED50: 2.15 g/kg). However, other insulin signaling molecules, specifically p-S6 (T1/2: 10.0 min, ED50: 0 g/kg) and p-ERK (T1/2: 10.0 min, ED50: 0.46 g/kg), were more rapidly phosphorylated in response to glucose administration and more sensitive to glucose doses. In addition, most of the molecules with a rapid response time had a T1/2 value of 10 min, because the first measured time point was 20 min and most of the rapid-responsive molecules reached a maximum within 20 min.
On the other hand, transcriptional regulation such as the gene expression of key glucose metabolism enzymes (e.g., G6pc and Gck) responded much slower (T1/2: 56.0 and 54.5 min) than blood glucose after glucose administration. However, the glucose responsiveness of gene expression was similar to metabolites in glycogenesis such as glycogen (T1/2: 59.19 min, ED50: 2.15 g/kg) and UDP-glucose (T1/2: 53.20 min, ED50: 1.91 g/kg) (Fig. 5, Table 3).
Construction of the dose- and time-dependent glucose-responsive transomic network
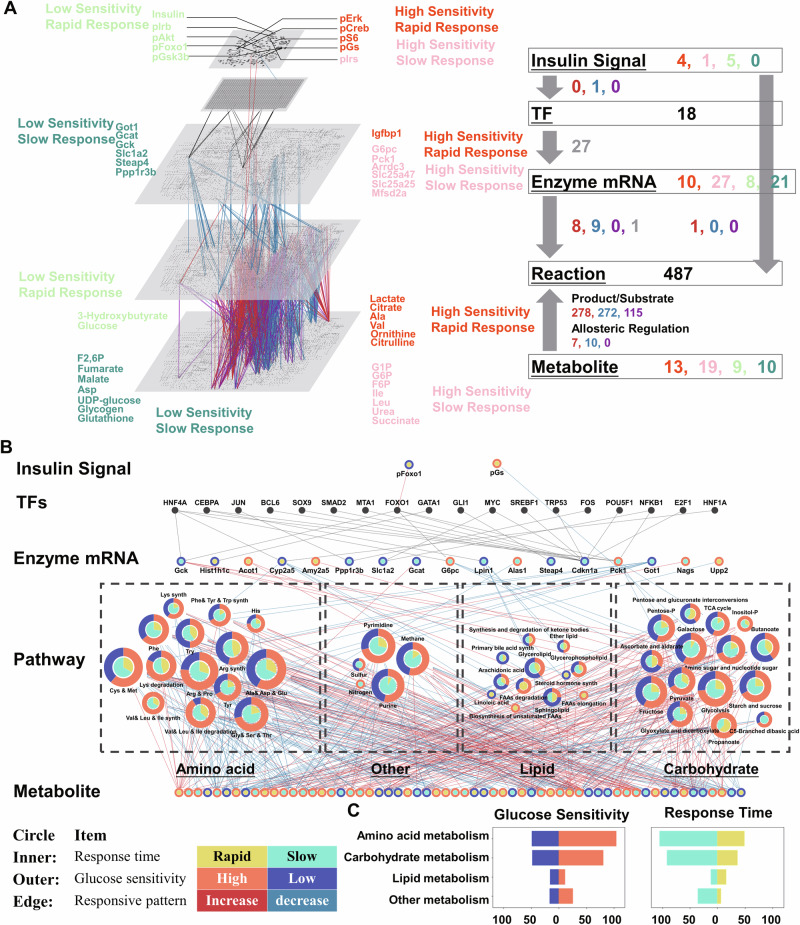
Using all of the identified dose-dependent glucose-responsive molecules, we constructed a global transomic network consisting of five layers, namely, Insulin Signal, TF, Enzyme mRNA, Reaction, and Metabolite layers, according to our previous method24,25 (Fig. 6A, Supplementary Data 9). The nodes of the Insulin Signal layer included all of the identified dose-dependent glucose-responsive phosphorylated insulin signaling molecules. The nodes of the TF layer included all of the deduced TFs regulating gene expression or having dose-dependent glucose-responsive phosphorylation. The nodes of the Enzyme layer included all of the identified dose-dependent glucose-responsive genes encoding metabolic enzymes. The nodes of the Reaction layer included metabolic reactions in the KEGG reaction database in which at least one of the associated substrates, products, and enzymes were included in the Enzyme or Metabolite layer (see below). The Metabolite layer included the dose-dependent glucose-responsive metabolites.
Fig. 6. Construction of the dose- and time-dependent glucose-responsive transomic network.
A The regulatory transomic network for dose-dependent glucose-responsive metabolic reactions. The left diagram represents the network as colored nodes in the layers and edges between the layers. Colored nodes represent the responsiveness of dose-dependent glucose-responsive molecules: Orange, high glucose sensitivity and rapid; Pink, high glucose sensitivity and slow; Light green, low glucose sensitivity and rapid; Aquamarine, low glucose sensitivity and slow. Colored edges represent interlayer regulatory connections: Red, upregulated regulations; Blue, downregulated regulations; Purple, both upregulated and downregulated regulations; Gray, other regulations such as TF regulations and ambiguous regulations. The numbers of each type of glucose-responsive node and edge are shown with the same colors in the network summary to the right. The insulin signal layer is the insulin signaling pathway constructed in our previous phosphoproteomic study25. The enzyme, reaction, and metabolite layers are organized into a global metabolic pathway (mmu01100) in the KEGG database. B The condensed dose-dependent glucose-responsive regulatory transomic network of the hepatic response to glucose in mice liver. The color of the outer circle of nodes represents the response time of a glucose-responsive molecule or the share of classified response time that is connected to a pathway (Yellow, rapid; Aquamarine, slow). The color of the inner circle of nodes represents the glucose sensitivity of a glucose-responsive molecule or the share of classified glucose sensitivity that is connected to a pathway (Orange, high glucose sensitivity; Blue, low glucose sensitivity). The color of the edges represents the responsive pattern of each regulation (Red, high glucose sensitivity; Blue, low glucose sensitivity). Dashed boxes show the type of metabolism these pathways. C The number of dose-dependent glucose-responsive reactions classified according to their glucose responsiveness across various types of metabolism. (e.g., carbohydrate metabolism, amino acid metabolism).
We connected nodes between layers with edges representing dose-dependent glucose-responsive regulations between layers (Fig. 6A, Supplementary Fig. 5A). We used the KEGG database to identify substrate/product regulations between the Reaction layer and the Metabolite layer. We also connected regulations of the Reaction layer and the Enzyme layer with the KEGG database. We included the inferred TF regulations from the TF layer to the Enzyme layer and allosteric regulations from the Metabolite layer to the Reaction layer, which resulted in the transomic network (Fig. 6A, Supplementary Fig. 5).
The global transomic network included nodes of 10 insulin signaling molecules, 18 TFs, 67 genes encoding metabolic enzyme mRNAs, 483 reactions, and 51 metabolites (Fig. 6A). All nodes in the network were classified according to their glucose dose sensitivity and response time. In the Insulin Signal layer, all signaling molecules showed rapid responses. The AKT pathway including p-Akt, p-FOXO1, and p-GSK3β showed low glucose dose sensitivity, whereas the ERK pathway including p-ERK and p-CREB showed high glucose dose sensitivity. The molecules in other layers including the Enzyme mRNA layer and Metabolite layer showed a wide range of glucose dose sensitivity and rapid/slow responses.
To understand the types of metabolism regulation, we further constructed a condensed transomic network and merged the metabolic reactions into nodes that contained metabolic pathway information, and determined the glucose responsiveness of pathways according to the type of metabolism (e.g., carbohydrate metabolism, amino acid metabolism) (Fig. 6B)25. We identified all pathways that included glucose dose-responsive metabolic reactions from the original global transomic system network according to their KEGG pathway classification (Supplementary Fig. 7C). The condensed network for dose-dependent glucose metabolism in the mouse liver included five omics layers, namely Insulin Signal Molecule, TF, Enzyme RNA (encoding enzyme), Pathway, and Metabolite. By condensing metabolic reactions into pathway nodes, we found that most dose-dependent glucose-responsive reactions were connected to pathways in carbohydrate metabolism and amino acid metabolism (Fig. 6B). Among them, allosteric and substrate regulations rather than enzyme regulations were responsible for most of the dose-dependent glucose-responsive regulations (Fig. 6B, Supplementary Fig. 7C). The most regulated pathways were alanine, aspartic acid, and glutamate metabolism (mmu00250); arginine and proline metabolism (mmu00330); cysteine and methionine metabolism (mmu00270); glycolysis/gluconeogenesis (mmu00010); glycine, serine, and threonine metabolism (mmu00260); and starch and sucrose metabolism (mmu00500).
Regarding the glucose responsiveness of pathways, high glucose dose-sensitive regulations were more abundant in amino acid than carbohydrate metabolism (Fig. 6B). The majority of pathways in lipid metabolism showed low glucose dose sensitivity but a rapid response time. These differences in response time and glucose dose sensitivities suggest different glucose responsiveness of different types of metabolism. The metabolites and regulators with low glucose dose sensitivity were mainly molecules such as UDP-glucose (ED50: 1.91 g/kg), glycogen (ED50: 2.15 g/kg), Gck (ED50: 1.65 g/kg), and ketone bodies (ED50: 1.61 g/kg) in glycogenesis or upper insulin signaling molecules including insulin (ED50: 2.15 g/kg) and p-FOXO1 (Fig. 6A). As these metabolites or regulators are critical for the energy conversion of glucose into other sources such as glycogen, fatty acid, or proteins, we compared the ratio of classified glucose dose sensitivity of amino acid and lipid metabolism in degradative and synthetic pathways. We found that synthetic reactions were less dose-sensitive to glucose compared with degradative reactions in both amino acid and lipid metabolism (Supplementary Fig. 7B).
in silico dynamic analysis using the kinetic modeling of metabolic fluxes
As the omics analysis only catches static snapshots of metabolites, we further used in silico kinetic modeling to estimate metabolic flux after glucose metabolism. Metabolic flux is the turnover rate of molecules through a metabolic reaction and is important for understanding dynamic metabolism. To examine dynamic metabolic fluxes of glucose metabolism, we performed kinetic modeling of metabolic fluxes based on the dose-dependent glucose-responsive transomic network. To reduce the complexity of the metabolic network, we focused on the reactions in glycogenolysis; glycolysis; gluconeogenesis; lactate, Asp, and Ala metabolism; and the TCA cycle (Fig. 7A, Supplementary Fig. 7, Supplementary Data 10). The metabolic fluxes were modeled using the experimental measured metabolites of blood glucose, citrate, alanine, glycerophosphate, aspartic acid, malate, lactate, and steady-state fluxes.
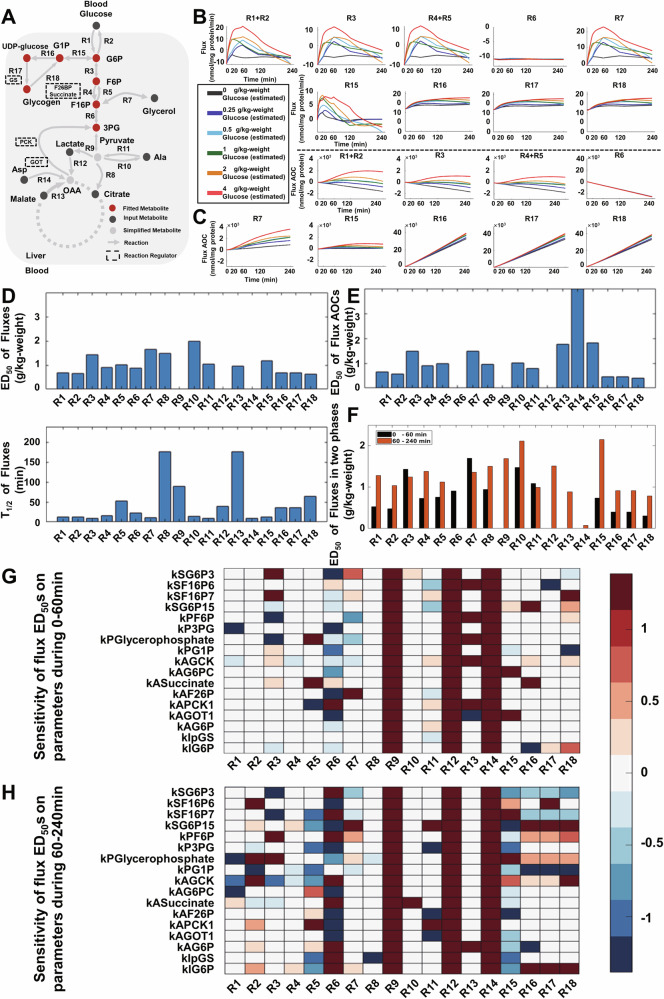
Fig. 7. In silico kinetic modeling of metabolic fluxes and their glucose responsiveness.
A Metabolic network used for kinetic modeling. Ret dots represent fitted metabolites. Black dots represent input metabolites and gray dots represent simplified metabolites that were not measured. Arrows represent metabolic reaction fluxes. Molecules in dotted boxes represent metabolic regulators. B The selected time courses of simulated reaction fluxes for the modeled metabolic network. C The selected time courses of simulated reaction fluxes AOC for the modeled metabolic network. D Bar plot of ED50 and T1/2 values for simulated fluxes. E Bar plot of ED50 values for simulated fluxes AOC. F Bar plot of ED50 values for fluxes from 0–60 min (black) and 60–240 min (red). G Heatmap of regulatory parameter sensitivity analysis on the ED50 for estimated metabolic fluxes during 0–60 min. H Heatmap of regulatory parameter sensitivity analysis on the ED50 for estimated metabolic fluxes during 60–240 min.
The estimated fluxes of reactions in glycolysis and gluconeogenesis, especially those in upper glycolysis (R1 + R2, R3, and R4 + R5), increased in a glucose dose-dependent manner (Fig. 7B, Supplementary Data 11). It is worth noting that both R1 + R2 and R4 + R5 were combined because the estimated fluxes of both directions were identical or the reaction was not glucose-responsive (Supplementary Fig. 8). Estimated flux of reactions of blood glucose transport (R1 + R2) was glucose responsive as it reflected the high Km value of hepatic glucokinase41. Fluxes of reactions in lower glycolysis and gluconeogenesis (R6 and R7) and glycogenesis (R15), however, responded differently. Fluxes of reactions of the conversion between F16P and 3PG (R6) in lower glycolysis and gluconeogenesis were generally stable, whereas fluxes of other reactions such as the glycerol synthesis (R7) and glycogen synthesis of the mutual conversion of G6P and G1P (R15) were transiently increased. Contrary to the transient increase in net glycogen synthesis (R15), the fluxes of reactions in glycogenesis and glycogenolysis such as the conversion of G1P to UDP-glucose (R16), conversion of UDP-glucose to glycogen (R17), and conversion of glycogen to G1P (R18) showed a sustained increase. We calculated the area of the curve (AOC) (see “Methods” section) of the metabolic fluxes, which reflected the total amounts of metabolites conserved in reaction fluxes (Fig. 7C, Supplementary Fig. 9). The AOCs of fluxes in glucose transport (R1 + R2), mutual conversion of G6P and F6P (R3), conversion between F6P and F16P (R4 + R5), glycerol synthesis (R7), and glycogen synthesis (R15) exhibited a clear dose-dependent increase, indicating that these fluxes contributed to the conversion of glucose into other energy sources such as glycerol and glycogen. It is worth noting that although some steady-state fluxes (e.g., R7 + R15) in the estimation were calibrated based on experiments in a previous study42,43, distributions between R7 and R15 in the combined fluxes were not calibrated and may not have accurately reflected the real fluxes. This may explain the larger estimated flux AOC values in glycerol synthesis (R7) than in glycogen synthesis (R15) in our flux estimation.
To investigate the dose- and time-dependency of fluxes after glucose administration, we calculated the ED50 values of flux and flux AOC, and the T1/2 values of flux and flux AOC for each reaction with the same calculation method as used in the transomic analysis (Fig. 7D, E, Supplementary Fig. 10, Supplementary Data 12). Flux ED50 values were similar between reactions, whereas flux T1/2 values were different between reactions. T1/2 values of flux R5 (52 min), R8 (177 min), R9 (90 min), R13 (177 min), and R18 (64 min) were larger than those of other fluxes. Specifically, the response time of glycogenolysis flux (R18) was larger than fluxes in glycogenesis (R16 and R17), indicating a slower response in glycogen degradation flux than its synthesis. The ED50 values of the flux AOCs were different between reactions and the ED50 values of the flux AOCs in net glycogen synthesis (R15) were larger than those of glycogenesis (R16 and R17) and glycogenolysis (R18), indicating the lower dose sensitivity of glycogen synthesis than other fluxes. These results support the hypothesis from the transomic analysis that reactions with low glucose dose sensitivity are a potential indicator of energy conversion (Figs. 6, 7).
Because of the different T1/2 values between reactions, we performed principal component analysis (PCA) for each time point and dose of z-score normalized fluxes (Supplementary Fig. 10). PC1 (41.93% of the total contribution of a variable) scores separated 0 min and other time points, whereas PC2 scores (22.22% of the total contribution of a variable) separated 20 min and other time points. The PCA results indicated that the flux time course could be divided into the early phase (0–60 min) and the late phase (60–240 min). We calculated the corresponding glucose-responsiveness indicator of ED50 for estimated fluxes in the early and late phases (Fig. 7F, Supplementary Fig. 10). Most ED50 values of estimated fluxes in the late phase (60–240 min) were larger than those in the early phase (0–60 min). These results showed that the glucose dose sensitivities of fluxes after glucose administration were heterogeneous during different time periods. Specifically, the glucose dose sensitivity in net glycogen synthesis flux (R15) was significantly lower during the late phase than in the early phase. Thus, the estimated fluxes were used to elucidate the conversion of glucose into other energy sources especially glycogen during the late phase, whereas metabolic regulations reduced the blood glucose level during the early phase of glucose metabolism (Fig. 2A).
To understand to what extent kinetic parameters influence the fluxes of glucose metabolism, we conducted parameter sensitivity analysis of the flux ED50 values in the early phase of 0–60 min and late phase of 60–240 min (Fig. 7G, H, Supplementary Data 13). Few flux ED50 values during the early phase were sensitive to parameter changes, especially the regulatory parameters (kI and kA). However, there were exceptions such as the kAPCK and kASuccinate to R5 (conversion of F16P to F6P), KAF26P, KAGOT1, and KAPCK1 to R6 (mutual conversion between F16P and 3PG), which are consistent with previous reports suggesting that changes in the transcription of Pck1 and G6pc determine the gluconeogenic capacity of the liver and the allosteric regulations of F26P regulated the glycolysis flux44,45. By contrast, glycolysis (R1–R5) and glycogenesis (R15–R18) in the late phase were sensitive to changes in the parameters of maximum reaction rate (k1) and thermodynamic constant (k2) during the late phase (Supplementary Fig. 13). Fluxes in glycogenesis (R15–R18) were also sensitive to the Michaelis constants for the substrate and production (kSG6P15, kPG1P) and constants for allosteric regulation (kIG6P, kAG6P) in addition to the parameters of k1 and k2. These results indicate that there are more regulations for glycolysis and glycogenesis in the late phase than in the early phase.
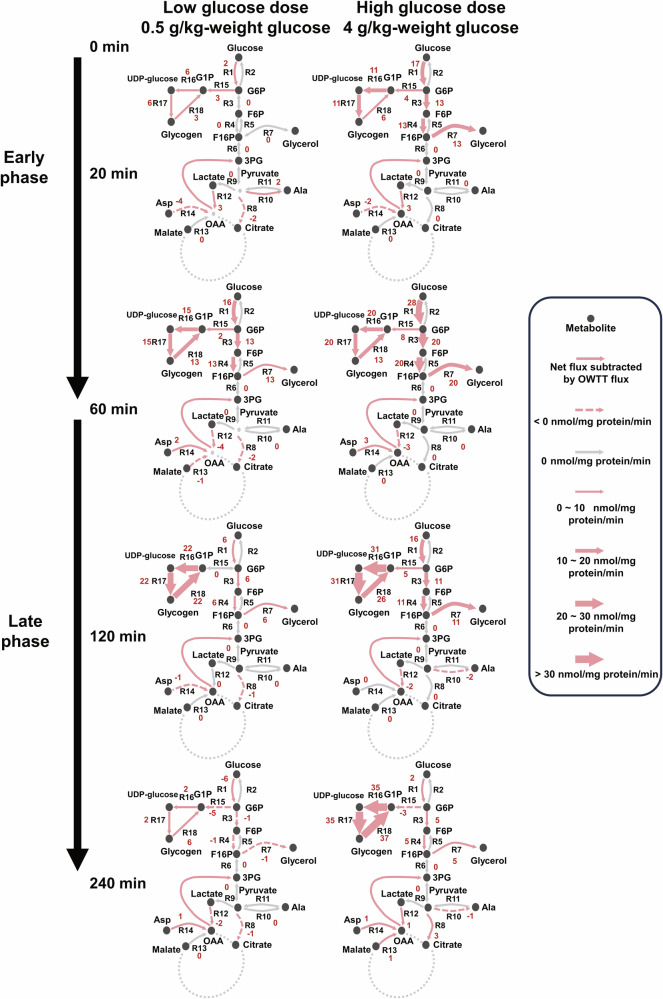
Taken together, we proposed a two-phase model of time- and dose-dependent selective glucose metabolism in the liver (Fig. 8). During the early phase of hepatic glucose metabolism after glucose administration (20 and 60 min), at both low (0.5 g/kg) and high (4 g/kg) glucose dose administration, blood glucose level similarly returned to basal level (Fig. 2A), and fluxes showed a similar balance in each branch at the low and high glucose doses, although the absolute fluxes were larger with the high glucose dose (Fig. 8). These results suggest that fluxes are controlled for glucose homeostasis in the early phase regardless of glucose dose. By contrast, in the late phase (120 and 240 min), glycogenesis (R15, R16, R17, and R18) and glyceroneogenesis (R7) were dominant at high glucose doses, resulting in more energy conversion of glucose into glycogen and glycerol-only at a high dose of glucose. Thus, in the early phase, fluxes flowed for glucose homeostasis at both the low and high glucose doses, whereas in the late phase, fluxes flowed for energy conversion only at high glucose doses. Together, these results demonstrate the time- and dose-dependent selective glucose metabolism for glucose homeostasis and energy conversion in the liver.
Fig. 8. Time- and dose-dependent selective glucose flux control for glucose homeostasis and energy conversion.
Numbers besides reactions are the optimal estimates of fluxes subtracted by OWTT fluxes with the unit of nmol/mg-protein/min. The direction of catabolic reaction in bidirectional reactions is regarded as positive.
Discussion
In this study, we measured the glucose dose-dependent time course of multi-omics data including metabolome, transcriptome, and phosphorylation in the mouse liver. We identified metabolites, genes, and phosphorylation of signaling molecules that dose-dependently responded to glucose administration and their responsive patterns. With these identified molecules, we elucidated the metabolic reactions, TFs, and allosteric regulations that are involved in the metabolic regulations and constructed a dose-dependent glucose-responsive transomic network of the mouse liver after glucose administration. We found that the overwhelming majority of metabolic regulations after glucose administration were upstream regulations including the product and substrate regulation and allosteric regulation, consistent with our previous studies25,29.
Dose-dependent analysis also allows more specificity in identifying glucose-responsive molecules. Instead of thousands of responsive molecules that are usually identified in single-dose analysis25,28, we narrowed down the number of responsive molecules into a significantly smaller number using dose-dependent analysis that excluded the water effect compared with our previous study which identified 2420 (1369 increased and 1151 decreased) glucose-responsive genes in WT mice. Among the identified dose-dependent glucose-responsive genes, most of the genes encoding known key enzymes for glucose metabolism, such as Gck, Pck1, and G6pc, have been identified46–49. This method identified some clear dose-responsive but less studied genes such as Arrdc3, Igfbp1, and those in the SLC families, which exhibits its potential for identifying novel candidate responsive molecules50,51.
The transomic analysis revealed features of multiple types of metabolism after glucose administration including carbohydrate, amino acid, and lipid metabolism. We found that the response of reactions in amino acid metabolism was rapid and dose-sensitive to glucose administration compared with carbohydrate metabolism, whereas lipid metabolism was rapid and with low glucose dose sensitivity. We previously reported the selective response by basal and induced insulin stimulation in vitro across multiple omics layers30,52,53. Basal insulin stimulates signaling through p-FOXO1 and transcriptional regulation, whereas induced insulin stimulation activates the phosphorylation of pS6 and protein synthesis. In this study, we calculated the glucose responsiveness of response time and glucose dose sensitivity of dose-dependent glucose-responsive molecules and classified them into four groups according to their glucose responsiveness. We found that molecules in insulin signaling pathways across omics layers exhibited different glucose dose sensitivities. Upstream insulin signaling molecules triggered by basal insulin stimulation including p-FOXO1 and p-IRβ had low glucose dose sensitivities, whereas some of their downstream regulators including genes such as Pck1, G6pc, and the pS6 signaling molecule showed higher glucose dose sensitivities. Although the higher glucose dose sensitivities of these molecules were similar to the high insulin sensitivity in the insulin-stimulated cell model of our previous study24, p-FOXO1, which had high insulin sensitivity in our previous study, appeared to have low glucose dose sensitivity in this study. However, in this study, p-FOXO1 was more glucose dose-sensitive than its upstream molecule p-AKT (Fig. 5), consistent with our previous study where p-FOXO1 was more insulin-sensitive than p-AKT53. In addition to glucose dose sensitivity, we also elucidated the different characteristics of response time in each omics layer. We found that the phosphorylation of insulin signaling molecules was rapid, whereas the transcriptomic expression of genes was slow in response to glucose administration. Metabolites, however, exhibited different response times in accordance with their time courses using clustering analysis. Metabolites in amino acid metabolism and lipid metabolism such as Val, Ala, and ketone bodies were rapid, whereas the response time of metabolites in upper central carbohydrate metabolism including G6P and glycogen was slow and even sustained after blood glucose returned to its equilibrium. The long response time of many metabolites indicated that the regulatory mechanism of glucose metabolism is effectively longer than the course of the blood glucose level returning to its equilibrium. Most of the calculated T1/2 values were consistent with the time constant calculated in our previous studies in the glucose-administered mouse model, except metabolites such as UDP-glucose and Leu24,25. Furthermore, the heterogeneity of response time and glucose dose sensitivity in molecules, especially those in the same type of metabolism, suggest that glucose responsiveness could be a potential feature for differentiating different types of metabolism from their biological functions.
After glucose administration, the regulation of metabolism through allosteric and phosphorylation regulations responded rapidly in accordance with the reduction of blood glucose level. Synthetic reactions and the energy source of glucose metabolism such as glycogen and ketone bodies exhibited lower glucose dose sensitivities than degradative reactions and intermediated metabolites. These results indicate that two different types of metabolism may exist after glucose administration that are either responsible for translating the excess glucose into other energy sources with low glucose dose sensitivity or maintaining blood glucose homeostasis with high glucose dose sensitivity. Other evidence for this hypothesis was the low glucose dose sensitivity of hepatic ketone bodies in this study (ED50: 1.61 g/kg). As a well-known alternative energy source for glucose, blood ketone bodies were previously recognized as being sensitive to insulin54; however, the results of this study suggest that hepatic ketone bodies have low glucose dose sensitivity similar to blood glucose and insulin in the liver. The low glucose dose sensitivity of hepatic ketone could be the result of a compensatory downregulation for the increased utilization of glucose for energy sources after glucose administration. Given the above glucose-responsiveness features of molecules and regulatory pathways, we considered low glucose dose sensitivity to be a potential indicator of glucose conversion after glucose administration.
In this study, we observed that glucose responses varied significantly across different omics layers, exhibiting different glucose dose sensitivities and response times. These responses were systematic and complex, making it challenging to categorize them into precise biological terms with our current knowledge. As the regulation of glucose metabolism after glucose administration mainly serves two biological objectives: maintaining glucose homeostasis, and energy conversion of glucose into metabolites including glycogen, lipids, amino acids, and lactate7,47. We therefore used the concepts of glucose homeostasis and energy conversion to summarize the potential biological functionalities of these systematic responses with different glucose sensitivities. We believe these concepts best capture the functionalities of these indicators, providing a clearer framework to understand their roles in metabolic regulation. We found that molecules and reactions that responded after glucose administration exhibited distinct glucose dose sensitivities and response times. Regulation by phosphorylation in insulin signaling pathways and allosteric regulation exhibited rapid response times in accordance with the rapid responses of insulin and blood glucose. These results indicate the potential role of these types of metabolic regulations in glucose homeostasis maintenance after glucose administration. By contrast, transcriptomic regulations and some substrate and product regulations, especially those in upper glycolysis, exhibited slow responses and low glucose dose sensitivities, suggesting that metabolic regulations with slow responses and low glucose dose sensitivities may be related to metabolic functions other than glucose homeostasis maintenance after glucose administration. In addition, those molecules and reactions with low glucose dose sensitivities are typically related to the conversion of glucose and synthesis of energy sources55. Hence, low glucose dose sensitivity may reflect the conversion of blood glucose into other energy sources.
We simulated the dynamic fluxes of glucose metabolism after glucose administration using kinetic modeling and calculated their indicators of glucose responsiveness and the dose sensitivity of each parameter based on measured omics data and steady-state flux value. The reconstructed dynamic modeling gave us a glimpse of the possible metabolism of central carbohydrate metabolism. The estimated fluxes and their AOCs suggested low glucose dose sensitivities in fluxes that were mainly responsible for the conversion of glucose in the liver, including net glycogenesis and glycerol synthesis. The model showed that the sustained upregulation of glycogenesis at higher glucose doses resulted in more conversion of glucose into hepatic glycogen. This result indicated that glucose was converted into hepatic glycogen mainly because of the different response times between the response of glycogenesis and glycogenolysis. Furthermore, we found high Pearson correlations between the time course of Gck expression (0.87), G6P (0.82), and glycogenesis fluxes (R16 and R17) as well as the high dose sensitivity of glycogenesis flux ED50 values (R15) to parameters related to G6P allosteric regulations and Gck transcriptional regulation during 60–240 min (Fig. 7H, Supplementary Fig. 11). These results are consistent with previous studies suggesting that the Gck- and G6P-mediated activation of liver glycogen synthase are key regulators of glycogenesis and glycolysis46,47,56. In addition to the different sensitivities of flux ED50 to parameters during two time periods, the sensitivity of flux for net glycogen synthesis (R15) was different from that in glycogenesis (R16, R17) and glycogenolysis (R18) during 60–240 min (Fig. 7H). The net glycogen synthesis (R15) was sensitive to changes in the parameters of p-GS, Pck, and Gck regulation, whereas fluxes of glycogenesis (R16, R17) and glycogenolysis (R18) were not. This further suggested the heterogeneity of dynamic regulations between the net glycogen synthesis flux and unidirectional fluxes of glycogenesis or glycogenolysis. Based on the estimated fluxes, we proposed a potential dynamic mechanism of glucose metabolism that involved two phases with different glucose dose sensitivities and selective controls: an early phase with high glucose dose-sensitive regulations that help maintain glucose homeostasis to keep blood glucose level at its equilibrium, and a late phase of low glucose dose-sensitive regulations that dose-dependently convert glucose into glycogen (Fig. 8).
Our study revealed the heterogeneity of glucose dose sensitivity for metabolic regulations in relation to different objectives. However, questions remain regarding the mechanism underlying this heterogeneity of glucose dose sensitivity. A possible explanation for this would be the different natures of control systems required for these two objectives. Understanding the mechanisms underlying glucose metabolism, especially those for maintaining glucose homeostasis, is important for understanding the pathologies of metabolic disorders such as diabetes. This may also contribute to drug development for these diseases. Our study offers a novel perspective of the complex glucose metabolism through glucose responsiveness, especially the glucose dose sensitivity of molecules and regulations. Additional studies into these two objectives of energy conversion and the maintenance of glucose homeostasis may reveal more regulatory details of glucose metabolism.
Mathematical modeling plays a pivotal role in advancing our understanding of biological systems by providing a framework to quantitatively analyze the behavior of complex biological processes. In this study, our kinetic transomic model enabled the quantitative analysis of in vivo glucose metabolism and insulin signaling pathways in a time- and dose-dependent and dynamic manner. The use of deterministic models like ours allows for a systematic examination of how different factors, such as enzyme activities and metabolite concentrations, interact over time. However, to capture the inherent randomness and fluctuations in biological processes, stochastic models are invaluable as well57,58. These models account for the probabilistic nature of molecular interactions and the variability observed in biological systems, which deterministic models might overlook. By incorporating stochastic elements, researchers can gain a deeper understanding of the robustness and variability in metabolic processes, thereby improving the accuracy of predictions and identifying key regulatory mechanisms59.
Moreover, the integration of AI and machine learning (ML) techniques with mathematical modeling has emerged as a powerful approach to handle the complexity of biological data in recent years. AI/ML can optimize model parameters, identify key features and biomarkers, and integrate multi-omics data more effectively60. Incorporating these advanced methodologies in future research could further advance our understanding of glucose metabolism and its regulation, leading to more precise and comprehensive insights into the underlying biological processes.
The potential mechanism of hepatic glucose metabolism presented in this study may not reflect the direct causal relationship and should be validated in future experiments. In this study, we fasted the mice for 16 h to stabilize the concentrations of metabolites. However, some previous reports suggested that the fasting period (5 h) are more recapitulating to human than overnight (16–18 h)61. Regarding transomic analysis, the limitations include experimental variation during the measurement of omics data and possible deficiencies of regulation estimation because of the inconsistency between the model and prior knowledge from species, organs, and experimental variations in the omics databases. Our calculation results of glucose-responsiveness indicators, namely the ED50 and T1/2, may have also been affected by experimental variation when the response in the time course was less significant. Furthermore, our constructed transomic network did not cover all metabolites and signaling molecules, including those of lipidome and glucagon pathways, which also play important roles after the glucose administration62,63. The high and low glucose dose sensitivities in this study were defined by the calculated threshold of ED50. However, the exact threshold value cannot be generalized to other studies and can vary across different omics layers. This variability can lead to a lack of clarity in the precise definitions of these terms, highlighting the difficulty and limitation in accurately delineating systematic differences for biological functionality.
Regarding the in silico kinetic modeling of dynamic fluxes, the label-free estimation of fluxes used in this study may have had larger errors or inaccuracies in terms of flux calculation compared with traditional isotope-labeled flux analysis. There are also technical reasons that protein-level measurements are difficult and some of the gene expression levels are associate with protein-level changes. We used transcription-level changes instead of protein-level changes for quantifying enzyme activities in this study for both the omics analysis and flux simulation. Some of the fluxes modeled in this study, especially in the downstream of glycolysis and unidirectional reactions including the conversion between 3PG and Ala or Asp, and the distributions of steady-state fluxes between glycogenesis and glycerol synthesis were not calibrated by experimental measured fluxes64. In addition, the network used in our kinetic modeling included simplified reactions and metabolites as well as unknown regulators such as the pyruvate of metabolites and TFs including CREB112,65–67. We also omitted interorgan interactions for the simplification of in silico modeling. These simplified molecules, reactions, and interactions were not measured or modeled but may have important regulatory impacts on central carbohydrate metabolism. We used glucose level derived from the tail vein rather than the portal vein for the flux simulation. As the glucose level in the portal vein is known to be higher than the tail vein after glucose administration, this may affect the result of simulated fluxes. Lastly, as the error and confidence analysis aren’t directly applicable for ODE functions, there are also limitations of transparently elucidating uncertainties in the flux modeling.
Methods
Mouse studies
Mouse experiments were approved by the animal ethics committee of The University of Tokyo and according to the ARRIVE guidelines and the University of Tokyo guidelines for the care and use of laboratory animals. Ten-week-old male C57BL/6 J wild-type (WT) mice were purchased from Japan SLC Inc. After overnight fasting (16 h), mice were administered 0, 0.25, 0.5, 1, 2, 4 g/kg body weight glucose or the same amount of water orally. Blood glucose level was measured from the tail vein at 0, 20, 60, 120, and 240 min after the glucose administration (ACCU-CHECK, Roche). After the measurement of blood glucose level, mice were euthanized by cervical dislocation, and the liver was dissected and frozen in liquid nitrogen immediately. The frozen liver was pulverized with ShakeMaster NEO (BMS) followed by multi-omic measurements. Plasma insulin concentration was determined using LBIS Mouse Insulin ELISA Kit (U-type) (633-03411, Wako).
Metabolomic analysis
From the liver, total metabolites and proteins were extracted with methanol:chloroform: water (2.5:2.5:1) extraction as previously described3. Briefly, about 40 mg of the liver was suspended in 500 µl of ice-cold methanol with internal standards [20 µM l-methionine sulfone (Wako), 2-morpholinoethanesulfonic acid, monohydrate (Dojindo), and d-camphor-10-sulfonic acid (Wako)] for normalization among MS runs. Then, 500 µl of chloroform and 200 µl of water were added. Following to the centrifugation at 4600 × g for 15 min at 4 °C, the aqueous layer was filtered using a 5-kDa-cutoff filter (Millipore) to remove protein contamination. The filtrate was dissolved in 50 µl of water containing reference compounds [200 µM each of trimesate (Wako) and 3-aminopyrrolidine (Sigma–Aldrich)], following to the lyophilization and subjected to MS analysis. The protein was precipitated by the addition of 800 µl of ice-cold methanol after the removal of the aqueous layer. Following to the centrifugation at 12,000 × g for 15 min at 4 °C, the resultant pellet was washed with 1 ml of ice-cold 80% methanol. The pellet was sonicated with Bioruptor UCW-310 (Sonicbio Co., Ltd.) in 500 µl of water, followed by the addition of the same volume of sample buffer containing 2% SDS and 100 mM Tris-HCl (pH 8.8). After the incubation at 4 °C for 60 min, the total protein concentration was determined by bicinchoninic acid (BCA) assay for normalization of metabolite concentration among samples.
All CE-TOFMS experiments were conducted using an Agilent 1600 Capillary Electrophoresis system (Agilent Technologies), a G1603A Agilent CE-MS adapter kit, and a G1607A Agilent CE electrospray ionization (ESI)–MS sprayer kit as previously described3. For cationic compounds, a fused silica capillary [50 µm internal diameter (i.d.) × 100 cm] was used with 1 M formic acid as the electrolyte68.
Methanol/water (50%, v/v) containing 0.01 µM hexakis (2,2-difluoroethoxy) phosphazene was used as the sheath liquid and the speed was set to 10 µl/min. ESI–time-of-flight (TOF) MS was set to positive ion mode, and the capillary voltage was 4 kV. Automatic recalibration for normalization of each acquired spectrum was performed using the masses of the reference standards [13 C isotopic ion of a protonated methanol dimer (2 MeOH + H)]+, mass/charge ratio (m/z) 66.0631 and [hexakis(2,2-difluoroethoxy) phosphazene + H]+, m/z 622.0290. To identify metabolites, the relative migration times of all peaks were calculated using reference compound (3-aminopyrrolidine). The metabolites were identified by referring their m/z values and relative migration times to the standards. Quantification was conducted by comparing peak areas to calibration curves generated using internal standardization techniques with methionine sulfone. The other conditions were the same as described previously69. For the anionic metabolites, COSMO (+) (chemically coated with cationic polymer) capillary (50 µm i.d. by 105 cm) (Nacalai Tesque, Kyoto, Japan) was used with a 50 mM ammonium acetate solution (pH 8.5) as the electrolyte. Ammonium acetate (5 mM) in MeOH/Water (50%, v/v) containing 0.01 μM Hexakis(2,2-difluoroethoxy) phosphazene was used as the sheath liquid at the speed of 10 µl/min. ESI-TOFMS was performed in negative-ion mode, and the capillary voltage was 3.5 kV. Trimesate and d-camphor-10-sulfonic acid were used as the reference and the internal standards, respectively. The other conditions were identical to those described previously70. Data analysis was performed Agilent MassHunter software (Agilent Technologies)69–71.
For the measurement of F1,6P and F2,6P separately, IC-QEMS72 analysis was conducted. The metabolites were separated with a Dionex IonPac AS11-HC-4 µm column (250 × 0.4 mm, 4 µm; Thermo Fisher Scientific)72 at 35 °C. KOH was used as an eluent at the speed of 0.02 mL/min, and the gradient was as follows: 1 mM from 0 to 2 min, 20 mM at 16 min, 100 mM at 35 min. Isopropanol containing 0.1% acetic acid was used as sheath solution at the speed of 5 µl/min. The mass spectrometric measurement was conducted in the ESI negative-ion mode. The ESI parameters are as follows: sheath gas, 20 (arbitrary units); auxiliary gas, 10 (arbitrary units); spray voltage, 4.0 kV; capillary temperature, 300 °C; S-lens, 50 (arbitrary units). Data were acquired in full MS scan mode. Parameters of the scanning were as follows: resolution, 70,000; auto-gain control target, 3 × 106; maximum ion injection time, 100 ms; scan range, 70–1000 m/z.
RNA sequencing
RNAeasy Mini Kit (QIAGEN) and QIAshredder (QIAGEN) were used to extract total RNA from 10 mg of liver samples following to the manufacture’s protocol. The quantity and the quality of the extracted RNA were assessed by Nanodrop (Thermo Fisher Scientific) and the 2100 Bioanalyzer (Agilent Technologies). Sequencing library was prepared as previously described73 and subjected to sequencing using HiSeq 2500 (Illumina).
Quality filter and adapter trimming for fastaq files of sequences performed with Trimmomatic (0.39). Mouse reference genome was built from the Ensembl database (GRCm38/mm10, Ensembl release 97) using bowtie2-2.3.5.1 and RSEM (v1.3.0)74,75. Pre-processed sequences were mapped on each reference and quantified using bowtie and RSEM for estimating the number of transcripts as an indication of gene expression76. The number of transcripts was shown as Transcripts Per Kilobase Million (TPM).
Western blotting
Total proteins were extracted from liver samples as described above (see metabolomic measurement section). The lysate was boiled in sample buffer (58.28 mM Tirs-HCl, pH 6.8, 4.7% glycerol, 2.82% SDS, 6% β-Mercaptoethanol, and 0.0094% bromophenol blue). Samples (10–40 µg for phospho-proteins) were subsequently separated by SDS-PAGE and transferred to nitrocellulose membrane followed by immunoblotting. Antibodies for total Akt (#9272), phospho-Akt (Ser473) (#9271), total Erk1/2 (#9102), phospho-Erk1/2 (Thr202/Tyr204) (#9101), total cAMP responsive element-binding protein (Creb) (#9197), phospho-Creb (Ser133) (#9198), total Foxo1 (#9462), phosphor-Foxo1 (Ser256) (#9461), phosphor-Irβ (Tyr1150/Tyr1151) (#3024), total Irs1 (#2382), total mTor (#2972), phospho-mTor (Ser2448) (#2971), total S6 (#2217), phospho-S6 (Ser235/Ser236) (#2211), total S6k (#9202), phospho-S6k (Thr 389) (#9205), total eukaryotic translation initiation factor 4e (eif4e) (#9742), phospho-Eif4e (Ser209) (#9741), total Gsk3β (#9315), phospho-Gsk3β (Ser9) (#9336), total Gs (#3886), phospho-Gs (Ser641) (#3891), and total Acc (#3662) were purchased from Cell Signaling Technology. Antibodies for phosphor-Irs1 (Tyr612) (09-432) and total-Irs2 (MABS15) were purchased from Millipore, for total-Irβ was from Santa Cruz Biotechnology, and for phospho-Acc (Ser79) (07-303) from Upstate. A Peroxidase (HRP)-conjugated anti-rabbit antibody (NA9340V), anti-mouse antibody (NXA931), and anti-goat antibody (A5420) were purchased from GE Healthcare (rabbit, mouse) and Sigma (goat). Immunodetection was performed using Immobilon Western Chemiluminescent HRP Substrate (Millipore) or SuperSignal West Pico PLUS Chemiluminescent Substrate (Thermo Fisher Scientific) and the signals were measured by a luminoimage analyzer (Fusion System Solo 7S; M&S Instruments Inc). Quantification, brightness adjustment, and treatment were performed with the Fiji software (ImageJ; National Institutes of Health)77. For the images with high background, the subtract background function in the Fiji software was used. The images were converted and the conversion to 8-bit image was carried out by Photoshop CS6 (Adobe).
Glycogen content assay
Glycogen content in the liver was determined as previously described78. Briefly, approximately 20 mg of liver was digested by incubating for 1 h at 95 °C in 1 ml of 30% (w/v) potassium hydroxide solution. Lysate (50 µl) was collected into another 1.5 mL tube and neutralized in 15.3 μl of glacial acetic acid. The total protein concentration of the liver digest was measured by using BCA assay and the protein concentration was adjusted to 1 μg/µl. The Bligh and Dyer method was performed to remove lipids and extract glycogen. Samples (50 µl) was mixed with mixed with 120 μl of ice-cold methanol, 50 μl of chloroform, 10 μl of 1% (w/v) linear polyacrylamide, and 70 μl of water, followed by centrifugation at 12,000 × g to remove the aqueous layer after ice-incubation for 30 min. Methanol (200 µl) was added and centrifuged at 12,000 × g for 30 min at 4 °C to precipitate glycogen. After washing with ice-cold 80% (v/v) methanol, samples were dried up, and glycogen pellets were resuspended in 20 μl of amyloglucosidase (0.1 mg/ml; Sigma–Aldrich) in 50 mM sodium acetate buffer. Then the samples were incubated for 2 h at 55 °C to digest glycogen. The concentration of glucose produced from the glycogen was measured by using the Amplex Red Glucose/Glucose Oxidase Assay kit glucose assay (Thermo Fisher Scientific), according to the manufacturer’s instructions.
Omics data preprocessing
As outliers from measurement error and high missing data ratio for a molecule may affect the result of quantitative analysis of time course. We preprocessed the measured omics data by excluding outliers and molecules with a high ratio of missing data before the analysis. In this study, we defined an outlier using the boxplot method79. We considered those out of the 1.5 interquartile range (IQR) from the median value of any time point at a specific dose outlier data. In addition, molecules that have less than 3 measurable replicates (non-NAN for metabolites or proteins or TPM > 0.1 for genes) among 5 replicates at any time point of any dose were excluded from further analysis.
Identification of dose-dependent glucose-responsive molecules
We identified molecules that have a false discovery rate (FDR)–adjusted P value (q value) using the Benjamini-Hochberg (BH) method less than 0.1 using the ANOVA test in any of its glucose administration doses as temporally changed80. The phosphorylation level of an insulin signaling molecule would be considered temporally responsive when either its total protein or its phosphorylated protein changed temporally. Metabolites, gene expressions, and phosphorylation levels of signaling molecules that have a foldchange larger than 1.2 in their Area Of the Curve (AOC) ratio of any glucose administration from 0 min to 240 min were regarded as water-independent changes. We calculated the AOC ratio of a molecule which is the ratio of the area of the curve between its responsive doses added/subtracted by the difference between glucose and water doses by its responsive pattern. However, since some of the phosphorylation levels of insulin signaling molecules and metabolites responded rapidly, we also used both the 240 min curve AOC ratio and 120 min curve of AOC for calculating the AOC ratio. We considered a molecule increased after a glucose dose administration if the AOC ratio was larger than 1.2 and decreased if it was smaller than 0.83 (1/1.2). We defined dose-dependent glucose-responsive molecules as those that responded both temporally and to glucose in any dose after glucose administration (Supplementary Fig. 1A). For a molecule in general, we considered a dose-dependent glucose-responsive molecule increased (decreased) if it increased (decreased) but not decreased (increased) in any of its glucose administration doses. Those who had both increased and decreased doses were considered as ambiguously responded.
Method for calculating glucose-responsive indicators of ED50 and T1/2
We calculated the ED50 and T1/2 from the simulated time course of molecules with a time-dependent function (Supplementary Fig. 1B). Best-fitted parameter sets in the function for each molecule are obtained by minimizing the sum of squared residues between the output of the function and the experiment results with the interior-point method. We defined ED50 as the in the logistic function. We defined the value of T1/2 by interpolating the fitted glucose effect and finding the time to half of the maximum glucose effect. We obtained ED50 and T1/2 values from the best-fitting result among 10 iterations of simulation. As indicators of glucose responsiveness of a molecule, larger ED50, and T1/2 value suggests lower glucose sensitivity and slower response time of this molecule, respectively.
Method for the inference of regulatory allosteric regulations after glucose administration
To infer allosteric regulations, we used a method similar to our previous study25. We obtained the entries for the responsible metabolic enzymes from the BRaunschweig ENzyme DAtabase (BRENDA) database81 and extracted their allosteric effector (activator and inhibitor) information and inhibitory half-saturation constants (Ki) values, as reported for Homo sapiens, Mus musculus, and Rattus norvegicus. If a pair of allosteric effectors of metabolites and the responsible metabolic enzyme has more than one Ki value among three species, we calculated the geometric mean of the Ki values and used it as the Ki value for that paired regulation. When multiple Ki values for the same enzyme and metabolite were present, we used their geometric mean. To compare with the metabolomic data, we changed the unit of the metabolomic data using the weight of protein per volume in the mouse liver (0.2 g/ml).
Here, we quantified the log foldchange effect of allosteric inhibition to metabolic flux as. is the elasticity of the allosteric inhibition and reflects how fluctuations in the concentration of a metabolite c affect the rate of the reaction v. is the log foldchange between the maximum concentration and 0 min concentration of allosteric regulators. The elasticity of non-cooperative, non-competitive inhibitors is described as 82. We tested whether the concentration between maximum response and 0 min of an allosteric effector for each metabolic reaction by identifying statistical differences using the two-tailed Welch’s t-test with a q value less than 0.1. The q values were calculated by the Storey procedure83. We determined an allosteric regulation if the reaction has a larger than and showed a statistical difference in their concentrations between its maximum response time point and 0 min. An increased responsive pattern of the concentration of allosteric effector metabolite was regarded as inhibiting allosteric regulation and decreased responsive pattern as activating allosteric regulation.
However, Ki values of some important allosteric regulations are not available in the BRENDA database81. We thus added those regulations that were previously reported critical for glucose metabolism in mice to our result manually. Those regulations were the allosteric regulations of 6-phosphofructokinase from succinate, malate, and F2,6P, Glycogen synthase, and Glycogen phosphorylase from G6P. As a result, we predicted 21 regulatory allosteric regulations including 7 inhibiting and 14 activating regulations between 12 enzymes and 10 metabolites.
Method for the prediction of TF regulations after glucose administration
To infer TF regulations, we used a literature-curated method described in Luz Garcia-Alonso et al.39 The literature-curated collections were from three publicly available databases namely Kyoto Encyclopedia of Genes and Genomes (KEGG)84, TFactS85 and Transcriptional Regulatory Relationships Unraveled by Sentence-based Text mining (TRRUST)86. We directly retrieved all the TF–target interactions as indicated in the corresponding databases and recognized TF regulations as those whose regulatory genes were dose-dependent glucose-responsive in more than one database. As a result, we predicted 27 TF regulations between 18 TFs and 10 genes.
Identification of synthesis and degradation reactions of amino acid and lipid metabolism
We identified synthesis and degradation reactions of amino acid and lipid metabolism according to the KEGG pathway database84. We consider a reaction degradation or synthesis if it is included in a degradation or synthesis pathway of amino acid and lipid metabolism. The detailed classification of pathways and reactions is shown in Supplementary Data 9. Using this method, we obtained the number and percentage of each class of glucose responsiveness in degradation or synthesis pathways of amino acid and lipid metabolism. (Supplementary Fig. 7).
In silico simulation of metabolic fluxes
The metabolic network in the reconstructed model is shown in Supplementary Fig. 8A. The network includes simplified glycolysis, glycogen pathway, a part of the TCA cycle, and lactate and alanine metabolism. These simplified reactions include R7 (the mutual conversion between F16P and Glycerophosphate), R8, R9, R10 (the conversion of 3PG through pyruvate to citrate, lactate, and alanine), R11, R12 (the conversion of lactate and alanine through pyruvate and oxaloacetate to 3PG), R13 and R14 (the conversion of aspartate and malate through oxaloacetate to 3PG). Those reactions estimated dynamic fluxes of glycolysis, gluconeogenesis, glycogenolysis, and glycogenesis. The model consists of 16 metabolites, 4 enzyme gene expressions, and 1 phosphorylation of insulin signaling molecules. The dose-dependent glucose-responsive time-course data of 6 metabolites namely G6P, G1P, F1,6P, 3PG, UDP-glucose, and glycogen were fitted while the measured time-course of other molecules were used as the input of the model. We used the mass balance equations to estimate changes of a molecule
| 1 |
where y denoted the estimated amount of a metabolite and V denoted the inflow and outflow fluxes to metabolites. We also used the formalism of Modular Rate Law and particularly the common modular with complete activation/inhibition22,87
| 2 |
so that it could consider the contribution of activators, inhibitors, and substrate and product effects to the reaction rate. In the modular rate law, V denotes the reaction rate, which is the flux of a metabolic reaction. , , , and denote the maximum reaction rate, the function of substrate and products, the function of inhibitory regulation, and the function of activatory regulations, respectively. For the function of substrate and products, we used different formations to simulate irreversible and reversible reactions:
| 3 |
where , and denote the concentrations of substrates, productions, and the stoichiometric coefficient. In the function of substrate and products, k2 denoted the thermodynamic constant representing the ratio between the concentrations of the products and the substrates at equilibrium while KS and KP denoted the Michaelis constants for the substrate and the production for the underlying reaction, respectively. For the function of inhibitory regulation , the formation is expressed as , where denotes the concentration of inhibitor j and denotes the inhibitory constant. Similarly, the function of activating regulation is expressed as , where , denotes concentration of the activator i and denotes the activatory constant. The contribution of phosphorylation to the reaction rate is considered either an activator or an inhibitor according to our dose-dependent glucose-responsive transomic network constructed in this study. Consequently, the kinetic model comprises the rate equations in Supplementary Data 10.
The estimates for the kinetic rate constants were calculated using the flux distribution predicted by a kinetic simulation model. We determined the initial values of the flux estimate as follows. We first generated a random set of parameters within the predetermined ranges. We set the upper bound for parameter as and the lower bound as . We set the upper bound for parameter , , , and as 100 times of the digit of the maximum level. Similarly, we set the lower bound for parameter , , , and as 1% of the digit of the minimum level of its underlying molecule. When a random set of parameters is generated, we then examined the generated set of initial parameters and whether they are confined to a steady state of metabolic flux for 24 hours before the glucose administration using the experimentally measured molecule concentrations as the initial values. We determined a steady state for a particular set of parameters was reached when the concentration changes of all simulated metabolites were less than 1% of their steady-state fluxes at 0 min within the last 10 min of the steady-state simulation.
The simulation of dynamic fluxes after glucose administration is conducted following the steady-state simulation. We used the final concentration of fitted metabolites in the steady-state estimation as the initial value of the dynamic fluxes. The same set of parameters for the kinetic simulation model was used for both the steady-state estimation and dynamic flux simulation. In order to reflect the positive glycolysis after glucose administration, we set a positive constraint of flux in R3 at 60 min to simulate the flux of glycolysis after glucose intake doses (0.25, 0.5, 1, 2, 4 g/kg-weight).
We evaluated the fitting using the residual sum of squares (RSS) of both the experimentally measured metabolite concentration and steady-state flux:
| 4 |
where the function or is the value of estimated steady-state flux for reactions (R) or concentrations of metabolites (M). M includes six metabolites of G6P, G1P, F1,6P, 3PG, UDP-glucose, and glycogen, T includes the time points of 0, 20, 60, 120, and 240 min and D includes the 0, 0.5, 1, 2, 4 g/kg-weight glucose dose which were the time points and doses measured by experiments. R includes combinations of the steady-state fluxes of reactions namely the sum of reactions R15 and R7, the sum of reactions R11, R12, R13, and R14, the sum of reactions R8, R9, and R10, and the subtraction of reactions R9 from R12 which are the equivalent fluxes to those experimentally measured in a previous study42. yM is the experimentally measured concentrations of metabolites in this study and yR is the experimentally measured fluxes in the liver of fasting mice in the previous study. N is the number of data. The residues were normalized by the experimentally measured concentrations or flux as well as the number of data.
The parameters of the kinetic model were estimated by minimizing RSS using a covariance matrix adaptation evolution strategy (CMA-ES)88 to approach the neighborhood of the local minimum followed by the interior-point algorithm for constrained nonlinear multivariable function89 to reach the local minimum.
After 50 independent estimations of the model, we selected the parameter values that resulted in the minimum RSS. The parameters and equations used in this study are shown in Supplementary Data 10. We confirmed that the best-fitted model had similar time courses of metabolites and steady-state fluxes to the experimentally measured data in this or previous studies. We performed the simulations and the parameter estimations using MATLAB software (version R2021a; MathWorks) and on the supercomputer system from the National Institute of Genetics in Japan. Using the best estimation result. Time courses of fluxes were presented in Supplementary Fig. 7. Pearson correlation coefficients between time courses of fluxes and molecules were also calculated (Supplementary Fig. 9).
Calculation of flux AOCs
We calculated the time course Area Of the Curve ( for estimated fluxes as follows:
| 5 |
where is the simulated flux value and is time. The time courses of flux AOCs were shown in Supplementary Fig. 7.
Parameter sensitivity analysis for the ED50s and T1/2s of estimated fluxes
We defined the individual model parameter sensitivity (S) as follows:
| 6 |
where x is the parameter value and f(x) is the ED50 or T1/2 for estimated fluxes. The differentiation is numerically approximated by the central difference
| 7 |
and is set to 1% of . We examined the parameter sensitivity for 53 parameters of maximum reaction rate , substrate constants , product constants , thermodynamic constant , inhibitory constants and activatory constants related to doses of administrated glucose. The higher the absolute value of parameter sensitivity, the larger the effect of the parameter on the ED50 or T1/2. The results of the sensitivity analysis are presented in Supplementary Fig. 9.
Implementation
Statistical tests, transomic network analysis, fluxes simulation, and analysis were performed using MATLAB 2021a (The Mathworks Inc.). The statistical identification of glucose-responsive genes was conducted using R (v1.1.456) and EdgR (3.30.3) package90. Visualization of transomic network in Graph Modeling Language (GML) formats was performed using Python 3.7 and VANTED (2.8.2)91.
Supplementary information
Acknowledgements
We thank the team of Prof. Tomoyoshi Soga (Keio University) for their technical assistance with metabolomics analysis using capillary electrophoresis time-of-flight mass spectrometry and IC-QEMS. We thank our laboratory members for critically reading this manuscript and for their technical assistance with the experiments. The computational analysis of this work was performed in part with the support of the supercomputer system of the National Institute of Genetics (NIG), Research Organization of Information and Systems (ROIS). This study was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI (Grant Nos. JP17H06300, JP17H06299, JP18H03979, JP21H04759, JP22K15034), CREST, the Japan Science and Technology Agency (JST) (Grant No. JPMJCR2123), and by The Uehara Memorial Foundation. T.K. receives funding from a Grant-in-Aid for Early-Career Scientists (No. JP21K16349). K.M. receives funding from a Grant-in-Aid for Early-Career Scientists (No. JP21K15342). S.O. receives funding from a Grant-in-Aid for Early-Career Scientists (No. JP21K14467) and the Takeda Science Foundation. This work was supported by AMED Grant Number JP21zf0127001 (T.S.), JST, CREST Grant Number JPMJCR2123 (T.S.), MEXT KAKENHI Grant Number JP23H04946(T.S.) and World Premier International Research Center Initiative (WPI), Human Biology-Microbiome-Quantum Research Center (Bio2Q) (T.S.), MEXT, Japan.
Author contributions
Y.P., A.Hatano., and S.K. conceived and supervised the project; Y.P. designed and performed the data analyses; A.Hatano. designed and performed the animal experiments, sample preparation of omics measurements, and glycogen content assay; Y.P. and S.O. developed methods for the indicator calculation and flux analysis; K.M. performed the western blot analyses; Y.P., T.K., Y.B., H.S., R.E., A.T., H.M., D.L., S.U., and S.F. performed the transomic analysis; A.Hirayama. and T.S. performed the metabolomic measurements; A.N. performed transcriptomic sequencing; Y.P., S.O., K.M., H.I., Y.I., and S.K. wrote the manuscript; All authors read and approved the final manuscript.
Data availability
Additional data are made available in supplementary tables of this manuscript. Accession codes of fastq data will be available before publication.
Code availability
All software used for data analysis is available in the main text or the supplementary materials. Custom codes are available on request from the authors.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Yifei Pan, Atsushi Hatano.
Supplementary information
The online version contains supplementary material available at 10.1038/s41540-024-00437-2.
References
- 1.Floriane, B., Planchais, J., Dentin, R., Guilmeau, S. & Postic, C. Integration of ChREBP-mediated glucose sensing into whole body metabolism. Physiology30, 428–437 (2015). [DOI] [PubMed] [Google Scholar]
- 2.Szablewski, L. Glucose homeostasis–mechanism and defects. Diabetes-Damages and Treatments 2 (2011).
- 3.Klover, P. J. & Mooney, R. A. Hepatocytes: critical for glucose homeostasis. Int. J. Biochem. Cell Biol.36, 753–758 (2004). [DOI] [PubMed] [Google Scholar]
- 4.Han, H.-S. et al. Regulation of glucose metabolism from a liver-centric perspective. Exp. Mol. Med.48, e218 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.König, M., Bulik, S. & Holzhütter, H. G. Quantifying the contribution of the liver to glucose homeostasis: a detailed kinetic model of human hepatic glucose metabolism. PLoS Comput. Biol.8, e1002577 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hers, H.-G. Mechanisms of blood glucose homeostasis. J. Inherit. Metab. Dis.13, 395–410 (1990). [DOI] [PubMed] [Google Scholar]
- 7.Moore, M. C., Coate, K. C., Winnick, J. J., An, Z. & Cherrington, A. D. Regulation of hepatic glucose uptake and storage in vivo. Adv. Nutr.3, 286–294 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nakrani, M. N., Wineland, R. H. & Anjum, F. Physiology, Glucose Metabolism (StatPearls Publishing LLC: Tampa, FL, USA, 2022). [PubMed]
- 9.Lépine, G. et al. Investigating the postprandial metabolome after challenge tests to assess metabolic flexibility and dysregulations associated with cardiometabolic diseases. Nutrients14, 472 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ward, C. W. & Lawrence, M. C. Landmarks in insulin research. Front. Endocrinol.2, 76 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dimitriadis, G. D., Maratou, E., Kountouri, A., Board, M. & Lambadiari, V. Regulation of postabsorptive and postprandial glucose metabolism by insulin-dependent and insulin-independent mechanisms: an integrative approach. Nutrients13, 159 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wilcox, G. Insulin and insulin resistance. Clin. Biochem. Rev.26, 19–39 (2005). [PMC free article] [PubMed] [Google Scholar]
- 13.Ekberg, K. et al. Contributions by kidney and liver to glucose production in the postabsorptive state and after 60 h of fasting. Diabetes48, 292–298 (1999). [DOI] [PubMed] [Google Scholar]
- 14.Lizcano, J. M. & Alessi, D. R. The insulin signalling pathway. Curr. Biol.12, R236–R238 (2002). [DOI] [PubMed] [Google Scholar]
- 15.Saltiel, A. R. & Kahn, C. R. Insulin signalling and the regulation of glucose and lipid metabolism. Nature414, 799–806 (2001). [DOI] [PubMed] [Google Scholar]
- 16.Titchenell, P. M., Lazar, M. A. & Birnbaum, M. J. Unraveling the regulation of hepatic metabolism by insulin. Trends Endocrinol. Metab.28, 497–505 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lin Lin, H. V. & Accili, D. Hormonal regulation of hepatic glucose production in health and disease. Cell Metab.14, 9–19 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lindsay, J. R. et al. Meal-induced 24-hour profile of circulating glycated insulin in type 2 diabetic subjects measured by a novel radioimmunoassay. Metabolism52, 631–635 (2003). [DOI] [PubMed] [Google Scholar]
- 19.Wasserman, D. H. et al. The physiological regulation of glucose flux into muscle in vivo. J. Exp. Biol.214, 254–262 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hasenour, C. M. et al. Mass spectrometry-based microassay of 2H and 13C plasma glucose labeling to quantify liver metabolic fluxes in vivo. Am. J. Physiol. Endocrinol. Metab.309, E191–E203 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yugi, K., Kubota, H., Hatano, A. & Kuroda, S. Trans-omics: how to reconstruct biochemical networks across multiple ‘omic’ layers. Trends Biotechnol.34, 276–290 (2016). [DOI] [PubMed] [Google Scholar]
- 22.Yugi, K. et al. Reconstruction of insulin signal flow from phosphoproteome and metabolome data. Cell Rep.8, 1171–1183 (2014). [DOI] [PubMed] [Google Scholar]
- 23.Yugi, K., Ohno, S., Krycer, J. R., James, D. E. & Kuroda, S. Rate-oriented trans-omics: integration of multiple omic data on the basis of reaction kinetics. Curr. Opin. Syst. Biol.15, 109–120 (2019). [Google Scholar]
- 24.Kawata, K. et al. Trans-omic analysis reveals selective responses to induced and basal insulin across signaling, transcriptional, and metabolic networks. iScience7, 212–229 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kokaji, T. et al. Transomics analysis reveals allosteric and gene regulation axes for altered hepatic glucose-responsive metabolism in obesity. Sci. Signal.13, eaaz1236 (2020). [DOI] [PubMed] [Google Scholar]
- 26.Egami, R. et al. Trans-omic analysis reveals obesity-associated dysregulation of inter-organ metabolic cycles between the liver and skeletal muscle. iScience24, 102217 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Terakawa, A. et al. Trans-omics analysis of insulin action reveals a cell growth subnetwork which co-regulates anabolic processes. iScience25, 104231 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kokaji, T. et al. In vivo transomic analyses of glucose-responsive metabolism in skeletal muscle reveal core differences between the healthy and obese states. Sci. Rep.12, 1–19 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bai, Y. et al. Trans-omic analysis reveals opposite metabolic dysregulation between feeding and fasting in liver associated with obesity. iScience27.3, (2024). [DOI] [PMC free article] [PubMed]
- 30.Kubota, H. et al. Temporal coding of insulin action through multiplexing of the AKT pathway. Mol. Cell46, 1–13 (2012). [DOI] [PubMed] [Google Scholar]
- 31.McGill, R., Tukey, J. W. & Larsen, W. A. Variations of boxplots. Am. Stat.32, 12–16 (1978). [Google Scholar]
- 32.Kanehisa, M. & Susumu, G. KEGG: kyoto encyclopedia of genes and genomes. Nucleic Acids Res.28, 27–30 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schomburg, I. et al. BRENDA: a resource for enzyme data and metabolic information. Trends Biochem. Sci.27, 54–56 (2002). [DOI] [PubMed] [Google Scholar]
- 34.Rousseeuw, P. J. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math.20, 53–65 (1987). [Google Scholar]
- 35.McKight, P. E. & Najab, J. Kruskal‐Wallis test. In The Corsini Encyclopedia of Psychology (2010).
- 36.Batista, T. M. et al. Arrestin domain-containing 3 (Arrdc3) modulates insulin action and glucose metabolism in liver. Proc. Natl Acad. Sci. USA117, 6733–6740 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mehta, M. B. et al. Hepatic protein phosphatase 1 regulatory subunit 3B (Ppp1r3b) promotes hepatic glycogen synthesis and thereby regulates fasting energy homeostasis. J. Biol. Chem.292, 10444–10454 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Berger, J. H., Charron, M. J. & Silver, D. L. Major facilitator superfamily domain-containing protein 2a (MFSD2A) has roles in body growth, motor function, and lipid metabolism. PLoS ONE7, e50629 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Garcia-Alonso, L. et al. Benchmark and integration of resources for the estimation of human transcription factor activities. Genome Res.29, 1363–1375 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zack, G. W., Rogers, W. E. & Latt, S. A. Automatic measurement of sister chromatid exchange frequency. J. Histochem. Cytochem.25, 741–753 (1977). [DOI] [PubMed] [Google Scholar]
- 41.Iynedjian, P. B. Mammalian glucokinase and its gene. Biochem. J.293, 1 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hasenour, C. M., Rahim, M. & Young, J. D. In vivo estimates of liver metabolic flux assessed by 13C-propionate and 13C-lactate are impacted by tracer recycling and equilibrium assumptions. Cell Rep.32, 107986 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ferre, T. et al. Evidence from transgenic mice that glucokinase is rate limiting for glucose utilization in the liver. FASEB J.10, 1213–1218 (1996). [DOI] [PubMed] [Google Scholar]
- 44.Hatting, M. et al. Insulin regulation of gluconeogenesis. Ann. N. Y. Acad. Sci. USA1411, 21–35 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rider, M. H. et al. 6-phosphofructo-2-kinase/fructose-2, 6-bisphosphatase: head-to-head with a bifunctional enzyme that controls glycolysis. Biochem. J.381, 561–579 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Nozaki, Y. et al. Metabolic control analysis of hepatic glycogen synthesis in vivo. Proc. Natl Acad. Sci. USA117, 8166–8176 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Meyer, C. et al. Role of human liver, kidney, and skeletal muscle in postprandial glucose homeostasis. Am. J. Physiol. Endocrinol. Metab.282, E419–E427 (2002). [DOI] [PubMed] [Google Scholar]
- 48.Beale, E. G. et al. Disregulated glyceroneogenesis: PCK1 as a candidate diabetes and obesity gene. Trends Endocrinol. Metab.15, 129–135 (2004). [DOI] [PubMed] [Google Scholar]
- 49.Chou, J. Y. & Mansfield, B. C. Mutations in the glucose‐6‐phosphatase‐α (G6PC) gene that cause type Ia glycogen storage disease. Hum. Mutat.29, 921–930 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Schumann, T. et al. Solute carrier transporters as potential targets for the treatment of metabolic disease. Pharmacol. Rev.72, 343–379 (2020). [DOI] [PubMed] [Google Scholar]
- 51.Bae, J.-H., Song, D.-K. & Im, S.-S. Regulation of IGFBP-1 in metabolic diseases. J. lifestyle Med.3, 73 (2013). [PMC free article] [PubMed] [Google Scholar]
- 52.Sano, T. et al. Selective control of up-regulated and down-regulated genes by temporal patterns and doses of insulin. Sci. Signal.22, ra112 (2016). [DOI] [PubMed] [Google Scholar]
- 53.Kubota, H., Uda, S., Matsuzaki, F., Yamauchi, Y. & Kuroda, S. In vivo decoding mechanisms of the temporal patterns of blood insulin by the insulin-AKT pathway in the liver. Cell Syst.7, 1–11 (2018). [DOI] [PubMed] [Google Scholar]
- 54.Veech, R. L. The therapeutic implications of ketone bodies: the effects of ketone bodies in pathological conditions: ketosis, ketogenic diet, redox states, insulin resistance, and mitochondrial metabolism. Prostaglandins Leukot. Essent. Fatty Acids70, 309–319 (2004). [DOI] [PubMed] [Google Scholar]
- 55.Rui, L. Energy metabolism in the liver. Compr. Physiol.4, 177 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.von Wilamowitz-Moellendorff, A. et al. Glucose-6-phosphate–mediated activation of liver glycogen synthase plays a key role in hepatic glycogen synthesis. Diabetes62, 4070–4082 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hahl, S. K. & Kremling, A. A comparison of deterministic and stochastic modeling approaches for biochemical reaction systems: On fixed points, means, and modes. Front. Genet.7, 157 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Levine, E. & Hwa, T. Stochastic fluctuations in metabolic pathways. Proc. Natl Acad. Sci. USA104, 9224–9229 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Clement, E. J. et al. Stochastic simulation of cellular metabolism. IEEE Access8, 79734–79744 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Reel, P. S. et al. Using machine learning approaches for multi-omics data analysis: a review. Biotechnol. Adv.49, 107739 (2021). [DOI] [PubMed] [Google Scholar]
- 61.Jensen, T. L. et al. Fasting of mice: a review. Lab. Anim.47, 225–240 (2013). [DOI] [PubMed] [Google Scholar]
- 62.Jiang, G. & Zhang, B. B. Glucagon and regulation of glucose metabolism. Am. J. Physiol. Endocrinol. Metab.284, E671–E678 (2003). [DOI] [PubMed] [Google Scholar]
- 63.Masoodi, M. et al. Metabolomics and lipidomics in NAFLD: biomarkers and non-invasive diagnostic tests. Nat. Rev. Gastroenterol. Hepatol.18, 835–856 (2021). [DOI] [PubMed] [Google Scholar]
- 64.Uematsu, S. et al. Multi-omics-based label-free metabolic flux inference reveals obesity-associated dysregulatory mechanisms in liver glucose metabolism. iScience25, 103787 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lam, T. K. T. et al. Regulation of blood glucose by hypothalamic pyruvate metabolism. Science309, 943–947 (2005). [DOI] [PubMed] [Google Scholar]
- 66.Gray, L. R., Tompkins, S. C. & Taylor, E. B. Regulation of pyruvate metabolism and human disease. Cell. Mol. Life Sci.71, 2577–2604 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Yu, X. et al. The role of calcium/calmodulin-dependent protein kinase cascade in glucose upregulation of insulin gene expression. Diabetes53, 1475–1481 (2004). [DOI] [PubMed] [Google Scholar]
- 68.Soga, T. & Heiger, D. N. Amino acid analysis by capillary electrophoresis electrospray ionization mass spectrometry. Anal. Chem.72, 1236–1241 (2000). [DOI] [PubMed] [Google Scholar]
- 69.Soga, T. et al. Differential metabolomics reveals ophthalmic acid as an oxidative stress biomarker indicating hepatic glutathione consumption. J. Biol. Chem.281, 16768–16776 (2006). [DOI] [PubMed] [Google Scholar]
- 70.Soga, T. et al. Metabolomic profiling of anionic metabolites by capillary electrophoresis mass spectrometry. Anal. Chem.81, 6165–6174 (2009). [DOI] [PubMed] [Google Scholar]
- 71.Ishii, N. et al. Multiple high-throughput analyses monitor the response of E. coli to perturbations. Science316, 593–597 (2007). [DOI] [PubMed] [Google Scholar]
- 72.Hirayama, A. et al. The use of a double coaxial electrospray ionization sprayer improves the peak resolutions of anionic metabolites in capillary ion chromatography-mass spectrometry. J. Chromatogr. A1619, 460914 (2020). [DOI] [PubMed] [Google Scholar]
- 73.Kamitani, M. et al. Lasy-Seq: a high-throughput library preparation method for RNA-Seq and its application in the analysis of plant responses to fluctuating temperatures. Sci. Rep.9, 7091 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Bolger, A. M., Lohse, M. & Usadel, B. Trimmomatic: a flexible trimmer for Illumina sequence data. Bioinformatics30, 2114–2120 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Li, B. & Dewey, C. N. RSEM: accurate transcript quantification from RNA-Seq data with or without a reference genome. BMC Bioinform.12, 1–16 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Langmead, B. & Salzberg, S. L. Fast gapped-read alignment with Bowtie 2. Nat. Methods9, 357–359 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Schindelin, J. et al. Fiji: an open-source platform for biological-image analysis. Nat. Methods9, 676–682 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Noguchi, R. et al. The selective control of glycolysis, gluconeogenesis and glycogenesis by temporal insulin patterns. Mol. Syst. Biol.9, 664 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Heckert, N. Alan, et al. Handbook 151: NIST/SEMATECH e-Handbook of Statistical Methods. NIST Interagency/Internal Report (NISTIR) (2002).
- 80.Benjamini, Y. & Hochberg, Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc.57, 289–300 (1995). [Google Scholar]
- 81.Schomburg, I., Chang, A. & Schomburg, D. BRENDA, enzyme data and metabolic information. Nucleic Acids Res.30, 47–49 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Reznik, E. et al. Genome-scale architecture of small molecule regulatory networks and the fundamental trade-off between regulation and enzymatic activity. Cell Rep.20, 2666–2677 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Storey, J. D. & Tibshirani, R. Statistical significance for genomewide studies. Proc. Nat. Acad. Sci. USA100, 9440–9445 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Kanehisa, M. The KEGG database. In ‘In Silico’ Simulation of Biological Processes: Novartis Foundation Symposium, Vol. 247 (John Wiley & Sons, Ltd, Chichester, UK, 2002).
- 85.Essaghir, A. et al. Transcription factor regulation can be accurately predicted from the presence of target gene signatures in microarray gene expression data. Nucleic Acids Res.38, e120 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Han, H. et al. TRRUST v2: an expanded reference database of human and mouse transcriptional regulatory interactions. Nucleic Acids Res.46, D380–D386 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Liebermeister, W., Uhlendorf, J. & Klipp, E. Modular rate laws for enzymatic reactions: thermodynamics, elasticities and implementation. Bioinformatics26, 1528–1534 (2010). [DOI] [PubMed] [Google Scholar]
- 88.Auger, A. & Hansen, N. Tutorial CMA-ES: evolution strategies and covariance matrix adaptation. In Proc. 14th Annual Conference Companion on Genetic and Evolutionary Computation (2012).
- 89.Byrd, R. H., Hribar, M. E. & Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim.9, 877–900 (1999). [Google Scholar]
- 90.Robinson, M. D., McCarthy, D. J. & Smyth, G. K. edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. bioinformatics 26, 139–140 (2010).. [DOI] [PMC free article] [PubMed]
- 91.Junker, B. H., Klukas, C. & Schreiber, F. VANTED: a system for advanced data analysis and visualization in the context of biological networks. BMC Bioinform.7, 1–13 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Additional data are made available in supplementary tables of this manuscript. Accession codes of fastq data will be available before publication.
All software used for data analysis is available in the main text or the supplementary materials. Custom codes are available on request from the authors.