Dynamical structure-function correlations provide robust and generalizable signatures of consciousness in humans

Abstract

Resting-state functional magnetic resonance imaging evolves through a repertoire of functional connectivity patterns which might reflect ongoing cognition, as well as the contents of conscious awareness. We investigated whether the dynamic exploration of these states can provide robust and generalizable markers for the state of consciousness in human participants, across loss of consciousness induced by general anaesthesia or slow wave sleep. By clustering transient states of functional connectivity, we demonstrated that brain activity during unconsciousness is dominated by a recurrent pattern primarily mediated by structural connectivity and with a reduced capacity to transition to other patterns. Our results provide evidence supporting the pronounced differences between conscious and unconscious brain states in terms of whole-brain dynamics; in particular, the maintenance of rich brain dynamics measured by entropy is a critical aspect of conscious awareness. Collectively, our results may have significant implications for our understanding of consciousness and the neural basis of human awareness, as well as for the discovery of robust signatures of consciousness that are generalizable among different brain conditions.

Dynamical analysis of resting-state fMRI networks reveals a consistent increase in structure-function correlation and entropy decrease upon both general anesthesia-induced and deep sleep-induced loss of consciousness in humans.

Introduction

The identification of reliable markers for determining the presence or absence of human consciousness from brain signals remains a major unresolved problem in neuroscience^1–9. The spontaneous dynamics of the brain can be measured using resting-state functional magnetic resonance imaging (rs-fMRI)^10–14, consisting of the recording of functional magnetic resonance imaging while no task is explicitly performed (i.e., during rest). Using this approach, it has been shown that the brain exhibits dynamic transitions between various transient configurations, each serving distinct cognitive functions^15–26. The nature of signals during the resting state suggests that they might reflect complex neural processes related to ongoing cognition and consciousness, prompting the search for signatures of consciousness in the dynamics of spontaneous brain activity^2,27–33. For instance, differences in the sequences and prevalence of transient brain states measured in macaques can distinguish between wakefulness and general anaesthesia induced by propofol, ketamine, and sevoflurane^29,34, a finding that was replicated in human individuals suffering from disorders of consciousness^2,30,35.

One of the major obstacles behind the aforementioned challenge consists of determining robust and generalizable markers of consciousness^36–38. In this context, robustness indicates markers that do not require fine-tuning of parameters for each different dataset where they are applied; moreover, robustness also stands for the independence of the consciousness state of the individuals. Generalizability refers to the capacity to successfully detect consciousness markers in different datasets obtained using heterogeneous acquisition parameters and under potentially divergent experimental conditions. Currently, few papers explicitly address these two requirements, especially in combination. This represents an important obstacle, both for the study of fundamental principles underlying consciousness, and for the translation to the clinics.

Here we focused on determining markers of consciousness based on the dynamics of functional connectivity measured using rs-fMRI in human participants, contrasting the awake state with general anaesthesia (intravenous propofol) and deep sleep, two different brain states characterised by diminished or absent conscious awareness, and corresponding to two datasets acquired by different research groups using different parameters of data acquisition. Our results provide evidence that consciousness exhibits specific features that are grounded in the temporal dynamics of ongoing brain activity, which are common to different brain states, and robust against changes in experimental acquisition protocols.

Methods

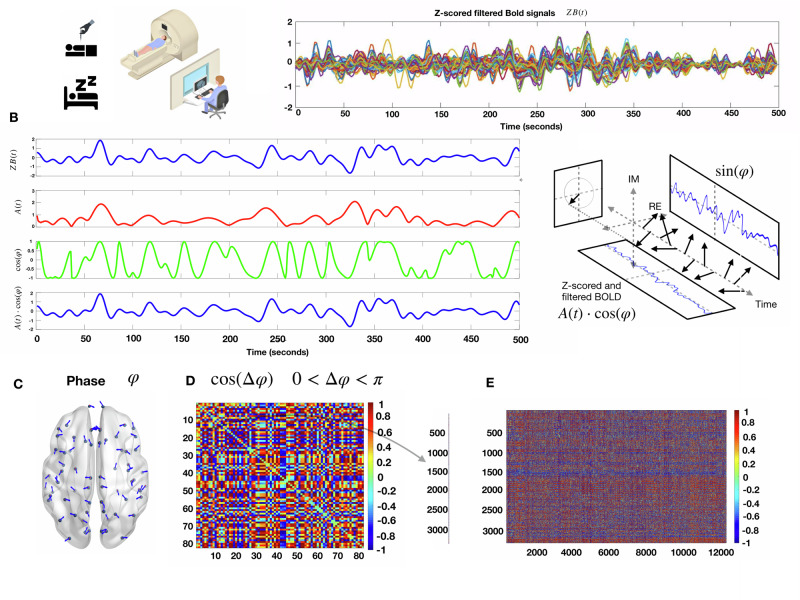
Before entering into the details, we describe here the general idea of the methodology for which a summary can be seen in Fig. 1. We first consider in both datasets blood-oxygen-level-dependent (BOLD) signals of healthy volunteers. For each participant, we computed the Z-scored BOLD time series (Fig. 1A). Secondly, we computed the Hilbert transform of the said signals to extract the phase of the signal for each region of interest (ROI) at each repetition time (TR) (Fig. 1B, C). We next compare every ROI pair of these phases at every TR to determine brain regions’ synchronizations and anti-synchronizations evolving through time (Fig. 1D). We did not use Global Signal Regression, in neither of the two databases used, because it is well-known that it can induce spurious anticorrelations, which are known to be relevant for tracking consciousness. Previous studies showed that the global signal can contain information pertaining to pathological and pharmacological perturbations of consciousness³⁹.

Fig. 1. Phase-based dynamic functional patterns.

A Left, In the general anesthesia dataset, 16 healthy volunteers were scanned in three conditions (awake, G.A, and recovery), and in the sleep database, 18 healthy volunteers were scanned in two conditions (awake and N3 sleep). Right) Example of Z-scored filtered BOLD time series for one participant of the anesthesia database in the awake condition, 250 time points with a TR of 2 s. B Hilbert transform the z-scored BOLD signal of one ROI into its time-varying amplitude A(t) (red) and the real part of the phase φ (green). In blue, we recover the original z-scored BOLD signal as A(t)cos(φ). C Example of the phase of each brain region at one TR. D Symmetric matrix of cosines of the phase differences between all pairs of brain regions. E We concatenated the vectorized form of the triangular superior of the phase difference matrices for all TR’s for all participants, in all the conditions for both datasets separately.

Instantaneous phase

The analytic representation of a real-valued signal x(t) is a complex signal $\tilde{x}\left(t\right)$ with the same Fourier transform as the real-valued signal, but defined only for positive frequencies. The analytic signal can be built from the real-valued signal using the Hilbert transform H:

$$\tilde{x}\left(t\right)=x\left(t\right)+iH\left[x\left(t\right)\right]$$

Where i is the imaginary unit. The main advantages of using the analytic signal are that, given some real-value data (for example BOLD signals), we can determine two functions of time to better access meaningful properties of the signal. We consider now a narrowband signal that can be written as an amplitude-modulated low-pass signal A(t) with carrier frequency expressed by $\varphi \left(t\right)$:

$$x\left(t\right)=A\left(t\right)cos\left[\varphi \left(t\right)\right].$$

If the Fourier transforms of A(t) and $cos\left[\varphi \left(t\right)\right]$ have separate supports, then the analytic signal of a narrowband signal can be rewritten as the product of two meaningful components

$$\tilde{x}\left(t\right)=A\left(t\right)e^{i\varphi \left(t\right)}.$$

Where A(t) is the instantaneous amplitude and $\varphi \left(t\right)$ is the instantaneous phase obtained from the Hilbert transform H[x(t)].

The narrower the bandwidth of the signal of interest, the better the Hilbert transform produces an analytic signal with a meaningful envelope and phase⁴⁰. Adopting a band-pass filtered version of the BOLD time series improves the separation between the phase and envelope spectra.

The BOLD signals were first z-scored, and subsequently, we computed the Hilbert transform (Fig. 1B), to obtain the phase of each signal at each TR, i.e., one time sample. Then, each instantaneous phase pattern was represented as a vector with N elements (here N = 68 or 90, since we used the Desikan–Killiany and AAL atlas, comprising these number of ROIs), each element represents the projection of the phase (indicated by an arrow with an angle in Fig. 1C) of each brain area. Then, we built the matrix of phase coherence patterns (Fig. 1D) for each TR, as well as for each participant and condition.

Phase-based dynamic functional coordination

To circumvent the issue of arbitrarily choosing the time window and overlapping in capturing temporal oscillations employing a sliding-window methodology^12,29,41,42, the use of phase-based dynamic functional coordination was preferred^13,43,44.

Analytic representations of signals were employed to derive a phase signal corresponding to the BOLD time series. We computed the instantaneous phase ${\varphi }_n\left(t\right)$ of the BOLD signals across all ROI $n\in \left\{\mathrm{1,\; ...,}N\right\}$ for each TR $t\in \mathrm{\{2,}\dots ,T-\mathrm{1\}}$, the first and last TR’s of each fMRI scan were excluded due to possible signal distortions induced by the Hilbert transform⁴⁵.

The instantaneous phase was computed using Euler’s formula from the analytic signal, which was then “wrapped” within the range of −π to π, facilitating the calculation of inter-ROI phase differences. To obtain a whole-brain pattern of BOLD phase differences, the phase coherence between areas k and j at each time t, PC(k, j, t), was estimated using the pairwise phase coherence

$$PC\left(k,j,t\right)=cos\left({\varphi }_k\left(t\right)-{\varphi }_j\left(t\right)\right).$$

When areas k and j have synchronized BOLD signals at time t, phase coherence takes value 1 and, when areas k and j in anti-phase at time t phase coherence is −1, all the rest of the cases lies in between the interval [−1,1]. This computation was repeated for all subjects. For each subject, the resulting PC was a three-dimensional tensor with dimension N × N × T, where N is the number of regions in the parcellation considered (here 68 regions for general anaesthesia and 90 regions for the deep sleep) and T is the number of TR in each fMRI session.

K-means clustering

To assess recurring coordination patterns among individuals in both datasets, a multistep methodology was employed. First, by taking advantage of the symmetry of the phase coherence matrices, we concatenated only the vectorized triangular superior parts of the phase coherence matrices for every time step together. Thus, the scanning sessions were transformed into matrices, wherein one dimension represented instantaneous phase differences (feature space) and the other dimension represented time (see Fig. 1E) for all participants and all conditions. The resulting matrix was subjected to the K-means clustering algorithm utilising the L2 distance metric, as implemented in Python programming language (Scikit learn package). This resulted in a discrete set of k coordination patterns and their corresponding occurrence across time for each participant and each condition.

This process yielded k cluster centroids, which served as representatives of the recurring coordination patterns, accompanied by a label indicating the pattern to which each phase coherence matrix belongs according to the K-Means algorithm. The number of clusters was determined from a range from k = 3 to k = 10 (see Supplementary Figs.). Using the implementation of the K-means algorithm provided by Scikit Learn Python library using the ‘k-means++’ initialization method, the clustering was applied 200 times to avoid local minima using a random initialization of centroid positions in each iteration. This means that at initialization, random starting points were chosen from random samples of the coherence feature space, and then the K-Means algorithm ran from there for a maximum of 300 iterations (default value of the algorithm implementation) before stopping and re-initializing again, doing so 200 times.

Shannon entropy

We make the histogram associated to the frequency of visits to each pattern for each participant in the different states. For each of the normalized histogram of occurrence, we compute the Shannon entropy S as follows:

$$S=-\sum _i^k{P}_i{log}_2{P}_i$$ 1

Where P_i is the probability (normalized histogram) of visit for each pattern for each participant in each brain state.

Structure-function correlation

To investigate the dependence of brain dynamics on the state of consciousness, we defined a measure of similarity between functional and structural connectivity. We resorted to a widely used group estimate of human anatomical connectivity, measured with the noninvasive technique of diffusion tensor imaging (DTI). We computed the linear correlation coefficient between the entries of both matrices (K-means centroids/anatomical connectome) using the Pearson correlation. However, as shown in Figure S5, our results generalise using non-parametric measures, such as Spearman correlation or Kendall’s tau. This was performed for each phase-based coordination pattern obtained using the K-means algorithm, and was denoted SFC (see Figs. 2 and 3). Last, for each participant, we computed the linear slope coefficient of the relationship between the occurrence rate of each centroid and the corresponding centroid/anatomical correlation.

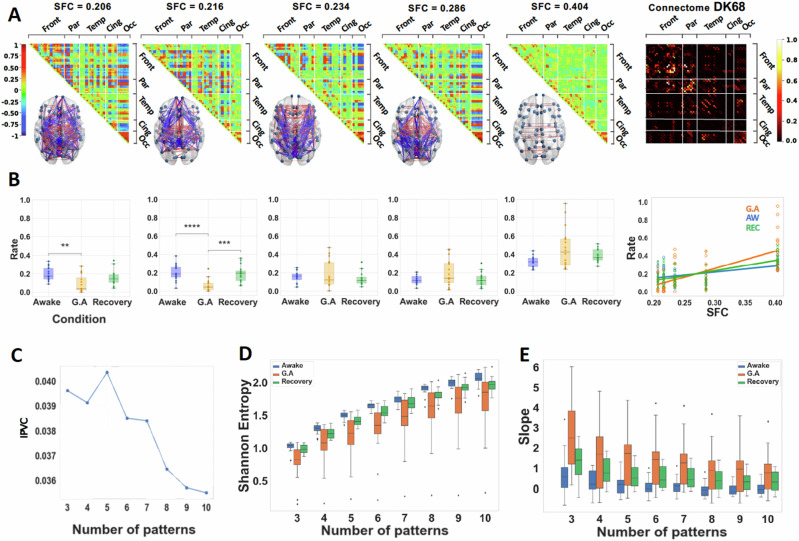
Fig. 2. Anesthesia increases structure-function coupling and decreases Shannon entropy of distributions of occupancies of patterns.

A Matrix representation of the brain coordination patterns obtained for k = 5, which is the number of clusters that maximizes the inter-pattern correlation variance (IPVC) for $3\le k\le 10$, ordered by increasing SFC (from left to right). Only the strongest elements were depicted on the brain representation; in red, the positive coherence > +0.4, and in blue, the negative coherence < −0.4. Right: (normalized) connectome using the Desikan–Killiany parcellation represented in its matrix form. B Distribution of rates of occurrence for each of the above brain patterns across all 3 conditions. Significance markers as brackets indicate what conditions are compared, and on top, stars indicate the degree of significance following the following p-value convention. **: between 0.01 and 0.001 ; *** : between 0.001 and 0.0001 ; ****: between 0.0001 and 0.00001. Right: Rate of the brain patterns as a function of their SFC. A linear regression is fitted with the mean rate of each brain pattern per condition. C IPVC as a function of the number of patterns. D Shannon Entropy of the distribution of occurrences of the k brain patterns $3\le k\le 10$ for the three conditions. Across all values of k analyzed, the Shannon entropy is lower under general anesthesia than in wakeful states. E Slopes of the linear regression for $3\le k\le 10$, computed for each participant. All boxplots extend from the first to the third quartile, with a line at the median and outliers shown as grey diamonds.

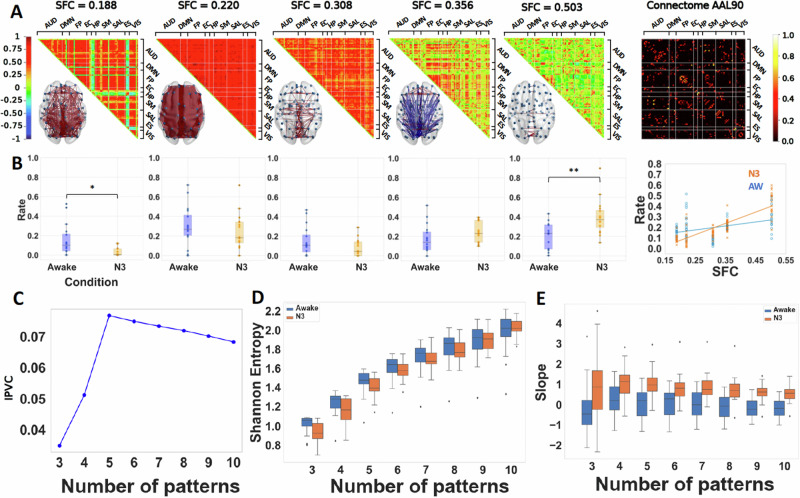
Fig. 3. Deep sleep increases structure-function coupling and decreases Shannon entropy of distributions of occupancies of patterns.

A Matrix representation of the brain coordination patterns obtained for k = 5, which is the number of clusters that maximizes the inter-pattern correlation variance for $3\le k\le 10$, ordered by increasing SFC (from left to right). Only the strongest elements were depicted on the brain representation, in red the synchronizations > +0.4 and in blue anti-synchronizations < −0.4. Right: (normalized) connectome in the AAL90 parcellation (90 × 90). B Distribution of rates of visit for each of the above brain patterns across the two conditions (Awake, N3 sleep). Paired t test was used for comparison between conditions. Rate of the brain patterns as a function of their structure-function correlation (SFC). Significance markers as brackets indicate what conditions are compared, and on top stars indicate the degree of significance following the following p value convention. *: between 0.05 and 0.01 ; **: between 0.01 and 0.001. A linear regression is fitted with the mean rate of each brain pattern per condition, showing that, during deep sleep, the brain dynamics favor brain patterns with higher SFC unlike in the wakeful condition. C Inter-pattern correlation variance (metric used to determine the number of brain patterns). D Shannon Entropy of the distribution of rates of the k brain patterns $3\le k\le 10$ for two conditions. Across all values of k, the same relative difference is found, during deep sleep, the Shannon entropy is lower than in wakeful states. E Slopes of the linear regressions for $3\le k\le 10$, computed for each participant, showing a tendency for anatomically dictated dynamics in deep sleep. Paired t test was used for comparison between conditions.

Markov chains

For every time-point, the K-Means clustering assigns the index of the closest centroid to the empirical phase coherence matrix, resulting in a chain of indexes (integers, between 1 and k). We consider that sequence of centroids, or “patterns visited” for each participant at each time, as a sequence of random variables that jumps from one pattern to another pattern with a certain probability given by the empirical frequencies in which these events happen in the data. From this information we built a Markov Chain, as done previously².

More precisely, we counted the number of transitions between all pairs of patterns, excluding self-transitions that correspond to remaining in the same pattern, and normalized them to have a Markov transition matrix, where the sum of the rows is equal to one. We only include transitions of states of the same individual participant (see Figs. 4 and 5), meaning the last state visited by a given patient and the first state visited by the next patient cannot be counted as a transition of state.

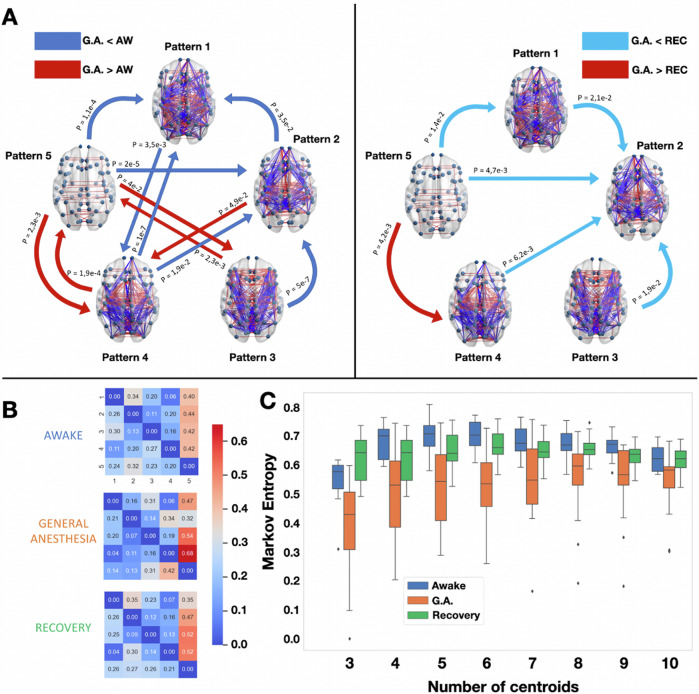
Fig. 4. Propofol anesthesia decreases Markov entropy of transitions between patterns and produces robust transition differences with the conscious states, both awake and recovery.

A Brain network representations of the five different brain patterns and the statistical significance of the Markov transition probabilities using a two-sample paired t test. Left: the awake condition is compared to general anesthesia (and vice-versa). Right: The general anesthesia condition is compared to the recovery condition. In blue are represented the transitions that were favoured in the wakeful conditions (awake and recovery), and in red the ones favoured in the unconscious condition. Only the transitions that passed the intermediate bootstrap check (CI = 95%) were considered. Comparisons were made through paired t tests. B Markov transition probabilities for the three conditions computed for k = 5. C Kolmgorov–Sinai entropy of the Markov chains obtained for $3\le k\le 10$. The Kolmgorov–Sinai entropy was consistently lower under general anesthesia. All boxplots show median, 1st, and 3rd quartile of the distributions, and outliers are diamonds. One-way repeated measure ANOVA was used to compute statistical differences between the conditions and paired t tests as post-hoc analysis as shown in Supplementary Tables.

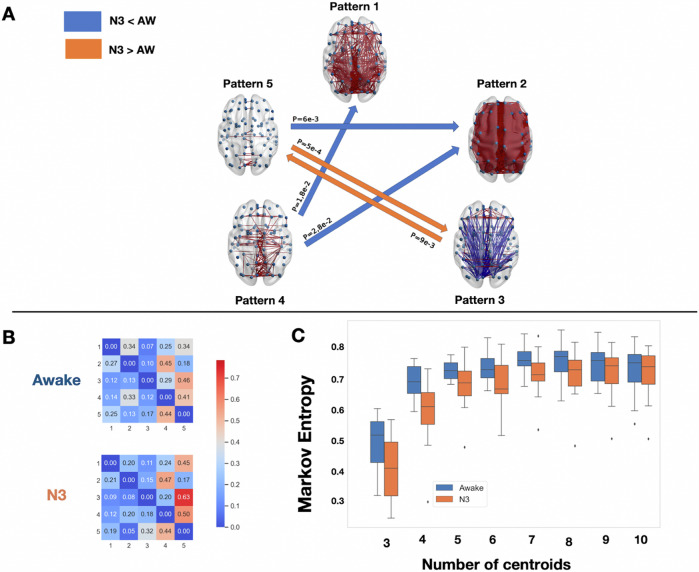
Fig. 5. Deep sleep decrease Markov entropy of transitions between patterns and produce robust transition differences with the conscious states awake and recovery.

A Brain network representations of the four different brain patterns and the statistical significance of the Markov transition probabilities using a t test. The awake condition is compared to sleep (and vice-versa). In blue are represented the transitions that were favored in the awake condition, and in orange the ones favored in the deep sleep condition (N3). Again, only the transitions that passed the intermediate bootstrap check (CI = 95%) are showed. B On the left are the Markov transition probabilities for the two conditions computed for k = 5. C The entropy of the Markov chains obtained for $3\le k\le 10$ obtained using formula (2). The Markov entropy was consistently lower under deep sleep N3 condition. All boxplots extend from the first to the third quartile, with line at the median and outliers shown as grey diamonds.

In order to generalize the notion of uncertainty of a probability distribution given by its Shannon entropy, here we quantify the degree of randomness or uncertainty there is in a sequence of random variables characterised by a discrete Markov Chain. For each participant from their Markov transition matrix, we obtained the stationary distribution μ represented as a row vector whose entries are probabilities, where μ_i corresponds to the stationary probability of observing pattern i (i.e., over the long run, independent of the starting pattern, the proportion of time the chain spends in state i is approximately μ_i for all i). The stationary probability is computed as follows: μP = μ, where P is the Markov transition matrix.

Then, we calculate the entropy rate, or Kolmogorov–Sinai entropy, of the Markov chains as follows:

$$S_M=-\sum _{ij}{\mu }_i{P}_{ij}{log}_2{P}_{ij}$$ 2

where P_ij corresponds to the transition probability from pattern i to pattern j.

Statistical methods

To assess the statistical significance of the differences between conditions in, transition probabilities, slope’s coefficients, Shannon and Markov entropies, we performed a repeated measure ANOVA to know whether there are statistically significant differences in the three-group comparison, followed by post-hoc to statistically test pairs of conditions: two paired t test with Bonferroni correction were performed between the awake and general anaesthesia conditions, and between the recovery and general anaesthesia ones. Similarly, for the sleep dataset, we performed one paired t test to compare the N3-associated measurements and the awake ones. Details about the statistical analyses are available in Tables S1 and S2 in the supplementary material.

Then, in order to ensure that the transition probabilities differences between conditions were indeed due to the specificity of the brain conditions, we resorted to a bootstrap method for each subject. For every individual, we randomly shuffled the indexes from the chain of states 10,000 times and computed as many transition matrices, thus breaking any temporal dependencies of the transitions between specific states. We then verified if the actual transitions did not belong to a confidence interval, successively designed by a confidence level of 90%, 95%, and 99%, defined by the shuffled transitions matrices. Only transitions that passed at least the 90% confidence level were then considered.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Results

We investigated a dataset of general anaesthesia with the intravenous agent propofol, where the BOLD signals of 16 participants during three conditions (awake, general anaesthesia and recovery) and a dataset of deep sleep consisting of 18 participants in two conditions (awake and N3 sleep). Both datasets were obtained following the procedures indicated in detail in the section “fMRI acquisition, experimental design and processing”.

Our phase-based analysis consistently unveiled discernible cerebral patterns of brain dynamics, demonstrating robustness against the choice of the number of clusters in the K-means algorithm (see Supplementary Figs. S1 and S2). Notably, the brain pattern possessing the lowest correlation with the connectome exhibited higher occurrence during the awake state in comparison to participants under general anaesthesia (Fig. 2B) and N3 sleep (Fig. 3B). In stark contrast, a pattern indicative of heightened structure-function correlation was more frequently observed in participants under general anaesthesia and deep sleep, as opposed to those in the awake state (see Figs. 2B and 3B).

To illustrate our results we choose the number of patterns k that maximized the inter-pattern correlation variance as in previous studies², that turns out to be five for the general anaesthesia and for deep sleep dataset. In Figs. 2A and 3A, we illustrate the five centroids in the matrix representation ordered by increasing SFC (from left to right). Only the strongest elements in absolute value were depicted on the brain graph representation, in red the positive coherence > +0.4 and in blue the negative coherence < −0.4. We show five patterns only for illustration, as shown throughout this article, our results are robust independently of the choice of the number of clusters from three to ten.

The robustness of our results are in terms of the slope of structure-function correlation, the Shannon and Markov entropies, which show differences between states of consciousness (awake versus loss of conscisouness) independently of the choice of the number of centroids in the K-means algorithm. In particular, we show that the slope of structure-function correlation with respect to the rate of occurrence of the patterns is higher when consciousness is suppressed either by general anaesthesia or deep sleep (Fig. 2B right and 4B right) independently of the choice of the number of centroids (patterns) in the K-means algorithm (Figs. 2E and 3E). We also show that the Shannon entropy computed from the normalized histograms (probability distributions) of occurrences of each brain pattern for each condition is higher in the awake and recovery conditions with respect to general anaesthesia (Fig. 2D). A similar behavior is observed in the deep sleep dataset, where the Shannon entropy is higher in the awake state with respect to the N3 stage (Fig. 3D). In both datasets the results are robust to the choice of the number of centroids (see Figs. 2–5). Furthermore, to demonstrate the robustness of our findings across different analytical approaches, we present in Figure S3 an increase in the slope of the SFC and a reduction in Shannon Entropy in unconscious states using sliding-window correlation in both datasets. Additionally, employing a pass-band filter of 0.04 to 0.07 Hz yields similar results in both datasets as those obtained with a broader filter (0.01–0.1 Hz), indicating that our results are robust to variations in bandwidth filtering (Fig. S4).

Finally, to provide a more comprehensive description of the dynamic nature of pattern exploration, we computed a matrix for each participant in each state of consciousness that detailed the probabilities of transitions between patterns. We selected the statistically significant pattern transitions obtained by comparing pairs of conditions for general anaesthesia and deep sleep (Figs. 4 and 5). From the frequency of transitions between patterns we estimated Markov chains for each condition, from which we computed the Markov Entropy following Eq. (2).

To illustrate the transitions at the group level, we represent the Markov transition matrix corresponding to the average transition matrices across all participants in the same condition. We observed higher Markov entropy for the conscious states (awake and recovery) with respect to general anaesthesia, and a similar result contrasting the awake state versus N3. As shown in (Figs. 4B and 5B), both results generalize well with different choices of the number of centroids.

Discussion

The present study delves into the generalization of results obtained previously² about the dynamics of the human brain and how they are altered in states of loss of consciousness, by employing two complementary datasets of humans under general anaesthesia and N3 sleep. The ability to employ the same method effectively across independent datasets in different scenarios of low consciousness, emphasizes its reliability and underscores its potential to yield consistent outcomes in other datasets. Such cross-applicability is indicative of the robustness of the approach and the generalizability of the results. Specifically, loss of consciousness—whether due to spontaneous sleep, or induced by general anaesthesia—appears to reduce the repertoire of dynamical states that the brain visits, with increased prevalence of the most structurally coupled pattern.

Our results demonstrate that sustaining rich brain dynamics is essential for consciousness and can serve as a biomarker for consciousness. While the awake state exhibits a richer dynamic exploration of the functional repertoire as exhibited by the Shannon entropy analyzing the histograms (Figs. 2C and 3C) and the Markov entropy for the Markov chains (Figs. 4B and 5B), the dynamic exploration is consistently reduced under anaesthesia and N3 sleep for all the different choices for the number of clusters. This result is well aligned with the entropic brain hypothesis^46–48. This diversity in state exploration is also related to recent results in the mouse using calcium imaging under different drugs of general anaesthesia, which show that under anaesthesia, the brain explores less states than the awake brain⁴⁹, and recent results of the structure-function interdependence of the macaque brain under loss of consciousness induced by three different anaesthetics (sevoflurane, propofol, ketamine) and restoration of consciousness by deep brain stimulation (DBS)⁵⁰. Furthermore, the more prevalent functional connectivity patterns during anaesthesia correlate with the anatomical connectivity, consistent with previous findings. As in previous studies², here we find that the slope of occurrence probability versus structure-function correlation increases in the states of low consciousness. Here, we show that those earlier results generalize to other mechanism of loss of conscisouiness such as general anaesthesia and N3 sleep and different number of brain patterns.

A notable feature of the phase-based methodology is that it does not need meticulous adjustment of the width of sliding windows. This autonomy from fine-tuning aspects diminishes the potential for bias introduced by window length selection, highlighting again the robustness of the methodology.

The sporadic emergence of patterns more present in states of low consciousness during periods of conscious wakefulness, and vice-versa, raises pertinent questions about the boundaries between these brain states. The co-occurrence of seemingly contrasting states within the same individual challenges conventional notions of discrete consciousness states. This observation requires further investigation into the underlying mechanisms that give rise to these sporadic occurrences and offers a unique perspective on the dynamic nature of consciousness^32,51–53. The alterations induced by propofol in the body and the brain are not only reduced to consciousness, as elucidated by ref. ⁵⁴. Discrimination between changes stemming directly from the loss of consciousness and those arising from ancillary effects of propofol on cerebral processes remains challenging. A comparable challenge is encountered in the realm of sleep research, as underscored by ref. ⁵⁵, wherein deep sleep is acknowledged as more than mere unconsciousness. Additionally, diminished vigilance is observed independently of attenuated awareness⁵⁶.

The question arises concerning the generalizability of the findings through alternative brain recording techniques, bypassing the reliance on functional Magnetic Resonance Imaging (fMRI). The prospect of employing different data sources, such as electroencephalography (EEG) or magnetoencephalography, to substantiate the identified consciousness states introduces an avenue for expanding the horizon of the current methodology, and enhances the robustness of the method and the findings^25,57–59. Generalisations of the present method to EEG are under development⁶⁰, and may be of particular relevance, for example, for the study of unconsciousness induced by epileptic seizures. Alternatively, other species under general anaesthesia can be studied as has been done in the past with the sliding-window technique^29,34. Envisioning a broader context, the study prompts consideration of consciousness-altering scenarios beyond those encountered within wakefulness or unconscious states.

However, it is important to acknowledge the limitations inherent in the study. Important gaps remain in understanding how these dynamics are influenced by brain structure and anaesthesia agents. For example, another widely used anaesthetic, sevoflurane, has been shown to resemble propofol in terms of its effects on brain dynamics, both in humans^27,35,61 and macaques^34,62. Another important limitation is that we do not know which changes are a consequence of propofol reducing consciousness, and which appear because propofol does other things in the brain⁵⁴. The same problem is present for sleep, since deep sleep is not only loss of consciousness (consciousness may be present as shown by Siclari, Tononi et al.⁵⁵), and reduced vigilance occurs independently of reduced awareness⁵⁶. The generality of the method is also partly a weakness because, as can be seen in Figs. 2 and 3, the patterns of general anaesthesia and deep sleep are quite different. This may be because they are obtained from data obtained by different research groups using different data acquisition parameters, with different preprocessing protocols and different participants under different conditions of loss of consciousness and different levels of global signal contribution. In Supplementary Fig. S6, we illustrate that the sleep dataset exhibits significantly higher levels of global signal compared to the anaesthesia dataset. There are multiple reasons why this may have come about. Methodologically, the two datasets were denoised differently; RETROICOR⁶³ (sleep) versus aCompCor (anaesthesia). Although global signal regression is not part of either method, the two procedures may have removed different amounts of global signal. Physiologically, the sleep dataset participants may have been more drowsy even during the awake scans, since they were scanned at 7 pm in the evening. This disparity partially accounts for the pronounced differences between the centroids derived from the two datasets, as well as the presence of hyper-synchronized patterns in the sleep dataset. These findings suggest that our approach remains robust despite varying levels of global signal across different datasets.

Future studies could address this issue following the approach taken in ref. ², which uses data from different research groups and applies a unique preprocessing method and parcellation. Despite these limitations, the method appears to be robust and generalisable; the question then remains: how broad is the generalisability of the present findings?

In conclusion, the present study highlights the generalisation and robustness of previous results employing a uniform methodology across varying states exhibited by different cohorts, in different consciousness states. By leveraging the complementary nature of our results, we provide a comprehensive characterization of the dynamic features of brain networks and how consciousness reshapes the dynamics of the human brain and its relation with the connectome. This study contributes to the broader discourse on consciousness and methodology, paving the way for future investigations into the relationship of consciousness and dynamical brain patterns and to identify potential markers that may be utilized in the future to distinguish between conscious and unconscious states.

fMRI acquisition, experimental design and processing

Anaesthesia data: recruitment

The propofol data employed in this study have been published before^27,64–66. For clarity and consistency of reporting, where applicable we use the same wording as our previous studies. The propofol data were collected between May and November 2014 at the Robarts Research Institute in London, Ontario (Canada)²⁷. The study received ethical approval from the Health Sciences Research Ethics Board and Psychology Research Ethics Board of Western University (Ontario, Canada). Healthy volunteers (n = 19) were recruited (18–40 years; 13 males). Volunteers were right-handed, native English speakers, and had no history of neurological disorders. In accordance with relevant ethical guidelines, each volunteer provided written informed consent, and received monetary compensation for their time. Due to equipment malfunction or physiological impediments to anaesthesia in the scanner, data from n = 3 participants (1 male) were excluded from analyses, leaving a total n = 16 for analysis.

Anaesthesia data: procedure

Resting-state fMRI data were acquired at different propofol levels: no sedation (Awake), and Deep anaesthesia (corresponding to Ramsay score of 5). As previously reported²⁷, for each condition, fMRI acquisition began after two anaesthesiologists and one anaesthesia nurse independently assessed Ramsay level in the scanning room. The anaesthesiologists and the anaesthesia nurse could not be blinded to experimental condition, since part of their role involved determining the participants’ level of anaesthesia. Note that the Ramsay score is designed for critical care patients, and therefore, participants did not receive a score during the Awake condition before propofol administration; rather, they were required to be fully awake, alert, and communicating appropriately. To provide a further, independent evaluation of participants’ level of responsiveness, they were asked to perform two tasks: a test of verbal memory recall, and a computer-based auditory target-detection task. Wakefulness was also monitored using an infrared camera placed inside the scanner.

Propofol (a potent agonist of inhibitory GABA-A receptors^67,68 was administered intravenously using an AS50 auto syringe infusion pump (Baxter Healthcare, Singapore); an effect-site/plasma steering algorithm combined with the computer-controlled infusion pump was used to achieve step-wise sedation increments, followed by manual adjustments as required to reach the desired target concentrations of propofol according to the TIVA Trainer (European Society for Intravenous Aneaesthesia, eurosiva.eu) pharmacokinetic simulation program. This software also specified the blood concentrations of propofol, following the Marsh 3-compartment model, which were used as targets for the pharmacokinetic model providing target-controlled infusion. After an initial propofol target effect-site concentration of 0.6 µg mL⁻¹, concentration was gradually increased by increments of 0.3 µg mL⁻¹, and Ramsay score was assessed after each increment: a further increment occurred if the Ramsay score was lower than 5. The mean estimated effect-site and plasma propofol concentrations were kept stable by the pharmacokinetic model delivered via the TIVA Trainer infusion pump. Ramsay level 5 was achieved when participants stopped responding to verbal commands, were unable to engage in conversation, and were rousable only to physical stimulation. Once both anaesthesiologists and the anaesthesia nurse all agreed that Ramsay sedation level 5 had been reached, and participants stopped responding to both tasks, data acquisition was initiated. The mean estimated effect-site propofol concentration was 2.48 (1.82–3.14) µg mL⁻¹, and the mean estimated plasma propofol concentration was 2.68 (1.92–3.44) µg mL⁻¹. Mean total mass of propofol administered was 486.58 (373.30–599.86) mg. These values of variability are typical for the pharmacokinetics and pharmacodynamics of propofol. Oxygen was titrated to maintain SpO2 above 96%. At Ramsay 5 level, participants remained capable of spontaneous cardiovascular function and ventilation. However, the sedation procedure did not take place in a hospital setting; therefore, intubation during scanning could not be used to ensure airway security during scanning. Consequently, although two anaesthesiologists closely monitored each participant, scanner time was minimised to ensure return to normal breathing following deep sedation. No state changes or movement were noted during the deep sedation scanning for any of the participants included in the study. Written informed consent was asked to all participants before the experiment. All ethical regulations relevant to human research participants were followed.

Anaesthesia data: design

As previously reported²⁷, once in the scanner participants were instructed to relax with closed eyes, without falling asleep. Resting-state functional MRI in the absence of any tasks was acquired for 8 min for each participant. A further scan was also acquired during auditory presentation of a plot-driven story through headphones (5 min long). Participants were instructed to listen while keeping their eyes closed. The present analysis focuses on the resting-state data only; the story scan data have been published separately⁶⁶.

Anaesthesia data: fMRI data acquisition

As previously reported²⁷, MRI scanning was performed using a 3-Tesla Siemens Tim Trio scanner (32-channel coil), and 256 functional volumes (echo-planar images, EPI) were collected from each participant, with the following parameters: slices = 33, with 25% inter-slice gap; resolution = 3 mm isotropic; TR = 2000 ms; TE = 30 ms; flip angle = 75 degrees; matrix size = 64 × 64. The order of acquisition was interleaved, bottom-up. Anatomical scanning was also performed, acquiring a high-resolution T1-weighted volume (32-channel coil, 1 mm isotropic voxel size) with a 3D MPRAGE sequence, using the following parameters: TA = 5 min, TE = 4.25 ms, 240 × 256 matrix size, 9 degrees flip angle²⁷.

Sleep data: recruitment

A total of 63 healthy subjects (36 females, mean ± SD, 23.4 ± 3.3 years) were selected from a dataset previously described in a sleep-related study by Tagliazucchi and Laufs⁶⁹. Participants entered the scanner at 7 PM and were asked to relax, close their eyes, and not fight the sleep onset. A total of 52 minutes of resting-state activity were measured with a simultaneous combination of EEG and fMRI. According to the rules of the American Academy of Sleep Medicine, the polysomnography signals (including the scalp potentials measured with EEG) determine the classification of data into four stages (wakefulness, N1, N2, and N3 sleep).

We selected 18 subjects with contiguous resting-state time series of at least 200 volumes to perform our analysis. The local ethics committee approved the experimental protocol (Goethe-Universität Frankfurt, Germany, protocol number: 305/07), and written informed consent was asked to all participants before the experiment. The study was conducted according to the Helsinki Declaration on ethical research. All ethical regulations relevant to human research participants were followed.

Sleep data: MRI data acquisition

MRI images were acquired on a 3-Tesla Siemens Trio scanner (Erlangen, Germany) and fMRI acquisition parameters were 1505 volumes of T2-weighted EPIs, TR/TE = 2080 ms/30 ms, matrix 64 × 64, voxel size 3 × 3 × 3 mm³, distance factor 50%; FOV 192 mm². An optimized polysomnographic setting was employed (chin and tibial EMG, ECG, EOG recorded bipolarly [sampling rate 5 kHz, low-pass filter 1 kHz] with 30 EEG channels recorded with FCz as the reference [sampling rate 5 kHz, low-pass filter 250 Hz]. Pulse oximetry and respiration were recorded via sensors from the Trio [sampling rate 50 Hz]) and MR scanner-compatible devices (BrainAmp MR+, BrainAmpExG; Brain Products, Gilching, Germany), facilitating sleep scoring during fMRI acquisition. The method RETROICOR⁶³, was uses to model physiological noise (Respiration effects and cardiac pulsatility) and use it to denoise the data.

Sleep data: brain parcellation AAL90 to extract BOLD time series and filtering

To extract the time series of BOLD signals from each participant in a coarse parcellation, we used the AAL90 parcellation with 90 brain areas anatomically defined in [25]. BOLD signals (empirical or simulated) were filtered with a Butterworth (order 2) band-pass filter in the 0.01–0.1 Hz frequency range.

DWI preprocessing and tractography anaesthesia dataset

The diffusion data were preprocessed with MRtrix3 tools. This is the same pipeline adopted in our previous work for clarity and consistency of reporting, where applicable we use the same wording as in our previous publications,⁷⁰. After manually removing diffusion-weighted volumes with substantial distortion, the pipeline involved the following steps: (i) DWI data denoising by exploiting data redundancy in the PCA domain⁷¹ (dwidenoise command); (ii) Correction for distortions induced by eddy currents and subject motion by registering all DWIs to b0, using FSL’s eddy tool (through MRtrix3 dwipreproc command); (iii) rotation of the diffusion gradient vectors to account for subject motion estimated by eddy⁷² (iv) b1 field inhomogeneity correction for DWI volumes (dwibiascorrect command); (v) generation of a brain mask through a combination of MRtrix3 dwi2mask and FSL BET commands.

After preprocessing, the DTI data were reconstructed using the model-free q-space diffeomorphic reconstruction algorithm (QSDR) implemented in DSI Studio (www.dsi-studio.labsolver.org), following our previous work⁷⁰. The use of QSDR is desirable when investigating group differences because this algorithm preserves the continuity of fiber geometry for subsequent tracking since it reconstructs the distribution of the density of diffusing water in standard space. QSDR initially reconstructs DWI data in native space, and subsequently computes values of quantitative anisotropy (QA) in each voxel, based on which DSI Studio performs a nonlinear warp from native space to a template QA volume in Montreal Neurological Institute (MNI) space. Once in MNI standard space, spin density functions are reconstructed, with a mean diffusion distance of 1.25 mm with three fiber orientations per voxel⁷³.

Finally, fiber tracking was carried out using DSI Studio’s own FACT deterministic tractography algorithm, requesting 1000,000 streamlines according to widely adopted parameters: angular cutoff = 55°, step size = 1.0 mm, tract length between 10 mm (minimum) and 400 mm (maximum), no spin density function smoothing, and QA threshold determined by DWI signal in the cerebrospinal fluid. Streamlines were automatically rejected if they presented improper termination locations, based on a white matter mask automatically generated by applying a default anisotropy threshold of 0.6 Otsu’s threshold to the anisotropy values of the spin density function.

Brain parcellation

For both BOLD and DWI data, brains were parcellated into 68 cortical ROIs, according to the Desikan-Killiany anatomical atlas⁷⁴.

DWI preprocessing and tractography Sleep dataset

The data was obtained from 16 healthy right-handed participants (11 men and five women, mean age: 24.75 ± 2.54). Data were collected at Aarhus University, Denmark. Participants with psychiatric or neurologic disorders (or a history thereof) were excluded from participation in this study. The MRI data (structural MRI, DTI) were collected in one session on a 3 T Siemens Skyra scanner at Aarhus University, Denmark. The parameters for the structural MRI T1 scan were as follows: voxel size of 1 mm3; reconstructed matrix size 256 × 256; echo time (TE) of 3.8 ms and TR of 2300 ms.

The DTI data were collected using TR = 9000 ms, TE = 84 ms, flip angle = 90°, reconstructed matrix size of 106 × 106, voxel size of 1.98 × 1.98 mm with slice thickness of 2 mm and a bandwidth of 1745 Hz/Px. Furthermore, the data were collected with 62 optimal nonlinear diffusion gradient directions at b = 1500 s/mm². Approximately one nondiffusion-weighted image (DWI; b = 0) per 10 diffusion-weighted images was acquired. Additionally, the DTI images were collected with different phase encoding directions. One set was collected using anterior to posterior phase encoding direction and the second acquisition was performed in the opposite direction. For the parcellation, we used the AAL template to parcellate the entire brain into 90 regions (76 cortical regions, adding 14 subcortical regions, AAL90). The parcellation consists of regions distributed in each hemisphere⁷⁵. The linear registration tool from the FSL toolbox (www.fmrib.ox.ac.uk/fsl, FMRIB⁷⁶) was used to coregister the EPI image to the T1-weighted structural image. The T1-weighted image was coregistered to the T1 template of ICBM152 in MNI space. The resulting transformations were concatenated and inversed and further applied to warp the AAL template from MNI space to the EPI native space, where interpolation using nearest-neighbor method ensured that the discrete labeling values were preserved. Thus the brain parcellations were conducted in each individual’s native space. We generated the SC maps for each participant using the DTI data acquired. We processed the two datasets acquired (each with different phase encoding to optimize signal in difficult regions). The construction of these SC maps or structural brain networks consisted of a three-step process. First, the regions of the whole-brain network were defined using the AAL template as used in the functional MRI data. Second, the connections between nodes in the whole-brain network (i.e., edges) were estimated using probabilistic tractography. Third, data were averaged across participants. Similar to the functional data, we applied the AAL90 template using the FLIRT tool from the FSL toolbox (www.fmrib.ox.ac.uk/fsl, FMRIB) to coregister the b0 image in diffusion MRI space to the T1-weighted structural image and then to the T1 template of ICBM152 in MNI space⁷⁷. The two transformation matrices from these coregistration steps were concatenated and inversed to subsequently be applied to warp the AAL templates from MNI space to the diffusion MRI native space.

Brain parcellation

For both BOLD and DWI data, brains were parcellated into 90 ROIs, according to the AAL anatomical atlas⁷⁵.

Author contributions

R.C. and A.D. conceived the project. E.T., L.N., and A.O. designed the experimental protocols. A.L. preprocessed the anesthesia dataset and E.T. the Sleep dataset. P.C. and R.C. performed the data analysis. J.D.S., Y.S.P. developed the computational models. A.L. and J.D.S. contributed to data interpretation and provided critical insights. R.C., A.L., E.T., P.C., and A.D. wrote the manuscript with input from all authors. All authors discussed the results and contributed to the final manuscript.

Peer review

Peer review information

Communications Biology thanks Hyunwoo Jang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Christina Karlsson-Rosenthal. A peer review file is available.

Data availability

The dataset of general anaesthesia is openly available and can be found in the following link https://openneuro.org/datasets/ds003171/versions/1.0.0⁷⁸. The dataset of sleep is available on request from nztglzcch@gmail.com.

Code availability

All analyses were carried out using custom scripts written in Python and openly available https://github.com/Krigsa/phase_coherence_kmeans⁷⁹.

Competing interests

The authors declare that they have no competing interests. E.T. is an Editorial Board Member for Communications Biology but was not involved in the editorial review of, nor the decision to publish, this article.

Supplementary information

The online version contains supplementary material available at 10.1038/s42003-024-06858-3.