Abstract

The conversion of lignin can produce biomass-derived aromatic compounds such as 2-pyrone-4,6-dicarboxylic acid (PDC), which is a potential sustainable precursor of bioplastics. PDC is a pseudoaromatic dicarboxylic acid that can aggregate in aqueous solution. Aggregation depends upon PDC–PDC, PDC-water, and PDC-ion interactions that are representative of interactions in similar charged, aromatic compounds. These interactions both dictate PDC aggregation and the likelihood that PDC aggregates exhibit parallel stacking configurations that may promote PDC crystallization, which can be leveraged to separate PDC from solution. However, the interplay of interactions that drive aggregation and structure formation, and how these depend upon the charge of PDC and ionic species present in solution, remains unclear. In this work, we investigate PDC aggregation in diverse ionic solutions using all-atom molecular dynamics simulations and molecular clustering analysis. We consider ion-induced dipole interactions by using a modified Lennard-Jones nonbonded model for divalent ions in solutions. From molecular clustering analysis, we derive characteristic parameters to quantify aggregate sizes and parallel stacking configurations. We show that acid dissociation facilitates PDC aggregation in ionic solutions via ion-mediated interactions, and different ionic solutions influence both the likelihood of aggregation and the formation of parallel aggregates. In particular, we find that parallel stacking is primarily found in solutions with monovalent ions, whereas divalent ions promote larger, but less structured, aggregates. These results provide molecular-scale insight into the effects of specific ions on the aggregation of like-charged PDC molecules to inform understanding of related separation processes.
1. Introduction
Lignocellulosic biomass is an abundant renewable feedstock which can potentially be used for the sustainable production of fuels and high-value chemicals, thereby reducing dependence upon petroleum and contributing to decarbonization.1,2 A pathway for biomass valorization is through the conversion of lignin, one of the three primary components of biomass, to diverse bioproducts with rich functional groups.3 One product that can be obtained from the microbial conversion of lignin is 2-pyrone-4,6-dicarboxylic acid (PDC), a pseudoaromatic dicarboxylic acid.4 PDC shows promise as a precursor for the production of bioplastics and epoxy adhesives.5,6 However, the production of PDC requires its separation from the aqueous fermentation broth utilized in microbial conversion processes. A common separation method for obtaining high-purity PDC is crystallization, which is mediated by added salt such as sodium chloride.7 The resulting crystal structure of Na(PDC)2 has PDC molecules oriented with their pyran rings packed against each other and sodium ions bridging between carboxylic acid groups. This structure suggests the importance of ion-mediated interactions in promoting PDC crystallization; such interactions will depend upon the identity of the salt added to induce crystallization. Given the complex composition of fermentation broth, including the presence of multiple different ionic species, further improving separation processes of PDC or related molecules via crystallization requires insight into the effect of solution pH and ion identity on intermolecular interactions with PDC.
In general, crystallization involves the (1) nucleation of a crystal after the aggregation of molecules into a stable cluster and (2) growth of the crystal through packing of molecules on its surface.8,9 The initial aggregation of molecules into clusters is thus a critical step in the crystallization process.10,11 More broadly, molecular aggregation is relevant to numerous industrial applications in pharmaceuticals, solar cells, sensing, detergents, coatings, and food.12−14 Aggregation is usually driven by noncovalent interactions that are sufficiently attractive to overcome the unfavorable entropy change associated with spontaneous aggregation.15−17 Noncovalent interactions can include electrostatic interactions, hydrogen bonding, dipole–dipole interactions, and van der Waals interactions. The solvent environment can also influence the magnitude of these interactions. For example, cosolvents can strengthen the hydrogen-bond network of water to modulate the function and stability of aggregated structures,18 solvent-mediated hydrophobic interactions can mediate the assembly of nonpolar aggregates,19 and pH and ionic strength can alter the formation and properties of molecular aggregates.20,21 Understanding the balance of the interactions that contribute to the thermodynamic stability of aggregated structures can provide insight into conditions that facilitate molecular aggregation as a precursor to crystallization.22,23
Based on the PDC crystal structure,24,25 two less common interactions may influence PDC aggregation: stacking interactions and ion-mediated interactions. In molecules with planar, aromatic or pseudoaromatic rings, stacking interactions promote the formation of structures with rings attractively packed in close contact,26 which we refer to as “parallel molecular stacking” due to the alignment of rings. Ion-mediated interactions can counterintuitively promote the aggregation of like-charged molecules, in contrast to conventional expectations from Debye–Hückel theory,27 by increasing the charge density in the spatial region between charged molecules.28,29 For instance, Lavagna et al.30 and Petretto et al.31 found that ion-mediated interactions drive the aggregation of like-charge nanoparticles on lipid membranes or in aqueous salt solution through ion bridges. Moreover, the identity and concentration of ions influence ion-mediated interactions’ strength. In particular, metal cations lead to ion-mediated interactions by providing an interaction center with a large attractive interaction energy that can promote specific orientations of the interacting species.32 Lee et al. showed that a high concentration of metal ions promotes the formation of oligomers for amyloid β aggregates, and zinc ions can more effectively destabilize fibril structures for amyloid β aggregates than copper ions.33 Ions with smaller radii can also lead to higher aggregation numbers, as has been shown for charged polymers.34 Thus, a competition between stacking interactions, ion-mediated interactions, and other noncovalent interactions can determine PDC aggregation and the resulting structure of PDC aggregates. The fundamental open question is as follows: How do the charge of PDC and the identity of other ions in solution influence this competition between molecular interactions?
A challenge in studying the PDC aggregation process is resolving molecular-scale details of aggregate structure. Although experiments have revealed the precipitation of PDC in solutions containing alkali metal ions,25 limited work has studied the aggregation of PDC, or similar pseudoaromatic carboxylic acid molecules, to reveal the influence of ion identity on PDC aggregation. Doing so requires methods to accurately resolve the effect of varying ions on ion-mediated interactions and to quantitatively characterize differences in aggregate structures. As an alternative to experimental characterization of molecular aggregates, computational modeling can provide insight into aggregation mechanisms35−37 and reveal parameters influencing aggregate structures.38,39 One commonly used method to study molecular-scale aggregation in ionic solutions is classical molecular dynamics (MD) simulation.40 For instance, MD simulations have been used to investigate how ion-mediated interactions influence protein stabilization on nanoparticle surfaces.41 Dai et al. used MD simulations to investigate ion-mediated attractive interactions between DNA molecules and rationalized this attractive force through the formation of ion bridges.42 Lewis et al. leveraged MD simulations to investigate the role of ionic interactions in aqueous lithium bistriflimide solutions as a function of concentration and found that highly interconnected ion-rich network forms in the superconcentrated regime.43 Petretto et al. found that the aggregation of weakly charged hydrophilic polyelectrolytes with biguanide groups in water or in monovalent ionic solutions is driven by the like-charged pairing of the biguanide units and is favored by increasing salt concentration.44 These studies indicate that MD simulations are suitable for analyzing the factors contributing to PDC aggregation as a precursor to crystallization.
In this work, we perform all-atom MD simulations to study factors that influence PDC aggregation. In particular, we seek to understand how the pH and specific ionic species present in solution influence the competition of stacking interactions, ion-mediated interactions, and noncovalent interactions between PDC and water to dictate the structure of the resulting aggregates. Specifically, we focus on determining conditions that lead to aggregates with parallel molecular stacking, which are consistent with the PDC crystal structure. To do so, we systematically model PDC molecules with different degrees of acid dissociation (to investigate the role of pH) and in the presence of various metal ions. We develop a method to identify PDC aggregates and compute two order parameters that characterize aggregates in terms of concentration and degree to which PDC molecules pack pyran rings against each other. Our results show that the dissociation of PDC molecules and addition of Na+, K+, Rb+, Cs+, Be2+, Mg2+, and Ca2+ ions facilitate PDC aggregation. These results provide insight into how adjustment to solution pH and selection of appropriate ionic species can promote PDC aggregation into highly ordered structures with parallel molecular stacking.
2. Methods
2.1. Molecular Dynamics Simulations
Classical molecular dynamics (MD) simulations were performed to analyze PDC aggregation in water or in various ionic solutions. All MD simulations were performed in the isothermal–isobaric (NPT) ensemble using Gromacs 2018.45Figure 1 shows the PDC chemical structure and an example snapshot of a simulation system. As shown in Figure 1a, PDC is a planar, pseudoaromatic compound with two carboxylic acid groups of varying pKa:46 (1) the carboxylic acid group in the green box dissociates first when the pH is low (pKa = 1.13), and (2) the carboxylic acid group in the red box dissociates second when the pH is further increased (pKa = 2.52). All systems were initiated in a cubic simulation box with dimensions of 6 nm in all directions. Each simulation system contained 100 PDC molecules (of varying net charge; vide infra) and 6088–6196 water molecules, with the number of water molecules determined using gmx solvate). Either 50, 100, or 200 metal ions were added to neutralize the system depending upon the charge of the PDC molecules and added metal ions.
Figure 1.

Simulation systems used to investigate PDC aggregation in various ionic solutions. a) PDC chemical structure with two carboxylic acid groups indicated. The group in green dissociates first and the group in red dissociates second when the pH is increased. b) Snapshot of 100 PDC− ions in a solution with Li+ counterions. PDC− ions are in blue, metal ions are in pink and water is not shown for visual clarity. The images at right illustrate the range of monovalent and divalent metal ions studied in this work.
As shown in Figure 1, a number of monovalent and divalent metal ions were considered. For comparison, we also considered a system consisting of 100 neutral PDC molecules and 6246 water molecules without additional ions. The resulting PDC concentration was approximately 0.77 mol/L, which is comparable to concentrations produced experimentally.7,47
PDC molecules were parametrized using the Generalized AMBER force field.48 Water molecules were modeled using the SPC/E model. To more accurately capture interactions with divalent metal cations, referred to as M(II) ions, the functional form of the standard Lennard-Jones (LJ) potential was modified following the approach by Li and coworkers:49
| 1 |
Here, 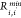 is the distance between two atoms corresponding
to the minimum value of the LJ potential and
is the distance between two atoms corresponding
to the minimum value of the LJ potential and 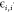 is the depth of the LJ minimum.
is the depth of the LJ minimum. 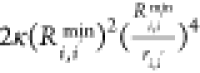 is an additional term that represents ion-induced
dipole interactions when M(II) ions are present in the system, with
κ = 0 if only monovalent M(I) ions are present in the system.
If M(II) ions are present in the system, we took the value of
is an additional term that represents ion-induced
dipole interactions when M(II) ions are present in the system, with
κ = 0 if only monovalent M(I) ions are present in the system.
If M(II) ions are present in the system, we took the value of  ,
, 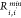 , and κ from ref. (49)eq 1 was implemented using tabulated potentials
in Gromacs 2018. In constructing the parameter matrix for the nonbonded
LJ parameters, we used Lorentz–Berthelot combining rules.48
, and κ from ref. (49)eq 1 was implemented using tabulated potentials
in Gromacs 2018. In constructing the parameter matrix for the nonbonded
LJ parameters, we used Lorentz–Berthelot combining rules.48
Each simulation system was equilibrated for 2 ns at 293.15 K (based on experimental conditions25) and 1 bar using the velocity-rescale thermostat and Berendsen barostat. A 100 ns simulation was then performed at the same temperature and pressure using the Nose-Hoover thermostat and Parrinello–Rahman barostat. Simulations were performed using the leapfrog algorithm with a 2 fs time step for most simulations and a 1 fs time step for simulations that exhibited numerical instabilities. van der Waals interactions were modeled with a shifted LJ potential and Verlet cutoff scheme that was smoothly shifted to zero at 1.2 nm. Electrostatic interactions were calculated using the smooth particle mesh Ewald method with a short-range cutoff of 1.2 nm, a grid spacing of 0.14 nm, and fourth-order interpolation. Bonds were constrained using the LINCS algorithm. All thermostats used a 2.0 ps time constant, and all barostats used a 2.0 ps time constant with 4.5 × 10–5 bar–1 as the isothermal compressibility.
2.2. Identification of PDC Aggregates and Parallel Clusters
We developed and implemented a clustering method
to identify PDC molecular aggregates and the degree to which PDC molecules
stack in parallel configurations within these aggregates. We calculated
two quantities to determine PDC aggregates: (1) the minimum pairwise
molecular distance between molecules, 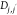 , and (2) the dihedral angle between pairs
of molecules, Aj,j′. We use j∈J to denote
a PDC molecule (neutral or charged) and t∈T to denote an atom in molecule j. Dj,j′ is determined
as follows:
, and (2) the dihedral angle between pairs
of molecules, Aj,j′. We use j∈J to denote
a PDC molecule (neutral or charged) and t∈T to denote an atom in molecule j. Dj,j′ is determined
as follows:
| 2 |
Here, 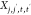 ,
, 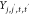 , and
, and 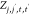 are pairwise distances between atom t (in molecule j) and t′ (in molecule j′) projected onto the x-axis, y-axis,
and z-axis, respectively.
are pairwise distances between atom t (in molecule j) and t′ (in molecule j′) projected onto the x-axis, y-axis,
and z-axis, respectively.
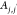 is determined as follows:
is determined as follows:
| 3 |
The vector nj is the normal
vector to the plane of molecule j. The molecular
plane is defined by two vectors, which are computed based on the positions
of carbon atoms C08, C09, C10; see Figure 2. The cross-product of these two vectors
determines the normal vector nj (shown
in Figure 2). 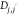 and
and 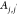 were computed using MDTraj.50
were computed using MDTraj.50
Figure 2.

Geometries and stacking structures between two PDC molecules. a) Geometries and computation of dihedral angle between two PDC molecules. The molecular plane is determined using carbon atoms C08, C09, C10, and the cross-product of vectors between C09–C08 and C09–C10 define the normal vector to the molecular plane. The dot product of a pair of normal vectors for different PDC molecules determines the dihedral angle between them. b) Snapshot of stacking structures of two PDC− ions in a solution with Li+ counterions. PDC− ions are in blue while other components are not shown. PDC− ions that satisfy eq 4 but do not exhibit parallel stacking are shown at left, whereas PDC− ions that satisfy both eqs 4 and 5 and exhibit parallel stacking are shown at right.
We identified aggregates by using a clustering
algorithm detailed
in Section S2. Briefly, the method involves
determining 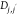 and
and 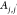 for each pair of PDC molecules in each
simulation configuration. PDC molecules were assigned to aggregates
based on the following two equations:
for each pair of PDC molecules in each
simulation configuration. PDC molecules were assigned to aggregates
based on the following two equations:
| 4 |
| 5 |
Pairs of PDC molecules that satisfy eq 4 were assigned to the same aggregate. Pairs of PDC molecules within the same aggregate that further satisfy eq 5 were considered to be in a parallel stacking configuration and were defined as being within the same parallel cluster; each aggregate could contain multiple parallel clusters. The cutoff value A0 was set to 20◦. The cutoff value D0 was set to 0.31 nm based on sensitivity analysis of several potential cutoff values (Figure S1). This cutoff value is comparable to the interplanar distance of stacked pairwise pyrone rings, which is unusually short potentially caused by the strong antiparallel dipolar interactions of the carbonyl moieties of the pyrone ring as well as of the carboxylic acids.46 Because the clustering algorithm was performed separately for different simulation configurations, the number and distribution of both aggregates and parallel clusters fluctuate throughout the simulation trajectory.
2.3. Aggregate Order Parameters
We defined
two order parameters to compare the tendency of PDC to assemble into
aggregates that exhibit parallel molecular stacking. The first order
parameter, Rc, quantifies
the degree of parallel molecular stacking for parallel clusters. To
compute Rc, we first
implemented the clustering method (Algorithm 1 of Supporting Information) described in the prior section by
applying eq 4 and not eq 5 to determine a set of
aggregates (i.e., PDC molecules were assigned to aggregates without
considering parallel molecular stacking). For each aggregate p in this set, we define the aggregation number Lp as the total number of molecules
within the aggregate. The number of parallelly stacked PDC molecules
was counted by further applying eq 5 to pairs of PDC molecules, thereby generating a set
of parallel clusters. We note that multiple distinct parallel clusters
are possible per aggregate. We define Nc as the number of PDC molecules within parallel cluster c that are contained in aggregate p; hence, 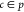 . Finally, we define Rc as
. Finally, we define Rc as
| 6 |
Thus, Rc is the ratio of the number of PDC molecules in parallel cluster c to the total number of PDC molecules within aggregate p that contains parallel cluster c. Rc is a continuous parameter with a value between 0 and 1: Rc = 0 indicates that no molecules in aggregate p are in parallel stacking configurations whereas Rc = 1 indicates that all molecules in aggregate p are in parallel stacking configurations.
The second order parameter, Mc, quantifies the total number of PDC molecules in parallel clusters. For the set of parallel clusters defined by applying eqs 4 and 5 to all pairs of PDC molecules, Nc was defined as the number of PDC molecules within parallel cluster c and F(Nc) was defined as the number of parallel clusters with a given value of Nc. Since each aggregate defined using eq 4, can contain zero, one, or multiple parallel clusters, F(Nc) is not necessarily equal to the number of aggregates. We then define Mc as follows:
| 7 |
Hence, Mc counts the total number of PDC molecules in parallel clusters
containing Nc molecules.
Note that 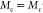 for two different parallel clusters c and c′ if
for two different parallel clusters c and c′ if 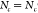 . Larger values of Mc indicate an overall increased propensity
for PDC molecules to exhibit parallel molecular stacking regardless
of whether the PDC molecules are in a large number of small parallel
clusters (i.e., small Nc, large F(Nc)) or a small number of large parallel clusters (i.e., large Nc, small F(Nc)), whereas reporting
the distribution of Nc alone may lead to peaks at small values of Nc without revealing the overall extent of
parallel stacking with the system.
. Larger values of Mc indicate an overall increased propensity
for PDC molecules to exhibit parallel molecular stacking regardless
of whether the PDC molecules are in a large number of small parallel
clusters (i.e., small Nc, large F(Nc)) or a small number of large parallel clusters (i.e., large Nc, small F(Nc)), whereas reporting
the distribution of Nc alone may lead to peaks at small values of Nc without revealing the overall extent of
parallel stacking with the system.
The probability distributions of Mc and Rc are generated based on all values of Mc and Rc determined for each parallel cluster c (using eqs 6 and 7, respectively) for each simulation configuration output after the number of clusters stabilized. The time required for the number of clusters to stabilize varied from 20–30 ns for each system, as reported in Section S5 and Figures S3 – S7. Simulation configurations were output every 1 ns. An illustrative example of determining Rc and Mc for the PDC-water-Li+ system is given in Section S4.
2.4. Spatial Distribution Function
The spatial distribution function (SDF) describes the probability of finding a molecule at a certain position in the 3D space around a given reference molecule. Another distribution function is the radial distribution function (RDF), which measures the probability of finding a particle at a certain distance away from a given reference particle. The advantage of the SDF over the RDF is that the SDF can present more detailed information regarding the 3D local solvation structure in molecular liquids.51 Each SDF is stored in a Gaussian cube file, which consists of a reference molecule structure (a.xyz coordinate file) and an isosurface depicting the probability of the observed atom or molecule. We used the Gromacs tool gmx spatial to determine SDFs and generate Gaussian cube files, then Visual Molecular Dynamics (VMD) was used for visualization.52 We selected the reference PDC molecule as the one found in a parallel cluster with the highest frequency across all simulation configurations. Reference molecules for all simulation systems are shown in Section S6. When visualizing SDFs, a different isovalue was selected for each molecule (80 for PDC, 8 for water, and 100 for ions) based on the amount of information expected to be shown.
3. Results and Discussion
This section presents results and analysis of PDC aggregation in water and various ionic solutions. Additional data quantifying aggregation from the simulation trajectories for each system are provided in the Section S5. We discuss the effects of acid dissociation, monovalent metal ions, and divalent metal ions on PDC aggregation.
3.1. Neutral PDC-Water System
We first simulated a neutral PDC-water system. Although this system would correspond physically to a low pH in which both carboxylic acid groups are protonated, the primary goal of these simulations is to serve as a comparison to other PDC-water–ion systems in subsequent sections. PDC molecules rapidly aggregate within 20 ns (Figure S3) to form aggregates that remain stable for the duration of the simulation.
Figure 3a shows a snapshot of the final simulation configuration after 100 ns in which a single large aggregate structure (spanning the periodic boundaries) is present along with several smaller isolated PDC molecules; parallel stacking between aggregated PDC molecules is not clearly observed in the snapshot. Figure 3b shows the SDF to more clearly quantify preferred configurations of molecular aggregates. The regions of highest PDC density (indicated by the blue surface in Figure 3b) encircle the PDC molecule, indicating that surrounding PDC molecules can interact with the reference PDC molecule at positions on or below the surface of the pyran ring. This suggests that stacking interactions are not the dominant interaction driving the PDC aggregation since parallel stacking is not the only configuration observed. Moreover, water molecules preferentially occupy spatial regions (indicated by the green surfaces) near the (protonated) carboxylic acid groups, indicating the formation of strong PDC-water hydrogen bonds.
Figure 3.

Aggregation of neutral PDC molecules in water. a) Snapshot of the PDC-water system after 100 ns. PDC molecules are drawn in blue and water molecules are not shown. The lines indicate periodic boundaries. b) Spatial distribution function (SDF) centered on a reference PDC molecule. For the reference model, carbon, oxygen, and hydrogen atoms are in cyan, red, and white, respectively. The isosurface in blue indicates PDC molecular density and the isosurface in green indicates water molecular density. c) Concentration indicator of aggregated PDC (Mc). d) Degree of parallel stacking for PDC (Rc). Red and blue curves in Figure 3c,d are Gaussian process regression fits of the probability distribution.
Figure 3c,d show probability distributions for Mc and Rc computed from the simulation trajectory to quantify the propensity for PDC aggregation into parallel stacking configurations. To better visualize trends, we fit the probability distributions using Gaussian process regression implemented with the MATLAB function fitrgp (fits are shown as red and blue curves in Figure 3c,d). Figure 3c shows that the probability distribution for Mc is peaked near 17 with a small value near 0 and a long tail for larger values of Mc. Figure 3d further shows that the probability distribution for Rc is strongly peaked near zero, indicating that PDC aggregates in pure water lack a high degree of parallel molecular stacking, which is consistent with the simulation snapshot in Figure 3a and the SDF in Figure 3b. Since larger values of Mc indicate either a large number of small clusters with parallel stacking or a small number of large clusters with parallel stacking, with Figure 3c,d, the distribution of Mc suggests a strong propensity for neutral PDC molecules to aggregate in pure water without a high degree of parallel stacking despite the strong PDC-water hydrogen bonding. Together, these data indicate that the interactions of neutral PDC molecules in water are sufficiently favorable that aggregation (Mc > 1) is preferred, which we can attribute to the generally hydrophobic nature of PDC in its neutral form. However, aggregation is not driven by PDC–PDC stacking interactions and PDC molecules maintain strong hydrogen bonds with water. These factors lead to disordered, randomly packed structures that are unlikely to be precursors to PDC crystals due to the lack of parallel molecular stacking.
3.2. Effect of Acid Dissociation on PDC Aggregation in Li+ Solution
The formation of randomly packed structures by neutral PDC molecules suggests a role for ion-mediated interactions in promoting parallel stacking. To investigate the effect of such interactions, we next investigated how the addition of Li+ ions to solution would influence the aggregation of PDC ions. Li+ is a common metal ion with a small radius compared with other metal ions. We performed simulations for both PDC– and PDC2–, reflecting both possible protonation states of the carboxylic acids and hence effects of pH on the competition between stacking interactions, Li+-mediated PDC interactions, and hydrogen bonding interactions between PDC and water. Simulation snapshots of these systems are presented in the Section S6.
For PDC– in the presence of Li+ ions, the probability distribution for Mc is peaked near 30 (Figure 4a). Compared to the prior system of neutral PDC molecules, the shift of Mc to larger values indicates a stronger tendency of PDC– to aggregate into structures that exhibit parallel molecular stacking (specifically, a small number of large parallel clusters). Similarly, the distribution of Rc also indicates a high probability of Rc = 1, which indicates that parallel stacking is favorable. Given that charged PDC ions might be expected to repel each other and be more strongly solvated by water, this result instead suggests that Li+ ions promote favorable PDC–PDC interactions. The SDF in Figure 4a indicates that there is significant Li+ density located near the carboxylic acid group, indicating that Li+ ions outcompete water molecules when comparing to Figure 3b. The PDC density located immediately above and below the pyran ring is due to the stacking interactions, and water molecules instead occupy only a region around the periphery of the ring. Together, these results indicate that the Li+ ions are able to promote favorable PDC–PDC interactions by occupying regions in between negatively charged carboxylic acid groups while permitting pyran rings to pack against each other in parallel stacking configurations.
Figure 4.
Effect of acid dissociation on PDC aggregation in Li+ solution. a) At the first degree of acid dissociation, b) at the second degree of acid dissociation. Left: concentration indicator of aggregated PDC molecules (Mc). Middle: degree of parallel stacking for PDC (Rc). Right: SDFs (The isosurfaces in blue, green, and pink indicate PDC molecular density, water molecular density, and Li+ density, respectively). For the reference model, carbon atoms are in cyan, oxygen atoms in red, and hydrogen atoms in white. Red and blue curves in Figure 4a and 4b are Gaussian process regression fits of probability distribution.
For PDC2– in the presence of Li+ ions, the probability distribution for Mc is peaked near 24 (Figure 4b), representing a reduced peak compared to PDC–, and the distribution of Rc also indicates a high probability of Rc = 0. Together, these quantities indicate that the second degree of acid dissociation and the corresponding increase in PDC charge disrupts the parallel stacking of PDC ions. Comparison of the SDFs in Figure 4a,b indicates that the increase of PDC’s charge through acid dissociation attracts more water around the reference molecule. These water molecules occupy the space that initially accommodated Li+ and PDC ions (Figure 4a Right), which disrupts the parallel stacking of PDC ions. We attribute this to the strong solvation of the charged ions (PDC and Li) by water outcompeting the stacking interactions between pyran rings. Compared to the case of neutral PDC, the analysis of PDC– and PDC2– indicates that parallel stacking is only observed for PDC– due to the combination of Li+-mediated attraction and stacking interactions; for neutral PDC, the absence of ion-mediated interactions disrupt parallel stacking, whereas for PDC2–, the strong solvation of ions disrupts parallel stacking.
3.3. Effect of Monovalent Metal Ions on PDC Aggregation
To extend the analysis of PDC aggregation in Li+ solutions, we further compare and analyze the effects of different monovalent metal ions on aggregation behavior for PDC– and PDC2–. Figure 5 summarizes aggregation trends in all studied monovalent metal ionic solutions.
Figure 5.
Effect of monovalent metal ions on PDC aggregation. a) Concentration indicator of aggregated PDC (Mc), and b) degree of parallel stacking (Rc), and c) SDFs for PDC-water–ion systems. The isosurfaces in blue, green, and pink indicate the PDC molecular density, water molecular density, and Li+ density, respectively. The isosurfaces for other ionic densities are negligible when using the isovalue of 100 and are not shown. In Figure 5a,b, left and right figures are for PDC– and PDC2–, respectively. Solid curves or lines in Figure 5a,b are Gaussian process regression fits of probability distribution.
For PDC–, all solutions promote the formation of PDC aggregates and the probability distribution of Mc is peaked near 30 (Figure 5a, left). Moreover, all solutions strongly favor the parallel stacking of aggregated PDC ions (Figure 5b, left) as shown by the peaks in Rc near 1. High values of Rc like these correspond to aggregates in which multiple PDC ions form parallel stacking configurations throughout the aggregate as shown in Figures S9 and S10. Highly favored parallel stacking thus leads to aggregates that exhibit order over length scales longer than single molecular sizes, although the aggregates remain of finite size. The outlier is Li+; compared with the other ions, Li+ leads to more PDC aggregates with a high concentration and a low degree of parallel stacking. Since Na+ is typically used to crystallize PDC,7 the preference for monovalent ions to promote parallel stacking as a presumed precursor to crystallization is consistent with experimental observations.
For PDC2–, the Li+ solution leads to different PDC stacking behavior compared with other M(I) ionic solutions by not facilitating PDC aggregation (Figure 5a Right) or promoting a high degree of parallel stacking (Figure 5b Right). Hence, at the second degree of acid dissociation, the Li+ solution leads to PDC aggregates with disordered and randomly packed structures, which are unlikely to be the precursors to PDC crystals. All other solutions facilitate the formation of PDC aggregates that exhibit more parallelly stacked structures (with Rc near 1) and the probability distribution of Mc value is more sharply near 30 compared to PDC– and has a longer tail to the distribution with Mc as high as 80 (Figure 5a Right). The Na+, K+, Rb+, and Cs+ ions show the strongest effects in facilitating PDC aggregation (the peaked probability value of Mc probability distribution in Figure 5a Left is near 0.1–0.11 while the peaked probability value of Mc probability distribution in Figure 5a Right is higher than 0.18). Furthermore, all other solutions (except Li+ solution) facilitate the parallel stacking of PDC ions (Figure 5b Right).
Figure 5c compares the M(I) ions’ influence on the SDFs of PDC-water–ion systems for PDC– and PDC2–. For all solutions (except Li+ solutions), the counterintuitive observation is that more PDC ions aggregate around the reference molecule at the second degree of acid even though the increased charge on PDC ions should increase like-charge repulsion. The resulting SDFs have clear layers of PDC density consistent with parallel stacking. This result is consistent with the observation that the second degree of acid dissociation facilitates the PDC2– aggregation as shown in Figure 5a Right (the peaked probability value of Mc probability distribution for PDC2– is higher than that for PDC–). Furthermore, Figure 5c elucidates the competition among various intermolecular interactions. For all solutions (except Li+ solutions), near the edge of PDC’s pyran ring, the hydrogen bonding interactions between PDC ions and water are stronger than ion-mediated interactions and stacking interactions between pairs of PDC ions, leading to enriched water density. Above and below PDC’s pyran ring, the stacking interactions between pairs of PDC ions are stronger than the ion-mediated interactions and hydrogen bonding interactions between PDC ions and water. We attribute the unique behavior of Li+ solutions, compared to other monovalent metal ions, to the small ionic radius of Li+, which results in a higher charge density and lower steric hindrance. These factors permit Li+ to more easily interact with PDC ions to disrupt packing, as observed in the SDFs (Figure 5c). This analysis indicates that increasing pH in the solutions of monovalent metal ions (except the Li+ solution) to facilitate acid dissociation can lead to PDC aggregates with large aggregation numbers and parallel stacking, which can serve as precursors of PDC crystals.
3.4. Effect of Divalent Metal Ions on PDC Aggregation
As discussed in the previous section, we observe diverse PDC aggregation patterns within the solutions of monovalent metal ions, with an increase in aggregation and parallel stacking observed for the higher charge density PDC2– ions. These observations further motivate the investigation of how divalent metal ions affect PDC aggregation, as shown in Figure 6.
Figure 6.
Effect of divalent metal ions on the PDC aggregation. a) Concentration indicator of aggregated PDC (Mc), and b) degree of parallel stacking (Rc), and c) SDFs for PDC-water–ion systems. The isosurfaces in blue and green indicate the PDC molecular density and water molecular density, respectively. In Figure 6a,b, left figures are for PDC– and right figures are for PDC2–. Solid curves or lines in Figure 6a,b are Gaussian process regression fits of probability distribution.
For PDC–, solutions of Be2+, Ca2+, Sr2+, and Ba2+ facilitate the formation of aggregated PDC ions with the probability distribution of Mc peaked near 25–30 (Figure 6a Left), which is similar to observations for monovalent ions. Be2+ and Ca2+ solutions facilitate parallel stacking of PDC ions while the rest of the solutions do not (Figure 6b Left). For PDC2–, Mg2+ and Ba2+ solutions facilitate PDC aggregation with the Mc probability distribution peaked near 30–35 (Figure 6a Right). Notably, the Ba2+ solution leads to aggregated PDC with the probability distribution Mc peaked near 35 and with a higher peaked probability value than other metal ions. Moreover, the Mg2+ solution leads to a high degree of parallel stacking of PDC ions (the probability distribution of Rc is peaked near one in Figure 6b Right). This indicates that the Mg2+ solution leads to aggregated PDC ions with a higher degree of parallel stacking compared with the rest of ionic solutions. These two results indicate that divalent Mg2+ solutions could be ideal for crystallizing PDC at a pH that promotes dissociation of both carboxylic acid groups, but other divalent metal ions may preferentially form large, disordered aggregates that are less likely to lead to crystallization.
The SDFs in Figure 6c further indicate behaviors related to the probability distribution of Mc and Rc. For PDC–, the Be2+, Mg2+, and Ca2+ solutions lead to more aggregated PDC ions and metal ions than aggregated water molecules around the reference molecule, with the plots again similar to monovalent ions. For PDC2–, all solutions of divalent metal ions (except Mg2+), lead to more aggregated water molecules than aggregated PDC ions and metal ions around the reference PDC ion. This result suggests that the strong electrostatic interactions between the PDC2– and metal ions and hydration of metal ions by water disrupts parallel stacking. This also indicates that for these solutions of metal ions, the hydrogen bonding interactions between PDC ions and water are stronger than the stacking interactions between pairs of PDC ions and ion-mediated interactions between PDC ions and metal ions.
For Sr2+ and Ba2+ solutions, water and metal ions disrupt the parallel stacking of PDC ions around the reference PDC ion. This indicates that for Sr2+ and Ba2+ solutions at all degrees of acid dissociation, the hydrogen bonding interactions between PDC ions and water, and ion-mediated interactions between PDC ions and metal ions are stronger than the stacking interactions between pairs of PDC ions. However, for Mg2+ solution, around the reference molecule, there are more aggregated Mg2+ at the second degree of acid dissociation than aggregated Mg2+ at the first degree of acid dissociation. This disrupts the aggregation of water and hence allows more space for PDC aggregation around the reference PDC ion. This also indicates that for Mg2+ solution, at the second degree of acid dissociation, stacking interactions between pairwise PDC ions and ion-mediated interactions between PDC ions and Mg2+ are stronger than the hydrogen bonding interactions between PDC ions and water.
Compared to solutions with monovalent metal ions (Figure 5), the peaked value for the probability distribution of Rc for PDC ions in solutions with divalent metal ions tends to be lower for both PDC– and PDC2–. This result is due to enhanced hydrogen bonding interactions between PDC ions and water, and ion-mediated interactions between PDC ions and divalent metal ions, compared with the stacking interactions between pairs of PDC ions. This attracts more water or metal ions around the reference PDC ion, which disrupts the parallel stacking of PDC ions. In summary, we show solutions with Be2+ and Ca2+ facilitate PDC– aggregation with large aggregation numbers and high degree of parallel stacking (at low pH) while Mg2+ facilitates PDC2– aggregation with large aggregation numbers and parallel stacking structures.
4. Conclusions
Understanding molecular aggregation is critical for designing crystallization processes for PDC separation. In this work, we investigate PDC aggregation in solutions containing monovalent or divalent metal ions to determine ions that promote the aggregation of PDC into structures with parallel stacking, which is expected to lead to favorable crystallization. First, we perform atomistic molecular dynamics simulations of PDC at different degrees of acid dissociation and in various metal ion solutions. We then implement molecular clustering analysis based on the minimum distance and the dihedral angle between pairs of PDC molecules. From molecular clustering analysis, we compute order parameters for PDC aggregation to indicate the concentration of PDC aggregates and their preference for parallel stacking structures. The results show that the dissociation of PDC can contribute to PDC aggregation in the solutions of metal ion despite apparent like-charge repulsion. For both PDC– and PDC2–, solutions of Na+, K+, Rb+, and Cs+ facilitate the formation of PDC aggregates with large aggregation numbers and parallel stacking structures, which is consistent with the experimental utilization of Na+ to promote PDC crystallization. For divalent metal ions, Be2+ and Ca2+ solutions facilitate the formation of PDC– aggregates with large aggregation numbers and parallel stacking, while only Mg2+ solutions facilitate the formation of PDC2– with large aggregation numbers and parallel stacking. These results indicate that the choice of ion in solution can impact the relative interplay of PDC–PDC stacking interactions, PDC-water hydrogen bonding interactions, and electrostatic interactions that influences aggregate structures. In particular, we observe that when the hydrogen bonding interactions between water and PDC are weaker than stacking interactions between pairs of PDC ions and ion-mediated interactions between PDC ions and metal ions, the PDC aggregates exhibit parallel stacking configurations. We note that in this work we have focused on a single PDC concentration that is comparable to concentrations produced experimentally; future work will further investigate the effect of PDC and ion concentration on aggregation processes. The results also indicate that future separation processes should consider the addition of divalent cations, and particularly Mg2+, to further promote PDC crystallization.
Acknowledgments
This material is based upon work supported by the Great Lakes Bioenergy Research Center, U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research under Award Nos. DE-SC0018409. Jianping Li acknowledges support through the Keegstra Fellowship by the Great Lakes Bioenergy Research Center, U.S. Department of Energy. Part of this research was conducted with computing resources provided by Princeton Research Computing.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c05431.
Nomenclature, determination of distance cutoff value and aggregate order parameters, implementation and molecular simulation trajectories, simulation snapshots and index of the reference molecule. The force field parameters for all simulation systems are provided in this GitHub repository: https://github.com/jlianl/PDC_Aggregation (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Larson E. D.; Fiorese G.; Liu G.; Williams R. H.; Kreutz T. G.; Consonni S. Co-production of decarbonized synfuels and electricity from coal + biomass with CO2 capture and storage: an Illinois case study. Energy Environ. Sci. 2010, 3, 28–42. 10.1039/B911529C. [DOI] [Google Scholar]
- Dossow M.; Klüh D.; Umeki K.; Gaderer M.; Spliethoff H.; Fendt S. Electrification of gasification-based biomass-to-X processes – a critical review and in-depth assessment. Energy Environ. Sci. 2024, 17, 925–973. 10.1039/D3EE02876C. [DOI] [Google Scholar]
- Ragauskas A. J.; Beckham G. T.; Biddy M. J.; Chandra R.; Chen F.; Davis M. F.; Davison B. H.; Dixon R. A.; Gilna P.; Keller M.; et al. Lignin valorization: improving lignin processing in the biorefinery. Science 2014, 344, 1246843. 10.1126/science.1246843. [DOI] [PubMed] [Google Scholar]
- Otsuka Y.; Nakamura M.; Shigehara K.; Sugimura K.; Masai E.; Ohara S.; Katayama Y. Efficient production of 2-pyrone 4, 6-dicarboxylic acid as a novel polymer-based material from protocatechuate by microbial function. Appl. Microbiol. Biotechnol. 2006, 71, 608–614. 10.1007/s00253-005-0203-7. [DOI] [PubMed] [Google Scholar]
- Hishida M.; Shikinaka K.; Katayama Y.; Kajita S.; Masai E.; Nakamura M.; Otsuka Y.; Ohara S.; Shigehara K. Polyesters of 2-pyrone-4, 6-dicarboxylic acid (PDC) as bio-based plastics exhibiting strong adhering properties. Polym. J. 2009, 41, 297–302. 10.1295/polymj.PJ2008291. [DOI] [Google Scholar]
- Li J. Sustainable Process Intensification for Biomass Valorization. Springer Books 2023, 3355–3373. 10.1007/978-3-030-97940-9_170. [DOI] [Google Scholar]
- Perez J. M.; Sener C.; Misra S.; Umana G. E.; Coplien J.; Haak D.; Li Y.; Maravelias C. T.; Karlen S. D.; Ralph J.; et al. Integrating lignin depolymerization with microbial funneling processes using agronomically relevant feedstocks. Green Chem. 2022, 24, 2795–2811. 10.1039/D1GC03592D. [DOI] [Google Scholar]
- Mullin J. W.Crystallization; Elsevier, 2001. [Google Scholar]
- Liu H.; Jiang H.; Liu X.; Wang X. Physicochemical understanding of biomineralization by molecular vibrational spectroscopy: From mechanism to nature. Exploration 2023, 3, 20230033. 10.1002/EXP.20230033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gavezzotti A.Molecular aggregation: structure analysis and molecular simulation of crystals and liquids; OUP Oxford, 2006; Vol. 19. [Google Scholar]
- Jiang S.; Ter Horst J. H. Crystal nucleation rates from probability distributions of induction times. Cryst. Growth Des. 2011, 11, 256–261. 10.1021/cg101213q. [DOI] [Google Scholar]
- Israelachvili J.; MarČelja S.; Horn R. G. Physical principles of membrane organization. Q. Rev. Biophys. 1980, 13, 121–200. 10.1017/S0033583500001645. [DOI] [PubMed] [Google Scholar]
- Deng X.; Xie L.; Wang S.; Li C.; Wang A.; Yuan Y.; Cao Z.; Li T.; Ding L.; Hao F. Ionic liquids engineering for high-efficiency and stable perovskite solar cells. Chem. Eng. J. 2020, 398, 125594. 10.1016/j.cej.2020.125594. [DOI] [Google Scholar]
- Sumer Z.; Striolo A. Nanoparticles shape-specific emergent behaviour on liquid crystal droplets. Mol. Syst. Design Eng. 2020, 5, 449–460. 10.1039/C9ME00153K. [DOI] [Google Scholar]
- Israelachvili J. N.Intermolecular and surface forces, third ed. ed.; Academic Press, 2011. [Google Scholar]
- Menger F. M. Supramolecular chemistry and self-assembly. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 4818–4822. 10.1073/pnas.062524299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergström L. M. Thermodynamics of self-assembly. Appl. Thermodyn. Biol. Mater. Sci. 2011, 11, 289–314. [Google Scholar]
- Nandakumar A.; Ito Y.; Ueda M. Solvent effects on the self-assembly of an amphiphilic polypeptide incorporating α-helical hydrophobic blocks. J. Am. Chem. Soc. 2020, 142, 20994–21003. 10.1021/jacs.0c03425. [DOI] [PubMed] [Google Scholar]
- van der Vegt N. F.; Nayar D. The hydrophobic effect and the role of cosolvents. J. Phys. Chem. B 2017, 121, 9986–9998. 10.1021/acs.jpcb.7b06453. [DOI] [PubMed] [Google Scholar]
- Lukanov B.; Firoozabadi A. Specific ion effects on the self-assembly of ionic surfactants: a molecular thermodynamic theory of micellization with dispersion forces. Langmuir 2014, 30, 6373–6383. 10.1021/la501008x. [DOI] [PubMed] [Google Scholar]
- Korolovych V. F.; Ledin P. A.; Stryutsky A.; Shevchenko V. V.; Sobko O.; Xu W.; Bulavin L. A.; Tsukruk V. V. Assembly of amphiphilic hyperbranched polymeric ionic liquids in aqueous media at different pH and ionic strength. Macromolecules 2016, 49, 8697–8710. 10.1021/acs.macromol.6b01562. [DOI] [Google Scholar]
- Chen J.; Trout B. L. Computational study of solvent effects on the molecular self-assembly of tetrolic acid in solution and implications for the polymorph formed from crystallization. J. Phys. Chem. B 2008, 112, 7794–7802. 10.1021/jp7106582. [DOI] [PubMed] [Google Scholar]
- Orehek J.; Teslic D.; Likozar B. Continuous crystallization processes in pharmaceutical manufacturing: A review. Org. Process Res. Dev. 2021, 25, 16–42. 10.1021/acs.oprd.0c00398. [DOI] [Google Scholar]
- Shikinaka K.; Otsuka Y.; Iguchi Y.; Nakamura M.; Itoh Y.; Masai E.; Katayama Y.; Shigehara K. Preferential cesium ion trapping by 2-pyrone-4, 6-dicarboxylic acid (PDC) obtained from a metabolic intermediate of lignin, a woody biomass resource. J. Nucl. Sci. Technol. 2016, 53, 1256–1259. 10.1080/00223131.2016.1160806. [DOI] [Google Scholar]
- Bito M.; Otsuka Y.; Nakamura M.; Masai E.; Katayama Y.; Shigehara K.; Shikinaka K. Unique complexation behavior of alkali metal ions and 2-pyrone-4, 6-dicarboxylic acid (PDC) obtained from a metabolic intermediate of lignin. Waste Biomass Valorization 2019, 10, 1261–1265. 10.1007/s12649-017-0147-z. [DOI] [Google Scholar]
- Thakuria R.; Nath N. K.; Saha B. K. The nature and applications of π–π interactions: a perspective. Cryst. Growth Des. 2019, 19, 523–528. 10.1021/acs.cgd.8b01630. [DOI] [Google Scholar]
- Xiao T.; Song X. A molecular Debye-Hückel theory and its applications to electrolyte solutions. J. Chem. Phys. 2011, 135, 104104. 10.1063/1.3632052. [DOI] [PubMed] [Google Scholar]
- Wu J.; Bratko D.; Prausnitz J. M. Interaction between like-charged colloidal spheres in electrolyte solutions. Proc. Natl. Acad. Sci. U. S. A. 1998, 95, 15169–15172. 10.1073/pnas.95.26.15169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelmakh A.; Cai W.; Baumketner A. Attraction between Like-Charged Macroions Mediated by Specific Counterion Configurations. J. Phys. Chem. B 2019, 123, 9971–9983. 10.1021/acs.jpcb.9b06545. [DOI] [PubMed] [Google Scholar]
- Lavagna E.; Bochicchio D.; De Marco A. L.; Güven Z. P.; Stellacci F.; Rossi G. Ion-bridges and lipids drive aggregation of same-charge nanoparticles on lipid membranes. Nanoscale 2022, 14, 6912–6921. 10.1039/D1NR08543C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petretto E.; Ong Q. K.; Olgiati F.; Mao T.; Campomanes P.; Stellacci F.; Vanni S. Monovalent ion-mediated charge–charge interactions drive aggregation of surface-functionalized gold nanoparticles. Nanoscale 2022, 14, 15181–15192. 10.1039/D2NR02824G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller-Dethlefs K.; Hobza P. Noncovalent interactions: a challenge for experiment and theory. Chem. Rev. 2000, 100, 143–168. 10.1021/cr9900331. [DOI] [PubMed] [Google Scholar]
- Lee M.; Kim J. I.; Na S.; Eom K. Metal ions affect the formation and stability of amyloid β aggregates at multiple length scales. Phys. Chem. Chem. Phys. 2018, 20, 8951–8961. 10.1039/C7CP05072K. [DOI] [PubMed] [Google Scholar]
- Moffitt M.; Eisenberg A. Scaling relations and size control of block ionomer microreactors containing different metal ions. Macromolecules 1997, 30, 4363–4373. 10.1021/ma961577x. [DOI] [Google Scholar]
- McCullagh M.; Prytkova T.; Tonzani S.; Winter N. D.; Schatz G. C. Modeling self-assembly processes driven by nonbonded interactions in soft materials. J. Phys. Chem. B 2008, 112, 10388–10398. 10.1021/jp803192u. [DOI] [PubMed] [Google Scholar]
- Van Lehn R. C.; Alexander-Katz A. Structure of mixed-monolayer-protected nanoparticles in aqueous salt solution from atomistic molecular dynamics simulations. J. Phys. Chem. C 2013, 117, 20104–20115. 10.1021/jp406035e. [DOI] [Google Scholar]
- Gahan C. G.; Patel S. J.; Boursier M. E.; Nyffeler K. E.; Jennings J.; Abbott N. L.; Blackwell H. E.; Van Lehn R. C.; Lynn D. M. Bacterial quorum sensing signals self-assemble in aqueous media to form micelles and vesicles: an integrated experimental and molecular dynamics study. J. Phys. Chem. B 2020, 124, 3616–3628. 10.1021/acs.jpcb.0c00496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adjiman C.; Galindo A.; Pistikopoulos E. N.; Georgiadis M. C.; Dua V.. Molecular systems engineering; John Wiley & Sons, 2010; Vol. 6. [Google Scholar]
- Van Lehn R. C.; Alexander-Katz A. Ligand-mediated short-range attraction drives aggregation of charged monolayer-protected gold nanoparticles. Langmuir 2013, 29, 8788–8798. 10.1021/la400756z. [DOI] [PubMed] [Google Scholar]
- Maginn E.; Elliott J. Historical perspective and current outlook for molecular dynamics as a chemical engineering tool. Ind. Eng. Chem. Res. 2010, 49, 3059–3078. 10.1021/ie901898k. [DOI] [Google Scholar]
- Sharma A.; Mondal S.; Ahuja T.; Karmakar T.; Siddhanta S. Ion-Mediated Protein Stabilization on Nanoscopic Surfaces. Langmuir 2023, 39, 1227–1237. 10.1021/acs.langmuir.2c03010. [DOI] [PubMed] [Google Scholar]
- Dai L.; Mu Y.; Nordenskiöld L.; van der Maarel J. R. Molecular dynamics simulation of multivalent-ion mediated attraction between DNA molecules. Phys. Rev. Lett. 2008, 100, 118301. 10.1103/PhysRevLett.100.118301. [DOI] [PubMed] [Google Scholar]
- Lewis N. H.; Zhang Y.; Dereka B.; Carino E. V.; Maginn E. J.; Tokmakoff A. Signatures of ion pairing and aggregation in the vibrational spectroscopy of super-concentrated aqueous lithium bistriflimide solutions. J. Phys. Chem. C 2020, 124, 3470–3481. 10.1021/acs.jpcc.9b10477. [DOI] [Google Scholar]
- Zaki A. M.; Troisi A.; Carbone P. Unexpected like-charge self-assembly of a Biguanide-based antimicrobial polyelectrolyte. J. Phys. Chem. Lett. 2016, 7, 3730–3735. 10.1021/acs.jpclett.6b01631. [DOI] [PubMed] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Michinobu T.; Bito M.; Yamada Y.; Katayama Y.; Noguchi K.; Masai E.; Nakamura M.; Ohara S.; Shigehara K. Molecular properties of 2-pyrone-4, 6-dicarboxylic acid (PDC) as a stable metabolic intermediate of lignin isolated by fractional precipitation with Na+ ion. Bull. Chem. Soc. Jpn. 2007, 80, 2436–2442. 10.1246/bcsj.80.2436. [DOI] [Google Scholar]
- Otsuka Y.; Araki T.; Suzuki Y.; Nakamura M.; Kamimura N.; Masai E. High-level production of 2-pyrone-4, 6-dicarboxylic acid from vanillic acid as a lignin-related aromatic compound by metabolically engineered fermentation to realize industrial valorization processes of lignin. Bioresour. Technol. 2023, 377, 128956. 10.1016/j.biortech.2023.128956. [DOI] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Li P.; Merz J. K. M. Taking into account the ion-induced dipole interaction in the nonbonded model of ions. J. Chem. Theory Comput. 2014, 10, 289–297. 10.1021/ct400751u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGibbon R. T.; Beauchamp K. A.; Harrigan M. P.; Klein C.; Swails J. M.; Hernández C. X.; Schwantes C. R.; Wang L.-P.; Lane T. J.; Pande V. S. MDTraj: a modern open library for the analysis of molecular dynamics trajectories. Biophys. J. 2015, 109, 1528–1532. 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergman D. L.; Laaksonen L.; Laaksonen A. Visualization of solvation structures in liquid mixtures. J. Mol. Graphics Modell 1997, 15, 301–306. 10.1016/S1093-3263(98)00003-5. [DOI] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD: visual molecular dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.





